Ion electrodiffusion governs silk electrogelation
Nikola
Kojic
a,
Matthew J.
Panzer
b,
Gary G.
Leisk
c,
Waseem K.
Raja
a,
Milos
Kojic
d and
David L.
Kaplan
*a
aDepartment of Biomedical Engineering, Tufts University, 4 Colby St., Medford, MA 02155, USA. E-mail: david.kaplan@tufts.edu; Fax: +1-617-627-3231; Tel: +1-617-627-3251
bDepartment of Chemical and Biological Engineering, Tufts University, Medford, MA 02155, USA
cDepartment of Mechanical Engineering, Tufts University, Medford, MA 02155, USA
dDepartment of Nanomedicine, The Methodist Hospital Research Institute, Houston, TX 77030, USA
First published on 28th May 2012
Abstract
Silk electrogelation involves the transition of an aqueous silk fibroin solution to a gel state (E-gel) in the presence of an electric current. The process is based on local pH changes as a result of water electrolysis – generating H+ and OH− ions at the (+) and (−) electrodes, respectively. Silk fibroin has a pI = 4.2 and when local pH < pI, E-gel forms. An experimental system was constructed that allowed the measurement of E-gel growth and pH distribution for an applied current. To explain the observed rectangular pH profile of pHgel ≈ 4 surrounded by pHsilk-solution ≈ 10, a finite-element ion electrodiffusion model was developed. The model relies on electrodiffusion of the generated H+ and OH− ions. Initially, inputs into the model were the measured E-gel and voltage curves. The governing ion electrodiffusion equations were solved and the calculated pH matched the experimental pH profile, indicating that ion electrodiffusion dictates local pH changes and E-gel growth. Furthermore, the model predicted the constant currents (2 mA and 3 mA) necessary for two hypothetical E-gel growth curves and these results were then validated experimentally. The model thus shows how ion electrodiffusion governs the electrogelation process and also provides predictable outcomes for fundamental and practical E-gel applications.
Introduction
The use of electric fields to induce the assembly of biopolymers has been utilized in the field of biomaterials, where the goal has been to design and control material structure for various biomedical applications.1–6 One of these applications has involved the formation of a biocompatible medical adhesive based on a silk-protein hydrogels.2,7 In the presence of low-voltage direct-current (DC), an aqueous reconstituted silk fibroin solution undergoes a sol–gel transition.2,7 This process, termed electrogelation, produces a soft gel (E-gel) that has excellent adhesive properties.2,7 Furthermore, the gelation kinetics can be controlled by changing the value of the applied DC current. Other factors influencing the electrogelation process include pH and silk fibroin concentration, the effects of which have been evaluated using rheological tools.7Silk fibroin, the main protein constituent of silkworm silk, is a high molecular weight block copolymer comprised of a heavy (∼370 kDa) and light chain (∼26 kDa)8 and has a large number of acidic domains leading to a relatively low pI value of 4.2.9 Therefore, when the local pH decreases below the pI value the fibroin undergoes conformational changes that lead to the formation of the meta-stable E-gel.7 Besides electrogelation, reconstituted silk fibroin has been processed in different ways for numerous biomedical scenarios, such as 3-D tissue/cell scaffolds, drug-eluting films, electrospun fibers, and others.10–16
Silk hydrogels have also been formed by inducing gelation via a number of techniques that involved energy input or loss of water around the protein chains, including: vortexing,17 ultra-sonication,18 and the presence of high ionic strength and temperature.12 The use of electrical currents produces a silk hydrogel with interesting viscoelastic and adhesive properties,7 including reversibility as the E-gel dissolves back into solution upon reversal of the electrical polarity.2 These unique properties make the E-gel an interesting biomedical and biotechnological material, further highlighting the need for a better understanding of what factors control the electrogelation process.
In the present study we present a numerical finite-element model that examines how electrodiffusion of H+ and OH− ions generated during electrogelation dictate the growth of the E-gel. We first analyzed a set of experiments as inputs, and then used the model to calculate a corresponding pH profile. This profile was then shown to agree with experimentally measured pH values indicating that ion electrodiffusion, and the resulting local pH, was central to the electrogelation process. The model was then employed to examine two hypothetical E-gel growth curves and yielded a prediction of the constant currents needed to achieve the prescribed E-gel growth. Subsequent experiments performed with these predicted currents demonstrated good agreement between the model predictions and actual E-gel growth curves. Therefore, the computational model developed here provides insight into the underlying electrogelation mechanism and also has predictive capabilities important for future E-gel needs.
Theory and methods
Preparation of aqueous silk fibroin solution
Silk fibroin aqueous solutions were prepared as previously described.19 Briefly, Bombyx mori cocoons were boiled for 30 min in an aqueous solution of 0.02 M sodium carbonate and then rinsed thoroughly with deionized water. After overnight drying, the silk fibroin was dissolved in an aqueous solution containing 9.3 M LiBr at 60 °C for 6 hours. The solution was dialyzed against deionized water using Slide-a Lyzer dialysis cassettes (MWCO 3500, Pierce, Rockford, IL) for two days to remove the residual salt. The final concentration of the silk fibroin was roughly 7 wt%.Experimental setup
The experimental setup consisted of an acrylic reservoir that holds ∼2.5 mL of silk solution and two gold-coated acrylic plates (Fig. 1a). The bottom surface of the reservoir has laser-etched gratings separated at a distance of 0.05 mm. The gratings served as a scale bar to assess E-gel growth over time. The two plates were coated with a thin layer of gold, ∼300 nm thick, in order to provide a conductive surface. The plates were placed into the etched slots at the edge of the reservoir and electrically connected with alligator clips to the top corner of the plates to a programmable DC power supply (2602A Dual-channel System Source Meter Instrument, Keithley Instruments, Cleveland, OH) whose maximum voltage output was 40 V (Fig. 1a–c). Then, 2.5 mL of silk aqueous solution (pH ≈ 6.5) was used to fill the reservoir. The plate surface in contact with the silk solution was 1.8 cm width × 1.25 cm height = 2.25 cm2. The closed electrical circuit therefore consisted of: power supply → (+) plate → silk solution → (−) plate → power supply. | ||
| Fig. 1 Experimental setup for the electrogelation process. (A) Two gold-coated acrylic plates (connected to a power supply) serve as the (+) and (−) electrodes. The reservoir chamber is used to store the silk solution between the two plates (separated at a distance of 1 cm). (B) Side-view of electrogelation showing the E-gel (appearing as a white gel) growing from the (+) towards the (−) plate. Black scale bar is 0.5 cm. (C) A pH probe used to measure pH is placed into the E-gel. (D) pH-sensitive dye (phenol red) added to the silk solution turns yellow in acidic (pH < 6) and pink in basic environments (pH > 8). The silk solution is 7 wt% reconstituted silkworm silk protein and 93 wt% water. Black scale bar is 0.5 cm. | ||
After setting the power supply to a prescribed constant value of current, the power was turned on and the resulting voltage necessary to maintain the constant current was documented. A camera was used to record the E-gel growth, due to the opacity of the gel upon formation, both from below of the reservoir and from the edge-on view (Fig. 1b). The E-gel was a relatively uniform, opaque front growing from the (+) towards the (−) electrode, consistent with previous experiments.2
To determine how the pH changed during electrogelation, a pH probe, a pH-sensitive dye, and pH indicator paper strips were utilized. The pH probe (Orion 9810BN Micro pH Electrode, Thermo Scientific, Asheville, NC) has a small 1.3 mm tip designed to measure a wide range of pH (0–14) in gels as well as solutions. The probe was connected to a pH meter (Orion 2-Star pH meter kit, Thermo Scientific, Asheville, NC) to read out the pH value. Measurements were taken at several points in both the gel and the silk solution by direct contact with the probe tip (Fig. 1c). In the E-gel and the silk solutions, the tip was submerged ∼5 mm below the surface to minimize potential surface effects. The probe readings were confirmed by pH indicator paper strips and by using a pH-sensitive dye, phenol red, which is a water soluble pH indicator that turns yellow for pH < 6.8 and pink for pH > 8.2 (Fig. 1d). Commercially available phenol red powder (Sigma Aldrich, St. Louis, MO) was dissolved in deionized water to a stock concentration of 300 mg L−1 and this stock concentration was added, in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 volume ratio, to the silk solution yielding a final phenol red concentration of 15 mg L−1.
20 volume ratio, to the silk solution yielding a final phenol red concentration of 15 mg L−1.
Rate of ion generation due to water electrolysis
During the electrogelation process the applied current causes electrolysis of the water, which comprises 93 wt% of the silk solution. This can be seen by the appearance of bubbles on both of the electrodes and the bubbles remain present throughout the process (Fig. 1b). The governing electrochemical reactions at the (+) and (−) plates are: | (1) |
 | (2) |
The bubbles at the (+) and (−) plates are oxygen and hydrogen gas, respectively. Furthermore, H+ ions are generated at the (+) and OH− at the (−) plates. We can formulate the rate of ion generation (as a surface flux) by employing the following relation:
 | (3) |
For a given constant current, the ion influx is constant and equal in value for the H+ ions at the (+) and OH− ions at the (−) plate.
Governing equations
The constant generation (i.e. influx) of ions at the electrodes induces a local increase in concentration of H+ at the (+) and OH− at the (−) plate. The ions then start diffusing toward the opposite electrode, down their concentration gradient. Additionally, the presence of an electric field also moves the ions toward the oppositely charged plate. Therefore, in order to describe the dynamic movement of ions in the reservoir both the diffusion and electric field components must be taken into account.The Nernst–Planck equation extends Fick's law of diffusion for the case when the diffusing particles (i.e. ions) are moved by the electric field with respect to the fluid.20 In our case we have two types of diffusing ions and thus the governing equations are:
 | (4) |
 | (5) |
| H+: pH = −log10[CH+] | (6) |
| OH−: pH = 14 + log10[COH−] | (7) |
Finite element model
In order to solve the above equations and examine local concentration changes occurring during an actual electrogelation experiment, we developed a computational model based on the finite-element method.21,22 First, the model geometry was taken to encompass the space between the (+) and (−) plates. This space has a constant cross-section equal to the plate surface area in contact with the silk solution (2.25 cm2) and is 1 cm long (the separation distance between the two plates). The space was discretized by dividing a 1 cm line into 500 finite-elements (Fig. 2). We assumed, based on experimental evidence, that the E-gel growth is essentially a 1-D process and therefore we neglected small variations in the uniformity of the E-gel forming front. | ||
| Fig. 2 Schematic of the finite-element electrodiffusion model with the governing equations and boundary conditions for the H+ and OH− ions (constant influx q at the plates and C = 0 at the edge of the E-gel, i.e. at the E-gel forming front). The E-gel (yellow) grows from the (+) towards the (−) plate. The x = 0 coordinate is the surface of the (+) plate, x = Lg is the E-gel depth, i.e. the distance from the (+) plate to the E-gel forming front, and x = L = 1 cm is the coordinate of the (−) plate. The ions have an additional “velocity” V due to the presence of the electric field, which tends the move the H+ ion towards the (−) and the OH− ion towards the (+) plate. The velocity is defined as V = zDFE/(RT). The space is discretized between x = 0 and x = L into 500 finite-elements (not to scale in schematic). Green circles: finite-element nodes, blue circle: H+ ion, red circle: OH− ion. | ||
After applying the standard Galerkin procedure21,22 to eqn (4) and (5) the corresponding balance equations for a finite-element are:
| MĊ + KC = Q + Qconv | (8) |
 | (9) |
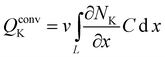 | (10) |
The boundary conditions for the model are: constant influx of H+ ions at x = 0 and OH− ions at x = L = 1 cm (based on eqn (3)) and a concentration of C = 0 for both ions at the E-gel forming front (Fig. 2). The latter boundary condition comes from experimental measurements which showed a neutral pH immediately next to E-gel forming front, as well as a sharp pH gradient at the edge of the E-gel (Fig. 1d). The neutral pH = 7 (corresponding to C = 0.1 nmol cm−3) is three orders-of-magnitude lower than the measured E-gel pH of 4 (CH+ = 100 nmol cm−3) and the silk solution pH of 10 (COH− = 100 nmol cm−3), and thus for numerical purposes the concentrations are assumed to be zero at the E-gel forming front.
Besides the ion diffusion coefficients, the other model inputs are: the applied current, the voltage curve as a function of time, and the E-gel growth curve as a function of time (Fig. 3). The resulting ion concentration profiles were then calculated and converted to a pH profile, using eqn (6) and (7). This pH distribution can then be compared with experimental pH values.
 | ||
| Fig. 3 Experimentally measured time-dependent values for a constant current of 0.4 mA – the minimum current needed to initiate E-gel formation. (A) Voltage necessary to maintain the constant current of 0.4 mA using the setup of Fig. 1. (B) E-gel growth curve for 0.4 mA. E-gel depth Lg is defined as the distance from the E-gel forming front to the (+) electrode (Fig. 2). Error bars are standard deviation from N = 4 experiments. | ||
Another aspect of the model is that it can be used in cases where E-gel growth and voltage curves are prescribed but the necessary current is unknown. In this scenario a range of entrance concentration values for the H+ ions can be specified and then successive iterations are used to perform the calculations until the x = 0 concentration is within the given range. Initial experiments can be used to make estimates about the entrance concentration and the model can then provide predictions for the constant current needed to achieve the desired kinetics of E-gel growth.
Results
The initial task was to determine the minimum constant current that would induce electrogelation. This minimum current was 0.4 mA, and the corresponding voltage curve was recorded from the Keithley power supply (Fig. 3a). The voltage increased over time, consistent with gas bubble production at the electrodes (eqn (1) and (2)).24 The growth of the E-gel was also measured (Fig. 3b, error bars are standard deviations from 4 independent experiments). The E-gel depth Lg is defined as the distance from the (+) plate (x = 0) to the E-gel forming front (Fig. 2).The time-dependent voltage and E-gel growth curves of Fig. 3 were then used as input for the finite-element model (Fig. 2). Other inputs into the model were:
(1) Ion diffusion coefficients (assumed to be as in water): DH+ = 9.31 × 10−5 cm2 s−1 and DOH− = 5.24 × 10−5 cm2 s−1.25
(2) Standard values of constants: Faraday constant F = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1, valence z = 1, R = 8.314 m2 kg s−2 K−1 mol−2, T = 298 K.
485 C mol−1, valence z = 1, R = 8.314 m2 kg s−2 K−1 mol−2, T = 298 K.
(3) Electric field was calculated by dividing the voltage by the distance separating the two plates (1 cm), giving the field in terms of V cm−1.
(4) The current was specified as 0.4 mA, and the corresponding ion influx was calculated using eqn (3) and employed in the model, along with the assumption of zero-concentration at the E-gel forming front (Fig. 2).
With the above input, the concentration profile (Fig. 4a) at the end of the experiment (t = 90 min) was calculated. For clarity, the concentration of OH− was inverted and plotted as “negative”, even though the actual calculated value of the OH− ions was positive. The dashed line in Fig. 4a indicates the “positive” and “negative” domains separating the H+ and OH− concentrations, respectively. The units of concentration are nmol cm−3 and the x-axis is the spatial coordinate, taken to be x = 0 at the (+) plate and x = L = 1 cm at the (−) plate (Fig. 2). From Fig. 4 it is apparent that the E-gel and silk solution zero-concentration boundary is at x = 0.6 cm, which is the final value of the E-gel growth curve from Fig. 3b.
 | ||
| Fig. 4 (A) Model results for the ion concentrations based on the experimentally measured voltage and E-gel growth curves (Fig. 3). For clarity, concentrations of H+ ions are displayed as positive and OH− concentrations are inverted and appear as negative. The dashed line indicates the separation between the H+ and OH− domains. The boundary between the E-gel and the silk solution is x = 0.6 cm, the final value of the E-gel depth in Fig. 3b. (B) pH profile calculated by converting ion concentration values of (A) into pH (eqn (6) and (7)). The numerical pH results agree well with the experimentally measured pH distribution obtained using the pH probe (Fig. 1c and d). The coordinate x = 0 is the (+) plate and x = L = 1 cm is the (−) plate (Fig. 2). | ||
The concentrations were then converted to pH using the relations from eqn (6) and (7) (Fig. 4b). The calculated numerical pH profile corresponds to the concentration profile of Fig. 4a. The experimental pH profile was measured by pH probe (Fig. 1c) and is shown for comparison. It should be noted that the pH probe electrically measures the pH and the presence of moving charged ions could induce some error. Therefore, the pH paper and the pH sensitive dye (Fig. 1d) were used for additional measurements, all of which confirmed the pH probe values of pH ≈ 4 throughout the gel and pH ≈ 10 in the silk solution (Fig. 1d). These pH measurements were also repeated in all other experiments, with the same profile and values found; pH ≈ 4 in the gel and pH ≈ 10 in the silk solution.
To examine the effect of the strength of the applied current, an experiment was performed with a current value of 0.8 mA. The resulting voltage and E-gel growth curves were measured (Fig. 5a and b) and plotted together with the previous 0.4 mA case. Following the same procedure as before, the voltage and growth curves, and the value of the current, were input into the computational model. The calculated concentration and pH profiles for 0.8 mA are plotted alongside the 0.4 mA case (Fig. 5c and d).
 | ||
| Fig. 5 (A) Experimental voltage curve for 0.8 mA (red curve) and the 0.4 mA voltage (blue curve). (B) The measured E-gel growth for 0.8 mA (red curve) and the 0.4 mA case (blue curve). (C) Calculated ion concentrations for the 0.8 mA (solid red line) and 0.4 mA (dashed blue line) experiments. Values from (A) and (B) were used as inputs for the model. (D) Resulting pH profiles (converted from the ion concentrations of (C)) for the 0.8 mA (solid red line) and 0.4 mA (dashed blue line) experiments. The coordinate x = 0 is the (+) plate and x = L = 1 cm is the (−) plate (Fig. 2). | ||
In order to probe the predictive capabilities of the model, two test cases were chosen: one with an E-gel growth rate twice (labeled 2× Rate) that of the 0.8 mA case, and the other at four times the growth rate (labeled 4× Rate). The hypothetical E-gel growth curves and the measured 0.8 mA case are shown in Fig. 6a. Prior to proceeding to calculate the current needed to produce the hypothetical growth curves, the corresponding voltage curves had to be approximated. A simple assumption was made based on the results of the 0.4 mA and 0.8 mA experiments: the ratio between the voltage values of 0.4 and 0.8 mA was assumed to be equal for the 2× and 4× cases. In other words, the relative voltage increase for doubling the current from 0.4 to 0.8 mA would be assumed for doubling the E-gel growth rate (2× case). Therefore, the initial (t = 1 min) voltage ratio between the 0.8 and 0.4 mA (Fig. 5a) was (V0.8 mA_initial = 4.4 V)/(V0.4 mA_initial = 3.4 V) = 1.3. Applying this to the 2× case: V2×_initial/(V0.8 mA_initial = 4.4 V) = 1.3 → V2×_initial = 5.72 V, and to the 4× case: V4×_initial = 1.3 × (V2×_initial = 5.72 V) = 7.44 V. The voltage values at the end of the hypothetical 2× and 4× cases were similarly obtained by assuming the same ratio holds for the voltage values of 0.8 and 0.4 mA at the corresponding time when the E-gel depth of 0.6 cm was reached for 0.8 mA. Thus, (V0.8 mA_t = 30 min = 11.4 V)/(V0.4 mA_t = 30 min = 4.9 V) = 2.33 and it follows for the 2× case V2×_t = 15 min = 2.33 × (V0.8 mA_t = 30 min = 11.4 V) = 26.6 V and the 4× case V4×_t = 7.5 min = 2.33 × (V2×_t = 15 min = 26.6 V) = 62 V. In the 4× case, we assume that the final value will be V4×_t = 7.5 min = 40 V, since that is the maximum voltage that our power supply can output. The presumed voltage curves for the 2× and 4× cases are shown in Fig. 6b along with the 0.8 mA case. Another input parameter that had to be estimated was the concentration range at x = 0. Based on the 0.4 and 0.8 mA values, which were C0.4 mA(x = 0) = 68 nmol cm−3 and C0.8 mA(x = 0) = 89 nmol cm−3 (Fig. 5c), and assuming that the concentration should be less than 100 nmol cm−3 (pH = 4), we presume a range of 95–100 nmol cm−3. This means that the x = 0 concentration will be slightly higher than the 0.8 mA case, but does not fall below pH = 4.
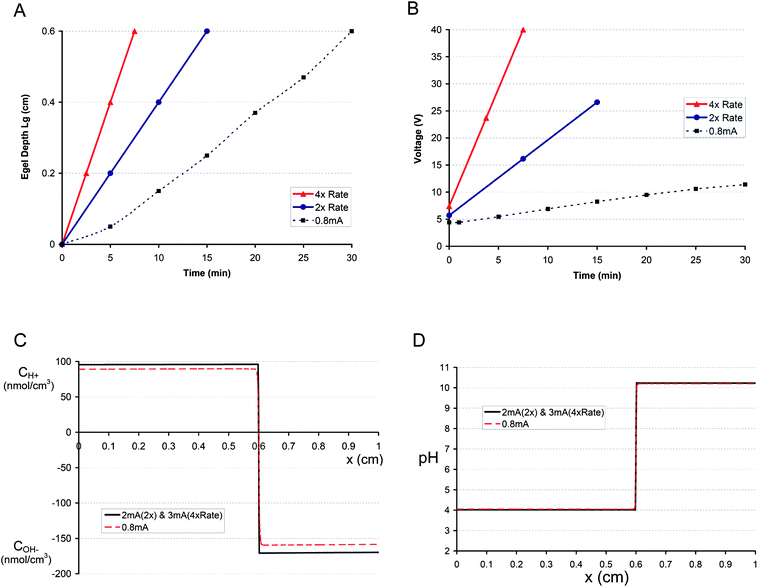 | ||
| Fig. 6 (A) Hypothetical E-gel growth curves (solid lines) and the measured 0.8 mA growth curve (dashed line). The solid blue line represents a growth rate that is twice that of the 0.8 mA case (labeled as 2× Rate), whereas the solid red line is 4-times the 0.8 mA growth rate (labeled as 4× Rate). (B) Corresponding voltage curves (solid lines, see Results for more details on how voltage was estimated) for the hypothetical E-gel growth curves (2× and 4× Rate) and the observed 0.8 mA voltage (dashed line). (C) The model predicts that a current of 2 mA is needed to achieve the E-gel growth curve of 2× Rate, and 3 mA is necessary for the 4× Rate. The resulting concentration profiles for the 2 mA and 3 mA cases are essentially the same (solid black line). The 0.8 mA concentration profile (dashed red line) is plotted for comparison. The profiles correspond to different time points but the same E-gel depth (x = 0.6 cm) (D) pH distributions, essentially identical for the 2 mA and 3 mA cases (solid black line) and the 0.8 mA case (dashed red line). | ||
Along with the above input values (E-gel growth curve, voltage curve, x = 0 concentration range), we also need to specify an initial estimate of the current (I0) from which an iterative process will start. After each iteration, a check is performed to determine whether the x = 0 concentration falls within the prescribed x = 0 range (95–100 nmol cm−3) and the next iteration is performed with a current increased or decreased by a selected increment, in our case: 0.1 mA. These adjustments of the current will continue until the x = 0 concentration falls within the given range, after which the program terminates. For the 2× case an initial current value of 1.4 mA was arbitrarily chosen, whereas for the 4× case an I0 = 2.8 mA was selected.
Inputting all of the above, the model outputted values of 2 mA for the 2× case and 3 mA for the 4× case. The solution was reached after 7 iterations for the 2× case, which started with an initial current value of 1.4 mA, and after 3 iterations for the 4× case (I0 = 2.8 mA). The corresponding concentration and pH profiles for the 2× and 4× cases are shown in Fig. 6c and d along with the 0.8 mA case. The concentration profiles for the 2× and 4× were essentially identical (Fig. 6c), and the same holds for the pH profiles (Fig. 6d).
To test the predictions of 2 mA for the 2× case and 3 mA for the 4× case, experiments were subsequently performed by applying a constant current of 2 mA and 3 mA. For each of the experiments the voltage and E-gel growth curves were measured (Fig. 7). The solid lines indicate the recorded voltage for the 2 mA and 3 mA cases, whereas the dashed lines represent the assumed voltage curves (labeled Numerical). The E-gel growth curves (Fig. 7b) were similarly displayed with the dashed lines indicating the presumed 2× (labeled 2 mA Numerical) and 4× (labeled 3 mA Numerical) growth rate (Fig. 6a), whereas the solid lines show the experimentally measured values for the 2 mA and 3 mA cases.
 | ||
| Fig. 7 (A) Voltage curves: dashed blue line (labeled 2 mA numerical) was the 2× Rate curve from Fig. 6b used in the calculations that yielded 2 mA; solid blue line (labeled 2 mA Experimental) represents measured voltage curve for a 2 mA experiment; dashed red line (labeled 3 mA numerical) was the 4× Rate curve from Fig. 6b used in the 3 mA calculations; solid red line (labeled 2 mA Experimental) indicates measured voltage values for the 3 mA experiment. (B) E-gel growth curves: Dashed blue line (labeled 2 mA numerical) was the hypothetical 2× Rate curve from Fig. 6a used in the calculations that yielded 2 mA; solid blue line (labeled 2 mA Experimental) is experimentally measured E-gel growth for 2 mA; dashed red line (labeled 3 mA numerical) was the hypothetical 4× Rate curve from Fig. 6a used to determine the value of 3 mA; solid red line (labeled 3 mA Experimental) indicates E-gel growth for the 3 mA experiment. | ||
Discussion
In previous work we have employed finite-element transport models in various scenarios, including water removal during spider silk fiber spinning,26 determination of solvent diffusion coefficients in a concentrated polymer solution,27 diffusion of molecules through nanochannels,28,29 and cellular mechanotransduction.30–32 In each case, the coupling of the computational models with experimental observations yielded a deeper understanding of the underlying mechanisms. Along those lines, in the present work we developed a finite-element electrodiffusion model in order to gain insight into what controls the electrogelation process.The formation of E-gel involves a decrease in local pH of the aqueous silk fibroin solution (normally at pH ≈ 6.5 (ref. 7)) to below the silk fibroin isoelectric point of pH = 4.2,9 allowing for conformational changes and a sol–gel transition. During electrogelation, water electrolysis generates H+ ions at the (+) and OH− ions at the (−) electrode (eqn (1) and (2)). These ions then diffuse down their concentration gradient and are also moved toward the oppositely charged electrode by the electric field. In such conditions, the redistribution of the ions results in pH variations, whereby the (+) plate becomes acidic and the (−) plate basic (Fig. 1d). To examine the importance of the ion, and thus pH, distribution in electrogelation, we developed a numerical finite-element model (Fig. 2) that could calculate the pH profile for a given experiment. The model relies on the following key experimental parameters: value of the current being applied, voltage needed to maintain the current, and the E-gel growth curve. Inputting these parameters, the model then solves the Nernst–Planck electrodiffusion equations (eqn (4) and (5)) for the ion concentration distribution. The concentrations are converted to pH using the appropriate relation (eqn (6) and (7)) and the numerically determined pH profile can be compared to the experimentally measured results. The first analyzed experiment was with the minimum constant current (0.4 mA) necessary to initiate E-gel formation. The recorded voltage and E-gel growth curves (Fig. 3) were used as input into the model. The calculated pH profile was in agreement with the measured pH distribution (Fig. 4b), capturing the large step-like jump in pH from pH = 4 → 10 at the E-gel/silk solution boundary (Fig. 1b and 4b).
Reproducing the experimental pH profile with the model allowed us to conclude that electrodiffusion of the generated H+ and OH− ions is central to the silk electrogelation process. The model helps to connect the experimental observations and explains the measured pH values and profile. This mechanistic insight was then used to make testable predictions about E-gel growth.
Two hypothetical E-gel growth curves (Fig. 6a) were chosen and the following question was posed: what is the constant current that needs to be applied in order to achieve the desired E-gel growth? Prior to answering this question, we had to make several assumptions about the corresponding voltage curves and the range of expected H+ concentrations at the (+) plate (Fig. 2). By analyzing another experiment (0.8 mA, Fig. 5) and comparing it to the 0.4 mA case, we could estimate the voltage curves (Fig. 6b) and the range of CH+(x = 0) values for our two hypothetical cases. Based on these inputs, the model went through iterations adjusting the initial, arbitrary value of the current after each iteration until the calculated CH+(x = 0) was within the specified range. For the 2× Rate case, where the rate of the E-gel growth is twice that of 0.8 mA, Fig. 6a, the model predicted that the 2 mA was needed, whereas 3 mA was required for the 4× Rate case (Fig. 6). These numerical predictions were then tested by performing experiments with 2 mA and 3 mA. The measured voltage curve for the 2 mA case agreed with the assumed voltage used in the model (Fig. 7a). However, for 3 mA there was an overestimate in the numerical case (Fig. 7a), especially in the final value (40 V vs. 28 V). A potential reason for this discrepancy could be that high currents, such as large ion and bubble production rates, accentuate non-linear effects caused by generated gas bubbles (see electrolysis reactions eqn (1) and (2)).24 At present, the model does not take into account the presence of bubbles and the potential mixing of fluid induced at high currents.
In contrast, the assumed numerical E-gel growth was in good agreement with experimentally measured growth curves (Fig. 7b) for both the 2 mA and 3 mA case, differing by <4% for 2 mA and <11% for 3 mA. Therefore, the model predictions for the current needed to achieve a desired E-gel growth curve, were validated experimentally. This provides further evidence that ion electrodiffusion governs silk electrogelation.
Conclusions
A finite-element model was developed that describes how ion electrodiffusion controls E-gel growth. The calculated rectangular pH profile agrees with the experimentally measured profile, indicating that ion electrodiffusion governs pH distribution and as such is central to electrogelation. Furthermore, the model was utilized to predict the value of the current needed for two hypothetical E-gel growth curves. These predictions were then confirmed experimentally, suggesting that the model could be employed to calculate the amount of current required for a desired E-gel growth profile under various conditions. This could be important for practical applications where precise control of E-gel growth is required, such as producing in situ medical adhesive coatings, or generating thin reversible E-gel layers to prevent biofouling of surfaces.The model can be further expanded to incorporate dynamic flow conditions, such as those found in microfluidic devices, where the silk solution flows across an electrically charged surface. The ability to form E-gel in a microfluidic device, where the flow would induce additional silk protein alignment, could be used to modify/enhance the E-gel's mechanical properties. Other flow scenarios would be encountered in various filtration and drug delivery applications, where the E-gel first encapsulates and then, when needed, releases the desired molecules or drugs. The ability to examine in silico a wide range of flow conditions would help optimize the E-gel formation and alignment process.
Future work will focus on how the reversal of polarity causes the E-gel to dissolve back into solution. Moreover, a molecular dynamics approach, similar to that used to examine how silk monomers assemble into fiber structures,33 could be employed to determine how the E-gel forms on a molecular level. This approach, which explores the pH-induced conformational changes of the silk protein, could then be coupled to our present finite-element model. Such a multiscale model would provide insight into the fundamentals of the silk electrogelation process and could potentially reveal the origins of E-gel's exceptional adhesion properties.
Acknowledgements
This work was supported by the NIH (DE017207, EB003210 and EB002520), the AFOSR, and the Ministry of Education and Science of Serbia (Grants OI 174028 and III 41007).References
- V. Kishore, J. A. Uquillas, A. Dubikovsky, M. A. Alshehabat, P. W. Snyder, G. J. Breur and O. Akkus, J. Biomed. Mater. Res., Part B, 2012, 100B, 400–408 CrossRef CAS.
- G. G. Leisk, T. J. Lo, T. Yucel, Q. Lu and D. L. Kaplan, Adv. Mater., 2010, 22, 711–715 CrossRef CAS.
- Q. Lu, Y. L. Huang, M. Z. Li, B. Q. Zuo, S. Z. Lu, J. N. Wang, H. S. Zhu and D. L. Kaplan, Acta Biomater., 2011, 7, 2394–2400 CrossRef CAS.
- E. Servoli, D. Maniglio, A. Motta and C. Migliaresi, Macromol. Biosci., 2008, 8, 827–835 CrossRef CAS.
- A. Michelman-Ribeiro, R. Nossal, R. Morris, S. Lange, C. S. Kuo and R. Bansil, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 1–10 CrossRef.
- E. K. Johnson, D. J. Adams and P. J. Cameron, J. Am. Chem. Soc., 2010, 132, 5130–5136 CrossRef CAS.
- T. Yucel, N. Kojic, G. G. Leisk, T. J. Lo and D. L. Kaplan, J. Struct. Biol., 2010, 170, 406–412 CrossRef CAS.
- S. Inoue, K. Tanaka, F. Arisaka, S. Kimura, K. Ohtomo and S. Mizuno, J. Biol. Chem., 2000, 275, 40517–40528 CrossRef CAS.
- C. Z. Zhou, F. Confalonieri, N. Medina, Y. Zivanovic, C. Esnault, T. Yang, M. Jacquet, J. Janin, M. Duguet, R. Perasso and Z. G. Li, Nucleic Acids Res., 2000, 28, 2413–2419 CrossRef CAS.
- H. J. Jin, S. V. Fridrikh, G. C. Rutledge and D. L. Kaplan, Biomacromolecules, 2002, 3, 1233–1239 CrossRef CAS.
- H. J. Jin, J. Park, R. Valluzzi, P. Cebe and D. L. Kaplan, Biomacromolecules, 2004, 5, 711–717 CrossRef CAS.
- U. J. Kim, J. Y. Park, C. M. Li, H. J. Jin, R. Valluzzi and D. L. Kaplan, Biomacromolecules, 2004, 5, 786–792 CrossRef CAS.
- F. G. Omenetto and D. L. Kaplan, Science, 2010, 329, 528–531 CrossRef CAS.
- C. Vepari and D. L. Kaplan, Prog. Polym. Sci., 2007, 32, 991–1007 CrossRef CAS.
- M. Wang, H. J. Jin, D. L. Kaplan and G. C. Rutledge, Macromolecules, 2004, 37, 6856–6864 CrossRef CAS.
- Y. Wang, D. D. Rudym, A. Walsh, L. Abrahamsen, H. J. Kim, H. S. Kim, C. Kirker-Head and D. L. Kaplan, Biomaterials, 2008, 29, 3415–3428 CrossRef CAS.
- T. Yucel, P. Cebe and D. L. Kaplan, Biophys. J., 2009, 97, 2044–2050 CrossRef CAS.
- X. Wang, J. A. Kluge, G. G. Leisk and D. L. Kaplan, Biomaterials, 2008, 29, 1054–1064 CrossRef CAS.
- S. Sofia, M. B. McCarthy, G. Gronowicz and D. L. Kaplan, J. Biomed. Mater. Res., 2001, 54, 139–148 CrossRef CAS.
- B. J. Kirby, Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices, Cambridge University Press, New York, NY, 2010 Search PubMed.
- T. J. R. Hughes, The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Prentice Hall, Englewood Cliffs, NJ, 1987 Search PubMed.
- M. Kojic, N. Filipovic, B. Stojanovic and N. Kojic, Computer Modeling in Bioengineering: Theoretical Background, Examples and Software, John Wiley & Sons, Chichester, United Kingdom, 2008 Search PubMed.
- M. Kojic, R. Slavkovic, M. Zivkovic, N. Grujovic and N. Filipovic, PAK Finite Element Program for Solid and Fluid Mechanics, Mass and Heat Transfer, Coupled Problems and Biomechanics, Mech. Eng. Dept. University of Kragujevac and R&D Center for Bioengineering Kragujevac, Serbia, 2010 Search PubMed.
- C. Sillen, E. Barendrecht, L. J. J. Janssen and S. J. D. Vanstralen, Int. J. Hydrogen Energy, 1982, 7, 577–587 CrossRef CAS.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, New York, NY, 2009 Search PubMed.
- N. Kojic, M. Kojic, S. Gudlavalleti and G. McKinley, Biomacromolecules, 2004, 5, 1698–1707 CrossRef CAS.
- N. Kojic, A. Kojic and M. Kojic, Comm. Numer. Meth. Eng., 2006, 22, 1003–1013 CrossRef.
- M. Kojic, A. Ziemys, M. Milosevic, V. Isailovic, N. Kojic, M. Rosic, N. Filipovic and M. Ferrari, Journal of the Serbian Society for Computational Mechanics, 2011, 5, 101–128 Search PubMed.
- A. Ziemys, M. Kojic, M. Milosevic, N. Kojic, F. Hussain, M. Ferrari and A. Grattoni, J. Comput. Phys., 2011, 230, 5722–5731 CrossRef CAS.
- N. Kojic, E. Chung, A. T. Kho, J.-A. Park, A. Huang, P. T. C. So and D. J. Tschumperlin, FASEB J., 2010, 24, 1604–1615 CrossRef CAS.
- N. Kojic, A. Huang, E. Chung, M. Ivanovic, N. Filipovic, M. Kojic and D. J. Tschumperlin, Biophys. J., 2010, 99, 3517–3525 CrossRef CAS.
- N. Kojic, M. Kojic and D. J. Tschumperlin, Biophys. J., 2006, 90, 4261–4270 CrossRef CAS.
- S. Keten and M. J. Buehler, J. R. Soc. Interface, 2010, 7, 1709–1721 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
