Interfacial viscoelasticity controls buckling, wrinkling and arrest in emulsion drops undergoing mass transfer

Abstract

Contrary to the notion that ‘oil and water do not mix’, many oils possess a residual diffusive mobility through water, causing the drop sizes in oil-in-water emulsions to slowly evolve with time. Liquid interfaces are therefore typically stabilized with polymeric or particulate emulsifiers. Upon adsorption, these may induce strong, localized viscoelasticity in the interfacial region. Here, we show that shrinkage of oil drops due to bulk mass transfer may render such adsorption layers mechanically unstable, causing them to buckle, crumple and, finally, to attain a stationary shape and size. We demonstrate using two types of model interfaces that this only occurs if the adsorption layer has a high interfacial shear elasticity. This is typically the case for adsorbed layers that are cross-linked or ‘jammed’. Conversely, interfacial compression elasticity alone is a poor predictor of interface buckling or arrest. These results provide a new perspective on the role of interfacial rheology for compositional ripening in emulsions. Moreover, they directly affect a variety of applications, including the rapid screening of amphiphilic biopolymers such as the Acacia gum or the octenyl succinic anhydride modified starch used here, the interpretation of light scattering data for size measurements of emulsion drops, or the formulation of delivery systems for encapsulation and release of drugs and volatiles.

---

Introduction

Oil droplets in emulsions relevant for foods, consumer products or pharmaceutical applications are mixtures of compounds with a wide range of hydrophobicities and partition coefficients. As a consequence, they tend to be compositionally unstable and undergo ripening due to inter-droplet gradients in the chemical potential.^1–3 For mobile, slightly water-soluble oils, the drop volume steadily decreases if a second, highly hydrophobic and immobile oil phase is present. The drops eventually disappear^1,4 if the oil–water interface is ‘simple’, i.e. if its only relevant mechanical characteristic is the interfacial tension. This is typically the case for pure liquids and for solutions of low molecular weight surfactants.^3–5 Mass transfer is thought to occur via the following sequence:^5,6 (i) dissolution of the mobile oil into the water phase, (ii) molecular diffusion, and (iii) dissolution into an immobile oil drop or reservoir, which acts as a compositional ‘sink’.

If the compositional gradient between the two different oils is large, the effects of compositional ripening typically dominate those due to differences in the Laplace pressure.^1–3 Compositional ripening and Laplace pressure (Ostwald) ripening can be differentiated via the Kelvin effect: since the Laplace term in the chemical potential of the disperse phase depends on the size as Δμ_LP(R) ∝ 2σV_m/R (where V_m is the molar volume, R is the drop radius and σ is the interfacial tension), curvature effects become less important than compositional ripening effects for relatively large drops.

Ripening in emulsions composed of drops with chemical potential gradients has been observed for pure systems,² for surfactant-stabilized interfaces,³ and for particle-covered drops.⁷ For emulsions stabilized by ionic or nonionic surfactants, the rate of compositional ripening depends on the solubility of the mobile oil in the micellar surfactant solution.³ The transport mechanisms for the oil through the water phase and across the oil–water phase boundary and the roles of micellation, interfacial properties, oil types, and the balance between the Laplace pressure and the osmotic pressure have been studied by several authors;^3–5,8–11 our assumption for this paper is that the compositional ripening process is limited by bulk-phase transport.

Emulsions are often stabilized with polymeric or particulate emulsifiers or surfactants.^{1–4,7,9,10,12–14} Upon adsorption, many of them not only modify the interfacial tension, but impose viscoelastic properties onto liquid interfaces.^15–17 The field of interfacial rheology is concerned with the stresses and deformations of adsorption layers at liquid interfaces.^16,18,19 These properties are emerging to have a profound impact on the stability and flow of emulsions and foams.^16,20–24

Despite the widespread use of particulate and polymeric emulsifiers, mass transfer and ripening processes in emulsions with complex, non-Newtonian interfaces have received very little attention, and in the existing studies^4,5,25–27 the detailed role of interfacial rheology was not discussed, or the approach was based on the a priori assumption that only the interfacial compression elasticity matters.

In this paper, we first demonstrate how the presence of adsorption layers with interfacial viscoelasticity can have a dramatic effect on the morphologies and sizes of emulsion droplets undergoing compositional ripening. For the model immobile oil we use squalane, a highly hydrophobic triterpene with near-perfect insolubility in water. The mobile oil used for the shrinking drops is β-ionone, an important carotenoid-derived fragrance compound. We quantify the temporal evolution of the drop sizes and identify mechanical instabilities at the oil–water interface using a custom-built microchannel cell, microscopy and image analysis. To elucidate the role of interfacial rheology in mass transfer driven shrinking, we study droplets stabilized with two different types of interfacial adsorption layers that are either very rigid or very compliant. For the rigid interfaces, we use adsorbed Acacia gum, a compact peptide–polysaccharide hybrid; for the compliant interfaces we use octenyl succinic anhydride (OSA) starch, a polysaccharide-based emulsifier with a flexible, random coil molecular structure. To obtain a comprehensive picture of the interfacial rheology of these model adsorption layers, we characterize their viscoelastic properties in the two primary interface deformation modes. We distinguish all interfacial viscoelastic parameters by the kinematics of the interface deformation: interfacial shear rheology involves shape deformations of an interfacial area element at constant area;^17,28,29 interfacial compression rheology deals with interfacial momentum and mass transfer upon changes in size of an interfacial area element while retaining its shape,^17,30 either by uniformly compressing or dilating it. We next discuss the role of interfacial viscoelasticity for mechanical instabilities occurring on macroscopic drops with radii greater than the capillary length, again comparing the rigid and the compliant interface types. Finally, we point out implications for the interpretation of drop size distributions obtained by small angle light scattering, for rapid screening of surface-active biopolymers, and for the design and formulation of emulsion-based delivery systems.

Results

Shrinking emulsion drops with complex interfaces

We first investigate the evolution of a population of oil drops as they undergo compositional ripening using optical microscopy in a microchannel cell. Experiments on compositional ripening are typically performed by preparing ternary oil-in-water emulsions with two populations of oil drops (one mobile and the other immobile) and observing the evolution of their size distributions either by microscopy⁷ or by small angle light scattering.³ Here we simplify the system by only using a single population of mobile oil drops dispersed in the aqueous continuous phase in the vicinity of a large reservoir of immobile oil (see Fig. 1). We estimate the water solubility of the mobile oil (β-ionone, see Fig. 1) as 8.2 × 10⁻⁴ g l⁻¹, using the method of Marrero and Gani;³¹ for the immobile oil reservoir (squalane) we assume immiscibility with the continuous water phase. These different mobilities are mirrored in the very different partition coefficients of these two oils; log K_ow is 14.63 for squalane and 3.84 for β-ionone (K_ow is the octanol–water partition coefficient).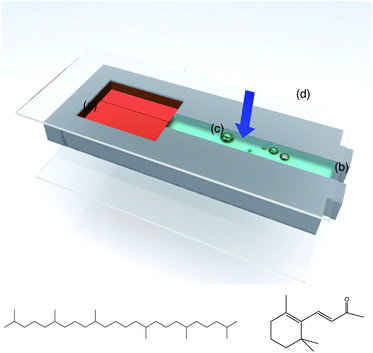

Fig. 1 Schematic of the experiment to study compositional ripening of mobile oil drops near an immobile oil reservoir by brightfield microscopy in a microchannel cell. (a) Immobile oil reservoir; (b) aqueous solution of amphiphilic polymer (Acacia gum or octenyl succinic anhydride (OSA) starch); (c) droplets of the mobile oil; and (d) cover glass. The arrow indicates the direction of observation in the microscope. Also shown are the model oils used for the shrinking experiments: squalane (left) is used for the immobile oil reservoir; β-ionone is used for the mobile drops.

We perform identical ripening experiments with two different types of interfaces. The first type is formed by adsorbed Acacia gum, a complex protein–polysaccharide hybrid;^32,33 it has a high interfacial shear elasticity and behaves as a 2D soft solid material under interfacial shear deformation.¹² This important biopolymeric emulsifier is frequently used to stabilize emulsions^34,35 or suspensions.³⁶ Among the three main fractions of Acacia gum, a high molecular weight (M_w ≈ 1.45 × 10⁶ g mol⁻¹) arabinogalactan–protein (AGP) complex is now known to be the primary surface-active fraction responsible for the strong amphiphilicity.^12,32,33 The other type of interface, formed by octenyl succinic anhydride (OSA) starch, exhibits no interfacial shear elasticity at all. This second emulsifier is derived from partially hydrophobized fractions of waxy maize starch, which is rendered amphiphilic by non-polar alkenyl succinate side-groups grafted onto the amylopectin backbone.³⁷ Both interfaces possess a moderate compression elasticity; we provide more details on the interfacial rheology of these two model interfaces below.

Fig. 2 shows the time-evolution of a population of mobile β-ionone oil droplets with adsorbed Acacia gum. The image region of interest is chosen such that drops of different sizes can be tracked simultaneously. The sequence shown in Fig. 2 reveals several phenomena: (i) all β-ionone drops shrink over time; (ii) the relative rate of change in drop volume (with respect to their original size) is different, depending on the initial drop size; (iii) over the course of the experiment, the oil–water interface buckles and becomes mechanically unstable as the drop volume decreases; (iv) this interfacial instability sets in at different times and at different relative volumes of the shrinking drops: the smallest one buckles first, then the second smallest, etc. The final radii of the shrunken drops are in the range of 10–45 μm; (v) finally, all drops stop shrinking and attain a stationary shape; we define a ‘jammed’ drop as one that has attained a stationary Feret radius and that does not shrink further.

Fig. 2 Mobile oil drops with interfacial shear rigidity undergoing compositional ripening. Dashed lines indicate the onset of buckling for each drop: the smallest drop buckles first, followed by drops of monotonically increasing radius. Oil phase: β-ionone and water phase: Acacia gum solution. Time is in minutes for each frame; the scale bar indicates 100 μm.

R(t) curves of drops with different initial radii R₀ cannot be superimposed (Fig. 3a): they buckle and undergo arrest at different times and interface compression ratios. The transition from shrinking drops to stationary ghosts is abrupt for small drops, but gradual for larger ones. However, drops with the same R₀ consistently shrink along identical R(t) trajectories; they also buckle at identical times t_B and compression ratios ΔA_B/A₀ and stop shrinking at the same time. The time at which the mechanical instability sets in, t_B, is plotted as a function of the initial drop radius R₀ in Fig. 3b. Within the range of sizes observed here, the relation is approximately linear. We speculate that as the drops shrink beyond the buckling threshold and the shapes begin to deviate from sphericity, the interfacial stress boundary condition changes from a purely interfacial tension-controlled state to a state where interfacial viscoelastic contributions become important.^38–40 Extrapolating the linear fit shown in the graph to smaller length scales, we can estimate a critical drop size for which we would expect the interface to buckle as soon as mass transfer starts. As indicated by the red shaded ‘problem zone’, t_B for μm-sized small drops becomes as short as a few minutes – which is dangerously close to typical timescales needed for emulsification or for sample preparation in physicochemical measurements on emulsions. Indeed, in this size range the collapsed ghosts may therefore easily be mistaken for stable oil droplets if non-discriminative methods are used; an example is small angle light scattering for size analysis of emulsions along with the commonly used Fraunhofer diffraction optical model. The inset of Fig. 3b emphasizes the role of the initial drop size for the intermediate regime between buckling and arrest: large drops continue to shrink even beyond the onset of the mechanical instability, developing increasingly corrugated and crumpled interface morphologies. In this regime, they shrink at a reduced rate, likely due to the combined effects of interfacial tension and interfacial viscoelasticity.

Fig. 3 Evolution of the droplet morphology with time for emulsions with dominant interfacial shear elasticity. (a) Feret radius R(t) for mobile β-ionone droplets with adsorbed Acacia gum undergoing compositionally induced shrinkage. Drops are considered to be ‘jammed’ when R attains a constant value. R(t) trajectories of drops with different initial sizes cannot be superimposed; buckling and arrest occur at different times and interface compression ratios ΔA_B = A₀, and are more abrupt for small drops. Inset: drops with the same initial size consistently shrink with reproducible R(t) trajectories; they also buckle and stop shrinking at identical times and compression ratios. (b) Time at the onset of buckling t_B as a function of the initial drop radius R₀. The solid line is a linear fit through all data; the dotted red line is an extrapolation to small drop sizes. Red shaded area: ‘problem zone’ where t_B approaches typical timescales relevant for dispersion processes or light scattering measurements. In the inset the time to reach the arrested state t_J is plotted against t_B. Once t_B is reached, large drops (indicated in green) continue to shrink and crumple for a relatively longer time until they attain a stationary size and shape as compared to small drops.

At the end of the experiment, all drops have shrunken, undergone the mechanical interface instability, and sedimented to the bottom of the sample cell as ‘ghosts’. These leftovers are highly non-uniform and non-spherical in shape. By analogy with surfactant-stabilized mobile drops with ‘simple interfaces’ (which completely disappear upon ripening⁷) we assume that these residual structures are devoid of the original oil phase and consist of an emptied, mechanically collapsed biopolymer skin. Centrifugation of the ghosts produces a dense pellet but no separated oil, further supporting this hypothesis. This implies that ultimately the oil phase needs to delaminate from the jammed biopolymer shell; below, we will show that this indeed happens even on the macroscopic scale with larger drops.

In a direct comparison with the jammed, shear-elastic interfaces formed by Acacia gum, the more compliant and stabilized OSA interfaces possess a much weaker resistance against shrinking. For drops stabilized with OSA, the drop diameter decreases uniformly and eventually stabilizes at values below 1–2 μm. Remarkably, for these drops with absent interfacial shear elasticity, a master curve can be constructed by a simple time shift of the drop size data (Fig. 4). The existence of this master curve indicates that for the OSA type interfaces a drop's shrinking rate at a given size does not depend on its initial radius.

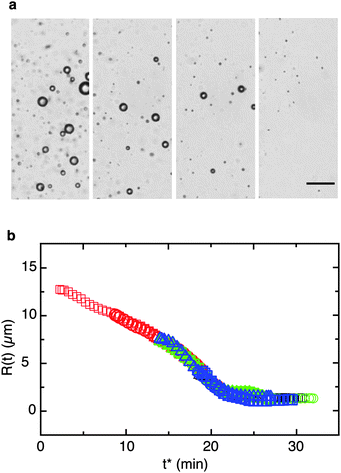Fig. 4 Mobile oil drops with compliant interfaces undergoing compositional ripening. (a) Micrograph sequence of β-ionone oil drops in an aqueous solution of octenyl succinic anhydride (OSA) starch. Scale bar: 50 μm; time increment between images: 4 min. (b) For drops without interfacial shear elasticity the shrinking process is size-invariant. A master curve can be constructed by a simple time shift of the drop size data. Drop sizes vs. shifted time t* are shown for emulsions without interfacial shear elasticity, undergoing shrinkage due to mass transfer; the diameter axis was not shifted.

Mass transfer continues until only particles with sizes of a few μm and below are left. These residual particles of OSA-stabilized oil droplets might be collapsed structures formed by a strongly adsorbed minority component desorbing less easily upon compression as compared to the majority of the OSA polymer;³⁷ in this view, they appear similar to the residual buckled shells described above, but with a mechanical instability occurring much later in the compression history, and only at very extreme interface compression ratios. Alternatively, it is possible that these small units are merely small droplets of β-ionone, stabilized by the interfacial compression elasticity. However, an open question is whether the magnitude of the compression moduli expected here would be sufficient to balance the large gradients in the chemical potential associated with compositionally different oil phases. In the following section, we will investigate the role of interfacial viscoelasticity.

Interfacial viscoelasticity: shear and compression

The interfacial compression modulus has traditionally been thought to be a key parameter for stabilization against ripening,^5,25–27 whereas the interfacial shear rheology has received far less attention. At first sight, this is not surprising since the shape evolution of ripening drops gives rise to a purely compressional deformation of the interface as long as the drops remain spherical. For the two types of interfaces studied here, we distinguish between interfacial shear and compressional viscoelasticity and measure the interfacial shear (G) and compression (E) moduli, summarized in Fig. 5a–d. We use symbols without subscripts for the interfacial moduli; all interfacial stresses (isotropic or extra) and moduli have the units of an interfacial tension, i.e. force per length (which is dimensionally equivalent to a bulk pressure × length).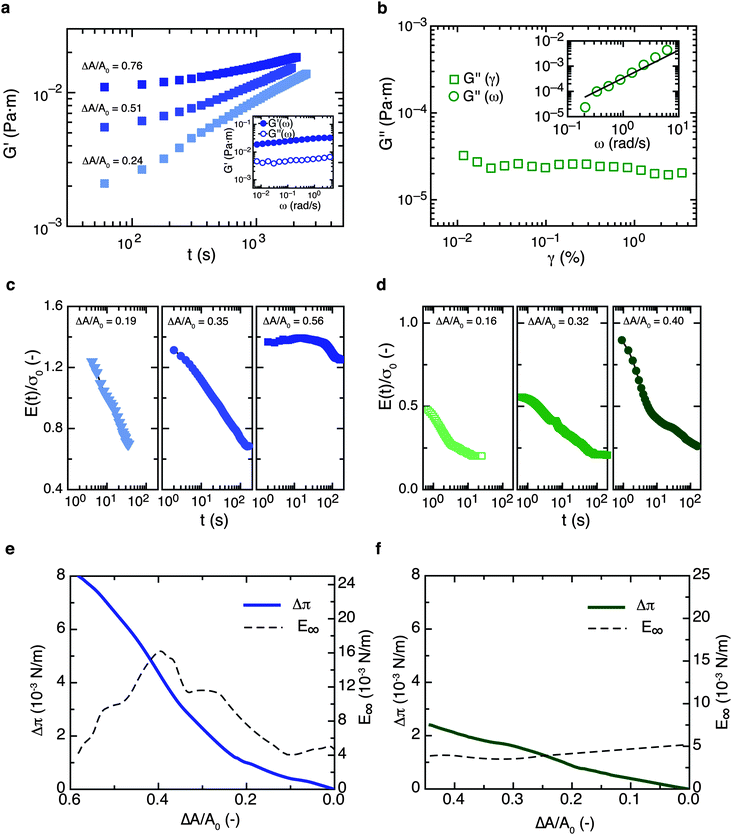

Fig. 5 Interfacial rheology for Acacia gum (left-hand panels) and OSA (right-hand panels) at the oil–water interface. (a) Shear rheology of Acacia gum layers; the interfacial shear elastic modulus is plotted as a function of time for different interface pre-compression ratios. These are obtained using measuring cells with different cup radii. The inset shows the interfacial elastic (G′) and viscous (G′′) shear moduli in a typical frequency sweep experiment, indicating a characteristic ‘soft solid’ type rheological response. (b) Interfacial shear rheology of OSA solutions; only a weak viscous shear modulus of the interface G′′ is detectable, whereas no elastic interfacial shear modulus G′ can be measured. Data are only shown for the highest interface pre-compression ratio ΔA/A₀ = 0.76; for lower pre-compression ratios we did not detect any interfacial shear response. The inset shows the interfacial shear viscous modulus G′′ as a function of the oscillation frequency ω; the line corresponds to a power law G′′ ∝ ω^1.1, indicating that the interface is liquid-like under shear. (c) Interfacial compression modulus E(t) for Acacia gum, following step compression ending at t = 0 s. Interfacial compression strains ΔA/A₀ are indicated with each experiment; the curves are normalized with respect to the equilibrium interfacial tension, σ₀ = 12.1 mN m⁻¹. (d) Interfacial compression modulus E(t) for OSA; curves are normalized with σ₀ = 9.8 mN m⁻¹. (e) Interfacial pressure increase Δπ as a function of ΔA/A₀ and static compression elasticity E_∞ for Acacia gum. (f) Δπ and E_∞ for OSA. The oil phase is β-ionone in all cases.

The difference between the two types of interfaces is most evident in interfacial shear deformation: Acacia gum interfaces are very strongly shear-elastic (G′ > G′′ → 0) and exhibit non-linear interfacial shear rheology indicative of 2D soft solid behavior. OSA interfaces on the other hand only possess a very weak shear response, and the absolute values of the complex interfacial shear viscosity are orders of magnitude lower. There is no detectable shear elasticity, and G′′ > G′ at all conditions.

A probe with conical geometry immersed into the subphase through an interfacial adsorption layer compresses the interface in a manner similar to a Langmuir film balance, as shown recently by Zang et al.⁴¹ for partially hydrophobic silica nanoparticles. We use this approach here to emulate the compression history of shrinking oil drops in the interfacial shear rheometer and create interfaces with different ΔA/A₀ by using measuring cells with different radii. Fig. 5a shows the time evolution of the interfacial shear elasticity for Acacia gum interfaces. G′(t) strongly depends on the compressional pre-strain, with the highest values found for the most highly compressed interface. The interfaces are already shear-elastic (G′ > G′′) during first few minutes of the experiments even at low compression ratios. A frequency sweep response for Acacia gum layers is plotted in the inset of Fig. 5a, showing typical weak scaling of both moduli with frequency and elastic behavior at all time scales. The ratio G′′/G′ slightly decreases with time and with compressional pre-strain (not shown here), but qualitatively the response remains characteristic of a 2D soft solid at all times and compression ratios (we note that with our method we do not have access to the first 3 minutes after the oil–water interface is created, and we are unable to observe an initial crossover of G′ and G′′). The interfacial shear rheology of OSA interfaces is rather unspectacular – in this case the interfacial shear modulus is purely viscous, the values are not evolving in time, and the frequency response indicates a scaling close to a Newtonian fluid. We only detect a very weak shear response at the highest pre-compression ratio of ΔA/A₀ = 0.76; in all other cases, there is no measurable interfacial shear response.

The static interfacial tensions are σ₀ = 0.0121 N m⁻¹ for Acacia gum and σ₀ = 0.0098 N m⁻¹ for OSA. To measure the interfacial compression modulus E, we perform step compression experiments in a drop shape tensiometer on millimetre-sized, rising oil drops that have been equilibrated to σ₀ (see Fig. 6a, b and h–j for sample images). Drops are compressed to different compressional strains ΔA/A₀ at time t = 0, and E(t) is calculated from the interfacial pressure response Δπ = σ₀ − σ(t). Both interfaces give strong, viscoelastic responses in pure compression, with overall values of the compression elasticity in the range of the static interfacial tension (0.5 < E/σ₀ < 1.5), the values for Acacia gum again exceeding those of OSA.

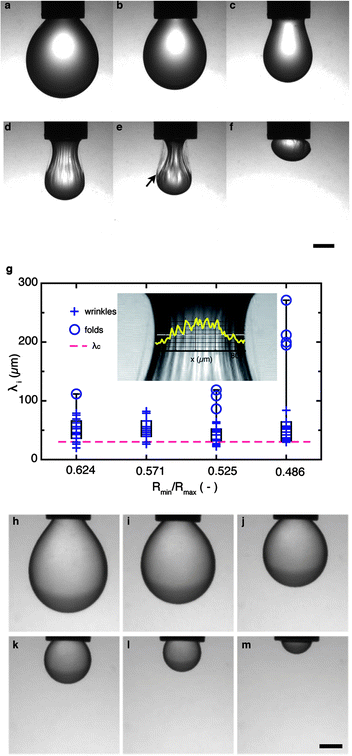Fig. 6 Drops larger than the capillary length: interface morphology of drops with and without interfacial shear elasticity. (a–f) Formation of wrinkles and multiple bag structures on interfaces with dominant interfacial shear elasticity (G′ > G′′ > 0): evolution of a drop of β-ionone immersed in a solution of Acacia gum upon compression externally driven by negative pressure in the syringe. The wrinkles on the drop surface are characteristic of interfaces with high shear elasticity. An intact, free-standing biopolymer film is left behind by the delaminating oil drop (see arrow). (g) Analysis of interface wrinkles. An intensity profile obtained by image analysis is overlaid on the zoomed necking region of a drop; the minimum drop radius is 0.447 mm (left). Wrinkle wavelength distributions in the form of box plots for four different compression states of the same drop; the ratio of the minimum (R_min) and maximum (R_max) radii indicates the curvature at the neck of the drop. For narrow necks (R_min/R_max < 0.55), several folds with much longer wavelengths form, plotted as circles in the λ_i distribution. The dashed line indicates the calculated value λ_c = 31 μm. (h–k) Compression of drops in the absence of interfacial shear elasticity (G′ ≪ G′′ < E). Interface between an OSA solution and β-ionone. Scale bars: 750 μm.

Within the time scales investigated, E(t) does not fully relax to zero for either type of interface and at any compression ratio studied. To obtain more information at longer time scales, we perform quasistatic compression experiments, again performed on rising oil drops pre-equilibrated to σ₀. The resulting interfacial pressure isotherms Δπ = f(ΔA/A₀) and the static compression moduli E_∞ derived from them are shown in Fig. 5. For Acacia gum interfaces the interfacial pressure is raised by about 8 × 10⁻³ N m⁻¹ upon a 60% decrease in interface area; for OSA solutions the value is only as low as 2 to 3 × 10⁻³ N m⁻¹. Assuming that E_∞ is associated with effectively irreversible desorption of the layer upon compression,³⁵ it appears that a non-zero compressional elasticity seems to be the first and most general ‘ingredient’ for the interfacial morphologies observed in this paper. However, a look at typical surfactants^17,42 with E > 0 suggests that this cannot be the only criterion, as for most of these surfactants none of the phenomena described in this paper are observed. Comparing Acacia gum with OSA interfaces, we note that for the former, which are prone to mechanical buckling, the ratio of the interfacial compressional elasticity and the interfacial tension is typically greater than unity.

In summary, for Acacia gum we find G′, G′′ > 0, |G*|/σ > 1 and E/σ > 1. For OSA, E/σ ≲ 1 but |G*|/σ ≪ 1 and G′′ > G′. For a third reference case, not discussed in detail here, we would expect that low molecular weight surfactants (nonionic, cationic or anionic) present at excess concentrations and slow interface deformations to be typically be characterized^13,16 by G′, G′′ → 0 and E/σ → 0, meaning shear elasticity is irrelevant, interfacial tension gradients upon compression are very rapidly rebalanced, and the static interfacial tension is the only mechanical property of the interface.

Drops larger than the capillary length: strain-induced wrinkles

A different type of interfacial instability occurs if the drop size exceeds the capillary length, l_c = σ₀(Δρg)⁻¹. In this case, gravitational effects become important and pendant or rising drops assume a non-spherical ‘pear’ shape that is highly sensitive to the interfacial tension.^39,43 Typical images of such drops are shown in Fig. 6. The drops of both types of interface are first left to equilibrate to a constant value of the static interfacial tension σ₀ (Fig. 6a and g); we then rapidly compress the interface by applying a negative pressure in the suspending capillary, thereby retracting the drop and decreasing its volume and interfacial area. The compliant OSA interface allows the drop to retract uniformly, decreasing its size until only a hemispherical cap is left at the capillary. In contrast, the rigid Acacia interface forms wrinkles upon retraction. These wrinkles are globally oriented in the vertical direction and only form on the ‘neck’ of the drop. They first appear relatively uniform, but grow more complex and hierarchically organized as the compression proceeds (Fig. 6c–f). For drop sizes above l_c, the competition between interfacial tension and gravity results in a net tensile force on the drop. If we view the interface of the drop as a thin elastic or viscoelastic layer, this configuration is a sheet-like structure under tensile strain. Stretched soft solids or elastic sheets form wrinkles in a variety of systems,^44,45 including elastomer or gel surfaces used for self-assembly, or skin; these wrinkles are thought to occur because elastic films tend to bend more easily than they stretch.⁴⁶

Indeed, these similarities suggest that the physics of wrinkle formation may be used as a sensitive indicator of interfacial rheology. A general expression⁴⁶ for the wrinkle wavelength is . This relation refers to intermediate wavelengths that become most dominant on a wrinkled thin sheet due to a balance between bending resistance and substrate stiffness:⁴⁶ short wavelengths are penalized by the bending resistance of the sheet (true in our case); long wavelengths are penalized by the presence of an ‘effective elastic support’ (to be verified in our case). To link λ to the interfacial viscoelastic properties, we use the flexure rigidity of a sheet B = Yh³/(1 − ν²) and approximate a pseudo-bulk value Y = Y_sh⁻¹ for the Young's modulus of the layer material via the relation^15,47Y_s = 2G′(1 + ν), which links the measured interfacial shear modulus G′ with the interface (2D) Young's modulus Y_s; h is the characteristic thickness of the interfacial film. Using the values l = 2.1 mm, ν = 0.5 (as suggested previously for rigid interfacial adsorption layers^48,49), a tension T = 0.004 N m⁻¹, a layer thickness h = 30 nm and an interfacial shear modulus G′ = 0.02 N m⁻¹ we obtain an approximate value for the wavelength of λ_c ≈ 31 μm.

In Fig. 6, we do not observe a single wavelength, but rather a distribution of wavelengths f(λ_i). The calculated λ compares reasonably well with the measured shortest wavelengths. This may have several causes: (i) there is not enough ‘effective elastic support’ to suppress longer wavelengths in our system consisting of jammed, but essentially non-crosslinked thin biopolymer adsorption layers on a fluid support. This is different from the thicker polymer films or plastic sheets studied previously;⁵⁰ (ii) the overall rotational geometry of the pendant drop may play a role in the formation of folds larger than the primary wrinkles. Indeed, as the global curvature of the neck increases upon volume decrease of the neck, an increasing number of primary wrinkles organize into larger folds. A detailed quantification of the roles of curvature in the necking region and the tensile strain exerted by the liquid drop is beyond the range of this paper, but would certainly merit further investigation. If the lowest reasonable value for the adsorption layer thickness of 8 nm were to be used (based on the molecular dimensions of the interfacially active AGP fraction⁵¹), the calculated wavelength would be λ_c = 16 μm, all other parameters being identical. In contrast, the value chosen here for h is based on published values of the film density indicating multilayer adsorption;³⁴ this value of h slightly overpredicts the minimum experimental wavelength measured using image analysis. Approaching the problem from the other end, the minimum wrinkle wavelength on a pendant drop could also be used as a sensitive indicator of the film thickness if the interfacial shear modulus is known.

The out-of-plane instabilities of pendant drops seem not to be restricted to Acacia interfaces studied here, but are relevant for a wide range of sytems.^13,52–54 In contrast, an intriguing feature not observed elsewhere is the ‘double bag’ structure seen in Fig. 6: the mass transfer-driven shrinkage allows the oil–water interface to delaminate from a collapsed biopolymer skin, leaving behind a free-standing bag-like structure. Fig. 6 suggests that this outer free-standing polymer film is permeable to the continuous phase liquid, since the oil drop remains intact and upon further reduction of the volume, the oil–water interface again wrinkles. Liquid drops encapsulated with crosslinked polysiloxane membranes were shown to develop wrinkles when they were de-formed in a simple shear flow;⁴⁷ there also, the global alignment was parallel to the longer axis of the deforming drops, i.e. in the direction of stretching from a spherical to an elongated ellipsoid shape.

In summary, as a pendant drop shrinks, wrinkle morphologies occur on the drop surface only if the system has a high interfacial shear elasticity. As the oil drop shrinks further, we surprisingly observe a ‘double bag’ which eventually delaminates from the oil–water interface, with the outer liquid phase permeating through the bag to fill the volume vacated by the shrunken oil drop; wrinkling is vertically oriented in the direction of gravity. We do not observe folding, wrinkling or delamination if interfacial shear viscoelasticity is absent or negligible (OSA case). In contrast, both types of interfaces studied possess significant compressional elasticities, indicating that this property alone is not predictive of the wrinkles seen in Fig. 6.

Discussion

Emulsion drops undergoing mass transfer-driven shrinking develop mechanical instabilities at the oil–water interface if a dense adsorption layer with significant interfacial shear elasticity is present. Unlike emulsions stabilized by micellar surfactants, where a disappearing drop leaves behind a surfactant micelle (or a microemulsion droplet if some residual oil remains solubilized in the core of the micelle), the residues of the collapsed, rigid interfacial layers may be orders of magnitude larger in size up to the μm range. The morphology of mobile, shrinking emulsion drops with high interfacial shear elasticity is size-dependent: drops of different initial sizes buckle and jam at different times and at different compression ratios, leading to a population of residual ‘ghosts’ with a wide distribution of sizes and shapes. In contrast, for drops with negligible interfacial shear elasticity the shrinking process is size-invariant, and a master curve can be constructed by a simple time shift of the drop size data.

For buckling, wrinkling and jamming to occur in oil-in-water emulsions, there are three necessary ingredients: (i) the interfacial compression elasticity should be non-zero; (ii) there should be a significant interfacial shear elasticity, G′ > G′′; typically the interfacial shear modulus is greater than the interfacial tension, |G*| > σ₀, and similar to or greater than the interfacial compression modulus, |G*| ≳ E; and (iii) to obtain wrinkles on emulsion droplets, conditions (i) and (ii) need to be met, and the drop size needs to exceed the wrinkle wavelength λ. Additionally, to observe wrinkles on pendant drops under gravity, the drop size is required to be greater than the capillary length, l_drop > l_c to obtain a gravitationally induced tensile strain on the drop. The shear moduli measured here are in the linear viscoelastic regime at each compressional pre-strain. In contrast, the static compression moduli derived from the isotherms in Fig. 5e and f change strongly with the compressional strain; the values used here for the apparent modulus E are therefore in the nonlinear viscoelastic regime for compression. As the 2D Young's modulus Y_s used above¹⁵ relies on definitions made for the linear viscoelastic regime, this point merits further investigation (in particular, local strains in typical compression experiments can be quite large, and real linear compression moduli may be difficult to measure, especially if the interface also has a high shear elasticity). We also note that our model experiments are designed such that all drops necessarily shrink and the mobile oil is caught in a reservoir. In contrast, if the oil migrates towards a second population of larger or more hydrophobic drops, an additional dilatational force term due to interface expansion in the receiving drops arises.

Acacia gum is a prototypical surface-active polymer for which both conditions (i) and (ii) are met; a look at the literature suggests that this interfacial rheological profile is shared by quite a number of other systems. Some examples are globular proteins,^15,20 including lysozyme, β-lactoglobulin, ovalbumin, bovine serum albumin; hydrophobins;⁵³ saponins⁵⁴ with interfacial shear elasticity; colloidal particle layers, for example those formed by SiO₂, TiO₂ or silver nanoparticles^7,55,56 or latex microparticles;⁵⁷ ionically crosslinked diblock copolymers;⁵⁸ polyelectrolyte nanocomposites made by layer-by-layer deposition;⁵⁹ polymerized membranes such as polyamides;⁴⁷ complexes of ionic surfactants with oppositely charged polyelectrolytes;^27,60 or adsorbed hydrophobic bacteria.⁶¹ Similar behaviour observed for particle-stabilised bubbles⁶² suggests that there also interfacial rheology might play a similar role.

The effects demonstrated above may also give rise to misinterpretations of ‘drop size distributions’ measured by small angle light scattering methods. In particular, the arrested ghosts left behind by emptied ionone drops may be misinterpreted as small emulsion drops. In contrast to emulsions stabilized with soluble surfactants, where disappearing drops can simply be identified by a dramatic loss in scattering intensity, the collapsed interfacial films observed here still scatter light and may be difficult to distinguish from actual emulsion drops if size distributions are analyzed using Fraunhofer diffraction as an optical model.

Ripening experiments with a mobile oil are straightforward to implement yet they are highly sensitive to interfacial viscoelasticity and to adsorption layer densities. Performed with different amphiphilic polymers and mixtures thereof, or with biopolymers of different origins and varying fractional compositions, these tests have the potential to be an efficient screening tool for such materials.

Similarly, these results are also expected to provide detailed knowledge of the interplay between the partitioning behavior of fluid mixtures and the interfacial properties in emulsions or microcapsules; this is important for the design and engineering of delivery systems, in particular for applications with a wide spectrum of oil hydrophobicities, such as pharmaceuticals, phytochemicals, and flavor or fragrance compounds.

Experimental section

Materials

β-Ionone ((3E)-4-(2,6,6-trimethylcyclohex-1-en-1-yl)but-3-en-2-one) and squalane (2,6,10,15,19,23-hexamethyltetracosane), both from Sigma-Aldrich, were used as received. Acacia gum (Efficacia) was obtained from CNI (Rouen, France) and was hydrated overnight in Millipore water under stirring, centrifuged for 10 minutes at 1000 rpm and passed through 5 μm pore size filters; the pH value was 4.5 and no salt was added. The mass concentration in the final solution was 10 ± 0.1% w/w (quantified by thermogravimetry); for interfacial rheology, additional solutions were prepared at 5% w/w for reference. For a discussion of the composition and the role of different fractions in this hybrid biopolymer we refer to an elaborate analytical study performed by Renard et al.³³ Octenyl succinic anhydride (OSA) starch (National Starch, Bridgewater, NJ) is dissolved in Millipore water and passed through 5 μm and 0.45 μm pore size syringe filters; the pH value is 4.4 and no salt is added. The surfaces in contact with the liquids are cleaned consecutively with Hellmanex III (VWR) detergent dissolved in hot water, followed by Millipore® water, isopropanol, ethanol and are then dried under nitrogen before and after every measurement.

Microscopy of emulsion drops

We image drops using a microchannel glass cell, depicted schematically in Fig. 1. The immobile oil phase (squalane) fills a reservoir at one end of the observation chamber. For a typical experiment, a volume of 100 μl of the mobile oil (β-ionone) is emulsified into 9.9 ml of the biopolymer solution by vortex-mixing a 10 ml glass flask; the resulting dilute, polydisperse emulsion is immediately filled into the narrow end of the microchannel and the cell is closed with a cover glass. The small dimensions of the microchannel (100 μm in height and 400 μm in width) minimize convective flow in the cell and facilitate observation of the evolving drops across the field of view. Due to the adsorbed amphiphilic layers the droplets do not coalesce either with each other or with the immobile oil reservoir (if coalescence does occur, it is easily identified by the sudden disappearance of the drops, accompanied by bulk motion of the fluids; in that case the experiment is completely discarded). Micrograph sequences are processed with the ImageJ software (National Institutes of Health, available free of charge at http://rsbweb.nih.gov/ij/) using its built-in size measurement functions; we characterize non-spherical drops using the Feret radius (defined as half the largest diameter measured on an irregularly shaped particle; for spherical drops, this is identical to the drop radius). The temperature is 23.0 ± 0.3 °C in all cases.

Interfacial shear rheology

For interfacial shear rheology we use a biconical disk (‘2D Couette’) fixture mounted on a Physica MCR300 rheometer (Anton Paar, Germany). The disk is positioned at the interface using the normal force transducer of the instrument; it rotates or oscillates with a controlled torque while the resulting deformation is measured. Torque values are transformed into interfacial shear stresses via the interfacial velocity calculated from the Stokes equation between two immiscible liquids.^29,63 Interfacial shear rheological parameters follow from the Boussinesq–Scriven law describing the interfacial stress boundary condition.^18,64 In oscillatory experiments, the shear strain γ(t) changes sinusoidally with time; in the linear viscoelastic regime, the response function is a sinusoidally changing interfacial shear stress, and the complex interfacial shear modulus G* = G′ + iG′′ is derived from these stress and strain waves (G′: interfacial shear elastic (storage) modulus and G′′: interfacial shear viscous (loss) modulus). The experiments performed here are time sweeps (measuring G*(t) at constant frequency ω and deformation amplitude γ₀), frequency sweeps (constant γ₀ and varying ω), and deformation sweeps (constant ω and varying γ₀); all interfacial shear rheology is performed in the linear viscoelastic regime. Stresses and deformations in interfacial shear rheometry are very small compared to bulk rheometry, therefore the electronically commutated motor needs to be precision-adjusted prior to every measurement. We calculate the interfacial shear deformations and moduli off-line from the deflection raw values of the instrument using suitable geometry factors.

To emulate the different degrees of compressional strain that shrinking oil drops undergo during ripening, we impose different compressional pre-strains onto the interfaces prior to the shear measurements. Three different measuring cells with different radii are used (R = 39.25, 47.5 and 70 mm), whereas the rotating disk is the same in all cases (R = 34.14 mm). This results in three different compressional pre-strains A/A₀ = 0.76, 0.51 and 0.25. After filling the cell with the aqueous polymer solution, the biconical disk is brought into contact with the liquid after a wait time of 540 seconds, after which the surface tension decreases by less than 10⁻⁴ N m⁻¹ per minute.¹² Upon detection of a normal force signal, indicating contact with the liquid, the vertical translation speed is reduced and the disk is slowly brought to its final position. Due to the cone shape on the fixture, this amounts to a slow compression of the liquid surface to an annular shape, with different final area and with different final compression ratios. The upper oil phase is immediately added after this compression via a Teflon tube mounted above the disk (this protocol in which a pre-formed air–water surface is compressed, followed by subsequent addition of the of the oil phase, is preferred here; in contrast, we found that driving the biconical disk through a pre-formed oil–water system results in an ill-defined oil–water–solid contact line). No wrinkles were observed on the flat interfaces studied using interfacial shear rheometry.

Interfacial compression rheology and tensiometry

Interfacial tensions and apparent compressional moduli are measured by pendant drop tensiometry (Drop Shape Analysis System DSA 10 Mk2, Krüss, Germany). A pendant or rising drop is suspended from a capillary into the continuous liquid phase to obtain a profile image of the drop contour. The Laplace–Young equation is fitted to this experimental profile by a numerical procedure.^39,43 Pendant drop images are used for tensiometry only if the drops are smooth and mechanical instabilities (wrinkles or folds) are absent. Drops with wrinkles are only used to assess the interface morphology or to extract wrinkle wavelengths by image analysis, but not for pendant drop tensiometry.⁵⁸ Wavelengths were measured by image analysis and corrected with a projection factor accounting for the rotational geometry of the drop. In addition to static interfacial tension measurements, we use the method to measure the interfacial compression modulus E(t). We used a custom-built syringe controller to impose small area changes on the drop and measured the interfacial tension response after a step compression. The transient compression modulus E(t) = Δπ(t)/(ΔA/A₀) follows from the surface pressure jump π = σ₀ − σ(t) with respect to the equilibrium value σ₀ after a small jump in surface area A/A₀ at time t = 0. Compression experiments are always performed on fresh drops that have been left to ‘equilibrate’ to a constant value of the interfacial tension σ₀. We use the transient compression modulus E(t) rather than frequency-dependent moduli E′ and E′′ (the two forms can be interchanged via a Fourier transform⁴²). Here, the advantage of measuring E(t) is that a step compression experiment takes a relatively short time to complete, providing data at time scales of 2–3 orders of magnitude yet avoiding the long waiting times needed for oscillatory experiments at several frequencies and thereby minimizing the influence of interface ageing. In this article we use the term ‘compressional elasticity’ since in all cases the interface decreases in area; the terms ‘dilatational’ or ‘dilational elasticity’ are used for the same property, especially when the experiments are performed in oscillatory mode. Interfacial pressure isotherms Δπ = f(A/A₀) are measured by slow, stepwise compression following equilibration to σ₀. We calculate the static compressional elasticity E_∞ = −A/(Δπ/A₀) from the slope of the isotherm.^16,17 In the absence of the adsorption layers, the interfacial tension of the neat liquids is constant in time, it does not change upon compression of the interface, and no interfacial rheological response is detectable.

Acknowledgements

We thank Nathalie Thiebaut for help with the tensiometry experiments.

Notes and references

1. J. Ugelstad, P. C. Mork, K. H. Kagerud, T. Ellingsen and A. Berge, Adv. Colloid Interface Sci., 1980, 13, 101–140.
2. B. P. Binks, J. H. Clint, P. D. I. Fletcher and S. Rippon, Langmuir, 1998, 14, 5402–5411.
3. B. P. Binks, J. H. Clint, P. D. I. Fletcher, S. Rippon, S. D. Lubetkin and P. J. Mulqueen, Langmuir, 1999, 15, 4495–4501.
4. A. A. Peña and C. A. Miller, Adv. Colloid Interface Sci., 2006, 123, 241–257.
5. A. Kabalnov, J. Dispersion Sci. Technol., 2001, 22, 1–12.
6. A. Kabalnov, Langmuir, 1994, 10, 680–684.
7. B. P. Binks, P. D. I. Fletcher, B. L. Holt, O. Kuc, P. Beaussoubre and K. Wong, Phys. Chem. Chem. Phys., 2010, 12, 2219–2226.
8. T. J. Wooster, M. Golding and P. Sanguansri, Langmuir, 2008, 24, 12758–12765.
9. S. Ariyaprakai and S. R. Dungan, J. Colloid Interface Sci., 2010, 343, 102–108; S. Ariyaprakai and S. R. Dungan, Langmuir, 2008, 24, 3061–3069.
10. S. S. Lim, M. Y. Baik, E. A. Decker, L. Henson, M. Popplewell, D. J. McClements and S. J. Choi, Food Chem., 2011, 128, 1023–1028.
11. A. J. Webster and M. E. Cates, Langmuir, 1998, 14, 2068–2079.
12. P. Erni, E. J. Windhab, R. Gunde, M. Graber, B. Pfister, A. Parker and P. Fischer, Biomacromolecules, 2007, 8, 3458–3466; P. Erni and A. Parker, Langmuir, 2012, 28, 7757–7767.
13. P. Erni, P. Fischer, V. Herle, M. Haug and E. J. Windhab, ChemPhysChem, 2008, 9, 1833–1837.
14. C.-T. Tan, in Food Flavors: Formation, Analysis and Packaging Influence, ed. E. T. Contiset al., Elsevier, Amsterdam, 1998, pp. 29–42.
15. L. M. C. Sagis, Rev. Mod. Phys., 2011, 83, 1367–1403.
16. D. A. Edwards, H. Brenner and D. T. Wasan, Interfacial Transport Processes and Rheology, Butterworth-Heinemann, Stoneham, MA, 1991.
17. R. Miller, N. Wüstneck, J. Krägel and G. Kretzschmar, Colloids Surf., A, 1996, 111, 75–118.
18. J. C. Slattery, L. Sagis and E.-S. Oh, Interfacial Transport Phenomena, Springer, New York, 2nd edn, 2007.
19. L. M. C. Sagis, Phys. A, 2010, 389, 673–684.
20. P. Erni, Soft Matter, 2011, 7, 7586–7600.
21. S. Vandebril, J. Vermant and P. Moldenaers, Soft Matter, 2010, 6, 3353–3362.
22. P. M. Vlahovska, Y. N. Young, G. Danker and C. Misbah, J. Fluid Mech., 2011, 678, 221–247.
23. J. D. Martin, J. N. Marhefka, K. B. Migler and S. D. Hudson, Adv. Mater., 2011, 23, 426–432.
24. J. T. Schwalbe, J. F. R. Phelan, P. M. Vlahovska and S. D. Hudson, Soft Matter, 2011, 7, 7797–7804.
25. M. B. J. Meinders, W. Kloek and T. van Vliet, Langmuir, 2001, 17, 3923–3929.
26. M. B. J. Meinders and T. van Vliet, Adv. Colloid Interface Sci., 2004, 108–109, 119–126.
27. S. Mun and D. J. McClements, Langmuir, 2006, 22, 1551–1554.
28. J. Kraegel and S. R. Derkatch, Curr. Opin. Colloid Interface Sci., 2010, 15, 246–255; S. Majumdar, R. Krishnaswamy and A. K. Sood, Soft Matter, 2011, 7, 7805–7812.
29. S.-G. Oh and J. C. Slattery, J. Colloid Interface Sci., 1978, 67, 516–525.
30. J. Benjamins, A. Cagna and E. H. Lucassen-Reynders, Colloids Surf., A, 1996, 114, 245–254.
31. J. Marrero and R. Gani, Fluid Phase Equilib., 2001, 183, 183–208.
32. R. C. Randall, G. O. Phillips and P. A. Williams, Food Hydrocolloids, 1988, 2, 131–140.
33. D. Renard, L. Lavenant-Gourgeon, M.-C. Ralet and C. Sanchez, Biomacromolecules, 2006, 7, 2637–2649.
34. S. R. Padala, P. A. Williams and G. O. Phillips, J. Agric. Food Chem., 2010, 57, 4964–4973.
35. E. Dickinson, D. J. Elverson and B. S. Murray, Food Hydrocolloids, 1989, 3, 101–114.
36. R. Bandyopadhyaya, E. Nativ-Roth, O. Regev and R. Yerushalmi-Rozen, Nano Lett., 2002, 2, 25–28.
37. L. Nilsson and B. Bergenståhl, J. Agric. Food Chem., 2007, 55, 1469–1474.
38. J. K. Ferri, P. Carl, N. Gorevski, T. P. Russell, Q. Wang, A. Boker and A. Fery, Soft Matter, 2008, 4, 2259–2266.
39. J. K. Ferri, C. Kotsmar and R. Miller, Adv. Colloid Interface Sci., 2010, 161, 145–153.
40. A. Yeung and L. Zhang, Langmuir, 2006, 22, 693–701.
41. D. Y. Zang, Y. J. Zhang and Q. W. Hou, Colloids Surf., A, 2012, 395, 262–266.
42. R. Miller, G. Loglio, U. Tesei and K. H. Schano, Adv. Colloid Interface Sci., 1991, 37, 73–96.
43. P. G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena, Springer, New York, 2004.
44. S. Mora, M. Abkarian, H. Tabuteau and Y. Pomeau, Soft Matter, 2011, 7, 10612–10619.
45. J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310–323.
46. E. Cerda and L. Mahadevan, Phys. Rev. Lett., 2003, 90, 074302.
47. A. Walter, H. Rehage and H. Leonhard, Colloids Surf., A, 2001, 183, 123–132.
48. E. Aumaitre, D. Vella and P. Cicuta, Soft Matter, 2011, 7, 2530–2537.
49. D. Vella, P. Aussillous and L. Mahadevan, Europhys. Lett., 2004, 68, 212–218.
50. J. Huang, M. Juszkiewicz, W. de Jeu, E. Cerda, T. Emrick, N. Menon and T. Russell, Science, 2007, 317, 650–653.
51. C. Sanchez, C. Schmitt, E. Kolodziejczyk, A. Lapp, C. Gaillard and D. Renard, Biophys. J., 2008, 94, 629–639.
52. J. B. Li, Y. Zhang and L. L. Yan, Angew. Chem., Int. Ed., 2001, 40, 891–894.
53. E. S. Basheva, P. A. Kralchevsky, N. C. Christov, K. D. Danov, S. D. Stoyanov, T. B. J. Blijdenstein, H.-J. Kim, E. G. Pelan and A. Lips, Langmuir, 2011, 27, 2382–2392.
54. R. Stanimirova, K. Marinova, S. Tcholakova, N. D. Denkov, S. Stoyanov and E. Pelan, Langmuir, 2011, 27, 12486.
55. S. S. Datta, H. C. Shum and D. A. Weitz, Langmuir, 2010, 26, 18612–18616.
56. R. Krishnaswamy, S. Majumdar, R. Ganapathy, V. V. Agarwal, A. K. Sood and C. N. R. Rao, Langmuir, 2007, 23, 3084–3087.
57. M. Abkarian, A. B. Subramaniam, S. H. Kim, R. J. Larsen, S. M. Yang and H. A. Stone, Phys. Rev. Lett., 2007, 99, 188301.
58. D. Carvajal, E. J. Laprade, K. J. Henderson and K. R. Shull, Soft Matter, 2011, 7, 10508–10519.
59. J. K. Ferri, W.-F. Dong, R. Miller and H. Möhwald, Macromolecules, 2006, 39, 1532–1537.
60. C. Monteux, C. E. Williams, J. Meunier, O. Anthony and V. Bergeron, Langmuir, 2004, 20, 57–63.
61. Z. Kang, A. Yeung, J. M. Foght and M. R. Gray, Colloids Surf., B, 2008, 62, 273–279.
62. A. B. Subramaniam, C. Mejean, M. Abkarian and H. A. Stone, Langmuir, 2006, 22, 5986–5990.
63. P. Erni, P. Fischer, E. J. Windhab, V. Kusnezov, H. Stettin and J. Läuger, Rev. Sci. Instrum., 2003, 74, 4916–4924.
64. L. E. Scriven, Chem. Eng. Sci., 1960, 12, 98–108.

---