 Open Access Article
Open Access ArticleX-Ray propagation imaging of a lipid bilayer in solution†
André
Beerlink
*ab,
Shashi
Thutupalli
c,
Michael
Mell
bd,
Matthias
Bartels
b,
Peter
Cloetens
e,
Stephan
Herminghaus
c and
Tim
Salditt
*b
aCurrent address: Deutsches Elektronen-Synchrotron, Notkestraße 85, 22605, Hamburg, Germany. E-mail: andre.beerlink@desy.de; Fax: +49(0)40 8994 1985; Tel: +49(0)40 8998 1985
bInstitut für Röntgenphysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077, Göttingen, Germany. E-mail: tsaldit@gwdg.de
cMax-Planck-Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077, Göttingen, Germany
dCurrent address: Mechanics of Biological Membranes and Biorheology, Departamento de Quimica Fisica I, Universidad Complutense, 28040 Madrid, Spain
eEuropean Synchrotron Radiation Facility, 6 Rue Jules Horowitz, 38043, Grenoble Cedex, France
First published on 13th March 2012
Abstract
We have used X-ray propagation imaging to visualize a less than 5 nm thick native lipid bilayer membrane freely suspended in aqueous solution. Contrast is formed by free space propagation of hard X-rays, with the membrane illuminated by a nano-focused, partially coherent synchrotron beam, at a controllable distance (defocus) behind the focal spot. Quantitative fitting of the magnified Fresnel fringes shows the transition from membranes swollen with solvent to the native bilayer, containing structural information at near-molecular resolution along the dimension perpendicular to the bilayer. We show first applications of this hybrid technique of propagation imaging and near-field diffraction to the investigation of ultra-thin organic films formed in micro-fluidic devices, namely the formation of a lipid bilayer by the adhesion of two constitutive monolayers.
1 Introduction
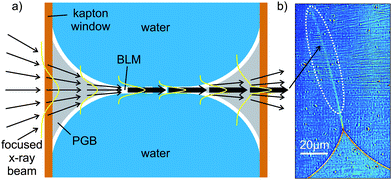
As the basic building blocks for biological membranes and many soft composite materials, lipid bilayers and liquid crystalline surfactant phases have for a long time been studied on molecular length scales by X-ray and neutron diffraction.1 As in many complex fluids and biomolecular assemblies, functionally relevant states and properties depend crucially on hydrated environmental conditions. X-ray and neutron probes are compatible with a multitude of sample environments, and yield the ensemble averaged structure at high resolution. However, in contrast to microscopy, local deviations from the mean and complex non-homogeneous samples with a hierarchy of length scales are generally not accessible by diffraction. Small-angle X-ray diffraction from membrane suspensions, for example, requires several microliters of relatively homogeneous samples. Contrarily, optical microscopy enables a direct visualization of membranes, however, not at the resolution needed to probe the molecular structure of the bilayer. Molecular details at the membrane surface and membrane proteins can be imaged by scanning force microscopy in solution, but three dimensional and buried structures are not accessible.2–4 Finally, electron microscopy offers the desired resolution, but is limited by high vacuum conditions and invasive sample preparation, including cryogenic or chemical fixation, staining, and/or sectioning. What has been missing so far is a probe that is capable of deducing quantitative structural information down to the molecular scale, while at the same time preserving local real space representation without the usual ensemble averaging. Also it needs to be compatible with a hydrated and functionally relevant sample environment. The developments in X-ray microscopy, both in the form of the earlier soft X-ray zone plate microscopy5–7 or the more recently developed lensless coherent X-ray diffractive imaging (CXDI) methods,8,9 have held the promise to fill the gap. Specific advantages such as (i) the potentially high resolution, (ii) the kinematic nature of the scattering process enabling quantitative image analysis, (iii) element specific contrast variation, and (iv) compatibility with unsliced (three-dimensionally extended), unstained and hydrated specimens have often been stressed. However, due to radiation damage, image quality, to date, has been satisfactory only for freeze dried or frozen hydrated samples, and moreover the lipid bilayer structure has almost eluded X-ray microscopy.Here we present a hybrid approach combining dose efficient free space X-ray propagation imaging and near-field diffraction to locally resolve thickness, density, and more generally the density profile of soft interfaces in particular membranes. The approach is compatible with full hydration without any indications of radiation damage. While certainly not applicable to all samples and isotropic three-dimensional structure analysis, our method can contribute significantly to the imaging of membrane based materials and to the structure analysis of soft matter interfaces at near-molecular resolution. Under hydrated conditions, it will close the gap between conventional scattering studies on the one hand, carried out over large ensembles, and conventional microscopy studies on the other hand, including X-ray microscopy, concerning resolution, interaction volume and complexity of the system studied. Such an investigative tool would be particularly appealing in micro fluidic sample environment as micro fluidics has emerged as a very powerful tool for the controlled investigation of complex biochemical and physical phenomena, particularly soft interfacial phenomena.10–13 The combination of the method with micro fluidics can therefore yield structural information on the interfaces during (hydro)dynamic processes, such as the formation of bilayers, thinning, or bulging, as well as membrane fusion,14 down to the length scale of a few nanometers.
We demonstrate the approach in two steps. First we image a single freely suspended lipid bilayer using a well known setup of membrane electrophysiology, the so-called black lipid membranes (BLM), an established model system in membrane biophysics.15,16 The bilayer spans two separated, aqueous compartments (differing in pH, ion concentrations etc.), allowing for studies of functional transport across the bilayer at controlled compositional and environmental parameters, such as protein concentration, ionic strength, pH, and electrical field. In previous studies we have adapted this system to in situ X-ray structural studies,17,18 and have shown that BLMs swollen with organic solvent can be imaged by means of hard X-ray Fresnel diffraction (propagation imaging), with phase contrast arising from free space propagation of a partially coherent, parallel X-ray beam traversing the sample.19,20 To quantitatively monitor the BLM thickness and its changes during the thinning process of BLMs, the intensity fringes in the Fresnel diffraction image were recorded and analyzed down to about 200 nm thickness, where contrast and resolution were lost. In the present work, we show that by replacing the previously used parallel beam illumination by a highly focused and partially coherent multi-keV X-ray beam, the Fresnel oscillations of native lipid bilayers with a thickness in the region of d = 5 nm can be detected and analyzed with respect to the local structure at molecular length scales, see Fig. 1. This phase contrast projection imaging scheme locally averages the structure in the plane of the membrane over a length scale of the order of 5–20 μm, which is, however, orders of magnitude lower than conventional diffraction methods. At the same time, the molecular structure along the bilayer normal can be detected at a resolution high enough to distinguish the native membrane thickness from solvent swollen bilayers. Importantly, local deviations and profiles become accessible and the setup is fully compatible with excess solution and complex environments, since the beam penetrates several millimeters of bulk water. The approach differs from a simple diffraction experiment since it gives a real-space visualization of the membrane contour, and is thus compatible with external control parameters such as exerted forces, out-of-equilibrium transport, local fields etc.
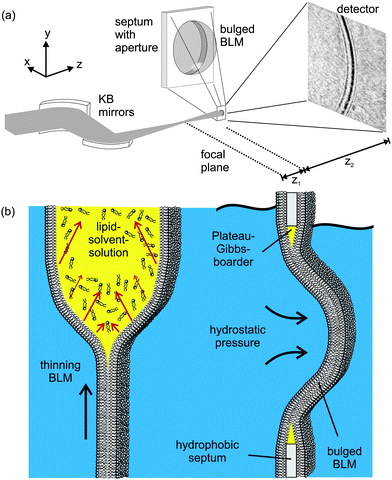 | ||
| Fig. 1 (a) Experimental setup: a highly focused X-ray beam coherently illuminates a spherically bulged black lipid membrane (BLM), spanning a micro-machined hole in the septum, located in the object plane at a controllable distance z1 downstream from the focal plane of the KB-mirror. The image is formed by free propagation of the wave field behind the sample over a distance z2 to the detector, where the intensity I(x) of the diffraction profile is recorded. (b) Schematic of the formation and bulging process of a BLM. Organic solvent, used to dissolve the lipid molecules, diffuses towards the outer rim of the aperture in the hydrophobic septum supporting the membrane. The BLM starts to thin until the two monolayers at the oil–water interfaces approach to finally form a bilayer lipid membrane. Application of hydrostatic pressure to one side of the BLM leads to the bulging of the interface. | ||
Moreover, dynamic processes such as membrane fusion can be followed with simultaneous high resolution structure analysis by least squares fitting of the oscillations. Importantly, the approach also differs from previous forms of X-ray imaging, since the high resolution information is not limited by the pixel size of the real-space imaging, but is extracted from intensity oscillations similar to other forms of diffraction. Thus, the hybrid approach combines the respective strengths and benefits of real and reciprocal space visualizations. It works best for samples which are sparse in the sense that electron density variations are limited to isolated parts of the field of view, such as in the present case to the interface regions.
Based on the first imaging results obtained from completely thinned membranes with native bilayer thickness, we then present a second step of application more geared towards studies of dynamic processes. We replace the macroscopic sample chamber by a micro-fluidic device designed to observe the formation of a reconstituted lipid bilayer by fusion of two monolayers, denoted here as micro-fluidic BLM (mfBLM).10–12 Briefly, the bilayers are prepared in a crossed channel micro-fluidic device, where two monolayers of surfactant molecules, assembled at the interface of an oil and water reservoir, are brought into contact to form a bilayer membrane. We take advantage of a fully automated preparation process, enabling bilayer formation via remote computer controlled motorized pumps. This system is particularly well suited for the in situ observation with synchrotron radiation, as no access to the experimental setup is required. Importantly, the throughput of this system is extremely high, with regard to the supply of new material (lipids, solvent, and buffer), change of parameters (pressure, concentration) or simply the formation of a new bilayer after rupture. Both systems, BLMs and mfBLMs can be electrically excited by the implementation of electrodes into the aqueous channels.
2 Experimental setup and data treatment
The experimental scheme is shown in Fig. 1. Black lipid membranes (BLMs) of 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhyPC) (Avanti Polar Lipids; Alabaster, USA) were prepared using the painting method of Müller and Rudin,16 using n-decane (Sigma-Aldrich; Germany) (20 mg mL−1) as a solvent, see ref. 17 and Fig. 1(b). micro-fluidic bilayer membranes have been prepared from oily solutions consisting of either DPhyPC in n-decane (see BLM formation) or Monoolein (Avanti Polar Lipids; Alabaster, USA) in Squalene (Merck; Germany), both at a concentration of 10 mg mL−1. Deionized and distilled water (MilliQ, Millipore; Germany) or buffer solutions with 150 mM NaCl, 5 mM Hepes, and pH = 7.0 are used as the aqueous phase during the preparation. Both techniques are described in further detail in the ESI†. The experiment at the ID22NI undulator station of the European Synchrotron Radiation Facility (ESRF, Grenoble, France), as skeched in Fig. 1(a), was carried out operating the beamline in the so-called pink mode (no crystal monochromators) at a photon energy of E = 17.5 keV. This corresponds to a wavelength of 0.708 Å, using the intrinsic monochromaticity of the undulators and the bandpass of the adaptive multilayer Kirkpatrick–Baez (KB) mirror system. The KB focal spot size was Dhoriz = 130 nm (FWHM) in the horizontal and Dvert = 140 nm (FWHM) in the vertical direction, respectively, as measured by knife edge and fluorescence scans performed on nano-structured test patterns. A drilled mirror allowed for the simultaneous detection of light microscope and X-ray images and thus a faster alignment of the sample in the beam. The position z1 of the sample was varied in a range of defocusing distances z1 = 3 mm ≤ z1 ≤ 200 mm, with respect to the KB mirror focus, see Fig. 1(a). Images were recorded after free space propagation over a distance z2 by using the Fast-REadout, LOw-Noise FRELON 2000 CCD camera, placed z1 + z2 = 526 mm behind the KB focus. It is equipped with a 24 μm thick LSO:Tb (terbium doped lutetium-oxyorthosilicate, Lu2SiO5) scintillator, which is optimized for high resolution imaging21 and has, in combination with the optical imaging setup, a pixel size of 0.96 μm. The minimum illumination time and thus time resolution of detectable processes was 200 ms, solely limited by the camera read-out time in full resolution mode and not the photon flux of the X-ray beam. The image recording procedure is analogous to the previously reported parallel beam imaging experiments.18 After flat (empty beam) and dark field correction of the raw images, the measured I(x,z) is then considered as the squared output of the 1D Fresnel operator acting on the one-dimensional optical transmission function, which for a pure phase object can be written as T(x) = eiφ(x). T(x) reflects the structure of the membrane patch along its local normal axis in a plane directly behind the sample, see Fig. 2(a). Note that for simplicity and robustness with respect to noise, we chose the one-dimensional description for the intensity profile I(x,z) along the direction perpendicular to the interface. The signal is averaged for a beam path through the sample of the order of 10 μm along the optical axis, depending on the bilayer thickness d and radius R. Further averaging of intensity profiles in the plane orthogonal to the optical axis, i.e. along the contour of the membrane, can be used in a controlled way to increase the signal level. The associated contour range could be adjusted from one to several hundred pixels in the detector.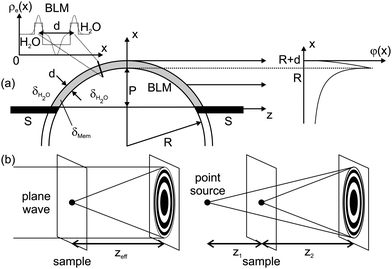 | ||
| Fig. 2 (a) The bulged BLM can be modelled in the simplest approach by an constant electron density ρe(x) across the hydrophobic membrane thickness d. In line with experimental observation, the BLM is sketched as a spherically bulged slab with radius R. The phase shift φ(x) is calculated from the refractive index difference (contrast) Δδ between the BLM δMem, and the surrounding water δH2O. It is subsequently projected along the z-axis onto the exit plane behind the membrane. (b) According to the Fresnel scaling theorem, the diffraction image recorded with a point-source is equivalent to a magnified image of the wave field recorded with parallel beam illumination at an effective focal distance zeff = z1z2/(z1 + z2). | ||
3 Theoretical model for propagation imaging
For simplicity, we first consider the simplest membrane structure with constant electron density, see Fig. 2(a), which is well suited for black lipid membranes swollen with organic solvent before the thinning transition takes place, see Fig. 1(b). The phase profile behind the object (exit wave) is then simply φ(x) ≃ −kΔδL(x), where Δδ is the refractive index difference with respect to the surrounding water, L the propagation length in the sample, and k the wave number, see Fig. 2(a) and in detail Fig. S4 in the ESI†. Subsequent Fresnel propagation is carried out by using the paraxial approximation of the (1D) Fresnel–Kirchhoff equation, for the given propagation distance z: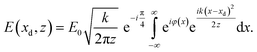 | (1) |
The prefactor indicates that for a given (fixed) phase profile φ(x) the contrast actually decreases on increasing the wavelength λ! By controlling the membrane curvature, one can always adjust the phase shift by the tangential beam path through the membrane to a sizable value. The disregard of absorption for weakly scattering objects of the given size is well justified for the chosen photon energy in the hard X-ray regime. The resulting intensity I(x,z) = |E(x,z)|2 of the phase contrast image was computed by numerical integration of φ(x) carried out in terms of a sum of Fresnel sine and cosine functions. To obtain the complete field E(x) = Ec(x) + El(x) + Er(x), the fields El(x) and Er(x) due to the source points in the left and right half-planes have to be added. For these regions the phase shifts are φl = φr = 0, since only the electron density difference with respect to the surrounding water is considered here. The simplest model of constant electron density, used to analyze the profiles of black lipid membranes by least squares fitting, is characterized by the following parameters: membrane thickness d, refractive index contrast Δδ, and the local radius of curvature R, as well as the propagation distance z and wave number k, while the fit accuracy is indicated by χ2. d was varied freely in the fit, while Δδ was in most cases fixed to the theoretical values of water and lipid/oil, for the given wave number k. The propagation distance z was measured, but a refinement of the measured values within a reasonable range was allowed during the fit. Finally, the calculated intensity was convoluted with a Gaussian function including a convolution parameter σ according to the Gaussian Shell model (GSM),22,23 taking into account the finite lateral coherence length of the partially coherent synchrotron beam. For the experimental parameters of high magnification the point spread function of the detector does not influence the extracted profiles. Note that the magnified Fresnel images are highly oversampled due to the use of a high resolution detector. A series of simulations showing the influence of the relevant fitting parameters are presented as Fig. S7 and S8 in the ESI†.
Simple estimates show that detector pixel size and the typical housing and sample chamber sizes impede the detection of phase contrast signals on a molecular scale. However, changing from a plane wave (parallel beam) to a point-beam illumination with spherical wavefronts (cone beam), impinging on the sample at distance z1 from the focus (quasi point source), and propagating a distance z2 ≫ z1 towards the detector, this short range imaging regime can be achieved. The relation between phase contrast increase and effective propagation distance decrease is described in more detail in the ESI†. By a simple variable transformation in the Fresnel–Kirchhoff diffraction integral, the point-beam case can be mapped onto an equivalent parallel-beam geometry,24 see Fig. 2(b), with a demagnified detector pixel size of ΔD/M, a demagnification factor of M = (z1 + z2)/z1, and an effective sample-detector distance zeff = z1z2/(z1 + z2) = z2/M. Note that compared to the parallel beam imaging, much smaller effective detector pixel sizes can be achieved, as well as smaller defocus values, along with much higher photon flux densities.
4 Results on bulged black lipid membranes
Fig. 3(a,b) shows a representative image recorded at relatively large effective defocus distances of zeff = 50.14 mm with correspondingly moderate magnification M = 9.37 as well as a large field of view (FOV = 164 μm). The values of d, σ and χ2 are given in the legend. The extracted values from profile 1 show an increase in the resolution below the minimum membrane thickness of 200 nm detectable in the previously reported parallel imaging geometry,18 which now reaches down to values below 100 nm. In this case, membrane motion may dominate the profile broadening and yield larger σ values than predicted by the GSM. The information contained in the oscillation amplitudes and oscillation phase with respect to the envelope encode the thickness and refractive index of the membrane, see ESI†.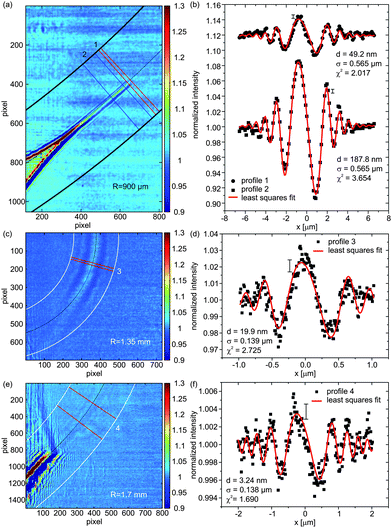 | ||
| Fig. 3 Corrected X-ray phase contrast images showing the bulged BLMs and their ‘anchoring’ at the so-called Plateau–Gibbs border. Intensity profiles on the right are extracted from the regions of interest (ROIs) on the left. The values for the local membrane thickness d are shown in the legend, as determined from the least squares fit. Errors of I(x) are approximately constant along the profile and are indicated by a single representative error bar. (a) Image recorded at an effective propagation distance of zeff = 50.14 mm along with (b) the respective intensity profiles being shifted for clarity. (c) Image of a nearly thinned BLM with clearly resolved contrast at an effective propagation distance zeff = 3.20 mm, and (d) corresponding analysis of the Fresnel fringes yielding a thickness of d = 19.9 nm, far below the resolution limit obtainable by plane wave illumination. (e) Image of a completely thinned section of a membrane visualized by X-ray phase contrast imaging recorded at parameters zeff = 6.75 mm, R = 1.7 mm, M = 76.93 and an illumination time of 0.5 s, with the analysis (f) yielding a thickness of d = 3.24 nm. | ||
Errors of the membrane thicknesses, which are achieved from the least squares fitting procedure with a refraction index fixed to the expected value, are 24% (profile 1) and 7% (profile 2). However, as expected, moderate magnification M does not allow for the detection of thinned native bilayers, and contrast is lost as the membrane thins by driving out solvent. Time series of solvent dynamics and the effect of applied electric fields on solvent suction were also recorded, and are presented as movies in the ESI†.
In the next step, we decreased zeff in order to increase the magnification M, the contrast, and the resolution, according to the expected scaling behavior (eqn (10) in ESI†). By reducing zeff to 3.20 mm a BLM (profile 3), see Fig. 3(c,d), of d ≃ 20 nm (±30%) can now be clearly resolved in the form of a strongly oversampled broad central oscillation accompanied by three to four side oscillations. This nearly thinned BLM is easily detectable, even without lateral averaging. In addition, we were able to record and analyze the signal of several completely thinned membrane sections at, however, very small contrast levels related to the small thickness of d = 3.24 nm. A representative example (profile 4) is depicted in Fig. 3(e,f), recorded at zeff = 6.75 mm and in Fig. S9 in the ESI†. Note that optimization of zeff is not an easy task since the coherence increases with zeff for the non-ideal partially coherent focusing scheme available in this experiment. This fact outlines the strategy for future improvements. The details of the fitting model, the resolution perpendicular to the membrane and the perspective of resolving intra-bilayer structure are further discussed in the ESI†. Aside from defocus distance, coherence and wave front aberrations, important future optimization parameters are the photon energy and radius of curvature R. Larger R and lower photon energy lead to stronger induced phase shifts based on longer propagation of the beam in the bilayer and, respectively, an enhanced interaction with the sample material. However, already for the present experiment, after image correction and integrating over neighboring cross-sections, the signal of a thinned bilayer is picked up above noise with an analyzable lineshape with contrast amplitudes of the order of 0.2–0.4% above the flat field level. Note that the high photon flux of the instrument provides a sufficiently low shot noise of the images, and the contrast limit is dictated primarily by the stability.
5 Results on bilayer formation in a micro-fluidic device
Fig. 4(a) shows a representative diffraction pattern of a mfBLM. The film is still swollen with solvent, leading to the excellent visibility of Fresnel fringes. Extracted profile 5 is depicted in (b), along with a least squares fit to the data. In contrast to the bulged membranes, the intensity profile of the mfBLM is much more symmetric as expected for a plane interface with vanishing curvature. However, residual pressure gradients Δp across the membrane induced by the two pumps will always lead to small motion of the membrane inside the channel. Only when the pumps are stopped, will the membrane stay at a fixed position. In this case, given Δp = 0, the membrane should favor a planar orientation to minimize its surface tension. Since it is composed of symmetric monolayers, we can model the intensity profile in the simplest approach by a symmetric phase slit.18 From the corresponding fit, a thickness of d = 383.5 nm is obtained, showing that the monolayers are still separated by oil and have not fused yet. The fit result of φ = 0.593 reflects the stoichiometric composition (index of refraction) of the oil phase, and the path length of the X-rays through the membrane. From a priori known refractive index difference and the fitted phase shift we obtain the path length, i.e. the diameter of the membrane patch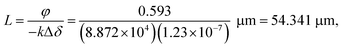 | (2) |
 | ||
| Fig. 4 (a) Diffraction pattern of a micro-fluidic BLM (mfBLM) prepared from a Monoolein–squalene solution/water at an effective propagation distance of 29.67 mm. The Fresnel fringes are detected up to high orders (deflection angles). Glue residues at the surface of the self-adhesive kapton window material produce parasitic features in the image. (b) Profile 5 extracted from the ROI in (a). Due to planar sample geometry it can be fitted using a symmetric phase slit model, which is characterized by two parameters, phase shift φ and the thickness d. | ||
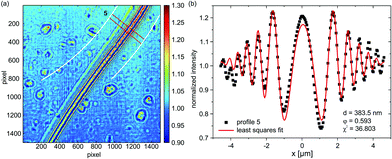
Fig. 5(a) shows the transition region between the Plateau–Gibbs border (PGB) and the bimolecular region of an mfBLM, which is formed through a “zipper-like” process. The Fresnel fringes close to the PGB are more strongly pronounced than in the thinner regions. Profile 6 in Fig. 5(b) is extracted from a position in Fig. 5(a), where a domain of residual organic solvent migrates towards the PGB. Fig. 5(c) shows profile 7, which is extracted from the ROI in the transition region. Here the fringe amplitudes have decreased, reflecting the thinning process. The fit results are d = 625.2 nm for profile 6 and φ = 0.268, corresponding to a path length L = 24.6 μm. In the central section, close to the region where monolayer fusion has already taken place, the Fresnel intensity pattern is dominated by a strong central maximum, see profile 7 depicted in Fig. 5(c).
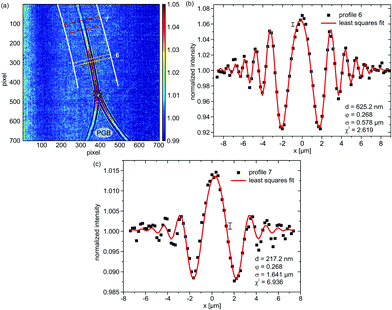 | ||
| Fig. 5 (a) Diffraction pattern of the transition region during the “zipper-like” effect of a micro-fluidic BLM (mfBLM) close to the Plateau–Gibbs border (PGB) (Monoolein–squalene/water, zeff = 94.21 mm). The Fresnel fringes disappear in regions where the membrane has already thinned and only a single maximum is left. (b) Profile 6, along with a reasonable least squares fit, showing a large thickness at the position of a thick domain of residual solvent. (c) Profile 7, which is located close to the bimolecular membrane region, cannot be fitted comparably accurately due to a notable contribution of the PGB to the diffraction pattern. | ||
The higher order oscillations are strongly damped. To capture this strong decay, the fit algorithm increases the FWHM of the convolution term (Lorentzian taking into account partial coherence and detector resolution) up to σ = 1.614 μm, compared to only σ = 0.578 μm in profile 6. This is unrealistic, since the imaging conditions were kept constant. In proportion to the increased broadening and damping effect, the oscillation amplitude in the model strongly decreases, which can only be compensated by an increase in the thickness. A value of d = 217.2 nm is unexpectedly high for a profile at a position so close to the bilayer part of the film. However, when profile 7 is fitted with σ fixed to the value of profile 6, a more reasonable thickness of 78.4 nm is obtained. Except for the central maximum, the higher order fringes are fitted more accurately with this constraint. The schematic representation in Fig. 6(a) gives a possible explanation for problems associated with the simple “phase-slit model”, which can not capture the lineshape in the center of the Fresnel diffraction pattern. This problem persists for the intensity profiles recorded after membrane thinning (see Fig. 6(b)). We attribute it to additional phase shifts by penetration of the Plateau–Gibbs border, which has to be crossed by the beam near the channel walls. The impinging X-rays can be reflected/refracted at the PGB–water interface, leading to a concentration of intensity in the central region, i.e. a “focusing” effect. The resulting far-field projection image at the detector can be considered as a superposition of the diffraction pattern of the fused bilayer and the central intensity peak and therefore does not conform to the present model. Note that this effect should be fully quantifiable by using an extended model in combination with a tomographic tilt series, in order to disentangle the two contributions.
 | ||
| Fig. 6 (a) Schematic representation of the “focusing” effect of the Plateau–Gibbs border. This results in an intensity maximum in (b) at the position of the thinned membrane. | ||
Finally, we show an exemplary image series of the “zipper-like” process, which occurs during the transformation from a bulk film to a bimolecular membrane, as shown in Fig. 7. It can be nicely visualized due to the interfacial geometry of the micro-fluidic setup. Two monolayers of monoolein molecules, which assemble at the squalene–water interface, get in contact and strong Fresnel fringes appear in the diffraction pattern (1). Driven first by adhesive and subsequently by van der Waals forces the domains of solvent in the gap between the two monolayers are expelled to the Plateau–Gibbs border (2–6). Finally, a thin bilayer membrane forms (7). Based on free energy arguments, one can show that the bifacial tension of the BLM γBLM is smaller than twice the interfacial tension of the monolayers γML (7). Consequently a force occurs, which results in BLM expansion (8) and sets the BLM under tension. Accordingly, the free energy difference ΔF between two monolayers and the thinning film increases with the contact angle. Starting from the swollen state, when the two monolayers meet at small contact angle, almost tangentially, the contact angle increases to approximately θ = 52° for the bimolecular membrane (9), where ΔF reaches an extremum. Using the standard pendant drop method, we have obtained γML = 1.77 ± 0.11 mN m−1. Our result for the membrane free energy is thus  mN m−1. The formation of the membrane is therefore accompanied by a gain in free energy of ΔF = 2γML − γBLM = 0.31 ± 0.02 mN m−1.
mN m−1. The formation of the membrane is therefore accompanied by a gain in free energy of ΔF = 2γML − γBLM = 0.31 ± 0.02 mN m−1.
 | ||
| Fig. 7 Image series of the “zipper-like” effect, which occurs during the transformation from a bulk film (1) to a bimolecular membrane (7). The migration of solvent (2–6) and the change in contact angle between the lipid monolayers and the BLM (4,9) is shown. See text for details. | ||
6 Conclusions
In summary, we have shown that a native thinned lipid membrane of less than 5 nm thickness can be imaged by hard X-ray propagation imaging in cone beam geometry, and that the profile can be analyzed quantitatively in terms of the membrane thickness. More complex models and data allow revelation of the vertical density profiles ρe(z) for a given point of the contour. While the detection limit for the local membrane thickness of the order of d ≃ 200 nm was previously encountered in a parallel beam setup,18 we have now achieved near-molecular resolution by means of magnification in a highly focused partially coherent synchrotron beam. With current progress in X-ray focusing optics breaking the 10 nm limit (in one dimension) by adaptive mirrors25 and/or a sub-15 nm beam (in two dimensions),26 achieved by waveguide optics, future improvements can be anticipated and are needed to extract structural details of more complex soft matter systems than the model bilayers studied here, along with an increased resolution. Notably, a (1D) resolution to below 1 nm can be expected, by further decrease of z1, possible using highly coherent focusing optics based on coherently illuminated KB mirrors, compound refractive lenses or X-ray waveguides. On the side of the analysis, using a box model for local quantitative analysis of the membrane interface structure, an extension to more general and complex profiles ρe(z) of soft matter interfaces and macromolecular assemblies can be carried out in a straightforward manner.Near-molecular resolution was achieved only in one dimension, after a local average over a region in the plane of the membrane with cross sections of the order of 10 μm. However, in many important applications of colloids and macromolecular assemblies the local architecture includes quasi planar configurations or rod like structures, both of which do not require isotropic nanoscale resolution along all three dimensions. Contrarily, full 3D X-ray microscopy at 5 nm resolution using far-field coherent diffraction or zone-plate X-ray microscopes, if at all achievable, necessitates cryogenic fixation, for reasons of radiation damage.27 A particular advantage of the present approach is the relatively low dose needed to visualize the membrane, compatible with room temperature and full hydration. In the present experiment, the sample was positioned in defocus as this reduces flux density, but data acquisition times down to 100 ms were already sufficient to detect membrane contours. At the same time, membranes suspended in solution were stable for several hours in the synchrotron beam before rupturing. In the future, problems like membrane fusion, membrane phase transitions, local membrane topology and thickness variations, e.g. resulting from external fields and ion concentration gradients across the bilayer, or phenomena associated with transport of molecules through the bilayers become thus accessible. More generally, local nanoscale structures in many hydrated and soft matter interfaces including more complex topologies can be investigated by this approach.
We acknowledge financial support by Deutsche Forschungsgemeinschaft through SFB755 Nanoscale Photonic Imaging. It is also a pleasure to thank Remi Tucoulou for his support at the ID22NI.
References
- J. Daillant, Curr. Opin. Colloid Interface Sci., 2009, 14, 396 CrossRef CAS.
- A. Janshoff and C. Steinem, ChemBioChem, 2011, 2, 798–808 CrossRef.
- M. Dong, S. Husale and O. Sahin, Nat. Nanotechnol., 2009, 4, 514–517 CrossRef CAS.
- I. Medalsy, U. Hensen and D. J. Muller, Angew. Chem., 2011, 123, 12309–12314 CrossRef.
- X-Ray microscopy, ed. G. Schmahl and D. Rudolph, Springer, Heidelberg, Germany, 1984 Search PubMed.
- J. Kirz, C. Jacobsen and M. Howells, Q. Rev. Biophys., 1995, 28, 33–130 CrossRef CAS.
- W. Meyer-Ilse, T. Warwick and D. Attwood, Proceedings of the Sixth International Conference, 2000 Search PubMed.
- H. Chapman and K. Nugent, Nat. Photonics, 2010, 4, 833–839 CrossRef CAS.
- X. Huang, J. Nelson, J. Kirz, E. Lima, S. Marchesini, H. Miao, A. Neiman, D. Shapiro, J. Steinbrener, A. Stewart, J. Turner and C. Jacobsen, Phys. Rev. Lett., 2009, 103, 198101 CrossRef.
- K. Funakoshi, H. Suzuki and S. Takeuchi, Anal. Chem., 2006, 78, 8169 CrossRef CAS.
- M. Holden, D. Needham and H. Bayley, J. Am. Chem. Soc., 2007, 129, 8650 CrossRef CAS.
- S. Ota, W.-H. Tan, H. Suzuki and S. Takeuchi, memo - Magazine of European Medical Oncology, 2008, 1, 18 CrossRef CAS.
- S. Thutupalli, S. Herminghaus and R. Seemann, Soft Matter, 2011, 7, 1312–1320 RSC.
- G. v. d. Bogaart, S. Thutupalli, J. Risselada, K. Meyenberg, M. Holt, D. Riedel, U. Diederichsen, S. Herminghaus, H. Grubmüller and R. Jahn, Nat. Struct. Mol. Biol., 2011, 18, 805–812 Search PubMed.
- H. Tien and A. Ottova-Leitmannova, Membrane Biophysics, Elsevier Science B.V., 2000 Search PubMed.
- P. Müller, D. Rudin, H. Tien and W. Wescott, Nature, 1962, 194, 979–980 CrossRef.
- A. Beerlink, P.-J. Wilbrandt, E. Ziegler, D. Carbone, T. Metzger and T. Salditt, Langmuir, 2008, 24, 4952 CrossRef CAS.
- A. Beerlink, M. Mell, M. Tolkiehn and T. Salditt, Appl. Phys. Lett., 2009, 95, 203703 CrossRef.
- D. Paganin, Coherent X-Ray Optics, Oxford University Press, 2006 Search PubMed.
- K. Nugent, Adv. Phys., 2010, 59, 1 CrossRef.
- P. Douissard, A. Cecilia, T. Martin, V. Chevalier, M. Couchaud, T. Baumbach, K. Dupre, M. Kühbacher and A. Rack, J. Synchrotron Radiat., 2010, 17, 571–583 CrossRef CAS.
- I. Vartanyants and A. Singer, New J. Phys., 2010, 12, 035004 CrossRef.
- T. Salditt, S. Kalbfleisch, M. Osterhoff, S. Krüger, M. Bartels, K. Giewekemeyer, H. Neubauer and M. Sprung, Opt. Express, 2011, 19, 9656–9675 CrossRef CAS.
- S. Mayo, P. Miller, A. Wilkins, T. Davis, D. Gao, T. Gureyev, D. Paganin, D. Parry, A. Pogany and A. Stevenson, J. Microsc., 2002, 207, 79 CrossRef CAS.
- H. Mimura, S. Handa, T. Kimura, H. Yumoto, D. Yamakawa, H. Yokoyama, S. Matsuyama, K. Inagaki, K. Yamamura, Y. Sano, K. Tamasaku, Y. Nishino, M. Yabashi, T. Ishikawa and K. Yamauchi, Nat. Phys., 2010, 6, 122–125 CrossRef CAS.
- S. Krüger, K. Giewekemeyer, S. Kalbfleisch, M. Bartels, H. Neubauer and T. Salditt, Opt. Express, 2010, 18, 13492–13501 CrossRef.
- M. Howells, T. Beetz, H. Chapman, C. Cui, J. Holton, C. Jacobsen, J. Kirz, E. Lima, S. Marchesini, H. Miao, D. Sayre, D. Shapiro, J. Spence and D. Starodub, J. Electron Spectrosc. Relat. Phenom., 2009, 170, 4–12 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information about membrane preparation, theoretical description of phase propagation, fitting model and process, coherence aspects, an additional result, and two movies showing membrane dynamics. See DOI: 10.1039/c2sm00032f |
| This journal is © The Royal Society of Chemistry 2012 |
