Chemical control of octahedral tilting and off-axis A cation displacement allows ferroelectric switching in a bismuth-based perovskite

Abstract

Bi(Fe_2/8Mg_3/8Ti_3/8)O₃ (BFTM) is a member of a small class of pure Bi³⁺ A site perovskites which are stable without recourse to high pressure synthesis. BFTM is polar in the R3c space group, but ferroelectric switching of the polarisation is not attainable in bulk ceramics. Formation of solid solutions with BaTiO₃ produces enhanced functional behaviour. The composition 0.75Bi(Fe_2/8Mg_3/8Ti_3/8)O₃–0.25BaTiO₃ displays ferroelectric hysteresis loops and piezoelectric response (high field d₃₃ of 85 pC N⁻¹ at 0.1 Hz and low field d₃₃ of 16 pC N⁻¹). This change in functional behaviour is associated with significant changes in the average structure, where the rhombohedral distortion is reduced and transformed to a pseudo-cubic R3m space group, as substitution of the larger Ba²⁺ cation suppresses tilting of the BO₆ octahedra. Polar Bi displacements are refined solely along the pseudocubic <111>_p direction of the perovskite subcell, with the off-axis displacements characteristic of BFTM being suppressed. The local structure deviates from the average structure in a similar way to PZT as shown by diffuse scattering in selected area electron diffraction, suggesting correlated <111>_p displacements along directions other than the average rhombohedral unique axis. The switchable polarisation measured by PUND measurements is considerably smaller than the remanence measured in P(E) loops.

---

Introduction

Lead based perovskite-structured piezoelectric ceramics, in particular Pb(Zr_xTi_1−x)O₃ (PZT) have been studied extensively due to their high performance in a wide range of electronic devices such as actuators, sensors, and transducers.¹ Piezoelectric materials generate an electric field in response to applied stress or change dimensions under an applied field. The required polar structures are generated by the 6s² lone pair of the lead cation, with displacements along the [001]_p and [111]_p directions of the parent cubic perovskite unit cell producing tetragonal (T) and rhombohedral (R) ferroelectric structures respectively. Combinations of these displacements produce a monoclinic structure which has also been assigned to coexisting nanodomains of the R and T structures.² There are two possible R structures in space groups R3m and R3c depending on whether antiphase octahedral tilting about [111]_p is present, affording R3c. In PZT, the piezoelectric properties quantified by the piezoelectric coefficient, d₃₃ (ranging from 200–600 pC N⁻¹ in commercial PZT)³ and strain (0.3%)⁴ are optimal at the morphotropic phase boundary (MPB) where the ferroelectric rhombohedral and tetragonal phases of a solid solution meet. Piezoelectrics containing lead are highly effective primarily because the 6s² lone pair can easily become stereoactive resulting in a large structural distortion and strong coupling between the electronic and structural degrees of freedom.⁵ The large piezoelectric response of PZT is assigned to polarization rotation at the MPB or in the monoclinic phase and to a high contribution (up to 70%) from the domain wall motion to the piezoelectric properties.^3,6

There is current interest in evaluating lead-free materials as alternatives to PZT for regulatory reasons, although the demands in coming up with a readily processable material to approach PZT performance metrics are considerable. A-site bismuth perovskites could be a viable alternative, as Bi³⁺ ions will also have lone-pair distortions similar in magnitude to their lead-based counterparts. Although replacing lead with bismuth may seem straightforward, it adds a layer of complexity as few A-site bismuth perovskites are stable under ambient pressure (due to the small size of the Bi³⁺ ion, which can cause instability in the AO₁₂ polyhedra) with BiFeO₃, Bi₂(Mn_4/3Ni_2/3)O₆, and Bi(Fe_2/8Mg_3/8Ti_3/8)O₃ as the only examples.^7–9

Bi(Fe_2/8Ti_3/8Mg_3/8)O₃ (BFTM) crystallizes in the rhombohedral R3c space group which arises from A-site and B-site displacements along [111]_p in relation to the Pm3̄m parent perovskite structure. In this space group, the BO₆ polyhedra belong to the tilt system a⁻a⁻a⁻, which means that the tilt angles are of equal magnitude and each octahedron rotates with an anti-phase tilt in relation to its neighbouring octahedra. The hysteresis loop of BFTM is not saturated and the remanent polarization is only ∼0.5 μC cm⁻², because the polarisation is not switchable at fields below dielectric breakdown.⁹ However, literature suggests that it is possible to achieve improved hysteresis loops and piezoelectric response through either doping and/or forming solid solutions.^10–12 The purpose of this study is to synthesize solid solutions between Bi(Fe_2/8Mg_3/8Ti_3/8)O₃ and BaTiO₃. BaTiO₃ is a classical ferroelectric material, which crystallizes in the P4mm tetragonal space group, due to the polar Ti displacement from the centroid of the oxide octahedron.

Experimental

Starting materials of BaCO₃ (Alfa Aesar, 99.997%), Bi₂O₃ (Alfa Aesar, 99.9995%), Fe₂O₃ (Alfa Aesar, 99.998), MgO (Alfa Aesar 99.998%), and TiO₂ (Alfa Aesar, 99.995%) were mixed in stoichiometric amounts under acetone with an agate mortar and pestle then calcined at 600 °C for 12 h. The resulting powders were pressed into pellets and placed in an alumina crucible lined with Pt foil on the bottom to prevent reaction with the alumina while heating. The pellets were then fired at different temperatures with grinding and repelletizing in the intermediate stages. The synthetic procedure is based on the synthesis of BFTM: 750 °C 12 h, 800 °C 12 h/800 °C 3 h, 850 °C 12 h/850 °C 3 h, 900 °C 12 h.⁹ Ball milling the starting materials produced an Aurivillius type phase as an impurity. Phase pure powder used for physical measurements was ball milled overnight in an ethanol slurry with a binder of 2 wt% polyvinyl butyral resin. The ball milling was done in a planetary mill with eight 10 mm yttria-stabilized zirconia balls, for 45 cycles with each cycle consisting of 15 min forward, 15 min rest, then 15 min reverse milling direction at a rate of 350 rpm. Pellets were pressed in a 10 mm die then vacuum sealed in a latex bag and pressed at 2000 bar using an isostatic cold press and sintered at 950 °C 1 h; 875 °C for 15 h to achieve a density greater than 95% as measured by an Archimedes balance. The pellets were then polished down to <0.5mm thickness (for ferroelectric and piezoelectric measurements) and polished to a mirror finish on a polishing wheel with a series of P800, P1200, then P2400 grit grinding paper (Buehler, Germany).

Powder X-ray diffraction data were collected using a Panalytical X'Pert Pro diffractometer with Co Kα₁ radiation (λ = 1.78901 Å). Data were collected over a 2θ range from 20°–130°. Synchrotron powder X-ray diffraction data were collected at ESRF on the ID31 beamline with λ = 0.39986 Å at room temperature and 10 K. Data were collected over a 2θ range from 2–44° at room temperature in a quartz capillary. Neutron data were collected at the ISIS spallation neutron source at the Rutherford Appleton Laboratory on the HRPD beam line. Data collected on the backscattering banks were used in the refinement. Low temperature neutron data was also collected at the ISIS spallation neutron source on the GEM beam line at a temperature of 10 K. Refinements were performed using the software GSAS/EXPGUI^13,14 and Topas Academic.¹⁵ Electron diffraction data were collected with a JEOL 2000FX electron microscope at room temperature. Samples were prepared by crushing the powder in ethanol and the crystallites in suspension were deposited onto a holey carbon film.

To prepare the pellets for impedance measurements, Pt paste electrodes were applied and fired at 800 °C for 0.5 h. Pt wires were used to make electrical contact. Impedance measurements were performed using a Solartron 1255B Frequency Response Analyzer and a Solatron 1296 dielectric interface. Measurements were taken over the frequency range of 1 Hz to 1 MHz over a temperature range from 25 °C to 900 °C on heating and cooling.

Ferroelectric characterization was performed with a Radiant Ferroelectric Tester Precision LC with a Radiant Precision high voltage interface and a Trek 609B high voltage amplifier. Measurements were performed at room temperature on thin pellets with gold sputtered electrodes at a frequency of 1 Hz and P(E) loops were collected at successively higher voltages until eventually dielectric breakdown occurred. Positive-up negative-down (PUND) measurements were also performed with the same instrument. A series of 5 voltage pulses were applied with a delay time of 1000 ms and a pulse width of 1000 ms. The net switched polarization is calculated by subtracting the non-switched polarization (P^{^}) from the total polarization of the switching pulse (P^*).¹⁶ High-field converse piezoelectric measurements were performed using a Fotonic sensor MTI-2100 combined with a commercial Radiant Ferroelectric Tester Precision LC, in line with a Trek 5/80 high voltage amplifier, and Radiant high voltage interface. In order to measure the piezoelectric coefficient d₃₃, poling was performed on pellets sputtered with Au electrodes on the parallel plane faces. The pellet was poled in silicon oil at 200 °C. The voltage was increased slowly to up to 110 kV cm⁻¹ and left for 20 min. Then the sample was slowly cooled to room temperature with the applied electric field before removing from the silicon oil, taking approximately three hours. d₃₃ was determined with a conventional Berlincourt meter (Piezotest PM300, London, UK). The measurements were carried out by applying an alternating force of 0.25 N and a frequency of 110 Hz.

Results

Structural characterization

BFTM-BT materials were synthesised at 10, 25, 50 and 75% BT content. The substitution of 10% BT into BFTM to afford Bi_0.9Ba_0.1(Fe_0.22Ti_0.44Mg_0.34)O₃ (0.9BFTM–0.1BT) changes the diffraction pattern significantly, with weakening of the R3c tilting peak (absent in the XRD data). At this composition, two rhombohedral phases are apparent in the neutron diffraction pattern together with a weakened ½(111)_p reflection characteristic of the R3c phase. Le Bail analysis shows that this material consists of two phases: R3c and R3m. The weakening of the tilt signature compared with the BFTM parent is shown in Fig. 1(a) and (b).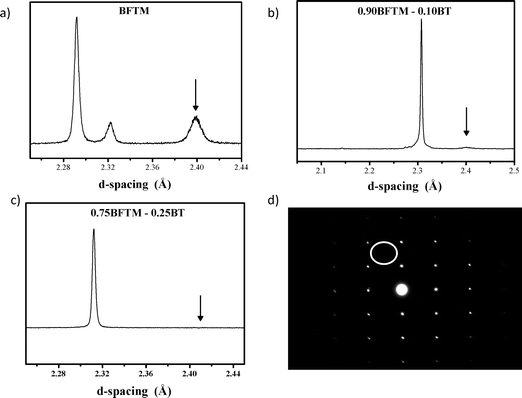

Fig. 1 Neutron diffraction from a) BFTM, b) 0.9BFTM-0.1BT and c) 0.75BFTM-0.25BT and d) SAED of 0.75BFTM–0.25BT showing the evolution from the R3c to R3m space group. The arrows in the neutron patterns indicate the presence/absence of a tilting peak. The SAED of 0.75BFTM–0.25BT can be indexed solely as a cubic perovskite. The white circle in the SAED pattern shows where the superstructure spot would be expected if tilting were present in the structure.

Bi_0.75Ba_0.25(Fe_0.188Mg_0.281Ti_0.531)O₃ (0.75BFTM-0.25BT) does not have the R3c space group of the parent BFTM as shown by the absence of the R3c ½(111)_p tilting peak in the neutron data and the lack of the tilt reflection in the [110] zone axis in the selected area electron diffraction (SAED) pattern, Fig. 1(c–d). The rhombohedral distortion is also strongly suppressed and the diffraction pattern appears cubic. Room temperature X-ray and neutron diffraction data were fitted to several different models by Rietveld refinement. The models used were Pm3̄m, the “distorted” Pm3̄m model applied to PMN,^17,18 and R3m. Upon inspection of the data, the space group Pm3̄m was chosen for the initial refinement as there was no characteristic peak splitting to indicate a lowering of symmetry. The fits of the combined X-ray and neutron data gave an R_wp value of 7.01 (χ² = 5.56) but showed a large mismatch of the model intensities of several of the peaks, which indicated that the space group was incorrect as shown in Figure S1 (Supporting Information†). The distorted Pm3̄m model, which gave an R_wp of 6.61 (χ² = 4.19) was based on an ideal cubic perovskite where the atoms are displaced from their special positions along the common disordered directions of [100], [110], and [111] as shown in Figure S2†. The R3m refinements were run with the standard atomic positions with A and B-site displacements along the <111>_p direction, but different models were also examined where 1) the A-site was changed from the (x,x,x) special position to the (x,y,z) general position corresponding to displacement away from the [111]_p direction, 2) the three B-site cations were refined with each on a separate position or 3) the magnesium and iron were refined to the same position with the titanium being allowed to refine separately. All of the models except the standard R3m space group resulted in very unreasonable thermal parameters or diverged upon refining. The best refinement came from the R3m space group with an R_wp = 6.19 (χ² = 3.67). Great care was taken in the refinements to keep all instrument parameters (background and profile) the same so that any difference in the goodness of fit was based on a difference in the model only. Therefore, R3m was chosen as the space group for the average structure and the combined X-ray/neutron Rietveld refinement is shown in Fig. 2a and 2b. The lattice parameters show the unit cell is nearly cubic with a = 4.00361(1) Å, α = 90.0025(3)°. The refined parameters and bond lengths are given in Table 1 and Table 2.

Fig. 2 Rietveld refinement of combined a) synchrotron XRD and b) neutron diffraction patterns for 0.75BFTM–0.25BT. The circles represent the observed data while the solid line represents the model and the difference curve is below.

Table 1 Atomic parameters for 0.75BFTM–0.25BT from Rietveld refinement at 300 K. Space group: R3m, lattice parameters: a = 4.00361(1) Å, α = 90.0025(3)°

Atom	x	y	z	B eq/Å^2	Occ
Bi/Ba	−0.0476(3)	−0.0476(3)	−0.0476(3)	7.30(6)	0.75/0.25
Fe/Mg/Ti	0.4713(6)	0.4713(6)	0.4713(6)	1.22(5)	0.19/0.28/0.53
O	0.4853(3)	0.4853(3)	0.0138(4)	3.85(1)	1

---

Table 2 Bond lengths and angles of 0.75BFTM–0.25BT at 300 K

Atoms	Bond length/Å
Bi/Ba–O	3 × 26480(4)
	6 × 2.84050(5)
	3 × 3.02056(6)
Fe/Mg/Ti–O	3 × 1.943866(4)
	3 × 2.062996(4)

---

Atoms	Angle/°
O–Fe/Mg/Ti–O	89.858(2) × 2, 93.249(2) × 2, 175.4738(8) × 2
O–Bi/Ba–O	55.779(2) × 3, 57.6677(8) × 6, 59.65929(2) × 3, 59.9043(2) × 3, 61.986(1) × 6, 64.766(2) × 3, 86.1161(3) × 6, 93.6193(3) × 6, 113.429(1) × 6, 119.3482(7) × 6, 119.626(2) × 6, 126.7215(9) × 6, 170.6873(5) × 3, 174.4914(9) × 3

---

Diffraction (10 K) and DSC (RT to 100 K—Fig. S4†) was performed at low temperatures, but no structural phase transition occurred. Combined neutron/XRD refinements were performed and the R3m model gave the best fit with an R_wp of 3.213% (χ² = 2.12) (Fig. S3 in the Supporting Information†). The refined displacement parameters (B_eq(A-site) = 6.64(4) Ų, B_eq(B-site) = 0.84(2) Ų, and B_eq(O) = 2.36(4) Ų) are similar to those at room temperature suggesting static displacements at low temperature.

SAED of 0.75BFTM–0.25BT shows that the material has a perovskite unit cell with nearly cubic lattice parameters which is consistent with the overall structure proposed by the Rietveld refinements. Along with the Bragg diffraction, diffuse streaks in SAED patterns along minor axes are observed, as shown in Fig. 3 which consists of four patterns along the [321], [139], [431] and [3̄71] zone axes as examples. Diffuse scattering is typically very weak, and these patterns can only be observed in the higher order zone axes or when tilted slightly off-axis away from the lower zone axes. This is due to a number of factors which are described in detail elsewhere¹⁹ but one of the main reasons is that when looking down a low order axis with strong Bragg reflections, any disorder is averaged out over the depth of the atomic columns, resulting in zero net modulation.

Fig. 3 Diffuse streaks present in SAED patterns of the a) [321], b) [139], c) [431] and d) [371] zone axes of 0.75BFTM–0.25BT. The intense diffuse streaks are marked by the arrows with indexes showing their directions in reciprocal space. The indexing is according to the cubic ideal perovskite.

In the case of the [321] pattern (Fig.3a), diffuse streaks are observed along [3̄25]* and [14̄5]* which are perpendicular to [11̄1] and [1̄11], respectively. And for the [139], [431] and[3̄71] patterns (Fig. 3b–d), the diffuse streaks are along [3̄2̄1]* and [6̄51̄]*, [4̄37]* and [2̄57]*, [415]*, and [3̄2̄5]* which are perpendicular to [11̄1] and [111̄], [11̄1] and [1̄11], [111̄] and [111] respectively. These transverse polarized diffuse streaks running through the Bragg reflections build up continuous {111}* sheets in reciprocal space. The transverse polarized nature of the diffuse streaks occurs when the displacement eigenvector of the most heavily displaced atoms is perpendicular to the modulation wave vector itself and requires that the atomic displacements are perpendicular to the sheets, which means the displacements producing the diffuse scattering occur along the <111>_p directions.²⁰

Dielectric characterization

Room temperature impedance measurement of both relative permittivity and loss show frequency dispersion (Fig. 4). The permittivity increases with increasing BT content from 144 for BFTM to 265 for 0.9BFTM–0.1BT, and 345 for 0.75BFTM–0.25BT at 1 kHz at room temperature. The loss however, does not follow this trend, with values at 1 kHz of 0.040 for BFTM, 0.076 for 0.9BFTM–0.1BTO and 0.049 for 0.75BFTM–0.25BT.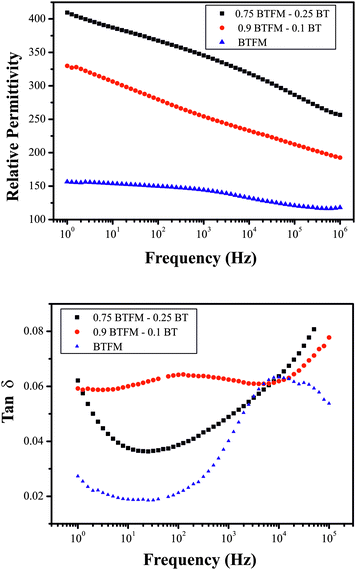

Fig. 4 a) Dielectric constant and b) loss tangent as a function of frequency at room temperature for BFTM and 10% and 25% BT substituted materials.

The temperature dependence of the permittivity from 0.75BFTM–0.25BT shows a broad peak at around 400 °C, and a second sharper peak at about 600 °C (Fig. 5). The broad lower temperature peak shifts to higher temperatures as the frequency is increased while the second sharper peak does not shift significantly with increasing frequency if the data taken on heating is considered. However, the second higher temperature peak is suppressed (i.e. the magnitude of the permittivity maximum is decreased) as the frequency is increased. The higher temperature peak shows hysteresis on heating/cooling which does not occur at lower temperature.

Fig. 5 Relative permittivity of 0.75BFTM–0.25BT as a function of temperature.

Ferroelectric hysteresis

Ferroelectric P–E hysteresis loop measurements were performed for both 0.9BFTM–0.1BT and 0.75BFTM–0.25BT as shown in Fig. 6a and b. P(E) loops for both compositions show a change in slope as the applied voltage is increased, suggesting non-linearity and therefore genuine domain wall motion.²¹ However, the shape of the loop for 0.9BFTM–0.1BT is not near saturation, possibly due to the inability to apply sufficient electric fields and therefore the loop shows sub-switching field behaviour.²² In contrast to the loop of 0.9BFTM–0.1BT, it is evident from the shape that the loop for 0.75BFTM–0.25BT is nearly saturated at a field of 90 kV cm⁻¹. The real switched polarization (ΔP) values are obtained using PUND measurements²³ by subtracting the non-switched polarization (P^{^}) from the total polarization of the switching pulse (P^*) and dividing by 2 and is shown in Fig. 6c. The pulse width used was 1000 ms and the delay time between the pulses was 1000 ms. The switched ΔP obtained from PUND is small (2.4 μC cm⁻² compared to the total maximum polarization of 20 μC cm⁻²).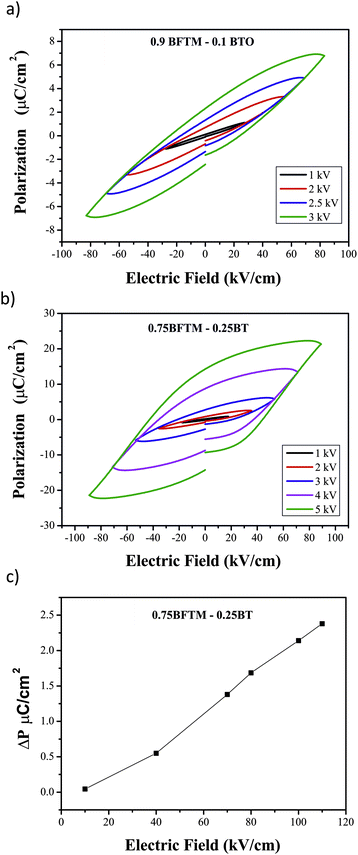

Fig. 6 P(E) hysteresis for a) 0.9BFTM–0.1BT and b) 0.75BFTM–0.25BT. c) PUND data for 0.75BFTM–0.25BT showing the true switched polarization.

Piezoelectric properties

Strain–electric field measurements for 0.75BFTM–0.25BT show a characteristic butterfly strain loop (Fig. 7a) which is evidence for ferroelectric switching and bulk piezoelectricity. Fig. 7b shows the strain response under unipolar drive at both 1 Hz and 0.1 Hz. The measured displacement is larger at 0.1 Hz, which suggests that application of electric field of lower frequency enables more efficient switching of domains in the material. This type of frequency dependence is observed for BiFeO₃,²⁴ PZT,²⁵ PMN-PT,²⁶ and PZN-PT²⁷ and explained by switching of predominantly non-180° domains. The high field piezoelectric coefficient d₃₃ calculated from the unipolar strain data is approximately 53 pC N⁻¹ at 1 Hz and 85 pC N⁻¹ at 0.1 Hz. The piezoelectric coefficient, d₃₃ measured was 16 pC N⁻¹ with the sample poled at 110 kV cm⁻¹ for 20 min at 200 °C. The d₃₃ of BFTM was also measured and was found to be 0.6 pC N⁻¹.

Fig. 7 a) Butterfly loop from strain-electric field measurements of 0.75BFTM–0.25BT and b) strain response of 0.75BFTM–0.25BT under unipolar drive.

Discussion

The introduction of the Ba²⁺ cation into BFTM produces significant structural and functional changes. The octahedral tilting is suppressed, producing a change in space group from R3c to a pseudocubic structure best described on average as R3m (Fig. 8), but with strong indications from diffuse scattering of a more intricate local structure. In a perovskite, BO₆ octahedra are prone to tilting when there is a need to optimise the anion coordination because the A-cation is too small for the 12 coordinate site of the AO₁₂ polyhedra as is the case in BFTM (tolerance factor = 0.948). In the solid solution of 0.75BFTM-0.25BT (tolerance factor = 0.98), a percentage of the bismuth ions which have a 12 CN ionic radius of 1.34 Ų⁸ are replaced by barium ions which have a larger ionic radius of 1.61 Ų⁹ increasing the V_A/V_B ratio of the polyhedra which decreases the average tilt angle to zero, resulting in a transition of the space group from R3c to R3m.³⁰ The A-site is occupied by bismuth and barium with average A–O bond lengths of 3 × 2.64799(4) Å, 6 × 2.84050(5) Å, 3 × 3.02056(6) Å which give a highly under-bonded bismuth atom (bond valence = 2.2) and a highly over-bonded barium atom (bond valence sum 2.7). The octahedral B site is occupied by iron, titanium, and magnesium in a disordered manner with bond lengths of 3 × 1.94386(4) Å and 3 × 2.06299(4) Å. The bond lengths result in bond valence sums of 3.1 for iron, 2.6 for Mg which is over-bonded and 3.7 for Ti which is under-bonded. Both the A and B cations are displaced along the <111>_p direction, with average structure displacements from the centroids of their anion polyhedra of 0.23 Å (A cation) and 0.10 Å (B cation). The B-site displacement is smaller than in BFTM (0.24 Å) but similar to that in the R3m phase of PZT (0.11 Å). The A-cation displacement is much smaller than that found in BFTM (0.66 Å) and just over half that of R3m PZT (0.40 Å).³¹ This difference in the A-site displacement between BFTM-BT and both BFTM and PZT is assigned to occupation of 25% of the sites in BFTM-BT by barium, which is not prone to the lone pair distortion seen in bismuth and lead. This is also apparent when comparing mean A–O bond lengths of 2.9(4) Å in BFTM and 2.84(2) Å in 0.75BFTM-0.25BT, where the spread in distances is greatly reduced in the Ba-doped system. The distribution of B–O bond lengths (BFTM 2.08(8) Å vs. 2.00(6) Å in 0.75BFTM-0.25BT) is almost unchanged, reflecting the decreased A-site distortion in the average structure. The nature of the A site displacements from the anion centroids differs from the parent BFTM, where there are disordered static local Bi displacements away from the threefold axis along the <110>_p direction, which are not observed in the average structure of 0.75BFTM–0.25BT. The absence of octahedral tilting and the introduction of the Ba²⁺ cation which prefers higher symmetry environments may be linked to the suppression of these off-axis displacements. The pseudocubic nature of the diffraction pattern and the ambiguity of the refined displacement directions (i.e. the similar figures of merit established for refined A site displacements along [001]_p and [111]_p) suggest similarities from the average structure analysis to PMN and other pseudo-cubic relaxor materials where well defined long-range order of polar displacements does not occur.^18,32

Fig. 8 a) BFTM in the R3c space group with octahedral tilting, b) 0.75BFTM-0.25BT in R3m, which is untilted c) BFTM viewed down the [001] axis to show the tilting scheme. d) 0.75BFTM-0.25BT viewed down the [111] direction, showing the loss of the octahedral tilt. e) A-site polyhedra of BFTM, multiple bismuth atoms are visible because of the multiplicity of the off-axis displacement f) A-site polyhedra in 0.75BFTM–0.25BT, g) B site octahedra of BFTM and h) B site octahedra of 0.75BFTM–0.25BT. The centroid of each polyhedra is represented as the white sphere. In e and f, bonds are colored according to short (green), medium (black) and long (blue) bond lengths.

The presence of static or dynamic disorder is normally signalled in average structure analyses by the atomic displacement parameters. The displacement parameters of the B-site cations can be considered normal with a B_eq value of 1.22(5) Ų (U = 0.015 Ų). However, the oxygen and A-site thermal parameters are abnormally large and temperature-independent, suggesting a significant static disorder component which is superimposed on the average structure. The large displacement parameters of the A-site and the oxygen combined with the severe over/under bonding of the A-site cations are indicative of considerable local strain, which is consistent with the diffuse scattering in the electron diffraction patterns.

Despite the reduced displacements in 0.75BFTM-0.25BT compared to BFTM, the solid solution has enhanced ferroelectric properties. This can be associated with the change in structure due to the suppression of the octahedral tilt which is caused by the addition of barium atoms on the A-site. In the lead-based PZT system, diffraction contrast imaging by Randall and Eitel³³ shows that the antiphase boundaries (APB) associated with the octahedral tilt coincide with non-180° ferroelectric domain walls, consistent with the conclusion from the frequency dependence of the strain–field measurements that this is the switching path. These APB regions have a strain mismatch between each tilt variant which pin the domain wall motion and suppress the extrinsic response in the R3c phase, but are not present in the R3m phase due to the absence of tilting. The introduction of barium on the A site has the same effect on the average structure of BFTM, providing an explanation for the enhanced ease of polarisation switching here.

On a local scale, the pattern of diffuse scattering in 0.75BFTM–0.25BT is similar to that of the well-known piezoelectric materials Pb(Zr,Ti)O₃ (PZT) and Pb,La(Zr,Ti)O₃ (PLZT).^19,34,35 The transverse polarized diffuse streaks indicate the cation displacements run perpendicular to the diffuse sheets along the [111]_p axes. This means the A-site and B-site displacements are strongly correlated along a one dimensional chain in different <111>_p directions with little to no correlation between each chain. The correlation length is estimated approximately as 5–10 unit cells calculated from the width, in reciprocal space, of the diffuse streaking—instrumental factors which are not easily measurable contribute to the width of the streaking. While this result seems to be in conflict with the average structure, which shows a displacement in only one <111>_p direction, a study of the diffuse scattering of PZT by Welberry et al. used Monte Carlo techniques to show how this disordered model can include the local diffuse scattering while at the same time satisfying the Bragg conditions of the average structure.³⁵ They developed models with more than 50% of the cations being displaced along a single <111>_p direction with the remaining cation displacements distributed between each of the other seven <111>_p directions. It was shown that these models will produce a diffraction pattern where the Bragg peaks fit an average structure that assumes no disorder while at the same time giving rise to the diffuse scattering patterns that were observed with electron diffraction. It is important to note that diffuse scattering can still be observed despite the fact that there will be a random distribution of 25% barium atoms on the A-site and 28% magnesium on the B-site, neither of which are prone to distortion. This does not affect the presence of diffuse scattering, but could potentially affect the correlation length.

The combined average structure and diffuse scattering information show that the present material is distinct from both ferroelectric PZT and relaxor PMN. The diffuse scattering in PMN condenses into rods, corresponding to correlated sheets of displacement, around the <110> type Bragg peaks rather than sheets in reciprocal space,^36,37 whereas the average structure in PZT permits decisive identification of the displacement directions. In BFTM–BT the mean A cation displacement along the rhombohedral [111]_p direction of 0.24 Å is less than the static incoherent displacement of 0.30 Å deduced from the temperature invariance of the displacement parameters. The component of this three-dimensionally incoherent displacement along the non-rhombohedral [111]_p directions (i.e. those body diagonal directions of the original cubic cell not selected for the three dimensionally correlated distortion) is correlated along each direction but not between them as shown by the pattern of diffuse scattering. The Pm3̄m refinements show that other displacement directions are likely to be present but the diffuse scattering patterns indicate that these displacements are not correlated. These structural differences from the canonical relaxor and ferroelectric materials should impact the functional behaviour.

The ferroelectric properties of 0.75BFTM–0.25BT change quite profoundly from the parent material BFTM. The impedance data from BFTM shows a sharp single peak at 730 °C indicating a ferroelectric (FE) to paraelectric (PE) transition from R3c to the ideal cubic perovskite with the space group Pm3̄m. The addition of BT (T_c = 120 °C) lowers the transition temperature as expected, but in the case of BFTM–BT, there are two distinct peaks that can be seen in the variable temperature impedance data. The frequency dispersive nature of the low temperature anomaly suggests that it can be attributed to the freezing of polar nanoregions. On the other hand, the position of the high temperature anomaly is invariant and more experiments will be needed to clarify its origin, but it is indicative of a polar transition to a polar nanoregion (PNR) state. This is a common effect and can be seen in NBT–BT,³⁸ NBT–KBT,³⁹ and BFO–BT.⁴⁰ The high temperature peak is attributed to the phase transition while the low temperature peak is described as a relaxation associated with a reorientation of the polarization of the polar nanoregions due to the thermal fluctuations and both peaks are part of the same phenomenon.³⁸

The room temperature permittivity as a function of frequency shows that 0.75BFTM–0.25BT has a much higher permittivity than both BFTM and 0.9BFTM–0.1BT across the whole frequency range. As the BT content increases, the coercive field and Curie temperature decreases and ferroelectric hysteresis loops evolve as is discussed in the following paragraph. Therefore, it is expected that the relative permittivity i.e. electrical polarizability increases with increasing BT content. The relative permittivity shows a strong frequency dependence increasing with a decrease in frequency. Dielectric loss of the samples decreases with increasing frequency in the low frequency regime (with the exception of the 0.9BFTM–0.1BT composition, where a broad relaxation peak dominates the low frequency behaviour), while an increase is obvious at high frequencies. The increase at low frequencies can be assigned to hopping conduction,⁴¹ while that at the highest frequencies may be due to inductive contribution from the wires.⁴² For BFTM, a broad loss peak at high frequencies is evident, suggesting the presence of a relaxation phenomenon. A similar peak in loss is also observed for 0.9BFTM–0.1BT at low frequencies, while in 0.75BFTM–0.25BT this feature cannot be seen. Corresponding to the peaks in the dielectric loss, the slope of the dielectric constant curves changes with frequency. Cole–Cole plots (Figure S5†) reveal clearly one semicircle for BFTM, showing that dielectric relaxation occurs; the tails at high and low frequency ends correspond to the increase in dielectric loss at the lowest and highest frequencies. For both 0.9BFTM–0.1BT and 0.75BFTM–0.25BT compositions, a semicircle can also be assigned, while the shape is not well-defined due to the contribution from high and low frequency tails. The magnitude of dielectric constant rules out the possibility of contribution from extrinsic charge carriers of interfacial charges at grain boundaries or electrodes.⁴³ Thus, we conclude that the dipoles that take part in the dielectric relaxation process, which are responsible for frequency dispersion of dielectric constant and loss, are intrinsic. The loss values at 1 kHz do not seem to follow a trend with values of 0.040, 0.076, and 0.049 for BFTM, 0.9BFTM–0.1BT, and 0.75BFTM–0.25BT respectively. The loss of other well known ferroelectrics is: BaTiO₃ (0.014),⁴⁴ PZT (0.015),⁴⁵ and 0.67BFO–0.33PZT (0.18).⁴⁶ The loss of BiFeO₃ has been reported at 0.03 in non-quenched samples which do not have saturated P(E) loops and 0.1 in quenched samples with saturated P(E) loops.⁴⁷

The ferroelectric properties evolve significantly upon addition of BT to BFTM. The P(E) loop for BFTM clearly does not reach saturation even at applied electric fields of approximately 140 kV cm⁻¹. This is likely due to the high T_c of BFTM and a large coercive field. Although the P_r value for 0.9BFTM–0.1BT (2.3 μC cm⁻²) is higher than BFTM (0.5 μC cm⁻²), the P(E) curve of 0.9BFTM–0.1BT is comparable to the parent compound as both show non-saturated loops at sub-switching fields. 0.75BFTM–0.25BT shows the best ferroelectric properties of the three materials. 0.75BFTM–0.25BT, which has a smaller T_c than BTFM has a P(E) loop which indicates switching behaviour and becomes nearly saturated at an applied field of 90 kV cm⁻¹. The loops of this material show a large remanent polarization despite a coercive field of 44 kV cm⁻¹ at the frequency of the measurement. PUND measurements were essential to characterise the switchable component of this polarisation, which is of the order of 10% of the total. The difference between the remanent and saturation polarisations in P(E) (which contain field-driven contributions such as conductivity, capacitance and non-permanent polarisation) and the true permanent switchable polarisation in PUND indicates that although the switchability is improved over BFTM there are mechanisms which dissipate the polarisation in 0.75BFTM-0.25BT. One of the main contributions to the discrepancy between the observed remanence and switchable polarization could be from PNRs which reorient during the P–E cycle, adding to the hysteresis and observed remanent polarization, but thermally relax between the pulses of the PUND measurement. The regions producing the polarisation response also generate the observed piezoelectric behaviour.

In regards to the piezoelectric properties, the maximum strain value obtained is 0.068%, which is lower than that of PZT (0.3%)⁴ and BiFeO₃ (0.17%)²⁴ but is of a similar magnitude to NBT-BT solid solution (0.06%).⁴⁸ The measured d₃₃ value of 16 pC N⁻¹ for 0.75BFTM–0.25BT is a significant improvement from the d₃₃ of BFTM which was found to be 0.6pC N⁻¹. The d₃₃ of 0.75BFTM-0.25BT is one-third of the high field value obtained from the unipolar strain field measured at 1Hz. This is not uncommon as piezoelectric coefficients obtained from induced strain measurements can be significantly higher than those obtained from direct measurements due to the possibility of better poling under larger fields that cannot be reached before breakdown or the domain walls may be more prone to displacement under large unipolar electric fields.⁴⁹ The dielectric and ferroelectric results show that the sample has a high T_c and large E_c, which also causes the difficulties in poling the sample completely. A similar phenomenon was also found in other lead-free piezoelectrics, such as (Bi_0.5Na_0.5)TiO₃ (E_c = 73kV cm⁻¹),^50,51 and Bi_0.5K_0.5TiO₃ (E_c = 52.5 kV cm⁻¹).⁵² Two materials that can easily be poled are BaTiO₃ which has an E_c of 26 kV cm⁻¹⁵³ and PZT which has an E_c of 7kV cm⁻¹.⁵⁴ The d₃₃ of common piezoelectric materials are BiFeO₃: 16 pC N⁻¹,^55,56 BaTiO₃: 190 pC N⁻¹,⁵⁷ and PZT 53/47: 220 pC N⁻¹.^58,59 The functional properties of the Pb-based systems vary sharply with composition e.g. the PbTiO₃ end member of PZT is not switchable, suggesting that further property improvement will require more detailed compositional variation.

Conclusions

The introduction of BaTiO₃ into BFTM increases the tolerance factor, suppresses the octahedral tilting and induces a phase transition from the polar space group R3c to a pseudocubic structure (at 25% BT doping) best described by polar space group R3m. Although the displacements in 0.75BFTM–0.25BT are smaller, the absence of the octahedral tilt allows for easier ferroelectric switching, which enhances the ferroelectric and piezoelectric properties over those of BFTM. The switchable polarisation is only 10% of the total observed in P(E) measurements. The combination of average and local structure shown by the Bragg diffraction and diffuse scattering shows that the nature of the A-site displacements in BFTM-BT differs from the classical ferroelectric and relaxor materials. Displacements are correlated three-dimensionally along a privileged [111]_p axis which confers a small metric rhombohedral distortion but the displacements along the other 7 initial cubic [111]_p directions are one-dimensionally correlated, producing a pseudo-cubic average structure with different extents of [111]_p displacement correlation combined with displacements along other directions. This combination of long-range and local distortions affects the average structure by making the component of the total Bi/Ba displacement which is not three-dimensionally correlated along the unique rhombohedral axis larger than the coherent displacement along the rhombohedral direction. This structural change is coupled with the observed enhancement of the functional behaviour.

Acknowledgements

This work is funded by the European Research Council (ERC Grant agreement 227987 RLUCIM), the Knowledge Centre for Materials Chemistry and the EPSRC (EP/H000925).

References

1. Y. Saito, H. Takai, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamur, Nature, 2004, 432, 84.
2. R. Guo, L. Cross, S. Park, B. Noheda, D. E. Cox and G. Shirane, Phys. Rev. Lett., 2000, 84, 5423.
3. D. Damjanovic, N. Klein, J. Li and V. Prorkhonskyy, Funct. Mater. Lett., 2010, 3, 5.
4. J. Rodel, W. Jo, K. T. P. Seifert, E.-M. Anton, T. Granzow and D. Damjanovic, J. Am. Ceram. Soc., 2009, 92, 1153.
5. P. K. Panda, J. Mater. Sci., 2009, 44, 5049.
6. D. Damjanovic, Appl. Phys. Lett., 2010, 97, 062906.
7. V. S. Filip'ev, N. P. Smolyaninov, E. G. Fesenko and I. N. Belyaev, Kristallografiya, 1960, 5, 958.
8. H. Hughes, M. Allix, C. A. Bridges, J. B. Claridge, X. Kuang, H. Niu, S. Taylor, W. Song and M. J. Rosseinsky, J. Am. Chem. Soc., 2005, 127, 13790.
9. C. A. Bridges, M. Allix, M. R. Suchomel, X. Kuang, I. Sterianou, D. C. Sinclair and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2007, 46, 8785.
10. R. Rai, I. Bdikin, M. A. Valente and A. L. Kholkin, Mater. Chem. Phys., 2010, 119, 539.
11. G. L. Yuan and S. W. Or, Appl. Phys. Lett., 2006, 88, 062905.
12. W. M. Zhu and Z. G. Ye, Appl. Phys. Lett., 2006, 89, 232904.
13. A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report, 1994 , LAUR 86–748.
14. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
15. A. A. Coelho, J. Appl. Crystallogr., 2000, 33, 899.
16. K. Rabe, C. Ahn, H. and J.-M. Triscone, ed., Physics of Ferroelectrics: A Modern Perspective, Springer Press, 2007.
17. P. Bonneau, P. Garnier, E. Husson and A. Morell, Mater. Res. Bull., 1989, 24, 201.
18. P. Bonneau, P. Garnier, G. Calvarin, E. Husson, J. R. Gavarri, A. W. Hewat and A. Morell, J. Solid State Chem., 1991, 91, 350.
19. K. Z. Baba-Kishi, T. R. Welberry and R. L. Withers, J. Appl. Crystallogr., 2008, 41, 930.
20. R. L. Withers, Adv. Imaging Electron Phys., 2008, 152, 303.
21. S. Li, W. Cao and L. Cross, J. Appl. Phys., 1991, 69, 7219.
22. I. Mayergoyz and G. Bertotti, ed., The Science of Hysteresis, Elsevier, 2005.
23. S. Y. Yang, F. Zavaliche, L. Mohaddes-ardabili, V. Vaithyanathan, D. Schlom, Y. J. Lee, Y. H. Chu, M. P. Cruz, Q. Zhan, T. Zhao and R. Ramesh, Appl. Phys. Lett., 2005, 87, 102903.
24. T. Rojac, M. Kosec and D. Damjanovic, J. Am. Ceram. Soc., 2011, 94, 4108–4111.
25. D. Zhou, M. Kamlah and D. Munz, Proc. SPIE–Int. Soc. Opt. Eng., 2001, 4333, 64.
26. Y. H. Chen and D. Viehland, Appl. Phys. Lett., 2000, 77, 133.
27. J. E. Daniels, T. R. Finlayson, M. Davis, D. Damjanovic, A. J. Studer, M. Hoffman and J. L. Jones, J. Appl. Phys., 2007, 101, 104108.
28. R. E. Eitel, C. A. Randall, T. Shrout, P. W. Rehrig, W. Hackenberger and S. Park, Jpn. J. Appl. Phys., 2001, 40, 5999.
29. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
30. N. Thomas and A. Beitollahi, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 549.
31. Z. Jirak and T. Kala, Ferroelectrics, 1988, 82, 79.
32. N. Thomas, S. A. Ivanov, S. Ananta, R. Tellgren and H. Rundlof, J. Eur. Ceram. Soc., 1999, 19, 2667.
33. R. E. Eitel and C. A. Randall, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094106.
34. R. L. Withers, Y. Liu and T. R. Welberry, J. Solid State Chem., 2009, 182, 348–355.
35. T. R. Welberry, D. J. Goossens, R. L. Withers and K. Z. Baba-Kishi, Metallurgical and Materials Transations A, 2010, 41A, 1110–1118.
36. S. Miao, J. Zhu, X. Zhang and Z. Y. Cheng, Phys. Rev. B: Condens. Matter, 2001, 65, 052101.
37. P. Ganesh, E. Cockayne, M. Ahart, R. E. Cohen, B. Burton, R. J. Hemley, Y. Ren, W. Yang and Z. G. Ye, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144102.
38. W. Jo, S. Schaab, E. Sapper, L. A. Schmitt, H.-J. Kleebe, A. J. Bell and J. Rodel, J. Appl. Phys., 2011, 110, 074106.
39. V. A. Isupov, Ferroelectrics, 2005, 315, 123.
40. S. O. Leontsev and R. E. Eitel, J. Am. Ceram. Soc., 2009, 92, 2957.
41. P. Lunkenheimer, S. Krohn, S. Riegg, S. Ebbinhaus, A. Reller and A. Loidl, Eur. Phys. J. Spec. Top., 2010, 180, 61.
42. S. Mukherjee, R. Gupta, A. Garg, V. Bansal and S. Bhargava, J. Appl. Phys., 2010, 107, 123535.
43. V. Bobnar, A. Levstik, C. Huang and Q. M. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 041202.
44. A. Von Hippel, Rev. Mod. Phys., 1950, 22, 221.
45. B. Zhu, D. Wu, Q. Zhou, J. Shi and K. Shung, Appl. Phys. Lett., 2008, 93, 012905.
46. W. M. Zhu and Z. G. Ye, Ceram. Int., 2004, 30, 1435–1442.
47. T. Rojac, M. Kosec, B. Budic, N. Setter and D. Damjanovic, J. Appl. Phys., 2010, 108, 074107.
48. Q. Zhang, Y. Zhang, F. Wang, Y. Wang, D. Lin, X. Zhao, H. Luo, W. Ge and D. Viehland, Appl. Phys. Lett., 2009, 95, 102904.
49. E. Hollenstein, M. Davis, D. Damjanovic and N. Setter, Appl. Phys. Lett., 2005, 87, 182905.
50. T. Takenaka, H. Nagata and Y. Hiruma, Jpn. J. Appl. Phys., 2008, 47, 3787.
51. K. Sakata and Y. Masuda, Ferroelectrics, 1974, 7, 347.
52. Y. Hiruma, R. Aoyagi, H. Nagata and T. Takenaka, Jpn. J. Appl. Phys., 2005, 44, 5040.
53. B. Jaffe, W. R. Cook and H. Jaffe, Piezoelectric Ceramics, Academic Press, 1971.
54. Y. Rattikorn, L.Y. and S. Wongsaenmai, J. Phys. D: Appl. Phys., 2006, 39, 759.
55. S. Zhang, T. Xia and T. Shrout, J. Electroceram., 2007, 19, 251.
56. Z. Zhang, H. Yan, X. Dong and Y. Wang, Mater. Res. Bull., 2003, 38, 241.
57. H. Jaffe, J. Am. Ceram. Soc., 1958, 41, 494.
58. D. Berlincourt, C. Cmolik and H. Jaffe, Proc. IRE, 1960, 48, 220.
59. S. Park and T. Shrout, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 1997, 44, 1140.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sc01115h

‡ This work is funded by the European Research Council (ERC Grant agreement 227987 RLUCIM) and the EPSRC.

---