Thermodynamic analysis of Xe/Kr selectivity in over 137 000 hypothetical metal–organic frameworks

Abstract

Metal–organic frameworks (MOFs) are porous crystals with the potential to improve many industrial gas separation processes. Because there is a practically unlimited number of different MOFs, which vary in their pore geometry and chemical composition, it is challenging to find the best MOF for a given application. Here, we applied high-throughput computational methods to rapidly explore thousands of possible MOFs, given a library of starting materials, in the context of Xe/Kr separation. We generated over 137 000 structurally diverse hypothetical MOFs from a library of chemical building blocks and screened them for Xe/Kr separation. For each MOF, we calculated geometric properties via Delaunay tessellation and predicted thermodynamic Xe/Kr adsorption behavior via multicomponent grand canonical Monte Carlo simulations. Specifically, we calculated the pore limiting diameter, largest cavity diameter, accessible void volume, as well as xenon and krypton adsorption at 1.0, 5.0 and 10 bar at 273 K. From these data we show that MOFs with pores just large enough to fit a single xenon atom, and having morphologies resembling tubes of uniform width, are ideal for Xe/Kr separation. Finally, we compare our generated MOFs to several known structures (IRMOF-1, HKUST-1, ZIF-8, Pd-MOF, & MOF-505) and conclude that significantly improved materials remain to be synthesized. All crystal structure files are freely available for download and browsing in an online database.

---

1 Introduction

Xenon and krypton, in pure form, are both valuable commodities that are used in medical applications (e.g., anesthesia, imaging) and lighting (e.g., fluorescent signs, airport runway lights).^1–3 Both gases are present in ambient air, but only in small quantities (1.14 ppm Kr, 0.086 ppm Xe), making extraction difficult. Typically, in producing pure nitrogen and pure oxygen, a series of distillation steps are performed on air until one of the side product streams has an 80/20 molar ratio of krypton to xenon.⁴ Nearly pure xenon (or krypton) can then be obtained in a final cryogenic distillation step. However, cryogenic distillation is energetically and monetarily costly, and the purity of the resulting gases is insufficient for some applications, e.g., removing radioactive ⁸⁵Kr from spent nuclear fuel.⁵

An alternative to cryogenic distillation is selective adsorption onto microporous adsorbents. Here, one gas from a mixture preferentially adsorbs onto the surface of the adsorbent material. Such selective adsorption techniques could not only reduce the overall cost of Xe and Kr production, but potentially achieve higher purity xenon, as well. Recently there have been a number of experimental and computational studies of Xe/Kr separation in zeolites and metal–organic frameworks (MOFs).^5–8 Zeolites NaX and NaA have been shown to have selectivities of ∼6 and ∼4, respectively, for xenon over krypton.⁵ Mueller et al.⁶ used a breakthrough system filled with the MOF HKUST-1⁹ to purify a 94/6 molar mixture of Kr/Xe to over 99% krypton and less than 50 ppm xenon. Ryan et al.⁷ performed molecular simulations on eight structurally diverse MOFs and found that Pd-MOF¹⁰ had very high xenon selectivity (∼18.0–19.4 over a wide pressure range) but poor adsorption capacity, while MOF-505¹¹ had the best combination of selectivity and capacity.

To date, only a small number of adsorbents have been explored for Xe/Kr separation. One goal of this work was to screen a much larger number of MOFs for their ability to selectively adsorb Xe over Kr and to relate this behavior to the nature of the pore structure. There have been several reports on the geometrical analysis of large adsorbent databases, which point to the utility of such an approach. Foster et al. determined the largest cavity diameter (LCD) and pore limiting diameter (PLD) for each of the known zeolites.¹² Haldoupis et al. performed a similar geometric analysis and calculated the Henry's constants for hundreds of MOFs reported in the Cambridge Structural Database.^13,14 First et al. determined the LCDs, PLDs, accessible and inaccessible volumes, and structure morphologies for all known zeolites.¹⁵ Willems et al. also described tools for high-throughput geometrical analysis of porous crystals.¹⁶ These studies revealed some broad insights and identified materials that may be useful for separation of small molecules such as CO₂, CH₄, and H₂ based on kinetic effects. Both First and Haldoupis extended their work^15,17 to the large database of hypothetical zeolites created by Deem and co-workers.^18,19 Some interesting trends emerged from the analysis, but synthesis of a novel hypothetical zeolite is a significant challenge; less than 200 different zeolite structures have been synthesized to date,²⁰ compared to thousands of MOFs over a much shorter time period.²¹

Here, we screened over 137 000 hypothetical MOFs²² for their capability to separate xenon from krypton at various pressures (structures and data available online at http://hmofs.northwestern.edu). The LCD, PLD and other geometric data (e.g., accessible void volume) were obtained via Delaunay tessellation methods, and equilibrium Xe/Kr adsorption properties were obtained via multicomponent grand canonical Monte Carlo (GCMC) simulations. We demonstrate how these methods can be combined to efficiently screen a large number of hypothetical MOFs for equilibrium-based adsorption separations and to discover novel structure-property relationships as well as design rules. For example, we identified candidate MOFs with very high xenon selectivity and used the associated geometrical data to show that the ideal materials have pores just large enough for a single xenon atom and have morphologies resembling tubes of uniform width. We also compared our generated MOFs to several known MOFs, IRMOF-1,²³ HKUST-1,⁹ ZIF-8,²⁴ Pd-MOF,¹⁰ & MOF-505,¹¹ and concluded that significantly improved materials remain to be synthesized.

2 Computational methods

The Xe/Kr screening approach described here required three distinct methods: hypothetical MOF generation, geometric analysis via Delaunay tessellation, and thermodynamic analysis via multicomponent GCMC simulations. A brief overview is given below, and additional details are available in the Supplementary Information.†

2.1 Hypothetical MOF generation

Our method, recently described in detail elsewhere,²² leverages the predictable assembly of building blocks into MOFs by systematically generating every possible structure given an input library of chemical building blocks. Hypothetical MOFs are generated by recombining building blocks derived from crystallographic data of already synthesized MOFs (see Fig. 1). Atoms are grouped into building blocks based on reagents used in the actual synthesis. Any building block can combine with any other building block provided that the geometry and chemical composition local to the point of connection are the same as in crystallographically determined structures. Building blocks are combined stepwise, and when an atomic overlap occurs at a particular step, a different building block is chosen or a different connection site, until all possibilities are exhausted. When no more building blocks can be added, the crystal generation procedure is complete. (For more details, see the ESI†). Note that no force field (or quantum mechanical) energy minimizations are involved; the pieces are connected according to the geometric rules that govern how the building blocks are connected in existing MOFs. The approach is very much like snapping Tinkertoys or Lego bricks together.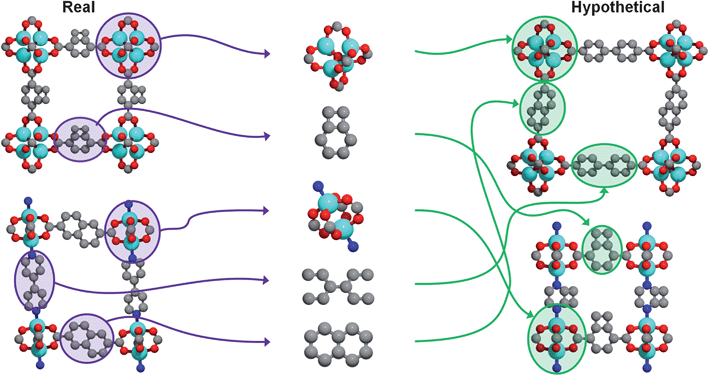

Fig. 1 Visual summary of the hypothetical MOF generation strategy. Crystal structures of existing metal–organic frameworks are obtained from X-ray diffraction data (left) and are subsequently divided into building blocks (middle) that can then be recombined to form new, hypothetical metal–organic frameworks (right). Figure adapted from Ref. 22.

For the generation procedure we chose 102 building blocks that varied significantly in their geometries, number of connection sites and chemical composition. All building blocks used are listed in the Supplementary Information.† The building blocks fall conceptually into three groups: inorganic, organic and functional groups. We constrained the generation algorithm to produce crystals with at most one kind of inorganic building block, two kinds of organic building blocks, and one kind of functional group. This constraint resulted in MOFs that were reasonable synthetic targets, with similar complexity to those commonly reported in the literature. By attempting every combination of building blocks subject to the above constraints, over 137 000 hypothetical MOF structures were generated. Note that all of the generated frameworks are neutral, with no charge-compensating ions.

2.2 Geometric analysis

The objectives of our geometric analysis were to find: 1) the largest hard sphere that could percolate a given structure (i.e., the pore limiting diameter or PLD), 2) the largest sphere that could fit inside a given structure (i.e., the largest cavity diameter or LCD), 3) the volume of the void space, or “empty space,” of a structure, and 4) a qualitative picture of the morphology of the pores. While many approaches suffice when considering only a few structures (e.g., visual inspection in commercially available crystal viewing software), methods that cannot be automated are impractical for a large database of structures. Our geometric analysis program, modified from the work of Greenfield and Theodorou,²⁵ is able to rapidly calculate the LCD, PLD, void volume and pore morphology data in three steps: 1) the structure is tessellated into Delaunay tetrahedra, 2) volumes are calculated inside each tetrahedron using spherical probe molecules, and 3) solvent accessible tetrahedra are grouped based on their adjacency to determine whether or not they form percolating channels.

The Delaunay tessellation maps a set of points in Cartesian space to a unique‡ set of tetrahedra that completely fill the space. The points become the vertices of the tetrahedra, and the sphere that intersects all four points (i.e., the circumsphere) of any tetrahedron must contain no other points. (In cases of high symmetry, a circumsphere can intersect five or more points. Our approach explicitly calculates the resulting polyhedra and their connectivity, and the polyhedra are included in subsequent references to tetrahedra.) In the case of the hypothetical MOFs, the atoms in the unit cell end up being the vertices of the tetrahedra. Tanemura's algorithm was used for the tessellation and is described elsewhere.^27,28

We used a range of spherical probes (with diameters from 0 to 40 Å in 0.05 Å increments) to find the probe size that would no longer be able to percolate the structure. Quantities such as pore limiting diameters and accessible void volumes require subdividing the Delaunay tetrahedra into categorized volumes (see Fig. 2). These categorized volumes are determined analytically using published algorithms.^25,29 For each tetrahedron, the occupied volume is defined as the region occupied by the framework atoms that protrude into the tetrahedron. Here, each framework atom is considered a sphere with a radius equal to the van der Waals radius of the atom it represents. The unoccupied volume is defined by the region inside the tetrahedron that is not occupied by the framework atoms. The volume accessible to a probe molecule is found by first increasing the radius of each framework atom by the radius of the probe and then recalculating the unoccupied volume.

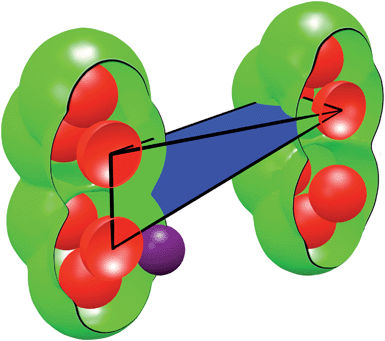Fig. 2 Anatomy of a single Delaunay tetrahedron. The framework atoms (red spheres) are connected via edges to form tetrahedra. A sample tetrahedron (black wire-cage) is shown and its volume is subdivided into three categories: occupied volume (red), unoccupied volume (green + blue), and accessible volume (blue). The accessible volume is a function of the size of the probe used (purple sphere).

Each Delaunay tetrahedron is connected to four other tetrahedra via their shared faces. If the shared face of two connected tetrahedra is wide enough to allow a spherical probe to pass through it (taking into account the volume occupied by the framework atoms), then those two tetrahedra are considered part of a cluster. If the connections between all of the tetrahedra are considered in this way, then the resulting clusters of tetrahedra indicate the regions within the structure where the probe molecule can freely travel.²⁵ A cluster statistics algorithm³⁰ was used to convert from direct connectivity between tetrahedra to indirect connectivity that spans multiple tetrahedra. Importantly, if any one of the clusters forms a pathway that connects to an image of itself across a periodic boundary, then a probe molecule that is able to freely travel in that cluster is said to percolate the structure.

2.3 Thermodynamic analysis

To calculate the adsorption equilibrium of Xe/Kr mixtures in the hypothetical MOFs, we performed multicomponent, atomistic GCMC simulations, as has been previously reported.⁷ The gas phase in equilibrium with the MOFs had a fixed 80/20 molar composition of krypton to xenon to be representative of an industrial mixture. Adsorption data were calculated for every MOF at 1.0, 5.0 and 10 bar at 273 K. All GCMC simulations included an M-cycle equilibration period followed by an M-cycle production run, where M was 1000, 5000, or 10 000 depending on the statistical accuracy desired. A cycle consists of N Monte Carlo steps, where N is the number of molecules (which fluctuates during a GCMC simulation). Insertion, deletion, translation and identity change moves (e.g., change xenon to krypton) were considered. We show in the Supplementary Information that 1000 cycles are sufficiently accurate for the purpose of high throughput screening. Note that the adsorption simulations have some limitations; the MOF frameworks were assumed to be rigid, defect free, and solvent free throughout the simulations.

Interaction energies between non-bonded atoms were computed through the Lennard–Jones (LJ) potential:

r_ij is the distance between atoms i and j, and ε_ij and σ_ij are the LJ well depth and diameter, respectively. LJ parameters between atoms of different types were calculated using the Lorentz–Berthelot mixing rules (i.e., geometric average of well depths and arithmetic average of diameters). LJ parameters for framework atoms were taken from the Universal Force Field (UFF).³¹ Xenon and krypton force field parameters were taken from Hirschfelder et al.³² and Talu and Myers,³³ respectively. No electrostatic charges were considered. We found 27 structures within the top 100 most selective hypothetical MOFs that have polar functional groups. The effect of these polar functional groups on polarizable molecules, like Xe, is an interesting area for future research. Selectivities were calculated from the standard definition:where x_i and y_i are the adsorbed phase mole fraction and gas phase mole fraction, respectively, of species i.

3 Results

We applied our geometric analysis method to compute the LCD and PLD for over 137 000 hypothetical MOFs. The resulting LCD values range from micropores to mesopores (from 2 Å to over 30 Å) as seen in Fig. 3a. The PLD values for the hypothetical MOFs also show significant diversity. A few structures allow molecules larger than 24 Å in diameter to percolate, while some structures have pores too small for helium atoms to percolate the pores as shown in Fig. 3b. Although beyond the scope of this investigation, it is worth noting that the broad spectrum of PLDs identified in the database could allow one to choose an ideal MOF for size-selective kinetic (or molecular sieving) separations given practically any conceivable binary mixture. By taking the ratio of the LCD to the PLD we are able create an approximate picture of the pore morphology within the hypothetical MOFs (see Fig. 3c). A ratio of 1.0 indicates that the percolating channels within a framework have the same diameter as the largest cavities—i.e., tubes of uniform width. The higher the ratio, the more the structure resembles a network of large cavities connected by narrow channels or windows. We found that the hypothetical MOFs had LCD/PLD values ranging from close to 1 to just over 6, with the majority of the structures being between 1 and 2.

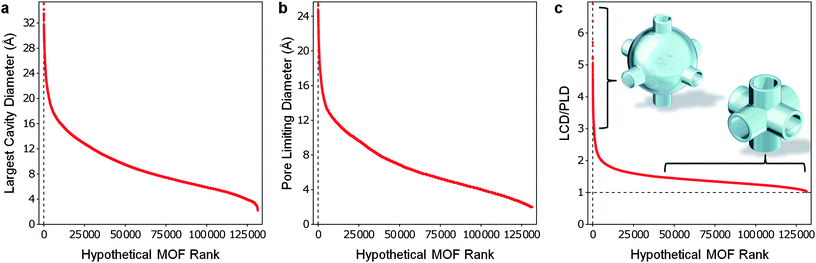Fig. 3 All hypothetical MOFs sorted by their LCD, PLD and LCD/PLD ratio. The database contains MOFs with a wide spectrum of (a) LCDs, (b) PLDs, and (c) pore morphologies, as defined by the LCD/PLD ratio.

To obtain thermodynamic data via GCMC simulations on such a large database, we adopted an adaptive strategy of performing simulations with successively higher quality. See Fig. 4 for a demonstration using the selectivity data at 5 bar. Our GCMC simulations predict that the top 350 MOFs have higher xenon to krypton selectivities than the highest previously reported value for a MOF material (∼19 in Pd-MOF).⁷ Interestingly, some MOFs demonstrate selectivity instead for krypton over xenon; over one hundred of them by a factor of more than ∼500 : 1, although some caution is required in this case due to significant statistical uncertainty. If high krypton selectivity were of interest, the same adaptive strategy could be adopted to identify MOFs with high krypton to xenon selectivities with greater statistical accuracy.

Fig. 4 All hypothetical MOFs sorted by their selectivity for xenon over krypton at 5 bar—in three stages. (a) In the initial stage, over 137 000 MOFs were screened for Xe/Kr selectivity at 5 bar via short simulations. The top 5% of the first stage (b) and then the top 5% of the second stage (c) were recalculated (and resorted) using successively longer simulations, reducing the statistical error significantly each time.

While selectivity is an important factor in separation processes, it must be balanced against the total adsorption capacity. As mentioned above, Pd-MOF has a high selectivity for xenon but a low adsorption capacity, limiting its potential for industrial use. The ideal structures have both high selectivity and high adsorption capacity. Fig. 5 shows selectivity plotted against absolute adsorption of xenon at 1 bar and 10 bar (see Figure S8 in the ESI† for data at other pressures); the most promising MOFs correspond to the dots in the upper right quadrant. We find that as the pressure is increased, there is a general decrease in selectivity accompanied by an increase in total adsorption. While MOF-505, shown in Fig. 5, is clearly superior to the known structures against which it was compared by Ryan et al.,⁷ there are thousands of hypothetical MOFs in our database predicted to be better in both selectivity and total adsorption capacity.

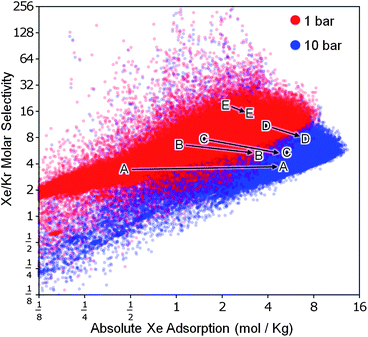Fig. 5 Performance limits for Xe/Kr separation using metal–organic frameworks. Our analysis of the database confirmed that there is a trade-off between selectivity and total adsorption capacity. We also found that when the pressure is increased, here shown going from 1 bar (red) to 10 bar (blue), selectivity generally decreases but total adsorption increases. Simulated data from five known structures⁷ provide context and help show the change in selectivity and adsorption with pressure: (A) IRMOF-1,²³(B) ZIF-8,²⁴(C) HKUST-1,⁹(D) MOF-505¹¹ and (E) Pd-MOF.¹⁰

Sometimes it can be beneficial to relate thermodynamic material properties to data that are either easier to measure or less costly to compute. In this spirit, we sought to correlate the thermodynamic selectivity data with geometric data (the latter being easier to obtain if the MOF crystal structure is known). Recent literature has suggested that in Xe/Ar and Xe/Kr separations, pore geometries play an important role.^7,34,35 Van Tassel et al.³⁴ simulated xenon and argon mixed-gas adsorption in the NaA zeolite and found that argon was favored at high pressure because its small size allowed tighter packing in the pore. Keffer et al.³⁵ later simulated competitive xenon and argon adsorption in theoretical slit, cylindrical, and spherical nanopores. These structures were always selective for xenon over argon at low pressures so long as the structure had cavities large enough to fit at least a single xenon atom. Ryan et al.⁷ predicted that structures with cavity sizes just large enough to hold one xenon atom, and having channels of uniform widths, have the highest Xe/Kr selectivity.

We found Xe/Kr selectivity to correlate strongly with the LCD (Fig. 6a) as well as the pore morphology, which can be inferred from the LCD to PLD ratio (Fig. 6b). The selectivity is sharply peaked when the LCD is slightly larger than a xenon atom and decreases rapidly as cavity size increases. We also found that selectivity is highest when the LCD/PLD ratio is between 1 and 2 (similar sized channels and cavities), and selectivity decreases as the ratio of LCD/PLD increases past 2 (cavities twice or more the size of the channel). This verifies, with the aid of over 137 000 structures, the hypothesis put forth by Ryan et al. when they examined only 8 structures.

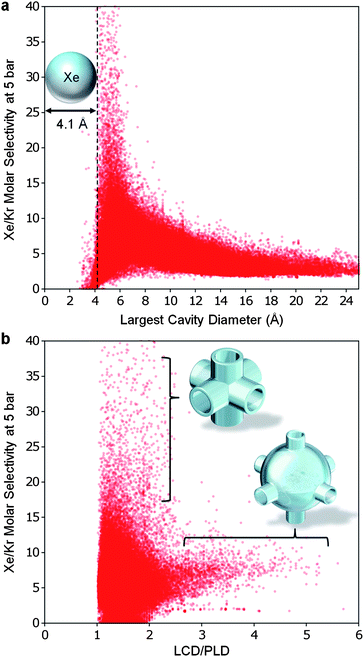Fig. 6 The geometry of an optimal MOF for Xe/Kr separation. (a) In all of the hypothetical MOFs, the highest selectivities were shared amongst the narrow subset of structures with LCD slightly greater than the diameter of a xenon atom. (b) The least selective MOFs had large cavities connected by narrow channels (LCD/PLD ratio greater than 2) while the best MOFs had tube-like pore morphologies (LCD/PLD ratio between 1 and 2). In both graphs, the selectivity has been cutoff at 40 for clarity.

We also attempted to search for a correlation between the geometric properties and some measure that combines selectivity and adsorption capacity. As shown in Fig. 7, we defined a performance metric for Xe/Kr separation that is simply the product of xenon selectivity and absolute adsorption. When comparing this performance metric to the LCD, we observed a large peak around ∼4.1 Å and a slightly smaller peak around ∼8.2 Å, after which the performance drops off precipitously. Apparently for pore diameters approximately the size of two xenon atoms, the discrete jump in additional capacity temporarily offsets the loss of selectivity. The structures best suited for Xe/Kr separation are still those that have LCDs between ∼4 Å and ∼8 Å, as hypothesized by Ryan et al.⁷

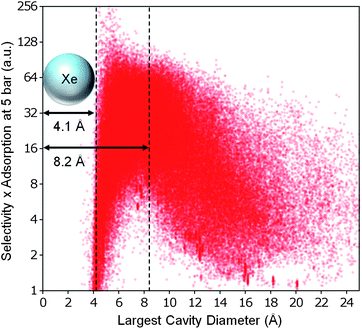Fig. 7 The best overall structures for Xe/Kr separation. Weighting selectivity and total adsorption capacity equally, the best structures for Xe/Kr separation are predicted to have LCDs slightly larger than a xenon atom. The axes have been chosen for clarity; see Figure S9c (ESI†) for the full data set.

4 Conclusions

We have applied a high-throughput computational method to identify candidate MOFs for the separation of xenon from krypton. By using both a geometric and thermodynamic analysis on a database of over 137 000 hypothetical structures, we were able to confirm a previous hypothesis that suggested cavities that could hold at least one, but not more than one, Xe atom would have the highest selectivity. We were also able to propose structures with higher selectivities than any currently synthesized MOFs. Selectivity is maximized when the structures have pore morphologies resembling tubes of uniform width (LCD/PLD between 1 and 2).

Acknowledgements

R.Q.S. gratefully acknowledges support by the U.S. Department of Energy (DEFG02-08ER15967) and the Defense Threat Reduction Agency (grant no. HDTRA1-09-1-0007). Computational work was supported through the resources provided by Information Technology at Northwestern University as part of its shared cluster program, Quest. C.E.W. gratefully acknowledges support from an ISEN Fellowship from the Initiative for Sustainability and Energy at Northwestern and a Ryan Fellowship from the Northwestern University International Institute for Nanotechnology, as well as Walter P. Murphy and Royal E. Cabell Fellowships.

References

1. S. C. Cullen and E. G. Gross, Science, 1951, 113, 580–582.
2. E. Gowin, in Fifth Cryogenics ‘98 IIR International Conference, Proceedings, Int. Inst. Refrigeration, Paris, France, 1998, ch. Specialty Gases - production and their application - What to do with the ‘unknown’ rare gases Neon, Krypton and Xenon - From history to application, pp. 174–177.
3. T. F. Holstraeter, M. Georgieff, K. J. Foehr, W. Klingler, M. E. Uhl, T. Walker, S. Koester, G. Groen and O. Adolph, Anesthesiology, 2011, 115, 398–407.
4. F. G. Kerry, Industrial Gas Handbook: Gas Separation and Purification, CRC Press, Boca Raton, Florida, 2007.
5. J. Izumi, in Handbook of Zeolite Science and Technology, ed. S. M. Auerbach, K. A. Carrado and P. K. Dutta, Marcel Dekker, New York, 2003, ch. Waste gas treatment using zeolites in nuclear-related industries.
6. U. Mueller, M. Schubert, F. Teich, H. Puetter, K. Schierle-Arndt and J. Pastré, J. Mater. Chem., 2006, 16, 626–636.
7. P. Ryan, O. K. Farha, L. J. Broadbelt and R. Q. Snurr, AIChE J., 2011, 57, 1759–1766.
8. J. A. Greathouse, T. L. Kinnibrugh and M. D. Allendorf, Ind. Eng. Chem. Res., 2009, 48, 3425–3431.
9. S. S. Chui, S. M. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150.
10. F. X. Llabrés i Xamena, A. Abad, A. Corma and H. Garcia, J. Catal., 2007, 250, 294–298.
11. B. Chen, N. W. Ockwig, A. R. Millward, D. S. Contreras and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4745–4749.
12. M. D. Foster, I. Rivin, M. M. J. Treacy and O. D. Friedrichs, Microporous Mesoporous Mater., 2006, 90, 32–38.
13. E. Haldoupis, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2010, 132, 7528–7539.
14. Cambridge Crystallographic Data Centre, Cambridge Structural Database (CSD): http://www.ccdc.cam.ac.uk/.
15. E. L. First, C. E. Gounaris, J. Wei and C. A. Floudas, Phys. Chem. Chem. Phys., 2011, 13, 17339–17358.
16. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141.
17. E. Haldoupis, S. Nair and D. S. Sholl, Phys. Chem. Chem. Phys., 2011, 13, 5053–60.
18. D. J. Earl and M. W. Deem, Ind. Eng. Chem. Res., 2006, 45, 5449–5454.
19. R. Pophale, P. A. Cheeseman and M. W. Deem, Phys. Chem. Chem. Phys., 2011, 13, 12407–12412.
20. Ch. Baerlocher & L. B. McCusker, Database of zeolite structures: http://www.iza-structure.org/databases/.
21. N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176–182.
22. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89.
23. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
24. K. S. Park, Z. Ni, A. P. Cté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O’Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
25. M. L. Greenfield and D. N. Theodorou, Macromolecules, 1993, 26, 5461–5472.
26. B. N. Delaunay, B. Acad. Sci. USSR, 1934, 7, 793–800.
27. M. Tanemura, T. Ogawa and N. Ogita, J. Comput. Phys., 1983, 51, 191–207.
28. S. Arizzi, P. H. Mott and U. W. Suter, J. Polym. Sci., Part B: Polym. Phys., 1992, 30, 415–426.
29. L. R. Dodd and D. N. Theodorou, Mol. Phys., 1991, 72, 1313–1345.
30. E. M. Sevick, P. A. Monson and J. M. Ottino, J. Chem. Phys., 1988, 88, 1198–1206.
31. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
32. J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, New York, 1965.
33. O. Talu and A. L. Myers, Colloids Surf., A, 2001, 187–188, 83–93.
34. P. R. Van Tassel, H. T. Davis and A. V. McCormick, Langmuir, 1994, 10, 1257–1267.
35. D. Keffer, H. T. Davis and A. V. McCormick, J. Phys. Chem., 1996, 100, 638–645.

---

Footnotes

† Electronic supplementary information (ESI) available: List of modular building blocks used (Section S1), crystal generator algorithm (Section S2), and link to online database (Section S3). Monte Carlo simulation details and statistical benchmarking (Section S4), and additional results (Sections S5–S7). See DOI: 10.1039/c2sc01097f

‡ In general, there are many ways to map points to tetrahedra, but only one way (including degenerate cases to account for high symmetry) satisfies the Delaunay criteria.²⁶

---