An analytical tool to determine undergraduate students' use of volume and pressure when describing expansion work and technical work

Abstract

In undergraduate chemical thermodynamics teachers often include equations and view manipulations of variables as understanding. Undergraduate students are often not able to describe the meaning of these equations. In chemistry, enthalpy and its change are introduced to describe some features of chemical reactions. In the process of measuring heat at constant pressure, work is often disregarded. Therefore, we investigated how undergraduate students describe expansion work and technical work in relation to enthalpy and its change. Three empirical studies (n_tot = 64, n_tot = 22, n_tot = 10) with undergraduate chemistry students taking their first or fifth chemistry course at two Swedish universities were conducted. Questions on enthalpy and its change, internal energy and its change, heat and work were administered in questionnaires, exam questions, hand-ins and interviews. An analytical matrix was developed and qualitative categories with respect to pressure and volume were formed. The results indicate that work in general and even more so expansion work and technical work are difficult processes to describe and relate to the definition and formula of enthalpy change. Work is mainly described without reference to pressure and volume. The properties of volume are more likely to be described correctly than the properties of pressure. The definition of enthalpy change at constant pressure is generalised to constant volume/varying pressure cases. This study gives further insight into the way in which students use pressure and volume as they describe expansion work and technical work as well as the contextual correctness of these descriptions. The matrix and categories can be used by researchers, teachers and students.

---

Introduction

The laws and theories of chemical thermodynamics can be used to explain, predict and model what we meet in our daily lives; hence in a broad perspective thermodynamics is important for everyone. However, thermodynamics is often only studied by secondary and tertiary students interested in science and researchers have stated that chemical thermodynamics is problematic for chemistry students (Carson and Watson, 1999; Tsaparlis, 2008). For chemistry as a discipline and undergraduate chemistry education this is a problem since thermodynamics is used as a tool in research laboratories and in the industry (Goedhart and Kaper, 2002). Another problem is that science teaching in general and the teaching of thermodynamic concepts in particular are based on algorithms. In fact, empirical evidence suggests that this is a real problem (Johnstone et al., 1977; Mazur, 1997; Carson and Watson, 1999; Carson and Watson, 2002; Kim and Pak, 2002).

Although mathematics is needed for solving problems in thermodynamics, teachers often justify their emphasis on numerical problem solving by arguing for enhanced conceptual understanding. In fact one of the most important contributions of research has been the revelation of how poorly students may understand the ideas underlying numerical problems they have answered correctly (Bodner and Herron, 2002). Since algorithmic problem solving exercises do not promote conceptual understanding students will, most likely, never get there (Gabel, 2003).

Also, in the introduction of new concepts (e.g., enthalpy) other concepts like energy, heat and work are used and students' understanding of these concepts are taken for granted by teachers (Carson and Watson, 1999). For instance, in upper secondary school and at the undergraduate level many chemical reactions are explained using the state function enthalpy H and its change ΔH instead of internal energy U and its change ΔU. By using ΔU heat and work are also introduced, often related to the forms of energy framework (van Roon et al., 1994; Carson and Watson, 1999; Goedhart and Kaper, 2002). The same concepts are used in different ways and the students are often faced with problems involving heat at constant pressure when only expansion work is allowed. However, work is often a mechanical concept (van Roon et al., 1994).

Theoretical background

Although different thermodynamic concepts and functions, such as Gibbs energy or function, are related to work this study focuses on Enthalpy, H, which is a description of a physical state, hence both the state of the matter (i.e. solid, liquid or gas) and the state variables (i.e. volume, pressure, temperature and amount of substance) affect the value of H and its change. Enthalpy is a state function since U, p and V are state functions. A change of the state function enthalpy is defined as dH = dU + d(pV) or ΔH = H₂ − H₁. The expression d(pV) indicates that the pressure and volume change from the initial state p₁V₁ to a final state p₂V₂. Since it is a change of a product, mathematics states that d(pV) = pdV + Vdp. The overall change of H does not depend on the path taken from H₁ to H₂.

In order to determine the change in internal energy both heat and work must be monitored: dU = đq + đw + đw′, where đq is an infinitesimal change in heat, đw is an infinitesimal change in expansion work and đw′ is an infinitesimal change in all other works (e.g., electrical work) (Laidler et al., 2003; Atkins and de Paula, 2005). The equation for dU probably contains mathematical notions that undergraduate chemistry students are unaware of. Here đ is used to indicate that the variable is path dependent (IUPAC, 2007). Heat and work are inexact integrals which means that their values depend on the path taken from U₁ to U₂.

In practical situations it is more difficult to determine the expansion work than to measure heat. Therefore, one reason for the introduction of enthalpy and its change is that the expansion work is disregarded by the definition of enthalpy change. As a chemical reaction occurs, or a physical transformation, the enthalpy of the system is changed due to the changes in U, p and V, dH = dU + d(pV) or dH = đq + đw + đw′ + pdV + Vdp. A more simple way, although not entirely correct, is to express the definition as ΔH = q + w + Δ(pV) ⇒ ΔH = q + w + pΔV + VΔp.

If expansion work is defined as đw = −p_exdV where p_ex is the external pressure (i.e., the pressure the system does work against in order to expand), hence p_ex = p, the equation becomes dH = đq + đw′ + Vdp which integrated becomes ΔH = q + w′ + VΔp. If the pressure is constant, as in many chemical reactions, Δp = 0, and no other work is allowed, w′ = 0, then the enthalpy change is heat at constant pressure ΔH = q_p.

Enthalpy changes may also be determined as dH = đq + đw + đw′ + pdV + Vdp, which at constant volume dV = 0 and no other work is allowed, becomes dH = đq + Vdp or integrated ΔH = q + VΔp, where VΔp is technical work. Depending on the properties of the system the enthalpy change may be determined in different ways. However, the first way, constant pressure and only expansion work, is emphasised in many textbooks at undergraduate level (e.g., Chang, 2007; Zumdahl and Zumdahl, 2007). Also note that ΔU = q + w is valid if the system is closed (Atkins and de Paula, 2005).

Research literature

Research has shown that work in general is problematic for students, for instance in the first law of thermodynamics and the relation to heat (Johnstone et al., 1977; Hadfield and Wieman, 2010). Also, work is often described as a mechanical concept (e.g., van Roon et al., 1994). Carson and Watson (1999), also described in Carson (2001), and Sözbilir (2001) explicitly focused on expansion work in their studies. Carson and Watsons' (1999) research framework includes a conceptual change perspective and therefore they are able to state that work is sensitized post teaching, even though the meaning is still unclear. Post teaching, 4 out of 22 students explain expansion work acceptably, while 8 students have a range of alternative conceptions. The most common one, held by three students, is that gas only does work when it pushes a piston. The results also suggest that students perceive work as raising weights, hence work is considered a mechanical concept as previously stated by van Roon et al. (1994). According to Carson and Watson (1999), one problem is that teachers assume that students know some concepts, for instance heat and work. In the study by Carson and Watson it is suggested that thermodynamic entities are defined qualitatively before they are defined quantitatively. This idea is further elaborated in Carson (2001). One example supporting the argument is the empirical evidence that suggests that students have limited understanding of the expression ΔH = ΔU + pΔV, since they can read it but do not know the meaning of the symbols. In the study by Hadfield and Wieman (2010) students tend to describe the expression w = −∫pdV as energy conversion and conservation or that w and −∫pdV represent different forms of energy.

It is obvious that enthalpy change does not necessarily offer students new ways of solving, anticipating and explaining problems. However, there is also a problem since students describe enthalpy change as heat at constant volume (Carson, 2001; Sözbilir, 2001). Carson (2001) asks the students explicitly during interviews, while Sözbilir's (2001) result is based on a questionnaire. According to both authors there are connections between enthalpy change and expansion work since students argue that the enthalpy change is the heat when no work is done (ΔV = 0). Five out of 22 students in Carson's (2001) study and 19 out of 44 students in Sözbilir's (2001) study state that constant volume is necessary.

Aim

Since research suggests that work, enthalpy change and constant pressure/constant volume are problematic concepts for students, the aim of this study is to develop an analytical tool in order to analyse students' answers regarding expansion work and technical work with respect to volume, pressure and context.

Methodology

In this section research design and sample as well as data collection and analysis are addressed.

Research design and sample

The research design was flexible, explorative and small-scale. An explorative design tries to find out what is happening, seeks new insights and searches for possible results that can be further investigated. It generates hypotheses rather than confirmations (Robson, 2002). Three studies were performed, first a pilot study (PS, n_tot = 64) in which different hypotheses/results for further research were generated. One hypothesis was H13: The students have trouble understanding that ΔH is measured as heat at constant pressure and only expansion work is allowed. A related result was H22: Work is not a chemical concept, (a) Work is only a physical concept, (b) Students are not aware of expansion work, (c) Expansion work is only done if a gas pushes a piston.

Based on experiences from the pilot study, the main study (HS) was designed. It became small-scale during the on-going empirical studies due to the cancellation of the chemistry programs at the university. Instead of n ≈ 60, a total number of 22 students participated. During the main study, the study focused on undergraduate students’ description of work (i.e., expansion work) as qualitative/conceptual questions were included. Tasks from the research literature were included to more thoroughly investigate the hypotheses (e.g., Sözbilir, 2001). Since the whole chemistry department was shut down the sampling became one of convenience (Bryman, 2008). However, the interviews (see data collection below) were purposely sampled to provide a heterogeneous sample of students (Bryman, 2008). The procedure gave empirical evidence with both depth and width. With respect to the focused aim of the study, a matrix and categories describing students' answers were created (see data analysis below).

In order to validate the results in the main study another small-scale follow-up study (FS, n_tot = 10) was conducted at a different university. In the follow-up study the matrix and categories were evaluated. The plan was to include a similar group at a different university, but the teacher at that university found the tasks too advanced for his course. Instead, he recommended another group taking a course in chemical thermodynamics at the same university. However, that course required at least one semester of undergraduate chemistry studies. All students taking the course were asked to participate.

How participants are chosen affects the generalisability and, as volunteering is important, the entire sampling process is already biased. The cancellation of the chemistry course made purposive or statistical sampling impossible. Therefore the generalisability of the results will be addressed in the section Discussion and concluding remarks.

Data collection

In the pilot study, different data collection methods were used, both pre and post questionnaires and interviews. The pre questionnaire design was based on previous research (de Vos and Verdonk, 1986; Bethge, 1988; Boo, 1998; Barker and Millar, 1999; Carson and Watson, 1999; Barker and Millar, 2000; Boo and Watson, 2001) and upper secondary school textbooks in order to pose questions appropriate to the students (Thylander and Johansson, 1999; Andersson et al., 2000, 2001).

In a general description one can say that the first empirical study covered different subject matter in chemical thermodynamics (e.g., enthalpy, bonds, boiling point and equilibrium). In the post questionnaire, the theory introduced during the teaching process was investigated, hence there was a minor shift in aim during the empirical investigation. More tasks included Gibbs energy and its change, hence both enthalpy and its change and entropy and its change were investigated simultaneously. All included tasks are not presented here in detail (see Nilsson, 2011). The interviews were semi-structured (Kvale, 1996; Drechsler, 2005). The results of the pilot study were hypotheses, see examples above.

The main study was designed to explicitly probe these hypotheses, hence the purpose was focused. The tasks were formulated to address qualitative aspects of the theory but all did not include work. Those that did were taken from previous research (e.g.,Carson, 2001; Sözbilir, 2001) and redesigned to fit the Swedish setting or were newly developed. The three major written tasks (X, Y, Z) were

• X. The reaction between sodium metal and water. The task was divided in three different ways (a) an open beaker, (b) balloon fitted beaker or (c) syringe fitted beaker as described below (cf. Interview study by Carson, 2001).

(a) A chemical reaction between sodium and water takes place and hydrogen gas is formed. The formed hydrogen gas is allowed to disappear. Is any work being done? Yes () No () Do not know ()

Motivate:....................

(b) A chemical reaction between sodium and water takes place and hydrogen gas is formed. The volume of the formed hydrogen gas can be determined by leading the gas into a syringe. Is any work being done? Yes () No () Do not know ()

Motivate:....................

(c) A chemical reaction between sodium and water takes place and hydrogen gas is formed. The formed hydrogen gas blows up a balloon. Is any work being done? Yes () No () Do not know ()

Motivate:....................

• Y. As a chemical reaction occurs the enthalpy change of a reaction ΔH might be different from the change in internal energy ΔU for the reaction. (a) Give an example of a reaction where ΔH ≠ ΔU and (b) motivate why your reaction supports ΔH ≠ ΔU. (New)

• Z. The reaction between magnesium metal and hydrochloric acid in a closed apparatus at either constant pressure A or constant volume B with the questions, (a) In which set of apparatus, A, B or both, do you think most heat is given out to the surroundings? (b) In which set of apparatus, A, B or both, does energy transferred as heat equal the reaction enthalpy? (cf.Sözbilir, 2001).

The written task X was used in pre and post questionnaires and the two written tasks Y, Z were included in one exam during the course and the post questionnaire. Five students were interviewed pre teaching and four students post teaching. During the interviews, the students explained three or more of the following reactions taking place in front of them: The endothermic dissolution of ammonium chloride, the exothermic dissolution of sodium hydroxide, the decomposition of sodium hydrogen carbonate and the reaction between magnesium and hydrochloric acid. These reactions have been used before in chemistry education research (e.g.,Boo, 1998; Carson, 2001; de Vos and Verdonk, 1986). The interview technique was White and Gunstone's (1992) “Interviews about Instances and Events” (p. 65). The result in HS was an outline to a matrix and categories regarding work and expansion work.

The follow-up study was designed to explicitly test the matrix and categories regarding work and expansion work. This means that the aim was further focused on enthalpy, its change and related concepts; hence only the most useful written tasks X, Y, Z were included. The tasks were used in pre and post questionnaires, hand-ins and exam questions. During the research process the ethical guidelines developed by the Swedish Research Council have been followed (Vetenskapsrådet, 2002).

Data analysis

During the analytical process a descriptive category was formulated: “Work is a concept needed to describe the enthalpy change”. It was later developed into “Students mainly understand expansion work as a function of volume”. This category can be described as a feeling coming from the continuous reading of students' responses (Nilsson, 2011). In order to investigate this feeling an analytical instrument was developed. The analytical instrument is a logical matrix, see Table 1 below, for determining students' use of pressure and volume in their explanations of the tasks. Table 1 shows the three different ways to express volume and pressure respectively, as constant, varying or not at all. All these possibilities are described in the matrix. Each square in the table indicated a specific description of how students use volume and pressure in order to describe work and expansion work, or, in the follow-up study, technical work. For instance, the intersection between ΔP = 0 and ΔV ≠ 0 indicates that the pressure is constant and the volume changes which indicates a proper definition of expansion work (pΔV). The analytical process is visualized in Fig. 1.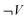

Table 1 Matrix for determining students' use of pressure and volume. ΔV = 0 means that volume is expressed as constant, ΔV ≠ 0 means varying volume and means that volume is not expressed. For pressure, P, the analogous explanation holds

	ΔV = 0	ΔV ≠ 0
ΔP = 0
ΔP ≠ 0

---

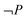
Fig. 1 Connection between the theoretical codes and the iterative analytical process. The analytical process is a development from Niedderer (2001).

By using Table 1 students' answers including work could be analysed. In the following example the student answers the question: Give an example of a reaction where ΔH ≠ ΔU. The student answers: E.g. the combustion of a substance which increases in volume (S8, HS Exam 1, task Ya). The combustion of a substance which increases in volume is a correct example and, as described above, there are several correct scientific answers that supports ΔH ≠ ΔU, since ΔH = ΔU + Δ(pV). However, the student had been introduced to enthalpy change as ΔH = ΔU + pΔV. Therefore the sought explanation lies in the intersection between ΔP = 0 and ΔV ≠ 0 since pΔV ≠ 0. The student only expresses the volume change and the answer is described by the intersection and ΔV ≠ 0.

All answers regarding expansion work, in general or specifically, could be described using the matrix but when using the matrix two limitations became obvious. First the question must include something regarding work and second the student had to explicitly explain what he or she meant by work.

As a consequence, answers without any explicit references to work could not be analysed using the matrix. Answers including work without any reference to pressure or volume were categorized as and 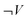. Finally, when work was expressed, for instance ΔP = 0 and ΔV ≠ 0 it could still be a contextually incorrect description. The matrix was insufficient in analysing the contextual correctness of each answer.

Therefore a category system was developed in order to analyse students' responses with respect to contextual correctness. The analytical approach follows the description given by B. Andersson and Wallin (2000) “[…] answers may include several factors that explain a certain phenomenon, and most answers may contain a unique combination of factors. In this case, the category system consists of definitions of the factors, and the categorizing is simply to record what factors are present in each answer.” (p. 1100).

The developed categories were based on a contextual interpretation of each answer. The first author gave each task a correct response with respect to pressure and volume, for instance in task Z where a completely correct description of apparatus B would be changing pressure (ΔP ≠ 0) and constant volume (ΔV = 0). All answers on task Z were analysed with respect to this correct description of apparatus B. For instance: ΔH = q in B The enthalpy change is transformed into heat energy when there is no change in pressure and volume (SK4, FS Exam, task Zb).

Here the student answers the question (b) In which set of apparatus, A, B or both, does energy transferred as heat equal the reaction enthalpy? Apparatus B is described as no change in pressure and volume which is interpreted as constant pressure (ΔP = 0) and constant volume (ΔV = 0). The answer clearly deviates from the correct response given by the first author. However, constant volume is contextually correct and even if the entire answer as such is considered to be incorrect it still contains correct elements.

Therefore, the answer is considered contextually correct with respect to volume but contextually incorrect with respect to pressure. This feature of each student's answer was coded. If the volume was described contextually correct by a student it was coded V1. If the volume was not mentioned by the student it was coded as V2. Contextually incorrect descriptions made by a student were coded as V3. The analogous reasoning holds for pressure (P1, P2 and P3), hence each student’s answer was given two codes and these codes together yield nine (3 × 3) different qualitative combinations (VxPx) as they are combined. The combinations (VxPx) say something about the correctness of the answers, how students may describe situations where expansion work and technical work are part of the answers and if some features of theory are more commonly present in their answers.

By developing these categories the results given by the analysis using Table 1 could be understood more completely. The categories based on the different qualitative combinations (VxPx) are given in Table 2.

Table 2 Categories used to analyse students' answers regarding work, expansion work and technical work. Correct description of volume is coded as V1, no description of volume is coded V2 and incorrect description of volume is coded V3 (identical description for P1, P2 and P3 with respect to pressure). W is the category

Description of the category	Description of sub category	Example	Combination of V and P
W1 are contextually correct explanations of expansion work and technical work with respect to V and p	W1.1 Scientifically accepted explanations of expansion work	The pressure is constant and the system expands No work, pressure is constant and there is no volume change	V1P1
	W1.2 Scientifically accepted explanations of technical work	A pressure change at constant volume No work, the volume is constant and there is no change in pressure
W2 are incomplete descriptions of expansion work and technical work with respect to V and p	W2.1 The volume is described correctly but the pressure is not mentioned	In A the volume increases	V1P2
	W2.2 The pressure is described correctly but the volume is not mentioned	The pressure is constant in A	V2P1
W3 are incorrect descriptions of expansion work and technical work with respect to V and/or p	W3.1 The volume is described correctly but the pressure is described incorrectly	In A the volume increases and so does the pressure	V1P3
	W3.2 The volume is described incorrectly but the pressure is described correctly	In A both volume and pressure are constant	V3P1
	W3.3 Either volume and pressure are described incorrectly or one is describe incorrectly whilst the other is not mentioned	In A the volume is constant	V3P3 V3P2/V2P3
W4 are general descriptions of work	W4.1 Incomplete descriptions. It is impossible to analyse the answer with respect to pressure or volume even though similar words are used.	The gas pushes the piston, where pushes could indicate increased pressure and/or a volume change.	V2P2
	W4.2 All answers including work without any reference to pressure or volume as described in W1–W3	In A work is done

---

Results

In this section only the results of the analysis using the matrix (Table 1) and descriptive categories (Table 2) are given. A deeper qualitative analysis of the answers has been made (Nilsson, 2011). Of the total number of 969 written answers in the main study and 222 in the follow-up study, 156 (16%) and 133 (60%) answers, respectively, were analysed with respect to work, expansion work and technical work. The difference in percentages indicates the focused aim in the follow-up study. In 64 (41%) and 84 (63%) of the 156 and 133 answers, respectively, work was included by the students. In three answers in the follow-up study work was described in more than one way, thus the total number of answers is less than the total number of explanations of work.

Results not considering contextual correctness

Table 3 shows the first categorization when no respect to contextual correctness was considered. Since no reference is made to contextual correctness the table is interpreted with respect to each column, row and intersection, hence

• The most common way to describe work is without reference to volume and pressure . It means that work is described generally. This pattern can be found in both studies (HS: 37.5% and FS: 31.0%, Table 3).

• Specific descriptions of volume and its change are more common than specific descriptions of pressure. As can be seen in Table 3 the students in the main study describe the properties of volume (ΔV = 0/ΔV ≠ 0) in 54.7% (6.3% + 48.4%) of the answers while the properties of pressure (ΔP = 0/ΔP ≠ 0) are only described in 32.8% (21.9% + 10.9%) of the answers. In the follow-up study the frequencies are 60.9% (10.3% + 50.6%) and 49.4% (37.9% + 11.5%), respectively.

• If volume is described as constant (ΔV = 0) in the main study the students mainly describe pressure as constant (ΔP = 0). Constant pressure is described in three of four answers in the column (ΔV = 0). Students in the follow-up study mainly describe constant volume (ΔV = 0) with varying pressure (ΔP ≠ 0), since eight out of nine answers in the column (ΔV = 0) is a combination of these two.

• If volume is described as varying (ΔV ≠ 0) by the students in the main study, pressure is excluded in 18 out of 31 answers , see Table 3. The remainder of answers are divided between constant pressure (ΔP = 0) and varying pressure (ΔP ≠ 0), hence varying volume is combined with different features of pressure. If volume is described as varying (ΔV ≠ 0) by the students in the follow-up study, pressure is excluded in 17 out of 44 answers . In 26 of the remaining 27 answers students combine varying volume with constant pressure (ΔP = 0), hence work is either varying volume or varying volume at constant pressure.

• As described in the first point above any answers without reference to volume are often associated with general descriptions of work. The column in Table 3 shows that 24 of 29 answers in the main study and 27 of 34 in the follow-up study are categorized as . But, the remaining answers categorised as are mostly combined with constant pressure. Four out of five of the remaining answers in the main study and six out of seven in the follow-up study are combinations of .

• If pressure is constant (ΔP = 0) Table 3 shows that students in the main study tend to describe the volume either as constant (ΔV = 0), varying (ΔV ≠ 0) or not at all . In the follow-up study students mainly describe volume as varying (ΔP ≠ 0) or not at all .

• In six out of seven answers in the main study students explain varying pressure (ΔP ≠ 0) together with varying volume (ΔV ≠ 0). In eight out of ten answers in the follow-up study students explain varying pressure (ΔP ≠ 0) together with constant volume (ΔV = 0).

• As described in the first point above any answers without reference to volume are often associated with general descriptions of work. The row in Table 3 shows that 24 out of 43 answers in the main study and 27 out of 44 in the follow-up study are categorized as 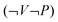. However, the remaining answers categorised as are mostly combined with varying volume. 18 out of 19 remaining answers in the main study and all in the follow-up study are combinations of .

• Pressure is more often excluded than volume when work is explained. This is a fair interpretation of all the points above. Table 3 shows that 67.2% of the answers in the main study and 50.6% of the answers in the follow-up study are categorised as , while 45.3% of the answers in the main study and 39.1% in the follow-up study are categorised as . Hence, work is mainly a function of volume.

Table 3 Analysis using Table 1. How students use volume and/or pressure to explain work, expansion work and technical work, not looking for correct or incorrect answers. ΔV = 0 indicates constant volume, ΔV ≠ 0 indicates volume change and indicates that volume is not mentioned. ΔP = 0, ΔP ≠ 0, are analogues for pressure, n main study = 64, n follow-up study = 87. The total sum may differ from 100%

		ΔV = 0		ΔV ≠ 0				Sum
		HS	FS	HS	FS	HS	FS	HS	FS
ΔP = 0	N	3	1	7	26	4	6	14	33
	%	4.7	1.1	10.9	29.9	6.3	6.9	21.9	37.9
ΔP ≠ 0	N	0	8	6	1	1	1	7	10
	%	0	9.2	9.4	1.1	1.6	1.1	10.9	11.5
	N	1	0	18	17	24	27	43	44
	%	1.6	0	28.1	19.5	37.5	31.0	67.2	50.6
Sum	N	4	9	31	44	29	34	64	87
	%	6.3	10.3	48.4	50.6	45.3	39.1

---

The results without contextual correctness can be summarised as follows: 59% of the answers in the main study and 37% of the answers in the follow-up study are blank. If answers are given, a majority of the students include work in a general manner, hence indicating that the students are aware of work but they do not explicitly explain work, in the current task, with respect to volume and pressure. If volume and pressure are explicitly expressed students tend to describe the properties of volume to a greater extent than the properties of pressure.

However, Table 3 does not indicate the number of correct responses and therefore the contextual analysis based on Table 2 is important.

Results including a consideration of contextual correctness

Table 4 shows how common the categories in Table 2 are in the data set. This results section is divided into six parts. The first part below addresses general description of work. In the second part expansion work and the proper use of volume is addressed. The third part includes technical work as well as the proper use of pressure. The fourth part gives insight in the incorrect answers and the fifth part describes when the categories are active. The sixth and final part is a summary of the results.

Table 4 Analysis using Table 2. Contextual analysis of answers regarding work expansion work and technical work, n main study = 64, n follow-up study = 87. The total sum may differ from 100%

Sub Category	Number of answers HS	Number of answers FS	Sum
W1.1 Correct	9 (14.1%)	21 (24.1%)	30
W1.2 Correct	0 (0%)	6 (6.9%)	6
W2.1 Incomplete	17 (26.6%)	11 (12.6%)	28
W2.2 Incomplete	1 (1.6%)	4 (4.6%)	5
W3.1 Incorrect	5 (7.8%)	0 (0%)	5
W3.2 Incorrect	1 (1.6%)	1 (1.1%)	2
W3.3 Incorrect	3 (4.7%)	7 (8.0%)	10
W4.1 Incomplete	5 (7.8%)	10 (11.5%)	15
W4.2 Incomplete	23 (35.9%)	27 (31.0%)	50
Sum	64 (100.1%)	87 (99.8%)	151

---

The general description of work (W4.1/W4.2)

Again Table 4 shows the general description of work since 23 answers (35.9%) in the main study and 27 answers (31%) in the follow-up study are categorized as W4.2. This categorization can be compared to the intersection in Table 3. The difference in frequencies is due to context. In another five answers (7.8%) in the main study, and ten answers (11.5%) in the follow-up study, students do not express volume or pressure explicitly which makes it impossible to determine if the answers are correct or not. Examples are for instance: the gas pushes the piston, or the gas fills the syringe. Without words like the gas expands, or ΔV ≠ 0 the answer the gas fills the syringe is categorized as W4.1.

Expansion work (W1.1) and the proper use of volume (W2.1/W3.1)

Expansion work, w = pΔV, is explained in a contextually correct way in nine answers (14.1%) in the main study and 21 answers (24.1%) in the follow-up study (W1.1), see Table 4. This means two things: Either students describe work as a volume change at constant pressure, or the absence of work if volume and pressure are constant. Since there is a difference in the relative frequencies between the studies, students in the follow-up study more often express expansion work correctly, hence educational level may be important. These frequencies suggest that many students are not able to describe the expansion work correctly when faced with actual situations. However, the picture is slightly changed when contextually correct descriptions of volume are also included. Work as function of only volume is described in a contextually correct way in 17 answers (26.6%) in the main study and 11 answers (12.6%) in the follow-up study (W2.1).

Furthermore, a contextually correct volume together with a contextually incorrect pressure is expressed in five answers (7.8%) in the main study (W3.1). These results indicate that it is likely for students in the main study to express work as a function of volume correctly (tot: 48.5%). The difference between the studies, hence educational levels, seems to be how pressure is used together with volume to explain work. Students seem to have more difficulties with the relation between work and pressure than the relation between volume and work.

Technical work (W1.2) and the proper use of pressure (W2.2/W3.2)

However, do note that technical work is described in a contextually correct way in six answers (6.9%) in the follow-up study (W1.2), see Table 4. Pressure is described correctly while volume is not described at all in one answer (1.6%) in the main study and four answers (4.6%) in the follow-up study (W2.2). Correctly described pressure together with incorrectly described volume can be found in one answer (1.6%) in the main study and one answer (1.1%) in the follow-up study (W3.2). These results indicate that technical work is not often described and that pressure in general seems to be less present in the descriptions of work.

Incorrect contextual descriptions of work

Table 4 shows that completely incorrect contextual descriptions of work are given in three answers (4.7%) in the main study and seven answers (8%) in the follow-up study (W3.3). The reasons for completely incorrect contextual answers are

• Pressure and volume need to change at the same time (S7, HS, Exam 1, task Ya). It is considered incorrect since the student does not give any further explanation of what he means and the fact that students in the main study were introduced to the definition of enthalpy change at constant pressure ΔH = ΔU + pΔV. However, it is still possible that S7 actually refers to the general definition ΔH = ΔU + Δ(pV).

• Students refer to the definition of enthalpy H = U + pV when describing work. Their argument is based on fixed values of p and V (S2 and S18, HS, Exam 1, task Zb/SK1 and SK5, FS, Hand in 3, task Yb).

• Processes carried out at constant pressure are explained using technical work w = Vdp or VΔp, which is contextually incorrect since volume changes (SK1, SK6 and SK7, FS, Hand in 2, Zb).

• An open vessel equals free expansion (SK1 and SK9, FS, Post questionnaire Xa). However, the use of free expansion as an explanation might be due to the fact that the surrounding is not described explicitly.

Only students in the follow-up study use technical work and free expansion incorrectly. This is not surprising since students in the main study are not introduced to technical work during teaching. Since the theoretical background changed between the two studies, one of the major revisions taking place was in fact that technical work (Vdp) was included in the descriptive categories.

The presence of categories over time

Table 5 below lists when the different descriptive categories are activated. Table 5 shows that pre teaching three categories are visible in the data (W2.1/W4.1/W4.2). This indicates that prior to teaching, as students begin their tertiary level education (HS) or as the students begin their second chemistry semester (FS), work, expansion work and/or technical work are described as a volume change, generally or in such a way that makes it impossible to determine how pressure and volume are used.

Table 5 When the descriptive categories are active. √ = active, — = not active, * = only HS, ** = only FS

Sub category	Pre teaching (questionnaires)	During teaching (hand ins and exams)	Post teaching (questionnaires)
W1.1	—	√	√**
W1.2	—	√**	—
W2.1	√	√	√
W2.2	—	√	—
W3.1	—	√*	—
W3.2	—	√	—
W3.3	—	√	√**
W4.1	√	√	√
W4.2	√	√	√

---

During teaching all descriptive categories are active and post teaching one correct category (W1.1) and one incorrect category (W3.3) were found in the data from the follow-up study. It is also notable that during the interviews in the main study not one correct description of expansion work was given.

Summary of results

In order to summarise the results it is important to keep in mind that close to 74% of the answers in the main study and 57% of the answers in the follow-up study were blank.

Of the analysable answers the most common description of work did not include any reference to pressure or volume (W4.2). It is more common for students in the follow-up study to describe work, expansion work and technical work correctly.

The incorrect descriptions of work, expansion work and/or technical work (W3.1–W3.3) are not common, but together with the incomplete descriptions, work is most often viewed as only a function of volume.

Discussion and concluding remark

When viewing the results it is important to emphasize that the analysed answers are given to questions explicitly probing work, expansion work, technical work and the difference between enthalpy change and change in internal energy. The general result is that students tend to describe work as a function of volume. At the same time pressure can be constant, varying or not mentioned at all. In the follow-up study work is not limited to expansion work, instead technical work w = Vdp or VΔp is also included in the course content. As students refer to technical work it indicates the use of the general definition of enthalpy change dH = dU + d(pV) or ΔH = ΔU + Δ(pV). However, in three of nine answers regarding technical work the descriptions are incorrect, hence the general definition of enthalpy change creates new opportunities for students in the follow-up study to explain the tasks, but the general definition does not automatically lead to correct answers. The absence of the category W1.2 in the main study is probably due to no explicit reference to technical work during teaching. In fact the teacher explicitly stated that he did not focus on such processes. Therefore, enthalpy change was only described as ΔH = ΔU + pΔV.

Regardless if the general definition of enthalpy change or the applied definition at constant pressure is used, the definitions do not seem to support students' arguments unless the conditions constant pressure or constant volume are considered first. Only then is it possible to apply the proper definition. It is also possible to argue that constant volume/varying pressure cases should not be compared to constant pressure/varying volume cases if students have only been introduced to ΔH = ΔU + pΔV, since the definition is not valid for constant volume/varying pressure cases.

In research, the investigate aspect of work has not been given much attention, but it is known that work in general, and specifically expansion work is problematic for chemistry students (e.g.,Carson, 2001; Hadfield and Wiedman, 2010; Johnstone et al., 1977; Sözbilir, 2001; van Roon et al., 1994). Both Carson (2001) and Sözbilir (2001) report that students state that enthalpy change is heat when no work is done, hence volume is constant. Carson (2001) points out that when students apply the definition for enthalpy change expansion work and/or constant pressure are often excluded. In none of the previous results is it clarified how students actually use volume and pressure to describe work. This study gives insights both into the ways work is described as well as the contextual correctness of these descriptions.

The problems seem to be perceiving work as a function of two variables, pressure and volume, and determining when the definition of enthalpy change as heat at constant pressure is valid. This study indicates that one possible explanation is the generalized use of the definition ΔH = ΔU + pΔV.

The generalisability of the study must also be addressed. Of course the generalisability is limited by the small sample size, but in these two cases (HS and FS) all answers from all students were analysed and therefore it is a fair picture we present here. It is difficult to say anything about the differences due to educational levels since the teachers address the course content differently. Processes where either pressure or volume changes are addressed in the follow-up study. This leads to a natural tendency towards more answers regarding expansion work, hence w = pΔV. The results in Tables 3 and 4 can only be fully understood under these limitations. However, it is possible that similar studies carried out elsewhere using exam questions, hand-ins or questionnaires would yield a similar result.

In fact neither the matrix nor the descriptive categories are constructed from data in this study. Instead they are logical patterns used on data, hence they could have been formulated without empirical evidence. However, without the continuous reading of empirical evidence early in the analytical process, the feeling that led to the results would never have come. The matrix and the categories are applicable when applied to empirical evidence from written tasks. If the aim is to use the matrix and the categories on interview data a revised interview design and questions must be prepared, thus focusing much more explicitly on expansion work and technical work. In this study the interviews took place before the continuous reading and therefore had a different purpose.

Despite this limitation we are certain that a more focused interview would allow us to use the matrix and categories on interview data also. In our mind the evolution of the matrix and categories is important since both teachers and researchers can use the analytical tools. Teachers may use them in class or on written responses (exams) in order to gain insight into possible learning difficulties. Larger sets of data can be analysed by researchers and, in fact, students can also use the matrix. However, the descriptive categories require contextual awareness and therefore we argue that primarily teachers and researchers should use them unless they are part of a teaching unit. In this teaching unit the analytical tools can be used as teaching tools in order to allow students to test themselves, hence different descriptions can be addressed by the teacher, thus opening a classroom dialogue.

Since each category describes a qualitatively different aspect of how students use volume and pressure, teachers or researchers may find many interesting results when analysing students' answers on certain tasks. There exist other qualitative categories which explain some of the patterns found here, but due to the scope of this article they will not be presented here (see Nilsson, 2011).

Acknowledgements

We would like to thank the Swedish National Graduate School in Science, Technology and Mathematics Education Research (FontD) for their financial support.

References

1. Andersson B. and Wallin A., (2000), Students' Understanding of the Greenhouse Effect, the Societal Consequences of Reducing CO2 Emissions and the Problem of Ozone Layer Depletion, J. Res. Sci. Teach., 37, 1096–1111.
2. Andersson S., Sonesson A., Stålhandske B., Tullberg A. and Rydén L., (2000), Gymnasiekemi A [Upper Secondary Chemistry A], Stockholm: Liber AB.
3. Andersson S., Sonesson A., Stålhandske B., Tullberg A. and Rydén L., (2001), Gymnasiekemi B [Upper Secondary Chemistry B], Stockholm: Liber AB.
4. Atkins P. W. and de Paula J., (2005), Elements of Physical Chemistry, Oxford: Oxford University Press.
5. Barker V. and Millar R., (1999), Students' reasoning about chemical reactions: What changes occur during a context-based post-16 chemistry course, Int. J. Sci. Educ., 21, 645–666.
6. Barker V. and Millar R., (2000), Students' reasoning about basic chemical thermodynamics and chemical bonding: What changes occur during a context-based post-16 chemistry course? Int. J. Sci. Educ., 22, 1171–1200.
7. Bethge T., (1988), Aspekte des Schülervorverständnisses zu grundlegenden Begriffen der Atomphysik, Bremen: Universität Bremen.
8. Bodner G. M. and Herron J. D., (2002), Problem-Solving in Chemistry, In J. K. Gilbert, O. de Jong, R. Justi, D. F. Treagust and J. van Driel (ed.), Chemical Education: Towards Research-Based Practice (pp. 235–266), Dordrecht: Kluwer Academic Publishers.
9. Boo H.-K., (1998), Students' Understanding of Chemical Bonds and the Energetics of Chemical reactions, J. Res. Sci. Teach., 35, 569–581.
10. Boo H.-K. and Watson J. R., (2001), Progression in High School Students' (aged 16–18) Conceptualizations about Chemical Reactions in Solution, Sci. Educ., 85, 568–585.
11. Bryman A., (2008), Social Research Methods (3rd ed.), Oxford: Oxford University Press.
12. Carson E., (2001), A Study of Undergraduate Students' Understanding of Selected Concepts in Chemical Thermodynamics, Unpublished PhD University of London, School of education.
13. Carson E. and Watson J. R., (1999), Undergraduate students' understanding of enthalpy change, U. Chem. Ed., 3, 46–51.
14. Carson E. and Watson J. R., (2002), Undergraduate students' understandings of entropy and Gibbs free energy, U. Chem. Ed., 6, 4–12.
15. Chang R., (2007), Chemistry (9th ed.), Boston: McGraw-Hill Higher Education.
16. de Vos W. and Verdonk A. H., (1986), A new road to reactions: Part 3. Teaching the heat effects of reactions, J. Chem. Educ., 63, 972–974.
17. Drechsler M., (2005), Textbooks', teachers', and students' understanding of models used to explain acid-base reactions, Licentiate thesis, Karlstad: Karlstad University.
18. Gabel D., (2003), Enhancing the Conceptual Understanding of Science, Educ. Horiz., 81, 70–76.
19. Goedhart M. J. and Kaper W., (2002), From Chemical Energetics to Chemical Thermodynamics, In J. K. Gilbert, O. de Jong, R. Justi, D. F. Treagust and J. van Driel (ed.), Chemical Education: Towards Research-Based Practice (pp. 339–362), Dordrecht: Kluwer Academic Publishers.
20. Hadfield L. C. and Wieman C. E., (2010), Student Interpretations of Equations Related to the First Law of Thermodynamics, J. Chem. Educ., 87, 750–755.
21. IUPAC, (2007), Quantities, Units and Symbols in Physical Chemistry (3rd ed.), Cambridge: Royal Society of Chemistry.
22. Johnstone A. H., MacDonald J. J. and Webb G., (1977), Misconceptions in school thermodynamics, Phys. Educ., 12, 248–251.
23. Kim E. and Pak S.-J., (2002), Students do not overcome conceptual difficulties after solving 1000 traditional problems, Am. J. Phys., 70, 759–765.
24. Kvale S., (1996), Interviews: An Introduction to Qualitative Research Interviewing, Thousand Oaks, Calif.: Sage.
25. Laidler K. J., Meiser J. H. and Sanctuary B. C., (2003), Physical Chemistry (4th ed.), Boston: Houghton Mifflin.
26. Mazur E., (1997), Peer Instruction, Upper Sadle River, NJ: Prentice Hall.
27. Niedderer H., (2001), Analyse von Lehr-Lern-Prozessen beim elektrischen Stromkreis aus Videodaten, In S. von Aufschneiter and M. Welzel (ed.), Nutzung von Videodaten zur Untersuchung von Lern-Lehr-Prozessen–Aktuelle Methoden empirischer pädagogischer Forschung, Münster: Waxmann.
28. Nilsson T., (2011), Kemistudenters föreställningar om entalpi och relaterade begrepp [Undergraduate chemistry students' conceptions of enthalpy and related concepts], Doctoral Thesis, Västerås: Mälardalen University.
29. Robson C., (2002), Real world research: a resource for social scientists and practitioner-researchers (2nd ed.), Oxford: Blackwell Publishing.
30. Sözbilir M., (2001), A Study of Undergraduates' Understandings of Key Chemical Ideas in Thermodynamics, Unpublished PhD University of York, Department of educational studies.
31. Thylander E. and Johansson B., (1999), Kemi 1000 övningsuppgifter i kemi på gymnasienivå med facit och fullständiga lösningar [Chemistry 1000 exercises in chemsitry for upper secondary level together with key and complete solutions], Göteborg: Konvergenta HB.
32. Tsaparlis G., (2008), Teaching and Learning Physical Chemistry: A review of Educational Research, In M. D. Ellison and T. A. Schoolcraft (ed.), Advances in Teaching Physical Chemistry, Washington, DC: American Chemical Society.
33. van Roon P. H., van Sprang H. F. and Verdonk A. H., (1994), ‘Work’ and ‘Heat’: on the road towards thermodynamics, Int. J. Sci. Educ., 16, 131–144.
34. Vetenskapsrådet, (2002), Forskningsetiska principer inom humanistisk-samhällsvetenskaplig forskning [research ethics principles in humanistic-social scientific research], Stockholm: Vetenskapsrådet.
35. White R. and Gunstone R., (1992), Probing Understanding, London: The Falmer Press.
36. Zumdahl S. S. and Zumdahl S. A., (2007), Chemistry (7th ed.), Boston, Mass.: Houghton Mifflin Co.

---