Is mathematics to blame? An investigation into high school students' difficulty in performing calculations in chemistry

Abstract

Mathematical ability is a major contributory factor to the success of a student in any science course. This paper aims to determine the source of the difficulty that students often find when performing calculations in chemistry. Through the design and analysis of a set of chemistry questions and analogous mathematics questions, set in a Standard Grade context, it is revealed that a basic grasp of mathematics is missing.

---

Introduction

The importance of mathematical ability as applied to chemical education has recently gained much attention in the media due to both the chemical industry and academia having commented on students' poor grasp thereof (Royal Society of Chemistry, 2009a). This has led to the development of a number of different initiatives and resources by the Royal Society of Chemistry, and collaborators, in order to ameliorate the situation (Royal Society of Chemistry, 2009b–c). With such a significant impact on the chemical sciences, and more broadly the scientific community as a whole, it would seem prudent to further investigate the origin of such difficulties that students display in carrying out chemical calculations.

Students' mathematical readiness for various stages of their chemical education has been known for some time to be an important contributor, perhaps even an indicator, to their effectiveness as fledgling chemists. As far back as 40 years ago researchers were developing “Mathematical Readiness” tests to ensure that students were satisfactorily equipped with the correct set of fundamental, mathematical skills to allow them to perform and understand chemical calculations. Weisman (1981) identifies a number of areas of a High School chemistry course that necessitate a mathematical proficiency, including: stoichiometry problems; Avogadro's number; and, balancing equations. Denny (1971) deconstructs the array of chemical calculations that a High School student was expected to be able to perform into 10 fundamental mathematical skills: computation; use of parentheses; signed number usage; use and manipulation of fractions; use of decimals; use of exponents, manipulation of numbers with exponents and logarithmic equivalence; use of percentage; manipulation of one-variable equations; use of ratio and proportion; and, producing and interpreting x, y graphs. Both of the aforementioned researchers then use their pedagogical knowledge to prepare tests that enable teachers to evaluate their students' mathematical knowledge in order to direct further teaching.

A myriad of researchers have extensively investigated the problems students face when presented with the more mathematically demanding aspects of a chemistry course: molar or stoichiometric calculations. Gable and Sherwood (1984) have identified the terminology “mole” to be a confusing factor for students. Novick and Menis (1976) suggest that the phonetic similarity to “molecule”, “molecular” etc., makes a significant impact. Even IUPAC appear to contribute to the confusion; Strömdahl et al. (1994) suggest that scientists and educators possess misconceptions about the definition of the mole, largely introduced through continued alterations to the definition by the regulatory body. Dierks et al. (1985) go as far to suggest an alternative to the mole when dealing with molecular quantities.

More mathematical and problem solving issues are alluded to by Lazonby et al. (1982) in which the inability to carry out the sequential application of basic mathematical operations is concluded to be detrimental overall. Further to this, the algorithmic approach of dimentional analysis, common in use and which would assist in obviating the observation of Lazonby et al. (1982), may generate the correct answer but does not confer understanding (Lythcott 1990). Some researchers have suggested that a more language rich version of dimensional analysis, with the inclusion of verbs and nouns in the description of the chemical system, may impart a greater degree of understanding compared to the classical approach (DeLorenzo, 1994).

A number of studies have been carried out that investigate the correlation between success in chemistry, and other science courses, and a multitude of variables. It has been suggested that theories of cognitive development can be related to scientific success in both High School level and Undergraduate education. (Bitner, 1991; Griffith, 1985; Hurst and Milkent, 1996). The non-cognitive variables, academic self-concept and student attitude, have been investigated by House (1995) and have been shown to be useful predictors of success in chemistry at an Undergraduate level. Each of these studies identifies appropriate mathematical skill as a necessary feature before the other factors can influence the success in the respective scientific discipline. At an undergraduate chemistry level, Leopold and Edgar (2008) have demonstrated that mathematical ability is correlated to success, and in particular they highlight the importance of non-calculator skills.

A number of factors clearly contribute to students' performance in chemical calculations, these being conceptual, numerical or problem solving in nature. It is an observation of the author that current High School students display an inadequate understanding of fundamental mathematical operations, like those identified by Denny (1971). As such, the aim of this research is to examine the performance of Scottish High School students when carrying out chemistry critical numerical operations.

Research methodology

In order to examine the difficulty that students have in performing chemistry calculations and to determine whether or not their numerical abilities are deficient to the extent in having a significantly detrimental effect, it was necessary to design a series of appropriate questions. A set of 8 chemistry questions were constructed that 4th year Standard Grade chemistry students, who are 16–17 years of age, are expected to be proficient in. These were used to design an analogous set of questions in which the chemical context was removed, leaving a set of questions that students would be expected to perform in a mathematics class; these will be referred to as the chemistry questions and the mathematics questions, respectively. The question set was subjected to review by the class teachers of the intended student cohort in order to ensure suitability of content and to ensure that the questions were constructed in a manner commensurate with student understanding.

Chem 1. Carbon has a formula mass of 12, how many moles are in 36 g of carbon?

Chem 2. What is the concentration of a 3 L solution that contains 6 moles of HCl?

Chem 3. Carbon has a formula mass of 12, how many moles are in 2 kg of carbon?

Chem 4. What is the concentration of a 100 mL solution that contains 0.2 moles of HCl?

Chem 5. Na has a formula mass of 23 and NaCl has a formula mass of 58.5. Calculate the percentage by mass of Na in NaCl.

Chem 6. Al has a formula mass of 27 and O has a formula mass of 16. Calculate the percentage by mass of Al in Al₂O₃.

Chem 7. The formula mass of C is 12, the formula mass of H is 1 and the formula mass of O is 16. Methane burns in oxygen to form carbon dioxide and water.

CH₄ + 2O₂ → CO₂ + 2H₂O

Given that 12 g of methane is burned, what mass of oxygen would be required?

Chem 8. Hydrochloric acid can react with magnesium hydroxide in a neutralisation reaction.

2HCl + Mg(OH)₂ → MgCl₂ + 2H₂O

Given that 2 L of a 2 mol/L solution of HCl are used, calculate the concentration required for a 1 L solution of magnesium hydroxide.

Chemistry calculations in the Standard Grade Chemistry course that involve using the mole concept fall broadly into two types: those requiring knowledge of the relationship between moles, mass and gram formula mass; and those between moles, concentration and volume. Both types are represented in this question set.

Questions Chem 1 and Chem 2 require a direct calculation involving the given data to generate the correct solution and, as such, form the most straightforward of the test questions in this study. Questions Chem 3 and Chem 4 are analogous to Chem 1 and Chem 2, respectively, and demonstrate a progression in difficulty due to the inclusion of a necessary unit conversion step. Moving away from the concept of the mole, Chem 5 and Chem 6 are assessing the students' capacity to calculate the percentage mass. Question Chem 5 has been worded to allow a direct calculation to take place; whereas, Chem 6 requires additional intermediate calculations to be performed before arriving at the solution. Questions Chem 7 and Chem 8 return to the mole concept and are examples of the most studied calculations in the literature pertaining to student performance. Despite being staple calculations in the Standard Grade Chemistry course (and most others of similar and higher level) these often present a great challenge for students. Both involve an initial calculation similar to Chem 1 or Chem 2, a method of relating the number of moles of two compounds and then a final calculation of similar complexity to the first.

This set of chemistry questions was used to develop an analogous set of mathematics questions in which the numerical complexity was similar but the chemistry context had been replaced with that which could be found in a Standard Grade Mathematics setting.

The numerical complexity of the two types of chemistry calculation involving the mole concept is identical; hence, one mathematics question could suffice as an analogue to both. This explains the fewer number of mathematics questions.

Math 1. A car travels 10 km in 2 hours. Calculate its speed in km/h.

Math 2. A plane travels 3000 m in 60 seconds. Calculate its speed in km/s.

Math 3. A cake that weighs 112 g in total has 5 g of sugar in it. What is the percentage by mass of sugar in the cake?

Math 4. The contents information on the side of a food product states the following:

Protein	0.02 g
Fat
Saturated	0.01 g
Unsaturated	0.02 g
Carbohydrate	0.02 g

What is the percentage by mass of the total fat content in the product?

Math 5. There are two different rectangles. The first has sides of length 4 m and m. The second has an area twice that of the first and one side of 2 m. What length is the other side?

Both Chem 1 and Chem 2 require one numerical operation and so a familiar concept from the Standard Grade Mathematics course that satisfies this requirement is the relationship between speed, distance and time; hence, question Math 1. This neatly allows for the introduction of a unit conversion to yield question Math 2, an analogue to both Chem 3 and Chem 4. Questions Math 3 and Math 4 are versions of the percentage by mass chemistry questions, Chem 5 and Chem 6, respectively. The first requires only a direct calculation; whereas, the stratification of the data in a table allows question Math 4 to more accurately simulate the steps required of question Chem 6. Finally, question Math 5 requires the same numerical procedure to both Chem 7 and Chem 8: an initial calculation using given data; numerical comparison between two items; and, another calculation. Table 1 summarises these pairing relationships between the chemistry and mathematics questions.

Table 1 Chemistry questions and their analogous mathematics questions

Chemistry question	Mathematics questions
Chem 1, Chem 2	Math 1
Chem 3, Chem 4	Math 2
Chem 5	Math 3
Chem 6	Math 4
Chem 7, Chem 8	Math 5

---

It was thought necessary that the students undergoing testing should not have prior knowledge of the reasons for the test. If students were made aware of the direct analogies between the chemistry and mathematics questions sets then performance on one set could potentially improve performance on the other. In obviation of this, the purpose of the test was purported to be probing the general numerical ability of the student body and the chemistry and mathematics questions were provided in a random sequence to mask any obvious similarities. Since students' ability in mental arithmetic was not under scrutiny in this investigation the cohort were allowed to utilise calculators. Additionally, the students were not subjected to any time constraints as this would likely increase the frequency of errors. It should also be noted that students were not penalised for the omission of units.

In order to obtain more information from this study, a short questionnaire was devised that could be administered to the students after completion of the initial test. This questionnaire first explained the purpose of the test and then demonstrated the analogies between each of the questions. The questionnaire then posed a series of exploratory questions in the hope of ascertaining student's awareness of the relationship between the two question sets (Table 2).

Table 2 Questionnaire questions

Question	Description
1	Whilst doing the questions did you realise that each chemistry question had a corresponding mathematics question?
2	Can you now see that the chemistry questions are related to the mathematics questions?
3	Can you easily recognise the chemistry questions from the mathematics questions?
4	Did you find the chemistry questions or the mathematics questions the most difficult?

---

Results and discussion

In order to ensure that adequate teaching time had been spent on concepts relevant to the content of the test, specifically the mole concept, it was decided to administer the test to pupils in 5th year, 16–17 years of age. The test material was thus completed by 52 pupils in a Scottish public school during a single Higher Chemistry class. This group comprised students from three different classes each of mixed ability and with a different teacher. Table 3 shows the student performance on each question.

Table 3 Student's performance

Chemistry question	% Correct answer	Mathematics questions	% Correct answer
Chem 1	88	Math 1	94
Chem 2	83	Math 2	69
Chem 3	65	Math 3	83
Chem 4	75	Math 4	79
Chem 5	73	Math 5	65
Chem 6	83
Chem 7	40
Chem 8	25

---

Student performance in the chemistry questions could be considered to be rather poor considering that the test was administered to students that were in the year above that for which the test was designed. This should mean that the students were comfortable with the entire content of the test as they were, at the time of sitting the test, expected to be able to perform calculations of increased complexity. Performance in questions Chem 7 and Chem 8 was particularly poor. This was of course expected as both of these questions involve the use of the mole concept, require several numerical operations and are of the type of question that was identified in the introduction as being particularly challenging for students to complete successfully. Despite this prior knowledge, the author was surprised to see a performance as low as 25% on question Chem 8.

The students' overall performance in the mathematics questions is more surprising still. With the exception of 94% correct for Math 1, the remaining performances are all poorer than expected. All of the questions in the mathematics question set could potentially be solved by students as young as 1st or 2nd year, perhaps even primary school for a few of them (Math 5 might be the exception as a close analogue of it could enter into the 4th year exams; however, the mathematics involved is not beyond those of earlier years). Although the mathematics question set is analogous to the chemistry question set in its numerical complexity, students have been carrying out similar questions in a mathematics setting for much longer. The knowledge required to carry out the chemistry calculations is only introduced to the students towards the end of 3rd year and therefore they are likely less familiar with it in comparison to the mathematics. This observation was even apparent to one of the students who made the following comment in the questionnaire:

“…maths has been done since primary school, granted not as hard as secondary but we are always taught how to deal with numbers whereas we only start chemistry properly in 3rd year as a standard grade”.

It would be expected that the students' performance on the mathematics question set should thus exceed the chemistry set.

Table 4 shows the other typical responses that the students gave in completing the questionnaire. The responses to questions 1 and 2 are not particularly informative; however, both questions 3 and 4 generate a few statements which are rather illuminating and will be made reference to further on.

Table 4 Questionnaire typical responses

Question	Typical response	% of Students giving similar response^a
a The percentages may not total to 100% as some of the students did not provide a response.
1	Yes	10%
	No	90%
2	Yes	100%
3	They are easily identifiable.	62%
	Yes, because elements from the periodic table are usually used in the chemistry questions.	23%
	Yes, the maths questions have specific methods to answer them.	12%
4	I found both sets of questions of equal difficulty. I think this is the case due to the similar simple skills we are using in both types of questions.	13%
	Chemistry was probably slightly harder but only just.	82%
	I found chemistry questions harder because the procedures were slightly different with each question and I had to think more about it.	5%

---

In order to establish whether or not there was a statistical difference between the scores achieved in each question set, a McNemar test was applied to the data. This was an appropriate statistical test to perform since a student's performance in a chemistry question and the corresponding mathematics question formed a matched pair of treatments. Table 5 summarises the results from the McNemar analysis of the data.

Table 5 McNemar test results

Question comparison	p-Value
Chem 1 and Math 1	0.453
Chem 2 and Math 1	0.109
Chem 3 and Math 2	0.824
Chem 4 and Math 2	0.383
Chem 5 and Math 3	0.125
Chem 6 and Math 4	0.774
Chem 7 and Math 5	0.021
Chem 8 and Math 5	0.000

---

In only two cases is the p-value below 0.05 and thus in only these cases can the null hypothesis, that the students’ performance in the two question sets is the same, be rejected: the comparison between Chem 7 and Math 5; and, the comparison between Chem 8 and Math 5. This indicates that there is no statistically significant difference in student performance between any of the other question pairs.

Taking into account the results of the McNemar test and the content of the question sets, a general observation can be made: there is no difference in student performance in the easier questions (Chem 1–Chem 6 and paired mathematics questions); whereas, in the harder questions, the students find the chemistry questions (Chem 7 and Chem 8) more challenging than the corresponding mathematics question (Math 5). This general observation in student performance is supported by the students' observations on their individual performances, as can be seen from the following example answers to question 4 in the questionnaire (Table 4).

In examining the solutions to the easier questions in the students' test scripts, the reasons for the incorrect answers were illuminated. Every single student attempted each question within the easy question set as might be expected due to the lack of difficulty. Considering the students' performance in Chem 1, Chem 2 and Math 1, the only reason for any incorrect answers was due to “silly” arithmetical mistakes such as not being able to perform simple arithmetic operations. Fig. 1 shows two such examples: on the left the student has been unable to carry out 2 divided by 12; on the right, the student has been unable to multiply 12 and 2.

Fig. 1 Examples of arithmetic errors.

Similarly, the incorrect answers to Chem 3, Chem 4 and Math 2 displayed poor grasp of division and also inability or not remembering to perform the required unit conversion. Fig. 2 shows another student’s attempt at one of the same questions from Fig. 1, although the correct number is achieved from the division, the student did not convert the 2 kg into 2000 g.

Fig. 2 Example of a student not performing a unit conversion.

The students' test scripts for the percentage mass questions, Chem 5, Chem 6, Math 3 and Math 4 all displayed consistent errors. Again, the inability to carry out a division correctly was the major source of error and, in addition to this, the students found Chem 6 and Math 4 to be more challenging as the numbers to use within the division needed to be generated for themselves. Fig. 3 illustrates a student unsuccessfully carrying out Math 4 due to the inability to extract and manipulate the correct information from the provided table prior to calculating the percentage.

Fig. 3 Example of a student not handling information correctly.

These observations in themselves do not generate much understanding of the inherent difficulties that students encounter with chemical calculations other than the possibility that the students may be deficient in the basic mathematical skills that are necessary to carry out the calculation.

By considering both the students' performance in the easier questions and their reflections on the comparison between the two question sets, it can be inferred that the normally stated reason for poor performance, the difficulty in understanding the concept of the mole, is unlikely to be the problem. If the molar concept was a problem for students then a difference in performance on the easier questions should have been seen. There was, however, a significant difference in the students' performance in the harder questions and since this cannot be explained by the notion of a difficulty in comprehension of the molar concept, an alternative explanation must be sought. The number of numerical operations to be carried out in solving a chemistry calculation is often deemed to significantly impact its difficulty. Whilst this is not being disputed, it does not explain the increase in difficulty experienced by the students as the analogous mathematics questions were designed to have the same number of numerical operations and thus this potential problem should have been factored out in this study. If the extra difficulties experienced in the chemistry set are neither due to the molar concept nor the number of mathematical operations, from where do they arise?

In order to answer this question it is necessary to examine the students' test scripts, paying attention to the answers provided for the harder questions (Chem 7, Chem 8 and Math 5). The following are a few choice examples from the students’ scripts that detail the spectrum of errors that were observed:

Fig. 4 Student's attempt at Chem 7.

Fig. 5 Student's attempt at Chem 7.

Fig. 6 Student's attempt at Math 5.

When attempting Chem 7 and Chem 8 there were primarily two types of common errors made. Students often managed to recognise the molar ratio between the two compounds of interest as being important yet are unable to utilise this fact successfully. Fig. 4 illustrates this as the student has used the balanced chemical equation to correctly write down the molar ratio between methane and oxygen; however, this was used to perform a conversion of mass, and not the moles, of the compound. Conversely, it was very common for students to exclude the necessary molar ratio step and thus obtain the incorrect solution. Fig. 5 shows that the student was able to obtain the number of moles of methane but used this directly, instead of involving the molar ratio, to calculate the mass of oxygen. For the mathematics question, the only incorrect solution that was encountered, other than no attempt being made, was using a familiar procedure from Standard Grade Mathematics: similar shapes. Fig. 6 clearly demonstrates a student applying this incorrect procedure.

In taking the incorrect answers and categorising them based on whether or not a student has demonstrated some understanding (got part of the question correct) or either not attempted the question or not provided any relevant working, an interesting pattern emerges (Table 6).

Table 6 Analysis of incorrect questions attempts

Question	Some understanding	Not attempted/Incorrect working
Chem 7	70%	30%
Chem 8	58%	42%
Math 5	12%	88%

---

Table 6 indicates that there is a tendency for the students to get the hard mathematics question either correct or incorrect; whereas, with the hard chemistry questions the students appear to be able to demonstrate some evidence of understanding.

This idea of students having a better understanding of the chemistry questions in comparison to the maths questions can be further exemplified in examining the correct answers provided by the students in their test scripts. In looking at the solutions to Chem 7, a number of different strategies were used. Fig. 7 shows a student using a very simple ratio approach in order to obtain the mass of oxygen. In contrast to this, another student has chosen to employ a more mathematically rich and complex approach, shown in Fig. 8, which has involved multiple calculations.

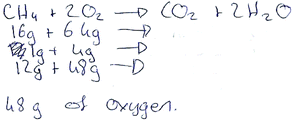Fig. 7 Student's correct solution to Chem 7.

Fig. 8 Student's correct solution to Chem 7.

Question Chem 8 presents a similar spectrum of techniques to obtain the correct answer. Fig. 9 shows a student using a similar set of workings as that demonstrated in Fig. 8, with all details of the calculation fully exposed. Contrary to this, the student's work illustrated in Fig. 10 shows another technique that begins with a simple equation to relate the quantities of a base to a neutralising acid.

Fig. 9 Student's correct solution to Chem 8.

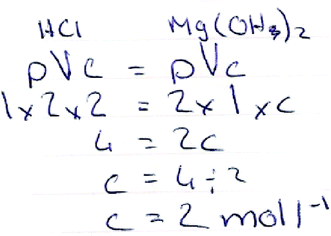Fig. 10 Student's correct solution to Chem 8.

The students that managed to provide the correct answer to Math 5 all used the same working to arrive at the solution. Fig. 11 demonstrates a typical example of the layout of the method that the students used. This example indicates a very logical and well practised approach to this type of question which was seen in all the other students' correct solutions. The responses to the questionnaire (Table 4) illustrate this idea as a number of the students indicated that “the maths questions have specific methods to answer them”.

Fig. 11 Student's correct solution to Math 5.

In order to establish the significance of the students' similarly presented solutions to Math 5, the same question in isolation was given to a small group of 7 6th year students, with an age range of 17–18. These pupils were selected to be of upper range mathematical ability with the view that their presumed greater understanding of basic mathematical principals would generate a diverse set of solutions. This was indeed the case and Fig. 12 illustrates a few of the students' solutions. The solution in the upper region of Fig. 12 is similar that of the original cohort of students with the exception that this one is more condensed in presentation. The solutions shown in the lower left and lower right both display different routes to the same correct answer which provides some evidence to the significance of the similarity in the solutions given by the students from the first question set.

Fig. 12 Students' diverse solution to Math 5.

The ability of the first cohort of students to utilise a number of different strategies to obtain a solution to the chemistry questions but using only one method in solving the maths question suggests that a fuller grasp of the chemistry, rather than the mathematics, may be present.

Conclusions

Mathematical ability is intrinsically involved in a student's performance in chemical calculations. This study looked at the performance of a cohort of 52 5th year Scottish High School students in a test comprised of chemistry questions and analogous maths questions. The aim was to elucidate any significant differences in ability between the two question sets and to use the students' solutions to determine the reasons for any such differences.

This study has identified no significant difference between the easier questions of the chemistry set in comparison to the mathematics set. This is an important discovery as it suggests that the “mole concept” is not necessarily the reason behind the students' poor success at calculations in chemistry. The primary reason for failure in the easier questions was due to a lack of understanding of basic mathematical operations such as division and multiplication, particularly when used in conjunction with fractions or ratios.

There was a significant difference with respect to the more difficult questions between each set. The students performed least well in the chemistry questions in comparison to the mathematics questions. It is thought that the solutions provided by the students suggest that the reason behind this is not due to a better understanding of the mathematics questions but a greater amount of practice in these questions. Since the mathematics questions are analogous to the chemistry questions, any practice at one should transfer some improved ability at the other; however, this does not appear to translate from mathematics to chemistry. The observation that all the correct solutions to the hard mathematics question were almost identical suggests that these questions are being completed in an algorithmic fashion whereas the correct chemistry questions displayed a variety of solutions and hence are better understood. If the underlying mathematics is not fully grasped and only “understood” through an algorithmic approach then one could expect to see students encountering difficulties with chemical calculations.

This study has identified two clear messages from a teaching perspective. Firstly, students are deficient in basic mathematical skills which have an obvious knock on effect on chemical calculations. The routine use of mathematical readiness tests would be a simple tool to identify and circumvent this problem. Secondly, it appears that students' mathematical skills may not be well understood and so utilised algorithmically. This algorithmic approach to mathematics teaching hinders problem solving ability in other subjects, most notably in the sciences. This is a more challenging issue to solve in which the action to be taken would be in the mathematics classroom rather than the science classroom. An improved communication between science departments and mathematics departments will be important in solving this problem.

Acknowledgements

The author would like to thank Maggie McAleavy, Lynn Jamison and Sonja Smith of Gryffe High School for their assistance in the completion of this study.

Notes and references

1. Bitner B. L., (1991), Formal operational reasoning modes: Predictors of critical thinking abilities and grades assignes by teachers in science and mathematics for students in grades nine through twelve, J. Res. Sci. Teach., 28, 265–274.
2. DeLorenzo R., (1994), Expanded dimensional analysis, J. Chem. Educ., 71, 789–791.
3. Denny Rita T., (1971), The mathematics skill test (MAST) for chemistry, J. Chem. Educ., 48, 845–846.
4. Dierks W., Weninger J. and Herron J. D., (1985), Mathematics in the chemistry classroom, J. Chem. Educ., 62, 1021–1023.
5. Gable D. and Sherwood R., (1984), Analysing difficulties with mole-concept tasks by using familiar analog task, J. Res. Sci. Teach., 21, 843–851.
6. Griffith W. T., (1985), Factors affecting performance in introductory physics courses, Am. J. Phys., 53, 839–842.
7. House J. D., (1995), Noncognitive predictors of achievement in introductory college chemistry, Res. High. Educ., 36, 473–490.
8. Hurst R. W. and Milkent M. M., (1996), Facilitating successful prediction problem solving in biology through application of skill theory, J. Res. Sci., Teach., 33, 541–552.
9. Lazonby, J., Morris, J. E. and Waddington D. J., (1982), The muddlesome mole, Educ. Chem., 19, 109–111.
10. Leopold D. G. and Edgar B., (2008), Degree of Mathematics Fluency and Success in Second-Semester Introductory Chemistry, J. Chem. Educ., 85, 724–731.
11. Lythcott J., (1990), Problem solving and requisite knowledge of chemistry, J. Chem. Educ., 67, 248–252.
12. Novick S. and Menis J., (1976), A study of student perceptions of the mole concept, J. Chem. Educ., 53, 720–722.
13. Weisman Rence L., (1981), A mathematics readiness test for prospective chemistry students, J. Chem. Educ., 58, 564–565.
14. Royal Society of Chemistry, (2009a), www.rsc.org/images/ACMERSCResponse_tcm18-170564.pdf, date accessed 10/11/11.
15. Royal Society of Chemistry, (2009b), http://www.rsc.org/images/Bulletin10_tcm18-134605.pdf, date accessed 10/11/11.
16. Royal Society of Chemistry, (2009c), http://discovermaths.rsc.org, date accessed 10/11/11.
17. Strömdahl H., Tullberg A. and Lybeck L., (1994), The qualitatively different conceptions of 1 mol, Int. J. Sci. Ed., 16, 17–26.

---