Quantitative Nanostructure–Activity Relationship modelling of nanoparticles†
Yi Ting
Chau
and
Chun Wei
Yap
*
Pharmaceutical Data Exploration Laboratory, Department of Pharmacy, National University of Singapore, Block S4, 18 Science Drive 4, Singapore 117543. E-mail: phayapc@nus.edu.sg; Fax: 065-67791554; Tel: 065-65165971
First published on 20th July 2012
Abstract
In recent years, the interest of the pharmaceutical industry to explore the use of nanoparticles for disease treatment or drug delivery has increased the need to evaluate their therapeutic efficacy or toxicity. However, evaluation of such properties using experimental means is time-consuming and costly. Thus, researchers are investigating the potential of using Quantitative Nanostructure–Activity Relationship (QNAR) models to predict the properties of nanoparticles prior to their synthesis. In this study, we developed a reliable, user-friendly and freely-accessible QNAR model to predict the cellular uptake of 105 nanoparticles with a single metal core by pancreatic cancer cells. Four modelling methods, namely Naïve Bayes, Logistic Regression, k nearest neighbour and support vector machine, were used to develop candidate models. A final consensus model was then developed using the top 5 candidate models. Validation of the final consensus model was done using a rigorous process by repeating the entire model development process five times using different combinations of training and validation sets. The final consensus model had a sensitivity of 86.7 to 98.2% and specificity of 67.3 to 76.6%. The majority of the wrong predictions were due to nanoparticles which had O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O–C
C–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding. Descriptors that were included in the final consensus models were mainly related to lipophilicity and hydrogen bonding. With the recent advances in QNAR methodology and its encouraging prediction toward virtual nanoparticles, the full potential of QNAR modelling should be exploited in the future to provide critical support to experimental studies over the design of nanomaterials.
O bonding. Descriptors that were included in the final consensus models were mainly related to lipophilicity and hydrogen bonding. With the recent advances in QNAR methodology and its encouraging prediction toward virtual nanoparticles, the full potential of QNAR modelling should be exploited in the future to provide critical support to experimental studies over the design of nanomaterials.
1. Introduction
Nanotechnology is the manipulation of sub-100 nanometer scale matter1 at the atomic level to create better and entirely new materials, known as nanomaterials.2 The rapid growth of nanomaterials production represents a scientific revolution in material design3 where nanomaterials with novel physiochemical properties are receiving increasing attention for their promise in bringing miracles to the biomedical, engineering and information technology fields.4 Part of this will necessitate large scale production of nanoparticles with new formulations and surface properties to meet novel demands. It is projected that commercialization of nanomaterials and nano-enabled devices could grow into a $1 trillion industry by 2015.3,5With the successful implementation of nanotechnology, there has been a growing number of pharmaceutical industries interested in exploring the use of manufactured nanoparticles (MNPs) for several applications. Fullerenes, which are the most established type of carbon nanoparticles, have unique physiochemical properties (light weight, high tensile strength, thermal/chemical stability and conductivity) that generated several applications including use in biomedical materials and devices such as tissue scaffolds, drug-delivery agents, and fluorescent-contrast agents.6 As a result of increased human exposure to these MNPs, this situation is calling for the need to evaluate the biological activity or toxicity of these MNPs to design efficacious and safe nanomaterials.
The evaluation of the biological or toxic effects was usually performed using in vitro and in vivo studies. However, experimental methods are laborious, time consuming and resource intensive. Therefore, researchers have been investigating the potential of using in silico methods, such as Quantitative Structure–Activity Relationship (QSAR) methodology to construct Quantitative Nanostructure–Activity Relationship (QNAR) models to predict the properties of MNP in biological systems in a fast and cost-effective manner prior to their synthesis.
The QSAR methodology to model drug-like compounds is well established and is a useful tool for predicting the properties of chemical compounds.7,8 It was first formulated in 1962 based on the assumption that the variations in biological activity of the compounds are determined by their variations in molecular structure. With the QSAR methodology, if toxicological data are available only for some compounds in a group, one is able to determine the toxicological properties of the other compounds in the same group using only calculated molecular descriptors and a suitable mathematical model.8,9 Hence, the QSAR paradigm is extensively applied in the areas of drug discovery and chemical toxicity modelling to guide the experimental design of chemical compounds. Its growing importance is also reflected in regulatory frameworks such as the European REACH (Registration Evaluation Authorisation and Restriction of Chemical Substances) system for new chemical management where the QSAR methodology is promoted as an acceptable method for filling in knowledge gaps for untested chemicals under certain conditions,10 and an alternative method for toxicity testing.8
Thus, similar to the general QSAR modelling strategies, the overall objective of QNAR models is to develop a mathematical and statistically significant model to describe the relationship between the measured biological (e.g. cell viability, cellular uptake) or toxicological activity profiles of MNPs and a set of calculated or experimentally measured descriptors that characterises MNPs.11–15 Such predictive knowledge can then be used to fill large nano-biological data gaps and significantly reduce the time and costs of the experimental work.8 It can be applied to newly designed or commercially available MNPs, allowing researchers to quickly and efficiently assess their potential biological effects,13 streamline and prioritize them for in vivo and in vitro testing, and design those with improved activity.11–14
While QSAR methodology is mature,9 the concept of QNAR is relative new and thus it has not been established whether QSAR methodology is equally applicable for MNPs.8 Preliminary works on QNAR for MNPs have shown the success of QNAR in establishing predictive relationships between structural attributes and biological activity of MNPs. Recently, Puzyn et al.16 reported on the development of a QSAR model to predict the cytotoxicity of various metal oxide nanoparticles and suggested that QSAR modelling can be used in computational nanotoxicology studies. However, this study was done on a relatively small number of nanoparticles (<20). In another study by Shaw et al.,17 51 MNPs with four different metal cores were tested in vitro against four cell lines in different assays to study their induced biological effects such as apoptosis. Different statistical techniques were applied to find the correlations between the biological activity profiles of MNPs and to discover hidden structure–property relationships. Currently, the numbers of QNAR models existing in the literature are very scarce. In order to provide guidance for future design of safe MNPs and to improve the success rate of experimental MNPs screening,18 it is of interest to develop widely accessible and reliable computational QNAR models using different modelling methods.
In this work, we aim to employ QSAR methods to develop a reliable, user-friendly and freely-accessible QNAR model to predict the biological activity of nanoparticles from an appropriate dataset using their physical, chemical and/or geometrical properties. The hypothesis that drove this study was that it is practical to use the physical, chemical and/or geometrical activity to develop predictive QNAR models.
2. Methodology
2.1 Data curation
Weissleder's19 dataset (Appendix 2†) which contained 146 nanoparticles with significant variations in cellular uptakes in pancreatic cancer cell lines was selected for this study due to its relatively larger sample size compared to the other two datasets. These nanoparticles have the same metal core with different surface-modifying organic molecules. In Weissleder's work, FITC (fluorescein isothiocyanate) was added to the surface of the nanoparticles to make them magneto-fluorescent and the nanoparticles were then screened against different cell lines. One of the cell lines tested was PaCa2 human pancreatic cancer cell due to the lack of efficient molecules for early detection of pancreatic cancer.21 It was found that the cellular uptake in PaCa2 was more diverse and highly dependent on surface modifications when compared to the other cell lines.12 Thus in this work, we selected the cellular uptake in PaCa2 as the end point of interest. To test our hypothesis, we aim to build a QNAR model that can predict the cellular uptake of nanoparticles in PaCa2 using their physical, chemical and/or geometrical properties.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 nanoparticles per cell. Based on the definition given in the Weissleder et al. paper,19 14 nanoparticles showed significant uptake into PaCa2, which corresponds to a threshold of more than 11
542 nanoparticles per cell. Based on the definition given in the Weissleder et al. paper,19 14 nanoparticles showed significant uptake into PaCa2, which corresponds to a threshold of more than 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 481.5 nanoparticles per cell to identify nanoparticles with good cellular uptake. However, it is also useful to identify nanoparticles which showed moderate cellular uptake as these could potentially be modified to have better cellular uptake. Thus, for our work, we lowered the threshold value to 5000 nanoparticles per cell. A total of 56 nanoparticles with cellular uptake of more than 5000 nanoparticles per cell were considered to have good/moderate (henceforth referred to as good for brevity) cellular uptake (positive class), while 49 nanoparticles with cellular uptake of less than 5000 nanoparticles per cell were considered to have poor cellular uptake (negative class).
481.5 nanoparticles per cell to identify nanoparticles with good cellular uptake. However, it is also useful to identify nanoparticles which showed moderate cellular uptake as these could potentially be modified to have better cellular uptake. Thus, for our work, we lowered the threshold value to 5000 nanoparticles per cell. A total of 56 nanoparticles with cellular uptake of more than 5000 nanoparticles per cell were considered to have good/moderate (henceforth referred to as good for brevity) cellular uptake (positive class), while 49 nanoparticles with cellular uptake of less than 5000 nanoparticles per cell were considered to have poor cellular uptake (negative class).
2.2 Calculating molecular descriptors
Since the nanoparticles have the same metal core with different surface-modifying organic molecules, they can be characterized using conventional chemical descriptors for the surface-modifying organic molecules. Chemical descriptors are quantitative representations of structural and physicochemical features of molecules, and have been extensively used in QSAR.22 A total of 679 1D, 2D chemical descriptors were calculated using PaDEL-Descriptor v2.8 software. After removing those descriptors that showed no variance for all the nanoparticles, 367 chemical descriptors were retained and those which were redundant or irrelevant were further removed by using descriptor selection methods which will be discussed later.2.3 Model development
Fig. 1 shows an overview of the model development process. It consists of 4 main steps: (i) selecting a modelling algorithm, (ii) generating candidate models (iii) building consensus model, and (iv) validating consensus model. By choosing different combinations of modelling algorithms and attribute subsets, many diverse models were produced and the final consensus model was developed from these models. | ||
| Fig. 1 An overview of the model development process. | ||
a. Logistic regression (LR)23,24. Logistic regression is based on the assumption that a logistic relationship exists between the probability of class membership and one or more descriptors. The probability, y, is calculated using
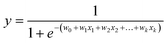 | (1) |
where x1, … , xk are chemical descriptors and w0 is the bias and w1, … , wk are coefficients corresponding to the descriptors x1 to xk.
b. Naïve Bayes (NB). Naïve Bayes gives a posterior probability of data within each class and was based on conditional probabilities. It used Bayes' Theorem, a formula that calculated a probability by counting the frequency of values and combinations of values in the historical data.
Bayes' Theorem found the probability of an event occurring given the probability of another event that had already occurred. If H represents the dependent event (Hypothesis) and E represents the prior event (Evidence), Bayes' theorem can be stated as follow
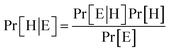 | (2) |
Where Pr[H|E] – probability of hypothesis H given the evidence E, Pr[E|H] – probability of evidence E conditional on hypothesis H, Pr[H] – prior probability of hypothesis H, Pr[E] – probability of evidence E.
c. k Nearest Neighbour (kNN)23,24. In kNN, the Euclidean distance between a to-be-predicted vector x and each individual vector xi in the training set was measured. In this study, vector x is the chemical descriptors for a nanoparticle. The k value represented the number of nearest neighbours. A total of k vectors nearest to the to-be-predicted vector x were used to determine the class of that vector by choosing the class of the majority of the k nearest neighbours as the predicted class of the vector x. For instance, in Fig. 2, let green represent nanoparticles with good cellular uptake, red represents nanoparticles with poor cellular uptake while black represents a nanoparticle with unknown biological property. If k = 7 and 5 of its nearest neighbours showed good cellular uptake while 2 showed poor cellular uptake, this nanoparticle would thus be predicted as having good cellular uptake. In this study, the k values used to develop the candidate models were 3, 4, 5, …, 10, 11.
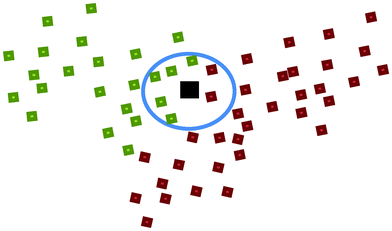 | ||
| Fig. 2 An illustration of the k Nearest Neighbour (kNN) method. | ||
d. Support Vector Machine (SVM)7. The SVM approach made use of hyperplanes which define decision boundaries separating between nanoparticles of different classes.25 It was trained by using a Gaussian kernel function with an adjustable parameter σ. SVM mapped the vectors into a higher dimensional feature space using the Gaussian kernel function and linear SVM was then applied to this feature space. In this study, sequential variation of σ (1e−9, 1e−8, … , 1e−2, 1e−1 and the empirical value of the inverse of the number of compounds in the training set) was used to develop the candidate models.
a. Selecting relevant descriptors. Descriptor selection was implemented to improve the predictive performance of the candidate models by removing redundant or irrelevant molecular descriptors and selecting those descriptors that were relevant to a particular study.22
We first performed a randomisation process on the entire set of 367 molecular descriptors such that 100 different pools with varying numbers of descriptors would be created. Forward selection was then applied to each pool of descriptors. A single descriptor that best correlated with the dependent property was first identified and the next most contributing descriptor was then added in the subsequent steps. The selection was stopped when the addition of a descriptor did not improve the model's performance. The use of forward selection on each pool of descriptors would identify a good descriptor subset for each model. From the 100 pools of descriptors created, 100 models, each with a distinct descriptor subset, were developed. This process of descriptor selection was repeated for each modelling method, and for kNN and SVM, the process was repeated for each value of k and σ respectively. Thus, a total of 2100 candidate models were developed (900 kNN, 1000 SVM, 100 LR and 100 NB models).
b. Building candidate models with applicability domain. To reliably predict and classify the cellular uptake property of the nanoparticles, each candidate model was built with an applicability domain (AD) defined using the multiple threshold method proposed by Fumera et al.26
Different modelling methods had different algorithms to compute a confidence value for the predicted cellular uptake classification of a nanoparticle. For example, in kNN, the confidence value for predicting a nanoparticle to have good cellular uptake was computed as the proportion of k nearest neighbours of the nanoparticle that have good cellular uptakes. Thus, if k is 5 and the number of nearest neighbours of the nanoparticle that have good cellular uptakes is 4, the confidence value for predicting the nanoparticle to have good cellular uptake will be 0.8.
Usually in a binary classification modelling method, a threshold of 0.5 for the confidence value is used such that if the confidence value is more than 0.5, the nanoparticle will be predicted as having good cellular uptake. Otherwise, it will be predicted as having poor cellular uptake.
In this work, we adopted the multiple thresholds method whereby two thresholds were determined for each candidate model. If the confidence value is greater than the higher threshold value, the nanoparticle will be predicted as having good cellular uptake. Conversely, if the confidence value is smaller than the lower threshold value, the nanoparticle will be predicted as having poor cellular uptake. When the confidence value lies between the two threshold values, the nanoparticle will be considered as out of the AD of the model and its degree of cellular uptake will not be predicted.
c. Characterizing candidate model performance. The candidate models were characterized by their predictive performance on the dataset and five-fold cross validation. To determine the predictive performance using five-fold cross validation, the dataset was first divided into 5 different portions. Four portions were used to form a training set to develop a model, while the remaining portion formed the testing set to determine the predictive performance of the model. This step was repeated until each subset was being used as the testing set. The five-fold cross validation predictive performance was then calculated as the average predictive performance on these five testing sets.
For each candidate model, the predictive performance consisted of the quantity of true positives TP, true negatives TN, false positives FP, false negatives FN, nanoparticles in the positive class which are out of the AD, nanoparticles in the negative class which are out of the AD, sensitivity SE = TP/(TP + FN) which is the prediction accuracy for the nanoparticles with good cellular uptake in this work, and specificity SP = TN/(TN + FP) which is the prediction accuracy for the nanoparticles with poor cellular uptake in this work. The Matthews correlation coefficient (MCC) was also used to measure the overall prediction accuracy of the model and was calculated using7
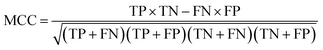 | (3) |
(i) Difference between dataset MCC and cross-validation MCC < 0.1. Rationale: to ensure that candidate models are not over-fitted.
(ii) <10% of the nanoparticles in the dataset are defined to be outside the AD of the candidate models. Rationale: more useful to have candidate models with larger AD so that they can be used to predict the properties for more diverse nanoparticles.
From the candidate models that satisfied the two criteria, the top five candidate models, determined using their cross-validation MCC values, were then selected to construct the final consensus model. The AD of the final consensus model was defined based on the collective predicted class of the candidate models. Nanoparticles were defined to be out of the AD of the final consensus model when all the five candidate models identified the nanoparticle to be out of their individual AD, or if there was a tie in the predictions (i.e. an equal number of candidate models predicted the nanoparticles to have good cellular uptake and poor cellular uptake). Otherwise, the nanoparticles were defined to be within the AD of the final consensus model and their classes were predicted based on majority voting of the candidate models. In addition, confidence values for the predictions were also computed using a similar algorithm as that was used in kNN.
Fig. 3 shows the process for constructing the various training and validation sets. The positive class, which contained nanoparticles with good cellular uptake, was randomly divided into five subsets of approximately equal size. The same procedure was done to the negative class. For each run, the training set consisted of 4 of the subsets from each class while the validation set consisted of the remaining subset from each class. For instance, in run 1, positive subset 1 and negative subset 1 formed the validation set while the remaining subsets formed the training set. More details on the distribution of the nanoparticles in the training and validation sets can be found in Appendix 3.†
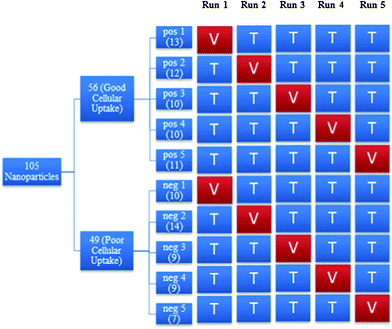 | ||
| Fig. 3 An overview of the process to construct training and validation sets in each run. Where pos: positive class, neg: negative class, V: validation set, T: training set. | ||
The training sets were subsequently used to develop the models using exactly the same approach described from Sections 2.3.1 to 2.3.3 while the validation sets, which were not used in the derivation of the models, were used to estimate the prediction capability of the consensus models. The average values of true positives, true negatives, false positives, false negatives, number of nanoparticles which were out of AD, sensitivity, specificity and MCC of the validation results from the 5 runs represented the cross-validated results of the final consensus model.
3. Results
3.1 Selection of candidate models for consensus modelling
Out of the 2100 candidate models that were developed, only 102 models (approximately 5%) were selected as suitable candidate models for consensus modelling. These comprised of 44 kNN, 38 SVM, 3 LR and 17 NB candidate models. The top 5 candidate models chosen to build the final consensus model consisted of 3 kNN, 1 SVM and 1 NB models. Results for the 5 runs in the rigorous validation process are similar and can be found in Appendix 3.†3.2 Model performance
Table 1 shows the performance of the final consensus model that was determined using the dataset and the rigorous validation process. The average sensitivity and specificity values of the 5 runs served as the cross-validated results of the final consensus model.| Test | No. of Nanoparticles | Within ADe | Out of AD | SEf(%) | SPg(%) | MCC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total | Pos | Neg | TPa | FNb | TNc | FPd | Pos | Neg | |||||
| a True Positive. b False Negative. c True Negative. d False Positive. e Applicability Domain. f Sensitivity. g Specificity. | |||||||||||||
| Dataset | 105 | 56 | 49 | 55 | 1 | 36 | 11 | 0 | 2 | 98.2 | 76.6 | 0.777 | |
| Rigorous validation | Run 1 | 23 | 13 | 10 | 12 | 1 | 7 | 3 | 0 | 0 | 92.3 | 70.0 | 0.649 |
| Run 2 | 26 | 12 | 14 | 10 | 2 | 9 | 5 | 0 | 0 | 83.3 | 64.3 | 0.480 | |
| Run 3 | 19 | 10 | 9 | 8 | 2 | 5 | 4 | 0 | 0 | 80.0 | 55.6 | 0.368 | |
| Run 4 | 19 | 10 | 9 | 7 | 2 | 6 | 2 | 1 | 1 | 77.8 | 75.0 | 0.528 | |
| Run 5 | 18 | 11 | 7 | 10 | 0 | 5 | 2 | 1 | 0 | 100.0 | 71.4 | 0.772 | |
| Average | — | — | — | — | — | — | — | — | — | 86.7 | 67.3 | 0.559 | |
3.3 Selection of descriptors
Descriptors that were commonly selected in the top 5 candidate models include number of CH2 groups, primary, secondary and tertiary nitrogens, halogens (fluorine, bromine, iodine), sulphur atoms, fused rings and hydrogen bonding.4. Discussion
4.1 Selection of candidate models
While some LR models were selected as suitable candidate models for consensus modelling, none was selected for the final consensus model. This is because LR models generally had lower predictive performance compared to kNN and SVM models. Similar results were generally seen in the 5 runs of the rigorous validation process. A possible reason for this is because logistic regression assumes a logistic relationship between the target property and molecular descriptors, which may not be true. Thus, kNN and SVM, which do not make such assumptions, may be more suitable for predicting cellular uptakes.4.2 Model performance
The final consensus model achieved a good sensitivity of 98.2% and specificity of 76.6% for the dataset. The rigorous validation results also showed similar sensitivity and specificity values of 86.7 and 67.3% respectively. The similar results for both the dataset and rigorous validation suggest that the final consensus model is less likely to be over-fitted. The results showed that the consensus model had a tendency to predict nanoparticles as having good cellular uptake. This bias is desirable as it reduces the accidental rejection of potentially useful surface-modifying organic molecules.Currently, there are no other existing QNAR studies for comparison with our model because the model generated by Fourches et al.12,13 predicted the cellular uptake values rather than classifying them as good or poor cellular uptake. In addition, they did not provide the individual predicted cellular uptake values for the nanoparticles and thus it is not possible to convert their predictions to good or poor cellular uptake for comparison. Nonetheless, a tentative comparison with the Shaw et al.17 study which had an accuracy of 73% for apoptosis prediction using 51 MNPs with four different metal cores suggests that our final consensus model is potentially useful for predicting the cellular uptakes in PaCa2 cells.
The final consensus model also performed well in predicting the properties of the 14 nanoparticles which have significant cellular uptake (as defined by Weissleder et al.19). Results from the rigorous validation process shows that 12 out of these 14 nanoparticles were predicted correctly, giving a success rate 85.7% for the final consensus model.
Among the 12 nanoparticles that were predicted wrongly by the final consensus model, one was a false negative result. This wrong prediction was probably due to the cellular uptake of the nanoparticle (5888 nanoparticles per cell) being near to the threshold value of 5000 nanoparticles per cell. Similarly, 7 out of remaining 11 nanoparticles which had false positive results also had cellular uptakes that were near to the threshold value. For the remaining 4 nanoparticles which had false positive results, a common feature that can be seen in the structure of the surface modifying organic molecules is the presence of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O–C
C–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding. This substructure can also be found in all the nanoparticles which have been predicted wrongly and in the 2 nanoparticles (261-14-12 and 261-16-13) that were defined to be out of the applicability domain, with the exception of nanoparticle 261-45-7 (false positive) and 261-46-1 (false negative). Among the 105 nanoparticles, a total of 60 nanoparticles (57.1%) contained this substructure. However, among the 14 nanoparticles which were predicted wrongly or out of AD (Fig. 4), the corresponding percentage of nanoparticles that contained this substructure is 85.7%. Thus, this suggests that the current set of descriptors may not be able to describe such substructures well, leading to increased wrong predictions for nanoparticles containing such substructures.
O bonding. This substructure can also be found in all the nanoparticles which have been predicted wrongly and in the 2 nanoparticles (261-14-12 and 261-16-13) that were defined to be out of the applicability domain, with the exception of nanoparticle 261-45-7 (false positive) and 261-46-1 (false negative). Among the 105 nanoparticles, a total of 60 nanoparticles (57.1%) contained this substructure. However, among the 14 nanoparticles which were predicted wrongly or out of AD (Fig. 4), the corresponding percentage of nanoparticles that contained this substructure is 85.7%. Thus, this suggests that the current set of descriptors may not be able to describe such substructures well, leading to increased wrong predictions for nanoparticles containing such substructures.
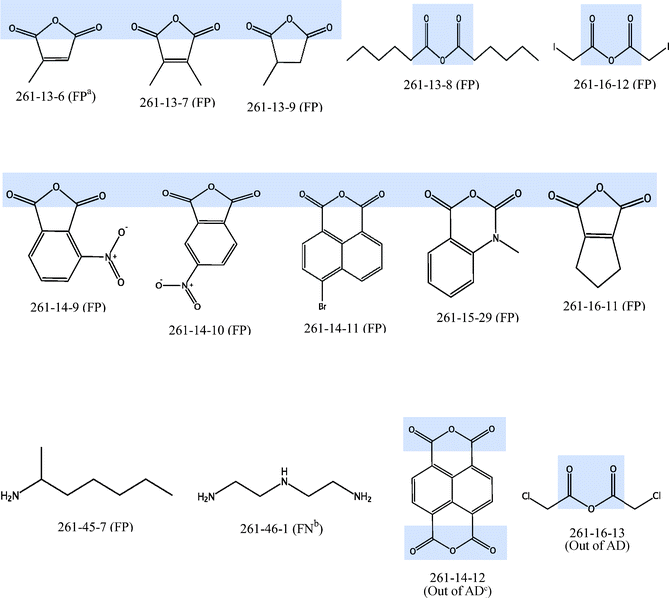 | ||
Fig. 4 Structures of 12 nanoparticles with wrong prediction and 2 nanoparticles which are defined to be out of AD (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O–C C–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O substructure shaded in blue) aFP: False Positive, bFN: False Negative, cAD: Applicability Domain. O substructure shaded in blue) aFP: False Positive, bFN: False Negative, cAD: Applicability Domain. | ||
4.3 Selection of descriptors
Most of the descriptors that were selected in the top 5 candidate models were related to lipophilicity, which is one of the major factors in determining the passive transport of chemicals across biological membranes. Examples of such descriptors include those associated with number of lipophilic groups (CH2, fused rings). Other than lipophilicity, hydrogen bonding descriptors such as hydrogen bonding between nitrogen and hydrogen, and other types of descriptors such as sulphur and various halogen atoms were found to be important for the prediction of the cellular uptake of nanoparticles in PaCa2. This is in agreement with the study done by Fourches et al.12,13 Hence, the results suggest that the factors affecting cellular uptake of nanoparticles into PaCa2 are similar to those affecting cellular uptake of chemicals. These findings also imply that the cellular uptake behaviour of a nanoparticle library is dependent on its surface-modifying organic molecules and QNAR models could be used to find a surface-modifying organic molecule that repels proteins or biomembranes for controlling the cellular uptake and the biodistribution of nanomaterials.104.4 Future work
In our study, suitable candidate models for consensus modelling were required to have less than 10% of the nanoparticles in the dataset which were outside their AD. The purpose of setting this criterion was to select candidate models with larger AD so that they can be used to predict the properties for more diverse nanoparticles. However, this also means that candidate models which may be more accurate would be identified as unsuitable for consensus modelling if they had more than 10% of the nanoparticles in the dataset which were out of their AD. Hence, it would be interesting to explore the use of such candidate models with smaller AD in future studies. By including such candidate models, the consensus model may have slightly smaller AD but may be more accurate than our current final consensus model. In addition, a different consensus modelling system could also be adopted whereby more accurate models with smaller AD will be used to predict the properties of the nanoparticles first. Nanoparticles which fall outside the AD of such models will then be predicted by models that are less accurate but with larger AD.In order to predict the cellular uptake of the nanoparticles, the current final consensus model used majority voting with the minimum number of voting members as one (i.e. if one of the top five models predicts a nanoparticle to have good cellular uptake, and the rest of the models define the nanoparticle to be out of their AD, the nanoparticle will be predicted as having good cellular uptake). This is based on the assumption that such model is confident in its prediction and thus its prediction should be regarded as accurate. Nevertheless, it may not be reliable or accurate to predict the biological property based on just one model. Thus, we hypothesise that increasing the minimum number of voting members of the consensus model could potentially improve the predictive performance of the consensus model.
5. Conclusion
In this work, we studied the feasibility of using QNAR methodology to predict the cellular uptake of nanoparticles in PaCa2 cells using their physical, chemical and/or geometrical properties. Our final consensus model was able to accurately predict 86.7 to 98.2% of the nanoparticles with good cellular uptake and 67.3 to 76.6% of the nanoparticles with poor cellular uptake. This provides support for our hypothesis that it is practical to use the physical, chemical and/or geometrical activity to develop predictive QNAR models.The recent advances in QNAR methodology and its prediction toward virtual nanoparticles can significantly reduce the time and costs of the experimental work scientists are currently facing and also aid in filling large nanoparticles data gaps. Hence the full potential of QNAR modelling should be exploited in future to provide critical support to experimental studies over the design of nanomaterials.
In an effort to support critical evaluation of our model by independent parties and the use of our model by experimental scientists, we have made our model available via the free software PaDEL-DDPredictor (http://padel.nus.edu.sg/software/padelddpredictor/).
Acknowledgements
This work was supported by the Ministry of Education Academic Research Fund Tier 1 grant (R-148-000-136-112) to Chun Wei Yap, and NUS Department of Pharmacy Final Year Project grant (R-148-000-003-001) to Yi Ting Chau.References
- K. Donaldson, V. Stone, C. L. Tran, W. Kreyling and P. J. Borm, Occup. Environ. Med., 2004, 61, 727–728 CrossRef CAS.
- D. N. J. Uldrich, The Next Big Thing is Really Small, Crown Business, New York, 2003 Search PubMed.
- H. X. T. Meng, S. George and A. Nel, ACS Nano, 2009, 3, 1620–1627 CrossRef CAS.
- H. M. Kipen and D. L. Laskin, Am. J. Physiol.: Lung Cell. Mol. Phys., 2005, 289, L696–697 CrossRef CAS.
- T. Xia, N. Li and A. E. Nel, Annu. Rev. Public Health, 2009, 30, 137–150 CrossRef.
- N. Lewinski, V. Colvin and R. Drezek, Small, 2008, 4, 26–49 CrossRef CAS.
- C. W. Yap, Y. Xue, H. Li, Z. R. Li, C. Y. Ung, L. Y. Han, C. J. Zheng, Z. W. Cao and Y. Z. Chen, Mini-Rev. Med. Chem., 2006, 6, 449–459 CrossRef CAS.
- T. Puzyn, D. Leszczynska and J. Leszczynski, Small, 2009, 5, 2494–2509 CrossRef CAS.
- T. W. Schultz, M. T. D. Cronin, J. D. Walker and A. O. Aptula, THEOCHEM, 2003, 622, 1–22 CrossRef CAS.
- E. Burello and A. P. Worth, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2011, 3, 298–306 CrossRef CAS.
- E. Burello and A. P. Worth, Nat. Nanotechnol., 2011, 6, 138–139 CrossRef CAS.
- D. Fourches, D. Pu and A. Tropsha, Comb. Chem. High Throughput Screening, 2011, 14, 217–225 CrossRef CAS.
- D. Fourches, D. Pu, C. Tassa, R. Weissleder, S. Y. Shaw, R. J. Mumper and A. Tropsha, ACS Nano, 2010, 4, 5703–5712 CrossRef CAS.
- D. Leszczynska and J. Leszczynski, AIP Conference Proceedings, 2010, 1229, 23–28 CrossRef CAS.
- A. Tropsha, Mol. Inf., 2010, 29, 476–488 CrossRef CAS.
- T. Puzyn, Nat. Nanotechnol., 2011, 6 Search PubMed.
- S. Y. Shaw, E. C. Westly, M. J. Pittet, A. Subramanian, S. L. Schreiber and R. Weissleder, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7387–7392 CrossRef CAS.
- A. T. a. A. Golbraikh, Curr. Pharm. Des., 2007, 13, 3494–3504 CrossRef.
- R. Weissleder, K. Kelly, E. Y. Sun, T. Shtatland and L. Josephson, Nat. Biotechnol., 2005, 23, 1418–1423 CrossRef CAS.
- H. Zhou, Nano Lett., 2008, 8, 859–865 CrossRef CAS.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107 Search PubMed.
- H. H. Lin, L. Y. Han, C. W. Yap, Y. Xue, X. H. Liu, F. Zhu and Y. Z. Chen, J. Mol. Graphics Modell., 2007, 26, 505–518 CrossRef CAS.
- C. W. Yap, Z. R. Li and Y. Z. Chen, J. Mol. Graphics Modell., 2006, 24, 383–395 CrossRef CAS.
- H. Li, C. W. Yap, Y. Xue, Z. R. Li, C. Y. Ung, L. Y. Han and Y. Z. Chen, Drug Dev. Res., 2005, 66, 245–259 CrossRef CAS.
- C. J. C. Burges, Data Min. Knowl. Discovery, 1998, 2, 121–167 CrossRef.
- G. Fumera, F. Roli and G. Giacinto, Pattern Recognit., 2000, 33, 2099–2101 CrossRef.
- I. V. Tetko, I. Sushko, A. K. Pandey, H. Zhu, A. Tropsha, E. Papa, T. Oberg, R. Todeschini, D. Fourches and A. Varnek, J. Chem. Inf. Model., 2008, 48, 1733–1746 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ra21489j |
| This journal is © The Royal Society of Chemistry 2012 |
