Formation of cyclodextrin-stabilized nanoemulsions and microemulsions and exploitation of their solubilization behavior†
Khushwinder
Kaur
*,
Nidhi
Kaur Bhatia
and
S. K.
Mehta
*
Department of Chemistry and Centre of Advanced Studies in Chemistry, Panjab University, Chandigarh - 160 014, India. E-mail: skmehta@pu.ac.in; makkarkhushi@gmail.com; Fax: +91-172-2545074; Tel: +91-172-2534423
First published on 13th July 2012
Abstract
This paper describes the formation and stability of cyclodextrin (CD) encapsulated micromulsions and nanoemulsions by a percolation and phase inversion temperature (PIT) emulsification method using AOT and Tween+lecithin as surfactants. The stability of the formulated system has been checked by visible absorption spectroscopy and particle size estimations. The results show that the particle size of the nanoemulsion increased slightly over a period of one month whereas the AOT based microemulsion has been reported to be stable over months. However, it was found that nanoemulsions form a better host for the assimilation of various CDs such as α-CD, β-CD and β-CD-hydrate whereas microemulsions have been reported to host hp-β-CD only. The study of interactions has been carried out using FTIR and fluorescence studies. The structural transitions within the microemulsions and nanoemulsions have also been studied with visible absorption spectroscopy.
1. Introduction
Oil-in-water nanoemulsions contain small oil droplets (d < 500 nm) dispersed within a watery continuous phase, with each oil droplet being surrounded by a protective coating of emulsifier molecules.1,2 The stability, physicochemical properties and functional performance of nanoemulsions can be controlled by altering their composition and preparation conditions so as to produce emulsions with different droplet concentrations.3 A small droplet size makes them stable against sedimentation and creaming for a long time, hence increasing the overall stability of the emulsions. However, nanoemulsions are thermodynamically unstable and droplet size tends to increase with time.4 Microemulsions, transparent dispersions of two immiscible liquids stabilized by an interfacial film of surfactants, are however thermodynamically stable. They form spontaneously when aqueous, oily and amphiphilic components are brought into contact. One major drawback of microemulsions is that formation requires high surfactant concentration, usually about 20 wt% or higher, which causes toxicity when used in pharmaceutical applications. In contrast, nanoemulsions can be prepared using lower surfactant concentrations typically between 3 and 10 wt%.5 Nanoemulsions have a number of unique functional attributes which make them useful in industrial products, including foods, pharmaceuticals, cosmetics, personal care products, and chemicals.Cyclodextrins (CD), which are ring molecules presenting the remarkable ability to include guest molecule within their internal cavity, are the subject of a dramatically high number of patents and scientific papers. Cyclodextrins can, in fact, solubilize and stabilize active compounds, increase their bioavailability, decrease their undesirable side effects, mask unpleasant flavors or odors or transform gases or liquids into solid powders, inter alia. Such fascinating properties explain their presence in many patented products intended for the agro-food industry as well as in cosmetology and pharmacy.6 However, natural cyclodextrins, find limited aqueous solubility meaning that complexes resulting from the interaction of lipophiles with these cyclodextrins can be of limited solubility resulting in precipitation of solid cyclodextrin complexes from water and other aqueous systems. In fact, the aqueous solubility of natural cyclodextrins is much lower than that of comparable acyclic saccharides. This is thought to be due to relatively strong intermolecular hydrogen bonding in the crystal state. Substitution of any of the hydrogen bond forming hydroxyl groups, even by lipophilic methoxy functions, results in a dramatic improvement in their aqueous solubility. Water-soluble cyclodextrin derivatives of commercial interest include the hydroxypropyl derivatives of β-CD (hp-β-CD) and β-CD hydrate.7
It is known that a unique microenvironment for carrying out a variety of chemical and biochemical reactions is found in the polar core of microemulsions and the hydrophobic cavity of CDs. Microemulsions have been used as model systems for studying various reactions in confinement, for example enzymatic reactions or micellar catalysis.8–10 Despite their simplicity, they provide an excellent method to study the fundamental effects of confinement. Due to the unique catalytic properties of microemulsions and chiral properties of the CD cavity, attempts have been made to solubilize hp-β-CD in different zones within the aggregates of a water–AOT–isooctane–hp-β-CD microemulsion. Other CDs such as α-CD, β-CD, β-CD hydrate have been assimilated in water–Tween 80+lecithin–ethyl oleate based nanoemulsions. The idea is to try to create a novel medium with different confined regions in the same aggregate: the polar core of the microemulsions and the chiral hydrophobic cavity of the cyclodextrins may be used as a chiral nanoreactor.
In the field of nutraceuticals and functional foods, there has been growing interest in taking advantage of nanoemulsions for solving the problems of solubility as well as stability of nutraceuticals and food additives in aqueous solution. The techniques and applications of nanoparticles in nutraceutical delivery systems have been discussed and reviewed significantly over the past few years.11–15 Recent studies in food microemulsions have focused on using food-grade, non-ionic surfactants derived from natural products. The solubilization of lycopene and lutein derivatives in aqueous media was successfully improved by Amar et al.16 using microemulsion technology. Construction of lecithin-based microemulsions with a wide range of food-acceptable surfactants in food application has also been reported.17,18 Compared with the high-energy formation of nanoemulsions, the low-energy emulsification method has strong appeal in the development of drug delivery systems, which can take advantage of phase behavior, industrial scale-up, reduced physical destruction of drugs, and the formation of smaller droplets.17,18 However, to the best of our knowledge, no report is available for the encapsulation of cyclodextrins with regard to food-grade concerns.
Therefore, the main aim of this study is to create a novel medium with different confined regions in the same aggregate: the polar core of the microemulsion and the chiral hydrophobic cavity of the cyclodextrins may be used as a chiral nanoreactor, and to find stable nanoemulsions and microemulsions containing cyclodextrins encapsulated with food-acceptable ingredients, lecithin and polysorbate 80 (Tween 80), to enhance the stability of cyclodextrins in food components.
2. Experimental
Materials
Sodium bis(2-ethylhexyl) sulfosuccinate, AOT, (Fluka, purity > 99%), lecithin, LC, extracted from soybeans, (Fluka, purity > 95%), isooctane, (E-Merck, purity > 99%), Tween 80, (Fluka, purity > 99%), ethyl oleate, (Sigma, purity > 70%), cyclodextrins, viz., α-CD and β-CD, (Higmedia, purity > 96%), hp-β-CD and β-CD hydrate (Fluka, purity > 98%) and methylene blue (MB) (British Laboratories) were used as received. Triple distilled water with conductance less than 3 μ Scm−1 was used for the preparation of the microemulsions and nanoemulsions.Methods
Preparation of samples
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Tween 80] = 0.3
[Tween 80] = 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water
water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO = 10
EO = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.7
1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 in wt ratio, and CD in a test tube, was kept at 50 °C and well mixed using a vortex mixer. The choice of components is based on the fact that all of them are GRAS (generally recognized as safe) by the FDA. The water was then added to the mixture in a sonicator bath until a transparent and isotropic nanoemulsion were obtained. The mixture was then allowed to cool slowly to room temperature. The aim of this slow cooling step was to ensure complete solubilization of the oil phase into a bicontinuous microemulsion at the HLB temperature, which is the requirement for formation of nanoemulsions. Table 1 depicts the assimilation behavior of the added CDs.
0.4 in wt ratio, and CD in a test tube, was kept at 50 °C and well mixed using a vortex mixer. The choice of components is based on the fact that all of them are GRAS (generally recognized as safe) by the FDA. The water was then added to the mixture in a sonicator bath until a transparent and isotropic nanoemulsion were obtained. The mixture was then allowed to cool slowly to room temperature. The aim of this slow cooling step was to ensure complete solubilization of the oil phase into a bicontinuous microemulsion at the HLB temperature, which is the requirement for formation of nanoemulsions. Table 1 depicts the assimilation behavior of the added CDs.
| CD assimilated | Water–AOT–isooctane (ME-I) | Water–tween 80–LC–EO (ME-II) |
|---|---|---|
| α- CD | Turbid | Assimilated |
| β- CD | Turbid | Assimilated |
| β- CD hydrate | Turbid | Assimilated |
| hp-β-CD | Assimilated | Turbid |
| γ-CD | Turbid | Turbid |
It turns out that α-, β-, and γ-CD cannot be solubilized in the ME-I at any ω value. Perhaps the hydrogen bond interaction between the CD hydroxyl group and the AOT polar headgroup, although a very effective H-bond acceptor, is not strong enough to solubilize these cyclodextrins. It is known19 that OH groups of cyclodextrins and in particular α-CD form very strong intramolecular hydrogen bonds, and it may be possible that the polar headgroup of AOT cannot compete with these intramolecular interactions resulting in poor solubility of the CD in ME-I. The hp-β-CD which has their OH groups substituted by the hydroxypropyl group has weaker intramolecular hydrogen bonds and thus a greater tendency to interact with the AOT environment resulting in solubilization in ME-I. However, suitably oriented and strong H-bonds seem to be formed in ME-II, which might be responsible for the solubility of α-CD, β-CD and β-CD hydrate. However, γ-CD cannot be assimilated in both the systems because γ-CD is a non-coplanar molecule with a more flexible structure. So the formation of H-bonds is distorted leads to low solubility.19
Results and discussion
Stability of CD encapsulated ME
The stability of the nanoemulsion–microemulsion produced has been assessed by measuring the change in droplet sizes at room temperature. The ME-I at [AOT] = 0.5 M and ω = 22.0 and ME-II with a surfactant ratio of [LC]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Tween 80] = 0.3 were selected for stability studies. The nanoemulsion–microemulsion prepared displayed good stability; and there was no phase separation. However, after several weeks, an increase in droplet size was noted with time. The stabilities of these CD-encapsulated microemulsions were determined by measuring their particle size and absorbance when stored in the dark for one month. The results show that the absorbance decreased from 1.98 to 0.95 with a corresponding red shift of 7 nm in pure ME-II and the absorbance decreased from 1.5 to 0.99 with corresponding red shift of 5 nm in β-CD hydrate assimilated ME-II. The results have been depicted in Fig. 1. The shift is a clear indication of weakening of bonding interactions and thus decreasing stability. However, no significant shifts were seen in the hp-β-CD system assimilated and in pure ME-I (Fig. 2).
[Tween 80] = 0.3 were selected for stability studies. The nanoemulsion–microemulsion prepared displayed good stability; and there was no phase separation. However, after several weeks, an increase in droplet size was noted with time. The stabilities of these CD-encapsulated microemulsions were determined by measuring their particle size and absorbance when stored in the dark for one month. The results show that the absorbance decreased from 1.98 to 0.95 with a corresponding red shift of 7 nm in pure ME-II and the absorbance decreased from 1.5 to 0.99 with corresponding red shift of 5 nm in β-CD hydrate assimilated ME-II. The results have been depicted in Fig. 1. The shift is a clear indication of weakening of bonding interactions and thus decreasing stability. However, no significant shifts were seen in the hp-β-CD system assimilated and in pure ME-I (Fig. 2).
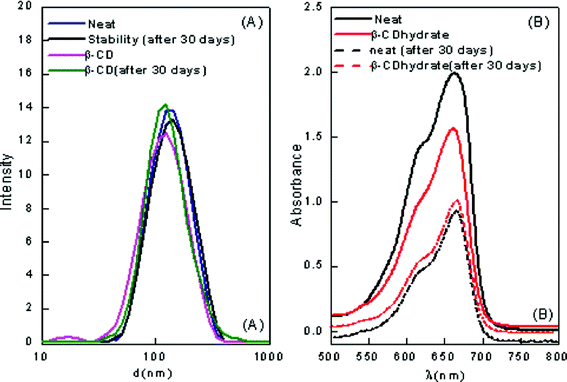 | ||
| Fig. 1 (A) Particle size distribution of pure and β-CD encapsulated ME-II (B) The visible absorption of the β-CD hydrate encapsulated ME-II after storage at room temperature for one month. | ||
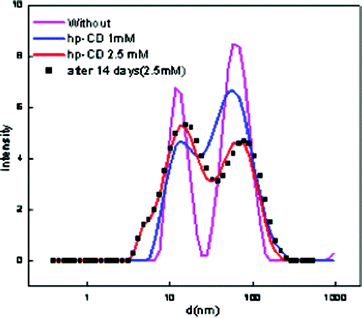 | ||
| Fig. 2 Particle size distribution of pure and hp-β-CD encapsulated ME-I. | ||
The particle size results reveal that the average size in the emulsion was in the range of 112–195 nm, which is a satisfactory range and classifies the formation as a nanoemulsion. Therefore, the formation of ME-II has been confirmed as nanoemulsion whereas ME-I is a microemulsion.20 The PDI values below 0.2 indicate a narrow size distribution; this indicates good long-term stability of the prepared systems due to reduction of degradation processes like Ostwald ripening.21,22
Particle size estimations have been depicted in Table 2 for ME-I and ME-II. The results indicate that the particle size of ME-II increased ∼10 nm after one month. This indicates that the stability of the nanoemulsion slightly decreases over a time period whereas ME-I has been reported to be stable. Also, it has been seen that the observed droplet size of ME-II decreases with the assimilation of CDs. Table 2 summarizes the mean droplet sizes and polydispersity indices for the freshly prepared emulsions at 25 °C for ME-I and ME-II produced at different CD concentrations. The decrease in size of ME-II with the incorporation of CD might be because the CD gets engulfed in the ME cavity. However, the size remains the same after encapsulation in ME-I, indicating that solubilization of any of the cyclodextrins in the ME-I change neither their size nor shape and the microemulsions are not perturbed by dissolution of these molecules.
| CD assimilated | Conc. (mM) | Diameter (nm) | PDI | Stability (1 month) | PDI |
|---|---|---|---|---|---|
| — | ME-I | ||||
| Neat | 33.80 | 0.57 | 33.20 | 0.59 | |
| hp-β-CD | |||||
| 1 | 27.11 | 0.43 | 27.01 | 0.45 | |
| 2.5 | 23.11 | 0.47 | 22.22 | 0.49 | |
| 5 | 20.60 | 0.42 | 19.22 | 0.46 | |
| — | ME-II | ||||
| Neat | – | 123.39 | 0.29 | 134.56 | 0.26 |
| α-CD | 2.5 | 113.20 | 0.29 | 121.26 | 0.28 |
| β-CD | 2.5 | 104.83 | 0.31 | 123.42 | 0.23 |
| β-CD hydrate | 2.5 | 110.99 | 0.35 | 121.61 | 0.30 |
Conductivity measurements
| CD | Conc. (mM) | logσi | logσf | θ c(K) | ω p | |
|---|---|---|---|---|---|---|
| Differential | SBE | |||||
| ME-I | ||||||
| Without | −0.59 ± 0.03 | 2.90 ± 0.02 | 315.2 0 | 316.80 ± 0.09 | 41.0 | |
| hp-β-CD | 1 | −0.86 ± 0.03 | 3.04 ± 0.05 | 317.00 | 317.01 ± 0.12 | 29.6 |
| 2.5 | −0.98 ± 0.14 | 3.72 ± 0.21 | 320.20 | 319.16 ± 0.3 | 42.1 | |
| 5 | −2.51 ± 1.27 | 6.51 ± 2.8 | 323.30 | 325.20 ± 0.05 | 43.0 | |
| ME-II | ||||||
| PIT (θ (K)) | ||||||
| Without | – | 53.0 | ||||
| α-CD | 1 | 41.5 | ||||
| 1.5 | 38.0 | |||||
| 2.5 | 36.5 | |||||
| β-CD | 1 | 47.0 | ||||
| 1.5 | 41.0 | |||||
| 2.5 | 37.5 | |||||
| β-CD hydrate | 1 | 41.0 | ||||
| 1.5 | 36.5 | |||||
| 2.5 | 34.5 | |||||
The data show that θc increases with the increase in concentration of hp-β-CD. The value of θc for all concentrations under study varies as 5 mM > 2.5 mM > 1 mM > without additive. The percolation threshold has also been obtained from the Sigmoidal Boltzmann fitting (SBE) procedure reported by Hait et al.23 Fitted curves of σ–θ are depicted in Fig. I (B) (supplementary material†).
The results depict that the addition of hp-β-CD delays the percolation process. The addition of CD in microemulsions causes variations in the effective polar area of the surfactant due to an increase in the screening of the electrostatic charges of the head groups and therefore a decrease in the electrostatic repulsions. This alters the geometric parameters, thus increasing the negative natural curvature of the surfactant and its tendency to produce reverse structures.24
In the present study, moderate concentrations of hp-β-CD have been found to delay the temperature induced percolation process. The results are depicted in Table 3. The delay in θc becomes more pronounced with an increase in concentration of hp-β-CD. This behavior of CD molecules is contrary to that found when organic compounds like urea and thiourea are added to microemulsions.25 This has been explained on the basis of binding of additives to the AOT head group, which induces greater disorder in the surfactant environment, thus preventing the interdroplet interactions. Bommarius et al.26 have shown that the mechanism of solubilizate exchange involves the formation of short-lived dimers, which deform the surfactant layer followed by their separation. Further, hp-β-CD is a water soluble entity and the –OH group of hp-β-CD has the tendency to H-bond with the water molecules at the interface of the microemulsion resulting in an increase in rigidity of the interface and hence the percolation temperature.
One of the best methods to study nanoemulsions is the phase inversion temperature (PIT) method, which is based on the changes in the solubility of polyoxyethylene-type non-ionic surfactants with temperature.27 The surfactant is hydrophilic at low temperatures but becomes lipophilic with increasing temperature due to dehydration of the polyoxyethylene chains. At low temperatures, the surfactant monolayer has a large positive spontaneous curvature forming oil-swollen micellar solution phases (or o–w microemulsions) which may coexist with an excess oil phase. At high temperatures, the spontaneous curvature becomes negative and water swollen reverse micelles (or w–o microemulsions) coexist with excess water phase. At a critical temperature, the hydrophilic–lipophilic balance (HLB) temperature, and the spontaneous curvature is zero and a bicontinuous microemulsion phase containing comparable amounts of water and oil phases coexists with both excess water and oil phases.28
To determine the PIT, the relationship between the conductivity and the temperature for the emulsions at different CD concentrations has been measured and is shown in Fig. 3 and Table 3. It has been observed that, the decrease in conductivity after reaching the maximum is not continuous and another well-defined maximum is observed. Some researchers29,30 have also reported similar results, and this phenomenon has been attributed to the formation of liquid crystalline phases during the transition from o/w emulsions to w/o emulsions. In these cases, the PIT is also taken as the average between the highest and the lowest conductivity values (i.e. neglecting the intermediate well-defined maximum). It is further observed that the PIT of the emulsions decreases with the increase in concentration of the assimilated CD. This effect is attributed to the ability of CD molecules to penetrate between the surfactant interface, thereby altering the optimum molecular geometry of the surfactant layer at the oil–water interface. The insertion of CD molecules therefore leads to the formation of a planer surfactant curvature. Therefore, they have to be heated to a lower temperature before the curvature tended towards unity and hence would have lower PIT. The PIT of emulsions accurately reflects that the real HLB of a surfactant in a given system changes sensitively with the amount and kinds of added salts.31
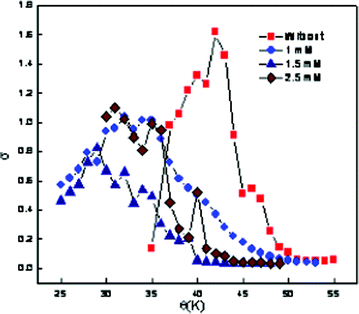 | ||
| Fig. 3 Variation of electrical conductivity as a function of temperature at different concentrations of β-CD hydrate for ME-II. | ||
Spectroscopic investigations
In any reverse micellar formulation, the OH band is a good probe to get an insight of the state of water. This is because the change in the relative populations of differently H-bonded molecules is revealed by the change in OH band shape and width.32,33 It has already been reported by Mehta et al.34 that water close to the biological membranes or protein interface exhibits behavior markedly different from that of bulk water. The water solubilized in reverse micelles, in any respect, is similar to the interfacial water present near the biological membranes or at the protein surfaces. It has restricted mobility and a depressed freezing point and lacks the normal H-bonded structure present in the bulk. Curve fitting of ME-I data shows that there are four types of water molecules in the formulated system. The high-frequency peak at (3610 ± 20) cm−1 is ascribed to trapped water in the palisade layer of microemulsions.35 The peak at (3540 ± 20) cm−1 is attributed to bound water in water pool, which is hydrogen to sulfo-group of AOT. The peak (3420 ± 20) cm−1 is assigned to the free water. The low frequency peak (3230 ± 20) cm−1 results from bound water with a sodium counterion.36Fig. 4 depicts the changes occurring in the OH band by the addition of CD and the data tabulated in Table 4 reveals that the bands associated with all the four types of water molecules shows red shifts with the incorporation hp-β-CD in ME-I. The downward frequency shift indicates significantly strong H-bonding interactions among the water and hp-β-CD molecules with the incorporation of hp-β-CD suggesting that water–water H-bonds are being replaced by hp-β-CD OH-water H-bonds. Other contributions to the shift can arise from structural disorder within the H-bonded molecular cluster confined within the micellar core.
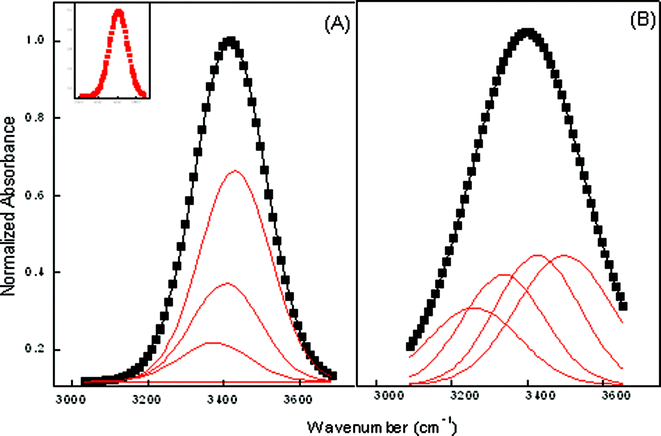 | ||
| Fig. 4 Deconvoluted FTIR spectra of ME-I at ω = 22 (A) Pure (B) hp-β-CD. Inset shows the reference peak. | ||
| — | Water with sodium counterion | Free water | Bound water in water pool hydrogen to sulfo-group of AOT | Trapped water in the palisade layer |
|---|---|---|---|---|
| ME-I | ||||
| Pure | 3307.5 | 3391.2 | 3431.0 | 3441.5 |
| Fraction of water | 0.00534 | 0.4964 | 0.1402 | 0.3850 |
| hp beta CD | 3230.5 | 3322.2 | 3414.0 | 3422.5 |
| Fraction of water | 0.1126 | 0.2855 | 0.2855 | 0.0011 |
| ME-II | ||||
| ω | Bound with Tween 80 | Free water | Phosphate of lecithin | Palisade layer |
| 4.9 | No conspicuous peak | |||
| 9.8 | No conspicuous peak | |||
| 14.71 | 3275.9 | 3350.3 | 3416.0 | 3477.09 |
| 19.62 | 3291.0 | 3400.6 | 3470.1 | 3528.8 |
| 24.52 | 3315.1 | 3419.1 | 3492.2 | 3546.2 |
| 28.26 | 3320.9 | 3428.3 | 3495.2 | 3555.0 |
| α CD | 3284.1 | 3392.3 | 3447.3 | 3482.7 |
| Fraction of water (PF) | 0.2783 | 0.3311 | 0.3276 | 6.979 × 10−6 |
| β CD | 3284.8 | 3388.7 | 3459.0 | 3523.3 |
| Fraction of water (PF) | 0.2419 | 0.3381 | 0.3334 | 0.0864 |
| β CD hydrate | 3288.4 | 3439.6 | 3386.4 | 3502.7 |
| Fraction of water (PF) | 0.49763 | 0.262 | 0.2181 | 0.0015 |
Also, the total peak area of the OH stretching band of water has been found to increase with water content. As water is composed of four different states of water in the system, viz. bound water, trapped water, and free water, it is reasonable to assume that the total peak area corresponding to the water band is the sum of the peak areas of the different states of water.
Thus, total peak area is given by
| GTotal = G1 + G2 + G3 | (1) |
If PF is the fraction of free water corresponding to the 3290 ± 20 cm−1 peak, PB is the fraction of bound water corresponding to the 3490 ± 20 cm−1 peak, and PT (water bound to the surfactant head group and counterion) is the fraction of trapped water corresponding to the 3610 ± 10 cm−1 peak, then their respective values can be calculated from the following relations
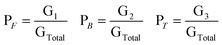 | (2) |
To further support the results in ME-II, the data has been subjected to deconvolution to find the actual state of water in the systems. Whereas in pure ME-II, the OH band at low water content is diffused with no sharp maxima (Fig. 5). However, with the assimilation of CDs viz. α, β and β-CD hydrate, sharp maxima are observed. As CDs are comprised of glucopyranose units with the cavity lined by the H-atom and the glycosidic oxygen bridges, this results in the appearance of sharp bands in the assimilated CD. Curve fitting of ME-II data shows that there are four types of water molecules in the formulated system (Fig. 5, Table 4). The high-frequency peak at (3510 ± 30) cm−1 is ascribed to trapped water in the palisade layer of the nanoemulsions. The peak at (3440 ± 30) cm−1 is attributed to phosphate of lecithin in the water pool. The peak (3320 ± 30) cm−1 is assigned to the free water whereas the low frequency is assigned to water bound with Tween 80. The results further reveal that with the incorporation of CD at low water content, the water pool begins to be formed with no conspicuous difference in the number of molecules associated to a particular type of water. The added water molecules first hydrate the surfactant head group and then form the core of the ME system. However, on the basis of fraction of water estimated (Table 4) in the presence of cyclodextrins viz. α CD, β CD, β CD hydrate in the water pool, it is observed that the maximum quantity of water is bound to Tween 80, whereas the palisade layer has the minimum amount. The results further indicate that there is not much change in the peak position of water bound to Tween 80 with the incorporation of cyclodextrins.
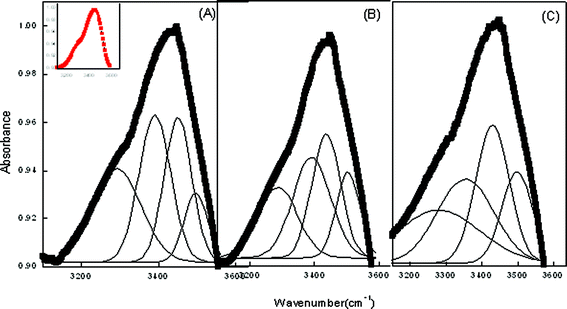 | ||
| Fig. 5 Deconvoluted FTIR spectra of ME-II at ω = 4.9 respectively in the presence (A) α-CD (B) β-CD (C) β-CD hydrate. Inset shows the reference peak. | ||
Methylene blue is a water soluble probe. MB is known to exhibit absorption maxima at 612 (dimer) and 666 nm (monomer), respectively.39 Since the peaks fall in the visible region, the word visible will be used instead of UV-Visible in the remaining text. However, with the incorporation in ME-I, only the monomer peak is observed. This clearly indicates suppression of the dimer formation by inclusion of the MB monomer in the ME-I cavity. The absorption spectra of ME-I assimilated with 2 mM hp-β-CD is depicted in Fig. 6 (A). A blue shift of 9 nm is observed with the incorporation of 1 mM hp-β-CD whereas a red shift of 11 and 13 nm, is seen in the presence of 3 and 4 mM hp-β-CD. With the increase in ω of ME-I, at a particular concentration of hp-β-CD, a red shift is observed. This indicates that hp-β-CD is located at the interface at low ω but with the increase in ω, it migrates to the core. The results also confirm that the concentration of hp-β-CD higher than 1mM have the tendency to migrate to the water pool.
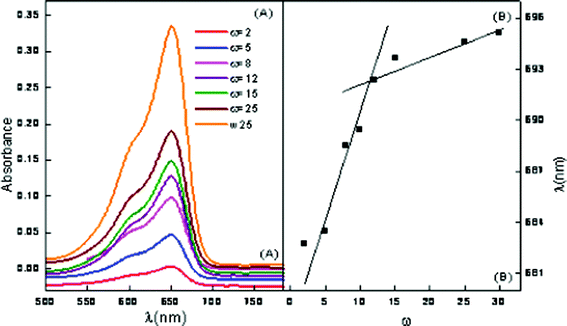 | ||
| Fig. 6 Vis absorption spectra of ME-I (A) variation of ω in the presence of 2 mM hp-β-CD (B) wavelength of maximum absorption vs. ω. | ||
The plots of wavelength at maximum intensity of ME-I, using MB as a function of ω are presented in Fig. 6 (B). The breakpoint in the plot in Fig. 6 (B) corresponds to the ω′ value where the reverse micelle changes to a microemulsion. This also indicates that the cationic dye (MB) is localized at the vicinity of the anionic sulfonate groups due to electrostatic attraction.
Similar studies have been carried out in the ME-II system to elucidate the behavior and interactions of other assimilated CDs. Fig. 7 shows the behavior of pure ME-II and a conspicuous change in the behavior has been observed at ω = 9.8. Here, MB shows absorption maxima at 614 (dimer) and 664 nm (monomer), respectively towards the red end side of the electromagnetic region as compared to the pure MB. A sharp change in behavior is observed at ω = 9.8 where conspicuous monomer and dimer peaks vanish and instead only flattened monomer peak is observed. At ω = 19.62, broad monomer peak at 684.8 nm and a sharp peak corresponding to the dimer is observed at 587.9 nm. All the spectral changes observed have been assigned to sudden structural transformations in ME-II from o/w to bicontinuous to w/o. This has been depicted in Fig. 7(B).
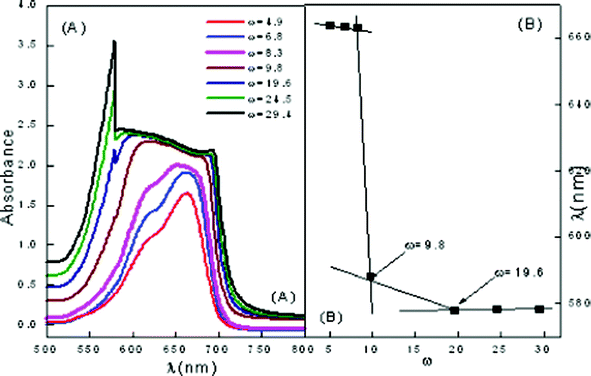 | ||
| Fig. 7 Vis absorption spectra of ME-II (A) variation of ω in pure ME-II (B) wavelength of maximum absorption vs. ω. | ||
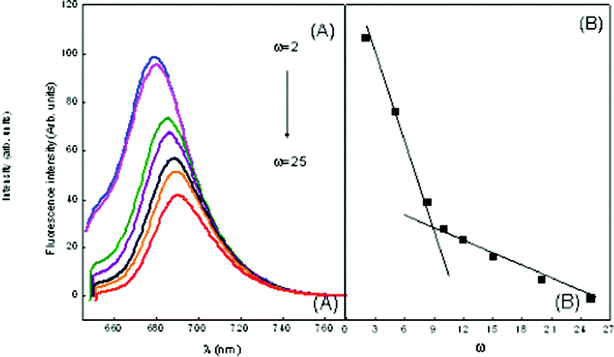 | ||
| Fig. 8 Emission spectra of MB in ME-I (A) variation of ω in the presence of 1 mM hp-β-CD (B) wavelength of maximum absorption vs. ω marking the formation of free water pool. | ||
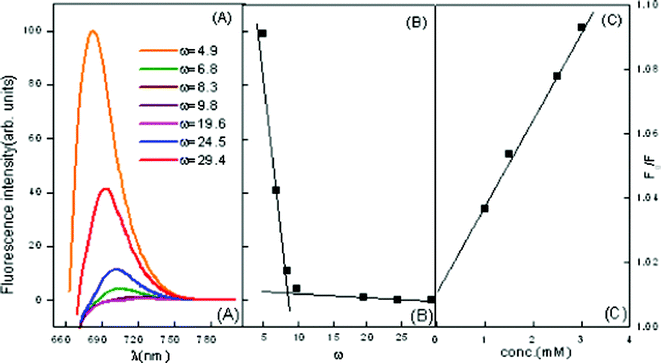 | ||
| Fig. 9 Emission spectra of MB in ME-II (A) variation of ω in the presence of β-CD = 2.5 mM (B) wavelength of maximum absorption vs. ω marking the formation of free water pool (C) Stern–Volmer plot for quenching of MB in the presence of β-CD = 2.5 mM. | ||
The fluorescence intensity of MB decreases in the presence of a quencher molecule (CD) in microemulsion media. The Stern–Volmer constant (KSV)40 have been evaluated using eqn (1)
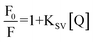 | (3) |
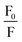 vs. quencher concentration [Q] (Fig. 9(c)). The values of KSV are depicted in Table 5.
vs. quencher concentration [Q] (Fig. 9(c)). The values of KSV are depicted in Table 5.
| ω | KSV (ME-I) | N | ω | KSV (ME-II) | N |
|---|---|---|---|---|---|
| 2 | 1.26 | 20.26 | 4.9 | 2.23 | 9.20 |
| 5 | 1.19 | 22.88 | 6.8 | 2.02 | 12.6 |
| 8 | 0.17 | 24.62 | 8.3 | 1.96 | 18.0 |
| 10 | 0.12 | 26.62 | 9.8 | 1.75 | 28.0 |
| 12 | 0.87 | 28.95 | 19.6 | 1.42 | 36.5 |
| 15 | 0.57 | 32.00 | 24.5 | 0.98 | 40.5 |
| 22 | 0.33 | 39.20 | 29.4 | 0.86 | 56.3 |
| 25 | 0.04 | 46.91 | – | – | – |
The KSV decreases with an increase in ω, i.e. with increasing amount of water in the interior water pool of ME-I and ME-II respectively. As the ratio of the number of water molecules to that of the surfactant (ω) decreases, the size of the water pool decreases. With a decrease in the size of the reverse micellar core, the quencher molecules become restricted into it and the interaction occurs easily, resulting in higher values of KSV. Another reason may be because of the high “local concentration” of the quencher ion in the reverse micellar core than in the bulk. All Stern–Volmer plots for the quencher ions were found to be linear, suggesting that collisional (dynamic) quenching plays a major role in the quenching process.
During a collision between quencher and fluorophore, there is a possibility of electron transfer occurring. Also, as the size of the core increases, the local concentration decreases, hence quenching decreases. The decrease in value of Ksv is more or less proportional to ω and a break point is observed at ω = 9.5 in ME-I (Fig. 8) and ω = 9.8 in ME-II (Fig. 9(B)), marking the beginning of free water in the system.
Also, the results depict that in ME-I, MB has λmaxfl 682 nm (same as pure MB) i.e. there is no shift in the emission maxima, the dye molecules are most likely to reside at the water–surfactant interface, i.e., on the surface of a micelle on a polar disposition. A red shift from 682 nm to 694.12 nm and gradual decrease in fluorescence intensity with increasing ω of the reverse micelles has also been observed. This indicates that MB molecules are initially located at the interface of reverse micelles but migrates to the core at higher ω.
Similar studies have also been carried out in ME-II. A decrease in KSV with the increase in ω is observed in Fig. 9(C) . The results have in depicted in and Table 5. Here also florescence intensity decreases with an increase in ω indicating the quenching capability of assimilated MB and its initial location at the micellar interface and its consequent migration to the water pool. However, in this case a sharp decrease in intensity is observed after ω = 8.3, indicating a conspicuous change in the microstructure of the microemulsion at this ω.
The results also depict a conspicuous red shift in λmaxfl with the increase in ω in the presence of CD, which indicates that the initial location of CD is the micellar interface with its consequent migration to the water pool.
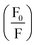 in the presence of quencher [Q] to that in the absence is related to the micellar concentration by the expression
in the presence of quencher [Q] to that in the absence is related to the micellar concentration by the expression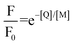 | (4) |
Here, effective micellar concentration [M] = ([S] − cmc)/N where [S] is the concentration of the surfactant and N is the micellar aggregation number:
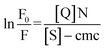 | (5) |
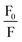 against [Q] and it has been considered as the average aggregation number of the micelles. The values of N have been tabulated in Table 5. The values of N are higher for ME-I as compared to ME-II.
against [Q] and it has been considered as the average aggregation number of the micelles. The values of N have been tabulated in Table 5. The values of N are higher for ME-I as compared to ME-II.
Differential scanning calorimetry
We followed the method utilized by Senatra et al.42,43 in which the endothermic scanning mode was applied and the peaks representing various states of water were identified and analyzed. The method differentiates between three types of water. By analyzing samples with DSC, changes in the cooling–heating curve can be observed. For characterization of our nanoemulsions, both heating and cooling curves have been found to be important. The complete spectrum has been presented in Fig. 10. The thermogram reveals the presence of four different types of water molecules present in both pure and cyclodextrin assimilated nanoemulsion.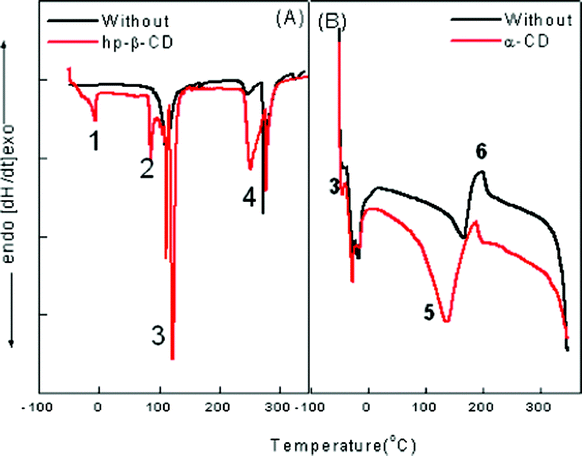 | ||
| Fig. 10 Thermogram for (A) ME-I and (B) ME-II representing various types of water molecules associated with the system where (1) is free water, (2) is Na+ counterion bound water; (3) is trapped water in the palisade layer; (4) is the AOT head group bound water; (5) is pure super cooled water at −15 °C; (6) is Tween 80 and phosphate surfactant head group bound water. | ||
In ME-I, the water inside a micelle “acts” as bulk water of smaller volume. DSC cooling curves in Fig. 10 (A) show the curves for pure and hp-β-CD assimilated microemulsions. The results show:
1. The peak for free water is not sharp in the case of pure microemulsion, however, with the assimilation of hp-β-CD, a sharp peak appears at −6.5 °C.
2. Water bound to the sodium counter ion and AOT head group appears at 250 °C and 278 °C.
3. The water trapped in the palisade region appears at 115 °C. However, the sharp peak vanishes with the assimilation of hp-β-CD due to maximum H-bonding in this region.
However, ME-II shows a different behavior that can be described as follows:
1. “Free” water, which is water with properties that are similar to those of bulk water. It melts at 0 °C.
2. “Interfacial” water, which is the water confined within the region separating the aqueous core from the oleic acid dispersing phase. This region is considered to be a finite in extent and not just an imaginary line which serves as a border between the two phases. The interphasial water melts at 167 °C for a pure nanoemulsion whereas with the assimilation of α-CD it shifts to 137 °C.
3. “Bound” water, which is bound to hydrophilic groups and counterions, and which melts at temperature slower than −40.5 °C.
Conclusions
This study presents the investigation of novel microemulsions (AOT/water/isooctane) with assimilation of cyclodextrins: hp-β-CD and nanoemulsions (water/Tween-80/lecithin/ethyl oleate) with the assimilation of α-CD, β-CD, β-CD hydrate. The results show, for the first time, that microemulsions and nanoemulsions with a chiral hydrophobic and hydrophilic nanostructured cavity in the same aggregates can be formed. The incorporation of CD in reverse micelles has been reported to significantly affect their solubilization, electric percolation phenomenon and the water pool properties. Conductivity results depict that PIT of the system decreases with the increase in concentration of added CD. The insertion of CD molecules leads to the formation of a planer surfactant curvature. Therefore, they have to be heated to a lower temperature before the curvature tends towards unity and hence would have lower PIT. FTIR spectroscopy and DSC studies clearly indicates the presence of four different types of water molecules in the formulated system that show shift with the incorporation of various CDs.The results allow exploration of the functionality of the interfaces, and it may be possible that these systems can be used as delivery vehicles for various food components, an area that we are currently investigating.
Acknowledgements
K. K. is thankful to Inspire DST for fellowship. S. K. M. is grateful to DST for financial assistance.References
- M. Porras, C. Solans, C. González, A. Martínez, A. Guinart and J. M. Gutiérrez, Colloids Surf., A, 2004, 249, 115–118 CrossRef CAS
.
- E. P. Melo, M. R. Aires-Barros and J. M. S. Cabral, Biotechnol. Annu. Rev., 2007, 1, 87–96 Search PubMed
.
- L. Wang, X. Li, G. Zhang, J. Dong and J. Eastoe, J. Colloid Interface Sci., 2007, 314, 230–235 CrossRef CAS
.
- C. M. Pey, A. Maestro, I. Solé, C. González, C. Solans and J. M. Gutiérrez, Colloids Surf., A, 2006, 288, 144–150 CrossRef CAS
.
- K. Bouchemal, S. Briancon, E. Perrier and H. Fessi, Int. J. Pharm., 2004, 280, 241–251 CrossRef CAS
.
- E. Almenar, R. Auras, M. Rubino and B. Harte, Int. J. Food Microbiol., 2007, 118, 164–172 CrossRef CAS
.
- R. J. Bergeron, M. J. Channing, G. J. Gibeily and D. M. Pillor, J. Am. Chem. Soc., 1977, 99, 5146–5151 CrossRef CAS
.
- R. D Falcone, M. A. Biasutti, N. M. Correa, J. J. Silber, E. Lissi and E. Abuin, Langmuir, 2004, 20, 5732–5737 CrossRef
.
- K. Martinek, A.V. Levashov, N. L. Klyachko, Y. L. Khmelnitski and Y. V. Berezin, Eur. J. Biochem., 1986, 155, 453–468 CrossRef CAS
.
- C. N. Durfor, R. J. Bolin, R. J. Sugasawara, R. J. Massey, J. W. Jacobs and P. G. J. Schultz, J. Am. Chem. Soc., 1988, 110, 8713–8714 CrossRef CAS
.
- E. Acosta, Curr. Opin. Colloid Interface Sci., 2009, 14, 3–15 CrossRef CAS
.
- J. Flanagana, K. Kortegaarda, D. N. Pinderb, T. Rades and H. Singha, Food Hydrocolloids, 2005, 20, 253–260 CrossRef
.
- J. Flanagan and H. Singh, Crit. Rev. Food Sci. Nutr., 2006, 46, 221–237 CrossRef CAS
.
- N. Garti, A. Yaghmur, M. E. Leser, V. Clement and H. J. Watzke, J. Agric. Food Chem., 2001, 49, 2552–2562 CrossRef CAS
.
- N. Patel, U. Schmid and M. J. Lawrence, J. Agric. Food Chem., 2006, 54, 7817–7824 CrossRef CAS
.
- I. Amar, A. Aserin and N. Garti, J. Agric. Food Chem., 2003, 51, 4775–4779 CrossRef CAS
.
- J. Flanagana, K. Kortegaarda, D. N. Pinderb, T. Rades and H. Singha, Food Hydrocolloids, 2005, 20, 253–260 CrossRef
.
- N. Patel, U. Schmid and M. J. Lawrence, J. Agric. Food Chem., 2006, 54, 7817–7824 CrossRef CAS
.
- G. Astray, C. Gonzalez-Barreiro, J. C. Mejuto, R. Rial-Otero and J. Simal-Gándara, Food Hydrocolloids, 2009, 23, 1631–1640 CrossRef CAS
.
- F. A. Araújo, R. G. Kelmann, B. V. Araújo, R. B. Finatto, H. F. Teixeira and L. S. Koester, Eur. J. Pharm. Sci., 2010, 42, 238–245 CrossRef
.
- P. Izquierdo, J. Esquena, T. F. Tadros, C. Dederen, M. J. Garcia, N. Azemar and C. Solans, Langmuir, 2002, 18, 26–30 CrossRef CAS
.
- N. Uson, M. J. Garcia and C. Solans, Colloids Surf., A, 2004, 250, 415–421 CrossRef CAS
.
- S. K. Hait, S. P. Moulik and R. Palepu, Langmuir, 2002, 18, 2471–2476 CrossRef CAS
.
- D. F. Evans, D. J. Mitchell and B. W. Ninham, J. Phys. Chem., 1986, 90, 2817–2825 CrossRef CAS
.
- L. Garcia-Rio, J. R. Leis, J. C. Mejuto and M. E. Pena, Langmuir, 1994, 10, 1676–1683 CrossRef CAS
.
- A. S. Bommarius, J. F. Holzwarth, D. I. C. Wang and T. A. Hatton, J. Phys. Chem., 1990, 94, 7232–7239 CrossRef CAS
.
- K. Shinoda, J. Colloid Interface Sci., 1968, 24, 4–9 CrossRef
.
- K. Shinoda and H. Saito, J. Colloid Interface Sci., 1969, 30, 258–263 CrossRef CAS
.
- P. Izquierdo, J. Esquena, T. F. Tadros, C. Dederen, M. J. Garcia, N. Azemar and C. Solans, Langmuir, 2002, 18, 11126–11135 CrossRef
.
- H. Kunieda, Y. Fukui, H. Uchiyama and C. Solans, Langmuir, 1996, 12, 2136–2140 CrossRef CAS
.
- D. Morales, J. M. Gutiérrez, J. M. Garcia-Celma and C. Solans, Langmuir, 2003, 19, 7196–7200 CrossRef CAS
.
-
(a) E. Caponetti, D. C. Martino, F. Ferrante, L. Pedone, A. Ruggirello and V. T. Liveri, Langmuir, 2003, 19, 4913–4922 CrossRef CAS
; (b) G. Giammona, F. Goffredi, V. T. Liveri and G. Vassallo, J. Colloid Interface Sci., 1992, 154, 411–415 CrossRef CAS
.
- K. K. Karustis, A. A. Frazier, D. S. Martula and J. A. Whiles, J. Phys. Chem., 1996, 100, 11113–11119 CrossRef
.
- S. K. Mehta and K. Kaur, Colloids Surf., A, 2010, 368, 37–43 CrossRef CAS
.
- T. K. Jain, M. Varshney and A. Maitra, J. Phys. Chem., 1989, 93, 7409–7416 CrossRef CAS
.
- H. MacDonald, B. Bedwell and E. Gulari, Langmuir, 1986, 2, 704–708 CrossRef CAS
.
- S. Biswas, S. C. Bhattacharya and S. P. Moulik, J. Colloid Interface Sci., 2004, 271, 157–162 CrossRef CAS
.
- J. Czapkiewicz, M. Dlugolecka and B. Tutaj, J. Colloid Interface Sci., 2004, 276, 227–230 CrossRef CAS
.
- G. Zhang, S. Shuang, C. Dong and J. Pan, Spectrochim. Acta, Part A, 2003, 59, 2935–2941 CrossRef
.
- R. G. Alargova, I. I. Kochijashky, M. L. Sierra and R. Zana, Langmuir, 1998, 14, 5412–5418 CrossRef CAS
.
- M. J. P. Gallego, C. B. Diaz and E. G. Romero, Colloids Surf., A, 2004, 249, 25–28 CrossRef
.
- D. Senatra, Adv. Colloid Interface Sci., 2006, 123, 415–424 CrossRef
.
- D. Senatra and G. Giubilaro, J. Colloid Interface Sci., 1978, 67, 448–453 CrossRef CAS
.
Footnote |
| † Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra21114a/ |
| This journal is © The Royal Society of Chemistry 2012 |
