Vibrational and electronic circular dichroism spectroscopies and DFT calculations for the assignment of the absolute configuration of hydroxy-substituted 2-tetralols

Abstract

The absolute configuration of 1-and 2-tetralol (1a and 2a), of 5-hydroxy- and 8-hydroxy-2-tetralol (2b and 2c), and of 1-aminotetralin (1b) has been established by comparison of experimental infrared vibrational absorption (VA) and vibrational circular dichroism (VCD) spectra and density functional theory (DFT) calculations. DFT calculations using B3PW91 functional with TZ2P basis set were carried out to predict the VA and VCD spectra. Electronic circular dichroism (ECD) spectra were also measured and compared to time-dependent DFT calculations. The VCD data have been found to be more specific than ECD.

---

Introduction

1,2,3,4-Tetrahydro-1-naphthols (1-tetralols) and 1,2,3,4-tetrahydro-2-naphthols (2-tetralols) are versatile intermediates in organic synthesis since they are suitable for elaboration into various tetralin derivatives.¹ The tetralin unit is the core structural element of many compounds exhibiting a diverse range of biological activities and is also incorporated in a number of natural products.² For example, 2-aminotetralins bearing hydroxy and/or methoxy groups in the aromatic ring are well known dopaminergic, serotoninergic, adrenergic, as well as melatoninergic agents³ and are used for the treatment of many central nervous system related disorders.⁴ In addition, they have been reported to possess a variety of actions, including cardiovascular effects and potent antifungal activities.⁵ It is worth noting that 2-aminotetralin activity has been found to be strongly dependent on both the substitution pattern of the aromatic ring and the configuration of the stereogenic center in 2-position.^3b,6 For these reasons, considerable effort has been directed towards the synthesis of tetralin derivatives in enantiomerically pure forms.⁷

Some of the authors have recently reported that 2-tetralol (2a), 5-hydroxy- and 8-hydroxy-2-tetralol (2c and 2d) can be prepared in moderate to very high enantiomeric excess (up to 99% ee) by enzymatic resolution of the corresponding racemic butyrates.⁸

Provided that the conformational preferences of the molecules under study are known, electronic circular dichroism (ECD) and subsequent applications of empirically derived sector rules have been frequently used to assign the absolute configuration (AC) of such compounds. Several correlations between CD spectra and the conformation/absolute configuration of structures containing a tetralin moiety have been reported.⁹ In particular, Snatzke and Ho univocally related the sign of the ECD band in the 260–290 nm range corresponding to the ¹L_b transition of the benzene chromophore in tetralins, to the chirality sense of the cyclohexene ring.¹⁰ Snatzke's helicity rules have been verified and proven to be correct for a number of tetralin derivatives.¹¹ However, failures of the rules have been encountered in some instances.¹²

A powerful non-empirical method to determine the AC of molecules in solution has emerged in recent years, i.e. measuring vibrational circular dichroism (VCD)¹³ and/or electronic circular dichroism (ECD) and comparing the experimental spectra with those predicted by density functional theory (DFT) and time-dependent DFT (TDDFT) calculations.¹⁴

In this work, we indeed use VCD and ECD in tandem with DFT and TDDFT calculations to determine the AC of 2-tetralol (2a) and its hydroxy-substituted derivatives (2b and 2c) (see Scheme 1), previously obtained by an empirical assignment. These studies have also been extended to 1-tetralol (1a) and 1-aminotetralin (1b). To the best of our knowledge, no VCD spectra of tetralin derivatives has so far been reported. We anticipate that VCD will be more specific than ECD in distinguishing different molecules and in establishing their absolute configuration (AC). All of these compounds bear a chiral center remote from the aromatic moiety, which provides the electronic transitions. Thus, the gross features of the ECD spectra are similar in all cases and just minor aspects change. We faced a similar problem in ref. 15, where a chiral center was close to an aromatic paracyclophane moiety.

Scheme 1

Results and discussion

Conformational analysis

Scheme 1 presents the structures of all tetralols here studied. They differ in the position (1 or 2) of the OH substituent in the alicyclic ring and in the substitution pattern of the aromatic ring.

A detailed conformational analysis has been performed in vacuo to determine the conformer populations of the investigated compounds. We expected 1a and 2a to possess six conformers corresponding to the OH (OD) group in 1 or 2 being either on the axial or equatorial position for a skewed chair conformation of the cyclohexene ring and for three possible rotational states of the OH (OD) group about the C–O bond. This expectation has been checked by scanning energies along τ (H₂C₂C₁O) and φ (C₉–C₁–OH) dihedral angles for 1a and τ (H₁C₁C₂O) and φ (C₁–C₂–OH) for 2a with Gaussian03^16,17 at the B3LYP/6-31G(d,p) level of theory, as reported in Figs SI-1 and SI-2 of the supplementary information‡. The boat-type conformation at ca. τ = 100° about which the two possible half-chairs (τ ≈ 60° and τ ≈ 160°) interconvert, is found at higher energy, close to the transition state situation.¹⁸

The high mobility for the hindered rotation of the OH group is a notorious fact in phenols and for this reason we have run a scan of the energy for molecules 2b and 2c. Notwithstanding the facile rotation of such OH, one may observe that the lowest energies occur for the relevant HOCC dihedral angles χ = 0° and 180°. This double possibility is composed with the other six conformation possibilities, giving a total of twelve possible conformers (see Figs SI-3 and SI-4‡).

The geometries of the conformers A–F (for 1a, 1b and 2a) and A–L (for 2b and 2c) for the (R)-enantiomers were optimized with DFT calculations at the B3PW91/TZ2P level. The IR and VCD spectra have been calculated for all of the optimized geometries of Figs SI-5–SI-9‡. The relative energies and free energies of the stable conformations with the corresponding populations are listed in Figs SI-5 and SI-6 for 1a and 2a, respectively, together with the optimized structures and in Figs SI-7, SI-8 and SI-9 for 2b, 2c and 1b, respectively‡.

Since, hydrogen–deuterium exchange takes place at the hydroxyl group in methanol-d₄ solutions, calculations in vacuo and in solution were carried out using D-substituted hydroxyl groups.

1-Tetralol (1a)

In vacuo, the most abundant conformers (A and B) are characterized by the hydroxyl group at C₁ being in the pseudo-axial position (Fig. SI-5‡). The hydrogen atom on the hydroxyl group is trans to the hydrogen atom at C₁ for conformer A (around 45% population) and oriented towards the benzene ring in conformer B (around 28% population). At higher energy (0.62 kcal mol⁻¹), the OH substituent on C₁ assumes the pseudo-equatorial position in the conformer C (about 16% population) with H atom on the OH trans to H₁. The other conformers bearing the OH group in the pseudo-equatorial position (conformer D with the hydroxyl group oriented towards the phenyl ring) and conformer E with OH directed towards H₂ are not very likely (around 4% population). Finally, the least populated conformer (F with 3% population) is characterized by the OH group in the pseudo-axial position with OH gauche with respect to C₁–H₁.

2-Tetralol (2a)

In the three most populated conformers, which have been labelled A, B and C, for a total 78% population, the hydroxyl group at the C₂ stands in the equatorial position. (Fig. SI-6‡) The first and the third most populated conformers (conformer A, 29%, and conformer C, 24%) are characterized by the OH bond in gauche with respect to C₂–H₂. The second most abundant conformer (conformer B, around 25% population) has the hydrogen atom on the OH group trans with respect to H₂. The first three conformers are almost iso-energetic. In the three least populated conformations, the hydroxyl group at C₂ is axial; in conformer D (about 9% population) the hydrogen of the OH is trans with respect to H₂, in conformers E (8%) and F (5% population) the OH is gauche with respect to C₂–H₂.

The somewhat unusual behaviour of the hydroxyl group in the pseudo-axial position being slightly more stable in compound 1a (around 0.3 kcal mol⁻¹) than the pseudo-equatorial forms can have several explanations: either weak hydrogen bonding is more likely to take place in this situation between the positive H of the OH and the electron-rich aromatic moiety or the steric interactions between the OH at C₁ and the hydrogen atoms of the aromatic ring in the peri-position are minimized.^15,19

NMR studies²⁰ have confirmed the pseudo-axial character of the substituent in position C₁ in 1a.

For compound 2a, these types of interactions are less likely and conformers with the OH in the equatorial position are more stable, as expected.

The effects of solvation by chloroform and methanol on the optimized geometry and energy were examined here by IEF-PCM model at the B3PW91/TZ2P level and compiled in Figs SI-5 and SI-6‡ with Gibbs free energy values for each conformer. In the polarizable continuum model (IEF-PCM) for 1a, the geometry of the six conformers is preserved and the lowest-energy conformations coincide with conformers A, B and C found previously with the vacuum model. However, a switch in the relative population of conformers A and B in chloroform and of B and C in methanol takes place. We also noticed that PCM-relative-energy of pseudo-axial and pseudo-equatorial conformers A and C ratio in methanol is almost 1. This is expected since the OH/phenyl interactions are screened by the solvent and some intramolecular H-bonding may be sequestered by the solvent.

For compound 2a, where H-phenyl interactions are less important, we confirmed that the effect of polar solvent, such as methanol, on the structure and relative energy is less significant.

To sum up, both 1a and 2a are quite flexible molecules, due to the mobility of the cyclohexene ring and to the pseudo-rotation of the OH about the CO bond. However, 1a differs from 2a in the fact that, in most of the conformers, the OH group in 1a is pseudo-axial, while in 2a it is equatorial. For this reason, we report in Fig. 1 the most populated conformers calculated in vacuo for 1a (left) and 2a (right); the remaining conformers are depicted in the supporting information‡. The addition of continuum (implicit) solvent does not change the conclusions.

Fig. 1 The most populated conformers calculated in vacuo1a (left) and 2a (right).

The structures of all twelve expected conformers of 2b and 2c have been optimized at the B3PW91/TZ2P level of theory in vacuo and in methanol. The relative free energies of the twelve conformers were calculated and the results are summarized in Figs SI-7 and SI-8 for 2b and 2c, respectively, together with the corresponding structures‡.

In methanol-d₄ solutions, hydrogen–deuterium exchange takes place at both hydroxyl groups. Therefore, calculations in vacuo and in solution were carried out using deuterium substitution of both the hydroxyl groups in the benzene and alicyclic rings.

5-Hydroxy-2-tetralol (2b) and 8-hydroxy-2-tetralol (2c)

In 2b, except conformer F, all of the most populated conformers (A–G) bear the alicyclic OH group in the equatorial position (Fig. SI-7‡). Conformer F is characterized by the hydroxyl group at C₂ in the axial-position with the H of the hydroxyl trans to H₂. The OH at C₅ (always in the plane of the benzene ring), for conformers A (22% population), B and C (16% population) is directed towards the hydrogen at C₆. In conformers A, C, D and E, the hydroxyl group at the C₂ is oriented gauche and in conformer B and Gtrans with respect to C₂–H₂.

For compound 2c (Fig. SI-8‡), the prevalence of the conformers with the alicyclic OH moiety in the equatorial position (lowest energy structures) with respect to the axial position (highest energy structures) is less clear than for compound 2b. Even if the most populated conformers have the alicyclic OH equatorial (conformer A with 18% population, conformer B with 16% population, conformer C with 15% and conformer D with 15%) alternation of the equatorial and axial alicyclic OH moiety for the next structures is noticed. Finally, the least populated structures are all axial (conformers I, J, K and L), like in compound 2b. The most populated conformers (A–C and F), which altogether give a 56% population, have the benzyl OH moiety directed towards the hydrogen at the C₆.

1-Aminotetralin (1b)

In compound 1b, where an amino group replaces the hydroxyl group at C₁, conformer population changes slightly. In 1b, unlike 1a, the major conformer A (27%) bears the amine group in pseudo-equatorial position. The next conformers B (21% population) and C (18% population) have the pseudo-axial substituent. For 1b, conformers with the amine group in pseudo-axial position represent just 54% of the total population compared to 76% for 1a.

VA and VCD spectra

The experimental IR-VA and VCD spectra of 1a and 2a recorded in CDCl₃ and in CD₃OD compared to the calculated IR-VA and VCD are presented in Fig. 2 and 3, respectively. Herein, we consider the average spectra according to statistical weights from the calculated Gibbs free energy. When comparing calculations and experiment, we should keep in mind that no scaling was applied.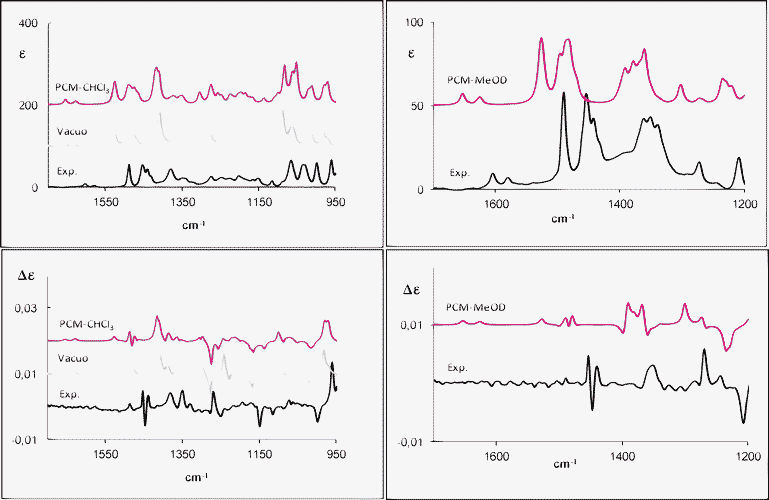

Fig. 2 Experimental and calculated (weighted sum; B3PW91/TZ2P) IR (top) and VCD (bottom) spectra of (R)-(−)-1-tetralol (1a) in CDCl₃ (left) and in CD₃OD (right).

Fig. 3 Experimental and calculated (weighted sum; B3PW91/TZ2P) IR (top) and VCD (bottom) spectra of (R)-(+)-2-tetralol (2a) in CDCl₃ (left) and in CD₃OD (right).

The IR and VCD spectra on the left panels of Fig. 2 are in reasonable agreement with the experimental data. There are few features that are not reproduced, but on the basis of VCD data one can state that the AC assignment is safe and, on account of both VCD and IR data, the conformational analysis presented above is acceptable. The most critical region is the central one, between 1150 cm⁻¹ and 1350 cm⁻¹. In particular, we point out that at 1281 cm⁻¹ we calculate a strong negative VCD peak by B3PW91/TZ2P in vacuo, as well as with PCM–CHCl₃. Such a VCD band is mainly due to conformer B, even though in general experimental VCD is weak here and no dominant VCD spectrum is identified for any conformer (see Fig. SI-10‡). Secondly, the presence of a strong positive VCD peak at 1244 cm⁻¹ without any correspondence to the experimental data is also noted in vacuo; by contrast, this band disappears using the PCM–CHCl₃ model.

Besides, the (+, −, +) features observed at 1455–1440 cm⁻¹ are not correctly predicted by the calculations in vacuo and for the PCM–CHCl₃ model even though, in the latter case, the correct shape is predicted and just the overall intensity is calculated too low.

In Fig. 2, right panels, the experimental IR and VCD spectra of 1a in methanol-d₄ together with the PCM calculated ones are given. The solvent may have profound effects on the IR and VCD spectra; in general, it may alter geometries of the solute molecule with a change of frequencies and intensities. Besides, it can modify the population-weighted spectra.¹⁷

The experimental and calculated IR and VCD spectra compare pretty well: the sign and the absolute intensities of most VCD signals are well reproduced by the continuum model, except for the (+,−,+) signals at 1493–1487–1482 cm⁻¹, which are underestimated in the VCD calculation. The calculated VCD spectrum also presents a bisignate signal at 1393–1370 cm⁻¹, which is more structured than the experimental broad feature. As evidenced in Fig. SI-10‡, the sign of this couplet, especially due to the in-plane and out-of-plane CH bending of the C₁H₁, is characteristic of the pseudo-axial or pseudo-equatorial position, respectively.

The analysis of Figs SI-10 and SI-5 shows that the calculated features of Fig. 2 result from a weighted sum of quite different spectra‡. The correct evaluation of statistical weights of different conformers is crucial; in the past, Grimme and collaborators²¹ pointed out that the choice of adequate functional is essential for determining the thermodynamic properties. In Table SI-1‡, we compare the population factors (based on ΔG) of 1a obtained with two different functionals, one of which (B97D) incorporates some dispersion effects, within the PCM approximation for CHCl₃. The results are of comparable quality and the predicted VCD spectra are similar, even though not identical (see Fig. SI-19‡). In any case, the same AC assignment is made with all approaches, though with different accuracy.

For 2-tetralol (2a), the calculated spectra in vacuo are in good overall qualitative agreement with the experimental spectra, as shown in Fig. 3. The calculated features in the absorption spectra at 1427 cm⁻¹ and around 1391 cm⁻¹ are not visible in the experimental spectra. The corresponding (−,+), (−,+) VCD couplets are in agreement with experimental features at ca. 1350 cm⁻¹, even if the experimental VCD signals are weaker than the calculated one. Also, the calculated VCD triplet (+,−,+) around 1334, 1309 and 1298 cm⁻¹ corresponds to weaker experimental VCD signals. The use of PCM for chloroform allows one to obtain a slightly better agreement with experimental features, in particular around 1055 cm⁻¹. In any case, the data univocally confirm the AC assignment. In the second part of Table SI-1‡, we compare the population factors of the various conformers of 2a calculated with the two functionals BP3W91 and B97D, within implicit solvent approximation (CHCl₃). Similar conclusions can be drawn as those for 1a.

The experimental IR and VCD spectra of 2a in methanol-d₄ are presented in Fig. 3 (right panel). Calculated and experimental IR and VCD spectra in the IEF-PCM approximation are consistent. VCD intensities and signs of the observed bands are well reproduced by the weighted average and the AC assignment is still confirmed. Interestingly, the VCD signals (+,−,+) at 1535–1500–1494 cm⁻¹, which are the signature of the equatorial substitution, confirm the predominance of the equatorial conformers for the compound 2a. (Fig. SI-11‡) Finally, if one compares IR and VCD data from d₄-methanol solutions for 1a and 2a, one may notice that while the IR data are quite similar, instead VCD are different, so that one concludes, as in ref. 15, that VCD allows one to well characterize the interactions of the chiral center with other removed moieties.

For 2b and 2c, experiments were performed only in methanol due to their poor solubility in chloroform at the concentrations needed for VCD measurements. The experimental IR and VCD spectra of 2b and 2c in methanol-d₄ are presented in Fig. 4 and 5, respectively, (see also Figs SI-12 and SI-13 for the single conformers‡). Immediately, we can tell that differences in VCD spectra are present between 2b and 2c, while the IR spectra are almost identical.

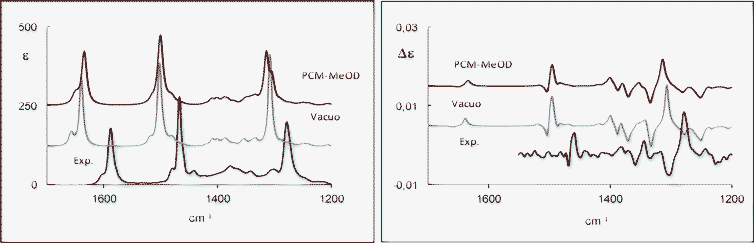Fig. 4 IR (left) and VCD (right) spectra of (R)-(+)-5-hydroxy-2-tetralol (2b) in MeOH-d₄: experimental and calculated (weighted sum; B3PW91/TZ2P) in vacuo spectra (middle) and with IEF-PCM model (top).

Fig. 5 IR (left) and VCD (right) spectra of (R)-(+)-8-hydroxy-2-tetralol (2c) in MeOH-d₄: experimental (bottom) and calculated (weighted sum; B3PW91/TZ2P) in vacuo spectra (middle) and with the IEF-PCM model (top).

For compounds 2b and 2c, the calculations are more complex due to the presence of twelve stable conformers.

The agreement between experimental and calculated in vacuo VCD spectra is very good, except for the experimental bisignate VCD signal for 2b (+,−) at 1346 and 1337 cm⁻¹, which is not well reproduced by the calculations. Calculations in vacuo and with the PCM model give comparable results. A bisignate (−,+) VCD signal at 1507–1497 cm⁻¹ typical of the equatorial conformers, which are the more populated ones, can also be observed.

For compound 2c, the agreement between experimental and calculated IR and VCD spectra in vacuo is quantitatively good, with the exception of the negative VCD signals observed at 1323, 1315 cm⁻¹, which were predicted with a weaker intensity, and of the intense positive VCD signal at 1287 cm⁻¹, which was not predicted by calculations. Using PCM, the agreement slightly improves.

The VCD signals (−,+,+) calculated at 1506, 1496 and 1479 cm⁻¹ correspond to the broad absorption band centered at 1502 cm⁻¹ and are well reproduced by the vacuum and PCM calculations. As previously observed for 2a and 2b, the bisignate VCD signal (−,+) at 1506 and 1496 cm⁻¹ is the signature of the equatorial conformers.

For compound 1b, the use of B3PW91/TZ2P functional/basis set for the isolated molecule in vacuo provides the calculated IR and VCD spectra reported in Fig. 6. The agreement between the experimental and calculated IR and VCD spectra is good, except for the following features: the IR signal calculated at 1624 cm⁻¹ is too intense; it corresponds to a predicted intense negative VCD couplet. This feature correlates with the much broader IR band observed at ∼1600 cm⁻¹ and to a structured VCD signal. Also, the negative VCD signal observed at 1447 cm⁻¹ is not correctly predicted by calculations, while the corresponding IR feature is well accounted for.

Fig. 6 Experimental IR (left) and VCD (right) spectra of (R)-(−)-1-aminotetralin (solid line) and (S)-(+)-1-aminotetralin (dashed line) (1b) in CCl₄ compared to in vacuo calculated spectra for (R)-1-aminotetralin (weighted sum; B3PW91/TZ2P).

ECD spectra

The ECD spectra of both enantiomers of 1a, 1b, 2a, 2b and 2c measured in CH₃CN are shown in Fig. 7–11. (For the absorption UV spectra of 1a, 1b, 2a, 2b and 2c see Fig. SI-18 in the supporting information‡)

Fig. 7 Calculated (weighted sum) ECD spectra of (R)-1-tetralol (dotted line) compared with the experimental data for (R)-(−)-1-tetralol (black bold solid line) and (S)-(+)-1-tetralol (grey bold solid line) (1a).

Fig. 8 Calculated (weighted sum) ECD spectra of (R)-2-tetralol (dotted line) compared with the experimental data for (R)-(+)-2-tetralol (black bold solid line) and (S)-(−)-2-tetralol (grey bold solid line) (2a).

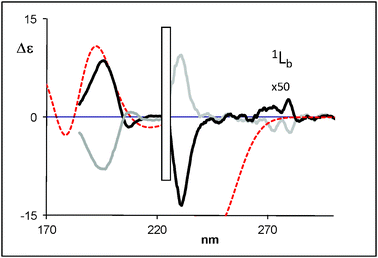Fig. 9 Calculated (weighted sum) ECD spectra of (R)-5-hydroxy-2-tetralol (dotted line) compared with the experimental data for (R)-(+)-5-hydroxy-2-tetralol (black bold solid line) and (S)-(−)-5-hydroxy-2-tetralol (grey bold solid line) (2b).

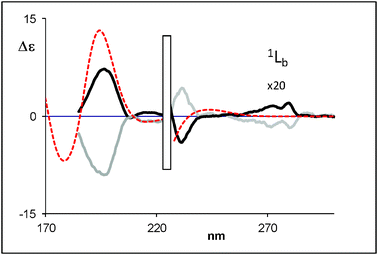Fig. 10 Calculated (weighted sum) ECD spectra of (R)-(+)-8-hydroxy-2-tetralol (dotted line) compared with the experimental data for (R)-(+)-8-hydroxy-2-tetralol (black bold solid line) and (S)-(−)-8-hydroxy-2-tetralol (grey bold solid line) (2c).

Fig. 11 Calculated (weighted sum) ECD spectra of (R)-1-aminotetralin (dotted line) compared with the experimental data for (R)-(−)-1-aminotetralin (black bold solid line) and (S)-(+)-1-aminotetralin (grey bold solid line) (1b).

The UV spectra of 1a, 2a, 2b and 2c show three main regions of absorption: the first one with a broad band with two maxima at 270 and 267 nm (1a and 2a); at 277 and 270 nm (2b and 2c) corresponding to the ¹L_b, followed by a more intense band at 217 nm (¹L_a transition), and the third one with high-intensity absorption at 195 nm (¹B_b transition).

For 1b in Fig. SI-18‡ one notices the three main absorption regions: the broad band at 270 and 262 nm at lower energy, a shoulder at 216 nm and finally at higher energy the band at 191 nm.

In the CD spectra, at least three Cotton effects can be noticed: for 1a and 2a, the lowest energy Cotton effect with a fine structure is centered at 265 nm (¹L_b) followed by another Cotton effect at 220 nm that corresponds to the ¹L_a CD band. These Cotton effects have opposite signs for compound 1a (¹L_b band is positive and ¹L_a is negative for (−)-1- tetralol) and same sign for 2b (positive for (+)-2-tetralol). For 2b and 2c the ¹L_b fine structured CD band is centered at 275 nm and followed the ¹L_a CD band at 230 nm with the opposite sign (the latter feature being negative for the (+) enantiomer).

At higher energy (¹B_b), 1a presents a bisignate signal (−,+) at 198 and 186 nm for the (−)-1-tetralol in correspondence of the absorption band at 195 nm.

2a, 2b and 2c present for the (+) enantiomer a positive CD signal around 195 nm corresponding to the maximum of absorption. Fig. 11 reports for the (−)1b a positive CD signal around 189 nm. However, as discussed in the introduction, not much use of the ¹B_b band has been made for AC determination and researchers have concentrated mostly on ¹L_b (and ¹L_a) transitions (see also refs. 22–24).

However, all compounds studied in the present work exhibit a ¹L_b Cotton effect with the same sign. This is not very helpful, unless one can deal with sufficient confidence the evaluation of vibronic coupling. Instead, the VCD spectra are rather different for these compounds. In any case, let us see whether the modern TDDFT technology¹³ allows one to interpret and use UV and ECD spectra.

TDDFT calculations

TDDFT calculations in vacuo of the CD spectra were performed first on compounds 1a and 2a in view of their lower number of conformers and the opposite sign of the bands at 198 and 216 nm. The calculations have been performed with the hybrid functional B3LYP and the same statistical conformational average as used for VCD was employed. The sign and the relative intensity of ¹B_b and ¹L_a Cotton effects are well reproduced for 1a, 1b and 2a.

On the basis of results obtained with 1a and 2a (Fig. 7 and 8, respectively, see also Fig. SI-15‡), we have performed TDDFT calculations of 2b and 2c with the same functional and basis set. The intensity and the sign of ¹B_b and ¹L_a Cotton effects are quite well reproduced by the theoretical calculation for 2b and 2c (Fig. 9 and 10, respectively, see also Fig. SI-16‡). It is clear that the TDDFT calculations used in this study do not include vibronic effects and are not able to predict the ¹L_b bands.

Direct comparison of theoretical and experimental ECD data demonstrates that the (−) 1-tetralol (1a), (+) 2-tetralol (2a), (+) 5-hydroxy-2-tetralol (2b) and (+) 8-hydroxy-2-tetralol (2c) enantiomers possess the R absolute configuration, in agreement with the Snatzke empirical assignment based on ¹L_b. Yet, due to the weakness of the ¹L_b transitions and to the prediction of imprecise wavelengths for electronic transitions, the AC assignment made on this basis is less convincing than that made on the VCD data.

Experimental

Sample preparation

(R)-(−) and (S)-(+)-1-tetralol (1a) and R)-(−) and (S)-(+)-1-aminotetralin (1b) were purchased from Sigma-Aldrich and used without further purification. (R)-(+) and (S)-(−)-2-tetralol (2a), (R)-(+) and (S)-(−)-5-hydroxy-2-tetralol (2b) and (R)-(+) and (S)-(−)-8-hydroxy-2-tetralol (2c) were prepared as previously reported.⁸

ECD and VCD spectroscopy

ECD spectra were obtained with a JASCO 815SE instrument from 300 to 185 nm under the following experimental conditions: integration time τ = 2 s, scan speed 100 nm min⁻¹, 2 nm resolution, 5 or 10 scans. The spectra were obtained for ∼3 × 10⁻³ M solutions in CH₃CN, CHCl₃ and CH₃OH in 0.1 or 1 mm quartz cuvettes. Since no difference was observed, we just report data for the first solvent.

IR Vibrational absorption (VA) and VCD spectra have been collected on a JASCO FVS4000 apparatus equipped with a liquid N₂-cooled MCT detector in the 900–1600 cm⁻¹ region at 4 cm⁻¹ resolution. The samples were dissolved in CDCl₃ (CCl₄ for 1-aminotetralin) and/or methanol-d₄ (concentration: 0.2–0.6 M) and then placed in a 100 μm path length cell with BaF₂ windows. For the VCD measurements, we decided to prepare just methanol-d₄ solutions of 2b and 2c due their poor solubility in CDCl₃.

CDCl₃ was purchased from Sigma-Aldrich and methanol-d₄ was obtained from Cambridge Isotope Laboratories. Due to CD₃OD absorption, the VA and VCD spectra are limited below to 1200 cm⁻¹, while for CDCl₃ solutions spectra run to 950 cm⁻¹.

ECD and VCD spectra were recorded for both enantiomers, however, for the VCD, only the spectra for the (R) enantiomers have been presented due to the poor enantiomeric excess of S-2a, 2b and 2c. In all absorption spectra, the solvent absorption was subtracted and for the VCD spectra the same procedure was applied as well with the solvent or the racemic mixture (when possible) under identical conditions.

Computational methods

Geometry optimization and harmonic frequency analysis were performed using DFT calculations at the B3PW91/TZ2P and B97D/TZ2P level of theory with the Gaussian 03 and 09 suite of programs.^16a The TZ2P basis set is built from the Huzinaga-Dunning TZ set, with the addition of two sets of polarization functions from Dunning's cc-pVTZ, as available from the internet.^16b

Vibrational harmonic frequencies, IR and VCD intensities were calculated at the same level of theory. The convoluted spectra have been calculated applying Lorentzian bands with half widths of 10 cm⁻¹ to the vibrational transitions centered at the calculated frequencies and with areas equal to the intensities, either IR or VCD. No scaling factor has been applied. The spectra have been calculated for the isolated molecule in vacuo and in implicit solvent, to compare with data in CDCl₃ and in CD₃OD. We used the integral equation formalism (IEF) version of the static isodensity surface polarized continuum model (IPCM).¹⁷

Averaged IR and VCD spectra were calculated with the Boltzmann weighted populations for the individual conformers.

ECD calculations using the TDDFT method were run at the B3LYP/TZVP level of theory with G03W using DFT-optimized geometries in vacuo and the same population factors used for VCD. 20 singly exited states were considered and CD spectra were generated by applying a Gaussian band with 0.2 eV half-height width.

Conclusions

The determination of the absolute configuration of optically active 1-tetralol (1a), 2-tetralol (2a), 5-hydroxy-2-tetralol (2b), 8-hydroxy-2-tetralol (2c) and 1-aminotetralin (1b) has been performed. This was achieved by ECD and VCD coupled with DFT and TDDFT calculations, which proved to be accurate enough, notwithstanding the large number of conformers. The latter fact in part hampers the agreement of the calculations and experiments. VCD shows here a high specificity in the AC assignment and is found to be superior to ECD to this scope; this is thought to be due to the fact that ECD is determined by electronic transitions residing on the aromatic moiety. The slight perturbation brought by the substitutions on either the cyclohexane or the aromatic moiety affects in a specific way only the weak ¹L_b transitions. On the contrary, the same substitutions have a more profound influence on the VCD spectra. Even the IR-VA spectra are not as sensitive; all of this had been observed in another instance.¹⁵ The superiority of VCD with respect to ECD as a method for AC assignment is irrespective of the many difficulties encountered above in the calculations, related to the conformational richness of the molecules. Above, we pointed out that the choice of the functional and the approximation of the solvents (in vacuo, implicit) can affect the results. However, we verified that overall the predicted AC is common to all approaches.

In these conclusive notes we surmise that the sensitiveness of ¹L_b ECD feature to substitutions is due, among other causes,^22–24 to its vibrational (vibronic) structure.

Finally, this study has allowed us to learn an important aspect of the conformations of these systems; that is the prevalence of axial conformers in 1-tetralol and of the more common equatorial conformers in 2-tetralols. This finding of the pseudo-axial conformer has been also pointed out in another context by Muñoz et al.,²⁵ This work will be useful to compare other natural products data to.²⁶

We think that the above conclusions, regarding the assignment of the absolute configuration and the conformations, are valid independent of the type of substituent in the cyclohexane moiety; this is seen by comparing 1a and 1b (1-tetralol and 1-aminotetralin), though with different population factors. We expect this to be valid also for 2-tetralol and 2-aminotetralin, for which studies are under way. We also think that the computational method does not affect, up to certain point, this conclusion.

References

1. (a) T. Honda, A. Fujii, K. Inoue, Y. Yasohara, Y. Itagaki, K. Maehara, T. Takeda and Y. Ueda, PCT Int. Appl. WO 2003046197, 2003; (b) F. Orsini, G. Sello, E. Travaini and P. Di Gennaro, Tetrahedron: Asymmetry, 2002, 13, 253.
2. (a) S. Kotha and N. G. Krishna, Curr. Sci., 2011, 7, 923; (b) J. M. Cassady, J. Nat. Prod., 1990, 53, 23.
3. (a) A. K. Dutta, X.-S. Fei and M. E. A. Reith, Bioorg. Med. Chem. Lett., 2002, 12, 619; (b) E. J. Homan, S. Copinga, L. Elfström, T. van der Veen, J.-P. Hallema, N. Mohell, L. Unelius, R. Johansson, H. V. Wikström and C. J. Grol, Bioorg. Med. Chem., 1998, 6, 2111; (c) S. Copinga, P. G. Tepper, C. J. Grol, A. S. Horn and M. L. Dubocovich, J. Med. Chem., 1993, 36, 2891.
4. (a) For example, for the preventive treatment of Parkinson's disease: D. Scheller and F. Dressen, PCT Int. Appl. WO 2005063238 A1 20050714, 2005; (b) for the treatment of depression: D. Scheller, A. Breidenbach and N. Selve, PCT Int. Appl. WO 2005009425 A1 20050203, 2005; (c) for treatment of various types of pain: B. Beyreuther, D. Scheller, J. Freitag and J. Bianchine, PCT Int. Appl. WO 2007147556 A1 20071227, 2007.
5. (a) S. Montanari, P. Cavalleri, F. Santangelo and F. Marchini, PCT Int. Appl. WO 9838155 A1 19980903, 1998; (b) B. Yao, H. Ji, Y. Cao, Y. Zhou, J. Zhu, J. Lü, Y. Li, J. Chen, C. Zheng, Y. Jiang, R. Liang and H. Tang, J. Med. Chem., 2007, 50, 5293.
6. (a) N. Rodenhuis, W. Timmerman, H. V. Wikström and D. Dijkstra, Eur. J. Pharmacol., 2000, 394, 255; (b) H. Yu, Y. Liu, Å. Malmberg, N. Mohell, U. Hacksell and T. Lewander, Eur. J. Pharmacol., 1996, 303, 151.
7. (a) J. S. Yadav, G. S. K. K. Reddy, G. Sabitha, A. D. Krishna, A. R. Prasad, H.-U. Rahaman, K. V. Rao and A. B. Rao, Tetrahedron: Asymmetry, 2007, 18, 717; (b) M. Mogi, K. Fuji and M. Node, Tetrahedron: Asymmetry, 2004, 15, 3715 and references cited therein; (c) P. Manitto, G. Speranza, D. Monti, G. Fontana and E. Panosetti, Tetrahedron, 1995, 51, 11531.
8. (a) P. Bonomi, P. Cairoli, D. Ubiali, C. F. Morelli, M. Filice, I. Nieto, M. Pregnolato, P. Manitto and G. Speranza, Tetrahedron: Asymmetry, 2009, 20, 467; (b) I. Nieto, S. Rocchietti, D. Ubiali, G. Speranza, C. F. Morelli, I. E. Fuentes, A. R. Alcantara and M. Terreni, Enzyme Microb. Technol., 2005, 37, 514.
9. (a) J. C. Craig, S. Y. C. Lee, R. P. K. Chan and I. Y.-F. Wang, J. Am. Chem. Soc., 1977, 99, 7996; (b) J. Barry, H. B. Kagan and G. Snatzke, Tetrahedron, 1971, 27, 4737; (c) P. Crabbè and W. Klyne, Tetrahedron, 1967, 23, 3449.
10. G. Snatzke and P. C. Ho, Tetrahedron, 1971, 27, 3645.
11. (a) G. Speranza, P. Manitto, D. Pezzuto and D. Monti, Chirality, 1991, 3, 263; (b) G. Snatzke, M. Kajtár and F. Snatzke, Aromatic chromophores, in: Fundamental Aspects and Recent Developments in Optical Rotatory Dispersion and Circular Dichroism, eds F. Ciardelli and P. Salvadori,Heyden & Son, London, 1973, 148.
12. J. M. Jansen, A. M. Johansson, A. Karlén and U. Hacksell, Chirality, 1995, 7, 82.
13. VCD General references: (a) P. J. Stephens, in Computational Medicinal Chemistry for Drug Discovery, ed. P. Bultinck, H. de Winter, W. Langenaecker and J. Tollenaere, Dekker, New York, 2003,chap. 26, pp 699–725; (b) P. J. Stephens, F. J. Devlin and J. J. Pan, Chirality, 2008, 20, 643; (c) L. A. Nafie and T. B. Freedman, in Circular Dichroism: Principles and Applications, ed. K. Nakanishi, N. Berova and R. W. Woody, Wiley-VCH Publishers, New York, 2000, chap. 4, pp. 97–152; (d) L. A. Nafie, Vibrational Optical Activity, Principles and Applications, John Wiley and Sons, New York, 2011; (e) T. A. Keiderling, in Circular Dichroism: Principles and Applications, ed. K. Nakanishi, N. Berova and R. W. Woody, , Wiley-VCH Publishers, New York, 2000, chap. 22, p 621–666; (f) P. L. Polavarapu and C. Zhao, Fresenius' J. Anal. Chem., 2000, 366, 727; (g) V. P. Nicu, J. Neugebauer and E. J. Baerends, J. Phys. Chem. A, 2008, 112, 6978; (h) V. P. Nicu, E. Debie, W. Herrebout, B. Van Der Veken, P. Bultink and E. J. Baerends, Chirality, 2010, 21, E287; (i) P. L. Polavarapu, J. Frelek and M. Woznica M., Tetrahedron: Asymmetry, 2011, 22, 1720; (j) A. Bouchet, T. Brotin, M. Linares, H. Agren, D. Cavagnat and T. Buffeteau, J. Org. Chem., 2011, 76, 1572; (k) P. J. Stephens, F. J. Devlin, F. Gasparrini, A. Ciogli, D. Spinelli and B. Cosimelli, J. Org. Chem., 2007, 72, 4707.
14. ECD, general references: (a) F. Furche, R. Ahlrichs, C. Wachsmann, E. Weber, A. Sonbaski, F. Voegtle and S. Grimme, J. Am. Chem. Soc., 2000, 122, 1717; (b) J. Autschbach, Chirality, 2009, 21, E116; (c) T. D. Crawford, Theor. Chem. Acc., 2006, 115, 227.
15. S. Abbate, F. Lebon, S. Lepri, G. Longhi, R. Gangemi, S. Spizzichino, G. Bellachioma and R. Ruzziconi, ChemPhysChem, 2011, 12(18), 3519.
16. (a) Gaussian 03, Revision C.02, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian, Inc., Wallingford CT, 2004; (b) URL: http://www.emsl.pnl.gov/forms/basisform.html..
17. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
18. F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry (3rd edn), Plenum Press, New York, 2008.
19. F. Johnson, Chem. Rev., 1968, 68, 375.
20. Y. Senda, J. Ishiyama, S. Imaizumi and K. Hanaya, J. Chem. Soc., Perkin Trans. I, 1977, 217.
21. (a) T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398; (b) S. Grimme, Angew. Chem., Int. Ed., 2006, 45, 4460.
22. E. Dornhege and G. Snatzke, Tetrahedron, 1970, 26(12), 3059.
23. G. Snatzke, M. Kajtar and F. Snatzke, in Fundamental Aspects and Developments in Optical Rotatory Dispersion and Circular Dichroism, ed. F. Ciardelli and P. Salvadori, Heyden & Son Ltd., London, 1973, 148.
24. (a) D. A. Lightner and J. E. Gurst, Organic Conformational Analysis and Stereochemistry from Circular Dichroism Spectroscopy, Wiley-VCH, New-York, 2000, chap. 13, pp. 409–415; (b) G. Pescitelli, L. Di Bari, A. M. Caporusso and P. Salvadori, Chirality, 2008, 20, 393.
25. (a) M. A. Muñoz, C. Areche, A. San Martin, J. Rovirosa and P. Joseph-Nathan, Nat. Prod. Comm., 2009, 4, 1037; (b) L. A. Nafie, Nat. Prod. Comm., 2008, 3, 451.
26. S. Abbate, L. F. Burgi, E. Castiglioni, F. Lebon, G. Longhi, E. Toscano and S. Caccamese, Chirality, 2009, 21, 436.

---

Footnotes

† We dedicate this work to the late Professor Paolo Manitto.

‡ Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra21080k

---