Reflections on the chemistry of the Fischer–Tropsch synthesis
Olusola O.
James
*abc,
Biswajit
Chowdhury
b,
M. Adediran
Mesubi
c and
Sudip
Maity
*a
aLiquid fuels Section, Central Institute of Mining and Fuels Research (Digwadih Campus), Dhanbad, India. E-mail: sudip_maity@yahoo.com; jamesoladele2003@yahoo.com
bIndian School of Mines, Dhanbad, India
cCovenant University, Canaan Land, Ota, Ogun State, Nigeria
First published on 25th April 2012
Abstract
Fischer–Tropsch synthesis (FTS) occupies a key position in the search for alternatives to petroleum for obtaining liquid hydrocarbons. Hydrocarbons can be produced from alternative carbonaceous resources (natural gas, coal, biomass and waste) through FTS and the use of biomass is particularly attractive from a carbon footprint point of view. However, the nature of biomass resources dictates a different exploration approach compared to fossil fuel resources. Compared to coal and natural gas based FTS processes where economics of scale is an advantage, a Biomass-to-Liquid (BTL) plant is more suited for smaller scale operation. Thus, the BTL process economy will benefit from a condensed FTS processes. Moreover, considering the expected role of FTS in regional and global hydrocarbon supply in the near future, it becomes pertinent to strive towards improving the process economy. This requires molecular and process engineering and detailed knowledge of the reaction is a pre-requisite to engineering the reaction at molecular level. Syngas to hydrocarbon involves consecutive steps of CO activation, C–C coupling, hydrogenation and desorption of the hydrocarbon product. Atomic details of the dynamics of these steps are still unclear. Recently, clearer pictures about activation are now available. However, over the course of ninety years since the first report on an FTS, proposed pathway of C–C coupling has come full cycle from oxygenate to nonoxygenate and back to oxygenate intermediates. To this end, we attempted an X-ray of progress made at providing answers to issues in the chemistry of FTS. The review focuses on product distribution, macro kinetics and the mechanism of FTS. We compare FTS with other C–C coupling reactions of CO, identify catalytic entities for controlling product selectivity and finally we offer an outlook on future directions of fundamental research towards resolving the lingering questions on the mechanism of C–C coupling in FTS.
 Olusola O. James | Olusola O. James received his B.Sc and M.Sc (chemistry) degrees from University of Ilorin, Ilorin, Nigeria. He is a doctoral researcher at Central Institute of Mining and Fuel Research (CIMFR), Dhanbad, India, courtesy TWAS-CSIR postgraduate fellowship. His research interests include heterogeneous catalysis with special focus on acid–base and redox reactions, Fischer–Tropsch synthesis and biomass conversions. |
 Biswajit Chowdhury | Biswajit Chowdhury obtained his B.Sc (Honors) and M.Sc from Jadavpur University, Calcutta, in 1993 and 1995. He did his doctoral research at the Indian Institute of Chemical Technology, Hyderabad, India. In 2002 he joined Research Laboratory of Hydrothermal Energy, Kochi University, Japan, as a post-doctoral researcher. In 2003 he moved to National Institute of Advanced Science and Technology (AIST), Tsukuba, as a visiting scientist, where he worked with Prof. Masatake Haruta. In 2007 he joined as an Assistant Professor in the Department of Applied Chemistry, Indian School of Mines, Dhanbad. His current research focus involves heterogeneous catalysis for green chemistry reactions. |
 M. Adediran Mesubi | Professor M Adediran Mesubi obtained B.Sc (Combined Hons) in Chemistry and Physics in from ABU, Zaria, Nigeria in 1966 and Ph.D (Chemistry) Kansas State University, USA in 1972. He became a Professor of Chemistry at University of Unilorin, Nigeria where did most of his research work in synthesis and spectroscopic studies of metal complexes. Presently, he is a senior Professor at Covenant University, Ota, Nigeria. His research interests now include Schiff base transition metal complexes and their biological studies, nanoscience & nanotechnology, electroplating technology, fine chemicals and renewable energy. He has many journal publications. |
 Sudip Maity | Sudip Maity is working as a scientist at the Central Institute of Mining and Fuel Research, FRI, Dhanbad, India for the last 12 years. He did his PhD in High Temperature & Pressure phase transitions studies. He is working in the field of catalyst research for Fischer–Tropsch synthesis for coal-to-oil and gas-to-oil technologies. He is also working on the molecular structure of coal using XRD and the production of hydrogen from renewable sources by non-thermal plasma techniques. He has several patents and publications. |
1 Introduction
For socio-political, economic and environmental reasons, there are quests for alternatives to petroleum for obtaining hydrocarbons.1–3 The ultimate goal in this quest is hydrocarbon production from renewable resources. At present, technologies for hydrocarbon production exclusively from renewable inputs are far from being competitive with the current petroleum based hydrocarbon economy.4,5 In the interim, attentions are on non-petroleum fossil fuels as alternatives resources for obtaining hydrocarbons. To this end, indirect liquefaction processes also known as feed-to-liquids, XTLs (where X: C-coal, G-natural gas, B-biomass or W-waste), are at the forefront among other technological options being explored for this purpose. The term ‘indirect liquefaction’ is often used for these conversions because irrespective of the physical state of the feed resources (gas or solid), the route to liquid hydrocarbon (fuel) involves a syngas (H2 + CO) intermediate.A typical XTL process involves a three step conversion : feed-to-syngas, syngas-to-syncrude and syncrude-to-product conversions.6 The syngas-to-syncrude conversion is basically Fischer–Tropsch synthesis (FTS) and is colloquially used to describe indirect liquefaction. Among the XTLs, CTL & GTL have attained commercial status. Existing CTL & GTL installations are being expanded and a number of new FT plants are at various stages of completion across the globe.7–11 This is an indication of the emerging role of XTL technology and the anticipated increasing share in global hydrocarbon supply in the near future.12 It also accounts for the increasing research attention on the topic in recent times. However, in spite of approximately a century since the first report on the FTS reaction, there are still debates about the detail of FTS chemistry. In this contribution, we highlight recent findings about the FTS reaction and chemistry.
Historically, the adoption of FT technology had been driven by political decisions, but in recent times interest in FT technology is motivated by economic viability, environmental and energy security concerns.13–17 Despite widespread concern about the effect of continued CO2 emissions on global warming and climate change, the pace of adoption of renewable energy options is rather slow, largely due to economic reasons (volume and or cost of production), which constitutes a major sustainability challenge for a paradigm shift from fossil fuels to renewable energy.18 It also brings to the fore the point that economic competitiveness appears to takes precedence over environmental benefits for the adoption of renewable energy technologies in the present globalised society.19–27
Solar and biomass are vast renewable energy resources that are receiving increasing attention in order to increase their share in global energy mix.28–30 Unlike fossil fuels in which large quantities of reserves are concentrated in specific geographical locations or geological formations, solar and biomass resources are diffuse and scattered over large area.31 This major difference in the nature of these energy resources requires different approaches for harnessing them. For example, exploitation of petroleum is characterised by the transportation of crude and refined products through pipelines over long distances and large refinery complexes. However, sustainable economic production of liquid hydrocarbon from biomass points in the opposite direction to that of petroleum. Moreover, compared to CTL & GTL, economic sustainability of BTL points in the direction of small scale distributed refineries and the short distance movement of raw materials and products.32–34
A recent economic feasibility report on BTL recommends a large plant (≥ 1 Mt a−1) like CTL & GTL which are mature FT technologies.35 Logistics of gathering of large biomass feed material is a major challenge for the success of a large scale BTL plant. Pre-densification of biomass by fast pyrolysis processes at regional centres prior to collection and central refining plant were suggested as strategies to reduce the transportation cost. The recommendation states further that densified biomass (or compact bioslurry) can then be processed directly to fuels via hydrotreating or indirectly via syngas generation for FT syncrude, methanol or hydrogen production. The hydrotreating option requires hydrogen input which will have to be produced from part of the feedstock, also the quality and range of fuel options here is limited. Although the syngas generation route affords a wider range of fuels, the pre-pyrolysis step before gasification as well as long distance distribution of finished product will further reduce the energy efficiency of this route. Moreover, hydrogen deficient syngas feeds (from coal and biomass) are characterised by low carbon utilisation and poor well-to-wheel ratio. Elimination of these additional steps in the chain from feedstock biomass to wheel will naturally enhance the energy efficiency.36 This implies adopting a distributed or regional processing strategy, but this option demands low capital investment to be economically viable. It has been shown that co-production of electricity along with liquid fuels has an economic advantage over a purely liquid fuel BTL plant.37 Since typical bio-syngas is hydrogen deficient, an efficient direct conversion of the bio-syngas to syncrude without in situ or prior water gas shift (WGS) can afford an energy rich exit gas for maximising electricity generation with a minimal compromise on liquid fuel production (Scheme 1).
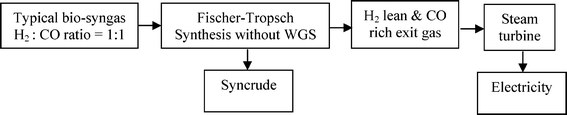 | ||
| Scheme 1 Flow chart of BTL with co-electricity production. | ||
The pursuit of low capital investment for a small scale BTL plant will involve miniaturisation, intensification and integration of the steps (feed-to-syngas, syngas-to-syncrude and syncrude-to-product conversions) in a traditional XTL process. The feed-to-syngas step accounts for more than fifty percent of the capital outlay in XTL processes. Significant process had been made in the design of biomass gasifiers, those based on entrained flow technology appeared to show greater potential in terms of energy efficiency and H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO ratio.38,39 A micro-channel reactor is also a compact technology with demonstrated feasibility for FT applications.40–42 Thus, a low capital investment for a small scale BTL plant may benefit from selecting the duo of an entrained flow type gasifier and micro-channel reactor technologies. It is also important to take into account that typical syncrude composition follows Anderson–Schulz–Flory (ASF) distribution. The selection of catalyst and reaction parameters should be guided by a carbon number range of desired hydrocarbons or intermediate products that can be most efficiently refined to the desired products.6
CO ratio.38,39 A micro-channel reactor is also a compact technology with demonstrated feasibility for FT applications.40–42 Thus, a low capital investment for a small scale BTL plant may benefit from selecting the duo of an entrained flow type gasifier and micro-channel reactor technologies. It is also important to take into account that typical syncrude composition follows Anderson–Schulz–Flory (ASF) distribution. The selection of catalyst and reaction parameters should be guided by a carbon number range of desired hydrocarbons or intermediate products that can be most efficiently refined to the desired products.6
In addition, the cost of fuel production can be minimised further by reducing the number of processing units. While a rigorous biomass-to-syngas step leading to clean syngas cannot be compromised, syngas-to-syncrude and syncrude-to-product step can be coupled into a single hybrid unit that leads to on-specification fuels or valuable chemicals.43–45 Also since FTS is a bottom-up process, it is envisaged that enhanced process economy of BTL can also be pursued by tailoring the synthesis to high value chemicals. These objectives require manipulations at the molecular level which in turn require detailed insight into the reaction mechanism. Efforts at elucidating the mechanism of FTS have come a long way, but general consensus on the detailed mechanism of FTS (and its sister process—methanol synthesis) are still under debate. The history of the FTS mechanism dates back to its discovery and there have been a number of periodic reviews on the subject along the line, yet it is very difficult to capture all the reports on the subject. In order to identify platforms for the molecular engineering of FTS, the present report is intended as a distillation of recent progress on the mechanism of FTS. The scope of this report is limited to thermodynamics and stoichiometry; product distribution, kinetic expression and highlights on convergence of findings on FT mechanism.
2 FT Thermodynamics and stoichiometry
Hydrocarbon formation from syngas is exothermic, it is driven by the co-formation of water and or carbon dioxide. For example,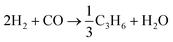 , ΔG°(227 °C) = −96 kJ mol−1.46 Heat release increases with increasing chain length and hence heat removal is a very important factor in reactor and process design. In practice, more than one reaction is possible on the catalyst surface in a FTS reactor. A list of likely reactions in an FT reactor is shown in Table 1. Thermodynamic product selectivity generally follows the order: alkanes > alkenes > alcohols, and the product distribution can vary significantly with catalyst type and reaction conditions. For simplicity, the stoichiometry of FTS is often approximated as:47
, ΔG°(227 °C) = −96 kJ mol−1.46 Heat release increases with increasing chain length and hence heat removal is a very important factor in reactor and process design. In practice, more than one reaction is possible on the catalyst surface in a FTS reactor. A list of likely reactions in an FT reactor is shown in Table 1. Thermodynamic product selectivity generally follows the order: alkanes > alkenes > alcohols, and the product distribution can vary significantly with catalyst type and reaction conditions. For simplicity, the stoichiometry of FTS is often approximated as:47| nCO + 2nH2 → –(CH2)n– + nH2O ΔHR(227 °C) = −165 kJ mol−1 |
| Main reactions | |
| 1. Methane | CO + 3H2 → CH4 + H2O |
| 2. Paraffins | (2n + 1)H2 + nCO → CnH2n+2 + nH2O |
| 3. Olefins | 2nH2+nCO → CnH2n + nH2O |
| 4. Water gas shift (WGS) reaction | CO + H2O → CO2 + H2 |
| Side reactions | |
| 5. Alcohols | 2nH2 + nCO → CnH2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1O + nH2O 1O + nH2O |
| 6. Boudouard reaction | 2CO → C + CO2 |
| Catalyst modifications | |
| 7. Catalyst oxidation/reduction | a. MxOy + yH2 → yH2O + xM |
| b. MxOy + yCO → yCO2 + xM | |
| 8. Bulk carbide formation | yC + xM → MxCy |
Stoichiometric requirements of the syngas feed for a FT process depends on its operation mode and catalyst properties. When reactants are in stoichiometric balance, the relationship, H2/(2CO + 3CO2), known as the Ribblett ratio, is one.49 It is generally believed that the WGS reaction has a profound effect on the reaction stoichiometry. Co-based catalysts generally require syngas of H2/CO ≈ 2. Fe based catalysts are generally WGS active, they can use H2/CO ≤ 2, depending on the reaction temperature. For high temperature (300–350 °C) operation mode, WGS proceeds to equilibrium and can complement hydrocarbon formation. For instance, the net reaction of FTS and WGS for hydrocarbon formation using syngas with H2/CO = 1 can be expressed as: 2CO + H2 → –CH2– + CO2. For low temperature (180–250 °C) operation mode, WGS proceeds below equilibrium but significant CO2 formation can occur. Under this operation mode, especially when using syngas of H2/CO = 2, WGS activity is unwanted. This accounts in part for the preference of Co based catalysts for GTL plant.
WGS is generally considered a pre-requisite for the hydrogenation of CO2, via the reverse reaction (rWGS) to CO before subsequent hydrogenation to hydrocarbon. However, Ni et al.50 had asserted that r-WGS is not an indispensable step for FTS using CO2. Fujiwara et al.51 and Rongxian et al.52 had also advanced that hydrogenation of CO2 to hydrocarbon over un-promoted and Zr promoted Fe–Zn FT catalyst proceeded largely through a methanol intermediate. A common feature of the catalysts in the three reports is the presence of the ZnFe2O4 spinel phase. The same spinel phase was identified in the series of reports on Fe–Zn iron catalysts by Iglesia and co-workers.53 These authors treated the spinel phase as a textural promoter which increases the surface area of the catalyst. One of the qualities of their catalyst is lower CO2 formation compared to Fe–SiO2 based iron catalysts. It appears that ZnFe2O4 is not only a textural promoter but also connected with the observed lower CO2 formation of the catalyst reported by Iglesia and co-workers. The above observation is particularly interesting from fundamental and applied perspectives and may open a new chapter in FT catalyst design. Therefore, more fundamental studies are required for insights on the properties and FT activity of the spinel, ZnFe2O4, and similar crystalline phases.
3 Fischer–Tropsch Synthesis Product Distribution
Syncrude is a spectrum of hydrocarbons ranging from C1 to C50–200. The typical gas chromatogram of FTS products is a complex spectrum of products, characterised by a notable degree of order in terms of carbon number and class of compounds.54 With cursory analysis of the chromatogram it was noticed that the mole fractions of the products declines exponentially with the carbon number. This behaviour being typical of polymerisation reactions led to the description of FTS as a surface polymerisation reaction which proceeds via the stepwise addition of a monomer carbon species, X (where X may be CO, H2CO, HCOH, HCO, CHO, COH, C, CH, CH2), and a termination step leading to products as shown in Scheme 2.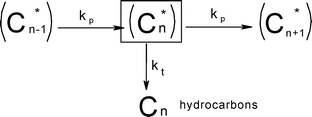 | ||
| Scheme 2 FTS chain growth in classical ASF model.55 | ||
Instead of a tabular list or pictorial presentation of the products, a simple and unambiguous model will provide a quicker comparison of product selectivities of different catalysts and reaction conditions. Such a model may also provide indirect insights about mechanism of product formation. An empirical statistical product distribution model known as “Anderson–Schultz–Flory” (ASF) distribution law emerged for this purpose. The mathematical description of ASF law is illustrated in eqn (1)–(4). Similar to polymer product distribution, graphical description of FT also become popular, as in Fig. 1 or 2.
mn = (1 − α)αn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1∞ 1∞ | (1) |
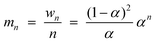 | (2) |
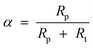 | (3) |
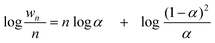 | (4) |
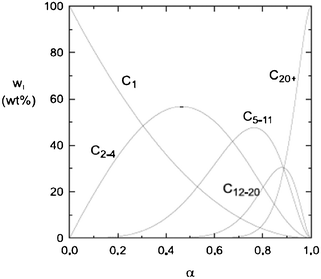 | ||
| Fig. 1 Ideal ASF FT product selectivity as function of the chain growth probability factor α. | ||
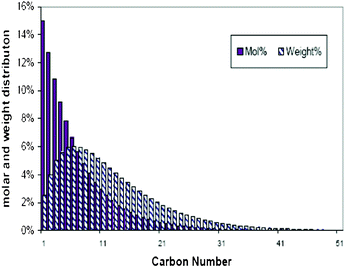 | ||
| Fig. 2 A typically theoretic FT synthesis distribution, α = 0.85. | ||
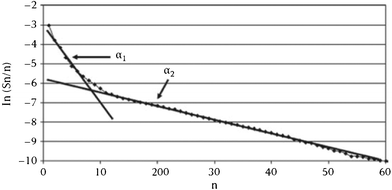
A semi-logarithmic plot of the product mole fraction as a function of carbon number should produce a straight line, and chain growth probability, α, can be readily obtained from the slope (Fig. 3). As mentioned above, the ASF distribution is based on the assumption that the chain growth probability is constant and saturated hydrocarbons are formed by stepwise addition of monomer to a growing chain.
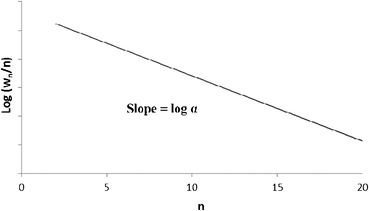 | ||
| Fig. 3 Classical Anderson–Schulz–Flory distribution of all products. | ||
3.1 Deviations from ASF distribution
Although ASF distribution law gives a fair description of FTS products, there are significant deviations in the FT product spectrum obtained from iron, cobalt, and ruthenium catalysts from what is predicted by ASF distribution law.56–61 The deviations are illustrated in Fig. 4 and listed as follows:62–65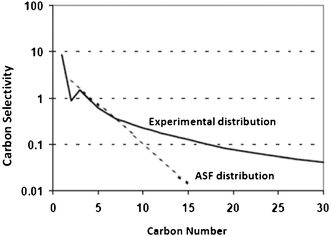 | ||
| Fig. 4 Experimental FT product distribution in comparison to ASF distribution law. | ||
- high molar methane content than predicted by ASF;
- an anomaly in C2 with relatively low molar contents than in the ASF diagram and low olefin contents in the C2 fraction;
- a curvature away from the ASF distribution at high carbon numbers; and
- chain length dependency of olefin contents.
While the deviations are generally attributed to the occurrence of secondary reactions (hydrogenation, isomerization, α-olefins re-insertion, and hydrogenolysis), van Dijk66 draws attention to the fact that FTS is not an ideal polymerization reaction assumed in the ASF model. He pointed out that FTS differs from an ideal polymerization reaction because of the following: the monomer has to be formed in situ on the catalyst surface from the reactants CO and H2; the rates of surface reactions are chain length dependent and the primary products can undergo secondary reactions that influence the product distribution. In agreement with van Dijk, Henricus also opined that these three dissimilarities of FTS from ideal polymerization kinetics account for the deviation of FTS product distribution from the ideal ASF distribution. He drew attention to the fact that erroneous product analyses can introduce systematic deviations that may be mistaken for mechanistic phenomena, especially in non-steady state operations.
According to Dry,67 simple empirical rate equations may be sufficient for the operation of pilot and commercial scale plants with a given catalyst. Moreover, general behaviour of Fischer–Tropsch catalysts at different process conditions are well known, hence, details of the Fischer–Tropsch mechanism are of little important from process engineering perspectives. However, empirical rate equations give little or no insight into surface chemistry of the reaction. Surface chemistry of heterogeneous catalytic reactions is an essential tool for catalyst design and optimization. Accurate description and identification of adsorbed species on a catalyst surface are pre-requisites to gaining insights to it surface chemistry. In addition, detailed profiles of the product distribution is also essential for thorough kinetic analyses towards development of holistic reaction mechanisms and modelling. Detailed descriptions of FTS products are experimentally demanding and mathematically challenging. Experimentally, it is crucial to collect and analyse all the products (tail gas, water, oil, and wax), and the search for simple unambiguous model to describe the product distribution has been very challenging. In the subsequent sections, we examine proposed post ASF products distribution models and reaction mechanisms.
3.2 Post ASF product distribution models
Because of the highlighted limitations of ASF distribution law, there had been quest for more encompassing models to describe FTS products. The ASF model describes the entire product range by a single parameter, α, the growth probability. Like the ideal gas law, the beauty and the attraction of ASF model is its mathematical simplicity. However, it appears the single parameter, α, is insufficient to describe the entire product range and the assumption of ASF that chain growth is independent of carbon number does not suffice in FTS. Approaches to post-ASF description of FT products are guided by this line of thoughts. The post ASF models to be discussed in next subsections are: double-α model, olefin re-insertion models and the chain-length-dependent desorption model.68–70mn = w1(1 − α1)α1n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + w2(1 − α2)α2n 1 + w2(1 − α2)α2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 | (5) |
It became necessary to introduce another parameter, ‘breaking point’ a hypothetical carbon number value (not necessarily an integer), to delineate contributions of each chain growth probabilities, α1 and α2. The breaking point, designated as μ, has no physiochemical relevance, it is defined as the total mole fraction of hydrocarbons formed with growth probability α1 (see eqn (6)). Thus, the model is characterised by three independent parameters: α1, α2 and μ.
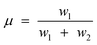 | (6) |
Detailed quantitative analysis of FTS products is sine qua non to successful assessments of product distribution models and mechanistic studies. Accuracy of mass balance is particularly critical for using double-α model for the description of FTS products. There had been significant advances in analytical techniques and procedures for providing reliable data for descriptions of FTS products. Bertoncini et al.,73 combined different types of gas chromatography techniques (e.g. low resolution, high resolution and two-dimensional gas chromatography) to provide enhanced molecular characterization of FTS products. The combined techniques afforded enhanced peak resolution and identification. Detailed composition of olefin and oxygenate by-products was achieved using the GC × GC techniques. The authors claimed that each of the three main class of FTS products (paraffin, olefin and oxygenates) present unique Anderson–Schulz–Flory (ASF) distributions. Westhuizen and associates74 also reported that GC × GC provides more accurate quantitative data for the evaluation of the effect of reaction variables on the deviation of FT product distribution from ASF distribution law.
Recent studies by Pour and co-workers on the effect of reaction variable on FTS product description using double-α model indicated that the deviations from ASF distribution law decrease with increasing H2/CO ratio over Ru-promoted Co/Al2O3. The deviations also decreases with decreasing particle size of Fe/Cu/La catalysts.75 It was also shows that the deviation was enhanced with increasing order of basicity of the promoter (X = Ca, Mg, La) in Fe/Cu/X catalysts.76 The reports of Pour and associates77 showed that the deviation from ASF law is a function of the reaction conditions and catalyst properties as opposed to the assumed occurrence of more than one chain growth mechanisms by advocates of the double-α model. Also the model parameters in the double α model are not independent or incompatible as assumed, the parameters are statistically prone to errors.71 A small variation in one parameter can easily be translated or propagated into the other parameter which can lead to erroneous prediction. For example, the value of μ depends on α1, thus, a small change in α1 will impact on the values of μ, and the change will also impact on the value of α2. However, there have been claims of experimental evidence in support of two incompatible chain growth mechanisms in FTS.78,79 Nevertheless, as shown in Fig. 5, the double α model focuses on shape deviation in the ASF distribution law at high carbon numbers. It offers no contribution to account for the other aspects of deviations from the ASF distribution law.
3.2.2.1 Diffusion enhanced olefin readsorption model. The diffusion enhanced olefin re-adsorption model was advanced by Iglesia and co-workers.80 They explained that chances of re-adsorption of an α-olefin increase the slower it diffuses away from the catalyst surface. Diffusivity of an α-olefin is a function of molecular size or carbon number, catalyst properties and reaction conditions. Decreasing the diffusivity or increasing the residence time increases the re-adsorption tendency of α-olefins. Hence, enhanced re-adsorption of α-olefins due to diffusion limitation leads to an increase in chain growth probability with increasing carbon number until a constant asymptotic value is reached for large carbon numbers.
These authors also correlate reaction conditions and catalyst properties with the re-adsorption of α-olefins. Low temperature, high pressure and low space velocity favour an increase in residence time and re-adsorption of α-olefins which in turn promotes selectivity to heavy hydrocarbons. It was added that catalyst pores are filled with liquid hydrocarbons produced during FTS; this condition restricts the diffusion of α-olefins out of the catalysts pores. The authors modified Scheme 2 by introducing the reversible olefin desorption–readsorption step to give Scheme 3. In a nutshell, this model proposed that chain growth is dependent on the carbon number and is favoured by inhibited-diffusion enhanced re-adsorption of α-olefins.
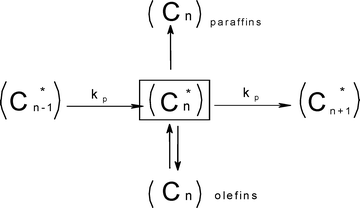 | ||
| Scheme 3 Diffusion enhanced olefin readsorption model, a modified form of the classical ASF with the termination step addition of reversible olefin desorption-readsorption step.81 | ||
Deviations of FTS products from ideal ASF distributions was explained in terms of a carbon number dependent diffusion parameter, Φ in eqn (7).
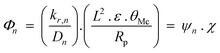 | (7) |
The first term of the equation, ψn, reflects the molecular properties of olefins with n carbon atoms which leads to the observed effect of chain size on termination probability and olefin content, while the second term of the equation, χ, depicts the structural parameter of catalyst (considered a guide for rational FT catalyst design catalyst).82
Carbon number dependent diffusivity of α-olefins was described by an empirical relation, Dnα e−0.3n, but the relation overestimates the diffusivity of the hydrocarbon. In addition the model could not account for experimentally observed exponential decreases of olefin/paraffin ratio as a function of carbon number.83,84 The report of Shi and Davis85 also showed that molecular diffusivity of hydrocarbon displayed lower dependency with their chain length. A recent report by Davis's group also indicated that diffusion enhanced re-adsorption of olefins is only significant for products with a carbon number greater than 17. They proposed that chain length–dependent solubility in the liquid phase is the predominant cause of chain length dependencies of secondary reactions of α-olefins.86
3.2.2.2 Solubility enhanced α-olefin re-adsorption model. As mentioned in the diffusion enhanced model, some authors are of the opinion that carbon number dependency of residence time of α-olefins is due to their solubility in the liquid reaction product (wax) in the reactor or catalysts pores.87–90 It was argued that solubility of olefins increases exponentially with carbon number and it has a much stronger carbon number dependency compared to diffusivity. In the solubility enhanced olefin re-adsorption model, catalyst pores or reactors filled with liquid/wax are considered an Eley–Rideal system in which interaction between the dissolved olefins and surface species on the catalyst is either diffusion or activation controlled. The interaction is considered activation controlled since experimental results have shown that diffusion alone does not sufficiently account for carbon number dependent re-adsorption of α-olefins. Olefin re-adsorption rate is considered dependent on the concentration of activated complex which also depends on solubility in the liquid phase, thus, using activated complex theory, the rate of α-olefin re-adsorption is shown in eqn (8),
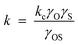 | (8) |
where, kc is gas phase or ideal solution rate constant, γO, γS and γOS, are activity coefficients of the dissolved olefin, surface species and their activated complex.
When γOS < 1, then kc > k ; the complex is more solvated than the reactants, then solubility enhances re-adsorption of α-olefins and chain growth initiation. Thus, carbon number dependent re-adsorption of olefins will be kinetically controlled rather than by thermodynamics. Solubilities of the α-olefins can also be related to vapor–liquid equilibria characteristics of FTS systems. Although estimates can be obtained using Raoult's or Henry's law, Derevich and associates91 commented that such empirical methods may not be accurate enough but a rigorous calculation based on the use of state equations with appropriate mixing rules would be needed.
In summary, the description of FT product distribution using solubility enhanced α-olefin re-adsorption model is characterised by the use of many parameters and complicated expression. Moreover, the assumption had been challenged from a thermodynamic point of view. At equilibrium, the activity/chemical potential of a substance is identical in liquid and gas phase, hence, the reactivity/olefin re-adsorption rate should be independent of concentration/solubility in the liquid phase.
3.2.2.3 Physisorption enhanced re-adsorption olefin model. Influence of the physisorption of olefins had also been suggested as an important factor that could influence the rate of re-adsorption of α-olefins. Generally, linear relationships are observed between the logarithm of equilibrium adsorption parameters and the carbon number. Carbon number dependent α-olefin re-adsorption over ruthenium catalysts under FT conditions has been described using Henry constant, Hnα e1.2n. And the carbon number dependency of physisorption for larger olefins has also been used to predict the increase of the chain growth probabilities with chain length.87,92
3.2.2.4 Combined solubility-physisorption enhanced α-olefin re-adsorption model. As highlighted in section 3.2.2.1, limitations of the diffusivity model motivated proposals in support of solubility and physisorption to account for re-adsorption of α-olefins. These factors are physical phenomena with common molecular origins but are manifested at different conditions. It is difficult to delineate which one is responsible for observed carbon number dependent enhancement of re-adsorption of α-olefins. However, Geerlings et al.,92 showed that the chain length dependent re-adsorption of α-olefins is weaker in the presence of a wax layer than on a wax free layer. They attributed their observation to differences in the effective heat of desorption. They explained that in the absence of a wax layer, the hydrocarbons desorb from a bare metal surface, whereas in the presence of a wax layer, desorption takes place through a liquid phase. The authors believed that the carbon number dependent re-adsorption of α-olefins originates from solubility and physisorption, rather than from inhibited diffusion. Hence, they introduce a transition point between the solubility and physisorption contributions to the re-adsorption of α-olefins in terms of critical chain growth probability, αc (defined as the maximum α value below which wax formation can be avoided). The FTS conditions with chain growth probability below and above the critical value are referred to as dry and wet operations respectively. Low conversions, high temperatures, and low pressures favour dry conditions. These reaction conditions are characterized by a smaller chain growth probability and correlation factor, β (which relates hydrocarbon vapor pressure with carbon number). From a large collection of experimental gas–liquid data, eqn (9) and (10) were obtained as empirical relations between temperature and vapour pressure of hydrocarbons.65
| Pi = Poβi, where Po = 1.78382 × 104 kPa | (9) |
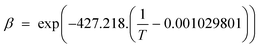 | (10) |
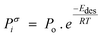 | (11) |
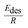 is effective enthalpy of desorption (or vaporisation) per –CH2– unit.
is effective enthalpy of desorption (or vaporisation) per –CH2– unit.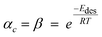 | (12) |
Taking physisorption as a transition state between the chemisorbed and the vapor or liquid phase hydrocarbons, Van der Laan and Beenackers93 relates the gas phase pressure to carbon number dependent concentration of olefins on a catalyst surface (see Fig. 6) and derived eqn (13) which combines solubility and physisorption contributions to re-adsorption of α-olefins in a single constant, c.
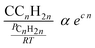 | (13) |
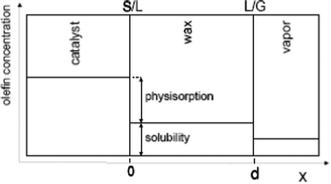 | ||
| Fig. 6 Olefin concentration profile near a Fischer–Tropsch catalyst illustrating solubility and physisorption contribution to re-adsorption of olefin94 | ||
Like the diffusion model, solubility and physisorption models focused on one aspect of the deviations from ASF law. The model offers little or no explanation for other deviations of the FTS product spectrum from ideal ASF law. Besides these models are distances away from the coveted simplicity of ASF law. We provide an appraisal of the re-adsorption models before we examine chain-length-dependent desorption model.
Appraisal of carbon dependent re-adsorption of olefin models. There are two key components in the assumptions of olefin re-adsorption models, ‘olefin re-adsorption’ and ‘chain initiation’. The models treated the first component as physical phenomenon but were silent on the second component. Perhaps it is an oversight or olefin re-adsorption was assumed to be the rate limiting step in the consecutive elementary processes. Hence, limitations of the models may be traceable to this oversight. Despite leading to more complex expressions, the success of the models is comparable irrespective of their different mathematic treatment; possibly because diffusion, solubility and physisorption are closely inter-related and it may be difficult to completely delineate their effects in FTS reaction conditions.
In the diffusion model, the carbon number dependence of the olefin/paraffin ratio was explained in terms of diffusivity of α-olefin in the liquid filled-catalyst pores. Although the model is silent about the influence of solubility, the model has indirectly incorporated solubility. Yet, it appears that solubility or the condition of catalyst pores being filled with liquid/wax product is not requisite for limited diffusion of the olefins. According to the classical law of diffusion of gasses (Graham's law of diffusion: at constant temperature and pressure, the rate of diffusion is inversely proportional to the square root of the molecular mass, expressed mathematically in eqn (14)), the diffusivity of hydrocarbons decreases (or their residence time increases) naturally with increasing molecular mass.
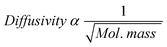 | (14) |
Fig. 7 shows a plot of reciprocals of square root of molecular masses of C2–C50 olefins (a measure of gas phase diffusivity) against their carbon numbers. The figure shows that C2 stands out having exceptionally high diffusivity compared to other olefins. Although diffusivity falls steeply after C2, C3–C6 olefins also have very high diffusivity and C7–C10 olefins can also be said to have high diffusivity. After C10 decrease of the gaps in diffusivity become less noticeable as carbon number increases.
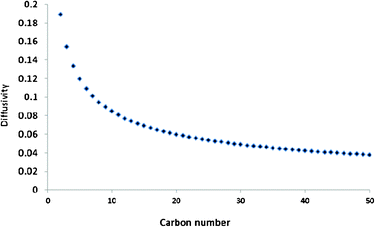 | ||
| Fig. 7 Graham's law diffusion illustration of diffusivity on the carbon number of olefins. y = 0.114e−0.02x, R2 = 0.868. | ||
Comparison of the shape/pattern of the curve in Fig. 4 with the curve in Fig. 7 shows that except for the C2 anomaly, the typical FTS product selectivity pattern reflects the diffusivity pattern of the hydrocarbons. This may suggest that the commonly observed curvature away from the ideal ASF distribution at high carbon numbers is due to natural low diffusivity of the FTS products (including olefins) but not their tendency to initiate chain growth after readsorption on the catalyst surface. It also suggests that other deviations of the FTS product spectrum from ideal ASF distribution law are most probably due to characteristic chemical behaviours of those constituent FTS products rather than physical behaviours as described in the olefin readsorption models. In general the olefin readsorption models are only able to describe the FTS product spectrum from C3+. They are unable to predict C1 and C2 selectivities without the introduction of special parameters. Perhaps a model that is based on the intrinsic chemical behaviour of C2 and C1 will be provide all-encompassing single parameter that will sufficiently/satisfactorily describe all the FTS product spectrum.
The above assertion is in line with findings of Schulz and Claeys.95 These authors conducted extensive studies on the kinetics of α-olefin re-insertion. α-olefins of carbon numbers C2–C11 were co-fed syngas in a gradientless stirred slurry reactor during FTS. Their observations are as follows:
- Added olefins undergo limited re-insertion but instead undergo hydrogenation and isomerisation reactions to a significant extent
- Reactivity and selectivity of olefin incorporation is not chain length dependent (with exception of ethene which is 10–25 times more reactive than other olefins).
- Conversion of the co-fed olefins except (C2, ethene) have no effect on olefin/paraffin ratio.
- Reaction conditions have a strong effect on the extent of reaction and selectivity of co-fed olefins (e.g. inhibition by CO and alkali in iron based FTS).
- Olefins with internal double bonds and paraffins do not participate in secondary chain growth
Despite the above findings, especially exceptional chemical behaviour of ethene compared to other olefins, the authors explained the deviation of the FTS product spectrum from ASF distribution law in terms of mean reactor residence of a FT product. They proposed that FT products revolve between a ternary phase (catalyst surface, wax or liquid phase and gas phase) system in the reactor in a convective cycle (Scheme 4). Preferential removal of a product from the convective cycle determines its mean reactor residence time which in turn governs re-adsorption of an α-olefin and by extension the FT product spectrum. The mean reactor residence time of a product is express as:
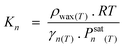 | (15) |
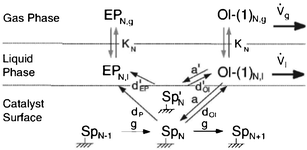 | ||
| Scheme 4 Mean reactor residence time model.95 | ||
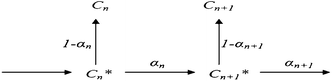 | ||
| Scheme 5 Scheme used to derive the relationship between selectivities of consecutive carbon numbers.96 | ||
Thus, the model parameters are chain growth, chain desorption and chain hydrogenation. Hydrogenation and desorption are considered chain termination steps, chain-growth probability as a function of the carbon number (αn) is described in terms of rate constants, k, of the three generic reactions as follows:
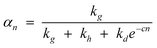 | (16) |
The k’s are catalyst properties, c is a physical desorption constant of the product (depending on process conditions—temperature and reactant partial pressures). The model states that competition between the three generic reactions rather than their absolute rates governs the product distribution and the relative rates are defined as follows:
Hence, olefin/paraffin ratio (O/P)n and chain growth probability as a function of the carbon number are then be expressed as follows:
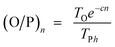 | (17) |
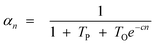 | (18) |
The only mathematical constraints in ‘a’ is that all three must assume positive values. The olefin/paraffin ratio will decrease exponentially with the carbon number, increasing pressure and decreasing temperature.
In previous models, prediction is limited to C3+ fractions of the product spectrum. The desorption model treated the C1 precursor like a higher Cn surface species and can terminate via either hydrogenation or desorption without considering the mechanistic implication of the desorption aspect. The methane formation rate was described satisfactorily, using parameter values that were obtained from higher Cn product fraction. To predict C2, the model was extended by invoking Dry's hypothesis that observed negative deviation in the total C2 selectivity is due to possibility of two active growth positions in C2 surface species. Eqn (18) was revised by dividing TP and TO by 2.
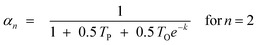 | (19) |
With the revision, total C2 formation rate was predicted almost perfectly, but the ethylene/ethane ratio is overestimated. This was attributed to the high tendency of ethylene to undergo secondary hydrogenation to ethane. Despite the overestimation, the model is the first model that successfully captures nearly all the deviations from ASF distribution law without introducing additional parameters to predict C1 and C2 selectivities.97
So far we had been examining descriptions of the FTS product spectrum, we started from ASF distribution law and its deficiencies to discussions on post ASF models. The models constitute an indirect or backdoor view of mechanism of FTS. To a first approximation, the ability of such models to fully describe the product spectrum is an indication of correctness of its assumptions with respect to the reaction dynamics. However, a front door or investigation of the reaction mechanism from starting reactant is necessary for confirmation. This leads us to examining macro kinetics and mechanisms of FTS in the remaining sections.
4 Kinetics of the FTS reaction
Accurate understanding of the mechanism of a chemical reaction is not only a pre-requisite for developing physically realistic mathematical models for the reaction, it is also a crucial requirement for the rational design of an efficient catalyst.98 The activity of FT catalysts depends on the choice of active metal and the preparation method. It is generally accepted that the order of specific activity of FT active metals follows the order: Ru > Ni > Co > Fe; although only iron and cobalt are commercially viable. There appears to be a preference for cobalt based catalysts in most new FT plants because of their higher activity and stability compared to iron. However, precursors of iron based catalysts are cheaper than those of cobalt. From a process economy point of view, it is desirable to develop iron based catalysts of comparable activity and stability as cobalt based.A macro kinetics study is a useful tool for gaining insight into reaction mechanisms. For simple reactions, macro kinetics studies may provide sufficient information to decipher the reaction mechanism, but it is usually insufficient to provide satisfactory details of about complex reactions. However, it can provide a starting platform for further probes of the reaction mechanism using other tools (isotopic, spectroscopic, theoretical).99–101 There are two common approaches in macro kinetics studies: deductive or inductive methods. The deductive approach often involves fitting experimental kinetic data with empirical or polynomial models. When the species (reactants, intermediates, products) involved in the reaction are not explicitly defined like in FTS, this approach may be associated with many fitted parameters which give little or no insight about the reaction mechanism. Moreover, extrapolation of the rate equations outside the region where data was collected may lead to significant deviations. In the inductive approach, rate equations are derived based on proposed mechanisms, the equation that best fits the experimental data is judged the most probable mechanism. Since the inductive approach is based on prior informed assumption or theories, it is expected that the kinetic expression which best fits the experimental data should be capable of predicting the reaction rate at all conditions. Absence of significant deviation of extrapolations from an equation is proof of validity of the assumptions or theories upon which the equation was derived.
Although FTS is generally considered polymerisation in nature, polymerisation kinetic expressions102,103 are not directly applicable because in FTS, the monomer species are formed in situ on the catalyst surface and more than one potential monomer is possible. At present, there is no clear consensus on the expression for the kinetics of the FT reaction over iron and cobalt based catalysts. Various equations proposed to describe the rate of FTS reaction over iron and cobalt based catalysts are shown in Tables 2 and 3. The rate expressions in Table 2 and 3 are of Langmuir–Hinshelwood–Hougen–Watson type models based on different assumptions. Without recourse to the various assumptions, cursory mechanistic interpretations can be drawn from the expressions based on a general form of useful kinetic equation for multi-step heterogeneous catalytic reactions given by Susu.104
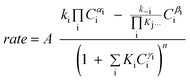 | (20) |
| Proponent(s) | Kinetic expression | Derivable mechanistic insight | ||
|---|---|---|---|---|
| n | Species involved in the rate determining step | |||
| a. | Anderson–Dry |
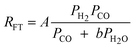
|
1 | Undissociated H2 or CO |
| b. | Ledakowicz–Nettelhoff |
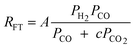
|
1 | Undissociated H2 or CO |
| c. | Satterfield–Huff |
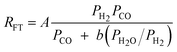
|
1 | Undissociated H2 or CO |
| d. | Van Berge |
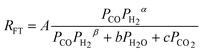 where β = maximum (α -1, 0) where β = maximum (α -1, 0) |
1 | Undissociated H2 or CO |
| e. | Van Steen |
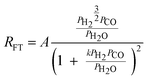
|
2 | Partially dissociated H2 and Undissociated CO |
| f. | Botes et al. |
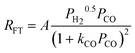
|
2 | Dissociated H2 and Undissociated CO |
| Proponent(s) | Kinetic expression | Derivable mechanistic insight | ||
|---|---|---|---|---|
| n | Species involved in the rate determining step | |||
| a. | Rautavuoma and Van der Baan |
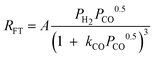
|
3 | Undissociated H2 and Dissociated CO |
| b. | Yates and Satterfield |
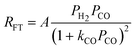
|
2 | Undissociated H2 and CO |
| c. | Sarup and Wojciechowski |
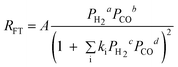 Where a, b, c and d could assume various values, including fractions such as 0.25 and 0.75. Where a, b, c and d could assume various values, including fractions such as 0.25 and 0.75. |
||
| c(1). |
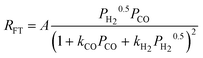
|
2 | Dissociated H2 and Undissociated CO | |
| c(2). |
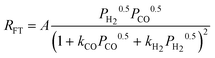
|
2 | Dissociated H2 and CO | |
| d. | Van Steen |
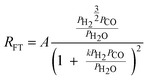
|
2 | Partially dissociated H2 and Undissociated CO |
| e. | Botes et al. |
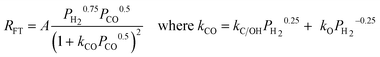
|
2 | Dissociated H2 and CO |
The rate expression was derived using principles of microscopic reversibility and steady state approximation. The exponent ’n’ in the denominator is a reflection of a number of colliding reacting species involved in the rate determining step (n ≤ 2, n > 2 is statistically less likely). The numerator terms are governed by assumptions of the elementary steps. To make kinetic sense, the exponents α, β, & γ, cannot take arbitrary values. They are related to the number of species that are involved in the elementary reactions (usually α, β, & γ ≤ 2). Kinetically, only positive integer values (1 or 2) are reasonable, but fractional values are also permitted as indicators of the dissociation of a reacting species. Since the rate expressions are usually a reflection of the rate determining step, mechanistic insights derivable from the rate expressions are also presented in the respective tables.
A comparison of the kinetic expressions in the Table 2 (except entry f.) revealed that H2O or CO2 are considered inhibition terms for the FT reaction on iron catalysts. This had been a long held view, but recently this long held view was subjected to critical analyses and was found invalid. The proponent of the equation in entry f showed that the effect of H2O on the FTS reaction rate is not statistically significant. They argued that there is no justification for the inclusion of H2O in the rate expression. These authors demonstrated that their proposed rate expression (without H2O and or CO2 as inhibition terms) described both historical and new kinetic data more accurately than those that have H2O or CO2 as inhibition terms.105 Although there are opposing views on the effect of water pressure in cobalt based FTS, it is generally accepted that water does not influence the FT rate over cobalt catalysts.106 Hence, the rate expressions for cobalt catalysts contains no water term.
Arguments advanced in entry f (Table 2) appear sufficient as proof of validity of the derivable mechanistic insights from it. Over cobalt based catalysts, a straight conclusion cannot be reached. More information beyond what is derivable from macro kinetics studies is required. Moreover, further validation of the preliminary inference in the case of iron based catalysts is necessary. Such information was recently made available via theoretical and isotopic studies. Theoretical calculations indicated that hydrogen assisted CO dissociation is more thermodynamically favoured over a direct CO dissociated path.107 Experimental data in support of this theoretical prompt was reported by Ojeda et al.108,109 They demonstrated that hydrogen-assisted CO activation is the predominant kinetically-relevant step on Fe and Co catalysts at conditions typical of FTS practice. These authors showed through theoretical calculations that H2 dissociates readily over Fe and Co, and H-atoms are involved in the CO dissociation elementary steps (see Scheme 6).
![CO activation paths on Fe(110) [blue] and Co(0001) [red]. The preferred H-assisted CO dissociation path is highlighted in blue. Values on the arrows refer to the individual barriers (in kJ mol−1) for each elementary step. (adapted from ref. 108).](/image/article/2012/RA/c2ra20519j/c2ra20519j-s6.gif) | ||
| Scheme 6 CO activation paths on Fe(110) [blue] and Co(0001) [red]. The preferred H-assisted CO dissociation path is highlighted in blue. Values on the arrows refer to the individual barriers (in kJ mol−1) for each elementary step. (adapted from ref. 108). | ||
This finding agrees with the mechanistic inference drawn from entry f (Table 2) for iron based catalysts. However over cobalt based catalyst, entry c1(Table 3) is the closest to the results of theoretical calculations and the same conclusion was arrived at recently by Bukur and co-workers.110
As shown above, it is only recently that questions about CO activation were resolved and it represents a major progress in the quest to unravel the mechanism of FTS. It engenders greater confidence in fitting macro kinetic data. However, mechanistic insights from macro kinetic studies did not extend to answering questions about the identity of the monomer species and pathway of monomer coupling. In the next section we examine studies in these areas.
5 Mechanism of FTS
Unlike conventional polymerisation reactions where feed reactants are monomers, in FTS monomers are first generated in situ from the syngas feed (CO and H2) and it is generally accepted that hydrocarbon formation proceeds in the following sequence: generation of the chain initiator; chain growth or propagation and chain growth termination or desorption. While a complete description of the mechanism of FTS will entail detailed atomic dynamics of the hydrocarbon formation sequence, it become rather more complicated with the inclusion of a monomer formation step. A picture of the situation can be inferred from the perspective of Krische et al.,111,112 who described FTS as a hydrogen mediated catalytic reductive polymerization of carbon monoxide. They suggested that organometallic intermediates arising transiently in the course of catalytic hydrogenation of CO may be intercepted and re-routed to C–C coupling products. A number of mechanisms have been proposed, we examine only the main rival mechanisms.5.1 Proposed main rival FTS mechanisms
The identity of the monomer species involved is central to gaining a clear picture about product formation and selectivity in FTS. From Scheme 6, it can be seen that the kinetically relevant path to the chain initiator is similar on Fe and Co. However, chain growth can occur via oxygenated or deoxygenated surface species and views about the FTS mechanism are along this divide. While we group highlights on proposed rival FTS mechanisms into oxygenated and deoxygenated surface species; we feel that the ability to control or engineer the catalyst surface to favour either of the possible chain growth species will provide leverage for controlling the C–C coupling pathway and product distribution.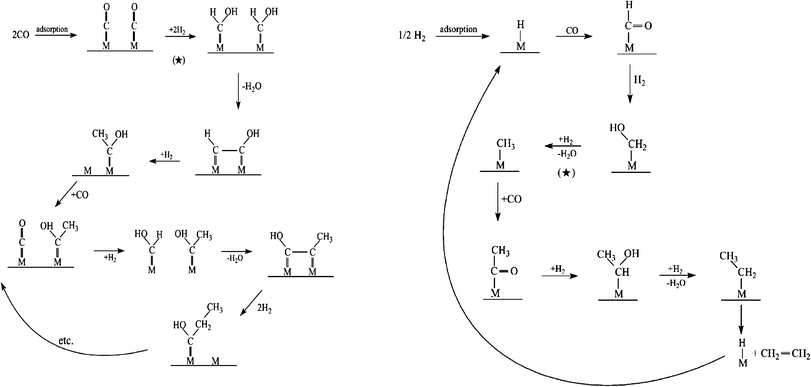 | ||
| Scheme 7 Proposed Fischer–Tropsch synthesis mechanisms via oxygenates monomer formation and chain propagation.113,114 | ||
| Pathway | Chain initiation | Chain propagation | Chain termination |
|---|---|---|---|
| CO insertion or Hydroformylation | m-H or m-R | CO insertion into m-H or m-R, followed by sequential hydrogenation and elimination of water | Hydrogenation to aldehydes or alcohols |
| Enol mechanism | m = CHOH | Condensation of adjacent m = CHOH, followed elimination of water | Dehydration of alcohols to 1-alkenes |
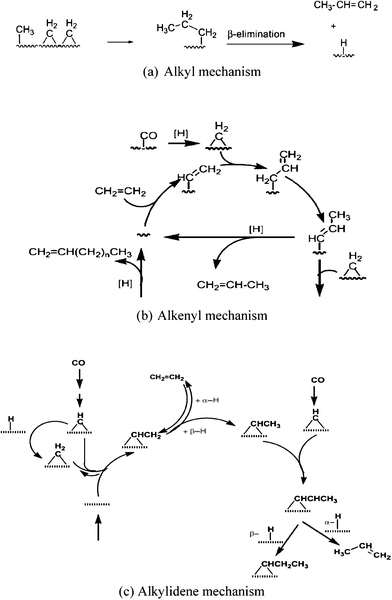
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, etc. But CH or CH2 are recognised as the chain initiators and propagators. The original carbide theory (Scheme 8) has undergone modifications in the light of new experimental and theoretical studies. It was later renamed a carbene mechanism. There are three mechanisms that are based on carbene intermediates and their main features are presented in Table 5 and Scheme 9.
CH2, etc. But CH or CH2 are recognised as the chain initiators and propagators. The original carbide theory (Scheme 8) has undergone modifications in the light of new experimental and theoretical studies. It was later renamed a carbene mechanism. There are three mechanisms that are based on carbene intermediates and their main features are presented in Table 5 and Scheme 9.
 | ||
| Scheme 8 Activation of CO on a metal surface giving surface carbide. | ||
 | ||
| Scheme 9 Proposed Fischer–Tropsch synthesis mechanisms via carbene monomer formation and chain propagation.115 | ||
| Pathway | Chain initiation | Chain propagation | Chain termination |
|---|---|---|---|
| Alkyl mechanism | m-CH3 or m-CH2R | CH2 | β-elimination to give 1-alkenes |
| Alkenyl mechanism |
m-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR CHR |
CH2 and sequential allyl–vinyl rearrangement step | β-elimination to give 1-alkenes |
| Alkylidene Mechanism | m = CH–CHR | CH and sequential H addition | β-elimination to give 1-alkenes |
For fundamental and application objectives it is desirable to unequivocally elucidate the detailed mechanism/pathway of FTS. Different monomer species were suggested in the selected rival mechanism. In fact, it has been commented that FTS does not have any close parallel in solution chemistry. According to Maitlis and Zanotti,115 there are as many views on the mechanism of interactions between the CO and H2 leading the alkene and alkane products, as there have been workers on the topic. However, there appears to be convergences of opinions from old literature and recent findings in support of an oxygenate species as a more probable chain propagator. The next section discusses and highlights studies on the C–C coupling pathways in FTS.
5.2.2.1 Iron catalysts. In a short account on the mechanism of the FTS reaction on iron catalysts compiled by Davis,113 the carbide mechanism was credited to Fischer even though he pre-supposed the oxygenate intermediates route for C–C coupling. The carbide mechanism enjoyed acceptance in the first fourteen years after the discovery of FTS. The next thirty years (1940–70) marked reports on oxygenated (enol) mechanisms on iron catalysts based on isotopic studies. From 1970, attention shifted back to the carbide mechanism and it dominates discussions on FTS afterwards. A series of reports on isotopic studies by Davis and co-workers strongly supports the oxygenate intermediates route to hydrocarbons over iron catalysts.116–121 They demonstrated that co-fed alcohols re-incorporate 50–100 times as much as alkene counterparts at initiating chain growth over iron catalysts. Investigations on the conversion of alcohols over iron oxide and iron carbides catalysts by Wang and Davis119 indicated that the substrates undergo dehydration, dehydrogenation and ketonisation (Tischenko condensation) for tertiary, secondary and primary alcohols respectively. Through 14C-tracer studies it was also shown that alcohol dehydration to olefin in FTS product spectrum is insignificant. Putting these observations together, Davis advanced that chain initiation over iron catalysts is most probably via formate species formed from either CO or CO2. But he added that propagation steps involve the addition of CO (or a surface species derived from CO) to a growing chain. The proposed mechanism is illustrated in Scheme 10. It is essentially the same as CO insertion mechanism in Table 4 but with oxygenates species as the initiator.116
 | ||
| Scheme 10 Chain initiation and chain propagation in modified oxygenate mechanism by Davis.116 | ||
Also a recent report by Durham et al.,122 also supports the CO insertion mechanism on iron catalysts. These authors carried out FTS over a Fe–Zn based catalyst in supercritical hexane media. In addition to alcohols as observed by Davis and associates, these authors obtained aldehydes and showed that aldehydes can initiate chain growth. They proposed that for n-alkanes and aldehydes as primary products, olefins are formed as both primary and secondary products, while CH4 and CO2 as secondary products.
5.2.2.2 Cobalt catalysts. Unlike iron catalysts in which there are older literatures which provide indications of the involvement of an oxygenate intermediates route to hydrocarbons, similar records are very scanty for cobalt catalysts. However, according to an account on the oxygenate mechanism compiled by Davis,116 in the early 1950–60s, British researchers while studying hydroformylation inferred that alcohols are the true primary products of the Fischer–Tropsch synthesis on both cobalt and iron catalysts. Wender and associates123 also proposed hydroformylation as the hydrocarbon formation route in the FT reaction. The next reports that indicated the oxygenated intermediate route to hydrocarbon formation on cobalt catalysts was about two decades later by Mims. He stressed that evidence from isotopic transient studies of FTS over cobalt catalysts showed that methanol shares the same oxygenate intermediate with hydrocarbon products. However, at about the time of report of Mims,124 the carbide mechanism had gained wide acceptance as the hydrocarbon formation route over cobalt catalysts. The original carbide mechanism was succeeded by carbene mechanisms which are also becoming disfavoured in the light of new findings.
After Fischer, Craxford and Rideal contributed to the carbide mechanism. Brady and Pettit were known for experiments which brought methylene to the fore as the monomer or intermediate in hydrocarbon chain growth. In honour of the contributions by Biloen and Sachtler, the alkyl-methylene C–C coupling mechanism was renamed Fischer–Tropsch–Brady–Pettit–Biloen–Sachtler Mechanism.125–127 This mechanism enjoyed wide acceptance for a short time but later became disfavoured because the alkyl–methylene C–C coupling pathway was found to be energetically unfavourable. Later an alkenyl–methylene mechanism was proposed by Maitlis et al.128 based on the consideration that achieving C–C coupling is more energetically favourable between alkenyl–methylene than alkyl–methylene. The mechanism hinged on the following:
- analyses of products of FT reactions with 13C labelled alkenes;
- decomposition of a model dinuclear complex bearing three or four C1 ligands, [(Cp*Rh)2(CH2)2(Me)(L)]+ or [(Cp*RhMe)2(CH2)2] to give propene MeCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 under oxidative (or thermal) conditions;
CH2 under oxidative (or thermal) conditions;
- experiments which showed that vinyl + methyl coupling proceed more readily than methyl + methyl over model organometallic compounds.
Validity of the above observations had been challenged by researchers. Shi and Davis129–131 pointed out that the 13C-data and other isotopic tracer data of Maitlis et al., were wrongly interpreted and do not provide direct evidence in support of surface bound vinyl intermediate as chain initiator. Ndlovu and associates132 also pointed out that the allyl–vinyl isomerisation/rearrangement step claim in the alkenyl mechanism cannot be replicated. They reported that under thermal treatment, only decomposition of Fe{[η5–C5H5](CO)2CH2CH.CH2} and Fe{[η5–C5(CH3)5](CO)2CH2CH.CH2}, iron counterpart of the dinuclear Rh complex, takes place. In hydrogen atmosphere, mere hydrogenation of the ligand or cleavage of the metal–carbon bond was observed, and no allyl–vinyl isomerisation. They concluded that if allyl and vinyl species exist under Fischer–Tropsch synthesis conditions, such species would desorb or be hydrogenated to alkyl species. Hence, the premise of the whole alkenyl mechanism is not a plausible route to chain growth mechanism in FTS.
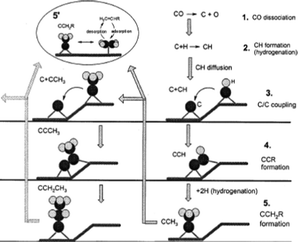
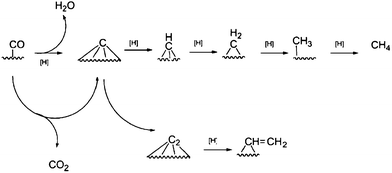
Experiments and theoretical calculations showed that CH2 is kinetically unstable, it readily decomposes to CH. Hence, Ciobica et al.,133 explored CH as a plausible monomer for hydrocarbon formation during FTS. In what is known as the alkylidene mechanism, he proposed that CH can be added to an alkylidene (RCH) or alkyl (CH3 or RCH2) and C–C coupling in each case is followed by hydrogenation. A theoretical evaluation of the mechanism was carried out using a Ru(0001) surface, using periodic ab initio calculations. The authors reported that the calculation results shows that the two C–C couplings share the same intermediate and can occur in parallel. Comparing the results obtained with Ru with similar results on different transition metals, the authors added that the stronger the M–C bond, the more difficult it is to hydrogenate toward methanation, they advanced that the C–C coupling transition state over the Ru(0001) surface is lower than the transition state for methanation. They concluded that the O atom is removed as water and the C atom is partially hydrogenated and will then enter in the C–C coupling cycle. In a similar investigation, Liu and Hu134 reported that C–CH coupling has the lowest activation energy among possible CHx species on Ru. They proposed a C + CR mechanism for FTS (Fig. 8).
The above theoretical studies in support of the C–CH coupling mechanism were based on Ru. Although Ru is the most active FTS metal, calculation data on Ru alone is not sufficient to generalise the validity of the mechanism. Reports of Cheng and co-workers135 may afford a more valid generalisation. These researchers investigated the reaction rates of all possible C1 + C1 coupling pathways on stepped Rh, Co, Ru, Fe, Re surfaces. Their calculations indicated that the structures of the transition states are similar on the surface of the metals but have different coupling barriers. They confirmed that CH2 + CH3 coupling is the least preferred pathway on the five metal surfaces due the low stability of the reacting species. Calculations of Cheng et al. indicated that CH3, RCH2 and RCH species are unstable as coupling partners of CH. They submitted that C–CH and CH–CH coupling play dominant roles in chain growth on the five metal surfaces. Indications of instability in the CH3, RCH2 and RCH species raise questions on the validity of mechanisms based on the species.
According to Morgan et al.,136 formyl is an unstable intermediate on Ru. However, recent findings point in the direction of oxygenate intermediates in C–C coupling over cobalt catalysts. Hydroformylation experiments on silica supported cobalt catalysts seems to have triggered attention on the possibility of oxygenate intermediates in C–C coupling on cobalt catalyst. Tsubaki and associates137–139 showed that Co/SiO2 catalysts are very active and selective for the synthesis of alcohols and aldehydes from syngas and 1-hexene under mild reaction conditions. Promotion of the cobalt with small amounts of noble metals was found to enhance the hydroformylation activity of the catalysts. It was also found that the use of methanol and ethanol as solvent improve oxygenate selectivities. Conventional homogeneous catalysis hydroformylation reactions are usually carried out at conditions more severe (higher T and P) than FTS. But these authors performed the hydroformylation reactions at conditions (pressure and temperature) typical of LTFT. The enhancement of oxygenate selectivity by use of solvents can be interpreted as having similar effects as supercritical fluid media in FTS by minimizing the extent of hydrogenation and other secondary reactions of the primary products.
Thus, it appears that by extrapolation there is a strong tendency for the presence of oxygenate intermediates on cobalt catalysts at FTS conditions. This inference is supported by the report of Sanchez-Escribano et al.140 who used IR spectroscopy to investigate the conversion of syngas and methanol over Cu–ZnO–Al2O3, Ni–Al2O3 and Co–Al2O3 (methanol synthesis, methanation and Fischer–Tropsch catalysts respectively). These authors showed that data obtained at low pressure provide clear evidence of the existence of oxygenate intermediates or pathways (formates, possibly dioxymethylene, methoxy groups) on the three catalysts. They suggested that an oxygenated surface species may be involved in the chain growth to give C2+ compounds over Co–Al2O3. And that the oxygenate mechanism most probably co-exists with the carbide mechanism.
Although theoretical calculations seem to lag behind the experimental studies, they nonetheless provide further leads towards the recognition of the oxygenate mechanism on cobalt catalysts. Experimental results motivated theoretical studies revisiting the FTS mechanism and exploring the possibility of oxygenates on cobalt catalysts. Cheng et al.,141 use DFT calculations to investigate the mechanism of the formation of aldehdyes and alcohols on a FT Co catalyst. They identified the CHO species as the favoured oxygenate intermediate and the CO-insertion mechanism was suggested as a likely route for the formation of long-chain oxygenates. In the calculation leading to the conclusion by Cheng et al., a pressure gap between surface science and heterogeneous catalysis was not taken into consideration. Inderwildi and co-workers142 attempted to bridge the pressure gap using microkinetic simulations. From DFT calculations and simulation results they asserted that preferred route of CO activation on a cobalt catalyst proceeded via a formyl species intermediate (CO → CHO → CH2O → CH2). They reasoned that since CH2 is an unstable species, it is less probable as the chain monomer. However, the formyl species was also found to have very short half-lives and may be difficult to observe experimentally but it may be detectable at high pressure.
Other DFT calculations by Inderwildi et al.143 and Zhuo et al.,144 showed that CO insertion is the most probable C–C coupling route to hydrocarbons over cobalt. Zhuo et al., reported that the TOF of CO consumption through CO insertion is double that of the formyl intermediate. In a more recent report, results of DFT calculations by Inderwildi and Mirwald145 ruled out the carbide mechanism as the main route to hydrocarbon formation over Ru surface. They also showed by micro-kinetic simulations that chain growth via direct reaction between surface CHx and CO is thermodynamically and kinetically more favoured compared to CO dissociation and chain initiation involving CO hydrogenation. Contrary to the anticipation of Inderwildi and co-workers that the experimental detection of oxygenate intermediates on cobalt catalysts will be difficult, reports of Sanchez-Escribano et al.,140 and Kollár et al.,146 filled this gap by providing evidence of stable oxygenate intermediates on cobalt catalysts using variable temperature in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) and optical diffuse reflectance (DRS) to identify oxygenate intermediates on cobalt catalysts.
From the above highlights, theoretical and experimental results converged on the likelihood of the oxygenate intermediates route to hydrocarbons on iron and cobalt catalysts. The results are in favour of CO insertion as the C–C coupling mechanism on the two catalyst types. Yet it may be too early to arrive at conclusions on the topic, more rigorous fundamental studies are require to provide decisive evidences. Meanwhile, it is also instructive to compare FTS with other related C–C coupling reactions of CO.
6 Related C–C coupling reactions of CO
Table 6 shows other C–C couplings of the reaction of CO. The closest to FTS in terms of co-reactant and product is isosynthesis. The key difference between the two reactions is the nature of the catalyst, hydrogenation metals and acid–base metal oxides for FTS and isosynthesis respectively. The metal catalysts can activate the reactants (H2 & CO) more efficiently than the oxide catalysts. This may account for the requirement of higher temperature and pressure conditions in isosynthesis compared to FTS. By extension, limited chain growth and branching in isosynthesis may also have a connection with the lower efficiency of the oxide catalysts at activating one or both reactants compared to metal catalysts in FTS. With this comparison, we are inclined to suggest that mechanisms of hydrocarbon formation in the two reactions are most probably similar if not identical.| CO reactions | Co-reactant | Catalyst | Reaction conditions | Major primary product | |
|---|---|---|---|---|---|
| Temp. (°C) | Press. (bar) | ||||
| FTS | H2 | Ru, Ni, Fe, Co | 180–350 | 10–20 | alkene & alkanes |
| Isosynthesis | H2 | ThO2, ZrO2 | 375–475 | 30–60 | isobutene & isobutane |
| Hydroformylation | Alkene, H2 | Rh, Co, Ni | 40–200 | 10–100 | aldehydes |
| Carbonylation | Alkyl cation precursors (alkene, alkanol, dialkylethers, alkylesters), aldehyde, acetals | Brønsted and Lewis acids, Rh, Co, Ni, Pd, Mo | 0–50 | 1–100 | Carboxylic acid, esters, anhydride |
It is generally agreed that C–C coupling during isosynthesis over ZrO2 involves carbonylation and aldol condensation. The major chain growth step occurs through CO insertion into the activated aldehyde or ketone, and alternative chain growth also occurs via condensation between methoxide and a surface bound enolate. The resulting intermediates can undergo further C–C coupling or hydrogenation to alcohols. This can be followed by hydrogenolysis or dehydration to the corresponding alkanes or alkenes respectively.147–150 CO insertion requires a Lewis acid site (metal or non-metal), while aldol condensation is favoured by basic sites.
It is worth noting that aldol condensation is recognised as a termination step which accounts for the branching and non-ASF product distribution in isosynthesis.151 A similar non-ASF product distribution are been observed in FTS over base (Ca) promoted cobalt152 and iron catalysts (unpublished results by these authors), in each case wax selectivity decreases and product distribution shifted primarily to middle distillate fractions. This could be a preliminary evidence in support of the earlier suggestion that the pathway to hydrocarbons in FTS and isosynthesis are similar. Similar non-ASF product distribution is therefore expected in potassium promoted FTS catalyst (especially iron based catalysts), however, there has not been a report of such cases. Group I & II metals are usually employed in the form of oxides, hydroxides or carbonates as promoters in FTS catalysts. The compounds of group I metals are more basic but also more water soluble than the corresponding group II metal compounds. Water is a co-product in FTS, and the group I metal promoters have a tendency of being leached out by water from the catalyst under the reaction conditions. Hence, their effect on product selectivity may be short-lived and less noticeable.
Carbonylation and hydroformylation are essentially CO insertion C–C coupling reactions, the differences between them consist of a co-reactant to CO and a post CO insertion reaction. In hydroformylation, an activated hydrogen atom is added to a π-coordinated alkene followed by CO insertion, then desorption of the product as an aldehyde, all the reaction steps take place on a single metal centre.153 Whereas in carbonylation, activation of the reactant occurs on different sites, CO on the Lewis acid centre (metal or non-metal) and the alkyl species is adsorbed as a conjugate base to a Brønsted acid site. After insertion of CO into the alkyl, the resulting product, the acyl cation intermediate can be desorbed as carboxylic acid or esters by a reaction with alcohol, ether154–158 or water (Koch reaction).159–160 Traditionally, the two reactions are homogeneous catalysis reactions carried out in the liquid phase which requires high pressure to achieve substantial CO dissolution in the liquid medium. Heterogenised processes permitted operations at pressures ranges used in FTS.161–164 Although the presence of hydrogen was indicated to promote carbonylation over metal catalyst,165,166 hydrogen assisted CO activation is not essential for initiation but product desorption is critical for the continuity of the catalytic cycle in carbonylation or hydroformylation.
From the above discussion we can conclude that C–C coupling in carbonylation and hydroformylation involves acidic site (Lewis and or Brønsted) CO insertion into an electrophilic carbon species. This is similar to the CO insertion reaction in isosynthesis discussed earlier. However, contrary to the need for a desorption step for the continuity of the catalytic cycle in carbonylation or hydroformylation, the coupled intermediate in isosynthesis remains at the active site for further chain propagation. Desorption can take place via another type (aldol) of C–C coupling reaction, as proposed and product distribution is a function of the relative rates of CO insertion and aldol C–C coupling reactions. As suggested earlier, C–C coupling in isosynthesis and FTS are most likely similar, then, by extrapolation ASF and non-ASF product distribution observed for a Ca promoted catalyst can be accounted for by the relative rates of CO insertion and aldol C–C coupling reactions. The reaction rates are a function of the strengths and densities of the respective sites. Typical FTS catalysts are made up of acidic sites species (active metals: Ru, Ni, Co, Fe; supports: SiO2, Al2O3, TiO2; promoters: Ru, Pt, Pd, ZrO2, MnO, etc). These species favours CO insertion C–C chain growth, and the absence of a strong basic site to promote aldol coupling leads to ASF production distribution. Non-ASF product distribution observed for the Ca promoted catalysts can be attributed to the presence of a strong basic site in substantial amounts, favouring competition between aldol coupling and the CO insertion route. The comparison and explanations in this section are untested hypothesis, but they are suggestions for fundamental studies on the subject.
7 Conclusion and outlook
FTS is a key technology for obtaining hydrocarbons from non-petroleum carbonaceous resources. In its early history, the commercial FTS process was driven by political decisions, but motivations for the reaction now are environmental concerns and economics. Striving at further improving the economics require, among other things, molecular engineering. This demands detailed insight into the chemistry of FTS. In its ninety years history, FTS has been an active area of research and tremendous efforts had been expended on the elucidation of details of the reaction. Although commendable progress has made over the years, clarifications on the chemistry of FTS are still necessary. FTS is generally considered a polymerisation type reaction involving: chain initiation, propagation and termination steps. Exact details of the FTS polymerisation steps are not fully clear at present.We have explored proposed macro kinetics expressions and product distribution models for indirect clues on the details. There is a high level of certainty with findings about pathway of chain initiation step as involving hydrogen assisted CO activation. Except for the desorption model, the proposed FTS product distribution models attribute olefin/paraffin ratio and curvature away from the ASF distribution at high carbon numbers to the re-adsorption of the primary olefin product. These models in themselves are unable to account for C1 and C2 selectivities. However, the desorption model captures all the observed deviations from ASF law. We believed that there are more to chain termination steps in the model than mere hydrogenation and desorption. Investigations are needed into the intermediates and the elementary steps to paraffin and olefin products. These details will contribute to the goal of unravelling the full mechanism of FTS. From macro kinetics, isotopic and theoretical studies, there is a high level of certainty that the chain initiation step involves hydrogen assisted CO activation. Also, there are increasing reports of evidence in support of CO insertion as the C–C coupling mechanism and oxygenate intermediate pathways to hydrocarbons for both the iron and cobalt catalyst. However, more fundamental studies are necessary to obtain further details and a clearer picture.
We compare FTS with other C–C coupling reactions of CO. Based on the similarity of isosynthesis to FTS, we proposed the same mechanisms for plausible C–C coupling in FTS. These pathways are promoted by different site types (electrophilic and nucleophilic for CO insertion and aldol condensation respectively), and the relative densities of the sites can influence product distribution. Thus, at this point we can draw that catalytic units for molecular manipulations (catalyst design) of FTS are hydrogenation, electrophilic and nucleophilic sites. Hydrogenation property is critical to high activity, electrophilicity and nucleophilicity influence product distribution. Electrophilicity have been well investigated, nucleophilicity is less recognised and combinations of the three are yet to be explored for possibilities.
Acknowledgements
Olusola O. James is grateful to TWAS (Trieste Italy) and CSIR (India) for TWAS-CSIR Postgraduate Fellowship Award.References
- M. Asif and T. Muneer, Renewable Sustainable Energy Rev., 2007, 11(7), 1388–1413 CrossRef.
- G. Bang, Energy Policy, 2010, 38(4), 1645–1653 CrossRef.
- A. Grunwald, Futures, 2011, 43(8), 820–830 CrossRef.
- A. Demirbas, Prog. Energy Combust. Sci., 2007, 33(1), 1–18 CrossRef CAS.
- G. Sorda, M. Banse and C. Kemfert, Energy Policy, 2010, 38(11), 6977–6988 CrossRef.
- A. de Klerk, Fischer–Tropsch Facilities at a Glance, in ‘Fischer–Tropsch Refining, Wiley-VCH Verlag GmbH & Co. KGaA, First Edition 2011 Search PubMed.
- (a) Sasol facts 2011 your blueprint to the world of sasol, http://www.sasol.com/sasol_internet/downloads/11029_Sasol_Facts_2011_1309786765289.pdf.; (b) GTL projects blossoming around the world, http://edj.net/sinor/sfr1-01art9.html; (c) JSPL to execute CTL project,Press release, http://www.jindalsteelpower.com/MediaFiles/PressRelease/PressRelease_2009_7_16_35_41_217.pdf.
- T. W. Patzek and G. D. Croft, Nat. Resour. Res., 2009, 18(3), 181–191 CrossRef CAS.
- E. D. Larson, G. Fiorese, G. Liu, R. H. Williams, T. G. Kreutz and S. Consonni, Energy Proc., 2009, 4371–4378 CrossRef CAS.
- H. C. Mantripragada and E. S. Rubin, Energy Proc., 2011, 2700–2707 CrossRef CAS.
- R. H. Williams, G. Liu, T. G. Kreutz and E. D. Larson, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 529–553 CrossRef CAS.
- T. Takeshita and K. Yamaji, Energy Policy, 2008, 36(8), 2773–2784 CrossRef.
- M. G. Salameh, Appl. Energy, 2003, 75(1-#x2013;2), 33–42 Search PubMed.
- W. A. Payne, Adv. Agron., 2010, 105, 1–46 CrossRef.
- M. de Wit, M. Junginger, S. Lensink, M. Londo and A. Faaij, Biomass Bioenergy, 2010, 34(2), 203–217 CrossRef.
- K. Sunde, A. Brekke and B. Solberg, Forest Policy and Economics, 2011, 13(8), 591–602 CrossRef.
- G. R. Timilsina and A. Shrestha, Energy, 2011, 36(4), 2055–2069 CrossRef.
- P. K. Swain, L. M. Das and S. N. Naik, Renewable Sustainable Energy Rev., 2011, 15(9), 4917–4933 CrossRef CAS.
- J. Shen, E. Schmetz, G. J. Stiegel, J. C. Winslow, R. M. Kornosky, D. R. Madden and S. C. Jain, Stud. Surf. Sci. Catal., 2007, 163, 315–325 CrossRef CAS.
- O. P. R. van Vliet, A. P. C. Faaij and W. C. Turkenburg, Energy Convers. Manage., 2009, 50(4), 855–876 CrossRef CAS.
- H. C. Mantripragada and E. S. Rubin, Energy Policy, 2011, 39(5), 2808–2816 CrossRef CAS.
- C. J. Lee and C. Han, Comput.-Aided Chem. Eng., 2009, 27, 1881–1886 CrossRef.
- L. Tock, M. Gassner and F. Maréchal, Biomass Bioenergy, 2010, 34(12), 1838–1854 CrossRef CAS.
- J. M. Seiler, C. Hohwiller, J. Imbach and J. F. Luciani, Energy, 2010, 35(9), 3587–3592 CrossRef CAS.
- Y. H. H. Chen, J. M. Reilly and S. Paltsev, Energy Policy, 39(9), 4713–4725 CrossRef.
- M. Erturk, Renewable Sustainable Energy Rev., 2011, 15(6), 2766–2771 CrossRef.
- F. Trippe, M. Fröhling, F. Schultmann, R. Stahl and E. Henrich, Fuel Process. Technol., 2011, 92(11), 2169–2184 CrossRef CAS.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS.
- C. E. Wyman and G. Huber, Biofuels, Bioprod. Biorefin., 2009, 3, 105–107 CrossRef CAS.
- L. R. Lynd, E. Larson, N. Greene, M. Laser, J. Sheehan, B. E. Dale, S. McLaughlin and M. Wang, Biofuels, Bioprod. Biorefin., 2009, 3, 113–123 CrossRef CAS.
- K. Yagi and T. Nakata, Biomass Bioenergy, 2011, 35(7), 2883–2892 CrossRef.
- A. C. Caputo, M. Palumbo, P. M. Pelagagge and F. Scacchia, Biomass Bioenergy, 2005, 28(1), 35–51 CrossRef.
- A. Kauriinoja, Small-scale biomass-to energy solutions for northern periphery area, M.Sc thesis, University of Oulu, 2010 Search PubMed.
- M. K. Delivand, M. Barz, S. H. Gheewala and B. Sajjakulnukit, Appl. Energy, 2011, 88(11), 3651–3658 CrossRef.
- E. Henrich, N. Dahmen and E. Dinjus, Biofuels, Bioprod. Biorefin., 2009, 3, 28–41 CrossRef CAS.
- J. Manganaro, B. Chen, J. Adeosun, S. Lakhapatri, D. Favetta and A. Lawal, Energy Fuels, 2011, 25, 2711–2720 CrossRef CAS.
- G. Liu, E. D. Larson, R. H. Williams, T. G. Kreutz and X. Guo, Energy Fuels, 2011, 25, 415–437 CrossRef CAS.
- K. Bienert, The status of the Choren Carbo V gasification, 2nd European Summer School on Renewable Motor Fuels, Warsaw, Poland, 29 – 31 August 2007 Search PubMed.
- J. Zhou, Q. Chen, H. Zhao, X. Cao, Q. Mei, Z. Luo and K. Cen, Biotechnol. Adv., 2009, 27(5), 606–611 CrossRef CAS.
- D. Atkinson and J. McDaniel, Chemical Engineering World, 2009, 28–36 CAS.
- S. R. Deshmukh, A. L. Y. Tonkovich, K. T. Jarosch, L. Schrader, S. P. Fitzgerald, D. R. Kilanowski, J. J. Lerou and T. J. Mazanec, Ind. Eng. Chem. Res., 2010, 49(21), 10883–10888 CrossRef CAS.
- J. J. Lerou, A. L. Tonkovich, L. Silva, S. Perry and J. McDaniel, Chem. Eng. Sci., 2010, 65(1), 380–385 CrossRef CAS.
- H. Jingjiang, L. Zhenlin, Y. Yoshiharu, N. Norikazu and T. Noritatsu, Chem.–Eur. J., 2006, 12, 8296–8304 CrossRef.
- S. Abelló and D. Montané, ChemSusChem, 2011, 4(11), 1538–56 CrossRef.
- B. Sun, M. Qiao, K. Fan, J. Ulrich and F. Tao, ChemCatChem, 2011, 3, 542–550 CrossRef CAS.
- P. M. Maitlis, J. Mol. Catal. A: Chem., 2003, 204-#x2013;205, 55–62 Search PubMed.
- T. J. Donnelly, Product Distributions of the Fischer–Tropsch Synthesis, Ph.D Thesis, Massachusetts Institute of Technology, 1989 Search PubMed.
- O. O. James, A. M. Mesubi, T. C. Ako and S. Maity, Fuel Process. Technol., 2010, 91, 136–144 CrossRef CAS.
- M. E. Dry, Chemical concepts used for engineering purposes, in ‘Fischer–Tropsch Technology’, ed. A. Steynberg, M. Dry, Elsevier, 2004 Search PubMed.
- X. Ni, Y. Tan, Y. Han and N. Tsubaki, Catal. Commun., 2007, 8, 1711–1714 CrossRef CAS.
- M. Fujiwara, R. Kieffer, H. Ando, Q. Xu and Y. Souma, Appl. Catal., A, 1997, 154, 87–101 CrossRef CAS.
- B. Rongxian, T. Yisheng and H. Yizhuo, Fuel Process. Technol., 2004, 86, 293–301 CrossRef.
- S. Li, A. Li, S. Krishnamoorthy and E. Iglesia, Catal. Lett., 2001, 77(4), 197–205 CrossRef CAS.
- M. Claeys and E. van Steen, Basic studies, in ‘Fischer–Tropsch Technology’, ed. A. Steynberg and M. Dry, Elsevier, Amsterdam, 2004 Search PubMed.
- G. P. Vander Laan, Ph.D Thesis, University of Groningen, 1999 Search PubMed.
- H. G. Stenger Jr. and C. F. Askonas, Ind. Eng. Chem. Fundam., 1986, 25(3), 410–413 Search PubMed.
- G. Henrici-Olivé and S. Olivé, Angew. Chem., Int. Ed. Engl., 1976, 15(3), 136–141 CrossRef.
- C. N. Satterfield and G. A. Huff Jr., J. Catal., 1982, 73(1), 187–197 CrossRef CAS.
- N. O. Egiebor, W. C. Cooper and B. W. Wojciechowski, Can. J. Chem. Eng., 1985, 63, 826–834 CrossRef CAS.
- G. A. Kliger, L. S. Glebov, T. P. Popova, E. V. Marchevskaya, V. G. Beryezkin and S. M. Loktev, J. Catal., 1988, 111(2), 418–420 CrossRef CAS.
- (a) This article is not included in your organization's subscription. However, you may be able to access this article under your organizaiton's agreement with Elsevier; (b) R. Snel, Catal. Lett., 1988, 1(10), 327–330 CrossRef CAS.
- N. O. Egiebor, W. C. Cooper and B. W. Wojciechowski, Can. J. Chem. Eng., 1985, 63(5), 826–834 CrossRef CAS.
- N. M. Rice, C. C. Hsu and B. W. Wojciechowski, Can. J. Chem. Eng., 1988, 66, 694–696 CrossRef CAS.
- P. Chaumette, C. Verdon and P. Boucot, Top. Catal., 1995, 2(1–4), 301–311 CrossRef CAS.
- W. Kuipers, C. Scheper, J. H. Wilson, I. H. Winkenburg and H. Oosterbeek, J. Catal., 1996, 158(1), 288–300 CrossRef.
- H. A. J. van Dijk, The Fischer–Tropsch synthesis: A mechanistic study using transient isotopic tracing, Ph.D Thesis, Technische Universiteit Eindhoven, Eindhoven, 2001 Search PubMed.
- M. E. Dry, Appl. Catal., A, 1996, 138, 319–344 CrossRef CAS.
- G. A. Huff Jr. and C. N. Satterfield, J. Catal., 1984, 85(2), 370–379 CrossRef.
- H. G. Stenger Jr., J. Catal., 1985, 92, 426–428 CrossRef.
- Y. Yang, S. Pen and B. Zhong, Catal. Lett., 1992, 16(3), 351–357 CrossRef CAS.
- F. G. Botes, Ph.D Thesis, Technische Universiteit Eindhoven, 2008 Search PubMed.
- J. Huyser, M. J. van Vuuren, G. Kupi, The Value of a Two Alpha Model in the Elucidation of a Full Product Spectrum for Fe-LTFT, in ‘Advances in Fischer–Tropsch Synthesis, Catalysts, and Catalysis, ed. Burtron H. Davis and Mario L. Occelli, CRC Press Taylor & Francis Group, 6000 Broken Sound Parkway NW 2010 Search PubMed.
- F. Bertoncini, M. C. Marion, N. Brodusch and S. Esnault, Oil Gas Sci. Technol., 2009, 64(1), 79–90 CrossRef CAS.
- R. van der Westhuizen, R. Crous, A. de Villiers and P. Sandra, J. Chromatogr., A, 2010, 1217(52), 8334–8339 CrossRef CAS.
- A. Tavasoli, A. N. Pour and M. G. Ahangari, J. Nat. Gas Chem., 2010, 19(6), 653–659 CrossRef CAS.
- A. N. Pour, M. R. Housaindokht, S. F. Tayyari and J. Zarkesh, J. Nat. Gas Chem., 2010, 19(2), 107–116 CrossRef CAS.
- A. N. Pour, M. Zare and Y. Zamani, J. Nat. Gas Chem., 2010, 19(1), 31–34 CrossRef CAS.
- J. Gaube and H. F. Klein, Appl. Catal., A, 2010, 374(1–2), 120–125 CrossRef CAS.
- J. Gaube and H.-F. Klein, J. Mol. Catal. A: Chem., 2008, 283, 60–68 CrossRef CAS.
- R. J. Madon and E. Iglesia, J. Catal., 1993, 139, 576–590 CrossRef CAS.
- E. Iglesia, S. L. Soled, R. A. Fiato and G. H. Via, J. Catal., 1993, 143, 345–368 CrossRef CAS.
- R. J. Madon and E. Iglesia, J. Catal., 1994, 149, 428–437 CrossRef CAS.
- E. Iglesia, S. L. Soled, J. E. Baumgartner and S. C. Reyes, J. Catal., 1995, 153, 108–122 CrossRef CAS.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS.
- B. Shi and B. H. Davis, Catal. Today, 2005, 106, 129–131 CrossRef CAS.
- C. M. Masuku, W. D. Shafer, W. Ma, M. K. Gnanamani, G. Jacobs, D. Hildebrandt, D. Glasser and B. H. Davis, J. Catal., 2012, 287, 93–101 CrossRef CAS.
- E. W. Kuipers, C. Scheper, J. H. Wilson and H. Oosterbeek, J. Catal., 1996, 158, 288–300 CrossRef CAS.
- E. W. Kuipers, I. H. Vinkenburg and H. Oosterbeek, J. Catal., 1995, 152, 137–146 CrossRef CAS.
- L. M. Tau, A. Dabbagh and B. H. Davis, Energy Fuels, 1990, 4, 94–99 CrossRef CAS.
- W. H. Zimmerman, D. B. Bukur and S. Ledakowicz, Chem. Eng. Sci., 1992, 47, 2707–2712 CrossRef CAS.
- I. V. Derevich, V. S. Ermolaev and V. Z. Mordkovich, Theor. Found. Chem. Eng., 2008, 42(2), 216–219 CrossRef CAS.
- J. J. C. Geerlings, J. H. Wilson, G. J. Kramer, H. P. C. E. Kuipers, A. Hoek and H. M. Huisman, Appl. Catal., A, 1999, 186, 27–40 CrossRef CAS.
- G. P. van der Laan and A. A. C. M. Beenackers, Ind. Eng. Chem. Res., 1999, 38(4), 1277–1290 CrossRef CAS.
- G. P. van der Laan, Kinetics, Selectivity and Scale Up of the Fischer–Tropsch Synthesis, Ph.D Thesis, 1999, University of Groningen. Search PubMed.
- H. Schulz and M. Claeys, Appl. Catal., A, 1999, 186(1–2), 71–90 CrossRef CAS.
- F. G. Botes, Energy Fuels, 2007, 21, 1379–1389 CrossRef CAS.
- F. G. Botes, Kinetic and Selectivity Modelling of the Iron-Based Low-Temperature Fischer–Tropsch Synthesis, PhD Thesis, Technische Universiteit Eindhoven, 2008 Search PubMed.
- G. Ertl, Angew. Chem., Int. Ed. Engl., 1990, 29(11), 1219–1227 CrossRef.
- S. T. Oyama and W. Li, Top. Catal., 1999, 8, 75–80 CrossRef CAS.
- R. D. Cortright and J. A. Dumesic, Adv. Catal., 2001, 46, 161–264 CrossRef CAS.
- H. Lynggaard, A. Andreasen, C. Stegelmann and P. Stoltze, Analysis of simple kinetic models in heterogeneous catalysis, Denmark, Elsevier, 2004, pp. 1–87 Search PubMed.
- E. van Steen and H. Schulz, Appl. Catal., A, 1999, 186, 309–320 CrossRef CAS.
- Y. N. Wang, W. P. Ma, Y. J. Lu, J. Yang, Y. Y. Xu, H. W. Xiang, Y. W. Lia, Y. L. Zhao and B. J. Zhang, Fuel, 2003, 82, 195–213 CrossRef CAS.
- A. A. Susu, Chemical kinetics and heterogeneous catalysis, CJC Press, Lagos, 1997 Search PubMed.
- F. G. Botes and B. B. Breman, Ind. Eng. Chem. Res., 2006, 45, 7415–7426 CrossRef CAS.
- F. G. Botes, Ind. Eng. Chem. Res., 2009, 48(4), 1859–1865 CrossRef CAS.
- S. Shetty, A. P. J. Jansen and R. A. van Santen, J. Am. Chem. Soc., 2009, 131, 12874–12875 CrossRef CAS.
- M. Ojeda, R. Nabar, A. U. Nilekar, A. Ishikawa, M. Mavrikakis and E. Iglesia, J. Catal., 2010, 272, 287–297 CrossRef CAS.
- M. Ojeda, A. Li, R. Nabar, A. U. Nilekar, M. Mavrikakis and E. Iglesia, J. Phys. Chem. C, 2010, 114, 19761–19770 CAS.
- T. Bhatelia, W. Ma, B. Davis, G. Jacobs and D. Bukur, Chemical Engineering Transactions, 2011, 25, 707–712 Search PubMed.
- H. Y. Jang and M. J. Krische, Acc. Chem. Res., 2004, 37, 653–661 CrossRef CAS.
- M. Y. Ngai, J. R. Kong and M. J. Krische, J. Org. Chem., 2007, 72, 1063–1072 CrossRef CAS.
- B. H. Davis, Fuel Process. Technol., 2001, 71, 157–166 CrossRef CAS.
- B. H. Davis, Fuel Chemistry Division Preprints, 2002, 47(1), 237–239 CAS.
- P. M. Maitlis and V. Zanotti, Chem. Commun., 2009, 1619–1634 RSC.
- B. H. Davis, Catal. Today, 2009, 141, 25–33 CrossRef CAS.
- L. M. Tau, H. A. Dabbagh, T. P. Wilson and B. H. Davis, Appl. Catal., 1989, 56, 95–106 CrossRef CAS.
- L. M. Tau, H. A. Dabbagh, J. Halasz and B. H. Davis, J. Mol. Catal., 1992, 71, 37–55 CrossRef CAS.
- Y. Wang and B. H. Davis, Appl. Catal., A, 1999, 180, 277–285 CrossRef CAS.
- B. Shi and B. H. Davis, Topics in Catalysis, 2003, 26(1–4), 57–161 Search PubMed.
- M. K. Gnanamani, R. A. Keogh, W. D. Shafer, B. Shi and B. H. Davis, Appl. Catal., A, 2010, 385, 46–51 CrossRef CAS.
- E. Durham, S. Zhang and C. Roberts, Appl. Catal., A, 2010, 386, 65–73 CrossRef CAS.
- I. Wender, H. W. Sternberg, R. A. Friedel, S. J. Metlin, R. E. Markby, The Chemistry and catalytic properties of cobalt and iron carbonyls, Technical Report, BM-BULL-600 (OSTI ID: 7193411), Bureau of Mines, Washington, D.C., 1962 Search PubMed.
- C. A. Mims, Catal. Lett., 1988, 1(8–9), 293–298 CrossRef CAS.
- P. M. Maitlis, Pure Appl. Chem., 1989, 61(10), 1747–1754 CrossRef CAS.
- R. Quyoum, V. Berdini, M. L. Turner, H. C. Long and P. Maitlis, J. Am. Chem. Soc., 1996, 118, 10888–10889 CrossRef CAS.
- R. Quyoum, V. Berdini, M. L. Turner, H. C. Long and P. M. Maitlis, J. Catal., 1998, 173, 355–365 CrossRef CAS.
- M. L. Turner, N. Marsih, B. E. Mann, R. Quyoum, H. C. Long and P. M. Maitlis, J. Am. Chem. Soc., 2002, 124(35), 10456–10472 CrossRef CAS.
- B. Shi and B. H. Davis, Catal. Today, 2000, 58, 255–261 CrossRef CAS.
- P. M. Maitlis and M. L. Turner, Catal. Today, 2001, 65, 91–93 CrossRef CAS.
- B. Shi and B. H. Davis, Catal. Today, 2001, 65, 95–97 CrossRef CAS.
- S. B. Ndlovu, N. S. Phala, M. Hearshaw-Timme, P. Beagly, J. R. Moss, M. Claeys and E. van Steen, Catal. Today, 2002, 71, 343–349 CrossRef CAS.
- I. M. Ciobıca, The Molecular Basis of the Fischer Tropsch Reaction, Ph.D Thesis, Technische Universiteit Eindhoven, 2002 Search PubMed.
- Z. P. Liu and P. Hu, J. Am. Chem. Soc., 2002, 124, 11568–11569 CrossRef CAS.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 6082–6086 CAS.
- G. A. Morgan, D. C. Sorescu Jr., T. Zubkov and J. T. Yates Jr., J. Phys. Chem. B, 2004, 108, 3614–3624 CrossRef CAS.
- X. Q. Qiu, N. Tsubaki, K. Fujimoto and Q. M. Zhu, Fuel Process. Technol., 2004, 85, 1193–1200 CrossRef CAS.
- Y. Zhang, K. Nagasaka, X. Qiu and N. Tsubaki, Catal. Today, 2005, 104, 48–54 CrossRef CAS.
- Y. Zhang, M. Shinoda, Y. Shiki and N. Tsubaki, Fuel, 2006, 85, 1194–1200 CrossRef CAS.
- V. Sanchez-Escribano, M. A. L. Vargas, E. Finocchio and G. Busca, Appl. Catal., A, 2007, 316, 68–74 CrossRef CAS.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 9464–9473 CAS.
- O. R. Inderwildi, S. J. Jenkins and D. A. King, J. Phys. Chem. C, 2008, 112(5), 1305–1307 CAS.
- O. R. Inderwildi, D. A. King and S. J. Jenkins, Phys. Chem. Chem. Phys., 2009, 11, 11110–11112 RSC.
- M. Zhuo, K. F. Tan, A. Borgna and M. Saeys, J. Phys. Chem. C, 2009, 113, 8357–8365 CAS.
- J. W. Mirwald and O. R. Inderwildi, Phys. Chem. Chem. Phys., 2012, 14, 7028–7031 RSC.
- M. Kollár, A. De Stefanis, H. E. Solt, M. R. Mihályi, J. Valyon and A. A. G. Tomlinson, J. Mol. Catal. A: Chem., 2010, 333, 37–45 CrossRef.
- S. C. Tseng, N. B. Jackson and J. G. Ekerdt, J. Catal., 1988, 109(2), 284–297 CrossRef CAS.
- N. B. Jackson and J. G. Ekerdt, J. Catal., 1990, 126(1), 31–45 CrossRef CAS.
- N. B. Jackson and J. G. Ekerdt, J. Catal., 1990, 126(1), 46–56 CrossRef CAS.
- A. Sofianos, Catal. Today, 1992, 15(1), 149–175 CrossRef CAS.
- T. J. Hazanec, J. Catal., 1986, 98(1), 115–125 CrossRef.
- A.R. de la Osa, A. De Lucas, A. Romero, J. L. Valverde and P. Sánchez, Fuel, 2011, 90(5), 1935–1945 CrossRef CAS.
- C. F. Huo, Y. W. Li, M. Beller and H. Jiao, Organometallics, 2003, 22, 4665–4677 CrossRef CAS.
- J. R. Zoeller, E. M. Blakely, R. M. Moncier and T. J. Dickson, Catal. Today, 1997, 36(3), 227–241 CrossRef CAS.
- J. Gong, Q. Fan and D. Jiang, J. Mol. Catal. A: Chem., 1999, 147(1–2), 113–124 CrossRef CAS.
- H. Jiang, Z. Liu, P. Pan and G. Yuan, J. Mol. Catal. A: Chem., 1999, 148(1–2), 215–225 CrossRef CAS.
- Q. Xu, S. Inoue, N. Tsumori, H. Mori, M. Kameda, M. Tanaka, M. Fujiwara and Y. Souma, J. Mol. Catal. A: Chem., 2001, 170(1–2), 147–153 CrossRef CAS.
- N. Tsumori, Q. Xu, Y. Souma and H. Mori, J. Mol. Catal. A: Chem., 2002, 179(1–2), 271–277 CrossRef CAS.
- H. Mori, A. Mori, Q. Xu and Y. Souma, Tetrahedron Lett., 2002, 43(44), 7871–7874 CrossRef CAS.
- K. Qiao and C. Yokoyama, Catal. Commun., 2006, 7(7), 450–453 CrossRef CAS.
- P. Cheung, A. Bhan, G. J. Sunley and E. Iglesia, Angew. Chem., Int. Ed., 2006, 45, 1617–1620 CrossRef CAS.
- F. E. Celik, T. J. Kim and A. T. Bell, Angew. Chem., Int. Ed., 2009, 48, 4813–4815 CrossRef CAS.
- F. E. Celik, T. Kim, A. N. Mlinar and A. T. Bell, J. Catal., 2010, 274, 150–162 CrossRef CAS.
- S. A. I. Barri and D. Chadwick, Catal. Lett., 2011, 141(6), 749–753 CrossRef CAS.
- K. Omata, K. Fujimoto, H. Yagita, H. Mazaki and H. Tominaga, Stud. Surf. Sci. Catal., 1988, 36, 245–249 CrossRef CAS.
- K. Fujimoto, S. Bischoff, K. Omata and H. Yagita, J. Catal., 1992, 133(2), 370–382 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |