Direct ab initio molecular dynamics (MD) study of the ionization on a benzene dimer†
Hiroto
Tachikawa
*
Division of Materials Chemistry, Graduate School of Engineering, Hokkaido University, Sapporo 060-8628, JAPAN. E-mail: hiroto@eng.hokudai.ac.jp; Fax: +81-11-706-7897
First published on 30th May 2012
Abstract
The ionization dynamics of a benzene dimer have been investigated by means of a direct ab initio molecular dynamics (MD) method in order to elucidate the reaction mechanism. Following the ionization, the T-shaped neutral benzene dimer was gradually changed to a π-stacked benzene dimer cation. The structural change and time evolution of the electronic absorption spectrum were completely visualized for the first time. The time scale of the dimer formation was estimated to be 1.0–1.5 ps. First, the benzene molecule at the stem position (Bz′) was ionized, and the structure of Bz′+ was rapidly deformed due to the Jahn–Teller effects. Next, the rotation of (Bz′)+ gradually occurred relative to Bz. Finally, a π-stacked benzene dimer cation was formed. TD-DFT calculations indicated that the absorption spectrum of (Bz)2+ is blue-shifted as a function of time. The formation mechanism of the benzene dimer cation was discussed on the basis of the theoretical results.
1. Introduction
The π–π stacking is a non-covalent interaction caused by overlapping of π-orbitals between π conjugated systems.1 The interaction plays an important role in structural arrangements and molecular assemblies in biology,2 chemistry,3 and materials science.4 Also, the interaction accounts for diverse phenomena such as nucleobase stacking, side-chain interactions in proteins, binding of drugs into DNA and RNA and organic crystal packing of aromatic molecules.5The benzene dimer is the simplest π–π prototype interaction system. Therefore, several investigations have been carried out to elucidate the nature of the interaction of benzene–benzene aromatic system.6–8 The neutral benzene dimer is only stable at low temperatures and is mostly prepared in a supersonic jet expansion, where different sized clusters are produced simultaneously. Using ionization-detected stimulated Raman spectroscopy (IDSRS), Henson et al. proposed a T-shaped dimer geometry of the benzene dimer.9 After that, a T-shaped structure and a nonpolar parallel-displaced structure have been proposed on the basis of the various results. A subsequent rotational spectrum measured by Arunan and Gutowsky suggested the intermolecular center-of-mass distance for benzene molecules is 4.96 Å in the T-shaped dimer.10
Dinadayalane and Leszczynski investigated theoretical configurations of the benzene dimer, i.e., perpendicular T-shaped, parallel-displaced (PD), sandwich, and V-shaped structures using second- and fourth-order Møller–Plesset perturbation (MP2 and MP4) theory.11 The T-shaped configuration has the lowest energy and it is stabilized by 0.17 kcal mol−1 over the PD configuration at the MP4(SDTQ)/aug-cc-pVDZ level. Pitonak et al. showed that the potential energy surface (PES) of the benzene dimer contains two energy minima, the T-shaped (TS) and PD structures.12 Sherrill et al.13 calculated potential energy curves of benzene dimers using the CCSD(T) complete basis set model. The sandwich, T-shaped, and parallel-displaced (PD) benzene dimers were examined. T-shaped and PD forms are almost equivalent in energy, although the T-shape is the lowest form energetically. However, the interaction energy of the benzene dimer (neutral) is negligibly small: Bz + Bz → (Bz)2.
Compared with the neutral benzene dimer, the formation energy of a benzene cation with neutral benzene is significantly larger, Bz+ + Bz → (Bz)2+ + ΔE(+). Experimentally, the dimer cation in the gas phase has been characterized by Ohashi et al.14–17 Photodissociation action spectra of (Bz)2 revealed that absorption bands are appeared at 1.07, 1.35, 2.14, and 2.82 eV. The former two bands are assigned as charge resonance (CR) bands, whereas the latter two bands are local excitations (LE) within the benzene ring. In low temperature matrices, γ-irradiated liquid benzene exhibits two bands at 1.36 eV (CR band) and 2.64 eV (LE band).18
Jahn–Teller (JT) distortions and charge localization in the benzene dimer cation were analyzed using the equation-of-motion coupled cluster (EOM-CCSD) method.19 Ionization of the dimer changes the bonding from non-covalent to covalent and induces significant geometrical distortions, e.g., shorter inter-fragment distance and JT displacements.
The electronic states of the neutral benzene dimer and benzene dimer cation have been well understood.20–32 However, the dynamics feature for the formation mechanism of the benzene dimer cation following the ionization of the neutral benzene dimer is scarcely known because there is no theoretical study on the reaction dynamics.
In the present study, the ionization dynamics of the benzene dimer has been investigated by means of a real time direct ab initio molecular dynamics (MD) method: (Bz)2 + Ip → [(Bz)2+]ver → (Bz)2+, where Ip means ionization potential of neutral benzene. We focus our attention on the reaction mechanism and time scale of the complex formation.
2. Method of calculation
First, the neutral structure of a benzene dimer (Bz)2 was optimized at the MP2/6-311G(d,p) level. Next, the structures and momenta of the atoms of (Bz)2+ were generated by thermal distribution around the equilibrium geometry of (Bz)2.33–35 The temperature of the simulation was 10 K. Direct ab initio molecular dynamics (MD) calculations36,37 were carried out at the B3LYP/6-311G(d,p) level of theory. The trajectory of (Bz)2+ following the vertical ionization from the neutral state was propagated from the vertical ionization point of the neutral (Bz)2. A total of 20 trajectories were run. The equations of motion for N atoms in a benzene dimer are given by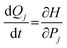 | (1) |
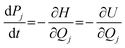 | (2) |
Static ab initio calculations were performed with the Gaussian 03 and 09 program packages38 using the cc-pVDZ, 6-311G(d) and 6-311++G(d,p) basis sets in order to obtain sufficiently accurate energetics. The derived structures and geometrical parameters of the stationary points are given in the supporting information.†
3. Results
A. Structures of the benzene dimer (Bz)2
First, the structure of the neutral benzene dimer (Bz)2 with the T-shape was fully optimized at the MP2/6-311G(d,p) level. The structure obtained is illustrated in Fig. 1. The hydrogen atom of Bz′ (H1′) orients toward the center of mass of Bz (denoted by c.m.). Hereafter, the benzene molecules in the dimer are classified into two molecules, Bz (hydrogen acceptor benzene) and Bz′ (hydrogen donor benzene). | ||
| Fig. 1 Optimized structure of T-shaped benzene dimer calculated at the MP2/6-311G(d,p) level. | ||
The intermolecular distance, r(H1′-c.m.), is calculated to be 1.400 Å. The C–C bond distances are r(C0–C1′) = 3.703 Å, and R1 = r(C0–C1′) = 3.707 Å. The angle is θ = 30.6°. The binding energy was calculated to be 4.2 kcal mol−1 at the MP2/6-311G(d,p) level.
The natural population analysis (NPA) was used as the charge calculation of molecules. NPA molecular charges on Bz and Bz′ of the neutral dimer are calculated to be 1.00 and 1.00, respectively, indicating that both Bz and Bz′ are neutral in charge.
B. Vertical ionization state of (Bz)2
NPA charges at the vertical ionized state, (Bz)2+, are calculated to be + 0.07 on Bz and + 0.93 on Bz′ at the MP2/6-311G(d,p) level. The result indicates that the charge distribution on the benzene dimer cation is schematically expressed by (Bz)(Bz′)+. Namely, the hole is localized on the hydrogen donor benzene molecule (Bz′).The ionization energy of (Bz)2 is calculated to be Ip(dimer) = 9.33 eV. The corresponding energy of the monomer is Ip(Bz) = 9.43 eV. The ionization energy of benzene decreases slightly with the dimer formation (ΔE = −0.1 eV).
C. Ionization dynamics of (Bz)2
Snapshots of (Bz)2+ following the ionization of the benzene dimer are illustrated in Fig. 2. At time zero, the structure of (Bz)2+ corresponds to that of a neutral benzene dimer. The hole is mainly localized on the benzene Bz′, which is schematically expressed by (Bz)(Bz′)+. The intermolecular distance between Bz+ and Bz′ is 3.707 Å for R1 distance (point a). | ||
| Fig. 2 Snapshots of benzene dimer cation (Bz)2+ following the ionization of a T-shaped benzene neutral dimer. Direct AIMD calculations were carried out at the B3LYP/6-311G(d,p) level. | ||
Following the ionization of the neutral dimer, Jahn–Teller distortion of (Bz′)+ occurs rapidly. The structure of benzene dimer cation is also deformed. The intermolecular distance is slightly elongated from R1 = 3.707 Å (0 fs) to 4.084 Å (480 fs). A rotation of (Bz′)+ takes place as shown in the arrows at 480 fs (point b). At 1095 fs (point c), (Bz′)+ is largely rotated with respect to the Bz. The carbon atom of (Bz′)+ (C1′) approaches gradually to the carbon atom of neutral benzene (C1). The distance of C1′ from C1 of Bz+ is r(C1′–C1) = 3.702 Å. The benzene cation (Bz′)+ is further rotated and the dimer cation is formed at 1340 fs (point d). This dimer cation corresponds to the (1–1′) dimer cation, i.e., one carbon atom of (Bz′)+ (denoted by C1′) interacts with one carbon atom of Bz′ (C1). The intermolecular distance is r(C1′–C1) = 2.935 Å. The collision between Bz+ and Bz′ occurs, and the distance reaches the minimum point at 1651 fs (point e). After the collision, the dimer cation vibrates largely around the equilibrium point of the dimer cation.
The potential energy of the system, intermolecular distance (R1), and angle (θ) are plotted as a function of time in Fig. 3. The zero level of potential energy corresponds to the energy of benzene dimer cation at the vertical ionization point from the neutral benzene dimer denoted by [(Bz–Bz′)+]ver. This structure corresponds to the optimized structure of the T-shape calculated at the MP2/6-311G(d,p) level (point a). At time zero, the structure of [(Bz–Bz′)+]ver has the distance R1 = 3.707 Å. By the ionization, the potential energy of the system of the dimer cation is suddenly reduced to −1.1 kcal mol−1. This energy reduction is due to the intramolecular deformation of (Bz′)+ caused by Jahn–Teller effects. The vibration caused by the Jahn–Teller effect manifests as the fine structure (sharp spike) in the potential energy during the reaction. The sharp spike disappears at 200 and 800 fs, which is due to the fact that the vibrational energy is efficiently transferred into the other modes. The intermolecular distance R1 increases and reaches a maximum at 480 fs (point b). Next, the intermolecular distance R1 decreases gradually with increasing time, which means that the potential energy of (Bz′)+ approaches that of Bz. The potential energy is still flat up to 1000 fs. The energy is suddenly decreased after 1000 fs and the dimer cation is formed with R1 = 2.90 Å at 1340 fs (point d). After that, the collision of Bz to (Bz′)+ occurs at 1500 fs. The potential energy increases from −5 kcal mol−1 to −1.5 kcal mol−1 by the time of the collision. The time profile of the angle θ indicates that the molecular rotation of (Bz′)+ takes place smoothly without an activation energy.
 | ||
| Fig. 3 Time profile of the potential energy curve of the system, intermolecular distance (R1) and angle (θ) of the trajectory of (Bz)2+. | ||
D. Time profile of bond population
The time profile of the population of the C1–C1′ bond, which is newly formed after the ionization, is given in Fig. 4. Before the ionization, the neutral complex (Bz)2 has a negative population (−0.002) that is close to zero. After the ionization, the population is suddenly changed to a positive value (5 × 10−2). This means that the C1–C1′ bond formation is changed from an anti-bonding to a bonding nature. After that, the complex (1–1) is gradually formed. The population is also gradually increased. Finally, the population is changed to + 0.010 and the (1–1) complex is completely formed at this point. Thus, from time profile of population and potential energy, it was found that a new C–C bond is spontaneously formed after the ionization of (Bz)2. | ||
| Fig. 4 Bond population of C1–C1′ atoms plotted as a function of time. Calculations were carried out at the B3LYP/6-311G(d,p) level. | ||
E. Absorption spectra
The time dependent absorption spectra of (Bz)2+ are illustrated in Fig. 5. The structure of (Bz)2+ at time zero is the T-shaped form optimized for the neutral dimer. Two peaks are found for the benzene dimer cation at time zero: the lower peak at 0.8 eV is assigned to an intermolecular charge resonance (CR) band corresponding to (Bz)(Bz′)+ → (Bz)+(Bz′). The higher peak at 3.2 eV is a local excitation band within the benzene cation (Bz+) expressed by (Bz)(Bz′)+ → (Bz)(Bz′*)+. | ||
| Fig. 5 Time profiles of the absorption spectra of (Bz)2+ after ionization of the neutral T-shaped benzene dimer. TD-DFT calculations were carried out at the B3LYP/6-311G(d,p) level. | ||
At time = 0.0 fs, the absorption maxima are at 0.80 eV with an intensity of I = 4000 and at 3.2 eV with I = 380. The CR band is gradually blue-shifted as a function of time, and the peak of the band is changed from 0.8 to 1.45 eV at the final state of the π-stacking. The intensity of the CR band increases significantly after the dimer cation formation. On the other hand, the local excitation band is hardly changed during the dimer formation.
F. Structures of benzene dimer cation
As shown in the previous section, the direct ab initio MD calculation suggested that the T-shaped form of (Bz)2 dimer is changed spontaneously to a benzene dimer cation with a π-stacking form. The (1–1′) complex was preferentially formed. In this section, the structures of (Bz)2+ are searched by static geometry optimization.First, each structure of the benzene molecule (Bz) and benzene cation radical (Bz+) was fully optimized at the B3LYP/6-311G(d,p) level. Second, several initial configurations of Bz relative to Bz+ were randomly generated (30 geometries), and then the geometries of Bz–Bz+ were fully optimized. Five conformations were obtained as the stable forms of benzene dimer cation (Bz)2+. The optimized structures are illustrated in Fig. 6 and the relative energies are given in Table 1.
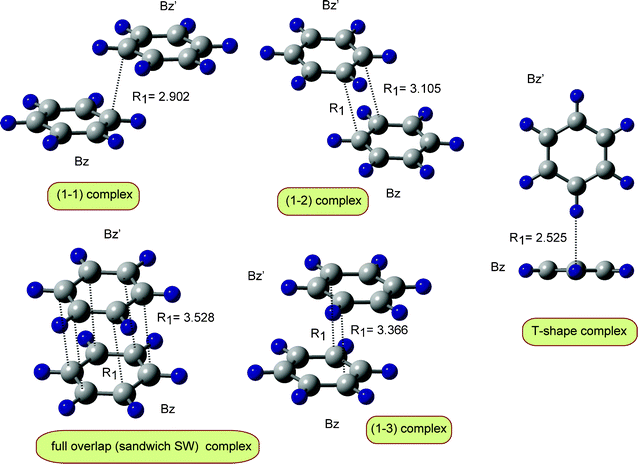 | ||
| Fig. 6 Optimized benzene dimer cations of (Bz)2+ obtained at the B3LYP/6-311G(d,p) level. Values indicate bond distance in Å. | ||
In the dimer cation of the (1–1′) complex, a carbon–carbon bond is formed between Bz+ and Bz. In the full overlap complex, all carbon atoms of Bz+ interact with all carbon atoms of Bz. In (1–2) and (1–3) complexes, two carbon atoms interact between Bz+ and Bz. The most stable form of the benzene dimer cation is the (1–1′) complex. However, the energy differences of the (1–2), (1–3) and full overlap complexes from the (1–1′) complex are significantly small (<1.0 kcal mol−1). This fact indicates that it is possible to form all the complexes equivalently in the reaction Bz+ + Bz.
The proton hyperfine coupling constants (H-hfcc's) of the benzene dimer cation were calculated and the results are given in Table 2. All the benzene dimer cations have H-hfcc's close to −6.0 MHz. Itagaki et al. measured EPR and ENDOR spectra of benzene dimer cations formed in X-ray irradiated halocarbon matrices containing a relatively high concentration of benzene molecules.24 They showed that the benzene dimer cation has an isotropic hyperfine coupling constant of −6.15 MHz. This value is in good agreement with the present values.
| Dimer cation | H-hfcc/in MHZ | — |
|---|---|---|
| (1–1′) complex | −5.71 | — |
| (1–2) complex | −5.90 | — |
| (1–3) complex | −6.18 | — |
| Full overlap (SW) | −6.25 | — |
| Experimental | −6.15 | (Bz)2+ in CFCl3 (130 K) |
| −6.03 | (Bz)2+ in CF3CCl3 (100 K) |
G. Spectrum shifts of benzene cation
The dynamics calculations showed that the electronic absorption spectrum of the T-shaped form is blue-shifted by the ionization due to the structural change from the T-shaped form of (Bz)2+ to the (1–1′) complex. In this section, the spectrum shift of a free benzene cation to form a benzene dimer cation, Bz+ + Bz → (Bz)2+, is investigated by means of TD-DFT calculations. All results are given in Fig. 7. The lowest excitation energy of free Bz+ was calculated to be 3.05 eV. After the dimer cation formation, the lowest excitation bands corresponding to the charge resonance (CR) band are around 1.5 eV in all the complexes except for the T-shaped form. The reaction is expressed by| Bz+ + Bz → (Bz)2+ red-shifted | (3) |
 | ||
| Fig. 7 Absorption spectra of the benzene dimer cations of (Bz)2+ calculated at the B3LYP/6-311G(d,p) level. Experimental values are given in the stick diagram. | ||
The T-shaped form showed an excitation band at 0.6 eV. Thus, the new charge resonance band is at 1.5 eV after the benzene dimer formation. This feature is in good agreement with the pulse radiolysis experiments.39 The reaction of the T-shaped form is expressed by
| T-shaped (Bz)2+ → π-stacked (Bz)2+ blue-shifted | (4) |
Thus, the spectral shift is dependent on the initial structure of Bz+.
H. Comparison with the experiments
Ohashi and Nishi observed the photodissociation of (C6H6)2+ at photon energies between 1.29 and 2.81 eV using a pulsed laser beam in the field-free region of a reflectron-type time-of-flight mass spectrometer. At a photon energy of 2.81 eV, the (C6H6)2+ ions are promoted to a bound upper state correlated to C6H6+(π–π) + C6H6(X). Absorption of a photon in the range of 1.29–2.14 eV induces a charge resonance transition to a repulsive upper state which correlates to C6H6+(X) + C6H6 (X). Three electronic transition bands observed by Ohashi and Nishi14 are given in Fig. 7 as stick diagrams. The calculated spectra are in good agreement with the experiments. The low energy band is assigned to a charge transfer band (a charge resonance band: X →A), and two low intensity bands are local excitation bands of (Bz)2+. Thus, the present calculations represent excellently the electronic states of (Bz)2+.I. Effects of initial structure of (Bz)2
To elucidate the effects of the initial configurations of the neutral dimer (Bz)2 on the time for dimer formation, T(φ), seven initial structures (φ = 0–30°) were selected and then the dynamics calculations were carried out. An increase of angle from the T-shape decreases the dimer formation time.Fig. 8A shows the effects of the initial angle (φ) on the time for the (Bz)2+ dimer formation. The angle φ is defined as an angle between the C6 axis of Bz (lower) and C2V axis of Bz (upper). For example, if the angle is φ = 0, (Bz)2 has a T-form. The larger angles cause a large deviation from the T-form. Three typical cases of potential energy (φ = 5, 20, and 30°) are plotted. T(φ) means a time period from zero to the time of the energy minimum corresponding to the dimer formation. The energy minima were at T(φ = 5) = 576 fs, T(φ = 20) = 396 fs, and T(φ = 30) = 335 fs. All values of T(φ) are plotted as a function of the angle φ in Fig. 8B. T(φ) is 1324 fs at φ = 0.0° (T-shape), and it gradually decreases with increasing φ. Thus, the initial angle φ strongly affects the dimer formation time. The deviation from the T-shaped structure accelerates the dimer formation reaction. From these results, it is predicted that an increase of temperature induces the dimer formation.
 | ||
| Fig. 8 Effects of the initial configurations of the neutral dimer (Bz)2 on the time for dimer formation. (A) Potential energies of sample trajectories with angles φ = 5, 20, and 30°, and (B) Time for dimer formation plotted as a function of the angle φ. | ||
In the present study, the initial structures in the dynamics calculations were based on the MP2/6-311G(d,p) optimized geometry of the neutral system. To check the method dependency on the product channels, several initial structures of the T-shaped form were examined in the dynamics calculation. The structures were obtained by the B3LYP/6-311G(d,p), MP2/3-21G(d) and PW91PW91/6-311G(d,p)//CCSD(T)/6-31G(d) methods. As shown in supporting information, all the methods gave the same product: i.e, a π-stacking form was only obtained from the dynamics calculations.†
J. Jahn–Teller effects in (Bz)2+
An important initial event at the vertical ionization point [(Bz) 2+]ver is the Jahn–Teller deformation of the dimer cation. The present direct ab initio MD calculation can describe clearly the Jahn–Teller deformation, because the present method can deal with all the degrees of freedom of the reaction system, i.e., full dimensional potential energy surface. The time evolution of the C–C bond distances of Bz are given in Fig. 9. At time zero, the C–C bond distances of Bz are 1.40 Å. After the ionization, the bond distances are rapidly varied as a function of time: r23 is elongated from 1.40 to 1.42 Å and it vibrated periodically. On the other hand, the C–C bond in vertical position (r12) is rapidly shortened from 1.40 Å to 1.38 Å, and it vibrates around 1.38 Å. The present calculation clearly represented the Jahn–Teller effect of the benzene dimer cation. | ||
| Fig. 9 Jahn–Teller effects on the structural deformation of a benzene dimer cation. (Upper) Structure of benzene dimer cation at time zero, and (lower) time profiles of C–C bond lengths of the benzene dimer cation. The dotted line indicates the C–C bond length at the equilibrium point of the neutral benzene dimer. | ||
4. Discussion
A. Reaction model
The neutral benzene dimer and the benzene dimer cation are a prototype system of C–H–π and π–π stacking interactions. Previously, the static ab initio calculations have been widely carried out for the structures and electronic states of benzene dimer and benzene dimer cation. However, the formation mechanism of benzene dimer cation was not clearly understood. In the present study, for the first time, the structural change from the T-shaped to the stacked form and the time evolution of the electronic transition caused by the change were completely visualized.A reaction model can be proposed on the basis of the present calculations. The potential energy curves (PECs) for the benzene dimer formation (neutral and cation) are illustrated in Fig. 10. The lower curve indicates that the neutral dimer is formed from two monomer molecules. The binding energy of two benzene molecules is expressed by ΔEbind(0). The binding energy is calculated to be 5.4 kcal mol−1 at the MP2/6-311G(d,p) level. The upper curve indicates the PEC of the formation of the benzene dimer cation. The benzene dimer cation is directly formed without an activation barrier. The benzene dimer cation denoted by [(Bz)2+]ver is a vertical ionization point from the neutral T-shaped dimer. The present calculation indicated that the T-shaped dimer cation leads to a (1–1′) π-stacking dimer. Hence, the reaction of this route is one of the half reactions of the full collision reaction Bz+ + Bz.
 | ||
| Fig. 10 Schematic illustration of the potential energy curves of the formation of the neutral and radical cations of benzene dimers. | ||
The intensity of the charge resonance (CR) band is small because the overlap integral between Bz and Bz+ in the T-shaped form at time zero is significantly small. The structure of [(Bz)2+]ver is gradually deformed by the attractive interaction between Bz+ and Bz. The CR band is also gradually blue-shifted and the intensity of the absorption spectrum increases. Finally, the benzene dimer cation, (1–1′) complex is completely formed at 1.0–1.5 ps. The wavelength of the spectrum is blue-shifted and the intensity increases at the final state.
B. Comparison with the benzene excimer
Hirata et al.40 (1999, Roos Ref. 10) investigated the excited states of (Bz)2 using spectroscopy of an expanded surpersonic jet with a pump–probe technique. They found that the T-shaped form of (Bz)2 is converted to the π-stacking form by the electronic excitation: (Bz)2* (excited state T-shape) → (Bz)2* (π-stacking excimer). The potential energy surface calculated by Roos and co-workers supported this conversion.41 The present calculations showed that the ionization of (Bz)2 leads to the formation of the π-stacking form of (Bz)2+ as well as the excimer of (Bz)2*.Acknowledgements
The author acknowledges a partial support from a Grant-in-Aid for Scientific Research (C) from the Japan Society for the Promotion of Science (JSPS) (Project No. 21550002).References
- Recent review article M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873 RSC.
- C. Lin, R. Chinnappan, K. Acharya, J. L. Pellequer and R. Jankowiak, Biophys. Chem., 2011, 154, 35 CrossRef CAS.
- T. Okamoto, K. Nakahara, A. Saeki, S. Seki, J. H. Oh, H. B. Akkerman, Z. N. Bao and Y. Matsuo, Chem. Mater., 2011, 23, 1646 CrossRef CAS.
- Y. Gao, G. Hu, W. Zhang, D. Ma and X. Baob, Dalton Trans., 2011, 40, 4542 RSC.
- V. Philip, J. Harris, R. Adams, D. Nguyen, J. Spiers, J. Baudry, E. E. Howell and R. J. Hinde, Biochemistry, 2011, 50, 2939 CrossRef CAS.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262 CrossRef CAS.
- M. Shibahara, M. Watanabe, C. Yuan, K. Goto and T. Shinmyozu, Tetrahedron Lett., 2011, 52, 3371 CrossRef CAS.
- J. Wang, J. D. Gu and J. Leszczynski, J. Phys. Chem. A, 2011, 115, 6376 CrossRef CAS.
- B. F. Henson, G. V. Hartland, V. A. Venturo, R. A. Hertz and P. M. Felker, Chem. Phys. Lett., 1991, 176, 91 CrossRef CAS.
- E. Arunan and H. S. Gutowsky, J. Chem. Phys., 1993, 98, 4294 CrossRef CAS.
- T.C. Dinadayalane and J. Leszczynski, Struct. Chem., 2009, 20, 11 CrossRef CAS.
- M. Pitonak, P. Neogrady, J. Rezac, P. Jurecka, M. Urban and P. Hobza, J. Chem. Theory Comput., 2008, 4, 1829 CrossRef CAS.
- C. D. Sherrill, T. Takatani and E. G. Hohenstein, J. Phys. Chem. A, 2009, 113, 10146 CrossRef CAS.
- K. Ohashi and N. Nishi, J. Chem. Phys., 1991, 95, 4002 CrossRef CAS.
- K. Ohashi and N. Nishi, J. Phys. Chem., 1992, 96, 2931 CrossRef CAS.
- K. Ohashi, Y. Nakai, T. Shibata and N. Nishi, Laser Chem., 1994, 14, 3 CrossRef CAS.
- K. Ohashi, Y. Inokuchi and N. Nishi, Chem. Phys. Lett., 1996, 263, 167 CrossRef CAS.
- T. Shida and W. H. Hamill, J. Chem. Phys., 1966, 44, 4372 CrossRef CAS.
- P. A. Pieniazek, S. E. Bradforth and A. I. Krylov, J. Chem. Phys., 2008, 129, 074104 CrossRef.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104–112 CrossRef CAS.
- R. A. DiStasio Jr, G. von Helden, R. P. Steele and M. Head-Gordon, Chem. Phys. Lett., 2007, 437, 277–283 CrossRef.
- P. A. Pieniazek, S. E. Bradforth and A. I. Krylov, J. Chem. Phys., 2008, 129, 074104–074111 CrossRef [(Bz)2+ binding energy = 0.23 eV].
- K. Muller-Dethlefs and J. B. Peel, J. Chem. Phys., 1999, 111, 10550–105514 CrossRef CAS.
- Y. Itagaki, N. P. Benetis, R. M. Kadam and A. Lund, Phys. Chem. Chem. Phys., 2000, 2, 2683–2689 RSC.
- J. L. Llanio-Trujillo, J. M. C. Marques and F. B. Pereira, J. Phys. Chem. A, 2011, 115, 2130–2138 CrossRef CAS.
- M. Pavone, N. Rega and V. Barone, Chem. Phys. Lett., 2008, 452, 333–339 CrossRef CAS.
- M. Mine, H. Hori, M. Ogata, K. Tanaka, T. Tsutsui and E. Miyoshi, Chem. Phys. Lett., 2007, 438, 157–161 CrossRef CAS.
- E. Misiyoshi, T. Ichikawa, T. Sumi, Y. Sakai and N. Shida, Chem. Phys. Lett., 1997, 275, 404 CrossRef.
- E. Miyoshi, N. Yamamoto, M. Sekiya and K. Tanaka, Mol. Phys., 2003, 101, 227 CrossRef CAS.
- R. Kusaka and T. Ebata, Angew. Chem., 2010, 122, 7143–7146 CrossRef.
- S. Yashonath, S. L. Price and I. R. McDonald, Mol. Phys., 1988, 64, 361–376 CrossRef CAS.
- P. Linse, S. Engstrom and B. Jonsson, Chem. Phys. Lett., 1985, 115, 95–100 CrossRef CAS.
- (a) H. Tachikawa, J. Phys. Chem. A, 2011, 115, 9091–9096 CrossRef CAS; (b) H. Tachikawa, Chem. Phys. Lett., 2011, 513, 94–98 CrossRef CAS.
- H. Tachikawa and T. Fukuzumi, Phys. Chem. Chem. Phys., 2011, 13, 5881–5887 RSC.
- H. Tachikawa, J. Phys. Chem. C, 2011, 115, 20406 CAS , in press.
- H. Tachikawa, J. Phys. Chem. A, 2011, 115, 9091–9096 CrossRef CAS.
- H. Tachikawa, Phys. Chem. Chem. Phys., 2011, 13, 11206–11212 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. PopleGaussian, Inc., Pittsburgh PA, 1998. Gaussian03, revision B.04; Gaussian, Inc.: Pittsburgh, PA, 2003.
- K. Okamoto, S. Seki and S. Tagawa, J. Phys. Chem. A, 2006, 110, 8073–8080 CrossRef CAS.
- T. Hirata, H. Ikeda and H. Saigusa, J. Phys. Chem. A, 1999, 103, 1014–1024 CrossRef CAS.
- T. Rocha-Rinza, L. De Vico, V. Veryazov and B. O. Roos, Chem. Phys. Lett., 2006, 426, 268–272 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available. See DOI: 10.1039/c2ra20246h/ |
| This journal is © The Royal Society of Chemistry 2012 |
