Gas-phase basicity of several common MALDI matrices measured by a simple experimental approach

Abstract

We present a combined experimental and theoretical study to determine the gas-phase basicity of several relatively small organic molecules that are used as matrices in MALDI: alpha-cyano-4-hydroxycynnamic acid (αCHCA), ferulic acid (FA), 3-hydroxypicolinic acid (HPA), sinapinic acid (SA), and 2,4,6-trihydroxyacetophenone (THAP). Our simple and fast experimental approach utilizes the ability of an electrosonic spray ionization (ESSI) source to produce high densities of gas-phase ions at ambient conditions, so that their gas-phase thermochemical properties can be probed in a bracketing-like experiment at atmospheric pressure, with no need for high vacuum. The reaction between the analyte and reference bases is monitored by a commercial mass spectrometer. We determined the following GB values of the MALDI matrices studied: 908.1 ± 0.8 (αCHCA), 863.8 ± 8.0 (FA), 876.3 ± 10.2 (HPA), 867.4 ± 1.4 (SA), and 864.2 ± 7.6 (THAP) kJ mol⁻¹. A good agreement between the experimentally measured and computationally predicted (DFT-B3LYP, G4MP2) gas-phase basicities for the studied compounds is found, except for αCHCA for which the calculations resulted in approximately 80 kJ mol⁻¹ lower GB. We attribute the observed discrepancy between the measured and calculated values to a gas-phase rearrangement of αCHCA into a heterocyclic aromatic isomer, 7-hydroxyquinoline-3-carboxylic acid (HQA). HQA is thermodynamically more stable and features higher GB than that of αCHCA (calculated at approximately 920 kJ mol⁻¹). The gas-phase basicity values of THAP and HPA are reported for the first time.

---

Introduction

Proton transfer reactions, i.e. protonation and deprotonation of a compound, are very widespread in nature. Not only are they the basis of fundamental acid–base chemistry, but they are employed in such vitally important biological processes as photosynthesis,^1–5cellular respiration,^6–8 and acid–base catalysis in enzymatic reactions.^9–13 Two thermochemical parameters are commonly used to describe proton transfer reactions, the proton affinity (PA) and the gas-phase basicity (GB).^14,15 These values can be obtained with relatively good accuracy via pulsed high-pressure mass spectrometry,^16–18 the kinetic method,^19,20 or bracketing. For instance, when the protonation reaction is not directly accessible it is common to use bracketing experiments.^14,15 In this case, the molecule of interest M can be reacted with a reference base, B that possesses well-known thermochemical properties:

MH⁺ + B ↔ M + BH⁺

By reacting a particular protonated base, MH⁺, with a set of reference bases one can evaluate the GB of M based on the equilibrium concentrations of the ions of interest.^14,15

In practice, measurements of PA and/or GB require sophisticated equipment which allows for the stable generation of protonated/deprotonated ions in sufficient number densities, with well-defined kinetic and internal energy profiles.^21–27 Complementary information to experimental measurement of GB and PA can be obtained through the use of theoretical calculation using modern quantum chemistry methods.¹⁵ The accuracy of the most advanced quantum chemical methods can be equal to or better than the chemical accuracy; however, the size of the systems that are accessible to quantum chemical methods can greatly increase the time required for such calculations.^28–34 However, the application of theoretical calculations to PA evaluation is much more frequent.

Recently, we reported a simple method for determining GBs of peptides and proteins at ambient conditions which can be carried out on most types of commercial electrospray mass spectrometers.^35,36 The gas-phase ions are produced at atmospheric pressure in the electrosonic spray ionization (ESSI) source, a variant of the traditional ESI source where the nebulizer gas possesses a supersonic flow velocity.³⁷ The ions react with vapors of the reference bases prior to the mass spectrometer inlet. In a manner similar to traditional bracketing experiments, the yield of a proton-transfer reaction between the analyte and a series of reference bases with known GB was monitored, allowing for the determination of the GB of the target compound. The major advantages of this method are short measurement times and the simplicity of the experimental setup, which utilizes an ESSI ion source and a commercial mass spectrometer.

In the present study, we extend the applicability of this method to a set of small molecules that are used as matrices in matrix-assisted laser desorption-ionization (MALDI). The motivation for the measurement of the GB of these molecules is that the proton transfer from protonated matrix ions to neutral analyte molecules is considered to play an important role in ion formation mechanisms in positive ion mode MALDI.^38–45 Despite the fact that GBs of matrix molecules are needed for a complete understanding of the fundamentals of the MALDI mechanism and for discovering new compounds with better characteristics for MALDI,^46–53 relatively limited data are available, often showing poor agreement and low accuracy.⁴⁴ Here, the GB of several commonly used MALDI matrices (Scheme 1) are measured by the simple ESSI-based experimental approach and compared to analogous data obtained from state-of-the-art quantum chemical calculations. For 2,4,6-trihydroxyacetophenone and 3-hydroxypicolinic acid, GB values are reported for the first time.

Scheme 1

Experimental

Alpha-cyano-4-hydroxycinnamic acid (αCHCA), 2-methoxypyridine, and 3-picoline-N-oxide were purchased from Sigma (Sigma-Aldrich Chemie GmbH, Buchs, Switzerland); sinapic acid (SA), 3-hydroxypicolinic acid (HPA), 2,4,6-trihydroxyacetophenone (THAP), pyridine, 3-hydroxypyridine, 4-chloroaniline, aniline, o-toluidine, 1,2-benzenediamine, p-anisidine, o-anisidine, 4-phenylpyridine, 4-picoline, 4-ethylpyridine, 2-ethylpyridine, 3,4-dimethylpyridine, and 4-ethylpyridine were purchased from Fluka (Fluka-Chemie AG, Buchs, Switzerland); ferulic acid (FA), 2-chloro-4-picoline, 3-aminophenol, and 2,6-dimethylaniline were obtained from Acros (Acros Organics, New Jersey, USA); 2-picoline was purchased from Aldrich (Aldrich-Fine Chemicals).

1 mM solutions of MALDI-matrices (0.1 mM in the case of 3-HPA) in a 1 : 1 (v : v) mixture of acetonitrile (Fluka, HPLC grade) and ultrapure water were acidified by the addition of up to 1% (v), (10% in case of αCHCA) acetic acid (Fluka, puris). Reference bases were used as pure substances in small aliquots deposited in microcentrifugal tubes (Eppendorf).

Mass spectrometry measurements

Mass spectrometry experiments were performed on a commercial hybrid quadrupole time-of-flight mass spectrometer (Q-TOF Ultima; Waters/Micromass Ltd., Manchester, UK) equipped with a Z-spray interface (Waters). The ion source was kept at room temperature. RF and DC voltages on ion guides were optimized in order to ensure the most efficient ion transmission in the range of m/z 50–500. Cesium iodide clusters (2 g L⁻¹CsI solution in a 1 : 1 water/2-propanol mixture) were used for mass calibration.

Working solutions of MALDI-matrices were directly electrosprayed via a home-built ESSI source. The design of the ESSI source has been described previously.³⁷ Briefly, it was composed of a T-piece (Swagelok, BGB Analytik AG, Switzerland), an outer and an inner fused silica capillary (inner diameters of 375 and 50 μm, respectively; BGB Analytik AG, Switzerland). The ESSI probe was mounted orthogonally to the mass spectrometer inlet on a XYZ-stage and its position was carefully optimized for maximum signal. Samples were delivered at a flow rate of 5–7 μL min⁻¹ (syringe pump, Harvard Apparatus, USA). A high voltage of 3.5 kV was applied to the ESSI probe, and an optimized nitrogen pressure between 10 and 20 bar was used.

Pure reference bases were deposited in small aliquots into sets of four microcentrifuge tubes mounted on a rack in such a way that they were evenly distributed under the ESSI plume to ensure prompt and uniform saturation of the plume volume with reference base vapors. The solutions containing the MALDI-matrices were sprayed continuously and vapors of the reference bases were introduced into the plume, one at a time. After about 20 to 30 s, a stable signal of the species [M + H]⁺ was achieved. This procedure was repeated at least three times for each reference base.

Data processing

MS data were recorded using commercial MassLynx software (v. 4.0, Waters, UK). Typically, 20 scans were combined per data point. The area under the MALDI-matrix [M + H]⁺ peak was used to calculate the relative signal drop in the presence of reference bases. The [M + H]⁺ peak areas in the presence of a reference base were related to the baseline, which was corrected over the whole series of measurements by a linear function to account for baseline drifts. Relative signal decrease was plotted against the GB's of the reference bases, and a sigmoid fitting of the form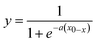 with the two parameters, a and x₀, was performed using MATLAB (2010a, The MathWorks, Natick, USA). Data points outlying the 95% confidence interval for the sigmoid fit were excluded.

The GBs of the MALDI matrices were extracted from the fitted sigmoidal curve. Different studies suggest using different points to determine the GB in bracketing experiments,^{35,36,54–58} since it is often difficult to observe a sharp transition in the extent of deprotonation of the ion monitored.⁵⁴ In the current work, the GB was assigned to a point where the increase of deprotonation rate was the highest by taking the X-coordinate of the minimum point on the second derivative of the fitted sigmoidal function—at approximately 80% of the [M + H]⁺ relative intensity. GBs determined in this way showed better agreement with the results of computational predictions than the inflection point x₀ of the sigmoidal fit, which corresponds to 50% of [M + H]⁺ deprotonation. The 95% confidence interval of GB was calculated based on the fitting parameter's errors.

Theoretical calculations

Quantum chemical calculations were performed using the Gaussian 03⁵⁹ and 09⁶⁰ software packages. Initial structures were optimized at the B3LYP/6-31G* level of theory. Selected (lowest energy) protonated and deprotonated structures were further optimized at the B3LYP/6-311+G** level and used for G4MP2⁶¹ calculations. Unfortunately, the size of the systems did not allow the application of G4 theory⁶² itself with our computational facilities. The Hessian matrix and vibrational frequencies were also calculated at B3LYP/6-31G* and B3LYP/6-311+G** levels of theory. The results of vibrational analysis were used for evaluating the entropy and the Gibbs free energy (in the RRHO approximation^59,60).

Results and discussion

Mass spectra recorded for αCHCA in the absence and presence of a reference base (Fig. 1a–b, respectively) clearly demonstrate the effect of the gas-phase proton transfer reaction: the [M + H]⁺ peak of αCHCA at m/z 190.05 is depleted from the spectrum upon introduction of reference base vapors while the peak of the protonated base, 2-chloropicoline (m/z 128.02), shows up.

Fig. 1 Positive ion mode ESSI mass spectra of αCHCA in the absence (a) and presence (b) of a reference base, 2-chloro-4-metylpyridine. (a) αCHCA produced protonated ([M + H]⁺) and sodiated ([M + Na]⁺) ion peaks at m/z 190.05 and 212.03, respectively. (b) Upon introduction of the reference base the corresponding protonated peak ([B + H]⁺) at m/z 128.02 dominated the spectrum. Some background ions originating from typical ion source contaminants, such as oleamide (m/z 282.29) or PEG (m/z 129.05), were also observed in the spectrum and had no interference with the target signal.⁷⁹

The yield of the gas-phase proton transfer from matrix ions to the neutral reference bases was monitored over time. Fig. 2 shows selected ion chromatograms of protonated αCHCA ions in the presence of two different reference bases, 4-ethylpyridine and 3-hydroxypyridine. It can be clearly seen that the signal of [M + H]⁺ (Fig. 2, upper panels) decreases exactly at the moment when the signal of the protonated reference base ([RB + H]⁺) appears (Fig. 2, lower panels). The introduction of a weaker reference base, 3-hydroxypyridine (GB = 897.7 kJ mol⁻¹),¹⁵ did not result in strong depletion of [M + H]⁺ (Fig. 2a–b). In contrast (Fig. 2c–d), the signal of [M + H]⁺ almost vanished in the presence of a stronger reference base, 4-ethylpyridine (GB = 915.5 kJ mol⁻¹).¹⁵ ESSI-MS experiments were highly reproducible, showing essentially no carry-over effects (Fig. 2b–d), and sufficient baseline stability (Fig. 2a–c). A similar behavior was found for all the compounds studied.

Fig. 2 Ion current traces of the protonated αCHCA ion [M + H]⁺ (a, c) upon introduction of reference bases: 3-hydroxypyridine (a–b) and 4-ethylpyridine (c–d). Selected ion chromatograms of the respective protonated reference bases are also shown (b, d).

To access the gas-phase thermochemical properties of a compound the following prerequisite should be fulfilled: the reaction should take place in the gas phase under conditions of chemical and thermal equilibrium. Recently, Chingin et al.⁶³ showed that abundant gas-phase ions can be produced by ESI and ESSI at atmospheric pressure, before entering the mass spectrometer. ESSI,³⁷ where a high nebulizing gas pressure (up to 20 bars) is used, provides a higher degree of desolvation compared to the conventional ESI, such that gas-phase reactions occurring in the ESSI plume can be easily accessed at ambient conditions. Additionally, ESSI allows the placement of the spray emitter far enough (10 to 20 cm) from the mass spectrometer inlet, so that gas-phase ions generated at the very beginning of the ESSI plume travel through the ambient background for a few hundred μs.³⁶ According to ref. 64 and references therein, a minimum of 10 collisions are needed to equilibrate individual molecules. Under the experimental conditions used, the ions are estimated⁶⁵ to undergo approximately 10⁵ collisions, which is more than sufficient to ensure equilibration of the system. Reference bases will reach high concentration in the gas phase and quickly saturate the plume volume thanks to their high volatility and uniform distribution of the test tubes along the ESSI path. Moreover, the reference bases were selected based on their structure in order to minimize the difference in the steric factor of reaction: different substituted analogs of pyridine and aniline were used throughout the study (Table 1). We can therefore assume with a high degree of confidence that our setup fulfils all the requirements for studying the gas-phase proton-transfer reactions and the data provides us with the true GB value.

Table 1 Gas-phase basicity of reference bases¹⁵

Reference base	Gas-phase basicity/kJ mol^−1	Reference base	Gas-phase basicity/kJ mol^−1
p-chloroaniline	842.0	pyridine	898.1
aniline	850.6	2-methoxypyridine	902.8
o-toluidine	859.1	4-phenylpyridine	907.8
1,2-benzenediamine	865.8	3-picoline-N-oxide	910.9
3-hydroxyaniline	866.9	4-methylpyridine	915.3
p-anisidine	868.5	4-ethylpyridine	915.5
2,6-dimathylaniline	869.8	2-methylpyridine	917.3
o-anisidine	873.3	2-ethylpyridine	920.6
2-chloro-4-picoline	889.4	3,4-dimethylpyridine	925.5
3-hydroxypyridine	897.7

---

The extent of [M + H]⁺ deprotonation by the various reference bases was evaluated based on the ratio of [M + H]⁺ signal intensity in the presence and in the absence of a reference base. The relative intensities of [M + H]⁺ were plotted against the GB values of the reference bases and fitted by the two-parametric sigmoidal function (Fig. 3). Typically, five to six measured data points, together with two manually added ones (1 for the low GB and 0 for the high GB) were used for fitting. The X-coordinate of the point on the fitted sigmoidal function where the increase in deprotonation rate reached its maximum was taken as the GB of a MALDI matrix. The determined GB values are summarized in Table 2.

Fig. 3 Sigmoid fit of the [M + H]⁺ ion relative signal intensity versus the GB of reference bases plotted for (a) αCHCA, (b) FA, (c) HPA, (d) SA, and (e) THAP. Two data points with the relative signal intensity equal to one and to zero for the low and high GB values, respectively, were added manually to simplify the fitting procedure. The 95% confidence interval for sigmoid curve is shown as dotted lines. The MALDI matrix's GB was determined as the point where the change of deprotonation rate was maximal (shown with the dashed arrow).

Table 2 Gas-phase basicity of MALDI matrices

MALDI matrix	GB, kJ mol^−1
	literature	calculated			experimental
		G4MP2	B3LYP/6-311+G*
aCHCA	900 ± 8.5;^66 826.2^68	815.6	831.0		908.1	±	0.8
FA	862.4^67	861.5	862.6		863.8	±	8.0
HPA		885.4	871.2		876.3	±	10.2
SA	860.5 ± 11.5;^66 869.0^67	845.1	866.6		867.4	±	1.4
THAP		846.0	866.6		864.2	±	7.6
HQA		918.0	924.3		908.1	±	0.8

---

In all cases, the measured data points followed a clear trend, allowing for a fitting with sufficiently high correlation to the model equation (R² > 0.9350). This allowed for quite accurate determination of the value corresponding to GB of a compound. As can clearly be seen from Table 2, the uncertainty of GB determination was close to or better than the chemical accuracy (± 1 kcal mol⁻¹ or ± 4.18 kJ mol⁻¹). The determined GB values were in an excellent agreement with some of previously published ones for SA, FA and αCHCA.^66,67 For the other two compounds, the GB was determined for the first time.

It is noteworthy to point out that the deprotonation of MALDI matrix ions occurred as a single sharp transition within the narrow window of GB of the reference bases (Fig. 3), which is expected for small molecules with a single proton-binding site. In comparison, the deprotonation rates reported earlier in analogous studies of peptide and protein ions were lower, possibly due to the multiplicity of available protonation sites and a large number of possible conformations.^35,36

Comparison of measured GBs to calculations

Here, we employed DFT-based methods and one of the so-called compound methods, G4MP2,⁶¹ to theoretically predict the GBs of the MALDI matrices studied. GBs were calculated based on the difference in energy of the neutral and the protonated form of a molecule. The MALDI matrices studied here allow for several possible protonation sites, which may differ in energy. Thus, selecting a wrong protonated structure for calculation would result in an erroneous GB. For this reason, we performed a careful selection of the protonated structures for GB calculations. Geometries of alternative protonated forms of every MALDI matrix were first optimized using the DFT method and the resulting structures were then compared in energy. The most stable forms, having the lowest energy, were used further for high-level DFT and G4MP2-based calculations of the thermochemical parameters. This approach is consistent with the requirement of the system being at chemical and thermodynamic equilibrium. We can therefore exclude alternative protonated structures as a source of error in quantum chemical calculations.

When the DFT-calculated values were compared to the measured GBs an excellent agreement was found for four of the studied compounds, with the exception of αCHCA where the experimentally measured GB appeared to be higher by 77 kJ mol⁻¹ than the calculated one (Table 2, Fig. 4). The calculated values were in equally good agreement with the previously published GB values for FA and SA (Table 2). A very similar result was obtained in G4MP2 calculations (Table 2, Fig. 4). Surprisingly, the agreement between the G4MP2 results and the experiment was worse for the DFT calculations, even though G4MP2 was specifically designed for calculations of thermochemical parameters, such as the enthalpy of formation or the PA, and was reported to have a very high accuracy (higher accuracy compared to DFT methods).⁶¹ However, computational prediction of the GBs involves calculation of entropy based on predicted harmonic vibrational frequencies. In G4MP2, geometry optimization and calculation of harmonic frequencies is done using a double-ζ basis set compared to a triple-ζ we utilized in the DFT-based calculations here: B3LYP/6-31G(2df,p) vs. B3LYP/6-311+G(d,p), respectively.⁶¹ We can therefore attribute the overall poorer agreement of G4MP2 results with the experimental data to the lower accuracy of the entropy calculations.

Fig. 4 Correlation plot showing the agreement between the experimental and calculated values of the GB of MALDI matrices studied. Error bars represent 95% confidence intervals for the experimental values. The unit correlation line is shown with the chemical accuracy (± 4.18 kJ mol⁻¹).

Remarkably, the GB value predicted for αCHCA by calculations in the current work matched very well to one of the previously published numbers that was also derived from quantum chemical calculations,⁶⁸ while the other experimentally determined value available from the literature was very close to the GB measured by our approach.⁶⁶ Such a pronounced discrepancy between the calculated and experimentally measured value of GB of αCHCA cannot be simply attributed to experimental errors or inaccuracy of the quantum chemical methods. We hypothesized that a structural rearrangement of αCHCA would lead to the formation of an isomer that is more stable and a stronger base. The most probable structure that would satisfy the criteria is a heterocyclic aromatic isomer of αCHCA, 7-hydroxyquinoline-3-carboxylic acid (HQA; Scheme 2). The energy of aromatization drives the formation of the second condensed heterocyclic ring and makes HQA thermodynamically more stable than αCHCA by approximately 80 kJ mol⁻¹, according to quantum chemical calculations. HQA should also be a much stronger base than αCHCA, since the nitrogen atom in the quinoline core presents a more favorable protonation site. The GB of unsubstituted quinoline equals 921.4 kJ mol⁻¹, as reported in the NIST Ion Thermochemistry database.¹⁵ Very similar rearrangement pathways involving decarboxylation and cyclization of αCHCA were recently described by Tarzi et al.⁶⁹ and further support our hypothesis. Finally, we ran calculations to predict the GB of HQA and obtained values which are much closer to those measured in experiment with αCHCA (Table 2, Fig. 4): 924.3 (DFT) and 918.0 (G4MP2) kJ mol⁻¹vs. 908.1 ± 0.8 kJ mol⁻¹ in the experiment. We attribute the residual differences between the experimental data and calculated values to the generic imperfection of quantum chemical methods for the determination of the Gibbs free energy originating from the low accuracy of the entropy term calculation due to the use of RRHO approximation. This shortcoming restricts the applicability of quantum chemical calculations for accurate determination of thermochemical values in reasonable-size systems to prediction of PAs only.

Scheme 2 Gas-phase rearrangement of αCHCA to protonated 7-hydroxyquinoline-3-carboxylic acid (HQA).

With the proposed gas-phase rearrangement of αCHCA to HQA, we can eliminate the outlier in the correlation plot in Fig. 4 and bring all the points very close to the unit correlation line. The validity of the suggested hypothesis should certainly be further tested using the state-of-the-art experimental techniques such as ion mobility spectrometry^70–73 and gas-phase ion spectroscopy.^74–78 Nevertheless, the formation of HQA in MALDI and its influence on ion formation is most probably negligible due to its much shorter timescale.

Conclusions

In the present study of several commonly used MALDI matrices, we successfully demonstrated the applicability of our simple ESSI mass spectrometry-based approach for the rapid and precise measurement of the GB of small molecules. The accuracy of GB determination was very high, close to or at the level of the chemical accuracy of ± 1 kcal mol⁻¹ (± 4.18 kJ mol⁻¹). Our results extended the set of measured GBs to two more MALDI matrices, THAP and HPA.

The method showed an excellent agreement of results with the previously reported values for αCHCA, SA, and FA. A reasonable agreement between the experimental data and results of complimentary quantum chemical calculations was achieved. B3LYP/6-311+G(d,p) showed better agreement with the experimental data than G4MP2, probably, due to more accurate calculation of entropy. The only pronounced difference between the calculated and measured GB was found for αCHCA, which had the predicted GB by approximately 80 kJ mol⁻¹ lower that the experimental value. Notably, the analysis of previously published literature revealed a very similar discrepancy between the computationally and experimentally determined GB of αCHCA. We hypothesize a gas-phase isomerization of αCHCA to HQA that is thermodynamically more stable and has a higher GB. The calculated GB of HQA is much closer to the value measured in the experiment. The proposed rearrangement of αCHCA to HQA resolves the disagreement between the measured and predicted GB of αCHCA. However, the relevance of the proposed gas-phase rearrangement reaction to the processes actually taking place in the MALDI plume remains questionable due to a great difference in the timescale.

Notably, our simple experimental approach and quantum chemistry methods complement each other and allow for reciprocal compensation of their inabilities: while GB can be easily accessed in experiment, the more demanding measurement of PA can be substituted with theoretical prediction. Moreover, the data that can be generated by this combined approach may serve for further optimization of modern quantum chemistry methods for thermochemical calculations.

Acknowledgements

The work was financially supported by the Swiss National Science foundation (grant no. 200020-124663) and by a Novartis Doctoral fellowship to KB. Quantum chemical calculations were performed on the Obelix cluster at the Competence Center for Computational Chemistry, ETH Zurich, and the Brutus cluster, ETH Zurich. We also thank Dr A. Fedorov for fruitful discussions of the manuscript.

References

1. M. Y. Okamura and G. Feher, Annu. Rev. Biochem., 1992, 61, 861–896.
2. T. Friedrich, K. Steinmuller and H. Weiss, FEBS Lett., 1995, 367, 107–111.
3. J. F. Allen, Cell, 2002, 110, 273–276.
4. T. J. Meyer, M. H. V. Huynh and H. H. Thorp, Angew. Chem., Int. Ed., 2007, 46, 5284–5304.
5. G. Renger, Biochim. Biophys. Acta, Bioenerg., 2004, 1655, 195–204.
6. G. T. Babcock and M. Wikstrom, Nature, 1992, 356, 301–309.
7. P. D. Boyer, Annu. Rev. Biochem., 1997, 66, 717–749.
8. B. E. Schultz and S. I. Chan, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 23–65.
9. M. Eigen, Angew. Chem., Int. Ed. Engl., 1964, 3, 1–19.
10. W. P. Jencks, Chem. Rev., 1972, 72, 705–718.
11. J. Kraut, Annu. Rev. Biochem., 1977, 46, 331–358.
12. D. B. Northrop, Acc. Chem. Res., 2001, 34, 790–797.
13. L. Hedstrom, Chem. Rev., 2002, 102, 4501–4523.
14. S. G. Lias, J. F. Liebman and R. D. Levin, J. Phys. Chem. Ref. Data, 1984, 13, 695–808.
15. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
16. T. B. McMahon and P. Kebarle, Can. J. Chem., 1985, 63, 3160–3167.
17. J. E. Szulejko and T. B. McMahon, Int. J. Mass Spectrom. Ion Processes, 1991, 109, 279–294.
18. R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2007, 129, 569–580.
19. S. A. McLuckey, D. Cameron and R. G. Cooks, J. Am. Chem. Soc., 1981, 103, 1313–1317.
20. R. G. Cooks, J. S. Patrick, T. Kotiaho and S. A. McLuckey, Mass Spectrom. Rev., 1994, 13, 287–339.
21. R. M. Moision and P. B. Armentrout, J. Am. Soc. Mass Spectrom., 2007, 18, 1124–1134.
22. S. H. Hoke, S. S. Yang, R. G. Cooks, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 1994, 116, 4888–4892.
23. J. C. Mathurin, T. Faye, A. Brunet and J. C. Tabet, Anal. Chem., 2000, 72, 5055–5062.
24. O. E. Schroeder, E. J. Andriole, K. L. Carver, K. E. Colyer and J. C. Poutsma, J. Phys. Chem. A, 2004, 108, 326–332.
25. K. A. Schug, W. Lindner and K. Lemr, J. Am. Soc. Mass Spectrom., 2004, 15, 840–847.
26. A. Likholyot, J. K. Hovey and T. M. Seward, Int. J. Mass Spectrom., 2005, 243, 49–62.
27. P. Kebarle, Annu. Rev. Phys. Chem., 1977, 28, 445–476.
28. I. Y. Zhang and X. Xu, Int. Rev. Phys. Chem., 2011, 30, 115–160.
29. M. S. Schuurman, S. R. Muir, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2004, 120, 11586–11599.
30. T. Helgaker, W. Klopper and D. P. Tew, Mol. Phys., 2008, 106, 2107–2143.
31. A. Karton, A. Tarnopolsky, J.-F. Lamere, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886.
32. G. Czako, B. Nagy, G. Tasi, A. Somogyi, J. Simunek, J. Noga, B. J. Braams, J. M. Bowman and A. G. Csaszar, Int. J. Quantum Chem., 2009, 109, 2393–2409.
33. A. Karton, S. Parthiban and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 4802–4816.
34. F. Neese, T. Schwabe, S. Kossmann, B. Schirmer and S. Grimme, J. Chem. Theory Comput., 2009, 5, 3060–3073.
35. D. Touboul, M. C. Jecklin and R. Zenobi, J. Phys. Chem. B, 2007, 111, 11629–11631.
36. D. Touboul, M. C. Jecklin and R. Zenobi, J. Am. Soc. Mass Spectrom., 2008, 19, 455–466.
37. Z. Takats, J. M. Wiseman, B. Gologan and R. G. Cooks, Anal. Chem., 2004, 76, 4050–4058.
38. R. Zenobi and R. Knochenmuss, Mass Spectrom. Rev., 1998, 17, 337–366.
39. R. Knochenmuss, A. Stortelder, K. Breuker and R. Zenobi, J. Mass Spectrom., 2000, 35, 1237–1245.
40. R. Knochenmuss and R. Zenobi, Chem. Rev., 2003, 103, 441–452.
41. F. Hillenkamp, E. Waefler, M. C. Jecklin and R. Zenobi, Int. J. Mass Spectrom., 2009, 285, 114–119.
42. M. Karas, M. Gluckmann and J. Schafer, J. Mass Spectrom., 2000, 35, 1–12.
43. M. Karas and R. Kruger, Chem. Rev., 2003, 103, 427–439.
44. R. Knochenmuss, Analyst, 2006, 131, 966–986.
45. T. W. Jaskolla and M. Karas, J. Am. Soc. Mass Spectrom., 2011, 22, 976–988.
46. T. W. Jaskolla, W.-D. Lehmann and M. Karas, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12200–12205.
47. C. Yang, X. Hu, A. V. Loboda and R. H. Lipson, J. Am. Soc. Mass Spectrom., 2011, 21, 294–299.
48. T. Meyer, M. Kunkel, A. W. Frahm and D. Waidelich, J. Am. Soc. Mass Spectrom., 2001, 12, 911–925.
49. S. Laugesen and P. Roepstorff, J. Am. Soc. Mass Spectrom., 2003, 14, 992–1002.
50. F. H. Song, Rapid Commun. Mass Spectrom., 2003, 17, 1802–1807.
51. S. P. Mirza, N. P. Raju, S. S. Madhavendra and M. Vairamani, Rapid Commun. Mass Spectrom., 2004, 18, 1666–1674.
52. M. R. Kumar, N. P. Raju, T. J. Reddy, A. Narahari, M. J. R. Reddy and M. Vairamani, Rapid Commun. Mass Spectrom., 2005, 19, 3171–3174.
53. M. A. R. Meier, N. Adams and U. S. Schubert, Anal. Chem., 2007, 79, 863–869.
54. P. D. Schnier, D. S. Gross and E. R. Williams, J. Am. Chem. Soc., 1995, 117, 6747–6757.
55. N. P. Ewing, G. A. Pallante, X. Zhang and C. J. Cassady, J. Mass Spectrom., 2001, 36, 875–881.
56. G. Bouchoux, J. Y. Salpin and D. Leblanc, Int. J. Mass Spectrom. Ion Processes, 1996, 153, 37–48.
57. J. Wu and C. B. Lebrilla, J. Am. Chem. Soc., 1993, 115, 3270–3275.
58. J. Wu and C. Lebrilla, J. Am. Soc. Mass Spectrom., 1995, 6, 91–101.
59. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, A. Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, 2003.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09 and Revision A.02, in Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, Wallingford CT, 2009.
61. L. A. Curtiss, P. C. Redfern and K. Raghavachari, Journal of Chemical Physics, 2007, 127 article number 124105.
62. L. A. Curtiss, P. C. Redfern and K. Raghavachari, Journal of Chemical Physics, 2007, 126, arcticle number, 084108.
63. K. Chingin, V. Frankevich, R. M. Balabin, K. Barylyuk, H. W. Chen, R. Wang and R. Zenobi, Angewandte Chemie-International Edition, 2010, 49, 2358–2361.
64. G. Tejeda, B. Mate, J. M. Fernandez Sanchez and S. Montero, Phys. Rev. Lett., 1996, 76, 34–37.
65. B. R. Eichelberger, T. P. Snow and V. M. Bierbaum, J. Am. Soc. Mass Spectrom., 2003, 14, 501–505.
66. R. Steenvoorden, K. Breuker and R. Zenobi, Eur. J. Mass Spectrom., 1997, 3, 339–346.
67. F. H. Yassin and D. S. Marynick, THEOCHEM, 2006, 766, 137–141.
68. G. R. Kinsel, D. Q. Yao, F. H. Yassin and D. S. Marynick, Eur. J. Mass Spectrom., 2006, 12, 359–367.
69. O. I. Tarzi, H. Nonami and R. Erra-Balsells, J. Mass Spectrom., 2009, 44, 260–277.
70. P. Dwivedi, C. Wu, L. M. Matz, B. H. Clowers, W. F. Siems and H. H. Hill, Anal. Chem., 2006, 78, 8200–8206.
71. P. Martinez-Lozano and J. Rus, J. Am. Soc. Mass Spectrom., 2010, 21, 1129–1132.
72. T. W. Knapman, J. T. Berryman, I. Campuzano, S. A. Harris and A. E. Ashcroft, Int. J. Mass Spectrom., 2010, 298, 17–23.
73. A. B. Kanu, P. Dwivedi, M. Tam, L. Matz and H. H. Hill, J. Mass Spectrom., 2008, 43, 1–22.
74. J. S. Prell, T. M. Chang, J. A. Biles, G. Berden, J. Oomens and E. R. Williams, J. Phys. Chem. A, 2011, 115, 2745–2751.
75. A. Lagutschenkov, J. Langer, G. Berden, J. Oomens and O. Dopfer, Phys. Chem. Chem. Phys., 2011, 13, 2815–2823.
76. A. Lagutschenkov, J. Langer, G. Berden, J. Oomens and O. Dopfer, Phys. Chem. Chem. Phys., 2011, 13, 15644–15656.
77. A. Lagutschenkov, J. Langer, G. Berden, J. Oomens and O. Dopfer, J. Phys. Chem. A, 2010, 114, 13268–13276.
78. R. Wu and T. B. McMahon, ChemPhysChem, 2008, 9, 2826–2835.
79. B. O. Keller, J. Suj, A. B. Young and R. M. Whittal, Anal. Chim. Acta, 2008, 627, 71–81.

---