Quantum-chemical embedding methods for treating local electronic excitations in complex chemical systems
André
Severo Pereira Gomes
*a and
Christoph R.
Jacob
*b
aUniversité de Lille 1, Laboratoire PhLAM, CNRS UMR 8532, Bat P5, 59655 Villeneuve d’Ascq Cedex, France. E-mail: andre.gomes@univ-lille1.fr
bKarlsruhe Institute of Technology (KIT), Center for Functional Nanostructures, Wolfgang-Gaede-Str. 1a, 76131 Karlsruhe, Germany. E-mail: christoph.jacob@kit.edu
First published on 3rd April 2012
Abstract
Quantum chemistry has become an invaluable tool for studying the electronic excitation phenomena underlying many important chemical, biological, and technological processes. Here, we review quantum-chemical approaches for modeling such phenomena. In particular, embedding methods can be particularly useful for treating localized excitations in complex chemical systems. These split the total system into a number of interacting subsystems. The electronic excitations processes occurring in the subsystem of interest are then treated with high accuracy, while its environment is taken into account in a more approximate way. In this review, we use a formulation based on the formally exact frozen-density embedding theory as our starting point. This provides a common framework for discussing the different embedding approaches that are currently available. Moreover, it also forms the basis of emerging methods that allow for a seamless coupling of density-functional theory and wavefunction based approaches, both for ground and excited states. These provide new possibilities for studying electronic excitations in large systems with predictive quantum-chemical methods.
1 Introduction
Processes involving excited electronic states are crucial for many functions of biological or chemical systems. Examples include light absorption and energy transfer in photosynthetic proteins1 or photovoltatic devices2,3 as well as light emission from luminescent proteins4 or from organic materials.5 Over the past years, quantum chemistry has made significant progress in unraveling the underlying electronic processes (see, e.g., ref. 4, 6). This includes the emergence of accurate and efficient computational methods for the treatment of excited states as well as the development of embedding and subsystem approaches that make an application of these quantum-chemical methods to complex systems possible (for reviews, see, e.g., ref. 7–9). In particular, subsystem and embedding methods that allow for a seamless coupling of different quantum chemical methods have recently become available.10–12 These open the way to a theoretical design of functional materials and chemical systems in the future.A quantum-chemical description of electronic excitations requires methods that are capable of describing both ground and excited states with similar accuracy. Such methods have been developed extensively over the past decades (for reviews, see, e.g., ref. 13–15). While time-dependent density-functional theory (TDDFT) offers a good cost–accuracy ratio and is applicable to rather large molecular systems with up to a few hundreds of atoms, it is also prone to unsystematic errors. On the other hand, wavefunction theory (WFT) based methods for excited states offer the potential for a systematic improvement, but their applicability is usually limited to rather small molecules. Thus, for isolated small molecules (e.g., in gas-phase experiments), they can often provide very accurate predictions. Nevertheless, in difficult cases already for medium-sized molecules with only 10–20 atoms it can be impossible to obtain sufficiently accurate predictions (for an example, see ref. 16, and for a review highlighting some of the current challenges of quantum-chemical methods for excited states, see ref. 15).
It is therefore not surprising that the treatment of electronic excitations in even larger and more complex chemical systems presents a significant challenge for computational chemistry. Examples of such large systems are molecules in the condensed phase (i.e., solvated molecules or molecular materials), biomolecules or biomolecular assemblies, molecular nanostructures (e.g., metal organic frameworks or assemblies of molecular clusters), or complex solid-state system such as impurities in materials as well as molecules adsorbed on surfaces.
Such large systems present several challenges: First, the need to control the computational cost of quantum-chemical calculations, since these increase with the size of the system at a much faster rate than that of the availability of computer resources. This is partially addressed by the development of efficient (linear-scaling) algorithms and their implementation in modern program packages. These efforts are, however, offset by the need to account for dynamical effects, as is often mandatory for large systems. In particular for molecules in solution and for biological systems, it will be necessary to account for the structural flexibility by considering many different molecular structures. Second, even if calculations on rather large systems are possible, the choice of quantum-chemical methods is severely restricted. Often, approximate DFT calculations are the only available option and it is not possible to improve the description by applying more accurate wavefunction based methods. Finally, quantum-chemical calculations on large systems are also difficult to interpret. Usually, a very delocalized picture is obtained that makes it difficult to identify the important aspects.17,18 In particular when local electronic excitation are of interest, these can be difficult to isolate among the many excited states of a large system. On the other hand, even delocalized excitation phenomena are best understood within a local picture.8
Already due to the increased computational cost, a full treatment of the complete system is in most cases out of reach for the calculation of excitation energies. However, many electronic excitations are local, i.e., the change in the electronic structure upon excitation is mainly restricted to a comparably small part of the full system—for instance, a particular molecule in a complex environment, a particular chromophore in a bimolecular system, or an impurity in a solid. Under these circumstances, it is possible to apply additional simplifications and drastically reduce the total computational cost while retaining accuracy for the subsystem of interest. This is the goal of embedding methods, which restrict the explicit treatment to a small subsystem of interest while approximating that of its environment, effectively extending the applicability of accurate quantum chemical methods from small isolated molecules to complex chemical systems. At the same time, such a treatment simplifies the interpretation of the computational results considerably.
Our aim here is to highlight some of the currently available quantum chemical embedding approaches, with a particular focus on their application for describing local electronic excitations. The review is organized as follows: First, we give an overview of quantum-chemical methods for the treatment of excited states in section 2. Subsequently, embedding methods in quantum chemistry will be introduced. To this end, we outline an exact theoretical framework for quantum-chemical embedding methods, the frozen-density embedding (FDE) theory in section 3, before presenting an attempt of a classification and an overview of a variety of approximate embedding methods in section 4. Finally, we discuss two case studies for comparing some of these approaches in section 5.
2 Quantum chemistry for excited states
For predicting excitation energies, quantum-chemical methods that can treat both the ground-state and excited states are necessary. Here, we will provide an overview of the most important theoretical approaches. These can be divided into two groups that tackle the problem from two formally equivalent, but conceptually very different directions.First, time-independent approaches take the stationary Schrödinger equation,
| Ĥ|Ψk〉 = Ek|Ψk〉, | (1) |
On the other hand, time-dependent approaches start from a stationary ground-state wavefunction |Ψ0〉 and consider the time evolution of this initial state after switching on a time-dependent external perturbation. Here, we will only consider an oscillating electric dipole perturbation with frequency ω, i.e.,
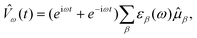 | (2) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β is the β-component (β = x,y,z) of the time-independent electric dipole operator and εβ(ω) denotes the associated perturbation strength. The time evolution of the wavefunction could be obtained by solving the time-dependent Schrödinger equation
β is the β-component (β = x,y,z) of the time-independent electric dipole operator and εβ(ω) denotes the associated perturbation strength. The time evolution of the wavefunction could be obtained by solving the time-dependent Schrödinger equation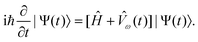 | (3) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α, expressed as a series expansion,
α, expressed as a series expansion,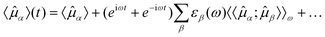 | (4) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α〉 is the time-independent expectation value and 〈〈
α〉 is the time-independent expectation value and 〈〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α;
α;![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β〉〉ω is the linear electric dipole–electric dipole response function describing the oscillations of the α-component of the dipole moment in response to an oscillating electric dipole field in β-direction. To first order, only oscillations with frequency ω appear in this expansion. Terms involving higher-order response functions have been omitted here, and we refer the reader to the thorough derivations of higher-order response theory available in the literature.19
β〉〉ω is the linear electric dipole–electric dipole response function describing the oscillations of the α-component of the dipole moment in response to an oscillating electric dipole field in β-direction. To first order, only oscillations with frequency ω appear in this expansion. Terms involving higher-order response functions have been omitted here, and we refer the reader to the thorough derivations of higher-order response theory available in the literature.19
Within an exact treatment based on time-dependent perturbation theory (see, e.g., ref. 20) the linear response function is given by the sum-over-states expression
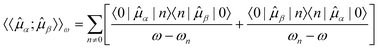 | (5) |
The sum-over-states expression for the linear response function would require the solution of the time-independent Schrödinger equation for all excited states. However, when combined with approximate parametrizations of the many-electron wave-function it becomes possible to determine the linear response function directly by solving a linear system of equations, thus avoiding the explicit calculation of excited state wavefunctions.19,21 Such a response theory can, for instance, be obtained by using the quasienergy formalism, which will be outlined in section 2.2. Subsequently, excitation energies can be determined by identifying the poles of the linear response function.
While for an exact treatment, time-independent approaches (which construct a wavefunction for each excited state explicitly) and time-dependent approaches based on response theory (which avoid the calculation of excited state wavefunctions) are equivalent, this is usually not the case anymore for approximate quantum-chemical methods. Both time-independent and time-dependent approaches are widely used for the quantum chemical calculation of excitation energies, and some of the most important methods will be highlighted in the following.
2.1 Time-independent approaches
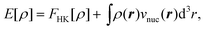 | (6) |
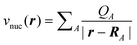 is the Coulomb potential of the nuclei at positions RA and with the charges QA. Furthermore, the Hohenberg–Kohn theorem provides a variational principle for calculating the ground-state energy E0 and the corresponding ground-state electron density ρ0 by minimizing this energy functional, i.e., E0=minρE[ρ].
is the Coulomb potential of the nuclei at positions RA and with the charges QA. Furthermore, the Hohenberg–Kohn theorem provides a variational principle for calculating the ground-state energy E0 and the corresponding ground-state electron density ρ0 by minimizing this energy functional, i.e., E0=minρE[ρ].
In Kohn–Sham (KS) DFT,23 the energy functional is decomposed as,
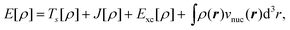 | (7) |
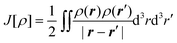 is the classical Coulomb interaction of the electron density with itself, and the exchange–correlation functional Exc[ρ] collects all the remaining energy terms. This energy functional is then minimized by introducing a wavefunction for the reference system of noninteracting electrons, which is given by a single Slater determinant |Φs〉 built from the orbitals {ϕi}. These Kohn–Sham orbitals can then be determined by solving the KS equations,
is the classical Coulomb interaction of the electron density with itself, and the exchange–correlation functional Exc[ρ] collects all the remaining energy terms. This energy functional is then minimized by introducing a wavefunction for the reference system of noninteracting electrons, which is given by a single Slater determinant |Φs〉 built from the orbitals {ϕi}. These Kohn–Sham orbitals can then be determined by solving the KS equations,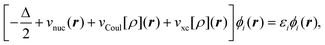 | (8) |
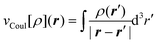 is the classical Coulomb potential of the electrons and
is the classical Coulomb potential of the electrons and 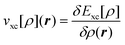 is the exchange–correlation potential. Since these potentials both depend on the electron density, the KS equations have to be solved in self-consistent field (SCF) iterations. Even though KS-DFT provides a formally exact theory for calculating the ground-state density, the exact exchange–correlation functional is not know and approximate functionals have to be introduced. For overviews of the currently available approximate functionals, see, e.g., ref. 24–26, and for a discussion of their limitations, see, e.g., ref. 27 and 28.
is the exchange–correlation potential. Since these potentials both depend on the electron density, the KS equations have to be solved in self-consistent field (SCF) iterations. Even though KS-DFT provides a formally exact theory for calculating the ground-state density, the exact exchange–correlation functional is not know and approximate functionals have to be introduced. For overviews of the currently available approximate functionals, see, e.g., ref. 24–26, and for a discussion of their limitations, see, e.g., ref. 27 and 28.
Even though the Hohenberg–Kohn theorem was initially formulated only for the ground state, it can easily be extended to the lowest state in each spin or spacial symmetry.29,30 However, in this case the Hohenberg–Kohn functional FHK[ρ] is no longer universal, but becomes symmetry-specific. In practice, this symmetry-specific functional is unknown, and one usually resorts to impose the symmetry constraints on the noninteracting reference system, i.e., the Slater determinant formed from the KS orbitals. Note, however, that in the exact theory neither the spin nor the spatial symmetry of the wavefunction of this reference system correspond to the one of the true wavefunction.31
Despite the lack of a formal justification,32 excited states have been targeted in variational KS-DFT calculations by employing excited-state wavefunctions for the noninteracting reference system. In the simplest case, this corresponds to replacing an occupied KS orbital by an unoccupied one (i.e., a non-Aufbau solution), but it might also be necessary to form linear combinations of different Slater determinants for specific states.33 In particular, this ΔDFT approach has been applied to study multiplet energies in transition metal complexes with DFT.34 This approach can be extended to a ΔSCF-DFT scheme, in which the orbitals of the excited Slater determinants constructed for the noninteracting reference system are re-optimized.35 In this case, it has to be ensured that the SCF procedure does not collapse to the ground-state.36
For the calculation of excitation energies with DFT, the application of such ΔSCF-DFT calculations has been rather limited. Usually, time-dependent DFT (discussed in section 2.2.1) provides more accurate results and avoids the rather cumbersome optimization of the KS orbitals of excited Slater determinants. There is a revived interest in the use ΔSCF-DFT and related methods for overcoming some of the limitations of TDDFT, such as for the description of Rydberg states37 or of large conjugated organic molecules.38 An interesting related approach is the constricted variational DFT method by Ziegler and coworkers,39,40 that is based on the determination of stationary points of the energy functional, subject to the condition that the density difference corresponds to an electronic excitation. Both ΔSCF-DFT and TDDFT emerge from this formulation.
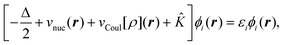 | (9) |
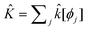 with
with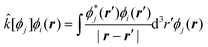 | (10) |
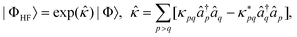 | (11) |
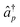 and âq are the operators creating or annihilating an electron in orbital p or q, respectively. The advantage of this parametrization is that it introduces only non-redundant parameters by ensuring the orthogonality of the HF orbitals. Therefore, the parameters κpq can be determined from an unconstrained optimization of the HF energy.
and âq are the operators creating or annihilating an electron in orbital p or q, respectively. The advantage of this parametrization is that it introduces only non-redundant parameters by ensuring the orthogonality of the HF orbitals. Therefore, the parameters κpq can be determined from an unconstrained optimization of the HF energy.
Electron correlation can then be included by employing a more general ansatz for the wavefunction that also includes excited Slater determinants, i.e., determinants in which one or more of the occupied HF orbitals are replaced by virtual ones. In configuration interaction (CI) methods,42 the many-electron wavefunction |Ψk〉 for a given electron state k is expanded in a basis of Slater determinants as
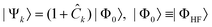 | (12) |
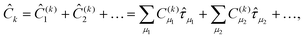 | (13) |
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) μ of different ranks. Here, μ1 and μ2 represent single and double excitations from occupied to virtual orbitals, and the corresponding excitation operators are
μ of different ranks. Here, μ1 and μ2 represent single and double excitations from occupied to virtual orbitals, and the corresponding excitation operators are 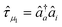 and
and 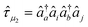 , where indices i,j,k,… refer to occupied orbitals whereas indices a,b,c,… label virtual orbitals. Note that the coefficients C(k)μ are different for each electronic state k.
, where indices i,j,k,… refer to occupied orbitals whereas indices a,b,c,… label virtual orbitals. Note that the coefficients C(k)μ are different for each electronic state k.
The coefficients Cμ can then be determined using the variational principle, i.e., by minimizing the energy with respect to these coefficients. This leads to the Hamiltonian matrix in the basis of the HF and excited determinants,
| Hij = 〈Ψi|Ĥ|Ψj〉 | (14) |
While in single-reference CI methods the HF determinant is used as reference state |Φ0〉, this is a poor choice in situations where there are other close-lying excited states. This is often the case in open-shell systems such as transition metal complexes. One is then better served by multi-reference configuration interaction (MR-CI) methods, which use a reference based on a multi-configurational (MC) wavefunction,
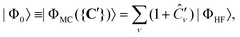 | (15) |
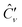 instead of Ĉν. There are different approaches for generating the determinants in eqn (15), the most widely used is the complete active space (CAS), where a full CI is performed within the active space.
instead of Ĉν. There are different approaches for generating the determinants in eqn (15), the most widely used is the complete active space (CAS), where a full CI is performed within the active space.
A further improvement consists in taking the orbital coefficients κpq as additional variational parameters,
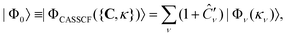 | (16) |
Irrespective of the construction of the reference wavefunction and even when the (MR)-CI expansion is truncated at the SD level, calculations on all but relatively small molecules remain computationally infeasible. This has motivated the development of specialized approximations where the size of the CI expansions is reduced by removing of certain classes of excitation on the basis of physical arguments. One such approach is the difference-dedicated CI (DDCI), where configurations that contribute in approximately the same way to both the ground and excited states (e.g., determinants that are doubly excited with respect to inactive orbitals) are disregarded. This way, energy differences between the states can still be determined accurately, whereas total energies are in general rather inaccurate. In its different flavors,53–55 DDCI has been extensively used for determining the different spin states in relatively large molecules containing one or more magnetic centers,56–58 as well as the electronic spectra of transition metal complexes.59,60
Finally, it is also worth mentioning that—unlike full CI—all truncated CI methods (with the exception of CIS) are not size-extensive. Thus, upon extending the size of the system a spurious decrease in the correlation energy occurs. As a result, excitation energies are not size-intensive, i.e., they can spuriously change as the size of the system is increased (e.g., when studying the effect of the solvation shell on the spectrum of a solute molecule), which may even change the results qualitatively. This can be approximately corrected by using suitable correction schemes,61 but a more rigorous way for achieving size-extensivity of the correlation energy and size-intensivity of excitation energies is provided by coupled-cluster methods, that will be discussed in the following section.
|Ψ0〉 = exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉 )|ΦHF〉 | (17) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is of the same form as the excitation operator Ĉk in CI methods, but different labels are now used for the expansion coefficients to distinguish these different methods,
is of the same form as the excitation operator Ĉk in CI methods, but different labels are now used for the expansion coefficients to distinguish these different methods,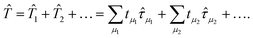 | (18) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is truncated, because terms such as
is truncated, because terms such as ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 21,
21, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1
1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2, and
2, and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 22 now occur, which correspond to certain double, triple, and quadruple excitations, respectively. By construction, the exponential parametrization of the wavefunction ensures that the resulting energies will be size-extensive.
22 now occur, which correspond to certain double, triple, and quadruple excitations, respectively. By construction, the exponential parametrization of the wavefunction ensures that the resulting energies will be size-extensive.
Since a variational determination of the coupled cluster amplitudes tμ is not feasible, projection techniques are used instead. To this end, the Schrödinger equation is left-multiplied by 〈μi|exp(−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ), resulting in the ground-state energy
), resulting in the ground-state energy
E0 = 〈ΦHF|Ĥexp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉 )|ΦHF〉 | (19) |
Ωμi = 〈μi|exp(−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )Ĥexp( )Ĥexp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉 = 0 )|ΦHF〉 = 0 | (20) |
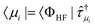 with μi running over all possible excited determinants of excitation rank i. The amplitudes will have the general form
with μi running over all possible excited determinants of excitation rank i. The amplitudes will have the general form | (21) |
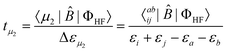 | (22) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) are operators involving the product of Ĥ and
are operators involving the product of Ĥ and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) operators. As the expressions for the former depend on the truncation level, we refer to the literature for concrete examples.41,62
operators. As the expressions for the former depend on the truncation level, we refer to the literature for concrete examples.41,62
Because of the projective nature of the coupled cluster method, it is not possible to invoke a variational principle in order to obtain excited states. Therefore, to construct excited state wavefunctions one would need to employ different reference states. This could, for instance, be an open-shell determinant corresponding to a single excitation with respect to |ΦHF〉. This approach has several disadvantages. First, the above coupled cluster equations would have to be solved for each excited state, which can become computationally rather demanding. Second, different electronic states will no longer be orthogonal, which complicates the calculation of transition moments. Finally, excited states that are not dominated by a single determinant cannot be easily described, as they would require a multi-reference coupled cluster method.
An alternative that remedies part of these difficulties is the equation-of-motion coupled cluster method for excitation energies (EOM-EE), where one introduces the parametrization
|Ψk〉 = Ĉk exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉 )|ΦHF〉 | (23) |
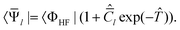 | (24) |
![[capital Psi, Greek, macron]](https://www.rsc.org/images/entities/char_e1f7.gif) l| are neither Hermitian conjugate nor orthogonal among themselves, but rather biorthogonal, i.e., 〈
l| are neither Hermitian conjugate nor orthogonal among themselves, but rather biorthogonal, i.e., 〈![[capital Psi, Greek, macron]](https://www.rsc.org/images/entities/char_e1f7.gif) l|Ψk〉 = δkl. This parametrization allows for a Hamiltonian matrix
l|Ψk〉 = δkl. This parametrization allows for a Hamiltonian matrix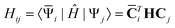 | (25) |
![[capital Psi, Greek, macron]](https://www.rsc.org/images/entities/char_e1f7.gif) l| the matrix H is obtained as
l| the matrix H is obtained as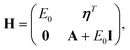 | (26) |
ην = 〈ΦHF|[Ĥ,![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) ν]exp( ν]exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉, )|ΦHF〉, | (27) |
Aμν = 〈μ|exp(−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )[Ĥ, )[Ĥ,![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) ν]exp( ν]exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ΦHF〉. )|ΦHF〉. | (28) |
These excitation energies are size-intensive,63 thus presenting a significant advantage over CI approaches. The CI-like parametrization for the excited-states makes the calculation of transition moments and other expectation values rather simple, even though both left and right eigenvectors need to be calculated because A is not Hermitian. However, these transition moments are not size-intensive64 and therefore in general not reliable for large systems.
All multi-reference methods define a reference (or model) space P, consisting of a set of determinants {|φi〉}. Usually, this is achieved by defining an active space, and all determinants contributing to a full CI expansion within this active space are considered. In MRCI methods this is usually the active space obtained from a CASSCF calculation, whereas in multi-reference coupled-cluster methods the HF orbitals are used directly without reoptimization. Of course, it is important that this model space contains all relevant configurations for the states that are of interest.62 All other possible contributions to the exact wavefunctions that are not contained in the model space P are within its orthogonal complement Q.
This model space then serves as the starting point for obtaining a set {|Ψk〉} of exact solutions of the Schrödinger equation with the same dimension as P. The correspondence between wavefunctions in the model space {|φk〉} and the exact wavefunctions {|Ψk〉} is then established through a projection operator 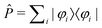 so that
so that
|φk〉 = ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |Ψk〉. |Ψk〉. | (29) |
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) that establishes the reverse mapping and generate the exact wavefunction from one belonging to the model space,
that establishes the reverse mapping and generate the exact wavefunction from one belonging to the model space,|Ψk〉 = ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) |φk〉. |φk〉. | (30) |
Ĥeff|φm〉 = ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) −1Ĥ −1Ĥ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) |φm〉 = Em|φm〉, |φm〉 = Em|φm〉, | (31) |
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) and, consequently, the effective Hamiltonian Ĥeff can be defined via the solution of the so-called Bloch equation. For details, we refer to ref. 75.
and, consequently, the effective Hamiltonian Ĥeff can be defined via the solution of the so-called Bloch equation. For details, we refer to ref. 75.
Once ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) is obtained, Ĥeff in eqn (31) can be constructed and its matrix representation can be diagonalized to obtain the energies {Em}. In multi-reference coupled cluster, an exponential parametrization is used as ansatz for the wave operator
is obtained, Ĥeff in eqn (31) can be constructed and its matrix representation can be diagonalized to obtain the energies {Em}. In multi-reference coupled cluster, an exponential parametrization is used as ansatz for the wave operator ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) ,
,
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) = exp(Ŝ) = exp(Ŝ) | (32) |
| Ŝ = Ŝ(0,0) + Ŝ(1,0) + Ŝ(0,1) + Ŝ(1,1) + … | (33) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) and
and ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) . Using this decomposition, the amplitudes can be determined in a hierarchical fashion for the different sectors. For instance, in order to obtain the contributions from the (a,b) sector to Ŝ, one must first solve all (m,n) sectors for which m < a, n < b.75,76 For a given sector, one obtains amplitude equations of the form
. Using this decomposition, the amplitudes can be determined in a hierarchical fashion for the different sectors. For instance, in order to obtain the contributions from the (a,b) sector to Ŝ, one must first solve all (m,n) sectors for which m < a, n < b.75,76 For a given sector, one obtains amplitude equations of the form〈χ(m,n)j|Ĥ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) − − ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) Ĥ(m,n)eff|φ(m,n)i〉 = 0 Ĥ(m,n)eff|φ(m,n)i〉 = 0 | (34) |
However, in their original formulation FSCC methods are plagued by the so-called intruder state problem.77 This occurs during the iterative solution of eqn (34). When certain low-lying states belonging to Q(m,n) turn out to have energies close to (or even lower than) the higher-lying states from P(m,n) in some amplitudes equations (which are similar to those in eqn (21) and (22)) might have very small energy denominators and prevent the solution of the linear system. The larger the P(m,n) space, the more serious this problem becomes, as accidental degeneracies with Q states become increasingly likely. To alleviate this difficulty, approaches based on an intermediate Hamiltonian formulation (IHFSCC) have been introduced.78–82 These divide the P space as P = Pm + Pi and Pm now serves as the basis for projecting the lower exact solutions, whereas for Pi this requirement is relaxed. This provides enough flexibility so that when Q states interact strongly with the higher-lying Pi states, the corresponding amplitude equations can be approximated to assure convergence. The IHFSCC approach has become the de facto standard for treating (small) molecules containing heavy elements.67,68,71,74,83,84
For situations where the reference is a closed-shell determinant it is instructive to compare the EOM-EE and Fock-space approaches. Starting from the definitions in eqn (32), we can write the wavefunction for state k as
|Ψ(FS)k〉 = ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) FS|Φ0〉 = exp(Ŝ)|Φ0〉 = exp(Ŝ − FS|Φ0〉 = exp(Ŝ)|Φ0〉 = exp(Ŝ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )exp( )exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|Φ0〉. )|Φ0〉. | (35) |
Being based on perturbation theory, one now starts from a partitioning of the Hamiltonian into a zeroth-order contribution Ĥ0 and a perturbing part ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ,
,
Ĥ = Ĥ0 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) | (36) |
| Ĥ0|φm〉 = E0,m|φm〉. | (37) |
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) PT2 that provide the mapping between the model space and the exact solutions. Instead of the exponential parametrization in coupled cluster methods,
PT2 that provide the mapping between the model space and the exact solutions. Instead of the exponential parametrization in coupled cluster methods, ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) PT2 is now expressed as a linear expansion in the orders of perturbation, and only the terms up to first order are retained,
PT2 is now expressed as a linear expansion in the orders of perturbation, and only the terms up to first order are retained,![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) PT2 = 1 + PT2 = 1 + ![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) (1) (1) | (38) |
![[capital Omega, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1e5.gif) PT2 can be expressed as a linear combination of state-specific90,91 wave operators,
PT2 can be expressed as a linear combination of state-specific90,91 wave operators,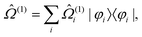 | (39) |
Using such a formalism, one arrives at the equations for the individual states
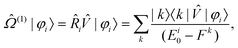 | (40) |
The main weakness of CASPT2 is its susceptibility to intruder states, that is, states that belong to Q and are thus outside of active spaces, but that have energies close to Ei0. These will makes the expression for ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) i go to infinity, causing the perturbation expansion to diverge. Instead of adopting the intermediate Hamiltonian technique as done in the coupled cluster case, Roos and coworkers92–94 as well as others95 devised practical solutions based on the modification of such denominators by the application of a global level shift parameter that modifies the Hamiltonian in such a way that any effects due to the quasidegeneracy of Ei0 and Fk can be avoided. This approach has been found to work very well in practice for the so-called “weak” intruder states that do not interact too strongly with the reference. For more strongly interacting states other solutions must be sought (e.g., including them into the active space), otherwise one should employ alternative formulations such as the NEVPT2 approach96 that avoid intruder states by construction.
i go to infinity, causing the perturbation expansion to diverge. Instead of adopting the intermediate Hamiltonian technique as done in the coupled cluster case, Roos and coworkers92–94 as well as others95 devised practical solutions based on the modification of such denominators by the application of a global level shift parameter that modifies the Hamiltonian in such a way that any effects due to the quasidegeneracy of Ei0 and Fk can be avoided. This approach has been found to work very well in practice for the so-called “weak” intruder states that do not interact too strongly with the reference. For more strongly interacting states other solutions must be sought (e.g., including them into the active space), otherwise one should employ alternative formulations such as the NEVPT2 approach96 that avoid intruder states by construction.
The performance of CASPT2 relative to methods such as MRCI, EOM-EE or IHFSCC has been evaluated for a number of cases, for instance in heavy-element chemistry.71,73,74,84,97,98 In general, CASPT2 yields excitation energies rather close to those obtained with methods that are formally more accurate at a fraction of the computational cost. However, their relative position and the corresponding symmetry classification are often less reliable, which can be attributed to the relatively low accuracy in which dynamical correlation is taken into account. In spite of that, CASPT2 remains one of the few methods (along with MRCI approaches discussed earlier) that can accurately describe both static and dynamic correlation effects for large molecular complexes containing centers with a number of half-filled d or f shells such as those containing (bi)metallic centers.57,99,100 It is also routinely employed to study the spectra and photochemistry of other complexes of transition metals and heavy elements.72,101–105
2.2 Time-dependent approaches based on response theory
Instead of explicitly calculating the wavefunctions of the different excited states, approaches based on response theory set out to calculated the linear response function 〈〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α;
α;![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β〉〉ω (see eqn (5)). A common theoretical framework for achieving this with different methods of quantum chemistry is provided by the quasienergy formalism pioneered by Christiansen and coworkers.19,106 It defines a quasienergy as the time-dependent generalization of the energy,
β〉〉ω (see eqn (5)). A common theoretical framework for achieving this with different methods of quantum chemistry is provided by the quasienergy formalism pioneered by Christiansen and coworkers.19,106 It defines a quasienergy as the time-dependent generalization of the energy,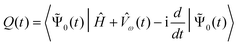 | (41) |
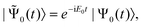 | (42) |
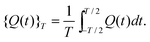 | (43) |
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/char_e11c.gif) 0(t)〉 can be determined by making the time-averaged quasienergy stationary with respect to variations in the wavefunction,
0(t)〉 can be determined by making the time-averaged quasienergy stationary with respect to variations in the wavefunction,| δ{Q(t)}T = 0. | (44) |
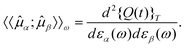 | (45) |
In any quantum chemical method, a parametrization of the wavefunction is introduced, i.e., the wavefunction depends on a set of parameters λ. In so-called variational methods these parameters are in the time-independent case determined by minimizing the energy expectation value. In the time-dependent case, the corresponding parameters can be determined by minimizing the time-averaged quasienergy {Q(t,λ)}T. However, a number of important quantum-chemical methods, such as coupled cluster theory, are not variational, i.e., the wavefunction parameters λ are determined from other conditions. In this case, one can replace Q(t,λ) by the Lagrangian
L(t,λ,![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) ) = Q(t,λ) + ) = Q(t,λ) + ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) g(λ). g(λ). | (46) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) are the Lagrange multipliers and g(λ) = 0 is a set of auxiliary time-dependent equations. Both the parameters λ and the Lagrange multipliers
are the Lagrange multipliers and g(λ) = 0 is a set of auxiliary time-dependent equations. Both the parameters λ and the Lagrange multipliers ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) can then be treated as variational parameters.
can then be treated as variational parameters.
The parameters and possibly also the multipliers can then be determined using variational perturbation theory by expanding the quasienergy Lagrangian in orders of the perturbation strengths and taking the time average,
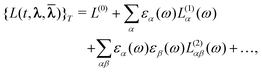 | (47) |
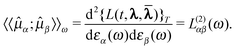 | (48) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) can be expanded as
can be expanded as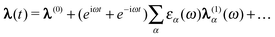 | (49) |
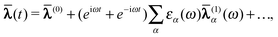 | (50) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) (1)(ω) to refer to the first order terms in these expansions. These can then be determined from the variational conditions
(1)(ω) to refer to the first order terms in these expansions. These can then be determined from the variational conditions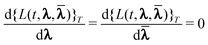 | (51) |
Taking the second derivative of {L(t,λ,![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) )}T with respect to the perturbation strengths εα(ω) and εβ(ω) while taking the implicit dependence of λ and
)}T with respect to the perturbation strengths εα(ω) and εβ(ω) while taking the implicit dependence of λ and ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) on the perturbation strengths into account via the chain rule leads to19
on the perturbation strengths into account via the chain rule leads to19
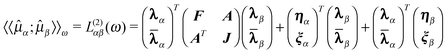 | (52) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) α/β =
α/β = ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) α/β(1) to simplify the notation and define the abbreviations for the partial derivatives with respect to the parameters and multipliers
α/β(1) to simplify the notation and define the abbreviations for the partial derivatives with respect to the parameters and multipliers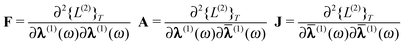 | (53) |
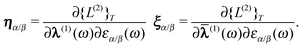 | (54) |
The first-order parameters λα/β and multipliers ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) α,β can be determined from the variational conditions of eqn (51). They only appear in the second-order term Lαβ(2)(ω) and setting the derivative of eqn (52) with respect to λα and
α,β can be determined from the variational conditions of eqn (51). They only appear in the second-order term Lαβ(2)(ω) and setting the derivative of eqn (52) with respect to λα and ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) α to zero leads to the linear equations
α to zero leads to the linear equations
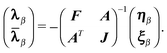 | (55) |
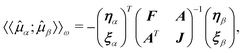 | (56) |
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/char_e0db.gif) s(t)〉, where the KS orbitals
s(t)〉, where the KS orbitals ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) i(r,t) now become time-dependent. This gives rise to the time-dependent density
i(r,t) now become time-dependent. This gives rise to the time-dependent density 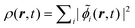 . Within the adiabatic approximation any explicit time or history dependence of the exchange-correlation contribution is neglected, and one arrives at the time-averaged quasienergy functional109,110
. Within the adiabatic approximation any explicit time or history dependence of the exchange-correlation contribution is neglected, and one arrives at the time-averaged quasienergy functional109,110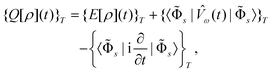 | (57) |
In order to obtain expressions for the response equations and the linear response function one introduces a parametrization of the time-dependent KS determinant |![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/char_e0db.gif) s〉. This can be achieved by using an exponential parametrization acting upon the ground-state Kohn-Sham determinant |Φs〉 (cf.eqn (11))
s〉. This can be achieved by using an exponential parametrization acting upon the ground-state Kohn-Sham determinant |Φs〉 (cf.eqn (11))
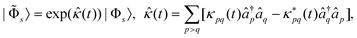 | (58) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (t). This parametrization automatically ensures the orthogonality of the time-dependent KS orbitals without introducing additional Lagrange multipliers. Using this parametrization, the linear response function can be determined by differentiating the time-averaged quasienergy with respect to the parameters κpq(t).
(t). This parametrization automatically ensures the orthogonality of the time-dependent KS orbitals without introducing additional Lagrange multipliers. Using this parametrization, the linear response function can be determined by differentiating the time-averaged quasienergy with respect to the parameters κpq(t).
Because these parameters can be determined variationally, no additional Lagrange multipliers are needed and the linear response function is given by
〈〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α; α;![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β〉〉ω = − ηαF(ω)−1ηβ β〉〉ω = − ηαF(ω)−1ηβ | (59) |
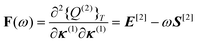 | (60) |
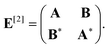 | (61) |
| Aia,jb = δijδab(εa − εi) + 2(ia|bj) + (ia|fxc|bj), | (62) |
| Bia,jb = 2(ia|jb) + (ia|fxc|jb), | (63) |
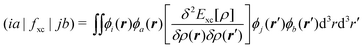 | (64) |
TDDFT has been widely used for studying excited states in medium to large molecules.112–114 Its main advantage is its excellent cost–accuracy ratio. For a broad range of chemical applications, TDDFT is capable of providing results which are qualitatively correct, and often come close to the accuracy of more sophisticated wavefunction-based methods such as CASPT2. This has been demonstrated in a number of recent benchmarking studies on light115–121 and heavy-element containing73 molecules. However, the accuracy often depends on the proper choice of the exchange–correlation functional and kernel, and choosing these appropriately for a particular application is based on experience and often requires careful comparison with more accurate wavefunction based calculations.
However, with the currently available approximations, TDDFT also has some severe shortcomings.122 First, with standard non-hybrid exchange–correlation functionals, it does not provide a correct description of Rydberg states. This is caused by the wrong asymptotic form of the exchange–correlation potential.123 This problem can be addressed by constructing approximations for the exchange–correlation potential that enforce the correct asymptotic behavior, for instance by using orbital-dependent model potentials.124 Alternatively, range-separated hybrid functionals can be used that also result in asymptotically correct exchange–correlation potentials.28 Second, charge-transfer excitations are not described correctly. For detailed discussions of this problem and possible solutions, we refer to ref. 125–127. Finally, within the adiabatic approximation TDDFT does not include double excitations. This could in principle be addressed by using a frequency-dependent exchange–correlation kernel,128,129 but such approximations are not suitable for general applications yet.
|![[capital Psi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b0.gif) 〉 = exp( 〉 = exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (t))|ΦHF〉, (t))|ΦHF〉, | (65) |
Q(t;t) = 〈ΦHF|(Ĥ + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ω(t))exp( ω(t))exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (t))|ΦHF〉 (t))|ΦHF〉 | (66) |
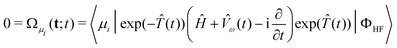 | (67) |
As in the time-independent case, the coupled-cluster wavefunction is not determined variationally. Therefore, the coupled-cluster Lagrangian19,106
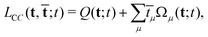 | (68) |
![[t with combining macron]](https://www.rsc.org/images/entities/b_char_0074_0304.gif) have been introduced and the amplitude equations Ωμ(t;t) serve as constraints. The linear response function can then be determined by taking the derivative of the time-averaged Lagrangian {LCC(t,
have been introduced and the amplitude equations Ωμ(t;t) serve as constraints. The linear response function can then be determined by taking the derivative of the time-averaged Lagrangian {LCC(t,![[t with combining macron]](https://www.rsc.org/images/entities/b_char_0074_0304.gif) ;t)}T, yielding the linear response function (cf.eqn (56))
;t)}T, yielding the linear response function (cf.eqn (56))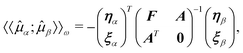 | (69) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) only appear linearly in the Lagrangian. This response function can be rewritten as
only appear linearly in the Lagrangian. This response function can be rewritten as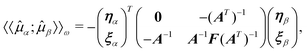 | (70) |
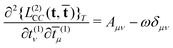 | (71) |
While feasible for small molecules, the relatively large computational cost of calculating and diagonalizing the CCSD Jacobian have motivated the development of more approximate coupled cluster methods based on perturbative approaches that yield energies correct to second order or higher. The first of these is the CC2 method,131 where the main idea is to retain the singles equation Ωμ1 as in CCSD but to approximate the doubles equation Ωμ2. This results in a Jacobian in which the doubles–doubles block is diagonal, thus resulting in significant computational gains. To make these linear response coupled-cluster methods, in particular CC2, applicable to truly large molecular systems, there has been significant work in recent years to combine it with efficient computational techniques.132,133
3 Embedding methods: basic ideas and exact theory
All quantum-chemical methods for excited states discussed in the previous section show a rather steep increase of the computational effort with the size of the system. This is particularly the case for wavefunction based methods where there are well-defined hierarchies that allow for a systematic improvement of the calculation. Thus, their applicability is limited to comparably small molecules and a treatment of electronic excitations in complex chemical systems remains a challenge. However, if only local excitations are of interest, additional simplifications can be introduced.The simplest possibility for exploiting this locality is the truncation of the full system to a smaller model. Such a model contains only the part of the system where the local excitations of interest take place and of its environment. For the case of a chromophore molecule in solution the definition of such cluster models is rather straightforward: In the simplest case, one starts from an isolated chromophore, which is then progressively surrounded by solvent molecules up to some limit e.g. to include a complete solvation shell. Similar constructions can be used for chromophores in protein environments by only including specific amino acid residues that are close to the chromophore. Also for treating impurities in solids truncated cluster models can be set up by including only atoms within a certain distance from the impurity. Even though such a truncation of the full system may be a rather crude approximation, the results obtained with such cluster models will eventually converge towards a full calculation if the size of the model system is systematically enlarged. However, this convergence can be rather slow and, therefore, cluster models that provide sufficiently accurate results will often be rather large and contain hundreds or thousands of atoms. Thus, a full quantum-chemical treatment of sufficiently large truncated models is rarely possible with accurate quantum-chemical methods.
Embedding methods follow an intermediate strategy between a full quantum-chemical treatment and the use of small truncated model systems: They still restrict the accurate treatment to a small subsystem of interest, but instead of neglecting the environment of this model system, it is included in a more approximate manner. As with truncated model systems, the results obtained with such embedding schemes will eventually converge towards those of a full treatment when enlarging the size of the explicitly treated subsystem. However, since the environment is always included, this convergence should be much faster, which makes it possible to restrict the size of the active subsystem considerably if only local excitations or other local spectroscopic properties are of interest.
Formally, such embedding approaches can be formulated as an exact theory as outlined in the following subsection. From this exact embedding theory one always obtains the same results as with a full quantum-chemical treatment, independent of the chosen size of the active subsystem. However, such a treatment is not suitable for practical applications since its computational cost would be comparable to (or even larger than) the one of a full quantum-chemical treatment. Therefore, approximations have to be applied for the description of the environment. The quality of these approximations determines how fast the results of embedding calculations converge with the size of the explicitly treated subsystem. More accurate embedding methodologies will allow for the use of a smaller active subsystem, which in turn makes it possible to apply more sophisticated and more accurate quantum-chemical methods for the description of the local excitations of interest. It should also be noted that embedding approaches also simplify the interpretation of the computational results significantly, since information from the parts of the system not treated explicitly will, in effect, be filtered away by construction.
3.1 Frozen-density embedding theory
Embedding approaches start from a partitioning of the total system into a subsystem of interest (subsystem I in the following) and its environment (subsystem II). The frozen-density embedding (FDE) theory formulated by Wesolowski and Warshel134—following earlier work of Senatore and Subbaswamy135,136 and of Cortona137—provides a formally exact theoretical framework for introducing such a partitioning. It is based on the formally exact DFT (i.e., considering exact density functionals) and uses the electron density of the total system ρtot(r) as its starting point. This total density is partitioned into the electron densities of the active subsystem, ρI(r), and of the environment, ρII(r), i.e.,| ρtot(r) = ρI(r) + ρII(r). | (72) |
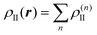 | (73) |
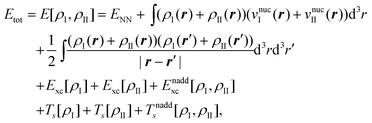 | (74) |
| Enaddxc[ρI,ρII]=Exc[ρI+ρII] − Exc[ρI] − Exc[ρII] | (75) |
| Tnadds[ρI,ρII]=Ts[ρI+ρII] − Ts[ρI] − Ts[ρII], | (76) |
The total energy given in eqn (74) can be partitioned as,
| Etot = EI + EII + Eint, | (77) |
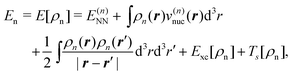 | (78) |
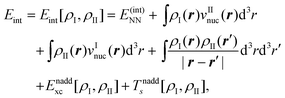 | (79) |
Eqn (79) provides an exact expression for the interaction energy between two subsystems with fixed electron densities ρI and ρII. The first four terms add up to the classical electrostatic interaction energy between the nuclei and electron densities of the two subsystems. In addition, the nonadditive exchange–correlation energy Enaddxc[ρI,ρII] and the nonadditive kinetic energy Tnadds[ρI,ρII] account for the non-classical contributions to the interaction energy. While the classical terms can be calculated directly for any two subsystems once the nuclear charges and positions as well as the subsystem electron densities are known, the evaluation of the non-classical contributions requires the knowledge of the exchange–correlation and kinetic-energy functionals, Exc[ρ] and Ts[ρ]. Even though these are not know, eqn (79) provides a useful starting point for the development of embedding methods. We note that its applicability is not limited to DFT calculations since an electron density can always be defined within any theoretical framework and then used to evaluate an interaction energy within FDE theory.
For the case of a KS-DFT description, the density of the active subsystem I can be obtained from the KS orbitals {ϕIi} as 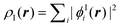 . Note that in this case the noninteracting kinetic energy Ts[ρI] can also be calculated directly from the KS orbitals. For a given frozen electron density ρII(r) in subsystem II, the KS orbitals (and the electron density) of the active subsystem I can then be determined by minimizing the total energy given in eqn (74) with respect to ρI, while keeping ρII frozen. Performing this minimization under the constraint that the number of electrons NI in subsystem I is conserved leads to a set of equations for the KS orbitals of subsystem I,
. Note that in this case the noninteracting kinetic energy Ts[ρI] can also be calculated directly from the KS orbitals. For a given frozen electron density ρII(r) in subsystem II, the KS orbitals (and the electron density) of the active subsystem I can then be determined by minimizing the total energy given in eqn (74) with respect to ρI, while keeping ρII frozen. Performing this minimization under the constraint that the number of electrons NI in subsystem I is conserved leads to a set of equations for the KS orbitals of subsystem I,
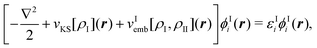 | (80) |
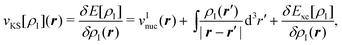 | (81) |
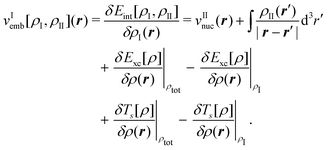 | (82) |
The first two terms of the embedding potential of eqn (82) describe the classical electrostatic potential of the nuclei and of the electrons in the frozen environment. In addition, the embedding potential also contains an exchange–correlation component and a kinetic-energy component. These account for the non-classical contributions, such as the Pauli (exchange) repulsion of the electrons in the frozen subsystem and chemical bonding (i.e., orbital interactions) between the subsystems. While the electrostatic part of the embedding potential can be evaluated directly for given subsystem densities, this is not possible for the exchange–correlation and kinetic energy parts, as these require the knowledge of the corresponding exact functionals.
The same embedding potential can also be derived for the case that a wavefunction based description is used for the active subsystem.142,143 In this case a wavefunction ΨI(r1, s1, r2, s2,…) is used to represent the electron density ρI(r) of subsystem I. By using that
EI = E[ρI] = E(I)NN + 〈ΨI|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Inuc + Inuc + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ee|ΨI〉, ee|ΨI〉, | (83) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ,
, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Inuc, and
Inuc, and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ee are the operators of the kinetic energy, the electron–nuclear attraction energy, and of the electron–electron interaction, respectively, the total energy of eqn (74) and (77) can be rewritten as
ee are the operators of the kinetic energy, the electron–nuclear attraction energy, and of the electron–electron interaction, respectively, the total energy of eqn (74) and (77) can be rewritten asEtot = E[ΨI,ρII] = E(I)NN + 〈ΨI|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Inuc + Inuc + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ee|ΨI〉 + Eint[ρI,ρII] + EII, ee|ΨI〉 + Eint[ρI,ρII] + EII, | (84) |
The wavefunction describing subsystem I in the presence of the frozen density ρII(r) can then be obtained by minimizing this total energy functional with respect to ΨI while keeping the electron density ρII of the environment frozen, under the constraint that the number of electron NI in subsystem I is conserved. This leads to the condition,
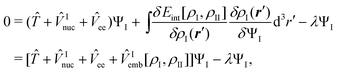 | (85) |
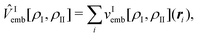 | (86) |
For solving this embedded Schrödinger equation, the common approximations of wavefunction based quantum chemistry can be applied. Note that the derivation given here differs from the one in ref. 143, where an approximate wavefunction of subsystem I was introduced before performing the energy minimization. In this case, the embedding potential contains an additional term correcting for the difference between the approximate and the exact wavefunctions. However, it can be argued that a correction for deficiencies of an employed wavefunction approximation should not be contained in the embedding potential.70,144 Therefore, the derivation given here avoids this correction by introducing an approximate wavefunction only at a later stage.
However, such an agreement with the results of a full calculation is only possible if the frozen density fulfills certain conditions.145,146 In particular, the frozen density ρII has to be smaller than or equal to the correct total density ρtot at every point in space, i.e., ρII(r) ≤ ρtot(r). Otherwise, the complementary density of the active system would have to be negative, which is not possible. In addition, this complementary density ρtot − ρII has to be noninteracting vs-representable in the case of a KS-DFT description for the active system or interacting v-representable in the case of a wavefunction based treatment.
In particular the first condition is usually not fulfilled for most approximate frozen densities. Usually, these will be too small in some regions and too large in others. Consequently, the application of the embedding potential of eqn (82) does not lead to the exact total density with such choices for ρII. This problem can be alleviated by switching from an embedding method to a subsystem approach in which both the densities of subsystem I and II are determined. That is, the densities of both subsystems are determined separately, but in each case the (frozen) density of the other subsystem is taken into account. When using KS-DFT, this can be formulated as a set of coupled equations for the KS orbitals of the two subsystems,
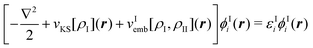 | (87) |
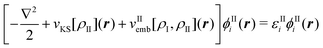 | (88) |
The simplest strategy for solving these coupled equations for the two subsystems is through so-called freeze-and-thaw iterations.147 First the density of subsystem I is determined in the presence of an approximate frozen density for subsystem II. Subsequently, the roles of the two subsystems are interchanged and the density calculated for subsystem I in the previous step is now frozen, whereas an updated density is determined for subsystem II. This is repeated iteratively until convergence is reached. Alternatively, the two sets of equations (eqn (87) and (88)) can be solved simultaneously.139 Note that the resulting partitioning into subsystems is not unique, because density can be moved between the two subsystems without changing the total electron density. However, a unique partitioning can be obtained when requiring that both subsystems share the same embedding potential, i.e., that vIemb[ρI,ρII] = vIIemb[ρI,ρII].11,138
When focussing on one subsystem of interest, such an iterative subsystem scheme can be considered as an embedding scheme that not only accounts for the effect of the environment on the active subsystem but also includes the polarization of the environment caused by the active subsystem. Thus, such a polarizable embedding goes beyond a scheme in which a fixed frozen density is employed for the environment. Consequently, it will always converge to the same density as a full treatment, irrespective of the initial choice of ρII if no further approximations are introduced.
In a formalism based on response theory,149–152 the (time-dependent) electron densities ρI(r,t) and ρII(r,t) of the two subsystems are in a KS-DFT framework represented by two separate Slater determinants |![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/char_e0db.gif) I〉 and |
I〉 and |![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/char_e0db.gif) II〉, respectively. Consequently, the total time-averaged quasi-energy can be expressed as
II〉, respectively. Consequently, the total time-averaged quasi-energy can be expressed as
| {Q(t)}T = {Q[ρI](t)}T + {Q[ρII](t)}T + {Eint[ρI,ρII](t)}T, | (89) |
| ρ(r,t) = ρI(r,κI) + ρII(r,κII). | (90) |
With this parametrization, the matrix F, which determines the poles of the response function, assumes a block structure,
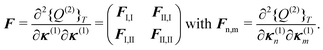 | (91) |
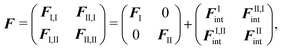 | (92) |
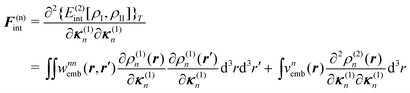 | (93) |
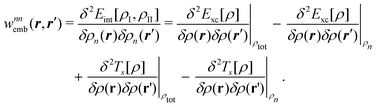 | (94) |
| Annia,jb = δijδab(εna − εni) + 2(ia|bj) + (ia|fxc|bj) + (ia|wnnemb|bj), | (95) |
| Bnnia,jb = 2(ia|jb) + (ia|fxc|jb)+(ia|wnnemb|jb), | (96) |
Second, the off-diagonal blocks introduce a coupling between the subsystems, which is given by
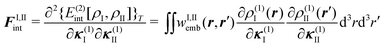 | (97) |
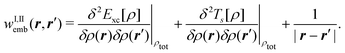 | (98) |
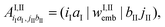 | (99) |
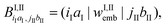 | (100) |
In should be noted that the subsystem response theory discussed above in the framework of TDDFT can also be generalized to a wavefunction based description of the active subsystem. In this case, the DFT quasi-energy of subsystem I in eqn (89) is replaced by the quasi-energy Lagrangian of a wavefunction based method, i.e.,
| {L(t)}T = {L[ρI](t)}T + {Q[ρII](t)}T + {Eint[ρI,ρII](t)}T, | (101) |
ρ(r,t) = ρI(r,λI,![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) I) + ρII(r,κII) I) + ρII(r,κII) | (102) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0cc.gif) I. Embedding contributions to the isolated subsystem matrices FI, AI, and JI as appearing in the response function (eqn (56)) can then be derived by differentiating the interaction energy with respect to the parameters and multipliers. As in the TDDFT case, these will introduce both embedding contributions entering into the subsystem response and embedding contributions that couple the two subsystems. In general, linear-response function in eqn (56) will now involve the matrix152
I. Embedding contributions to the isolated subsystem matrices FI, AI, and JI as appearing in the response function (eqn (56)) can then be derived by differentiating the interaction energy with respect to the parameters and multipliers. As in the TDDFT case, these will introduce both embedding contributions entering into the subsystem response and embedding contributions that couple the two subsystems. In general, linear-response function in eqn (56) will now involve the matrix152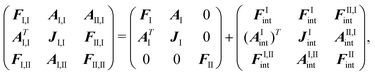 | (103) |
4 Approximate embedding methods
While the FDE theory presented in the previous section provides an exact theoretical framework for embedding methods in quantum chemistry, it is not directly suitable for numerical applications. In particular, it requires the knowledge of the exact nonadditive kinetic-energy functional, which is not easily available in practice. Therefore, numerous approximate embedding schemes have been developed instead. For discussing these in the following section, it is useful to establish a classification scheme for such methods.One scheme for classifying approximate embedding methods has been proposed by Bakowies and Thiel (BT)153 and follows the steps taken above for presenting the FDE theory.
• Mechanical coupling: The simplest way to setup an embedding scheme is to treat each subsystem individually and introduce the coupling only through the total energy. To this end, an interaction energy between the subsystems is calculated according to eqn (79) or some approximation to it. With such a simple scheme only the geometrical structure of the active subsystem is altered. All electronic properties, in particular the electron density, are identical to those obtained when treating the subsystem of interest in isolation.
• Electronic coupling: Embedding schemes that include the effect of the environment in the quantum-chemical treatment of the active subsystem in some way form the next category. This can be achieved by including the embedding potential of eqn (82) both in a KS-DFT or in a wavefunction based treatment of the subsystem of interest. In practice, this embedding potential is usually approximated. With such a coupling through an embedding potential, the electronic properties of the subsystem of interest can be affected by its environment.
• Polarizable embedding: In the simplest case of embedding schemes with electronic coupling, the (approximate) embedding potential is determined solely by the geometric structure of the environment. For instance, the frozen electron density calculated for the isolated environment (i.e., in the absence of the subsystem of interest) can be used in eqn (82). More advanced schemes can be set up by including the polarization of the environment due to the presence of the active subsystem. This leads to schemes where the embedding potential has to be determined iteratively.
• Embedding including environment response: When treating electronic excitation energies or other response properties, a fourth category—not contained in the original BT classification—can be introduced. In this case one can distinguish whether or not the response of the environment to the electronic excitation is included. With state-specific methods, this can be achieved by iteratively updating the environment density for each excited state instead of employing one common frozen environment density for all excited states. Within response theory, the response of the environment can be included through the additional subsystem and coupling contributions to the response matrices discussed in the previous section. Several different strategies can be introduced to approximate these contributions. First, the coupling contributions can be neglected and only those modifying the subsystem response are retained. Second, the coupling contributions can be included in an approximate fashion. Finally, it is also possible to fold the contributions of the environment as well as the coupling in an approximate fashion into the response matrices of the active subsystem. While this will not account for coupling between individual excitation energies, it does allow for an efficient inclusion of the polarization of the environment density.
Among those groups, different methods can be classified according to the approximations that are introduced for calculating the interaction energy and the embedding potential. First, in continuum solvation models the discrete molecular structure of the environment is neglected and replaced by a dielectric continuum. Next, a large variety of embedding methods uses a discrete description for the environment and models the electrostatic part of the environment using point charges or localized multipole moments. Such a purely electrostatic description can be augmented with additional terms accounting for non-classical interactions. As a further step, there are embedding methods that retain a full electron density for the environment using the embedding potential of eqn (82), but employing an approximate electron density for the environment and introduce approximations for the nonadditive kinetic-energy functional. Finally, embedding methods that do not introduce such approximations have also been proposed for embedding accurate wavefunction theory calculations into an environment treated with DFT.
In the following, we will discuss these different approximations. We note, however, that a classification in terms of sophistication does not imply an equivalence in terms of accuracy. Often, seemingly simple schemes have been parametrized so that they provide rather accurate results. At all levels of approximations, embedding methods can operate in the different categories in the BT classification scheme. This is sketched in the two-dimensional overview in Fig. 1. In all cases further distinctions can be made according to the methods used for describing the active subsystems. However, in most cases this does not affect the embedding methodology significantly, so we will only make this distinction in a few cases.
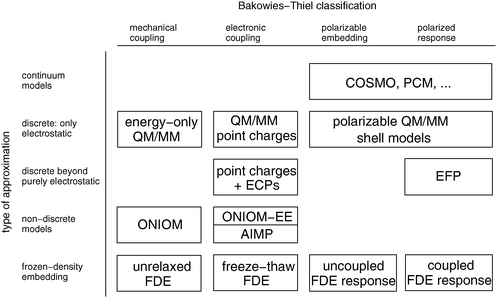 | ||
| Fig. 1 Overview of some of the available approximate embedding scheme. On the horizontal axis are the categories of the extended Bakowies–Thiel classification, while the vertical axis sorts different approaches according to the models employed for the environment. | ||
4.1 Continuum models
The simplest possible way to account for environment effects in quantum-chemical calculations are continuum models. These neglect the specific molecular structure of the environment and replace it by a continuum characterized by its dielectric constant ε(env). The subsystem of interest is then placed in a cavity inside this dielectric continuum. The nuclear charges and the electron density of the active subsystem induce charges on the surface of this cavity (apparent surface charges), and the electrostatic potential of these surface charges is included in the quantum-chemical treatment of the active subsystem as an embedding potential.Commonly, the cavity surface is discretized, and a distribution of point charges qs at positions rs on the cavity surface is used to approximate the apparent surface charges. The resulting embedding potential is then given by
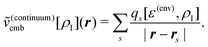 | (104) |
Continuum models are particularly suited for modeling solvent effects. They model not the effect of a specific molecular structure of the solvent environment but rather an implicit average over the different solvent configurations. Therefore, they provide an efficient way of including the dynamics of the solvent without considering many different molecular structures explicitly. Instead of providing an interaction energy according to eqn (79) for a specific structure, they try to approximate the free energy of the solvated molecule and the free solvation energy.
While for the dielectric constant ε(env) one commonly uses the experimentally determined one for a specific solvent, the size and shape of the cavity are parametrized to reproduce free energies. Usually, this requires a solvent-specific parametrization. Thus, the embedding potential used in continuum models is not just an approximation to the electrostatic part of eqn (82), but implicitly also includes non-electrostatic contributions as well as the aforementioned dynamical averaging. Since by construction the embedding potential depends on the density of the active subsystem, continuum models can be categorized as polarizable embedding methods in the BT classification.
Continuum models can be easily combined with a variety of quantum-chemical methods, given the simplicity of the embedding potential in eqn (104). However, for determining the surface apparent charges qs the electron density of the active subsystem is required. While this is directly available in HF and DFT calculations, its calculation can be more involved with wavefunction based correlation methods and a fully self-consistent determination of the surface charges can become computationally rather demanding. Therefore, approximate schemes for the combination of continuum models with, e.g., perturbation theory162 or coupled cluster theory163 have been devised.
For the calculation of excitation energies, continuum models allow for a rather straightforward inclusion of the response of the environment (for a review, see ref. 164). With state-specific methods, this is achieved by determining a different set of surface charges for each excited state of interest, i.e., the difference in the electron density of the active subsystem induce a change Δqs in the surface charges. Such a fully self-consistent state-specific treatment is, for instance, possible for including solvent effects in CASSCF calculations.165,166 Similarly, when employing response theory for the calculation of excitation energies, the response of the environment can be included by accounting for the response of the surface charges by an embedding kernel, which in the case of TDDFT has the form
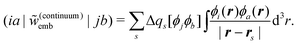 | (105) |
A detail that is worth discussing is the meaning of the response of the surface charges Δqs when treating excited states. Because the continuum model implicitly accounts for the dynamics of the solvent environment, the environment response not only accounts for the response of the electron density of the environment, but also includes the structural relaxation of the solvent after the electronic excitation. This is usually referred to as equilibrium solvation. However, it is possible to decompose the environment response into a fast contribution Δq(fast)s (corresponding to the response of the solvent electrons) and a slow contribution Δq(slow)s (corresponding to the response of the nuclei in the environment). By separating these two contributions and including only the fast one in the quantum-chemical calculation it is possible to access vertical excitation energies (for details, see, e.g.ref. 164).
The simplicity of continuum models has made them the method of choice for obtaining a first estimate of solvent effects on excitation energies.159,164 However, the neglect of the explicit structure of the environment is at the same time the biggest disadvantage of continuum models, in particular if specific solvent–solute interactions such as hydrogen bonding are present. In this case, usually several solvent molecules have to be included explicitly in the active subsystem.172–174 For the same reason, continuum models are less successful for describing the effect of structured environments, such as in proteins or solid-state systems, even though they are often still used to model the bulk contribution of the outer shells of the such environments.
4.2 Discrete approximations: electrostatic embedding
A next step beyond continuum models are discrete approximations, in which molecular structures are considered and determine the interaction energy and the embedding potential. In contrast to continuum models, these discrete models will make an explicit treatment of the dynamics of the environment necessary. In particular for describing solvent effects or biomolecular environments, this usually requires calculations for a large number of different molecular structures of the environment in combination with a suitable averaging.The simplest discrete approximation to the interaction energy and the embedding potential can be obtained by using a classical molecular mechanics (MM) model. The combination of the quantum mechanical (QM) treatment of the subsystem of interest with a MM description of the environment and its interaction with the active subsystem leads to so-called QM/MM methods. Such QM/MM models are common both for describing solvent effects and biomolecular structures as well as for the treatment of solid state systems and surfaces. These were first pioneered by Warshel and Levitt,175 and have been further developed by numerous researchers in the past decades. Several excellent recent reviews are available on QM/MM methods, mostly with a focus on their use for biological systems.176–180 Therefore, we will only highlight the most important ideas in the following and put a special focus on the application of QM/MM methods for studying excited states.
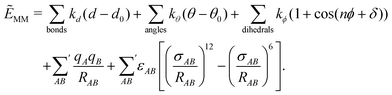 | (106) |
QM/MM methods replace the energy of the environment EII and the interaction energy Eint in eqn (77) by the corresponding energy from a classical force field, while a full quantum-chemical description is only retained for the energy of the active subsystem EI. This is possible because the total MM energy of eqn (106) can usually be partitioned according to eqn (77) in a straightforward way. If there are no covalent bonds between the active subsystem and its environment, this leads to an interaction energy of the form
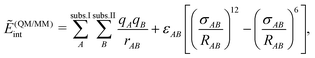 | (107) |
Instead of evaluating the electrostatic part of the interaction energy completely at the molecular mechanics level, the true charge density of the active subsystem can also be used instead of molecular mechanics charges for this subsystem, i.e.,
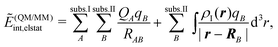 | (108) |
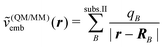 | (109) |
QM/MM calculations employing an electrostatic embedding potential are in many cases the method of choice for describing local excitations in protein environments. Two widely studied examples are rhodopsins, where the protein environment plays an important role in tuning the absorption energy of the retinal chromophore,181–185 and green fluorescent protein.186–189 For these photoactive proteins, a large variety of quantum-chemical methods, ranging from TDDFT to CI and quantum Monte–Carlo calculations, have been employed in combination with an electrostatic embedding potential. While some of these studies have employed only a single static structure for the protein environment, others have included an explicit averaging over different protein conformations by sampling a number of snapshots from molecular dynamics simulations.
Note that the electrostatic embedding potential in such QM/MM calculations is independent of the electron density of the active subsystem. Therefore, no additional response contributions appear in the calculation of excitation energies, i.e., the response of the environment is not included, and the presence of the environment only enters via a shift of the orbital energies. However, for the treatment of excitations in photoactive proteins an adequate quantum-chemical description of the isolated chromophore is already challenging.16,181 Moreover, it has been pointed out that already the environment effect obtained with a fixed electrostatic embedding potential sensitively depends on the correct description of the transition dipole moments, which again is often difficult to achieve.181 Thus, polarizable embedding approaches (discussed in section 4.2) have so far not been extended to photoactive proteins.
The most obvious difference is that the environment has a periodic structure and an infinite summation over the environment charges is in principle required, i.e., the point-charge embedding potential now has the form
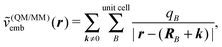 | (110) |
A different approach to the infinite series in eqn (110) is Ewald summation,197 where the series is split into a short-range part that is summed in real space and a long-range part for which the summation is performed in reciprocal space, both of which converge quickly. The resulting potential can then be fitted to a finite array of point charges, from which the embedding potential is constructed.193,198–200 Alternatively, an approach that uses the potential resulting from the Ewald summation directly in a quantum-chemical calculation has been developed by Burow et al. based on the periodic fast multipole method.201
Such periodic point-charge environments have been combined with a variety of quantum-chemical methods for studying local excitations in solid-state systems. Examples include the description of color centers in bulk ZnO with CASSCF calculations,202 of local excitations at the Cr2O3(0001) surface with CASSCF and CI-based methods,203 and of surface and bulk excitations in KBr with TDDFT and with EOM-CC methods.204 These studies always employ a fixed embedding potential, i.e., the response of the environment is not included.
In all applications of point-charge embedded cluster models, several options exist for defining these charges. The simplest is to use the formal charges corresponding to the oxidation states of the respective ions, another possibility is the use of partial charges, which could be derived from full quantum-chemical calculations using different schemes. For an overview and a discussion, we refer to ref. 192. If homogenous periodic systems (i.e., bulk structures) are considered, the environment charges can be updated iteratively to correspond to those obtained for the embedded cluster. This is done, for instance, in the embedded ion methods and its extensions192,205 and a similar scheme can be employed in QM/MM embedding calculations for molecular crystals.206,207 Such schemes implicitly account for ground-state polarization of the environment by the embedded cluster.
For studying impurities in ionic crystals, this polarization is more difficult to include and has to be modeled explicitly. The use of atomic polarizabilities at the site of the ions in the environment (see below) is less common in studies of solid-state systems. Instead, shell models208 are often employed,209–211 in which one augments the ionic charges with a shell of the opposite charge connected to the ion by a harmonic spring. This shell can then ``move'' in response to the electric fields generated by the embedded cluster to account for the polarization of the environment.
One possibility of setting up such a polarizable QM/MM scheme is the discrete reaction field (DRF) model,212 in which an embedding potential of the form
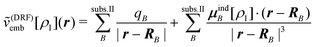 | (111) |
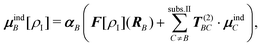 | (112) |
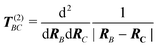 is the dipole interaction tensor and F is the electric field generated by the charge density of the active subsystem and all atomic partial charges of the environment,
is the dipole interaction tensor and F is the electric field generated by the charge density of the active subsystem and all atomic partial charges of the environment, | (113) |
For the calculation of excitation energies, such a polarizable embedding potential can be applied within response theory. In this case, the dependence of the embedding potential on the density of the active subsystem leads to additional embedding contributions to the response matrices. In the case of TDDFT, this results in the embedding kernel215
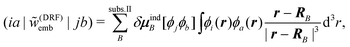 | (114) |
Such polarizable QM/MM embedding potentials have been combined with (TD-)DFT214–216 as well as with linear-response coupled cluster methods171,217,218—where, as for the continuum models, the approximation of neglecting JI,I is used. The latter have been applied in numerous studies of solvent effects on excitation energies.219–221 Note that QM/MM approaches for the description of solvent effects always require an explicit averaging over a large number of snapshots from molecular dynamics simulations.
A slightly improved formalism and implementation, both for TDDFT and for coupled cluster, have been presented recently by Kongsted and coworkers.222–224 The main difference of this polarizable embedding scheme is the use of not only partial charges, but also of dipole, quadrupole, and possibly higher multipole moments in the static part of the electrostatic embedding potential, whereas the polarizable part is still modeled with induced dipole moments. However, both for the static and for the polarizable part solvent models have been parametrized that in addition to those at the positions of nuclei include partial charges, dipoles, etc. also at additional locations. Such polarizable QM/MM schemes can be further combined with continuum models to account for outer solvation shells.225
4.3 Discrete approximations: beyond purely electrostatic embedding
The approximate embedding potentials discussed above only contain an electrostatic component. Depending on their parametrization, these can implicitly also account for some of the non-electrostatic contributions in the exact local embedding potential (eqn (82)). However, the absence of these explicit non-electrostatic contributions can pose a severe problem. This becomes particularly obvious in point-charge embedding methods modeling an ionic crystal environment, as discussed in section 4.2. If the basis set employed for the active subsystem is sufficiently flexible, positive charges in the environment can act as artificial nuclei and orbitals spuriously localize at these centers.226 This problem is particularly severe if formal charges are employed.A simple way of fixing such problems is the introduction of pseudopotentials modeling the core electrons at these centers.227–229 Such effective core pseudopotentials are widely used in quantum chemistry and are readily available for most atoms. Note that these pseudopotentials contain nonlocal projection operators and do therefore not emerge in the FDE theory outlined above, but are derived within a different theoretical framework. However, their use for describing environment effects can only be considered a pragmatic solution, as such effective core pseudopotentials are derived in a very different context. For a discussion of the pseudopotential approximation in quantum chemistry, see ref. 230. A more rigorous way of deriving nonlocal embedding potentials is provided by the ab initio model potential (AIMP) method, which will be discussed below.
| Ẽ(EFP-1)int = ECoul + Epol + Erep, | (115) |
| ṽ(EFP-1)emb[ρI](r) = vCoul(r) + vpol[ρI](r) + vrep(r), | (116) |
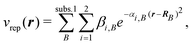 | (117) |
Subsequently, the EFP scheme has been refined and extended to arbitrary solvents.232,235,236 In this EFP-2 method, the interaction energy is modeled as
| Ẽ(EFP-2)int = ECoul + Epol + Eexrep + Edisp + Ect, | (118) |
4.4 Beyond a discrete representation of the environment
| Ẽ(ONIOM)int = Elowtot − (ElowI + ElowII), | (119) |
| Ẽ(ONIOM)tot = EhighI + Elowtot − ElowI, | (120) |
where the superscript “high” denotes energies calculated with an accurate quantum-chemical method, whereas the superscript “low” indicates energies calculated with a more approximate method. This could, for instance, be an accurate wavefunction based method combined with DFT as more approximate method. Thus, the ONIOM scheme allows for the combination of different quantum chemical methods. However, in its original formulation, the energies EhighI and Elowtot are calculated for the isolated active subsystem, i.e., only mechanical coupling is included.
This has been extended to include an electrostatic embedding potential as in eqn (109), where the partial charges are extracted from the quantum-chemical calculation performed for the environment with a more approximate quantum-chemical method.241,242 Recently, a ONIOM electrostatic embedding scheme has been devised that uses the full electrostatic embedding potential,243i.e.,
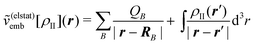 | (121) |
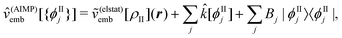 | (122) |
The AIMP method has been used extensively in studies of electronic excitations in solid-state systems using a variety of wavefunction based quantum chemical methods, for instance for studying transition metal253 or lanthanide and actinide centers254–256 in ionic crystals. In this case, the environment can be described by an array at atomic ions. Thus, the environment orbitals can be pre-calculated and the resulting embedding potentials can be stored and reused. It must be noted that for ionic solids, an AIMP description of the first shells of the environment usually has to be combined with a further point-charge embedding to account for the long-range electrostatic interactions.257 To account for the polarization of the environment, the AIMP method can be combined with shell-models,249,258 where the electrostatic part of the embedding potential is modified.
4.5 Frozen-density embedding with approximate kinetic-energy functionals
The frozen-density embedding (FDE) scheme aims at providing a full description of environment effects by approximating the exact embedding potential of eqn (82). However, for the exchange–correlation functional Exc[ρ] and for the nonadditive kinetic-energy functional Tnadds[ρI,ρII] (eqn (76)) and its functional derivative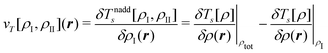 | (123) |
If both the active subsystem and its environment are described with DFT using an approximate exchange–correlation functional that depends only locally on the electron density (i.e., LDA or GGA functionals), the exchange–correlation contribution can be treated consistently. With hybrid functionals or with orbital-dependent exchange–correlation potentials, a local functional has to be used for the nonadditive exchange–correlation contributions, which constitutes an additional approximation.266,267
The simplest class of approximations applies an approximate kinetic energy functional in eqn (76) as well as for the functional derivative in eqn (123). These are referred to as decomposable approximations. Early studies employed the well-known Thomas–Fermi functional, but following a series of tests for hydrogen-bonded systems,274,275 Wesolowski proposed the use of generalized-gradient approximation (GGA) kinetic-energy functionals within the FDE scheme. In particular, he recommended275 the use of the PW91k functional of Lembarki and Chermette,276 which has been used almost exclusively in applications of the FDE scheme in the past decades. More recently, new GGA kinetic-energy functionals have also been proposed for the use in decomposable approximations to the kinetic-energy component of the FDE interaction energy and embedding potential.273
Several studies have assessed the quality of the available decomposable approximations. Generally, these provide a good accuracy of the electron densities and molecular properties as long as the interaction between the subsystems in dominated by weak, non-covalent interactions such as hydrogen bonding. This has, for instance, been demonstrated by comparing the electron densities obtained in FDE calculations to those of a full treatment.277,278 For interaction energies, the PW91k approximation provides a typical accuracy of ca. 1–2 kcal/mol in hydrogen bonded complexes.272
Even though successful for weak interactions between the subsystems, several shortcomings of the available decomposable approximations based on GGA functionals have been pointed out. In the limit of infinitely separated subsystems the potential shows a wrong form at the frozen subsystem, which affect the resulting orbital energies and can lead to spuriously low excitation energies.279 This shortcoming can partly be addressed with so-called non-decomposable approximations,271,279 in which the non-additive kinetic energy or the potential vT[ρI,ρII] are approximated directly. Even more severe is the failure of all presently available approximations for subsystems connected by covalent bonds,278 even if these covalent bonds are very weak.280 These problems have so far not been addressed satisfactorily, but recent work provides some possible directions for future improvements.146 Alternatively, the insufficiencies of the currently available approximations can be circumvented by using a more general partitioning that introduces capping groups.281
The applications discussed so far focussed on ground-state properties. Excited states can be treated in such DFT-in-DFT embedding calculations either with a state-specific approach or within response theory. A state-specific approach is realized if excited states of the active subsystem are described using a ΔDFT or ΔSCF-DFT approach (see section 2.1.1). This was applied by Wesolowski and coworkers to study crystal field splittings for impurities in ionic crystals,288–290 using the ground-state embedding potential also for the excited states.
As outlined in section 3.1.4, the FDE theory can also be extended to a description of excited states within response theory, in particular with TDDFT. In applications of such an approach, one usually—in addition to the use of approximations to the kinetic-energy contribution to the embedding kernel—introduces approximations for the treatment of the embedding contributions to the response equations (eqn (92)). The simplest approximation is to neglect the off-diagonal coupling blocks FI,IIint and FII,Iint arising from the embedding contribution.291 This leads to a decoupling of the response equations of the two subsystems, and the energies of local excitations of the active subsystem can be determined by considering only the matrix FI,I = FI + FI,Iint, where the additional embedding contribution is determined by the embedding kernel given in eqn (94). This approximation corresponds to a neglect of the response of the environment.
Such a scheme can be employed for the calculation of solvent effects on local excitation energies by combining it with approximate construction of the solvent electron density.292 Because the TDDFT response calculation is limited to the active subsystem describing the solute molecule this results in an efficient treatment and allows for the inclusion of large frozen solvent shells as well as an averaging over a sufficient number of solvent structures. The simplest approximation for the solvent density is to use the sum of the densities of isolated water molecules. Such a description can be further refined by updating the density of a few solvent molecules close to the active subsystem in freeze-and-thaw iterations.140,293 Similar schemes can be used to treat local excitations in protein environments.294,295
With a fixed frozen density, such FDE calculations correspond to electronic embedding in the BT classification. Accounting for the ground-state polarization of the environment leads to a polarizable embedding scheme, but within the approximation discussed so far the polarized response of the environment density is not included. A discussion of these different contributions and a comparison to a polarizable QM/MM description can be found in ref. 296.
A computational strategy for an efficient treatment of the full embedding contributions to the response matrices has been devised by Neugebauer.150,151 In his subsystem TDDFT scheme, off-diagonal coupling contributions to the response matrices are not neglected. Instead, the excitation energies of the individual subsystems are determined first, and in a second step the coupling contributions are included only for those excitations that are of interest. This allows for an efficient treatment of both the polarization of the environment151,297 and of couplings between local excitations.150 Neugebauer and coworkers have employed their scheme in several studies of photosynthetic systems, in particular light harvesting complexes.294,298 Recent reviews on the calculation of excitation energies with subsystem TDDFT and on the related applications are available.6,8,9
The limitations of these scheme where addressed in later work, in which the constraint that the total density is kept fixed was relaxed.302,303 Instead, the environment density is chosen as ρII = ρtot − ρbareI, where the total density is obtained from a periodic DFT calculation and ρbareI is the density of the isolated subsystem I. This environment density is then kept frozen, i.e., the polarization of the environment is only included through the periodic DFT description, but not updated according to the wavefunction based calculation. This scheme has been applied in a number of studies of ground state properties304–307 and of local excited states.229 For a review of these WFT-in-DFT embedding approaches and their applications, see ref. 7.
For the calculation of excitation energies, wavefunction based methods are often required because of the well-known limitations of TDDFT, but nevertheless a DFT calculation provides an adequate ground-state density. Therefore, a simplified WFT-in-DFT embedding scheme, in which the embedding potential is obtained from a DFT-in-DFT embedding calculation (either using a fixed approximate environment density or an environment density polarized in freeze-and-thaw iterations) has been proposed.70 This simplified scheme has been applied to study electronic excitations of NpO2+2 impurities embedded in ionic crystals using IHFSCC methods.
In applications of in WFT-in-DFT embedding, the response of the environment has not yet been accounted for. With the state-specific wavefunction based methods that were mainly employed (i.e., CASSCF, CI, and IHFSCC), this would be possible by using state-specific embedding potentials.148 However, this approach has not been attempted in practice so far, and would introduce additional problems in the calculation of transition moments since the different electronic states of the active subsystem will no longer be orthogonal. Therefore, an inclusion of the environment response should be easier within response theory, and the corresponding theory as well as working equations for linear-response coupled-cluster methods have been derived recently.152
4.6 Frozen-density embedding with optimized effective potentials
For calculating local excitations and other local molecular properties, FDE calculations employing approximate kinetic-energy functional can provide an accurate description of environment effects in certain cases. In particular, the available approximations are applicable if the interaction between the subsystem of interest and its environment is weak or dominated by electrostatic interactions. However, even in these cases the available approximations to the kinetic-energy component vT[ρI,ρII] of the embedding potential have deficiencies. These inevitably introduce small, but sometimes not negligible errors into the calculated excitation energies. These can be reduced by increasing the size of the active subsystem, but especially in WFT-in-DFT embedding calculations this is not desirable and often not feasible. On the other hand, a description of covalent bonds between subsystems is not possible with the currently available approximations.Therefore, variants of the FDE scheme that avoid such approximations for the kinetic-energy functional or its functional derivative have been developed in recent years by several groups. The evaluation of the kinetic-energy component vT[ρI,ρII] of the embedding potential requires the evaluation of the functional derivative of the noninteracting kinetic-energy functional Ts[ρ] for two different densities, the total density ρtot = ρI + ρII and the density of the active subsystem ρI. By using the Euler–Lagrange equation for the KS system of noninteracting electron with a given, fixed density ρ(r) this functional derivative can be related to the local potential vs[ρ](r) that has this density ρ(r) as its ground state,308
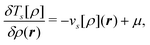 | (124) |
| vT[ρI,ρII](r) = vs[ρI](r) − vs[ρtot](r) + Δμ | (125) |
Within DFT-in-DFT embedding schemes, approaches calculating an approximate embedding potential are usually computationally not advantageous. For determining the embedding potential, one or more calculations on the full system are required, which embedding schemes usually aim to avoid. Nevertheless, such calculations can be employed to demonstrate that schemes based on the embedding potential of eqn (82) do indeed reproduce the electron density of a full calculation. Moreover, the reconstruction of accurate embedding potentials can further guide the development of new approximations to the kinetic-energy component of the embedding potential vT[ρI,ρII]. The latter was the aim of a recent study of Fux et al.,146 and a similar study was performed by Goodpaster et al.311 However, such schemes are not suitable for practical calculations. Therefore, Goodpaster et al. extended their scheme312 by introducing a pairwise approximation that relies on a further partitioning of the frozen environment density (see eqn (73). Instead of calculating the kinetic-energy component of the embedding potential as in eqn (125), it is approximated as
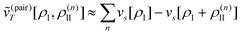 | (126) |
Within WFT-in-DFT embedding schemes, a DFT calculation on the full system is often feasible, while the correlated WFT calculation on the small subsystem of interest becomes the bottleneck. Thus, the use of accurate embedding potentials becomes feasible in this case. This was realized by Roncero et al., who were the first to propose the use of OEP methods in the context of WFT-in-DFT embedding.10 Their scheme starts with a DFT or HF calculation on the full system, from which the total electron density ρtot(r) is obtained. This density is then partitioned into an active subsystem and its environment, and an accurate embedding potential for the active subsystem is determined with the ZMP algorithm by requiring that the chosen density of the active subsystem is reproduced in a DFT or HF calculation. This potential is then included in the wavefunction based treatment of the active subsystem. Note that, even though no approximate kinetic-energy functional is used, such a scheme still introduces several approximations: First, the total electron density is calculated with approximate DFT or HF. Second, neither the total density nor the embedding potential are refined to account for the difference between the DFT or HF electron density and the one obtained from a correlated wavefunction based treatment (i.e., an accurate DFT-in-DFT embedding potential is used as approximation to the WFT-in-DFT embedding potential). Finally, when constructing a suitable partitioning of the total density, it is difficult to ensure that the subsystem densities are vs-representable. In particular when localized orbitals are employed, these densities usually contain nodes, which makes them difficult to reproduce with a local potential expanded in a finite basis set (see also the discussion in ref. 146, 313, 314). To address the latter problem, Roncero et al. extended their scheme to allow for an iterative refinement of the density partitioning.315
However, as for the DFT-in-DFT studies in ref. 146 and 311 discussed above, the resulting density partitioning—and thus also the embedding potential—are not unique. This shortcoming was addressed by Carter and co-workers, who defined a unique partitioning by using the idea of partition density-functional theory (P-DFT) of Wasserman and co-workers138,316 to require that the active subsystems and its environment share a common embedding potential.11 Subsequently, they presented a reformulation of the embedding theory in terms of an optimization of the embedding potential, that allows for a conceptually simple implementation of WFT-in-DFT embedding schemes that do not rely on approximate kinetic-energy functionals.12 Even though results were only presented for DFT-in-DFT embedding calculations, this scheme can be easily extended to obtain accurate WFT-in-DFT embedding potentials, provided a correlated WFT method that allows for an efficient calculation of the electron density is used.
In such a complete WFT-in-DFT scheme (i.e., one in which the density calculated with WFT is used to construct an accurate embedding potential), the only remaining approximations are those inherent to the (approximate) WFT treatment of the subsystem of interest and the (approximate) DFT treatment of the environment as well as the use of an approximate functional for the exchange–correlation component of the embedding potential. However, all these approximations are justified and controllable. The largest remaining obstacle for such complete WFT-in-DFT schemes is the need for OEP methods. In combination with a finite orbital basis set the reconstruction of the local potential corresponding to a given density is an ill-posed problem.317,318 Therefore, the embedding potentials obtained with finite-basis set OEP methods are in general not unique. This will affect the energy and density from a correlated WFT calculation on the active subsystem as well as molecular properties. Thus, numerically stable OEP methods that provide unambiguous embedding potentials are required319–321 and a new approach addressing these issues has been developed recently.322
The existing complete WFT-in-DFT methods using accurate embedding potentials11,12 can also be applied directly to a state-specific WFT approaches for calculating excited states. This can either be done in an approximate fashion using a common frozen environment density or in a full treatment that determines a state-specific embedding potential. However, the extension to response theory is still an open issue, because this will also require the calculation of an accurate kinetic-energy contribution to the embedding kernel.
5 Case studies
5.1 Excited states of acetone in aqueous solution
The determination of solvatochromic shifts of acetone in water is one of the de facto standards for evaluating the performance of theoretical approaches for describing solvent effects on excitation energies. Numerous studies have employed a range of electronic structure methods and embedding approaches (see ref. 221 for a non-exaustive summary up to 2005). In Table 1, some of these results are summarized.| Method | Basis | Solvent | E | Shift |
|---|---|---|---|---|
| Supermolecular calculations | ||||
| CASPT2323 | ANO | S(2) | 4.54 | 0.18 |
| TDDFT/BLYP324 | plane wave | S(periodic) | 4.37 | 0.19 |
| TDDFT/PBE0325 | plane wave | S(periodic) | 4.51 | 0.20 |
| Continuum solvation models | ||||
| TDDFT/CAM-B3LYP224 | aug-cc-pVDZ | PCM | 4.59 | 0.08 |
| CASSCF326 | 6–31G* | S(1) + PCM | 4.49 | 0.21 |
| CASPT2323 | ANO | S(2) + DC | 4.50 | 0.14 |
| QM/MM with non-polarizable force fields | ||||
| TDDFT/CAM-B3LYP224 | aug-cc-pVDZ | M2P0 | 4.63 | 0.12 |
| CCSD224 | aug-cc-pVDZ | M2P0 | 4.69 | 0.11 |
| QM/MM with polarizable force fields | ||||
| TDDFT/CAM-B3LYP224 | aug-cc-pVDZ | M2P2 | 4.75 | 0.24 |
| S(1) + M2P2 | 4.70 | 0.19 | ||
| S(2) + M2P2 | 4.68 | 0.17 | ||
| CCSD224 | aug-cc-pVDZ | M2P2 | 4.80 | 0.22 |
| TDDFT/B3LYP234 | Dunning-Hay | EFP-1 | 4.59 | 0.21 |
| TDDFT/B3LYP225 | aug-cc-pVTZ | MM-5 | 4.53 | 0.12 |
| MM-5 + PCM | 4.57 | 0.16 | ||
| Frozen Density Embedding (PW91k approximation) | ||||
| TDDFT/SAOP292 | TZP | LDA/DZ | 4.67 | 0.20 |
| TDDFT/SAOP70 | TZ2P | LDA/DZP | 4.63 | 0.16 |
| CC270 | aug-cc-pVDZ | LDA/DZP | 4.55 | 0.20 |
| Exp.327–329 | 4.68–4.69 | 0.19–0.21 | ||
The simplest approach are supermolecular calculations, where acetone and a number of water molecules are considered explicitly. However, such a treatment is computationally costly and often only a small number of solvent molecules can be considered. For instance, Serrano-Andrés et al.323 performed CASPT2 calculations in which the effect of the solvent was modeled by only two additional water molecules. For these small clusters, static structures with an optimized geometry were used. While this resulted in a good agreement with experiment, it cannot be expected that these results are converged with respect to the size of the solvent shell. Moreover, dynamical effects resulting from the many different possible solvent structures and the associated temperature effects such as peak broadening are not included.
Alternatively, a treatment with periodic boundary conditions avoids errors introduced by a truncation of the system, and in combination with molecular dynamics allows for an inclusion of temperature effects by averaging over a number of snapshots. Such a treatment was employed by Bernasconi et al.324 using Car-Parrinello molecular dynamics (CPMD) in combination with TDDFT. However, with non-hybrid functionals spurious charge-transfer excitations can obscure the picture, which can be alleviated with hybrid functionals.325
Another possibility is the use of continuum solvation models for including the effect of the environment. As discussed above, such an approach implicitly accounts for the dynamics of the solvent, but cannot describe specific interactions, in particular hydrogen bonding. Therefore, the agreement with experiment can be rather poor.224 The popular solution for this shortcoming is the inclusion of a few solvent molecules to the active subsystem.323,326 However, it should be noted that this again requires a suitable averaging over different solvent configurations.
A QM/MM description can significantly improve results with respect to continuum methods, while being significantly cheaper than the full quantum-mechanical treatment including solvent dynamics. Nevertheless, an averaging over a large number of solvent configurations is still required. The relative importance of different parameters characterizing the force fields used to represent the environment have been investigated in the recent benchmark studies of Sneskov et al.330 and of Schwabe et al.,224 using DFT and LR-CCSD cluster for the active subsystem. In the M2P0 model, static partial charges, dipoles, and quadrupoles are used to represent the solvent, but the polarization of the environment is not included. As shown in Table 1, such models underestimate the solvent shift.
Including the polarization of the environment through induced dipoles in the M2P2 model improves the solvatochromic shifts significantly. Furthermore, the analysis of Sneskov et al.330 shows that for acetone, the main effect of the solvent polarization is captured already in the description of the ground-state, with only minor contributions to excited state. A curious finding is that for the better force field models (M2P2), the excitation energies are slightly overestimated for both DFT and coupled cluster. Furthermore, including two water molecules explicitly in the active subsystem results in an improvement of the excitation energies, while the shift remains accurate with respect to experiment. As the change in the shift is much less than for the excitation energies, this could indicate that there are electronic effects that are not captured by the QM/MM description. Moreover, the differences to the results obtained with effective fragment potentials234 indicates that these results are still quite sensitive to the parametrization of the MM model.
In QM/MM calculations, another important question is the size of the MM environment. The studies discussed so far always employed rather large solvent shells because the electrostatic effects are of long range. As a large MM part will necessarily mean more expensive molecular dynamics calculations, Steindal et al.225 have devised a three-level approach, where specific interactions are included with a polarizable QM/MM model (in the Table, MM-5 indicates that waters within a radius of 5 Å are treated explicitly), whereas the bulk contribution is treated with a continuum model. This leads to a faster convergence of the excitation energy with respect to the size of the explicit solvent environment.
The application of approaches based on FDE with approximations for the kinetic energy part of the embedding potential to study solvatochromic shifts has been pioneered by Neugebauer et al.292 They employed snapshots from CPMD simulations of both the gas phase and the solution to obtain geometries of acetone surrounded by 88 water molecules. For those TDDFT calculations were carried out, in which the solvent environment was included via the FDE embedding potential. One important finding of ref. 292 was that nearly identical solvent shifts are obtained when the FDE embedding potential is constructed from an approximate density. Thus, they suggested to use a superposition of densities obtained for isolated water molecules. This approach was subsequently also used70 in combination with CC2 calculations for the active subsystem. Both with TDDFT and with CC2 a very good agreement with experiment is found for the solvatochromic shifts. However, with CC2 the absolute excitation energies are systematically underestimated both in the gas-phase and for solvated acetone, which could be attributed to the approximate treatment of correlation in CC2 and possibly also the use of BLYP-generated structures that do not yield proper C=O distances.
It should be noted that the FDE calculations of Neugebauer et al.292 use a fixed embedding potential which does not include the polarization of the environment, neither for the ground nor for the excited state. In ref. 70, only the ground-state polarization was included via freeze-and-thaw iterations. Both studies include only the uncoupled embedding contributions in the response part, i.e., the response of the environment is not included. Thus, polarizable QM/MM approaches guard an advantage over uncoupled FDE in this respect.296 However, the recent developments for including this polarization at the response level also for FDE should make the two methods comparable for general response properties. On the other hand, FDE keeps the advantage of retaining a full electron density for the solvent and should, therefore, provide a more accurate embedding potential, in particular at shorter distances.296
5.2 Electronic spectra in solid oxides: MgO in bulk and in the presence of defects
Unlike the case of a molecule in solution, there is no single model system for evaluating new methodologies in solid-state applications. Here, we have chosen to discuss MgO because it is a relatively simple ionic material and well-characterized experimentally. Therefore, it has been the subject of several theoretical studies of electronic states arising from excitations in the bulk, surfaces, or of so-called F+or F-centers, which are due to vacant oxygen sites. The results of some of these studies are summarized in Table 2.| Method | Cluster | Environment | E | |
|---|---|---|---|---|
| a Polarizable force field using a semiempirical shell-model for the ion polarizabilities. b Formal point charges (±2) on the site positions on the atoms in the environment, with effective core potentials at positions of Mg atoms close to the cluster. c Fractional point charges from a periodic calculation. d Calculated on a reoptimized geometry in the presence of the vacancy. | ||||
| Bulk MgO | ||||
| ΔDFT/PBE229 | Periodic | 4.48 | ||
| GW/BSE331–333 | Periodic | 7.2–7.7 | ||
| CIS44 | Mg4O4 | (MgO)108 | Force fielda | 8.9 |
| CISD44 | 7.5 | |||
| CASPT2229 | Mg4O4 | (MgO)252 | Madelungb | 6.62 |
| Madelungc | 6.87 | |||
| MRCISD229 | Mg4O4 | (MgO)252 | FDE | 5.63 |
| Exp.334,335 | 7.5–7.8 | |||
| F center (neutral O vacancy defect, 2 electrons trapped) | ||||
| ΔSCF-HF336 | Mg14O12 | (MgO)1674 | Madelung | 2.62 |
| (MgO)168 | AIMP | 7.45 | ||
| MRCI337 | Mg14O12 | Mg2+24 | AIMP | 6.00 |
| CASPT2338 | 5.59 | |||
| CASSCF339 | Mg14O12 | Mg2+157 O2−159 | AIMP | 6.45 |
| CASPT2339 | 5.47 (5.01d) | |||
| Exp.340 | 5.03 | |||
| F+ center (O− vacancy defect, one electron trapped) | ||||
| MRCI337 | Mg14O12 | Mg2+24 | AIMP | 5.75 |
| CASPT2338 | 5.95 | |||
| CASSCF339 | Mg14O12 | Mg2+157 O2−159 | AIMP | 6.73 |
| CASPT2339 | 5.96 (5.22d) | |||
| Exp.340 | 4.96 | |||
Excitations in the bulk have been studied by plane-wave DFT/PBE229 as well as embedded clusters44,229 and correlated solid-state approaches.331–333 Unsurprisingly, one sees that the latter yield the best agreement with experiment, whereas DFT calculations severely underestimate the excitation energies. On the other hand, embedded cluster calculations employing wavefunction based methods perform rather well. Already CIS is significantly closer to experiment than the DFT/PBE calculations. The CISD calculation of Shluger et al.44 using a polarizable force field to describe the environment yields results in excellent agreement with experiment. However, one cannot rule out a such a good agreement is not due to fortuitous error cancellation.
On the other hand, the results of Carter and coworkers229 employing a better correlation method (CASPT2) in combination with a static point charge description of the environment are about 1 eV below experiment. Moreover, the change in excitation energies with increased cluster size in these calculations229 does not show a clear convergence trend and the results are sensitive to the choice of the point charges for the environment. This could be due to an insufficient inclusion of Pauli repulsion via effective core pseudopotentials at of Mg2+atoms close to the embedded clusters.
It is also interesting to see that an FDE description of the environment in combination with a MR-CISD treatment of the active subsystem also underestimates the excitation energies rather strongly. This is apparently in contrast to the good performance of FDE for other local excitations for impurities in ionic solids.70,288–290 This could be due to an insufficient account of Pauli repulsion by the kinetic energy functionals in use, even though the authors argue from an analysis of the embedding potential that this is not the cause of the problem.229 Nevertheless, it might merit further investigation, for instance with the recently developed FDE scheme employing accurate optimized embedding potentials.11,12 In addition, it should be pointed out that the FDE calculations do not account for the response of the environment, since the fixed embedding potential obtained for the ground-state is also employed for the excited states.
Finally, we turn to local excitations of defect sites, which represent a situation also encountered when describing materials with impurities or doping agents. Comparing the results of Miyoski et al.336 with point-charge embedding and AIMPs clearly shows the importance of the inclusion of non-classical, repulsive parts of the embedding potential. With a purely electrostatic embedding potential, a spurious delocalization of the embedded cluster wavefunction over the environment occurs. The use of AIMPs prevents this,257,336 even though the ΔSCF-HF calculation overestimates the experimental excitation energy significantly. This can be improved if electron correlation is included in an appropriate fashion.338,339 Moreover, comparing the two CASPT2 results shows that a sufficiently large environment and a more flexible description of the buffer region are still important.
For the defects another important aspect is the proper description of the geometry. Relaxation effects due to the creation of the vacancies need to be included. In the examples discussed here, these were found to be as important as electron correlation, as they lower the excitation energies of the F and F+ centers by about 0.5 and 0.8 eV, respectively. If these are included, the CASPT2 results are in very good agreement with the experimental values. It should be noted here that the same accuracy is not achieved for both defects. This is due to the more delocalized nature of the excited states for the F+ centers, which would likely require larger clusters for the active subsystem as well as extended basis sets.
6 Concluding remarks
In this review we have presented the ingredients needed for a quantum-chemical description of electronic excitations in complex chemical systems. This includes electronic structure methods capable of treating excited states as well as embedding methods for extending their applicability from relatively small molecules to larger systems. In this respect, we have attempted to outline the strengths and weaknesses of the different approaches in practical applications, with a particular focus on the treatment of local electronic excitations. From these it becomes evident that both a proper inclusion of electron correlation in the electronic structure calculation and an appropriate inclusion of non-classical contributions to the embedding potential at short range as well as of long-range electrostatic effects are all decisive. However, no single method or combination of methods can claim to be accurate, computationally affordable, and generally applicable at the same time.Thus, when considering quantum-chemical embedding schemes it is more relevant to think of them as a framework in which different approximations can be made in practice, in order to arrive at a good balance between accuracy and computational cost. We believe that the FDE theory can provide such a framework. First, for the ground-state it allows the seamless combination of density-functional and wavefunction theory-based electronic structure methods through their interaction via a formally exact DFT-based embedding potential. Second, in combination with response theory, the same can be achieved for electronically excited states. Going beyond local excited states, FDE-based approaches offer the additional advantage that they are able to describe the coupling of electronic excitations of different subsystems, since a quantum-mechanical description is retained for all parts.
Nevertheless, there are still several challenges FDE-based approaches should address in the future. The first one is the development of approximations to the kinetic-energy component of the embedding potential that are both computationally efficient and sufficiently accurate to describe, for instance, situations where the active subsystem and its environment are linked by strong interactions such as covalent bonds. Methods based on the use of accurate optimized embedding potentials might prove to be a valuable tool in this respect, but these will probably only be feasible within WFT-in-DFT embedding schemes. Second, with the recent emergence of WFT-in-DFT approaches for calculating excited states and other molecular properties with response theory, the proper inclusion of couplings between the subsystem remains a challenge and will require additional methodological developments as well as flexible computer implementations and applications of such schemes.
Acknowledgements
C.R.J. gratefully acknowledges funding from the DFG-Center for Functional Nanostructures at KIT. A.S.P.G. acknowledges support from PhLAM (Laboratoire de Physique des Lasers, Atomes et Molécules, Unité Mixte de Recherche de l'Université de Lille 1 et du CNRS).References
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nature Chem., 2011, 3, 763–774 CrossRef CAS.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS.
- B. M. van der Ende, L. Aarts and A. Meijerink, Phys. Chem. Chem. Phys., 2009, 11, 11081–11095 RSC.
- I. Navizet, Y.-J. Liu, N. Ferré, D. Roca-Sanjuán and R. Lindh, ChemPhysChem, 2011, 12, 3064–3076 CrossRef CAS.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef.
- C. König and J. Neugebauer, ChemPhysChem, 2012, 13, 386–425 CrossRef.
- P. Huang and E. A. Carter, Annu. Rev. Phys. Chem., 2008, 59, 261–290 CrossRef CAS.
- J. Neugebauer, ChemPhysChem, 2009, 10, 3148–3173 CrossRef CAS.
- J. Neugebauer, Phys. Rep., 2010, 489, 1–87 CrossRef CAS.
- O. Roncero, M. P. de Lara-Castells, P. Villarreal, F. Flores, J. Ortega, M. Paniagua and A. Aguado, J. Chem. Phys., 2008, 129, 184104 CrossRef CAS.
- C. Huang, M. Pavone and E. A. Carter, J. Chem. Phys., 2011, 134, 154110 CrossRef.
- C. Huang and E. A. Carter, J. Chem. Phys., 2011, 135, 194104 CrossRef.
- S. Grimme, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz, R. Larter and T. R. Cundari, Wiley, 2004, vol. 20, pp. 153–218 Search PubMed.
- P. H. P. Harbach and A. Dreuw, in Modeling of Molecular Properties, ed. P. Comba, Wiley, 2011, pp. 29–47 Search PubMed.
- L. González, D. Escudero and L. Serrano-Andrés, ChemPhysChem, 2012, 13, 28–51 CrossRef.
- C. Filippi, M. Zaccheddu and F. Buda, J. Chem. Theory Comput., 2009, 5, 2074–2087 CrossRef CAS.
- Ch. R. Jacob and M. Reiher, J. Chem. Phys., 2009, 130, 084106 CrossRef.
- Ch. R. Jacob, S. Luber and M. Reiher, Chem.-Eur. J., 2009, 15, 13491–13508 CrossRef CAS.
- O. Christiansen, P. Jørgensen and C. Hättig, Int. J. Quantum Chem., 1998, 68, 1–52 CrossRef CAS.
- D. J. Tannor, Introduction to Quantum Mechanics: A Time-Dependent Perspective, University Science Books, 2006 Search PubMed.
- T. Helgaker, S. Coriani, P. Jorgensen, K. Kristensen, J. Olsen and K. Ruud, Chem. Rev., 2012, 112, 543–631 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2nd edn., 2001 Search PubMed.
- J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C, 2006, 102, 203–226 RSC.
- D. Rappoport, N. R. M. Crawford, F. Furche and K. Burke, in Computational Inorganic and Bioinorganic Chemistry, ed. E. I. Solomon, R. A. Scott and R. B. King, Wiley, 2009, pp. 159–172 Search PubMed.
- A. J. Cohen, P. Mori-Sanchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS.
- O. Gunnarsson and B. I. Lundqvist, Phys. Rev. B, 1976, 13, 4274–4298 CrossRef CAS.
- U. von Barth, Phys. Rev. A, 1979, 20, 1693–1703 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902–908 CrossRef CAS.
- R. Gaudoin and K. Burke, Phys. Rev. Lett., 2004, 93, 173001 CrossRef CAS.
- T. Ziegler, A. Rauk and E. J. Baerends, Theor. Chim. Acta, 1977, 43, 261–271 CrossRef CAS.
- C. Daul, Int. J. Quantum Chem., 1994, 52, 867–877 CrossRef CAS.
- M. Levy and A. Nagy, Phys. Rev. Lett., 1999, 83, 4361–4364 CrossRef CAS.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS.
- C.-L. Cheng, Q. Wu and T. Van Voorhis, J. Chem. Phys., 2008, 129, 124112 CrossRef.
- T. Kowalczyk, S. R. Yost and T. V. Voorhis, J. Chem. Phys., 2011, 134, 054128 CrossRef.
- T. Ziegler, M. Seth, M. Krykunov, J. Autschbach and F. Wang, J. Chem. Phys., 2009, 130, 154102 CrossRef.
- J. Cullen, M. Krykunov and T. Ziegler, Chem. Phys., 2011, 391, 11–18 CrossRef CAS.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure Theory, John Wiley & Sons, Chichester, 2000 Search PubMed.
- R. G. Szalay, T. M. an G. Gidofalvi, H. Lischka and R. Shepard, Chem. Rev., 2012, 112, 108–181 CrossRef.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS.
- A. L. Shluger, P. V. Sushko and L. N. Kantorovich, Phys. Rev. B, 1999, 59, 2417–2430 CrossRef CAS.
- P. V. Sushko and A. L. Shluger, Surf. Sci., 1999, 421, L157–L165 CrossRef CAS.
- L. Goerigk and S. Grimme, J. Chem. Phys., 2010, 132, 184103 CrossRef.
- H. H. Falden, K. R. Falster-Hansen, K. L. Bak, S. Rettrup and S. A. Sauer, J. Phys. Chem. A, 2009, 113, 11995–12012 CrossRef CAS.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, Chem. Phys. Lett., 1994, 219, 21–29 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- G. Li Manni, A. L. Dzubak, A. Mulla, D. W. Brogden, J. F. Berry and L. Gagliardi, Chem.-Eur. J., 2012, 18, 1737–1749 CrossRef CAS.
- G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS.
- K. H. Marti and M. Reiher, Phys. Chem. Chem. Phys., 2011, 13, 6750–6759 RSC.
- J. Miralles, O. Castell, R. Caballol and J.-P. Malrieu, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- V. M. Garcia, R. Caballol and J.-P. Malrieu, J. Chem. Phys., 1998, 109, 504–511 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2003, 119, 9428–9443 CrossRef CAS.
- I. Negodaev, C. de Graaf and R. Caballol, J. Phys. Chem. A, 2010, 114, 7553–7560 CrossRef CAS.
- C. de Graaf, X. López, J. L. Ramos and J. M. Poblet, Phys. Chem. Chem. Phys., 2010, 12, 2716–2721 RSC.
- R. Maurice, A. M. Pradipto, N. Guihéry, R. Broer and C. de Graaf, J. Chem. Theory Comput., 2010, 6, 3092–3101 CrossRef CAS.
- F. Neese, J. Inorg. Biochem., 2006, 100, 716–726 CrossRef CAS.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2008, 128, 114117 CrossRef.
- A. Venkatnathan, A. B. Szilva, D. Walter, R. J. Gdanitz and E. A. Carter, J. Chem. Phys., 2004, 120, 1693–1704 CrossRef CAS.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–351 CrossRef CAS.
- H. Koch, H. J. A. Jensen, P. Jorgensen and T. Helgaker, J. Chem. Phys., 1990, 93, 3345–3350 CrossRef CAS.
- H. Koch, R. Kobayashi, A. S. de Meras and P. Jorgensen, J. Chem. Phys., 1994, 100, 4393–4400 CrossRef CAS.
- D. I. Lyakh, M. Musial, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS.
- V. V. Ivanov, D. I. Lyakh and L. Adamowicz, Phys. Chem. Chem. Phys., 2009, 11, 2355–2370 RSC.
- I. Infante, E. Eliav, M. J. Vilkas, Y. Ishikawa, U. Kaldor and L. Visscher, J. Chem. Phys., 2007, 127, 124308 CrossRef.
- I. Infante, A. S. P. Gomes and L. Visscher, J. Chem. Phys., 2006, 125, 074301 CrossRef.
- C. Danilo, V. Vallet, J.-P. Flament and U. Wahlgren, Phys. Chem. Chem. Phys., 2009, 12, 1116–1130 RSC.
- A. S. P. Gomes, Ch. R. Jacob and L. Visscher, Phys. Chem. Chem. Phys., 2008, 10, 5353–5362 RSC.
- F. Real, A. S. P. Gomes, L. Visscher, V. Vallet and E. Eliav, J. Phys. Chem. A, 2009, 113, 12504–12511 CrossRef CAS.
- F. Ruipérez, C. Danilo, F. Réal, J.-P. Flament, V. Vallet and U. Wahlgren, J. Phys. Chem. A, 2009, 113, 1420–1428 CrossRef.
- P. Tecmer, A. S. P. Gomes, U. Ekström and L. Visscher, Phys. Chem. Chem. Phys., 2011, 13, 6249–6259 RSC.
- J.-B. Rota, S. Knecht, T. Fleig, D. Ganyushin, T. Saue, F. Neese and H. Bolvin, J. Chem. Phys., 2011, 135, 114106 CrossRef.
- I. Lindgren and D. Mukherjee, Phys. Rep., 1987, 151, 93–127 CrossRef CAS.
- D. Mukhopadhyay, S. Mukhopadhyay, R. Chaudhuri and D. Mukherjee, Theor. Chim. Acta, 1991, 80, 441–467 CrossRef CAS.
- U. Kaldor, Theor. Chem. Acc, 1991, 80, 427–439 CAS.
- L. Meissner, J. Chem. Phys., 1998, 108, 9227–9235 CrossRef CAS.
- L. Meissner and M. Musiał, in Recent Progress in Coupled Cluster Methods, ed. P. Ćársky, Springer, 2010, p. 395 Search PubMed.
- A. Landau, E. Eliav, Y. Ishikawa and U. Kaldor, J. Chem. Phys., 2000, 113, 9905–9910 CrossRef CAS.
- A. Landau, E. Eliav, Y. Ishikawa and U. Kaldor, J. Chem. Phys., 2001, 115, 6862–6865 CrossRef CAS.
- E. Eliav, A. Borschevsky, K. R. Shamasundar, S. Pal and U. Kaldor, Int. J. Quantum Chem., 2009, 109, 2909–2915 CrossRef CAS.
- N. Vaval, P. Manohar and S. Pal, Collect. Czech. Chem. Commun., 2005, 70, 851–863 CrossRef CAS.
- A. S. P. Gomes, L. Visscher, H. Bolvin, T. Saue, S. Knecht, T. Fleig and E. Eliav, J. Chem. Phys., 2010, 133, 064305 CrossRef.
- M. Musial and R. J. Bartlett, J. Chem. Phys., 2008, 129, 044101 CrossRef.
- M. Musial and R. J. Bartlett, J. Chem. Phys., 2008, 129, 134105 CrossRef.
- M. Musial and R. J. Bartlett, Chem. Phys. Lett., 2008, 457, 267–270 CrossRef CAS.
- K. Andersson, P.-A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- J. Finley, P.-A. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- J. P. Finley, Chem. Phys. Lett., 1998, 283, 277–282 CrossRef CAS.
- B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223 CrossRef CAS.
- N. Forsberg and P.-A. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- G. Ghigo, B. O. Roos and P.-A. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- H. A. Witek, Y.-K. Choe, J. P. Finley and K. Hirao, J. Comput. Chem., 1998, 108, 1081–1088 Search PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- G. La Macchia, I. Infante, R. Juraj, J. K. Gibson and L. Gagliardi, Phys. Chem. Chem. Phys., 2008, 10, 7278–7283 RSC.
- I. Infante, A. Kovacs, G. L. Macchia, A. R. M. Shahi, J. K. Gibson and L. Gagliardi, J. Phys. Chem. A, 2010, 114, 6997–6015 CrossRef.
- C. de Graaf, C. Sousa, I. de P. R. Moreira and F. Illas, J. Phys. Chem. A, 2001, 105, 11371–11378 CrossRef CAS.
- A. Ghosh and P. R. Taylor, Curr. Opin. Chem. Biol., 2003, 7, 113–124 CrossRef CAS.
- K. Pierloot, Mol. Phys., 2003, 101, 2083–2094 CrossRef CAS.
- S. Villaume, A. Strich, C. Daniel, S. A. Perera and R. J. Bartlett, Phys. Chem. Chem. Phys., 2007, 9, 6115–6122 RSC.
- S. Vancoillie, H. Zhao, M. Radon and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582 CrossRef CAS.
- K. Pierloot and E. van Besien, J. Chem. Phys., 2005, 123, 204309 CrossRef.
- P. Wahlin, V. Vallet, U. Wahlgren and I. Grenthe, Inorg. Chem., 2009, 48, 11310–11313 CrossRef CAS.
- O. Christiansen, A. Halkier, H. Koch, P. Jorgensen and T. Helgaker, J. Chem. Phys., 1998, 108, 2801–2816 CrossRef.
- E. K. U. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255–291 CrossRef CAS.
- M. E. Casida, in Recent Advances in Density-Functional Methods, ed. D. P. Chong, World Scientific, Singapore, 1995, pp. 155–192 Search PubMed.
- P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, J. Chem. Phys., 2002, 117, 9630–9645 CrossRef.
- P. Sałek, T. Helgaker and T. Saue, Chem. Phys., 2005, 311, 187–201 CrossRef.
- A. Kovyrshin and J. Neugebauer, J. Chem. Phys., 2010, 133, 174114 CrossRef.
- J. Autschbach and T. Ziegler, Coord. Chem. Rev., 2003, 238–239, 83–126 CrossRef CAS.
- F. Furche and D. Rappoport, Computational Photochemistry, in Computational and Theoretical Chemistry, ed. M. Olivucci, Elsevier, Amsterdam, 2005, vol. 16 Search PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- D. Jacquemin, E. A. Perpéte, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2010, 6, 1532–1537 CrossRef CAS.
- J. Preat, D. Jacquemin, J.-M. A. V. Wathelet and E. A. Perpéte, J. Phys. Chem. A, 2006, 110, 8144–8150 CrossRef CAS.
- D. Jacquemin, V. Wathelet, E. A. Perpéte, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Phys. Chem., 2009, 130, 054112 CrossRef.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103 CrossRef.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2010, 133, 174318 CrossRef.
- D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2000, 2, 2117–2121 RSC.
- R. van Leeuwen and E. J. Baerends, Phys. Rev. A, 1994, 49, 2421–2431 CrossRef CAS.
- P. R. T. Schipper, O. V. Gritsenko, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2000, 112, 1344–1352 CrossRef CAS.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2004, 121, 655–660 CrossRef CAS.
- J. Autschbach, ChemPhysChem, 2009, 10, 1757–1760 CrossRef CAS.
- M. E. Casida, J. Chem. Phys., 2005, 122, 054111 CrossRef.
- N. T. Maitra, F. Zhang, R. J. Cave and K. Burke, J. Chem. Phys., 2004, 120, 5932–5937 CrossRef CAS.
- O. Christiansen, A. Halkier, H. Koch, P. Jorgensen and T. Helgaker, J. Chem. Phys., 1998, 108, 2801–2815 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- D. Kats, T. Korona and M. Schütz, J. Chem. Phys., 2006, 125, 104106 CrossRef.
- T. A. Wesolowski and A. Warshel, J. Phys. Chem., 1993, 97, 8050–8053 CrossRef CAS.
- G. Senatore and K. R. Subbaswamy, Phys. Rev. B, 1986, 34, 5754–5757 CrossRef CAS.
- M. D. Johnson, K. R. Subbaswamy and G. Senatore, Phys. Rev. B, 1987, 36, 9202–9211 CrossRef CAS.
- P. Cortona, Phys. Rev. B, 1991, 44, 8454–8458 CrossRef.
- P. Elliott, K. Burke, M. H. Cohen and A. Wasserman, Phys. Rev. A, 2010, 82, 024501 CrossRef.
- M. Iannuzzi, B. Kirchner and J. Hutter, Chem. Phys. Lett., 2006, 421, 16–20 CrossRef CAS.
- Ch. R. Jacob, J. Neugebauer and L. Visscher, J. Comput. Chem., 2008, 29, 1011–1018 CrossRef CAS.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672 CrossRef CAS.
- N. Govind, Y. A. Wang and E. A. Carter, J. Chem. Phys., 1999, 110, 7677–7688 CrossRef CAS.
- T. A. Wesolowski, Phys. Rev. A, 2008, 77, 012504 CrossRef.
- F. Aquilante and T. A. Wesolowski, J. Chem. Phys., 2011, 135, 084120 CrossRef.
- T. A. Wesolowski, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszczynski, World Scientific, Singapore, 2006, vol. 10, pp. 1–82 Search PubMed.
- S. Fux, Ch. R. Jacob, J. Neugebauer, L. Visscher and M. Reiher, J. Chem. Phys., 2010, 132, 164101 CrossRef.
- T. A. Wesolowski and J. Weber, Chem. Phys. Lett., 1996, 248, 71–76 CrossRef CAS.
- Y. G. Khait and M. R. Hoffmann, J. Chem. Phys., 2010, 133, 044107 CrossRef.
- M. E. Casida and T. A. Wesolowski, Int. J. Quantum Chem., 2004, 96, 577–588 CrossRef CAS.
- J. Neugebauer, J. Chem. Phys., 2007, 126, 134116 CrossRef.
- J. Neugebauer, J. Chem. Phys., 2009, 131, 084104 CrossRef.
- S. Höfener, A. Severo Pereira Gomes and L. Visscher, J. Chem. Phys., 2012, 136, 044104 CrossRef.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- Ch. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- J. Tomasi, Theor. Chem. Acc., 2004, 112, 184–203 CrossRef CAS.
- B. Mennucci and R. Cammi, Continuum Solvation Models in Chemical Physics: From Theory to Applications, Wiley, 1st edn., 2008 Search PubMed.
- A. Pedone, M. Biczysko and V. Barone, ChemPhysChem, 2010, 11, 1812–1832 CAS.
- B. Mennucci, J. Phys. Chem. Lett., 2010, 1, 1666–1674 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805 Search PubMed.
- R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 1999, 103, 9100–9108 CrossRef CAS.
- O. Christiansen and K. V. Mikkelsen, J. Chem. Phys., 1999, 110, 1365–1375 CrossRef CAS.
- B. Mennucci, C. Cappelli, C. A. Guido, R. Cammi and J. Tomasi, J. Phys. Chem. A, 2009, 113, 3009–3020 CrossRef CAS.
- M. Cossi, V. Barone and M. A. Robb, J. Chem. Phys., 1999, 111, 5295–5302 CrossRef CAS.
- R. Cammi, L. Frediani, B. Mennucci, J. Tomasi, K. Ruud and K. V. Mikkelsen, J. Chem. Phys., 2002, 117, 13–26 CrossRef CAS.
- O. Christiansen and K. V. Mikkelsen, J. Chem. Phys., 1999, 110, 8348–8360 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2003, 119, 10519–10535 CrossRef CAS.
- C. B. Nielsen, S. P. A. Sauer and K. V. Mikkelsen, J. Chem. Phys., 2003, 119, 3849–3870 CrossRef CAS.
- J. Kongsted, T. B. Pedersen, A. Osted, A. E. Hansen, K. V. Mikkelsen and O. Christiansen, J. Phys. Chem. A, 2004, 108, 3632–3641 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2003, 118, 1620–1633 CrossRef CAS.
- G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2006, 125, 164515 CrossRef.
- J. Kongsted and B. Mennucci, J. Phys. Chem. A, 2007, 111, 9890–9900 CrossRef CAS.
- J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. B, 2008, 112, 1456–1464 CrossRef CAS.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS.
- J. Gao, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, VCH, New York, 1995, vol. 7, pp. 119–185 Search PubMed.
- P. Sherwood, in Modern Methods and Algorithms of Quantum Chemistry, of NIC Series, ed. J. Grotendorst, John von Neumann Institute for Computing, Jülich, 2000, vol. 1, pp. 257–277 Search PubMed.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2006, 117, 185–199 CrossRef.
- H. M. Senn and W. Thiel, Top. Curr. Chem., 2007, 268, 173–290 CrossRef CAS.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS.
- M. Wanko, M. Hoffmann, P. Strodel, A. Koslowski, W. Thiel, F. Neese, T. Frauenheim and M. Elstner, J. Phys. Chem. B, 2005, 109, 3606–3615 CrossRef CAS.
- M. Hoffmann, M. Wanko, P. Strodel, P. H. König, T. Frauenheim, K. Schulten, W. Thiel, E. Tajkhorshid and M. Elstner, J. Am. Chem. Soc., 2006, 128, 10808–10818 CrossRef CAS.
- K. Fujimoto, S. Hayashi, J.-y. Hasegawa and H. Nakatsuji, J. Chem. Theory Comput., 2007, 3, 605–618 CrossRef CAS.
- J. S. Frähmcke, M. Wanko, P. Phatak, M. A. Mroginski and M. Elstner, J. Phys. Chem. B, 2010, 114, 11338–11352 CrossRef.
- J.-y. Hasegawa, K. J. Fujimoto and H. Nakatsuji, ChemPhysChem, 2011, 12, 3106–3115 CrossRef CAS.
- M. A. L. Marques, X. López, D. Varsano, A. Castro and A. Rubio, Phys. Rev. Lett., 2003, 90, 258101 CrossRef.
- E. Epifanovsky, I. Polyakov, B. Grigorenko, A. Nemukhin and A. I. Krylov, J. Chem. Theory Comput., 2009, 5, 1895–1906 CrossRef CAS.
- C. Filippi, F. Buda, L. Guidoni and A. Sinicropi, J. Chem. Theory Comput., 2011, 8, 112–124 CrossRef.
- K. B. Bravaya, M. G. Khrenova, B. L. Grigorenko, A. V. Nemukhin and A. I. Krylov, J. Phys. Chem. B, 2011, 115, 8296–8303 CrossRef CAS.
- J. Sauer, Chem. Rev., 1989, 89, 199–255 CrossRef CAS.
- K. Jug and T. Bredow, J. Comput. Chem., 2004, 25, 1551–1567 CrossRef CAS.
- J. Weber and J. Schmedt auf der Günne, Phys. Chem. Chem. Phys., 2010, 12, 583–603 RSC.
- E. V. Stefanovich and T. N. Truong, J. Phys. Chem. B, 1998, 102, 3018–3022 CrossRef CAS.
- H. M. Evjen, Phys. Rev., 1932, 39, 675–687 CrossRef CAS.
- A. Gellé and M.-B. Lepetit, J. Chem. Phys., 2008, 128, 244716 CrossRef.
- P. V. Sushko and I. V. Abarenkov, J. Chem. Theory Comput., 2010, 6, 1323–1333 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- S. E. Derenzo, M. K. Klintenberg and M. J. Weber, J. Chem. Phys., 2000, 112, 2074–2081 CrossRef CAS.
- M. Klintenberg, S. E. Derenzo and M. J. Weber, Comput. Phys. Commun., 2000, 131, 120–128 CrossRef CAS.
- B. Herschend, M. Baudin and K. Hermansson, J. Chem. Phys., 2004, 120, 4939–4948 CrossRef CAS.
- A. M. Burow, M. Sierka, J. Döbler and J. Sauer, J. Chem. Phys., 2009, 130, 174710 CrossRef.
- K. Fink, Phys. Chem. Chem. Phys., 2005, 7, 2999–3004 RSC.
- J. A. Mejias, V. Staemmler and H. J. Freund, J. Phys. Condens. Matter, 1999, 11, 7881–7891 CrossRef CAS.
- N. Govind, P. V. Sushko, W. P. Hess, M. Valiev and K. Kowalski, Chem. Phys. Lett., 2009, 470, 353–357 CrossRef CAS.
- D. Stueber, F. N. Guenneau and D. M. Grant, J. Chem. Phys., 2001, 114, 9236–9243 CrossRef CAS.
- J. Torras, S. Bromley, O. Bertran and F. Illas, Chem. Phys. Lett., 2008, 457, 154–158 CrossRef CAS.
- R. Bjornsson and M. Bühl, J. Chem. Theory Comput., 2012, 8, 498–508 CrossRef CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- J. M. Vail, J. Phys. Chem. Solids, 1990, 51, 589–607 CrossRef CAS.
- V. E. Puchin, E. V. Stefanovich and T. N. Truong, Chem. Phys. Lett., 1999, 304, 258–264 CrossRef CAS.
- V. A. Nasluzov, E. A. Ivanova, A. M. Shor, G. N. Vayssilov, U. Birkenheuer and N. Rösch, J. Phys. Chem. B, 2003, 107, 2228–2241 CrossRef CAS.
- B. T. Thole and P. T. van Duijnen, Theor. Chim. Acta, 1980, 55, 307–318 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- L. Jensen, P. T. van Duijnen and J. G. Snijders, J. Chem. Phys., 2003, 118, 514–521 CrossRef CAS.
- L. Jensen, P. T. van Duijnen and J. G. Snijders, J. Chem. Phys., 2003, 119, 3800–3809 CrossRef CAS.
- C. B. Nielsen, O. Christiansen, K. V. Mikkelsen and J. Kongsted, J. Chem. Phys., 2007, 126, 154112 CrossRef.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Phys. Chem. A, 2003, 107, 2578–2588 CrossRef CAS.
- A. Osted, J. Kongsted, K. V. Mikkelsen and O. Christiansen, Mol. Phys., 2003, 101, 2055–2071 CrossRef CAS.
- J. Kongsted, A. E. Hansen, T. B. Pedersen, A. Osted, K. V. Mikkelsen and O. Christiansen, Chem. Phys. Lett., 2004, 391, 259–266 CrossRef CAS.
- J. Kongsted, A. Osted, T. B. Pedersen, K. V. Mikkelsen and O. Christiansen, J. Phys. Chem. A, 2004, 108, 8624–8632 CrossRef CAS.
- K. Aidas, J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Phys. Chem. A, 2005, 109, 8001–8010 CrossRef CAS.
- J. M. Olsen, K. Aidas and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 3721–3734 CrossRef CAS.
- K. Sneskov, T. Schwabe, J. Kongsted and O. Christiansen, J. Chem. Phys., 2011, 134, 104108 CrossRef.
- T. Schwabe, J. M. H. Olsen, K. Sneskov, J. Kongsted and O. Christiansen, J. Chem. Theory Comput., 2011, 7, 2209–2217 CrossRef CAS.
- A. H. Steindal, K. Ruud, L. Frediani, K. Aidas and J. Kongsted, J. Phys. Chem. B, 2011, 115, 3027–3037 CrossRef CAS.
- I. V. Yudanov, V. A. Nasluzov, K. M. Neyman and N. Rösch, Int. J. Quantum Chem., 1997, 65, 975–986 CrossRef CAS.
- N. W. Winter, R. M. Pitzer and D. K. Temple, J. Chem. Phys., 1987, 86, 3549–3556 CrossRef CAS.
- G. Rossmüller, V. Kleinschmidt, J. Kossmann and C. Hättig, J. Phys. Chem. C, 2009, 113, 1418–1425 Search PubMed.
- D. K. Kanan, S. Sharifzadeh and E. A. Carter, Chem. Phys. Lett., 2012, 519–520, 18–24 CrossRef CAS.
- P. Schwerdtfeger, ChemPhysChem, 2011, 12, 3143–3155 CrossRef CAS.
- P. N. Day, J. H. Jensen, M. S. Gordon, S. P. Webb, W. J. Stevens, M. Krauss, D. Garmer, H. Basch and D. Cohen, J. Chem. Phys., 1996, 105, 1968–1986 CrossRef CAS.
- M. S. Gordon, M. A. Freitag, P. Bandyopadhyay, J. H. Jensen, V. Kairys and W. J. Stevens, J. Phys. Chem. A, 2001, 105, 293–307 CrossRef CAS.
- P. Arora, L. V. Slipchenko, S. P. Webb, A. DeFusco and M. S. Gordon, J. Phys. Chem. A, 2010, 114, 6742–6750 CrossRef CAS.
- S. Yoo, F. Zahariev, S. Sok and M. S. Gordon, J. Chem. Phys., 2008, 129, 144112 CrossRef.
- M. S. Gordon, J. M. Mullin, S. R. Pruitt, L. B. Roskop, L. V. Slipchenko and J. A. Boatz, J. Phys. Chem. B, 2009, 113, 9646–9663 CrossRef CAS.
- D. Ghosh, D. Kosenkov, V. Vanovschi, Ch. F. Williams, J. M. Herbert, M. S. Gordon, M. W. Schmidt, L. V. Slipchenko and A. I. Krylov, J. Phys. Chem. A, 2010, 114, 12739–12754 CrossRef CAS.
- D. D. Kemp, J. M. Rintelman, M. S. Gordon and J. H. Jensen, Theor. Chem. Acc., 2010, 125, 481–491 CrossRef CAS.
- S. Humbel, S. Sieber and K. Morokuma, J. Chem. Phys., 1996, 105, 1959–1967 CrossRef CAS.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363 CrossRef CAS.
- T. Vreven and K. Morokuma, J. Comput. Chem., 2000, 21, 1419–1432 CrossRef CAS.
- H. P. Hratchian, P. V. Parandekar, K. Raghavachari, M. J. Frisch and T. Vreven, J. Chem. Phys., 2008, 128, 034107 CrossRef.
- N. J. Mayhall, K. Raghavachari and H. P. Hratchian, J. Chem. Phys., 2010, 132, 114107 CrossRef.
- H. P. Hratchian, A. V. Krukau, P. V. Parandekar, M. J. Frisch and K. Raghavachari, J. Chem. Phys., 2011, 135, 014105 CrossRef.
- D. G. Fedorov and K. Kitaura, J. Phys. Chem. A, 2007, 111, 6904–6914 CrossRef CAS.
- E. E. Dahlke and D. G. Truhlar, J. Chem. Theory Comput., 2006, 3, 46–53 CrossRef.
- J. L. Pascual, J. Schamps, Z. Barandiarán and L. Seijo, Phys. Rev. B, 2006, 74, 104105 CrossRef.
- G. Fradelos and T. A. Wesolowski, J. Phys. Chem. A, 2011, 115, 10018–10026 CrossRef CAS.
- G. Fradelos and T. A. Wesolowski, J. Chem. Theory Comput., 2011, 7, 213–222 CrossRef CAS.
- L. Seijo and Z. Barandiarán, in Computational Chemistry: Reviews of Current Trends, ed. J. Leszczynski, World Scientific, Singapore, 1999, vol. 4, p. 55 Search PubMed.
- B. Swerts, L. F. Chibotaru, R. Lindh, L. Seijo, Z. Barandiaran, S. Clima, K. Pierloot and M. F. A. Hendrickx, J. Chem. Theory Comput., 2008, 4, 586–594 CrossRef CAS.
- J. L. Pascual, N. Barros, Z. Barandiarán and L. Seijo, J. Phys. Chem. A, 2009, 113, 12454–12460 CrossRef CAS.
- L. Seijo and Z. Barandiarán, Int. J. Quantum Chem., 1996, 60, 617–634 CrossRef CAS.
- R. Llusar, M. Casarrubios, Z. Barandiarán and L. Seijo, J. Chem. Phys., 1996, 105, 5321–5330 CrossRef CAS.
- J. L. Pascual, Z. Barandiarán and L. Seijo, Phys. Rev. B, 2007, 76, 104109 CrossRef.
- B. Ordejón, L. Seijo and Z. Barandiarán, J. Chem. Phys., 2007, 126, 194712 CrossRef.
- F. Real, B. Ordejon, V. Vallet, J.-P. Flament and J. Schamps, J. Chem. Phys., 2009, 131, 194501 CrossRef.
- J. L. Pascual and L. G. M. Pettersson, Chem. Phys. Lett., 1997, 270, 351–356 CrossRef CAS.
- J. L. Pascual and L. Seijo, J. Chem. Phys., 1995, 102, 5368–5376 CrossRef CAS.
- J. L. Whitten and H. Yang, Int. J. Quantum Chem., 1995, 56, 41–47 CrossRef.
- U. Gutdeutsch, U. Birkenheuer, S. Krüger and N. Rösch, J. Chem. Phys., 1997, 106, 6020–6030 CrossRef CAS.
- T. M. Henderson, J. Chem. Phys., 2006, 125, 014105 CrossRef.
- R. J. Buenker, H. P. Liebermann, D. B. Kokh, E. I. Izgorodina and J. L. Whitten, Chem. Phys., 2003, 291, 115–124 CrossRef CAS.
- B. Paulus, Phys. Rep., 2006, 428, 1–52 CrossRef CAS.
- R. G. Gordon and Y. S. Kim, J. Chem. Phys., 1972, 56, 3122–3133 CrossRef CAS.
- Y. S. Kim and R. G. Gordon, J. Chem. Phys., 1974, 60, 1842–1850 CrossRef CAS.
- Ch. R. Jacob, T. A. Wesolowski and L. Visscher, J. Chem. Phys., 2005, 123, 174104 CrossRef.
- S. Laricchia, E. Fabiano and F. Della Sala, J. Chem. Phys., 2010, 133, 164111 CrossRef CAS.
- T. A. Wesolowski and J. Weber, Int. J. Quantum Chem., 1997, 61, 303–311 CrossRef CAS.
- Y. A. Wang and E. A. Carter, in Theoretical Methods in Condensed Phase Chemistry, ed. S. D. Schwartz, Kluwer, Dordrecht, 2000, pp. 117–184 Search PubMed.
- F. Tran and T. A. Wesolowski, Int. J. Quantum Chem., 2002, 89, 441–446 CrossRef CAS.
- J. M. Garcia Lastra, J. W. Kaminski and T. A. Wesolowski, J. Chem. Phys., 2008, 129, 074107 CrossRef.
- A. W. Götz, S. M. Beyhan and L. Visscher, J. Chem. Theory Comput., 2009, 5, 3161–3174 CrossRef.
- S. Laricchia, E. Fabiano, L. A. Constantin and F. Della Sala, J. Chem. Theory Comput., 2011, 7, 2439–2451 CrossRef CAS.
- T. A. Wesolowski, H. Chermette and J. Weber, J. Chem. Phys., 1996, 105, 9182–9190 CrossRef CAS.
- T. A. Wesolowski, J. Chem. Phys., 1997, 106, 8516–8526 CrossRef CAS.
- A. Lembarki and H. Chermette, Phys. Rev. A, 1994, 50, 5328–5331 CrossRef CAS.
- K. Kiewisch, G. Eickerling, M. Reiher and J. Neugebauer, J. Chem. Phys., 2008, 128, 044114 CrossRef.
- S. Fux, K. Kiewisch, Ch. R. Jacob, J. Neugebauer and M. Reiher, Chem. Phys. Lett., 2008, 461, 353–359 CrossRef CAS.
- Ch. R. Jacob, S. M. Beyhan and L. Visscher, J. Chem. Phys., 2007, 126, 234116 CrossRef.
- S. M. Beyhan, A. W. Götz, Ch. R. Jacob and L. Visscher, J. Chem. Phys., 2010, 132, 044114 CrossRef.
- Ch. R. Jacob and L. Visscher, J. Chem. Phys., 2008, 128, 155102 CrossRef.
- P. Cortona and A. Villafiorita Monteleone, Int. J. Quantum Chem., 1994, 52, 987–992 CrossRef CAS.
- P. Cortona, A. Villafiorita Monteleone and P. Becker, Int. J. Quantum Chem., 1995, 56, 831–837 CrossRef.
- J.-M. Gillet and P. Cortona, Phys. Rev. B, 1999, 60, 8569–8574 CrossRef CAS.
- L. L. Boyer and M. J. Mehl, Ferroelectrics, 1993, 150, 13–24 CrossRef.
- W. N. Mei, L. L. Boyer, M. J. Mehl, M. M. Ossowski and H. T. Stokes, Phys. Rev. B, 2000, 61, 11425–11431 CrossRef CAS.
- M. M. Ossowski, L. L. Boyer, M. J. Mehl and H. T. Stokes, Phys. Rev. B, 2002, 66, 224302 CrossRef.
- J. M. García-Lastra, T. Wesolowski, M. T. Barriuso, J. A. Aramburu and M. Moreno, J. Phys.: Condens. Matter, 2006, 18, 1519–1534 CrossRef.
- M. Zbiri, M. Atanasov, C. Daul, J. M. Garcia-Lastra and T. A. Wesolowski, Chem. Phys. Lett., 2004, 397, 441–446 CrossRef CAS.
- M. Zbiri, C. A. Daul and T. A. Wesolowski, J. Chem. Theory Comput., 2006, 2, 1106–1111 CrossRef CAS.
- T. A. Wesolowski, J. Am. Chem. Soc., 2004, 126, 11444–11445 CrossRef CAS.
- J. Neugebauer, M. J. Louwerse, E. J. Baerends and T. A. Wesolowski, J. Chem. Phys., 2005, 122, 094115 CrossRef.
- J. Neugebauer, Ch. R. Jacob, T. A. Wesolowski and E. J. Baerends, J. Phys. Chem. A, 2005, 109, 7805–7814 CrossRef CAS.
- J. Neugebauer, J. Phys. Chem. B, 2008, 112, 2207–2217 CrossRef CAS.
- J. Neugebauer, J. Veldstra and F. Buda, J. Phys. Chem. B, 2011, 115, 3216–3225 CrossRef CAS.
- Ch. R. Jacob, J. Neugebauer, L. Jensen and L. Visscher, Phys. Chem. Chem. Phys., 2006, 8, 2349–2359 RSC.
- J. Neugebauer, C. Curutchet, A. Muñoz Losa and B. Mennucci, J. Chem. Theory Comput., 2010, 6, 1843–1851 CrossRef CAS.
- C. König and J. Neugebauer, Phys. Chem. Chem. Phys., 2011, 13, 10475–10490 RSC.
- N. Govind, Y. A. Wang, A. J. R. da Silva and E. A. Carter, Chem. Phys. Lett., 1998, 295, 129–134 CrossRef CAS.
- T. Klüner, N. Govind, Y. A. Wang and E. A. Carter, Phys. Rev. Lett., 2001, 86, 5954–5957 CrossRef.
- T. Klüner, N. Govind, Y. A. Wang and E. A. Carter, J. Chem. Phys., 2002, 116, 42–54 CrossRef.
- P. Huang and E. A. Carter, J. Chem. Phys., 2006, 125, 084102 CrossRef.
- D. Lahav and T. Klüner, J. Phys. Condens. Matter, 2007, 19, 226001 CrossRef.
- P. Huang and E. A. Carter, Nano Lett., 2006, 6, 1146–1150 CrossRef CAS.
- S. Sharifzadeh, P. Huang and E. Carter, J. Phys. Chem. C, 2008, 112, 4649–4657 CAS.
- P. Huang and E. A. Carter, Nano Lett., 2008, 8, 1265–1269 CrossRef CAS.
- S. Sharifzadeh, P. Huang and E. A. Carter, Chem. Phys. Lett., 2009, 470, 347–352 CrossRef CAS.
- S. Liu and P. W. Ayers, Phys. Rev. A, 2004, 70, 022501 CrossRef.
- Q. Zhao, R. C. Morrison and R. G. Parr, Phys. Rev. A, 1994, 50, 2138–2142 CrossRef CAS.
- Q. Wu and W. Yang, J. Chem. Phys., 2003, 118, 2498–2509 CrossRef CAS.
- J. D. Goodpaster, N. Ananth, F. R. Manby and T. F. Miller, J. Chem. Phys., 2010, 133, 084103 CrossRef.
- J. D. Goodpaster, T. A. Barnes and T. F. Miller, J. Chem. Phys., 2011, 134, 164108 CrossRef.
- T. A. Wesolowski, J. Chem. Phys., 2011, 135, 027101 CrossRef.
- S. Fux, Ch. R. Jacob, J. Neugebauer, L. Visscher and M. Reiher, J. Chem. Phys., 2011, 135, 027102 CrossRef.
- O. Roncero, A. Zanchet, P. Villarreal and A. Aguado, J. Chem. Phys., 2009, 131, 234110 CrossRef CAS.
- J. Nafziger, Q. Wu and A. Wasserman, J. Chem. Phys., 2011, 135, 234101 CrossRef.
- S. Hirata, S. Ivanov, I. Grabowski, R. J. Bartlett, K. Burke and J. D. Talman, J. Chem. Phys., 2001, 115, 1635–1649 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria and E. R. Davidson, J. Chem. Phys., 2006, 124, 141103 CrossRef.
- A. Heßelmann, A. W. Götz, F. Della Sala and A. Görling, J. Chem. Phys., 2007, 127, 054102 CrossRef.
- T. Heaton-Burgess, F. A. Bulat and W. Yang, Phys. Rev. Lett., 2007, 98, 256401 CrossRef.
- T. Heaton-Burgess and W. Yang, J. Chem. Phys., 2008, 129, 194102 CrossRef.
- Ch. R. Jacob, J. Chem. Phys., 2011, 135, 244102 CrossRef.
- L. Serrano-Andrés and M. P. Fülscher, and G. Kallström, Int. J. Quantum Chem., 1997, 65, 167–181 CrossRef.
- L. Bernasconi, M. Sprik and J. Hutter, J. Chem. Phys., 2003, 119, 12417–12431 CrossRef CAS.
- L. Bernasconi, M. Sprik and J. Hutter, Chem. Phys. Lett., 2004, 394, 141–146 CrossRef CAS.
- M. Cossi and V. Barone, J. Chem. Phys., 2000, 112, 2427–2435 CrossRef CAS.
- C. W. Portern and C. Iddings, J. Am. Chem. Soc., 1926, 48, 40–44 CrossRef.
- N. S. Bayliss and R. G. McRae, J. Phys. Chem., 1954, 58, 1006–1011 CrossRef CAS.
- N. S. Bayliss and G. Wills-Johnson, Spectrochim. Acta, Part A, 1968, 24, 551–561 CrossRef CAS.
- K. Sneskov, T. Schwabe, O. Christiansen and J. Kongsted, Phys. Chem. Chem. Phys., 2011, 13, 18551–18560 RSC.
- A. Schleife, C. Rödl, F. Fuchs, J. Furthmüller and F. Bechstedt, Phys. Rev. B, 2009, 80, 035112 CrossRef.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. Lett., 1998, 80, 4514–4517 CrossRef CAS.
- N. P. Wang, M. Rohfling, P. Kruger and J. Pollman, Appl. Phys. A, 2004, 78, 213–221 CrossRef CAS.
- M. L. Bortz, R. H. French, D. J. Jones, R. V. Kasowski and F. S. Ohuchi, Phys. Scr., 1990, 41, 537–541 CrossRef CAS.
- D. M. Roessler and W. C. Walter, Phys. Rev., 1967, 159, 733–738 CrossRef CAS.
- E. Miyoshi, Y. Miyake, S. Katsuki and Y. Sakai, J. Mol. Struct., 1998, 451, 81–88 CrossRef CAS.
- C. Sousa, G. Pacchioni and F. Illas, Surf. Sci., 1999, 429, 217–228 CrossRef CAS.
- C. Sousa and F. Illas, J. Chem. Phys., 2001, 115, 1435–1439 CrossRef CAS.
- D. Dominguez-Ariza, C. Sousa, F. Illas, D. Ricci and G. Pacchioni, Phys. Rev. B, 2003, 68, 054101 CrossRef.
- Y. Chen, R. T. Williams and W. A. Sibley, Phys. Rev., 1969, 182, 960–964 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
