An interaction stress analysis of nanoscale elastic asperity contacts
Meysam
Rahmat
,
Hossein
Ghiasi
and
Pascal
Hubert
*
Department of Mechanical Engineering, McGill University, 817 Sherbrooke St West, Montreal, Quebec, Canada H3A 2K6. E-mail: pascal.hubert@mcgill.ca
First published on 9th November 2011
Abstract
A new contact mechanics model is presented and experimentally examined at the nanoscale. The current work addresses the well-established field of contact mechanics, but at the nanoscale where interaction stresses seem to be effective. The new model combines the classic Hertz theory with the new interaction stress concept to provide the stress field in contact bodies with adhesion. Hence, it benefits from the simplicity of non-adhesive models, while offering the same applicability as more complicated models. In order to examine the model, a set of atomic force microscopy experiments were performed on substrates made from single-walled carbon nanotube buckypaper. The stress field in the substrate was obtained by superposition of the Hertzian stress field and the interaction stress field, and then compared to other contact models. Finally, the effect of indentation depth on the stress field was studied for the interaction model as well as for the Hertz, Derjaguin–Muller–Toporov, and Johnson–Kendall–Roberts models. Thus, the amount of error introduced by using the Hertz theory to model contacts with adhesion was found for different indentation depths. It was observed that in the absence of interaction stress data, the Hertz theory predictions led to smaller errors compared to other contact-with-adhesion models.
1. Introduction
Contact mechanics,1 as one of the main branches of solid mechanics, has always been of great importance. During the past hundred years, numerous studies have addressed various aspects of contact mechanics. The application of this branch, however, is not limited to solid mechanics. Different fields of science including biology,2,3 physics,4–6 chemistry,7,8 and materials science9–11 have benefitted from the variety of contact models. These models were designed to fit the experimental results attained in various subsections of the aforementioned fields.12 Today, there are several models that try to capture the physics of contact and predict the characteristics of the system under study.13The Hertz model14 for contact mechanics is the most famous, and arguably, the most successful contact model, since it is still used over one-hundred years later.15 This model was first introduced in 1882 to examine the effect of elastic contact on the optical interference of glass lenses. Hertz made a few assumptions in his model: the objects are continuous and non-conforming, the surfaces are frictionless, and the involved strains are small. He also considered the solids as half-spaces in order to ignore the effect of boundaries on the stress field. Hertz validated his model by measuring the contact area under an optical microscope. Ninety years later, Johnson, Kendall, and Roberts16 proposed their model, which was aptly named the JKR model, to account for contacts with attractive forces between the solids. They employed the concept of surface energy to understand the contact of elastic solids with adhesion. Their model proved to be successful especially for relatively large and compliant solids with strong adhesion. A few years later, Derjaguin, Muller, and Toporov17 incorporated the contact deformation, as well as the molecular attraction, into their contact model and called it the DMT model. They employed the Hamaker theory18 to model the van der Waals interactions and proved the effectiveness in their model particularly for smaller and stiffer contact bodies with weak adhesion. Afterwards, Tabor19 proposed a criterion that could distinguish the validity range of both the JKR and DMT models for a given system. The criterion used geometric and elastic properties of the system along with the surface energy between the contact bodies. The JKR model was expanded by Maugis20 to account for systems with large contact areas and highly deformed solids. The model employed the maximum force in the Lennard–Jones potential, which led to more accurate predictions, but with the cost of adding complexities to the JKR model. The other improvement in the field of contact models was done by Tatara21 who expanded the Hertz model to nonelastic regimes (i.e., deformations of more than 30 percent22). Along with these significant achievements throughout the years, several other models such as those of Sneddon23 and Sokolov24 were also proposed to simulate contact and interaction phenomena. However, a simple model, such as the Hertz model, to capture the behaviour of a contact system with adhesion was still missing in the literature.
Experimental investigations of contact mechanics benefit from instruments with high precision of force measurements including nanoindenter25,26 and atomic force microscope.27 High force sensitivity,28 along with small tip radius,29 has made atomic force microscopy (AFM) an excellent candidate for experimental studies of contact mechanics.30 The AFM force measurements are not limited to interaction studies,31,32 but also extend to extremely sensitive applications such as measuring the strength of one chemical bond33 or manipulation of single atoms.34,35 A mere force curve, obtained from the AFM, can provide all the information required to model the contact between two objects. Recently, Rahmat and Hubert36 introduced the new concept of interaction stress. They used AFM force curves and presented a method to obtain the non-contact stress field induced in adjacent objects.
In the current study, a new approach to modelling contact mechanics is presented. This approach combines the simplicity of the Hertz theory with the new concept of interaction stress and provides the stress field in contact systems with adhesive interaction. A set of AFM experiments was performed on carbon nanotube buckypaper substrates and the new approach was applied to find the stress field in the samples.
In the following sections, the theory of different contact models, including the proposed model, is described. The results of the AFM experiments are then presented. The discussion section includes the comparison between the new model and its older counterparts, and the conclusion highlights the main contributions of the current study.
2. Theory
The common contact models in the literature, which include Hertz, JKR, and DMT, are detailed in this section. The relationship between the indentation depth, indentation force, and contact area is described. Moreover, the procedure of extracting the stress field in the substrate is also explained in detail. At the end of the section, the new approach for modelling contact with adhesion is proposed. This model uses the interaction stress along with the simple Hertz model.2.1. Hertz model
According to the Hertz theory, the amount of force, F, required to indent an elastic sphere to a depth of δ by means of an elastic spherical indenter can be determined from: | (1) |
 | (2) |
 | (3) |
 | (4) |
 | ||
| Fig. 1 Schematic of the indentation of a flat surface with a spherical indenter. The indentation depth, δ, and the contact radius, a, are illustrated. According to eqn (2) in this case the effective radius of contact bodies, R, is equal to the radius of the spherical indenter since the radius of the flat substrate is equal to infinity. The bottom part shows the top view of the contact area. The blue mesh on the contact area and in the substrate indicates the meshing step to obtain the local pressure on the surface, and the stress filed in the substrate, respectively. | ||
Using the Hertz theory, the radial distribution of contact pressure can be represented by:
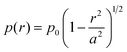 | (5) |
 | (6) |
In order to find the stress field in the substrate subjected to a Hertz contact, a superposition of stresses obtained from the Boussinesq theory37 may be used. Boussinesq presented the stress field in a half-space substrate subjected to a concentrated load on the surface. However, in a Hertz contact, we need to find the stress field in a substrate subjected to a pressure profile as the one expressed by eqn (5). Therefore, the contact area is meshed, and the continuous pressure profile is replaced by individual concentrated loads at the centre of each element. The Boussinesq stress field due to each of the concentrated loads is determined, and by superposing all these stresses, the actual stress field of a Hertz contact is simulated.
2.2. Johnson–Kendall–Roberts model
The effect of surface energy on the contact of elastic solids was investigated by Johnson, Kendall, and Roberts.16 They explained that two solids with adhesion at the surface attract each other; hence, unlike the Hertz model, the contact area at zero external force is not zero. An energy-based approach was followed and it was demonstrated that the force required to separate the two solids with adhesion, Fad, only depends on the effective radius, R, and the work of adhesion of both surfaces, γ, as: | (7) |
Due to the attractive force between the solids in this case, the contact radius of solids under the external load F is larger than the Hertz contact, and can be obtained from:
 | (8) |
 | (9) |
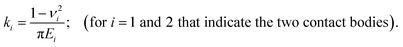 | (10) |
Based on these updates, the indentation depth, δ, is given by
 | (11) |
The contact pressure profile in the JKR theory considers the effect of adhesion forces between the two solids. Compared to Hertz, the JKR theory considers an extra term and can be formulated as follows:1
 | (12) |
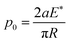 | (13) |
 | (14) |
The JKR theory is a good model for contacts with relatively large contact area and systems with high values of work of adhesion.38 When the attraction force is negligible (i.e., when the work of adhesion is small), all the extra terms in the formulation go to zero, and the JKR theory is back to Hertz contact.
2.3. Derjaguin–Muller–Toporov model
A new contact model, which considers the contact deformation and molecular attraction, was proposed by Derjaguin, Muller, and Toporov.17 According to the DMT model, the adhesion force is obtained from:| Fad = −2γπR | (15) |
 | (16) |
 | (17) |
In order to find the stress field in the substrate, the DMT model uses a pressure profile similar to the Hertz theory, but in the external load considers the adhesion force, as well.
2.4. Contact with interaction stress
The concept of interaction stress was first introduced by Rahmat and Hubert.36 They defined interaction stress as “the state of stress (i.e., a tensor) at any given point of an object as a result of its vicinity to a secondary object”. According to this definition, an AFM experiment was designed and the concept was proved to agree with the Hamaker theory,18 for a system of a silicon nitride probe with a silicon dioxide substrate under water. A brief explanation of the stepwise discretization method which results in obtaining the interaction stress data is presented here.The stepwise discretization method starts with a typical AFM force curve, which shows the evolution of the force applied to the AFM probe as a function of its position with respect to the substrate. This force, F, can be expressed as:
| F = (meff + mhydro)a + Fdrag + kΔzdeflect | (18) |
 | (19) |
| mhydro = (0.6ρfL1/2b3/2)Vcant | (20) |
 | (21) |
The stepwise discretization method finds the interaction stress level as a function of tip–substrate distance. It starts from the cutoff distance, where the tip–substrate interaction is negligible, and hence the interaction stress is zero. The interaction stress at each step is obtained based on the interaction stress at the previous step, the interaction force F (obtained from eqn (18)) and the geometry of the AFM tip as follows:
 | (22) |
 | (23) |
Based on the concept of interaction stress and the Hertz model, a new contact model with adhesion is proposed here. According to Rahmat and Hubert,36 the interaction stress is a non-contact stress field and is originated from van der Waals forces. The interaction stress field is induced in adjacent objects located at a given distance from each other, but is negligible for large distances (i.e., beyond several nanometres). On the other hand, the Hertz theory successfully predicts the contact stresses when there is no attraction considered between the solids. Therefore, by combining these two concepts and employing the principle of superposition, the stress field associated with contact with adhesion is obtained. It should be mentioned that the principle of superposition is applicable to linear elastic materials, and hence, the use of this principle for nonlinear material systems leads to errors in predictions. Single-walled carbon nanotube (SWNT) buckypaper shows nonlinear behaviour, especially at high indentation depths (above 10 nm); however, at low indentation depth, the deviation from linear behaviour may be ignored and the principle of superposition may be applied to have a reasonable estimation of the material properties. Fig. 2 shows the Hertz and interaction stress fields, separately. The Hertz theory (Fig. 2a) accurately predicts the stress field in contact bodies with no adhesion, while the interaction stress theory (Fig. 2b) captures the adhesion effect on the stress field. Therefore, the stress field in objects with adhesion, 〈Ψadhesion〉, can be presented as:
| 〈Ψadhesion〉 = 〈ΨHertz〉 + 〈ΨInteraction〉 | (24) |
 | ||
| Fig. 2 (a) The Hertz contact stress field; the stress contour is composed of spheres tangential to the substrate's surface at the point of contact. (b) The interaction stress caused by adhesion forces. The stress contours present concentric spheres around the centre of the spherical indenter. A contact with adhesion is modelled by superposing the stress fields shown in (a) and (b). Point A shows a random point in the stress field, where the stresses may be obtained according to the procedure described in the text. | ||
All the required parameters (e.g., Young's modulus and work of adhesion) can be obtained from a single AFM force curve experiment. During this experiment, the AFM lowers its probe from a distance towards the substrate and records forces applied to the probe as a function of its location. When the probe is far from the substrate, the AFM senses no force, but at close distances, the AFM records an attraction force towards the substrate. Once the probe reaches the substrate and starts to apply a contact force, a repulsive force is registered by the AFM.
The raw force curve is then processed to remove the effect of the AFM cantilever's deflection and account for drag and inertia forces.36 Before the contact happens, an attraction force bends the AFM cantilever towards the substrate, and thus the tip of the AFM probe is actually closer to the substrate than the root of the cantilever (even if the cantilever is not tilted initially). However, when the probe is in contact with the substrate, the cantilever bends off the surface. In this case, because of the cantilever's deflection, the indentation depth is less than the amount that the cantilever's root moves towards the substrate.
As explained previously,36 the interaction stress data can be found from the non-contact section of the processed AFM force curve. When the origin of the spherical coordinate system is the centre of the indenter, the interaction stress is a tensor with only one nonzero component, which is the normal radial stress.
The minimum point in the semi-contact regime (Fig. 3) shows the amount of adhesion force. In the absence of hysteresis loss, the approach and retract data of the AFM experiment are identical (as was observed for this case). Therefore, Fig. 3 can be used to find the work of adhesion from eqn (7) or (15). Finally, the Young's modulus and indentation force versus indentation depth data can be extracted from the contact section of the processed AFM force curve. Hence, all the information required by the Hertz theory is provided and the Hertz stress field is obtained.
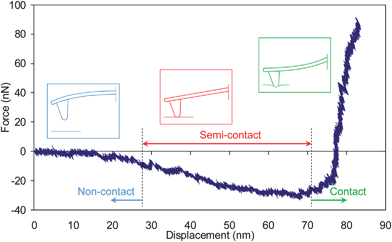 | ||
| Fig. 3 Processed AFM force curve data for the approach phase of a poly(methyl methacrylate) coated AFM probe towards a single-walled carbon nanotube buckypaper substrate. The experiment was performed under distilled water. The cantilever deflection effect is compensated, and the drag and inertia forces are considered. Three regimes of non-contact, semi-contact, and contact are separated in the graph. Schematics of the probe–substrate interaction are also shown. In the non-contact regime, the cantilever bends towards the substrate, while in the contact regime, it bends off the surface. | ||
The stress tensor at a random point A (Fig. 2) in contact bodies with adhesion is obtained as follows:
(1) The normal radial interaction stress at point A is obtained from the interaction stress graph (e.g., Fig. 6a). All other components of the interaction stress tensor are zero.
(2) The interaction stress tensor obtained in step (1) is converted into a Cartesian coordinate system with the contact point as the origin.
(3) The contact stress tensor at point A is calculated from the Hertz theory.
(4) The stress field obtained in step (3) is converted into a Cartesian coordinate system with the contact point as the origin.
(5) The stress tensors obtained in steps (2) and (4) are added tensorially to obtain the net contact-with-adhesion stress tensor at point A.
The next section explains the details of AFM contact experiments.
3. Results
In order to investigate the validity of the proposed model, a SWNT buckypaper was selected to use as the substrate. The entangled mat of carbon nanotubes has been of significant interest in the past few years.39 This random structure does not provide outstanding properties of the aligned carbon nanotubes;40–42 however, different actuating and structural applications43 have benefitted from carbon nanotubes in the buckypaper form. The processes of SWNT buckypaper synthesis are able to produce high quantities of nanotubes with high purity and control on the nanotubes' diameter and chirality.44 As a result, SWNT buckypaper was selected as an interesting candidate to obtain its mechanical properties and evaluate the proposed contact model. There are different challenges involved with this selection. For instance, SWNT buckypapers do not fall exactly in the category of continuous and homogeneous materials at the nanoscale. That leads to two important questions: (1) how repeatable and consistent are the results of nanoindentation on buckypaper substrate? and (2) how valid is the obtained stress field in the buckypaper based on the assumption of continuous and homogeneous substrate? To answer the first question, it should be noted that, due to nanotubes sliding and similar effects, measuring local properties at the nanoscale may lead to a vast distribution of values. Therefore, investigating such material systems calls for a complete statistical analysis before any conclusion is drawn. For example, modelling studies show that the mechanical properties of buckypapers depend on the type and diameter of nanotubes45 and buckypaper's Young's modulus varies between 0.2 and 3.1 GPa. These results are obtained for buckypapers with nanotubes of different types and diameters. In the current work, several indentations on different locations of the buckypaper were performed and a Young's modulus of 0.54 GPa with a standard deviation of 0.14 GPa was obtained. Therefore, it was expected that the response of the material does not depend on the position where the indentation is taken place. In this case, the buckypaper behaved similar to a homogeneous material. In order to answer the second question, it is understood that assuming the buckypaper to be a continuous and homogeneous medium will be the source of some errors in the final results. However, at this stage and as a first approximation, the substrate was considered to be continuous and other sources of error that are introduced based on the selected continuum model (e.g., Hertz, JKR, DMT or interaction theory) are investigated.Furthermore, it should be noted that the proposed theory in the current work is general and will lead to smaller errors when the substrate is continuous and homogeneous. In this work, SWNT buckypaper is only selected as a challenging demonstrative sample. Therefore, if the proposed approach can capture the physics of indentation on these kinds of samples, it can be freely applied to a vast variety of other samples (e.g., very soft materials, biological samples, non-isotropic materials, etc.)
The SWNT buckypaper used in the work was kindly provided by National Research Council Canada-Steacie Institute for Molecular Sciences. The unfunctionalized and highly pure buckypaper was produced by laser oven technique and had an impurity level below 10% by weight.46 The thickness of the buckypaper was measured by a micrometre at 15 different locations to find an average value of 56.3 μm, with a standard deviation of 7.6 μm. Fig. 4 shows a scanning electron microscopy (SEM) image of the buckypaper sample, as well as the distribution of the bundles' diameter. Several SEM micrographs were obtained from different locations of the buckypaper, and with different magnifications. From these images, one thousand measurements of the bundle's diameter were performed, and a mean diameter of 23 nm, with a standard deviation of 8 nm, was attained.
 | ||
| Fig. 4 (a) SEM micrograph of the unfunctionalized SWNT buckypaper at 150k× magnification. The S-4700 FE-SEM was set to an acceleration voltage of 10 kV and an emission current of 8 μA. The micrograph was taken at a working distance of 12 mm from the electron gun. The scale bar is 200 nm. (b) Statistical measurement of SWNT bundles' diameter. One thousand measurements were performed on several SEM micrographs at different locations of the buckypaper and with different magnifications. A Gaussian distribution is used to fit to the measurements. | ||
Prior to measuring the force curves, an AFM image was captured using a Veeco Dimension V atomic force microscope. Fig. 5 shows the AFM picture captured with a Veeco RFESP probe, which has a nominal tip diameter of 8 nm. When a probe with larger diameter is used, the local fluctuations vanish and the substrate appears smoother and more uniform.
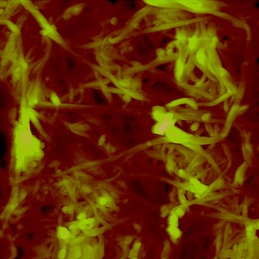 | ||
| Fig. 5 AFM image of the unfunctionalized SWNT buckypaper topography. It was captured in air and at room temperature. The spectrum of colors from bright to dark shows the elevation from 0 to 500 nm. The size of the image is 3 μm × 3 μm. | ||
In order to provide a better understanding of the local properties of the bundles and not only one bundle, an AFM probe with larger diameter was required. Therefore, a Veeco RFESP probe was coated with poly(methyl methacrylate) (PMMA). A spray coater deposited a thin layer of 950k PMMA A2 (from Microchem Inc., Newton, Massachusetts) on the RFESP probe. A tip diameter of 60 nm was measured through SEM micrographs of the apex.47 The spring constant of the cantilever was then measured using Sader technique48 and a value of 5.2 N m−1 was obtained. This combination of tip material and diameter, as well as the cantilever's spring constant, led to successful force curve measurements. Finally, in order to eliminate the influence of capillary forces caused by condensation of the atmospheric humidity, the force curve data were captured under distilled water and at room temperature.49
Several force curves were obtained and the initial processing step (as explained before) was carried out to achieve the processed force curves, such as the one shown in Fig. 3. By processing such graphs, the interaction stress and indentation data were obtained, as shown in Fig. 6. The detail of extracting interaction stress data was previously explained.36 The graph shown in Fig. 6a is achieved by multiplying the stress level measured under water by a factor of 3. This factor compensates the influence of liquid environment on the van der Waals forces,50 while keeping the work of adhesion constant, which is the case for rough surfaces.51
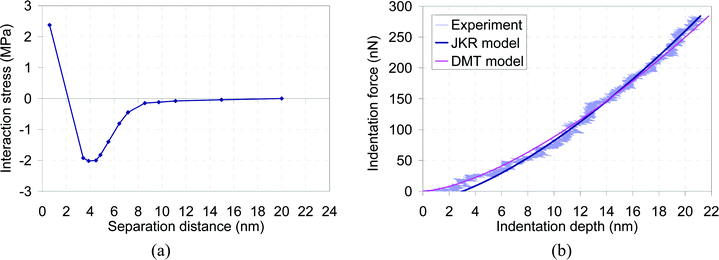 | ||
| Fig. 6 (a) Interaction stress data for a PMMA coated AFM probe and unfunctionalized SWNT buckypaper substrate. The measured data were averaged together. The data were multiplied by 3 to compensate the influence of water medium. The separation distance indicates the distance between the tip and the substrate. (b) A typical indentation plot obtained from an indentation of unfunctionalized SWNT buckypaper with a PMMA coated AFM probe. The JKR and DMT models were fit to the experimental data to extract the buckypaper's Young's modulus. In this case, the JKR and DMT models predicted Young's moduli of 0.47 and 0.42 GPa, respectively. An average modulus of 0.54 GPa was obtained as a result of several similar measurements. This value along with the interaction stress data shown in (a) were input into four contact models of Hertz, JKR, DMT and interaction theory to predict the stress field in the substrate. | ||
Because of the proper selection of the cantilever spring constant, no sudden jump to contact was observed, and the buckypaper substrate behaved elastically with no hysteresis. Therefore, the approach and retract lines of the force curve were almost identical. Forty force curves were generated and it was found that they had an average adhesion force of 29.2 nN with a standard deviation of 2.3 nN. This value was used to calculate the work of adhesion from eqn (7) and (15).
Finally, both of the JKR and DMT models were fit to the contact region of Fig. 3 to find the Young's modulus of SWNT buckypaper, Fig. 6b. The PMMA Young's modulus and Poisson's ratio were assumed to be 2.5 GPa and 0.4, respectively. Thus, with a Poisson's ratio of −0.2 for the buckypaper,52 the JKR and DMT models adjusted values of buckypaper Young's modulus to achieve the best fit to the experiments. Twenty curves (ten JKR and ten DMT) were fit to ten different experiments and an average Young's modulus of 0.54 GPa was found for the SWNT buckypaper. This value agrees with a prior measurement that used a Nanoindenter, in which the buckypaper was loaded under a combination of bending and indentation.25 From this measurement, a Young's modulus of 0.5 ± 0.2 GPa was obtained.46 As mentioned before, the mechanical properties of buckypaper samples are affected by the type and geometric characteristics of the nanotubes; however, the obtained value is within the range of reported literature. In order to obtain the stress field in the buckypaper substrate, the interaction stress data and material properties of the system were required. The interaction stress data were obtained as explained before and the results are shown in Fig. 6a. The Young's modulus of the buckypaper was obtained based on the best curve fits to the experimental results (Fig. 6b).
The force curve experiment fully characterized the SWNT buckypaper substrate. Therefore at this stage, the obtained material properties and geometric parameters could be input into various contact models to find the stress field in the substrate. Based on the models explained in the theory section, a code was generated in MATLAB® to simulate the indentation of a half-space with a spherical indenter. The mechanical properties of the indenter and substrate as well as the indenter's radius were the input. Furthermore, the value of work of adhesion was set based on the experiments. The pressure profiles on the contact area were discretized by meshing the circular contact area and finding the amount of force applied to each element. The pressure profile was then replaced by concentrated loads at the centre of each element. By this technique, the Boussinesq theory could be used along with the principle of superposition to obtain the state of stress at any point in the substrate. For the interaction theory, the Hertz tensor of stress in the substrate was added to the interaction stress. Prior to the summation step, a stress transformation step was applied to the interaction stress values to obtain Cartesian stresses, instead of radial stresses towards the centre of the indenter. In this way, the tensorial state of stress for the Hertz, interaction, DMT, and JKR models was determined. However, it is challenging to compare nine elements of different tensors together. Hence, the state of stress at each point was converted to von Mises stress.53 The von Mises theory uses the stress invariants and is usually used as a yield criterion. Fig. 7 shows the von Mises stresses in the buckypaper substrate subjected to an indentation of 8 nm. The effect of two-dimensional meshing at the contact area, as well as the three-dimensional meshing in the substrate, was investigated, and a trade-off between the converging results and simulation run-time was selected.
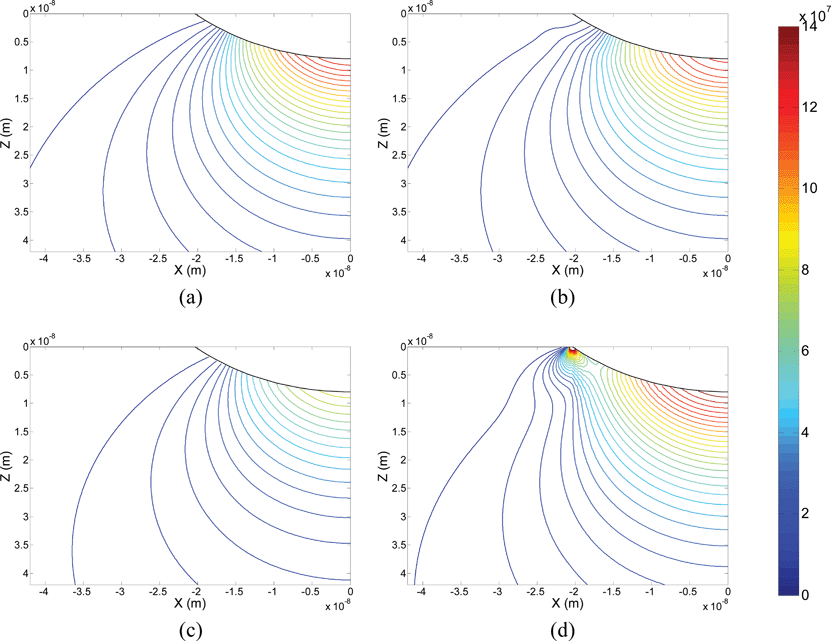 | ||
| Fig. 7 von Mises stress (Pa) field in the SWNT buckypaper substrate at an indentation depth of 8 nm. The stress field is asymmetric, and the results are shown at the plane of symmetry. The results of (a) Hertz, (b) interaction, (c) DMT, and (d) JKR models are shown. | ||
4. Discussion
The stress field at high indentation depths (above 10 nm in this case) becomes dominated by the contact stress, and the effect of adhesion is hard to distinguish. Moreover, at high indentations, the assumption of elastic behaviour may not be valid. On the other hand, in this case, the JKR model has a critical indentation depth of 5.2 nm. Therefore, the results shown in Fig. 7 were obtained at 8 nm indentation depth. The Hertz contact does not consider the influence of the adhesion and is used as a benchmark. The von Mises stress at a distance of 5 nm under the indenter is between 100 and 140 MPa, but decreases rapidly to a value of around 30 MPa at 30 nm below the central axis of the indenter. The interaction stress results are very similar to the Hertz values. That is predictable, because at 8 nm indentation depth, the contact stress levels are significantly higher than the maximum interaction stress. Nevertheless, there are small differences between Hertz and interaction contours at the peripheral regions of the indenter (i.e., near the edge of the contact area). Among the models shown in Fig. 7, the DMT theory seems to underestimate the stress level, compared to the other models. This model gives more accurate predictions for harder surfaces with weaker interactions. In the current case, the relatively strong adhesion caused the DMT model to predict a smaller value for the non-adhesive pressure profile, which led to lower stress values. On the other hand, the JKR model, which was designed for softer materials with stronger adhesion, shows stress contours similar to the interaction and Hertz models. The maximum stress value under the central axis of the indenter seems to be higher than the values predicted by Hertz and interaction models. The reason may lie in the new term added to the pressure profile to compensate the adhesion effect. Thus, the pressure profile applies higher pressure at the central parts of the contact area, while the negative value for the adhesion is dominant at the regions close to the edge of the contact area. Moreover, the JKR pressure profile, explained in eqn (12), results in singularities at the edge of the contact area (i.e., r = a). This means the model predicts an infinite attraction force at the edge of the contact area. The other limitation with the JKR model is related to the critical depth, where the model is incapable of contact force prediction at indentation depths lower than the critical depth. For the current system, the critical indentation depth was calculated to be 5.2 nm. Hence, with the JKR model, there are no results for indentation depths below 5.2 nm.Once the interaction results are compared to the well-known models in the literature, they could be employed to investigate scenarios where the other models, such as JKR, cannot predict the behaviour of the system. Fig. 8a shows the stress field, found based on the interaction theory, at a 2 nm indentation depth. The DMT model is not suitable for softer material systems with strong interaction, and the JKR model is not capable of modelling the contacts below its critical depth (i.e., 5.2 nm in our case). The interaction results are different from the Hertz results, especially where the substrate's distance to the indenter is less than 5 nm. The red regions under the central part of the indenter seem to be stretched vertically, while a wing-shaped pattern appears at the regions near the edge of the contact area. Hence, the effectiveness of the interaction model for systems with adhesion is obvious at lower indentation depths. Fig. 8b studies the difference among all models at various indentation depths. The maximum von Mises stress value along the central axis of the indenter is shown on the y-axis. The results show that the maximum stress level increased by increasing the indentation depth. The interaction stress predicted values close to the Hertz theory. The JKR model, starting after its critical depth limit, followed the same trend and seems to be an upper bound for the interaction model. The DMT model, however, underpredicted the stress level and approached the other models from below. It should be noted that the stress sign for the first three data points was considered negative. The DMT model was expected to be the lower bound of the interaction model predictions. The secondary axis of Fig. 8b shows the difference between the maximum stress obtained from Hertz and interaction models. This value is divided by the Hertz maximum stress and is presented in percentage. The results showed that the difference between Hertz and interaction models decreased from over 6% at 1 nm to below 2% at 9 nm indentation. Therefore, it is concluded that the effect of adhesion is particularly noticeable at lower indentations. According to Fig. 8, the conventional contact-with-adhesion models such as JKR and DMT were not very effective in this case, while a simple Hertz model predicted a more realistic stress field. By increasing the indentation depth, the results of all models converged to the real stress field (the interaction stress results), and the errors shown on the secondary axis of Fig. 8b decreased. The actual stress field in contact bodies with adhesion (the interaction stress model) is between DMT results (from below) and JKR results (from above). At small indentation depths (i.e., a few nanometres), the difference between the JKR and DMT models may be significant. The results of the Hertz model are also located between DMT and JKR results and lead to smaller errors. Therefore, in the absence of interaction stress data, using a simple Hertz model for low indentation depths may be more effective than conventional contact-with-adhesion models and lead to smaller errors.
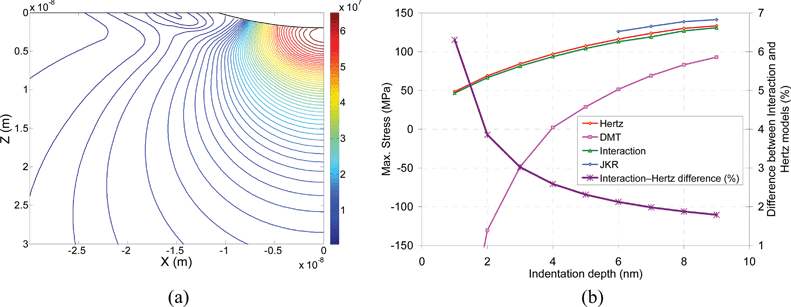 | ||
| Fig. 8 (a) von Mises stress (Pa) field in the SWNT buckypaper substrate obtained from the interaction model at 2 nm indentation. (b) Maximum von Mises stress obtained from Hertz, DMT, interaction, and JKR models at various indentation depths. The difference between Hertz and interaction models (%) is shown on the secondary axis. The interaction stress results are the actual stress fields in the contact bodies. The Hertz predictions are very close to the actual stress field and seem to predict more realistic results compared to other contact-with-adhesion models. | ||
5. Conclusions
The interaction contact model was presented and validated with a set of experiments. A superposition of the stress fields obtained from the Hertz theory and interaction stress theory was used to obtain the stress field in contact bodies with adhesion. The Hertz theory was used to predict the contact stress field without considering the effect of adhesion; while the adhesion effect was captured by the interaction stress theory. The proposed procedure benefits from simplicity of the classic Hertz theory, while at the same time it is able to account for contacts with adhesion. It does not have the limitations of the DMT model, where the stress field in the substrate is indeterminable for negative indentation depth. Moreover, it is not limited to a critical indentation depth and does not lead to singularities at the edge of the contact area, which are the limitations found in the JKR model. The theory of this model was explained and compared with the well-known models in the literature, and the validity of the interaction model was studied by AFM force curve experiments. As a challenging, and at the same time, interesting substrate, SWNT buckypaper samples were tested. The Young's modulus of the buckypaper substrate was measured at 0.54 GPa, which agrees with the value obtained from a previous investigation with a different approach. The study was concluded by a quantitative analysis of the stress field in the substrate predicted by different models. The interaction model seemed to lie between the DMT model approaching from below and the JKR model as an upper bound. It was shown that the results of JKR and DMT models differ significantly at low indentation depths. When the interaction stress data are not available, the results of a simple Hertz theory, which also lies between JKR and DMT bounds, may be closer to actual stress results.Acknowledgements
The project was funded by McGill University and Chemical, Biological, Radiological and Nuclear (CBRN) Research and Technology Initiative (CRTI), project CRTI107-121RD. The SWNT buckypapers were provided by National Research Council Canada-Steacie Institute for Molecular Sciences (NRC-SIMS), and the access to the atomic force microscope was provided by Professor Francois Barthelat. The authors thank Erin Quinlan for her assistance.References
-
K. L. Johnson, Contact Mechanics, Cambridge University Press, New York, 2003 Search PubMed
.
- K. D. Costa, A. J. Sim and F. C. P. Yin, J. Biomech. Eng., 2006, 128(2), 176 CrossRef
.
- C. J. Sullivan, S. Venkataraman, S. T. Retterer, D. P. Allison and M. J. Doktycz, Ultramicroscopy, 2007, 107(10–11), 934 CrossRef CAS
.
- K.-K. Liu, J. Phys. D: Appl. Phys., 2006, 39(11), R189 CrossRef CAS
.
- M. C. Strus, L. Zalamea, A. Raman, R. B. Pipes, C. V. Nguyen and E. A. Stach, Nano Lett., 2008, 8(2), 544 CrossRef CAS
.
- S. Decossas, G. Cappello, G. Poignant, L. Patrone, A. M. Bonnot, F. Comin and J. Chevrier, Europhys. Lett., 2001, 53(6), 742 CrossRef CAS
.
- Y. Sun, B. Akhremitchev and G. C. Walker, Langmuir, 2004, 20(14), 5837 CrossRef CAS
.
- Y. Sun and G. C. Walker, Langmuir, 2005, 21(19), 8694 CrossRef CAS
.
- M. S. Bischel, M. R. Vanlandingham, R. F. Eduljee, J. W. Gillespie and J. M. Schultz, J. Mater. Sci., 2000, 35(1), 221 CrossRef CAS
.
- R. W. Stark, T. Drobek, M. Weth, J. Fricke and W. M. Heckl, Ultramicroscopy, 1998, 75(3), 161 CrossRef CAS
.
- S. Tripathy and E. J. Berger, J. Biomech. Eng., 2009, 131(9), 094507 CrossRef CAS
.
- V. I. Uricanu, M. H. G. Duits, R. M. F. Nelissen, M. L. Bennink and J. Mellema, Langmuir, 2003, 19(20), 8182 CrossRef CAS
.
- C. Y. Zhang and Y. W. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(2), 021912 CrossRef CAS
.
- H. Hertz, Journal für die reine und angewandte, 1882, 92, 136 Search PubMed
.
- J. Erath, S. Schmidt and A. Fery, Soft Matter, 2010, 6(7), 1432 RSC
.
- K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324(1558), 301 CrossRef CAS
.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53(2), 314 CrossRef CAS
.
- H. C. Hamaker, Physica, 1937, 4, 1058 CrossRef CAS
.
- D. Tabor, J. Colloid Interface Sci., 1977, 58(1), 2 CrossRef CAS
.
- D. Maugis, J. Colloid Interface Sci., 1992, 150(1), 243 CrossRef CAS
.
- Y. Tatara, JSME Int. J., Ser. A, 1993, 36(2), 190 Search PubMed
.
- Y. Yan, Z. Zhang, J. R. Stokes, Q.-Z. Zhou, G.-H. Ma and M. J. Adams, Powder Technol., 2009, 192(1), 122 CrossRef CAS
.
- I. N. Sneddon, Int. J. Eng. Sci., 1965, 3(1), 47 CrossRef
.
- I. Y. Sokolov, Surf. Sci., 1994, 311(3), 287 CrossRef CAS
.
- P. Hubert, B. Ashrafi, K. Adhikari, J. Meredith, S. Vengallatore, J. Guan and B. Simard, Compos. Sci. Technol., 2009, 69(14), 2274 CrossRef CAS
.
- R. Saha and W. D. Nix, Mater. Sci. Eng., A, 2001, 319–321, 898 CrossRef
.
- M. Monclus, T. Young and D. Di Maio, J. Mater. Sci., 2010, 45(12), 3190 CrossRef CAS
.
- L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325(5944), 1110–1114 CrossRef CAS
.
- Y. Sugimoto, P. Pou, M. Abe, P. Jelinek, R. Perez, S. Morita and O. Custance, Nature, 2007, 446(7131), 64 CrossRef CAS
.
- M. Ashino, D. Obergfell, M. Haluska, S. Yang, A. N. Khlobystov, S. Roth and R. Wiesendanger, Nat. Nanotechnol., 2008, 3(6), 337 CrossRef CAS
.
- X. Li, W. Chen, Q. Zhan, L. Dai, L. Sowards, M. Pender and R. R. Naik, J. Phys. Chem. B, 2006, 110(25), 12621 CrossRef CAS
.
- R. P. Jaiswal, G. Kumar, C. M. Kilroy and S. P. Beaudoin, Langmuir, 2009, 25(18), 10612 CrossRef CAS
.
- R. W. Friddle, M. C. Lemieux, G. Cicero, A. B. Artyukhin, V. V. Tsukruk, J. C. Grossman, G. Galli and A. Noy, Nat. Nanotechnol., 2007, 2(11), 692 CrossRef CAS
.
- B. Kim, V. Putkaradze and T. Hikihara, Phys. Rev. Lett., 2009, 102(21), 215502 CrossRef
.
- Y. Sugimoto, P. Pou, O. Custance, P. Jelinek, M. Abe, R. Perez and S. Morita, Science, 2008, 322(5900), 413–417 CrossRef CAS
.
- M. Rahmat and P. Hubert, J. Phys. Chem. C, 2010, 114(35), 15029 CAS
.
-
J. Boussinesq, Application des potentials à l'étude de l'equilibre et du mouvementdes solides élastique, Gauthier-Villais, Paris, 1885 Search PubMed
.
- D. C. Lin, E. K. Dimitriadis and F. Horkay, J. Biomech. Eng., 2007, 129(6), 904 CrossRef
.
- Z. Wang, Z. Liang, B. Wang, C. Zhang and L. Kramer, Composites, Part A, 2004, 35(10), 1225 CrossRef
.
- W. Fei, Z. Weiping, Y. Wu, L. Guohua and Q. Weizhong, Polymer, 2005, 46(26), 12689 CrossRef
.
- C. H. Sun, F. Li, H. M. Cheng and G. Q. Lu, Appl. Phys. Lett., 2005, 87(19), 193101 CrossRef
.
- J.-P. Salvetat,
et al.
, Phys. Rev. Lett., 1999, 82(5), 944 CrossRef CAS
.
- B. Ashrafi, P. Hubert and S. Vengallatore, Nanotechnology, 2006, 17(19), 4895 CrossRef CAS
.
- C. T. Kingston, Z. J. Jakubek, S. Dénommée and B. Simard, Carbon, 2004, 42(8–9), 1657 CrossRef CAS
.
- S. W. Cranford and M. J. Buehler, Nanotechnology, 2010, 21(26), 265706 CrossRef
.
- B. Ashrafi, J. Guan, V. Mirjalili, P. Hubert, B. Simard and A. Johnston, Composites, Part A, 2010, 41(9), 1184 CrossRef
.
- M. Rahmat, K. Das and P. Hubert, ACS Appl. Mater. Interfaces, 2011, 3(9), 3425 CAS
.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70(10), 3967 CrossRef CAS
.
- D. Chabrier, B. Bhushan and S. Marsaudon, Appl. Surf. Sci., 2010, 256(14), 4672 CrossRef CAS
.
- J. N. Israelachvili and P. M. McGuiggan, Science, 1988, 241(4867), 795–800 CAS
.
- A. P. Serro, R. Colaço and B. Saramago, J. Colloid Interface Sci., 2008, 325(2), 573 CrossRef CAS
.
- L. J. Hall, V. R. Coluci, D. S. Galvao, M. E. Kozlov, M. Zhang, S.O. Dantas and R. H. Baughman, Science, 2008, 320(5875), 504–507 CrossRef CAS
.
-
W. Riley, L. Srurges and D. Morris, Mechanics of Materials, John Wiley & Sons, Inc., 2007 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2012 |
