Programmable microfluidic synthesis of spectrally encoded microspheres

Abstract

Spectrally encoded fluorescent beads are an attractive platform for assay miniaturization and multiplexing in the biological sciences. Here, we synthesize hydrophilic PEG–acrylate polymer beads encoded with lanthanide nanophosphors using a fully automated microfluidic synthesis device. These beads are encoded by including varying amounts of two lanthanide nanophosphors relative to a third reference nanophosphor to generate 24 distinct ratios. These codes differ by less than 3% from their target values and can be distinguished from each other with an error rate of <0.1%. The encoded bead synthesis strategy we have used is readily extensible to larger numbers of codes, potentially up to millions, providing a new platform technology for assay multiplexing.

---

Introduction

Over the past several years, advances in biomedical research technology have driven an unprecedented explosion of genomic and proteomic data, yet the challenge of translating new biomarkers of disease into actionable diagnostics and therapeutics remains daunting. To both validate and deploy the vast numbers of recent discoveries into clinical practice requires new approaches to multiplexing and high-throughput biomarker analysis. Despite intense research, few practically available cost-effective assays for multiplexing exist, and new approaches are needed. Beyond diagnostics, advances in multiplexing may have impact on basic research and development systems, including combinatorial drug discovery.

Multiplexed assays require that individual probes be reliably identified and tracked throughout an experiment. This identification and tracking is often done using planar arrays, where the identity of each probe is encoded by its physical position. An alternative approach uses encoded beads, where each probe is attached to a separate bead that is uniquely identifiable. Bead-based assays offer faster reaction kinetics, increased assay flexibility, and improved reproducibility and reduced costs due to the ability to attach probes to multiple particles at once.¹ However, technical challenges in bead encoding have limited their practical application to date.² Existing encoding methods^1–4 generally fall into two categories: spatial encoding and spectral encoding. Spatial encoding schemes create graphical patterns or bar codes in the particle material in a variety of ways.^5–9 However, spatial methods face difficulties in cost-effective fabrication, often require large particles to generate large code sets, and have slower and more challenging code readout than existing spectral methods due to orientation requirements.

Spectral encoding schemes incorporate mixtures of luminescent materials such as lanthanides,^10–12 quantum dots (QDs),^13–18 or fluorescent dyes^19,20 that emit light at different wavelengths to generate uniquely identifiable signatures. These schemes allow identification of codes in any orientation and are compatible with conventional bead synthesis procedures and standard detection optics, making them particularly attractive. Despite the promise of spectral encoding schemes, technical challenges have limited their practical code capacity. Organic dyes have broad emission spectra, narrow Stokes shifts, and limited photostability, making it difficult to deconvolve spectral signatures from multiple dyes and reducing the usable lifetime of the codes. Quantum dots offer relatively narrow and tuneable excitation spectra, and have therefore been the subject of considerable recent interest for encoding schemes. However, QDs have complicated photophysics and can undergo energy transfer and re-absorption when tightly packed together.^21–24 These effects limit the number of optical codes that can be created, due to re-absorption losses at higher concentrations in the beads.^25,26 As a result, the largest experimentally produced spectral code sets from organic dyes or quantum dots have fallen far short of theoretical expectations. The best known commercial system, Luminex,²⁷ has been limited to 500 unique codes and code sets synthesized in the literature have been even smaller.^{10,11,13–18}

Lanthanide nanophosphors are an attractive alternative to QDs. They have narrow emission peaks due to the Laporte forbidden f–f energy transitions within the rare earth emitter (e.g., Eu³⁺)²⁸ and are highly photostable.^29–31 A common host matrix (e.g., YVO₄) can be used with several individual emitters, resulting in families of nanophosphors with a shared excitation profile, but with distinct emission spectra (Fig. 1A). Unlike QDs, neither re-absorption nor self-reabsorption is observed in lanthanide nanophosphors. They are also less prone to bleaching, chemical or oxidative damage to their emission characteristics over time. Collectively, these properties make lanthanide nanophosphors an ideal luminescent material for spectral encoding.

Fig. 1 Characterization of the lanthanide nanophosphors synthesized for use in the automated microfluidic bead synthesizer. (A) Emission spectra for each of the nanophosphors (Dy- (green), Eu- (red), and Sm- (orange) doped Y_0.80Bi_0.15VO₄) when excited at 285 nm. Excitation spectra of all three nanophosphors (inset) are nearly identical. (B) Histogram showing particle size distribution for nanophosphors (as measured by dynamic light scattering), and a photograph of vials of nanophosphor suspensions illuminated with a UV lamp (inset).

Here, we present a novel approach to synthesize spectrally encoded polymer beads containing multiple lanthanide nanophosphors. To generate these beads, we use a custom and fully automated microfluidic device to mix different predetermined ratios of nanophosphors suspended in monomer, followed by photopolymerization, resulting in uniquely identifiable spectral codes. Using this device, we have produced, imaged, and characterized thousands of encoded beads with 24 distinct spectral codes. The beads are highly uniform in size and have a very tight distribution of lanthanide ratios around the programmed values, such that we can distinguish between the codes with <0.1% error. These results establish the practical feasibility of using lanthanide nanophosphors for spectral encoding, and lay the foundation for future high-throughput multiplexing of biological assays.

Methods

Lanthanide synthesis

The synthesis of nanophosphors is based on previously published preparations of similar compounds.^29,32,33 A detailed synthesis is described in the Supporting Information. All chemical reagents and polymers [poly(ethylene glycol) (PEG) and poly(acrylic acid) (PAA)] for nanophosphor synthesis were purchased from Sigma-Aldrich (St. Louis, MO) and were used without further purification. Microwave synthesis was performed using a Biotage Initiator (Biotage AB, Uppsala, Sweden). Purification of the synthesized nanophosphors was performed by ultrafiltration using Amicon Ultra-15 centrifugal filter units with a 50 000 MWCO (Millipore, Billerica, MA), resulting in suspensions with a nanophosphor concentration of ∼50 mg mL⁻¹ in water. Luminescence spectra were measured using a FluoroMax-3 (Horiba Scientific, Kyoto, Japan) spectrofluorometer and the nanophosphor particle size distributions were measured using a Zetasizer Nano (Malvern Instruments, Malvern, UK).

Microfluidic device production

Devices were fabricated in poly(dimethylsiloxane) (PDMS, RTV 615, Momentive Performance Materials, Albany, NY) by Multi-Layer Soft Lithography³⁴ using 4′′ test-grade silicon wafers (University Wafer, South Boston, MA) coated with multiple layers of SU8 (Microchem Corp., Newton, MA) and AZ50 XT photoresists (Capitol Scientific, Austin, TX) patterned by standard photolithography processes.

Bead synthesis

Encoded beads were generated by varying ratios of three pre-polymer input solutions each containing different lanthanide nanoparticles. The three monomer input solutions used in the microfluidic bead synthesizer all contained purified water with 42.8% v/v 700 MW PEG-diacrylate (Sigma-Aldrich), 6% v/v 2-hydroxy-4′-(2-hydroxyethoxy)-2-methylpropiophenone (“Irgacure 2959”, a photoinitiator, Sigma-Aldrich) dissolved in methanol at 0.33 g mL⁻¹, and 5% v/v YVO₄:Eu (25 mg mL⁻¹). One of the input solutions also contained 21.3% v/v YVO₄:Dy (10 mg mL⁻¹) and one of the others contained 21.3% v/v YVO₄:Sm (10 mg mL⁻¹). Droplets were formed into a continuous flowing stream of light mineral oil (Sigma-Aldrich) that contained 2% v/v Abil EM90 (Evonik Industries, Germany) and 0.05% v/v Span 80 (Sigma-Aldrich) as surfactants to eliminate droplet merging and sticking to the PDMS walls. On device UV illumination polymerizes the droplets into beads downstream of the T-junction.

Accurately programming spectral codes requires precise flow control from each of the lanthanide inputs. This was accomplished by performing a calibration routine to directly measure relative hydraulic resistances. The coupled flow eqn (1) and (2) were then solved to determine the required pressure (P_n) from each input (n) to achieve the desired flow rates (Q_n):

Where Q_tot is the total flow rate from all lanthanide inputs, P_mix is the pressure at the inlet to the mixing channel where all lanthanide input streams come together, and R_mix is the resistance of the mixing channel. The resistance of each input (R_n) was determined relative to a fixed reference standard, PEG-diacrylate with food coloring, flowed into one of the lanthanide inputs. The pressures at these two inputs were set to the same value and the flow rate ratio (Q_n/Q_ref) was determined by measuring the width taken up by each fluid in the channel. When the input pressures are equal, eqn (1) reduces to:

R _mix was determined by flowing lanthanide in pre-polymer at one of the lanthanide inputs at a fixed pressure and then measuring the pressure (P_mix) where the inputs come together at the entrance to the mixing channel. Under these conditions Q_tot = Q_n so from eqn (1) and (2):

P _mix was measured by opening the valve to a second lanthanide input followed by adjustment of the pressure until there was no flow at this position. Once the relative resistances for each of the lanthanide inputs (R_n) and the resistance downstream of the inputs (R_mix) is determined, the system of eqn (1) and (2) can be solved to obtain the pressures needed for the desired flow rates of each lanthanide in monomer for accurately hitting each targeted spectral code.

Bead imaging and data analysis

Bead imaging was performed on a Nikon Ti microscope with a custom UV transilluminator as shown in Fig. 3. The lanthanide emission was detected through six emission filters (Fig. 4) and recorded on an Andor DU-888 camera (Andor Technology plc., Belfast, Northern Ireland). Linear unmixing was performed using least squares fitting after background subtraction and flat-field correction of the images. Beads were identified by local thresholding on the Eu channel, and the median Dy/Eu and Sm/Eu ratios for each bead were recorded. A global scaling was applied to the beads from each image to best map the measured ratios to the programmed codes. All data analysis was performed in MATLAB (The MathWorks Inc., Natick, MA).

Results

Synthesis of lanthanide nanophosphors

The spectral encoding scheme we describe relies critically on stable, well-characterized lanthanide nanophosphors. Here, we have synthesized nanophosphors using a polymer-assisted hydrothermal approach combined with microwave irradiation.^35–37 The product is a crystalline YVO₄ nanoparticulate host containing one of the trivalent rare earth dopants (Eu³⁺, Sm³⁺, or Dy³⁺) (see Methods), resulting in materials with unique emission spectra (Fig. 1A) when excited with UV light (Fig. 1A, inset). The nanophosphors have a size distribution from 30–160 nm (Fig. 1B) and are coated with poly(acrylic acid) to create stable aqueous suspensions (Fig. 1B, inset, illuminated with a UV lamp). Bismuth (at a 5–15% atomic replacement of yttrium) has also been incorporated into these nanophosphors to increase their UV absorption.^35–38 Henceforth, the nanophosphors are referred to simply by the rare earth dopant present (e.g., Eu). To test the reproducibility of nanophosphor production, we synthesized multiple batches of each nanophosphor and compared their emission spectra (Fig. S1†). In all cases, these spectra were virtually identical, demonstrating the ability to consistently and reproducibly produce nanophosphors.

Synthesis of ratiometrically encoded polymeric beads

To incorporate these lanthanides into solid beads at programmed ratios, we have designed and fabricated a custom, fully-automated microfluidic device. The microfluidic bead synthesizer (Fig. 2A), operates in two stages. In stage one, the different lanthanides, suspended in poly(ethylene glycol) diacrylate, flow into the device and mix in a staggered herringbone mixer.³⁹ During this mixing, the relative flow rates from the different lanthanide inputs determine the relative abundance of each lanthanide in a bead. In stage two, droplets are generated by flowing the lanthanide mixture into an oil stream at a T-junction,^40,41 and then polymerized into beads through on-chip UV illumination.⁴² After producing beads with each mixture, the mixing channel is flushed with high-pressure water to clear the channel, the pressures are adjusted to pre-programmed values automatically for the next code, and the process repeats. Accurately achieving targeted spectral codes requires precise control over lanthanide flow rates, which is achieved by setting pressures based on a set of coupled flow equations and calibration parameters (see Methods). The actual device (Fig. 2C and D) is fabricated by standard Multi Layer Soft Lithography (MSL) techniques and incorporates controls for up to 8 lanthanide inputs.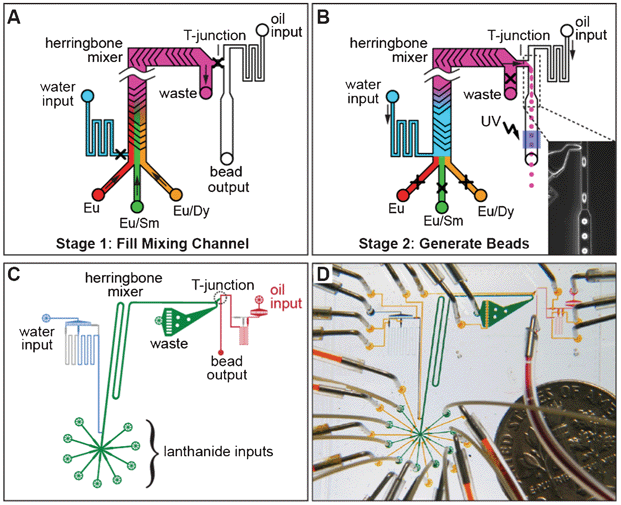

Fig. 2 Microfluidic bead synthesizer. (A) Stage 1 of bead synthesis. Mixtures of lanthanide nanoparticles (Eu alone (red), Eu/Sm (green), Eu/Dy (orange)) suspended in pre-polymer bead mixture flow into a microfluidic device at controlled ratios and are mixed on chip using a staggered herringbone mixer. (B) Stage 2 of bead synthesis. Water (blue) pushes the lanthanide mixture (pink) towards a T-junction containing a continuously flowing oil stream, producing droplets (shown in microscope image, inset). Droplets are polymerized into beads via illumination with UV light and collected for later use. (C) CAD drawing of the flow channels of the device showing the lanthanide inputs and herringbone mixer (green), water input and resistor (blue), and oil input and bead output (red). (D) Photograph of the bead synthesizer microfluidic device with food coloring in the channels and a dime for scale. Flow channels are colored as in panel C; control lines used to open and close on-chip valves are shown in yellow.

To test both the feasibility of using lanthanide nanophosphors to create uniquely identifiable spectral codes and the performance of this device, we synthesized a set of ratiometrically-encoded beads including varying levels of Dy and Sm and a constant level of Eu. Codes are determined by the relative ratios of Dy/Eu and Sm/Eu, with the constant level of Eu providing an internal normalization to correct for spatial and temporal variations in either excitation intensity or detection efficiency. We chose to synthesize a two-dimensional grid of 24 ratiometric codes containing 6 distinct levels of both Dy and Sm. The levels were chosen using an error model based on preliminary measurements that predicted levels that should be separated by roughly equal numbers of standard deviations. In three hours of fully automated unattended device operation, we produced a set of 24 spectral codes with each code consisting of approximately 1500 beads.

Imaging of spectrally encoded beads

To measure the lanthanide luminescence ratios in these beads, we developed an additional custom microfluidic device to create an ordered linear array of ∼190 beads within a narrow serpentine channel (Fig. 3A) covering a ∼1 mm² area. Beads in the serpentine can be loaded and unloaded using on-chip valves in the fluidic circuit, allowing for efficient imaging of large numbers of beads. A “sieve” valve at the end of the channel that allows fluid flow, but blocks solid beads can be closed during bead loading and imaging and then opened to flush the channel with buffer and load new beads, ensuring that no bead is imaged twice. Initial images of the beads showed that they are highly monodisperse, with a mean diameter of 46.4 ± 1.0 μm. Images of these beads at commonly used fluorescence wavelengths revealed minimal luminescence of the lanthanides in the fluorescein, Cy3, and Cy5 channels, indicating that these beads are compatible with assays using these dyes for detection (Fig. S2†).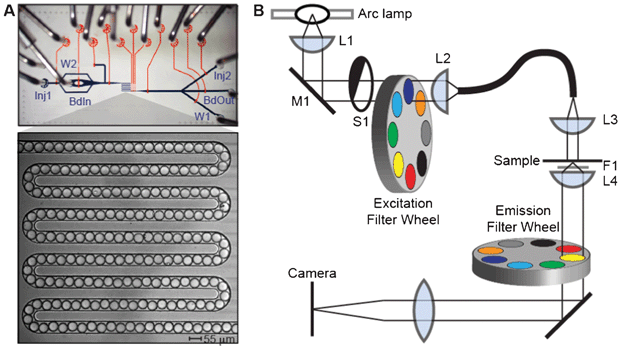

Fig. 3 Bead imaging setup. (A) Photograph of microfluidic imaging device with flow channels shown in blue and control channels shown in orange. Beads are injected into a 55 mm wide serpentine channel for imaging (photograph, inset); sieve valves at the end of the channel retain beads while permitting fluid flow to facilitate channel loading. Inputs (Inj1, BdIn, Inj2) and outputs (W1, W2, BdOut) at either end of the device provide bidirectional flow. (B) Schematic of the microscopy system used for imaging beads. Light from a full-spectrum 300 W Xenon arc lamp is collected (L1), reflected off a 400 nm long pass filter (M1) to reject visible light, and passed through a shutter (S1) and an excitation filter wheel (to switch between UV and visible transillumination) before being focused (L2) into a deep UV liquid light guide. The other end of the liquid light guide is mounted on the condenser mount of a Nikon Ti microscope, where the light is collimated by a fused silica lens (L3) and projected onto the sample. Emitted light from the sample is collected by a Plan Apo 4x/0.2 NA objective (L4), with a UV blocking filter placed between the sample and the objective. Emitted light is filtered through an emission filter wheel mounted beneath the objective before being focused onto the camera.

Because the lanthanides are best excited in the deep UV, which conventional microscope optics do not transmit, we built a custom UV transillumination microscope to image the beads (Fig. 3B). Luminescence emission from the beads was detected in six spectral bands defined by emission filters chosen to pass the characteristic emission peaks of each lanthanide (Fig. 1A and 4A). The intensities of individual lanthanides were then determined by linear unmixing, which expresses the measured images as a sum of component images multiplied by each component's characteristic spectrum.⁴³ Here, we used as our components the three lanthanides Dy, Eu, and Sm, as well as the autofluorescence of the microfluidic device within which the beads are held (Fig. 4B). The unmixing error (the difference between the measured images and the component images times their spectra) was <2% for a typical image set. A typical set of unmixed images is shown in Fig. 4C. To identify the lanthanide ratios in each bead, we first identified beads in the image by adaptive local thresholding of the Eu channel. For each identified bead (spanning ∼90 pixels), we then calculated the Dy/Eu and Sm/Eu ratios on a pixel by pixel basis, and record the median ratios for each bead.⁴⁴

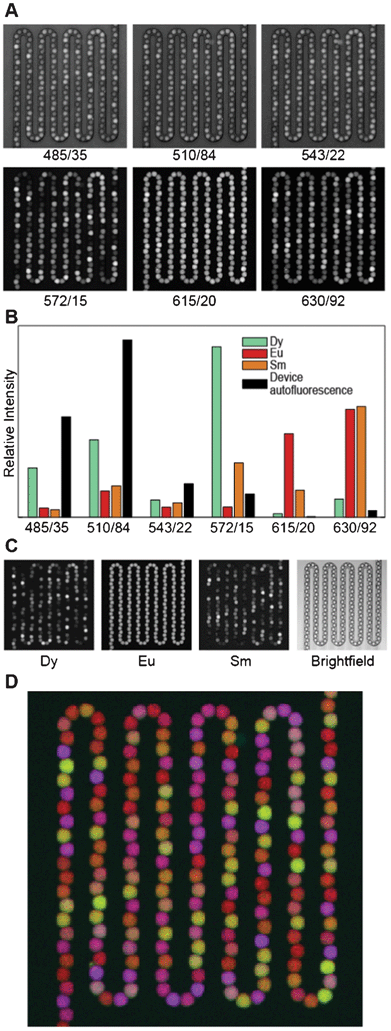Fig. 4 Analysis procedure. (A) Raw data in each of the six luminescence channels. Data are scaled linearly. Each channel is labelled by the center wavelength/passband width (in nm) of the imaging filter. (B) Reference spectra used for unmixing. (C) Left: Linearly scaled black and white images of unmixed data from each channel (Dy, Eu, and Sm), with black set to the minimum intensity in the image and white set to the maximum intensity. Right: Bright field image of the same field of view. (D) False color overlay of Dy, Eu, and Sm luminescence, colored blue, red, and green, respectively, with scaling as in Panel C.

Identification of spectral codes

To be practically useful, each code within an encoded bead set should cluster tightly around the predetermined, programmed ratios. The results of imaging 10 bead-filled serpentines containing a representative sample of 1926 beads from the 24 code set are shown in Fig. 5A. To determine cluster centroids for each code, we performed k-means clustering on the data, using the programmed values as the starting cluster centroids. The synthesized beads for each code cluster tightly, with the measured values for each code agreeing very well with the targeted values (inset Fig. 5A): the mean distance between the programmed ratios (0, 0.12, 0.27, 0.46, 0.70, and 1) and the measured ratios is only 0.014. Discounting the 0,0 code, the mean fractional error between the measured and programmed levels (distance from programmed to measured divided by distance of programmed to origin) is 2.9%. A second independently generated code set shows similarly precise agreement with the programmed levels (Fig. S3 and S4†), indicating that our synthesizer produces spectrally encoded beads with both high accuracy and repeatability. These code sets were synthesized independently with a three-week gap between the syntheses, and both code sets were imaged several additional weeks after the syntheses, demonstrating bead and reagent stability.

Fig. 5 A 24 code matrix. (A) Scatter plot of the median Dy/Eu and Sm/Eu luminescence ratios for 10 filled serpentines (1926 beads), with points false colored according to their Sm/Eu (red) and Dy/Eu (blue) ratios. Each point represents one bead. Grey ellipses around each code cluster illustrate three- and four-sigma contours derived from fitting a Gaussian mixture model to the data. Histograms of bead ratios in the Dy/Eu and Sm/Eu channels (black) and their corresponding Gaussian fits (red) are shown along each axis; these histograms group all codes together. Inset: Measured cluster centroids (red) and their corresponding programmed intensity ratios (blue); the root mean square deviation between the programmed ratios and the measured ratios is 0.014. (B) Standard deviations calculated from Gaussian fits to the bead ratio histograms in (A) as a function of ratio (filled circles, with blue for Dy and red for Sm). Square symbols illustrate the statistical standard deviation determined from replicated imaging of the same serpentine of beads.

Another critical requirement for a robust encoding scheme is that beads from different codes cluster tightly together and far from other codes, preventing misidentification of beads. The RMS deviation of individual beads from their code centroid, calculated as above, is 4%. To quantify how accurately we can assign beads to a code, we fit a two-dimensional Gaussian to each code cluster using a Gaussian mixture model. The three and four standard deviation ellipses around each code are shown in the grey lines in Fig. 5A. We find that 98.7% of all beads lie within three standard deviations of the cluster centroid, and only two of the 1926 beads fall more than four standard deviations away from the cluster centroid. From this model, we can also estimate the number of standard deviations at which the error ellipse of one code would begin to overlap with neighbouring codes; this is the number of standard deviations that a bead would have to fall from the cluster centroid to be misidentified. We find that this overlap occurs at about 5.5 standard deviations, corresponding to a misidentification rate of 4 × 10⁻⁸. Consistent with this, we performed 10-fold cross validation of the Gaussian mixture model and found that no beads were misidentified. Thus, not only do the code centroids fall close to the programmed values, the individual beads are tightly distributed around these values, indicating that each bead can be assigned to a code with a <0.1% chance of misidentification.

Understanding and minimizing errors is crucial to maximize the code space that can be achieved with a given encoding scheme. The distribution of measured bead ratios around their programmed values can result from both errors in bead synthesis and bead imaging. These synthesis and imaging errors, in turn, are composed of both a systematic, instrumental component as well as a statistical, shot noise (either photon or lanthanide nanoparticle number) component. To probe the relative contributions of these sources of error in our measurements, we calculated the mean error for each Dy/Eu level and each Sm/Eu level, independent of the concentration of the other lanthanide. The histograms of the Dy/Eu and Sm/Eu ratios for all beads are shown at the edges of the scatter plot in Fig. 5A, along with Gaussian fits to the data. The widths (standard deviations) from these Gaussian fits are plotted (Fig. 5B), along with the statistical measurement error (determined by repeated imaging of the same serpentine of beads). The statistical measurement error accounts for roughly one half of the total error in the Dy/Eu channel and between one half and one third of the total error in the Sm/Eu channel. While these other sources of error can be further reduced, the fact that we are within 2–3 fold of the measurement shot noise limit indicates that these other errors are relatively small.

Discussion

Here we have demonstrated a system to precisely generate beads containing ratiometric spectral codes using a microfluidic device and luminescent lanthanide nanophosphors. We have created 24 uniquely identifiable codes containing a single reference level of Eu and 6 levels each of both Sm and Dy. Measurements of ∼2000 beads from this code set establish both that the measured ratios closely match the desired programmed ratios and that these codes are easily distinguished from one another, validating the accuracy and precision of this technique. Importantly, both this scheme and the device that we have used to produce these codes can be extended to significantly larger code sets.

Previous microfluidic systems have been built for generating spectrally encoded beads using premixed solutions for each code,^13,45 five fixed ratios between two colors,¹⁸ or continuously varying ratios between two colors.¹⁷ Our device is unique in incorporating automated on-chip mixing with multiple input streams while accurately achieving programmed ratiometric codes (error <3%), with low variance within a code (4%), and precise control over bead size (CV < 2.5%). The current bead synthesizer incorporates eight lanthanide inputs and is scalable with respect to both the number of lanthanide inputs and the rate of bead synthesis. Because individual codes are produced one at a time, each code can be deposited into separate wells of a high-throughput assay plate for downstream applications. The current polymer and lanthanide nanophosphor formulations used are compatible with a wide range of aqueous buffers used in biological assays.

The ultimate performance of a spectral encoding scheme depends both on the number of encoding species and the number of intensity levels of each that can be reliably distinguished. The number of distinguishable intensity levels is inversely proportional to deviations from the programmed error level; therefore, minimization of synthesis and measurement errors is necessary to maximize the code space. Our results establish that we can synthesize beads with a mean deviation from the programmed ratio of 2.9%. This number is significantly smaller than deviations from programmed intensities seen for QDs²² indicating that lanthanide nanophosphors suffer much less from energy transfer and re-absorption between particles.

We envision a direct path to expanding our code set through both minimizing code variance and adding other lanthanides. If we assume that the errors in intensity ratios are normally distributed, and require that the midpoint between any two programmed codes is at least four standard deviations from each other (corresponding to a misidentification probability of less than 10⁻⁴), then our current intra-code variance of 4% should allow the resolution of seven intensity levels for Dy/Eu and Sm/Eu. If we were able to reduce the total error to the statistical measurement error in Fig. 5, the number of resolvable levels would increase to 12 per lanthanide while maintaining a code-calling accuracy rate greater than 99.99%.

A number of lanthanide nanophosphors with different dopants and distinct emission spectra have been synthesized, including erbium, thulium, holmium, and cerium/terbium.^38,46,47 Incorporation of additional nanophosphors such as these provides an alternative approach to expanding the code space. In addition to the current downconverting (UV-excited) YVO₄ nanophosphors, there are also upconverting lanthanide nanophosphors that emit in the visible region upon excitation in the near-IR. Syntheses of upconverting nanoparticles with the emitting species Dy, Er, Eu, Ho, Sm, Tb, and Tm have been reported.^48–51 A system combining upconverting and downconverting nanoparticles could potentially use as many as 14 orthogonal channels for encoding. As the overall coding capacity of the system scales as the number of distinguishable levels to the power of the number of dyes, extending the high precision with which we currently measure lanthanide abundance to these additional channels will allow a large increase in the coding capacity of this system, potentially up to millions of codes.

The methodology and device described here allows for simple and accurate synthesis of spectrally encoded beads using microfluidics and lanthanide nanophosphors. Given an expanded code space with additional lanthanide nanophosphors, this platform enables a multitude of diverse assays, including immuno-diagnostics, small molecule library screening, and combinatorial synthesis approaches.

Acknowledgements

This work was funded by a grant from the W.M. Keck Foundation. R.E.G was supported by a National Science Foundation Graduate Fellowship. P.M.F. was supported by a fellowship administered jointly by the Helen Hay Whitney Foundation and the Howard Hughes Medical Institute. Data for Fig. S2† was acquired in the Nikon Imaging Center at QB3/UCSF. Portions of this work were performed as a user project at the Molecular Foundry, funded by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank Ron Zuckermann for his guidance and valuable discussion, and Colin Campbell for assistance with photographing serpentine channel devices.

References

1. R. Wilson, A. R. Cossins and D. G. Spiller, Encoded Microcarriers For High-Throughput Multiplexed Detection, Angew. Chem., Int. Ed., 2006, 45, 6104–6117.
2. K. B. Cederquist, S. L. Dean and C. D. Keating, Encoded anisotropic particles for multiplexed bioanalysis, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2010, 2, 578–600.
3. K. Braeckmans, S. C. De Smedt, M. Leblans, R. Pauwels and J. Demeester, Encoding microcarriers: present and future technologies, Nat. Rev. Drug Discovery, 2002, 1, 447–456.
4. S. Birtwell and H. Morgan, Microparticle encoding technologies for high-throughput multiplexed suspension assays, Integr. Biol., 2009, 1, 345.
5. K. Braeckmans, et al., Encoding microcarriers by spatial selective photobleaching, Nat. Mater., 2003, 2, 169–173.
6. M. J. Dejneka, et al., Rare earth-doped glass microbarcodes, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 389–393.
7. S. R. Nicewarner-Peña, et al., Submicrometer Metallic Barcodes, Science, 2001, 294, 137–141.
8. H. Lee, J. Kim, H. Kim, J. Kim and S. Kwon, Colour-barcoded magnetic microparticles for multiplexed bioassays, Nat. Mater., 2010, 9, 745–749.
9. D. C. Pregibon, M. Toner and P. S. Doyle, Multifunctional Encoded Particles for High-Throughput Biomolecule Analysis, Science, 2007, 315, 1393–1396.
10. P. Schuetz and F. Caruso, Electrostatically Assembled Fluorescent Thin Films of Rare-Earth-Doped Lanthanum Phosphate Nanoparticles, Chem. Mater., 2002, 14, 4509–4516.
11. H. H. Gorris, R. Ali, S. M. Saleh and O. S. Wolfbeis, Tuning the Dual Emission of Photon-Upconverting Nanoparticles for Ratiometric Multiplexed Encoding, Adv. Mater., 2011, 23, 1652–1655.
12. F. Zhang, et al., Rare-Earth Upconverting Nanobarcodes for Multiplexed Biological Detection, Small, 2011, 7, 1972–1976.
13. S. Fournier-Bidoz, et al., Facile and Rapid One-Step Mass Preparation of Quantum-Dot Barcodes., Angew. Chem., Int. Ed., 2008, 47, 5577–5581.
14. Q. Wang, Y. Liu, C. Lin and H. Yan, Layer-by-layer growth of superparamagnetic, fluorescent barcode nanospheres, Nanotechnology, 2007, 18, 405604.
15. X. Gao and S. Nie, Quantum Dot-Encoded Mesoporous Beads with High Brightness and Uniformity: Rapid Readout Using Flow Cytometry, Anal. Chem., 2004, 76, 2406–2410.
16. M. Han, X. Gao, J. Z. Su and S. Nie, Quantum-dot-tagged microbeads for multiplexed optical coding of biomolecules, Nat. Biotechnol., 2001, 19, 631–635.
17. X.-H. Ji, et al., On-demand preparation of quantum dot-encoded microparticles using a droplet microfluidic system, Lab Chip, 2011, 11, 2561.
18. X.-H. Ji, et al., Integrated parallel microfluidic device for simultaneous preparation of multiplex optical-encoded microbeads with distinct quantum dot barcodes., J. Mater. Chem., 2011, 21, 13380.
19. G. A. Lawrie, B. J. Battersby and M. Trau, Synthesis of Optically Complex Core–Shell Colloidal Suspensions: Pathways to Multiplexed Biological Screening, Adv. Funct. Mater., 2003, 13, 887–896.
20. P. P. T. Surawski, et al., Flow cytometric detection of proteolysis in peptide libraries synthesised on optically encoded supports, Mol. BioSyst., 2008, 4, 774–778.
21. J. Lee, A. O. Govorov and N. A. Kotov, Nanoparticle Assemblies with Molecular Springs: A Nanoscale Thermometer, Angew. Chem., 2005, 117, 7605–7608.
22. S. Shojaei-Zadeh, J. F. Morris, A. Couzis and C. Maldarelli, Highly crosslinked poly(dimethylsiloxane) microbeads with uniformly dispersed quantum dot nanocrystals, J. Colloid Interface Sci., 2011, 363, 25–33.
23. W. G. J. H. M. van Sark, et al. Photooxidation and Photobleaching of Single CdSe/ZnS Quantum Dots Probed by Room-Temperature Time-Resolved Spectroscopy, J. Phys. Chem. B, 2001, 105, 8281–8284.
24. W. G. J. H. M. van Sark, P. L. T. M. Frederix, A. A. Bol, H. C. Gerritsen and A. Meijerink, Blueing, Bleaching, and Blinking of Single CdSe/ZnS Quantum Dots, ChemPhysChem, 2002, 3, 871–879.
25. K. Barnham, J. L. Marques, J. Hassard and P. O'Brien, Quantum-dot concentrator and thermodynamic model for the global redshift, Appl. Phys. Lett., 2000, 76, 1197–1199.
26. A. J. Chatten, K. W. J. Barnham, B. F. Buxton, N. J. Ekins-Daukes and M. A. Malik, A new approach to modelling quantum dot concentrators, Sol. Energy Mater. Sol. Cells, 2003, 75, 363–371.
27. R. J. Fulton, R. L. McDade, P. L. Smith, L. J. Kienker and J. R. Kettman, Advanced multiplexed analysis with the FlowMetrixTM system, Clinical Chemistry, 1997, 43, 1749–1756.
28. C. R. Ronda, T. Jüstel and H. Nikol, Rare earth phosphors: fundamentals and applications, J. Alloys Compd., 1998, 275–277, 669–676.
29. H. Xu, H. Wang, Y. Meng and H. Yan, Rapid synthesis of size-controllable YVO4 nanoparticles by microwave irradiation, Solid State Commun., 2004, 130, 465–468.
30. W. Xu, et al., YVO4: Eu3+,Bi3+ UV to visible conversion nano-films used for organic photovoltaic solar cells, J. Mater. Chem., 2011, 21, 12331–12336.
31. N. M. Idris, et al., Tracking transplanted cells in live animal using upconversion fluorescent nanoparticles, Biomaterials, 2009, 30, 5104–5113.
32. S. Choi, Y.-M. Moon and H.-K. Jung, Luminescent properties of PEG-added nanocrystalline YVO4:Eu3+ phosphor prepared by a hydrothermal method, J. Lumin., 2010, 130, 549–553.
33. F. Wang, X. J. Xue and X. G. Liu, Multicolor tuning of (Ln, P)-Doped YVO4 nanoparticles by single-wavelength excitation, Angew. Chem., Int. Ed., 2008, 47, 906–909.
34. M. A. Unger, H.-P. Chou, T. Thorsen, A. Scherer and S. R. Quake, Monolithic Microfabricated Valves and Pumps by Multilayer Soft Lithography, Science, 2000, 288, 113–116.
35. S. Neeraj, N. Kijima and A. K. Cheetham, Novel red phosphors for solid state lighting; the system BixLn1-xVO4; Eu3+/Sm3+ (Ln = Y, Gd), Solid State Commun., 2004, 131, 65–69.
36. S. Takeshita, T. Isobe and S. Niikura, Low-temperature wet chemical synthesis and photoluminescence properties of YVO4: Bi3+, Eu3+ nanophosphors, J. Lumin., 2008, 128, 1515–1522.
37. D. Chen, et al., Color-tunable luminescence for Bi3+/Ln3+:YVO4 (Ln = Eu, Sm, Dy, Ho) nanophosphors excitable by near-ultraviolet light, Phys. Chem. Chem. Phys., 2010, 12, 7775–7778.
38. X. Y. Huang, et al., Spectral conversion for solar cell efficiency enhancement using YVO4:Bi3+,Ln3+ (Ln=Dy, Er, Ho, Eu, Sm, and Yb) phosphors, J. Appl. Phys., 2011, 109, 113526.
39. A. Stroock, et al., Chaotic mixer for microchannels, Science, 2002, 295, 647–651.
40. T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device, Phys. Rev. Lett., 2001, 86, 4163–4166.
41. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Formation of droplets and bubbles in a microfluidic T-junction—scaling and mechanism of break-up, Lab Chip, 2006, 6, 437–446.
42. S. Xu, et al., Generation of Monodisperse Particles by Using Microfluidics: Control over Size, Shape, and Composition, Angew. Chem., Int. Ed., 2005, 44, 724–728.
43. T. Zimmermann, Spectral imaging and linear unmixing in light microscopy, Adv. Biochem. Eng. Biotechnol., 2005, 95, 245–265.
44. J. P. Brody, B. A. Williams, B. J. Wold and S. R. Quake, Significance and statistical errors in the analysis of DNA microarray data, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12975–12978.
45. Y. Zhao, et al., Microfluidic Generation of Multifunctional Quantum Dot Barcode Particles, J. Am. Chem. Soc., 2011, 133, 8790–8793.
46. M. Haase, K. Riwotzki, H. Meyssamy and A. Kornowski, Synthesis and properties of colloidal lanthanide-doped nanocrystals, J. Alloys Compd., 2000, 303–304, 191–197.
47. B. Yan and J. Wu, YVO4: RE3+ (RE=Eu, Sm, Dy, Er) Nanophosphors: Facile Hydrothermal Synthesis, Microstructure, and Photoluminescence, J. Mater. Res., 2009, 24, 3050–3056.
48. F. Wang, et al., Simultaneous phase and size control of upconversion nanocrystals through lanthanide doping, Nature, 2010, 463, 1061–1065.
49. F. Wang, et al., Tuning upconversion through energy migration in core-shell nanoparticles, Nat. Mater., 2011, 10, 968–973.
50. F. Wang and X. Liu, Recent advances in the chemistry of lanthanide-doped upconversion nanocrystals, Chem. Soc. Rev., 2009, 38, 976–989.
51. S. Wu, et al., Non-blinking and photostable upconverted luminescence from single lanthanide-doped nanocrystals, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10917–10921.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2lc40699c

‡ These authors contributed equally to this work, and the author order was chosen by random draw.

---