DOI:
10.1039/C1LC20770A
(Focus)
Lab Chip, 2012,
12, 20-28
Acoustofluidics 2: Perturbation theory and ultrasound resonance modes
Received
17th August 2011
, Accepted 9th September 2011
First published on 21st November 2011
Abstract
In the second part of the thematic tutorial series “Acoustofluidics – exploiting ultrasonic standing waves forces and acoustic streaming in microfluidic systems for cell and particle manipulation”, we develop the perturbation theory of the acoustic field in fluids and apply the result in a study of acoustic resonance modes in microfluidic channels.
 Henrik Bruus | Prof. Henrik Bruus received his B.Sc. in mathematics and physics from the University of Copenhagen in 1984 and his M.Sc. and Ph.D. degrees in physics from the Niels Bohr Institute, University of Copenhagen in 1986 and 1990, respectively. He was postdoctoral fellow at the Nordic Institute of Theoretical Physics 1990–92, Yale University 1992–94 and CNRS Grenoble 1994–96. He returned to the Niels Bohr Institute as an associate professor 1997–2001, before he joined the faculty at DTU Nanotech, Technical University of Denmark in 2002. He was promoted to full professor there in 2005. He has (co)authored more than 100 peer-reviewed journal papers on condensed matter physics and microfluidics, as well as 120 peer-reviewed conference contributions and two monographs, the latest being “Theoretical Microfluidics”, Oxford University Press (2008). |
Foreword
This is the second paper of 23 in the tutorial series on Acoustofluidics. Each of the forth coming Lab on a chip issues will contain a tutorial which will encompass a topic related to microfluidics and acoustic forces on fluids and particles in microenvironments. This tutorial, single authored by Henrik Bruus, develops the perturbation theory of the acoustic field in fluids and applies the result in a study of acoustic resonance modes in microfluidic channels. Both first- and second-order perturbation theory as well as acoustic resonances in viscous liquids is presented. Acoustic eigenmode analysis, taking into account the wall boundary conditions, is further discussed as the basis to understand the resonance modes observed in acoustofluidic microsystems. It is our hope that this tutorial will become a facilitating and comprehensive document for further discussions on acoustofluidics in the following issues of the series.
Andreas Lenshof & Thomas Laurell
|
I. Introduction
Ultrasound acoustics in the low MHz-range are well suited for applications within microfluidics, because frequencies f ≳ 1.5 MHz combined with the speed of sound in water at room temperature, cwa ≈ 1.5 × 103 m s−1, leads to wavelengths λwa ≲ 1 mm, which may fit into the submillimeter-sized channels and cavities in microfluidic systems and form standing pressure waves known as resonance modes. For several reasons it is often advantageous to operate an acoustofluidic device at these resonance modes: they are usually both stable and reproducible, their spatial patterns are controlled by the geometry of the microfluidic channel, and at resonance a maximum of acoustic power is delivered from the transducer to where it is needed in the system in the form of acoustic radiation force on suspended particles1–3 or acoustic streaming of the solvent.4–7 For microchips, the ultrasound is typically generated as bulk or surface acoustic waves driven by an ac voltage applied to externally mounted piezo-ceramic transducers8,9 or to interdigitated metal electrodes deposited internally on a piezo-electric substrate,10,11 respectively.
In the following section we derive the linear wave equation for the acoustic field in a fluid using regular, first order perturbation theory. A more complete treatment of this theory can be found in the textbooks by Lighthill,12 Pierce,13 and Landau & Lifshitz.14 Here, as in Part 1 of the Tutorial series presenting the governing equations of microfluidics,15 we shall use the notation of the textbook by Bruus.16 The derivation is based on a combination of the thermodynamic equation of state expressing pressure p in terms of density ρ, the kinematic continuity equation for ρ, and the dynamic Navier–Stokes equation for the velocity v (see more details in ref. 16),
| | | ρ∂tv = −∇p − ρ(v·∇)v + η∇2v + βη∇(∇·v). | (1c) |
For
water, the values of the viscosity
η and the viscosity ratio
β are given in
Table 1. Throughout this tutorial paper, we disregard for simplicity all external fields,
e.g. gravity and electromagnetism, and study only the isothermal case to avoid involving the heat transfer equation. Even so, the set
eqn (1) of coupled non-linear, partial differential equations is notoriously difficult to solve analytically. However, good and useful approximate solutions can be found by perturbation theory.
Table 1 Parameters at 25 °C used for acoustic modeling. For waterη = 1 mPa s, β ≈ 1.7, and (at f = 1 MHz) γ ≈ 10−6
| Material |
Longitudinal speed of sound |
Density |
Young's modulus |
Poisson's ratio |
|
Water
|
c
wa
= 1497 m s−1 |
ρ
wa
= 998 kg m−3 |
— |
— |
|
Polystyrene
|
c
ps = 2350 m s−1 |
ρ
ps = 1050 kg m−3 |
— |
— |
|
Silicon
|
c
si = 8490 m s−1 |
ρ
si = 2331 kg m−3 |
Y
si = 164 GPa |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) si = 0.10
si = 0.10 |
| Pyrex |
c
py
= 5661 m s−1 |
ρ
py = 2230 kg m−3 |
Y
py = 63 GPa |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) py = 0.22
py = 0.22 |
II. First-order perturbation theory and the acoustic wave equation
Consider a quiescent liquid, which before the presence of any acoustic wave has constant density ρ0 and pressure p0. Let an acoustic wave constitute tiny perturbations (subscript 1) in the fields of density ρ, pressure p, and velocity v,| | | ρ = ρ0 + ρ1, p = p0 + c2aρ1, and v = v1. | (2) |
In the (isentropic) expansion of the equation of state p(ρ) = p0 + (∂p/∂ρ)sρ1, the derivative has the dimension of a velocity squared, written as c2a. Below we find that ca can be identified with the (isentropic) speed of sound in the liquid. Inserting eqn (2) into eqn (1b) and (1c), and neglecting products of first-order terms, leads to the first-order continuity and Navier–Stokes equation,| | | ρ0∂tv1 = −c2a∇ρ1 + η∇2v1 + βη∇(∇·v1). | (3b) |
A single equation for ρ1 is obtained by taking the time derivative of eqn (3a) followed by insertion of eqn (3b) in the resulting expression,| | 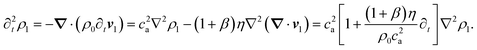 | (4) |
In microfluidics, even for a non-zero ν0, with v0 ≲ 0.1 m s−1, eqn (3) and (4) are approximately correct to order v0/ca ≲ 10−4, see ref. 14.
To make further analytical progress, we assume harmonic time dependence of all fields,
| | | ρ1(r, t) = ρ1(r)e−iωt, | (5a) |
| | | p1(r, t) = c2aρ1(r)e−iωt, | (5b) |
| | | v1(r, t) = v1(r)e−iωt, | (5c) |
where
ω = 2π
f is the angular frequency and
f the frequency of the acoustic field. The harmonic time dependence is expressed by the complex phase e
−iωt to ease the mathematical treatment. The physical fields are obtained simply by taking the real part. With this, each time derivative ∂
t in
eqn (4) gives a factor −i
ω, and the equation for the pressure becomes
| | 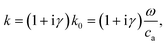 | (6b) |
| | 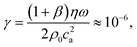 | (6c) |
where we have used
p1 =
c2aρ1 as well as introduced the wavenumber
k0, the complex-valued wavenumber
k, and the viscous damping factor
γ (for values see
Table I).
Eqn (6a) is the Helmholtz equation for a damped wave with wavenumber
k and angular frequency
ω. As
γ ≪ 1, we can neglect the viscosity in the bulk part of the acoustic wave, and going back to the explicitly time-dependent
eqn (4) using
ω → i∂
t, we obtain the wave equation
| | 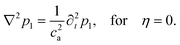 | (7) |
The solutions in 1D to this standard wave equation have the form
p1 =
p1(
x ±
cat) showing that a pressure perturbation
p1(
x) at
t = 0 propagates a distance ∓
cat in time
t, and thus that
ca indeed can be interpreted as the speed of sound. In the inviscid limit it furthermore follows by inserting
eqn (2) into
eqn (3b) that
v1 =
v(
r)e
−iωt is a gradient of a potential
ϕ1,
| | 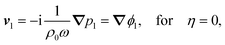 | (8a) |
| | 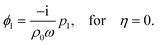 | (8b) |
Thus both the density
ρ1 and velocity
v1 can be calculated from the pressure
p1, which itself is determined by the Helmholtz equation and the boundary conditions.
III. Second-order perturbation theory and non-zero time averages
As the Navier–Stokes equation is nonlinear, the first-order fields calculated in the previous section cannot in general be an exact solution. A more accurate description may be obtained by continuing the first-order expansion in eqn (2) to second order,where all zero- and first-order terms are assumed to be known. These expansions are inserted into eqn (1), and upon collecting all second-order terms, we find that the second-order fields p2, ρ2, and v2 fulfil the following second-order equation of state, continuity and Navier–Stokes equation,| | 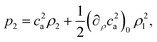 | (10a) |
| | | ∂tρ2 = −ρ0∇·v2 − ∇·(ρ1v1), | (10b) |
| | | ρ0∂tv2 = −∇p2 + η∇2v2 + βη∇(∇·v2) −ρ1∂tv1 − ρ0(v1·∇)v1. | (10c) |
Normally, the second-order fields would be negligible compared to the first-order fields. However, if the latter have a harmonic time dependence as in eqn (5), then they do not contribute to any time-averaged effect as 〈cos(ωt)〉 = 0, where 〈X〉 denotes the time average over a full oscillation period τ of a quantity X(t),
| | 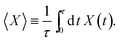 | (11) |
In contrast, the time average of a product of two first order terms both proportional to cos(
ωt) is non-zero, as
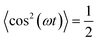
.
Assuming harmonic time dependence, the time average of the second-order continuity and Navier–Stokes eqn (10b) and (10c), becomes
| | | ρ0∇·〈v2〉 = −∇·〈ρ1v1〉, | (12a) |
| | | η∇2〈v2〉 + βη∇(∇·〈v2〉) − ∇〈p2〉 = 〈ρ1∂tv1〉 + ρ0〈(v1·∇)v1〉. | (12b) |
Clearly, the time-averaged, second-order fields will in general be non-zero, due to the time-averaged products of first-order terms acting as source terms in the governing equations. Physically, the non-zero velocity 〈
v2〉 is the so-called acoustic streaming, where the bulk fluid is moving steadily in time due to the absorption of energy and momentum from the acoustic wave, while the non-zero pressure 〈
p2〉 gives rise to the acoustic radiation force coming from the scattering of acoustic waves on the particles and causing acoustophoretic motion of the particles.
In Fig. 1 is shown an example from ref. 17 of these effects observed by measuring the motion of polystyrene tracer beads in a water-filled, square silicon/glass chamber of side length 2 mm and depth 0.2 mm, under the influence of an ultrasound field at the resonance frequency 2.17 MHz applied through an externally attached piezo transducer. Panel (a) is a color plot of the pressure field p1 at a given time calculated using the theory of Sections V and VI B. Red represents positive, blue negative, and green zero pressure. Half a cycle later the sign of the pressure field has changed, but the green pressure nodal lines remain fixed in space appearing as six horizontal sinusoidal waves undergoing three full oscillations across the chamber. In panel (b) is shown the result of measuring on 5-μm-diameter tracer beads. Initially, the beads are distributed homogeneously in the chamber. After the onset of the ultrasound field, the particles move away from the high pressure oscillations under the influence of the acoustic radiation force. The first 1 ms of this motion is recorded by micro particle image velocimetry (micro-PIV), and the obtained velocity of the particles is represented by the yellow arrows. After 1 s all tracer particles have moved to the nodal lines, where they appear as the black wavy line on the gray scale top-view photograph of the device. In panel (c) the same experiment is repeated with 1-μm-diameter tracer beads. For these smaller particles the acoustic radiation force is weak, and the particle motion is dominated by Stokes drag from the circulating acoustic streaming of the water. No particle accumulation at the nodal lines takes place, and instead the depicted 6 × 6 flow-roll pattern persists.
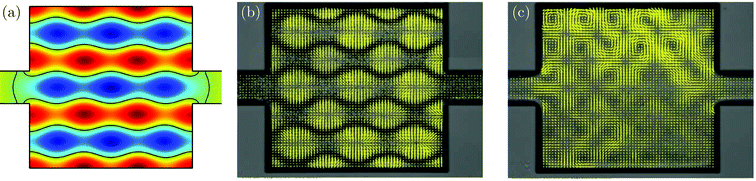 |
| | Fig. 1 Acoustic streaming and radiation forces at the 2.17 MHz-acoustic resonance in a square silicon/glass chamber of area 2 mm × 2 mm and depth 0.2 mm. (a) Color plot of the pressure field p1 (red: positive, green: zero, blue: negative) calculated by numerical simulation in the 2D chamber model of the 2.17 MHz pressure eigenmode. Nodal lines are shown in black. (b) Top-view gray-scale photograph of 5-μm-diameter polystyrene beads undergoing acoustophoretic motion in the water-filled chamber due to the acoustic radiation force. The particle velocity (overlaid yellow arrows) 1 ms after the onset of the 2.17 MHz ultrasound wave were measured by micro-PIV. After 1 s the particles have accumulated at the pressure nodal lines (black wavy lines). (c) Experiments on 1-μm-diameter polystyrene beads, under the same conditions as in the previous panel. In this case the acoustic radiation force is much weaker than the Stokes drag from the acoustic streaming motion of the water, so in the resulting 6 × 6 flow-roll pattern no particle accumulation at the pressure nodal lines is observed. Adapted from ref. 17. | |
The acoustic radiation force1–3 and the acoustic streaming4–7 are central concepts in acoustofluidics and will be studied in more detail throughout the Tutorial series. In the rest of this tutorial paper, we study the basics of the underlying first-order acoustic resonant modes.
IV. Basics of acoustic resonances in viscous liquids
As mentioned in the introduction, acoustic resonance modes are particularly useful to establish for acoustic handling of cells and particles in microfluidic systems. To illustrate the fundamental properties of such resonance modes, we study the simple 1D setup sketched in Fig. 2(a). Two planar walls are placed parallel to the yz-plane at x = −L and x = L, respectively, and the gap is filled with water. To mimic the action of the piezo transducer, the walls are forced to oscillate in anti-phase at a frequency f ≈ 1 MHz and with an amplitude ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 0.1 nm. As a simplification we neglect the actual tiny displacement of the walls and instead model the oscillation by the velocity boundary condition sketched in Fig. 2(a),
≈ 0.1 nm. As a simplification we neglect the actual tiny displacement of the walls and instead model the oscillation by the velocity boundary condition sketched in Fig. 2(a),| | v1(−L, t) = −ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt, e−iωt, | (13a) |
| | v1(+L, t) = +ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt. e−iωt. | (13b) |
Starting from rest the resonance builds up until the incoming power equals the heat dissipation due to viscosity, and a steady state at constant temperature is reached. The standing 1D wave v1 = f(x)e−iωtex has ∇ × v1 = 0, so v1 = ∇ϕ1 and ∂jvi = ∂ivj. To find the viscid velocity potential ϕ1, we note that ∂j∂jvi = ∂j∂ivj = ∂i∂jvj, i.e. ∇2v1 = ∇(∇·v1), and from eqn (3a) we have ∇·v1 = iωp1/(ρ0c2a). Inserting these two expressions together with v1 = ∇ϕ into eqn (3b), we find,| | 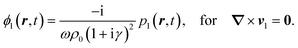 | (14) |
Because ϕ1 ∝ p1, the wave eqn (6a) also holds for ϕ1, and we can therefore write the solution for ϕ1 as a superposition of a pair of counter-propagating plane waves with a complex wave number k = k0(1 + iγ) and unknown coefficients ϕ+ and ϕ− to be determined,| | | ϕ1(x, t) = [ϕ+eikx + ϕ−e−ikx]e−iωt. | (15) |
The corresponding first-order velocity is| | | v1(x, t) = ∂xϕ1(x, t) = ik[ϕ+eikx − ϕ−e−ikx]e−iωt. | (16) |
The antisymmetric boundary condition on v1 in eqn (13) combined with eqn (16) leads to ϕ+ = ϕ−, as well as an expression for the coefficients,| | 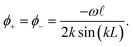 | (17) |
From this, we can obtain the following expression for v1,| | 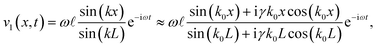 | (18) |
where we have used γk0L ≪ 1 to make Taylor expansions in kL around k0L. We note that when k0L differs sufficiently from integer multiples of π, i.e. γ ≪ |k0L − nπ|, then the imaginary part of the denominator can be neglected. This corresponds to off-resonance characterized by a small maximum magnitude |v1| of the velocity,| | 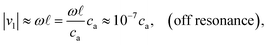 | (19) |
where the value is calculated by assuming ω ≈ 107 rad s−1, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 0.1 nm and ca ≈ 103 m s−1.
≈ 0.1 nm and ca ≈ 103 m s−1.
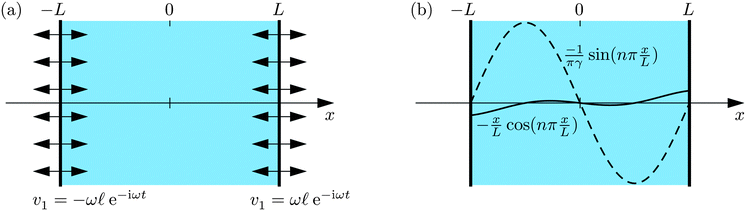 |
| | Fig. 2 (a) A liquid slab (blue) between two parallel planar walls (thick lines) that oscillate harmonically in counter-phase (double arrows). As the amplitude is minute, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≪ L, the wall positions are considered fixed, while the first-order velocity v1(t) at the walls is changing harmonically, v1(t) = ±ω ≪ L, the wall positions are considered fixed, while the first-order velocity v1(t) at the walls is changing harmonically, v1(t) = ±ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt. (b) Sketch of the two terms in the resonant velocity field v1eqn (22b). The small component (full line) proportional to (x/L) cos(πx/L) obeys the oscillatory boundary condition with amplitude ±ω e−iωt. (b) Sketch of the two terms in the resonant velocity field v1eqn (22b). The small component (full line) proportional to (x/L) cos(πx/L) obeys the oscillatory boundary condition with amplitude ±ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The large resonant component (dashed line) proportional to (1/πγ) sin(πx/L) is an eigenmode obeying the hard-wall condition with zero velocity amplitude. . The large resonant component (dashed line) proportional to (1/πγ) sin(πx/L) is an eigenmode obeying the hard-wall condition with zero velocity amplitude. | |
More interesting, perhaps, are the acoustic resonances, where the acoustic field acquires particularly large amplitudes and thus contains a large amount of stored energy, see Fig. 2(b). Theoretically, the resonances are identified by the minima in the denominators of v1 in eqn (18), i.e. by sin(k0L) = 0 or k0L = nπ, n = 1, 2, 3,…,
| | 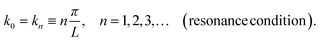 | (20) |
In practice, the resonance is achieved by tuning the frequency
ω to the resonance frequency
ωn given by
| | 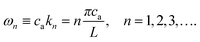 | (21) |
At the
nth resonance sin(
knL) = 0 and cos(
knL) = (−1)
n, so the acoustic fields become
| | 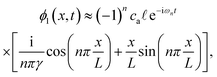 | (22a) |
| | 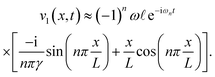 | (22b) |
From these expressions it follows that each of the fields acquires a resonant component with an amplitude that is a factor of 1/(
nπ
γ) ≈ (1/
n) × 10
5 larger than the non-resonant component,
e.g.| | 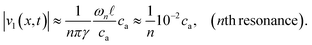 | (23) |
Despite the huge multiplication factor, 1/(π
γ) ≈ 10
4, the perturbation approach remains valid as the density fluctuation is small,
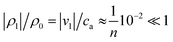
.
From eqn (22b) we see that the term actually obeying the velocity boundary condition v1(±L) = ±ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is 105 times smaller than the other term, which obeys the hard-wall condition v1(±L, t) = 0 and thus in fact is an eigenmode of the system. Consequently, when coupling into a system with a frequency near an eigenmode frequency, the corresponding eigenmode gets excited with a huge amplitude, approximately a factor 1/γ larger than the coupling amplitude, independent of the actual boundary condition, see Fig. 2(b).
is 105 times smaller than the other term, which obeys the hard-wall condition v1(±L, t) = 0 and thus in fact is an eigenmode of the system. Consequently, when coupling into a system with a frequency near an eigenmode frequency, the corresponding eigenmode gets excited with a huge amplitude, approximately a factor 1/γ larger than the coupling amplitude, independent of the actual boundary condition, see Fig. 2(b).
As the energy density Eac for an harmonically oscillating system is twice the time-averaged kinetic energy density, eqn (18) implies 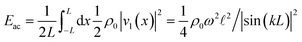 . By Taylor expanding this expression in
. By Taylor expanding this expression in 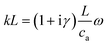 around the resonance knL = nπ, we find a Lorentzian line shape as a function of frequency,
around the resonance knL = nπ, we find a Lorentzian line shape as a function of frequency,
| | 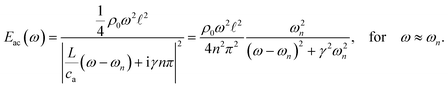 | (24) |
At resonance we find the energy density
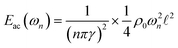
, which is much larger than the off-resonance energy density of about
ρ0ω2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2
2. At
ω =
ωn the energy density
Eac(
ω) is at its maximum, while it decreases to half of this value when changing the frequency to
ω =
ωn +
γωn. Therefore, the full width Δ
ω at half maximum of the resonance peak is seen to be Δ
ω = 2
γωn, and by definition the quality factor
Q of the resonance therefore becomes,
| | 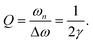 | (25) |
We emphasize that this result overestimates the Q-factor, because it builds on the simplifying assumption that viscous dissipation in the bulk liquid is the only source to loss of acoustic energy. In a real device, acoustic energy is also lost as viscous friction at the walls and as sound waves emitted into the chip holder and fluidic connectors as well as into the surrounding air.
18
V. Acoustic eigenmodes
The above result indicates that we can gain insight in the nature of acoustic resonances in externally driven systems by analyzing the eigenmodes pn = pn(r)e−iωnt of the equivalent isolated liquid-filled chamber. If more specific details are needed, it is necessary to calculate the acoustic response of the entire system driven by the piezo transducer, i.e. combining the wave equation of the liquid with the elastic equations of the surrounding solids. Such more complete descriptions will be discussed in Part 3 of this Tutorial series.19
A. Boundary conditions
In the simple chamber model of the liquid domain, the acoustic pressure eigenmodes pn = pn(r)e−iωnt in the liquid are determined by the Helmholtz eqn (6a) with appropriate boundary conditions. In the following we use either the soft-wall, the hard-wall, or the lossy-wall boundary condition.
The soft-wall condition is used when the medium interfacing with the liquid cannot sustain any appreciable pressure. Examples of this are a free liquid/air interface or, as in ref. 20, liquid surrounded by a thin glass wall and then air. The mathematical form of the boundary condition is
| | | p1 = 0, soft-wall boundary condition. | (26a) |
The hard-wall condition applies when the liquid is interfacing with an infinitely hard wall, not yielding to the velocity v1 of the liquid. Consequently, the normal velocity of the liquid at the wall is zero, which by eqn (8a) leads to a zero normal gradient of the pressure,
| | | n·∇p1 = 0, hard-wall boundary condition. | (26b) |
The lossy-wall condition is an approximative description of partial radiative acoustic losses from the liquid to the surrounding medium. Consider a planer configuration with the liquid placed in the half-space x < 0 next to an ideally absorbing medium (subscript m) at x > 0. A radiative loss can be described by a wave in the medium having only the right-ward propagating component: ϕm = A eikmx. From eqn (8) follows vm = ikmϕm and pm = iωρmϕm, and thus pm = ρmcmvm at the interface. Combining this with continuity in pressure (p1 = pm) and velocity (v1 = vm) across the interface, and with n·∇p1 = iωρ0n·v1 from eqn (8), we arrive at
| | 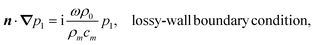 | (26c) |
where the planar case is generalized to any curved surface. The product
ρmcm is known as the specific acoustic impedance of the medium. The soft-wall condition
eqn (26a) is recovered from
eqn (26c) in the limit of zero impedance of the surrounding medium, while the hard-wall condition
eqn (26b) corresponds to infinitely large impedance. If the liquid and the medium have the same impedance, acoustic waves pass the interface without suffering any scattering.
Finally, we note that since (ρsicsi)/(ρwacwa) = 13.2 and (ρpycpy)/(ρwacwa) = 8.4 (using the longitudinal sound velocities of Table 1), it may be a reasonable first approximation to use the hard-wall boundary condition for water channels in silicon/glass chips.
B. An ideal water-filled rectangular channel
We proceed by studying the acoustic modes for a rectangular water-filled channel placed along the coordinate axes with its opposite corners at (0, 0, 0) and (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , w, h) surrounded by either hard or soft walls. As can be verified easily by direct substitution, the eigenmodes of this ideal rectangular channel are
, w, h) surrounded by either hard or soft walls. As can be verified easily by direct substitution, the eigenmodes of this ideal rectangular channel are| | 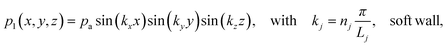 | (27a) |
| | 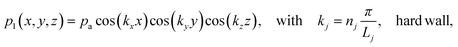 | (27b) |
where pa is the pressure amplitude, where (Lx, Ly, Lz) = (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , w, h), and where nj = (0),1, 2, 3,… is the number of half wavelengths (nj > 0 for the sine-waves). The corresponding three-index resonance frequencies fnx,ny,nz = ωnx,ny,nz/(2π) are
, w, h), and where nj = (0),1, 2, 3,… is the number of half wavelengths (nj > 0 for the sine-waves). The corresponding three-index resonance frequencies fnx,ny,nz = ωnx,ny,nz/(2π) are| | 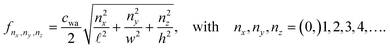 | (28) |
Examples of these analytically determined eigenmodes are shown in Fig. 3. Note the relatively low frequency of (d) and (e) having nz = 0 along the smallest dimension in contrast to nz = 1 of the other four eigenmodes. In (f) one half-length is squeezed in along the z-direction (nz = 1) and the frequency increases significantly. In fact, as (a) and (f) have the same indices they also have the same frequency, namely f1,1,1 despite their different boundary conditions. It turns out that the anti-symmetric resonance (d), having a perfect nodal plane in the vertical center plane, is an ideal configuration for acoustophoretic separation.
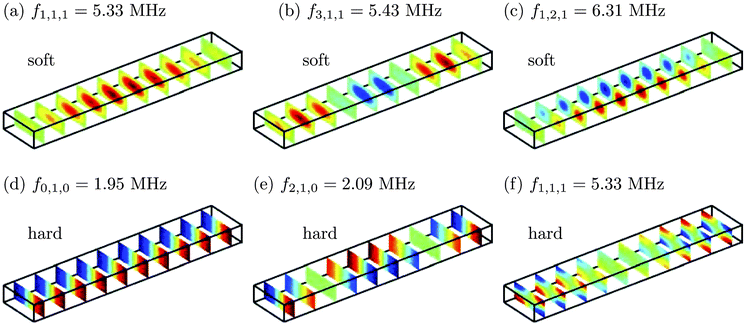 |
| | Fig. 3 Color slice plots (red: positive, green: zero, blue: negative) of some inviscid eigenmodes of the pressure field p1 in a rectangular, single, water-filled microchannel of length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 mm, width w = 0.38 mm, and height h = 0.15 mm. (a)–(c) Soft-wall boundary conditions p1 = 0 at the surface, i.e. a zero-density wall surrounds the channel. (d)–(f) Hard-wall boundary condition n·∇p1 = 0, i.e. the surrounding wall is of infinite density. Adapted from ref. 21. = 2 mm, width w = 0.38 mm, and height h = 0.15 mm. (a)–(c) Soft-wall boundary conditions p1 = 0 at the surface, i.e. a zero-density wall surrounds the channel. (d)–(f) Hard-wall boundary condition n·∇p1 = 0, i.e. the surrounding wall is of infinite density. Adapted from ref. 21. | |
C. Radiation loss in rectangular channels
When energy dissipates from the acoustic field near resonance, the resonance peak in the form of acoustic energy density plotted versus frequency acquires a finite full width at half maximum, Δω = ωn/Q, where Q is the quality factor of the resonance at frequency ωn. If the only source of energy dissipation is the viscous damping in the liquid, then it follows from eqn (6c) and (25) that the Q-factor is of the order Q ≈ 106 for water. However, it is found experimentally that typical Q-factors are in the range 100 < Q < 1000, see e.g.Fig. 4 and ref. 18, mainly due to the radiative losses to the sample holder, the surrounding air, and inlet/outlet tubes.
 |
| | Fig. 4 Experimental determination of the Q factor of an acoustic mode. (a) The silicon/glass chips containing straight channels of length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 40 mm, width w = 377 μm, and height h = 157 μm. The channels are etched down into the silicon chip of thickness 350 μm, and they are covered by a pyrex glass lid of thickness 1.13 mm. The chips are 50 mm long and have widths of 2.5 mm (α = 1), 4.7 mm (α = 2), 6.8 mm (α = 3), and 9.0 mm (α = 4). (b) A photograph of the experimental setup showing how a chip is coupled mechanically to the piezo actuator, the PMMA holder, and the inlet/outlet tubes. (c) Plot of the measured acoustic energy density Eacversus frequency f (red dots) for the α = 2 chip. The two observed acoustic resonance peaks are fitted well by the sum of two Lorentzian line shapes (eqn (24), blue line). The resonance frequencies are f1 = 2.0021 MHz and f1 = 1.9927 MHz, while the Q-factors are Q1 = 209 and Q2 = 577. Adapted from ref. 23. = 40 mm, width w = 377 μm, and height h = 157 μm. The channels are etched down into the silicon chip of thickness 350 μm, and they are covered by a pyrex glass lid of thickness 1.13 mm. The chips are 50 mm long and have widths of 2.5 mm (α = 1), 4.7 mm (α = 2), 6.8 mm (α = 3), and 9.0 mm (α = 4). (b) A photograph of the experimental setup showing how a chip is coupled mechanically to the piezo actuator, the PMMA holder, and the inlet/outlet tubes. (c) Plot of the measured acoustic energy density Eacversus frequency f (red dots) for the α = 2 chip. The two observed acoustic resonance peaks are fitted well by the sum of two Lorentzian line shapes (eqn (24), blue line). The resonance frequencies are f1 = 2.0021 MHz and f1 = 1.9927 MHz, while the Q-factors are Q1 = 209 and Q2 = 577. Adapted from ref. 23. | |
In the simple chamber model, this lowering of the Q-factor can be modeled using the lossy-wall boundary condition (26c) with the acoustic impedance ρmcm as a fitting parameter. For the rectangular channel, this can be argued as follows: Consider the transverse half-wavelength standing wave between the walls at y = ±![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /2 given by p1(y) = A sin[π(1 + i
/2 given by p1(y) = A sin[π(1 + i![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) )y/
)y/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ], where the unknown
], where the unknown ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) is the damping factor given by the radiative loss. Note that this form is similar to eqn (18), but with a different interpretation of
is the damping factor given by the radiative loss. Note that this form is similar to eqn (18), but with a different interpretation of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . In this case the lossy-wall boundary conditions become
. In this case the lossy-wall boundary conditions become
| | 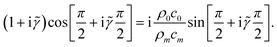 | (29) |
Assuming
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif)
≪ 1, a Taylor expansion leads to
| | 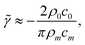 | (30) |
so that the damping factor
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif)
due to radiation loss can be thought of as a ratio between the impedances of
water and the surrounding (ideally absorbing) medium.
Radiative losses to ideally absorbing walls can lower the Q-factor to as much as Q ≈ 10. However, the real surroundings (sample holder, inlet/outlet tubes, and the air) are not completely absorbing, which is why the measured Q-factors are in the range Q ≈ 100–1000.
Experimentally, the global structure of the acoustic eigenmodes can be mapped out using an automated micro-PIV setup.22
VI. Geometrical effects
For geometrical shapes more irregular than rectangular it is in generally not possible to find analytical solutions to the acoustic wave equation and one must resort to numerical simulations. Below we sketch the basic principle of the finite element method (FEM), one of the most widely used numerical methods.
With numerical methods at hand, it is possible to study the effects of specific geometrical shapes on the resonance modes in the liquid domain. In fact, we have already seen an example of this in Fig. 1(a). According to eqn (27b), the corresponding pressure resonance of a perfect hard-walled square cavity of side length L in the xy-plane should have the form p1(x, y) = pacos(6πx/L) cos(6πy/L), which is symmetric along the diagonal x = y. However, the figure clearly shows that the presence of the inlet and outlet channels along the x-direction breaks this symmetry.
A. Finite element method (FEM) simulations
A general and versatile method to solve the acoustic wave equations (and other continuum field equations) is the so-called weak form suitable for implementation in the finite element method (FEM) used by the COMSOL Multiphysics software (www.comsol.com). In FEM analysis the governing equations are not satisfied in each and every point of the computational domain Ω, but only on average in each of the small regions defined by a mesh.
As a main example we study the Helmholtz equation 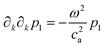 for acoustic waves, eqn (6a). To discretize this equation, the domain Ω is divided by a mesh into a large number M of small cellsm. A corresponding number of scalar test functions
for acoustic waves, eqn (6a). To discretize this equation, the domain Ω is divided by a mesh into a large number M of small cellsm. A corresponding number of scalar test functions ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) m are introduced, each being different from zero only in their respective cellm. The given field p1(r) is represented by a linear combination of test functions with coefficients Pm,
m are introduced, each being different from zero only in their respective cellm. The given field p1(r) is represented by a linear combination of test functions with coefficients Pm,
| | 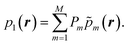 | (31) |
In the weak form, a given differential equation in the continuous space is transformed into
M equations, one for each coefficient
Pm, by multiplying it by each of the test functions, integrating of the domain, and demand that all these integrals should be zero,
| | 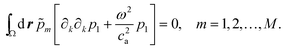 | (32) |
As a result the integrand is zero on average, and the equation
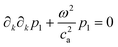
is fulfilled approximatively. By partial integration only first derivatives are left in the integrand, and a specific surface integral appears, through which the boundary conditions can be applied,
| | 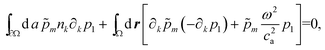 | (33) |
where
n is the outward-pointing surface normal of ∂Ω. The Neumann boundary condition
n·
∇p1 =
N(
r) is therefore imposed by
| | 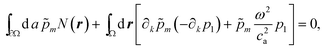 | (34) |
For the hard-wall condition
eqn (26b),
N(
r) = 0 and the surface integral vanishes.
The Dirichlet condition p1 = D(r) is more tricky to impose on the boundary. In this case the normal derivative on the boundary is free to vary such that the imposed Dirichlet boundary condition indeed is fulfilled. This case therefore requires the introduction of an auxiliary field f(r) on the boundary together with a number J of associated test functions ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) j(r), the so-called Lagrange multipliers, each defined the along the edges of the outer edges of the J mesh cells at the surface ∂Ω,
j(r), the so-called Lagrange multipliers, each defined the along the edges of the outer edges of the J mesh cells at the surface ∂Ω,
| | 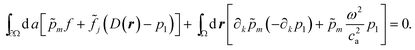 | (35) |
As the Lagrange multiplier test functions
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) j
j only exists on the boundary, the demand for zero-valued integrals forces the coefficient (
D(
r) −
p1) to be zero for any converged solution of the problem. On the other hand, the coefficient
f(
r) of the pressure test function
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) m
m is a dependent variable, which through
∇p1 couples to the terms of the volume integral. Since this coefficient is also the normal derivative of the pressure, we find that it has been determined as
n·
∇p1 =
f for a converged solution.
With this method we can calculate the acoustic resonance modes for any shape of acoustic cavities with any boundary condition. The soft-wall condition eqn (26a) is obtained by setting D(r) = 0, while the lossy-wall condition eqn (26c) requires 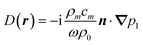 .
.
B. Symmetry breaking in acoustic resonances
As an example of the effects of non-trivial geometrical shapes on the acoustic resonances, we take the study of symmetry breaking in a water-filled silicon/glass microchamber of ref. 17, see Fig. 5. The 2-mm-by-2-mm square chamber has a depth of 0.2 mm, and two inlet/outlet channels of width 0.4 mm and unequal lengths (12.5 mm and 10.5 mm) are attached on opposite sides as sketched in panel (a). Experimentally, two close lying resonances of nearly identical resonance pattern are observed at 2.06 MHz and 2.08 MHz, see panels (b) and (c). The pattern of the lower-frequency resonance is shifted slightly to the left, towards the longer and thus less confining channel, while the opposite is the case of the higher-frequency resonance.
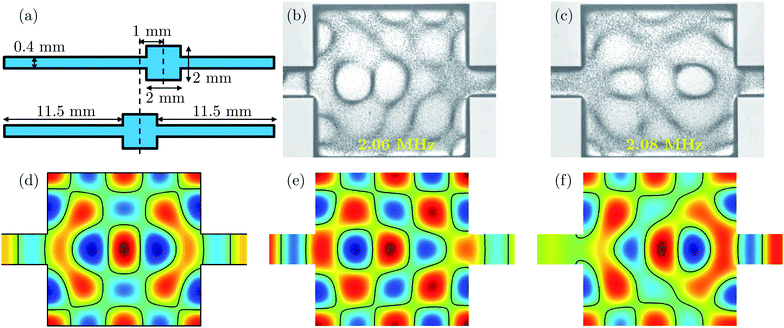 |
| | Fig. 5 (a) Sketches of a 2 mm square microfluidic chamber placed symmetrically and asymmetrically (shifted 1 mm to the right) relative to 0.4 mm wide and 11.5 mm long inlet/outlet channels (not drawn to scale). (b) Photograph of the position of 5-μm-diameter tracer beads (black bands) in a silicon/pyrex chip having the asymmetric geometry of panel (a) after 1 s of motion in the 2.06 MHz ultrasound resonance mode. (c) The same as the previous panel, but for the 2.08 MHz resonance mode. (d) Color plot of the pressure field p1 (blue: negative, green: zero, red: positive) of the resonance near the 2.1 MHz in the symmetric geometry with hard-wall boundary conditions found by numerical simulation using COMSOL. Notice the left-right symmetry of p1. (e) Same as the previous panel, except for the asymmetric device. Notice the slightly larger amplitude of p1 left of the symmetry line as in panel (b). (f) Same has the previous panel, but for the resonance mode with a frequency 0.028 MHz higher. Notice the slightly larger amplitude of p1 right of the symmetry line as in panel (c). Adapted from ref. 17. | |
A similar trend is seen in the numerical simulation presented in the color plots of the pressure field p1 in panels (d)–(f) obtained by solving the 2D Helmholtz eqn (6a) with the hard-wall condition (26b). In panel (d) is shown the result for the symmetric case of equal-length (11.5 mm) inlet/outlet channels: a left-right symmetric pressure field. To quantitatively explain the non-symmetric pressure modes observed experimentally, the pressure resonances are also calculated in the asymmetric case of inlet/outlet channels of unequal lengths (12.5 mm and 10.5 mm). Two nearly identical resonance patterns are found near the frequency of the symmetric case in panel (d), one mode with a frequency 0.028 MHz lower than the other similar to the observed frequency difference. In agreement with the experimental observations, the lower-frequency mode is seen to be shifted to towards the left inlet channel, which is longer and thus supports a resonance at a slightly lower frequency, while the other is shifted towards the short, right inlet channel thus giving rise to a slight increase in resonance frequency.
The simple acoustic model, where the chip surrounding the water channel is merely modeled as a hard wall, thus offers some qualitative insight in the behavior of acoustic resonance modes.
VII. Concluding remarks
In this tutorial paper we have used first-order perturbation theory to derive the governing equation for acoustic waves in fluids. We have noted that non-vanishing time-average effects can only be explained by applying second-order perturbation theory.
The acoustic wave theory was used to study various aspects of resonance modes including effects of viscous and radiative damping of systems driven by an externally applied ultrasound frequency. Furthermore, after establishing the soft-wall, the hard-wall, and the lossy-wall boundary conditions, the basic features of acoustic eigenmodes in 3D rectangular-shaped inviscid liquid domains were studied. And finally, it was shown by comparison to experiments that the simplified 2D chamber model, where the surrounding elastic solid has been decoupled, did offer qualitative insight into the physical nature of the resonance modes in flat microchambers. However, to obtain quantitative agreement between simulation and experiment, it is necessary to include modeling of the elastic walls and its coupling to the liquid-filled microchannels. This is the topic of Part 3 of this Tutorial series.19
Acknowledgements
This work was supported by the Danish Council for Independent Research, Technology and Production Sciences, Grant No. 274-09-0342.
References
- L. V. King, Proc. R. Soc. London, Ser. A, 1934, 147, 212–240 CrossRef.
- K. Yosioka and Y. Kawasima, Acustica, 1955, 5, 167–173 Search PubMed.
- L. P. Gorkov, Soviet Physics - Doklady, 1962, 6, 773–775 Search PubMed.
- Lord Rayleigh, Philos. Trans. R. Soc. London, 1884, 175, 1–21 CrossRef.
- H. Schlicthing, Physicalische Zetischrift, 1932, 327–335 Search PubMed.
- C. Eckart, Phys. Rev., 1948, 73, 68–76 CrossRef.
- J. Lighthill, J. Sound Vib., 1978, 61, 391–418 CrossRef.
- A. Nilsson, F. Petersson, H. Jönsson and T. Laurell, Lab Chip, 2004, 4, 131–5 RSC.
- O. Manneberg, J. Svennebring, H. M. Hertz and M. Wiklund, J. Micromech. Microeng., 2008, 18, 095025 CrossRef.
- Z. Guttenberg, H. Muller, H. Habermuller, A. Geisbauer, J. Pipper, J. Felbel, M. Kielpinski, J. Scriba and A. Wixforth, Lab Chip, 2005, 5, 308–317 RSC.
- J. Shi, H. Huang, Z. Stratton, Y. Huang and T. J. Huang, Lab Chip, 2009, 9, 3354–3359 RSC.
-
J. Lighthill, Waves in Fluids, Cambridge University Press, 2002 Search PubMed.
-
A. D. Pierce, Acoustics, Acoustical Society of America, Woodbury, 1991 Search PubMed.
-
L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, Oxford, 2nd edn, 1993, vol. 6, Course of Theoretical Physics Search PubMed.
- H. Bruus, Lab Chip, 2011, 11, 3742–3751 RSC.
-
H. Bruus, Theoretical Microfluidics, Oxford University Press, Oxford, 2008 Search PubMed.
- S. M. Hagsäter, T. G. Jensen, H. Bruus and J. P. Kutter, Lab Chip, 2007, 7, 1336–1344 RSC.
- M. Groschl, Acustica, 1998, 84, 432–447 Search PubMed.
- J. Dual and T. Schwarz, Lab Chip, 2011 10.1039/c1lc20837c.
- B. Hammarstrom, M. Evander, H. Barbeau, M. Bruzelius, J. Larsson, T. Laurell and J. Nillsson, Lab Chip, 2010, 10, 2251–2257 RSC.
- R. Barnkob and H. Bruus, Proc. Meet. Acoust., 2009, 6, 020001, DOI:10.1121/1.3186746.
- P. Augustsson, R. Barnkob, S. T. Wereley, H. Bruus and T. Laurell, Lab Chip, 2011 10.1039/c1lc20637k.
- R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Lab Chip, 2010, 10, 563–570 RSC.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) si = 0.10
si = 0.10![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) py = 0.22
py = 0.22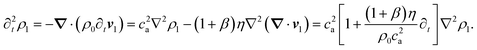
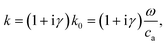
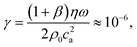
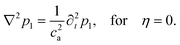
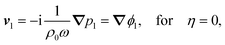
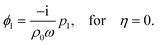
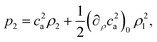
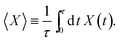
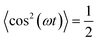 .
.

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 0.1 nm. As a simplification we neglect the actual tiny displacement of the walls and instead model the oscillation by the velocity boundary condition sketched in Fig. 2(a),
≈ 0.1 nm. As a simplification we neglect the actual tiny displacement of the walls and instead model the oscillation by the velocity boundary condition sketched in Fig. 2(a),![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt,
e−iωt,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt.
e−iωt.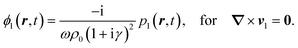
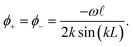
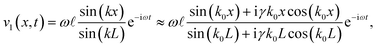
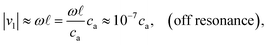
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 0.1 nm and ca ≈ 103 m s−1.
≈ 0.1 nm and ca ≈ 103 m s−1.

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≪ L, the wall positions are considered fixed, while the first-order velocity v1(t) at the walls is changing harmonically, v1(t) = ±ω
≪ L, the wall positions are considered fixed, while the first-order velocity v1(t) at the walls is changing harmonically, v1(t) = ±ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) e−iωt. (b) Sketch of the two terms in the resonant velocity field v1eqn (22b). The small component (full line) proportional to (x/L) cos(πx/L) obeys the oscillatory boundary condition with amplitude ±ω
e−iωt. (b) Sketch of the two terms in the resonant velocity field v1eqn (22b). The small component (full line) proportional to (x/L) cos(πx/L) obeys the oscillatory boundary condition with amplitude ±ω![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . The large resonant component (dashed line) proportional to (1/πγ) sin(πx/L) is an eigenmode obeying the hard-wall condition with zero velocity amplitude.
. The large resonant component (dashed line) proportional to (1/πγ) sin(πx/L) is an eigenmode obeying the hard-wall condition with zero velocity amplitude.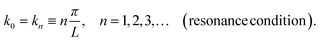
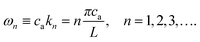
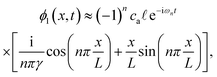
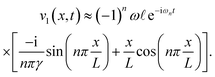
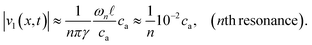
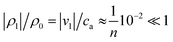 .
.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is 105 times smaller than the other term, which obeys the hard-wall condition v1(±L, t) = 0 and thus in fact is an eigenmode of the system. Consequently, when coupling into a system with a frequency near an eigenmode frequency, the corresponding eigenmode gets excited with a huge amplitude, approximately a factor 1/γ larger than the coupling amplitude, independent of the actual boundary condition, see Fig. 2(b).
is 105 times smaller than the other term, which obeys the hard-wall condition v1(±L, t) = 0 and thus in fact is an eigenmode of the system. Consequently, when coupling into a system with a frequency near an eigenmode frequency, the corresponding eigenmode gets excited with a huge amplitude, approximately a factor 1/γ larger than the coupling amplitude, independent of the actual boundary condition, see Fig. 2(b).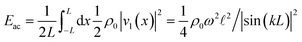 . By Taylor expanding this expression in
. By Taylor expanding this expression in 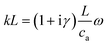 around the resonance knL = nπ, we find a Lorentzian line shape as a function of frequency,
around the resonance knL = nπ, we find a Lorentzian line shape as a function of frequency,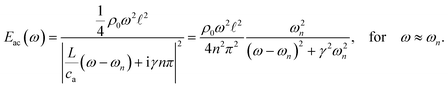
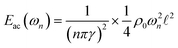 , which is much larger than the off-resonance energy density of about ρ0ω2
, which is much larger than the off-resonance energy density of about ρ0ω2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2. At ω = ωn the energy density Eac(ω) is at its maximum, while it decreases to half of this value when changing the frequency to ω = ωn + γωn. Therefore, the full width Δω at half maximum of the resonance peak is seen to be Δω = 2γωn, and by definition the quality factor Q of the resonance therefore becomes,
2. At ω = ωn the energy density Eac(ω) is at its maximum, while it decreases to half of this value when changing the frequency to ω = ωn + γωn. Therefore, the full width Δω at half maximum of the resonance peak is seen to be Δω = 2γωn, and by definition the quality factor Q of the resonance therefore becomes,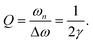
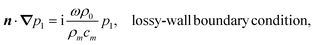
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , w, h) surrounded by either hard or soft walls. As can be verified easily by direct substitution, the eigenmodes of this ideal rectangular channel are
, w, h) surrounded by either hard or soft walls. As can be verified easily by direct substitution, the eigenmodes of this ideal rectangular channel are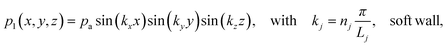
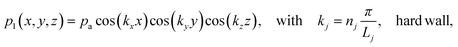
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , w, h), and where nj = (0),1, 2, 3,… is the number of half wavelengths (nj > 0 for the sine-waves). The corresponding three-index resonance frequencies fnx,ny,nz = ωnx,ny,nz/(2π) are
, w, h), and where nj = (0),1, 2, 3,… is the number of half wavelengths (nj > 0 for the sine-waves). The corresponding three-index resonance frequencies fnx,ny,nz = ωnx,ny,nz/(2π) are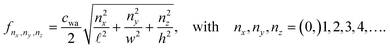

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 mm, width w = 0.38 mm, and height h = 0.15 mm. (a)–(c) Soft-wall boundary conditions p1 = 0 at the surface, i.e. a zero-density wall surrounds the channel. (d)–(f) Hard-wall boundary condition n·∇p1 = 0, i.e. the surrounding wall is of infinite density. Adapted from ref. 21.
= 2 mm, width w = 0.38 mm, and height h = 0.15 mm. (a)–(c) Soft-wall boundary conditions p1 = 0 at the surface, i.e. a zero-density wall surrounds the channel. (d)–(f) Hard-wall boundary condition n·∇p1 = 0, i.e. the surrounding wall is of infinite density. Adapted from ref. 21.
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 40 mm, width w = 377 μm, and height h = 157 μm. The channels are etched down into the silicon chip of thickness 350 μm, and they are covered by a pyrex glass lid of thickness 1.13 mm. The chips are 50 mm long and have widths of 2.5 mm (α = 1), 4.7 mm (α = 2), 6.8 mm (α = 3), and 9.0 mm (α = 4). (b) A photograph of the experimental setup showing how a chip is coupled mechanically to the piezo actuator, the PMMA holder, and the inlet/outlet tubes. (c) Plot of the measured acoustic energy density Eacversus frequency f (red dots) for the α = 2 chip. The two observed acoustic resonance peaks are fitted well by the sum of two Lorentzian line shapes (eqn (24), blue line). The resonance frequencies are f1 = 2.0021 MHz and f1 = 1.9927 MHz, while the Q-factors are Q1 = 209 and Q2 = 577. Adapted from ref. 23.
= 40 mm, width w = 377 μm, and height h = 157 μm. The channels are etched down into the silicon chip of thickness 350 μm, and they are covered by a pyrex glass lid of thickness 1.13 mm. The chips are 50 mm long and have widths of 2.5 mm (α = 1), 4.7 mm (α = 2), 6.8 mm (α = 3), and 9.0 mm (α = 4). (b) A photograph of the experimental setup showing how a chip is coupled mechanically to the piezo actuator, the PMMA holder, and the inlet/outlet tubes. (c) Plot of the measured acoustic energy density Eacversus frequency f (red dots) for the α = 2 chip. The two observed acoustic resonance peaks are fitted well by the sum of two Lorentzian line shapes (eqn (24), blue line). The resonance frequencies are f1 = 2.0021 MHz and f1 = 1.9927 MHz, while the Q-factors are Q1 = 209 and Q2 = 577. Adapted from ref. 23.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /2 given by p1(y) = A sin[π(1 + i
/2 given by p1(y) = A sin[π(1 + i![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) )y/
)y/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ], where the unknown
], where the unknown ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) is the damping factor given by the radiative loss. Note that this form is similar to eqn (18), but with a different interpretation of
is the damping factor given by the radiative loss. Note that this form is similar to eqn (18), but with a different interpretation of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . In this case the lossy-wall boundary conditions become
. In this case the lossy-wall boundary conditions become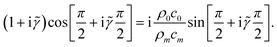
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ≪ 1, a Taylor expansion leads to
≪ 1, a Taylor expansion leads to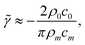
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) due to radiation loss can be thought of as a ratio between the impedances of water and the surrounding (ideally absorbing) medium.
due to radiation loss can be thought of as a ratio between the impedances of water and the surrounding (ideally absorbing) medium.
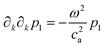 for acoustic waves, eqn (6a). To discretize this equation, the domain Ω is divided by a mesh into a large number M of small cellsm. A corresponding number of scalar test functions
for acoustic waves, eqn (6a). To discretize this equation, the domain Ω is divided by a mesh into a large number M of small cellsm. A corresponding number of scalar test functions ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) m are introduced, each being different from zero only in their respective cellm. The given field p1(r) is represented by a linear combination of test functions with coefficients Pm,
m are introduced, each being different from zero only in their respective cellm. The given field p1(r) is represented by a linear combination of test functions with coefficients Pm,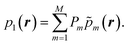
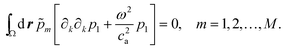
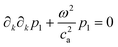 is fulfilled approximatively. By partial integration only first derivatives are left in the integrand, and a specific surface integral appears, through which the boundary conditions can be applied,
is fulfilled approximatively. By partial integration only first derivatives are left in the integrand, and a specific surface integral appears, through which the boundary conditions can be applied,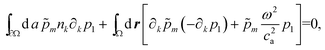
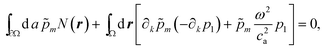
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) j(r), the so-called Lagrange multipliers, each defined the along the edges of the outer edges of the J mesh cells at the surface ∂Ω,
j(r), the so-called Lagrange multipliers, each defined the along the edges of the outer edges of the J mesh cells at the surface ∂Ω,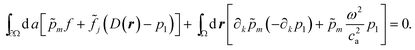
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) j only exists on the boundary, the demand for zero-valued integrals forces the coefficient (D(r) − p1) to be zero for any converged solution of the problem. On the other hand, the coefficient f(r) of the pressure test function
j only exists on the boundary, the demand for zero-valued integrals forces the coefficient (D(r) − p1) to be zero for any converged solution of the problem. On the other hand, the coefficient f(r) of the pressure test function ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) m is a dependent variable, which through ∇p1 couples to the terms of the volume integral. Since this coefficient is also the normal derivative of the pressure, we find that it has been determined as n·∇p1 = f for a converged solution.
m is a dependent variable, which through ∇p1 couples to the terms of the volume integral. Since this coefficient is also the normal derivative of the pressure, we find that it has been determined as n·∇p1 = f for a converged solution.
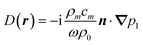 .
.
