 Open Access Article
Open Access ArticleQuantifying apatite formation and cation leaching from mesoporous bioactive glasses in vitro: a SEM, solid-state NMR and powder XRD study†
Philips N.
Gunawidjaja
a,
Isabel
Izquierdo-Barba
bc,
Renny
Mathew
a,
Kjell
Jansson
d,
Ana
García
bc,
Jekabs
Grins
d,
Daniel
Arcos
bc,
María
Vallet-Regí
bc and
Mattias
Edén
*a
aPhysical Chemistry Division, Department of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: mattias.eden@mmk.su.se; Fax: +46 8 152187; Tel: +46 8 162375
bDepartamento de Química Inorgánica y Bioinorgánica, Facultad de Farmacia, Universidad Complutense de Madrid, 28040 Madrid, Spain
cNetworking Research Center on Bioengineering, Biomaterials and Nanomedicine (CIBER-BBN), Madrid, Spain
dInorganic and Structural Chemistry Division, Department of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden
First published on 2nd March 2012
Abstract
By employing solid-state nuclear magnetic resonance (NMR) spectroscopy, powder X-ray diffraction (PXRD), and scanning electron microscopy coupled with energy-dispersive X-ray (EDX) spectroscopy, we compare the biomimetic growth of calcium hydroxyapatite (HA) from an ordered mesoporous bioactive glass (MBG) in simulated body fluid (SBF) and buffered water solutions. For the latter medium, we also examine the effects of using two different MBG concentrations. We evaluate the predicting powers of PXRD and 31P NMR for directly quantifying the relative amounts of biomimetic amorphous calcium phosphate (ACP) and HA: we observe a very good agreement between the two analytical techniques. Thanks to their mesoporous channel system, fluids readily penetrate throughout sub-mm sized MBG grains, as evidenced by EDX. The latter revealed distinct element-mappings across the material after its exposure to SBF compared to water. Under our in vitro conditions involving relatively high MBG-loadings in the solutions, the HA formation reduces in SBF relative to buffered water, particularly for increasing MBG concentration. These features stem from a high [Ca2+]/[PO3−4] ratio resulting in the fluid medium, which retards the HA crystallization by inducing a rapid ACP precipitation and an accompanying depletion of phosphate ions in the solution. This has bearings on the design of bioactivity comparisons of bioglasses exhibiting significantly different cation compositions.
1. Introduction
Thanks to their bone-bonding properties originating from a growing hydroxy-carbonate apatite (HCA) surface layer when subjected to body fluids, silicate-based bioactive glasses (BGs) have found several clinical and technological applications, such as in dentistry, as bone-filling materials and additives in toothpaste.1–5 The preparation routes of BGs have undergone significant developments, currently encompassing melt-quench, sol–gel, as well as evaporation-induced self-assembly (EISA)6 techniques: particularly the latter has been exploited recently for producing mesoporous bioactive glasses (MBGs).7–11 They feature an enhanced bioactivity mainly due to their ordered arrangement of mesopores and very large surface area,7–11 as well as a unique nano-structured pore-wall constitution.12–14Comparative in vitro “bioactivity” evaluations of (M)BGs displaying different compositions, textures or synthesis routes are traditionally assessed by the relative amounts of HCA formed at their surfaces per unit exposure-period in a simulated body fluid (SBF):1–3,15 the faster the in vitro HCA formation, the higher the bioactivity. However, such evaluations reported in the literature often differ substantially in their testing conditions. Disregarding controversial issues such as whether HCA-formation in SBF is a faithful indicator of the in vivo bone-bonding properties of BGs,16–18 a large number of both external and internal (i.e., inherent to the material) factors may affect the apparent in vitro bioactivity. External conditions encompass, for instance, the pH and temperature of the solution,18,19 if tests employ a “stationary” or “flowing” medium,20,21 or whether the specimen is in the form of a bulk piece/pellet, sub-mm sized grains or a fine powder. Furthermore, the BG concentration and the ratio between the surface area of the material and the volume of the solution may have profound bearings on the bioactivity assessment.22–25
In the quest for finding the “ideal” BG, it is normally its bioactivity-dependence on the internal material properties—such as its composition, structure, and texture—that constitute the desirable targets for evaluation. While the development and assessments of BGs have traditionally featured a high degree of empirical testing, several comprehensive studies are reported that unveil bioactivity/composition relations and to a lesser extent their link to the glass structure.26–32 Despite that elucidating the relationship between the internal material properties and the HCA formation is ideally targeted, the external conditions are often difficult to control precisely so as to provide unbiased comparisons of different bioglasses (or biomaterials vide infra).
Another complication for bioactivity evaluations is the potentially (very) different results emerging from the particular experimental technique employed for probing the HCA formation, which should ideally translate into a direct quantification of the “bioactivity” and its relationship to the internal (M)BG properties. Current investigations have predominantly utilized either powder X-ray diffraction (PXRD), infrared spectroscopy, or scanning and transmission electron microscopy (SEM/TEM),7–11,19–25 and less frequently solid-state nuclear magnetic resonance (NMR) spectroscopy.13,33–36 Yet, reports to date are qualitative rather than quantitative.
Herein, we consider the apatite growth at the surface of an “S85”9,10 (10CaO–85SiO2–5P2O5) MBG in SBF as well as in water buffered by tris(hydroxymethyl)-aminomethane (TRIS). We also investigate the consequences of employing two different S85 concentrations in the latter medium (labelled “TRIS” hereafter). Our S85-deriving specimens are henceforth referred to as “sbfτm” or “trisτm”, where τ denotes the soaking interval (8 h or 16 h) and m the mass of MBG per litre of SBF or TRIS solution, respectively. This work serves a three-fold purpose:
(i) The biomimetic calcium phosphate layer generated in vitro at the (M)BG surface over short time periods comprises a mixture of amorphous calcium phosphate (ACP) and structurally ordered HCA. We recently exploited solid-state 31P NMR to quantify the relative amounts of amorphous and crystalline phosphates,13 while PXRD has been applied routinely to qualitatively probe the in vitro apatite-formation of (M)BGs; e.g., see ref. 2,13,14,20,23,25,33–35,37 and 38. In situ XRD studies are also reported.39 However, PXRD has to our knowledge not yet been utilized to directly assess the ACP and HCA contents of the biomimetic surface layer. In Sections 2.1 and 2.2, we evaluate the relative merits of PXRD and solid-state 31P NMR for making such quantifications.
(ii) We explore the release of Ca, P and Si from the MBG, as probed either globally from analyzed cation concentrations in the solution following S85-soaking (Section 2.3) or over a ∼200 μm range within the leached S85 structure itself through an element-mapping by SEM coupled with energy-dispersive X-ray (EDX) spectroscopy (Section 2.4). SEM/EDX evidences a deep penetration of the surrounding fluid into the MBG structure, hence underlining/evidencing its highly efficient release of Ca and P observed herein, as well as in previous reports.7–10
(iii) In Sections 2.5 and 2.6, we compare and discuss the results of (i) and (ii) by illustrating how the particular design of the in vitro study may affect the HCA formation, and hence the apparent in vitro “bioactivity”. This concerns the medium employed for MBG soaking (SBF or TRIS solution) as well as the stoichiometric composition and concentration of the MBG. Under conditions of high S85-loadings, higher HCA formation is observed from the TRIS medium compared to SBF. Further, the failure of producing HCA from a previously evidenced bioactive “S58”9,10 (37CaO–58SiO2–5P2O5) MBG specimen will be rationalized as stemming from interferences of our particular in vitro conditions with the Ca-rich nature of this MBG.
2. Results and discussion
2.1 31P NMR results
Fig. 1 displays 31P magic-angle spinning (MAS) NMR spectra recorded by single pulses from pristine S85 and the sbfτ20 and trisτm specimens. Both the S85 MBG and a crystalline hydroxyapatite reference specimen (“HAref”) produce 31P NMR peak maxima around 3 ppm, as expected from their common calcium orthophosphate structural building blocks.12,40 However, the NMR response from the well-ordered HAref structure features a narrow Lorentzian peak, whereas that from the MBG is significantly broader and Gaussian-shaped: the latter NMR features are typical of structurally disordered phosphates.40 The Ca2+ and PO3−4 ions within/at the CaO–SiO2–P2O5 MBG pore-wall form nm-sized disordered clusters,12–14 henceforth referred to as “CaP”. They share several NMR characteristics with the ACP layer initially forming at the MBG surface on its contact with (simulated) body fluids, which underlines their similar local structural features.12,13,41 | ||
| Fig. 1 31P MAS NMR spectra acquired by single pulses from samples of (a) pristine S85 (black trace) and crystalline HAref (grey line), and after soaking S85 in TRIS or SBF solutions for (b) 8 h and (c) 16 h. The distinct colors identify each NMR spectrum by its respective sbfτ20 and trisτm specimen, with m given by 3 g L−1 or 20 g L−1. Numbers at the right specify the respective fwhm (in ppm) of the main orthophosphate 31P NMR peak. The grey rectangle in (a) marks a minor resonance assigned to P–O–Si moieties.12,13 | ||
The 31P NMR signals stemming from the SBF/TRIS-exposed S85 specimens are shown in Fig. 1(b and c). The NMR peak in each spectrum is a superposition of one narrow and one broad component, signifying the co-existence of an ordered (i.e., apatite) and one or several disordered (i.e., CaP and ACP) phases, respectively.13,41 In buffered water, ACP converts into HA, whereas the presence of additional ions in the SBF, notably CO2−3, leads to formation of HCA, as in biomineralized tissues.1–3 Henceforth, we use the label “H(C)A” when referring collectively to the biomimetic apatite produced either in SBF or TRIS solutions. While the NMR peak maximum remains at 3 ppm throughout, and all spectra in Fig. 1(b and c) manifest a noticeable peak-narrowing as the SBF or TRIS immersion period increases, the TRIS-soaked samples display consistently lower full-width at half maximum (fwhm) height values of their 31P NMR peaks. This signal-narrowing is even more pronounced for the tris16h3 sample compared to its tris16h20 counterpart. As the NMR peak-width reflects the structural order of the orthophosphate environments, the results in Fig. 1(b and c) evidence an accelerated ACP → HA conversion as the amount of MBG per solution volume decreases.
Table 1 lists the results from deconvoluting the peak of each 31P NMR spectrum into signals from the ACP and H(C)A components; see Fig. S1 of the ESI†. Further discussion and a justification for this procedure are provided by Gunawidjaja et al.13 The results reveal quantitatively the enhanced H(C)A formation as either (i) the MBG-soaking interval increases, (ii) a TRIS solution is employed instead of SBF and (iii) the concentration of the MBG (mS85/V) decreases from 20 g L−1 to 3 g L−1. The impact on the ACP → H(C)A conversion from each of these factors—where (ii) and (iii) are remarkably strong—is examined and rationalized in the remainder of this paper. We stress that the same pristine S85 MBG was employed throughout all in vitro studies, which highlights the profound influences from external factors on the “apparent bioactivity”. The three distinct specimens resulting after 16 h of SBF/TRIS immersion display variations between 0.43 and 0.61 in their estimated fractions of H(C)A (Table 1): this amounts to >30% relative difference in the bioactivity assessment of the same biomaterial.
| Sample | Net NMR peak | ACP [NMR] | H(C)A [NMR] | H(C)A [PXRD]b | |||||
|---|---|---|---|---|---|---|---|---|---|
| δ max (ppm) | fwhm (ppm) | δ (ppm) | fwhm (ppm) | Fraction | δ (ppm) | fwhm (ppm) | Fraction | ||
| a Results of deconvoluting each NMR peak in the spectra of Fig. 1 into contributions from amorphous (CaP/ACP) and ordered (H(C)A) phosphate components. The second and third columns list the peak maxima (δmax) and full-width at half maximum (fwhm) of the net 31P NMR peak; the uncertainty (±0.05 ppm) of δmax is primarily dictated by the external chemical shift referencing. Best-fit parameter-uncertainties: for ACP (δ ± 0.15 ppm; fwhm ± 0.2 ppm); for H(C)A (δ ± 0.08 ppm; fwhm ± 0.1 ppm); relative fractions ±0.025. b PXRD-determined fraction of H(C)A out of the total P content. | |||||||||
| S85 | 3.06 | 6.30 ± 0.08 | 2.83 | 6.22 | 1.00 | ||||
| sbf8h20 | 3.24 | 3.46 ± 0.05 | 3.40 | 5.58 | 0.66 | 3.24 | 2.13 | 0.34 | 0.26 |
| sbf16h20 | 3.22 | 2.81 ± 0.04 | 3.56 | 5.36 | 0.57 | 3.18 | 1.94 | 0.43 | 0.39 |
| tris8h20 | 3.04 | 2.78 ± 0.04 | 3.26 | 5.34 | 0.60 | 3.12 | 1.85 | 0.40 | 0.19 |
| tris16h20 | 3.06 | 2.50 ± 0.04 | 3.36 | 5.33 | 0.50 | 3.08 | 1.80 | 0.50 | 0.48 |
| tris16h3 | 3.06 | 1.91 ± 0.03 | 3.15 | 4.58 | 0.39 | 3.11 | 1.60 | 0.61 | 0.65 |
| HAref | 3.06 | 0.67 ± 0.02 | |||||||
2.2 Quantification of H(C)A: PXRD versus NMR
The PXRD patterns shown in Fig. 2 verify that the pristine S85 MBG exhibits the characteristics of an amorphous sample, whereas all diffraction peaks revealed from the sbfτ20 and trisτm specimens may be assigned to apatite. These results corroborate the trends inferred by 31P NMR: besides unambiguously evidencing the presence of H(C)A even at the shortest soaking interval of 8 h, PXRD confirms that when the MBG concentration remains constant at the high level of 20 g L−1, the apatite formation enhances in the TRIS medium relative to SBF. Further, it is significantly boosted either for increasing exposure period or as the mS85/V ratio decreases. | ||
| Fig. 2 Powder X-ray diffractograms obtained from HAref (bottom) and the as-indicated SBF or TRIS exposed S85 samples. | ||
The PXRD patterns were used to estimate the relative fraction of H(C)A out of the total phosphorus content of each sample, by using the Rietveld method and the FullProf program.42 A similar approach has been employed to derive the HCA fraction out of all crystalline phases (e.g., HCA, calcite and quartz) potentially forming on SBF-exposure of BGs.38 However, PXRD has to our knowledge hitherto not been utilized to determine the relative ACP and H(C)A contents of the biomimetic calcium phosphate layer.
Our procedure assumes that the in vitro-formed H(C)A exhibits the nominal HA stoichiometry, [Ca5(PO4)3(OH)]. Initial quantifications were obtained by dividing refined scale factors obtained from the MBG specimens by that of the HAref sample. However, several factors thwart a direct proportionality between the summed diffraction intensity of the H(C)A phase and its fraction, including variations of the X-ray absorption of the sample with the apatite content, insufficient thickness of the sample, as well as micro-absorption effects.43 The first factor is usually dominating, but it may readily be accounted for in the present two-phase mixture, provided that the distinct absorption characteristics of the H(C)A and amorphous SiO2-dominated MBG constituents are known. These X-ray mass absorption coefficients were employed to calculate a corrected weight fraction of H(C)A (denoted ccorrA), according to the procedure of ref. 43,
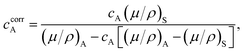 | (1) |
Despite that the H(C)A contents determined by PXRD are typically slightly lower than their NMR-derived counterparts (see Table 1), an excellent correlation is observed for four out of five estimations, as evidenced by Fig. 3. Each analytical technique is associated with its pros and cons: notwithstanding the relatively high receptivity of the 31P nucleus, MAS NMR experimentation is more time-consuming than that of PXRD for routine sample screening. However, NMR offers a decisive advantage in its straightforward extraction of the H(C)A content, only requiring signal-deconvolution into two components, while its element-specific feature makes the assessment-accuracy independent of the fraction of phosphate-bearing phases present in the specimen. Yet, when the molar ratio of H(C)A relative to ACP is small (<0.2), the 31P NMR signal-deconvolution becomes inherently inaccurate, then making quantifications by PXRD preferred.
 | ||
| Fig. 3 The correlation between the relative H(C)A fractions out of the total calcium phosphate content, as estimated by PXRD using eqn (1) (vertical axis) and by 31P NMR (horizontal) for the indicated samples. The straight line corresponds to the best-fit result (correlation coefficient R2 = 0.998) when excluding the result from the tris8h20 specimen. | ||
The main deficiency of our PXRD quantification procedure constitutes the assumption that the biomimetic H(C)A exhibits the HA stoichiometry. We have verified that its violation implies a relative error in the estimated fraction being roughly equal to the discrepancy between the stoichiometric nCa/nP ratio of the actual H(C)A phase and the as-assumed HA-value of nCa/nP = 5/3. Whereas the nCa/nP ratio may be determined by electron microscopy, the significantly increased efforts towards resolving this issue make 31P MAS NMR an attractive alternative for determining the relative H(C)A content.
In conclusion, we favour 31P MAS NMR as the method of choice for self-consistently estimating relative H(C)A contents, provided that a sufficiently large amount of the sample is available (>100 mg).
2.3 MBG dissolution in TRIS-buffered water
To assess the extent of degradation of the S85 MBG for the relatively short immersion periods of 8 h and 16 h employed herein, the concentrations of calcium-, silicon- and phosphorus-bearing ions were measured in the solution remaining after removal of each trisτm specimen (see Table 2). Fig. 4(a) plots the results together with the pH value of each solution, including that of the initial TRIS medium (pH = 7.45).| Sample | pH | [Si]/mmol L−1 | [Ca]/mmol L−1 | [P]/mmol L−1 | x Si | x Ca | x P | [Ca]/[P] |
|---|---|---|---|---|---|---|---|---|
| a Analyzed pH-value (uncertainty ±0.03) and molar concentrations (all within ±2.5%) of each solution remaining after removal of the respective trisτm solid phase. Each fraction xE (E = Si, Ca, P) is calculated from the net amount of element E present in the solution, divided by its respective initial amount of the pristine S85 sample. | ||||||||
| tris8h20 | 7.56 | 2.55 | 2.91 | 0.27 | 0.010 | 0.101 | 0.014 | 11 |
| tris16h20 | 7.59 | 2.55 | 2.56 | 0.06 | 0.010 | 0.089 | 0.003 | 45 |
| tris8h3 | 7.51 | 2.65 | 1.00 | 0.20 | 0.070 | 0.231 | 0.073 | 4.9 |
| tris16h3 | 7.51 | 2.56 | 1.16 | 0.36 | 0.068 | 0.268 | 0.128 | 3.3 |
 | ||
| Fig. 4 (a) Variations of the Si, Ca and P concentrations (left axis) and pH-values (right axis) in the solutions corresponding to the as-indicated TRIS-soaked S85 samples. The dotted horizontal line marks the initial pH-value of the TRIS solution. (b) Degree of dissolution, i.e., the fraction of each element present in the solution relative to the total amount initially present in the pristine S85 MBG. | ||
Whereas the pH value only increases marginally (by up to 0.15) over the 16 h of soaking, and the Si concentration remains essentially constant at ∼2.56 mmol L−1 (∼72 mg L−1)—indicating its saturation throughout all tests—the relative concentrations of Ca and P vary substantially. Due to the ACP/HA precipitation, they are overall higher in the solutions associated with shorter exposure periods, τ = 8 h, relative to those at 16 h. While the [Ca2+] is elevated throughout in the solutions comprising the higher amount of S85 (i.e., trisτ20), it does not change significantly for increasing soaking interval within each pair of {tris8h20, tris16h20} and {tris8h3, tris16h3} samples. However, [PO3−4] drops markedly when τ lengthens, signifying a very rapid initial ion release from S85, followed by a phosphorus consumption due to the subsequently dominating ACP/HA formation processes. Compare the Ca2+ and PO3−4 concentrations of the solutions belonging to the tris8h20 and tris16h20 specimens: the decrease in [Ca2+] matches well 1.66 times that of the accompanying decrease in [PO3−4], i.e., as expected for precipitation of a calcium phosphate of approximate HA composition. Such a directly interrelated reduction in the Ca2+ and PO3−4 concentrations is not observed from the two trisτ3 counterpart solutions, presumably as it is obscured by the non-negligible MBG dissolution that becomes emphasized under these more dilute conditions.
Fig. 4(b) displays the fraction of each element dissolved from S85 for each soaking-interval and MBG content per unit solution volume. This representation conveys more transparently the degree of ion-release from the MBG pore-walls when using S85 concentrations of either 3 g L−1 or 20 g L−1 (that relate by a factor of 6.67). The nearly constant [Si] in the TRIS solutions translates for the MBG mass/volume ratio of 20 g L−1 into a negligible Si release of ∼1% of the entire reservoir, whereas the dissolution is ∼6.7 times higher under the more dilute conditions of 3 g L−1, i.e., the trisτ3 specimens. They also display the largest dissolution degree for Ca and P, amounting roughly to 25% and 10%, respectively. The real extents of Ca and P release from the S85 sample during each immersion period are substantially larger than hinted from Fig. 4(b), as it merely reveals the net amounts of ions remaining in the solution after precipitation of ACP and its subsequent crystallization into HA. The latter process dominates at the longer exposure interval of 16 h.
2.4 SEM/EDX results
SEM/EDX was utilized to investigate the microstructure and composition gradients within the SBF/TRIS-leached S85 material. Fig. 5(a) shows a micrograph recorded from pristine S85. An EDX analysis of 50 spots from distinct grains provided the composition Ca0.11Si0.81P0.08O1.93, which accords well with the result from X-ray fluorescence (XRF) spectroscopy (see Section 3.1). The micrograph of Fig. 5(b) was obtained from the sbf16h20 specimen: it reveals a thin surface layer comprising numerous small HCA crystallites. Note that the lower right portion of the image resulted by scratching off the phosphate layer to reveal the underlying MBG surface. The variable MBG particle sizes are illustrated for the sbf16h20 specimen in Fig. 5(c), whose image depicts a collection of smaller particles clustered around the surface of a large grain. Fig. 5(d) shows the cross-section of one such small particle.![(a–d) SEM micrographs recorded from grains of the (a) pristine and (b–d) sbf16h20 specimens. (b) An image revealing the ACP/HCA-coated MBG surface. (c) A collection of small particles close to a large one. (d) Zoom around the cross-section of one small grain [marked by the dashed box in (c)]. Note the slightly varying thickness (1–2 μm) of the ACP/HCA surface layer (light grey). (e–g) EDX spectra recorded from (e) pristine S85 and at the as-indicated spots in the image of (d). The analyzed amounts of Si, Ca and P in at% (out of the cations) are specified in (c) and (e–g).](/image/article/2012/JM/c2jm15066b/c2jm15066b-f5.gif) | ||
| Fig. 5 (a–d) SEM micrographs recorded from grains of the (a) pristine and (b–d) sbf16h20 specimens. (b) An image revealing the ACP/HCA-coated MBG surface. (c) A collection of small particles close to a large one. (d) Zoom around the cross-section of one small grain [marked by the dashed box in (c)]. Note the slightly varying thickness (1–2 μm) of the ACP/HCA surface layer (light grey). (e–g) EDX spectra recorded from (e) pristine S85 and at the as-indicated spots in the image of (d). The analyzed amounts of Si, Ca and P in at% (out of the cations) are specified in (c) and (e–g). | ||
Thanks to the bicontinuous cubic mesoporous channel system of S85,9,10 surrounding fluids may readily access the centre of even sub-mm sized particles. The cation leaching discussed in Section 2.3 is mirrored in the EDX results at selected spots within the grain displayed in Fig. 5(c): they exhibit substantially lower amounts of Ca and P after 16 h of SBF treatment, which reflects the well known “silica-gel layer” discussed in the contexts of sol–gel- and melt-prepared BGs subjected to SBF.1,2,33,37,44–46 Generally, small MBG particles (<15 μm) manifest a total depletion of Ca and P across the material (Fig. 5(d and f)), whereas EDX spectra recorded at their surface evidence pure calcium phosphate, as shown for sbf16h20 in Fig. 5(g).
To probe the penetration depth of the fluid into the MBG and its bearings on the leaching of Ca2+ and PO3−4 ions, systematic EDX spot-analyses were performed on selected (large) grains of the tris16h20 and sbf16h20 specimens. Fig. 6 displays representative maps of their composition-gradients from the surface towards the particle interior. The XRF-analyzed content of each cation in S85 is indicated by the horizontal line in Fig. 6(a–c). Just beyond the 1–2 μm thick phosphate surface-layer, the tris16h20 grains reveal a domain (≤60 μm) of essentially pure silica, whereas those of sbf16h20 exhibit small but significant amounts of both Ca and P throughout the leached layer. The analyzed compositions gradually change towards that of the initial S85 composition, which for sbf16h20 and tris16h20 occur at about distances of 80 μm and 160 μm from the surface, respectively. The observed ion-concentration differences inside the leached S85 material in SBF and TRIS solutions are attributed to a more pronounced local precipitation of ACP occurring at the S85 pore-walls in the former medium (which is already supersaturated with respect to apatite), whereas the TRIS solution may dissolve larger fractions of Ca2+ and PO3−4 ions until ACP formation initiates.
 | ||
| Fig. 6 EDX spot analysis from large grains of the sbf16h20 (black squares) and tris16h20 (grey circles) specimens: the analyzed at% of each specified element is plotted against the distance from the particle surface. The corresponding value obtained by XRF is indicated by the horizontal line, with the estimated uncertainty (±1.5 percentage units) shown by the grey box. Note that (a–c) are plotted using the same vertical range of 20 percentage units (although the starting and ending values vary), whereas (d) employs an expanded scale. | ||
The corresponding analyzed sodium contents of sbf16h20 and tris16h20 are plotted in Fig. 6(d). Sodium is well-known to substitute into the HCA structure formed in vivo and is also incorporated into biomimetic phosphate layers grown at MBGs in SBF.13 Note that Na is present solely in the SBF medium,15 and traces thereof are indeed exclusively revealed from particles of sbf16h20 (as opposed to tris6h20) throughout the entire analyzed distance. This establishes a very deep penetration of the solution into the MBG material.
2.5 Dependence of ion release and H(C)A formation on MBG concentration
The S85 MBG constitutes the entire source of Ca and P in the biomimetic ACP/HA phases formed in the TRIS solution. As demonstrated by both PXRD (Fig. 2) and 31P NMR (Fig. 1 and Table 1), both the relative amount of HA and its crystallinity are higher in the trisτ3 samples obtained under more dilute soaking conditions compared to their trisτ20 counterparts. Hence, our results corroborate previous reports on melt-quench and sol–gel prepared BGs for variable amounts of bioglasses relative to the SBF volume,22,23 where diminished HCA formation was observed as the BG concentration in the solution increased above a critical value. The inhibited ACP → HA crystallization stems from a rapid and substantial precipitation of ACP, leaving very low P contents of the remaining solutions accompanying the tris8h20 and tris16h20 solid phases.The solutions associated with the trisτ3 samples display ratios of [Ca2+]/[PO3−4] ∼3–5 that remain closer to the value of ∼1.7 (i.e., the molar ratio nCa/nP in HA), as compared to the markedly higher values [Ca2+]/[PO3−4] > 10 in those employing mS85/V = 20 g L−1 (see Table 2). We suggest that the H(C)A crystallization is facilitated when the [Ca2+]/[PO3−4] ratio in the solution approximately matches the Ca3(PO4)2 stoichiometry (selected for simplicity, as its composition approximates well all other relevant phosphate phases that may form), whereas a ratio significantly higher than ∼1.5 retards the ACP → HA conversion. This may also explain the (counter-intuitive) observation of a reduced H(C)A growth observed from the SBF medium relative to TRIS under otherwise identical soaking conditions (Table 1 and Fig. 1 and 2). While the latter solution is devoid of both Ca2+ and PO3−4 ions, they are present in SBF. Yan et al. suggested that the ACP → H(C)A crystallization process stops when insufficient amounts of PO3−4 ions are available to ensure a critical thickness of the ACP layer to allow for crystallization.22 In the present case, this may be interpreted as follows: the fluid present inside the MBG pore system reaches a high local [Ca2+]/[PO3−4] ratio (primarily due to Ca2+ release from the pore-walls) that induces a rapid ACP formation: the accompanying depletion of PO3−4 ions thereby retards, or even inhibits, the H(C)A formation.
For both SBF-immersed melt- and sol–gel-derived BGs, Jones et al. also highlighted that the [Ca2+]/[PO3−4] ratio of the solution may constitute the primary factor dictating the degree of ACP → HCA conversion.23 However, this was attributed to calcite formation superseding that of HCA, stemming from significantly enhanced pH-values observed in their solutions as the BG concentration increased. This explanation is certainly adequate, and is corroborated by other groups;19,24 yet, it is doubtful if it applies to our present TRIS-treated samples, as (i) the TRIS solution is (formally) devoid of CO2−3 ions, and PXRD did not reveal any traces of calcium carbonates, while (ii) as opposed to previous studies,19,23 the pH-values of our solutions change marginally throughout the in vitro tests (see Table 2).
2.6 S58: MBG composition effects
Note that the resulting Ca2+ concentration of the medium employed for in vitro testing is directly related to both the amount of the (M)BG employed and its composition. Whereas P-bearing bioactive glasses comprise overall similar stoichiometric P contents (<10 at% out of the cations), their amounts of Ca2+ may vary significantly.1,2,8,9,28,29 Hence, the larger the Ca content of the M(BG), the higher the [Ca2+]/[PO3−4] ratio of the resulting solution, and the more pronounced local ACP precipitation across the material, as we suggested as an explanation for the local Ca and P composition differences observed within the sbf16h20 and tris16h20 specimens (Section 2.4). Our proposed dependence of the ACP → H(C)A crystallization on the [Ca2+]/[PO3−4] ratio of the SBF solution may explain previous results on the rate of HCA formation observed from S85 (of nominal composition 85SiO2–10CaO–5P2O5) relative to Ca-richer MBGs, such as S75 (75SiO2–20CaO–5P2O5) and S58 (58SiO2–37CaO–5P2O5):9 it was reported that the ACP formation increases along the series S85 < S75 < S58, whereas the degree of HCA crystallization displays the reversed trend.9,10 Identical conclusions were drawn from another study on similar MBG compositions.8Fig. 7 and 8 display the respective solid-state 31P NMR and PXRD results for SBF-soaked S58 specimens that are denoted S58-τ20, with the immersion period specified either in hours (h) or days (d). Their preparation employed otherwise identical in vitro conditions (20 g L−1) as for the S85-deriving sbfτ20 series. Now neither experimental technique reveals any trace of crystalline phases. The 31P NMR peak-width narrows marginally (by ∼10%) over one week of SBF-soaking, and remains consistently broader than that observed from the S85 specimen over a markedly shorter time-span of 8 h. Unfortunately, the ion concentrations were not analyzed in these SBF solutions, but we attribute the quenched HCA formation to a high [Ca2+]/[PO3−4] ratio in the solution, which is consistent with the previously reported elevated extent of Ca2+ release from this Ca-richer S58 MBG relative to that of S85.9,10 This results in an enhanced ACP precipitation occurring inside the S58 pores, compared to those of S85. These explanations are identical to those employed to rationalize the observed differences of the HCA formation in SBF versus TRIS solutions (Section 2.5). However, there the effects on the HCA crystallization originated from distinct initial cation concentrations among the in vitro media, whereas now, they arise from differences between the MBG compositions.
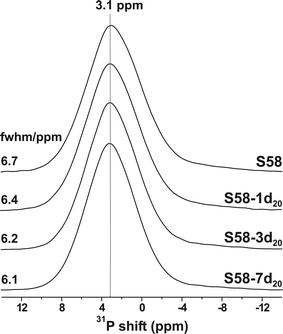 | ||
| Fig. 7 31P MAS NMR spectra recorded from pristine S58 (top) and after progressively prolonged SBF-immersion (τ) in hours (h) or days (d), as specified by each sample label S58-τ20. | ||
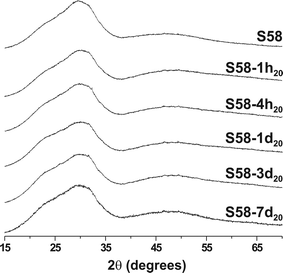 | ||
| Fig. 8 PXRD patterns recorded for the as-indicated set of SBF-soaked S58 samples. | ||
The Ca rich nature of the S58 MBG leads to an overall more depolymerised silicate network in its porewalls compared to the S85 structure.12,47 The two MBG structures feature distinct pore arrangements: 2D hexagonal for S58 and 3D bi-continuous cubic for S85.10 Their responses to solutions are different: while the S85 MBG does not reveal any significant alterations in neither of its textural parameters nor small angle PXRD patterns, these change markedly for the S58 MBG even over short exposure intervals (see the ESI†). The S58 surface area decreases, accompanied by an increase of the pore diameter from 9.45 nm to 15.2 nm over seven days in SBF (see the ESI†). The structural modifications are also reflected at a local structural level, where 29Si NMR evidences a progressive network fragmentation on SBF exposure.47
Our in vitro bioactivity tests on the S85 and S58 MBGs emphasize the difficulties of separating the effects of “internal” from “external” factors when assessing the bioactivity through the rate/amount of H(C)A formed: since the instantaneous Ca and P concentrations of the solution invariably depend on the chemical composition of the biomaterial, it may be difficult to ensure unbiased assessments of (M)BGs exhibiting widely differing compositions, unless very low concentrations are arranged. If the total amount of phosphorus in the surrounding fluid is not significantly larger than that of the bioactivity-probed (M)BG itself, a P-rich specimen may readily appear to exhibit a favourable in vitro bioactivity relative to a P-poor counterpart, as the primary source of the produced H(C)A then derives from the biomaterial itself. Conversely, a large stoichiometric nCa/nP ratio of the (M)BG combined with a (too) high concentration may also be detrimental for the observed bioactivity. Hence, the precise (M)BG-loading per solution-volume will be crucial for the apparent “in vitro bioactivity”, as discussed previously,22,23 and illustrated herein for the S85-deriving trisτ20 and trisτ3 samples.
3. Experimental
3.1 MBG sample preparations
The MBG synthesis involved an EISA process6 at 40 °C with the P123 triblock copolymer as a structure-directing agent.9 Tetraethyl orthosilicate (TEOS), triethyl phosphate (TEP) and Ca(NO3)2·4H2O served as precursors for introducing each of the elements Si, P and Ca, respectively. The reaction product was calcined at 700 °C for 6 h to eliminate organic species and nitrate ions. This procedure was employed to prepare two MBG specimens of nominal molar compositions 10CaO–85SiO2–5P2O5 and 37CaO–58SiO2–5P2O5, labeled “S85” and “S58”, respectively, according to their mol% of SiO2.The cation compositions of the pristine S85 and S58 samples were determined by XRF spectroscopy, using a Philips PANalytical AXIOS spectrometer (Philips Electronics NV), with X-rays generated by the Rh Kα line at λ = 0.614 Å. Except for some observed losses of P, the XRF-analyzed compositions of Ca0.098Si0.838P0.064O1.93 (S85) and Ca0.364Si0.554P0.082O1.68 (S58) were close to the nominal ones.
3.2 In vitro studies
An SBF solution was prepared according to Kokubo et al.,15 by dissolving NaCl, KCl, NaHCO3, K2HPO4·3H2O, MgCl2·6H2O, CaCl2, and Na2SO4 into distilled water. The solution was buffered at pH = 7.45 by using TRIS/HCl. It was passed through 0.22 μm Millipore filters to avoid bacterial contamination. Additionally, the in vitro studies involved a medium of distilled water, buffered by TRIS/HCl to provide the same pH-value as that of the SBF solution.Our in vitro studies used 1.00 g of S85 grains (see Section 3.3) in 50 mL of either SBF or TRIS solutions, equivalent to a mass/volume ratio mS85/V = 20 g L−1, whereas those involving TRIS immersion additionally utilized 0.600 g in 200 mL (i.e., mS85/V = 3 g L−1). All SBF/TRIS treatments were performed for 8 h or 16 h at 37 °C, employing a sealed polyethylene container under continuous orbital stirring (100 rpm) in an Ecotron HT incubator. Each sample was filtered, washed with water to quench the surface reactions, and subsequently vacuum-dried at 37 °C for several days.
The pH value was determined for each of the four TRIS solutions resulting after S85-immersion, by using an Ilyte system with ion-selective electrodes specific for Na+, K+ and Ca2+. The concentrations of Si, Ca and P were analyzed by inductively coupled plasma/optical emission spectrometry (ICP/OES) in a Perkin Elmer OPTIMA 3300 DV device. Four analyses were performed per solution and element, and their respective average values were calculated.
The bioactivity of S58 was tested for variable SBF-immersion periods between 1 h and 7 days. All tests involved solely SBF and one concentration (mS58/V = 20 g L−1), but employed otherwise identical conditions and procedures as described above.
3.3 Scanning electron microscopy
A scanning electron microscope (JSM 74001F; JEOL, Japan) equipped with an energy dispersive X-ray spectrometer (EDS-INCA system, Oxford Instruments) was used to investigate the chemical composition of the S85 MBG before and after SBF/TRIS exposure. Prior to analysis, cross-sections of large grains (>400 μm in diameter) were polished using an SM-09010-CP (JEOL) instrument, operating with an Ar-ion beam.The size-distribution of the pristine S85 particles (prior to in vitro soaking) was estimated by the intercept method,48 using a JEOL 6400 scanning electron microscope. Around 1900 particles were considered, and twenty straight lines were drawn on several SEM micrographs recorded at different magnifications. This revealed two maxima at ∼20 μm and ∼300 μm of the resulting size-distribution (see Fig. S3 of the ESI†).
3.4 Solid-state NMR
31P MAS NMR experiments used an Agilent/Varian/Chemagnetics Infinity-400 spectrometer and a magnetic field of 9.4 T, corresponding to a 31P Larmor frequency of −162.0 MHz. Finely ground powders of the S85- and S58-deriving samples were filled in 6 mm zirconia pencil rotors and spun at 9.0 kHz. Single-pulse (“Bloch-decay”) acquisitions employed ∼70° flip-angles at a 31P nutation frequency of 48 kHz, 600–900 s relaxation delays (selected from separate T1 saturation-recovery measurements), and the number of accumulated signal transients as follows: ∼340 (for S85), 128–296 (for S58), and 36 (for HAref). All NMR experimentation was performed without 1H decoupling: we verified on a selected set of samples that application of high-power decoupling did not affect the 31P NMR peak-widths perceptibly. No signal apodization was used in the data processing. Chemical shifts are reported relative to 85% H3PO4.3.5 Powder X-ray diffraction
PXRD patterns were recorded with Cu Kα radiation using a PANalytical X'Pert PRO MPD diffractometer equipped with an X'Celerator detector. A relatively thick layer (∼300 μm) of each powder was dispersed on zero-background Si plates. PXRD patterns were collected using variable slits and 4 cm2 irradiated area in the 2θ range of 10–80° for a total time of 12 h.4. Conclusions
We explored the ACP and H(C)A growth at the surface of an “S85” MBG of composition Ca0.098Si0.838P0.064O1.932 in both SBF and TRIS/HCl-buffered water, and for the latter solution also using two different MBG concentrations of 20 g L−1 and 3 g L−1. We examined the ion release from S85 after SBF- or TRIS-soaking, by determining the concentrations of Si, Ca and P in the surrounding solution, as well as inside the leached MBG structure, by using SEM/EDX. Whereas the tris16h20 grains displayed a ∼60 μm thick domain of almost pure silica, their sbf16h20 counterparts verified small but significant amounts of Ca and P throughout all particles of diameter >20 μm. This is attributed to more extensive local deposits of ACP at the MBG porewalls when they are subjected to SBF, as the latter medium is already supersaturated with respect to apatite.We demonstrated both PXRD and solid-state 31P NMR for estimating the relative amounts of H(C)A and ACP in the biomimetic phosphate layer, and their relative merits were discussed. Generally, the ACP → H(C)A crystallization was observed to enhance (i) in the TRIS medium as compared to SBF, as well as (ii) when using more dilute conditions (3 g L−1 of S85). All these findings were rationalized to stem from the relatively high MBG-loading used in our in vitro testing, where a fast Ca2+ release from the MBG leads to locally high [Ca2+]/[PO3−4] ratios of the fluid medium inside the pores. This stimulates phosphate-consuming ACP precipitation (particularly for the calcium- and phosphate-bearing SBF), thereby retarding the HCA crystallization due to insufficient PO3−4 amounts remaining in the fluid medium.22 This feature also explained the herein observed absence of HCA formation from a bioactive Ca-rich “S58” MBG (Ca0.364Si0.554P0.082O1.68), as well as rationalizing previous observations8–10 that the ACP formation accelerates for increasing amounts of Ca in the MBG, whereas the ACP → HCA crystallization diminishes.
Note that our results do not imply that TRIS solution is favourable for H(C)A formation per se, but merely that the apatite growth increases under more dilute SBF-soaking conditions (vide infra), as also reported previously.22–25 Problems associated with a retarded/inhibited H(C)A crystallization are expected to reduce in a flowing in vitro medium, and hence also under in vivo conditions. An optimal in vitro testing scenario is achieved when the total amounts of Ca2+ and (especially) PO3−4 ions available in the surrounding fluid grossly exceed those present in the biomaterial itself. Such conditions provide a more faithful indicator of the “real” in vitro bioactivity, by decoupling the influences from the MBG composition itself on the HCA growth.
Acknowledgements
This work was supported by the Swedish Research Council (projects VR-NT 2009-7551 and 2010-4943), the Faculty of Sciences at Stockholm University, CICYT Spain (project MAT 2008-00736) and the Comunidad Autónoma de Madrid (projects MAT 2008-0076 and CSO 2010-11384-E). P.N.G. was supported by a postdoctoral grant from the Carl Trygger Foundation. We thank Andy Y. H. Lo for help with recording some of the NMR spectra and Niklas Hedin for providing the hydroxyapatite reference sample.References
- L. L. Hench, J. Am. Ceram. Soc., 1991, 74, 1487–1510 CrossRef CAS.
- M. Vallet-Regí, C. V. Ragel and A. J. Salinas, Eur. J. Inorg. Chem., 2003, 1029–1042 CrossRef.
- D. Arcos and M. Vallet-Regí, Acta Biomater., 2010, 6, 2874–2888 CrossRef CAS.
- L. L. Hench and J. M. Polak, Science, 2002, 295, 1014–1017 CrossRef CAS.
- M. N. Rahaman, D. E. Day, B. Sonny Bal, Q. Fu, S. B. Jung, L. F. Bonewald and A. P. Tomsia, Acta Biomater., 2011, 7, 2355–2373 CrossRef CAS.
- C. J. Brinker, Y. F. Lu, A. Sellinger and H. Y. Fan, Adv. Mater., 1999, 11, 579–585 CrossRef CAS.
- X. X. Yan, C. Z. Yu, X. F. Zhou, J. W. Tang and D. Y. Zhao, Angew. Chem., Int. Ed., 2004, 43, 5980–5984 CrossRef CAS.
- X. X. Yan, X. H. Huang, C. Z. Yu, H. X. Deng, Y. Wang, Z. D. Zhang, S. Z. Qiao, G. Q. Lu and D. Y. Zhao, Biomaterials, 2006, 27, 3396–3403 CrossRef CAS.
- A. López-Noriega, D. Arcos, I. Izquierdo-Barba, Y. Sakamoto, O. Terasaki and M. Vallet-Regí, Chem. Mater., 2006, 18, 3137–3144 CrossRef.
- I. Izquierdo-Barba, D. Arcos, Y. Sakamoto, O. Terasaki, A. Lopez-Noriega and M. Vallet-Regí, Chem. Mater., 2008, 20, 3191–3198 CrossRef CAS.
- X. Li, X. P. Wang, H. R. Chen, P. Jiang, X. P. Dong and J. L. Shi, Chem. Mater., 2007, 19, 4322–4326 CrossRef CAS.
- E. Leonova, I. Izquierdo-Barba, D. Arcos, A. Lopez-Noriega, N. Hedin, M. Vallet-Regí and M. Edén, J. Phys. Chem. C, 2008, 112, 5552–5562 CAS.
- P. N. Gunawidjaja, A. Y. H. Lo, I. Izquierdo-Barba, A. García, D. Arcos, B. Stevensson, J. Grins, M. Vallet-Regí and M. Edén, J. Phys. Chem. C, 2010, 114, 19345–19356 CAS.
- A. García, M. Cicuéndez, I. Izquierdo-Barba, D. Arcos and M. Vallet-Regí, Chem. Mater., 2009, 21, 5474–5484 CrossRef.
- T. Kokubo, H. Kushitani, S. Sakka, T. Kitsugi and T. Yamamuro, J. Biomed. Mater. Res., 1990, 24, 721–734 CrossRef CAS.
- T. Kokubo and H. Takadama, Biomaterials, 2006, 27, 2907–2915 CrossRef CAS.
- M. Bohner and J. Lemaitre, Biomaterials, 2009, 30, 2175–2179 CrossRef CAS.
- H. B. Pan, X. L. Zhao, B. W. Darvell and W. W. Lu, Acta Biomater., 2010, 6, 4181–4188 CrossRef CAS.
- M. Cerruti, D. Greenspan and K. Powers, Biomaterials, 2005, 26, 1665–1674 CrossRef CAS.
- I. Izquierdo-Barba, A. J. Salinas and M. Vallet-Regí, J. Biomed. Mater. Res., 2000, 51, 191–199 CrossRef CAS.
- D. Zhang, M. Hupa, H. T. Aro and L. Hupa, Mater. Chem. Phys., 2008, 111, 497–502 CrossRef CAS.
- H. W. Yan, K. Zhang, C. F. Blanford, L. F. Francis and A. Stein, Chem. Mater., 2001, 13, 1374–1382 CrossRef CAS.
- J. R. Jones, P. Sepulveda and L. L. Hench, J. Biomed. Mater. Res., 2001, 58, 720–726 CrossRef CAS.
- P. Sepulveda, J. R. Jones and L. L. Hench, J. Biomed. Mater. Res., Part A, 2002, 61, 301–311 CrossRef CAS.
- K. Zhang, H. W. Yan, D. C. Bell, A. Stein and L. F. Francis, J. Biomed. Mater. Res., Part A, 2003, 66, 860–869 Search PubMed.
- R. D. Rawlings, J. Mater. Sci. Lett., 1992, 11, 1340–1343 CrossRef CAS.
- Z. Strnad, Biomaterials, 1992, 13, 317–321 CrossRef CAS.
- R. Hill, J. Mater. Sci. Lett., 1996, 15, 1122–1125 CrossRef CAS.
- I. Lebecq, F. Désanglois, A. Leriche and C. Follet-Houttemane, J. Biomed. Mater. Res., Part A, 2007, 83, 156–168 CrossRef CAS.
- M. D. O'Donnell, S. J. Watts, R. G. Hill and R. V. Law, J. Mater. Sci.: Mater. Med., 2009, 20, 1611–1618 CrossRef CAS.
- M. Edén, J. Non-Cryst. Solids, 2011, 357, 1595–1602 CrossRef.
- R. G. Hill and D. S. Brauer, J. Non-Cryst. Solids, 2011, 357, 3884–3887 CrossRef CAS.
- S. Hayakawa, K. Tsuru, C. Ohtsuki and A. Osaka, J. Am. Ceram. Soc., 1999, 82, 2155–2160 CrossRef CAS.
- K. S. K. Lin, Y. H. Tseng, Y. Mou, Y. C. Hsu, C. M. Yang and J. C. C. Chan, Chem. Mater., 2005, 17, 4493–4501 CrossRef CAS.
- L. J. Skipper, F. E. Sowrey, R. Rashid, R. J. Newport, Z. Lin and M. E. Smith, Phys. Chem. Glasses, 2005, 46, 372–376 CAS.
- E. Dietrich, H. Oudadesse, M. Le Floch, B. Bureau and T. Gloriant, Adv. Eng. Mater., 2009, 11, B98–B105 CrossRef.
- C. Ohtsuki, T. Kokubo and T. Yamamuro, J. Non-Cryst. Solids, 1992, 143, 84–92 CrossRef CAS.
- M. Bini, S. Grandi, D. Capsoni, P. Mustarelli, E. Saino and L. Visai, J. Phys. Chem. C, 2009, 113, 8821–8828 CAS.
- V. FitzGerald, K. O. Drake, J. R. Jones, M. E. Smith, V. Honkimaki, T. Buslaps, M. Kretzschmer and R. J. Newport, J. Synchrotron Radiat., 2007, 14, 492–499 CrossRef CAS.
- K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Pergamon Press, Amsterdam, 2002 Search PubMed.
- R. Mathew, P. N. Gunawidjaja, I. Izquierdo-Barba, K. Jansson, A. García, D. Arcos, M. Vallet-Regí and M. Edén, J. Phys. Chem. C, 2011, 115, 20572–20582 CAS.
- J. Rodriguez-Carvajal and T. Roisnel, “FULLPROF.98 and WINPLOTR New Windows 95/NT Applications for Diffraction,” Commission on Powder Diffraction, International Union of Crystallography, 1998, No. 20, pp. 35–36 Search PubMed.
- V. K. Pecharsky and P. Y. Zavalij, Fundamentals of Powder Diffraction and Structural Characterization of Materials, Springer, 2009 Search PubMed.
- M. Ogino and L. L. Hench, J. Non-Cryst. Solids, 1980, 38/39, 673–678 CrossRef.
- Ö. H. Andersson and K. H. Karlsson, J. Non-Cryst. Solids, 1991, 129, 145–151 CrossRef.
- V. Banchet, E. Jallot, J. Michel, L. Wortham, D. Laurent-Maquin and G. Balossier, Surf. Interface Anal., 2004, 36, 658–665 CrossRef CAS.
- P. N. Gunawidjaja, R. Mathew, I. Izquierdo-Barba, A. Y. H. Lo, A. García, D. Arcos, M. Vallet-Regí and M. Edén, Philos. Trans. R. Soc., A, 2012, 370, 1376–1399 CrossRef.
- ASTM E 384-84, Standard Test Method for Microhardness of Materials, Philadelphia, USA, ASTM Committee on Standards, 1984, pp. 384–89 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2jm15066b |
| This journal is © The Royal Society of Chemistry 2012 |
