Assessing PM₁₀ source reduction in urban agglomerations for air quality compliance

Abstract

The objective of this work was to study PM₁₀ and PM_2.5 concentration data available from monitoring stations in two large urban agglomerations in Greece and to estimate the emissions reduction required for compliance with the EU Air Quality Standards (AQS) for particulate matter. The cities studied are namely the Athens and Thessaloniki Metropolitan Areas (AMA and TMA, respectively). PM₁₀ concentrations during the period 2001–2010 have been evaluated for 15 air quality monitoring stations in the two urban areas. It was found that the concentrations of PM₁₀ during the period studied constantly exceeded the threshold values at the traffic and industrial stations in TMA and most of the traffic sites in AMA. Most of the occurrences of non-attainment to the daily AQSs were observed during the winter period at all stations (more pronounced for TMA stations). The reduction in current emission source strength to meet the air quality goal was calculated by the rollback equation using PM₁₀ day-averaged concentrations over the selected period at each station. Among the lognormal and Weibull distributions, the lognormal distribution was found to best fit the frequency distributions of PM₁₀ concentrations at the selected stations. The results showed that the minimum reduction required in order to meet the AQS in the AMA ranges from approximately 20 to 38% and up to 11% for traffic and background stations, respectively. Reductions in the range of 31% for traffic and 44% for industrial areas in TMA are also required. The same methodology was applied to PM_2.5 concentrations in the AMA and showed that emission reductions up to 31% are necessary in order to meet the 2020 EU AQS. Finally, continuous concentration data of organic (OC) and elementary carbon (EC) in PM_2.5 were used to study the possibility of achieving specific emission attenuation objectives in AMA.

---

Environmental impact

PM is of major concern to policy makers due to their role in climate change and human health. The objectives of this work were to study the characteristics of PM concentrations in two urban agglomerations suffering air pollution problems in Greece and to calculate the required emission reductions for compliance with the EU AQS. 10-Year concentration data from 15 monitoring stations were modelled with probability distribution functions and the rollback equation. We examined the possibility of achieving the calculated emission attenuation objectives using data on OC and EC concentrations in PM_2.5 and emission inventories. The results suggest that it is quite difficult for the areas to comply with the AQS, however reductions in traffic emissions would improve the air quality.

1. Introduction

Air quality and particularly atmospheric aerosols are of major concern to policy makers due to their role in climate change, local visibility and human health.^1–3 In order to protect human health the environmental authorities establish air quality standards (AQS) and target values for annual and daily mean concentrations. The European Union has set limit values for PM₁₀ annual and day averaged concentrations and an annual target value to be met by 2010 for PM_2.5 with the Directive 2008/50/EC.⁴ Specifically, it is required for annual mean PM₁₀ concentrations to be lower than 40 μg m⁻³ whereas the 24 hour limit value of 50 μg m⁻³ must not be exceeded more than 35 times in a calendar year. As regards PM_2.5 concentrations in the first stage an annual limit value of 25 μg m⁻³ has been established to be set in force in 2015 and in the second stage a limit of 20 μg m⁻³ must be met by 2020.

Local authorities develop emission abatement strategies in order to manage air quality in urban areas. Since the concentrations of pollutants are usually random variables influenced by emissions, meteorological conditions and topography, the knowledge of the characteristics of their frequency distribution is important in determining such measures. If the type of the frequency distribution is correctly determined for a pollutant, then the risk of exceeding air quality objectives can be assessed and the necessary emission reductions for attainment of the AQS calculated. Many types of probability distribution functions have been used to describe the distribution of air pollutants, i.e. the lognormal, Weibull, log logistic, Gamma, Beta, Inverse Gaussian, two parameter exponential and Gumbel asymptotic.^5–10 In particular for PM the most commonly applied distributions in recent studies are the lognormal, Weibull and Type V Pearson,^11–14 whereas high PM values are fitted by the two parameter exponential and Gumbel asymptotic distributions.^15–17

In this study the most common probability distributions for PM concentrations, namely the lognormal and Weibull, were tested against PM₁₀ and PM_2.5 concentration data from 15 air quality monitoring stations in the Athens and Thessaloniki Metropolitan areas (AMA and TMA, respectively), in Greece, during the period 2001–2010. The objectives of this work were to present the statistical characteristics of PM₁₀ and PM_2.5 concentrations in the two urban agglomerations and to calculate the required emission reductions in order to meet the EU AQS. In the beginning the data for the whole monitoring period, at each station, were fit by the distributions in order to examine whether a single uniform probability density function (PDF) could model the observed concentrations during the whole monitoring period, even during periods with missing values. Then the data were modelled separately for smaller time periods (ranging from 1–5 consecutive years) in order to reduce the observed variability due to the effect of varying meteorological parameters and emissions. The best fitting PDF at each station was determined using goodness of fit statistics. Based on the above results, the emission reduction required for compliance with the EU AQS in the areas around the stations was estimated using the rollback equation. The possibility of reducing the emissions to the required levels is discussed. In addition, data on organic and elemental carbon (OC and EC) concentrations in PM_2.5 at the NCSR Demokritos research station were analysed. Organic matter and elemental carbon are considered a major fraction of PM_2.5 and PM₁₀ in Athens. In particular, the contribution of the sum of primary organic matter (POM) and EC to PM_2.5 has been calculated at 31% for central Athens,¹⁸ whereas approximately 22–23% of PM₁₀ has been estimated to comprise of carbonaceous material.¹⁹OC and EC in PM_2.5 have been associated with serious health effects including carcinogenesis and mutagenesis.²⁰

2. Areas of interest and data origin

2.1. Athens Metropolitan Area

The Athens Metropolitan Area (Fig. 1) suffers air pollution problems like most metropolitan areas in the world due to high population density (approximately 3.6 million residents²¹) and the accumulation of major economic activities (half of the country's industrial and commercial activities²²) in the region. In addition, the topography of Athens and the prevailing meteorological conditions exacerbate the problem of air pollution. Specifically, Athens is located along a basin oriented SW-NE, surrounded by high mountains and open to the sea only towards the south. This topography results in wind blowing mostly from SW and NE over the area and hinders the dispersion of air pollutants. In particular, SW winds are either loaded with Saharan dust aerosols or occur by local circulation (sea breeze) and have low speeds which results in temperature inversions and therefore favour the production of photochemical pollutants.^23–25 As regards PM concentrations, many research studies during the last decade have shown the importance of particle pollution problems over the Athens area and the occurrence of severe episodes.^22,23,26

Fig. 1 PM concentration monitoring stations in the Athens and Thessaloniki Metropolitan Areas.

2.2. Thessaloniki Metropolitan Area

Thessaloniki is the second largest city in Greece and is considered to be one of the most polluted cities within Europe, especially with respect to airborne particles.²⁷ The metropolitan area of Thessaloniki (Fig. 1) includes the municipalities of Thessaloniki, Ampelokipon-Menemenis, Kalamaria, Kordeliou-Evosmou, Neapolis-Sykeon, and Pyleas-Chortiati and has a population of 813 630 inhabitants.²¹ Economic activities, mainly in the fields of manufacturing and commerce, are concentrated in the area. These activities along with heavy traffic, industrial units (in the northern and northwestern part), a very busy port and airport contribute to the air pollution in the area. Also the structure/plan of the city and the dominant meteorological conditions exacerbate the problem of air pollution (calm winds).²⁸

2.3. Data origin

In this study we analyse the concentrations of PM₁₀, PM_2.5, OC and EC in PM_2.5 during the period 2001–2010. The day-averaged PM₁₀ and PM_2.5 concentrations were retrieved from the European Air quality database²⁹ (release 4 March 2010) for the period 2001–2008 and filled with data for 2009 and 2010 from the Hellenic Ministry for the Environment, Energy and Climate Change (H.M.E.E.C.C.).³⁰ In the Athens Metropolitan Area the concentrations of PM were monitored at 9 stations (Fig. 1) operated by the H.M.E.E.C.C. during the period 2001–2010. In particular, PM₁₀ concentrations are recorded at 4 traffic urban stations (Aristotelous, Marousi, Pireaus-1 and Goudi) and at 5 background suburban stations (Lykovrisi, Agia Paraskevi, Thrakomakedones, Zografou and Koropi). Monitoring of PM_2.5 concentrations is performed at Lykovrisi, Pireaus-1, Agia Paraskevi and Goudi stations. In the Thessaloniki Metropolitan Area, a network of ground air quality monitoring stations (Fig. 1) is operated by the Region of Central Macedonia. PM₁₀ concentrations are recorded at Panorama, Sindos, Kordelio, Agia Sofia and Kalamaria stations. Details on the location, type and monitoring period at each station are given in Table S1 in the ESI†. The assessment of PM concentrations is performed by beta ray attenuation (FH 62 I-R, ESM Andersen GmbH) at all stations. Equivalence to the reference methods given in Directive 2008/50/EC has been previously shown in Grivas et al.²² More details on the sampling procedure and calibration are given by Grivas et al.²³ In addition, a thermal/Optical Aerosol Analyzer (Sunset Laboratory Inc) was used for the OC/EC analysis of the PM_2.5 samples at the NCSR Demokritos air quality monitoring station (located at a background area in AMA; 37.99°N, 23.82°E).

3. Methodology

3.1. Probability density functions of PM concentrations

The available PM₁₀ and PM_2.5 concentration data were fitted to two of the most common probability distributions for PM, namely the lognormal and Weibull distributions. The probability density function and the cumulative density function of the lognormal distribution are given in the ESI† (eqn (1) and (2)). The parameters of the lognormal distribution, i.e. the geometric mean concentration, μ_g, and the standard geometric deviation, σ_g, are estimated by the maximum likelihood method (see eqn (4) and (5) in the ESI†).³¹ Also the parameters λ and σ of the Weibull distribution are estimated by the maximum likelihood method⁵ (the probability density function, the complementary distribution function and the equations used to calculate the parameters λ and σ are given in the ESI†, eqn (6)–(9)). The distributions were fit to day-averaged concentrations at each station during the whole period 2001–2010, and separately for each year having at least 65% valid observations. The distribution that best fits the PM day-averaged concentrations over the selected period was found for each station using the goodness of fit criteria described below (Section 3.2). Based on the results of the fitting procedure, possible breakpoints in the time period 2001–2010 were detected (taking also into account other parameters, as discussed in Section 4.2). Thus the distributions were also fit for different periods at each station.

3.2. Goodness of fit criteria

The goodness of fit for the theoretical lognormal and Weibull distributions to the observed PM distributions was examined using several statistical indicators. In particular the mean bias error (MBE), the root mean square error (RMSE) and the index of agreement (IA) were estimated. The MBE value shows whether a model over or under predicts the observations. The RMSE is the most common indicator for model performance. RMSE evaluates the total deviation of the predicted values from the observed and should be approximately zero for a good model. However, its value can be significantly increased by few large mispredictions of the observed values. The index of agreement d is a relative and bounded measure for comparison between models, summarizing the accuracy of a model in predicting variations about the observed mean.³² Its value is limited to the range of 0–1, with better models having a value of d which approaches 1. The goodness of fit was also evaluated using the Kolmogorov–Smirnov and the Anderson–Darling, statistical indexes.³³ The Kolmogorov–Smirnov (K–S) statistic, D, is better in detecting discrepancies around the middle of the range of the distribution values whereas the Anderson–Darling (A–D) statistic highlights differences between the tails of the theoretical and the observed distributions. For each of these statistics the smaller the value is, the better the fit.

3.3. Calculation of changes in emission levels and emission reduction

Assuming that the source distribution remains the same (i.e. meteorological conditions, background concentrations and the spatial distribution of emission sources remain unchanged) and the pollutant is non-reactive, the reductionR (%) in current emission source strength to meet an air quality goal can be calculated by the rollback equation:³⁴where E{c} is the current actual annual mean of the pollutant concentration, E{c}_s is the annual mean corresponding to the air quality standard c_s, and c_b is the background concentration, assumed to be constant. The rollback equation assumes that under the abovementioned conditions, changes in emissions levels by a factor of k correspond to the same change in concentration levels.

The annual mean corresponding to the AQS can be estimated if the parent frequency distribution of the pollutant is known. According to the assumptions σ_g remains unchanged; therefore the geometric mean concentration of the best-fitting distribution corresponding to the AQS can be found by the complementary distribution function. For the lognormal distribution the annual mean corresponding to the AQS can be found by:

In particular, for PM₁₀ the E{C}_s is the expected day-averaged concentration of a distribution (with known σ_g) for which the probability of a concentration exceeding 50 μg m⁻³ equals 0.09589 (=35/365). It must be noted that the AQS for the day-averaged PM₁₀ concentrations was set in force in 2005. During the period 2001–2004 the limit value for day-averaged PM₁₀ concentrations was 70, 65, 60 and 55 μg m⁻³, whereas for the annual averaged concentration it was 46.4, 44.8, 43.2 and 41.6 μg m⁻³; respectively (margin of tolerance; Directive 1999/30/EC).³⁵ However emission reductions and changes in this study are calculated based on the current AQS.

The methodology was applied to day-averaged concentrations at PM monitoring stations in each metropolitan area. Time periods were selected based on the data availability for consecutive years, and also taking into account the assumptions of the rollback equation i.e. keeping meteorological conditions and spatial distribution of emission sources unchanged. The background concentration c_b was set initially to 0 μg m⁻³; thus the results apply to the minimum reduction required for compliance with the AQS. In the case of AMA, the annual averaged PM₁₀ concentration during 2010 at the Aliartos background station was used to derive the value of c_b. Although the data were available for only a small fraction of the year (39%) they have been collected during both seasons of the year and can be considered as representative of the background PM₁₀ concentration in the AMA. The derived value for c_b was 29.11 ± 15.35 μg m⁻³ which is in agreement with previous studies³⁶ for non-combustion related PM₁₀ concentrations in urban and suburban areas in Attica. In particular, Papanastasiou and Melas¹⁴ reported the results of two studies performed by Vardoulakis and Kassomenos³⁶ in AMA and by Assael et al.³⁷ in TMA, where the non-combustion related PM₁₀ concentrations were estimated in the range 20–40 μg m⁻³. Due to lack of more detailed data on PM₁₀ background concentrations in the areas of interest, it was decided to use the value of 30 μg m⁻³ for both AMA and TMA.

In addition emission changes between different years and periods were estimated with the rollback equation by setting E{c} as the reference year/period mean pollutant concentration and E{c}_s as the mean concentration of the target year/period. This was applied for PM₁₀ and PM_2.5 annual mean concentrations. For PM_2.5 there is no AQS for daily concentrations but a target value of 25 μg m⁻³ to be met by 1 January 2010 and an annual limit value of 25 μg m⁻³ to be met by 1 January 2015, with a tolerance of 20% on 1 June 2008, decreasing every year to reach 0% by 1 January 2015 (i.e. approximately 29.3 μg m⁻³ on 1 January 2009 and approximately 28.6, 27.9, 27.1, 26.4 and 25.7 μg m⁻³ on 1 January of the years thereafter; Directive 2008/50/EC).⁴ Therefore in the case of PM_2.5 concentrations the estimation of the required emission change to reach AQS was performed by setting the annual limit value as target and the actual annual averages of concentrations as reference values. Also by using the lognormal distribution and the above methodology inversely we estimated the day-averaged concentration that should not be exceeded more than 1 time per year in order to meet the annual AQS.

3.4. Calculation of exceedances

The calculation of cases of non-attainment to the daily AQS is of importance in the case of PM₁₀ concentrations. Therefore we evaluated the performance of the lognormal distribution in predicting exceedances of the daily AQS. The actual frequency of exceedances was calculated by counting the number of observations exceeding the threshold value of 50 μg m⁻³ and dividing it by the number of data available. The actual exceedances however may not be accurate since they do not include missing values, which can be up to 35% in our case. In this study, actual and predicted exceedances are compared with respect to the current AQS; however, discussion is given also on the number of cases of non-attainment to the daily AQS in force during the period 2001–2004.

4. Results and discussion

4.1. Particulate matter concentrations

In the AMA higher concentrations were observed mainly during the cold period (October–March: 23.3 ± 4.3 °C) at traffic urban stations and during the summer (April–September: 12.1 ± 3.3 °C) at background stations besides Lykovrisi. This is probably associated with central heating emissions during the cold period and increased photochemical activity and local dust resuspension during the warm period.^23,38 It was also observed that the current daily and annual AQS was frequently exceeded in the area during the period 2001–2010. In Fig. 2 the comparison of the annual limit value with annual averages of PM₁₀ concentrations is shown together with the number of exceedances of the current daily AQS. The data reported were derived from the EU Airbase dataset²⁹ and filled with data from the H.M.E.E.C.C.³⁰ It is observed in Fig. 2a that the annual averaged concentration of PM₁₀ during the monitoring period at each station shows fluctuations however it has decreased from the beginning to the end of the monitoring period at most of the stations besides Thrakomakedones and Koropi. There are still two stations that fail to comply with the annual AQS, namely the traffic urban stations Marousi and Aristotelous. In fact at those two stations the annual averaged PM₁₀ concentration has never reached values lower than the AQS since 2001 (except for 2004 at Marousi station). This is probably associated with the increase of traffic and urbanization in the areas around the stations. In particular at Marousi station the annual averaged concentrations have lowered during the period 2002–2004, probably due to the beginning of the operation of the Attiki odos highway,⁸ and were later increased due to the enhanced construction and accumulation of major economic activities in the area.

Fig. 2 Comparison of the annual limit values with annual averages of PM₁₀ concentrations in the (a) Athens (MARousi, ZOGrafou, THRakomakedones, AGia Paraskevi, LYKovrisi, PIReaus-1, ARIstotelous, GOUdi and KORopi stations) and (b) Thessaloniki (PANorama, AGia Sofia, KALamaria, SINdos and KORDelio stations) Metropolitan areas, and number of exceedances of the current daily AQS.

As regards the daily AQS for PM₁₀ concentrations, it was constantly exceeded through the period 2001–2010 at the Aristotelous, Marousi, Pireaus-1 (except for 2009) and Lykovrisi stations. On the other hand, at the three background stations Zografou, Agia Paraskevi and Thrakomakedones, the daily AQS was exceeded in the past. However, during the last years of the studied period, the levels of PM₁₀ have decreased and day-averaged concentrations remained lower than the AQS by the end of 2009. During 2010 a slight increase of day-averaged PM₁₀ concentrations was observed and the daily AQS was exceeded at the Thrakomakedones station. Most cases of non-attainment to AQS occurred during the cold period (see Fig. S1 in the ESI†), except for Zografou and Agia Paraskevi stations. Previous studies of PM₁₀ concentrations in Athens by Borge et al.³⁹ and Grivas et al.²³ have shown that some of the high PM concentration events occurring in Athens can be attributed to long range transported aerosols (e.g. desert dust events) and other natural sources. Especially during the warm period of the year, peaks in PM₁₀ concentrations at background suburban stations can be attributed to local dust resuspension.¹⁸

The PM_2.5 concentrations in the AMA were monitored at the stations Agia Paraskevi, Goudi, Lykovrisi and Pireaus-1 during the period 2007–2010, and had mean values of 17.8 ± 8.6, 22.4 ± 9.1, 27.4 ± 13.0, and 28.8 ± 12.9 μg m⁻³, respectively. Their values showed a clear decreasing trend during that period. On 1 January 2010, the target value of 25 μg m⁻³ was not exceeded at any station. In contrast with PM₁₀ concentrations, higher PM_2.5 concentrations were observed during the warm period. This is probably associated with secondary PM formation due to the increased photochemical activity. Also Theodosi et al.¹⁹ have shown that during the warm period of September 2005–August 2006 PM₁ concentrations at Lykovrisi and Goudi stations were mainly associated with long range transport. The average PM_2.5/PM₁₀ concentration ratio at the background stations Lykovrisi and Agia Paraskevi was 0.65, with values ranging from 0.52 during winter to 0.75 during summer. Moreover, PM_2.5 concentrations were monitored gravimetrically at Demokritos station during 2009–2010. Their mean concentration was 16.9 ± 11.8 μg m⁻³.

In addition, OC and EC concentrations in PM_2.5 were monitored at the NCSR Demokritos station during 2010. The results considering their annual and seasonal averaged values and the ratio OC/EC are given in Table 1. Previous studies at Western and Central European sites have shown that EC is generally related to fossil fuel combustion sources (mainly traffic) which are active throughout the year, whereas OC is mostly associated with primary biomass burning and space heating emissions during the cold period and is considered primarily biogenic (from gas-to-particle conversion) during the warm period of the year.^41,45 Also Sciare et al.⁴⁷ have shown that at a remote site in the Eastern Mediterranean, the observed EC and OC concentrations during the early spring and summer are associated with biomass burning emissions due to agricultural waste burning practices. In this study the values of OC and EC concentrations and of OC/EC ratio were approximately the same during all seasons. For EC concentrations the small increase observed during the spring could be attributed to biomass burning emissions, whereas for OC the slightly higher values during spring and summer compared to the cold season could result from biogenic sources. In addition, strong correlation (Pearson R > 0.7) between OC and EC concentrations was found during most of the seasons except for autumn (Pearson R was approximately 0.77 for winter, 0.73 for summer, 0.80 for spring and 0.65 for autumn) indicating that they probably originate from the same sources or sources in the same location. On the other hand, no correlation between OC and EC with PM_2.5 concentrations was found during any season except for summer (R: 0.7 for OC, 0.71 for EC). The values of OC and EC concentrations observed during 2010 at the Demokritos station were generally lower compared to results from studies at other urban background sites (see Table 1), whereas the OC/EC ratio was in the same range as in other studies during the warn season. It is also observed in Table 1 that the value of the OC/EC ratio was larger than 2 during all seasons. Values of the OC/EC ratio larger than 2 (ref. 50) or 2.2 (ref. 51) are indicative of the presence of secondary organic aerosols in the atmosphere.

Table 1 Level of carbonaceous PM_2.5 and the OC/EC ratio found in this study and in the recent literature

Area	Site type	Period	Season^a	OC/μg m^−3	EC/μg m^−3	OC/EC	PM2.5/μg m^−3
a AY: All year, W: Winter, Sp: Spring, S: Summer, A: Autumn, and MA: Monthly Averaged. b Refer to PM1.5 measurements.
Athens/NCSR Demokritos station	Background Suburban	2010	AY	2.43 ± 0.95	0.67 ± 0.32	4.03 ± 1.88	16.59 ± 11.97
			W	2.38 ± 1.05	0.67 ± 0.38	4.29 ± 2.69	15.43 ± 16.04
			Sp	2.46 ± 0.80	0.71 ± 0.23	3.71 ± 1.87	18.86 ± 13.93
			S	2.64 ± 1.15	0.64 ± 0.24	4.17 ± 1.24	19.13 ± 8.96
			A	2.29 ± 0.85	0.64 ± 0.40	4.09 ± 1.62	13.04 ± 6.52
Marseille^40	Background Urban (industrial influence)	2008	S	4.7 (2.9–9.6)	1.3 (0.66–3.4)
Hungary and Portugal^41	Rural/Remote (low level)	2002–2004	S	3.47–4.52	0.53–0.57
			W	8.91–12.3	1.74–1.80
Beijing^42	Urban	11/2005–10/2006	W	20 ± 19		3.3 ± 0.8
			Sp	12 ± 7		2.6 ± 1.1
			S	10 ± 5		2.2 ± 1.1
			A	18 ± 11		2.2 ± 1.1
North Belgium^43	Industrial	2001–2003	A	4.1 ± 1.3	1.1 ± 0.8	3.7	21 ± 12
			W	2.3 ± 1.3	0.4 ± 0.3	5.8
	Traffic		A–W	2.5 ± 1.1	1.3 ± 1.0	1.9	45 ± 22
			W–Sp	2.9 ± 1.3	1.5 ± 0.6	1.9
	Suburban Traffic		W	2.6 ± 1.5	0.6 ± 0.5	6.5	16 ± 8
	Suburban Industrial		A	2.7 ± 1.1	0.3 ± 0.2	9	16 ± 8
	Suburban Industrial		A–W	4.2 ± 1.6	0.5 ± 0.3	8.4	24 ± 13
UK^44	Urban Background	05/2007–04/2008	AY	2.8	1.5		11.6
			S	3.1	1.5		13.2
			W	2.5	1.4		10.1
	Rural		AY	2.5	1.1		10.5
			S	2.9	0.93		12.5
			W	2.1	1.2		8.5
Milan^45	Urban Background	08/2002–12/2003	AY	9.2 ± 7.2	1.4 ± 0.7	6.5 ± 4.3	40 ± 26.4
			Warm	5.2 ± 2.8	1.2 ± 0.5	4.2 ± 2.2	24.5 ± 9.9
			Cold	14 ± 7.9	1.6 ± 0.8	8.6 ± 4.8	58.3 ± 28
SW Spain^46	Background Urban (industrial influence)	06/2005–06/2006	AY	2.9	1.1	2.9	21
	Rural		AY	3	0.6	4.7	21
Finokalia Greece^b (ref. 47)	Remote	09/2001–04/2004	AY	1.74 ± 0.35	0.31 ± 0.07		8.47 ± 1.30
New York^48	Urban (impacted by traffic)	2006–2008	MA	1–4.1	0.5–1.4
Hong Kong^49	Roadside	01/2004–05/2004	AY	11 ± 4.7	12.2 ± 4.4		52.3 ± 18.3
			W	13.2 ± 6	11 ± 4.7		54.1 ± 21.1

---

The annual averaged PM₁₀ concentrations at all the monitoring stations in TMA are depicted in Fig. 2b along with the number of exceedances of the current daily AQS. It is observed that the current daily AQS was frequently exceeded in the area during the period 2001–2010. In particular at traffic and industrial urban stations (Agia Sofia, Kordelio and Sindos) the annual and daily AQS were constantly exceeded. At the background suburban station Panorama the daily AQS was exceeded only in the past, whereas at the traffic suburban station Kalamaria PM₁₀ concentration has decreased to values lower than the annual AQS during the last two years of the study and the daily AQS is not exceeded. At all the stations located in the metropolitan area of Thessaloniki most cases of non-attainment to the daily AQS occurred during the cold period (see Fig. S2 in the ESI†; 22.1 ± 4.3 °C). In addition, higher concentrations were observed mainly during the cold period at all stations besides the traffic suburban station in Kalamaria. As previously reported for AMA, also for TMA this is probably associated with space heating emissions which are predominant during winter. The annual mean PM₁₀ concentration has dropped at all stations at the end of the studied period compared to the 2001 levels; however, a clear decreasing trend was observed only at the Panorama and Kalamaria stations.

4.2. Statistical distributions of PM concentrations

The parameters of the empirical (observed), lognormal and Weibull distributions describing the measured concentrations were calculated at each station separately for each year and for the whole monitoring period. The lognormal distribution was found to best fit (based on the K–S and A–D statistical indexes) the observed concentrations distribution for all periods at most of the PM₁₀ and PM_2.5 monitoring stations in AMA and TMA (e.g. see Fig. 3a for Agia Paraskevi station; for the lognormal distribution K–S: 0.041; A–D: 7.07, for the Weibull distribution K–S: 0.109; A–D: 97.60). In particular, at PM₁₀ monitoring stations in Athens the Weibull distribution was found to fit better than the lognormal distribution the observed concentrations of PM₁₀ during the whole monitoring period (including data from years with data availability less than 65%) at Marousi (Fig. 3b; for the lognormal distribution K–S: 0.072; A–D: 21.92, for the Weibull distribution K–S: 0.065; A–D: 24.25) and Goudi stations; however, the results found separately for each year showed that data were better described by the lognormal distribution. In addition the comparison of actual with estimated probability of exceedances of the daily AQS showed that the use of the Weibull distribution (theoretical probability approximately 0.4046) significantly overpredicted the observed exceedances (actual probability 0.3395) at Marousi station during the period 2001–2010. Therefore the lognormal probability distribution function was chosen as the best fitting for the whole dataset in the analysis that follows.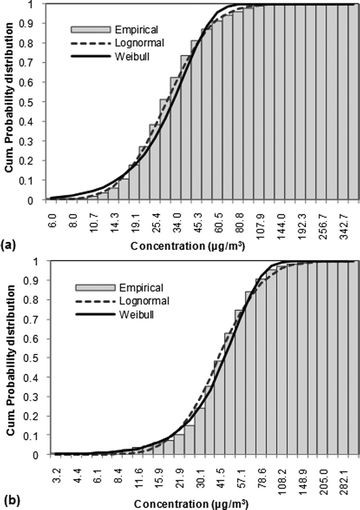

Fig. 3 Comparison of the empirical cumulative probability distribution with the theoretical lognormal and Weibull cumulative probability distributions for the period 2001–2010 at (a) Agia Paraskevi and (b) Marousi stations.

Descriptive statistics for PM₁₀ concentrations in Athens stations during the whole monitoring period are depicted in Table 2 along with the predicted (theoretical) mean concentration (μ) and standard deviation (σ_g) of the lognormal distribution. The goodness of fit criteria for the lognormal distributions fitting the PM₁₀ concentrations during the whole monitoring period at each station (see Table S2 in the ESI†) showed that the lognormal distribution underestimates the observed mean concentrations; however, the overall deviation between actual and predicted values is rather small (the maximum MBE value was 0.0008 at Koropi station, and the maximum RMSE value was 0.013 at Marousi station). In addition the index of agreement approximates 1 at all stations, indicating that the lognormal distribution can successfully model the observed concentration data. A closer look at the performance of the lognormal distribution in modelling the values around the middle and the tails of the empirical distribution of concentrations is provided by the K–S and A–D test statistics. It is observed that the K–S value is small at all stations indicating good agreement between measured and modelled concentrations around the median concentrations whereas the A–D values are rather high. However, since the AQS for day-averaged concentrations is closer to the middle than the tails of our empirical distributions (the range and median concentrations are depicted in Table 2) the derived lognormal distributions are not expected to predict with large discrepancies of the number of exceedances of the daily limit value. Nonetheless the accurate calculation of exceedances of the daily AQS is important for the protection of human health.

Table 2 Descriptive statistics for PM₁₀ concentrations and characteristics of the lognormal distribution (μ: geo. mean concentration; σ_g: standard deviation) fitting the data acquired during the whole period 2001–2010

Station^a	Period	Characteristics of PM10 concentration distribution/μg m^−3
		Observed						Predicted
		Mean	Median	Mode	SD	Min.	Max.	μ	σ g
a B: background, I: industrial, T: traffic, U: urban, and S: suburban.
Marousi (TU)	2001–2010	46.75	42.00	34.00	25.65	3.22	331.00	40.67	22.41
Goudi (TU)	2001–2007	38.08	34.50	36.00	20.37	3.96	144.17	32.86	18.56
Zografou (BS)	2001–2007	31.83	28.00	28.00	18.23	3.00	387.00	28.40	13.30
Thrakomakedones (BS)	2001–2010	30.41	26.00	19.00	21.14	2.00	441.00	26.15	14.08
Agia Paraskevi (BS)	2001–2010	34.38	29.00	23.00	21.90	6.00	396.00	29.98	15.10
Lykovrisi (BS)	2001–2010	54.41	49.08	45.00	27.90	5.00	438.00	48.72	23.06
Pireaus-1 (TU)	2001–2010	46.90	42.63	33.00	22.52	11.00	236.00	42.29	19.27
Koropi (BS)	2008–2010	35.46	31.00	31.00	23.80	5.00	332.00	31.27	14.82
Aristotelous (TU)	2001–2010	53.74	49.00	40.00	24.84	10.83	421.00	49.59	19.32
Panorama (BS)	2001–2009	31.43	29.00	21.00	14.62	4.00	213.00	28.47	12.87
Kalamaria (TS)	2007–2010	35.09	31.00	27.00	17.38	8.00	206.00	31.75	13.94
Agia Sofia (TU)	2001–2010	56.04	50.00	35.00	27.42	12.00	265.25	50.73	22.22
Kordelio (IU)	2001–2010	58.87	52.00	44.00	30.24	9.00	226.42	52.08	26.04
Sindos (IU)	2001–2009	48.27	45.00	45.00	21.27	10.00	211.58	44.26	18.47

---

The comparison of the actual with the theoretical (calculated based on the probability distribution for the whole monitoring period) probability of exceedance of the daily AQS for PM₁₀ concentrations at Athens monitoring stations is presented in Table 3. It is observed that the difference between the actual and predicted number of exceedances was indeed rather small at most of the stations and can be attributed to missing values in the dataset; however, at Zografou and Thrakomakedones stations the number of exceedances is highly overestimated by the lognormal distribution. Although the observed and predicted number of exceedances agree for the whole period at most of the stations, we found significant discrepancies between the theoretical and the actual annual number of exceedances at most of the stations (data not shown). For example at Zografou and Thrakomakedones stations the theoretical lognormal distribution predicts the exceedances quite correctly during the period 2001–2004 whereas it overestimates the exceedances during the period 2005–2007 and 2006–2010, respectively (2005 was not taken into account at Thrakomakedones station due to limited data availability). The same applies for Koropi station with 21 more exceedances (than the actual) of the AQS according to the theoretical PM₁₀ distribution. Therefore we searched for breakpoints in the time series of concentrations that could be associated with changes in the spatial distribution of emission sources in the areas around the stations. Common patterns in annual empirical distributions could be identified based on the above results.

Table 3 Comparisons of actual with estimated probability of exceedance of the PM₁₀ daily AQS

Station^a	Actual probability	Theoretical probability	Difference in exceedances (days)
a B: background, I: industrial, T: traffic, U: urban, and S: suburban.
Marousi (TU)	0.33948	0.35394	4
Goudi (TU)	0.23477	0.22867	−2
Zografou (BS)	0.09080	0.11361	20
Thrakomakedones (BS)	0.09215	0.11431	20
Agia Paraskevi (BS)	0.14044	0.15481	9
Lykovrisi (BS)	0.46106	0.47805	3
Pireaus-1 (TU)	0.37063	0.35659	−4
Koropi (BS)	0.12768	0.16105	21
Aristotelous (TU)	0.46427	0.49144	5
Panorama (BS)	0.09433	0.10643	11
Kalamaria (TS)	0.14894	0.15040	1
Agia Sofia (TU)	0.49481	0.51320	3
Kordelio (IU)	0.52932	0.53240	1
Sindos (IU)	0.37260	0.38508	3

---

An example on the identification of breakpoints in the time series of PM₁₀ concentrations based on the comparison of their empirical with theoretical distributions is presented in Fig. 4 for the period 2001–2010 at Agia Paraskevi station. It is observed that the lognormal distribution (for the whole monitoring period) significantly underestimates PM₁₀ concentrations in the lower range of data while it overestimates PM₁₀ concentrations in the upper range of data during the period 2007–2010. The opposite occurs for the period 2001–2005 whereas the fit for 2006 is not examined due to limited data availability. For that reason the concentration data for each period were fit separately by lognormal distributions, also depicted in Fig. 4. The difference between the actual and the new theoretical days with exceedances for the periods 2001–2005, 2007–2010 is approximately 30 and 2, respectively. In addition, according to the values of the statistical indexes, the theoretical distributions slightly overpredict the observed concentrations (MBE equals to 1.12 × 10⁻⁴ and 2.43 × 10⁻⁴, respectively), though they generally agree with the data (d = 1) (Table S3 in the ESI†).

Fig. 4 Comparison of the annual empirical probability distribution with the theoretical (lognormal) probability distribution for the periods 2001–2010, 2001–2005 and 2007–2010, at Agia Paraskevi station in AMA.

By following the abovementioned procedure for each station, we found the periods that should be examined separately in emissions reduction calculations. The periods examined for PM₁₀ emission reduction calculations in the AMA are 2001–2005 and 2007–2010 at Agia Paraskevi station, 2005–2010 at Aristotelous and Marousi stations, 2001–2008 and 2009–2010 at Lykovrisi station, 2001–2004 and 2005–2007 at Zografou, 2007–2010 at Pireaus-1, 2001–2004 and 2006–2010 at Thrakomakedones station, 2009–2010 at Koropi station. Years with data capture less than 65% were excluded from the analysis. The lognormal distributions for the most recent periods at each station are given in Fig. 5. Overall the new theoretical distributions have approximately the same small RMSE (0.003–0.016), with those for the whole monitoring periods, small MBE (0.00004–0.002 in absolute values), an index of agreement equal to 1 and fit better the middles and tails of the distributions (Table S3 in the ESI†).

Fig. 5 Estimated lognormal probability distributions of PM₁₀ concentrations for the period 2001–2010 at AMA and TMA stations.

As regards the PM_2.5 concentrations in the AMA, the characteristics of the lognormal distributions fitting the data are depicted in Table 4 along with the values of the statistical indexes indicating the goodness of fit. It is observed that the theoretical distributions slightly underpredict the observed concentrations (MBE value up to −2.4 × 10⁻⁵) but generally agree with the data (RMSE values 0.008–0.011; d ranges from 0.97–0.99). The lognormal distributions can also successfully predict the values in the middle (K–S value up to 0.06) and the tails (A–D value up to 2.4) of the empirical distributions of PM_2.5 concentrations.

Table 4 Descriptive statistics for PM_2.5 concentrations and characteristics of the lognormal distribution (μ: geo. mean concentration; σ_g: standard deviation) fitting the data acquired during the whole period 2007–2010

Station^a	Period	Characteristics of PM2.5 concentration distribution/μg m^−3
		Observed			Predicted		Goodness of fit criteria
		Median	Min.	Max.	μ	σ g	MBE	RMSE	d	K–S	A–D
a B: background, T: traffic, U: urban, and S: suburban.
Demokritos (BS)	2009–2010	13.94	1.34	87.89	14.26	8.22	−2.4 × 10^−5	1.1 × 10^−2	0.97	0.048	1.09
Lykovrisi (BS)	2007–2010	25.10	6.00	135.10	24.84	11.01	−5.1 × 10^−7	8.9 × 10^−3	0.99	0.044	2.38
Agia Paraskevi (BS)	2007–2010	16.10	4.10	74.10	16.09	7.19	−5.4 × 10^−9	1.3 × 10^−2	0.97	0.043	2.08
Goudi (TU)	2007–2009	21.10	5.10	64.10	20.57	8.70	−2.4 × 10^−8	1.3 × 10^−2	0.98	0.061	2.31
Pireaus-1 (TU)	2007–2010	27.10	5.00	157.10	26.24	11.30	−5.3 × 10^−7	8.1 × 10^−3	0.99	0.056	1.69

---

Likewise the OC and EC concentration distributions were best fitted by the lognormal distribution (OC K–S: 0.04, A–D: 0.34; EC K–S: 0.06, A–D: 1.92). The geometric mean concentration and standard deviation of the OC and EC in PM_2.5 lognormal distributions were 2.27 μm and 1.45, 0.60 μm and 1.57, respectively. It should be noted that for OC and EC concentrations no particular AQS exists. For the analysis performed in Section 4.3 we set a limit value for OC and EC in PM_2.5 that should not be exceeded more than 1 time per year equal to the 90^th percentile of their current (2010) concentration. The value was thus set to approximately 1 μg m⁻³ for EC and to 3.55 μg m⁻³ for OC. Based on the above definition of the limit values, the actual probability of exceeding them is 0.1 whereas the estimated theoretical probability (lognormal distributions) was found approximately equal to 0.11 for OC and 0.13 for EC.

The same analysis was performed for the PM₁₀ concentrations in the TMA. Descriptive statistics for PM₁₀ concentrations in TMA stations during the whole monitoring period are depicted in Table 2 along with the predicted (theoretical) mean concentration (μ) and standard deviation (σ_g) of the lognormal distribution. Similarly to the results for AMA, the goodness of fit criteria (Table S2 in the ESI†) showed that the lognormal distribution generally underestimates (with the exception of Kordelio station) slightly the observed mean concentrations (the maximum MBE value was −0.000003 at Agia Sofia station); however, the overall deviation between actual and predicted values is rather small (the maximum RMSE value was 0.0081 at Kalamaria station) and the theoretical distributions agree with the measured data (index of agreement approximates 1). In addition the values of K–S and A–D statistical indexes are small (except for A–D at Panorama and Sindos stations). Also the comparison of the actual with the theoretical probability of exceedance of the daily AQS for PM₁₀ concentrations at TMA monitoring stations is presented in Table 3. It is observed that the difference between the actual and predicted number of exceedances was rather small at all stations except for Panorama. Likewise we searched for breakpoints in the time series of concentrations that could be associated with changes in the spatial distribution of emission sources in the areas around the stations. The periods examined for PM₁₀ emission reduction calculations in the TMA are 2001–2003 and 2007–2010 at Agia Sofia and Kordelio stations, 2001–2004 and 2006–2007 at Panorama, 2001–2004 and 2006–2008 at Sindos, 2007–2008 and 2009–2010 at Kalamaria station. Years with data capture less than 65% were excluded from the analysis. The lognormal distributions for the most recent periods at each station are given in Fig. 5.

4.3. Emission changes and required emission reduction to meet AQS

The required emission reduction in order to meet the current AQS was estimated separately for each period at each station. The mean value of measured PM₁₀ concentrations in AMA and TMA along with the estimated expected mean concentrations, the minimum emission reduction required in order to meet the daily AQS for PM₁₀ concentrations and the emission change between different periods at each station are given in Table 5 for each station. The results indicate that measures leading to emission reductions should be applied to most of the stations in order to comply with the AQS. In particular, the current minimum reduction (results for the whole period 2001–2010 are given in Table S4 in the ESI†) ranges from approximately 20 to 38% for traffic stations and is up to 11% at background stations in the AMA (Lykovrisi station was accounted for as traffic station). In the TMA the minimum required emissions reduction is up to 31% at traffic stations and in the range of 35% to 44% at industrial areas. At the stations Thrakomakedones, Zografou, Agia Paraskevi in the AMA and Panorama and Kalamaria in the TMA there is no need to apply emission mitigation measures in order to meet the daily AQS (negative values of R; see also Fig. 4). This is in agreement with the observed decrease in concentrations at these areas. It is also shown in Table 5 the emission change through the period 2001–2010 at the monitoring stations. At most of the stations emissions were lowered by 12.2% to 31.0% in the AMA and by 18.2% to 29.0% at the TMA. However, by setting the background concentration equal to 30 μg m⁻³ the required emissions reduction ranges from 85% to 95% at traffic urban stations, from 90% to 102% at industrial urban stations and is 98% at background suburban stations (R was calculated only for the latest period at stations which still fail to comply with the EU AQS on annual, day or both averaged PM₁₀ concentrations). The later results indicate the difficulty for the AMA and TMA to comply with the EU AQS. Since the background concentration of PM₁₀ is significant compared to the EU AQS for annual averaged concentrations, local abatement measures might not be sufficient to reduce local PM concentrations as indicated by values of R close to or larger than 100.

Table 5 Level of PM₁₀ emissions minimum reduction required for compliance with the 24 h average EU AQS and calculated emission change at each monitoring station (different monitoring periods at each station are given in brackets) in the (a) Athens Metropolitan Area and (b) Thessaloniki Metropolitan Area. Values in brackets correspond to the required emission reduction calculated using 30 μg m⁻³ as background PM₁₀ concentration

Monitoring Station (Period)	Mean concentration/μg m^−3	E{C}s/μg m^−3	Required emission reduction^e (%)	Emission change (%)
a Traffic urban. b Background suburban. c Industrial urban. d Traffic suburban. e Values in brackets correspond to the required emission reduction calculated using 30 μg m^−3 as cb in eqn (1).
(a) Athens Metropolitan Area
Aristotelous (2005–2010)^a	52.69	32.51	38.31 (88.96)
Marousi (2005–2010)^a	45.89	31.63	31.07 (89.72)
Pireaus-1 (2007–2010)^a	39.31	31.21	20.61 (87.01)
Lykovrisi (2001–2008)^b	58.20	30.94	46.85
Lykovrisi (2009–2010)^b	40.76	30.53	25.11 (95.10)	29.97
Thrakomakedones (2001–2004)^b	32.41	28.75	11.31
Thrakomakedones (2006–2010)^b	28.47	28.64	−0.60	12.17
Zografou (2001–2004)^b	34.10	30.34	11.02
Zografou (2005–2007)^b	28.75	30.69	−6.76	15.70
Agia Paraskevi (2001–2005)^b	40.05	29.79	25.61
Agia Paraskevi (2007–2010)^b	27.63	30.48	−10.32	31.01
Goudi (2007)^a	38.06	32.63	14.27
Koropi (2009–2010)^b	33.70	30.09	10.72 (97.56)
(b) Thessaloniki Metropolitan Area
Agia Sofia (2001–2003)^a	66.4	31.41	52.68
Agia Sofia (2007–2010)^a	47.13	32.55	30.92 (85.10)	29.01
Kordelio (2001–2003)^c	67.20	30.55	54.54
Kordelio (2006–2010)^c	52.79	29.57	43.99 (101.90)	21.44
Panorama (2001–2004)^b	34.18	31.14	8.88
Panorama (2006–2007)^b	27.97	30.89	−10.44	18.17
Sindos (2001–2004)^c	48.86	31.65	35.23
Sindos (2006–2008)^c	49.03	31.85	35.04 (90.28)	−0.35
Kalamaria (2007–2008)^d	40.57	30.57	24.64
Kalamaria (2009–2010)^d	29.47	33.14	−12.47	27.37

---

In Table 6 the required emission changes in order to meet the annual AQS for PM_2.5 that will be set in force in 2015 and 2020 are depicted. It was found that at first emission abatement measures must be taken in the areas of Lykovrisi and Pireaus-1 stations in order to comply with the 2015 AQS. The 2020 AQS will be exceeded also at the area of Goudi station if emissions remain unchanged. Also in Table 6 is depicted the concentration that should not be exceeded for more than 1 time per year in order for the annual concentration to comply with the AQS. This concentration was estimated using the theoretical distributions fitting the observed PM_2.5 data and eqn (1) and eqn (2)†. It was found that the derived value is above the maximum observed concentration at Demokritos, Agia Paraskevi and Goudi stations (maximum concentrations of 87.89, 74.10 and 64.10 μg m⁻³, respectively) and above the 99^th percentile of observed concentrations at the Lykovrisi and Pireaus-1 stations. In addition, as regards the attenuation of OC and EC concentrations in PM_2.5, reductions of approximately 44% and 52% should be applied to their emission sources.

Table 6 Level of PM_2.5 emission changes required for compliance with the annual EU AQS at each monitoring station and estimated 24 hour average concentration that should not be exceeded more than one time per year in order to meet the annual EU AQS

Station^a	Emission change (%) (2015)	Emission change (%) (2020)	Estimated maximum daily concentration to meet AQS
a B: background, T: traffic, U: urban, and S: suburban.
Demokritos (BS)	−41.47	−13.17	106.20
Lykovrisi (BS)	8.72	26.98	77.61
AgiaParaskevi (BS)	−40.48	−12.38	78.24
Goudi (TU)	−11.66	10.67	73.97
Pireaus-1 (TU)	13.08	30.46	75.38

---

In order to evaluate whether such emission reductions can be achieved, we estimated primary and secondary emissions in AMA and TMA during 2008.⁵² The results are based on the primary anthropogenic PM emissions given in the UNECE/EMEP database (CEIP, Emission from Greece during 2008 as used in EMEP models⁵³—latest year with available data) and the methodology on spatial emission mapping and natural emissions calculation described in the study of Aleksandropoulou et al.³⁸ Emissions of secondary PM were calculated using the methodology of de Leeuw.⁵⁴ According to the above methodology, emissions of each precursor gas can be weighted to account for potential secondary aerosol formation. The weighting factors account for the fraction of emissions of pollutant changing into aerosol and the molecular weight difference. Their values have been derived on a European level and are 1 for primary PM, 0.54 for SO₂, 0.88 for NO_x, 0.64 for NH₃ and 0.02 for NMVOCs. Emissions of each pollutant are multiplied by the aerosol formation potential and results are reported in PM₁₀ equivalents. The results showed that during 2008 the contribution of natural sources (soil dust, marine aerosols and biogenic emissions) to primary and secondary PM₁₀ emissions in AMA and TMA were 44.52% and 40.16%, respectively. Primary natural PM emissions dominate the PM emissions, especially in the coarse mode during the cold season. The above values are only indicative since large uncertainties are associated with natural emissions calculation. However, they reflect the difficulty in reducing PM concentrations in the examined areas due to the large contribution of natural sources in emissions. It should be noted here that the contribution of natural PM sources (African dust, sea salt and windblown dust) to PM concentrations has been evaluated to 17 μg m⁻³ during the period 2001–2002 on a European scale, whereas particularly for Mediterranean sites the value was approximately 19.3 μg m⁻³ (Moussiopoulos et al.⁵⁵ and references therein). Although primary emissions from natural sources cannot be reduced because they are subject to meteorological conditions, the production of secondary aerosols from pollutants emitted from natural sources can be suppressed by reducing the emissions from anthropogenic sources. This is supported by results of studies on secondary organic aerosol (SOA) production. In particular, Kanakidou et al.⁵⁶ found with a global model that approximately 75% of biogenic SOA production may be induced by human activities.⁴¹

Besides natural emissions, previous studies on sources of PM in the AMA have shown that most of the PM related pollution is attributed to traffic sources (i.e. vehicle exhaust, road dust). In particular, the study by Karanasiou et al.⁵⁷ showed, using source apportionment techniques, that during March–December 2002, at 3 sites located at the periphery of Athens city centre, most of the PM₁₀ mass collected was associated with motor vehicles exhaust and road dust (53%), whereas 18% was marine aerosols, 13% resuspended soil particles, 7% industrial emissions (could also include fuel oil combustion for central heating), and 8% was attributed to particles emitted from biomass burning (with peaks during winter due to residential wood burning). The same study also found contributions of 54%, 19%, 15% and 12% from traffic, marine, biomass burning, and industrial sources, respectively, in PM₂. Also Grivas et al.²³ have shown that the observed PM₁₀ concentration levels in Athens during the period 2001–2004 at background stations is mainly the result of seasonal climatic conditions (long range transport, local natural sources, secondary PM formation) and of the transport of aerosols from more polluted areas within the same region, whereas at traffic stations the vehicular traffic overwhelms the effect of local stationary sources. In addition, Theodosi et al.¹⁹ have shown that only 1/3 of coarse particles collected during the period September 2005–August 2006 at Lykovrisi and Goudi stations are of natural origin and suggested traffic related sources for the rest at both sites. In the TMA road transport has been associated with 15.5% of total PM₁₀ primary anthropogenic emissions during 2002,⁵⁵ whereas Manoli et al.⁵⁸ have shown that the contribution of traffic related sources to PM concentrations in TMA was approximately 66% (38% exhaust and 28% road dust) for fine particles and dominated coarse particle concentration (57% was road dust). Therefore, reducing emissions of traffic related sources would lead to attenuation of PM₁₀ concentrations. Such reductions have been observed at the AMA in the past, specifically during 2004, when the Attica peripheral road and the suburban railway commenced operation. More reductions of traffic related PM emissions are expected in the following years due to the extension of the Athens subway network and the scheduled gradual replacement of buses used for public transport needs with new models driven by natural gas and/or diesel.⁵⁹

Another important source of PM during the cold period is fuel combustion for space heating. In particular, during 2008 emissions from space heating over the greater area of Athens have been estimated to correspond approximately to half of the anthropogenic PM_2.5 emissions and just over 1/3 of anthropogenic PM₁₀ emissions.⁵² In TMA space heating emissions particularly during 2007 comprised 65% of primary anthropogenic PM₁₀ emissions in the area. Towards the direction of lowering emissions from space heating and the building sector in general, a major operational programme has recently been established by the Greek Ministry of Environment, Energy and Climate Change with the objective to reduce the energy demand of buildings and homes. Taking into account that the directive on the energy performance of buildings⁶⁰ has only recently been implemented in the Greek legislation, positive results on PM concentrations reduction are expected in the following period.

Particularly for Thessaloniki, another important source of PM₁₀ emissions is the industrial combustion. During 2002, 69.3% of the anthropogenic PM₁₀ emissions in TMA have been associated with industrial activities.⁵⁵ Also their contribution to PM₁₀ concentrations has been reported in the range of 7% at the city centre to 30% at the western suburbs during 2004.⁶¹ Therefore, changes in industrial facilities emissions would mainly affect the PM₁₀ concentrations at the areas in their vicinity (industrial sites).

5. Summary and conclusions

In this study the lognormal and Weibull distributions were fitted to PM₁₀ and PM_2.5 concentration data measured at 15 stations in the Athens and Thessaloniki metropolitan areas during the period 2001–2010. According to the goodness of fit statistical indexes the lognormal distribution was found to best fit the observed concentrations data. The theoretical distributions predicted with accuracy the exceedances of the daily AQS at most of the stations. Still the deviation between modelled and measured exceedances was significant, particularly at background suburban stations in both urban areas. This discrepancy in the characteristics of the theoretical and empirical distributions was attributed to substantial changes in meteorological conditions and the spatial distribution of emissions during the period. Therefore the period 2001–2010 was split into smaller time periods having approximately the same frequency distribution of PM₁₀ concentrations. Based on the fitted distributions the minimum reduction required in order to attain the daily AQS was estimated using the rollback equation.

The results indicated that emission mitigation measures have to be applied at the traffic and industrial stations at AMA and TMA. The background concentration is significant compared to the EU AQS for PM₁₀; thus it is quite difficult for the areas to comply with the AQS. However, actions towards reducing traffic related emissions would improve the air quality at traffic stations and also at industrial and background stations in both areas.

Acknowledgements

This work was supported by the European Union's LIFE Programme under grant LIFE 09 ENV/GR/000289.

References

1. C. A. Pope, R. T. Burnett, M. J. Thun, E. E. Calle, D. Krewski, K. Ito and G. D. Thurston, JAMA, J. Am. Med. Assoc., 2002, 287, 1132–1141.
2. C. A. Pope and D. Dockery, J. Air Waste Manage. Assoc., 2006, 56, 709–742.
3. A. G. Russell and B. Brunekreef, Environ. Sci. Technol., 2009, 43, 4620–4625.
4. Directive 2008/50/EC, Off. J. Eur. Communities: Legis., 2008, 152, 1–44.
5. P. G. Georgopoulos and J. H. Seinfeld, Environ. Sci. Technol., 1982, 16, 401A–416A.
6. A. S. Kao and S. K. Friedlander, Environ. Sci. Technol., 1995, 29, 19–28.
7. F. Karaca, O. Alagha and F. Ertürk, Chemosphere, 2005, 59, 1183–1190.
8. P. Kassomenos, A. Lykoudis and A. Chaloulakou, Environ. Int., 2010, 36, 281–289.
9. D. T. Mage and W. R. Ott, Atmos. Environ., 1984, 18, 163–171.
10. B. Morel, S. Yeh and L. Cifuentes, Atmos. Environ., 1999, 33, 2575–2585.
11. I. Gavriil, G. Grivas, P. Kassomenos, A. Chaloulakou and N. Spyrellis, Global NEST Journal, 2006, 8(3), 241–251.
12. G. M. Giavis, H. D. Kambezidis and S. P. Lykoudis, Int. J. Environ. Pollut., 2009, 36, 99–109.
13. H. C. Lu, Atmos. Environ., 2002, 36, 491–502.
14. D. K. Papanastasiou and D. Melas, Water, Air, Soil Pollut., 2010, 207, 115–122.
15. H. C. Lu and G. C. Fang, Atmos. Environ., 2003, 37, 3491–3499.
16. H. C. Lu, Chemosphere, 2004, 54, 805–814.
17. Z. Mijic, M. Tasic, S. Rajsic and V. Novakovic, Atmos. Res., 2009, 92, 420–426.
18. G. Grivas, A. Chaloulakou and N. Spyrellis, Proceedings of the European Aerosol Conference, Thessaloniki, 2008.
19. C. Theodosi, G. Grivas, P. Zarmpas, A. Chaloulakou and N. Mihalopoulos, Atmos. Chem. Phys. Discuss., 2011, 11, 7659–7691.
20. J. L. Mauderly and J. C. Chow, Inhalation Toxicol., 2008, 20, 257–288.
21. Hellenic Statistical Authority, Population census 2001, Actual population per prefecture, municipality, municipal district and thorp, ΦEK (gazette) 715/12-06-02 no. B., EL.STAT, Athens, 2002.
22. G. Grivas, A. Chaloulakou, C. Samara and N. Spyrellis, Water, Air, Soil Pollut., 2004, 158, 357–371.
23. G. Grivas, A. Chaloulakou and P. Kassomenos, Sci. Total Environ., 2008, 389, 165–177.
24. Hellenic Ministry for the Environment, Physical Planning and Public Works, Air pollution in Athens for 2006, H.M.E.P.P.P.W., Athens, 2007.
25. D. Melas, I. Kioutsioukis and M. Lazaridis, in NATO Science Series: IV: Earth and Environmental Sciences—Advances of Air Pollution Modelling for Environmental Security, ed. I. Farago, K. Georgiev and A. Havasi, Springer, Dordrecht, 2005, vol. 54, pp. 285–296.
26. A. Chaloulakou, P. Kassomenos, N. Spyrellis, P. Demokritou and P. Koutrakis, Atmos. Environ., 2003, 37, 649–660.
27. C. Vlachokostas, C. Achillas, N. Moussiopoulos, K. Kalogeropoulos, G. Sigalas, E. A. Kalognomou and G. Banias, Air Qual., Atmos. Health, 2010 DOI:10.1007/s11869-010-0096-1.
28. C. Samara and D. Voutsa, Chemosphere, 2005, 59, 1197–1206.
29. The European air quality database, http://www.eea.europa.eu/data-and-maps/data/airbase-the-european-air-quality-database-3, 2011.
30. Hellenic Ministry of environment, energy and climate change, Air quality measurement data for the period 1984–2010, (http://www.ypeka.gr, H.M.E.E.C.C., Athens, 2011.
31. D. M. Holland and T. Fitz-Simons, Atmos. Environ., 1982, 16, 1071–1076.
32. C. J. Willmott, Bull. Am. Meteorol. Soc., 1982, 63, 1309–1313.
33. O. Thas, Comparing Distributions, Springer, New York, 2009, p. 353.
34. J. H. Sheinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: from Air Pollution to Climate Change, Wiley, New York, 1998, p. 1326.
35. Council Directive 1999/30/EC, Off. J. Eur. Communities: Legis., 1999, 163, 41–50.
36. S. Vardoulakis and P. Kassomenos, Atmos. Environ., 2008, 42, 3949–3963.
37. M. J. Assael, M. Delaki and K. E. Kakosimos, Atmos. Environ., 2008, 42, 65–77.
38. V. Aleksandropoulou, K. Torseth and M. Lazaridis, Water, Air, Soil Pollut., 2011, 219, 507–526.
39. R. Borge, J. Lumbreras, S. Vardoulakis, P. Kassomenos and E. Rodriguez, Atmos. Environ., 2007, 41, 4434–4450.
40. I. El Haddad, N. Marchand, H. Wortham, C. Piot, J. L. Besombes, J. Cozic, C. Chauvel, A. Armengaud, D. Robin and J. L. Jaffrezo, Atmos. Chem. Phys., 2011, 11, 2039–2058.
41. A. Gelencser, B. May, D. Simpson, A. Sanchez-Ochoa, A. Kasper-Giebl, H. Puxbaum, A. Caseiro, C. Pio and M. Legrand, J. Geophys. Res., 2007,(112), D23S04.
42. P. Lin, M. Hu, Z. Deng, J. Slanina, S. Han, Y. Kondo, N. Takegawa, Y. Miyazaki, Y. Zhao and N. Sugimoto, J. Geophys. Res., 2009,(114), D00G11.
43. L. Bencs, K. Ravindra, J. de Hoog, Z. Spolnik, N. Bleux, P. Berghmans, F. Deutsch, E. Roekens and R. Van Grieken, Environ. Pollut., 2010, 158, 3421–3430.
44. R. M. Harrison and J. Yin, J. Environ. Monit., 2010, 12, 1404–1414.
45. G. Lonati, S. Ozgen and M. Giuglian, Atmos. Environ., 2007, 41, 4599–4610.
46. A. M. S. de la Campa, C. Pio, J. D. de la Rosa, X. Querol, A. Alastuey and Y. Gonzalez-Castanedo, Environ. Res., 2009, 109, 671–681.
47. J. Sciare, K. Oikonomou, O. Favez, E. Liakakou, Z. Markaki, H. Cachier and N. Mihalopoulos, Atmos. Chem. Phys., 2008, 8, 5551–5563.
48. O. V. Rattigan, H. D. Felton, M.-S. Bae, J. J. Schwab and K. L. Demerjian, Atmos. Environ., 2010, 44, 2043–2053.
49. S. C. Lee, Y. Cheng, K. F. Ho, J. J. Cao, P. K.-K. Louie, J. C. Chow and J. G. Watson, Aerosol Sci. Technol., 2006, 40, 157–165.
50. J. C. Chow, J. G. Watson, Z. Q. Lu, D. H. Lowenthal, C. A. Frazier, P. A. Solomon, R. H. Thuillier and K. Magliano, Atmos. Environ., 1996, 30, 2079–2112.
51. B. J. Turpin and J. J. Huntzicker, Atmos. Environ., Part A, 1991, 25, 207–215.
52. V. Aleksandropoulou and M. Lazaridis, unpublished work.
53. EMEP/CLRTAP, Emission from Greece during 2008 as used in EMEP models, http://www.ceip.at/emission-data-webdab/emissions-as-used-in-emep-models/, EMEP Centre on Emission Inventories and Projections (CEIP), Vienna, 2011.
54. F. de Leeuw, Environ. Sci. Policy, 2002, 5, 135–145.
55. N. Moussiopoulos, Ch. Vlachokostas, G. Tsilingiridis, I. Douros, E. Hourdakis, C. Naneris and C. Sidiropoulos, Sci. Total Environ., 2009, 407, 1268–1285.
56. M. Kanakidou, K. Tsigaridis, F. J. Dentener and P. J. Crutzen, J. Geophys. Res., 2000, 105(D7), 9243–9254.
57. A. A. Karanasiou, P. A. Siskos and K. Eleftheriadis, Atmos. Environ., 2009, 43, 3385–3395.
58. E. Manoli, D. Voutsa and C. Samara, Atmos. Environ., 2002, 36, 949–961.
59. S. A. Attiko Metro, Historical data on transit in Athens, http://www.ametro.gr/, 2007.
60. Directive 2002/91/EC, Off. J. Eur. Communities: Legis., 2002, 1, 65–71.
61. K. E. Kakosimos, A. S. Katsarou and M. J. Assael, Proceedings of the 4th Environmental Conference of Macedonia region, Thessaloniki, 2011.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1em10673b

---