Conduction band energy determination by variable temperature spectroelectrochemistry

Abstract

The conduction and valence band energy positions of nanostructured semiconductors are arguably the most important physical parameters of these materials; however they have also proven the most problematic to measure. In this work, we describe a new method of variable temperature spectroelectrochemistry, which is a simple way to directly measure the absolute conduction band energy of nanostructured electrodes with minimal assumptions. In addition, the extinction coefficient of free conduction band electrons is simultaneously determined by this method. Results of variable temperature spectroelectrochemistry measurements of nanoparticle TiO₂ electrodes are presented. Values of −0.761 to −0.936 V vs. Ag/AgCl were determined for the conduction band energy, which was found to shift with E_F in excellent agreement with literature estimates. We believe this method will be applicable to a large variety of materials and systems.

---

Broader context

The absolute conduction and valence band energies of nanostructured semiconductor materials are probably the most important physical parameters in understanding their behavior. For example, knowledge of the band energies is essential in determining the driving force for key charge-transfer reactions, such as recombination in DSSCs or water reduction/oxidation in photocatalytic water splitting. However, accurate determination of nanostructured semiconductor band energies has thus far proven elusive. In this work we present a new, simple method to directly measure the band energies of nanostructured semiconductor materials. As a proof-of-concept we provided the measurement of the conduction band energy of nanoparticle TiO₂; a material that has been of significant interest in various aspects of energy and environmental science over the past several decades. Our results further provide the first direct evidence of band edge unpinning for nanoparticle TiO₂ electrodes. In addition, the determination of the extinction coefficient of free conduction band electrons is presented.

Introduction

Nanostructured semiconductor electrodes are an important class of materials exhibiting remarkable performance in energy conversion paradigms such as dye-sensitized solar cells, DSSCs, and photocatalysis.^1–7 The most important electronic parameters of these materials are the conduction and valence band edge positions; knowledge of these energies is crucial in understanding the photophysical and chemical behavior. For example, it is essential in determining the driving force for key charge-transfer reactions, such as recombination in DSSCs or water reduction/oxidation in photocatalytic water splitting.^3,7–9 Remarkably, however, there is no reliable method to measure the absolute band edge positions. Herein we describe a simple new method to measure the band energies.

Mott–Schottky analysis is the most commonly used method to measure band edge positions of flat crystalline semiconducting electrodes; however this cannot be accurately applied to nanostructured electrodes. The Mott–Schottky equation is derived from modeling the depletion region capacitance as a parallel plate capacitor, and is thus applicable to flat semiconductor–electrolyte interfaces. The use of nanoparticles, for example, immersed in an electrolyte would require solution of Poisson's equation in spherical coordinates,¹⁰ analogous to that derived for nanorods.¹¹ In addition, the depletion region for nanoparticle based semiconductors is typically larger than the radius of the nanoparticle, making the film unable to support traditional band-bending required for such techniques.^12–14 Furthermore, Mott–Schottky analysis describes the depletion region capacitance in terms of the dopant density, N_D; however a nanoparticle based film comprised of 10 nm diameter particles of a semiconductor with N_D = 10¹⁷ cm⁻³, which has been measured for thin dense films of anatase TiO₂ annealed in air to 500 °C,¹⁵ translates to one dopant for every twenty nanoparticles. Clearly a homogeneous depletion region capacitance would not be produced under such conditions.

During the 1990s Fitzmaurice and co-workers conducted a series of studies focused on using spectroelectrochemistry to determine the conduction band position in mesoporous nanoparticle based transparent semiconducting films.^16–22 This method relies on determining the concentration of electrons in the conduction band of the semiconducting film by measuring the absorption of sub-band gap energy photons, typically near-IR, by these electrons as a function of applied potential. The absorbance spectrum of electrons in mesoporous TiO₂ has garnered much debate over the past twenty years.^{14,16–18,21,23–28} This debate arises from very broad absorption features and wildly ranging conditions in which measurements are taken (protic vs. aprotic solvents, pH, presence of intercalating cations, etc.). Nevertheless, the resulting estimates for E_cb in TiO₂ from spectroelectrochemistry studies have been used for nearly twenty years, despite several drawbacks that have become apparent with these measurements. These problems include: (1) the assumption of a flat interface and an accumulation layer is maintained throughout the film,¹⁷ an assumption that has been demonstrated to be highly unlikely.^12,14,29 (2) The requirement that a large negative bias be applied to the electrode to achieve a substantial accumulation layer irreversibly alters the electrode during the measurement when electrolytes contain small cations that can intercalate.^19,21,23,30 (3) The extinction coefficient of conduction band electrons and the dopant density must be known or easily estimated.^22,31 (4) Monitoring the absorbance of TiO₂ during a cyclic voltammogram results in a large hysteresis and a scan rate dependence on the absorbance indicating steady-state electron filling is not achieved.²¹

In this work we introduce a steady-state variable temperature spectroelectrochemical measurement to determine the conduction band edge in transparent mesoporous semiconducting electrodes which overcomes the limitations of Mott–Schottky and spectroelectrochemical techniques applied previously. The absorbance of conduction band electrons, following Beer's Law, is given by A = εln_cb, where ε is the molar extinction coefficient, l is the effective path length and n_cb is the electron concentration in the conduction band of TiO₂. The quantity n_cb can be calculated according to the equation:^32,33

where k_B is Boltzmann's constant, T is temperature, E_cb is the energy of the conduction band minimum, E_F is the Fermi level energy and N_c is the effective conduction band density of states. N_c can be calculated according to:^32,34where m^*_c is the effective mass of an electron (m^*_c ≈ 10m_e for TiO₂)³⁵ and ℏ is Planck's constant divided by 2π. Inserting eqn (1) into Beer's law, and taking the natural log for an Arrhenius-type temperature dependent equation results in the following equation:

Thus, a plot of ln(A) vs. 1/T should be linear with a slope that produces the conduction band energy directly. In addition, the intercept yields the extinction coefficient of conduction band electrons. We note that there is a slight temperature dependence of the density of states function, described by eqn (2), which additionally needs to be accounted for to accurately determine the extinction coefficient. As a point of reference, at 300 K a value of N_c = 7.94 × 10²⁰ cm⁻³ is obtained from eqn (2).

Results

An example of a typical optical absorption spectrum of a mesoporous TiO₂ electrode, taken as the difference spectra between 0.5 V and −0.8 V vs. Ag/AgCl, is displayed in Fig. 1. The characteristic features are the bleach of absorbance at wavelengths less than ∼380 nm attributed to a Burstein shift, signifying that conduction band filling is occurring.^22,36 The second characteristic is a lack of local absorbance maxima, indicating that lithium intercalation is not appreciable and trapped electrons are not significantly absorbing as both have been shown to present local maxima in the range 700–770 nm.^{21,24–26,28} An additional absorption of trapped electrons appears near 400 nm and has been correlated to surface traps.²⁰ See ESI† for a plot depicting local maxima from trapped electrons. The third characteristic is the observed monotonic increase in absorbance with wavelength, distinctive of a delocalized electron absorption.^26,37,38 The fourth characteristic is the interference pattern signifying a highly uniform TiO₂ film.^16,20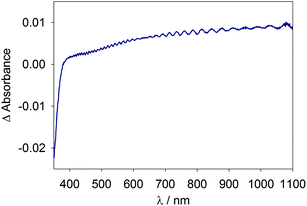

Fig. 1 Change in absorbance of a TiO₂ electrode when potential is stepped from +0.5 to −0.8 V vs. Ag/AgCl.

In order to obtain reliable and reproducible results, it is necessary to avoid strong accumulation conditions in the TiO₂ which leads to lithium intercalation and the formation of lithium titanate according to eqn (4).^24,25,30

xLi⁺ + xe_TiO2⁻ + TiO₂ → Li_xTiO₂ (4)

To this end we determined a potential range in which Li⁺ was not noticeably intercalated into the TiO₂ electrode. An example of a measurement of the percent transmittance, %T, at 800 nm while performing 25 cycles of cyclic voltammetry from 0 to −2 V vs. Ag/AgCl, similar to the wavelength and potential range used in past spectroelectrochemical measurements containing lithium, is shown in ESI (Fig. SI2†).^19,21 It is apparent that the electrode is strongly intercalating lithium, leading to an ever increasing absorbance with each additional scan. In addition to the bands shifting more positive, an absorption peak at 700 nm grows into the spectrum at negative potentials, see ESI.† In contrast, performing 25 cycles of cyclic voltammetry from 0 to −1 V vs. Ag/AgCl results in consistent %T changes and constant electron absorption features such as shown in Fig. 1, indicating that Li⁺ intercalation is not interfering with measurements over this potential range. The remainder of the results presented will be limited to monitoring the %T at potentials positive of −1 V vs. Ag/AgCl. An additional problem with fitting the absorbance measured during cyclic voltammetry arises from scan rate dependence of the absorbance. This point is demonstrated by plotting the absorbance as a function of potential at several scan rates; the absorbance at any given potential increases as the scan rate is decreased (see ESI, Fig. SI3†). Therefore the electrode must be held at a constant potential (E_F) to achieve steady state conditions in order to determine an accurate absorbance measurement at a given temperature.

The results of monitoring %T at 950 nm of a TiO₂ film while performing chronoamperometry are displayed in Fig. 2. As expected, both increasing the applied potential (moving from left to right in the figure) and increasing the temperature (moving down the plot) decreased the %T of the film. The decreasing %T (thus increasing A) indicates an increased concentration of free conduction band electrons as predicted by eqn (1).

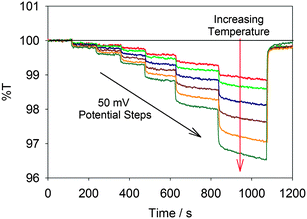Fig. 2 Plot of %T at 950 nm while stepping the potential from 0.50 to −0.45, −0.50, −0.55, −0.60, −0.65, −0.70, and back to +0.50 V vs. Ag/AgCl. Each trace represents a different temperature (288, 294, 301, 308, 314, 320 and 327 K), with increasing temperatures resulting in decreasing %T.

The absorbance values averaged for the last 60 seconds of each applied potential at each temperature are plotted in Fig. 3. In order to account for the slight temperature dependence of N_c, eqn (2) was incorporated into eqn (3) to produce the following final equation:

Fig. 3 Plot of ln(A) vs. T⁻¹ each line represents a different potential from −0.70 to −0.45 V vs. Ag/AgCl in 50 mV increments from top to bottom. The temperatures correspond to 288, 294, 301, 308, 314, 320 and 327 K. Error bars represent one standard deviation. The solid lines depict a global fit result to eqn (5) as described in the text.

The solid lines in Fig. 3 represent the results of a non-linear least-squares fit to eqn (5) for the data obtained at potentials between −0.45 and −0.70 V vs. Ag/AgCl. A global fit to all the data was performed to produce a single value for the extinction coefficient with a conduction band energy that was allowed to float. This fit produced a value of ε = 1 ± 0.3 × 10⁵ M⁻¹ cm⁻¹; the fit results for E_cb are displayed in Table 1. We note that potentials more positive than −0.45 V vs. Ag/AgCl did not elicit a change in %T that could be accurately measured, as can be seen in Fig. 2.

Table 1 Fit results of absorbance vs. temperature to eqn (3)

E F (mV vs. Ag/AgCl)	E cb/q (mV vs. Ag/AgCl)
−450	−761 ± 6
−500	−794 ± 6
−550	−828 ± 6
−600	−863 ± 6
−650	−899 ± 6
−700	−936 ± 6

---

Discussion

Due to the problems with obtaining accurate values for E_cb with Mott–Schottky or spectroelectrochemical methods as described above, direct comparison to previous literature reports is problematic. However, boundary values for E_cb can be readily determined by considering the energetics in a DSSC; the E_cb must lie somewhere between the dye excited potential, E°^*, and the quasi Fermi level, E_F, at V_oc. For a typical DSSC employing the N3 sensitizer, E°^* = −1.05 V vs. Ag/AgCl.^39,40 The V_oc is the difference between the solution potential, E_redox, and E_F; thus E_F can be estimated from subtracting V_oc from E_redox.⁴¹ Considering the I₃⁻/I⁻ redox shuttle with a E_redox ∼0.06 V vs. Ag/AgCl,^2,40,42,43 and a maximal V_oc of 0.8 V,⁴⁴ a value of E_F = −0.74 V vs. Ag/AgCl is produced.⁴⁵ This places a limit of −1.05 < E_cb/q < −0.74 V vs. Ag/AgCl; in excellent agreement with our measured values.

The results displayed in Table 1 also show an increasing E_cb with applied potential, consistent with a model of band edge unpinning (also referred to as Fermi-level pinning). This model is based on a semiconductor with a high concentration of electrically active surface states. Band edge unpinning will occur when the charge in the surface states becomes greater than the charge in the space charge region, resulting in further applied potential being dropped across the Helmholtz layer instead of the semiconductor.⁴⁶ Fermi-level pinning is more generally observed rather than an accumulation layer for n-type semiconductors/liquid junctions.^14,23,46,47 This is particularly expected, and has been reported, for porous nanocrystalline TiO₂ due to its very high surface area and known high density of surface states.^14,47,48

The fit results for ε are significantly higher than those that have been presented previously. Literature values of ε for the wavelengths 700–1000 nm are in the range 470–3400 M⁻¹ cm⁻¹.^{17,27,28,49,50} These literature values are typically determined by measuring the concentration of electrons in the TiO₂, either by chronoamperometry^28,49 or titration,⁵⁰ and comparing this to the measured absorbance. Using chronoamperometry to determine ε from the data displayed in Fig. 3 results in ε ≈ 1000–3000 M⁻¹ cm⁻¹, in good agreement with previous studies. However, these techniques measure the total concentration of charge in the TiO₂ film, both trapped and free electrons, and could substantially over estimate the concentration of electrons contributing to the measured absorbance. Accounting for the relative concentration of trapped and free electrons would easily increase the measured extinction coefficients by one or two orders of magnitude. Indeed, the multiple trapping model used to describe electron transport through nanoparticle TiO₂ electrodes is based on the fact that the vast majority of electrons in the film are trapped, not free.^51–54 Further, as noted above, the model of band edge unpinning is also based on the idea that most electrons are trapped and it has been demonstrated that trapped electrons absorb light differently than free electrons (see ESI SI1†). We therefore argue that our measured value of ε = 1 ± 0.3 × 10⁵ M⁻¹ cm⁻¹ is in excellent agreement with the reasoning that the majority of electrons in the film are indeed trapped and do not participate in the measured absorption.

Finally, we compare the variable temperature spectroelectrochemical method presented in this work with previous spectroelectrochemical methods. As discussed in the introduction, there are several problems concerning the previous spectroelectrochemical measurements that were employed to determine the conduction band edge. It is worth pointing out, however, that in principle careful spectroelectrochemical measurements could produce E_cb by incorporation of eqn (1) into Beers law. Since the measured absorbance is proportional to ε, this would only produce an accurate value of E_cb if an accurate value of ε was independently known. Our results indicate that determination of ε by charge extraction underestimates ε by approximately two orders of magnitude for TiO₂, however, which would produce an error of E_cb by ∼0.12 eV. Therefore, a significant advantage of the method presented herein is that the temperature variation effect on the absorbance is independent of ε, thus allowing for a more direct and accurate determination of E_cb with minimal assumptions or prior knowledge. An additional advantage is that ε is determined simultaneously with E_cb; however we reiterate that accurate determination of ε requires taking into account the temperature dependence of the density of states as shown above. In addition, we note that there may be a small dependence of the band gap and dielectric constant of TiO₂ over the modest temperature variation employed here which was not accounted for.³⁴ Since the E_cb values reported in Table 1 can be obtained at a fixed temperature using our fitted value of ε, i.e. all the data is self-consistent, we believe these effects are negligible. Further work to clarify such subtleties is in progress, however we believe the new variable temperature spectroelectrochemical method as described herein represents the best way to determine band edge positions of nanostructured semiconductor materials.

Conclusion

The method described herein for conduction band edge determination is relatively simple; it is quick, makes a minimal number of assumptions, does not require a priori knowledge of ε for free electrons, and does not require band-gap excitation. The only demands of this method are the preparation of an electrode with good optical quality and detectable free electron absorption. Additionally, this method is remarkably versatile; we expect this method will allow band edge determination in a variety of porous semiconductor materials. This work is currently in progress in our lab.

Experimental

An ∼8 μm thick film of nominally 5 nm radii TiO₂ nanoparticles was deposited on fluorine doped tin oxide, FTO, via a doctor blade technique using Solaronix T/SP TiO₂ paste. A custom jacketed three electrode electrochemical cell was incorporated into a Perkin Elmer Lamda 35 UV-Vis spectrophotometer such that the mesoporous TiO₂ film was positioned normal to the optical path. The temperature of the electrochemical cell was controlled using a Neslab chiller/circulator. The specific temperatures used were 15.0, 21.1, 27.5, 34.5, 40.9, 47.3 and 53.8 °C. Practical limitations prohibited expanding the temperature range, at cooler temperatures condensation formed on the outside of the cell and warmer temperatures were avoided in order to maintain reference electrode stability. Cyclic voltammetry and potential step voltammetry (chronoamperometry), using an AutoLab potentiostat, were performed while monitoring the percent transmittance, %T, of the TiO₂ electrode. For the potential step measurements the potential started at 0.5 V, stepped to −0.45 and then stepped in 50 mV increments to −0.7 V before being returned to 0.5 V. Between measurements the potential was held at 0.5 V vs. Ag/AgCl to drain excess electrons from the TiO₂, %T returned to 100%. All %T measurements are given setting the %T at 0.5 V as 100 %T. A control was constructed using a bare FTO electrode to confirm the absence of any contribution to the %T measurement from the FTO due to varying either potential or temperature. The potential was measured vs. a Ag/AgCl reference electrode (EDAQ ET072) determined to be −400 mV vs. ferrocene, and a platinum wire was used as a counter electrode. All measurements reported here where made using an electrolyte of 0.20 M LiClO₄ in acetonitrile, replaced every hour to prevent an appreciable concentration of Ag⁺ or Cl⁻ from building up due to migration through the reference electrode frit.

Acknowledgements

TWH would like to thank the Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy grant no. DE-FG02-11ER16245 for support of this work.

References

1. S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115.
2. A. Hagfeldt, G. Boschloo, L. C. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595.
3. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446.
4. X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503.
5. D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890.
6. W. J. Youngblood, S.-H. A. Lee, K. Maeda and T. E. Mallouk, Acc. Chem. Res., 2009, 42, 1966.
7. A. Kay, I. Cesar and M. Gratzel, J. Am. Chem. Soc., 2006, 128, 15714.
8. J. W. Ondersma and T. W. Hamann, J. Am. Chem. Soc., 2011, 133, 8264.
9. C. M. McShane and K. S. Choi, J. Am. Chem. Soc., 2009, 131, 2561.
10. L. M. Peter, Phys. Chem. Chem. Phys., 2007, 9, 2630.
11. I. Mora-Sero, F. Fabregat-Santiago, B. Denier, J. Bisquert, R. Tena-Zaera, J. Elias and C. Levy-Clement, Appl. Phys. Lett., 2006, 89, 203117.
12. W. J. Albery and P. N. Bartlett, J. Electrochem. Soc., 1984, 131, 315.
13. G. Hodes, I. D. J. Howell and L. M. Peter, J. Electrochem. Soc., 1992, 139, 3136.
14. F. Cao, G. Oskam, P. C. Searson, J. M. Stipkala, T. A. Heimer, F. Farzad and G. J. Meyer, J. Phys. Chem., 1995, 99, 11974.
15. H. X. Wang, P. G. Nicholson, L. Peter, S. M. Zakeeruddin and M. Gratzel, J. Phys. Chem. C, 2010, 114, 14300.
16. B. O'Regan, M. Gratzel and D. Fitzmaurice, Chem. Phys. Lett., 1991, 183, 89.
17. G. Rothenberger, D. Fitzmaurice and M. Gratzel, J. Phys. Chem., 1992, 96, 5983.
18. B. O'Regan, M. Gratzel and D. Fitzmaurice, J. Phys. Chem., 1991, 95, 10525.
19. G. Redmond and D. Fitzmaurice, J. Phys. Chem., 1993, 97, 1426.
20. G. Boschloo and D. Fitzmaurice, J. Phys. Chem. B, 1999, 103, 2228.
21. G. Boschloo and D. Fitzmaurice, J. Phys. Chem. B, 1999, 103, 7860.
22. D. Fitzmaurice, Sol. Energy Mater. Sol. Cells, 1994, 32, 289.
23. L. A. Lyon and J. T. Hupp, J. Phys. Chem., 1995, 99, 15718.
24. H. Lindstrom, S. Sodergren, A. Solbrand, H. Rensmo, J. Hjelm, A. Hagfeldt and S.-E. Lindquist, J. Phys. Chem. B, 1997, 101, 7710.
25. H. Lindstrom, S. Sodergren, A. Solbrand, H. Rensmo, J. Hjelm, A. Hagfeldt and S.-E. Lindquist, J. Phys. Chem. B, 1997, 101, 7717.
26. Nanophotonics: Integrating Photochemistry, Optics, and Nano/Bio Materials, ed. H. Masuhara and S. Kawata, Elsevier, San Diego, 1st edn, 2004, vol. 1.
27. M. Ohta, N. Koumura, K. Hara and S. Mori, Electrochem. Commun., 2011, 13, 778.
28. Y. R. Liu, J. R. Jennings, Y. Huang, Q. Wang, S. M. Zakeeruddin and M. Gratzel, J. Phys. Chem. C, 2011, 115, 18847.
29. A. Hagfeldt and M. Gratzel, Chem. Rev., 1995, 95, 49.
30. N. Kopidakis, K. D. Benkstein, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2003, 107, 11307.
31. B. Enright, G. Redmond and D. Fitzmaurice, J. Phys. Chem., 1994, 98, 6195.
32. J. Nelson, The Physics of Solar Cells, Imperial College Press, London, 2003.
33. ****, To clarify notation used throughout this work an italicized E denotes potential while a bold E denotes energy; thus E = E/q.
34. S. M. Sze, The Physics of Semiconductor Devices, Wiley, New York, 2nd edn, 1981.
35. B. Enright and D. Fitzmaurice, J. Phys. Chem., 1996, 100, 1027.
36. E. Burstein, Phys. Rev., 1954, 93, 632.
37. J. I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York, 1975.
38. R. van de Krol, A. Goossens and E. A. Meulenkamp, J. Appl. Phys., 2001, 90, 2235.
39. G. Sauve, M. E. Cass, G. Coia, S. J. Doig, I. Lauermann, K. E. Pomykal and N. S. Lewis, J. Phys. Chem. B, 2000, 104, 6821.
40. S. K. Sarkar, J. Y. Kim, D. N. Goldstein, N. R. Neale, K. Zhu, C. M. Elliot, A. J. Frank and S. M. George, J. Phys. Chem. C, 2010, 114, 8032.
41. T. W. Hamann and J. W. Ondersma, Energy Environ. Sci., 2011, 4, 370.
42. M. Zhang, J. Y. Liu, Y. H. Wang, D. F. Zhou and P. Wang, Chem. Sci., 2011, 2, 1401.
43. G. Boschloo and A. Hagfeldt, Acc. Chem. Res., 2009, 42, 1819.
44. M. Gratzel, Inorg. Chem., 2005, 44, 6841.
45. ****, The AgCl reference used herein was determined to be −0.40 V vs. Fc in MeCN. This value was used to convert literature potentials considering the E° for Fc is 0.45 V vs. SCE and 0.69 vs. NHE.
46. A. J. Bard, A. B. Bocarsly, F. R. F. Fan, E. G. Walton and M. S. Wrighton, J. Am. Chem. Soc., 1980, 102, 3671.
47. G. Schlichthorl, S. Y. Huang, J. Sprague and A. J. Frank, J. Phys. Chem. B, 1997, 101, 8141.
48. F. Fabregat-Santiago, I. Mora-Sero, G. Garcia-Belmonte and J. Bisquert, J. Phys. Chem. B, 2003, 107, 758.
49. D. Kuciauskas, J. E. Monat, R. Villahermosa, H. B. Gray, N. S. Lewis and J. K. McCusker, J. Phys. Chem. B, 2002, 106, 9347.
50. J. Y. Liu, J. Zhang, M. F. Xu, D. F. Zhou, X. Y. Jing and P. Wang, Energy Environ. Sci., 2011, 4, 3021.
51. J. Bisquert and V. S. Vikhrenko, J. Phys. Chem. B, 2004, 108, 2313.
52. J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 4292.
53. A. C. Fisher, L. M. Peter, E. A. Ponomarev, A. B. Walker and K. G. U. Wijayantha, J. Phys. Chem. B, 2000, 104, 949.
54. E. A. Gibson, A. L. Smeigh, L. Le Pleux, L. Hammarstrom, F. Odobel, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2011, 115, 9772.

---

Footnote

† Electronic supplementary information (ESI) available: Absorbance plots displaying the instability of TiO₂ at negative potentials and the peaks created by lithium intercalation as well as a plot showing the scan rate dependence of the absorbance at 950 nm. See DOI: 10.1039/c2ee22926a

---