The Kubas interaction in M(II) (M = Ti, V, Cr) hydrazine-based hydrogen storage materials: a DFT study

Abstract

The Cr(II) binding sites of an experimentally realised hydrazine linked hydrogen storage material have been studied computationally using density functional theory. Both the experimentally determined rise in H₂ binding enthalpy upon alteration of the ancillary ligand from bis[(trimethylsilyl)methyl] to hydride, and the number of H₂ molecules per Cr centre, are reproduced reasonably well. Comparison with analogous Ti(II), V(II) and Mn(II) systems suggests that future experiments should focus on the earliest 3d metals, and also suggests that 5 and 7 wt% H₂ storage may be possible for V(II) and Ti(II) respectively. Alteration of the metal does not have a large effect on the M–H₂ interaction energy, while alteration of the ancillary ligand bound to the metal centre, from bis[(trimethylsilyl)methyl] or hydride to two hydride ligands, THF and only hydrazine based ligands, indicates that ancillary ligands that are poor π-acceptors give stronger M–H₂ interactions. Good evidence is found that the M–H₂ interaction is Kubas type. Orbitals showing σ-donation from H₂ to the metal and π-back-donation from the metal to the dihydrogen are identified, and atoms-in-molecules analysis indicates that the electron density at the bond critical points of the bound H₂ is similar to that of classical Kubas systems. The Kubas interaction is dominated by σ-donation from the H₂ to the metal for Cr(II), but is more balanced between σ-donation and π-back-donation for the Ti(II) and V(II) analogues. This difference in behaviour is traced to a lowering in energy of the metal 3d orbitals across the transition series.

---

1 Introduction

The practical implementation of hydrogen as a fuel for road vehicles has several problems, including storage of the hydrogen in a compact space. Liquid storage has a high energy cost due to the cooling required, and hydrogen is lost during boil off, whilst high pressures (in excess of 300 bar) require specialist materials for the tanks. To circumvent these issues it has been suggested to incorporate within pressurised tanks a storage material to which the hydrogen can bind, to increase the storage capacity of the tank at a lower pressure. The United States Department of Energy (DOE) has targets to be met by 2015 for such storage systems. These include a gravimetric storage density of 5.5 wt%, a volumetric storage capacity of 40 g L⁻¹ and a 3.3 min refuelling time for a 5 kg tank.¹

Many different types of hydrogen storage materials have been investigated, and may be categorised according to the strength of the bond between the hydrogen and the material. At one end of this scale are metal hydrides, which bind the H atoms with a strong covalent bond (40–80 kJ mol⁻¹),^2,3 whilst at the other end are materials such as zeolites or carbon based frameworks that physisorb H₂ molecules through weak van der Waals forces (3–6 kJ mol⁻¹).⁴ The high storage capacities of the metal hydrides are offset by the energy costs of cooling the material during uptake, and heating the material to drive off the H₂ for use, while the ease with which the H₂ may be removed from materials that physisorb hydrogen is balanced by their low storage capacities (generally less than 1 wt% at room temperature). It has been calculated that a storage material-hydrogen binding enthalpy of between 20–30 kJ mol^−1 5,6 would give the best balance between storage capacity and the energy required to release the hydrogen.

In order to achieve an enthalpy in this range metals may be incorporated into the storage materials, to which H₂ may bind in a Kubas fashion. A Kubas interaction^7,8 is consistent with a lengthening of the H–H bond without breakage and involves σ-donation from the filled H–H σ-bonding orbital into an empty d orbital of a metal, and simultaneous π-back-donation from a filled metal d orbital into the vacant σ* anti-bonding orbital of the H₂ molecule. This is similar to the synergic bonding described by the Dewar–Chatt–Duncanson model for the interaction of, for example, CO with transition metals.^9,10 The fabrication of solid state materials which use the Kubas interaction to store hydrogen is a great challenge because it is difficult to synthesize a material that has both a high concentration of low valent, low coordinate binding sites (transition metals in the solid state prefer to be 6-coordinate in most cases), light weight, and enough porosity to allow hydrogen to diffuse through the structure.

Previously, we have investigated, both experimentally and computationally, hydrogen storage materials with first row transition metals in the +3 oxidation state.^2,11–17 Our first computational study was of a storage material based on an experimentally confirmed mesoporous silicate with titanium benzyl binding sites,¹¹ and the second was a hydrazine linked system containing vanadium binding sites.¹⁵ This latter system is of particular interest because the excess volumetric densities at 77 K (60 kg m⁻³) were reported to be greater than that of a metal organic framework (MOF). In both of these systems the experimental enthalpies in the 20–40 kJ mol⁻¹ range are believed to be due to the Kubas interaction, and this was verified by our calculations,^14,17 which also showed that the highest H₂ binding enthalpies would occur in systems based on early transition metals with hydride ancillary ligands.

In our experimentally characterised systems we observe a trend of rising H₂ binding enthalpy with increased coverage, opposite to the behaviour seen during physisorption. For the silica based systems this was rationalised through a molecular orbital analysis; the binding of one hydrogen molecule alters the energy of the frontier orbitals of the binding site such that the HOMO and LUMO are closer in energy to the HOMO and LUMO of free H₂, making the binding of the next H₂ molecule more favourable.¹⁴ By contrast, for the hydrazine linked material an analogous molecular orbital analysis proved inconclusive. We suggested that the rising enthalpy trends may be due to cooperativity between the metals of adjacent binding sites, thought to be possible due to the observed metallic conductivity, but the calculations did not include these effects.¹⁷ Rising enthalpies have also been observed recently in KC24 and attributed to lattice expansion effects.¹⁸

In this contribution we study computationally molecular models of the H₂ binding sites of an experimentally characterised Cr gel in which the metal centres are linked by hydrazine based ligands.¹⁹ The best experimentally verified material possesses the highest gravimetric and volumetric storage of any Kubas based material at 298 K (3.2 wt% and 42 kg m⁻³ at 170 bar without saturation). The materials are largely amorphous‡ with Cr(II), Cr(III) and Cr(IV) sites, although the majority are Cr(II). X-ray photoelectron spectroscopy shows that the binding mode of the hydrazine and the way that it links the binding sites together also vary, although mostly it links in a –NH–NH₂– fashion. During synthesis, each Cr(II) has a bis[(trimethylsilyl)methyl] ligand bound to it initially, which is then hydrogenated off. Proposed structures for the Cr(II) sites within the gel before and after hydrogenation are shown in Fig. 1A and 1B respectively, although the coordination number and the geometry of the ligands about the metals are not known for certain. This is because the air sensitive, paramagnetic, and amorphous nature of these materials precludes most detailed methods of structural characterization.

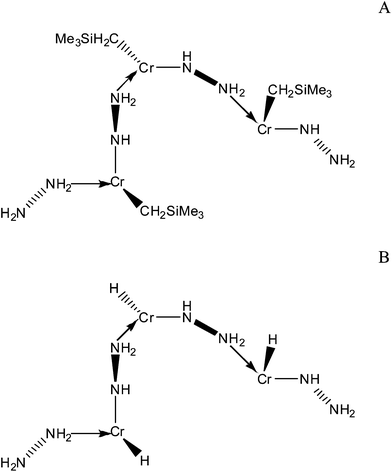Fig. 1 Schematic representations of the proposed structures¹⁹ of the Cr(II) hydrazine linked systems; (A) before hydrogenation, and (B) after hydrogenation.

As with our previous computational studies of M(III) silica- and hydrazine-based materials, we here employ molecular models of the binding sites, and probe their interaction with H₂. We initially benchmark our method against experimental data before investigating the effect of altering the ancillary (i.e. non hydrazine-based) ligand bound to the metal, and the effect of altering the metal from Cr to V and Ti. We also compare the results to those of our previous study of hydrazine linked hydrogen storage materials with transition metals in the +3 oxidation state.¹⁷

2 Computational details

Spin-unrestricted DFT, with the Perdew–Burke–Ernzerhof (PBE)^20,21 exchange correlation functional, was used throughout. This functional was chosen because of its success in our previous studies on the benzyl titanium binding sites of a mesoporous silica¹⁴ and on the vanadium binding sites of a hydrazine linked material,¹⁷ and because it has been shown by Sun et al. to be the best functional to balance computational speed and accuracy when looking at dihydrogen bound to metal centres.²² It is certainly a commonly used functional in this area of research.^23–28

The Gaussian 09 code²⁹ was used for all geometry optimisations, and the 6-311++G** basis^30–36 sets were used on all atoms. An ultrafine integration grid was used and the RMS force geometry convergence criterion was set to 0.000667 a.u. using IOP 1/7. Stationary points were analysed by performing analytical frequency calculations.

Atoms-in-molecules (AIM) calculations were performed using the AIMALLPro³⁷ programme on the electron densities at the Gaussian optimised geometries, employing formatted Gaussian checkpoint files as input.

Partial atomic charges were quantified using the Mulliken, Voronoi and Hirshfeld scales. These were calculated at the Gaussian optimised geometries using the Amsterdam Density Functional (ADF) program,^38–40 with the PBE functional, TZ2P basis sets^41–45 on all the atoms and the parameter controlling the integration grid set to 6.0. Mulliken charges were also calculated using the Gaussian code and atoms-in-molecules charges were taken from the AIMALLPro output.

The average energy of interaction between the metal and the H₂ units (M–H₂) was calculated in ADF as follows. Using the same calculation settings employed for the partial charges, a single point calculation on the geometry of the binding site representation with H₂ molecules bound (BSR(H₂)_n) was performed. Two further single point calculations were then performed breaking the molecule into two fragments; the metal-containing fragment (spin-unrestricted) and the (H₂)_n fragment (spin restricted). The average energy of interaction between the metal and the H₂ units was calculated as

E for all species was taken as the SCF energy. This fragment method of calculating the energy of the M–H₂ interaction was used successfully in our analysis of the amorphous silica based hydrogen storage materials¹⁴ and a variation on this method was used for the analysis of the hydrazine linked hydrogen storage materials with vanadium binding sites.¹⁷ In the silica study we evaluated the effects of basis set superposition error, concluding that it was only about 1 kJ mol⁻¹ per H₂. We have therefore not included corrections for basis set superposition error in the present work.

Whilst searching for alternative structures with different metals and ligands it was found that there were multiple possible true minimum geometries for the same set of ligand, metal and number of H₂ molecules. For example, with Ti(II), a hydride ancillary ligand and one bound H₂, it is possible to converge several structures with a capped square planar geometry with different relative positioning of the ligands, and also a trigonal bipyramidal structure. These geometries are within 32 kJ mol⁻¹. Due to the difficulty in locating all possible conformers (and as the geometry about the metal in the experimental system is not known) it was thought best to focus on a single conformer with one bound H₂ when making comparisons between metals and ligands. Therefore, all comparisons, in terms of the energy of the M–H₂ interactions, are made with reference to the binding of one H₂ molecule in a standard molecular conformation. This conformer is not necessarily the global minimum for all combinations of ligands and metals but is a true minimum. The chosen conformers for each of the ligand sets are shown in Fig. 2.

Fig. 2 Schematic representations of the conformers chosen for binding the first H₂ molecule to the binding site representations; (A) bis[(trimethylsilyl)methyl] ancillary ligand, (B) hydride ancillary ligand, (C) hydrazide ancillary ligand, (D) THF ancillary ligand and (E) two hydride ancillary ligands.

3 Results and discussion

3.1 Benchmarking against experimental data

The Cr(II) hydrazine systems studied experimentally show rising H₂ binding enthalpies with increasing coverage. For the materials with a bis[(trimethylsilyl)methyl] ancillary ligand the enthalpy rises to a maximum of −17.86 kJ mol⁻¹, and when this ligand is replaced with a hydride the maximum in the enthalpy increases to −51.58 kJ mol⁻¹, a rise in enthalpy after hydrogenation of −33.72 kJ mol⁻¹.¹⁹

The coordination number of the metal is not known experimentally and we have therefore investigated three, four and five coordinate molecular binding site representations (BSRs) (Fig. 3). The coordination number was increased using hydrazine ligands whilst maintaining the +2 oxidation state of the metal.§ The five coordinate BSRs did not bind H₂ molecules and so were discounted. The three coordinate BSR with a hydride ancillary ligand bound the first H₂ molecule as two hydride ligands (Fig. 4B) and so three coordinate BSRs were not considered further as this would imply irreversible hydrogen storage, which has not been seen experimentally. The four coordinate BSRs with a bis[(trimethylsilyl)methyl] ancillary ligand bind one H₂ molecule with an energy of −28.33 kJ mol⁻¹, rising to −48.52 kJ mol⁻¹ with a hydride ancillary ligand (Table 1, Fig. 5). This rise in enthalpy upon altering the ancillary ligand (−20.19 kJ mol⁻¹) is in reasonable agreement with experiment. Only one H₂ molecule is found to bind to the four coordinate BSRs, also in reasonable agreement with the 1.58 H₂/Cr seen experimentally (H₂ physisorbed within the pores of the framework is not accounted for in our model). Furthermore, four coordinate BSRs were found to best reproduce the experimental data for the V(III) hydrazine linked system studied previously,¹⁷ and we therefore focus on four coordinate BSRs for the remainder of this work.

Fig. 3 Schematic representations of the binding site representations chosen for the possible coordination numbers of the Cr(II) hydrazine linked experimental system; (A) three coordinate, (B) four coordinate and (C) five coordinate. L = H or bis[(trimethylsilyl)methyl].

Fig. 4 Ball and stick representations of the optimised geometries of three coordinate binding site representations with Cr(II) and a hydride ancillary ligand; (A) no bound H₂, (B) one H₂ bound as a dihydride and (C) two H₂ bound (one as a dihydride).

Fig. 5 Ball and stick representations of the optimised geometries of four coordinate binding site representations with Cr(II) and a hydride ancillary ligand; (A) no bound H₂ and (B) one H₂ bound, and with a bis[(trimethylsilyl)methyl] ancillary ligand; (C) no H₂ bound and (D) one H₂ bound.

Table 1 H–H bond lengths, frequencies and bond critical point (BCP) densities, and average M–H₂ interaction energies for all of the binding site representations studied computationally with 4 coordinating ligands. In all cases the number of non-ancillary hydrazine and hydrazide ligands was chosen so as to maintain the M(II) oxidation state. / = no geometry optimised for that combination. — = no calculation with that combination was attempted

Ancillary ligand(s)	No. of H2 bound	H–H bond lengths/Å			H–H stretching frequencies/cm^−1			M–H2 interaction energies/kJ mol^−1			H–H BCP densities/e bohr^−3
		Ti^2+	V^2+	Cr^2+	Ti^2+	V^2+	Cr^2+	Ti^2+	V^2+	Cr^2+	Ti^2+	V^2+	Cr^2+
(Trimethylsilyl)methyl	1	0.813	0.795	0.784	3278	3580	3783	−31.32	−30.09	−28.33	0.222	0.233	0.239
	2	0.803	0.790	/	3456	3645	/	−40.33	−23.34	/	0.227	0.234	/
		0.805	0.809		3364	3372					0.225	0.225
	3	0.805	/	—	3404	/	—	−217.32	/	—	0.225	/	—
		0.840			2965						0.206
		2.159			N/A						N/A
Hydride	1	0.810	0.837	0.811	3342	3004	3377	−44.11	−54.33	−48.52	0.224	0.211	0.225
	2	0.788	0.792	/	3700	3632	/	−41.78	−33.34	/	0.237	0.229	/
		0.806	0.803		3408	3485					0.226	0.234
	3	0.794	/	—	3606	/	—	−26.58	/	—	0.234	/	—
		0.798			3535						0.230
		0.800			3468						0.229
Two hydrides	1	0.810	0.816	0.818	3359	3296	3308	−59.69	−61.16	−68.78	0.224	0.223	0.223
	2	0.809	0.810	/	3383	3380	/	−42.16	−51.28	/	0.225	0.226	/
		0.810	0.819		3333	3264					0.224	0.222
	3	0.802	/	—	3463	/	—	−35.57	/	—	0.229	/	—
		0.816			3276						0.222
		0.822			3183						0.217
Two hydrazides	1	0.828	0.795	0.792	3062	3574	3636	−46.22	−37.33	−37.75	0.212	0.232	0.234
	2	0.792	0.782	/	3593	3769	/	−58.18	−8.93	/	0.224	0.239	/
		0.809	0.808		3333	3386					0.234	0.227
THF	1	0.810	0.802	—	3304	3465	—	−31.43	−49.00	—	0.223	0.228	—
	2	0.792	0.794		3595	3590		−45.78	−27.49		0.233	0.233
		0.817	0.803		3225	3465					0.219	0.229

---

3.2 Altering the metal

We extended our study to other early first row transition metals by substituting the Cr(II) with Ti(II), V(II) or Mn(II) to see if, as with our work with metals in the +3 oxidation state,¹⁴ there is a trend to fewer bound H₂ molecules as the periodic table is crossed. Fig. 6 shows that this is indeed the case for hydride ancillary ligands, as the number of H₂ molecules bound to the BSRs reduces as the metal is altered, with Ti(II), V(II) and Cr(II) binding three, two and one H₂ molecules, respectively (Mn(II) was found not to bind any H₂). This is also the case for the bis[(trimethylsilyl)methyl] ancillary ligand (Fig. 7) where only one H₂ molecule may be bound to Cr(II) but two to Ti(II) or V(II).

Fig. 6 The M–H₂ interaction energy as a function of the number of bound H₂ molecules for four coordinate Ti, V and Cr BSRs with a hydride ancillary ligand.

Fig. 7 The M–H₂ interaction energy as a function of the number of bound H₂ molecules for four coordinate Ti, V and Cr BSRs with a bis[(trimethylsilyl)methyl] ancillary ligand.

We also observed previously¹⁷ that the M–H₂ interaction energy is not much affected on changing the metal, and this is again the case; Fig. 6 and 7 show the M–H₂ interaction energies to be within 10 kJ mol⁻¹ of each other when one H₂ is bound.

3.3 Altering the ancillary ligand

The ancillary ligand was altered from hydride or bis[(trimethylsilyl)methyl] to all N-donor ligands, to two hydride ligands and to tetrahydrofuran (THF). THF may be used as a solvent during the preparation of the experimental materials¹⁶ and may remain bound to the metal centres, and so could be present in the final material.

Previously with first row transition metals in the +3 oxidation state it was observed that ancillary ligands that did not accept electron density via π-back-donation from the metal enhanced the M–H₂ binding energy, presumably due to increased back-donation to H₂.¹⁷ This is also the case with the metals in the +2 oxidation state. The generally accepted order of the ancillary ligands’ ability to accept π-electron density is two hydrides < one hydride < hydrazide < bis[(trimethylsilyl)methyl] and Table 1 indicates that the M–H₂ interaction energy generally reduces in that order. The fact that changing the alkyl group to a hydride does not alter the number of H₂/metal but only the strength of binding suggests that the hydride induced amplification of hydrogen storage capacity to 3.2 wt% at 170 bar and 298 K on hydrogenation in the experimental Cr system is due to the loss of weight in the system on alkyl loss as opposed to greater numbers of H₂ binding per site. On the basis of the molecular weight of the Cr hydrazine system (ca. 80 g mol⁻¹) the 3.2 wt% would be very close to saturation, although saturation was not observed at the pressures in this study.¹⁸ This also suggests that V(II) materials should be able to bind a maximum of ca. 5 wt% and Ti(II) materials a maximum of ca. 7 wt% on the basis of 2 and 3 H₂/M respectively, and molecular weights of ca. 80 g mol⁻¹ based on a 1 : 1 M : hydrazine ratio.

3.4 The nature of the M–H₂ interaction

As in our previous work on the Ti sites of the silica based systems¹⁴ and the V binding sites of the hydrazine linked systems¹⁷ we again observe evidence for the M–H₂ interaction being of a Kubas type. Experimentally the Kubas interaction is characterised by a lengthening of the H–H bond of the H₂ molecule and a reduction in its stretching frequency upon binding. In our representation of the Cr experimental system the H–H bond lengthens upon binding from its free (computational) value of 0.752 Å to 0.784 Å when there is a bis[(trimethylsilyl)methyl] ancillary ligand and to 0.811 Å with hydride (Table 1). The vibrational frequency concomitantly decreases from 4317 cm⁻¹ to 3783 and 3377 cm⁻¹ respectively (Table 1).¶ The experimental binding enthalpies¹⁹ of −17.86 kJ mol⁻¹ with a bis[(trimethylsilyl)methyl] ancillary ligand and −51.58 kJ mol⁻¹ with a hydride ligand are in the Kubas range and are reproduced reasonably well computationally (Table 1). Molecular orbitals featuring the two synergic interactions of the Kubas bond, π-back-donation from the metal to the H₂ molecule and σ-donation from the H₂ molecule to the metal, are shown in Fig. 8A and 8B, respectively.

Fig. 8 Molecular orbitals of the Cr(II) BSR with a bis[(trimethylsilyl)methyl] ancillary ligand and one bound H₂; (A) HOMO-1 (π-back-donation) and (B) HOMO-44 (σ-donation). Image C shows the bare ball and stick framework.

In our previous paper on the V(III) binding sites of a hydrazine linked hydrogen storage material, we studied the M–H₂ interaction via atoms-in-molecules (AIM) theory and benchmarked our analysis against prototypical Kubas systems.¹⁷ In AIM theory, two atoms are considered to be bonding when there is a bond critical point (BCP) between them. The BCP is the minimum on the line of maximum electron density connecting two nuclei (the bond path), and is a maximum in a plane perpendicular to the bond path. The electron density at the BCP is correlated with the strength of the bond. We found the density at the BCP of the H–H bond of the bound H₂ molecule for the classically Kubas systems to be between 0.202–0.219 e bohr⁻³.¹⁷ Here, the density at the BCP of the H₂ molecule bound to the BSR of the Cr experimental system is 0.239 and 0.225 e bohr⁻³ with bis[(trimethylsilyl)methyl] and hydride ancillary ligands, respectively (Table 1). These values are both higher than those of the classically Kubas systems but close to those found for the BSR of the V hydrazine linked gel, studied previously, of 0.238–0.240 e bohr⁻³.¹⁷ As for the V hydrazine linked gel, this suggests that the present M–H₂ bonds are weaker than in the classically Kubas systems; there is reduction in the electron density at the BCP of the H₂ molecule from the free H₂ molecule BCP value of 0.256 e bohr⁻³, but not quite as much as with the classically Kubas systems. Table 1 also shows that, in general, the electron density at the H–H BCPs increases as the number of bound H₂ units increases. This is in line with the general reduction of the calculated M–H₂ interaction energy as more H₂ are bound.

Previously, in our studies of the V(III) hydrazine linked gel¹⁷ and the Ti(III) sites of the silica based systems,¹⁴ we found that the Kubas interaction was dominated by the σ-donation from the H₂ to the metal such that the partial charge on the metal reduced, in most cases, upon binding H₂. This is also the case for the BSRs of the experimentally realised Cr(II) system where out of all of the combinations of ancillary ligands and methods of calculating the partial charge, in 15 cases the partial charge on the metal reduces as more H₂ molecules are bound and in only five cases the partial charge increases (Table S2†). For example, the partial charge on the Cr in the four coordinate binding site with a hydride ancillary ligand is shown in Fig. 9. However, when the metal is altered computationally to Ti or V the partial charge neither decreases nor increases significantly in most cases, suggesting a balance between the two synergic components of the Kubas bond. Examples for four coordinate BSRs with Ti or V with a hydride ligand are shown in Fig. 10 and 11 respectively. An increase in the π back-bonding component of the Kubas interaction might be expected in M(II) vs. M(III), and also that the effect would be smallest for Cr(II), due to the stabilisation of the 3d orbitals across the periodic table. This is illustrated in Table 2; the occupied orbitals that interact with the H₂ molecule are generally the two lowest d-based orbitals for all of the metals, and those for Cr are much lower in energy than those of Ti or V. The more stable the d-based MOs, the less they will interact with the LUMO of the H₂ molecule (+0.72 eV) and the smaller the π-back-donation component of the M–H₂ bond.

Fig. 9 The partial charge on the Cr as a function of the number of H₂ molecules bound for a four coordinate BSR with a hydride ancillary ligand.

Fig. 10 The partial charge on the Ti as a function of the number of H₂ molecules bound for a four coordinate BSR with a hydride ancillary ligand.

Fig. 11 The partial charge on the V as a function of the number of H₂ molecules bound for a four coordinate BSR with a hydride ancillary ligand.

Table 2 Energies of metal d-based molecular orbitals of four coordinate BSRs with either bis[(trimethylsilyl)methyl] or hydride ancillary ligands, as a function of metal and number of bound H₂ molecules

Metal	Orbital	Bis[(trimethylsilyl)methyl]		Hydride
		No H2 bound	1 H2 bound	No H2 bound	1 H2 bound
Ti	LUMO	−1.50	−1.27	−1.31	−1.28
	HOMO	−2.27	−2.34	−2.15	−2.24
	HOMO-1	−2.34	−2.50	−2.23	−2.52
V	LUMO	−1.41	−1.18	−1.31	−1.28
	HOMO	−2.66	−2.54	−2.40	−2.54
	HOMO-1	−2.70	−2.84	−2.70	−2.84
	HOMO-2	−2.85	−2.92	−2.86	−2.92
Cr	LUMO	−1.10	−1.23	−1.09	−1.31
	HOMO	−2.87	−2.95	−2.86	−2.76
	HOMO-1	−3.60	−3.85	−3.57	−3.19
	HOMO-2	−3.70	−3.73	−3.77	−3.58
	HOMO-3	−3.78	−3.80	−3.88	−3.93

---

In previous work¹⁷ we have examined the AIM bond paths formed between the H₂ molecules and the metal centres. It would be expected that there would be a bond path between the H atoms, two bond paths from the metal (one to each of the H atoms) and that at the centre of this triangle there would be a ring critical point. However, for every M/H₂ system we have studied, we have found a bond catastrophe in which the ring critical point and the bond critical points are so close together that a ring critical point and one of the bond critical points cancel each other out,¹⁷ as observed previously by Sparkes et al. for the interaction of a C=C double bond with a metal.⁴⁶ Thus, there is only one bond path between the metal and one of the H atoms. We have used this bond path to assess the balance of π-back-donation and σ-donation in the Kubas interaction; if the bond path lies mainly on the straight line between the metal and the BCP of the H–H bond, then we concluded that the bond is dominated by σ-donation, but if the bond path is curved away from this line there is a larger π-back-donation component to the bond. We have attempted a similar analysis of the molecular graphs of the present targets, but unfortunately no clear cut pattern emerged to give a clear indication of the effect of altering the metal on the extent of π-back-donating versus σ-donating components of the M–H₂ bonds. Selected molecular graphs are given in the ESI (Fig. S1 and S2†).

4 Conclusions

The Cr(II) binding sites of an experimentally realised hydrazine linked hydrogen storage material have been studied computationally and the experimental results have been reproduced reasonably well. This includes the rise in H₂ binding enthalpy upon alteration of the ancillary ligand from bis[(trimethylsilyl)methyl] to hydride (−17.86 to −51.58 kJ mol⁻¹, vs. −28.33 to −48.52 kJ mol⁻¹ computationally) and the number of H₂ molecules per Cr centre.

The study has been extended to Ti(II), V(II) and Mn(II). It was not possible to bind any H₂ to the latter and hence we predict that Mn(II) based hydrogen storage materials would not perform well. However, Ti(II) and V(II) based systems seem more promising as more H₂ molecules could be bound to these binding site representations than for Cr(II), suggesting that future experiments should focus on the earliest 3d metals. Indeed, calculations for V(II) and Ti(II) suggest 5 and 7 wt%, respectively. Alteration of the metal did not have a large effect on the M–H₂ interaction energy.

The study was also extended to investigate the effect of altering the ancillary ligand bound to the metal centre, from bis[(trimethylsilyl)methyl] or hydride to two hydride ligands, THF and only N-donor ligands. As in our previous work on M(III) systems,^14,17 it was found computationally that the ancillary ligands that are poor π-acceptors, such as hydrides, give stronger M–H₂ interactions as more of the metal's electron density is available to back donate to the incoming H₂. The M–H₂ interaction energies therefore reduced with the ancillary ligand in the order two hydrides > hydride > hydrazide > THF ≅ bis[(trimethylsilyl)methyl].

Strong evidence is found that the M–H₂ interaction is Kubas type. We have identified orbitals showing the synergic components of the Kubas bond, i.e. σ-donation from H₂ to the metal and π-back-donation from the metal to the dihydrogen, and AIM analysis indicates that the electron density at the bond critical points of the bound H₂ is similar to that of classical Kubas systems. Previously, with Ti(III), V(III) and Cr(III) systems, we found that the M–H₂ Kubas interaction is dominated by σ-donation from the H₂ to the metal. This is also the case for the present Cr(II) systems but is more balanced between σ-donation and π-back-donation for the Ti(II) and V(II) analogues. This difference in behaviour is traced to a lowering in energy of the metal 3d orbitals across the transition series.

Acknowledgements

We are grateful to the UCL Graduate School for a scholarship to CVJS, and for computing resources via UCL's Research Computing “Legion” cluster and associated services.

References

1. U.S.A. Department of Energy, Targets for Onboard Hydrogen Storage Systems for Light-Duty Vehicles, http://www1.eere.energy.gov/hydrogenandfuelcells/storage/pdfs/targets_onboard_hydro_storage_explanation.pdf.
2. T. K. A. Hoang and D. M. Antonelli, Adv. Mater., 2009, 21, 1787.
3. S. I. Orimo, Y. Nakamori, J. R. Eliseo, A. Zuttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111.
4. A. W. C. van den Berg and C. O. Arean, Chem. Commun., 2008, 668.
5. R. C. Lochan and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 1357.
6. J. L. C. Rowsell and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4670.
7. G. J. Kubas, J. Organomet. Chem., 2001, 635, 37.
8. G. J. Kubas, J. Organomet. Chem., 2009, 694, 2648.
9. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C71–C79.
10. J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939.
11. A. Hamaed, M. Trudeau and D. M. Antonelli, J. Am. Chem. Soc., 2008, 130, 6992.
12. A. Hamaed, T. K. A. Hoang, M. Trudeau and D. M. Antonelli, J. Organomet. Chem., 2009, 694, 2793.
13. A. Hamaed, H. Van Mai, T. K. A. Hoang, M. Trudeau and D. Antonelli, J. Phys. Chem. C, 2010, 114, 8651.
14. C. V. J. Skipper, A. Hamaed, D. M. Antonelli and N. Kaltsoyannis, J. Am. Chem. Soc., 2010, 132, 17296.
15. T. K. A. Hoang, A. Hamaed, G. Moula, R. Aroca, M. Trudeau and D. M. Antonelli, J. Am. Chem. Soc., 2011, 133, 4955.
16. T. K. A. Hoang, M. I. Webb, H. V. Mai, A. Hamaed, C. J. Walsby, M. Trudeau and D. M. Antonelli, J. Am. Chem. Soc., 2010, 132, 11792.
17. C. V. J. Skipper, T. K. A. Hoang, D. M. Antonelli and N. Kaltsoyannis, Chem.–Eur. J., 2012, 18, 1750.
18. J. J. Purewal, J. B. Keith, C. C. Ahn, B. Fultz, C. M. Brown and M. Tyagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 054305.
19. A. Hamaed, T. K. A. Hoang, G. Moula, R. Aroca, M. L. Trudeau and D. M. Antonelli, J. Am. Chem. Soc., 2011, 133, 15434.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
22. Y. Y. Sun, K. Lee, L. Wang, Y. H. Kim, W. Chen, Z. F. Chen and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 073401.
23. H. Lee, M. C. Nguyen and J. Ihm, Solid State Commun., 2008, 146, 431.
24. C. G. Zhang, R. W. Zhang, Z. X. Wang, Z. Zhou, S. B. Zhang and Z. F. Chen, Chem.–Eur. J., 2009, 15, 5910.
25. A. Mavrandonakis, E. Klontzas, E. Tylianakis and G. E. Froudakis, J. Am. Chem. Soc., 2009, 131, 13410.
26. W. Zhou, T. Yildirim, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085434.
27. Y. F. Zhao, Y. H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2005, 94, 155504.
28. H. Lee, W. I. Choi and J. Ihm, Phys. Rev. Lett., 2006, 97, 056104.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.2), Gaussian, Inc., Wallingford, CT, 2009.
30. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639.
31. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
32. A. J. Wachters, J. Chem. Phys., 1970, 52, 1033.
33. P. J. Hay, J. Chem. Phys., 1977, 66, 4377.
34. K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062.
35. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. Schleyer, J. Comput. Chem., 1983, 4, 294.
36. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265.
37. T. A. Keith, AIMALL, Revision 11.04.03, TK Gristmill Software, Overland Park KS, USA, 2011 (aim.tkgristmill.com).
38. G. T. Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
39. C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391.
40. ADF, Revision 2009.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2009.
41. R. C. Raffenetti, J. Chem. Phys., 1973, 59, 5936.
42. D. P. Chong, Can. J. Chem., 1995, 73, 79.
43. G. D. Zeiss, W. R. Scott, N. Suzuki, D. P. Chong and S. R. Langhoff, Mol. Phys., 1979, 37, 1543.
44. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142.
45. D. P. Chong, E. Van Lenthe, S. Van Gisbergen and E. J. Baerends, J. Comput. Chem., 2004, 25, 1030.
46. H. A. Sparkes, A. B. Chaplin, A. S. Weller and J. A. K. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 503.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2dt30383c

‡ XRD shows broad, low-intensity reflections from 2θ = 30 to 35° that do not correspond to any known Cr–N phase.

§ The molecular BSRs we employ feature a combination of formally neutral, two-electron donor hydrazine (NH₂NH₂) and formally monoanionic, one-electron donor hydrazide (NHNH₂) ligands. By varying the number of the former, we can alter the coordination number of the metal whilst leaving the oxidation state unaltered. Whilst recognising that quantum chemically calculated partial charges never mimic formal charges exactly, Table S1† presents the charges on parts of the Cr(II) BSR shown in Fig. 3B. It is clear that the formally anionic hydride and hydrazide ligands carry a significantly negative partial charge, while the hydrazine ligands have an overall, smaller positive charge. In this manuscript we use the term “hydrazine-based” to refer to ligand environments containing both hydrazine and hydrazide ligands, specifying the number of each where necessary.

¶ The decrease is some way short of the experimental Raman value (2285 cm⁻¹). However, since these spectra were acquired at atmospheric pressure where the hydrogen binding is minimal and the zero coverage enthalpies generally lower than 20 kJ mol⁻¹, the Raman band may represent binding of H₂ to a very small number of high enthalpy binding sites that do not represent the bulk sample.

---