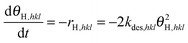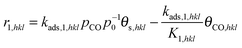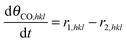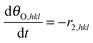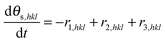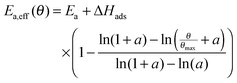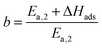On the interaction of carbon monoxide with ternary Cu/ZnO/Al2O3 catalysts: modeling of dynamic morphological changes and the influence on elementary step kinetics†
Received
29th March 2012
, Accepted 29th May 2012
First published on 2nd July 2012
Abstract
This paper focuses on gas-phase induced dynamic morphological changes of the catalyst, in particular by carbon monoxide. Those structural changes are studied in terms of hydrogen temperature-programmed desorption (TPD) from carbon monoxide pre-treated surfaces. Modeling the hydrogen TPD from the pre-treated catalyst shows activation of Cu(110) and Cu(100) planes. This is in good agreement with previously shown morphological changes in different gas atmospheres observed from in situ EXAFS and TEM measurements and observed transient maxima of methanol synthesis upon CO pre-treatment which has been reported in the literature. The obtained hydrogen desorption energies for the respective copper surfaces are physically reasonable. This surface heterogeneity is further implemented in a microkinetic model to describe the temperature-programmed surface reaction (TPSR) between carbon monoxide and adsorbed oxygen. It is found that a logarithmic coverage-dependence on adsorbed oxygen is essential for obtaining good agreement between simulation and experiment. For high oxygen loadings the apparent activation energy is essentially constant, which is in good agreement with literature results.
Introduction
Nowadays, methanol counts among the top ten basic chemicals and becomes even more important as a chemical energy carrier.1,2 With receding coal and gas reserves methanol can act as an alternative way for energy storage and directly as a fuel.1 Methanol is commercially produced via synthesis gas (CO2, CO and hydrogen) over Cu/ZnO/Al2O3 catalysts. Hereby, methanol is mainly produced by the hydrogenation of carbon dioxide.3–5 However, typically carbon monoxide is not separated from carbon dioxide, but can be converted to carbon dioxide by the water-gas-shift reaction. This suppresses the formation of water, which is known to inhibit the methanol production and to enhance deactivation of the catalyst.6,7 Copper particles have been identified as active sites8,9 and are known to undergo dynamic morphological changes, depending on the gas atmosphere.10–14 Wilmer and Hinrichsen14 and later Vesborg et al.13 found that the methanol production rate strongly depends on the pre-treatment conditions. Treatment with carbon monoxide before methanol synthesis leads to a transient maximum in methanol production. This dynamic effect was also observed by the development of highly sensitive in situ methods, such as Extended X-ray Absorption Fine Structure (EXAFS) and Transmission Electron Microscopy (TEM) measurements.10–13 From these experiments it was proposed that the morphological changes of metallic copper are mainly attributed to the Cu/ZnO interface energy. Clausen et al.10 used the Wulff construction to relate the equilibrium shape of the fcc particles to the contact surface free energy. This concept was later incorporated into a microkinetic model for the methanol synthesis.15,16 Subsequently, Hansen et al.12 and Vesborg et al.13 quantified these effects by calculating the energy changes with data extracted from in situ TEM measurements. The gas environment is not only responsible for changes in surface area but also for changes in the ratio of different surface facets. The microkinetic model proposed by Ovesen et al.16 has incorporated different rates for methanol synthesis over the three low-index planes Cu(111), Cu(110) and Cu(100). It is assumed that a change in the ratio of those planes may also enhance the methanol productivity.
Besides EXAFS and TEM measurements temperature-programmed (TP) experiments, i.e. TP adsorption and TP desorption, have always been a subject of great interest for catalyst characterization and also for extraction of parameters for elementary step kinetics.17–22 A profound survey can be found in the case of copper catalysts in the literature.23–28 First, UHV methods were applied to extract the kinetics of the sorption processes, later flow set-ups under ambient pressure were used to quantify the energies of adsorption and desorption. However, this was not the only subject of interest, as Muhler et al.25,29 established the hydrogen temperature-programmed desorption as a tool to quantify the active copper surface area. This method was found to be more mild and less destructive, compared to the widely used N2O frontal chromatography.30,31 Wilmer and Hinrichsen14 used the hydrogen desorption from the copper catalyst to study dynamic changes in the catalyst. The catalyst was pre-treated by flushing it with either synthesis gas or carbon monoxide before dosing the hydrogen. With synthesis gas a symmetrical TPD signal was observed, whereas for different CO/He pre-treatment the signal became asymmetrical in shape, being more significant for longer pre-treatment times. A second shoulder was assigned to a different surface site, evolving with a severe reducing pre-treatment.14
This paper studies the interaction of carbon monoxide with the ternary copper catalyst. Numerical procedures are used to quantitatively evaluate the effect of catalyst pre-treatment with carbon monoxide. Simple kinetics and the ratio of exposed copper facets are extracted from those experiments, which provide interesting information in addition to the in situ measurements by Hansen et al.12 and Vesborg et al.13 In a second part, the kinetics of carbon monoxide oxidation to carbon dioxide, an important elementary step for the methanol synthesis or water-gas shift reaction,15,16,32–34 is studied in great detail, giving a relation for the coverage-dependence of carbon monoxide oxidation.
Experimental and computational details
The fixed-bed reactor can be modeled either as a continuously stirred-tank reactor (CSTR) or as a plug flow reactor (PFR), within the limits of total and negligible back-mixing in the catalytic bed. The corresponding equations for the CSTR and PFR are given as:26,35| |  | (1) |
| |  | (2) |
The overall rate rtotal,i for a specific compound describes the averaged rate over different catalytic active surface planes.
In a previous study we already showed that the hydrogen TPD from the copper catalyst under the evaluated conditions can safely be treated using a CSTR reactor model.26 The calculations concerning the TPSR of carbon monoxide and adsorbed oxygen to yield carbon dioxide were performed with both reactor models to rule out a reactor model limitation.
Surface species are further calculated by an ordinary differential equation:
| |  | (3) |
MATLAB® R2010b was used to solve the governing equations. MATLAB® comprises a built-in sparse system ODE solver (ode15s). The absolute tolerances were set to a value of 10
−10. For the PFR reactor model partial differential equations were discretized by the methods of lines,
36 using a backward differences scheme. Numerical convergence and mass conservation were tested for all models. For fittings, either the MATLAB® nonlinear least-squares fitting “lsqnonlin” or the constrained nonlinear optimization “fmincon” was implemented. The “fmincon” routine can solve optimization problems including both linear and nonlinear bound constraints. The termination tolerance on the function value was chosen to be 10
−15. For each experiment a well defined temperature interval was chosen. For the hydrogen desorption experiments,
experimental data from the onset to the end of the signal were included in the objective function, as the signals became highly unsymmetrical upon treatment with CO/He.
14 However, for the TPSR experiments a fit around the maximum of the mole fraction of CO
2 in the outlet flow was used in order to avoid limitations by the tailing of the experimental signal.
26,37
The quality of the respective model fit was evaluated by introducing a dimensionless scaled root mean square error between the experimental value f1 and the modeling result f2:
| |  | (4) |
Here, the root mean square error is divided by the maximum experimental concentration in the outlet flow of the respective experiment,
Xref. For SRMSE values below 0.045 two responses are considered to be equal, corresponding to a deviation below experimental certainty.
35
The results for the pre-treated hydrogen temperature-programmed desorption experiments were taken from Wilmer and Hinrichsen.14 Before dosing the hydrogen, the catalyst was pre-treated with either methanol synthesis gas or CO/He at 493 K. An adsorbate-free surface was achieved by flushing the catalyst with He at 493 K. Subsequently, saturation coverage of hydrogen was achieved by dosing the hydrogen at 240 K and 15 bar for half an hour.24 The pressure was reduced to atmospheric pressure and the reactor was cooled to 78 K. Subsequent to an additional He treatment for 30 minutes, desorption flow experiments were initialized by changing the temperature linearly up to 493 K in the He flow.14
For the CO temperature-programmed surface reaction, experimental results were taken from Hinrichsen et al.37 Before each experimental run methanol synthesis was carried out overnight. Subsequently, the catalyst was flushed with He at 493 K to achieve an adsorbate-free surface. Saturation coverage of adsorbed oxygen (ΘO = 0.5) was then achieved by switching to N2O/He. Consequently the temperature was lowered to 78 K and the gas flow was changed to CO/He, followed by starting a linear temperature ramp to 300 K.37
Results
Part 1 – Dynamic behavior of the Cu/ZnO/Al2O3 catalyst
Fig. 1 shows the results for hydrogen TPD obtained by Wilmer and Hinrichsen14 (solid lines) subsequent to pre-treating the copper catalyst either with methanol synthesis gas or carbon monoxide in helium. Trace A shows the results for the catalyst pre-treated with methanol synthesis gas. This signal is very symmetrical and is equal in shape and Tmax position compared to experiments at full coverage, already presented elsewhere.26 Traces B, C and D were recorded after different times of CO/He pre-treatment. After one hour the amount of adsorbed hydrogen drops by about 13% and the shape becomes slightly asymmetrical (trace B). After 18 hours the amount further decreases and a second shoulder evolves (trace C). Finally after a severe treatment for 64 hours with CO/He, a second maximum can clearly be observed. These changes in symmetry were proven to be reversible.14 Hence, no irreversible surface reconstruction was observed. The unsymmetrical peaks suggest that desorption takes place from different active sites, comprising different desorption parameters. While the symmetric peak in trace A was often referred to desorption from mainly Cu(111),24,26,27 the low temperature shoulder (traces B–D) can be explained by a second crystal facet. Furthermore, the second maximum is shifted to higher temperatures at saturation coverage, which suggests that a third kind of active site is activated during such a pre-treatment.
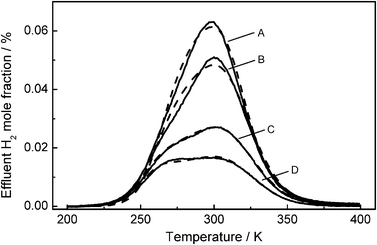 |
| | Fig. 1 Experimental H2 TPD spectra (solid lines) and simulated curves (dashed lines), after pre-treatment of the catalyst with CO/He for: (A) 0 h (SRMSE = 0.022), (B) 1 h (SRMSE = 0.027), (C) 18 h (SRMSE=0.014), (D) 64 h (SRMSE = 0.019). Experimental conditions: QHe = 100 Nml min−1, β = 6 K min−1, ωcat = 0.2 g, ΘH = 1. | |
Three different active sites were considered, for the Cu(111) facets kinetic values were taken from ref. 26 (see also Table 1). Hereby Nrtotal is given by:
| |  | (5) |
and
| |  | (6) |
Since it was already shown that re-
adsorption is negligible under the evaluated experimental conditions,
26 only desorption of hydrogen has to be considered, thus the rate for surface hydrogen reads in the case of recombinative desorption:
| | 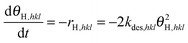 | (7) |
The mass conservation is given by:
| |  | (8) |
Hence, the specific moles
nH2,des,hkl desorbed from one surface plane can be calculated by the conservation law. To avoid unreasonable values the following constraint was implemented, using the “fmincon” fitting routine:
A more rigorous approach using the “lsqnonlin” fitting routine without this constraint leads to imaginary values during the first iterations but results in the same parameters at the end of the model fitting.
Fig. 1 compares experimental and modeled traces of the hydrogen desorption for different pre-treatments. Kinetic parameters for the unknown surfaces, which we assign to Cu(110) and Cu(100), and the specific mol number of desorbing hydrogen were subject of the model fit, yielding the kinetic parameters
Edes,100 = 63.7 kJ mol
−1 and
Edes,110 = 81.2 kJ mol
−1, respectively. All results are displayed in
Table 1. Hereby, we kept the Arrhenius factor of the desorption constant at 3.75 × 10
10 s
−1 (
=Ades,111), to avoid physical unreasonable values. In a recent paper we already showed that a proper choice of
Ades, while fitting
Edes, might lead to reasonable values for the desorption energy.
26 In order to determine which sites are evolving, hydrogen desorption experiments under UHV from different low-index planes by Anger
et al.23 are analyzed, in particular the
Tmax position of the desorption maxima. In their study the
Tmax positions at full coverage follow the order Cu(100) < Cu(111) < Cu(110). Since the signal for a fresh or syngas treated polycrystalline copper
catalyst was previously attributed to show Cu(111) desorption kinetics,
24,26,27 it can be concluded that the high temperature hydrogen signal is caused by hydrogen desorbing from Cu(110) surface sites. In the study of Anger
et al.23 the evaluation of Cu(100), on the other hand, was not possible due to complex surface reconstruction processes. However, the position of
Tmax at full coverage indicates that Cu(100) planes are most likely responsible for the low temperature maximum in our study. Limitations by surface reconstruction were not observed for the evaluation method presented in this study, since all experiments were reversible and even the spectra under most reducing conditions could be reproduced in good agreement.
14 Therefore, it is straightforward to conclude that the extracted parameters with the higher activation energy should be attributed to Cu(110) surface planes, whereas the low energy maximum is caused by exposed Cu(100) planes. As can be seen modeled and measured
spectra are in great agreement. This is also indicated by SRMSE values below 0.03. It should be mentioned that it was not possible to properly describe all signals with only one new type of crystal plane. Besides Cu(111), two more crystal facets are needed to describe the desorption. As an example,
Fig. 2 summarizes the contribution of each surface plane to the overall signal. Here, Cu(110) has the lowest fraction, followed by Cu(100). For all pre-treatments, Cu(111) has the highest fraction.
Fig. 3 shows the trend for the distribution of active sites for the different surface planes, calculated from the amount of desorbed hydrogen (see also
Table 1). The amount of Cu(111) drops with longer exposure to CO/He, while the amount of Cu(110) first rises and slightly drops after 18 hours. The amount of Cu(100), however, rises steadily for all experiments, with a higher slope at a lower pre-treatment time.
Table 1 Parameters derived from hydrogen TPD with different CO/He pre-treatment times
| Parameter |
Value |
95% confidence interval |
Fraction |
|
Values taken from ref. 26.
|
|
E
a,111
a (kJ mol−1) |
75−5.5 θH2.6 |
— |
— |
|
E
a,110 (kJ mol−1) |
81.2 |
±0.2 |
— |
|
E
a,100 (kJ mol−1) |
63.7 |
±0.1 |
— |
|
n
H2,des,111,1h (μmol) |
20.7 |
±0.2 |
0.88 |
|
n
H2,des,100,1h (μmol) |
1.0 |
±0.1 |
0.04 |
|
n
H2,des,111,18h (μmol) |
11.3 |
±0.1 |
0.77 |
|
n
H2,des,100,18h (μmol) |
1.8 |
±0.1 |
0.12 |
|
n
H2,des,111,64h (μmol) |
7.1 |
±0.1 |
0.72 |
|
n
H2,des,100,64h (μmol) |
1.9 |
±0.04 |
0.19 |
 |
| | Fig. 2 Experimental H2 TPD spectrum (black) and simulated curves (grey), after pre-treatment of the catalyst with CO/He for 18 h, contributions from different copper facets: Cu(111) dashed, Cu(100) dotted and Cu(110) dashed dotted. Experimental conditions: QHe = 100 Nml min−1, β = 6 K min−1, ωcat = 0.2 g, ΘH = 1. | |
 |
| | Fig. 3 Morphological change due to different long pre-treatments of the catalyst with CO/He, ■ Cu(111), □ Cu(100) and ● Cu(110). | |
Part 2 – Temperature-programmed surface reaction
Hinrichsen et al.37 investigated the CO oxidation over the ternary copper catalyst. The CO oxidation was determined to be the rate determining/slow step during the water-gas shift and methanol synthesis reaction.15,16,32–34 The following reaction scheme was implemented to describe the surface reaction:| | | CO(g) + shkl ⇌ COshkl | (reaction 1) |
| | | COshkl + Oshkl ⇌ CO2shkl + shkl | (reaction 2) |
| | | CO2shkl ⇌ CO2(g) + shkl | (reaction 3) |
All reactions are part of the redox mechanism and equilibrium reactions.15,16,32–34 First, carbon monoxide adsorbs on the surface site shkl. The oxygenated surface was achieved by the method described before. Subsequently, the surface reaction proceeds via a Langmuir–Hinshelwood mechanism.38,39 After the reaction, carbon dioxide desorbs and is removed by the purging gas. The kinetics for the sorption steps 1 and 3 are calculated by means of collision theory, assuming non-activated adsorption. The site density for the surface atoms is taken from Evans et al.40 For carbon monoxide a sticking coefficient of one was used, also suggested by Domagala and Campbell41 and Cox and Schulz.42 For the molecular adsorption of carbon dioxide a sticking coefficient of one is assumed.43 However, calculations with varying Arrhenius parameters of several magnitudes did not show any deviations for the resulting TPSR signals, neither for carbon monoxide nor for carbon dioxide. The equilibrium constants couple the rate constants in forward and reverse directions as follows:| |  | (10) |
For steps 1–3, the equilibrium constants are calculated by means of statistical thermodynamics.44,45 Especially for the water-gas shift and methanol reaction this was explained in great detail elsewhere.15,16,32–34 In our model the respective thermodynamic input for the partition functions was taken from ref. 16 and 32 (see also ESI†).
This yields the following reaction rates for step 1 through 3:
| | 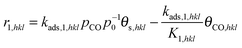 | (11) |
| |  | (12) |
| |  | (13) |
Now it is straightforward to define the differential equations for the surface species:
| | 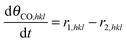 | (14) |
| |  | (15) |
| | 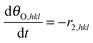 | (16) |
The corresponding equation for the uncovered sites reads:
| | 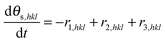 | (17) |
which can also be calculated by a site balance according to:
| |  | (18) |
At high coverages of educts often lower apparent
activation energies for reactions are observed. This apparent
activation energy
Ea,app is given by the true activation energy
Ea and the adsorption energy of the educts Δ
Hads:
Usually the adsorption enthalpy is negative, which means that the apparent activation energy is lowered by the modulus of Δ
Hads. In order to account for the coverage-dependent apparent
activation energy between the limits of
Ea,app and
Ea, a function in the form of
Ea,eff =
f(
Θ) is implemented. Keskitalo
et al.46 found the following mathematical expression to account for different types of dependencies:
| |  | (20) |
Here,
b represents the minimum of the function in the range of 0 ≤
Θ/
Θmax ≤ 1, which is reached when
Θ equals
Θmax, as shown in
Fig. 4. The factor
a describes the type of the dependence. For
a greater than one, the dependence is almost linear,
i.e. Temkin-like. The smaller the value of
a, the greater the range, where the apparent activation energy is almost constant. On the other hand, the transition area is shifted towards smaller coverages and steeper slopes. For lim
a → 0 a constant value of
b is obtained, whereas for
b = 1 always the maximum value is reached. A nonlinear coverage relationship between the apparent and true
activation energy
Ea in the form of
can be formulated. Finally, coupling
eqn (20) and (21) yields the effective activation energy:
| | 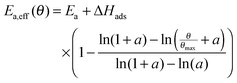 | (22) |
with
| | 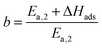 | (23) |
This equation can now be used to describe the behavior of the experimental data. The factor
a is, besides the kinetic parameters, subject of the model fit. However, only reasonable initial values for
a were chosen, indicated by Habraken
et al.47 who found an almost constant apparent
activation energy for wide ranges of
ΘO. This means that
a should be very small to describe the experimental behavior.
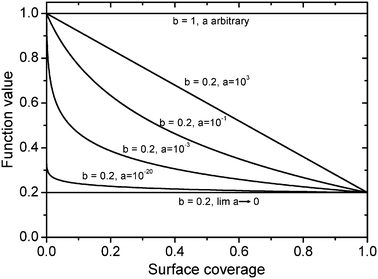 |
| | Fig. 4 Logarithmic coverage-dependence based on information given in ref. 46. | |
As indicated in part 1, different types of surface sites are involved in the kinetics when the catalyst is treated with a flow of carbon monoxide in helium. Therefore the contribution to the overall rate for gaseous species, rtotal,i, can be written as:
| | | rtotal,i = ηr100,i + εr110,i + (1 − η − ε)r111,i | (24) |
where
η is the ratio of sites on Cu(100) relative to the overall active sites and
ε is the ratio of sites on Cu(110) relative to the overall active sites and
rtotal,i can be interpreted as the average rate over an active site. Ovesen
et al.16 reported the kinetic parameters for the surface reaction (
reaction 2) for the three low-index surface planes Cu(111), Cu(110) and Cu(100). These values were used as a starting point. Keeping the ratio of the Arrhenius parameters for different active sites constant, the number of unknown kinetic parameters is lowered to only
A2,111 and
Ea,2,111. When keeping the ratios of
k2,hkl constant, essentially the same results were obtained. Furthermore, the fractions of the different surface sites were chosen to be 0.8 for Cu(111), 0.1 for Cu(110) and 0.1 for Cu(100). These numbers can be regarded as averaged extracted values from the pre-treated hydrogen desorption experiments after exposure to CO/He (see also part 1). Closer analysis of the kinetic constants found by Ovesen
et al.16 reveals that the Cu(100) structure has a much higher
activation energy compared to the other two low-index planes. On the other hand the modulus of the adsorption enthalpy is low compared to the Cu(110) structure, which increases the apparent activation energy (see also
eqn (19)). The higher
activation energy means that the CO
2 signal is shifted to temperatures around 300 K, which is not related to the signal of the experiments. Hinrichsen
et al.37 and Genger
48 suggested the investigation of the first signal; hence, we omitted this plane from our calculations, which could be confirmed by comparative simulations. The number of active sites per
catalyst weight,
N, was determined by Hinrichsen
et al.37 to be 236 μmol g
cat−1. This corresponds to a N
2O consumption rate of 118 μmol g
cat−1. However, only about 30% of the provided oxygen was converted to yield carbon dioxide.
37 Integration for the molar coverage of oxygen was done for each experiment up to 275 K, corresponding to the first maximum of the measurement.
37Table 2 gives an overview of the reactive oxygen and temperature intervals for SRMSE determination used in our computations. As a starting point, the
catalyst was initialized by half a monolayer of oxygen, for which the previously mentioned amount was set to be active for CO
oxidation. Furthermore at
t = 0 s the coverage of carbon monoxide was set to a value of
ΘCO = 0.5, which enhances the computational time significantly. This is physically reasonable for low starting temperatures,
i.e. T = 160 K, the adsorbed state is highly preferred. Reference calculations show a coverage of 0.5 way before the surface reaction starts, when the flow is switched from pure He to the CO/He mixture.
Table 2 Calculated amount of reactive oxygen for CO and O* TPSR and SRMSE intervals for analysis
| Heating rate (K min−1) |
6 |
10 |
15 |
|
n
O,reactive (μmol g−1) |
35.9 |
29.7 |
26.9 |
| SRMSE – Interval (K) |
160–240 |
160–250 |
160–250 |
Fig. 5 compares the respective simulated and experimental responses, by assuming complete back-mixing (CSTR). The PFR model yields the same signal of CO2 in the outlet flow, with an SRMSE value below 4 × 10−3, when comparing the modeled signals. As can be seen, the agreement between simulation and experiment is very high. This can be confirmed by SRMSE values below 0.04. The corresponding kinetic constants are listed in Table 3. The factor a results in a low value of 4.4 × 10−12, which was expected to accurately describe the experiments. Since no reaction takes place, the activation energy is low and constant at the beginning of the experiment (Fig. 6). The simulated CO2 signal ascends around T = 170 K and the activation energy for Cu(111) does not change by more than 10% until 90% of the reactive oxygen is removed via the surface reaction. Subsequently, the activation energy is further slightly rising. The remaining (reactive) oxygen coverage is about 5 × 10−5 on Cu(111), hence the apparent activation energy does not reach the limit Ea in our elevated temperature interval. The effective activation energy for Cu(111) is smaller than for Cu(110), thus the reaction first proceeds over Cu(111). At the end of the experiment, the signal levels off. This was mainly attributed to the CO oxidation by reduction of ZnO.48Fig. 7 shows the contributions from Cu(111) and Cu(110) and for completeness also Cu(100) planes, which are omitted in the calculation of the first maximum. It can be seen that the Cu(100) structure is not involved during the evaluated temperature range, but partly responsible for the tailing, resulting in a second maximum. However, this effect cannot be separated from ZnO reduction and therefore a discussion is not reasonable and the exception of this plane seems to be adequate.48Fig. 8 shows the coverage of the surface intermediates as a function of the temperature. It can clearly be seen that the second maximum is not due to re-adsorption of CO2 as the amount of adsorbed CO2 is very low, i.e. for β = 6 K min−1 and Cu(111) below 10−7. This can be explained by the highly competitive adsorption of carbon monoxide and the sorption equilibrium of carbon dioxide, the latter being almost complete on the gas phase for the evaluated temperature interval. The amount of adsorbed (reactive) oxygen drops when the temperature reaches about 170 K and the surface reaction starts. At the same time the coverage of carbon monoxide rises, which corresponds to strong adsorption at this temperature and the oxygen being irreversibly removed. Subsequently, the coverage of carbon monoxide starts to drop at a temperature around 250 K since at this temperature desorption of carbon monoxide quantitatively takes place.
 |
| | Fig. 5 Experimental TPSR of CO and O* spectra (solid) and simulated curves (dashed), using different heating rates, (A) β = 6 K min−1 (SRMSE = 0.038), (B) β = 10 K min−1 (SRMSE = 0.037), (C) β = 15 K min−1 (SRMSE = 0.021). Experimental conditions: QCO/He = 10 Nml min−1, ωcat = 0.2 g. | |
Table 3 Parameters derived from CO and O* TPSR at different heating rates
| Parameter |
Value |
95% confidence interval |
Re-parameterized |
|
E
a,2,111 (kJ mol−1) |
83.4 |
±1.6 |
83.4 |
| ln(A2,111) (s−1) |
15.4 |
±1.0 |
4.9 × 106 |
|
a = 10−parameter |
11.4 |
±1.3 |
4.4 × 10−12 |
|
E
a,2,110 (kJ mol−1) |
— |
— |
98.6 |
|
A
2,110 (s−1) |
— |
— |
8.0 × 106 |
|
E
a,2,100 (kJ mol−1) |
— |
— |
100.3 |
|
A
2,100 (s−1) |
— |
— |
8.0 × 106 |
 |
| | Fig. 6 Trend of apparent activation energy for Cu(111) (solid) and Cu(110) (dashed). Experimental conditions: QCO/He = 10 Nml min−1, β = 6 K min−1, ωcat = 0.2 g. | |
 |
| | Fig. 7 Experimental TPSR of CO and O* spectra (solid) and simulated curves. Contributions from different copper facets: Cu(111) dashed, Cu(100) dotted and Cu(110) dashed dotted. Experimental conditions: QCO/He = 10 Nml min−1, β = 6 K min−1, ωcat = 0.2 g. | |
 |
| | Fig. 8 Trend of surface coverages, ΘCO (solid, black), reactive ΘO (dashed, black) and ΘCO2 (solid, grey). Experimental conditions: QCO/He = 10 Nml min−1, β = 6 K min−1, ωcat = 0.2 g. | |
Discussion
In a recent paper the desorption kinetics from a ternary copper catalyst were studied in great detail.26 Hereby, it was found that the catalyst mainly exposed Cu(111) planes, which is consistent with other literature studies.24,27,28 Furthermore, we could show that a coverage-dependent activation energy can give a quantitative good fit for different hydrogen surface coverages as well as for a fresh and an aged catalyst. Hence it is straightforward to conclude that the (reversible) changes in the shape of the desorption spectra observed by Wilmer and Hinrichsen14 originate from a dynamic change of the copper catalyst. In our modeling approach we implemented two new copper facets to describe the experimental spectra. Upon carbon monoxide pre-treatment, Sakakini et al.49 proposed, besides Cu(110), an increasing fraction of Cu(211) being exposed. However, the Topsøe group used in situ methods, such as EXAFS and TEM, to study the dynamic changes in the catalyst morphology.10–13 They found the most stable surface planes being exposed to be (100), (110) and (111). Under reducing conditions, a reversible change in the exposed low-index copper facets was observed. These results were also described using the Wulff construction10 and could be implemented in a microkinetic model.16 Anger et al.23 studied the temperature-programmed desorption of hydrogen from copper single crystals under UHV conditions. Hereby, only kinetic values for Cu(111) and Cu(110) could be determined since surface reconstruction over Cu(100) limited their analysis. Coverage-dependent activation energies for Cu(111) and Cu(110) were found. In our calculations we did not include coverage-dependencies for the Cu(110) and Cu(100) planes. Therefore, the extracted parameters in Table 1 can be seen as mean values for the different surface planes and are well in the range of previously reported parameters for Cu(111).23,24,26–28 The trend for the exposed surface planes shows that under mild reaction conditions the catalyst mainly exposes Cu(111), while the catalyst undergoes morphological changes under strong reducing conditions, with increasing amounts of Cu(110) and Cu(100). This is consistent with previously observed transient methanol production rates.13,14 Reducing pre-treatments before methanol synthesis showed transient maxima in the methanol production. This can be correlated to our experiments by the findings of Ovesen et al.16 The different low-index planes have increasing activities in methanol synthesis, in the order Cu(111) < Cu(100) < Cu(110). We could show that a reducing pre-treatment increases the amount of the highly active 110 and 100 structures, which leads to a higher methanol production rate.16 This is independent of the proposed highly active ZnOx, which additionally enhances the methanol production rate.11,14 The results are also in good qualitative agreement with the surface plane distribution calculated by the Wulff construction.10,16 The crystal structure is described depending on the contact-surface free energy and the gaseous environment, however, with the limitation that it is always restricted by one copper low-index plane bound to the ZnO interface and the surface free energies of the unbound facets used in the Wulff construction of the crystal. For 64 h pre-treatment almost similar ratios of exposed copper planes under reducing conditions (γ/γ0 < 0) can be found. Only for extremely low values of γ/γ0 the ratios are remarkably different. Except for these low values of the contact-surface free energy, the Cu(111) plane always exhibits a higher fraction than Cu(110) and Cu(100), which is consistent with our results. However, Vesborg et al.13 found that only a mixture of hydrogen and carbon monoxide may lead to extremely low values of γ/γ0. Under working conditions copper binds to the substrate via all kinds of planes, suggesting that the real crystal structure is a mixture of all planes being able to bind to ZnO. Our ratios are extracted under working conditions; therefore one may conclude that they can be interpreted as mean values. Hansen et al.12 found activation of Cu(100) in a carbon monoxide atmosphere, which is in good agreement with our experiments with increasing pre-treatment time of up to 64 h. This long pre-treatment may be assigned to an equilibrated reconstruction, as the shape of a 62 h and 64 h pre-treated catalyst is essentially constant.14
The parameter estimation of the carbon monoxide pre-treatment shows great agreement between experiment and simulation. The shapes and the position of the temperature maximum are reproduced quite exactly. The assumption of coverage-independent adsorption enthalpies may explain the small deviations at the onset of the signal for all spectra. At the beginning of the experiments, the catalytic active surface is completely covered with oxygen and carbon monoxide. This limiting case leads to a maximum interaction between the adsorbed molecules, leading to different influences on the binding of the adsorbates, which may also influence the adsorption energy. However, this assumption did not influence the quality of the extracted data. The pre-exponential factor extracted in this study is in reasonable agreement with a factor of 6 × 105 s−1 to 1 × 106 s−1, determined by Genger,48 assuming pseudo first-order kinetics and plotting ln(T2max/β) against 1/Tmax. The introduced logarithmic coverage-dependence of the activation energy leads to a behavior described by Habraken et al.,47 where the apparent activation energy was found to be essentially constant for a large range of ΘO. Fig. 7 shows the contributions of the different surface planes to the signal in the outlet flow. Only Cu(111) and Cu(110) contribute to the measured signal, the tailing is mainly caused by ZnO reduction and surface reaction over Cu(100). However, as these two effects cannot be separated, they are not taken into account in this study. Besides, the lower reactivity over Cu(100) was already outlined before.47,50–52 The second shoulder could also be caused by re-adsorption effects. However, as seen in Fig. 8, the surface concentration of carbon dioxide is very low (<1 × 10−7). This is caused by a highly competitive adsorption between carbon monoxide and dioxide. The equilibrium of gas-phase and adsorbed carbon dioxide is almost completely on the gas phase for evaluated temperatures. The activation energy of the oxidation step over Cu(111) is with a value of 83.4 ± 1.6 kJ mol−1 in reasonable agreement with values obtained in previous studies.37,48,51,53,54 Habraken et al.51 determined a value of 79 to 84 kJ mol−1, independent of the crystal structure. Gokhale et al.54 calculated a value of 79 kJ mol−1 for Cu(111), using density functional theory. Nakamura et al.,53 Hinrichsen et al.,37 Genger48 and Habraken et al.47 reported apparent activation energies in the range of 28 to 33.5 ± 2.5 kJ mol−1, which makes it difficult to compare. However, when we use eqn (19) to calculate the apparent activation energy of Cu(111) for our experiments we obtain a value of 34.4 ± 1.6 kJ mol−1 in reasonable agreement with previously reported ones. Campbell and Ernst55 reported a value of 79 kJ mol−1 for Cu(110) comparable to Cu(111), however Ovesen et al.16 later introduced structure sensitivity in their microkinetic model of methanol synthesis. They reported a very low activation energy for Cu(111) of 72 kJ mol−1 and activation energies being 13 and 15 kJ mol−1 higher for Cu(110) and Cu(100) compared to their value for Cu(111). We used this difference in reactivity as model basis. The activation energies of Cu(100) and Cu(110) presented here are higher than reported in the literature, but both signals are subject to tailing effects, which originate from the reduction of zinc oxide, and their fraction on the overall active surface is very low in our calculations. Therefore, we constrained the model only to optimize the Arrhenius parameters with respect to the Cu(111) plane. The results are still reasonable when only Cu(111), corresponding to equal kinetics for all low-index planes, is considered (indicated by Fig. 7). The differences in the resulting Arrhenius parameters are in the range of the parameter confidence intervals.
To summarize, the experimental approach by Wilmer and Hinrichsen,14 combined with the evaluation presented here may act as a simple fingerprint method to investigate the intrinsic activity of different methanol synthesis catalysts. Since methanol synthesis comprises structure sensitive reaction steps,16,56e.g. the oxidation of carbon monoxide, the distribution of the different copper surface planes is supposed to have a significant influence on the catalysts activity. Recently, Kaluza et al.57 studied a novel synthesis route for ternary copper catalysts. Their continuous approach led to a catalyst which showed a 50% higher copper area-related activity than the commercial reference catalyst employed in their study. It would be interesting to study these catalysts by our method in order to understand the differences in the methanol synthesis activity regarding structure–activity relationship. Moreover, other pre-treatments than CO/He could reveal even further reconstruction effects, i.e. a mixture of CO and H2, as suggested by Vesborg et al.13 Concerning the deactivation behavior of catalysts for methanol synthesis, pre-treatments with oxidizing gases, i.e. carbon dioxide or water, and subsequent evaluation as presented here may further guide experiments to design a more stable catalyst for methanol synthesis.
Conclusions
Temperature-programmed flow experiments were used to model the interaction of carbon monoxide with a ternary copper catalyst under ambient pressure. CO/He treatment prior to hydrogen temperature-programmed desorption experiments showed that the copper catalyst undergoes dynamic morphological changes. Cu(100) and Cu(110) were found to be activated during such a procedure, with slightly different desorption parameters than on Cu(111). The ratio of the exposed surface planes changes during such a pre-treatment, which is in good agreement with the maximum in the methanol production rate. The kinetics of carbon monoxide oxidation over different copper low-index planes, an important step in water-gas shift and methanol synthesis reaction, was studied in some detail and exhibited a logarithmic coverage-dependence on oxygen. The new parameters of hydrogen desorption and the surface reactions could enhance the performance of microkinetic models, especially when experimental conditions are changed and different crystal surfaces are involved. The extracted parameters may help to enhance the bridging of the pressure and material gaps between UHV and industrially important process conditions.
Symbols used
|
A
| Arrhenius factor [s−1] |
|
c
| concentration [mol m−3] |
|
E
a
| activation energy [kJ mol−1] |
|
E
a,app
| apparent activation energy [kJ mol−1] |
|
E
a,eff
| effective activation energy at specific coverage [kJ mol−1] |
|
f
1/2
| experimental/modeling result [mol%] |
|
hkl
| Miller indices [–] |
|
j
| running variable [–] |
|
k
| reaction rate constant, forward (+), reverse (−) [s−1] |
|
K
| equilibrium constant [–] |
|
L
| length of the reactor bed [m] |
|
N
| coverage/number of active sites per catalyst weight [μmol gcat−1] |
| No | Number of data points [–] |
|
n
H2,des
| amount of hydrogen desorbed [μmol] |
|
p
i
| partial pressure [Pa] |
|
p
0
| thermodynamic reference pressure [Pa] |
|
R
| ideal gas constant [J mol−1 K−1] |
|
r
| reaction rate [s−1] |
|
T
| temperature, at peak maximum (max) [K] |
|
t
| time [s] |
|
u
| superficial velocity [m s−1] |
|
X
ref
| reference value [mol%] |
|
x
| dimensionless reactor coordinate [–] |
Greek symbols
|
β
| heating rate [K min−1] |
|
ε
b
| bed porosity [–] |
|
ε
| fraction of Cu(110) [–] |
|
η
| fraction of Cu(100) [–] |
|
ρ
p
| particle density [kg m−3] |
|
τ
| residence time [s] |
|
Θ
| degree of coverage [–] |
|
ν
i,j
| stoichiometric coefficient [–] |
|
ω
cat
| catalyst weight [gcat] |
References
- G. A. Olah, Angew. Chem., Int. Ed., 2005, 44, 2636–2639 CrossRef CAS.
-
J. B. Hansen and P. E. Højlund Nielsen, in Handbook of Heterogeneous Catalysis, eds. G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Wiley-VCH, 2008, vol. 6, pp. 2920–2949 Search PubMed.
- G. C. Chinchen, P. J. Denny, D. G. Parker, M. S. Spencer and D. A. Whan, Appl. Catal., 1987, 30, 333–338 CrossRef CAS.
- G. Liu, D. Willcox, M. Garland and H. H. Kung, J. Catal., 1985, 96, 251–260 CrossRef CAS.
- M. Muhler, E. Törnqvist, L. P. Nielsen, B. S. Clausen and H. Topsøe, Catal. Lett., 1994, 25, 1–10 CrossRef CAS.
- H. H. Kung, Catal. Today, 1992, 11, 443–453 CrossRef CAS.
- M. Sahibzada, I. S. Metcalfe and D. Chadwick, J. Catal., 1998, 174, 111–118 CrossRef CAS.
- G. C. Chinchen, K. C. Waugh and D. A. Whan, Appl. Catal, 1986, 25, 101–107 CrossRef CAS.
- W. X. Pan, R. Cao, D. L. Roberts and G. L. Griffin, J. Catal., 1988, 114, 440–446 CrossRef CAS.
- B. S. Clausen, J. Schiøtz, L. Grabaek, C. V. Ovesen, K. W. Jacobsen, J. K. Nørskov and H. Topsøe, Top. Catal., 1994, 1, 367–376 CrossRef CAS.
- J. D. Grunwaldt, A. M. Molenbroek, N. Y. Topsøe, H. Topsøe and B. S. Clausen, J. Catal., 2000, 194, 452–460 CrossRef CAS.
- P. L. Hansen, J. B. Wagner, S. Helveg, J. R. Rostrup-Nielsen, B. S. Clausen and H. Topsøe, Science, 2002, 295, 2053–2055 CrossRef CAS.
- P. C. K. Vesborg, I. Chorkendorff, I. Knudsen, O. Balmes, J. Nerlov, A. M. Molenbroek, B. S. Clausen and S. Helveg, J. Catal., 2009, 262, 65–72 CrossRef CAS.
- H. Wilmer and O. Hinrichsen, Catal. Lett., 2002, 82, 117–122 CrossRef CAS.
- T. S. Askgaard, J. K. Nørskov, C. V. Ovesen and P. Stoltze, J. Catal., 1995, 156, 229–242 CrossRef CAS.
- C. V. Ovesen, B. S. Clausen, J. Schiøtz, P. Stoltze, H. Topsøe and J. K. Nørskov, J. Catal., 1997, 168, 133–142 CrossRef CAS.
- A. M. de Jong and J. W. Niemantsverdriet, Surf. Sci., 1990, 233, 355–365 CrossRef CAS.
-
J. A. Dumesic, D. F. Rudd, L. M. Aparicio, J. E. Rekoske and A. A. Treviño, The Microkinetics of Heterogeneous Catalysis, ACS Professional Reference Book, 1993 Search PubMed.
- J. L. Falconer and J. A. Schwarz, Catal. Rev., 1983, 25, 141–227 CAS.
- J. B. Miller, H. R. Siddique, S. M. Gates, J. N. Russell Jr., J. T. Yates Jr., J. C. Tully and M. J. Cardillo, J. Chem. Phys., 1987, 87, 6725–6732 CrossRef CAS.
-
J. W. Niemantsverdriet, Spectroscopy in Catalysis, Wiley-VCH, 2007 Search PubMed.
-
O. Hinrichsen, in Handbook of Heterogeneous Catalysis, eds. G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Wiley-VCH, 2008, vol. 3, pp. 1543–1560 Search PubMed.
- G. Anger, A. Winkler and K. D. Rendulic, Surf. Sci., 1989, 220, 1–17 CrossRef CAS.
- T. Genger, O. Hinrichsen and M. Muhler, Catal. Lett., 1999, 59, 137–141 CrossRef CAS.
- M. Muhler, L. P. Nielsen, E. Törnqvist, B. S. Clausen and H. Topsøe, Catal. Lett., 1992, 14, 241–249 CrossRef CAS.
- M. Peter, J. Fendt, H. Wilmer and O. Hinrichsen, Catal. Lett., 2012, 142, 547–556 CrossRef CAS.
- J. Tabatabaei, B. H. Sakakini, M. J. Watson and K. C. Waugh, Catal. Lett., 1999, 59, 143–149 CrossRef CAS.
- H. Wilmer, T. Genger and O. Hinrichsen, J. Catal., 2003, 215, 188–198 CrossRef CAS.
- O. Hinrichsen, T. Genger and M. Muhler, Chem. Eng. Technol., 2000, 23, 956–959 CrossRef CAS.
- G. C. Chinchen, C. M. Hay, H. D. Vanderwell and K. C. Waugh, J. Catal., 1987, 103, 79–86 CrossRef CAS.
- J. J. F. Scholten and J. A. Konvalinka, Trans. Faraday Soc., 1969, 65, 2465–2473 RSC.
-
C. V. Ovesen, PhD thesis, Technical University of Denmark, 1992.
- C. V. Ovesen, B. S. Clausen, B. S. Hammershshøi, G. Steffensen, T. Askgaard, I. Chorkendorff, J. K. Nørskov, P. B. Rasmussen, P. Stoltze and P. Taylor, J. Catal., 1996, 158, 170–180 CrossRef CAS.
- C. V. Ovesen, P. Stoltze, J. K. Nørskov and C. T. Campbell, J. Catal, 1992, 134, 445–468 CrossRef CAS.
- J. M. Kanervo, T. J. Keskitalo, R. I. Slioor and A. O. I. Krause, J. Catal., 2006, 238, 382–393 CrossRef CAS.
-
A. Löwe, Chemische Reaktionstechnik, Wiley-VCH, 2001 Search PubMed.
- O. Hinrichsen, T. Genger and M. Muhler, Stud. Surf. Sci. Catal., 2000, 130, 3825–3830 CrossRef.
- K. I. Choi and M. A. Vannice, J. Catal., 1991, 131, 22–35 CrossRef CAS.
- O. P. Van Pruissena, M. M. M. Dingsa and O. L. J. Gijzemana, Surf. Sci., 1987, 179, 377–386 CrossRef.
- J. W. Evans, M. S. Wainwright, A. J. Bridgewater and D. J. Young, Appl. Catal., 1983, 7, 75–83 CrossRef CAS.
- M. E. Domagala and C. T. Campbell, Catal. Lett., 1991, 9, 65–70 CrossRef CAS.
- D. F. Cox and K. H. Schulz, Surf. Sci., 1991, 249, 138–148 CrossRef CAS.
- P. B. Rasmussen, P. A. Taylor and I. Chorkendorff, Surf. Sci., 1992, 269–270, 352–359 CrossRef CAS.
-
I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, 2003 Search PubMed.
-
T. L. Hill, An Introduction to Statistical Thermodynamics, Dover Publications, Inc, New York, 1986 Search PubMed.
- T. J. Keskitalo, M. K. V. Niemelae and A. O. I. Krause, Langmuir, 2007, 23, 7612–7619 CrossRef CAS.
- F. H. P. M. Habraken, E. P. Kieffer and G. A. Bootsma, Surf. Sci., 1979, 83, 45–59 CrossRef CAS.
-
T. Genger, PhD thesis, Ruhr-Universität Bochum, 2000.
- B. H. Sakakini, J. Tabatabaei, M. J. Watson and K. C. Waugh, J. Mol. Catal. A: Chem., 2000, 162, 297–306 CrossRef CAS.
- F. H. P. M. Habraken and G. A. Bootsma, Surf. Sci., 1979, 87, 333–347 CrossRef CAS.
- F. H. P. M. Habraken, C. M. A. M. Mesters and G. A. Bootsma, Surf. Sci., 1980, 97, 264–282 CrossRef CAS.
- P. B. Rasmussen, P. A. Taylor and I. Chorkendorff, Surf. Sci., 1992, 269–270, 352–359 CrossRef CAS.
- J. Nakamura, J. M. Campbell and C. T. Campbell, J. Chem. Soc., Faraday Trans., 1990, 86, 2725–2734 RSC.
- A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402–1414 CrossRef CAS.
- C. T. Campbell and K. Ernst, ACS Symp. Ser., 1992, 482, 130–142 CrossRef CAS.
- I. Nakamura, T. Fujitani, T. Uchijima and J. Nakamura, J. Vac. Sci. Technol., A, 1996, 14, 1464–1468 CAS.
- S. Kaluza, M. Behrens, N. Schiefenhövel, B. Kniep, R. Fischer, R. Schlögl and M. Muhler, ChemCatChem, 2011, 3, 189–199 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2cy20189e |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.