3D-QSPR models for predicting the enantioselectivity and the activity for asymmetric hydroformylation of styrene catalyzed by Rh–diphosphane

Abstract

This paper describes the development of quantitative structure–enantioselectivity and–activity relationships for the asymmetric hydroformylation of styrene by Rh–diphosphane. We used 3D steric- and electrostatic-type interaction fields derived from DFT calculations, and generated alignment-independent descriptors using GRid INdependent Descriptor (GRIND) methodology. The obtained QSPR models showed statistical significance and predictive ability. The most predictive model for enantioselectivity was obtained using steric-type 3D fields (MSF) based on the local curvature electron density isosurface that accounts for catalyst shape (r² = 0.92, q² = 0.68). We obtained the most predictive model for activity using a combination of shape- and electrostatic-based 3D fields (r² = 0.99, q² = 0.74). The use of chemically meaningful descriptors provides insight into the factors governing catalytic activity and selectivity. The worst predicted ligand, kelliphite, showed the lowest preference for equatorial–apical coordination and low selectivity, which suggests that its intrinsic enantiotopic differentiation capacity can be lost through the occurrence of bis-equatorial paths. The selective catalysts Rh–chiraphite, –binapine, –diazaphospholane, and –yanphos showed the same pattern as Rh–binaphos, for which the origin of stereoinduction is known: the chirality at the apical site discriminates one alkene coordination path and one enantiomer. Ligands with electron withdrawing groups at phosphorus atoms such as chiraphite, kelliphite, binaphos, and diazaphospholane reduce ligand basicity and promote catalytic activity effectively. However, more complex relationships underlie the origin of activity, and the shape of the catalyst also needs to be considered such as for the Ph-BPE ligand. Comparison with previous studies suggests that reduction of the steric hindrance at the reaction centre which favors alkene coordination and insertion would also promote catalytic activity.

---

Introduction

In asymmetric synthesis, hydrogenation is probably the most used, if not the only widely used, homogeneous catalytic process. Besides that, asymmetric hydroformylation (AHF) offers a potentially very useful synthetic route to enantiomerically pure aldehydes (Scheme 1), which can be used as precursors of biologically active compounds and fine chemicals.¹ Thus, much effort has been devoted during last few years to design efficient asymmetric catalysts. However, a broad applicability of the reaction is still a goal to achieve because of the intrinsic difficulties of controlling selectivity, and simultaneously, obtaining highly active catalysts. Most of the selective catalysts are based on Rh and chelating P-donor ligands, including C₁- and C₂-symmetric and diverse phosphorus groups. The most prominent ligands in AHF of styrene are the (2R,4R)-chiraphite² (1, see Fig. 1) diphosphite ligand, the (R,S)-binaphos³ (5) phosphane-phosphite, the diazaphospholane (7),^4a the (R,R)-Ph-BPE (13) diphospholane,^4b the (S,S)-binapine (6) and (S,S,R,R)-tangphos diphosphanes,⁵ and the yanphos phosphane phosphoramidite.⁶

Scheme 1

Fig. 1 Ligand dataset and catalytic outcome for asymmetric hydroformylation of styrene by rhodium complexes (%ee/%conv).

For establishing empirical relationships between catalyst structures and selectivity in hydroformylation, some researchers carried out systematic experimental studies on small ligand families that ideally vary in a single ligand variable.^7,8 For a series of biaryl-bridged diphosphite ligands, Klosin, Whiteker and co-workers found a linear relationship with the dihedral angle of bridging aryl moieties, which, in turn, correlates with the computed bite angles in the intermediates.^7a However, for a particular family of diphospholane ligands, the same type of correlation was unclear.^7b Klosin and co-workers explored a wider set and identified bis-phosphacycle structures as a promising class of ligands.⁵ Unfortunately, these studies did not provide clear insight into the factors governing enantioselectivity.

Computational studies on asymmetric hydroformylation are scarce. The first contributions considered binaphos and a series of C₂-symmetric diphosphane ligands by using semiquantitative “QM then MM” methods.⁹ Then, we provided for the first time quantitative theoretical assessment of the enantioselectivity in aminophosphane phosphinite (AMPP)¹⁰ and binaphos¹¹ systems by means of quantum mechanics/molecular mechanics (QM/MM) methods. Recently, Zhang and co-workers proposed a qualitative model based on MM calculations for the yanphos system.¹² In all these computational studies, enantioselectivity was assessed assuming that the alkene insertion into the Rh–H bond is the enantioselectivity-determining step. On the basis of these models and kinetic data, Landis and co-workers proposed a two-dimensional quadrant steric map for the qualitative rationalization of enantioselectivity for the Rh–(S,S,S)-bisdiazaphos catalyst.¹³ Recently, we extended this model to account for two possible alkene coordination paths, and provided quantitative measures of quadrant hindrance through the distance-weighted volume (V_W) descriptor for the Rh–binaphos catalyst.¹¹

Catalytic activity has been one of the most studied aspects of hydroformylation. We have recently shown that, in Rh–diphosphane catalyzed hydroformylation, the overall activity is determined by a set of reaction steps: CO dissociation, alkene coordination, and the final hydride migration.¹⁴ Thus, ligands that promote any of these steps may yield higher catalytic turnovers. Besides understanding the factors influencing the individual steps of the catalytic cycle, some systematic correlation studies attempted to establish relationships between ligand structure and catalytic activity. For monodentate P-donor ligands, it was experimentally shown that a relationship exists between ligand basicity and the activity of the catalyst; thus, the least basic phosphanes enhance the activity.¹⁵ This was attributed to the decreased electron density at the metal centre, which should facilitate CO/alkene exchange and the hydride migration.¹⁶ Theoretical studies had shown that electron-withdrawing ligands facilitate the hydride migration step.¹⁷ The contribution of back-donation to the metal–alkene bond is small, leading to facile rotation of the alkene moiety to reach the transition state (TS). For bidentate cyclic phosphanes, Pringle and co-workers found a correlation between the C–P–C angles and catalytic activity for a series of isoelectronic and isosteric ligands.¹⁸ The smaller ring size imposes small valence angles around the phosphorus atom, which seems to become a worse σ-donor and a better π-acceptor. In all these studies, differences in catalytic activity have been related to the electronic features of the ligands, setting aside their steric properties.

Our previous studies on AHF revealed that TS-based modelling has some limitations. We showed that QM/MM methods overestimate ligand–substrate interactions when stabilized arene–arene type interactions are involved, whereas full DFT calculations are unable to describe these noncovalent interactions.¹⁰ Moreover, for the Rh–binaphos system, the discrimination of one of the paths does not occur at the selectivity-determining step but at a previous step of the catalytic cycle, forcing to handle multiple kinetic scenarios.¹¹ Alternatively, more sophisticated computational approaches defined molecular descriptors from ground-state structures, to look for quantitative relationships between descriptors and enantioselectivity, in an analogous way to that of Quantitative Structure–Activity Relationship (QSAR) or –Property Relationship (QSPR) approaches used in drug design.¹⁹ One of the most attractive aspects of these methods is that they generate simple equations, which allow predicting catalytic activity or selectivity a priori. Although QSAR techniques are not of common use in homogenous catalysis, there are some outstanding examples that correlate catalytic activity and selectivity.²⁰

In asymmetric catalysis, the situation is even more challenging because the energy differences responsible for enantiomeric enrichment can be as low as 1–3 kcal mol⁻¹. Identification of quantitative structure–enantioselectivity relationships, in principle, accounting for 3D features of the chiral catalyst is needed in order to reflect its enantiotopic differentiation capacity. It is possible to use geometrical descriptors based on steric size,²¹ molecular topology,²² continuous chirality quantification methods²³ that indirectly account for 3-dimensionality, or 3D molecular interaction field (MIF) descriptors. Geometrical descriptors include easily accessible parameters from classical physical organic chemistry such as the Taft–Charton steric parameters,²¹ but these are only defined for some specific functional groups, so cannot be applied to more complex ligand architectures.

The MIF-based approaches became the standard 3D-QSAR methods used in drug design, the CoMFA (Comparative Molecular Field Analysis) approach being the most popular.²⁴ The generation of CoMFA descriptors involves three stages: (i) generation of the molecular structures; (ii) alignment of structures to obtain reproducible predictive spaces; and (iii) computation of the MIFs at each point of a 3D grid surrounding the molecule. Initially, those methods used MM-based interactions, but semiempirical²⁵ and QM²⁶ interaction energies have been also used. CoMFA-like approaches enabled obtaining fairly good results in some asymmetric catalytic processes as well.^25–27 For Rh–diphosphane AHF catalysis, we have shown that two different orientations of the catalysts are required to explain enantioinduction;¹¹ and consequently, it is not possible to apply an alignment-dependent approach straightforwardly because several alignment hypotheses should be combined simultaneously. Pastor and co-workers have introduced the GRid-INdependent Descriptors (GRIND), for which the alignment hypothesis is not required.²⁸ GRIND methods combined with empirical molecular interaction fields have shown their effectiveness in several asymmetric organometallic catalytic processes.²⁹ Similarly, we have developed a CoMFA-like alignment-independent (GRIND) protocol based on 3D molecular descriptors, which are derived from DFT calculations directly, named Q-QSSR.³⁰ A limitation of alignment-independent methodologies is the fact that molecular descriptors are not chiral, and thus unable to predict the absolute configuration of the product. Nevertheless, as we will show below, they are well suited to assess enantiomeric excess quantitatively.

Our recent research efforts have been aimed at rationalizing the enantioselectivity outcome in Rh-catalyzed hydroformylation for specific ligand families: AMPP¹⁰ and binaphos.¹¹ Herein, we introduce models for correlating catalyst structure with enantioselectivity and activity quantitatively for a set of 21 Rh–diphosphane catalysts. The dataset includes a variety of ligands that have different substituents, backbones and phosphane types. Our approach will combine the 3D alignment-independent protocol³⁰ together with our previous mechanistic knowledge.^{10,11,14,17,31} The use of chemically meaningful descriptors provides, in addition to the predictive models, chemical information to orient the design of ligands.

Theory and methods

Data set and structure generation

The data in this study are formed by a library of 21 Rh–diphosphorus catalysts, which were mainly obtained from ref. 5 (ligands 1–19), and thus we made sure that reactions were conducted in the same laboratory and under comparable conditions (solvent, temperature, catalyst loading, etc.). Additionally, we add two ligands (20 and 21) from ref. 32. The experimental conditions differ only slightly, and the catalysts can then be used to check the chemical meaning of the QSPR model and the descriptors by comparison with our previously obtained stereo-chemical models based on transition state determinations.¹⁰ Moreover, the selection shown in Fig. 1 encompasses wide enantioselectivity and activity ranges for the asymmetric hydroformylation of styrene by Rh–diphosphane complexes. Nevertheless, the number of catalysts in the dataset is relatively low; and this may cause chance correlations and overfitting in the QSPR models limiting their applicability. Unfortunately in the available experimental data (ref. 5), the catalysts with high selectivity constitute the smallest class. Therefore, we reduced the number of non-selective catalysts in order to avoid an imbalanced or biased dataset. Thus, the validation of the QSPR models should be carefully performed. The response variable for selectivity is the percentage of enantiomeric excess (ee) whereas for activity it is the percentage of conversion (conv). Fig. 1 shows these values in parentheses.

The molecular structures were obtained by means of quantum mechanics/molecular mechanics (QM/MM) calculations³³ using the ADF2006.01 package.³⁴ The QM part was [HRhCO(PH₃)₂] for diphosphane ligands, [HRhCO(P(OH)₃)₂] for diphosphite ligands, whereas the geometry of dissymmetric ligands (5, 20 and 21) was taken from our previous studies.^10,11 For the QM part, we selected the DFT method with the BP86 functional³⁵ and the TZP basis set.³⁶ SYBYL force field³⁷ was used to describe the atoms included in the MM part.³⁸ To search for conformational isomers, we defined a protocol based on restricted Molecular Dynamics (MD) simulations as implemented in the ADF software.³⁴ This protocol had been used successfully in our previous study of the Rh–binaphos catalyst¹¹ (see ESI† for details). The resulting lowest energy isomer was then used to compute the DFT-based molecular interaction fields.

3D-QSPR approach

We selected the 3D-QSPR approach developed by Bo and co-workers, Q-QSSR, which uses alignment-independent 3D descriptors derived from DFT calculations.³⁰ Once the 3D structures are obtained, we can divide the working protocol into four stages: (i) generation of the DFT molecular interaction fields; (ii) filtering of the grid points; (iii) computation of the molecular descriptors using GRIND methodology;²⁸ and (iv) multivariate analysis.

We firstly generated the molecular surface from the DFT-derived electronic density distribution by performing single point calculations at the BP86/TZP level on the structures. The molecular surface was defined by an electronic density isosurface at a value of 0.002 au in a rectangular grid of points, which expands 5 Å beyond molecular boundaries and spaces 0.2 Å. Then, at each of the points of the isodensity surface we computed two different fields: the Molecular Shape Field (MSF) and the Molecular Electrostatic Potential (MEP). The MSF is a geometrical parameter based on the local curvature of the isodensity surface and tries to account for steric effects of the catalyst.^28b The MEP tries to assess the electronic properties of the catalyst.

The number of surface data points (from ∼5000 to ∼20 000 depending on ligand size) needs to be filtered to reduce the dataset size and to select the most chemically relevant regions. We used two types of criteria for node selection: the shape MSF- and electrostatic MEP-based filtering. As in previous application of the Q-QSSR approach,³⁰ we selected the most convex areas of the isosurface (CONV) as being the most descriptive of the molecular shape by keeping one node out of 15. In addition, we also explored filtering of the points based on the MEP field for selecting the most basic areas of the catalyst (BAS), which contains the nodes that have the most negative values. In this case, a distance-based correction was introduced in the algorithms in order to avoid the selection of too few representative regions (see ESI†). The details of this procedure will be published elsewhere. Fig. 2 shows the result of shape and electrostatic filtering for ligand 1, where differences are clearly seen. In line with our general understanding, we can observe that the MSF filtering selects the bulky groups of the catalysts while the MEP filtering selects the basic areas of the catalyst such as oxygen and aromatic groups.

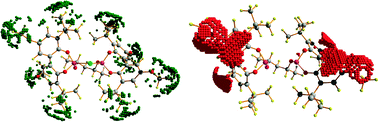Fig. 2 Example of the difference between convexity MSF-based filtering (CONV, left hand-side) and basicity MEP-based filtering (BAS, right hand-side) for ligand 1. The CONV filtering selects ligand's regions associated with bulky groups such as ^tBu and OMe, whereas the BAS filtering selects those associated with basic moieties such as the phenyl groups and the oxygens.

Grid alignment independence was achieved using the GRIND methodology proposed by Pastor et al.²⁸ Within this methodology, we compute the product of the molecular fields (MSF and MEP) for each pair of filtered grid points and then select the highest values of these products for each distance range. Thus, one builds the correlograms (see Fig. 3), which are the true molecular descriptors that will enter multivariate analysis. We tested correlograms with distance intervals of 0.25, 0.5 and 1.0 Å and with distance range between 3 and 10 Å, 3 and 15 Å, and 3 and 20 Å. An optimal interval of 0.25 Å was found, and products of MSF and MEP values were computed between 3 and 20 Å. To sum up, with two molecular fields and two filtering criteria, we can build 4 different correlograms, that is, 4 different descriptors: MSF–MSF_CONV, MEP–MEP_CONV, MSF–MSF_BAS and MEP–MEP_BAS. Additionally, we compared the results with those of a similar commercially-available alignment-independent approach (GRIND), which uses empirical interaction fields instead, as implemented in the ALMOND software.³⁹ The alignment-independent descriptors were built from the empirical TIP interactions generated with C3 probes (an atom of carbon with sp³ hybridization), which evaluate the shape of the catalyst in a similar way as MSF does (the results are provided in the ESI†).

Fig. 3 Example of MSF–MSF_CONV and MEP–MEP_BAS correlograms (the descriptors) for catalyst 1. The highest values of the products between field values for pairs of filtered points (normalized) vs. distances between the nodes (in Å).

Multivariate analysis

We used the Partial Least Squares Regression (PLSR)⁴⁰ as the multivariate regression technique. External and full-cross validations were considered for model building and evaluation. Different statistical parameters were employed for evaluating the predictive ability of models during the fitting and test stages, namely: the Pearson correlation coefficient (r²), the determination coefficient (q²), the sample standard error, and the slope and intercept of the fitted/predicted vs. observed values.⁴¹

Results and discussion

Analysis of dataset and molecular structures

All previous attempts to rationalize asymmetric hydroformylation were based on the transition state for alkene insertion into the Rh–H bond.^9–12 We have shown that alkene insertion is also the key transition state that determines the catalytic activity for usual kinetics of Rh–diphosphorus catalysts.¹⁴ This TS has a pseudo five coordination environment. To mimic the ligand arrangement in TS geometry, we optimized ground-state geometries of a penta-coordinated hydrido-bicarbonyl complex [HRh(CO)₂(P–P)], in which the diphosphorus ligand can coordinate in equatorial–apical (ea) and bis-equatorial (ee) modes. Assuming an apical preference for a hydride ligand, there is one isomer for ea coordination (ea), and two for ee coordination when the ligand is C₁-symmetric (ee1 and ee2) (Fig. 4). Additionally, for dissymmetric diphosphorus ligands (5, 20 and 21), it is possible to distinguish two ea isomers depending on which ligand moiety is coordinated at the apical site. Their coordination preferences have already been studied theoretically by us,^10,11 and showed that the preferred moiety in the apical site is the phosphite for ligand 5 and the aminophosphane for ligands 20 and 21. Note, however, that for the alignment-independent methodologies the coordination mode of the ligand becomes less crucial because its shape is described by a two-dimensional graph, the correlogram.

Fig. 4 Schematic representation of 3 different geometrical isomers for hydrido carbonyl complex [HRh(CO)₂(P–P)].

For each geometrical isomer ea, ee1 and ee2, suitable initial structures were generated, when possible, from analogous X-ray penta-coordinated structures. Then, for the three isomers, we applied the conformational search protocol described in the previous section to locate the species with the lowest energy. Except for the (S,S)-kelliphite ligand (11), our results indicate that all the analyzed ligands coordinate preferably in an equatorial–apical manner. Ligand 11 showed the largest P–Rh–P bite angle (126° for ee coordination) along the dataset, the rest of the bite angles ranging from 86° for ligand 17 to 113° for 1. The energy difference between ea and ee isomers for 17 was 14 kJ mol⁻¹, decreasing to only 6 kJ mol⁻¹ for 1. Interestingly, all catalysts exhibiting high enantioselectivity showed preferred ea coordination. This reinforces our previous suggestion that ea coordination brings a higher degree of chirality to the apical site thus favoring diastereoisomeric ligand–substrate interactions.^10,11

The optimized structures of the coordinated ligands were used to calculate the molecular fields. The inclusion of the whole complex with the metal and auxiliary ligands hindered the effect of the ligands, and gave poor statistical parameters. This effect was previously observed by Higginson, Morao and co-workers in analogous 3D-QSPR studies on asymmetric organometallic catalysis.²⁹ Thus, the molecular interaction fields (MSF and MEP) were calculated on the isolated ligands at the geometry that they have in the penta-coordinated complex.

QSPR model for enantioselectivity. The molecular shape field

Initially, we tried to build a QSPR model for predicting ee values in the 21-catalyst dataset (set 1) using the shape field with convexity node selection (MSF–MSF_CONV) as a descriptor. After full cross-validation of the 21-catalyst dataset, the Pearson correlation coefficient (r²) of the fitting stage is 0.83, whereas the predictive ability (q²) calculated using the Leave-One-Out (LOO) cross-validation method is 0.51 (4 PLS factors). In drug design, a model is considered to be predictive when the q² is higher than 0.5 (halfway between perfect prediction 1.0 and no model at all 0.0). Thus, the value of 0.51 for q² indicates that the model is in the limit of what one can consider as predictive.

There may be outliers that influence the quality of the QSPR model. Indeed, ligand 11 has the largest residuals, the difference between experimental and predicted ee values for fitting and validation stages being 34% and 55%. As mentioned above, the most stable isomer was ea coordination for all the ligands but for 11, which showed a preference for ee coordination. This means that ligand 11 was an outlier associated not only with the analysis of the response space, but also with the analysis of the chemical space. One of the assumptions of QSPR modeling is that the interaction between the substrate and the catalyst occurs in the same way. In previous studies, we showed that the interactions governing enantioselectivity occur mainly between the substrate and the apical ligand.^10,11 Thus, for ee coordination, the substrate will meet an achiral CO group in apical, and yield a low enantioselectivity. Although the QSPR model reflects the potential enantioinduction of the ligand 11, the preferred ee coordination does not allow transmitting the chiral information efficiently. When we set aside ligand 11, the statistical parameters improved significantly, and this confirmed its nature as an outlier. The new QSPR model for the dataset of 20 ligands (set 2) had q² = 0.68 (in prediction) and r² = 0.92 (in fitting) with 4 PLS factors. Fig. 5 shows the experimental ee values plotted against the fitted ee values. The coefficients of the QSPR equation are provided in the ESI.† Moreover, the standard error in these enantiomeric excess predictions is 17% (0.2 kcal mol⁻¹), which is within the order of the discrepancy with experiments that is encountered for catalysts 20 (23%, 0.3 kcal mol⁻¹) using QM/MM calculations of transition-states.¹⁰

Fig. 5 Experimental vs. fitted %ee values for the dataset of 20 catalysts (set 2), using MSF–MSF_CONV correlograms as descriptors.

We also tried the full set of available descriptors within our methodology. It is clear from Table 1 that the best results are obtained for shape-based descriptors MSF–MSF_CONV and MEP–MEP_CONV (q² > 0.6). The models generated using basicity-based descriptors MEP–MEP_BAS and the MSF–MSF_BAS cannot be accepted as predictive (q² < 0.5). These results are consistent with the idea that enantioselectivity is mainly determined by molecular shape recognition. It is also possible to combine the interaction fields in the representation of molecular structures by simply concatenating the correlograms. We had observed that the MEP–MEP_CONV descriptor contains a second level of steric information, which derives from node selection based on convexity.³⁰ However, combination of MSF–MSF_CONV and MEP–MEP_CONV did not improve the model in this case (q² = 0.68 and r² = 0.93); and therefore, we used the simpler MSF–MSF_CONV model for further analysis.

Table 1 Statistical parameters of LOO cross-validation for enantioselectivity in set 2 using different descriptors and filtering criteria^a

Filtering criteria	Descriptor	q ^2	r ^2
a Acceptable models with the following statistical parameters (fitting/prediction): slope = 0.99/0.92, intercept = 3.4/3.7%, and prediction error = 17% for MSF–MSFCONV; slope = 0.97/0.95, intercept = 4.2/2.4%, and prediction error = 19.6% for MEP–MEPCONV.
Shape-based	MSF–MSFCONV	0.68	0.92
	MEP–MEPCONV	0.60	0.95
Basicity-based	MSF–MSFBAS	0.12	0.46
	MEP–MEPBAS	0.41	0.85

---

Although the number of samples was relatively low, we carried out an external validation of the MSF–MSF_CONV model by dividing the dataset into 4 series of training and test subsets of 15 and 5 catalysts, respectively. Then the 5 external catalysts were predicted with the model trained by the remaining catalysts. To ensure a balanced test subset on the %ee rank, we defined a procedure for selecting the subset randomly but covering a wide range of enantioselectivities (see ESI†). Table 2 shows the test subset composition for each run, the experimental and predicted %ee values in parentheses, and r² and q² for each test set. We observed good predictions for runs 1, 2, and 4, but not for run 3, in which the ligands 1 and 6 show the large discrepancies. This could very well be explained by the mediocre predicting ability (q² = 0.52) of the resulting training set,⁴² which has only one ligand with an ee over 90%. Consequently, we expect a poor modeling of systems with high enantioselectivities such as 6 (ee = 94%). Ligand 1, (2R,4R)-chiraphite, is predicted to have a high ee (90%) and, in fact, the ligand has shown ee values of up to 90% at low temperatures.² Nevertheless, in our dataset, the reaction was conducted at 80 °C yielding low–medium enantioselectivity (ee = 50%).⁵ This indicates that the ligand is highly selective, as predicted by the model, but very sensitive to experimental conditions. Interestingly, for 1 we computed the lowest preference for ea coordination among set 2 (see above), which suggests that a nonselective ee path may be also operative at high temperatures reducing the overall enantioinduction. In summary, despite the observed discrepancies, the external validation achieved a 75% success supporting further the predictive ability of the model.

Table 2 Experimental vs. predicted enantiomeric excess (ee in %) for different test subsets of 5 catalytic systems employing 3D-QSPR models generated from the corresponding training sets with MSF–MSF_CONV descriptors

Run	Ligand (exp,pred)	(r^2,q^2)^a
a The r^2 and q^2 values correspond to the test set in prediction.
1	2 (2,23); 4 (13,14); 16 (44,43); 19 (55,51); 18 (82,82)	(0.96,0.89)
2	8 (6,8); 9 (17,16); 12 (48,11); 20 (75,54); 14 (83,81)	(0.88,0.62)
3	10 (10,11); 3 (28,7); 1 (50,91); 7 (76,90); 6 (94,43)	(0.58,0.05)
4	21 (10,35); 17 (43,46); 15 (52,71); 5 (82,76); 13 (94,79)	(0.92,0.71)

---

In an external blind test, we tried to carry out a priori prediction of the performance of a ligand from an independent laboratory. We tested whether it had been possible to anticipate the excellent enantioselectivities (99% ee) of the recently tested phosphane-phosphoramidite ligand (yanphos).⁶ To obtain the molecular structure, we assumed an ea coordination with the phosphoramidite moiety at the apical position, as proposed by Zhang and co-workers,¹² and we optimized it at the QM/MM level. Then, we computed the MSF–MSF_CONV descriptor using the same parameters as those used for building the QSPR model. In excellent agreement with experiment, we calculated an ee of 90%, and what is more important, the ligand was correctly classified as highly enantioselective.

3D-QSPR model for activity. The molecular electrostatic potential

We generated a new dataset with 19 ligands (set 3), using the percentage of conversion as the dependent variable. We removed the ligands 20 and 21 because the different origin of the data does not allow comparing conversion values. Table 3 collects the main statistical parameters obtained for the different descriptors. All defined descriptors yield models with poor predictive capacity (q² around 0.5). This is an indication that a property such as the activity requires to be modeled by more sophisticate descriptors, including both shape and basicity. When we combined shape- and electrostatic-based 3D fields via concatenation of correlograms, acceptable models were obtained. The concatenation of MEP–MEP_CONV and MEP–MEP_BAS descriptors achieved q² values of up to 0.74. Fig. 6 shows the experimentally measured values plotted against the fitted conversion values.

Table 3 Statistical parameters of LOO cross-validation for activity in set 3 using different descriptors and filtering criteria

Filtering criteria	Descriptor	q ^2	r ^2
a Slope = 0.75 and 0.99, intercept = 0.49 and 15.8% for prediction and fitting, respectively, fitting error = 3.8% and predicting error = 16.6%.
Shape-based	MSF–MSFCONV	0.52	0.71
	MEP–MEPCONV	0.56	0.88
Basicity-based	MSF–MSFBAS	0.44	0.63
	MEP–MEPBAS	0.47	0.56
Combination^a	MEP–MEPCONV and MEP–MEPBAS	0.74	0.99

---

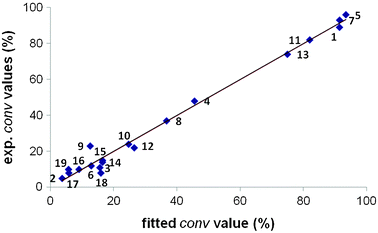Fig. 6 Experimental vs. fitted %conversion values for the dataset of 19 catalysts (set 3), using concatenated MEP–MEP_CONV and MEP–MEP_CONV descriptors for the 3D-QSPR modelling.

Again, we carried out 4 runs to evaluate the external predictive ability of the model despite the relatively low number of samples. Following the procedure described above, we divided the dataset into a training subset of 14 ligands and a test subset of 5, with the exception of run 4 consisting of 4 test ligands. Table 4 shows the test subset composition for each run, the experimental and predicted percentage of conversion, and the r² and q² for each test subset in prediction. We observed excellent predictions for three out of four external validations (runs 1, 2 and 4). In run 3, the predicted activity for ligands 13 and 5, both of which showed high conversion values (>70%), is rather poor. Looking at Fig. 6, we can observe that the available data are not uniformly distributed, and most of the systems show low conversion. This could explain the discrepancies of high-selective catalysts such as 13 and 5, especially when two of them are set aside of the training set such as in run 3.

Table 4 Experimental vs. predicted activity (conversion in %) for different test subsets of 5 ligands employing 3D-QSPR models generated from the corresponding training sets with concatenated MEP–MEP_CONV and MEP–MEP_BAS descriptors

Run	Ligand (exp,pred)	(r^2,q^2)^a
a The r^2 and q^2 values correspond to the test set in prediction. b 4 test ligands as a consequence of the employed algorithm for set splits (see the text).
1	2 (5,6); 19 (10,5); 14 (15,14); 8 (37,34); 1 (89,83)	(1.00,0.98)
2	3 (8,37); 18 (11,18); 12 (22,27); 4 (48,43); 7 (93,123)	(0.93,0.62)
3	17 (8,0); 6 (12,30); 9 (23,9); 13 (74,29); 5 (96,61)	(0.82,0.41)
4 ^b	16 (10,12); 15 (14,23); 10 (24,23); 11 (82,76)	(0.99,0.96)

---

Analysis of the enantioselectivity 3D-QSPR model and correlation with the stereochemical models

The main goal of QSPR approaches is to build mathematical models with predictive ability; however, obtaining additional chemical information to orient ligand design would be very valuable. To evaluate the exploratory ability of the QSPR models for understanding the mode of action of enantioinduction, we graphed the values of the product of the two-node molecular field (MSF–MSF) by the equation coefficients (Ci) at each distance range (Fig. 7).⁴³ This coefficient-weighted correlogram captures the 3D shape of catalyst structure and its impact on enantioselectivity, and transforms it into a quantitative 2D graph, as appearing in an experimental spectrum. The peaks indicate the most positive and the most negative contributions to enantioselectivity, and indentify those independent variables (two-node interactions) that are directly correlated with the dependent variable (%ee). From the largest coefficient-weighted nodal interactions, it is possible to retrieve 3D information and to identify the regions of the ligands that contribute the most to enantioselectivity (Fig. 8).

Fig. 7 Coefficient-weighted correlograms of the enantioselectivity model for ligands 5, 6, 13 and 20. Product of the MSF–MSF_CONV nodal interaction by the PLS coefficients at each distance range. In parentheses values of the enantiomeric excess (experimental/LOO predicted) are given.

Fig. 8 Backtracking of the most important MSF–MSF variables of the enantioselectivity model: (i) ligand 5, (ii) ligand 6, (iii) ligand 13, and (iv) ligand 20. Positive node interactions are indicated in dark blue, and negative in light yellow. The ligand substituents involved in key node interactions are highlighted in dark blue.

Fig. 7 shows the coefficient-weighted correlogram of the enantioselectivity MSF–MSF_CONV model for representative examples exhibiting either high enantioselectivities (5, 6 and 13) or with mechanisms of stereoinduction that are known (20). In the graph, we could identify different patterns depending on the number of peaks and the correlogram extent, which is related to the size of the ligand. For ligands 5 and 6, there were three important peaks along the profile: two positives at 14.5 and 17.0 Å (a and c), and one negative at 16.0 Å (b). In 5, backtracking of the variables associated with peaks a and b in 3D space highlighted very similar structural features. The two associated vectors were almost superimposed and connected the same ligand fragments (see Fig. 8(i)). This suggests that the contributions of peaks a and b are mutually cancelled. Consequently, the contribution of peak c, with the largest positive coefficient-weighted nodal interaction, is mainly responsible for the high computed enantioselectivity. In the 3D space, the c peak highlighted two patches: one at a phenyl substituent of a phosphane moiety and the other at a naphthyl group of the phosphite moiety (highlighted in Fig. 8(i)). Since the phenyl group does not belong to any stereogenic centre, it is reasonable to assign the key positive features to the steric hindrance of the naphthyl group. In our previous study on AHF by using an Rh–binaphos (5) system,¹¹ we found that the repulsive steric interactions between the substrate and the naphthyl groups of the apical phosphite are responsible for enantioinduction. This corroborates the interpretation of the QSPR model.

The coefficient-weighted correlogram of ligand 6 (binapine ligand) had a similar pattern to that of 5 (Fig. 7). Focusing on peak c, its contribution arose from two naphthyl groups not involved in the backbone. One of the nodes of peak c is very close to other node highlighted for its negative contribution in peak b (Fig. 8(ii)). Thus, the analysis of the QSPR model for 6 also identified a naphthyl group as the key fragment. Interestingly, in both ligands 5 and 6, the node describing the protrusion of the key naphthyl group was at 9 Å from the metal centre. These facts suggest that binapine (6) and binaphos (5) ligands possess some common 3D features responsible for the high enantioselectivity. Thus, we tested whether the stereochemical model proposed for 5 (Fig. 9)¹¹ is also valid for 6. The quadrant representation in Fig. 9 can be described as follows: (i) for ea coordination of the ligand, the plane of the quadrant contains the Rh–H bond and is parallel to the alkene plane, (ii) the quadrant delimited by the two phosphorus atoms is blocked by steric effects, and (iii) one of the two possible paths for the substrate approach (I or II) is sterically hindered in order to avoid mutual cancellation of enantioselectivities. To quantify the steric bulk of each quadrant and its impact on the metal center, we defined a geometrical descriptor called distance-weighted volume (V_W).¹¹ The V_W values for (S)-binapine (Fig. 9) agreed with the stereochemical model. There are one sterically small (uncoloured), two sterically large (dark grey), and one intermediate (light grey) quadrants. This map explains the observed preference for the product with S configuration;⁵ path I is favored over path II, and in path I, the pro-S transition state is more favored than the pro-R.

Fig. 9 Quadrant representation of the possible hydroformylation paths for the binapine ligand, values of V_W, and molecular structure of the [HRh(CO)₂{(S)-binapine}] complex oriented following the chiral hypothesis of the stereochemical model.

The analysis of the external yanphos system showed the same features as BINAPHOS (see ESI†): (i) the vectors associated with the positive a and the negative b peaks connect the same groups, cancelling each other; (ii) the highest positive peak c highlighted naphthyl groups in the apical phosphoramidite moiety; and (iii) the key node associated with a naphthyl fragment was located at ∼9 Å of the metal center. Other selective ligands such as (2R,4R)-chiraphite (1) and diazaphospholane (7) showed a similar pattern. For 1 the c peak highlighted the ^tBu groups, while for 7, it highlighted the chiral amine substituents. To sum up, the common 3D features of these ligands indicate that their enantioselectivity can be explained with the same stereochemical model as that proposed for Rh–BINAPHOS.¹¹

Ligands 20 and 13 (P-stereogenic AMPP and (R,R)-Ph-BPE) showed only one peak with positive contribution at 14.5 Å (peak a, Fig. 7). Backtracking the variables associated with peak a in 3D structure of 20 highlights two phenyls, one of the phosphinite moiety and the other one of the chiral aminophosphane (Fig. 8(iv)). The latter selectivity-increasing group had been identified as the key group in inducing enantioselectivity by previous QM/MM calculations on transition states.¹⁰ For ligand 13, the model also points out two Ph groups at distinct phosphorus moieties as the key selectivity-determining molecular fragments. Analogously to what was found for ligands 5 and 6, for ligands 13 and 20 the key nodes associated with the phenyl groups lie at the same distance from the metal centre (∼7 Å). It seems that the model has recognized an optimal placement of different functional groups for the interaction with the substrate, and that the effective placement is achieved by coordinating a phosphane moiety in the apical site, which is in agreement with previous hypotheses.^10–13 Thus, structural modifications around those specific areas would have a pronounced effect on enantioselectivity by tuning the interactions with the substrate.

Analysis of the activity 3D-QSPR model and correlation with ligand basicity

As stated in the Introduction, the correlation of catalytic activity with the ligand basicity has been observed for specific families of ligands.^15,18 Thus, additionally, we tried to establish a correlation between the activity and the ligand basicity for the set 3. We used the HOMO energy of free ligands, formally corresponding to phosphorus lone pairs, as a measure of their donation ability; the lower in energy the HOMO is, the less basic the diphosphane is. We were unable to find a correlation for the whole set. Nevertheless, if we only consider the diphospholane ligand family (14–19), or even the full family of phosphacycle moieties (1, 5–7, 11, 14–19), fair correlations are observed (Fig. 10). Ligands showing high activities (conv > 70%) have low-lying HOMOs (<−5.0 eV), whereas those showing low activities (conv < 20%) have high-lying HOMOs (>−5.0 eV). The use of HOMO energy as a descriptor can be proved via correlation with the Tolman electronic parameters (χ)⁴⁴ of the phosphacyclic substituents. The HOMO energies for 13, with the most electron-withdrawing Ph substituent (χ = 4.3), lie at −5.0 eV, whereas for ligands 14–19 with electron-donating Me, Et and ⁱPr groups (χ = 2.6, 1.8 and 1.0), the energies lie at ∼−4.7 eV.

Fig. 10 Correlation between the activity (percentage of conversion) and the HOMO energy (eV) of free diphosphanes. Circles correspond to diphospholane ligands and squares correspond to rest of the ligands with phosphacycle moieties.

Although some correlation between activity and basicity exists for specific ligand families, the 3D-QSPR modeling required shape-based descriptors in order to have predictive capacity for the whole set 3 (Table 3). Fig. 11 shows the coefficient-weighted correlograms of the activity model for selected examples. On the left-hand side of the graph, we plotted the shape-based MEP–MEP_CONV descriptor, which resembles that found for the enantioselectivity model (Fig. 7). Depending on the ligand bulkiness, we observed three peaks at 14.5, 16.0 and 17.0 Å (a, b and c), or one peak at 14.5 Å. On the right-hand side of the graph, the basicity-based MEP–MEP_BAS descriptor shows several positive peaks, the largest being at 7.0 Å (d), which vanishes for catalysts with low activities. Regarding the basicity-based descriptors, Fig. 12 shows the superimposed coefficient-weighted correlograms, amplified around the region of peak d. The height of peak d (5 > 13 ≈ 6 > 18) can be inversely correlated with the values of HOMO energy; the lowest for 5 (−5.4 eV), somewhat higher for 6 and 13 (−4.97 and −5.03 eV), and the highest for 18 (−4.7 eV). To explain the observed differences between ligands 6 and 13, we should look at the shape-based MEP–MEP_CONV descriptors. When going from 6 to 13, we observed that the negative contribution of peak b disappeared (Fig. 11). Thus, although binapine (6) and (R,R)-Ph-BPE (13) ligands have similar basicity, the shape of the (R,R)-Ph-BPE ligand has a positive effect on activity. Considering the mechanistic knowledge,^14,17 the positive effect could be very well related to a reduction of the steric hindrance on the reaction centre favoring the alkene coordination and hydride migration steps.

Fig. 11 Coefficient-weighted correlograms of the activity model for ligands 5, 6, 13 and 18. Product of the MEP–MEP_CONV (left) and MEP–MEP_BAS (right) nodal interaction by the PLS coefficients at each distance range. In parentheses Values of the conversion percentage (experimental/LOO predicted) are given.

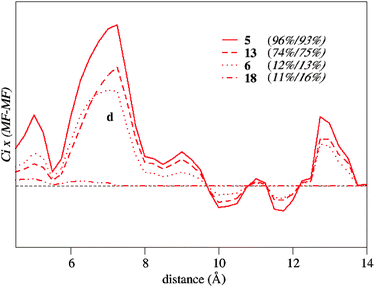Fig. 12 Coefficient-weighted correlograms of the activity model amplified around peak d for ligands 5, 6, 13 and 18. Product MEP–MEP_BAS interaction by the PLS coefficients. In parentheses Values of the conversion percentage (experimental/LOO predicted) are given.

Fig. 13 represents the backtracking of the variables associated with peak d for catalysts 5 and 13. In both cases, one of the nodes is located at the phosphorus lone pair, and the other node highlights an electron-withdrawing substituent; the oxygen atoms in BINAPHOS and the phenyl group in the (R,R)-Ph-BPE ligand. For the highly active catalysts chiraphite (1), diazaphospholane (7) and kelliphite (11), the vectors associated with peak d also connect a node located at the phosphorus lone pair and another node located near the heteroatom (O or N) substituents. This analysis further supports the correlation between high activity and low basicity, and highlights the importance of introducing electron-withdrawing groups to achieve more active catalysts.

Fig. 13 Backtracking of the most important MEP–MEP_BAS variables of the activity model: (i) ligand 5, and (ii) ligand 13.

Conclusions

Two 3D-QSPR models were generated for predicting the enantioselectivity and the activity for asymmetric hydroformylation of styrene catalyzed by rhodium–diphosphane catalysts, using a varied dataset of 21 ligands. The best predictive model for enantioselectivity was obtained using shape 3D fields (MSF) based on the local curvature of the electron density isosurface (r² = 0.92, q² = 0.68). Interestingly, the only ligand showing preference for bis-equatorial coordination (kelliphite) was identified as an outlier, and the worst predicted ligand in external validation was that with the lowest preference for equatorial–axial coordination, (2R,4R)-chiraphite. Although, the model predicts that both ligands are highly selective, low values of ee were observed. This suggests that the intrinsic enantiotopic differentiation capacity of kelliphite and chiraphite can be lost through the occurrence of non-selective bis-equatorial paths; and consequently, the equatorial–apical coordination is a prerequisite in Rh–diphosphane AHF. The most predictive model for activity was obtained using a combination of shape- and electrostatic-based 3D fields (r² = 0.99, q² = 0.74) for a dataset of 19 catalysts. The use of chemically meaningful descriptors provides insight into the factors governing catalytic activity and enantioselectivity. The models for enantioselectivity require shape-based descriptors to account for the steric effects induced by the ligand. In the case of the activity, it was possible to find a correlation with the ligand basicity, measured from the HOMO energies of free ligands, for structurally-related ligands. However, when a larger and more varied ligand set was considered, we required descriptors that accounted for both basicity and steric properties. Although in principle the QSPR models are only valid for styrene, we hope that the use of this model substrate can also help to identify selective and active catalysts for other substrates.

The QSPR analysis provides structural insight consistent with, and complementary to, the previously proposed stereochemical models for asymmetric hydroformylation. Thus, the stereochemical model previously proposed for an Rh–binaphos catalyst can be also applied to explain the high enantioinduction observed for Rh–chiraphite, –binapine, –diazaphospholane, and –yanphos systems. For binapine and yanphos ligands, we assigned the main contribution to the selectivity to the naphthyl groups, identifying regions where steric hindrance would favor selectivity. For chiraphite and diazaphospholane ligands, the analysis of the QSPR equation highlighted the ^tBu and chiral amine groups as the key enantioinducting moieties. Moreover, the effective placement of these groups to interact with the substrate is achieved through the coordination of phosphane moieties in the apical site of the complex.

The ligands that most effectively promote catalytic activity are those that carry electron-withdrawing groups in the vicinity of the phosphorus atoms via reduction of ligand basicity, as in chiraphite, binaphos, diazaphospholane and kelliphite ligands. Nevertheless, we found that more complex relationships account for the origin of activity. In the design of new active catalysts, the shape of the catalysts and the steric effects exerted on the reaction center are also important as in the (R,R)-Ph-BPE ligand. Based on previous mechanistic knowledge, it is reasonable to propose that reduction of the steric hindrance on the reaction centre will favor the alkene coordination and hydride migration steps. Finally, this computational methodology can be used to gain greater understanding of previously studied examples, to make predictions of the enantioselectivity and activity of new cases, and to derive guidelines for new ligand design.

Acknowledgements

The authors are grateful for financial support from the MINECO of Spain (Projects CTQ2011-29054-C02-01/BQU and CTQ2011-29054-C02-02/BQU), the DGR of the Generalitat de Catalunya, (2009SGR462, 2009SGR259 and XRQTC) and the European fund for regional development, FEDER (UNRV10-4E-1133) for economic support.

Notes and references

1. Rhodium Catalyzed Hydroformylation, ed. C. Claver and P. W. N. M. Leeuwen, Kluwer Academic Publishers, Dordrecht, 2000.
2. J. E. Babin and G. T. Whiteker, US Pat. 911518, 1992(WO 9303839).
3. K. Nozaki, Chem. Rec., 2005, 5, 376.
4. (a) T. P. Clark, C. R. Landis, S. L. Freed, J. Klosin and K. J. Abboud, J. Am. Chem. Soc., 2005, 127, 5040; (b) A. T. Axtell, C. J. Cobley, J. Klosin, G. T. Whiteker, A. Zanotti-Gerosa and K. A. Abboud, Angew. Chem., Int. Ed., 2005, 44, 5834.
5. A. T. Axtell, J. Klosin and K. A. Abboud, Organometallics, 2006, 25, 5003.
6. Y. Yan and X. Zhang, J. Am. Chem. Soc., 2006, 128, 7198.
7. (a) C. J. Cobley, R. D. J. Froese, J. Klosin, C. Quin and G. T. Whiteker, Organometallics, 2007, 26, 2986; (b) A. T. Axtell, J. Klosin and G. T. Whiteker, Organometallics, 2009, 28, 2993.
8. J. Mazuela, M. Coll, O. Pàmies and M. Diéguez, J. Org. Chem., 2009, 74, 5440.
9. (a) D. Gleich, R. Schmid and W. A. Herrmann, Organometallics, 1998, 17, 2141; (b) D. Gleich and W. A. Herrmann, Organometallics, 1999, 18, 4354.
10. J. J. Carbó, A. Lledós, D. Vogt and C. Bo, Chem.–Eur. J., 2006, 12, 1457.
11. S. Aguado-Ullate, S. Saureu, L. Guasch and J. J. Carbó, Chem.–Eur. J., 2012, 18, 995.
12. X. Zhang, B. Cao, S. Yu and X. Zhang, Chem.–Eur. J., 2010, 49, 4047.
13. A. L. Watkins and C. R. Landis, J. Am. Chem. Soc., 2010, 132, 10306.
14. E. Zuidema, L. Escorihuela, T. Eichelsheim, J. J. Carbó, C. Bo, P. C. J. Kamer and P. W. N. M. van Leeuwen, Chem.–Eur. J., 2008, 14, 1843.
15. (a) P. W. N. M. van Leeuwen and C. F. Roobeek, J. Organomet. Chem., 1983, 258, 343; (b) W. R. Moser, C. J. Papile, D. A. Brannon, R. A. Duwell and S. J. Weininger, J. Mol. Catal., 1987, 41, 271.
16. E. Zuidema, P. E. Goudriaan, B. H. G. Swennenhuis, P. C. J. Kamer, P. W. N. M. van Leeuwen, M. Lutz and A. L. Spek, Organometallics, 2010, 29, 1210.
17. E. Zuidema, E. Daura-Oller, J. J. Carbó, C. Bo and P. W. N. M. van Leeuwen, Organometallics, 2007, 26, 2234.
18. M. F. Haddow, A. J. Middleton, A. G. Orpen, P. G. Pringle and R. Papp, J. Chem. Soc., Dalton Trans., 2009, 202.
19. (a) A. G. Maldonado, J. A. Hageman, S. Mastroianni and G. Rothenber, Adv. Synth. Catal., 2009, 351, 387; (b) N. Fey and J. N. Harvey, Coord. Chem. Rev., 2009, 253, 704; (c) N. Fey, Dalton Trans., 2010, 39, 296; (d) J. A. Gillespie, D. L. Dodds and P. C. J. Kamer, Dalton Trans., 2010, 39, 2751.
20. (a) V. L. Cruz, J. Ramos, A. Muñoz-Escalona, A. Lafuente, B. Peña and J. Martínez-Salazar, Polymer, 2004, 45, 2061; (b) V. L. Cruz, J. Ramos, S. Martínez, A. Muñoz-Escalona and J. Martínez-Salazar, Organometallics, 2005, 24, 5095; (c) V. L. Cruz, J. Martínez, J. Martínez-Salazar, J. Ramos, M. L. Reyes, A. Toro-Labbe and S. Gutierrez-Oliva, Polymer, 2007, 48, 7672; (d) G. Occhipinti, H. R. Bjørsvik and V. R. Jensen, J. Am. Chem. Soc., 2006, 128, 6952; (e) G. Rothenberg and E. Burello, Adv. Synth. Catal., 2003, 345, 1334; (f) G. Rothenberg and E. Burello, Adv. Synth. Catal., 2004, 346, 467; (g) E. Burello, P. Marion, J. C. Galland, A. Chamard and G. Rothenberg, Adv. Synth. Catal., 2005, 347, 803; (h) J. A. Hageman, J. A. Westerhuis, H. W. Frühauf and G. Rothenberg, Adv. Synth. Catal., 2006, 348, 361; (i) Z. Strassberger, M. Mooijman, E. Ruijter, A. H. Alberts, A. G. Maldonado, R. V. A. Orru and G. Rothenberg, Adv. Synth. Catal., 2010, 352, 2201.
21. (a) J. J. Miller and M. S. Sigman, Angew. Chem., Int. Ed., 2008, 47, 771; (b) M. S. Sigman and J. J. Miller, J. Org. Chem., 2009, 74, 7633; (c) K. C. Harper and M. S. Sigman, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2179; (d) K. C. Harper and M. S. Sigman, Science, 2011, 333, 1875.
22. C. Jiang, Y. Li, Q. Tian and T. You, J. Chem. Inf. Model., 2003, 43, 1876.
23. (a) K. B. Lipkowitz, S. Schefzick and D. Avnir, J. Am. Chem. Soc., 2001, 123, 6710; (b) S. Alvarez, S. Schefzick, K. B. Lipkowitz and D. Avnir, Chem.–Eur. J., 2003, 9, 5832.
24. R. D. Cramer III, D. E. Patterson and J. D. Jeffrey, J. Am. Chem. Soc., 1988, 110, 5959.
25. S. Dixon, K. M. Merz Jr., G. Lauri and J. C. Ianni, J. Comput. Chem., 2005, 26, 23.
26. P.-W. Phuan, J. C. Ianni and M. C. Kozlowski, J. Am. Chem. Soc., 2004, 126, 15473.
27. (a) K. B. Lipkowitz and M. Pradhan, J. Org. Chem., 2003, 68, 4648; (b) M. C. Kozlowski, S. Dixon, M. Panda and G. Lauri, J. Am. Chem. Soc., 2003, 125, 6614; (c) M. Hoogenraad, G. M. Klaus, N. Elders, S. M. Hooijschuur, B. McKay, A. A. Smith and E. W. P. Damen, Tetrahedron: Asymmetry, 2004, 15, 519; (d) J. L. Melville, K. R. J. Lovelock, C. Wilson, B. Allbutt, E. K. Burke, B. Lygo and J. D. Hirst, J. Chem. Inf. Model., 2005, 45, 971; (e) J. C. Ianni, V. Annamalai, P.-W. Phuan and M. C. Kozlowski, Angew. Chem., Int. Ed., 2006, 45, 5502; (f) M. C. Kozlowski and J. C. Ianni, J. Mol. Catal. A: Chem., 2010, 324, 141; (g) S. E. Denmark, N. D. Gould and L. M. Wolf, J. Org. Chem., 2011, 76, 4337.
28. (a) M. Pastor, G. Cruciani, I. McLay, S. Pickett and S. Clementi, J. Med. Chem., 2000, 43, 3233; (b) F. Fontaine, M. Pastor and F. Sanz, J. Med. Chem., 2004, 47, 2805; (c) F. Fontaine, M. Pastor, I. Zamora and F. Sanz, J. Med. Chem., 2005, 48, 2687.
29. S. Sciabola, A. Alex, P. D. Higginson, J. C. Mitchell, M. J. Snowden and I. Morao, J. Org. Chem., 2005, 70, 9025.
30. M. Urbano-Cuadrado, J. J. Carbó, A. G. Maldonado and C. Bo, J. Chem. Inf. Model., 2007, 47, 2228.
31. J. J. Carbó, F. Maseras, C. Bo and P. W. N. M. van Leeuwen, J. Am. Chem. Soc., 2001, 123, 7630.
32. R. Ewalds, E. B. Eggeling, A. C. Hewat, P. C. J. Kamer, P. W. N. M. van Leeuwen and D. Vogt, Chem.–Eur. J., 2000, 6, 1496.
33. (a) F. Maseras and K. Morokuma, J. Comput. Chem., 1995, 16, 1170; (b) T. K. Woo, L. Cavallo and T. Ziegler, Theor. Chem. Acc., 1998, 100, 307.
34. (a) ADF 2007.01. Department of Theoretical Chemistry, Vrije Universiteit, Amsterdam; (b) E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41; (c) L. Versluis and T. Ziegler, J. Chem. Phys., 1988, 88, 322; (d) G. Te Velde and E. J. Baerends, J. Comput. Phys., 1992, 99, 84; (e) C. Fonseca Guerra, J. G. Snijders, G. Te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391; (f) G. Te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
35. Xα model with Becke's correction for describing exchange: (a) A. D. Becke, J. Chem. Phys., 1986, 84, 4524; (b) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 VWN parameterization with Perdew's correction for describing correlation: ; (c) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200; (d) J. P. Perdew, Phys. Rev. B, 1986, 33, 8822; (e) J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
36. Slater-type basis set, as included in ADF package. The 1s–3d electrons for Rh, the 1s electrons for C, N and O, and the 1s–2p electrons for P were treated as frozen cores. We applied scalar relativistic corrections to them via the zeroth-order regular approximation (ZORA) with the core potentials generated using the DIRAC program (ref. 34).
37. (a) M. Clark, R. D. Cramer III and N. van Opdenbosch, J. Comput. Chem., 1989, 10, 982; (b) U. C. Sing and P. A. Kollman, J. Comput. Chem., 1986, 7, 718.
38. The van der Waals parameters for Rh were taken from UFF force field: A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024.
39. ALMOND 3.3.0 from Molecular Discovery, London, UK.
40. (a) S. Wold, M. Sjostrom and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109; (b) P. Geladi and B. Kowlaski, Anal. Chim. Acta, 1985, 35, 1.
41. D. M. Hawkins, S. C. Basak and D. Mills, J. Chem. Inf. Comput. Sci., 2003, 23, 579.
42. For the training sets in the runs 1, 2, 3 and 4, the q² in prediction for the leave-one-out cross-validations are 0.62, 0.65, 0.52 and 0.63, respectively.
43. Related procedures have been used to retrieve information about stereochemical induction from QSPR models of asymmetric catalysis using Grid-Independent methodologies (see ref. 29 and 30).
44. C. A. Tolman, Chem. Rev., 1977, 77, 313.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed list of the relative energies of the different geometrical isomers obtained with the conformational search protocol, coefficients of the most predictive QSPR models, structural analysis of the enantioselectivity QSPR model for yanphos ligands, and some technical details. See DOI: 10.1039/c2cy20089a

---