Mapping the shape and phase of palladium nanocatalysts†
Amanda S.
Barnard
CSIRO Materials Science and Engineering, Parkville, 3052, VIC, Australia. E-mail: amanda.barnard@csiro.au; Fax: +61-3-9662-7145; Tel: +61-3-9662-7356
First published on 24th April 2012
Abstract
Understanding the size, shape and morphological transformations that may occur under different temperature conditions is vital to ensuring the long term stability of metal nanoparticle catalysts. This information can be conveniently captured in a nanoscale phase diagram, that maps the thermally stable structure as a function of size. This paper presents results of theoretical modeling, based on first principle computer simulations, exploring the equilibrium and non-equilibrium morphologies of palladium nanoparticles over the entire nanoscale. A total of 18 different ideal and imperfect structures and shapes are considered and compared, to reveal a delicate balance between the sphericity, the degree of twinning, and the surface anisotropy. The phase diagram is then discussed in relation to the experiments reported in the literature.
1 Introduction
Catalysis is a particularly important field in chemical and material sciences, and platinum-group metals are well established as superior heterogeneous oxidation catalysts1 in catalytic converters2 for the reduction of vehicle exhausts,3 and in modern fuel cells.4 In particular, interest in palladium nanocrystals has been growing steadily due to their ability to catalyze important organic reactions, such as cross-coupling reactions of aryl halides (Suzuki coupling reactions).5 Palladium also exhibits a remarkable capacity for hydrogen absorption,6,7 and structural changes that introduce a number of attractive features for energy applications.8 Hydrogenation reactions are particularly important,9–13 but each of these chemical and physical properties are intrinsically linked to the physical structure of nanoparticles,14 so one can see that it is highly desirable to be able to predict the conditions that give rise to particular morphologies, and the thermal conditions under which each morphology will be stable. In recent years numerous studies have focussed on shape-controlled synthesis of colloidal Pd nanocrystals.15–21 Although significant progress has been made in the development of new synthetic methods, and various nanostructures (including truncated octahedra, icosahedra, octahedra, decahedra, hexagonal and triangular thin plates, rectangular bars and cubes) have been synthesized,22 the ability to predict and understand the conditions that give rise to specific shapes is still challenging.23,24In general, Pd nanoparticles may take three different structural motifs when fast nucleation and growth are involved, including face-centred cubic motifs, decahedra, and icosahedra.25–27 The fcc motifs typically include a variety of shapes based on truncated cubes or octahedra, but other more complex geometries have also been routinely observed. This is perfectly exemplified by a recent study by Niu et al.28 who developed a framework for systematically and selectively synthesizing single-crystalline rhombic dodecahedral, cubic, and octahedral palladium nanocrystals (as well as their derivatives, with varying degrees of edge- and corner-truncation) by a seed-mediated method. By varying the concentration of KI and the reaction temperature, at the same ascorbic acid concentration, a series of Pd nanocrystals with varying shapes were obtained (in the presence of cetyltrimethylammonium bromide, CTAB). Under these conditions it was shown that {111} facets are favored at relatively low temperatures and medium KI concentrations; and {110} facets are favored at relatively high temperatures and medium KI concentrations; and that {100} facets are favored in the absence of KI, or at either very low or very high KI concentrations. The formation of different palladium facets were correlated with the growth conditions, and these correlations were explained in terms of surface energy and growth kinetics.28 While the role of the CTAB was not explicitly examined, another recent study found that cubic shapes prevailed if CTAB was the only capping agent, but in the presence of pseudo-halide thiocyanate ions (SCN−) truncated rhombic dodecahedra enclosed by twelve {110}, eight {111} and six {100} facets were preferred.29 It was presumed that SCN− ions may adsorb to the {110} facets and slow their rate of coarsening, leading to the formation of the high energy {110} facets. Pd nanoparticles may also be produced using a variety of other methods,30–43 with differing results.
The structure of Pd nanoparticles has been addressed computationally over the years, using empirical potentials,44–46 tight-binding47,48 methods, and most recently using density-functional theory (DFT).49–52 Many of these studies focussed on establishing the relative stability of selected morphologies, but consensus has not been reached. For example, since they can share the same number of atoms, ideal cuboctahedra and icosahedra are often compared, but Barreteau and co-workers47 have shown that icosahedra and cuboctahedra can be very close in energy once the second shell is filled. To complicate matters further Kaszkur found that pure Pd nanoparticles solidify into cubic structures with dislocations and grain boundaries.53 In addition to this, Pd nanoparticles have been frequently observed in alternative shapes that are typically excluded from these computational studies. It therefore remains a challenge to predict the relative stability of a more diverse groups of possible morphologies, and to make these predictions at sizes comparable with experiment, without fitting parameters or extrapolation.
One convenient way of capturing this information is to generate a map of the stable morphologies, as a function of size and temperature.54,55 In the present study predictive modeling has been used to identify the most stable shapes and structures of Pd nanoparticles as a function the number of atoms (NPd), or average diameter (〈D〉), and temperature (T). A large range of defect-free (monocrystalline) and twinned morphologies has been included in the virtual sample set, and the input materials parameters obtained from first principles electronic structure computer simulations. The preferred morphologies have been mapped in the 〈D,T〉 space, along with the predicted size-dependent melting temperatures, to generate the first complete nanoscale phase diagram of palladium. These predictions are then discussed in relation to experiments, reported in the literature.
2 Computational methods
The shape-dependent thermodynamic model used here includes contributions from the particle bulk, surfaces and planar defects,56 and has previously proven successful in predicting the size- and temperature-dependent shape of gold57 and platinum58,59 nanoparticles, without necessitating a large number of explicit simulations of individual structures.60 When concerned with nanoparticles >3 nm in diameter, the model for the temperature-dependent free energy, G(T), has the form: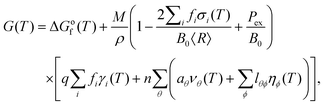 | (1) |
This version of the model requires the input of B0, γi(T), σi(T), νθ(T) and ηϕ(T), which must be calculated explicitly for all facets i, twin planes θ and line tensions ϕ of interest. These calculations were performed from first principles using Density Functional Theory (DFT) within the Generalized-Gradient Approximation (GGA), with the exchange–correlation functional of Perdew and Wang (PW91).64 This has been implemented via the Vienna Ab initio Simulation Package (VASP),65,66 which spans reciprocal space with a plane-wave basis expanded to a given kinetic energy cut-off (in this case 325 eV), and utilizes an iterative self-consistent scheme to solve the Kohn–Sham equations using an optimized charge–density mixing routine. All calculations were performed using the Projected Augmented Wave (PAW) potentials,67,68 with spin polarisation, to an energy convergence of 10−4 eV. Using this approach, the value of the bulk modulus was calculated to be 176 ± 1.15 GPa (see ESI† for comparison). This methodology has previously been used successfully to model the surfaces of Pt.58,59
In this paper the surfaces properties were computed using periodic 2 × 2 slabs generated by cleaving a three dimensional (periodic) super-cell along the crystallographic planes of interest, and adding a 15 Å layer of vacuum space. The (111) slab was 4.318 nm thick (containing 80 atoms), the (110) slab was 4.314 nm thick (containing 128 atoms), and the (100) slab was 4.527 nm thick (containing 96 atoms). In addition to this, the 〈111〉 twinning (or stacking fault) energy was calculated with a 96 atom periodic super-cell, where all atoms where relaxed while the cell parameters were fixed to the bulk values. The relaxations were performed using an efficient matrix-diagonalization routine based on a sequential band-by-band residual minimization method of single-electron energies69,70 with direct inversion in the iterative subspace.
This provides values of γ111 = 1.160 J m−2, γ110 = 1.594 J m−2, γ100 = 1.373 J m−2; σ111 = 1.443 J m−2, σ110 = 1.708 J m−2, σ100 = 1.591 J m−2; and ν111 = 0.086 J m−2 for Pd. These are the same types of configurations that have previously proven sufficient for simulating gold in ref. 54, and platinum in ref. 55. More information on these structures and a thorough comparison with others reported in the literature is available in the ESI.† The re-entrant line tensions of η111 = −0.0545 × 10−9 J m−1 and η100 = 0.0708 × 10−9 J m−1 were obtained by fitting to the total energies of isolated decahedral Pd nanoparticles calculated with the same computational settings (above), using the same technique described for the cases of gold and platinum.
At this point it should be pointed out that DFT has some issues in the simulation of surface and surface energies,71,72 and uncertainties will still be present. While it is, of course, possible to improve the accuracy of the individual calculations by increasing the computational complexity73 (and the computational cost), since these values are ultimately used to parameterise the model (which provides another level of approximation) all of these advantages are typically lost, when the systematic increase in accuracy cancels out (just as the systematic errors do). It is the relativity of the values that is important.
Since these DFT calculations have been performed at T ≈ 0, a number of simple expressions must be included to introduce the entropic contributions. There are a number of different ways of doing this, including the harmonic approximation (based on the vibrational density of states), lambda integration or thermodynamic integration;74 however, in the case of metals one may use the linear expression proposed by Guggenheim:75
 | (2) |
 | (3) |
3 Results and discussion
Using this established methodology, the temperature-dependent free energy was predicted for the range of monocrystalline shapes (free of twin planes) displayed in Fig. 1, as shown for the example of T = 300 K in Fig. 2. This collection of shapes including the tetrahedron, the minimally truncated tetrahedron, the truncated tetrahedron and the regular octahedron (which are all enclosed are exclusively by {111} facets); the minimally truncated octahedron, the truncated octahedron, the cuboctahedron the truncated regular hexahedron or truncated cube (enclosed by combinations of {111} and {100} facets); the regular hexahedron, or cube, (enclosed exclusively by {100} facets); and variations on the rhombic dodecahedron (enclosed by {110} facets) with truncations in the 〈100〉 and 〈111〉 directions.![The defect-free palladium nanomorphologies considered in this study. The first four shapes [(a) the regular tetrahedron, (b) the minimally-truncated tetrahedron, (c) the truncated tetrahedron, and (d) the octahedron] are entirely enclosed by {111} facets, whereas the following shapes [(e) the minimally-truncated octahedron, (f) the truncated octahedron, (g) the cuboctahedron and (h) truncated hexahedron] are enclosed by an increasingly large fraction of {100} facets, until we reach the hexahedron (i) which is entirely enclosed by {100} facets. The final shapes [(j) cubo-rhombic dodecahedron, (k) rhombic dodecahedron, and (l) octo-rhombic dodecahedron] are based on the rhombic dodecahedron, enclosed by a combination of {100} and {110} facets, entirely with {110} facets, and a combination of {111} and {110} facets, respectively.](/image/article/2012/CY/c2cy20017a/c2cy20017a-f1.gif) | ||
| Fig. 1 The defect-free palladium nanomorphologies considered in this study. The first four shapes [(a) the regular tetrahedron, (b) the minimally-truncated tetrahedron, (c) the truncated tetrahedron, and (d) the octahedron] are entirely enclosed by {111} facets, whereas the following shapes [(e) the minimally-truncated octahedron, (f) the truncated octahedron, (g) the cuboctahedron and (h) truncated hexahedron] are enclosed by an increasingly large fraction of {100} facets, until we reach the hexahedron (i) which is entirely enclosed by {100} facets. The final shapes [(j) cubo-rhombic dodecahedron, (k) rhombic dodecahedron, and (l) octo-rhombic dodecahedron] are based on the rhombic dodecahedron, enclosed by a combination of {100} and {110} facets, entirely with {110} facets, and a combination of {111} and {110} facets, respectively. | ||
 | ||
| Fig. 2 The free energy of each shape shown in Fig. 1, at T = 300 K. | ||
When G(T) is calculated for each of these shapes as a function of size there is a multitude of crossing points, indicative of the characteristic size and energy of the morphological transformation between pairs of shapes; though some are shallow, indicating kinetics are important. The majority of these morphological transformations are non-equilibrium events between high energy (unstable) shapes, and are therefore not relevant to the identification of the lowest energy morphologies. They are however, interesting if one were concerned with following a transformation trajectory that involved a cascade of transformations, but a study of this type should also include estimates of the transformation barriers (which are kinetic features, and are not considered here).
Of course, the lowest energy shapes, and therefore the size-dependent transformations of interest, change as a function of temperature. By combining all of these models, and systematically calculating the size-dependent free energy at 5 K intervals (from T = 0 K to T = 2000 K), it is possible to map the lowest energy fcc shape in 〈N,T〉 space, as shown in Fig. 3. In this diagram the lower limit is a consequence of the model, and is not related to palladium. At sizes below ∼3 nm there are a number of other thermodynamic influences (such as point defects, specific edge and corner reconstructions, or changes in symmetry) that may become important, but are not included in the model. Readers should also note due to the different cross-sections presented by shapes with equivalent numbers of atoms, it is preferable to identify morphological and phase transformations as a function of N, and then convert to relevant diameters later on.
 | ||
| Fig. 3 A restricted morphology map showing the lowest energy monocrystalline palladium nanoparticle shapes (from candidates shown in 1), as a function of the number of Pd atoms (NPd) and the temperature (T). The grey region is inaccessible to this theoretical treatment. | ||
Although 12 different monocrystalline morphologies were compared, this map reveals that very few of these shapes participate in the low energy landscape, and some obvious trends emerge. Firstly, no shapes with {110} facets are present, which indicates that the formation of these shapes must either be kinetically driven, or governed by variations in the surface chemistry. Secondly, size-dependence is only apparent below ∼30 nm, while temperature plays a more important role in determining the shape. And finally, the stability of the {100} facets decreases with temperature, evidenced by the preference for the truncated octahedron at T ≈ 0 K, the minimally truncated octahedron at T ≈ 300 K, and the octahedron and tetrahedron over T ≈ 450 K (f100 → 0 as T → Tm). In addition to the increase in f111 with temperature, there is also a relationship between the temperature and the total surface-to-volume ratio q. As the temperature increases the isovolumetric q increases, corresponding to a decrease in sphericity, due to the increased favourability of γ111(T). This is counter intuitive, but is consistent with similar predictions and the corresponding experimental observations for platinum nanoparticles.55
At higher temperatures, when the surface melting temperature has been exceeded, surface roughening is predicted; until eventually the size-dependent bulk melting temperature is breached and the most stable particles undergo the final solid–liquid transformation (described by eqn (3)). It has been previously shown that the melting temperature is sensitive to shape, as well as size, and that tetrahedral Pd nanoparticles will melt at lower temperatures than other shapes. The difference in the size-dependent melting temperatures for Pd nanoparticles of different shapes has been explored by Guisbiers et al.80
In addition to the monocrystalline particles (above), synthesis of Pd icosahedra and twinned structures may also be achieved by a variety of methods, such as blocking oxidative etching with citric acid or citrate ions.84 Therefore, the temperature-dependent free energy was also modelled for the range of twinned morphologies displayed in Fig. 4, where the location of the twin planes has been highlighted by marking the re-entrant edges around the circumference in blue. The shapes include the tetrahedral bipyramid, the truncated tetrahedral bipyramid (sometimes called a ‘trigon’), the symmetrically twinned octahedron which is referred to as the ‘prism’, and the symmetrically twinned truncated octahedron which is referred to as the ‘truncated prism’. Each successive shape may be obtained by truncating the most acute corners from the preceding shape when following the progression from Fig. 4(a) to (d). However, only when we reach the truncated prism (Fig. 4(d)) do we finally introduce {100} facets. In addition to these configurations, the multiply twinned decahedron and the multiply twinned icosahedron were also included (see Fig. 4(e) and (f), respectively).
 | ||
| Fig. 4 The twinned and multiply-twinned palladium nanomorphologies considered in this study. The shapes include (a) the tetrahedral bipyramid, (b) the truncated bipyramid, (c) the prism, (d) the truncated prism, (e) the decahedron, and (f) the icosahedron. The location of the twin planes has been highlighted by marking the re-entrant edges around the circumference in blue (regular edges appear in red). | ||
Like the monocrystalline shapes, a comparison of the size-dependent free energy of the six twinned morphologies reveals numerous crossing points, indicative the various morphological transformations that may be expected. The lowest energy shapes, and therefore the transformation sizes, change as a function of temperature, and once again, by calculating the size-dependent free energy at 5 K intervals (from T = 0 K to T = 2000 K) these twinned morphologies can also be mapped in 〈N,T〉 space. An example of these free energy curves, at T = 300 K, in shown in Fig. 5, and the mapped results are plotted in Fig. 6, where we can see that the high temperature behavior is similar to the monocrystalline particles. At higher temperatures, surface roughening is predicted when the surface melting temperature has been exceeded, and a quasi-molten region is predicted between the size-dependent bulk melting temperature for the tetrahedral bipyramid and the quasicrystalline icosahedron which typically survives annealing to higher temperatures than any other morphology. This behavior is characteristic of metal nanoparticles, and has been rigorously studied and confirmed in the case of gold.54,81–83
 | ||
| Fig. 5 The free energy of each shape shown in Fig. 4, at T = 300 K. | ||
 | ||
| Fig. 6 A restricted morphology map showing the lowest energy twinned palladium nanoparticle shapes (from candidates shown in 4), as a function of the number of Pd atoms (NPd) and the temperature (T). The grey region is inaccessible to this theoretical treatment. | ||
Below the surface roughening transition the tetrahedral bipyramid (Fig. 4a) and prism (Fig. 4b) morphologies are expected, which is also consistent with the monocrystalline phase map, as these are the twinned versions of the tetrahedron (Fig. 1a) and octahedron (Fig. 1d), respectively. However, in contrast to the monocrystalline results, this collection of particles does exhibit size-dependent shape selectivity at low temperatures. At small sizes the decahedron is preferred, and at large sizes the truncated prism (that can also be described as a symmetrically twinned truncated octahedron) is preferred. Between these shapes, at around room temperature, the icosahedron occupies a region of the phase map (between ∼25 to ∼60 nm, at room temperature), which is consistent with experimental observations.19,84–86 While all of these shapes display a high degree of sphericity, this ordering is particularly interesting as it reveals a delicate balance between the shape, the degree of twinning, and the anisotropy in the surface properties (including the surface melting temperatures).
As described above, while the twin plane is an endothermic feature in palladium (as it is in both gold and platinum), one re-entrant line tension is endothermic and the other is exothermic, so only certain configurations of the defect are stabilized. In the case of Pt both re-entrant line tensions are endothermic, so the defect is never stable. In Au both re-entrant line tensions are exothermic, so the stability of the defect decays as ∑ϕlθ,ϕ/aθ, which is always negative. Here the defect decays as ∑ϕlθϕ/aθ but the sign depends on the ratio of lθ,111 to lθ,100. If lθ,111/lθ,100 < |η111/η100| the defect is not stabilized. This means that both the size and shape of the defect plane are important; both of which are related to the size and shape of the particle as a whole. The decahedron has a significant defect density (n = 5/V) but lθ,111 ≈ 2lθ,100, so the defect is stabilized when the particles are sufficiently small. The truncated prism has a low defect density (n = 1/V), but lθ,111 = lθ,100 so the defect is less stable at small sizes where the contribution from the defect to the total free energy is greater. The icosahedron has a very high defect density (n = 20/V) so they are not as stable as the decahedron, but ∑lθ,100 = 0 so they are more stable at small sizes than the truncated prism.
By combining all of these results, and converting NPd to the average particle diameter 〈D〉, the lowest energy morphology can be mapped in 〈D,T〉 space, and we can generate the first nanoscale phase diagram of Pd (Fig. 7). This phase diagram relates specifically to isolated nanoparticles, and indicates that, with the addition of the quasi-molten region from the twinned morphology map, the predicted morphologies and the boundaries are all consistent with the monocrystalline map above ∼400 K. At lower temperatures the phase diagram is consistent with the monocrystalline map when the nanoparticles are >40 nm in average diameter. At smaller sizes the decahedron is thermodynamically stable, due to the contribution of the exothermic η111. The icosahedron and truncated prism no longer appear in this temperature regime, as they are unstable with respect to the truncated octahedron and the minimally truncated octahedron. These predictions may differ in the presence of a support.
 | ||
| Fig. 7 The equilibrium morphology map of nanoscale palladium, as a function of the average particle diameter (〈D〉) and the temperature (T). The grey region is inaccessible to this theoretical treatment. | ||
A survey of the extensive literature of Pd nanoparticle morphologies concludes that most relevant experimental studies are in good agreement with this morphology map, but direct comparison is difficult due to systemic bias toward making specific non-equilibrium shapes (suited to particular applications) rather than the equilibrium shapes. However, in a number of cases the formation of different competing shapes was addressed. As early as 2001 Jose-Yacaman et al.25 analyzed colloidal Pd nanoparticles in the range of 1–5 nm using high resolution electron microscopy (HREM) images and studied the corresponding diffraction patterns. The results identified the as-grown nanoparticles as fcc cuboctahedrons, icosahedrons, truncated decahedrons and single-twinned fcc configurations, but did not contain sufficient observations for a populations analysis or an estimate of relative stability. Using explicit computer simulations Barreteau and co-workers succeeded in identifying a transition between icosahedral and cuboctahedral structures below 561 atoms,47 but transitions to decahedra (and other ideal or twinned shapes) were not considered. This size is smaller than the range of applicability for the model used herein, but is consistent with the fact that icosahedra do not feature in the combined equilibrium morphology map (Fig. 7) and the fact that most Pd icosahedra are engineered using surfactants and specific synthesis techniques.19,84–86
For example, Kim et al. synthesized monodisperse Pd nanoparticles of 3.5, 5, and 7 nm in diameter, via the thermal decomposition of a Pd-surfactant complex at room temperature.87 In this case the size of Pd nanoparticles was controlled by varying the concentration of stabilizing trioctylphosphine surfactant. When trioctylphosphine was used as surfactant 3.5 nm particles were obtained, but when a mixture of TOP and oleylamine was used as surfactants and solvent, Pd nanoparticles with particle sizes of 5 and 7 nm were obtained. Some time later smaller monodispersed palladium nanoparticles with sizes ranging from 1.7 to 3.5 nm were synthesized using thioethers as stabilizing ligands by Ganesan et al.88 In addition to controlling size, surfactants are also useful in controlling shape. More recently Nguyen et al. prepared palladium nanoparticles by the polyol method and proposed techniques for controlling their size and shape simultaneously.89 In this case the polyvinylpyrrolidone (PVP) stabilized Pd nanoparticles included octahedrons (24 nm), tetrahedrons (22 nm) and cubes (20 nm), which were all obtained by alcohol reduction in ethanol with the addition of a hydrochloric acid catalyst.
This highlights the importance of complex surface chemistry in determining Pd nanoparticle morphology, but even at the most simple level, it has been shown that a coating of hydrogen has an important impact on shape.90 The interaction of atomic or molecular hydrogen with Pd has other technological applications in catalysis such as in the synthesis of ammonia or olefin hydrogenation.91 Using an explicit empirical potential and a combination of Monte Carlo and molecular dynamics simulations Calvo and Carré investigate the energetic, thermal and dynamical stability of hydrogenated Pd nanoparticles containing a few hundred atoms.90 It was found that icosahedra can absorb a larger quantity of hydrogen than cubic particles, but that hydrogen rich cubic particles undergo a structural transition toward icosahedra before melting occurs. This indicates that shape, shape stability, and thermochemical conditions are all correlated, so simplified diagram was proposed to account for the observed behavior.
Beyond hydrogenation, calculations of surface free energies of the low-index (111), (100) and (110) Pd surfaces exposed to oxygen adsorbates allowed Seriani and Mittendorfer92 to predict the adsorbate-induced changes in the thermodynamic equilibrium shape under oxidizing conditions. At a low oxygen chemical potential, corresponding to clean surfaces, they found that {111} facets dominate the nanomorphology, with a significant contribution from {100} facets, and a small contribution from higher energy {110} facets. As the degree of oxygen adsorption increases, the contribution from the {110} facets was also found to increase. At high oxygen partial pressures, surface oxides form, and the surfaces will display different chemical properties than the metal, and this will change the morphology altogether.
Before concluding it is also prudent to remind readers that the shape of Pd nanoparticles, like many other metallic nanoparticles, are a function of both kinetic and thermodynamic considerations. The morphological diversity of Pd nanoparticles is the most likely a combined effect of different (twinned and monocrystalline) seeds formed in the nucleation stage, followed by and selectively adsorption of monomers on one set of crystallographic facets over another during coarsening. These effects cannot be explored using the methods applied herein, and one must turn to complementary kinetic modeling techniques.93–98 Nevertheless, regardless of what it formed post-synthesis, the thermal and mechanical perturbations experienced by Pd nanoparticles during applications may drive morphological transformations, and a map of the expected morphology is useful in anticipating the outcomes.
4 Conclusions
In conclusion, based on first principles electronic structure computer simulations, and a well established shape-dependent thermodynamic model, the free energy of a large number of palladium nanoparticle morphologies has been compared, and the lowest energy structure predicted as a function of size and temperature. These predictions have been used to generate the first nanoscale phase diagram of Pd, which shows that (even though relative stability is influenced by surface anisotropy, degree of sphericity and the type of twinning configurations) monocrystalline shapes are thermodynamically preferred under most conditions. Only at low temperature, and small sizes, are multiply-twinned decahedra stable, due to the exothermic contribution of the re-entrant line tension where the twin plane intersects with a {111} surface. This work could be further refined, via the inclusion of higher index facets, to describe more rounded shapes or alternative structures, and this is ongoing.While the size of the nanoparticles determines the selectivity between the quasi-spherical decahedral and truncated octahedral shapes at low temperature, the morphology is far more heavily influenced by temperature. In general, the fraction of {111} facets increases with increasing temperature, due to the lower surface melting temperature, while the degree of sphericity decreases. This strong temperature dependence indicates that thermal fluctuations or incidental annealing may have impact catalytic performance, although arguably not as significantly as surface mass diffusion and other kinetic effects such as adsorbate induced restructuring. In addition to the catalytic properties, the shape will also have implications for the surface-enhanced Raman scattering (SERS) and magnetic properties of Pd nanostructures, which have also been previously reported.99–104
Based on these findings, future work will be directed toward determining how the transition boundaries are affected by varying the surface chemistry, which will be particularly important during catalytic reactions, and is influential in engineering shapes during synthesis (as discussed above). The inclusion of surface hydrogenation and oxidation (within the framework of ab initio thermodynamics) is on going, and it will be interesting to see how the morphology map varies under different conditions.
Acknowledgements
This project has been supported by the Australian Research Council (ARC) under grant number DP0986752. Computational resources for this project have been supplied by the National Computing Infrastructure (NCI) national facility under MAS Grant p00.References
- B. K. Hodnett, Heterogeneous Catalytic Oxidation, Wiley, NY, 2000 Search PubMed.
- H. S. Gandhi, G. W. Graham and R. W. McCabe, J. Catal., 2003, 216, 433 CrossRef CAS.
- Y. Nishihata, J. Mizuki, T. Kao, H. Tanaka, M. Enishi, M. Imura, T. Kamoto and N. Hamada, Nature, 2002, 418, 164 CrossRef CAS.
- Y. Suchorski and W. Drachsel, Top. Catal., 2007, 46, 201 CrossRef CAS.
- R. Narayanan and M. A. El-Sayed, Langmuir, 2005, 21, 2027 CrossRef CAS.
- A. Züttel, Mater. Today (Oxford, U. K.), 2003, 6, 24 Search PubMed.
- Y. Sun, Z. Tao, J. Chen, T. Herricks and Y. Xia, J. Am. Chem. Soc., 2004, 126, 5940 CrossRef CAS.
- F. Favier, E. C. Walter, M. P. Zach, T. Benter and R. M. Penner, Science, 2001, 293, 2227 CrossRef CAS.
- A. Molnár, A. Sárkány and M. Varga, J. Mol. Catal. A: Chem., 2001, 173, 185 CrossRef.
- D. Teschner, J. Borsodo, A. Wootsch, Z. Révay, M. Hävecker, A. Knop-Gericke, S. D. Jackson and R. Schlögl, Science, 2008, 320, 86 CrossRef CAS.
- M. García-Mota, B. Bridiera, J. Pérez-Ramíreza and N. López, J. Catal., 2011, 273, 92 CrossRef.
- B. Bridier and J. Pérez-Ramírez, J. Catal., 2011, 284, 165 CrossRef CAS.
- M. W. Tew, M. Janousch, T. Huthwelker and J. A. van Bokhoven, J. Catal., 2011, 283, 45 CrossRef CAS.
- M. Crespo-Quesada, A. Yarulin, M. Jin, Y. Xia and L. Kiwi-Minsker, J. Am. Chem. Soc., 2011, 133, 12787 CrossRef CAS.
- C. Burda, X. B. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025 CrossRef CAS.
- M. A. El-Sayed, Acc. Chem. Res., 2004, 37, 326 CrossRef CAS.
- S. E. Habas, H. Lee, V. Radmilovic, G. A. Somorjai and P. D. Yang, Nat. Mater., 2007, 6, 692 CrossRef CAS.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648 CrossRef CAS.
- Y. Xiong and Y. Xia, Adv. Mater., 2007, 19, 3385 CrossRef CAS.
- T. K. Sau and A. L. Rogach, Adv. Mater., 2010, 22, 1781 CrossRef CAS.
- S. Cheong, J. D. Watt and R. D. Tilley, Nanoscale, 2010, 2, 2045 RSC.
- B. Lim, M. J. Jiang, J. Tao, P. H. C. Camargo, Y. M. Zhu and Y. N. Xia, Adv. Funct. Mater., 2009, 19, 189 CrossRef CAS.
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310 CrossRef CAS.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60 CrossRef CAS.
- M. Jose-Yacaman, M. Marín-Almazo and J. A. Ascencio, J. Mol. Catal. A: Chem., 2001, 173, 61 CrossRef CAS.
- F. Baletto and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155408 CrossRef.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856 CrossRef CAS.
- W. Niu, L. Zhang and G. Xu, ACS Nano, 2010, 4, 1987 CrossRef CAS.
- L. Zhang, W. Niu and G. Xu, Nanoscale, 2011, 3, 678 RSC.
- J. M. Petroski, Z. L. Wang, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 3316 CrossRef CAS.
- T. Teranishi and M. Miyake, Chem. Mater., 1998, 10, 594 CrossRef CAS.
- J. H. Ding and D. L. Gin, Chem. Mater., 2000, 12, 22 CrossRef CAS.
- A. Henglein, J. Phys. Chem. B, 2000, 104, 6684 Search PubMed.
- X. M. Lin, H. M. Jaeger, C. M. Sorensen and K. J. Klabunde, J. Phys. Chem. B, 2001, 105, 3353 CrossRef CAS.
- Y. Li and M. A. El-Sayed, J. Phys. Chem. B, 2001, 105, 8938 CrossRef CAS.
- I. Quiros, M. Yamada, K. Kubo, J. Mizutani, M. Kurihara and H. Nishihara, Langmuir, 2002, 18, 1413 CrossRef CAS.
- J. E. Martin, J. P. Wilcoxon, J. Odinek and P. Provencio, J. Phys. Chem. B, 2002, 106, 971 CrossRef CAS.
- S. Stoeva, K. J. Klabunde, C. M. Sorensen and I. Dragieva, J. Am. Chem. Soc., 2002, 124, 2305 CrossRef CAS.
- B. L. V. Prasad, S. I. Stoeva, C. M. Sorensen and K. J. Klabunde, Chem. Mater., 2003, 15, 935 CrossRef CAS.
- S. I. Stoeva, B. L. V. Prasad, S. Uma, P. K. Stoimenov, V. Zaikovski, C. M. Sorensen and K. J. Klabunde, J. Phys. Chem. B, 2003, 107, 7441 CrossRef CAS.
- S.-W. Kim, J. Park, Y. Jang, Y. Chung, S. Hwang and T. Hyeon, Nano Lett., 2003, 3, 1289 CrossRef CAS.
- H. Song, F. Kim, S. Connor, G. A. Somorjai and P. Yang, J. Phys. Chem. B, 2005, 109, 188 CrossRef CAS.
- V. L. Nguyen, D. C. Nguyen, H. Hirata, M. Ohtaki, T. Hayakawa and M. Nogami, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2010, 1, 035012 CrossRef.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443 CrossRef CAS.
- R. J. Wolf, K. A. Mansour, M. W. Lee and J. R. Ray, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 8027 CrossRef CAS.
- C. Rey, L. J. Gallego, J. Garćýa-Rodeja, J. A. Alonso and M. P. Iñiguez, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 8253 CrossRef CAS.
- C. Barreteau, M. C. Desjonquères and D. Spanjaard, Eur. Phys. J. D, 2000, 11, 395 CrossRef CAS.
- Y. Xie and J. A. Blackman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195115 CrossRef.
- D. R. Jennison, P. A. Schultz and M. P. Sears, Chem. Phys., 1997, 106, 1856 CAS.
- S. Krüger, S. Vent, F. Nörtemann, M. Staufer and N. Rösch, J. Chem. Phys., 2001, 115, 2082 CrossRef.
- V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 144413 CrossRef.
- P. Nava, M. Sierka and R. Ahlrichs, Phys. Chem. Chem. Phys., 2003, 5, 3372 RSC.
- Z. Kaszkur, J. Appl. Crystallogr., 2000, 33, 1262 CrossRef CAS.
- A. S. Barnard, N. P. Young, A. I. Kirkland, M. A. van Huis and H. F. Xu, ACS Nano, 2009, 3, 1431 CrossRef CAS.
- A. S. Barnard, H. Konishi and H. F. Xu, Catal. Sci. Technol., 2011, 1, 1440 CAS.
- A. S. Barnard, Rep. Prog. Phys., 2010, 73, 086502 CrossRef.
- A. S. Barnard, X. M. Lin and L. A. Curtiss, J. Phys. Chem. B, 2005, 109, 24465 CrossRef CAS; A. S. Barnard and L. A. Curtiss, J. Mater. Chem., 2007, 17, 3315 RSC; A. S. Barnard, J. Phys. Chem. C, 2008, 112, 1385 Search PubMed.
- L.-Y. Chang, A. S. Barnard, L. C. Gontard and R. E. Dunin-Borkowski, Nano Lett., 2010, 10, 3073 CrossRef CAS.
- A. S. Barnard and L. Y. Chang, ACS Catal., 2011, 1, 76 CrossRef CAS.
- A. S. Barnard and L. A. Curtiss, ChemPhysChem, 2006, 7, 1544 CrossRef CAS.
- A. S. Barnard, Comput. Phys. Commun., 2011, 182, 11 CrossRef CAS.
- R. Lamber, S. Wetjen and N. I. Jaeger, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 10968 CrossRef CAS.
- A. S. Barnard, R. R. Yeredla and H. Xu, Nanotechnology, 2006, 17, 3039 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, RC558 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- D. M. Wood and A. Zunger, J. Phys. A: Math. Gen., 1985, 18, 1343 CrossRef CAS.
- A. Stroppa and G. Kresse, New J. Phys., 2008, 10, 063020 CrossRef.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741 CrossRef CAS.
- A. E. Mattson and W. Kohn, J. Chem. Phys., 2001, 115, 3441 CrossRef.
- J. M. Rickman and R. LeSar, Annu. Rev. Mater. Res., 2002, 32, 195 CrossRef CAS.
- E. A. Guggenheim, Thermodynamics, North Holland, 4th edn, 1993 Search PubMed.
- A. V. Grosse, J. Inorg. Nucl. Chem., 1962, 24, 147 CrossRef CAS.
- G. A. Somorjai, Introduction to surface chemistry and catalysis, John Wiley & Sons, Inc., New York, 1994 Search PubMed.
- P. Buffat and J. P. Borel, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 2287 CrossRef CAS.
- W. H. Qi and M. P. Wang, Mater. Chem. Phys., 2004, 88, 280 CrossRef CAS.
- G. Guisbiers, G. Abudukelimu and D. Hourlier, Nanoscale Res. Lett., 2011, 6, 396 CrossRef.
- K. Koga, T. Ikeshoji and K. Sugawara, Phys. Rev. Lett., 2004, 92, 115507 CrossRef.
- H.-S. Nam, N. M. Hwang, B. D. Yu and J.-K. Yoon, Phys. Rev. Lett., 2002, 89, 275502 CrossRef.
- Y. Wang, S. Teitel and C. Dellago, J. Chem. Phys., 2005, 122, 214722 CrossRef.
- Y. Xiong, J. M. McLellan, Y. Yin and Y. Xia, Angew. Chem., Int. Ed., 2007, 46, 790 CrossRef CAS.
- Y. Chen, B. He, T. Huang and H. Liu, Colloids Surf., A, 2009, 348, 145 CrossRef CAS.
- C. Li, R. Sato, M. Kanehara, H. Zeng, Y. Bando and T. Teranishi, Angew. Chem., Int. Ed., 2009, 48, 6883 CrossRef CAS.
- S.-W. Kim, J. Park, Y. Jang, Y. Chung, S. Hwang, T. Hyeon and Y. W. Kim, Nano Lett., 2003, 3, 1291 Search PubMed.
- M. Ganesan, R. G. Freemantle and S. O. Obare, Chem. Mater., 2007, 19, 3464 CrossRef CAS.
- V. L. Nguyen, D. C. Nguyen, H. Hirata, M. Ohtaki, T. Hayakawa and M. Nogami, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2010, 1, 035012 CrossRef.
- F. Calvo and A. Carré, Nanotechnology, 2006, 17, 1292 CrossRef CAS.
- D. A. King and D. P. Woodruff, The Chemical Physics of Solid Surfaces and Heterogeneous Catalysis, Elsevier, Amsterdam, 1982 Search PubMed.
- N. Seriani and F. Mittendorfer, J. Phys.: Condens. Matter, 2008, 20, 184023 CrossRef.
- A. S. Seyed-Razavi, I. K. Snook and A. S. Barnard, J. Mater. Chem., 2010, 20, 416 RSC.
- I. M. Lifshitz and V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35 CrossRef CAS; C. Wagner, Z. Electrochem., 1961, 65, 581 Search PubMed.
- T. Sugimoto, Adv. Colloid Interface Sci., 1987, 28, 65 CrossRef CAS.
- J. van Embden, J. E. Sader, M. Davidson and P. Mulvaney, J. Phys. Chem. C, 2009, 113, 16342 CAS.
- A. S. Seyed-Razavi, I. K. Snook and A. S. Barnard, Cryst. Growth Des., 2011, 11, 158 CAS.
- A. S. Barnard and Y. Chen, J. Mater. Chem., 2011, 21, 12239 RSC.
- J. M. McLellan, Y. J. Xiong, M. Hu and Y. N. Xia, Chem. Phys. Lett., 2006, 417, 230 CrossRef CAS.
- Z. Q. Tian, Z. L. Yang, B. Ren, J. F. Li, Y. Zhang, X. F. Lin, J. W. Hu and D. Y. Wu, Faraday Discuss., 2006, 132, 159 RSC.
- M. E. Abdelsalam, S. Mahajan, P. N. Bartlett, J. J. Baumberg and A. E. Russell, J. Am. Chem. Soc., 2007, 129, 7399 CrossRef CAS.
- T. Taniyama, E. Ohta and T. Sato, Europhys. Lett., 1997, 38, 195 CrossRef CAS.
- B. D. Shanina, A. M. Danishevskii, A. I. Veinger, A. A. Sitnikova, R. N. Kyutt, A. V. Shchukarev and S. K. Gordeev, J. Exp. Theor. Phys., 2009, 109, 609 CrossRef CAS.
- C. W. Xiao, H. Ding, C. M. Shen, T. Z. Yang, G. Hui and H. J. Gao, J. Phys. Chem. C, 2009, 113, 13466 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of electronic structure calculations and comparison of simulations results to values reported in the literature. See DOI: 10.1039/c2cy20017a |
| This journal is © The Royal Society of Chemistry 2012 |
