 Open Access Article
Open Access ArticleMixtures of ionic liquids
Heiko
Niedermeyer
,
Jason P.
Hallett
,
Ignacio J.
Villar-Garcia
,
Patricia A.
Hunt
and
Tom
Welton
*
Department of Chemistry, Imperial College London, London, SW7 2AZ, UK. E-mail: t.welton@imperial.ac.uk
First published on 13th August 2012
Abstract
Simple ionic liquids have long been held to be designer solvents, based upon the ability to independently vary their cations and anions. The formation of mixtures of ionic liquids increases this synthetic flexibility. We review the available literature of these ionic liquid mixtures to identify how their properties change and the possibility for their application.
 Heiko Niedermeyer | Dr Heiko Niedermeyer was awarded his undergraduate degree in Chemistry from the Philipps-Universität Marburg, Germany in 2008. During his undergraduate studies he undertook a student exchange project at Imperial College London in the groups of Prof. Tom Welton and Dr Patricia Hunt, where he returned for his PhD research. He was awarded his degree in 2011, working on the physical and physicochemical properties of mixtures of ionic liquids. In January 2012 he joined the group of Prof. Peter Wasserscheid at the Friedrich-Alexander Universität Erlangen-Nürnberg, Germany. |
 Jason P. Hallett | Jason P. Hallett received his PhD in Chemical Engineering from the Georgia Institute of Technology with Prof Charles Eckert and Prof Charles Liotta, studying homogenous catalysis and novel separations in high pressure CO2 mixtures with organic solvents and ionic liquids. He joined Imperial College in 2006 with a Marshall-Sherfield Postdoctoral Fellowship in Sustainable Chemistry and is now a Research Lecturer in the Department of Chemistry. He has authored over 50 articles and holds 4 patents. His current research interests involve the solvation behaviour of ionic liquids and the use of ionic liquids in the production of lignocellulosic biofuels. |
 Ignacio J. Villar-Garcia | Ignacio J. Villar-Garcia received his Chemical Engineering Degree and Masters from the University of Oviedo. He obtained his PhD at the University of Nottingham in 2009 under the supervision of Dr Peter Licence studying ionic liquids, ionic liquid catalytic solutions and mixtures of ionic liquids using X-ray photoelectron spectroscopy (XPS). He then spent two years as an Assistant Professor at Addis Ababa University, where he also worked on ionic liquid based projects. Currently, Ignacio works as a Research Associate in the Chemistry Department, Imperial College London. His research focuses on the study of mixtures of ionic liquids using different spectroscopic techniques. |
 Patricia Hunt | Patricia Hunt studied chemistry and physics at the University of Auckland, New Zealand, where she received her BSc, MSc, BA and then PhD (1998) working with Prof. Peter Schwerdtfeger. She then left New Zealand for King's College London and worked at the group of Prof. M. Robb (FRS). Patricia subsequently moved to Cambridge University, to work with Dr M. Sprik investigating condensed phase solvation dynamics using ab initio MD. In 2003 Patricia was awarded a Royal Society URF and has since established a research group at Imperial College London. Her main interests include theoretical and computational investigation of liquids, solvation, chemical reactivity and catalysis. |
 Tom Welton | Tom Welton, Head of the Department of Chemistry and the world’s first Professor of Sustainable Chemistry, is interested in using solvents to improve chemical processes. He has worked with ionic liquids throughout his research career and also with other solvents e.g. siloxanes, PEG's and solvents from renewable resources, all with a view to the development of sustainable solvent technologies. He is particularly interested in clean synthesis and catalysis and the central academic aim of his research is to understand the role that the immediate chemical environments in which reacting species find themselves influence the reaction process. |
Introduction
Ionic liquids are liquids that consist entirely of ions. The commonly used criterion that they should melt below 100 °C is arbitrary and has no physical meaning. However, it has become popular, largely because it represents a condition at which these are easier to handle than salts that melt at elevated temperatures. Many ionic liquids even melt below room-temperature. Since the beginning of this century, ionic liquids have undergone a transformation from interesting, but poorly known, materials to being the subjects of huge research activity.1 There has been an explosion of academic research2 and their introduction in industrial applications is well underway.3 Much of this interest has centred on their designation as “designer solvents”;4i.e., they can be fine-tuned by the independent selection of cation and anion to be the optimum solvent for a given application. It is even possible to use computational results to design an ionic liquid that has yet to be made. This designer solvent concept has led to intense study of how changing ionic liquid ions can affect their physico-chemical properties.1,2 As extensive as the ability to design ionic liquids by selection of cations and anions is, recently attempts have been made to take this idea further by using mixtures of ionic liquids. It is these mixtures that are the subjects of this review.Nomenclature
Ionic liquid mixtures
Most ionic liquids are [A][X] salts with one cation [A]+ and one anion [X]−, each with a single charge, and there has been no problem with describing these, but how should the mixtures of ionic liquids [A][X] + [B][X] or [A][X] + [A][Y] be named? Already different nomenclatures are appearing for mixed ionic liquids. There are two practices that have emerged in the literature. The overlap of terms between these makes for an extremely complicated situation and the reader is cautioned to take great care to be sure which is being used when reading any particular paper. The first is based upon the number of constituents in the product mixture while the second is based upon the number of components in the product mixture. The differences between these are subtle, but very important. We describe these below.5A constituent of a chemical system is any distinct chemical species, such as an individual molecule or ion, that is present in the system. A component is more precisely a chemically independent constituent. An ion is not a component, because it depends upon the presence of a counter ion to be stable.
Before going on to discuss ionic liquid mixtures, it is worth using a more familiar example of a salt solution in a molecular solvent to explain this. A mixture of ethanol and water has two constituents, ethanol and water; it also has two components, again ethanol and water. A solution of NaCl in water has three constituents (assuming that it is fully dissociated to free ions), water, Na+ and Cl−. However, it only has two components, water and NaCl. This is because the need for charge balance requires that the number of Na+ ions must be equal to the number of Cl− ions, so these are not chemically independent.
In both of the systems of ionic liquid nomenclature in use [A][X] + [B][X] is abbreviated to [A]a[B]b[X] (where a is the mole fraction of [A], X{[A]} and b is the mole fraction of [B], X{[B]}) and [A][X] + [A][Y] is abbreviated to [A][X]x[Y]y (where x = X{[X]} and y = X{[Y]}). If one classifies mixtures of ionic liquids by the number of constituents that are present in the system [A]a[B]b[X] are called ternary (3 constituent) ionic liquids. Following from this, [A]a[B]b[X]x[Y]y, [A]a[B]b[C]c[X] and [A]a[X]x[Y]y[Z]z are quaternary (4 constituent) ionic liquids and indeed [A][X] salts are binary ionic liquids. If, on the other hand, one classifies mixtures of ionic liquids by the number of components that are present in the system [A]a[B]b[X] and [A][X]x[Y]y are called binary (2 component) ionic liquids. This is because the phase diagram requires both, but only [A][X] and [B][X] in the former case and [A][X] and [A][Y] in the latter case for it to be fully described. So here, binary ionic liquid mixtures are those prepared by mixing two ionic liquids. Now let us consider the mixture [A]a[B]b[X]x[Y]y. If a ≠ x and b ≠ y, one needs to use three simple ionic liquids, such as [A][X], [B][Y] and [B][X], or [A][X], [B][Y] and [A][Y] to make this and three components to describe it. Such systems are called ternary reciprocal ionic liquids. The use of the designation reciprocal differentiates these from [A]a[B]b[C]c[Y] and [A][X]x[Y]y[Z]z systems, which are also ternary (3 component) ionic liquids. Finally, if one makes an ionic liquid [A]a[B]b[X]x[Y]y by mixing two simple ionic liquids, [A][X] and [B][Y], or [B][X] and [A][Y], this gives an extra constraint, a = x and b = y for the former, and b = x and a = y for the latter. This constraint reduces the number of components necessary to define the system to two, so these special cases can be designated as binary reciprocal ionic liquid mixtures. In this classification [A][X] salts are simple ionic liquids. Reading of the literature of molten salts shows that the distinction was rarely made between the different types of reciprocal molten salts and that they were all called reciprocal molten salts.
It is also necessary to consider the cases where a reaction occurs upon mixing to form new ions, such as the formation of complex ions in halogenometalate ionic liquids:
| [A][X] + MXn ⇌ [A][MXn+1] | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures there is no conflict between the two nomenclatures; both describe these as binary ionic liquids (two constituents [A]+ and [MXn+1]− and two components [A][X] and MXn). However, if these are not 1
1 mixtures there is no conflict between the two nomenclatures; both describe these as binary ionic liquids (two constituents [A]+ and [MXn+1]− and two components [A][X] and MXn). However, if these are not 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures complications again arise, e.g. if [A][X] is in excess:
1 mixtures complications again arise, e.g. if [A][X] is in excess:| 2[A][X] + MXn ⇌ [A][X] + [A][MXn+1] | (2) |
When different nomenclatures are in use, the question arises of which is the better. This can be tackled in several different ways:
(i) Simplicity. Simplicity and clarity are usually the best reasons to do anything. Many people prefer nomenclature based upon constituents, because at first glance it is relatively simple. You know which ions are present and count these. However, as described above, problems can arise for ionic liquid mixtures in which reactions occur. For example, since their introduction it has always been known that the anions in chloroaluminate ionic liquids enter into complex equilibria:6
| 2[AlCl4]− ⇌ [Al2Cl7]− + Cl− | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AlCl3
1 AlCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl− composition the [Al3Cl10]− ion was also present.7 So what would once have been considered to be a ternary ionic liquid ([A]+, [AlCl4]− and [Al2Cl7]−), must now be recognised to be a quaternary ionic liquid ([A]+, [AlCl4]−, [Al2Cl7]− and [Al3Cl10]−). Whereas, in spite of all of this, this is only ever a 2 component (binary) ionic liquid, usually written as [A]Cl–AlCl3.6
Cl− composition the [Al3Cl10]− ion was also present.7 So what would once have been considered to be a ternary ionic liquid ([A]+, [AlCl4]− and [Al2Cl7]−), must now be recognised to be a quaternary ionic liquid ([A]+, [AlCl4]−, [Al2Cl7]− and [Al3Cl10]−). Whereas, in spite of all of this, this is only ever a 2 component (binary) ionic liquid, usually written as [A]Cl–AlCl3.6
(ii) Thermodynamics. As with all chemistry, mixing is ultimately a thermodynamic process. At the heart of our understanding of the thermodynamics of mixing lies Raoult's law. Regardless of whether reactions occur or not, Raoult's law is based upon the mixing of components. If thermodynamic properties are being discussed, nomenclature based upon components is the most appropriate.
(iii) Semantics. Many people consider that when two (or more) ionic liquids are mixed, the product is a completely new ionic liquid. Indeed, this is the basis on which it is suggested that 1018 ionic liquids can be made.8 Alternatively, one can consider the product to be a mixture of ionic liquids. If one prefers the latter approach then the component based nomenclature is more appropriate, if one prefers the former then the constituent approach is closer. We suggest that the former approach can only be strictly applicable for ionic liquids of defined composition, i.e., [A]0.2[B]0.8[X] is a different ionic liquid to [A]0.3[B]0.7[X], again implied by suggestions of 1018 ionic liquids being possible. A more generalised description, i.e., [A]a[B]b[X], recognises that this is a mixture of varying composition.
(iv) Agreement with previous methodologies. Mixtures of molten salts have been known for a very long time. These have a well-established nomenclature, which is based upon the number of components in the system.9,10 While it is not necessary to stay with old methodologies, one should only break with these when there is a good reason to do so.
It is not possible, nor desirable, to dictate the behaviours of others, particularly when practices have already become established. However, while authors are free to choose the nomenclature that they prefer, we recommend strongly that they make it explicitly clear which they are using. Here we will use the nomenclature based upon components, i.e., [A]a[B]b[X] and [A][X]x[Y]y are called binary (2 component) ionic liquids (Table 1). To simplify further we will only include the subscripts when referring to a particular composition of the mixture, e.g., [A]0.2[B]0.8[X]; we will allow [A][B][X] to refer to the mixture in all compositions. Finally, we will follow the convention of listing all of the cations first, followed by the anions, with these each being listed in order of their masses.
| Mixture | Abbreviation | No. of components | No. of constituents | Name |
|---|---|---|---|---|
| None | [A][X] | 1 | 2 | Simple |
| [A][X] + [A][Y] or [A][X] + [B][X] | [A][X][Y] or [A][B][X] | 2 | 3 | Binary |
| [A][X] + [B][Y] | [A][B][X][Y] | 2 | 4 | Reciprocal binary |
| [A][X] + [B][X] + [B][Y] or [A][X] + [A][Y] + [B][Y] | [A][B][X][Y] | 3 | 4 | Reciprocal ternary |
| [A][X] + [A][Y] + [A][Z] or [A][X] + [B][X] + [C][X] | [A][X][Y][Z] or [A][B][C][X] | 3 | 4 | Ternary |
Ionic liquid abbreviations
Ionic liquids contain organic cations, usually quaternised aromatic and aliphatic ammonium ions. Alkylphosphonium and alkylsulfonium cations are also in use. A representative selection of common cations is shown in Fig. 1. Ionic liquid cations often have lengthy names, therefore a notation of the form [CnCm(CoCp)x(yz)] will be adopted throughout this paper, in which C signifies an alkyl chain (up to 4 alkyl chains can be attached to the cation core), with subscripts denoting the chain length (all methylene units plus the terminal methyl group) and x(yz) defines the cation core (e.g., N for ammonium, im for imidazolium, pyr for pyridinium and pyrr for pyrrolidinium salts).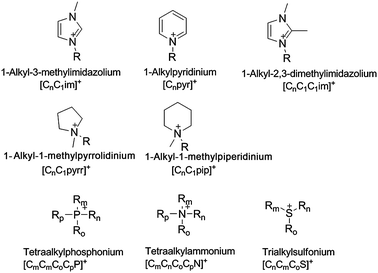 | ||
| Fig. 1 Some common cations used in ionic liquids, with their abbreviations. | ||
Ionic liquid anions are either inorganic or organic (Fig. 2). With the exception of halide anions, the negative charge is usually distributed over several atoms. Many anions are substituted with fluorine atoms, such as trifluoromethanesulfonate or tetrafluoroborate.
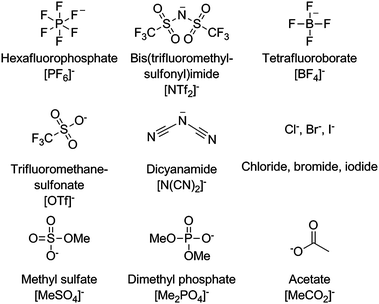 | ||
| Fig. 2 Some common anions used in ionic liquids and their abbreviations. | ||
Raoult's law and ideal solutions
This review is not a treatise on thermodynamics, but it is worth restating some of the fundamentals of mixing and particularly defining what is an ideal solution.5 The concept of an ideal mixture comes from the observations of François Raoult that at a given temperature the ratio of partial vapour pressure of a component A above a liquid mixture (pA) to its vapour pressure as a pure liquid (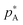 ) is approximately equal to its mole fraction in the liquid mixture (XA):
) is approximately equal to its mole fraction in the liquid mixture (XA):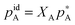 | (4) |
It is better to define ideality in terms of chemical potential. An ideal solution is the one in which the chemical potential of a component of a mixture (μA) can be related to the chemical potential of the pure component (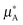 ) and its mole fraction in the solution such that:
) and its mole fraction in the solution such that:
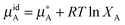 | (5) |
ΔGidmix = nRT(XA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XA + XB XA + XB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XB) XB) | (6) |
ΔSidmix = nR(XA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XA + XB XA + XB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XB) XB) | (7) |
| ΔHidmix = ΔGidmix +TΔSidmix = 0 | (8) |
The belief that all properties of an ideal solution should always change in a linear manner with changing composition of the mixture is a common mistake. Only those properties of an ideal solution that are directly thermodynamically related to eqn (5) and Raoult's law must be a linear function of composition (mole fraction of the components), others may be not so. For example, spectroscopic properties are often non-linear in ideal mixtures.11 When linear behaviour would be expected for ideal behaviour, deviation from the expected value is described as the excess function, e.g., the difference between the observed volume of mixing and the ideal volume of mixing is the excess volume of mixing, VE, which can take both positive and negative values.
The final definition of an ideal solution is that the activity coefficients (γ) of all constituents of the mixture are equal to 1. Values in excess of one indicate positive deviation from Raoult's law and values less than one indicate negative deviation from Raoult's law.
Regular solutions are those that have ideal entropies of mixing (eqn (7)), but non-zero enthalpies of mixing. In these cases, there is usually a simple relationship between activity coefficients and the mole fraction of the components. Many mixtures of molten salts, e.g. AgBr with Group 1 metal bromides,12 have been found to be regular solutions.
Finally, one should consider athermal solutions, which have ideal enthalpies of mixing (ΔHmix = 0), but non ideal entropies of mixing. This case has been found for mixtures of components that are similar in their chemical characteristics and have different sizes, such as mixtures of polystyrene with toluene or ethylbenzene and mixtures of polydimethylsiloxane with hexamethyldisiloxane.13
Thermodynamics of mixing ionic liquids, ΔHmix and ΔSmix
Very few direct measurements of the thermodynamics of mixing of ionic liquids have been reported in the literature, so it is particularly important to understand what has been learned from studies of molten salts. Much of the attention of those studying the thermodynamics of mixing of molten salts was focussed on the formation of metal complexes.14,15 For molten salts systems in which complex ions are not formed, nearly ideal behaviour could be observed and small values of ΔHmix have been measured,16 the main contribution to deviations from ideality being linked to differences in size of the mixed ions leading to changes in the Coulumbic interactions. This effect normally accounts for small, negative ΔHmix.17 Small, positive ΔHmix have been observed for molten salts mixtures where the difference in size of the ions is not significant.18 These changes were attributed to changes in the dispersion forces between the ions.It was first believed that molten salts have ideal entropies of mixing.19 However, small, negative entropies of mixing have been measured for many molten salt mixtures, both composed of a common anion and different cations and a common cation and different anions.16 Deviations from the ideal entropy of mixing were linked to deviations from the random distribution of ions in solution and modelled using conformational ion solution theory incorporating a non-random mixing term.20 This theory has been also used to calculate miscibility gaps of some molten salts systems and the Gibbs free energies for the related metathesis reactions.21 Again, these showed deviations from ideality driven by enthalpy rather than entropy.
Navia et al.22 used microcalorimetry to measure enthalpies of mixing for [CnC1im][C6C1im][BF4] (m = 2 or 4, Fig. 3), [C4C1im][BF4][PF6] and [C4C1im][BF4][MeSO4]. They found small positive excess enthalpies of mixing, HE, (net destruction of interactions) for the mixtures of different cations with a common anion. It is known that increasing the alkyl chain length of an imidazolium cation leads to cation–cation dispersion interactions, which one would expect to be disrupted upon addition of an ionic liquid with cations bearing shorter alkyl chains. This is not dissimilar to arguments used to explain the behaviours of some molten salts.18 Conversely, small negative HE (net creation of interactions) were found for the mixtures of different anions with a common cation.22 This can only be rationalized by considering that in one of the simple ionic liquids, the cation's ability to form bonds to anions has not been fully satisfied and that this ability gets better satisfied in the mixture.
![Excess molar enthalpies as a function of composition at T = 303.15 K: ▲, x [C6C1im][BF4] + (1 − x) [C2C1im][BF4]; ■, x [C4C1im][BF4] + (1 − x) [C6C1im][BF4]; ◆, x [C4C1im][PF6] + (1 − x) [C4C1im][BF4]; ●, x [C4C1im][BF4] + (1 − x) [C4C1im][MeSO4]. Reprinted with permission from ref. 22. 2012 Copyright, American Chemical Society.](/image/article/2012/CS/c2cs35177c/c2cs35177c-f3.gif) | ||
| Fig. 3 Excess molar enthalpies as a function of composition at T = 303.15 K: ▲, x [C6C1im][BF4] + (1 − x) [C2C1im][BF4]; ■, x [C4C1im][BF4] + (1 − x) [C6C1im][BF4]; ◆, x [C4C1im][PF6] + (1 − x) [C4C1im][BF4]; ●, x [C4C1im][BF4] + (1 − x) [C4C1im][MeSO4]. Reprinted with permission from ref. 22. 2012 Copyright, American Chemical Society. | ||
The partial immiscibilities of [CnC1im]Cl (n < 6) with [(C6)3C14P]Cl allowed Arce et al.23 to measure the temperature-dependent solubilities of the imidazolium salts in the [(C6)3C14P]Cl. This, in turn, allowed them to derive the enthalpies and entropies of these processes. It can be seen (Table 2) that as ΔH is slightly favourable for [C1C1im]Cl in [(C6)3C14P]Cl, but becomes less favourable as the alkyl chain length increases, but that the lack of mixing is dominated by the consistently negative ΔS values, regardless of the alkyl chain lengths.
| Alkyl group | ΔH/kJ mol−1 | ΔS/K−1 mol−1 |
|---|---|---|
| C1 | −21.7 | −100.3 |
| C2 | −2.29 | −39.1 |
| C3 | 1.03 | −25.5 |
| s-C4 | −1.14 | −26.7 |
| C4 | 1.35 | −20.3 |
| C5 | 1.51 | −15.7 |
Castejón and Lashock24 used molecular dynamics simulations to calculate the enthalpies of mixing of different binary mixtures of 1,2,3- and 1,2,4-triazolium ([123tr]+ and [124tr]+) and [C4C1im]+ based ionic liquids with [NO3]− and [ClO4]− anions. HE were found to be small for all cases, indicating again nearly ideal behaviour. In the cases when small and symmetrical ions were studied HE was very small and negative and its change with composition follows a symmetrical curve, typical behaviour for regular solutions. However, when the larger cation, [C4C1im]+, was one of the ions in the mixture HE were slightly larger and positive. Moreover, the curve for the change in HE with composition was found to be asymmetric, suggesting to the authors that structural changes in the solution due to the different interactions of the anions with the bulkier and more sterically crowded cation. However, this behaviour is not general for ionic liquids containing imidazolium type cations as the change in HE with composition was found to follow a nearly symmetrical line for all mixtures ([CnC1im][C6C1im][BF4] (m = 2 or 4), [C4C1im][BF4][PF6] and [C4C1im][BF4][MeSO4]) measured by Navia et al. (Fig. 3).22
Properties of ionic liquid mixtures
Density
The definition of ideal mixing in eqn (5) also leads to the excess volume of mixing being zero. Hence one should expect a linear change in the molar volume as the composition of the mixture changes between the two pure components. This is something that can be measured for ionic liquids in a comparatively straightforward manner. Molar volumes and hence densities of mixtures are directly related to chemical potentials. Therefore molar volumes are expected to be a linear function of the mole fraction of the components. Some caution does need to be applied to these measurements, because deviations from ideality in data generated by mixing liquids with very similar densities, as is often the case for ionic liquids, can be obscured by the narrow data range.In the first extensive work on the excess volumes of ionic liquid mixtures, Rebelo et al.25 analysed the volumes of mixing of the mixtures [CnC1im][CmC1im][NTf2], [C4C1im][PF6][NTf2], [C4C1im][BF4][NTf2] and [C4C1im][BF4][PF6]. All of these mixtures were found to exhibit almost linear mixing behaviour. VE for these mixtures was always found to be small – less than 0.1% of the overall volume and less than 1.5% of the difference in the molar volumes of the pure components. They were always slightly positive, indicating that there are no new strong favourable chemical interactions in the mixture, and were essentially insensitive to pressure and temperature. Thus, these mixtures can be considered to be nearly ideal, but with a consistent small deviation indicating some loss of interactions in the mixture. It was well demonstrated for [CnC1im][CmC1im][NTf2] that VE increased with the difference in the chain length of the two cations (Fig. 4). A similar dependence of VE upon the size difference of the ions was found for the ionic liquids with a common cation and different anions. The authors compared their results with those on mixtures of Group 1 halide salts, for which similar results have been found.26 It is clear from studies of mixtures of molten salts that differences in size account for most of the deviations from ideality observed.27 In those studies, large positive deviations from ideality were only observed when complex ions formed upon mixing of the neat molten salts.28 However, one cannot rule out the influence of dispersion forces and it should be noted that some of the longer chain ionic liquids used in the [CnC1im][CmC1im][NTf2] study are ones for which ‘nanostructures’ with polar and non-polar domains in the simple ionic liquid are possible.29 It is possible that the disruption of these by mixing with a cation that does not support these structures, e.g. in [C2C1im][C10C1im][NTf2], could make some contribution to the mixing thermodynamics. Further computational studies from the same authors calculated small, positive excess volumes also for [C2C1im][C6C1im][NTf2].30 These studies revealed that mesoscale segregation into polar and apolar domains in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of the ionic liquids, which was similar to the behaviour exhibited by the ionic liquid with an alkyl chain length that is halfway between those of the two cations in the mixture – [C4C1im][NTf2].
1 mixtures of the ionic liquids, which was similar to the behaviour exhibited by the ionic liquid with an alkyl chain length that is halfway between those of the two cations in the mixture – [C4C1im][NTf2].
![Excess molar volume at the equimolar composition as a function of the aliphatic chain length difference, |m − n|, between components [CnC1im][CmC1im][NTf2] (circles) and (CmOH + CnOH) (squares) systems. The crossed squares refer to alcohol mixtures containing methanol. Reprinted with permission from ref. 25. 2012 Copyright, American Chemical Society.](/image/article/2012/CS/c2cs35177c/c2cs35177c-f4.gif) | ||
| Fig. 4 Excess molar volume at the equimolar composition as a function of the aliphatic chain length difference, |m − n|, between components [CnC1im][CmC1im][NTf2] (circles) and (CmOH + CnOH) (squares) systems. The crossed squares refer to alcohol mixtures containing methanol. Reprinted with permission from ref. 25. 2012 Copyright, American Chemical Society. | ||
To compare to more well-known systems, the authors used mixtures of linear alcohols CmOH/CnOH and showed that their behaviours in this respect are remarkably similar. The excess volumes of mixtures containing different chain-lengths were compared to those found for mixtures of alcohols CmOH/CnOH and it was found that the reduced excess volume, VE/Vexp plotted against |m − n| were almost superimposable for both families of values. Flory theory was employed to allow semi-quantitative analysis of the results, however a final estimation of its applicability is not yet possible.25
Density measurements by Stoppa et al. and Larriba et al.,31 showed VE for [C2C1im][N(CN)2][BF4] and [C4C1pyrr][BF4][NTf2] respectively to be small and positive (<0.1%), in agreement with Rebelo et al. for [C4C1im][BF4][PF6].25 Navia et al. also found small positive VE for [C4C1im][BF4][PF6], but in contrast found small negative VE for [CnC1im][C6C1im][BF4] (n = 2 or 4) and [C4C1im][BF4][MeSO4].22 The agreement of the two results for [C4C1im][BF4][PF6] discounts any difference in experimental design leading to these different trends. As the corresponding cation mixtures were not included in the work of Rebelo et al.25 it is possible that they would form outliers in the linear correlation found in that work. It seems, however, more likely that the different behaviour is due to the variation in the chosen anion. Navia et al. suggest that the availability of free space in the [BF4]− ionic liquids could lead to packing effects that then lead on to the observed negative VE values.22 However, negative VE values have also been seen for mixtures of PbCl2 with CdCl2, for which this is an unlikely explanation,32 and other systems containing ions with small differences in size also exhibit negative deviations.29 Again, one cannot rule out the influence of dispersion forces. For [C4C1im][BF4][MeSO4] it is also possible that [MeSO4]− being a significantly stronger hydrogen bond acceptor than [BF4]− contributes to its negative VE.33
Aparicio and Atilhan used a combination of molecular dynamics simulations and infrared spectroscopy to study mixtures of pyridinium salts.34 They obtained small and positive VE for mixtures of [C4(C1)3pyr][BF4] and [C8(C1)3pyr][BF4] (where [C3(C1)3pyr] is 1-butyl-3-methylpyridinium and [C8(C1)3pyr] is 1-octyl-3-methylpyridinium), in agreement with Rebelo et al.25 For [C3(C1)3pyr][N(CN)2][BF4] they found small, negative VE in contrast to the small positive values found by Stoppa et al.31 for [C2C1im][N(CN)2][BF4]. The authors considered differences in the amount of free space, or changes in hydrogen bonding abilities of the cations in the two different systems as possible explanations for these different behaviours. Fox et al. recently reported that for [CnC1pyrr][CmC1pyrr][NTf2] the densities followed ideal mixing with simple additive behaviour observed in all cases.35 However, it should be pointed out that the differences between the densities of the ionic liquids used here were small and the small VE that have been noted in other studies would have been difficult to detect.
The most studied binary ionic liquids are undoubtedly those based upon mixtures of organic chloride salts with AlCl3.6 Of course, these are systems in which reactions occur and compound formation {[A][AlCl4]} at the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 composition is observed. However, if one considers these as two different mixtures above and below this composition, the resulting molar volumes remain approximately linear, for both regimes, although with more pronounced deviation than for ionic liquids without the potential for speciation.36
1 composition is observed. However, if one considers these as two different mixtures above and below this composition, the resulting molar volumes remain approximately linear, for both regimes, although with more pronounced deviation than for ionic liquids without the potential for speciation.36
A recent paper form the Rebelo group reported mixtures of the ionic liquids [C2C1im][C2SO4] or [C2C1im][CH3CO2] with the salt [NH4][SCN].37 This mixture is different from the others reported so far, in that, in all of the previous studies the mixtures had their cations be the common ion, or at least be similar to each other, whereas the size and chemistry of the [NH4]+ ion is very different to [C2C1im]+. For these mixtures, solubility limits were reached at ca. X{[NH4][SCN]} ≈ 0.5 in [C2C1im][C2SO4] and X{[NH4][SCN]} ≈ 0.35 in [C2C1im][CH3CO2]. The measured density values for [NH4][C2C1im][SCN][C2SO4] decrease in a nearly linear manner with increasing [NH4][SCN] concentration until the solubility limit is reached, whereupon it levels; whereas for [NH4][C2C1im][SCN][C2SO4] the density increases up to ca. X{[NH4][SCN]} ≈ 0.2, whereupon it levels. These results conflicted with others that they had measured (conductivity, viscosity and NMR spectra) or calculated (radial distribution functions by MD) for [NH4][C2C1im][SCN][CH3CO2] that showed a step change in the structure of the mixtures at ca. X{[NH4][SCN]} ≈ 0.33.
Vapour pressures
Vapour pressure measurements have long been used to calculate activity coefficients of mixtures of molten salts and many of these were found to follow nearly ideal behaviour.9,38 However, the low volatility of ionic liquids in general is an obvious problem in this respect. While recent results have demonstrated that, contrary to previous beliefs, vapour pressures can be measured for some ionic liquids, the results obtained do not provide a consensus as of yet. However, errors are found to be systematic and, in general, results show similar trends for various ionic liquids.39 While these methods may lack accuracy they are very precise, being able to observe relatively large changes in the vapour pressure with small changes in temperature.40It has been shown that ionic liquids and even ionic liquid mixtures can be distilled.41 The distillation results for mixtures show that the composition of the distillate has higher concentrations of the ionic liquid with the larger vapour pressure in comparison with the original mixture. However, it has not been possible to selectively distil (and hence purify) only one of the ionic liquids in the mixture.
It should be noted that the detection of a vapour over an ionic liquid mixture does not demonstrate that the vapour and liquid are in equilibrium. More fundamentally, Raoult's law assumes that the vapour in equilibrium with the liquid is a perfect gas. The calculation of activity coefficients from vapour pressures of mixtures of molten salts is complicated by the presence of polymeric clusters such as dimers, leading to significant intermolecular interactions.42 In this respect, measurements of vapour pressures of ionic liquids could be simpler as, to date, their vapours have been shown to consist solely of neutral ion pairs.43 The presence of higher order clusters has only been shown theoretically under conditions not achievable experimentally.44
More enthalpies of vaporisation have been measured than vapour pressures and there seems to be a greater consensus in the values.45 Taylor et al. suggested that measurements of enthalpies of vaporisation of the individual ionic liquid components within a mixture could be used to estimate the ideality of that mixture.46 They measured, via temperature programmed desorption (TPD) experiments, the heat of desorption of both components of a [C2C1im]0.95[C8C1im]0.05[NTf2] mixture to be the same, within experimental error, as the heat of desorption of the neat components [C2C1im][NTf2] and [C8C1im][NTf2]. It can then be calculated from a thermodynamic cycle that the enthalpy of mixing for that mixture should be zero, i.e. the mixture should be ideal or, at least, athermal.
EMF measurements
Activity coefficients, and hence deviations from ideality, can be calculated from electromotive force determinations. For example, a cell of the type Pb(l)/PbCl2 + KCl(l)/Cl2(g)/C was used to investigate the mixing of these molten salts.47 The standard potential of the cell is measured when using the pure component (PbCl2) as the electrolyte. The activities of PbCl2 are calculated by measuring the cell potentials and using the following equation at different compositions of the mixture: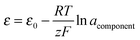 | (9) |
component = PbCl2.
Activities calculated by this method agreed with the ones calculated by measurements of vapour pressure in the absence of metal complex formation in the vapour phase.
Abbott et al.48 used a similar approach to measure the activity coefficients for solutions of AgX salts in [C2C1im]X (X = Cl, [SCN] or [CH3CO2]) ionic liquids, using a Ag/AgX ([C2C1im]X) (molality = 0.1 mol kg−1)//AgX ([C2C1im]X) (molality = x mol kg−1)/Ag cell. By assuming the very dilute m = 0.001 mol kg−1 solution to be ideal they calculated the activity coefficients (γ) for different solutions from the formula:
| E = RT/nF (mrefγref/mtestγtest) | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture of choline chloride and ethylene glycol) they saw Nernstian behaviour for AgCl, CuCl, and CuCl2. Bringing all of these results together suggests that some mixtures of ionic liquids are capable of forming ideal solutions of metal salts, at least in some concentration ranges.
2 mixture of choline chloride and ethylene glycol) they saw Nernstian behaviour for AgCl, CuCl, and CuCl2. Bringing all of these results together suggests that some mixtures of ionic liquids are capable of forming ideal solutions of metal salts, at least in some concentration ranges.
Phase behaviour
Measurements of the vapour pressures of molten salts was an important technique for investigating the thermodynamics of their mixing.10 However, probably for the technical reasons described above, these have yet to be investigated in detail for mixtures of ionic liquids. Licence and co-workers conducted variable temperature TPD measurements to investigate the thermodynamics of mixing behaviour in ionic liquids with the same anion and similar cations ([C2C1im][NTf2] and [C8C1im][NTf2]). While this is a non-equilibrium system, which led to deviations in T–P behaviour when compared to refluxing the same mixtures at vapour–liquid equilibrium (VLE) and limits the ability to form strong conclusions, the TPD behaviours were consistent with ideal mixing in the liquid phase.46Many simple ionic liquids are glass-transforming materials.1 This means that they will often super-cool and not display clear freezing points. Many examples never form a crystalline phase. As a general trend this problem is further exacerbated when making mixtures of ionic liquids.49 Hence, it is often difficult to obtain a full phase diagram.36,50–54 Also, it has been pointed out that thermograms may arise from samples that are not in thermodynamic equilibrium.35 For the binary system [C2C1im][OTf][NTf2] MacFarlane et al. found the glass transition temperature of the mixture to be a weighted average of the values for pure components.55 The same was generally true for [C2C1im][C4C1pyrr][B(CN)4], though no glass transition was found for low imidazolium concentrations.53
Most salt mixtures display a eutectic (a composition that freezes at a single temperature, without separation of the pure components, or a change in composition, and at the lowest temperature of any composition of the mixture) in their phase diagram.10,56 One way of exploiting this to get around the well-known problem of preparing ionic liquids in high purity has been offered by Dunstan and Caja, by making two ionic liquids that melt above room temperature, using recrystallization to purify these and then mixing them at their eutectic composition to create a highly pure ionic liquid mixture.57 For mixtures of [C2C1im][PF6] (mp. 61 °C) and [C2C1pz][PF6] (mp. 79 °C; [C2C1pz]+ = 1-ethyl-2-methylpyrazolium) a eutectic composition was found at X{[C2C1im]+} = 0.47 with a melting point of 23 °C. Eutectic compositions were also found for [C3C1pyrr][FSI][NTf2] (X{[FSI]−} = 0.67, mp. = 247 K, [FSI]− = bis(fluorosulfonyl)imide),58 and [C2C1im][C6C1im][NTf2] (X{[C2C1im]−} = 0.67, mp. = 247 K).59
Eutectic mixtures have also been found for a wide range of mixtures containing up to five different ions from a variety of quaternary ammonium cations with [NTf2]− and [OTf]− anions.60 While further depression of melting points was possible by adding additional ions to the mixture, the most pronounced effects were found for the binary ionic liquids, irrespective of whether an anion or a cation was added. For example, the melting point of the eutectic for [(C2)4N][(C4)4N][NTf2] was 40 °C below that of the lower melting simple salt; addition of [(C1)4N]+, [(C3)4N]+ or the tosylate anion to the eutectic mixture lowered the melting point further by only 14 °C, 11 °C or 22 °C respectively. Again, this is indicating a system in which chemical interactions are playing at most a secondary effect and entropy changes are dominating the observed behaviours. Raade and Padowitz,61 have used this approach to prepare an ‘all-inorganic’ quinary ionic liquid at its eutectic composition (Li0.15Na0.10K0.30Ca0.15Cs0.30[NO3]) with a melting point of 65 °C.
Contrary to most people's expectations not all salts, or ionic liquids, are fully miscible with each other. It has been shown that it is possible crystallize pure [C4C1im]Cl from [C4C1im][PF6].62 It has also been shown that it is possible to make mixtures of ionic liquids that form two separate liquid phases. These are often pairs of short chain imidazolium based cations together with long chain phosphonium based cations and small anions, such as [CnC1im]Cl (n < 6) and [(C6)3C14P]Cl.63,64 Replacing the chloride ion with the bulkier [NTf2]− however makes mixtures with n = 4 fully miscible. For these mixtures ΔH of dissolving the imidazolium salt in the phosphonium ionic liquid is usually small, as the main interaction of each ion is with another ion of the opposite charge, and no new combinations are made in the mixture. The corresponding ΔS, however, is significantly negative, thus preventing mixing.63 The importance of entropic contributions can be seen in the influence of the size of the cations on the solubilities of M[B(CN)4] (M = Li, Na or K) in [C2C1im][B(CN)4] which are low and show a strong alkali metal dependence,53 also in the moderate solubilities of [NH4][SCN] in [C2C1im][CH3CO2] or [C2C1im][C2SO4].37
Biphasic systems of two simple ionic liquids contain at least three, but potentially 4 species if all ions are different. Under these circumstances the partition coefficients can be significantly different for ions of the same liquid.63 The phase separation can be further fine-tuned by adding a third ionic liquid, thus mixing up to 6 ions. Even though not devised for concentrated electrolyte systems, the non-random two-liquid equation shows good predictive power for the phase behaviour of ionic liquid mixtures.36
In another example of unusual phase behaviour, when the ionic liquids [(C1)4P][Val] ([Val]− = valinate) and [C4C1im][NTf2] were mixed, a gel-like phase was formed. Under closer inspection this was found to contain a very fine powder suspended in a liquid.65 With centrifugation, these could be separated. The resultant liquid was [C4C1im][Val] while the solid was [(C1)4P][NTf2]. Clearly the two liquids had undergone a metathesis reaction to give a new liquid and an insoluble solid.
The W-shaped phase diagram for [C2C1im]Cl–AlCl3 must be the most abiding image of the chloroaluminate ionic liquids (Fig. 5). The underlying molecular behaviour giving rise to this phase diagram, due to formation of different chloroaluminate species, is well understood.36 As more AlCl3 is added to the chloride salt mixtures up to X{AlCl3} = 0.5 can be considered to be [A][X][Y] ([X] = Cl, [Y] = [AlCl4]) binary mixtures. For compositions richer in aluminium, further complex formation occurs and the liquids can be considered to be [A][Y][Z] ([Y] = [AlCl4], [Z] = [Al2Cl7]) binary mixtures up to a X{AlCl3} = 0.67 when [Al3Cl10]− begins to appear.
![[C2C1im]Cl–AlCl3 phase diagram.36](/image/article/2012/CS/c2cs35177c/c2cs35177c-f5.gif) | ||
| Fig. 5 [C2C1im]Cl–AlCl3 phase diagram.36 | ||
The full composition range can, therefore, be considered not one mixture, but two mixtures overlapping at a common point at X{AlCl3} = 0.5, the simple [AlCl4]− salt. Consequently a eutectic mixture with suppression of crystallisation (glass transformation) can be found on both sides of the equimolar mixture at approximately X{AlCl3} = 0.35 and X{AlCl3} = 0.65. The bromide analogues of these systems are known and follow similar behaviours.66 Of course, the earliest of this type of ionic liquid was formed by mixing AlCl3 with a bromide salt.67 No evidence has ever been presented that suggests that the bromide ions are anything other than randomly distributed across the whole range of halogenoaluminate species present in these ionic liquids.
The presence of high concentrations of halide ions together with a lack of competing potential ligands (e.g., H2O in aqueous solutions) leads to most metal halides forming complex ions in halide ionic liquids. Being from the same group of the Periodic Table, chlorogallates show very similar behaviour to the chloroaluminates.68 Chloroferrate ionic liquids have been shown to also form bimetallic species ([Fe2Cl7])− for compositions with X{FeCl3} > 0.5,69 as have chlorozincates,70 chloroaurates,71 chlorocuprates(I),72 chlorohafnates and chlorozirconates.73 In contrast, in chloroindate ionic liquids the indium species were found to be coordinatively saturated in the basic regime, [InCl6]3−, but no species richer in indium could be identified for acidic mixtures, as these precipitated as InCl3.68,74
Mixtures of [C4C1pyrr][NTf2] and AlCl3 show a series of different phase separations depending on composition, going from one phase over a two-phase region to one phase for nearly equimolar ratios to biphasic at equimolar mixtures of [C4C1pyrr][NTf2] and AlCl3.75 This could partly be attributed to a series of equilibria involving the progressive formation of species of the form [AlClx(NTf2)4−x]− as the composition of the mixture changed. Due to this speciation, aluminium deposition was possible from some phases and certain mixtures, even though this is known not to occur for [AlCl4]− in chloroaluminate ionic liquids. In further work on mixtures of [C4C1pyrr][NTf2] and AlCl3, evidence for the formation of similar species could be found, and the species active in the electrodeposition of aluminium was identified as [AlCl3(NTf2)]−. Furthermore, it was found that the equilibria could be influenced by changing temperature, such that deposition of aluminium was possible from compositions that did not allow this at room temperature.76 Similar results were concurrently found by Endres et al. for mixtures of [C2C1im][NTf2] or [C4C1pyrr][NTf2] with AlCl3.77
Viscosity
While not considered a mixture of ionic liquids at the time of writing, the work by Seddon et al. on chloride impurities in [C4C1im][BF4] should be considered in this context.78 An increase of the viscosity of the solution with increasing chloride concentration was found, with an approximately logarithmic relation between viscosity and the mole fraction of the chloride salt. The same was found for mixtures of Li[BF4] in [C2C1im][BF4].52The viscosities of four series of mixtures, [C2C1im][C6C1im][BF4], [C4C1im][C6C1im][BF4], [C4C1im][BF4][PF6] and [C4C1im][BF4][MeSO4], were measured and compared to different mixing laws from literature.79 Attempts to fit the data to a simple linear function of concentrations failed, but two other mixing laws gave very similar and quantitatively good results. The first was the ideal Katti and Chaudhri mixing law, which is based on the viscosities (η) and molar volumes (X) of the pure compounds:80
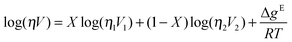 | (11) |
| log(η) = Xlog(η1) + (1 − X)log(η2) | (12) |
In good qualitative agreement with the aforementioned mixing laws, [C2C1im]Cl–AlCl3 shows two linear regimes on the logarithmic scale for mixtures above and below the equimolar composition.36
A third mixing law found to be in equally good agreement with the data for mixtures of [C2C1im][BF4] and [C2C1im][N(CN)2] is that according to Bingham, developed by analogy to electric resistors in a parallel circuit:82
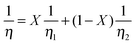 | (13) |
Superficially, approximately half of the data points fall on the curve of the Grunberg and Nissan mixing law, while the others seem to indicate the Bingham model. However, since these two liquids are very similar in viscosity and none of the three mixing laws gives significantly different results within the error of the experiment, this is probably just a coincidence. For larger differences of the simple salts, the Bingham model would give significantly lower viscosities for mixtures; which was found for mixtures of [C2C1im][AlCl4] with the corresponding lithium salt.83
The temperature dependence of the viscosities of Li[C2C1im][BF4] mixtures were found to follow a Vogel–Fulcher–Tamman behaviour, consistent with the results for simple ionic liquids and typical of glass-transforming materials.52
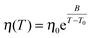 | (14) |
For mixtures of [C4C1pyrr]+ based ionic liquids with different perfluoroalkyl substituted bis-sulfonimide anions, the activation energies for flow, as calculated from the temperature dependence of the fluidity, were found to be lower than the weighted average of those of the simple liquids for mixtures of anions of similar size, whereas nearly ideal behaviour was found for mixtures with very different anion sizes.84 The authors did not have an explanation for this observation (one usually expects greater deviation from ideality for mixtures of unlike species than for mixtures of similar ones), other than it perhaps arises from competing effects cancelling themselves out, nor do we.
For the mixtures of [C2C1im][C2SO4] or [C2C1im][CH3CO2] ionic liquids with [NH4][SCN] there appears to be a (nearly) linear increase in viscosity as the [NH4][SCN] is added until its saturation concentration begins to be approached, whereupon it appears to level off ([C2C1im][CH3CO2], X{[NH4][SCN]} ≈ 0.25) or decline ([C2C1im][C2SO4], X{[NH4][SCN]} ≈ 0.35).37 This may suggest that there is a concentration range in which microscopic agglomeration of the [NH4][SCN] happens, but not precipitation.
Conductivity
For the conductivity of mixtures, there is no clear description of what would constitute ideal behaviour and therefore excess conductivity. MacFarlane et al. found positive deviation of the molar conductivity from a simple linear mixing rule for mixtures of [C2C1im][NTf2] and [C2C1im][OTf] exceeding the value of the higher conducting simple liquid for all of the compositions studied.55 The authors point out that this could potentially be explained by either a larger number of charge carriers or facilitated movement of the charge carriers. As the self-diffusion constants of the ions did not change significantly over the different compositions, they argued that decreased clustering of ions leading to reduced correlated ion movement and more independent charge carriers can explain the increased conductivity. A positive deviation from the linear mixing was also found for mixtures of [C2C1im][BF4] and [C2C1im][N(CN)2], but this time none of the values for the mixtures exceeded that of the most conducting pure component.85For mixtures of [C2C1im][BF4] and [C3C1im]Br, the conductivity was found to be less than to be expected from simple linear mixing, but not less than for the least conducting pure component, with no minima or maxima being identified.86 For mixtures of [C2C1im][BF4] and [C2C1im][NTf2] a negative deviation was found as well, with the conductivities of both of the mixtures studied being less than that of the least conducting pure component.87
MacFarlane et al. studied the conductivity of mixtures of Li[NTf2], [C3C1pyrr][NTf2] and [C3C1pyrr][FSI].58 For a solution with a fixed concentration of Li[NTf2], the conductivity was found to vary linearly on a logarithmic scale with the [FSI]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NTf2]− composition.
[NTf2]− composition.
When 10 wt% of the cyano-substituted quaternary ammonium salts [(NC)C1Cn(C1)2N][NTf2] (n = 1 or 2) is added to [C2C1im][NTf2] a sharp increase in conductivity is seen, in spite of the fact that the conductivities of the simple ammonium salts are considerably lower than that of [C2C1im][NTf2].88
[C2C1im]Cl–AlCl3 again falls into two distinct regions with linear behaviour on the logarithmic scale for both acidic and basic mixtures.36
Mixtures of [C4C1pyrr][NTf2] and [C3C1pyrr][FSI] doped with lithium salts (0.3 M) show approximately logarithmic behaviour in the room temperature region, however this is not the case for temperatures below −10 °C.89 For these temperatures, which are below the melting points of at least one of the pure components, the mixtures show significantly higher conductivities.
While its theoretical validity as a measure of ion association is currently under discussion, the calculated ratio of bulk conductivity to calculated conductivity from diffusion constants was calculated for the mixtures of [C2C1im][NTf2] and [C2C1im][OTf2] as well as the mixture of [C2C1im][BF4] with the Li[BF4]. In the first case a tendency towards conductivities higher than to be expected from linear mixing was found,55 while in the latter case no clear trend became apparent.52
As one would expect from the viscosity results above, the temperature dependences of the conductivities of ionic liquid mixtures follow Vogel–Fulcher–Tamman behaviour (eqn (14)), as do simple ionic liquids.52 This is very typical of glass-forming materials. It is likely that a number of the observations above also result from ionic liquid mixtures forming glasses.
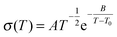 | (15) |
Overall, the conductivity of ionic liquids presents a somewhat unclear picture in terms of what “normal” behaviour would be. The majority of authors find approximately linear behaviour on the logarithmic scale. While this finding can be accepted at face value it is, furthermore, in good qualitative agreement with the Stokes–Einstein and Nernst–Einstein equations as well as the hole theory-based interpretation by Abbott,90 that all predict:
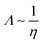 | (16) |
log Λ ∼ −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η ∼ X η ∼ X | (17) |
Of the available literature on the conductivity of mixtures, only two examples with significant positive deviation from this behaviour have been reported. One is the mixture of [C2C1im][BF4] with [N(CN)2]−.31 While both [C2C1im]+ and [BF4]− show typical behaviour in other studies of mixtures, no other mixtures involving the [N(CN)2]− anion have so far been published. It is, therefore, possible that the observed behaviour could be related to specific properties of this anion. The second example is the mixture of [C2C1im][NTf2] with [OTf]−. MacFarlane et al. explain their findings with properties that should be general to every binary mixture, however no similar behaviour is found for any other such system. Furthermore other mixtures with similar ions have been analysed in subsequent work by other groups, and no analogous behaviour was found. It is therefore unclear what is the cause of these findings.
An effect found for at least two mixtures is that while showing this typical behaviour over almost the full composition range, a sudden drop in conductivity is found for one of the pure compounds. This was found to be the case for [C2C1im]Br in its mixture with [BF4]−,86 and was more pronounced for [C2C1im][NTf2] in mixtures with cyano-substituted quaternary ammonium salts.88 Assuming no errors in measurement caused this behaviour, it might be indicative of a structural change in the ionic liquid upon mixing, and would therefore be worthy of further investigation.
As one would expect from their viscosity changes, the conductivities of [NH4][C2C1im][SCN][C2SO4] mixtures decrease to ca. X{[NH4][SCN]} ≈ 0.35 and then increase again.37 For [NH4][C2C1im][SCN][CH3CO2], the initial addition of [NH4][SCN] seems to have very little effect on the conductivity at all, in spite of the rising viscosity, but it then increases from ca. X{[NH4][SCN]} ≈ 0.2.37 This strongly suggests that there is some other effect that is working in the opposite direction to the viscosity changes throughout the composition range. The authors referred to the Waldon plot (log Λ vs. log 1/η) and the concept of ionicity, which, although not uncontroversial, is generally accepted to be an indicator of how ideally ionic an ionic liquid is,91 to solve this. They found that as they added [NH4][SCN] to the ionic liquids the deviation of the mixture from the ideal conductor (aqueous KCl) reduced to ca. X{[NH4][SCN]} ≈ 0.35 and then increases again, reflecting an initial increase in the number of charge carriers followed by a decrease at higher concentrations.
Diffusion
For mixtures of [C2C1im][BF4] with Li[BF4] the self-diffusion coefficients were found to qualitatively exhibit the expected behaviour of slower self-diffusion with higher viscosity on addition of the lithium salt.52 The relative order of the self-diffusion constants remains D([C2C1im]+) > D([BF4]−) > D(Li+) for all mixtures, a reversal of what would be predicted from the van-der-Waals radii and the Stokes–Einstein equation, however in line with what is known from simple ionic liquids. The activation energies for diffusion, as calculated from the Arrhenius plots, show a linear increase with the concentration of the lithium salt for the diffusion of the imidazolium cation. The two other ions, however, show a maximum for a Li[BF4] concentration of 0.75 mol L−1 and exhibit a parallel behaviour, taken by the authors as an indication of mutual diffusion.52 For mixtures of [C3C1pyrr][NTf2] and [C3C1pyrr][FSI] the same qualitative result could be found of the diffusion constants of the two anions changing in parallel – with the [FSI]− always diffusing faster – and the cation showing a different behaviour. The diffusion coefficients of the anions change almost linearly on a logarithmic scale with molar composition, with the less viscous liquid exhibiting faster diffusion. In contrast the cation shows a significantly less pronounced acceleration and a small maximum near the composition of the eutectic mixture.58For mixtures of [C4C1pyrr]+ based ionic liquids with different perfluoroalkyl substituted bis-sulfonimide anions the activation energy for self-diffusion of all ions in the mixture was generally found to be close to the value of the slowest diffusing ion in a simple ionic liquid when the mixtures were comprised of similarly sized ions. However, when the anions were different in size the activation energies converged to a single value, which was approximately 4 kJ mol−1 higher than the one for the cation. This implied a reduced correlation between the movements of oppositely charged ions, and is in good agreement with a remarkably high relative conductivity of the corresponding mixture.84
While no strict mixing rule is available for the diffusion in mixtures of ionic liquids, the Stokes–Einstein relation is able to give an estimate of the self-diffusion that can be expected for a given viscosity.
| Dη = const. | (18) |
For mixtures of [C3C1pyrr][NTf2] and [C4C1pyrr][NTf2] the average diffusion constants show a logarithmic change with the composition, however in [C3C1pyrr]+ rich compositions the [C4C1pyrr]+ cation diffuses notably slower. This was attributed to the larger cation having to diffuse trough a phase rich in the smaller cation.93
Due to the limited amount of data available on ion self-diffusion constants in mixtures of ionic liquids, it is difficult to give a precise assessment of their behaviour. For the relative order of the diffusion constants at a given mixture ratio, a similar picture emerges as for the pure liquids, with the cations diffusing faster than the anions and the relative order within each group consistent with the corresponding simple ionic liquids. On the grounds of the Stokes–Einstein equation and by analogy to the conductivity of mixtures, a logarithmic change of the diffusion constants with the molar composition can be expected. This is indeed found for some species,58 or averaged over all ions;93 however single ions can show different behaviour.
Structures of ionic liquid mixtures
Bulk structures
Coulomb forces between ions lead to most salts having highly ordered infinite ionic lattices, and so to their high melting points. The dramatic increase in conductivity displayed by simple salts as they melt, e.g., NaCl at 800 °C (solid) κ = 1 × 10−3 Ω−1 cm−1, at 900 °C (liquid) κ = 3.9 Ω−1 cm−1,94 shows that this has been accompanied by the freeing of ions to move from their lattice positions. At the same time their molar volumes increase upon melting, e.g., NaCl by 23%, KBr by 22%,95 as the structure of the salt breaks up and space is introduced. However, these changes are not accompanied by large differences in either the closest ion distances or their coordination numbers, which can even show greater short range ordering than the crystal.9 Neutron and X-ray diffraction studies of Group 1 metal halides have shown a reduction of average coordination numbers, a shortening of anion–cation distances, but an increase in anion–anion and cation–cation distances.96 X-ray diffraction patterns of solid and liquid [C2C1im]Br have shown the same kinds of changes, with the Br− ions closer to the cation ring atoms and more symmetrically distributed around the ring in the liquid than in the crystal.97 Organic salts with long alkyl chains have been shown to also form higher order structuring,98 such as liquid crystalline phases.99 Some ionic liquids have also been shown to contain structures in which ionic and non-polar domains separate,100 whereas others do not.101 While these structures should not be thought of as fixed and persistent, but rather more as fleeting and constantly changing, they do contribute to the overall properties of the ionic liquids in which they occur. So questions that arise for ionic liquids include: do they simply homogeneously and fully mix, under any, or all circumstances; if a ‘non-structured’ ionic liquid is added to a ‘structured’ ionic liquid are the structures disrupted and to what extent?Welton et al. studied the effect of concentration on the charge transfer UV spectra of 1-ethyl-4-(methoxycarbonyl)pyridinium iodide (Kosower's salt) in a range of ionic liquids [C4C1im]X (X = [BF4], [OTf], [SbF6] or [NTf2]), [C4C1pyrr][NTf2] and [C4C1C1im][NTf2], and showed that the mixture was fully mixed with statistically random ion contacts, i.e., there were neither attractive nor repulsive interactions leading to any solute ion pairing.102 They described this in terms of a ‘liquid pseudo-lattice model’ (Fig. 6). This model has all of the same features as the ‘cell model’ used to describe some mixtures of molten salts.10
 | ||
| Fig. 6 The cell model of ionic liquid mixtures, coloured ions represent the minor component, grey ions represent the major component.102 | ||
Support for this cell model comes from a study of the mid-IR spectra of [C4C1im]Br[NTf2] mixtures, which showed their spectra to be non-additive, as were the spectra of [C4C1im][BF4][PF6] and [C4C1im]Cl[PF6], suggesting that these are well mixed at the molecular level.103 Moreover, upon addition of water to the mixtures, absorptions characteristic of single water molecules coordinating to both anions at the same time were observed. The authors concluded that a structure like this would only be possible in a situation where the anions are well mixed. In contrast, mixtures of [C4C1im][NTf2] with [C4C1im]I were found to show perfect additivity in both their UV absorption and IR spectra, indicating that the I− ions in the mixtures were in the same environment as in [C4C1im]I itself.104 The authors discussed this mostly in terms of {[C4C1im]I} ion pairs and a microscopically phase separated structure. However, the crystal structure of the closely related [C2C1im]I clearly shows an extended hydrogen-bond networked structure, not one of isolated ion pairs.105 Thus, the results here are entirely consistent with a microscopically phase separated structure, as noted by the authors, but also with the cell model.
Kirchner et al., used ab initio MD calculations to study mixtures of [C2C1im][SCN] and [C2C1im]Cl.106 For both simple ionic liquids, it is well established that the main anion–cation interaction takes place through the most acidic proton at the C2 position of the imidazolium ring, with less pronounced contact through the two equivalent C4/5–H protons at the back of the ring. This is well reproduced by the radial distribution function (RDFs) of the pure liquids, with the intensities of the first peak following the order H2 > H4 ≈ H5. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture however this was not found to be the case for both ion pairs. While the qualitative results did not change for the chloride ion, the relative order inverted for the thiocyanate ion to H4 ≈ H5 > H2. This is indicative of the different ions competing for the available sites of interaction in the form of chemical equilibria, with the chloride ion as the more H-bond basic species replacing the thiocyanate ion at the most acidic position. This preference does not necessarily conflict with the cell structure, but it does introduce a new possibility; the anions may be randomly distributed throughout the ionic liquid on the bulk scale, but locally may favour one particular cation site. This can be imagined as having randomly distributed anions throughout the ionic liquid, with the orientations of the cations within their cells determined by the anions present in their local environment.
1 mixture however this was not found to be the case for both ion pairs. While the qualitative results did not change for the chloride ion, the relative order inverted for the thiocyanate ion to H4 ≈ H5 > H2. This is indicative of the different ions competing for the available sites of interaction in the form of chemical equilibria, with the chloride ion as the more H-bond basic species replacing the thiocyanate ion at the most acidic position. This preference does not necessarily conflict with the cell structure, but it does introduce a new possibility; the anions may be randomly distributed throughout the ionic liquid on the bulk scale, but locally may favour one particular cation site. This can be imagined as having randomly distributed anions throughout the ionic liquid, with the orientations of the cations within their cells determined by the anions present in their local environment.
In their study of solutions of [NH4][SCN] in [C2C1im][C2SO4] or [C2C1im][CH3CO2] the Rebelo group observed that the 1H NMR (in DMSO-d6) chemical shifts of the C2–H proton of the imidazolium ring moved to lower chemical shifts (decreased hydrogen bonding107) in both cases.37 For [NH4][SCN] in [C2C1im][C2SO4], for which spectra could be measured up to the X{[NH4][SCN]} ≈ 0.5 composition, a step-change in the chemical shifts of all of the ring protons was observed at ca. X{[NH4][SCN]} ≈ 0.33. In this experiment a weak hydrogen bond acceptor [SCN]− and a strong hydrogen bond donor [NH4]+ are added to the ionic liquid at the same time. The Kirchner results suggest that this could be interpreted as the strongest hydrogen bond donor [NH4]+ and acceptor [C2SO4]− have a sufficiently greater affinity for each other to draw the [C2SO4]− ions away from the [C2C1im]+ ring protons, first in a stepwise manner with concentration, but then forcing a structural shift. On the basis of MD simulations, the authors attributed this to a contraction of the overall structure at ca. X{[NH4][SCN]} ≈ 0.33. The same could not be observed for the [NH4][SCN] in [C2C1im][CH3CO2] solutions because this is the point at which the [NH4][SCN] reaches its saturation concentration. It is possible, but not clear as to whether these two observations are linked, or just a coincidence.
The analysis of optical Kerr effect (OKE) spectra for mixtures of ionic liquids by Quitevis et al. showed noticeably different behaviour for different mixtures.108 OKE spectra are governed by the intermolecular vibrational modes and are usually not additive for mixtures even of non-interacting liquids.109 However, for mixtures of [C5C1im]Br and [C5C1im][NTf2] almost perfect additivity was found, while the same was not true for mixtures of [C5C1im][PF6] and [C5C1im][CF3CO2].108 The authors argued that non-additivity arises from new interactions between the mixed species that cannot occur in the pure components and, therefore, that perfect additivity indicates that no new interactions are occurring in the mixture.
Quitevis et al. used the analogy of block and random co-polymers to explain these results (Fig. 7). In block co-polymers there are long strips with the same structure as the pure polymers and very few (therefore, spectroscopically insignificant) “intersections” at which the different species interact; this would be expected to give an additive spectrum. In a random co-polymer many “intersections” are formed and the resulting spectrum will be non-additive. The spectra of [C5C1im]Br[NTf2] are like the block co-polymer case and those of [C5C1im][CF3CO2][PF6] are like the random co-polymer case. The authors did, of course, recognise that the true situation is more complex and that in a bulk ionic liquid phase every cation is in contact with several of anions and vice versa,110 but the analogy does draw out the essential point that in the former case there is an appreciable degree of molecular-scale phase separation of the components and in the latter case they are intimately and randomly mixed. They proposed that this difference in behaviours arose because of the relative sizes of the anions in the two different mixtures, with a large difference in [C5C1im]Br[NTf2] and a much smaller one in the [C5C1im][CF3CO2][PF6]. Another possible explanation for their OKE data for [C5C1im]Br[NTf2] is that the interaction between the cation and anion may be so much stronger in [C5C1im]Br than in [C5C1im][NTf2] and that the intermolecular dynamics may be more local than collective with the OKE spectra reflecting the vibrational modes of these ion pairs instead of domains.111
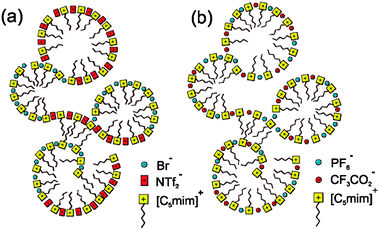 | ||
| Fig. 7 Possible ionic liquid structures that would lead to (a) additive and (b) non-additive spectra. Reprinted with permission from ref. 109. 2012 copyright, American Chemical Society. | ||
Rebelo et al. investigated a similar phenomenon with molecular dynamics calculations.112 They compared [C2C1im]0.5[C6C1im]0.5[NTf2] with pure [CnC1im][NTf2] (n = 2, 4 or 6). For the interactions where no direct cross interactions would be expected – namely anion–anion and anion–cation interactions – no significant difference was found for the RDF between the mixture and the pure compounds, with the mixture being most similar to the n = 4 pure liquid, however with all four systems very similar to each other.
The cation–cation interactions potentially offer the possibility for cross interactions. The radial distribution functions for the imidazolium rings can be expected to be very similar, as these remain largely unchanged by the nature of the side-chain. The RDFs of these however did not yield a clear picture, though the cation–cation interaction between different species gives a significantly weaker signal than the cation–cation interactions between equal ions.
As it is known that mesoscale phase-separation occurs in long chain imidazolium based ionic liquids, the RDFs between the methyl groups at the end of the side chains were also analysed.112 For the [C2C1im][C6C1im][NTf2] mixture it turned out that the contacts between equal cations were almost superimposable with the corresponding RDFs for the respective pure ionic liquids. The intensity of the cross signal was only weak, slightly more intense than the signal for ethyl–ethyl contacts, but significantly weaker than the signal in [C4C1im][NTf2]. This is consistent with the formation of non-polar domains according only to the length of the side chain, not to the overall volume occupied by the aliphatic chains. In other words, the ethyl groups remain dispersed in the polar framework as they would in pure [C2C1im][NTf2] and are not dragged into the non-polar domains formed by the hexyl groups of [C6C1im][NTf2].30 At the same time these calculations showed very small VE. Again this suggests that the phase separation is driven by entropic behaviour.
In an X-ray diffraction study of mixtures of [(Cn)3C1N][NTf2] (n = 4, 6 or 8) structures of interdigitated bilayers (Fig. 8) were found for all three pure ionic liquids, with a constant ratio of interdigitation vs. thickness of the non-polar layer, with the thickness being a linear function of n and the two other correlation distances, both properties of the densest packing of charged head groups in a layer, remaining unchanged.113 For the mixtures of the “adjacent” pure liquids, i.e. n = 4 with n = 6 or n = 6 with n = 8, the two latter distances remain constant as well, however the distance from one layer to the next increases linearly, with the simple salts and the mixtures falling on one function, indicating a smooth transition with no preference of any cation species for a specific position. The authors did also note that [(C4)3C1N][(C8)3C1N][NTf2], showed different behaviour, but no details were given.
![Interdigitated bilayers formed by mixtures of [(Cn)3C1N][NTf2] (n = 4, 6 or 8).113](/image/article/2012/CS/c2cs35177c/c2cs35177c-f8.gif) | ||
| Fig. 8 Interdigitated bilayers formed by mixtures of [(Cn)3C1N][NTf2] (n = 4, 6 or 8).113 | ||
In a similar study,114 a smooth transition of the correlation lengths was also found for mixtures of [C6C1im]Cl with [C10C1im]Cl, however with a significant positive deviation from linear behaviour, not falling on the same line as the [C8C1im]Cl data point. This is interpreted as the maintenance in the mixtures of the alkyl chain segregation to form non-polar domains that is seen in the simple ionic liquids, but with no differentiation of the domains with respect to the two different cations. That is, each non-polar domain contains both hexyl and decyl chains. This is in contrast to the results for [C2C1im][C6C1im][NTf2],30 which show that the ethyl groups of [C2C1im]+ do not enter into the non-polar domains formed by the hexyl groups of [C6C1im][NTf2]. This suggests that the ethyl chains of [C2C1im][C6C1im][NTf2] cannot enter into van der Waals dispersion interactions sufficiently to overcome those between the hexyl chains, hence the separation is maintained; whereas the hexyl and decyl chains of [C6C1im][C10C1im]Cl can both enter into van der Waals dispersion interactions and do so, allowing their intimate mixing.
Another X-ray diffraction study of a number of mixtures has shown a range of behaviours.115 For mixtures of ionic liquids that have a similar level of order in their pure state, e.g. [C2NH3][(HO)2C2NH3][CHO2] and [C2NH3][NO3][CHO2], the results showed an approximately linear relationship between composition of the mixture and the intensity of the signals. For [C5NH3][(HO)5C5NH3][NO3] the order of the system drops dramatically as [(HO)5C5NH3][NO3] is added to [C5NH3][NO3], until at approximately X{[C5NH3][NO3]} = 0.5 whereupon the mixture is almost as disordered as the pure [(HO)5C5NH3][NO3], further addition of which only leads to small changes. With the number of data points available from this study it is difficult to discern whether this is some continuous non-linear behaviour, or two linear regimes intersecting at roughly the equimolar composition. For behaviour that appears to be driven by the alkyl chain of the cation, it is remarkable that changing the anion to produce the [C5NH3][(HO)5C5NH3][CHO2] mixture leads to so much less order in the simple [C5NH3][CHO2] than in simple [C5NH3][NO3], and, therefore in the behaviour of the mixtures.
In the same study,115 non-linear behaviour was also found for mixtures of [C2NH3][NO3] and [C5NH3][NO3]. The peak assigned to the non-polar regions indicated larger distances for the pentyl based liquid as opposed to the ethyl based one, as expected. The mixtures show only a small drop in correlation length for molar concentrations of up to X{[C2NH3][NO3]} = 0.5, followed by a relatively steep decline for higher concentrations, together with a decline in peak intensity, indicating a lower degree of ordering. This suggests that the long chained cations force open the non-polar regions enough to accommodate the alkyl chains and that this persists so long as a threshold amount of these are present, but that the structures collapse below this concentration, leading to both shorter separations and less order. From an entirely qualitative point of view this could be similar to the behaviour of surfactants in a polar solvent, where a certain critical concentration is necessary to form larger structures such as micelles, and thus properties such as surface tension often show two separate linear regimes differing in slope depending on the concentration of solute.
Measurements of the activity of [C8C1im][NTf2] in water saturated [(C6)4N][NTf2] show only slight deviations from Raoult's law over most of composition range. However, a qualitative change in the dependence of the activity coefficient on the composition was found at X{[C8C1im][NTf2]} ≈ 0.3, indicative of a change in the microstructure of the mixture. It is unclear what this change might be.116
A similar result was found for water-saturated mixtures of [(C7)4N][NTf2] and [C14iso][NTf2] (where iso = isoquinolinium) where a change in the slope of the water–ionic liquid surface tension was found at ammonium concentrations of ∼10% and ∼80%, indicating changes in the structure of the ionic liquid liquid phase.117 While the authors did not offer a conclusive explanation for their findings, they consider simple micelle formation unlikely.
For mixtures of surfactant-like ionic liquids, with long alkyl chains, and less lipophilic ionic liquids, indications of the formation of aggregates have been found. For mixtures of [C16C1im]Cl or [C16C1im][BF4] in ethylammonium nitrate typical critical aggregation concentrations were approximately 10–100 times larger in ionic liquids than in water.118 The two different sets of mixtures showed different surface tensions depending on the anion of the imidazolium salts for concentrations up to 8% (w/w), which was taken as an indication that specific ion effects leading to a higher concentration of the two ions close to the surface despite the high concentration of nitrate anions present. For [CnC1im]Br (n = 10, 12, 14 or 16) in [C4C1im][BF4] surface tension measurements were used to imply aggregate formation, while transmission electron microscopy and dynamic light scattering were used to show that these were spherical in shape, but larger than traditional micelles (Fig. 9).119 The authors attributed this to greater cation–cation repulsion in the ionic liquids.
![Schematic representations of long-chain ionic liquid aggregates in (a) water and in (b) [C4C1im][BF4]. Hollow ellipses and hollow circles represent the [C4C1im]+ and [BF4]− in [C4C1im][BF4], respectively.119](/image/article/2012/CS/c2cs35177c/c2cs35177c-f9.gif) | ||
| Fig. 9 Schematic representations of long-chain ionic liquid aggregates in (a) water and in (b) [C4C1im][BF4]. Hollow ellipses and hollow circles represent the [C4C1im]+ and [BF4]− in [C4C1im][BF4], respectively.119 | ||
The behaviour of non-ionic surfactants in mixtures of ionic liquids can be “fine-tuned” over a wide range by changing the composition of the mixture.120 Hexaethylenealkyl ethers were found to be insoluble in [C2C1im][BF4], while in [C6C1im][BF4] they not only dissolve but show no aggregation behaviour. When the two ionic liquids are mixed and hexaethylenealkyl ethers added, decreasing critical micelle concentrations (cmc) and larger micelles were found with increasing concentration of the [C2C1im][BF4] in the mixture. The estimated standard free energy of micelle formation changed in a linear fashion with the molar composition of the ionic liquid mixture, thus allowing the prediction of cmc for the mixture. Furthermore, indications were found of a stronger interaction of the surfactant with the hexyl substituted cation than with the ethyl substituted one, indicating preferential solvation.
Structures in ionic liquid mixtures generally follow trends that are already well known from the simple ionic liquids. For mixtures of ionic liquids that have relatively short alkyl chains, ions are homogeneously and randomly mixed in solution in an analogous manner to the cell model used to describe molten salt mixtures. When the ions have longer alkyl chains that lead to the formation of non-polar nano-domains in the simple ionic liquids, these may persist in the mixtures. The formation of these domains, when mixing ionic liquids that have such structures in the pure liquid with those that do not, seems to be comparable to the formation of micelles in polar liquids, with a well-defined onset of structure formation at a certain critical concentration. When two ionic liquids are mixed that both show such structuring in the simple liquid, the transition is not always the same. While always smooth, the change of X-ray diffraction parameters over the composition of a mixture does not always fall on the same line as an intermediate pure ionic liquid (i.e. a 50% (n/n) mixture of a butyl- with an octyl-substituted ionic liquid does not always behave similar to a hexyl-substituted one).
Structures at interfaces
There has been a great deal of recent interest in how ionic liquids are structured at the interface with other phases.121 Few of these studies have considered ionic liquid mixtures. For studies of the ionic liquid–gas (or vacuum) interface different experiments, using different ionic liquids, have given different results for enrichment of the surface layer with one of the components of the ionic liquid. The presence of a long (n ≥ 4) alkyl chain on the cation leads to its surface enrichment in [CnC1im][NTf2] (n = 2–16), with this effect being greater the longer the chain, but not for [C2C1im][NTf2].122 This is in good agreement with work on [CnC1im][BF4] (n = 4–8),123 which did show surface enrichment with the alkyl chain and on [C2C1im][C2OSO3],124 which did not. This alkyl chain effect is not restricted to the cation. For [C2C1im][C8OSO3] surface enrichment with the alkyl chain was also observed.122 While the alkyl chain effect is dominant, it has been noted that for the same cation, [C8C1im]+, the enrichment of the surface layer decreases as the anion gets larger.125 This effect is greatest when the anions are small, when the difference between their sizes is relatively large, and diminishes as the anions become larger.The surface enrichment with the alkyl chain does not necessarily mean that the surface layer is enriched with the ion of which it is part (Fig. 10). For instance, for a [CnC1im]X salt it is possible that the anions are closely associated with the charged imidazolium ring and that the alkyl chain then protrudes into the vacuum. This would still give a surface enrichment of the alkyl chain, but with no surface enrichment of the cation itself. This is what one might expect from the bulk structures of ionic liquids.29,100 In fact, the available data supports the presence of such structures,126 even to the extent of showing examples that have a surface enrichment of anions and of the cation alkyl chain.127 It is probably best to think of the surface layer containing cations and anions, but with any lengthy (n > 4) alkyl chains directed into the vacuum.
 | ||
| Fig. 10 Ionic liquid–gas (or vacuum) interface with surface enhancement of alkyl chains and A – surface enhancement of cations, B – no surface enhancement of cations or anions, C – surface enhancement of anions. | ||
Given that it has been shown that the surface of [CnC1im][NTf2] (n = 4–16) at the ionic liquid–vacuum interface is enhanced with its alkyl chain, but that of [C2C1im][NTf2] is not,122 it might be expected that the surface of a mixture of [C2C1im][NTf2] with [C12C1im][NTf2] would be enriched with [C12C1im]+. However, no such enhancement for [C2C1im]0.9[C12C1im]0.1[Tf2N] was detected by X-ray photoelectron spectroscopy studies.128 Similarly, no such enhancement was seen for [C2C1im]0.5[C6C1im]0.5[Tf2N] by Rutherford backscattering (RBS).129 The anions in these mixtures are highly fluorinated and hence, likely to be surface active. These results suggest that the surface contains both cations and anions (i.e. not Fig. 10A) and for each cation its propensity to enter the surface layer is given by the difference of its energies at the surface and in the bulk, compared to the other cation. These energies arise from a complex combination of all potential interactions (e.g., Coulombic, hydrogen bonding, dipolar and dispersion). The data here would then simply suggest that these differences are similar for both cations; hence there is no favouring of one over the other at the surface.
A combined surface tension and XPS study observed a positive surface excess of the ionic surfactants Na[CnOSO3] (n = 8, 10, 12 or 14) and [N1,1,1,n]Br (n = 6, 8, 12 or 16) in [C2C1im][C2OSO3] and in bis(2-hydroxyethyl)dimethylammonium methylsulfonate [(CH3)2(C2H4OH)2N][C1SO3], with the degree of surface enrichment increasing with the alkyl chain length of the surfactant.130 At the same time, the level of the surfactants' counterions, Na+ or Br−, at the surfaces were below detection limits. Again this data indicates that the surface layers contain both cations and anions and that [N1,1,1,n]+ will displace ionic liquid cations at the surface, while [CnOSO3]− will displace ionic liquid anions at the surface. Interestingly, the surfaces were not found to be perfectly neutral, either for the mixtures or the simple ionic liquids. This was attributed to the differences in the sizes of the cations and anions. As above, the precise proportion of any of the ions found at the surface is given by the balance of its energies (relative to the other ions) at the surface and in the bulk. This results in [CnOSO3]− favouring the surface over [C2OSO3]− or [C1SO3]− and [N1,1,1,n]+ favouring the surface over either [C2C1im]+ or [(CH3)2(C2H4OH)2N]+. More recent work from the same group using surface tension measurements showed similar surface enhancements of [N1,1,1,n]Br (n = 8, 12, 14 or 16) in other of ionic liquids ([C4C1im][BF4], [C4C1pyrr][N(CN)2] and [C2NH3][NO3]).131
Ionic transition metal complexes have also been shown to concentrate at the liquid–vacuum interface of ionic liquids; e.g,. XPS studies found a significantly higher concentration of the ionic metal complex [Pt(NH3)4]Cl2 in the surface than in the bulk of the ionic liquid [C2C1im][C2OSO3].132 In another study, the charged phosphine tris(sulfonatophenyl)phosphine was found to concentrate at the surface of [C2C1im][C2OSO3].133 Consequently, when Rh(acac)(CO)2 was added, it also concentrated at the surface of the solution, in spite of the fact that when Rh(acac)(CO)2 itself was dissolved in [C2C1im][C2OSO3] it could not be detected at the surface. Care is needed not to over-interpret this finding as it may just be an artefact of its low solubility in this ionic liquid (0.19 mol%), because it could be detected at the surface of [C4C1im][C8OSO3], in which it is more soluble (2.89 mol%).
In general, there is much less work on the structures at the solid–liquid interface for ionic liquids, as direct investigation of buried interfaces is more challenging.134 Information on the electrode–ionic liquid mixtures interface would be very useful to understand applications, such as electrodeposition or dye sensitized solar cells, where mixtures of ionic liquids have been applied successfully. For the phase interface between a mercury electrode and a mixture of [C2C1im][BF4] with [C8C1im][BF4], preferential interaction of the octyl group with the electrode and consequently enrichment of the corresponding cation could be found.135 With such a limited data set currently available it is not possible to draw any general conclusions from these results.
Surfactant self-assembly in solution is largely controlled by the behaviour at the interface between the surfactant aggregates and the solvent, and the balance between hydrophilic and lipophilic components of the amphiphilic molecules.136 Inoue and Misono found that they could tune the self-assembly of polyoxyethylene surfactants by using mixtures of [C6C1im][BF4], in which the surfactants present no cloud point, and [C2C1im][BF4], in which they show no solubility.137
Chemical properties of ionic liquid mixtures
Polarity and solvent–solute interactions
Solvatochromic probes have been used extensively to understand how ionic liquids interact with potential solutes.1,2 The extension of this into mixtures of ionic liquids offers similar possibilities. However, it is important to understand that these probes respond to the solvent species that are present in their immediate environment, the cybotactic region. Even in mixtures of molecular solvents, the population of the cybotactic region has been shown to be a result of both the solvent species and the solute itself, with preferential solvation common.138 Hence, the composition of the cybotactic region does not necessarily reflect the composition of the bulk mixture. Pandey et al. have reiterated the importance of this for ionic liquid mixtures, in which unexpected behaviour could either be induced by the probe molecule itself, by either specific or non-specific interaction between it and the different solvent ions, thus enriching its solvation shell in a way that is not representative of the bulk liquid, or the ionic liquid mixture itself could form “micro-heterogeneities” which the probe molecule detects, but does not cause.139One case in which a strong deviation from simple linear behaviour on mixing was found was for solutions of pyrene in all possible binary mixtures of the ionic liquids [C4C1im][PF6], [C4C1im][NTf2] and [C2C1im][NTf2].139 The fluorescence spectrum of pyrene is used as a general measure of polarity; all three possible mixtures showed a strong deviation towards higher than expected polarities, with this measure exceeding the value found for the pure compounds.
E T N values of [C4C1im][C4C1C1im][NTf2] have also been shown to be non-linear.140 The deviation from linearity was modelled using a simple equilibrium:
R⋯[C4C1im]+ + [C4C1C1im]+ ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R⋯[C4C1C1im]+ + [C4C1im]+ R⋯[C4C1C1im]+ + [C4C1im]+ | (19) |
Pandey et al. also used the Kamlet–Taft system,139 using three dyes to calculate H-bond acidity (α), basicity (β) and general polarity/polarizability (π*). The problem of preferential solvation described above is further exacerbated when multi-probe systems are used. For these, it is not safe to assume, or even it is very unlikely, that the different probes will experience the same cybotactic region. This does not mean that these measurements are without use, but it does mean that the results must be interpreted with care. While it might be expected that the π* would reflect the behaviour found for pyrene, this was not the case, as linear mixing behaviour was found. However, the values for the pure components were very similar and it would be difficult to detect significant deviations from linear mixing with any great precision. Very little deviation from linear behaviour was also found for the H-bond basicity, again probably largely due to the small differences between the ionic liquids employed. The H-bond acidity however showed a strong deviation from linearity, deviating to higher acidity, however not significantly exceeding the values for the pure liquids. This is indicative of the dye “preferring” the energetically more favourable interaction with the more H-bond acidic species, without strong implications of a synergetic effect of the mixture. Qualitatively similar results were found for the ET(30) scale, which is measured with the same dye but not corrected for the π* value.
For mixtures of [C2C1im]+ based ionic liquids with amino acid anions, no systematic behaviour of the Kamlet–Taft parameters could be identified.141 While Ala–Val mixtures show no significant change in the π* parameter, Asp/Lys as well as Glu/Lys show strong deviation towards higher polarity, exceeding what can be found for the pure components. It seems likely that this is due to the fact that Asp and Glu both contain acid functionalities, while Lys carries an amine group, thus allowing a chemical interaction between the anions in the mixture. The H-bond acidity, α, is only given for the Asp–Lys mixture, showing a severely reduced acidity with increased amounts of Lys. While this can be rationalized with the additional basic amine functionality of Lys, it is noteworthy that all mixtures have an acidity at least as low as the simple ionic liquid and that the mixtures at 75% and 87.5% (n/n) even lower than that. This could well just be an artefact of the above stated problems regarding preferential solvation and/or the arithmetic of how these functions are calculated.
Kamlet–Taft parameters were also measured for a series of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (n/n) mixtures containing the ions [C4C1im]+, [C6C1im]+, [C4pyr]+, [NTf2]+ and [PF6]+. As none of these ions differ strongly in their respective properties, the corresponding results are to be analysed carefully, however they do seem to indicate a tendency towards positive deviation from linear mixing. For the H-bond acidity and basicity this can again be rationalized by the probe dyes being preferentially solvated by the ionic species with the highest Kamlet–Taft parameter values. There is however no obvious explanation for the π* results.142
1 (n/n) mixtures containing the ions [C4C1im]+, [C6C1im]+, [C4pyr]+, [NTf2]+ and [PF6]+. As none of these ions differ strongly in their respective properties, the corresponding results are to be analysed carefully, however they do seem to indicate a tendency towards positive deviation from linear mixing. For the H-bond acidity and basicity this can again be rationalized by the probe dyes being preferentially solvated by the ionic species with the highest Kamlet–Taft parameter values. There is however no obvious explanation for the π* results.142
In IR studies of water in ternary mixtures with [C4C1im][NTf2] and bromide and with [C4C1im][PF6] and chloride, using the water modes to assign to which anion hydrogen bonds were formed, a clear deviation from linear mixing behaviour, showing a preference towards interactions with the halide ions could be found.103
1,3-Bis(1-pyrenyl)propane, used as a molecular probe for microviscosity, shows a positive curvature of the viscosity for all mixtures of [C4C1im][NTf2], [C4C1im][PF6] and [C2C1im][NTf2] for almost the full composition range, but exhibiting a local maximum for compositions very rich in [C4C1im][PF6] or [C2C1im][NTf2] (∼95%), overall indicating lowered viscosities for these mixtures.143 Again, this is a measurement of the local viscosity of the cybotactic region of the probe and not necessarily indicative of the bulk viscosity of the mixture.
The Gutmann acceptor number, a measure of Lewis acidity established from the 31P NMR chemical shift of triethylphosphine oxide (TEPO), has been measured for mixtures of [C8C1im]Cl with MCl3 (M = Al, Ga, In).144 It was found to change according to the metal species present at a given concentration for indium and gallium, however remained constant for aluminium, as the interaction of the metal with the probe molecule was always strong enough to displace a chloride ion from the chloroaluminate complex, so making a new species ([AlCl3(TEPO)]).
Estimates of solvent–solute interactions can also be derived from solubility and gas chromatographic measurements.2,145 Mixtures containing the [C2C1im]+ cation and [NTf2]− and chloride in varying compositions have been used as stationary phases in gas chromatography.146 The system constants of these stationary phases were then evaluated according to the Abraham model of solvation.
As the chloride ion is significantly more basic than [NTf2]−, the mixtures differ mainly in their H-bond basicity parameter. This parameter changes in a largely linear manner with the composition, with the mixture being increasingly basic for higher chloride contents. The other parameter changing significantly was the generalised polarity parameter s, but no similarly clear trend could be found.
An analysis of the solubilities of N2, CO2 and CH4 in [C2C1im][BF4][NTf2] showed that these obey regular solution theory (RST) and can be predicted based on the molar volume of the mixtures.147 The data points thus obtained fall well onto the graph for pure ionic liquids. However, the selectivity for mixtures of CO2 with one of the other gases shows a notable dependence on the composition of the ionic liquid mixture. While the selectivity is generally better the lower the amount of [NTf2]− in the mixture – due to the lower molar volume – and can be well predicted using RST, there is a sharp drop in the selectivity when going to simple [C2C1im][BF4].
Thermal stability
The upper operating temperature of an ionic liquid is usually determined by the temperature at which it decomposes. Thermogravimetric heating traces were recorded to analyse the decomposition behaviour of mixtures of [C4C1pyrr][NTf2] and [C3C1pyrr][FSI] containing 0.3 M LiX.51 For X = [PF6]− the decomposition seems to progress in two distinct steps with the onset temperatures almost identical to the pure compounds. It is likely that these are the two ionic liquids decomposing separately. For X = [NTf2]− mixtures containing up to 13.2% (n/n) [C3C1pyrr][FSI] only one common decomposition temperature was found, however for higher concentrations the same step-wise decomposition of each ionic liquid occurs.Applications of ionic liquid mixtures
Solvents for chemical synthesis and process chemistry
Much of the activity surrounding the applications of ionic liquids has focused on their use as solvents for chemicals synthesis.1–3 It is likely that this will also be true for mixtures of ionic liquids. The first process available for commercialisation using ionic liquids was the Institut Français du Pétrole Difasol™ process.148 This is a biphasic process for the dimerization of olefins to make fuel upgrade additives with an ionic liquid phase that acts as a support for the nickel catalysts and a starting material/product phase that can be easily separated for product isolation. The Difasol™ process can either be used as a replacement for, or in addition to, the earlier homogeneous Dimersol™ process. The advantages of the use of the biphasic Difasol™ system are that it offers much more efficient catalyst use and therefore a reduced catalyst consumption, higher yield, better dimer selectivity and enhanced reactor space time yield. The process also gives energy savings over its predecessor.The Difasol™ process is based upon earlier work on the use of acidic compositions of [C2C1im]Cl–AlCl3 as a combination of solvent and co-catalyst for the dimerization of propene to hexenes with nickel(II) catalysts,149 which was subsequently extended to the oligomerization of butanes.150 Although this did provide the desired products, they were contaminated with the products of a fast cationic side reaction, arising from the superacidity of proton contamination of the ionic liquid. This problem was resolved by the addition of some ethylaluminium dichloride (really the dimer – Al2Et2Cl4).151 This leads to the formation of [AlEtCl3]− ions in the mixture, which can activate the cationic nickel catalysts and mop up any adventitious water. This is an example of the addition of a molecular species, Al2Et2Cl4, leading to the formation of new ions, [AlEtCl3]−, which then makes the solution a mixture of ionic liquids.
Another suggested use of mixtures of ionic liquids for catalysis is for ruthenium catalysed hydroformylation reactions in mixtures of [C4C1im][NTf2] with chloride, which showed increasing conversion rates with decreasing chloride concentrations indicating higher reactivity due to better solubility of the reactants. For less than roughly equimolar amounts of chloride the yield of the alcohol decreases again, potentially due to the aldol condensation of the intermediate products.152
For the formation of metal organic frameworks in ionic liquids it could be shown that the anion, even though not part of the final product, significantly influences the resulting structure, with mixtures of anions yielding different structures from the simple ionic liquids.153
It is well documented that some ionic liquids, notably [C4C1im]Cl, can dissolve cellulose. However to use cellulose as a feedstock for industrially more valuable chemicals, further processing is necessary, usually in the form of a second independent reaction step. However, by using mixtures of [(HO3S)4C4C1im]Cl (3.5 mmol) in [C4C1im]Cl (20 g) it was possible to realise this process in a one-pot reaction, where the cellulose is dissolved by the chloride and the acidic ionic liquid then catalyses the dehydration reaction.154 This yielded a complex mixture of products, including 2-(diethoxymethy)furan (the major component), polyols, aldehydes, ketones, ethers, furans, olefins, methyl esters and others.
The lipase-catalysed esterification of glucose with a fatty acid shows the highest glucose solubility and initial enzyme activity when hydrophilic ionic liquids are used, but the highest enzyme recyclability is found in hydrophobic ionic liquids. By using the combination of a hydrophobic and a hydrophilic ionic liquid, [C4C1im][OTf][NTf2], it was found that intermediate levels for solubility, activity and lifetime could be realized.155 The solubility showed negative deviations from linear behaviour, while the initial activity and the recyclability showed positive deviations. A later study, also made use of this strategy in an ultrasound irradiation study of lipase-catalysed esterification of fructose with palmitic acid with promising results.156
For the enzymatic hydrolysis of penicillin it was found that the by-product removal at a given pH of the aqueous phase and thus the selectivity of the process could be fine-tuned by varying the composition of [C4C1im][BF4][PF6], which was used as an extraction layer.157 In another extraction, Katsuta et al. could show that the extraction characteristics of Pd and Pt from hydrochloric acid solutions into hydrophobic protic ternary ionic liquid mixtures could be fine-tuned by varying the ratio of the coordinating anions, either Cl− or [NO3]− to the [NTf2]−.158 A relatively recent application of ionic liquid mixtures is for dispersive liquid–liquid micro-extraction.159 In this method a hydrophobic ionic liquid is injected together with a hydrophilic ionic liquid into an aqueous sample, to form a dispersion in which the large interface allows a rapid extraction of solutes from the water-phase into the ionic liquid. It was shown that such mixtures can not only be used as an analytical tool, but that the extraction performance can be influenced by varying the disperser as well as extraction solvent.
Concern over global climate change has led to an increased interest in CO2 capture technologies.160 It has been suggested that the non-volatile nature of ionic liquids gives these an advantage over conventional aqueous amine technologies.161,162 The high solubility of CO2 in [CnCmim][CH3CO2] ionic liquids, driven by the formation of a zwitterionic 1,3-dialkylimidazolium-2-carboxylates, is well known.163 Two moles of [CH3CO2]− are required for every one mole of CO2 absorbed, because the proton abstraction from the imidazolium salt that initiates the reaction leads to the formation of [H(CH3CO2)2]−. For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of [C2C1im][CH3CO2] and [C2C1im][CF3CO2] the CO2 solubility can be calculated using a simple weighted average of the solubility in the pure compounds.164 This indicated that the [CF3CO2]− is not capable of deprotonating the imidazolium cation, nor is it capable of stabilizing the proton by forming [H(CH3CO2)(CF3CO2)]−. What this study does show is the potential to use one ionic liquid with good physical properties as the solvent for another ionic liquid with the desired chemical properties, but poor physical properties in chemical processes.
1 mixture of [C2C1im][CH3CO2] and [C2C1im][CF3CO2] the CO2 solubility can be calculated using a simple weighted average of the solubility in the pure compounds.164 This indicated that the [CF3CO2]− is not capable of deprotonating the imidazolium cation, nor is it capable of stabilizing the proton by forming [H(CH3CO2)(CF3CO2)]−. What this study does show is the potential to use one ionic liquid with good physical properties as the solvent for another ionic liquid with the desired chemical properties, but poor physical properties in chemical processes.
Nucleophilic substitutions have been studied in a great deal of detail in ionic liquids.2 The kinetics of the reactions of a range of anionic nucleophiles (Cl−, Br−, I−, [CH3CO2]−, [CF3CO2]−, [CN]− and [SCN]−, Fig. 11) with methyl-p-nitrobenzene sulfonate (Me-p-NBS) in [C4C1im][NTf2], [C4C1pyrr][NTf2] or [C4C1pyrr][OTf] have been measured to elucidate the effects of the interactions between these anions and the ionic liquids.165 The anions were used as salts with the cation common to that of the ionic liquids in which the reaction was being conducted, so these should be described as binary mixtures with a common cation.
 | ||
| Fig. 11 The reactions of Me-p-NBS with anionic nucleophiles. | ||
These reactions were found to proceed smoothly in the ionic liquids with a typical SN2 mechanism and were amenable to analysis using the Kamlet–Taft linear solvation energy relationship (LSER) approach. Hydrogen bond donation by the ionic liquids, α, appeared in all of the LSERs generated and always had a negative value. This was attributed to slowing of the reaction by the solvent hydrogen bonding to the nucleophile, stabilising it with respect to the activated complex, which is a less strong hydrogen bond acceptor. Since the hydrogen bond donor property arises from the cation structure, this was seen as a strong cation effect. The strength of this effect was found to depend upon the hydrogen bond acceptor ability of the nucleophiles, except that an unusual result for [CN]− was interpreted as a hard/soft acid/base effect. I−, and [CH3CO2]−, had best fit LSERs with β included in the correlations, but with a much lower contribution that was attributed to the antagonistic hydrogen bonding effects. π* appeared in the best-fit LSERs for [CN]−, [CH3CO2]− and [CF3CO2]−.
When studying the activation parameters for these reactions in ionic liquids, it was noted that ΔS‡ for the reaction was more similar to the reaction of free solvated ions in molecular solvents, but ΔH‡ was more similar to that of the ion-paired nucleophiles in molecular solvents. It was concluded that this apparent anomaly is a direct result of the ionic association found in ionic liquids having some commonalities with ion-pairing in molecular solvents, but being far from the same thing. The results can be explained by the weakening of hydrogen bonds between the solvent and the anion as it loses its charge density decreases during the formation of the activated complex. This idea was further elaborated, when it was shown that while the reaction of chloride ions with cationic electrophiles is dominated by the behaviour of ion pairs, no kinetically significant ion pair derived behaviour could be seen in any ionic liquid, in spite of the fact that ion association is strong in these systems.166
The rate of hydrolysis of N-(p-fluorophenyldiphenylmethyl)-4-picolinium chloride in [C4C1im][NTf2], with added cations, such as [PBu4]+ and [C4C1C1im]+ showed distinct rate increases.140 This was attributed to the dilution of the [C4C1im]+, which slowed the reaction through its hydrogen bonding to the water. The preferential solvation of Reichardt's dye by the strong hydrogen bond constituent of the mixtures [C4C1im]+ prevented ETN values from being used to quantify this effect.
Electrochemical applications
Ionic liquids can be used as electrolytes in dye sensitized solar cells where good transport properties for iodine species are necessary.167 For optimum performance, a high concentration of iodide as well as high conductivity and diffusion coefficients are required. Mixtures of ionic liquids are known to perform well in these systems, as the beneficial transport properties of iodide based ionic liquids for I2 are combined by mixing with lower viscosity ionic liquids.168 A second approach is rather than mix two ionic liquids that each provide one property, to mix two or more ionic liquids based on iodide that are not liquid at the desired temperature, but show high conductivity above their melting points. Provided these form a sufficiently low melting (eutectic) mixture this can be combined with the inherently high iodide concentration to allow the construction of highly efficient solar cells.169 These ionic liquids can be further mixed with low viscosity ionic liquids, combining both approaches.170Use as battery electrolytes is another potential application of ionic liquid mixtures. The addition of lithium salts to ionic liquids in battery applications has been found to extend their electrochemical window.171 For applications in batteries it is often necessary to employ additives together with the ionic liquid to form a solid electrolyte interface covering the electrode, hence protecting the ionic liquid. Once the electrode has been fully covered no further improvement is achieved by adding more of the additive. Often a critical concentration of the additive exists at which it completely covers the electrode and is fully functional, but above which additional additive has no further benefit. However, when [C2C1im][FSI] (where [FSI] = N(SO2F)2]) was used as the solvent, fully reversible Li intercalation into a graphitized electrode could be achieved without the need for any additive.172 Hence, it was subsequently used as a additive to [C2C1im][NTf2] or [C2C1im][BF4] ionic liquids. However, its behaviour was not as simple as more traditional additives. It showed different behaviour in each ionic liquid, with the reversibility of the Li intercalation depending very strongly on the concentration of the [FSI]− ions and no critical concentration was observed in either case.173
A mixture of a [SMK][NTf2] salt (where SMK = 2-oxo-3,9-dioxa-6-azonia-spiro[5.5]undecane, Fig. 12) and [C3C1pyrr][NTf2] with added lithium salt was used as the electrolyte in a lithium battery cell.174 While the pure [SMK][NTf2] successfully suppressed dendrite formation, the high melting point, poor capacities and increasing passivation of the electrode prohibited its use alone, whereas the pyrrolidinium salt by itself caused dendrite formation at the lithium electrode, resulting in shorting of the cell. The same was true for mixtures with less than 0.2 mol kg−1 of the [SMK][NTf2]. However, higher concentrations largely supressed dendrite formation while showing good cycling of the cell with high capacities.
![The structure of the [SMK] cation.](/image/article/2012/CS/c2cs35177c/c2cs35177c-f12.gif) | ||
| Fig. 12 The structure of the [SMK] cation. | ||
Magnesium has been electrodeposited from a solution of Mg(CF3SO3)2 in mixtures of [C4C1im][BF4] and [C1C3pip][NTf2] (where [C1C3pip] N-methyl-N-propylpiperidinium) at different volume ratios (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 3
1, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).175 The addition of [C1C3pip][NTf2] to [C4C1im][BF4] increases the conductivity of the electrolyte system and the initial deposition–dissolution overpotentials were found to be lower in the mixtures than in any of the neat ionic liquids. The 4
1).175 The addition of [C1C3pip][NTf2] to [C4C1im][BF4] increases the conductivity of the electrolyte system and the initial deposition–dissolution overpotentials were found to be lower in the mixtures than in any of the neat ionic liquids. The 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture exhibited good conductivity and the lowest initial overpotential. Moreover, the reversible electrodeposition was maintained over 200 cycles.
1 mixture exhibited good conductivity and the lowest initial overpotential. Moreover, the reversible electrodeposition was maintained over 200 cycles.
Chromatography
The use of ionic liquids as stationary phases for gas chromatography is well established,145 and commercial columns are now available. It has been shown that mixtures of ionic liquids can be used to fine-tune the properties of these columns to provide enhanced separation selectivity of a mixture of alcohols and aromatic analytes.146Heat transfer fluids
Low-melting point inorganic nitrate salt mixtures have been proposed as heat transfer fluids and thermal energy storage media in solar energy applications, such as solar parabolic trough electrical power plant systems.61 The advantage of the all-inorganic nature of these mixtures is that they do not suffer the thermal instability problems of organic ionic liquids; while they are still liquid at low enough temperatures that they do not solidify under typical operating conditions.Overview
The analysis of the available literature presented above demonstrates that mixtures of ionic liquids have often shown a remarkable degree of predictability in many of their properties. However, care should be taken before too broad generalizations are made. The current data set is quite restricted and some properties have been investigated for one set of ionic liquids and other properties have been studied for others. It is possible that the differences could arise from different behaviours of the particular ionic liquids used in the studies, the effect being measured, or both. Fortunately, there is much that can be learned from past investigations on molten salts, to give a greater set of examples.Near ideal mixing is possible and has been demonstrated, but this does not imply that it will always be the case, nor even generally true. Only time and more examples will reveal this. Much mixing behaviour in ionic liquids has been shown to be entropy driven, with the number of components mixed being more important than their identities. Density and viscosity have both repeatedly been found in very good agreement with their corresponding mixing laws, namely the linear mixing of molar volumes and the linear mixing on the logarithmic scale of viscosities. Conversely, the phase transitions of mixtures of ionic liquids show promising potential in terms of the formation of eutectic mixtures, but these are difficult to predict. Glass forming behaviours are common and can lead to difficulties in even identifying the phase transition. Glasslike behaviour also has a dramatic effect upon dynamic properties. Timescales are long and predictability is very difficult to achieve.
So far, it is largely true that most people working in the area have used the typical, well known ionic liquids that are generally quite similar to each other and, with the exception of those interested in halogenometalate ionic liquids, have used mixtures composed of ions that do not react with each other. This is only a subset of those available. As the subject advances, more complex mixtures will be developed that are deliberately designed to escape these constraints. This will, undoubtedly, lead to interesting and useful additions to the properties that can be achieved with ionic liquids.
Acknowledgements
We would like to thank Prof. Amparo Galindo of the Chemical Engineering Department at Imperial College and Kevin Lovelock of the Chemistry Department at Imperial College. We would also like to thank the ERC for its generous support of our work on mixtures of ionic liquids.References
- (a) Ionic Liquids in Synthesis, ed. P. Wasserschied and T. Welton, VCH Wiley, Weinheim, 2nd edn, 2008 Search PubMed; (b) Electrodeposition from Ionic Liquids, ed. F. Endres, A. P. Abbott and D. R. MacFarlane, WILEY-VCH, Weinheim, 2008 Search PubMed; (c) Electrochemical Aspects of Ionic Liquids, ed. H. Ohno, John Wiley & Sons, NJ, 2005 Search PubMed; (d) “Ionic Liquids” Topics in Current Chemistry, ed. B. Kirchner, Springer, Heidelberg, 2009, vol. 290 Search PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508 CrossRef CAS.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123 RSC.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32 Search PubMed.
- P. Atkins and J. De Paula, Physical Chemistry, OUP, Oxford, 8th edn, 2006 Search PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071 CrossRef CAS.
- (a) A. K. Abdul-Sada, A. M. Greenway, K. R. Seddon and T. Welton, Org. Mass Spectrom., 1989, 24, 917 CrossRef CAS; (b) A. K. Abdul-Sada, A. M. Greenway, K. R. Seddon and T. Welton, Org. Mass Spectrom., 1993, 28, 759 CrossRef CAS.
- (a) K. R. Seddon, in The International George Papatheodorou Symposium: Proceedings, ed. S. Boghosian, V. Dracopoulos, C. G. Kontoyannis and G. A. Voyiatzis, Institute of Chemical Engineering and High Temperature Chemical Processes, Patras, 1999 Search PubMed; (b) J. D. Holbrey and K. R. Seddon, Clean Technol. Environ. Policy, 1999, 1, 223 CrossRef.
- H. Bloom, Pure Appl. Chem., 1963, 7, 389 CrossRef CAS.
- (a) Fused Salts, ed. B. R. Sundheim, McGraw-Hill, New York, 1964 Search PubMed; (b) O. J. Kleppa, Annu. Rev. Phys. Chem., 1965, 16, 187 CrossRef CAS; (c) S. V. Meschel and O. J. Kleppa, J. Chem. Phys., 1967, 46, 853 CrossRef.
- (a) L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486 CrossRef CAS; (b) A. Z. Tasic, B. D. Djordjevic and D. K. Grozdanic, J. Chem. Eng. Data, 1992, 37, 310 CrossRef CAS; (c) J. L. Gohres, C. L. Kitchens, J. P. Hallett, A. V. Popov, R. Hernandez, C. L. Liotta and C. A. Eckert, J. Phys. Chem. B, 2008, 112, 4666 CrossRef CAS.
- J. H. Hildebrand and E. J. Salstrom, J. Am. Chem. Soc., 1932, 54, 4257 CrossRef CAS.
- J. M. Prausnitz, R. N. Lichtenthaler and E. Gomes de Acevedo, Polymers: Solutions, Blends, Membranes, and Gels, in Molecular Thermodynamics of Fluid Phase Equilibria, Prentice Hall PTR, 1999, pp. 417–440 Search PubMed.
- J. Lumsden, Thermodynamics of molten salt mixtures, Academic Press, London, 1966 Search PubMed.
- O. J. Kleppa and F. G. McCarty, J. Phys. Chem., 1966, 70, 1249 CrossRef CAS.
- O. J. Kleppa, Annu. Rev. Phys. Chem., 1965, 16, 187 CrossRef CAS.
- O. J. Kleppa and L. S. Hersh, J. Chem. Phys., 1961, 34, 351 CrossRef CAS.
- O. J. Kleppa and S. V. Meschel, J. Phys. Chem., 1963, 67, 668 CrossRef CAS.
- J. H. Hildebrand and E. J. Salstrom, J. Am. Chem. Soc., 1932, 54, 4257 CrossRef CAS.
- M. L. Saboungi, C. Vallet and Y. Doucet, J. Phys. Chem., 1973, 77, 1699 CrossRef CAS.
- (a) M. L. Saboungi, H. Schnyders, M. S. Foster and M. Blander, J. Phys. Chem., 1974, 78, 1091 CrossRef CAS; (b) G. Flor, C. Margheritis and C. Sinistri, J. Chem. Eng. Data, 1978, 23, 336 CrossRef CAS.
- P. Navia, J. Troncoso and L. Romani, J. Chem. Eng. Data, 2007, 52, 1369 CrossRef CAS.
- A. Arce, M. J. Earle, S. P. Katdare, H. Rodriguez and K. R. Seddon, Chem. Commun., 2006, 2548 RSC.
- H. J. Castejón and R. J. Lashock, J. Mol. Liq., 2012, 167, 1 CrossRef.
- J. N. Canongia Lopes, T. C. Cordeiro, J. M. S. S. Esperanca, H. J. R. Guedes, S. Huq, L. P. N. Rebelo and K. R. Seddon, J. Phys. Chem. B, 2005, 109, 3519 CrossRef.
- Y. Tada, S. Hiraoka, Y. Katsimura and I. Yamada, Ind. Eng. Chem. Res., 1992, 31, 2010 CrossRef CAS.
- B. F. Powers, J. L. Katz and O. J. Kleppa, J. Phys. Chem., 1962, 66, 103 CrossRef CAS.
- H. Bloom, P. W. D. Boyd, J. L. Laver and J. Wong, Aust. J. Chem., 1966, 19, 1591 CrossRef CAS.
- J. N. C. Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330 CrossRef.
- K. Shimizu, M. Tariq, L. P. N. Rebelo and J. N. Canongia Lopes, J. Mol. Liq., 2010, 153, 52 CrossRef CAS.
- (a) A. Stoppa, R. Buchner and G. Hefter, J. Mol. Liq., 2010, 153, 46 CrossRef CAS; (b) M. Larriba, S. García, P. Navarro, J. García and F. Rodríguez, J. Chem. Eng. Data, 2012, 57, 1318 CrossRef CAS.
- N. K. Boardman, F. H. Dorman and E. Heymann, J. Phys. Colloid Chem., 1948, 53, 375 CrossRef.
- M. A. Ab Rani, A. Brandt, L. Crowhurst, A. Dolan, M. Lui, N. H. Hassan, J. P. Hallett, H. Niedermeyer, J. M. Perez-Arlandis, M. Schrems, T. To, T. Welton and R. Wilding, Phys. Chem. Chem. Phys., 2011, 13, 16831 RSC.
- S. Aparicio and M. Atilhan, J. Phys. Chem. B, 2012, 116, 2526 CrossRef CAS.
- E. T. Fox, J. E. F. Weaver and W. A. Henderson, J. Phys. Chem. C, 2012, 116, 5270 CAS.
- A. A. Fannin, D. A. Floreani, L. A. King, J. S. Landers, B. J. Piersma, D. J. Stech, R. L. Vaughn, J. S. Wilkes and J. L. Williams, J. Phys. Chem., 1984, 88, 2614 CrossRef CAS.
- A. B. Pereiro, J. M. M. Araújo, F. S. Oliveira, C. E. S. Bernardes, J. M. S. S. Esperança, J. N. Canongia Lopes, I. M. Marrucho and L. P. N. Rebelo, Chem. Commun., 2012, 48, 3656 RSC.
- (a) J. L. Barton and H. Bloom, Trans. Faraday Soc., 1959, 55 RSC; (b) H. Bloom and B. J. Welch, Trans. Faraday Soc., 1961, 57 RSC; (c) H. Bloom, S. Richards and D. Williams, Aust. J. Chem., 1972, 25, 2077 CrossRef CAS.
- (a) V. N. Emel'yanenko, S. P. Verevkin and A. Heintz, J. Am. Chem. Soc., 2007, 129, 3930 CrossRef CAS; (b) S. P. Verevkin, V. N. Emel'yanenko, D. H. Zaitsau, A. Heintz, C. D. Muzny and M. Frenkel, Phys. Chem. Chem. Phys., 2010, 12, 14994 RSC; (c) A. Seeberger, A. K. Andresen and A. Jess, Phys. Chem. Chem. Phys., 2009, 11, 9375 RSC; (d) F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Phys. Chem. Chem. Phys., 2010, 12, 12089 RSC; (e) F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Green Chem., 2011, 13, 1453 RSC; (f) M. A. A. Rocha, C. F. R. A. C. Lima, L. R. Gomes, B. Schröder, J. A. P. Coutinho, I. M. Marrucho, J. M. S. S. Esperança, L. P. N. Rebelo, K. Shimizu, J. N. Canongia Lopes and L. M. N. B. F. Santos, J. Phys. Chem. B, 2011, 115, 10919 CAS.
- D. H. Zaitsau, G. J. Kabo, A. A. Strechan, Y. U. Paulechka, A. Tschersich, S. P. Verevkin and A. Heintz, J. Phys. Chem. A, 2006, 110, 7303 CrossRef CAS.
- (a) M. J. Earle, J. M. S. S. Esperanca, M. A. Gilea, J. N. C. Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831 CrossRef CAS; (b) J. A. Widegren, Y.-M. Wang, W. A. Henderson and J. W. Magee, J. Phys. Chem. B, 2007, 111, 8959 CrossRef CAS.
- (a) A. Büchler, P. E. Blackburn and J. L. Stauffer, J. Phys. Chem., 1966, 70, 685 CrossRef; (b) E. E. Schrier and H. M. Clark, J. Phys. Chem., 1963, 67, 1259 CrossRef CAS.
- (a) J. P. Armstrong, C. Hurst, R. G. Jones, P. Licence, K. R. J. Lovelock, C. J. Satterley and I. J. Villar-Garcia, Phys. Chem. Chem. Phys., 2007, 9, 982 RSC; (b) L. P. N. Rebelo and K. R. Seddon, J. Phys. Chem. A, 2007, 111, 6176 CrossRef; (c) D. Strasser, F. Goulay, M. S. Kelkar, E. J. Maginn and S. R. Leone, J. Phys. Chem. A, 2007, 111, 3191 CrossRef CAS; (d) J. P. Leal, J. M. S. S. Esperança, M. E. M. da Piedade, J. N. Canongia Lopes, L. P. N. Rebelo and K. R. Seddon, J. Phys. Chem. A, 2007, 111, 6176 CrossRef CAS.
- P. Ballone, C. Pinilla, J. Kohanoff and M. G. Del Popolo, J. Phys. Chem. B, 2007, 111, 4938 CrossRef CAS.
- J. M. S. S. Esperanca, J. N. C. Lopes, M. Tariq, L. M. N. B. F. Santos, J. W. Magee and L. P. N. Rebelo, J. Chem. Eng. Data, 2010, 55, 3 CrossRef CAS.
- A. W. Taylor, K. R. J. Lovelock, A. Deyko, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2010, 12, 1772 RSC.
- J. L. Barton and H. Bloom, Trans. Faraday Soc., 1959, 55 Search PubMed.
- A. P. Abbott, G. Frisch, H. Garrett and J. Hartley, Chem. Commun., 2011, 47, 11876 RSC.
- M. Montanino, M. Moreno, F. Alessandrini, G. B. Appetecchi, S. Passerini, Q. Zhou and W. A. Henderson, Electrochim. Acta, 2012, 60, 163 CrossRef CAS.
- A. Arce, M. J. Earle, S. P. Katdare, H. Rodriguez and K. R. Seddon, Fluid Phase Equilib., 2007, 261, 427 CrossRef CAS.
- Q. Zhou, W. A. Henderson, G. B. Appetecchi and S. Passerini, J. Phys. Chem. C, 2010, 114, 6201 CAS.
- K. Hayamizu, Y. Aihara, H. Nakagawa, T. Nukuda and W. S. Price, J. Phys. Chem. B, 2004, 108, 19527 CrossRef CAS.
- J. Scheers, J. Pitawala, F. Thebault, J. K. Kim, J. H. Ahn, A. Matic, P. Johansson and P. Jacobsson, Phys. Chem. Chem. Phys., 2011, 13, 14953 RSC.
- M. Kunze, S. Jeong, E. Paillard, M. Winter and S. Passerini, J. Phys. Chem. C, 2010, 114, 12364 CAS.
- H. Every, A. G. Bishop, M. Forsyth and D. R. MacFarlane, Electrochim. Acta, 2000, 45, 1279 CrossRef CAS.
- V. I. Posypaiko and E. A. Alekseeva, Phase Equilibria in binary halides, Plenum, New York, 1987 Search PubMed.
- T. D. J. Dunstan and J. Caja, ECS Trans., 2007, 3, 21 CrossRef CAS.
- P. M. Bayley, A. S. Best, D. R. MacFarlane and M. Forsyth, ChemPhysChem, 2011, 12, 823 CrossRef CAS.
- Y. U. Pavlechko and G. Y. Kabo, Russ. J. Phys. Chem. A, 2008, 82, 1412 CrossRef CAS.
- J. Sun, M. Forsyth and D. R. MacFarlane, J. Phys. Chem. B, 1998, 102, 8858 CrossRef CAS.
- J. W. Raade and D. Padowitz, J. Sol. Energy Eng., 2011, 133, 031013 CrossRef.
- J. D. Holbrey, W. M. Reichert, M. Nieuwenhuyzen, S. Johnston, K. R. Seddon and R. D. Rogers, Chem. Commun., 2003, 1636 RSC.
- A. Arce, M. J. Earle, S. P. Katdare, H. Rodriguez and K. R. Seddon, Chem. Commun., 2006, 2548 RSC.
- A. Arce, M. J. Earle, S. P. Katdare, H. Rodriguez and K. R. Seddon, Phys. Chem. Chem. Phys., 2008, 10, 2538 RSC.
- J. Kagimoto, N. Nakamura, T. Kato and H. Ohno, Chem. Commun., 2009, 2405 RSC.
- J. R. Sanders, E. H. Ward and C. L. Hussey, J. Electrochem. Soc., 1986, 133, 325 CrossRef CAS.
- F. H. Hurley and T. P. Weir, J. Electrochem. Soc., 1951, 98, 203 CrossRef CAS.
- C. Hardacre, R. W. Murphy, K. R. Seddon, G. Srinivasan and M. Swadzba-Kwasny, Aust. J. Chem., 2010, 63, 845 CrossRef CAS.
- M. S. Sitze, E. R. Schreiter, E. V. Patterson and R. G. Freeman, Inorg. Chem., 2001, 40, 2298 CrossRef CAS.
- J. Estager, P. Nockemann, K. R. Seddon, M. Swadzba-Kwasny and S. Tyrrell, Inorg. Chem., 2011, 50, 5258 CrossRef CAS.
- E. R. Schreiter, J. E. Stevens, M. F. Ortwerth and R. G. Freeman, Inorg. Chem., 1999, 38, 3935 CrossRef CAS.
- (a) S. A. Bolkan and J. T. Yoke, J. Chem. Eng. Data, 1986, 31, 194 CrossRef CAS; (b) S. A. Bolkan and J. T. J. Yoke, Inorg. Chem., 1986, 25, 3587 CrossRef CAS.
- P. S. Campbell, C. C. Santini, D. Bouchu, B. Fenet, L. Rycerz, Y. Chauvin, M. Gaune-Escard, C. Bessada and A.-L. Rollet, Dalton Trans., 2010, 39, 1379 RSC.
- D. C. Apperley, C. Hardacre, P. Licence, R. W. Murphy, N. V. Plechkova, K. R. Seddon, G. Srinivasan, M. Swadzba-Kwasny and I. J. Villar-Garcia, Dalton Trans., 2010, 39, 8679 RSC.
- N. M. Rocher, E. I. Izgorodina, T. Ruther, M. Forsyth, D. R. MacFarlane, T. Rodopoulos, M. D. Horne and A. M. Bond, Chem.–Eur. J., 2009, 15, 3435 CrossRef CAS.
- T. Rodopoulos, L. Smith, M. D. Horne and T. Ruther, Chem.–Eur. J., 2010, 16, 3815 CrossRef CAS.
- P. Eiden, Q. Liu, S. Zein El Abedin, F. Endres and I. Krossing, Chem.–Eur. J., 2009, 15, 3426 CrossRef CAS.
- K. R. Seddon, A. Stark and M.-J. Torres, Pure Appl. Chem., 2000, 72, 2275 CrossRef CAS.
- P. Navia, J. Troncoso and L. Romani, J. Solution Chem., 2008, 37, 677 CrossRef CAS.
- (a) P. K. Katti and M. M. Chaudhri, J. Chem. Eng. Data, 1964, 9, 442 CrossRef CAS; (b) S. Glasstone, K. J. Laidler and H. Eyring, The Theory of Rate Processes, MacGraw-Hill, New York, 1941 Search PubMed; (c) R. E. Powell, W. E. Roseveare and H. Eyring, Ind. Eng. Chem., 1941, 33, 430 CrossRef CAS.
- L. Grunberg and A. H. Nissan, Nature, 1949, 164, 799 CrossRef CAS.
- (a) A. Stoppa, R. Buchner and G. Hefter, J. Mol. Liq., 2010, 153, 46 CrossRef CAS; (b) E. C. Bingham, Fluidity and plasticity, McGraw-Hill, New York, 1922 Search PubMed.
- Y. S. Fung and S. M. Chau, Inorg. Chem., 1995, 34, 2371 CrossRef CAS.
- F. Castiglione, G. Raos, G. B. Appetecchi, M. Montanino, S. Passerini, M. Moreno, A. Famulari and A. Mele, Phys. Chem. Chem. Phys., 2010, 12, 1784 RSC.
- A. Stoppa, R. Buchner and G. Hefter, J. Mol. Liq., 2010, 153, 46 CrossRef CAS.
- A. Jarosik, S. R. Krajewski, A. Lewandowski and P. Radzimski, J. Mol. Liq., 2006, 123, 43 CrossRef CAS.
- M. Egashira, S. Okada and J. Yamaki, Solid State Ionics, 2002, 148, 457 CrossRef CAS.
- M. Egashira, M. Nakagawa, L. Watanabe, S. Okada and J. I. Yamaki, J. Power Sources, 2005, 146, 685 CrossRef CAS.
- G. B. Appetecchi, M. Montanino, A. Balducci, S. F. Lux, M. Winterb and S. Passerini, J. Power Sources, 2009, 192, 599 CrossRef CAS.
- A. P. Abbott, ChemPhysChem, 2005, 6, 2502 CrossRef CAS.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649 RSC.
- M. Zistler, P. Wachter, P. Wasserscheid, D. Gerhard, A. Hinsch, R. Sastrawan and H. J. Gores, Electrochim. Acta, 2006, 52, 161 CrossRef CAS.
- G. Annat, D. R. MacFarlane and M. Forsyth, J. Phys. Chem. B, 2007, 111, 9018 CrossRef CAS.
- J. O'M. Bockris and A. K. N. Reddy, Modern Electrochemistry, Plenum, New York, 1970 Search PubMed.
- G. J. Landon and A. R. Ubbelohde, Trans. Faraday Soc., 1956, 52, 647 RSC.
- H. A. Levy, P. A. Agron, M. A. Bredig and M. D. Danford, Anal. N. Y. Acad. Sci., 1960, 79, 762 CrossRef CAS.
- B. Aoun, A. Goldbach, S. Kohara, J.-F. Wax, M. A. Gonzalez and M.-L. Saboungi, J. Phys. Chem. B, 2010, 114, 16838 CrossRef.
- C. M. Gordon, J. D. Holbrey, A. R. Kennedy and K. R. Seddon, J. Mater. Chem., 1998, 8, 2627 RSC.
- K. Binnemans, Chem. Rev., 2005, 105, 4148 CrossRef CAS.
- (a) J. N. C. Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330 CrossRef; (b) A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641 CrossRef CAS; (c) D. T. Bowron, D'Agostino, L. F. Gladden, C. Hardacre, J. D. Holbrey, M. C. Lagunas, J. McGregor, M. D. Mantle, C. L. Mullan and T. G. A. Youngs, J. Phys. Chem. B, 2010, 114, 7760 CrossRef CAS; (d) M. Macchiagodena, L. Gontrani, F. Ramondo, A. Triolo and R. Caminiti, J. Chem. Phys., 2011, 134, 114521 CrossRef; (e) O. Yamamuro, T. Yamada, M. Kofu1, M. Nakakoshi and M. Nagao, J. Chem. Phys., 2011, 135, 1089 CrossRef; (f) R. Hayes, S. Imberti, G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237 RSC; (g) R. Hayes, S. Imberti, G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 13544 RSC.
- C. Hardacre, J. D. Holbrey, C. L. Mullan, T. G. A. Youngs and D. T. Bowron, J. Chem. Phys., 2010, 133, 074510 CrossRef.
- M. Y. Lui, L. Crowhurst, J. P. Hallett, P. A. Hunt, H. Niedermeyer and T. Welton, Chem. Sci., 2011, 2, 1491 RSC.
- J.-M. Andanson, M. J. Beier and A. Baiker, J. Phys. Chem. Lett., 2011, 2, 2959 CrossRef CAS.
- R. Katoh, M. Hara and S. Tsuzuki, J. Phys. Chem. B, 2008, 112, 15426 CrossRef CAS.
- A. Elaiwi, P. B. Hitchcock, K. R. Seddon, N. Srinivasan, Y.-M. Tan, T. Welton and J. A. Zora, J. Chem. Soc., Dalton Trans., 1995, 3467 RSC.
- M. Brüssel, M. Brehm, T. Voigt and B. Kirchner, Phys. Chem. Chem. Phys., 2011, 13, 13617 RSC.
- A. G. Avent, P. A. Chaloner, M. P. Day, K. R. Seddon and T. Welton, J. Chem. Soc., Dalton Trans., 1994, 3405 RSC.
- (a) D. Xiao, J. R. Rajian, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2006, 110, 16174 CrossRef CAS; (b) D. Xiao, J. R. Rajian, L. G. Hines, S. Li, R. A. Bartsch and E. L. Quitevis, J. Phys. Chem. B, 2008, 112, 13316 CrossRef CAS.
- E. L. Quitevis, J. R. Rajian and B. R. Hyun, J. Phys. Chem. A, 2004, 108, 10107 CrossRef.
- C. Hardacre, J. D. Holbrey, S. E. J. McMath, D. T. Bowron and A. K. Soper, J. Chem. Phys., 2003, 118, 273 CrossRef CAS.
- E. L. Quitevis, personal communication.
- K. Shimizu, M. Tariq, L. P. N. Rebelo and J. N. C. Lopes, J. Mol. Liq., 2010, 153, 52 CrossRef CAS.
- T. Pott and P. Maleard, Phys. Chem. Chem. Phys., 2009, 11, 5469 RSC.
- O. Russina and A. Triolo, Faraday Discuss., 2012, 154, 97 RSC.
- T. L. Greaves, D. F. Kennedy, N. Kirby and C. J. Drummond, Phys. Chem. Chem. Phys., 2011, 13, 13501 RSC.
- Y. Hirohata, N. Nishi and T. Kakiuchi, J. Chem. Eng. Data, 2010, 55, 1980 CrossRef CAS.
- R. Ishimatsu, Y. Kitazumi, N. Nishi and T. Kakiuchi, J. Phys. Chem. B, 2009, 113, 9321 CrossRef CAS.
- S. Thomaier and W. Kunz, J. Mol. Liq., 2007, 130, 104 CrossRef CAS.
- N. Li, S. H. Zhang, L. Q. Zheng, B. Dong, X. W. Li and L. Yu, Phys. Chem. Chem. Phys., 2008, 10, 4375 RSC.
- T. Inoue, K. Kawashima and Y. Miyagawa, J. Colloid Interface Sci., 2011, 363, 295 CrossRef CAS.
- (a) R. Hayes, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709 RSC; (b) C. S. Santos and S. Baldelli, Chem. Soc. Rev., 2010, 39, 2136 RSC; (c) K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2012, 14, 5071 RSC.
- K. R. J. Lovelock, C. Kolbeck, T. Cremer, N. Paape, P. S. Schultz, P. Wasserscheid, F. Maier and H.-P. Steinrück, J. Phys. Chem. B, 2009, 113, 2854 CrossRef CAS.
- V. Lockett, R. Sedev, C. Bassell and J. Ralston, Phys. Chem. Chem. Phys., 2008, 10, 1330 RSC.
- (a) E. F. Smith, I. J. Villar-Garcia, D. Briggs and P. Licence, Chem. Commun., 2005, 5633 RSC; (b) J. M. Gottfried, F. Maier, J. Rossa, D. Gerhard, P. S. Schultz, P. Wasserscheid and H.-P. Steinrück, Z. Phys. Chem., 2006, 220, 1439 CrossRef CAS.
- C. Kolbeck, T. Cremer, K. R. J. Lovelock, N. Paape, P. S. Schultz, P. Wasserscheid, F. Maier and H.-P. Steinrück, J. Phys. Chem. B, 2009, 113, 8682 CrossRef CAS.
- (a) I. S. Martinez and S. Baldelli, J. Phys. Chem. C, 2010, 114, 11564 CrossRef CAS; (b) T. J. Gannon, G. Law, P. R. Watson, A. J. Carmichael and K. R. Seddon, Langmuir, 1999, 15, 8429 CrossRef CAS.
- V. Lockett, R. Sedev, S. Harmer, J. Ralston, M. Horne and T. Rodopoulos, Phys. Chem. Chem. Phys., 2010, 12, 13816 RSC.
- F. Maier, T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, P. S. Schulz, P. Wasserscheid and H. P. Steinruck, Phys. Chem. Chem. Phys., 2010, 12, 1905 RSC.
- K. Nakajima, A. Ohno, H. Hashimoto, M. Suzuki and K. Kimura, J. Chem. Phys., 2010, 133, 044702 CrossRef.
- L. G. Chen, R. V. Lerum, H. Aranda-Espinoza and H. Bermudez, J. Phys. Chem. B, 2010, 114, 11502 CrossRef CAS.
- L. G. Chen and H. Bermudez, Langmuir, 2012, 28, 1157 CrossRef CAS.
- F. Maier, J. M. Gottfried, J. Rossa, D. Gerhard, P. S. Schulz, W. Schwieger, P. Wasserscheid and H. P. Steinrück, Angew. Chem., Int. Ed., 2006, 45, 7778 CrossRef CAS.
- C. Kolbeck, N. Paape, T. Cremer, P. S. Schulz, F. Maier, H. P. Steinrück and P. Wasserscheid, Chem.–Eur. J., 2010, 16, 12083 CrossRef CAS.
- C. Aliaga, C. S. Santos and S. Baldelli, Phys. Chem. Chem. Phys., 2007, 9, 3683 RSC.
- M. T. Alam, M. M. Islam, T. Okajima and T. Ohsaka, J. Phys. Chem. C, 2009, 113, 6596 CAS.
- I. Hamley, in Introduction to soft matter: polymers, colloids, amphiphiles and liquid crystals, Wiley, 2007 Search PubMed.
- T. Inoue and T. Misono, J. Colloid Interface Sci., 2008, 326, 483 CrossRef CAS.
- E. B. Tada, L. P. Novaki and O. A. El Seoud, J. Phys. Org. Chem., 2000, 13, 679 CrossRef CAS.
- K. A. Fletcher, S. N. Baker, G. A. Baker and S. Pandey, New J. Chem., 2003, 27, 1706 RSC.
- C. C. Weber, A. F. Masters and T. Maschmeyer, J. Phys. Chem. B, 2012, 116, 1858 CrossRef CAS.
- J. Kagimoto, K. Noguchi, K. Murata, K. Fukumoto, N. Nakamura and H. Ohno, Chem. Lett., 2008, 37, 1026 CrossRef CAS.
- C. Chiappe and D. Pieraccini, J. Phys. Chem. A, 2006, 110, 4937 CrossRef CAS.
- K. A. Fletcher, S. N. Baker, G. A. Baker and S. Pandey, New J. Chem., 2003, 27, 1706 RSC.
- J. Estager, A. A. Oliferenko, K. R. Seddon and M. Swadzba-Kwasny, Dalton Trans., 2010, 39, 11375 RSC.
- (a) X. Han and D. W. Armstrong, Acc. Chem. Res., 2007, 40, 1079 CrossRef CAS; (b) C. F. Poole and S. K. Poole, J. Sep. Sci., 2011, 34, 888 CrossRef CAS.
- Q. Q. Baltazar, S. K. Leininger and J. L. Anderson, J. Chromatogr., A, 2008, 1182, 119 CrossRef CAS.
- A. Finotello, J. E. Bara, S. Narayan, D. Camper and R. D. Noble, J. Phys. Chem. B, 2008, 112, 2335 CrossRef CAS.
- (a) H. Olivier-Bourbigou, P. Travers and J. A. Chodorge, Petrol. Tech. Quat. Autumn, 1999, 141 Search PubMed; (b) B. Gilbert, H. Olivier-Bourbigou and F. Favre, Oil Gas Sci. Technol., 2007, 62, 745 CrossRef CAS.
- Y. Chauvin, B. Gilbert and I. Guibard, J. Chem. Soc., Chem. Commun., 1990, 1715 RSC.
- (a) Y. Chauvin, H. Olivier, C. N. Wyrvalski, L. C. Simon and R. F. de Souza, J. Catal., 1997, 165, 275 CrossRef CAS; (b) L. C. Simon, J. Dupont and R. F. de Souza, Appl. Catal., A, 1998, 175, 215 CrossRef CAS.
- Y. Chauvin, S. Einloft and H. Olivier, Ind. Eng. Chem. Res., 1995, 34, 1149 CrossRef CAS.
- K. Tominaga, Catal. Today, 2006, 115, 70 CrossRef CAS.
- Z. J. Lin, D. S. Wragg, J. E. Warren and R. E. Morris, J. Am. Chem. Soc., 2007, 129, 10334 CrossRef CAS.
- J. Long, B. Guo, X. Li, Y. Jiang, F. Wang, S. C. Tsang, L. Wang and K. M. K. Yu, Green Chem., 2011, 13, 2334 RSC.
- S. H. Lee, S. H. Ha, N. M. Hiep, W. J. Chang and Y. M. Koo, J. Biotechnol., 2008, 133, 486 CrossRef CAS.
- S. H. Ha, N. M. Hiep and Y.-M. Koo, Biotechnol. Bioprocess Eng., 2010, 15, 126 CrossRef CAS.
- Y. Y. Jiang, H. S. Xia, C. Guo, I. Mahmood and H. Z. Liu, Biotechnol. Prog., 2007, 23, 829 CAS.
- S. Katsuta, Y. Yoshimoto, M. Okai, Y. Takeda and K. Bessho, Ind. Eng. Chem. Res., 2011, 50, 12735 CrossRef CAS.
- (a) R. S. Zhao, X. Wang, L. L. Zhang, S. S. Wang and J. P. Yuan, Anal. Methods, 2011, 3, 831 RSC; (b) R. S. Zhao, X. Wang, F. W. Li, S. S. Wang, L. L. Zhang and C. G. Cheng, J. Sep. Sci., 2011, 34, 830 CrossRef CAS.
- N. MacDowell, N. Florin, A. Buchard, J. Hallett, A. Galindo, G. Jackson, C. S. Adjiman, C. K. Williams, N. Shah and P. Fennell, Energy Environ. Sci., 2010, 3, 1645 CAS.
- (a) E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, J. Am. Chem. Soc., 2002, 124, 926 CrossRef CAS; (b) B. Gurkan, B. F. Goodrich, E. M. Mindrup, L. E. Ficke, M. Massel, S. Seo, T. P. Senftle, H. Wu, M. F. Glaser, J. K. Shah, E. J. Maginn, J. F. Brennecke and W. F. Schneider, J. Phys. Chem. Lett., 2010, 1, 3494 CrossRef CAS.
- X. Zhang, X. Zhang, H. Dong, Z. Zhao, S. Zhang and Y. Huang, Energy Environ. Sci., 2012, 5, 6668 CAS.
- (a) G. Gurau, H. Rodríguez, S. P. Kelley, P. Janiczek, R. S. Kalb and R. D. Rogers, Angew. Chem., Int. Ed., 2011, 50, 12124 CrossRef; (b) M. Besnard, M. I. Cabaço, F. V. Chaávez, N. Pinaud, P. J. Sebastião, J. A. P. Coutinho and Y. Danten, Chem. Commun., 2012, 48, 1245 RSC.
- M. B. Shiflett and A. Yokozeki, J. Chem. Eng. Data, 2009, 54, 108 CrossRef CAS.
- L. Crowhurst, R. Falcone, N. L. Lancaster, V. Llopis-Mestre and T. Welton, J. Org. Chem., 2006, 71, 8847 CrossRef CAS.
- J. P. Hallett, C. L. Liotta, G. Ranieri and T. Welton, J. Org. Chem., 2008, 74, 1864–1868 CrossRef.
- M. Gorlov and L. Kloo, Dalton Trans., 2008, 2655 RSC.
- (a) P. Wang, S. M. Zakeeruddin, R. Humphry-Baker and M. Grätzel, Chem. Mater., 2004, 16, 2694 CrossRef CAS; (b) P. Wang, B. Wenger, R. Humphry-Baker, J. E. Moser, J. Teuscher, W. Kantlehner, J. Mezger, E. V. Stoyanov, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 6850 CrossRef CAS; (c) C. C. Xi, Y. M. Cao, Y. M. Cheng, M. K. Wang, X. Y. Jing, S. M. Zakeeruddin, M. Grätzel and P. Wang, J. Phys. Chem. C, 2008, 112, 11063 CrossRef CAS; (d) K. Fredin, M. Gorlov, H. Pettersson, A. Hagfeldt, L. Kloo and G. Boschloo, J. Phys. Chem. C, 2007, 111, 13261 CrossRef CAS.
- Y. Bai, Y. M. Cao, J. Zhang, M. Wang, R. Z. Li, P. Wang, S. M. Zakeeruddin and M. Grätzel, Nat. Mater., 2008, 7, 626 CrossRef CAS.
- Y. M. Cao, J. Zhang, Y. Bai, R. Z. Li, S. M. Zakeeruddin, M. Grätzel and P. Wang, J. Phys. Chem. C, 2008, 112, 13775 CAS.
- (a) H. Nakagawa, S. Izuchi, K. Kuwana, T. Nukuda and Y. Aihara, J. Electrochem. Soc., 2003, 150, A695 CrossRef CAS; (b) G. H. Lane, A. S. Best, D. R. MacFarlane, A. F. Hollenkamp and M. Forsyth, J. Electrochem. Soc., 2010, 157, A876 CrossRef CAS; (c) A. S. Best, A. I. Bhatt and A. F. Hollenkamp, J. Electrochem. Soc., 2010, 157, A903 CrossRef CAS.
- M. Ishikawa, T. Sugimoto, M. Kikuta, E. Ishiko and M. Kono, J. Power Sources, 2008, 183, 436 CrossRef.
- T. Sugimoto, Y. Atsumi, M. Kikuta, E. Ishiko, M. Kono and M. Ishikawa, J. Power Sources, 2009, 189, 802 CrossRef CAS.
- G. H. Lane, A. S. Best, D. R. MacFarlane, A. F. Hollenkamp and M. Forsyth, J. Electrochem. Soc., 2010, 157, A876 CrossRef CAS.
- P. Wang, Y. NuLi, J. Yang and Z. Feng, Surf. Coat. Technol., 2006, 201, 3783 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
