 Open Access Article
Open Access ArticleA practical guide to modelling enzyme-catalysed reactions
Richard
Lonsdale
,
Jeremy N.
Harvey
and
Adrian J.
Mulholland
*
Centre for Computational Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: adrian.mulholland@bris.ac.uk; Fax: +44 117 925 0612; Tel: +44 117 928 9097
First published on 26th January 2012
Abstract
Molecular modelling and simulation methods are increasingly at the forefront of elucidating mechanisms of enzyme-catalysed reactions, and shedding light on the determinants of specificity and efficiency of catalysis. These methods have the potential to assist in drug discovery and the design of novel protein catalysts. This Tutorial Review highlights some of the most widely used modelling methods and some successful applications. Modelling protocols commonly applied in studying enzyme-catalysed reactions are outlined here, and some practical implications are considered, with cytochrome P450 enzymes used as a specific example.
 Richard Lonsdale | Richard Lonsdale received his MChem in Chemistry from the University of Oxford in 2005. He completed his PhD in Chemistry at the University of Bristol in 2009, under the supervision of Adrian Mulholland. He is currently a post-doctoral research assistant at Bristol, uncovering the determinants of selectivity in drug metabolising enzymes, including the cytochromes P450. |
 Jeremy N. Harvey | Jeremy Harvey studied chemistry at the Université Catholique de Louvain in Belgium, where he completed a PhD on organic reaction mechanisms in 1995. After postdoctoral periods in Berlin and Jerusalem, he joined the academic staff in Bristol in 1999, where his research group focuses on using computational methods to understand chemical reactions. |
 Adrian J. Mulholland | Adrian Mulholland received his BSc in Chemistry from the University of Bristol in 1990. After a short period at ICI Pharmaceuticals, he obtained his DPhil from Oxford University in 1995. He was a Wellcome Trust Fellow at Harvard, then Bristol, and an EPSRC Advanced Research Fellow at Bristol (1998–2003). He is currently a Professor of Chemistry, with interests including biomolecular simulation and enzyme catalysis. |
1. Introduction
Enzymes are outstanding natural catalysts. Understanding the mechanisms of enzyme-catalysed reactions is fundamental to the study of biochemical processes. Potentially, better understanding can contribute to developing new medicines and new catalysts. Enzymes are complex and challenging, and it has proven difficult in many cases to establish the mechanisms of their catalysed reactions, and the origins of catalysis, from experiments alone. Molecular simulations and modelling are increasingly important here, complementing experimental techniques.Computational chemistry methods can provide information about enzyme-catalysed reactions that experiments cannot, such as the structures of transition states and reaction intermediates, once the mechanism has been established. Knowledge of such structures can help in the design of inhibitors, for example, as potential drug candidates. Modelling can identify catalytically important interactions. It can also provide insight into the factors that govern the high degree of stereo- and regioselectivity observed in many enzymes, which could be potentially exploited in chemical synthesis and catalyst design.1,2
This Tutorial Review describes some current computational methods for modelling enzyme-catalysed reactions. We discuss important practical considerations, such as the choice of method, and the preparation of a protein model for simulation. Careful preparation and testing is vital for successful modelling. As a practical example, we highlight the cytochrome P450 family of enzymes, which is involved in drug metabolism. Finally, we outline some examples of applications that show how biomolecular modelling and simulation can be applied, tested against experiment, and analysed to give unique insight into the fundamental mechanisms of biological catalysts.
2. Methods
Different types of computational molecular modelling and simulation methods are needed to investigate different aspects of enzymes. Perhaps the most obvious initial question is ‘what is the (chemical) mechanism of the reaction?’. As mentioned above, for many enzymes, experiments alone have not identified reaction mechanisms unambiguously, and many proposed and published mechanisms, even in biochemistry textbooks, are probably incorrect in important details (see e.g.Fig. 1). Establishing a mechanism means identifying which groups in the protein (and any cofactors) are involved in the reaction, and what their precise roles are. The structures and interactions of transition states and reaction intermediates should be determined. The energy barrier for a reaction step can be calculated as the difference in energy between the reactants and the transition state (see Fig. 2). For a good, realistic molecular model, if the barrier for a proposed mechanism is significantly larger than that derived from experiment (within the limits of accuracy of the computational method and experimental error), then that mechanism is unlikely. Calculations can now be performed for enzyme reactions with highly accurate methods, which allow predictions of barriers with close to chemical accuracy (1 kcal mol−1 ≈ 4 kJ mol−1) in the best cases.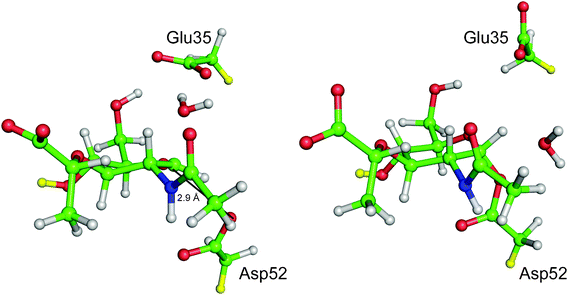 | ||
| Fig. 1 Lysozyme is an example of a classic ‘textbook’ enzyme, and was the first to have its mechanism proposed based on structural data. However, the previously commonly taught mechanism (where the reaction proceeds via a oxocarbenium ion) is probably wrong. Crystallography and electrospray ionization mass spectrometry of mutant hen egg white lysozyme, or a fluorinated substrate, support formation of a covalent intermediate. QM/MM calculations also support formation of the covalent intermediate in the wild type enzyme with the natural substrate.3 Representative snapshots from QM/MM (PM3/CHARMM22) umbrella sampling molecular dynamics simulations of the transition state (left hand side) and the covalent intermediate (right hand side) are shown. Only atoms in the QM region are shown, for clarity (i.e. the D site NAM sugar and the side-chains of Glu35 and Asp52). The distance between Asp52 Oδ2 and the D site NAM C1 decreases from ∼2.9 Å in transition state (indicated in the figure) to ∼1.4 Å in the covalent intermediate. ‘Link’ atoms are shown in yellow: these are QM hydrogen atoms added to the system at the QM/MM boundary to satisfy the bonding requirement of QM atoms where the boundary separates covalently bonded atoms. Reproduced from ref. 3 | ||
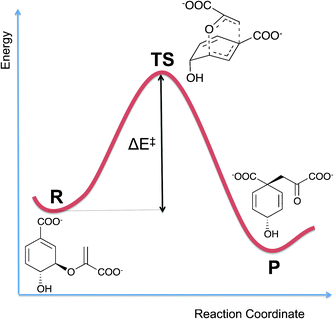 | ||
| Fig. 2 Energy profile for a reaction proceeding from reactants (R) to products (P) via a transition state (TS). The energy barrier for the reaction (ΔE‡) is the difference in energy between the reactants and transition state. The example reaction given here is the Claisen rearrangement of chorismate to form prephenate, which is catalysed by the enzyme chorismate mutase (see Section 5.2). | ||
Calculations can be performed with other aims, such as predicting the relative rates of reaction of different substrates, or mutant enzymes. Calculations of relative rates do not require such accurate methods as those needed for predictions of rates, and yet may be of more general practical use. Other experimental observables such as kinetic isotope effects can also be calculated and provide another useful link and validation. Calculations can examine hypotheses, even those not achievable in reality, to analyse important features of a reaction, such as identification of specific residues involved in transition state stabilization. It is also important to stress that to examine causes of catalysis, it is most informative to compare the enzyme-catalysed reaction with an equivalent reaction, e.g. an uncatalysed reaction in solution (see e.g.Fig. 11), or in a less active enzyme. It is arguably not meaningful to discuss catalysis (as opposed to mechanism) without making such a comparison. A complete understanding of enzyme activity also requires more than consideration of the chemical steps: specificity may be determined entirely by binding affinity, and techniques for predicting binding affinity may need to be used. Altogether, a wide variety of questions can be of interest for an enzyme, and different computational techniques are required for different types of question.
In the section below, we briefly outline some of the most widely-used methods for modelling the structure and dynamics of enzymes, and the reactions they catalyse. This is by no means a comprehensive account and the reader is directed elsewhere for a more detailed description.1,4,5 For example, the empirical valence bond (EVB) method has been used extensively for modelling enzyme-catalysed reactions,6 but is outside the scope of this Tutorial Review. In the EVB approach, reactions are modelled by empirical potential functions. Many of the same basic principles and aspects of protein modelling and simulations apply to EVB calculations, but here we focus on methods that use quantum mechanics to calculate the electronic structure of molecules for modelling enzyme-catalysed reaction mechanisms, and discuss empirical force field (MM) methods only for modelling structure and dynamics.
2.1 Molecular mechanics (MM) methods
Molecular mechanics (MM) methods are important in simulations of enzymes, even though typical MM methods cannot model chemical reactions. They are used for molecular dynamics simulations, or combined with quantum mechanical methods in QM/MM calculations on reactions (see below). MM methods allow long timescale (e.g. nano- to microsecond) simulations of the dynamics of proteins. This is possible because of the simple functional forms typically used in MM energy functions (force fields), e.g. harmonic terms represent the energy of bond stretching and valence angle bending, and simple periodic terms describe torsional angles. Van der Waals interactions are included by a simple Lennard-Jones function. Electrostatic interactions in MM force fields are usually described simply by using fixed atom-centred point charges. These atomic charges do not change in response to changes in the molecular environment or conformation, so changes in electronic polarization are not included.Some MM force fields for biological macromolecules represent all atoms in a protein explicitly, while others (united-atom force fields), treat only heavy (non-hydrogen) atoms and polar hydrogen atoms explicitly, while nonpolar hydrogen atoms are not represented explicitly, but instead are represented as part of the carbon atom to which they are bonded.
Standard MM potential functions cannot model the bond breaking and bond making, and electronic reorganization, involved in a chemical reaction: for example, the harmonic term for bonds does not allow them to break. Also, MM force field parameters are developed based on the properties of stable molecules, and so will usually not be applicable to unstable intermediates and transition states. It is possible to develop MM functions and parameters specifically for reactions, however, the parameters would generally apply only to a particular reaction, or small class of reactions, meaning that reparameterization is necessary for each problem studied. As mentioned above, protein MM force fields only include electronic polarization in an average, and invariant way. Polarizable force fields for biological molecules are the subject of a lot of current research; in future, MM force fields will probably include electronic polarization explicitly.
2.2 Quantum mechanical (QM) methods
Modelling a chemical reaction requires a method capable of describing the breaking and making of chemical bonds. Quantum mechanical (QM) (also called electronic structure or quantum chemical) methods model the distributions of electrons in molecules explicitly. They are widely used to study the geometries, electronic structure and reactions of small molecules. A number of different QM methods exist, and many (so called ‘wavefunction-based’ methods) involve finding the solution to the Schrödinger equation. The Schrödinger equation cannot be solved exactly for molecular systems containing more than one electron and hence approximations are required for many-body systems. Different QM methods differ depending on the approximations made, and can be divided roughly into three types: ab initio, density functional theory (DFT) and semi-empirical approaches.The simplest useful ab initio QM methods apply Hartree–Fock (HF) theory, in which it is approximated that each electron's spatial distribution is not dependent on the instantaneous motion of the other electrons. This approximation turns out to be the main flaw of HF theory: it ignores electron correlation, the tendency of electrons to avoid each other. The neglect of this effect in the calculation of the total energy has significant implications for chemistry: HF calculations on reactions often give large errors. Many ‘correlated’ ab initio methods, including those based on Møller–Plesset perturbation theory (e.g. MP2), configuration interaction (CI), or coupled cluster theory (CC), use HF wavefunctions as a starting point. These methods offer a significant improvement in accuracy over HF calculations, but also have much higher computational cost, which currently makes their application for systems with many tens of atoms difficult.
Density functional theory methods can offer accuracy approaching that of the correlated ab initio methods, but at substantially lower computational expense. The basis of DFT is that the ground-state energy of a molecule can be calculated just from a knowledge of the electron density distribution. The density is a function of only three variables and is thereby much simpler than the ab initio wavefunction, a function of 3N variables, where N is the number of electrons. However, the exact form of the functional relating the density to the energy is not known. Numerous approximate functionals have been developed based on a mixture of trial and error and known limiting features of the exact functional, but there is (as yet) no systematic way to improve them. One popular density functional is B3LYP, termed a ‘hybrid’ functional, in which a degree of HF exact exchange is mixed with contributions from other functionals including the Becke88 exchange functional and the Lee–Yang–Parr correlation functional.
Semi-empirical methods are the least computationally intensive of the QM methods mentioned here, but they are also typically the least accurate, unless specifically parameterized for a particular property. In fact, in some cases a MM treatment may be better than low levels of QM, such as semi-empirical methods. Semi-empirical methods can be applied to larger systems than DFT or correlated-HF methods (typically hundreds of atoms). They can also be used in molecular dynamics simulations.3 Examples of semi-empirical QM (molecular orbital) methods include those based on the Modified Neglect of Diatomic Differential Overlap (MNDO) approximation, such as AM1 and PM3. The self-consistent charge density functional tight-binding (SCC-DFTB) semi-empirical method is based on DFT and has been shown in many cases to provide geometries and relative energies comparable to DFT and ab initio calculations.7
An enzyme system typically consists of thousands of atoms, hence modelling an entire enzyme using QM methods is computationally demanding and whilst it is possible to perform a semi-empirical (e.g. AM1) QM calculation on a whole small protein, this is not yet possible for methods such as CC. One approach that is often used to model enzyme reactions with quantum chemical methods is to use a small ‘cluster’ model containing important functional groups (e.g. amino acid residues and substrate). The coordinates of these groups can be taken from X-ray crystal structures. It can be necessary to use restraints to keep the groups surrounding the reaction centre in place. This approach can be useful in modelling transition states and intermediates, and can identify probable mechanisms.8 It is likely that the surrounding enzyme environment and solvent have an effect on the reaction, however, and ideally should be included in the model. One simple and quick approach is to include an electrostatic continuum to represent the average overall effect of the protein and solvent environment. It is a good idea to test the sensitivity of the results to the size of the model used (number of atoms in the calculation), as well as to the treatment of the environment (e.g. the choice of dielectric constant), the choice of starting structure, and the level of theory used. Nowadays, calculations can be performed with good levels of QM theory on quite large active site models (over 100 atoms) with e.g. optimization of transition state structures. More atoms can be included in the calculation by hybrid quantum mechanics/molecular mechanics approaches (QM/MM), which can also more naturally allow e.g. molecular dynamics simulations. The main focus of this review is on QM/MM calculations, but many of the practical considerations described apply to modelling of an enzyme-catalysed reaction mechanism with other methods.
2.3 Quantum mechanics/molecular mechanics (QM/MM) methods
QM/MM methods simultaneously exploit the benefits of both the QM and MM methods described above. The region of most interest in the system (i.e. where the bond breaking/forming is taking place in the enzyme, along with selected surrounding catalytically relevant residues) is treated with a QM method. The rest of the enzyme is treated with a MM force field (Fig. 3). In many (but not all) QM/MM methodologies the two regions interact with each other, as described below.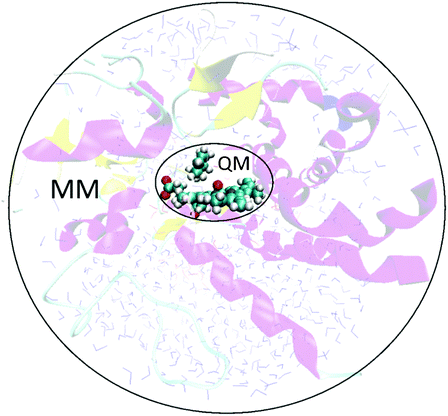 | ||
| Fig. 3 In a QM/MM calculation on an enzyme-catalysed reaction, the system is split into two regions: a small region encapsulating the reaction at the active site (shown here in ball and stick representation) is modelled with a QM method, while the rest of the enzyme (and surrounding solvent etc.) is modelled using MM. The enzyme illustrated is a (truncated) model of CYP101 (cytochrome P450cam) with cyclohexene bound.9 | ||
The underlying theory of the QM/MM approach has been covered by many different authors,4,10,11 so only a brief overview is given here. There are two main approaches to QM/MM calculations: the additive and subtractive approaches. In the subtractive approach (e.g. the ONIOM method in Gaussian12) the total energy, Etotalsub, is calculated using the following expression:
| Etotalsub = EMMtotal + EQMQMregion − EMMQMregion | (1) |
| Etotaladd = EQM(MM)QMregion + EMMMMregion + EQM/MM + Eboundary | (2) |
The energy of the QM atoms in the presence of the MM atoms, EQM(MM)QMregion, is calculated in a standard molecular orbital or DFT calculation. In an ab initio QM/MM calculation, the MM atomic charges are generally included directly through one-electron integrals. The MM atomic partial charges also interact with the nuclei of the atoms in the QM system. For semi-empirical QM/MM calculations, the interaction between the QM and MM partial charges is modelled slightly differently, because in semi-empirical QM methods such as AM1 and PM3, the inner electrons of atoms are combined with the nuclei to form ‘cores’, and only the valence electrons are treated explicitly: therefore usually the MM point charges are treated as cores. The energy of the atoms in the MM region, EMM, is given by a standard MM force field. The boundary energy, EBoundary, arises because the simulation system can only include a finite number of atoms, so terms to reproduce the effects of the surroundings must be included.
The QM/MM interaction energy, EQM/MM, represents the non-electrostatic interactions between the QM and MM regions. It typically consists of terms due to van der Waals interactions, and any bonded interaction terms. MM bonding terms (energies of bond stretching, angle bending, torsion angle rotation, etc.) are typically included for all QM/MM interactions which involve at least one MM atom.
QM/MM van der Waals interactions (representing dispersion attraction and exchange repulsion interactions between QM and MM atoms) are usually calculated by a molecular mechanics procedure (e.g. through Lennard-Jones terms), exactly as the corresponding interactions would be calculated between MM atoms not interacting through bonding terms. MM van der Waals parameters must therefore be assigned to each QM atom. The van der Waals terms are important in differentiating MM atom types in their interactions with the QM system. This is particularly important in differentiating between atoms of the same charge but different van der Waals radii (e.g. halide ions), which would otherwise be indistinguishable to the QM system; similarly, van der Waals interactions play a crucial role in determining the interaction of the QM system with MM atoms whose charges are close to zero. The van der Waals parameters are usually kept the same during the reaction. This is an approximation: changes in bonding mean that parameters appropriate for one state (e.g. reactants) may not be ideal for another (e.g. products). In general, van der Waals interactions are most significant at close range, playing an important part in determining QM/MM interaction energies and geometries. The van der Waals parameters chosen for QM atoms are, for convenience, typically the same as those for equivalent MM atoms in the force field. However, specifically optimized parameters can give more accurate results and may be necessary in some cases.13
3. Modelling an enzyme-catalysed reaction
Enzymes are large and complicated systems and present numerous challenges to the modeller. This section highlights some general factors to consider when modelling enzyme-catalysed reactions. The majority of these considerations only apply to large, entire (or truncated) enzyme models for MM or QM/MM simulations, but some also apply to small cluster models.3.1 Choice of starting structure
A detailed, accurate structure which closely resembles a point on the pathway of the chemical reaction is a basic requirement for modelling an enzyme-catalysed reaction. In practice, this usually means that a high-resolution X-ray crystallographic structure of an enzyme complex is needed. The structure used must accurately represent the reacting enzyme complex. A crystal structure of an enzyme alone, with no ligands bound at the active site, may be of little use, because it is difficult to predict binding modes and protein conformational changes associated with binding. Often, the crystallographic structure of an enzyme-inhibitor complex is a good choice. The inhibitor should closely resemble the substrate, product, transition state or an intermediate, in its bound conformation. It is generally not possible to determine experimentally the structures of active enzyme-substrate complexes, because these react too fast and cannot be isolated. It is sometimes possible to solve crystal structures of enzyme-substrate complexes for less efficient mutants or substrates, or by varying redox conditions, if the reaction is slow enough to enable the complex to be observed (Fig. 4).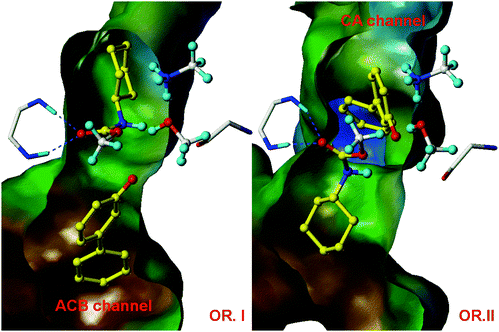 | ||
| Fig. 4 Fatty acid amide hydrolase (FAAH) is a promising pharmaceutical target for the treatment of pain, anxiety and depression. QM/MM calculations on the formation of the covalent adduct between FAAH and the O-arylcarbamate inhibitor URB524 showed that reaction was only possible in one of the two possible binding modes shown here (OR. II), thus identifying the productive binding mode. This prediction was subsequently validated by X-ray crystallography.14 Figure reproduced from ref. 15 | ||
The resolution of a protein structure determined by X-ray crystallography provides an indication of the level of accuracy. A high-resolution structure (less than 2 Å) is likely to give the positions of most heavy atoms very well, while at a very low resolution, it is probable that only the overall shape of the protein can be inferred. Modellers need to bear in mind that the quoted resolution (and the crystallographic R-factor) is only a measure of global model quality (dependent for example on the degree of ordering of the crystal and on the experimental conditions). Even in high-resolution structures, there can be considerable uncertainty in atomic positions for part of the system due to protein dynamics and conformational variability. Crystal structures represent an average over all the protein molecules in the crystal and over the whole time of data acquisition. One manifestation of this averaging is that the alternative conformations are observed for amino acid sidechains in many protein crystal structures: two or more well-ordered conformations are often observed for some groups. Similarly, some parts of the structure may not be resolved, such as surface loops or terminal regions of the protein: these regions may be very mobile and have no well-defined single conformation or position.
3.2 Setting-up an enzyme structural model for QM/MM calculations
Once an enzyme structure has been selected, it must be prepared for modelling. Hydrogen atoms are not usually resolved in X-ray crystallography of proteins, because of their low electron density. As a result, hydrogen atoms have to be added to a crystal structure prior to simulation. This can be done automatically by many software packages, for example in the HBUILD module of the CHARMM16 simulation program. For titratable amino acid residues such as aspartic acid, glutamic acid and histidine (see for example, Fig. 5), the protonation states of the residues need to be specified, and might not be obvious by inspection. Unexpected protonation states of amino acid side chains and other groups can be favoured within proteins, and predicting pKas in proteins remains a challenging problem. One method to aid in the selection of protonation states is to estimate the pKas of titratable residues based on their local environment (for example, using the PROPKA program17,18). In some cases, amino acid side chains such as asparagine, glutamine and histidine, which can exist as different rotamers, may have been built incorrectly: these should be evaluated individually, along with their local hydrogen bonding environment, to assess whether the right conformation has been assigned (e.g. by consideration of hydrogen bonding patterns; again this can be tested automatically by some programs). Another consideration is that crystal structures often contain alternative conformations of some side chains: it may be necessary to investigate the various possibilities. Caution is required about the structure of any ligands contained in a crystal structure, because these are more susceptible to error than protein structures. Crystal structures usually contain oxygen atoms corresponding to ordered water molecules that are often involved in hydrogen bonding with the enzyme. To create a full model, it is necessary to solvate the protein further, typically by placing the protein in a pre-equilibrated water box, and deleting any water molecules close to other atoms, in order to reproduce the effects of bulk solvation.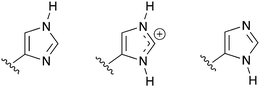 | ||
| Fig. 5 The three possible protonation states of a histidine side chain in the modelling of a protein. Care must be taken to choose the most-likely state for each histidine side chain in a protein model. This can be achieved by inspection of the local hydrogen-bonding environment. | ||
For MD and QM/MM calculations, once a molecular model has been created, a series of MM and/or QM/MM energy minimizations is usually carried out in order to optimize the geometries of both the added hydrogen atoms and the protein heavy atoms, as well as the added water molecules. In QM calculations on small cluster models, the crystal structure positions are usually used directly and no MM minimization is performed prior to QM optimization. There are several MM minimization algorithms, which vary in their ability to reach convergence and in their computational expense. The simplest of these, the steepest descent (SD) (or gradient descent) method, calculates the first derivative of the potential energy with respect to the atomic coordinates, producing a gradient vector. The minimum energy along this direction is estimated, giving an improved structure. The gradient is then recalculated to generate a new search direction. This is a quick and robust method of relaxing a starting geometry, but it tends to oscillate around the minimum energy path to the point of minimum energy, slowing down as it approaches this minimum. The conjugate gradient (CG) method avoids this oscillatory behaviour, by conducting each line search along a line which is conjugate to the previous gradient. The first step is equivalent to a SD step, however, all subsequent steps follow a direction determined by both the current gradient and the direction of the previous steps. CG methods hence have better convergence characteristics than SD but can lead to problems when poor starting geometries are chosen. The adopted basis Newton-Raphson (ABNR) method includes the second derivative of the potential energy surface and can hence find minima and saddle points. ABNR method can often converge very quickly, especially if started close to the energy minimum, but is impractical for large systems due to the expense of calculating the inverse of the Hessian. Quite often, a combination of methods is used, e.g. a protocol used by our group involves initial minimization of the hydrogen atoms, followed by all atoms using an appropriate number of SD, CG and then ABNR steps. The appropriate number of steps is that which is required to reach a certain energy threshold.
3.3 Molecular dynamics (MD) simulations
Molecular dynamics simulations are important in studies of enzymes, to investigate enzyme internal motions and conformational changes, to generate structures for mechanistic modelling, and for (QM/MM) calculations of free energy profiles for reactions. MD simulations can be performed with MM methods, or with low levels of QM/MM theory (e.g. semi-empirical QM). It is increasingly common to use MD structural ‘snapshots’ as a starting point for QM/MM calculations, rather than the crystal structure directly.In MD simulations, Newton's equations of motion are used to describe the motion of atoms on the potential energy surface. Ideally, the whole protein is simulated, e.g. under periodic boundary conditions. For QM/MM simulations particularly, the whole enzyme system is often truncated to reduce computational requirements: i.e. only a part of the whole protein (for example, a rough sphere around the active site) might be included in the simulation. When simulating a truncated protein system, it is necessary to include restraints or constraints in the boundary region to force the atoms belonging to it to remain close to their positions in the crystal structure. One common approach to simulations of truncated systems is the stochastic boundary MD method, in which the simulation system is divided into a reaction region and a buffer region.9,19 Typically, the whole simulation system might include all residues with one or more atoms within a distance of 15–25 Å of an atom in the active site. The buffer region often contains atoms in the outer layer of 5 Å or so. Atoms in the reaction region are treated by standard Newtonian MD, and are not subject to positional restraints. The protein heavy atoms in the buffer region are restrained to remain close to their (crystallographically determined) positions by harmonic forces tending to hold them in position, while a solvent deformable boundary potential prevents evaporation of water. Atoms in the buffer follow a Langevin equation of motion: they are subject to frictional and random forces to include approximately the exchange of energy with the surroundings. The charges of ionized residues in the buffer region are sometimes neutralized or scaled, in order to avoid unphysical interactions with the surrounding vacuum. Improvements to QM/MM simulations of truncated protein systems include the generalised solvent boundary potential (GSBP),20 in which the solvent surrounding the system is represented by a continuum dielectric.
3.4 QM/MM partitioning methods and schemes
In most QM/MM studies of enzymes, it is necessary to partition covalently bonded molecules into QM and MM regions, because usually part of the protein is directly involved in the reaction. Some amino acid side chains may participate directly in the reaction, undergoing chemical change as part of the mechanism, and must therefore be included in the QM region. Other side chains will play binding roles, and an MM representation could be inadequate in some cases, for example for particularly strong binding interactions. It may likewise be desirable to treat only the reactive parts of large cofactors or substrates by quantum chemical methods and to treat the rest by MM. There are two general QM/MM partitioning techniques that can be employed: firstly a frozen bond orbital to satisfy the valence shell of the QM atom at the QM/MM junction, for example the local self-consistent field (LSCF) method or the generalized hybrid orbital (GHO) method. Alternatively a QM atom (or QM pseudoatom) can be added to allow a proper bond at the QM/MM frontier, for example the link atom method or the connection atom method.4,11 (see Fig. 6) Link atoms are typically modelled as hydrogen atoms, and some of the interactions between these link atoms and the MM region are usually neglected. Generally, the positions of the link atoms are chosen such that they do not cut across any polar bonds, avoiding any unrealistic effects. Different methods require different positions for the boundary.21 In order to avoid the introduction of unbalanced charge interactions at the boundary between the QM and MM regions, the charges of MM groups adjacent to QM groups are commonly set to zero, although more complex electrostatic adjustments can also be made.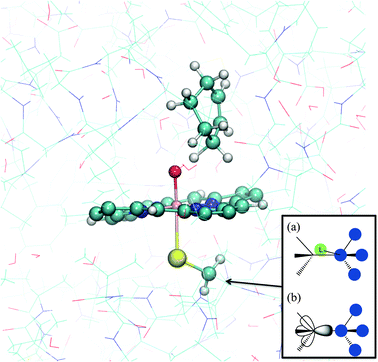 | ||
| Fig. 6 Typical QM/MM partitioning for modelling reactions of cytochrome P450 enzymes. The example shown here is cyclohexene in the active site of P450cam. The MM and QM atoms are shown in lines and ball and stick representation, respectively. Inset: (a) the link atom (L) and (b) frozen orbital methods for satisfying the valences of QM atoms at the QM/MM boundary. | ||
3.5 Treatment of the solvent
When simulating proteins it is important to consider the solvent environment. in vivo, proteins are solvated in water or e.g. partly in water and partly in a membrane (or associated with DNA). Different levels of approximation can be used to model the effects of solvation. Implicit solvent models do not include individual water molecules, and include the effect of the solvent e.g. by screening the charges of the protein atoms with a dielectric constant. The disadvantage of such methods is that specific solvent–solute interactions (e.g. hydrogen bonding to water molecules) cannot be modelled. In contrast, in explicit water models water molecules are represented explicitly: these therefore require longer equilibration times and the simulations take more time than simulations with an implicit water model. Most biomolecular MM forcefields have been developed to be compatible with simple point charge models of water, such as the TIP3P water model.22 There are some indications that for QM/MM simulations, particularly with higher levels of QM theory, the TIP4P model is preferable.23 Electronic polarization is included only in an approximate way in MM models such as TIP3P: for example, the dipole moment of such models is higher than that observed in the gas phase, thus including approximately the effects of polarization in the condensed phase.3.6 Calculating energy profiles and barriers for reactions
Structural and energetic information concerning the reactants, intermediates and transition states along the reaction path are the key objectives in modeling a chemical reaction, whether in a protein or in solution. Such information can be derived either from essentially static methods, in which single optimized structures are obtained for each key species, or using dynamical methods, in which ensembles of structures are generated. Focusing on static methods first, optimization of minimum energy structures has been described above and is usually relatively straightforward, even for the large systems typically involved in QM/MM studies. It should however be noted that typical optimization only leads to local minima, with the identification of global minima being much more difficult and very seldom attempted. In fact, because proteins have many minima of similar energy, it is more important to consider many of them.Optimization of saddle-points and reaction paths are more difficult problems. The algorithms commonly used for TS optimization in small systems are not always well suited to studies of large systems, such as enzymes. This is partly because such methods are demanding computationally (e.g. calculating and manipulating a full matrix of second derivatives becomes extremely expensive). Another reason relates to the point above about local minima: even when it is possible to locate a given TS, this is not very useful unless one is confident that the TS correlates along a smooth reaction path with the surrounding minima. Without this confidence, comparing their energies is essentially meaningless.
TS structures (saddlepoints) and associated reaction paths can be optimized in QM/MM calculations on enzymes; approximate TS structures generally have to be found as a prelude to such structural optimizations, and are often valuable in their own right for estimating potential energy barriers. One approach often used in locating approximate TSs and reaction paths on QM/MM potential energy surfaces is the so-called “adiabatic mapping” approach.11 In this method, a reaction coordinate is selected, e.g. the distance between two atoms. The energy of the system is then minimized while restraining this coordinate to a set of gradually incremented values, giving an energy profile. In favourable cases, if the ‘steps’ taken along the path are small, then a smooth reaction path is obtained, continuous both in energy and configuration space and can often give TS structures similar to fully optimized TSs. Discontinuities are observed frequently, however, due to structural relaxation to a conformationally distinct reaction path, possibly involving atoms situated very far from the reaction path. When this occurs, the energies obtained should not be used, and adiabatic mapping should be repeated in forward and reverse directions until a smooth energy profile is obtained. As continuous reaction paths rarely involve major motion of atoms far from the reacting centre, it is not a big approximation to freeze the positions of all atoms more than 10 Å or so from the reaction centre–this usually much improves convergence of the mapping procedure.
The difference in electronic energy (i.e. Etotaladd from (2)) between reactants and the transition state gives the potential energy barrier for the reaction, for that particular arrangement of reacting groups. By including a correction for zero-point energy (for the atoms in the QM region), and calculating vibrational frequencies, it is possible to obtain the activation energy, enthalpy, and free energy as one would do for a gas-phase reaction of small molecules. The free energy is particularly valuable as it can be directly compared to experiment. One may also be able to compute corrections to account for tunneling.24 However, doing this based on a single reaction path will not yield exact results, as the ‘real’ reaction involves barrier-crossing starting from a thermal ensemble of reactant conformations, which may all have different reaction barriers (see Fig. 7). To get a more realistic estimate, multiple reaction profiles can be calculated, using different starting structures taken, e.g., from MM molecular dynamics simulations. If all the barrier heights are similar, then one has a better estimate of (and more confidence in) the activation energy or free energy. Typically, though, they are somewhat different, and one may wish to use either the lowest barrier (if the corresponding reactant complex is not obviously anomalously unstable), or use some or other averaging method. Recent work has highlighted the importance of this type of sampling.9
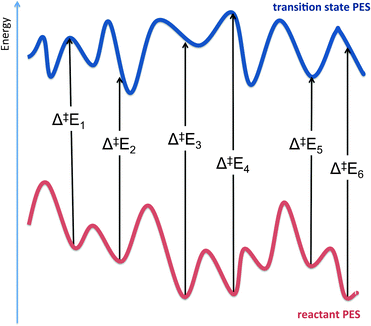 | ||
| Fig. 7 Two-dimensional representation of the potential energy surfaces (PESs) for a reactant and transition state for an enzyme catalysed reaction. Potential energy barriers (Δ‡E) calculated using adiabatic mapping are subject to variation, depending on the choice of starting structure when using different structures from MD simulations. This is due to the existence of many conformations for the reactant and the transition state. To obtain accurate barriers, it is often necessary to either average over many calculated barriers or to use a dynamical sampling method, such as umbrella sampling. | ||
Sampling reaction paths with umbrella sampling (or using related techniques) is quite challenging when computing the potential energy using QM/MM methods, since the underlying simulations require a very large number of computations of the potential energy and its gradient (105 or more). Hence this approach is currently only routinely applicable with low-level QM methods, such as AM1, PM3 and SCC-DFTB. Such low-level QM methods methods tend to yield rather inaccurate energy barriers. Another difficulty with such methods is that the free energy profile obtained may converge rather slowly with the length of each of the simulations performed along the reaction path, as one may not sample a truly equilibrium ensemble in the time available. The accuracy of QM/MM umbrella sampling free energy barriers based on low-level QM methods can be improved by applying a correction derived from adiabatic mapping studies at both the low level used for umbrella sampling and at a higher level.2 Also, accuracy can be improved by using specifically reparameterized semi-empirical methods for a particular system.13
Monte Carlo simulations can be used as an alternative to molecular dynamics simulations for sampling.
4. Modelling cytochrome P450 reactions
4.1 Introduction
Cytochrome P450 enzymes (P450s or CYPs) are very important in drug discovery, because they are involved in the metabolism of most drugs. They are also important in biosynthesis. They dominate Phase I drug metabolism, which involves the introduction of polar functional groups into non-polar molecules and can lead to inactivation or activation of drugs. The majority of P450-catalysed xenobiotic oxidation reactions in mammals occur in the liver. Most perform a detoxification function, but complications arise in some cases from the formation of reactive intermediates, such as epoxides. These intermediates can cause oxidative stress to cells, e.g. by reacting with proteins and DNA. P450s share a common active site haem (Fig. 8), that is bound to the enzyme via a cysteine residue. Information obtained from modelling could be potentially very useful in drug discovery, e.g. to help predict the formation of toxic metabolites in P450-mediated metabolism of lead compounds.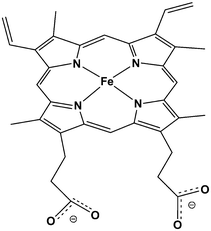 | ||
| Fig. 8 The haem prosthetic group found in cytochrome P450 proteins. The haem iron is bound to a cysteinate residue in the enzyme. | ||
The catalytic cycle of P450s involves the formation of a very reactive Fe(IV) oxo species, called Compound I (Cpd I), that is widely accepted to be the species that accounts for most of the substrate oxidation reactivity of P450s, as well as in other haem-containing monooxygenases.25 Computation has provided insight into the mechanisms by which oxidative metabolism is carried out by these enzymes, as well as the nature of Cpd I.26–32
P450s provide nice examples of how QM calculations with small cluster models (see 2.2) can provide insight into enzymes and their mechanisms. Typically, such small cluster models would be comprised of the haem group, with the substituents replaced by hydrogen atoms, bound to a −SH (or −SCH3) group to model the cysteinate bound to the iron. The B3LYP density functional gives the correct ground state spin configuration of Cpd I (a doublet), in agreement with experiment.29 As a consequence of a different alignment of the spins of the three unpaired electrons that exist in Cpd I, a quartet spin state exists that is slightly higher in energy than this doublet ground state (Fig. 3). The hydroxylation of small alkanes was modelled by Shaik et al., also using the B3LYP density functional.29 Hydroxylation by P450s follows the “rebound” mechanism, which consists of hydrogen abstraction by Cpd I, followed by radical recombination (or rebound). Hydroxylation displays “two-state reactivity”, in which the reaction proceeds on both the closely lying doublet and quartet spin surfaces. For methane, hydrogen abstration was found to have similar barriers on both spin surfaces. Radical recombination was found to be barrierless on the doublet spin surface, however, a small barrier was found for the quartet spin surface. This result explains the experimental finding of rearranged products with radical clock substrates.29
The solution of the crystal structure of P450cam (and subsequently of other isoforms), together with the development of QM(DFT)/MM methods, has enabled the electronic structure of Cpd I, and the mechanisms of oxidation reactions, to be modelled in the enzyme environment. The most extensively studied of these reactions is the hydroxylation of camphor at the 5-exo-position by P450cam, for which the entire catalytic cycle has been modelled with QM/MM methods.29,32 QM/MM modelling has helped to confirm the specific role of several active site amino acid residues in the catalytic cycle, previously suggested by experimental studies. The protein environment is believed to have an effect on the electronic structure of Cpd I, as differences have been observed between QM and QM/MM calculations. The main observed difference is in the distribution of the unpaired electron shared between the porphyrin ring and the cysteine sulfur. This difference arises due to the electrostatic polarization by the surrounding protein and solvent of the active site pocket, as well as through hydrogen bonding to the cysteinate sulfur.29,32,33 The electronic structure of Cpd I does not differ significantly, however, in different P450s.33
Some P450s catalyse the hydroxylation of aromatic rings, a process that can lead to formation of toxic products, such as arene oxides. Examples of modelling of this type of reaction include QM (DFT) studies of the hydroxylation of benzene with a cluster model27,28 and QM/MM modelling of the same process in the CYP2C9 enzyme.31 The calculations on small models led to the finding of a correlation between the calculated energy barriers for hydroxylation of different substituted benzenes, and experimentally derived Hammett constants.27 This type of relationship could be potentially extended to other substituents and could have applications in predicting drug metabolism.
4.2 Practical considerations
Modelling metalloenzymes, such as P450s, often require extra factors to be taken into account, such as obtaining convergence to the correct electronic state. Some of these factors are discussed below.The Fe(IV) oxo species is obviously central to P450 reactivity, so a method that can accurately model transition metals is required. Standard semi-empirical methods are not up to the task. Consequently, umbrella sampling QM/MM MD simulations on P450 reactions have not yet been reported, as the results are unlikely to be reliable. Correlated ab initio methods are also not a generally practical option for modelling these systems at present, due to computational expense. The B3LYP density functional is a popular method for modelling P450-catalysed reactions, and has been shown to perform well for this type of system.9,30–33,35 A significant drawback of B3LYP, and many other density functionals, is the lack of treatment of dispersion interactions, the attractive part of van der Waals interactions. The dispersion interaction is missing in many density functionals because of the approximate manner in which electron correlation is modelled. Whilst this does not have an effect on the calculated electronic structure of Cpd I, it can lead to errors (typically overestimation) in calculations of energy barriers when modelling reactions. Several empirical corrections to add dispersion interactions to B3LYP have been developed, such as those by Grimme.36 Recent calculations with such a method (B3LYP-D) on several hydroxylation and epoxidation reactions of Cpd I show the importance of including dispersion effects:37 better agreement with experiment was observed, compared with similar calculations without the correction. The energy barriers were lowered, because the dispersion correction is greater for the transition state than the Michaelis complex: the substrate is closer to Cpd I in the transition state, and so is stabilized more by dispersion interactions than the reactant complex, due the R−6 dependence of the correction.
It is common practice to treat by QM a truncated model of Cpd I, in which all of the haem substituents are replaced by hydrogen atoms: this model system has an overall charge of zero. Previous calculations on Cpd I of P450cam have shown the importance of allowing sufficient relaxation of the system in minimization, and correct treatment of protonation states and hydrogen bonding (e.g. of the haem propionates, if these are included in the QM region).30,38 The appropriate degree of truncation of the cysteinate ligand for QM or QM/MM calculations is a matter of debate. Some groups recommend modelling the cysteine side chain as a thiolate group (−SH), while others choose a methyl mercaptide ligand (−SCH3) or the entire cysteine residue, suitably ‘capped’ by hydrogen atoms. It has been suggested that the thiolate group results in a more accurate description of the Cpd I wavefunction in QM calculations on cluster models,32 whereas the methyl mercaptide ligand is more representative in QM/MM models. The differing suitability of the two different cysteine models is because small cluster models typically lack groups that donate hydrogen bonds to the thiolate group in the protein, but these hydrogen bonds are included in larger (e.g. QM/MM) models. The electronic structure of Cpd I is quite sensitive to the hydrogen-bonding environment of the cysteinate sulfur.33
To begin mechanistic calculations, the first step is to carry out a calculation on the QM or QM/MM model of Cpd I in its quartet state, using either a restricted or unrestricted open-shell DFT approach. The doublet ground state is more difficult to obtain initially, as is explained below. In the restricted approach the alpha and beta electrons are assigned to the same set of molecular orbitals, whereas in the unrestricted approach the alpha and beta electrons have separate orbitals. The latter approach is often required for open-shell systems. Convergence to the ‘correct’ quartet state (see above) is usually facile with modern electronic structure packages with high-quality initial guesses (see below) and good SCF optimization routines. The initial guess is the trial wavefunction that is used as a starting point for the electronic structure program. The quartet state has three unpaired electrons; two are located in Fe–O π* orbitals and the remaining one is distributed amongst the sulfur pπ orbital and the meso carbons of the haem (termed the a2u orbital), as shown in Fig. 9. As in QM studies of open-shell transition metal species, the converged solution should be carefully checked (by inspecting molecular orbitals, atomic charges, atomic spin densities etc.) to ensure that it corresponds to the expected one. This can be done either by detailed inspection of the output file or by visualization of the molecular orbitals. The doublet electronic state of Cpd I, in contrast, usually cannot be obtained from the software's initial guess, which tends to converge instead to higher energy doublet states with very different orbital occupations. The correct solution can be obtained by using a modified form of the converged orbitals for the quartet state, with orbital occupations changed to effectively switch the spin of the a2u electron. This is done most conveniently starting from a set of restricted open shell DFT orbitals. The resulting initial guess can then be used to optimize the doublet state wavefunction and then the associated geometry. An unrestricted open-shell density functional treatment is needed for these calculations, as the occupation pattern of alpha and beta orbitals differs. This approach should yield the correct ground-state (doublet) wavefunction for Cpd I.
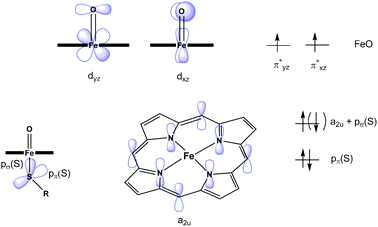 | ||
| Fig. 9 Schematic representation of the singly occupied molecular orbitals in a truncated model of Compound I, the active species in cytochrome P450, in the quartet spin state. The alternative spin orientation for the electron in the a2u + pσ (S) orbital shown in parentheses corresponds to the doublet spin state. The doublet and quartet spin states are close in energy and hence both can be involved in reaction.29,32,33 | ||
5. Comparison with experiment
The discussions above illustrate that modelling enzyme-catalysed reactions now can give useful, reliable and predictive results. Comparison with experiment is obviously an important test and allows validation of molecular models and computational techniques. There are now many examples where modelling techniques of the type described above have been used, with success, to model the reactions catalysed by enzymes giving qualitative (or, at best, quantitative) agreement with experiment.39 Some examples, and approaches for comparisons with experiments, are highlighted here.Transition state theory underlies the comparison of calculated barriers with experimental rate constants: there is much evidence that transition state theory provides a good general framework for enzyme-catalysed reactions. It is a theory that accounts for the rates of chemical reactions in terms of free energy differences between reactants and transition state; it is not the theory that enzymes stabilize the transition state (as first proposed by Pauling).
5.1 Comparison of activation energies and free energies with experimental rate constants
The rate of a reaction, kcat is related to the activation free energy, ΔG‡, by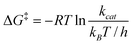 | (3) |
It is possible to calculate activation free energies for some enzyme reactions in very good agreement with experiment, as discussed in section 5.2 below. Even simple calculations of potential energy barriers can be useful and predictive, however. This is shown, for example, by the excellent correlation between potential energy barriers and (the log of) experimental rate constants for two enzymes, phenol hydroxylase (PH) and para-hydroxybenzoate hydroxylase (PHBH), for series of alternative substrates. PH and PHBH are flavin-dependent enzymes that catalyse the hydroxylation of phenols, with high specificity. This is an important step in the microbial degradation of aromatic compounds, such as lignin from wood. Various substituted phenols are also hydroxylated by these enzymes, including halophenols, hence reactions catalysed by PH and PHBH have potential applications in the detoxification of aromatic pollutants.
The PH-catalysed hydroxylation of phenol41 and PHBH-catalysed hydroxylation of p-hydroxybenzoate42 were studied using QM/MM methods, along with halogenated derivatives. The crystal structures of PH from Trichosporon cutaneum in complex with phenol and PHBH from Pseudomonas fluorescens in complex with p-hydroxybenzoic acid were used. QM/MM calculations were performed, using the CHARMM program, at the AM1/CHARMM22 level of theory. The QM region consisted of the flavin ring and the substrate (and the sidechain of Asp54 for PH). The proposed mechanism for both PH and PHBH is electrophilic aromatic substitution of the substrate by C4a-hydroperoxyflavin, resulting in the formation of a cyclohexadienone (Fig. 10). The reaction in PH was calculated to proceed stepwise via deprotonation of the hydroxyl moiety of the substrate by Asp54, activating the aromatic ring to enable hydroxylation by the hydroperoxyflavin molecule. For PHBH, the substrate was modelled with the hydroxyl group deprotonated. For PH, higher-level QM calculations were performed using a small gas phase model system at the HF, MP2 and B3LYP/6-31+G(d) levels of theory, to test the AM1 energies. AM1 was found to overestimate the activation energy for hydroxylation by around 10 kcal mol−1. This was apparent both from comparison with experimental kcat values and barriers calculated with higher levels of QM theory.
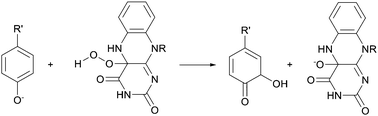 | ||
| Fig. 10 Electrophilic aromatic hydroxylation by hydroperoxyflavin catalysed by phenol hydroxylase (PH)41 and para-hydroxybenzoate hydroxylase (PHBH)42. R' is H in PH and CO−2 in PHBH. | ||
Energy barriers for hydroxylation in PH and PHBH were also computed for a variety of chlorinated and fluorinated substituted substrates (only fluorinated substrates in the case of PHBH). Overall, the substituents increased the energy barrier. On the basis that the electrophilic attack of the hydroperoxyflavin cofactor on the substrate is believed to be rate-limiting in the overall reaction cycle (for most of these substrates under typical conditions), the calculated energy barriers for the different substrates were compared to the experimental rate constants for their overall conversion by PH or PHBH. A linear correlation was found between the logarithm of the experimental rate constants (ln kcat) and the calculated energy barriers (ΔE‡) for the reaction of the hydroperoxyflavin cofactor with the substrate.
The good correlations indicate that the structural model and mechanism employed in this work provide an appropriate description of the rate-limiting step in the reaction cycles of PH and PHBH. The results also show that the enzyme-catalysed reaction is adequately described by transition state theory (and that activation entropies, and other factors, are similar for similar substrates). Although the calculated barriers were too high (because of the limitations of the AM1 method, which often significantly overestimates barriers as mentioned above), the results showed that the barriers are useful in a qualitative way. The correlation, which was observed for fluorinated substrates in PHBH, and both chlorinated and fluorinated substrates in PH, shows the potential of QM/MM methods for developing quantitative structure–activity relationships (QSARs). This is remarkable given that an adiabatic mapping approach was used with only a single pathway for each substrate. The good correlation shows that calculations of potential energy barriers, e.g. by adiabatic mapping, is a useful and predictive approach for some enzymes.
5.2 Towards chemical accuracy for energy barriers
PHBH has also been used to test and demonstrate high level QM/MM methods. As mentioned above, while relative barriers for different PHBH substrates are calculated usefully with a semi-empirical (QM/MM method (with the AM1 method), the absolute barriers are significantly too high. This is typical for semi-empirical methods, which often give barriers (and reaction energies) that are wrong by 10 kcal mol−1 or more. DFT methods give much better results, but suffer from some limitations (such as lack of dispersion in many functionals, and significant errors in energies in some cases).43 Higher level QM methods (such as the ab initio MP2 and CC methods) can be significantly more accurate, and can now be applied in QM/MM calculations on enzymes. A local treatment of correlation with these methods, and density fitting, reduces their computational expense without appreciably reducing their accuracy. This means that, in the best cases, it is now possible to calculate activation energies in enzymes to within chemical accuracy (within 1 kcal mol−1) using first principles methods (i.e. methods that are not specifically parameterized for a particular application). With such high level, computationally expensive methods, only potential energy barriers can be calculated directly. In fact, geometry optimization is usually not feasible at these levels either, so structures are typically optimized at a DFT/MM level, and ‘single point’ energies calculated for these structures at the higher level. Activation entropies can be estimated approximately from the difference between free energy and potential energy barriers at a (semi-empirical) QM/MM level, calculated with e.g. umbrella sampling and adiabatic mapping, respectively. The composite free energy barriers calculated in this way (i.e. high level QM/MM potential energy barriers, with thermal and zero-point vibrational corrections, added to the estimated activation entropy) can be compared to apparent activation energies derived from experimental rates using transition state theory (eqn (3)).These high level QM/MM calculations were first used to model reactivity in two well characterized enzymes:2 PHBH (see 5.1) and chorismate mutase (CM). CM catalyses a key step in the shikimate pathway, important to plants, funghi and bacteria in the production of aromatic amino acids. This step is the conversion of chorismate to prephenate, for which the mechanism is the same in the enzyme as it is in solution (Fig. 2). This feature has facilitated the discovery of the important factors that contribute to the rate acceleration (of >106) observed in the enzyme-catalysed reaction.
Claeyssens et al. performed B3LYP, MP2, LMP2 and LCCSD(T0) QM/MM calculations on PHBH and CM (the L in the acronyms indicates local correlation, CCSD(T0) denotes coupled-cluster theory with single and double excitations, and approximate treatment of triple excitations). The conformational flexibility of the enzymes was taken into account by averaging the results over multiple pathways (16 for CM, 10 for PHBH). Initial structures were sampled from AM1 QM/MM MD simulations and the reaction pathways optimized with B3LYP QM/MM. The computed average activation enthalpies with LCCSD(T0) were 13.1 (±1.1) and 13.3 (±1.5) kcal mol−1 for CM and PHBH respectively. These are in excellent agreement with the (apparent) experimental activation enthalpies of 12.7 and 12.0 kcal mol−1. HF (particularly), B3LYP and LMP2 showed poorer agreement with experiment, indicating that a high-level electron correlation treatment such as LCCSD(T0) is necessary to make quantitative predictions of activation energies in these enzymes. Activation entropies were estimated by comparing mean activation enthalpies with activation free energies (from lower-level AM1/CHARMM umbrella sampling calculations, as mentioned above). The resulting free energy barriers were very close to the values derived from experiments; they agreed within 1–2 kcal mol−1. These calculations show that QM/MM calculations can achieve near-chemical accuracy for enzyme-catalysed reactions. They also indicate that transition state theory provides a good general framework for the behaviour of enzymes. This is important because transition state theory underlies comparisons of calculated barriers with experimental kinetics.
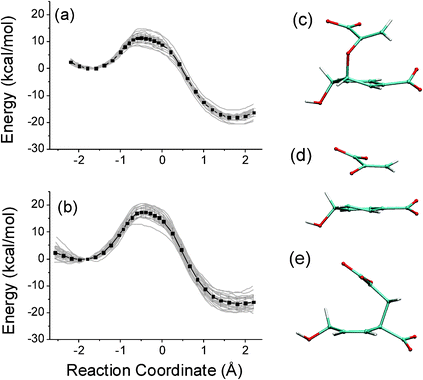 | ||
| Fig. 11 B3LYP/6-31(d)/CHARMM27 QM/MM energy profiles for the Claisen rearrangement of chorismate to prephenate in (a) water and (b) chorismate mutase. Representative structures are shown for (c) chorismate, (e) prephenate and (d) the transition state for the rearrangement. Reproduced from ref. 44. | ||
5.3 Predicting selectivity
For many types of problem, getting the absolute barrier height for an enzyme reaction is actually not particularly important; often the prediction of selectivity is a more practical (and useful) goal. The ability to predict the products formed during drug metabolism by P450s, for example, could help in the design of new drug molecules and avoid some of the effects associated with adverse drug reactions. Drug molecules often contain several sites at which oxidation may take place. Oxidation at one site may lead to detoxification, but oxidation at another position in the drug molecule may lead potentially to formation of a toxic metabolite. The preferred site of oxidation is often dictated by which site in the substrate is closest to the Cpd I oxygen: this is controlled by interactions between the substrate and the amino acid residues in the active site. Other more subtle geometrical factors, beyond a simple carbon-oxygen distance, can also play a role. In cases where more than one orientation of a substrate molecule is possible within the active site, the intrinsic reactivity of the oxidation sites may be the dominating factor in determining product formation. QM/MM methods are able potentially to account for both of these factors, as the QM part of the calculation takes Cpd I reactivity into account, and the effect of the substrate orientation is modelled by the inclusion of the protein environment in the MM region. It is critically important, however, to consider different possible binding modes (which could be generated practically e.g. by molecular dynamics simulations and/or docking).Oxidation of small alkenes such as propene and cyclohexene is an excellent test case for probing the ability of modelling methods to predict selectivity in product formation.9 In some bacterial P450 isoforms, the oxidation of propene results in formation of propene oxide, whereas the oxidation of cyclohexene results in both cyclohexene oxide and the allylic hydroxylation product (Fig. 12). This experimental observation is not trivial to explain. QM/MM energy profiles were calculated for different structures taken from MD simulations, to sample conformations of the enzyme-substrate complexes. These structures were selected based on angle and distance criteria such that the substrate was oriented in ‘reactive’ positions. The calculations showed that calculated relative energy barriers were in good agreement with experimentally observed product ratios, but only when multiple conformations were modelled. This example shows that QM/MM methods are a promising approach for predicting selectivity in P450 enzymes, but also highlights the need for extensive conformational sampling.
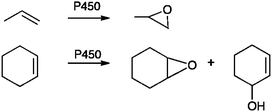 | ||
| Fig. 12 Oxidation of propene and cyclohexene by bacterial cytochrome P450 enzymes. These systems provide a test case for the prediction of selectivity using QM/MM methods.9,37 | ||
As in most studies of P450 reactions, DFT methods have been used to model these systems. As mentioned in section 4.2 above, many DFT methods do not include dispersion. Recent calculations on alkene oxidations in P450s show that it is important to include this effect.37 These calculations studied small models using DFT methods. The addition of the empirical dispersion correction was shown to result in improved selectivity predictions compared to calculations performed without the correction. On the basis of this and similar findings (and because the use of such a correction adds virtually no computational cost), we recommend the inclusion of this type of correction in all future B3LYP-based calculations on P450 enzymes, and indeed for other enzymes.
6. Conclusions
Enzymes are complex systems and to model their reaction mechanisms is no simple task. The potential benefits, from testing hypotheses for reaction mechanisms, to elucidating the factors that govern selectivity and catalysis, make the effort more than worthwhile. There are many different computational methods that can be used to study enzyme catalysed reactions, and the choice of an appropriate method is an important consideration. To model an enzyme-catalysed reaction, there are also many other details that require attention. Energy barriers for the chemical steps of enzyme reactions can now be calculated to a high degree of accuracy in the best cases, though less accurate calculations can also provide useful mechanistic insight. However, high accuracy is not needed for all types of application.Acknowledgements
The authors acknowledge colleagues involved in the work presented here and the EPSRC for funding. AJM is an EPSRC Leadership Fellow (grant number EP/G007705/1).References
- R. Lonsdale, K. E. Ranaghan and A. J. Mulholland, Chem. Commun., 2010, 46, 2354–2372 RSC.
- F. Claeyssens, J. N. Harvey, F. R. Manby, R. A. Mata, A. J. Mulholland, K. E. Ranaghan, M. Schütz, S. Thiel, W. Thiel and H.-J. Werner, Angew. Chem., Int. Ed., 2006, 45, 6856–6859 CrossRef CAS.
- A. L. Bowman, I. M. Grant and A. J. Mulholland, Chem. Commun., 2008, 4425–4427 RSC.
- H. M. Senn and W. Thiel, Top. Curr. Chem., 2007, 268, 173–290 CrossRef CAS.
- M. W. van der Kamp, K. E. Shaw, C. J. Woods and A. J. Mulholland, J. R. Soc. Interface, 2008, 5, S173–S190 CrossRef CAS.
- A. Warshel, Annu. Rev. Biophys. Biomol. Struct., 2003, 32, 425–443 CrossRef CAS.
- M. Elstner, T. Frauenheim and S. Suhai, THEOCHEM, 2003, 632, 29–41 CrossRef CAS.
- P. E. M. Siegbahn and F. Himo, JBIC, J. Biol. Inorg. Chem., 2009, 14, 643–651 CrossRef CAS.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, J. Phys. Chem. B, 2010, 114, 1156–1162 CrossRef CAS.
- R. A. Friesner and V. Guallar, Annu. Rev. Phys. Chem., 2005, 56, 389–427 CrossRef CAS.
- K. E. Ranaghan and A. J. Mulholland, Int. Rev. Phys. Chem., 2010, 29, 65–133 CrossRef CAS.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826 CrossRef CAS.
- L. Ridder, I. M. C. M. Rietjens, J. Vervoort and A. J. Mulholland, J. Am. Chem. Soc., 2002, 124, 9926–9936 CrossRef CAS.
- M. Mileni, S. Kamtekar, D. C. Wood, T. E. Benson, B. F. Cravatt and R. C. Stevens, J. Mol. Biol., 2010, 400, 743–754 CrossRef CAS.
- A. Lodola, M. Mor, S. Rivara, C. Christov, G. Tarzia, D. Piomelli and A. J. Mulholland, Chem. Commun., 2008, 214–216 RSC.
- http:// www.charmm.org .
- H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2005, 61, 704–721 CrossRef CAS.
- http:// propka.ki.ku.dk .
- K. E. Ranaghan, L. Ridder, B. Szefczyk, W. A. Sokalski, J. C. Hermann and A. J. Mulholland, Org. Biomol. Chem., 2004, 2, 968–980 CAS.
- W. Im, S. Berneche and B. Roux, J. Chem. Phys., 2001, 114, 2924–2937 CrossRef CAS.
- A. Rodríguez, C. Oliva, M. González, M. W. van der Kamp and A. J. Mulholland, J. Phys. Chem. B, 2007, 111, 12909–12915 CrossRef.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS.
- K. E. Shaw, C. J. Woods and A. J. Mulholland, J. Phys. Chem. Lett., 2010, 1, 219–223 CrossRef CAS.
- L. Masgrau, K. E. Ranaghan, N. S. Scrutton, A. J. Mulholland and M. J. Sutcliffe, J. Phys. Chem. B, 2007, 111, 3032–3047 CrossRef CAS.
- J. Rittle and M. T. Green, Science, 2010, 330, 933–937 CrossRef CAS.
- V. Guallar, M. Baik, S. Lippard and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 6998–7002 CrossRef CAS.
- C. M. Bathelt, L. Ridder, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2003, 125, 15004–15005 CrossRef CAS.
- C. M. Bathelt, L. Ridder, A. J. Mulholland and J. N. Harvey, Org. Biomol. Chem., 2004, 2, 2998–3005 CAS.
- S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS.
- J. Żurek, N. Foloppe, J. N. Harvey and A. J. Mulholland, Org. Biomol. Chem., 2006, 4, 3931–3937 Search PubMed.
- C. M. Bathelt, A. J. Mulholland and J. N. Harvey, J. Phys. Chem. A, 2008, 112, 13149–13156 CrossRef CAS.
- S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949–1017 CrossRef CAS.
- R. Lonsdale, J. Olàh, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2011, 133, 15464–15474 CrossRef CAS.
- J. N. Harvey, JBIC, J. Biol. Inorg. Chem., 2011, 16, 831–839 CrossRef CAS.
- J. N. Harvey, C. M. Bathelt and A. J. Mulholland, J. Comput. Chem., 2006, 27, 1352–1362 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, J. Phys. Chem. Lett., 2010, 1, 3232–3237 CrossRef CAS.
- A. Altun, S. Shaik and W. Thiel, J. Comput. Chem., 2006, 27, 1324–1337 CrossRef CAS.
- M. W. van der Kamp and A. J. Mulholland, Nat. Prod. Rep., 2008, 25, 1001–1014 RSC.
- M. Garcia-Viloca, J. Gao, M. Karplus and D. Truhlar, Science, 2004, 303, 186–195 CrossRef CAS.
- L. Ridder, A. J. Mulholland, I. M. C. M. Rietjens and J. Vervoort, J. Am. Chem. Soc., 2000, 122, 8728–8738 CrossRef CAS.
- L. Ridder, J. N. Harvey, I. M. C. M. Rietjens, J. Vervoort and A. J. Mulholland, J. Chem. Phys. B, 2003, 107, 2118–2126 CAS.
- M. W. van der Kamp, J. Żurek, F. R. Manby, J. N. Harvey and A. J. Mulholland, J. Phys. Chem. B, 2010, 114, 11303–14 CrossRef CAS.
- F. Claeyssens, K. E. Ranaghan, N. Lawan, S. J. Macrae, F. R. Manby, J. N. Harvey and A. J. Mulholland, Org. Biomol. Chem., 2011, 9, 1578–1590 CAS.
| This journal is © The Royal Society of Chemistry 2012 |
