Hetero triply-bridged dinuclear copper(II) compounds with ferromagnetic coupling: a challenge for current density functionals

Abstract

Seven new hetero triply-bridged dinuclear Cu(II) compounds have been synthesized and characterized corresponding to a series with general formula [Cu₂(L)₂(μ-OH)(μ-OH₂)(μ-O₂CR)]X₂ (where L = bpy = 2,2′-bipyridine, 4,4′-dmbpy = 4,4′-dimethyl-2,2′-bipyridine and 5,5′-dmbpy = 5,5′-dimethyl-2,2′-bipyridine; R = H for formate, CH₃ for acetate, CH₂CH₃ for propionate and C(CH₃)₃ for trimethylacetate and X = CF₃SO₃⁻ and ClO₄⁻). All compounds exhibit ferromagnetic behavior with the experimental J values derived from magnetic susceptibility measurements being in the 73–104 cm⁻¹ range. The overall qualitative behavior is reproduced by state of the art density functional theory based methods. However, none of the functionals is able to reproduce the fine details along the series which constitutes an excellent benchmark for future developments.

---

1. Introduction

The magnetochemistry of Cu(II) systems has received much attention because of their interesting structural and magnetic properties, as well as their application as molecular based materials.^1–3 In these materials, the Cu(II) ions exhibit a d⁹ electronic configuration and, hence, can be considered as suitable candidates representative of basic models of magnetic coordination compounds, especially in di- and polynuclear Cu(II) systems.^4,5 A deep understanding of magneto-structural correlations is highly desirable to be able to predict the magnitude of the coupling constant, its character and the corresponding physical mechanism, thus allowing one to design and synthesize new molecular based materials with improved magnetic properties. Hence, magneto-structural correlations for a series of compounds with different structural and magnetic properties are usually derived either from experimental measurements or theoretical calculations. Clearly, compounds with strong ferromagnetic coupling are of great interest for potential technological applications.^4–12

Among the different Cu(II) families with ferromagnetic properties, previous work has focused on the design, magnetic properties and magneto-structural correlations of the hetero triply-bridged dinuclear Cu(II) systems because this particular type of compound exhibits moderate to strong ferromagnetic interactions.^6–10 In this type of system, the magnetic interaction occurs via bridging ligands, although various pathways are possible,¹⁰ which depend on the coordination geometry of the Cu(II) ion, the Cu⋯Cu separation, the bond angles involving the bridging atoms, the dihedral angle between the planes containing the Cu(II) ions and the distance from the Cu(II) to the bridging ligands. Structurally, the Cu(II) ions are in a five-fold coordination which, however, corresponds to a rather broad range of geometries, from regular trigonal bipyramidal (TBP) to regular square-based pyramidal (SP). In a previous work,¹⁰ the possible topological arrangements of the dinuclear unit have been organized in six different classes: class A corresponds to co-planar bases with a square pyramidal geometry for both Cu(II) environments and the two bridges (aquo or hydroxo) lying in the equatorial positions; class B contains compounds with non-coplanar bases with a square pyramidal geometry for both Cu(II) ions with carboxylato and hydroxo bridges in the equatorial positions; class C includes compounds with non-coplanar bases with a square pyramidal geometry for both Cu(II) ions and two carboxylato bridges lying in the equatorial positions; class D stands for non-coplanar bases with a square pyramidal geometry for both Cu(II) ions, one single-atom or triatomic bridge in an equatorial–equatorial configuration and two carboxylato bridges in an axial–equatorial configuration; class E stands for non-coplanar bases with a trigonal bipyramidal geometry for both Cu(II) ions and one hydroxo bridge in an axial–axial configuration; and, finally, class F refers to non-coplanar bases with square pyramidal and trigonal bipyramidal geometries, two bridges occupying the axial–equatorial positions, with the third one in an equatorial–equatorial configuration. The knowledge of these topologies is useful to unravel the relationships between structural features and the value of the intramolecular magnetic exchange interaction in the triply-bridged dinuclear unit.

In previous studies, the magneto-structural correlations have been investigated for some of these compounds by the simple Extended Hückel (EH) method and a linear correlation has been found for class B compounds allowing a first step towards a proper understanding.¹⁰ However, to obtain more quantitative relationships it is necessary to go beyond the semi-empirical EH method and to make use of more reliable electronic structure methods as demonstrated by recent studies on other triply bridged dinuclear Cu(II) compounds which employed state of art density functional theory (DFT) based methods.^11,12 Six different exchange–correlation functionals have been used in order to fully understand the magneto-structural correlation and also to accurately predict the broad range of magnetic coupling constant (J) values exhibited by class B and class F compounds with ferro- and antiferromagnetic behavior, respectively. The DFT calculations have revealed that, for ferromagnetic class B compounds, the calculated J values almost quantitatively correlate with the sum of Addison's τ parameter¹³ of each Cu(II) ion. The calculated and experimental J values of all compounds are in agreement,¹² especially for the long-range separated hybrid LC-ωPBE method.¹⁴ In particular, the DFT calculations properly reproduce the magnitude of the magnetic coupling constants in the whole range of topologies studied. However, the calculated J values of class B compounds exhibit a rather large dependence on the type of hybrid exchange–correlation functional used and may even show noticeable deviations from the experimental values, especially in this type of ferromagnetic compound. Therefore, the precise interpretation of the magnetic interactions in class B compounds with ferromagnetic interactions still requires further attention and either accurate wave function based calculations or a more systematic study aimed precisely to better understand the performance of current DFT approaches in describing this type of system is needed. There is little doubt that wave function based calculations, using for instance the Difference Dedicated Configuration Interaction (DDCI) method, will properly describe these systems as highlighted in the review paper by Moreira and Illas.¹⁵ It is also clear that without a modeling of the external ligands, these calculations are likely to be computationally unfeasible. Therefore, in the present paper we focus on the second possibility and, to this end, we extend the investigation of the magneto-structural correlations and accurate prediction of intramolecular magnetic interactions of this series of compounds by adding seven newly synthesized compounds of class B and analyzing simultaneously the effect of the type of DFT method and of the basis set used to represent the electron density. We will show that the current exchange–correlation functionals, which properly describe magnetostructural correlations involving antiferromagnetic interactions,¹⁵ face difficulties in properly reproducing the J values and trends along the series of ferromagnetic compounds which, therefore, constitute a challenge for state of the art exchange–correlation functionals.

2. Experimental

The new compounds can be generally described as members of the [Cu₂(L)₂(μ-OH)(μ-OH₂)(μ-O₂CR)]X₂ series where L = bpy = 2,2′-bipyridine, 4,4′-dmbpy = 4,4′-dimethyl-2,2′-bipyridine and 5,5′-dmbpy = 5,5′-dimethyl-2,2′-bipyridine; R = H for formate, CH₃ for acetate, CH₂CH₃ for propionate and C(CH₃)₃ for trimethylacetate and X = CF₃SO₃⁻ and ClO₄⁻. In particular, the following compounds are considered: [Cu₂(bpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₃)](CF₃SO₃)₂ (1), [Cu₂(4,4′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CH)](ClO₄)₂ (2), [Cu₂(4,4′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₃)](ClO₄)₂ (3), [Cu₂(5,5′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₃)](ClO₄)₂ (4), [Cu₂(5,5′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CC(CH₃)₃)](ClO₄)₂ (5), [Cu₂(5,5′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₃)](CF₃SO₃)₂ (6) and [Cu₂(5,5′-dmbpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₂CH₃)](CF₃SO₃)₂ (7), for which structure can be easily understood by inspection of Scheme 1. The synthesis, crystal structures, magnetic properties and a systematic theoretical study are described in the forthcoming sections.

Scheme 1

2.1. Materials and measurements

2,2′-Bipyridyl, 4,4′-dimethyl-2,2′-bipyridine and 5,5′-dimethyl-2,2′-bipyridine were purchased as commercial chemicals from Aldrich. All reagents are commercial grade materials and were used without further purification. Elemental analyses (C, H, N) were performed on a Perkin–Elmer PE 2400 CHNS/O Analyzer. IR spectra were recorded on Spectrum One FT-IR spectrophotometer as KBr disc in the 4000–450 cm⁻¹ spectral range. Solid-state (diffuse reflectance) electronic spectra were measured as polycrystalline samples on a Perkin–Elmer Lambda2S spectrophotometer, over the range 8000–18 000 cm⁻¹.

Magnetic susceptibility measurements for compounds 1–7 were carried out with a Quantum Design SQUID MPMS-XL magnetometer working in the temperature range 2–300 K at magnetic fields of 500 G (2–30 K) and 10 kG (2–300 K). The EPR spectra of microcrystalline samples of 1–7 were recorded at X-band frequency (ν ∼ 9.4214 GHz) with a Brucker ES-200 spectrometer in the temperature range 300–4 K.

2.2. Synthesis

Here we describe in some detail the synthesis procedure and experimental conditions for [Cu₂(bpy)₂(μ-OH)(μ-OH₂)(μ-O₂CCH₃)](CF₃SO₃)₂ (1); the corresponding description for the rest of compounds (2 to 7) has similar routes and are described in more detail in the ESI† file.

A warmed methanol solution (10 ml) of bpy (0.156 g, 1.0 mmol) was added to a warmed aqueous solution (20 ml) of Cu(CF₃SO₃)₂ (0.361 g, 1.0 mmol). Then, an aqueous solution (5 ml) of NaO₂CCH₃ (0.204 g, 3.0 mmol) was slowly added. The mixture was warmed, with the addition of DMF (2 ml), yielding a clear dark blue solution. Upon slow evaporation at room temperature for 6 days, the product 1 was isolated as violet-blue block-shaped crystals. The crystals were filtered off, washed with the mother liquid and air-dried. Yield: ca. 75%. Anal. calc. for C₂₄H₂₂Cu₂F₆N₄O₁₀S₂: C, 34.62; H, 2.78; N, 6.73%. Found: C, 34.60; H, 2.80; N, 6.69%.

Caution. Perchlorate salts are potentially dangerous, only small quantities should be prepared.

2.3 Crystallography

X-ray data for single-crystal samples of compounds 1, 2, 4, 6 and 7 were collected at 100 K, whereas those of compound 3 and compound 5 were collected at 150 and 173 K, respectively. Reflection data were collected on a 1K Bruker SMART APEX CCD area-detector diffractometer using rotating mode, graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) at a detector distance of 4.5 cm and a swing angle of −30°. A hemisphere of the reciprocal space was covered by combination of three sets of exposures; each set had a different ϕ angle (0°, 88°, 180°) and each exposure of 40 s covered 0.3° in ω. Raw data frame integration was performed with the SAINT code,¹⁶ which also applied correction for Lorentz and Polarization effects. An empirical absorption correction by using the SADABS¹⁷ program was applied, which resulted in transmission coefficients ranging from 1.000 to 0.678, 0.746 to 0.603, 1.000 to 0.818, 1.000 to 0.850, 0.891 to 0.665, 0.945 to 0.614 and 0.746 to 0.614 for 1–7, respectively. The structures were solved by direct methods and refined by a full-matrix least-squares method on (F_obs)² using the SHELXTL-PC Version 6.12 software package.¹⁸

All hydrogen atoms of compound 1–4 were determined at the difference map and refined isotropically by riding with the heavy atoms. For compound 5, all hydrogen atoms on carbon atoms were fixed except O–H hydrogen atoms whose positions were refined. Also, one hydrogen atom of an aqua bridging molecule could not be located and the position was fixed according to geometry optimization from theoretical calculations. In addition, three methyl groups of trimethylacetate appear to be disordered. All hydrogen atoms on carbon atoms of compound 6 were fixed except O–H hydrogen atoms whose positions were refined. One triflate group was also found to be disordered. For compound 7, all H atoms were determined at the difference map and refined isotropically and bonded to the heavy atoms except hydrogen atoms on C(6) and C(8) which were fixed.

The crystal and refinement details for compounds 1–7 are listed in Table S1 (ESI†). Selected bond lengths and angles are given in Tables S2–S8 (ESI†).

3. Computational details

A series of DFT calculations with state of the art exchange–correlation functionals has been carried out considering the isolated dinuclear Cu(II) cationic complexes in vacuo. The electron density was described either explicitly considering all electrons or using small core (LANL2) effective core potential (ECP) for the Cu atoms which allows one to take scalar relativistic effects into account. For the all electron calculations we used a rather large standard basis set of Gaussian Type Orbitals (GTO) which is the same as in previous works^11,12 and is defined as follows: 6-3111+G extended with an f-function (exponent(f) = 0.528) for Cu and 6-31G(d) for the remaining atoms. For the calculations where the Cu innermost 10 electrons are described through a relativistic ECP, two different bases have been used which are either the standard LANL2DZ or the more extended standard LANL2TZ.¹⁹ The rest of atoms are described at the all electrons level with the 6-31G(d) basis set. We will refer to the three sets of calculations as AE, ECP-DZ and ECP-TZ, respectively.

The DFT calculations have been carried out using a variety of exchange–correlation functionals including hybrid schemes such as the well-known B3LYP and BHHLYP,^20,21 the M06 and M06-2X meta-GGA functionals developed by Zhao and Truhlar^22–24 and the short- (HSE)²⁵ and long-range (LC-ωPBE) functionals¹⁴ proposed by Scuseria and collaborators. In all cases the calculations were carried out within the unrestricted (spin-polarized) formalism. Clearly, in this type of formalism, the spin symmetry is not guaranteed.^26–28 Nevertheless, in the unrestricted Kohn–Sham formalism one can approximate the triplet (T) state using a single Slater determinant with two unpaired electrons (i.e., S_z = 1). However, to estimate the energy of the open shell singlet state it is possible to make use of the broken-symmetry (BS) approach imposing S_z = 0. In this way, the singlet–triplet gap energy has been obtained on the basis of the expectation value of the Heisenberg Hamiltonian as in eqn (1)

Ĥ = −JŜ₁·Ŝ₂ (1)

that using the appropriate mapping¹⁵ leads to the approximate relation:

J = 2[E(BS) − E(T)] (2)

where E(BS) is the energy of the broken-symmetry state and E(T) is the energy of the spin unrestricted approximation to the triplet state.²⁹ Here, it is important to stress that eqn (2) takes into account the so-called spin projection to approximately recover the spin symmetry lost in the BS approach and which is inherent to the use of a single Kohn–Sham determinant.^30–32 Here one must advert that alternative methods for calculating J couplings without the use of spin symmetry³³ lead to results that are not always accurate³⁴ when high quality range separated functionals like those employed in this paper are used. Nevertheless, one must admit that magnetostructural correlations involving mainly antiferromagnetic compounds do not suffer from this limitation. It has also been recently shown that, for a given functional, results obtained using the mapping procedure in eqn (2) are in agreement with those obtained using the spin flip Time Dependent DFT approach which properly accounts for spin symmetry in this type of system.³⁵

All calculations were carried out using the Gaussian09 suite of programs.³⁶

4. Results and discussions

4.1 Description of the crystal structures

The crystal structures of compounds 1–7 consist of a hetero triply-bridged dinuclear Cu(II) cationic unit and two counteranions (CF₃SO₃⁻ for compounds 1, 6 and 7; ClO₄⁻ for compounds 2–5). For each of the cationic units, two [Cu(L)] groups are linked together by three different bridging ligands: aquo, hydroxo and carboxylato. The environment of each Cu(II) center corresponds to a distorted square pyramidal geometry of the CuN₂O₂O′ chromophore, with τ values of 0.10 and 0.38 for the two Cu(II) centers. Let us recall that the Addison parameter is defined as τ = (α − β)/60, where α and β are the largest coordination angles. Hence, one has τ = 0 for square pyramidal (SP) and τ = 1 for trigonal bipyramidal (TBP) geometry.¹³ The coordination environment around each Cu(II) ion contains two N atoms of the chelate ligand (Cu–N 1.978(1)–2.012(6) Å), an oxygen atom of the carboxylato bridging ligand (Cu–O 1.941(1)–1.983(1) Å) and an oxygen atom of the hydroxo ligand (Cu–O 1.908(1)–1.938(5) Å) to form the square bases. The apical site of each Cu(II) atom is occupied by an oxygen atom of an aquo ligand at distances in range of 2.310(4)–2.442(1) Å. The syn,syn-coordinated carboxylato ligand bridges two equatorial planes of each Cu(II) chromophore, giving the Cu⋯Cu distances in the range of 2.979(1)–3.077(1) Å. The CuN₂O₂O′ chromophores are non-planar with dihedral angles (γ in Table 1) between the CuN₂ and CuO₂ planes in the range of 10.10(2)–28.62(1)°. The dihedral angles between the equatorial planes (ϕ in Table 1) are in the range of 112.07(1)–122.08(1)°. The bridging angles of Cu–OH–Cu are in the range of 100.80(7)–107.26(5)°. According to these structural features, compounds 1–7 are classified as class B (Scheme 1).

Table 1 Structural and magnetic data for Class B triply-bridged dinuclear copper(II) compounds^c

Compound^a	Geom ^b	τ	ϕ	γ	Cu⋯Cu	Cu–X		Cu–OH–Cu	J exp	Ref.^a
						Axial	Equatorial
a Abbreviations: bpy = 2,2′-bipyridine, 4,4′-dmbpy = 4,4′-dimethyl-2,2′-bipyridine, 5,5′-dmbpy = 5,5′-dimethyl-2,2′-bipyridine, n.d. = not determined, pw = present work. b SP = distorted square pyramid. c Geom stands for the coordination of Cu(1) and Cu(2), τ is the Addison structural parameter for Cu(II) center, ϕ is the angle between basal planes and γ is the tetrahedral twist angle, both in degrees. Cu⋯Cu and Cu–X distances are in Å and Cu–OH–Cu angles in degrees. Jexp is the experimentally derived magnetic coupling constant in cm^−1.
[Cu2(dpyam)2(μ-OH)(μ-OH2)(μ-O2CCH3)](S2O8) (I)	SP, SP	0.43	164.4	40.4	3.124	2.414	1.911–2.023	109.6	n.d.	10
[Cu2(bpy)2(μ-OH)(μ-OH2)(μ-O2CCH3)](NO3)2 (II)	SP, SP	0.21, 0.19	120.5	14.5, 11.6	3.049	2.347, 2.460	1.938–2.017	104.0	n.d.	10
[Cu2(phen)2(μ-OH)(μ-OH2)(μ-O2CCH3)](BF4)2·(H2O)0.5 (III)	SP, SP	0.21, 0.16	114.6	17.0, 8.6	3.002	2.374, 2.390	1.925–2.008	102.1	120.8	10
[Cu2(bpy)2(μ-OH)(μ-OH2)(μ-O2CCH3)](ClO4)2 (IV)	SP, SP	0.14, 0.25	118.1	—	3.035	2.379, 2.405	2.006–2.010	103.8	19.3	10
[Cu2(phen)2(μ-OH)(μ-OH2)(μ-O2CCH3)](ClO4)2 (V)	SP, SP	0.02, 0.14	113.8	16.4, 8.2	2.989	2.360, 2.375	1.933–2.020	101.3	120.0	10
[Cu2(bpy)2(μ-OH)(μ-OH2)(μ-O2CCH2CH3)](ClO4)2 (VI)	SP, SP	0.20, 0.16	120.1	15.0, 10.9	3.037	2.382, 2.415	1.920–2.005	104.5	148.9	10
[Cu2(bpy)2(μ-OH)(μ-O2CCH3)(μ-Cl)]Cl·(H2O)0.5 (VII)	SP, SP	0.41, 0.28	123.0	27.4, 18.9	3.040	2.632, 2.657	1.936–2.029	103.3	145.3	10
[Cu2(phen)2(μ-OH)(μ-OH2)(μ-O2CCH2CH3)](NO3)2 (VIII)	SP, SP	0.19, 0.21	122.3	14.6, 12.2	3.026	2.344, 2.368	1.925–2.029	103.6	98.4	12
[Cu2(phen)2(μ-OH)(μ-OH2)(μ-O2CC(CH3)3)](ClO4)2(CH3CH2OH) (IX)	SP, SP	0.10, 0.22	117.7,	9.9, 16.2	3.010	2.419, 2.379	1.911–2.015	103.8,	151.2	12
		0.08, 0.26	120.4	8.8, 21.2	3.034	2.425, 2.369	1.893–2.012	105.3
[Cu2(bpy)2(μ-OH)(μ-O2CCH2CH3)(μ-O2SOCF3)](CF3SO3)(DMF)0.5 (X)	SP, SP	0.14, 0.15	154.8	11.2, 11.8	3.341	2.351, 2.354	1.906–2.019	122.3	104.5	12
[Cu2(bpy)2(μ-OH)(μ-OH2) (μ-O2CCH3)](CF3SO3)2 (1)	SP, SP	0.24, 0.25	118.95	15.67, 18.73	3.024	2.394, 2.323	1.921–2.009	103.39	102.1	pw
[Cu2(4,4′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCH)](ClO4)2 (2)	SP, SP	0.10, 0.38	122.08	10.10, 28.62	3.077	2.324, 2.409	1.908–1.999	107.26	72.6	pw
[Cu2(4,4′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCCH3)](ClO4)2 (3)	SP, SP	0.11, 0.30	120.19	11.37, 25.20	3.055	2.323, 2.442	1.918–1.999	105.55	90.2	pw
[Cu2(5,5′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCCH3)](ClO4)2 (4)	SP, SP	0.21, 0.22	112.07	14.81, 15.64	2.984	2.329, 2.346	1.929–2.003	101.07	104.3	pw
[Cu2(5,5′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCC(CH3)3)](ClO4)2 (5)	SP, SP	0.17, 0.19	114.56	11.49, 13.99	3.008	2.320, 2.333	1.921–2.012	102.40	98.7	pw
[Cu2(5,5′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCCH3)](CF3SO3)2 (6)	SP, SP	0.34, 0.31	118.72	22.29, 20.60	3.007	2.310, 2.323	1.923–2.003	102.57	92.1	pw
[Cu2(5,5′-dmbpy)2(μ-OH)(μ-OH2)(μ-OCCH2CH3)](CF3SO3)2 (7)	SP, SP	0.23, 0.27	112.25	15.61, 18.04	2.979	2.321, 2.339	1.931–1.996	100.80	103.1	pw

---

The lattices of all compounds are stabilized by intermolecular π–π interactions between aromatic pyridine rings on chelate ligands of adjacent dinuclear cations and hydrogen bonding between the aquo and hydroxo bridges and triflate or perchlorate anions. The molecular structure of compound 1 is shown in Fig. 1 whereas the rest of structures are shown in Fig. S1–S6 (ESI†). For comparison purposes, the structural data of compounds 1–7 and of some other relevant hetero triply-bridged dinuclear Cu(II) compounds previously studied^10,12 are summarized in Table 1.

Fig. 1 Molecular structure and atomic numbering scheme for compound 1. Triflate counteranions are omitted for clarity.

4.2 Spectral characterizations

The infrared spectra display a broad band at 3510 cm⁻¹ for 1, 3519 cm⁻¹ for 2, 3524 cm⁻¹ for 3, 3434 cm⁻¹ for 4, 3401 cm⁻¹ for 5, 3475 cm⁻¹ for 6 and 3479 cm⁻¹ for 7, which can be assigned to the bridging OH vibration of the hydroxo ligands and/or lattice water. The spectra also exhibit the intense bands at 1557 and 1445 cm⁻¹ for 1, 1577 and 1413 cm⁻¹ for 2, 1554 and 1443 cm⁻¹ for 3, 1557 and 1479 cm⁻¹ for 4, 1540 and 1480 cm⁻¹ for 5, 1564 and 1481 cm⁻¹ for 6 and 1556 and 1479 cm⁻¹ for 7, corresponding to the ν_as(COO⁻) and ν_s(COO⁻) vibrations of carboxylato bridging ligands namely acetato for 1, 3, 4 and 6, formato for 2, trimethylacetato for 5 and propionato for 7, respectively. The spectra of compounds 1, 6 and 7 show the broad and intense bands of the stretching of CF₃SO₃⁻ at 1277 ν_as(S–O), 1153 ν_as(C–F), and 1029 ν_s(S–O) cm⁻¹ for 2; 1279 ν_as(S–O), 1161 ν_as(C–F) and 1031 ν_s(S–O) cm⁻¹ for 6 and 1281 ν_as(S–O), 1158 ν_as(C–F) and 1031 ν_s(S–O) cm⁻¹ for 7. The IR spectra of compounds 2–5 present the broad and intense bands of the stretching for the ionic ClO₄⁻ anion (1103 cm⁻¹ for 2, 1106 cm⁻¹ for 3, 1111 cm⁻¹ for 4 and 1120 cm⁻¹ for 5).

The diffuse reflectance spectra of compounds 1–7 display a broad band (16 530 cm⁻¹ for 1, 16 030 cm⁻¹ for 2, 16 340 cm⁻¹ for 3, 16 590 cm⁻¹ for 4, 16 490 cm⁻¹ for 5, 16 240 cm⁻¹ for 6 and 16 320 cm⁻¹ for 7) and a lower energy shoulder (13 880 cm⁻¹ for 1, 13 060 cm⁻¹ for 2, 13 620 cm⁻¹ for 3, 13 960 cm⁻¹ for 4, 13 600 cm⁻¹ for 5, 13 540 cm⁻¹ for 6 and 13 940 cm⁻¹ for 7). These features are typical and can be assigned to the d_xy, d_yz, d_xz → d_x²−y² and d_z² → d_x²−y² transitions for the square pyramidal geometry of the class B triply-bridged dinuclear Cu(II) compounds. Notice that according to strict symmetry considerations for the distorted square pyramidal geometry of compounds 1–7, the d_xy, d_yz, d_xz orbitals are not triply degenerated which is the origin of the broad band mentioned above.

4.3 Electron paramagnetic resonance spectra and magnetic properties

The Electron Paramagnetic Resonance Spectra (EPR) of compounds 1–7 (X-band, ν ∼ 9.4214 GHz) have been recorded at different temperatures between 4 and 300 K for polycrystalline solid samples. The general shape of the spectra is similar for all compounds; we show the EPR spectra of compound 4 in Fig. 2 as a representative example. A summary of data obtained from EPR measurements is reported in Table 2.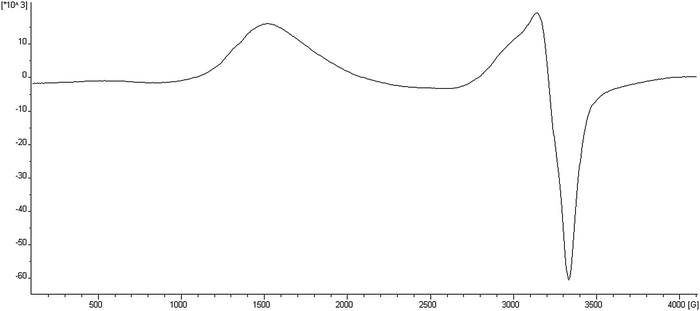

Fig. 2 EPR spectrum of compound 4 at 4 K.

Table 2 Experimental normal and half-field (at 4 K) EPR signals and best-fit susceptibility data to eqn (3) (g_iso, J_exp and θ) for compounds 1–7. Additional details corresponding to the fitting are reported in Table S9, ESI

Compound	g	g 1/2	g iso	J exp (cm^−1)	θ(K)	Nα(×10^−6)	R (×10^−4)
1	2.082	4.498	2.194	102	−0.39	30	2.4
2	2.095	4.350	2.163	73	−0.73	90	3.6
3	2.066	4.438	2.177	90	−0.58	60	3.3
4	2.092	4.429	2.167	104	−0.33	110	1.4
5	2.097	4.427	2.178	99	−0.31	50	2.1
6	2.074	4.426	2.196	92	−0.55	60	3.1
7	2.063	4.376	2.162	103	−0.38	40	2.3

---

As expected for ferromagnetic systems,³⁷ the principal transition band near g ∼ 2.1 (corresponding to Δm_s = 1) shows some asymmetry but maintains the center of the band as T goes from 300 to 4 K. No significant fine structure is observed. A broad band near g_1/2 ∼ 4.4 is also observed and assigned to the half field transition (corresponding to Δm_s = 2). Both bands slightly increase their intensity as temperature increases and the Δm_s = 2 half field transition band shows important intensity with respect to the Δm_s = 1 transition. This observation confirms the ferromagnetic character of these compounds.

Molar magnetic susceptibility (χ_M) measurements were carried out using microcrystalline samples of compounds 1–7 and diamagnetic corrections were calculated from the Pascal tables. The as measured χ_MT vs. T plots for all compounds are quite similar and display clear ferromagnetic behavior as shown in Fig. 3. At room temperature, the χ_MT values are in the 0.965–1.007 cm³ Kmol⁻¹ range, close to the value expected for two uncoupled Cu(II) ions. To account for the magnetic behavior of the dinuclear Cu(II) complexes and to evaluate the corresponding coupling constant J, defined as the singlet–triplet splitting, we fitted the raw experimental susceptibility data using the Bleaney–Bowers equation³⁸ with an additional temperature independent paramagnetism term, usually denoted as Nα. In addition, we corrected the Bleaney–Bowers expression with a mean-field Weiss θ parameter to account for the small antiferromagnetic intermolecular interactions detected in the low temperature region for these ferromagnetic dinuclear complexes:

Best-fit parameters were obtained by minimization of the error function R = Σ{[(χ_MT)_calc−(χ_MT)_exp]²/(χ_MT)_exp²}, and results are also shown in Table 2. In the view of the intrinsic low accuracy involving the fitting of ferromagnetically coupled Cu(II)–Cu(II) systems with rather large molecular weights one should avoid overparametrization. Therefore, the fitting was here consistently carried out for all compounds using the minimum possible number of parameters. Note that for these ferromagnetic compounds, χ_MT ranges from 0.9 to 1.2. Because of this small χ_MT range, small instrumental inaccuracies appear magnified and evidences as small discontinuities near 50K—attributable to the technical use of two different temperature probes for the high and low T ranges—although one must note that the J values are extracted from the high temperature part of the χ_MT versus T curve. The need for a small number of parameters in describing the χ_MT versus T curve of these ferromagnetic compounds also leads to a more difficult fitting to the magnetic model which affects especially the low T part of the χ_MT versus T curve. The g_iso values obtained from the fitting are consistent with those corresponding to Cu(II) systems and to the g values measured at 4 K which essentially correspond to the triplet state (Table 2). Here, we will mention the selected magnetic plot of compound 4 (Fig. 3) and the results of the remaining compounds are summarized in ESI† (Fig. S7–S12). The χ_MT vs. T plot of compound 4 shows a room temperature χ_MT product value of 1.01 cm³ Kmol⁻¹, slightly higher than that expected for two uncoupled Cu(II) ions. Lowering the temperature causes the χ_MT product to continuously increase until reaching a plateau value of 1.15 cm³ Kmol⁻¹ at 50 K. Upon further cooling, χ_MT shows an abrupt descent for all compounds, which clearly suggests that this quantity tends to zero when temperature tends to 0 K. This behavior can be explained by the existence of ferromagnetically coupled Cu(II) pairs responsible for the high temperature regime, where the low-lying triplet state was increasingly populated in detriment of the singlet state. Below liquid nitrogen temperature, small antiferromagnetic intermolecular interactions manifest and tend to couple the triplet states in such a way that the S = 1 spin moments of the different molecules cancel out each other and, as a result, a zero global magnetization is approached near the liquid helium temperature.

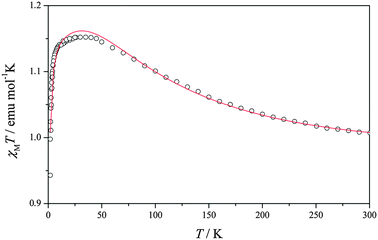Fig. 3 Plot of magnetic susceptibility-temperature product (χ_MT) versus temperature (T) for compound 4.

4.4 Magneto-structural correlations

Here we analyze the common magnetostructural correlations involving the experimental value of the magnetic coupling constant (J_exp) and the key feature of the molecular structure.^4,5Fig. 4 plots J_expversus the distance between the two Cu centers and Fig. 5 plots J_expversus the angle formed by the Cu–OH–Cu structural moiety where the OH corresponds to a monoatomic bridge that links two Cu centers at an equatorial position. Both plots exhibit a clear trend which is slightly more quantitative in the second case. These plots are important since they reveal a clear trend along the series indicating that the magnitude of the ferromagnetic coupling increases with decreasing Cu⋯Cu distance, as expected from simple arguments, and also increases with decreasing Cu–OH–Cu bond angle which can also be explained in terms of qualitative rules. Hence, these empirical correlations provide a very useful testing ground for theoretical methods.

Fig. 4 Plot of the experimental J (cm⁻¹) vs. Cu⋯Cu (Å) of compounds 1–7.

Fig. 5 Plot of the experimental J (cm⁻¹) vs. Cu–OH–Cu (deg.) of compounds 1–7.

In previous work it has been suggested that the aggregate Addison τ parameter also provides useful information about the relationship between structure and magnetic coupling. In fact, the Addison parameter allows one to properly define compounds 1–7 as belonging to class B. However, it does not provide a suitable magnetostructural correlation, which is at variance of previous work.¹¹ This is likely to be due to the fact that values of the magnetic coupling constant studied exhibited a broader range but also to their ferromagnetic character. This will be confirmed by the DFT calculations described in the next subsection.

4.5 Density functional theory based calculations

The calculated and experimental values of the magnetic coupling constants are summarized in Table 3 where the aggregate Addison τ parameter is also shown for comparison. All methods, including UHF which neglects electron correlation except for the part included by spin polarization, consistently predict these compounds to be ferromagnetic, in agreement with experiment and all methods regularly predict that all compounds have a similar value of the magnetic coupling constant, again in agreement with experiment. However, the fine details are more subtle, difficult to describe and do not always go in the expected direction. The calculated values of the magnetic coupling constant strongly depend on the type of exchange–correlation functional and, more precisely, on the amount of Fock exchange included in the exchange potential. This is not surprising and has been reported for quite a large number of systems although most of them exhibiting strong antiferromagnetic character.^15,30 The novelty here is that none of the studied methods is able to describe 2 as the compound with smallest J and 4 as the one with the largest. One can suggest that the experimental measurements and fitting procedures for these two compounds are intrinsically not enough and accurate, although the magnetostructural correlations in Fig. 4 and 5 will not support such a claim. Even accepting that these two compounds represent exceptions and excluding them from the statistical analysis, one will face the same problem since none of the methods will now predict that 3 is the compound with the smallest J and 7 the one with the largest.

Table 3 Calculated values of the coupling constant J (in cm⁻¹) for compounds 1–7, using hybrid and screened functionals compared to experimental magnetic values. AE and ECP stand for calculations with all electrons and effective core potentials respectively. For the ECP only results with the more extended TZ basis are shown

[a]	τ agg	J calc														J exp
		UHF		M06-2X		BHHLYP		LC-ωPBE		HSE		B3LYP		M06
		AE	ECP	AE	ECP	AE	ECP	AE	ECP	AE	ECP	AE	ECP	AE	ECP
1	0.49	37.1	38.1	67.1	95.8	83.5	85.6	135.3	143.1	147.7	155.5	169.5	170.5	238.9	301.9	102
2	0.48	37.6	39.4	66.5	96.7	82.1	85.3	133.1	143.0	146.0	155.7	165.8	168.6	231.0	299.1	73
3	0.41	38.3	39.4	67.9	96.9	84.1	86.3	134.2	141.8	148.1	155.7	170.0	170.7	240.3	304.0	90
4	0.43	36.0	37.2	65.8	94.5	81.9	84.6	132.3	141.4	145.2	154.4	167.0	169.7	236.8	300.5	104
5	0.36	34.8	35.5	64.8	93.5	80.0	81.9	133.0	141.9	145.9	155.0	168.7	171.2	240.3	308.7	99
6	0.65	37.1	38.5	68.0	100.0	84.0	87.2	138.3	148.8	150.7	161.5	173.4	177.0	249.0	326.1	92
7	0.50	36.3	38.0	66.1	96.7	82.4	86.2	133.2	143.7	146.0	157.1	168.0	172.5	237.6	305.7	103

---

In order to define in a more precise way the failure of all theoretical methods it is convenient to make some considerations. Let us start with the UHF results; here the calculated values for a given compound arising from the AE and ECP calculations are almost the same and even the effect of the basis set is almost negligible since going from the LANL2DZ to the LANL2TZ changes the calculated values by less than 2 cm⁻¹. This is consistent with the fact that UHF neglects correlation and that the main effect of increasing the basis set would be precisely in the description of the correlation effects. This is obvious in the case in which electron correlation is accounted for in a configuration interaction type wave function. In fact, DFT calculations with these two basis sets exhibit significant differences and, in the case of the LANL2DZ, deviates too much from the AE values. This is clearly an artifact of the limited basis set and will no longer be commented here. Let us now discuss the results obtained with the popular B3LYP functional which contains a 20% of Fock exchange and which is known to overestimate the magnetic coupling constant of antiferromagnetic Cu(II) dinuclear compounds by a factor of ∼2, provided the proper mapping (cf.eqn (2)) is used.^15,30 Results in Table 3 indicate that B3LYP calculated J values obtained at the AE level with the small core ECP and a triple-ζ valence basis set for the Cu atoms—hereafter referred to as ECP—are almost the same differing by at most 4 cm⁻¹ or 2%. However, the calculated values are significantly larger than the experimental values although, at variance of antiferromagnetic dinuclear Cu(II) compounds the deviation factor varies from 2.2 to 1.5. Interestingly, the M06 predicted values are much larger and, surprisingly, AE and ECP predicted values differ by a larger amount of ∼60 cm⁻¹. There is no clear explanation for these trends since M06 and B3LYP contain a similar amount of Fock exchange (27% and 20%, respectively) and one could perhaps conclude that these differences are a result of the parametrization of the M06 functional. This hypothesis seems to be confirmed by analysis of the results obtained by the BHHLYP and M06-2X functionals, containing 50% and 54% Fock exchange respectively. The BHHLYP calculated magnetic coupling constant values at the AE and ECP levels, as in the case of B3LYP, almost coincide with differences of at most ∼2 cm⁻¹. In addition, these calculated values are those closest to the experimental ones which, again, is at variance of existing experience with the family of antiferromagnetic dinuclear Cu(II) complexes. Interestingly, the values predicted by the M06-2X functional are almost in the experimental range but only when considering the results from ECP calculations which, as in the case of the M06 discussed above, deviate from the AE by ∼30–40 cm⁻¹. The difference between AE and ECP calculated values in the M06 and M06-2X functionals remains difficult to understand. Finally, we discuss the HSE and LC-ωPBE short- and long-range separated functionals which, for the dinuclear Cu(II) complexes database investigated up to now, provide the most accurate results in terms of agreement with experiment.^31,32 Results in Table 3 show that also here results obtained at the AE and ECP levels deviate although by ∼10–15 cm⁻¹, this is no doubt less than in the case of the M06 and M06-2X but still noticeable. Here, one will be tempted to attribute this difference to the range separation parameter which, as shown by Phillips and Peralta,³² has a significant influence on the calculated results. In the best scenario, the range separated functionals deviate from experiment by 30%.

The fact that exchange–correlation functionals that provide an almost quantitative description of antiferromagnetic compounds fail to describe the differences exhibited along a series of ferromagnetic dinuclear Cu(II) complexes is likely to be due to the different types of electronic correlation effects governing the magnetic coupling. In the case of antiferromagnetic compounds, the largest contributions correspond to metal to metal and metal to ligand excitations. The first ones correspond to the well-known superexchange mechanism^39,40 which appear already at the CASSCF level and are essentially the result of non-dynamical correlation. The second ones involve double excitations from the reference CASSCF wave function to the virtual orbitals^41,42 and are described reasonably well by second order perturbation theory based methods,⁴³ although one must also be aware of possible artifacts due to the slow convergence of the perturbation series.⁴⁴ In the case of ferromagnetic compounds, the main contribution comes from direct exchange^41,42 and it is necessary to go well beyond double excitation from the reference space to improve the description. It is likely that this is the origin of the difficulties of the present exchange–correlation functionals in describing ferromagnetic interactions.

5. Conclusions

A new series of seven dinuclear Cu(II) compounds with a common triple bridge consisting of hydroxo, aquo and carboxylato ligands has been synthesized, the crystal structures were solved and the magnetic properties studied by EPR and magnetic susceptibility measurements as a function of temperature. The seven compounds thus obtained exhibit ferromagnetic coupling which is a consequence of the topology introduced by the type of bridging ligands as previously shown.^10–12 Nevertheless, the magnetic coupling constant J between the Cu centers spans a rather broad range from 73 to 104 cm⁻¹ which is clearly governed by the different external ligands. These affect the Cu⋯Cu distance and the Cu–OH–Cu bonding angle which indeed appear to be reasonable structural parameters defining magnetostructural correlations. Nevertheless, these trends are far from being quantitative.

The magnetic coupling in these triple bridged dinuclear compounds has been examined by a series of density functional methods going from simple hybrids such as B3LYP and BHHLYP to the M06 and M06-2X meta-hybrid and including also the HSE and LC-ωPBE range separated functionals. Interestingly, all these methods consistently predict the compounds to be ferromagnetic but all fail to reproduce the variation from compound to compound. In fact, for a given functional, the calculated J values along the series are almost constant and, in some cases very far away from experiment. The best results are provided by the BHHLYP functional where results obtained at the AE and ECP levels are also close to each other. The M06-2X functional, which contains a similar amount of Fock exchange, also predicts values in the experimental range although here the AE and ECP calculated values differ by a noticeable amount. The popular B3LYP functional largely overestimates J and this is also the behavior of M06 which contains a similar amount of Fock exchange. In addition, M06 calculated values depend on whether the Cu core electrons are treated with AE or with a small core ECP. This is similar to the behavior described above for the M06-2X and the origin remains unclear. Finally, the HSE and LC-ωPBE range separated functionals which have found to perform the best in previous work dealing with a family of compounds spanning a broad range of values, from moderately ferromagnetic to strong antiferromagnetic, fail to reproduce the order of magnitude of J for the present new compounds. Furthermore, AE and ECP values obtained with the range separated functionals differ, which may be due to the inadequacy of the standard parameter governing range separation.

Therefore, the most important conclusion of the present work is that while the different exchange–correlation functionals explored in this work to investigate the magnetic coupling constant of the new ferromagnetic Cu(II) dinuclear compounds properly predict the qualitative nature of the experimental coupling, none of them is able to reproduce the trend in ferromagnetism along the series, and only BHHLYP predicts values in the experimental range. It is likely that the origin of the difficulties of the present exchange–correlation functionals in describing ferromagnetic interactions is due to the fact that a proper description in terms of wave function based methods requires including higher order terms in the perturbation treatment or, equivalently, to go beyond double excitations out of the CASSCF reference wave function defined by the magnetic orbitals only.⁴⁵ Clearly, the current density functional needs to be further improved to be able to properly describe ferromagnetism. The present series of compounds provides an excellent playground to test new and improved functionals.

Acknowledgements

Financial support has been provided by the Spanish MICINN (grant FIS2008-02238), Generalitat de Catalunya (grants 2009SGR1041 and XRQTC), The Thailand Research Fund, The Royal Golden Jubilee PhD Program (Grant No. PHD/0234/2550), the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission, through the Advanced Functional Materials Cluster of Khon Kaen University and the Center of Excellence for Innovation in Chemistry (PERCH-CIC), Office of the Higher Education Commission, Ministry of Education. Part of the computational time has been provided by the Centre de Supercomputació de Catalunya (CESCA) which is also gratefully acknowledged. F.I. acknowledges additional support through the ICREA Academia award for excellence in research.

References

1. J. R. Friedman, M. P. Sarachik, J. Tejada and R. Ziolo, Phys. Rev. Lett., 1996, 76, 3830.
2. G. L. J. A. Rikken and E. Raupach, Nature, 2000, 405, 932.
3. S. Tanase and J. Reedijk, Coord. Chem. Rev., 2006, 250, 2501.
4. O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993.
5. O. Kahn, Adv. Inorg. Chem., 1996, 43, 179.
6. G. Christou, S. P. Perlepes, E. Libby, K. Folting, J. C. Huffman, R. J. Webb and D. N. Hendrickson, Inorg. Chem., 1990, 29, 3657.
7. S. Youngme, C. Chailuecha, G. A. van Albada, C. Pakawatchai, N. Chaichit and J. Reedijk, Inorg. Chim. Acta, 2004, 357, 2532.
8. S. Youngme, C. Chailuecha, G. A. van Albada, C. Pakawatchai, N. Chaichit and J. Reedijk, Inorg. Chim. Acta, 2005, 358, 1068.
9. C. Chailuecha, S. Youngme, C. Pakawatchai, N. Chaichit, G. A. van Albada and J. Reedijk, Inorg. Chim. Acta, 2006, 359, 4168.
10. S. Youngme, J. Phatchimkun, N. Wannarit, N. Chaichit, S. Meejoo, G. A. van Albada and J. Reedijk, Polyhedron, 2008, 27, 304.
11. R. Costa, I. de P. R. Moreira, S. Youngme, K. Siriwong, N. Wannarit and F. Illas, Inorg. Chem., 2010, 49, 285.
12. N. Wannarit, K. Siriwong, N. Chaichit, S. Youngme, R. Costa, I. de P. R. Moreira and F. Illas, Inorg. Chem., 2011, 50, 10648.
13. A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349.
14. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109.
15. I. de P. R. Moreira and F. Illas, Phys. Chem. Chem. Phys., 2006, 8, 1645 and references therein.
16. Siemens SAINT, Version 4 Software Reference Manual, Siemens Analytical X-ray Systems, Inc., Madison, WI, USA, 1996.
17. G. M. Sheldrick, SADABS: Program for Empirical Absorption correction of Area Detector Data, University of Göttingen, Göttingen, Germany, 1996.
18. Bruker, XSHELL, Version 6.12 Reference Manual, Bruker AXS, Inc., Madison, WI, USA, 1999.
19. Basis set parameters have been extracted from the Basis Set Exchange web page at https://bse.pnl.gov/bse/portal.
20. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
21. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
22. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
23. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
25. J. Heyd, G. E. Scuseria and M. Ernzernhof, J. Chem. Phys., 2003, 518, 8207 bid. 2006, 124, 219906(E).
26. F. Illas, I. de P. R. Moreira, J. M. Bofill and M. Filatov, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 132414.
27. F. Illas, I. de P. R. Moreira, J. M. Bofill and M. Filatov, Theor. Chem. Acc., 2006, 115, 587.
28. I. de P. R. Moreira, R. Costa, M. Filatov and F. Illas, J. Chem. Theory Comput., 2007, 3, 764.
29. R. Caballol, O. Castell, F. Illas, J. P. Malrieu and I. de P. R. Moreira, J. Phys. Chem. A, 1997, 101, 7860.
30. R. Valero, R. Costa, I. de P. R. Moreira, D. G. Truhlar and F. Illas, J. Chem. Phys., 2008, 128, 114103.
31. P. Rivero, I. de P. R. Moreira, F. Illas and G. E. Scuseria, J. Chem. Phys., 2008, 129, 184110.
32. J. J. Phillips and J. E. Peralta, J. Chem. Phys., 2011, 134, 034108.
33. E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297.
34. E. Ruiz, J. Comput. Chem., 2011, 32, 1998.
35. R. Valero, F. Illas and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3523.
36. M. J. Frisch, et al., Gaussian 09, Revision A., 1, Gaussian, Inc., Wallingford CT, 2009.
37. A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer-Verlag, Berlin and Heidelberg, 1990.
38. B. Bleaney and K. D. Bowers, Proc. R. Soc. London, Ser. A, 1952, 97, 451.
39. P. W. Anderson, Phys. Rev., 1950, 79, 350.
40. P. W. Anderson, in Theory of the Magnetic Interaction: Exchange in Insulators and Superconductors, ed. F. Turnbull and F. Seitz, Academic Press, New York, 1963, vol. 14, p. 99.
41. C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 2728.
42. C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 3985.
43. C. de Graaf, C. Sousa, I. de P.R. Moreira and F. Illas, J. Phys. Chem. A, 2001, 105, 11371.
44. C. J. Calzado, C. Angeli, D. Taratiel, R. Caballol and J. P. Malrieu, J. Chem. Phys., 2009, 131, 044327.
45. Ph. de Loth, P. Karafiloglou, J. P. Daudey and O. Kahn, J. Am. Chem. Soc., 1988, 110, 76.

---

Footnote

† Electronic supplementary information (ESI) available. Synthesis conditions, structural and magnetic data for compounds 2–7 are provided. In addition CCDC numbers 907230–907236 contain the supplementary crystallographic data for compounds 1–7. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2cp43839a

---