 Open Access Article
Open Access ArticleUltracold fluorine production via Doppler cooled BeF
Ian C.
Lane
*
School of Chemistry and Chemical Engineering, Queen's University Belfast, Stranmillis Road, Belfast, UK BT9 5AG. E-mail: i.lane@qub.ac.uk
First published on 17th September 2012
Abstract
Large parts of the periodic table cannot be cooled by current laser-based methods. We investigate whether zero energy fragmentation of laser cooled fluorides is a potential source of ultracold fluorine atoms. We report new ab initio calculations on the lowest electronic states of the BeF diatomic molecule including spin–orbit coupling, the calculated minima for the valence electronic states being within 1 pm of the spectroscopic values. A four colour cooling scheme based on the A2Π ← X2Σ+ transition is shown to be feasible for this molecule. Multi-Reference Configuration Interaction (MRCI) potentials of the lowest energy Rydberg states are reported for the first time and found to be in good agreement with experimental data. A series of multi-pulse excitation schemes from a single rovibrational level of the cooled molecule are proposed to produce cold fluorine atoms.
1. Introduction
Ultracold molecules and atoms offer a unique opportunity to study chemical reactions at the quantum state level. Attractions include the ability to select individual rovibrational states of the reagents, the elimination of translational energy spread and the control of product quantum states using external fields. However, there has only been one reactive collision studied in this way.1 Problems with exploiting these reagents include the difficulty in cooling many of the elemental groups of the periodic table. For example, reactions involving halogen atoms are very rapid2 but Doppler cooling such atoms would require continuous-wave lasers operating in the VUV or XUV at milliWatt powers. Another practical problem concerns the very reactivity of many p-block elements that naturally makes them of special interest to chemists. This aggressive behaviour makes them unsuitable for the high vacuum apparatus used in today's cold atom experiments.3 In particular, fluorine is known to ruin the non-evaporated getter (NEG) surfaces of modern UHV pumps. What is required is a method to transport these reactive species to the centre of a trap without destroying the chamber, whereupon they can be released for study. Delivering the halogens in the form of a trapped, ultracold, parent molecular gas prior to in situ laser fragmentation elegantly resolves both these problems.Trapped ultracold fluorine atoms could be used as a source of highly reactive atoms for nanolithography. Wright and Lane4 have proposed studying the reaction of vibrationally excited ultracold Li2 dimers with fluorine atoms and have suggested quantum state selection of the reaction products is possible by selecting the initial vibrational state. Unfortunately, the production of trapped, cold halogen atoms presents perhaps one of the stiffest challenges for ultracold science. In particular, fluorine atoms are impossible to laser cool with current techniques as the lowest electric-dipole spin-allowed transition5 3s2P3/2 ← 2p4 2P3/2 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4731 cm−1) lies below 96 nm, a prohibitively short wavelength for a continuous wave laser. Furthermore, a single photon at this energy would impart a considerable momentum kick during spontaneous emission, leading to a significant recoil temperature. Hopes of using excited fluorine atoms and the 3p4D7/20 ← 3s4P5/2 transition at 685 nm were dashed6 by the relatively short lifetime (3.7 μs) of the metastable 3s4P5/2 state. Frustratingly, this lifetime is also too long for efficient optical cycling from the ground state. However, following the recent demonstration by Shuman et al. of Doppler cooled diatomic SrF7 it will not be long before trapped, ultracold fluorides can be prepared in the laboratory. Zero-energy fragmentation of such diatomics is a potential source of ultracold and trapped fluorine atoms.
4731 cm−1) lies below 96 nm, a prohibitively short wavelength for a continuous wave laser. Furthermore, a single photon at this energy would impart a considerable momentum kick during spontaneous emission, leading to a significant recoil temperature. Hopes of using excited fluorine atoms and the 3p4D7/20 ← 3s4P5/2 transition at 685 nm were dashed6 by the relatively short lifetime (3.7 μs) of the metastable 3s4P5/2 state. Frustratingly, this lifetime is also too long for efficient optical cycling from the ground state. However, following the recent demonstration by Shuman et al. of Doppler cooled diatomic SrF7 it will not be long before trapped, ultracold fluorides can be prepared in the laboratory. Zero-energy fragmentation of such diatomics is a potential source of ultracold and trapped fluorine atoms.
The alkaline earth diatomics are ionic compounds or, more precisely, they have an ion-pair potential as the lowest electronic state. SrF has a Franck–Condon (FC) factor between the lowest vibrational levels of the A2Π ← X2Σ+ transition8 of f00 > 0.98 making this a highly diagonal transition. Nevertheless, three vibronic transitions need to be pumped in order to close the cooling cycle. Ab initio work by Ornellas9 calculated the corresponding FC factors for BeF but revealed that the f00 value is approximately 0.90, much lower than SrF and consequently superficially appears much less suitable for cooling. On the contrary, we demonstrate that there is a viable laser cooling scheme based on four vibronic transitions similar to the one successfully deployed for SrF.
Unlike Doppler cooling of simple atoms, direct laser cooling of a molecular gas is complicated by its initial temperature, not because of the Maxwell Boltzmann velocities but the Boltzmann distribution of internal states. The larger energy separations between rovibrational levels in BeF will maximise the population in low v and J states when compared with heavier analogs like SrF or BaF. From a kinematic perspective, BeF is also the most attractive parent for the production of ultracold fluorine because its partner fragment has a smaller mass, and therefore will extract the majority of any surplus centre-of-mass dissociation energy. However, a viable transition pathway must be found to link the lowest vibrational levels of the ground state with the long range vibrational states at the dissociation limit. Such states form the basis of the Feshbach resonances required to access the continuum scattering states corresponding to the free atoms. Realistically, this population transfer must be done through an excited electronic state (to effect a great change in the internuclear separation) and key requirements are good FC factors and practical excitation energies for the efficient transfer of internal population. In this paper we use ab initio quantum chemistry to develop full potential curves of the lowest electronic states in BeF and we identify a viable fragmentation scheme to produce zero-energy fluorine atoms suitable for trapping.
Most of the detailed spectroscopic information of this fluoride is relatively dated and cannot match the quality of modern high resolution measurements. Datta10 first reported its spectra in 1922, identifying a bandhead at 309 nm with further bands extending to shorter wavelengths. Further analysis by Jenkins11 proved the emission was 2Π → 2Σ+ and measured the excited state bond length as 1.39 Å. The author assigned the spin–orbit A2Π1/2 state as lowest in energy but a later analysis of Λ-coupling constants by Walker and Barrow12 suggested that it is the A2Π3/2 component that is lower. This issue was finally resolved by theoretical analysis13 based on ab initio quantum chemistry. In 1965 Rao et al. reported14 emission spectra corresponding to the C2Σ+ → A2Π transition while a VUV study of the B2Σ+and C2Σ+ electronic states was published two years later by Novikov and Gurvich.15 The spectroscopy of the B2Σ+state was studied in further detail by Tai and Verma16 but only the lowest three vibrational levels have been interrogated in any great detail. The Russian study also reported red degraded bands at 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 66
000 cm−1 and 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 attributed to a pair of excited 2Π states but Tai and Verma indicated they did not observe these bands in their experiments.
000 cm−1 attributed to a pair of excited 2Π states but Tai and Verma indicated they did not observe these bands in their experiments.
Quantum chemistry is used here to address a number of key issues regarding the proposed method to form cold atoms, such as the availability of a barrier-less potential suitable for zero-energy fragmentation and whether the highest vibrational levels of this potential can be efficiently populated via accessible optical transitions. To answer these questions accurate potentials are naturally required but an additional motivation for this study is to provide generic valence potentials useful for the interpretation of the other alkaline fluorides too. The alkaline earth metals are not well served by the current generation of basis sets (even the best Be set is relatively small compared to other second row elements) and thus the lightest molecule in the series is the logical choice for reliable potentials.
Previous theoretical work has naturally concentrated on the lowest pair of electronic states. In particular, there has been some debate on the strength of the chemical bond and on the nature of the spin–orbit coupling in the A2Π state. Roach and Kuntz calculated a dissociation energy De of 3.94 eV17 for the X2Σ+ state which differed considerably from the experimental values of Hildenbrand and Murad18 (5.85 eV) and Farber and Srivastava19 (6.26 eV). A recent CCSD(T) study by Dixon is currently the most reliable theoretical study20 and reports the dissociation energy as 5.87 eV. Walker and Richards21 demonstrated that the observed spin–orbit coupling is consistent22 with a predominantly π4π configuration in the A2Π state with a considerable π3σ2 contribution and later work by Cooper, Prosser and Richards13 reconciled this picture with the Λ-coupling constants observed by Walker and Barrow. The spin–orbit coupling was later addressed at the MRCI level by Marian23 who also calculated constants for the D2Π state. The MRCI method also formed the basis of later studies on the dissociation energy24 and dipole moment25 of the X2Σ+ state. Such ab initio potentials were used by Ornellas et al. to calculate the ground26 and A2Π vibronic levels, rotational constants and lifetimes.27 The calculated FC factors suggest that the fundamental 0–0 transition has a much lower value than the equivalent vibronic transition in SrF. These calculations were repeated with better basis sets by Ornellas in 2005, confirming this result, while a V5Z/AV6Z study by Zhu et al. has recently been published.28 This final study also included the vibrational levels and spectroscopic constants of the B2Σ+ state but did not address transition dipoles or higher excited states. Previous theoretical studies have, in general, paid little attention to the excited state asymptote Be(3P) + F(2P). The only published potentials that illustrate this asymptote are those from Prosser and Richards,29 which are only computed at the Hartree–Fock level. Populating a vibronic level close to this dissociation limit may be crucial to the production of cold fluorine and it is therefore necessary to identify if a suitable bound state is available.
2. Ab initio calculations
The electronic states are found using Complete Active Space SCF (CASSCF) wavefunctions30 based on the valence orbital space 6a1, 2b1 and 2b2 (6220), though the lowest two a1 orbitals are treated as the core throughout. Dynamic electron correlation was calculated by Multi-Reference Configuration Interaction31 (MRCI), using the relaxed Davidson correction32 throughout. These calculations were augmented with additional points using the larger active spaces 7320 (for the Rydberg component of the Π states) and 8220 (for the Σ+ states). Only states of doublet multiplicity were calculated, and since all the 2Σ− valence states are repulsive they are not discussed further. Currently, the largest available correlation consistent basis set33 for Be is cc-pV5Z (V5Z) which lacks the diffuse functions for an accurate description of excited atomic levels of Be. The augmented cc-pV6Z (AV6Z) basis set is used for F and all calculations were performed using the MOLPRO suite of programs.343. Results
(a) A2Π ← X2Σ+ transition and laser cooling cycle
The ab initio potentials obtained are shown in Fig. 1. The ab initio data points were fitted using the LEVEL program (version 8.0)35 to obtain the bound rovibronic levels, spectroscopic constants (Table 1), FC factors and radiative lifetimes. The calculated v = 1–v = 0 energy separation in the X state is 1235.11 cm−1 in excellent agreement with the experimental value16 of 1246.70 cm−1. A similar relative error is found in the values of T00, where the experimental value is 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 cm−1 and the calculated one is 33
187 cm−1 and the calculated one is 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 cm−1 (0.9% discrepancy). The discrepancies between the calculated and experimental re values are <0.01 Å. The calculated bond dissociation energy D0(X2Σ+) is 47
511 cm−1 (0.9% discrepancy). The discrepancies between the calculated and experimental re values are <0.01 Å. The calculated bond dissociation energy D0(X2Σ+) is 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 cm−1 (5.838 eV) and D0(A2Π) is 13
092 cm−1 (5.838 eV) and D0(A2Π) is 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578 cm−1 (1.683 eV), the former within 1% of a recent high level CCSD(T) based calculation (47
578 cm−1 (1.683 eV), the former within 1% of a recent high level CCSD(T) based calculation (47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 cm−1) and smaller than the value reported by Zhu et al. Consistent with this, we find that the highest computed vibrational level is v = 64, within 1.5 cm−1 of the dissociation limit, rather lower than v = 74 reported in that work. Experimental X2Σ+ data only exists for vibrational levels up to v = 15 (17
350 cm−1) and smaller than the value reported by Zhu et al. Consistent with this, we find that the highest computed vibrational level is v = 64, within 1.5 cm−1 of the dissociation limit, rather lower than v = 74 reported in that work. Experimental X2Σ+ data only exists for vibrational levels up to v = 15 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 cm−1).
327 cm−1).
 | ||
Fig. 1 Valence MRCI potential energy curves of BeF calculated with V5Z basis set on Be and AV6Z basis set on F. Circles are ab initio points for 2Σ+ states and diamonds for 2Π. Be(23P) dissociation limit calculated as 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 cm−1 (experimental value 21 070 cm−1 (experimental value 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 cm−1) and Be(1P) as 43 980 cm−1) and Be(1P) as 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 cm−1 (experimental value 42 504 cm−1 (experimental value 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 cm−1). (b) Spin–orbit potentials associated with the fluorine ground state. 565 cm−1). (b) Spin–orbit potentials associated with the fluorine ground state. | ||
| BeF | T e (cm−1) | r e (Å) | v | T v (cm−1) | B v (cm−1) |
|---|---|---|---|---|---|
| a G. Tai and R. D. Verma, The UV Spectrum of BeF, J. Mol. Spec., 1995, 173, 1. b M. M. Novikov and L. U. Gurvich, Optics Spectrosc., 1966, 23, 173. c V. M. Tatevskii, L. N. Tunitskii and M. M. Novikov, Optika Spectrosk., 1958, 5, 520. d From r0 = 1.335. e Calculated as v = 6 (see text). | |||||
| X2Σ+ | 0 | 1.364 | 0 | 617.15[630.5]c | 1.4658[1.4801] |
| [1.3609] | 1 | 1852.26[1877.7]c | 1.4481[1.4625] | ||
| [1.3610]b | 2 | 3077.67[3106.7]c | 1.4312 | ||
| 3 | 4276.50[4317.5]c | 1.4157 | |||
| A2Π | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.8 542.8 |
1.399 | 0 | 588.45[585.6] | 1.4043[1.4115] |
[33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234] 234] |
[1.394] | 1 | 1755.74[1740.3] | 1.3887[1.3939] | |
| 2 | 2907.62 | 1.3706 | |||
| B2Σ+ | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182.8 182.8 |
1.334 | 0 | 680.88[777.63]a | 1.5347[1.5531]a |
[49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503.2]a 503.2]a |
[1.328]a,d | 1 | 1999.35[2113.84]a | 1.5090[1.5329]a | |
| 2e | 3293.69[3423.77]a | 1.4[1.5118]a | |||
| B2Σ+ (outer) | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117.8 117.8 |
2.775 | 0 | 201.8 | 0.362 |
| 1 | 600.6 | 0.368 | |||
| 2 | 993.2 | 0.373 | |||
| D2Π | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 249 |
2.015 | 0 | 520.4 | 0.6838 |
| 1 | 1476.6 | 0.7018 | |||
| C2Σ+ | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 295 295 |
1.324 | 0 | 736.4[652.5]a | 1.559[1.569]a |
[50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419] 419] |
[1.322]a | 1 | 2173.6[2049.4]a | 1.534[1.551]a | |
| 32Π | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612 612 |
1.340 | 0 | 821.0 | 1.541 |
| 1 | 2388.5 | 1.529 | |||
Like Ornellas et al., we calculate as many as 16 vibrational levels in the A2Π state, though only 13 have been experimentally observed. We find that v = 13 is the last A2Π vibrational level below the Be(1S) + F(2P) asymptote. Unlike the earlier study, we also computed the spin–orbit coupling in the A2Π state and used the lower component to determine the FC factors with the ground state. These are in good agreement with Ornellas (Fig. 2a) but despite the relatively small value of f00, a four colour laser cooling scheme can be found thanks to the additional spontaneous emission channels being tightly clustered around the 0–0 transition (Fig. 2b). The sum of all transitions beyond v = 3 is <6 × 10−5, similar to SrF. Fig. 2a also demonstrates the relative strengths of transition with Δv = 0, ±1 and ±2, the latter clearly increasing at higher v′′. The relative strength of the Δv = 0 transitions falls to a minimum for v′′ = 8 before rising again. The relative weakness of Δv = ±3 or higher explains why vibrational data on the X2Σ+ state is limited to v = 15 as the A2Π ← X2Σ+ transition is used in such studies. Large FC factors, however, are not enough to ensure a good cooling candidate as the rate of optical cycling must also be significant (105–108 s−1) to produce a strong Doppler force. The line strength (Einstein A coefficient) for the primary cooling transition is 1.35 × 108 s−1, giving a lifetime of 7.9 ns (about 1/3 that of the transition in SrF).
 | ||
| Fig. 2 (a) Calculated Franck–Condon factors (FC factors) in BeF for the lowest ten vibrational levels of the cooling transition A2Π ← X2Σ+ transition. Diagonal transitions in blue, Δv = ±1 in green and Δv = ±2 in red. (b) Proposed laser cooling scheme for BeF using the A2Π ← X2Σ+ transition. For each vibronic transition, only one rotational transition needs to be excited. The decay pathways are shown as single headed arrows while the cooling frequencies are represented by double headed ones. The Franck–Condon factors (FC factors) are the ones calculated in the present study. Both Be (I = 3/2) and F (I = 1/2) have nuclear spin leading to hyperfine structure (not illustrated). For each upper vibrational level, the sums over the remaining FC factors are f03+ < 0.00006 and f13+ < 0.0025. | ||
The hyperfine structure of 9BeF (100% abundance) is more complex than in 88SrF (82.5% of a natural sample) because the former metal has a nuclear spin of I = 3/2 (the same as 135Ba and 137Ba36) and this will complicate the laser cooling process. The rovibronic transitions in BeF can be labeled 2Π(case aαJ) ← 2Σ+(case bβJ) and the Fermi contact term bF in BeF37 has been reported as bF(Be) = 0.0098 cm−1. There are 7 hyperfine levels associated with 2Σ+(J = 3/2) N = 1 and 4 with 2Σ+(J = 1/2) N = 1 and these levels need to be pumped to complete the cooling cycle. In the excited state, an additional complication is the splitting of each rotational level (Λ-type doubling) as a consequence of the non-zero orbital electronic motion Λ. However, only one component of the Λ-doublet is populated during the cooling cycle (parity selection rule) and the hyperfine energy shifts can be compensated using acousto-optic modulators. In order to maximize the density of cooled molecules, a small internal population spread amongst the vibrational and rotational levels is desirable. Thus, perhaps a little paradoxically, it is the initial internal temperature that has a greater influence on the cooling of molecules than the translational temperature. Buffer gas cooling techniques can presently create intense beams (1011 cm−3 density) of even large molecules like naphthalene at temperatures of 6 K.38
Laser cooling creates a translationally cold molecule and ergo (almost) zero energy fragmentation of such molecules in a trap will retain the initial thermal energy of the ultracold parents. Such a scheme has been proposed by Wells and Lane for the production of C atoms from laser cooled CH radicals.39 The long range hyperfine structure in BeF is determined by the splitting in the ground 2P1/2 spin–orbit state of fluorine (I = 1/2, ΔE = 4.02 GHz) and its coupling with the nuclear spin on Be. The result is four hyperfine levels (F = 5/2, 3/2, 3/2 and 1/2) and their presence opens the door to populating a quasi-bound level above the lowest dissociation limit that can fragment into free atoms. It is necessary, therefore, to transfer the molecular population efficiently into this state from one of the vibrational levels populated via the laser cooling process (we chose v′′ = 2 for this study). A crucial issue is the long range behaviour of the potentials, since the presence of a barrier along the dissociation path will lead to unavoidable heating of the gas as the excess energy required to climb the barrier will have to be released in the form of kinetic energy in the atomic fragments. Therefore, we computed the spin orbit coupling for the molecular potentials correlated to the ground asymptote, using a VQZ basis set on each atom. By including just the X2Σ+ and A2Π states in the calculation we found poor agreement between the long range (50 Å) splitting and the known value for atomic F (286 cm−1versus the experimental value of 404.141 cm−1), but by extending the calculation to include the B2Σ+ and D2Π states as well, we calculated a value of 403.01 cm−1, in excellent agreement.40 The long range energies with spin–orbit coupling are shown in Fig. 1b and reveal no evidence of a barrier on the X2Σ+ potential curve.
(b) STIRAP population transfer via B2Σ+ state
Stimulated Rapid Adiabatic Passage41 (STIRAP), a fully coherent optical procedure for population transfer, has been used previously for the formation of ultracold molecules42 from cold atoms. For that application, a molecular rovibrational level above the atomic asymptote must be brought into resonance with the kinetic energy of colliding laser cooled atoms (creating a Feshbach resonance). A counterintuitive sequence of optical pulses then transfers the population from the quasi-bound state to a deeply bound rovibrational level. The STIRAP method produces low loss rates as adiabatic passage suppresses any decay via the intermediate excited state as demonstrated by Ye43 and co-workers for RbK. By reversing the pulse sequence and so using STIRAP to transfer molecules between the bound state and asymptote, microscopic reversibility ensures that zero-energy (centre of mass frame) atomic products can be formed with high transfer efficiency from a single quantum state in an ultracold molecule. While STIRAP has not been applied directly in this way, experiments44 with Cs2 by Danzl et al. have clearly demonstrated efficient population transfer back into a Feshbach resonance. It is important to note that we are not proposing excitation into a continuum of scattering states, but into a quasi-bound rovibrational level, the coupling of which with the continuum of atoms can be adjusted by external fields. The initial single quantum level of the ultracold molecule naturally does not have to be formed itself by STIRAP association of atoms, and the proposed method involves initial state preparation by direct laser cooling of a molecule like BeF.The states relevant for STIRAP production of fluorine atoms are presented in Fig. 3a, where the highest calculated vibrational states are shown for the X2Σ+ and B2Σ+ states (in both cases this is, coincidently, v = 64). In our study we use the calculated excited vibrational levels as surrogates for the Feshbach states (dominated by long-range dispersion forces) to explore possible excitation pathways and decay modes for the highly excited vibrational levels. For example, direct excitation to the highest vibrational level of the B2Σ+ state would appear to be a simple way for creating cold ground state fluorine atoms because although it is a higher energy asymptote it is the Be atom alone that is formed in an electronically excited state. Sadly, calculation of the spontaneous emission rate from B2Σ+v′ = 64 (Fig. 4a) reveals that the Feshbach will decay rapidly by photon emission rather than fragmentation into cold atoms. The corresponding Feshbach levels along the ground asymptote are the most suitable, and clearly only the X2Σ+ potential lacks a barrier. One complication is that since efficient laser cooling of molecules requires an excited state (here A2Π) below the lowest asymptote (to prevent predissociation destroying the cooling cycle), spontaneous emission from the threshold vibrational level back into this state is also unavoidable. However, we calculated the total spontaneous emission from X2Σ+v = 64 into the energetically accessible vibrational levels of the A2Π state as just
 | (1) |
 | ||
| Fig. 3 STIRAP pathway to produce cold fluorine atoms via the B2Σ+ state. (a) The states relevant for this study. In addition to those calculated, schematic versions of the two observed Rydberg states observed by Gurvich are shown, and the ground state of the BeF+ ion using the calculated dissociation energy reported by Ornellas et al. Also shown is the ion-pair asymptote Be+(2S) + F−(1S); (b) Four pulse scheme through D2Π and B2Σ+ states. The PUMP pulses are represented by the filled arrows. | ||
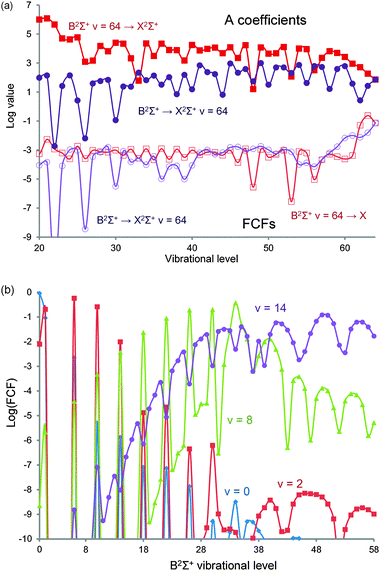 | ||
| Fig. 4 Calculated Franck–Condon factors (FC factors) in BeF as a function of vibrational quantum number. (a) The FC factors and A coefficients for vibronic transitions involving the v = 64 states of the B2Σ+ ↔ X2Σ+ transition. (b) The FC factors for the B2Σ+ ← X2Σ+ transition for v = 0, 2 and 14 for all upper vibrational levels up to v = 64. Note the logarithmic scale used in both plots. | ||
The B2Σ+ab initio points are fitted to a double well potential with the lowest vibrational level corresponding to a bound state in the inner well. Above v = 1 vibrational levels corresponding to the outer potential well appear and our calculated v = 2 level is consequently the lowest level of this potential minimum. The different states can be identified by the change in the rotational constant (from ≈1.5 cm−1 to ≈0.38 cm−1). The B2Σ+ and C2Σ+states were calculated with an active orbital space including two additional non-valence a1 orbitals (8220) because of the presence of Rydberg excitations. Ab initio quantum chemistry is less suitable for the Rydberg potentials, although we have expanded the active space to calculate the lowest energy examples. The accuracy achieved is not as strong as for the valence states as can be clearly seen in Table 1 comparing the calculated potentials for the B2Σ+ (valence) and C2Σ+ (Rydberg) states with the experimental data. The present calculations could be improved by using additional diffuse orbitals in the atomic basis sets. Nevertheless, the calculations of the excited C2Σ+ state are both consistent with the experimental results of Novikov and Gurvich15 and with X2Σ+ and C2Σ+ states belonging to the ‘s’2Σ+ series of Rydberg states. Consequently, the B2Σ+ state is the lowest member of the ‘p’2Σ+ series.45
As demonstrated in Fig. 4b, the FC factors from the ground state are negligible to the lowest vibrational states of this outer well. The sharp peaks in the figure correspond to vibronic transitions between the X2Σ+ state and the inner B2Σ+ potential. Clearly for efficient population transfer a large FC factor is desirable and unfortunately excitation from any of the vibrational states populated through the cooling cycle is very small. However, a six-order of magnitude improvement is achieved by starting from the v = 8 vibrational level (FC factor ≈ 0.002) or higher. To transfer vibrational population between vibrational levels in the X2Σ+ state a pair of STIRAP pulses are used, though in the illustrated scheme (Fig. 3b) the higher X2Σ+v = 14 level is populated via the excited D2Π v = 9 level. To populate a level close to the lowest asymptote, however, we find that the A coefficients reach a maximum (Fig. 4a) around B2Σ+v = 45 → X2Σ+v = 64 despite the fact that the FC factors improve all the way to the highest levels of the B2Σ+ state (0.1 for B2Σ+v = 64 → X2Σ+v = 64). This reflects the fact that the transition dipole moment falls rapidly with internuclear distance as the atomic transition correlated to these molecular states is spin forbidden (Be(3P) → Be(1S) with an estimated decay rate58 of just 0.4 s−1). This peak rate is a fairly modest 9.2 × 102 s−1. The A coefficients starting from levels in the D2Π state are even smaller, but this time the problem is the poor FC factors, not the transition dipole. We can understand this if we consider that the ion-pair potentials that form the minima of both the X2Σ+ and A2Π states are very similar, thus the vibrational quanta in each state must be similar to maximize the wavefunction overlap.
It should be remembered, however, that it is not the A coefficient that is directly relevant but the B coefficient as STIRAP involves a stimulated, not spontaneous, emission step. The two emission rates are naturally related, though the B coefficient can be defined in a number of slightly different forms. As experimentalists measure irradiance per unit area (typically cm−2) rather than unit volume we adopt a modified version of the definition popularised by Herzberg
 | (2) |
| Energy (cm−1) [λ (nm)] | A coefficient (s−1) | FC factor | B coefficient (J−1 (GHz) cm2) | |
|---|---|---|---|---|
| Scheme 1 | ||||
| D2Π ← X2Σ+ | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 299 |
1.8 × 106 | 3.2 × 10−2 | 5.9 × 1014 |
| 9 ← 2 | [174.6] | |||
| D2Π → X2Σ+ | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091 091 |
9.7 × 105 | 1.5 × 10−2 | 9.2 × 1014 |
| 9 → 14 | [217.0] | |||
| B2Σ+ ← X2Σ+ | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590 590 |
1.3 × 106 | 1.8 × 10−3 | 7.5 × 1014 |
| 45 ← 14 | [205.8] | |||
| B2Σ+ → X2Σ+ | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 013 |
9.2 × 102 | 1.4 × 10−3 | 6.8 × 1012 |
| 45 → 64 | [587.9] | |||
| Scheme 2 | ||||
| 42Π ← X2Σ+ | 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
5.3 × 106 | 2.8 × 10−2 | 5.0 × 1014 |
| 27 ← 2 | [115.8] | |||
| 42Π → X2Σ+ | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 552 |
6.3 × 105 | 2.6 × 10−3 | 5.3 × 1014 |
| 27 → 64 | [240.7] | |||
| Scheme 3 | ||||
| A2Π← X2Σ+ | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
7 × 106 | 1.9 × 10−1 | 1.0 × 1016 |
| 3 ← 2 | [289.8] | |||
| D2Π ← A2Π | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110 110 |
1.1 × 106 | 3.0 × 10−2 | 7.0 × 1015 |
| 6 ← 3 | [473.7] | |||
| D2Π → X2Σ+ | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
8.1 × 106 | 5.1 × 10−2 | 4.8 × 1015 |
| 6 → 10 | [214.0] | |||
| A2Π ← X2Σ+ | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 837 |
2.4 × 106 | 4 × 10−4 | 4.1 × 1015 |
| 10 ← 10 | [304.5] | |||
| B2Σ+ ← A2Π | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 278 |
5 × 105 | 7.0 × 10−2 | 3.6 × 1015 |
| 45 ← 10 | [493.1] | |||
| B2Σ+ → X2Σ+ | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 013 |
9.2 × 102 | 1.4 × 10−3 | 6.8 × 1012 |
| 45 → 64 | [587.9] | |||
(c) STIRAP population transfer via 42Π state
An alternative STIRAP scheme involving the 42Π state was also explored to circumvent the relatively weak transition dipole from the vibrational levels close to the 3P asymptote. To compute this state, a calculation of the lowest four 2Π states was conducted using a 7320 active space. At short range the second 2Π state is of Rydberg character, while at long range the 4th state is ion-pair in nature. The Rydberg component should have a strong absorption from the ground state but both the unconfirmed 2Π states observed by Novikov and Gurvich15 lie at a rather higher energy. In Fig. 1 and Table 1 we report this 32Π Rydberg potential as a bound state, analogous to the C2Π state in CaF, crossed by the inner wall of the lower ion-pair 2Π state. However, the lack of experimental evidence suggests that such a Rydberg potential may be very heavily predissociated, so in the rest of the paper it is treated as forming the inner part of the D2Π state.The 42Π state correlates to the Be(1P) atom product and therefore has a strong electric dipole transition with the ground state even at extended bond lengths. Transitions into X2Σ+v = 64 are strong and increase above v = 45 but as this transition is already very energetic (118 nm from X2Σ+v = 2) we use this state as a compromise (Fig. 5a). However a major difficulty arises from the high density of Rydberg states crossing this potential that will significantly increase the background coupling when compared to the B2Σ+ state. In Fig. 3 and 5 we have added a pair of schematic Rydberg potentials, based on our calculation for the lowest Rydberg, corresponding to those observed, exclusively to date, by Novikov and Gurvich. It should be noted that a vibrational progression was reported for both states so it appears that the predissociation suffered by these two states was not severe below the Be(3P) asymptote. Of more concern is the appearance of the ground potential of the BeF+ ion well below the 42Π state. We have modelled this using our Rydberg potential, the ionization energy of the Be atom and the dissociation energy (5.84 eV) calculated27 by Ornellas et al. Its presence will strongly reduce the efficiency of the STIRAP process and so the lower energy B2Σ+ state is preferred for population transfer to the asymptote of the X2Σ+ potential.
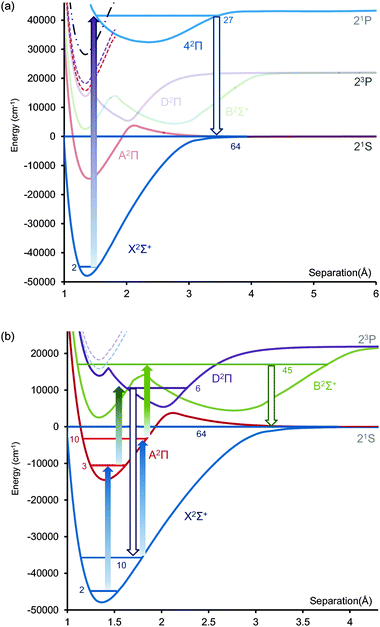 | ||
| Fig. 5 Alternative STIRAP pathways to produce cold fluorine atoms (the final destination state is a Feshbach state formed within the hyperfine structure of the lowest spin–orbit asymptote for the interaction of 9Be (1S0) and 19F (2P3/2) atoms). In the Hund's case (c) limit, the lowest state is J = 3/2. The nuclear spin on the 9Be atom is 3/2 and 1/2 on 19F producing hyperfine states F = 7/2, 5/2, 3/2 and 1/2. (a) Two pulse scheme with short wavelength (118 nm) pulse through the 42Π state; (b) 2 × 3-pulse scheme through D2Π and B2Σ+ states, using A2Π vibrational states as intermediate levels. The first group of pulses transfer population from X2Σ+v′′ = 2 to v′′ = 10. | ||
4. Discussion
(a) Technological requirements
The STIRAP fragmentation of ultracold BeF replaces the need to produce a high power, continuous wave laser source in the XUV with laser cooling at around 305 nm. Although the favoured STIRAP schemes involve the use of VUV light sources, the need for thousands of such photons for direct Doppler cooling has been replaced by, at most, a pair of laser pulses. In addition, even the shortest wavelength required in the STIRAP scheme here is significantly lower in energy than the F XUV cooling wavelength. Finally, while there is no known technology for the efficient production of a cw laser source in the XUV, the production of nanosecond pulses is possible in this wavelength region. Indeed, highly coherent, nanosecond XUV pulsed lasers have been developed for spectroscopy of atomic species such as He46 and molecules such as CO47 and N248 and operate at sub 100 nm wavelengths. These sources are based on sum-frequency generation in an intense beam of gas49 such as Xe, but the resulting pulse intensities are very low (0.01 μJ pulse−1). A tuneable VUV source operating over the range 110–170 nm has been developed that uses difference frequency generation in a similar arrangement50 and is capable of significantly higher pulse energies approaching 1 μJ pulse−1.For efficient STIRAP ultrafast pulses are usually ineffective but pulses of nanosecond duration have been used to demonstrate STIRAP in Ne51 atoms and NO52 molecules. However, in order to achieve the adiabaticity condition required for complete population transfer, shorter pulses need a higher intensity (in short, a high spectral intensity is necessary). Fortunately, in STIRAP the low power of the excitation pulse (PUMP) can be compensated using a more intense de-excitation (Stokes) pulse as the adiabaticity condition to be fulfilled is
 | (3) |
Thus far we have specifically considered simple STIRAP schemes that involve either one or two pairs of pulses, but schemes involving additional intermediate levels have been discussed in the literature and these expand greatly the number of possible excitation pathways. Coulston and Bergmann53 investigated four- and five-branch systems and still achieved high population transfer efficiency. One particularly attractive scheme is so-called “straddle STIRAP” proposed by Tannor and co-workers54 which uses a number of intermediate states instead on just one. This would replace the short wavelength D2Π ← X2Σ+ excitation step in Fig. 3b with a two photon chain, D2Π ← A2Π ← X2Σ+, replacing the VUV pulse with 300–500 nm pulses instead (Scheme 3, Table 2 and Fig. 5b). Now it is the turn of the intermediate D2Π ← A2Π pulse to be the most intense but this is clearly easy to achieve with the wavelengths necessary. The minimization of emission loss from the first intermediate A2Π level is important, but due to the strongly diagonal FC factors any population decay will feed back into the laser cooling cycling. The final excitation step can also be replaced with an equivalent B2Σ+ ← A2Π ← X2Σ+ sequence. This would relax the problem of fulfilling the adiabaticity condition above with VUV pulses.
Since the key requirement of the first pulse sequence is to simply populate a high vibrational level of the X2Σ+ state, such as v′′ = 10, an alternative method would be to exploit the growing strength of Δv = 1 and Δv = 2 vibrational changes in the A2Π ← X2Σ+ transition (Fig. 2a) to populate this vibronic state via the chain X2Σ+v′′ = 10 ← v′′ = 6 ← v′′ = 4 ← v′′ = 2. All the required excitation steps would lie in the UV/visible region.
(b) Further issues
The effect of background electronic states on the population transfer is a crucial issue because of the presence of Rydberg states below the excited dissociation limits studied here. Despite the presence of these Rydberg states in the vicinity of the B2Σ+state, numerous theoretical studies have shown that predissociation of the excited state is not a serious issue because in the STIRAP process the excited state is never actually populated. Kurkal and Rice55 have demonstrated that even for polyatomic molecules population transfer in the presence of off-resonance radiative coupling is insensitive to these background states. Furthermore, it is also possible to transfer into a predissociating state with unity efficiency, even if the process is not strictly adiabatic.56The exception to this general robustness is the presence of background ionization processes which would be unavoidable for excitation through the 42Π state. Furthermore, an infinite series of Rydberg states will cross the 42Π state at the inner wall as 42Π lies above the X1Σ+ ground state of the BeF+ ion. Indeed, any electronic state above the 1st excited 23P asymptote could suffer from extremely high decay rates. The presence of these Rydbergs also implies there may only be a small window of B2Σ+ vibrational levels suitable for complete population transfer. Note that the lowest vibrational levels of the two alleged 2Π Rydberg states15 lie above B2Σ+v = 45. A lower B2Σ+ vibrational level will suffer less overlap with Rydberg states but at a cost with respect to the final Stokes transition dipole (for example, the v = 41 level lies 1990 cm−1 below v = 45 but the corresponding A-coefficient is a third of the magnitude).
It is therefore worth estimating how many Rydberg states may exist below the B2Σ+v = 45 level. The highest Rydberg states we have calculated correspond to the lowest n = 3 states of 2Σ+ and 2Π symmetry and lie at lower energy. Such low lying Rydberg states tend to still have a strong valence component. However, the next shell states are more regular in nature which we can demonstrate by calculating the following
 | (4) |
| n* = n − μ | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1, more than 5000 cm−1 above B2Σ+v = 45. Consequently, there are a maximum of five missing Rydberg states in Fig. 1 that may predissociate this vibrational level, which should not severely interfere with the STIRAP process.
700 cm−1, more than 5000 cm−1 above B2Σ+v = 45. Consequently, there are a maximum of five missing Rydberg states in Fig. 1 that may predissociate this vibrational level, which should not severely interfere with the STIRAP process.
| Element | n | E ∞ | E n+2 | E R |
|---|---|---|---|---|
| a Energy of 5.88‘p’2Σ+ state. | ||||
| H | 1 | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 678 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 492 492 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186 186 |
| Li | 2 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469 469 |
7018 |
| Be+ | 2 | 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 882 |
118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
7030 |
| Na | 3 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449 449 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
6409 |
| Mg+ | 3 | 121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455 455 |
5953 |
| K | 4 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009 009 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 999 999 |
6010 |
| Ca+ | 4 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 751 751 |
74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484 484 |
5316 |
| Rb | 5 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 690 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 835 |
5855 |
| Sr+ | 5 | 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 964 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
5079 |
| Cs | 6 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
5698 |
| Ba+ | 6 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686 686 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 339 339 |
4836 |
| CaF | (4) | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 998 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826a 826a |
3172 |
A further advantage to the proposed scheme involves the elimination of photon recoil heating by the STIRAP sequence. There is no recoil heating effect from STIRAP because there is no spontaneous emission and therefore no dissipation. A momentum kick is inevitable, however, because there is (usually) a mismatch between the frequencies of the pump and dump pulses. This net momentum kick, however, is the same for all the parent molecules and serves to impart an impulse to the centre-of-mass and can be nullified by applying an external field and exploiting the paramagnetic nature of the fluorine atom.
5. Conclusion
We have calculated the low lying electronic states of BeF in order to investigate the possibility of laser cooling the molecule and then using optical pulses to effect a zero-energy fragmentation of the parent. A four colour laser scheme would appear to be effective for cooling. A STIRAP excitation process via the B2Σ+ state appears feasible though the transition dipole is small. Higher states are complicated by the presence of short range Rydberg states and the appearance of the ground state of the molecular ion well below the second excited asymptote of the neutral. Although STIRAP is an efficient technique, the production of ultracold parent molecules requires dense clouds of Doppler cooled diatomics and the multiple cooling wavelengths that entails. Crucially, however, the cold atoms formed can be elements that are difficult or impossible to cool with current technology. Thus, it is not a competitor to traditional laser cooling techniques but a technology to be adopted when these methods are inadequate.A more general observation concerns the need to fulfill the dual requirements of a parent diatomic that can be laser cooled and a molecule that can be subsequently fragmented at the dissociation limit via STIRAP. The best laser cooling candidates identified so far57 are either ionic compounds or hydrides and the former are characterised by very deep ground state potentials. Consequently, large energy separations need to be bridged, requiring either short wavelength photons or a chain of intermediate levels to break these molecules apart. However, the problem of absorbing tens of thousands of XUV photons (setting aside for one moment the lack of such laser sources in the foreseeable future) to cool a halogen has been reduced to using conventional cw lasers in concert with a series of excitation pulses in the UV and visible. The final temperature will not be limited by the concomitant large recoil heating that would be unavoidable in direct Doppler cooling of fluorine.
The lack of a zero spin, stable isotope of Be complicates the cooling sequence because of the increased number of hyperfine levels that need to be pumped within each vibronic transition. This problem must be addressed in the cooling of other fluorides, such as 137BaF. In addition, BeF possesses the largest dissociation energy of the alkaline earth fluorides. Alternative Group 2 fluorides with zero spin metal atoms, such as MgF, CaF or SrF, with simple hyperfine structures and weaker ionic bonds, may prove to be more practical fluorine sources.
While our calculations suggest grounds for cautious optimism, a number of important issues remain to be explored. A theoretical or spectroscopic determination of the quantum defects and a subsequent Quantum Defect Theory (QDT) analysis of the BeF Rydberg states would help clarify the feasibility of the proposed excitation scheme. A calculation of the long-range Feshbach states based on the atomic polarizabilities will refine the FC factors and A-coefficients estimated here. Finally, a simulation of the multi-pulse sequences proposed with realistic pulse energies and durations is desirable to determine under what precise conditions the populations of the penultimate level is zero and the first intermediate level is minimised.
Acknowledgements
The author would like to thank Adam Turner and Daniel Rogers for their help with the present calculations.References
- K.-K. Ni, S. Ospelkaus, D. Wang, G. Quemener, B. Neyenhuis, M. H. G. de Miranda, J. L. Bohn, J. Ye and D. S. Jin, Nature, 2010, 464, 1324–1328 CrossRef CAS.
- W. S. Struve, T. Kitagawa and D. R. Herschbach, J. Chem. Phys., 1971, 54, 2759–2761 CrossRef CAS.
- C. Liu and J. Noonan, Advanced Photon Source Accelerator Ultrahigh Vacuum Guide, ANL/APS/TB-16, Advanced Photon Source, Argonne National Laboratory, USA Search PubMed.
- K. W. A. Wright and I. C. Lane, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 032715 CrossRef.
- K. Lidén, Ark. Fys., 1949, 1, 229 Search PubMed.
- M. Shimizu, K. Yasutake, H. Ohmi, A. Takeuchi, H. Kakiuchi, K. Yoshii and Y. Mori, Appl. Phys. B: Lasers Opt., 2001, 72, 227–230 CrossRef CAS.
- E. S. Shuman, J. F. Barry and D. DeMille, Nature, 2010, 467, 820–823 CrossRef CAS.
- E. S. Shuman, J. F. Barry, D. R. Glenn and D. DeMille, Phys. Rev. Lett., 2009, 103, 223001 CrossRef CAS.
- M. Pelegrini, C. S. Vivacqua, O. Roberto-Neto, F. R. Ornellas and F. B. C. Machado, Braz. J. Phys., 2005, 35, 950–956 CrossRef CAS.
- S. Datta, Proc. R. Soc. London, Ser. A, 1922, 101, 187 CrossRef CAS.
- F. A. Jenkins, Phys. Rev., 1930, 35, 315–335 CrossRef CAS.
- T. E. H. Walker and R. F. Barrow, J. Phys. B: At., Mol. Phys., 1969, 2, 102–106 Search PubMed.
- D. L. Cooper, S. J. Prosser and W. G. Richards, J. Phys. B: At. Mol. Phys., 1981, 14, L487–L489 CrossRef CAS.
- K. M. Rao and P. T. Rao, Indian J. Pure Appl. Phys., 1965, 3, 177 CAS.
- M. M. Novikov and L. V. Gurvich, Opt. Spektrosk Engl. Transl., 1967, 23, 173 Search PubMed.
- G. Tai and R. D. Verma, J. Mol. Spectrosc., 1995, 173, 1–7 CrossRef CAS.
- A. C. Roach and P. J. Kuntz, Mol. Phys., 1982, 45, 853–856 CrossRef CAS.
- D. L. Hildenbrand and E. J. Murad, J. Chem. Phys., 1966, 44, 1524–1529 CrossRef CAS.
- M. Farber and R. D. Srivastava, J. Chem. Soc., Faraday Trans. 1, 1974, 70, 1581–1589 RSC.
- M. Vasiliu, D. Feller, J. L. Gole and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 9349–9358 CrossRef CAS.
- T. E. H. Walker and W. G. Richards, J. Phys. B: At. Mol. Phys., 1970, 3, 271–279 CrossRef CAS.
- T. E. H. Walker and W. G. Richards, Proc. Phys. Soc., 1967, 92, 285–290 CrossRef CAS.
- C. M. Marian, Chem. Phys., 1985, 100, 13–19 CrossRef CAS.
- S. R. Langhoff, C. W. Bauschlicher and H. Partridge, J. Chem. Phys., 1986, 84, 1687–1695 CrossRef CAS.
- S. R. Langhoff, C. W. Bauschlicher, H. Partridge and R. Ahlrichs, J. Chem. Phys., 1986, 84, 5025–5031 CrossRef CAS.
- F. B. C. Machado and F. R. Ornellas, Mol. Phys., 1989, 67, 1129–1140 CrossRef CAS.
- F. R. Ornellas, F. B. C. Machado and O. Roberto-Neto, Mol. Phys., 1992, 77(6), 1169–1185 CrossRef CAS.
- Z. L. Zhu, Q. P. Song, S. H. Kou, J. H. Lang and J. Feng, Int. J. Mol. Sci., 2012, 13, 2501–2514 CrossRef CAS.
- S. J. Prosser and W. G. Richards, J. Phys. B: At. Mol. Phys., 1980, 13, 2767–2772 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- D. E. Woon, T. H. Dunning Jr, unpublished CAS; D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CAS.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, G. Hetzer, T. Hrenar, G. Knizia, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, “Molpro, version 2010.1, a package of ab initio programs”, 2009 Search PubMed.
- R. J. Le Roy, LEVEL 8.0: A computer program for solving the radial Schrödinger equation for bound and quasibound Levels, Chemical Physics Research Report CP-663, University of Waterloo, 2007 Search PubMed the source code and manual for this program may be obtained from http://leroy.uwaterloo.ca/programs/.
- T. C. Steimle, S. Frey, A. Le, D. DeMille, D. A. Rahmlow and C. Linton, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 012508 CrossRef.
- L. B. Knight Jr., M. B. Wise, A. G. Childers, E. R. Davidson and W. R. Daasch, J. Chem. Phys., 1980, 73, 4198–4202 CrossRef.
- D. Patterson, E. Tsikata and J. M. Doyle, Phys. Chem. Chem. Phys., 2010, 12, 9736–9741 RSC.
- N. P. Wells and I. C. Lane, Phys. Chem. Chem. Phys., 2011, 13, 19036–19051 RSC.
- H. E. Radford, V. W. Hughes and V. Beltran-Lopez, Phys. Rev., 1961, 123, 153–160 CrossRef CAS.
- N. V. Vitanov, T. Halfmann, B. W. Shore and K. Bergmann, Annu. Rev. Phys. Chem., 2001, 52, 763–809 CrossRef CAS.
- K. Winkler, F. Lang, G. Thalhammer, P. V. D. Straten and J. H. Denschlag, Phys. Rev. Lett., 2007, 98, 043201 CrossRef CAS.
- S. Ospelkaus, K.-K. Ni, H. G. de Miranda, B. Neyenhuis, D. Wang, S. Kotochigova, P. S. Julienne, D. S. Jin and J. Ye, Faraday Discuss., 2009, 142, 351–360 RSC.
- J. G. Danzl, M. J. Mark, E. Haller, M. Gustavsson, R. Hart, J. Aldegunde, J. M. Hutson and H.-C. Nägerl, Nat. Phys., 2010, 6, 265–270 CrossRef CAS.
- J. J. Kay, S. L. Coy, B. M. Wong, C. Jungen and R. W. Field, J. Chem. Phys., 2011, 134, 114313 CrossRef.
- K. S. E. Eikema, W. Ubachs, W. Vassen and W. Hogervorst, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 1866–1884 CrossRef CAS.
- F. P. Levelt, W. Ubachs and W. Hogervorst, J. Chem. Phys., 1992, 97, 7160–7166 CrossRef.
- J. P. Sprengers, W. Ubachs, K. G. H. Baldwin, B. R. Lewis and W.-Ü L. Tchang-Brillet, J. Chem. Phys., 2003, 119, 3160–3173 CrossRef CAS.
- W. Ubachs, K. S. E. Eikema, W. Hogervorst and P. C. Cacciani, J. Opt. Soc. Am. B, 1997, 14, 2469–2476 CrossRef CAS.
- S. J. Hanna, P. Campuzano-Jost, E. A. Simpson, D. B. Robb, I. Burak, M. W. Blades, J. W. Hepburn and A. K. Bertram, Int. J. Mass Spectrom., 2009, 279, 134–146 CrossRef CAS.
- J. Martin, B. W. Shore and K. Bergmann, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 54, 1556–1569 CrossRef.
- A. Kuhn, S. Steuerwald and K. Bergmann, Eur. Phys. J. D, 1998, 1, 57–70 CrossRef CAS.
- G. W. Coulston and K. Bergmann, J. Chem. Phys., 1992, 96, 3467–3475 CrossRef CAS.
- V. S. Malinovsky and D. J. Tannor, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 4929–4937 CrossRef CAS.
- V. Kurkal and S. A. Rice, J. Phys. Chem. B, 2001, 105, 6488–6494 CrossRef CAS.
- V. Kurkal and S. A. Rice, J. Phys. Chem. A, 2002, 106, 10810–10817 CrossRef CAS.
- M. D. Di Rosa, Eur. Phys. J. D, 2004, 31, 395–402 CrossRef.
- As there is no experimental measurement available, this value is estimated from the calculated relative oscillator strengths of L. Głowacki and J. Migdałek, J. Phys. B: At. Mol. Opt. Phys., 2006, 39, 172 CrossRef and the experimental measurement (4.4 ms) in Mg I from P. L. Hansen, K. T. Therkildsen, N. Malossi, B. B. Jensen, E. D. van Ooijen, A. Brusch, J. H. Müller, J. Hald and J. W. Thomsen, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 062502 CrossRef.
| This journal is © the Owner Societies 2012 |
