Imaging ultrafast dynamics of molecules with laser-induced electron diffraction
C. D.
Lin
* and
Junliang
Xu
J. R. Macdonald Laboratory, Physics Department, Kansas State University, Manhattan, Kansas 66506-2604, USA. E-mail: cdlin@phys.ksu.edu; Fax: +1 785-532-6806; Tel: +1 785-532-1617
First published on 6th August 2012
Abstract
We introduce a laser-induced electron diffraction method (LIED) for imaging ultrafast dynamics of small molecules with femtosecond mid-infrared lasers. When molecules are placed in an intense laser field, both low- and high-energy photoelectrons are generated. According to quantitative rescattering (QRS) theory, high-energy electrons are produced by a rescattering process where electrons born at the early phase of the laser pulse are driven back to rescatter with the parent ion. From the high-energy electron momentum spectra, field-free elastic electron-ion scattering differential cross sections (DCS), or diffraction images, can be extracted. With mid-infrared lasers as the driving pulses, it is further shown that the DCS can be used to extract atomic positions in a molecule with sub-angstrom spatial resolution, in close analogy to the standard electron diffraction method. Since infrared lasers with pulse duration of a few to several tens of femtoseconds are already available, LIED can be used for imaging dynamics of molecules with sub-angstrom spatial and a few-femtosecond temporal resolution. The first experiment with LIED has shown that the bond length of oxygen molecules shortens by 0.1 Å in five femtoseconds after single ionization. The principle behind LIED and its future outlook as a tool for dynamic imaging of molecules are presented.
 C. D. Lin | Chii-Dong Lin is University Distinguished Professor at the Physics Department, Kansas State University, USA. Since 2002 he has worked on different aspects of strong field physics, including high-harmonic generation, laser-induced electron diffraction, nonsequential double ionization and attosecond physics. He received his PhD from University of Chicago in 1974 under Ugo Fano. Previously he studied many-body photoionization theory, classifications of doubly and triply excited states, ion–atom collisions and hyperspherical approach to three-body systems. |
 Junliang Xu | Junliang Xu is a postdoctoral researcher in the Agostini-DiMauro group at The Ohio State University. His research interest is ultrafast molecular dynamic imaging using laser-induced electron diffraction. He received his BS from University of Science and Technology at Hefei, China in 2006 and his PhD from Kansas State University in 2012 under the supervision of Prof. C. D. Lin. |
1 Introduction
1.1 The need of dynamic imaging for molecules
The determination of the structure and dynamics of a chemical reaction from reactants to products is of great importance in physics, chemistry and biology and it is the goal of ultrafast dynamic imaging methods. Future development of many areas of science and technology requires good knowledge of molecular dynamics at the atomic levels. Since the vibrational periods of molecules are in the order of tens to hundreds of femtoseconds and the shortest interatomic distances are in the order of one angstrom, it is obvious that dynamic imaging methods are required to have spatial resolution of one or fractional angstroms, and temporal resolution of a few to several tens of femtoseconds. Conventional X-ray and electron diffraction methods are capable of achieving sub-angstrom spatial resolution, but they have pulse lengths in the order of hundreds of picoseconds or more, they are not suitable for time-resolved X-ray diffraction or time-resolved electron diffraction.1In the past two decades, time-resolved chemical reaction dynamics have been widely studied using femtosecond (tens to hundreds of femtoseconds) light pulses, usually with infrared (IR) lasers and/or their second or third harmonics.2–6 In a typical pump–probe measurement, a reaction is initiated with an optical “pump” pulse. The evolution of the dynamic system is “probed” by another optical pulse as a function of the time delay between the two pulses. Since an optical probe pulse is sensitive to specific energy states, such methods only partially project out the wave packet created by the pump pulse, leaving out the important information of the global structure change versus time at the atomic level, such as atomic coordinates, bond lengths, bond angles, and torsion angles. To interpret such optical measurements, detailed knowledge of molecular structures of the ground and excited states beyond the equilibrium distance is needed. This is a monumental task for a molecule if its atomic configurations are not known.
Obviously, one way to accomplish femtosecond temporal and sub-angstrom spatial resolution for imaging molecular dynamics is to replace the optical probe pulses by femtosecond X-rays or femtosecond electron pulses. In the last two decades, great efforts have been devoted to finding new methods for the generation of femtosecond X-rays and femtosecond electron pulses.1,7–10 Much progress has been made and a few experiments using these new pulses as probes have been reported recently.11–14 In this article, we discuss an entirely different approach, called the laser-induced electron diffraction (LIED) method.15,16 The LIED takes advantage of the fact that intense infrared and mid-infrared lasers with duration of a few to several tens of femtoseconds are already available. If these lasers can be shown to be capable of achieving sub-angstrom spatial resolution, then LIED has the potential to develop into a competing tool for dynamic imaging of molecules. In fact, a proof-of-principle first experiment using LIED has been reported recently where the bond length of an oxygen molecule was found to shrink by 0.1 Å in about five femtoseconds.16 How is LIED compared to the more familiar femtosecond X-ray and femtosecond electron diffraction methods? How does LIED work? What is its future?
1.2 Comparison of femtosecond X-ray and electron diffractions with LIED
Unlike optical lasers, femtosecond X-ray lasers cannot be obtained simply just by compressing picosecond X-rays from 3rd generation synchrotron radiation lights. In fact, a complete new technology has to be developed. After several years of research and development, the first femtosecond X-ray free-electron lasers (XFELs) had arrived, with the Stanford LCLS (Linac coherent light source) began its operation since 2009. The XFELs are generated by self-amplified spontaneous emission from a linear electron accelerator with relativistic electron beams. The LCLS operates at around 30 Hz, with photon energy between 0.8 and 8 keV. Other facilities like the one in Japan began its operation in 2011, and the XFEL in Hamburg will be ready in 2014. More XFEL facilities in other countries are either under construction or in the planning stage. Clearly the future of XFELs is very bright. For imaging, at LCLS, diffraction images from nanocrystals and a single mimivirus particle have been taken and analyzed.11,17 At LCLS, using the maximum photon energy of 8 keV, the X-ray wavelength is 1.5 Å, thus spatial resolution achieved so far is limited to a few angstroms or worse. To reach better spatial resolution, higher photon energy pulses are needed in the future. In addition, each XFEL pulse is different from the previous one, thus the characterization of each pulse and synchronization with the kilohertz optical pump pulse pose additional complications in pump–probe experiments.18–20 The XFELs are built for a general imaging purpose of microscopic objects, including nanoparticles, condensed media, macromolecules, and biological systems such as cells and viruses. They are available only at large national facilities. Due to its high operational cost, the beam times available for individual experiments are expected to be severely limited. On the other hand, with the large number of people involved in XFELs, much progress has been made in target preparation, alignment or orientation of molecules, and powerful algorithms for data sorting and inversion.21 These achievements will prove to be useful for electron diffraction as well as LIED in the future. Recent works and issues related to XFELs can be found in these latest reports.19–25Electron diffraction is also a powerful tool for determining the structure of matter.26 Since electron scattering cross sections are five to six orders of magnitude higher than X-rays, electron diffraction has a lower penetration depth, making it useful for studying gas-phase molecules, thin films and surfaces. Since electron pulses can be readily manipulated in a compact unit, electron diffraction operates on table-tops and they are relatively much cheaper than XFEL's. To generate short electron pulses, femtosecond lasers are used to liberate them from metal surfaces. These electrons are then accelerated to tens of keV. Electron diffraction typically is capable of achieving 0.01 Å spatial resolution for static systems. However, electrons are charged, their temporal profiles tend to broaden by the presence of any charges, including other electrons. Thus existing ultrafast electron diffraction for gas-phase molecules has temporal resolution of about one picosecond or longer.8,9 Technological progress has made it possible recently to generate 100 fs pulses,27 but they have not been applied to study gas-phase molecules yet. On the other hand, interesting results on melting, phase transition in metals and semiconductors, and bond hardening, using a femtosecond electron diffraction method have been reported recently.12,13 To compress electron pulses to tens of femtoseconds, it has been suggested to use relativistic electron beams (for energy above 3 MeV).28 Programs are underway to produce even attosecond electron pulses. More details on the recent status in ultrafast electron diffraction can be found in recent reviews.13,29 We comment that measurements of durations of electron pulses and synchronization with optical pump pulses are also not as straightforward when compared to typical “pure” optical pump–probe experiments.
In short, in spite of significant technological advances in the past few decades, use of femtosecond X-rays or femtosecond electrons for probing time-resolved structural changes of molecules is still quite rare, especially when compared to typical optical pump–probe experiments that are found in many chemical laboratories today. In an optical pump–probe experiment, the two pulses come from the same “master” laser by beam-splitter and path-delay lines, thus the coherence between the pump and probe beams, the synchronization of the two, can be controlled to high precision.30,31 In LIED, the probe pulse is also an optical laser. Together with the optical pump pulse, both are derived from the same master laser. Thus the coherence and synchronization are easy to manipulate. In LIED, the probe pulse interacts not with the molecule via the absorption of photons, but via scattering by electrons liberated from the molecule itself. Thus LIED is based on electron diffraction, where the electrons are derived from the molecules. To understand how LIED works, a bit of the basic theory is needed.
2 The basic principle of LIED
The LIED is based on one of the rescattering phenomena32–34 that occur when an atom or molecule interacts with an intense femtosecond infrared laser pulse. Experimentally, it involves measuring the momentum distributions of high-energy photoelectrons, which are usually called high-energy above-threshold ionization photoelectrons. For LIED to work, several conditions have to be satisfied:(1) accurate laser-free electron-target ion differential cross sections (DCS) can be extracted from the high-energy photoelectron momentum spectra generated by the intense laser pulses;32–37
(2) DCS extracted can be “inverted” to reveal the target structure information.38,39
These first two conditions have been well established from theory and experiments for simple atomic targets. In the early experiments, the DCS were obtained from high-energy electron spectra generated by 800 nm Ti-Sapphire lasers.40–43 In these experiments the collision energies of the electrons are in the range of 15 to 50 eV, much smaller than those used in electron diffraction experiments.
For molecular targets, while the DCS can still be extracted from the high energy spectra,42,44 the DCS cannot be easily “inverted”. For easy inversion, in a standard electron diffraction method, high energy electrons at tens to hundreds of keV are used. At such high energies, the DCS is accurately approximated by the independent atom model (IAM).26 When this model is applicable, the positions of atoms in a molecule can be easily retrieved from the DCS directly.
(3) In LIED, the energy of the returning electrons can be increased with the use of longer wavelength mid-infrared lasers,45,46 but it is still not possible to reach tens or hundreds keV used in typical electron diffraction experiments. A key ingredient that makes LIED work is the realization that IAM can be applied to collisions at much lower energy, say as low as 100 eV, if the DCS is limited to the region of large scattering angles only.15 The high-energy electrons observed in the photoelectron spectra are precisely originated from these large-angle scatterings when mid-infrared lasers are the driving pulses.
This last third step provides the essential ingredient needed for LIED to achieve sub-angstrom spatial resolution. For temporal resolution, a few-ten to sub-ten femtoseconds mid-infrared lasers are already available today, thus paving the way for using LIED as a powerful tool for dynamic imaging of molecules.
Below we elaborate each of these steps.
2.1 Extracting field-free electron-ion DCS from photoelectron momentum spectra
The principle behind LIED is the three-step model of strong-field rescattering processes.47–49 Consider a molecule in a laser field. Fig. 1 depicts how the potential surface seen by an electron evolves in time over an optical period. At the far left, in the first step, when the electric field is near the maximum, an electron can tunnel out of the combined potential formed by the molecular ion and the laser's electric field. After tunnel ionization, most often, the electron will just drift away from the vicinity of the molecule and detected as a low-momentum event. At other times, in the second step, the laser field may drive the electron along a different path. As the potential surface changes within the sub-cycle, the electron is driven back to the core where it rescatters from the ion, at the time when the laser's electric field is near zero. If the electron is scattered into backward directions, it will gain additional momentum from the laser field and emerges as a high-energy photoelectron. LIED is based on the collision process in the third step where diffraction images are formed by electrons scattered off from the ion, not by photons absorbed by the molecule as in an optical process. Most importantly, from the instant that the electrons are born to the instant of scattering by the ion, all of the processes occur within one optical cycle. No external electric or magnetic fields are employed to guide or accelerate the electrons. Since electrons are released repeatedly at each half optical cycle, the diffraction images by LIED may display interference unless a few-cycle laser pulses are used.34,50 We comment that if the returning electron recombines with the ion to emit radiation, the process is called high-order harmonic generation (HHG). Since photo-recombination is an inverse process of photoionization, HHG spectra are also encoded with information about the structure of the target molecule and can be used as a probe.51–53 In fact, in recent years it has become quite popular to extract the wavefunction of the highest occupied molecular orbital of a molecule from the HHG spectra using the so-called tomographic method.52–54 However, the method is based on a number of assumptions that are not supported by basic photoionization theory, its general validity has been called into questions.55 | ||
| Fig. 1 Basic principle of Laser Induced Electron Diffraction for imaging ultrafast molecular dynamics. The LIED is based on the rescattering model, where the elementary processes: the birth of electrons, their acceleration, and the formation of diffraction images, all occur within one optical period of the laser, as depicted by its electric field (red line) here. The potential surfaces due to the combined field from the molecular ion and the electric field of the laser at different times are shown. An electron is first tunnel ionized near the peak of the field. The field first drives it away from the ion, but may drive it back to recollide with the ion, at about three quarters of an optical cycle after ionization. If the electron is scattered into the backward direction, it will be further accelerated by the laser field and emerges as a high energy electron which is registered by the detector shown on the far right. The diffraction images in LIED are extracted from the high energy photoelectron spectra; its basic mechanism is analogous to the conventional gas-phase electron diffraction method, but is accompanied by femtoseconds temporal resolution offered by the laser. | ||
For LIED to be able to work like an electron diffraction method, laser-free electron-ion differential cross section should be extracted from the high-energy photoelectron momentum spectra. This has been made possible with the recently developed quantitative rescattering (QRS) theory.32,34,56 Since experiments often are unable to determine the laser intensity accurately, we established the validity of the QRS theory by comparing the model to accurate numerical results obtained by solving the time-dependent Schrodinger equation for a simple model atom in a known laser field.34,56,57 In Fig. 2a, we depict the electric field of a linearly polarized laser and its vector potential. We choose a model Ar atom as a target, with the atom described by a simple one-electron approximation. Fig. 2b shows the calculated photoelectron energy distribution for the model Ar. The low-energy electron yield drops very quickly from the threshold to about 2UP, where UP is the quiver energy of a free electron in the laser field. It is given by UP (eV) = 9.33 × I (1014 W cm−2) λ2 (μm), where I is the peak intensity of the laser and λ is the wavelength. These low-energy electrons are not of interest for LIED. The high-energy electrons are from above 2UP to about 10UP. Note that high-energy electron yields are much smaller than the low-energy ones.
 | ||
| Fig. 2 Illustration of extracting field-free electron diffraction images from laser-induced photoelectron momentum spectra. (a) Typical electric field (E) and vector potential (A) versus time for a few-cycle laser pulses. Electrons are tunnel ionized at each half optical cycle near the peak of the field (marked by a and a′) and return to recollide with the target ion about three quarters of an optical period laser (marked by b and b′). (b) Typical electron yields vs. the kinetic energy of photoelectrons. For LIED, high energy electrons within (4–10) UP are used. (c) Photoelectron momentum spectra of a model Ar atom exposed to a laser pulse, obtained by solving the time-dependent Schrödinger equation “exactly”. To see the LIED events, in (d) the spectra in (c) are renormalized such that the total yield for a given photoelectron energy is the same. The center of each semicircle in (d) is displaced from the origin. The yields along each circle of (c) represent elastic scattering events, while the shift of the center is due to the additional momentum gained by the electron from the time of collision till the pulse is over. The photoelectron momentum vector p and the scattering electron momentum pr are drawn in (c), with momentum expressed in units of A0, which is the peak value of the vector potential. (e) The elastic scattering differential cross section between electron and Ar+ calculated at pr = 1.22 a.u. The DCS extracted from the photoelectron spectra at the same pr, but from two different laser intensities, are shown, demonstrating that accurate field-free e− − Ar+ scattering DCS can be extracted from the photoelectron momentum spectra, independent of the lasers used. (f) Similar DCS extracted from Xe target at pr = 0.92 a.u., but using a longer laser pulse. The extracted DCS show oscillations due to interference of scattering events from different optical cycles, but the envelope still falls on the field-free scattering DCS. These oscillations will be washed out in real experimental data where the spectra are collected from a focused laser pulse with continuously distributed intensities. Laser wavelength of 800 nm is used in the simulation. Figures are adopted from ref. 34 and 56. | ||
Fig. 2c shows the photoelectron momentum spectra, where the horizontal axis is the momentum component along the polarization axis of the laser, and the vertical axis is the perpendicular component. In this simple model, there is a cylindrical symmetry in the system. From the 2D momentum spectra in Fig. 2c, it is fair to say that little can be seen, especially when one recognizes that the logarithmic scale is used in the density plot. However, if the momentum spectrum is renormalized to the same value for each photoelectron energy, as shown in Fig. 2d, then prominent semicircles appear, where the center of the circle is displaced. The semicircle represents elastic scattering events, while the displacement of the origin is traced to the additional momentum gained by the photoelectron from the laser field after the collision as the electron exits the laser field. Thus for electron scattering in the laser field, according to QRS, the diffraction images can be expressed as
| I(p,θ) = W(pr)σ(pr, θr). | (1) |
This equation interprets that photoelectron momentum spectra I(p,θ) generated by the laser is proportional to the elastic differential cross section σ(pr,θr) by a laser-free electron with momentum pr, for a scattering angle θr. The proportional constant, W(pr), is interpreted as a wave packet, or more precisely, the electron flux integrated over the pulse duration. The two vectors, in atomic units, are related by p = pr − Ar, where the angles are defined in Fig. 2c. Here Ar = A(tr) is the vector potential at the time of electron recollision. In Fig. 2e we compare the field-free e− − Ar+ scattering DCS at pr = 1.22. To extract the DCS from the electron spectra in Fig. 2c, we read the yield along the circumference of the same pr = 1.22. Fig. 2e shows that the two curves agree with each other over the angular range from 120° to 180°. If the DCS is extracted from the electron spectra generated by a laser of different intensity, the DCS at the same pr extracted is the same. This result is important since it means that field-free electron-ion DCS thus obtained is independent of laser intensities. If a longer pulse is used, the extracted DCS will show oscillations due to interference by scattering from different optical cycles, as seen in Fig. 2f. In this case, the envelope of the extracted DCS agrees with the field-free one. When the laser intensity is changed, the oscillation shifts but the envelope remains the same. We note that these oscillations are washed out in experiments since in experiments focused laser beams are used where the intensities are continuously distributed within the focused volume.
In short, the validity of eqn (1) has been established theoretically and field-free elastic electron-ion scattering DCS can be extracted from the high energy electron momentum spectra.
2.2 Initial experimental tests of LIED using Ti–Sapphire lasers
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40–44,58 Since the highest returning electron energy is 3.2UP, in these experiments scattering energies are in the 15–50 eV range. From the experimental electron momentum spectra, the extracted DCS have been shown to be in good agreement with the theoretical DCS for electron-ion collisions in the absence of any laser fields. In one case, the extracted DCS has been compared directly with laboratory e− + Ar+ collision data.59 We comment that electron-ion collision experiments are difficult and very few data are available. Important conclusions from these earlier experiments confirmed that the DCS extracted are independent of the pulse duration, and of the laser's intensity.32,40–44,58 The DCS has also been extracted from data taken with short laser pulses where the carrier-envelope-phase was varied and the extracted DCS are independent of these phases.43
40–44,58 Since the highest returning electron energy is 3.2UP, in these experiments scattering energies are in the 15–50 eV range. From the experimental electron momentum spectra, the extracted DCS have been shown to be in good agreement with the theoretical DCS for electron-ion collisions in the absence of any laser fields. In one case, the extracted DCS has been compared directly with laboratory e− + Ar+ collision data.59 We comment that electron-ion collision experiments are difficult and very few data are available. Important conclusions from these earlier experiments confirmed that the DCS extracted are independent of the pulse duration, and of the laser's intensity.32,40–44,58 The DCS has also been extracted from data taken with short laser pulses where the carrier-envelope-phase was varied and the extracted DCS are independent of these phases.43
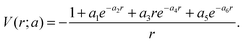 | (2) |
The parameters a = {ai; i = 1,…,6} are determined by fitting the calculated energy levels to the experimental energy levels of Ar.60 A model potential thus obtained is also expected to describe low-energy e− − Ar+ scattering cross sections. However, this model potential is not expected to be accurate enough to describe the same collision at high energies, say, at 500 eV or 5 keV. With this in mind, we ask if we can use the DCS extracted from the electron spectra, where the electron collision energy is from 15–50 eV, to recover the model potential, eqn (2), which was obtained from fitting the binding energies of the first few excited states of an atom?
This question was addressed by Xu et al.38 The goal of the “structure” retrieval is to determine the parameters {ai} in eqn (2) using the DCS extracted from the electron spectra. A genetic algorithm was used where the fitness function was chosen to be
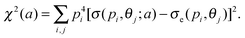 | (3) |
Here pi and θj are the discrete momentum points of the returning electrons and the elastic scattered angles, respectively, and σe(pi,θj) are the extracted DCS from the electron spectra. The GA returns the parameters {ai}, from which the model potential can be obtained.
This potential represents the “structure” of the many-electron argon atom. To demonstrate how well this “structure” retrieval works, in Fig. 3 we show the “experimental” DCS and the retrieved model potentials for the rare gas atoms, Ne, Ar, Kr and Xe. Since experimental data were not available for all of these targets, the DCS are actually obtained from R-matrix calculations.61 These DCS from advanced many-body calculations include effects of electron correlations. To mimic experimental data, a random error of 5–10% was introduced to each “experimental” point. From the fitted parameters, we obtained the effective charge Z(r) = − rV(r) for each atom. The resulting V(r) obtained from fitting the DCS and from fitting the energy levels are shown to agree very well in Fig. 3. In this example, the “structure” of the rare gas atom is represented by the effective model potential V(r). We note that the DCS for Ar and Kr look very similar to each other in the figures shown, but the genetic algorithm was able to retrieve the potentials that look rather different. As r approaches zero, the effective charge becomes close to the nuclear charge of the atom. This is a simple example of structure retrieval for atoms. Using actual electron spectra for these targets, in Morishita et al.,39 the same procedure was used to retrieve the model potential and similar conclusion was found.
 | ||
| Fig. 3 The DCS from 100° to 180° calculated using a many-body R-matrix method over a range of incident electron momenta from 0.4 to 2.0 a.u. for Ne, Ar, Kr and Xe atoms. These numerical results were treated as experimental data for structure retrieval. To extract the “structure” of each atom, the many-electron system is approximated by a single electron in an effective charge Z(r) = −rV(r), where V(r) is given in the form of eqn (2). Using the DCS data on the left side, the retrieved Z(r) for each target is shown to be in good agreement with the Z(r) retrieved from fitting the binding energies of the ground state and the first few excited states of the atom. Genetic algorithm is used for the fitting. For Xe, the correct answer comes from the 2nd best fit. Since Xe is larger in size, the small-r region is not probed by the low-energy electrons, thus the retrieved potential is not accurate in that region. DCS from higher collision energies are needed in order to retrieve the correct Xe potential at small r. Figures adopted from ref. 38. | ||
In short, we have clear evidence that laser-free electron-ion scattering DCS can be extracted from experimental electron momentum spectra and the results are independent of the properties of the lasers used.
| I(p,θ,ϕ;ΩL) = N(ΩL)W(pr)σ(pr,θr,ϕr;ΩL). | (4) |
Here the momentum of the photoelectron and the scattering electrons are given by p = (p,θ,ϕ), pr = (pr,θr,ϕr), in spherical coordinates, respectively. As before, p = pr − Ar. In eqn (4), we have pulled out the ΩL-dependent tunnel ionization rate N(ΩL) explicitly. If the molecular gas is partially aligned or oriented with an angular distribution A(ΩL), then the spectra are obtained by integrating the product A(ΩL)I(p,θ,ϕ;ΩL) over all the ΩL angles. For randomly distributed molecules, A(ΩL) = 1. For a focused laser beam, integration of eqn (4) over the spatial distribution of intensities would still give an expression similar to eqn (4) except that in a focused laser W(pr) is interpreted as the “wave packet” from the focused laser beam. Note that tunnel ionization rate N(ΩL) can be calculated using the molecular tunneling ionization theory64,65 or the strong-field approximation.66 The N(ΩL) does not depend on laser intensity much, thus for molecular targets, electron spectra from partially aligned/oriented molecules can still be expressed in the form
D(p,θ,ϕ) = W(pr)![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (pr,θr,ϕr), (pr,θr,ϕr), | (5) |
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (pr,θr,ϕr) = ∫N(ΩL)A(ΩL)σ(pr,θr,ϕr;ΩL)dΩL. (pr,θr,ϕr) = ∫N(ΩL)A(ΩL)σ(pr,θr,ϕr;ΩL)dΩL. | (6) |
Here ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) differs from standard elastic electron-molecular-ion scattering DCS only by the additional factor N(ΩL). Eqn (6) gives the “diffraction image” that can be extracted from the high-energy electron spectra for molecular targets. If molecules are randomly distributed or aligned in one dimension with respect to the laser polarization axis of the laser, then the dependence on the azimuthal angle ϕr drops out since the system has cylindrical symmetry. We comment that molecules can be impulsively aligned by an infrared laser67 or by other means.
differs from standard elastic electron-molecular-ion scattering DCS only by the additional factor N(ΩL). Eqn (6) gives the “diffraction image” that can be extracted from the high-energy electron spectra for molecular targets. If molecules are randomly distributed or aligned in one dimension with respect to the laser polarization axis of the laser, then the dependence on the azimuthal angle ϕr drops out since the system has cylindrical symmetry. We comment that molecules can be impulsively aligned by an infrared laser67 or by other means.
According to eqn (6), to compare the extracted ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (pr,θr,ϕr) with theory, the electron-molecular ion elastic scattering DCS, σ(pr,θr,ϕr;ΩL), for each fixed-in-space geometry, have to be calculated. Unfortunately such calculations are not readily available, nor are the experimental data. In most electron-molecule collisions, usually only the DCS from randomly distributed molecules are calculated. Recently, in connection with the DCS extracted from the electron spectra for CO2, N2, and O2, elastic DCS for collisions from fixed-in-space molecular ions have been reported in Okunishi et al. in 2011.42 Such calculations are complicated for collision energies below 100 eV. Simpler DCS calculations that account for alignment or orientation dependence have been reported recently.68
(pr,θr,ϕr) with theory, the electron-molecular ion elastic scattering DCS, σ(pr,θr,ϕr;ΩL), for each fixed-in-space geometry, have to be calculated. Unfortunately such calculations are not readily available, nor are the experimental data. In most electron-molecule collisions, usually only the DCS from randomly distributed molecules are calculated. Recently, in connection with the DCS extracted from the electron spectra for CO2, N2, and O2, elastic DCS for collisions from fixed-in-space molecular ions have been reported in Okunishi et al. in 2011.42 Such calculations are complicated for collision energies below 100 eV. Simpler DCS calculations that account for alignment or orientation dependence have been reported recently.68
3 Probing interatomic separations in molecules using LIED with mid-infrared lasers
3.1 Low- vs. high-energy electron diffractions: what structure information is made available?
In conventional gas-phase electron diffraction,26 one distinguishes low-energy electron diffraction from high-energy electron diffraction. To study rotation, vibration or outer-shell phenomena, low-energy elastic or inelastic collisions are carried out. These measurements probe the energy structure of a molecule, usually when it is in the ground state. These measurements do not reveal the elementary information such as the bond length and bond angles which define what a molecule is “like”. A simplest picture of a molecule is the ball-and-stick model. The atoms in it, the length between each pair of them and the direction of each of the “stick” are the first global information for a molecule, long before one has to worry about the chemical bonding or the correlation effects. Such information, however, is not sensitive to collisions where the electron energy is below 100 eV or so. Note that at 100 eV, the de Broglie wavelength of an electron is 1.22 Å, which is of the order of the size of a small molecule. Thus electron scattering DCS below 100 eV are not suitable for probing interatomic distances.Electron diffraction, which usually means electron diffraction images taken with electron energies in the tens to hundreds of keV, is used for gas-phase electron diffraction measurements. Bond length accurate to 0.01 Å can be routinely achieved. There are two advantages for using high energy electrons in gas-phase electron diffraction. First, it has a small de Broglie wavelength for better spatial resolution. Second, the scattering theory at large collision energies is usually simpler. In electron diffraction, it has been well established that the DCS at high energies can be calculated using the independent atom model, which is a model extended from the Born approximation. When IAM is valid, the calculation of the DCS is easy, and the “inversion” to retrieve “molecular structure” is simple. The structures retrieved from gas-phase electron diffraction are precisely the parameters that give the ball-and-stick model of a molecule.
In LIED, the maximum energy of the returning electrons is given by 3.2UP. While UP is proportional to Iλ2, where I is the laser intensity and λ the wavelength, it is not desirable to increase the intensity significantly since the molecules will be severely ionized. A convenient way to increase UP is to increase the wavelength λ. But it is still not realistic to increase the return energy to tens or hundreds of keV. First, such real long wavelength lasers are not available. Second, the returning electron flux drops roughly like λ−5.5, thus there will be a few electrons return to recollide with the target ion.45 It appears that LIED would not work in practice.
For LIED to spurn back to life, it takes another new idea.15 Does one really need tens to hundreds of keV electrons to achieve sub-angstrom spatial resolution? The answer is no. One needs only electrons with energies somewhat above 100 eV, and these electrons can be generated by present day mid-infrared lasers in many laboratories already.
3.2 The independent atom model and its region of validity
According to the independent atom model, the elastic scattering amplitude of a fixed-in-space molecule by a beam of electrons is given by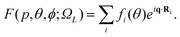 | (7) |
In IAM, a molecule is approximated as a collection of atoms fixed in space where the atomic nuclei are located at Ri. In the equation above, the complex electron–atom scattering amplitudes are given by {fi}. The momentum transfer q = p0 − p is the difference between the momentum of the incident and the scattered electron. For elastic scattering, p = |p| = |p0|, the magnitude of the momentum transfer is q = 2 p sin(θ/2), where θ is the angle between p and p0. In eqn (7), ΩL represents the spherical angles of the fixed-in-space molecular axis with respect to the incident direction of the electron beam, and θ and ϕ are the spherical angles of the scattered electrons.
The scattering DCS obtained from eqn (7) is given by
 | (8) |
| σ(θ) = 2σA(θ) + 2σA(θ)sin(qR)/qR. | (9) |
Here σA(θ) is the DCS for an individual atom. The ratio of the molecular interference term with respect to the atomic term is defined as the molecular contrast factor, γ. For the case of eqn (9), γ = sin(qR)/qR. If qR is not too small, the molecular interference term adds modulation to the smooth atomic DCS. If q is large, then a small change in R can result in a clear shift of the position of the maximum and minimum in the modulation term. In other words, if the internuclear distance changes only slightly, the shift of the fringe will still be quite visible. This is the underlying reason for the sensitivity of spatial resolution in electron diffraction. Since q = 2p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2), large q can be accomplished by large p and small θ. This is the condition used by the conventional electron diffraction method, where the electron energy is, say, at about 30 keV, and the scattering angle is limited to smaller than about 15° since beyond it the signal is too weak. The key to LIED is to use a smaller p, but larger angles θ. For electron energies of 100 to 200 eV and the range of angle θ from about 40° or 50° to 180°, the same range of momentum transfer q is spanned as in the conventional electron diffraction method.
sin(θ/2), large q can be accomplished by large p and small θ. This is the condition used by the conventional electron diffraction method, where the electron energy is, say, at about 30 keV, and the scattering angle is limited to smaller than about 15° since beyond it the signal is too weak. The key to LIED is to use a smaller p, but larger angles θ. For electron energies of 100 to 200 eV and the range of angle θ from about 40° or 50° to 180°, the same range of momentum transfer q is spanned as in the conventional electron diffraction method.
With sufficiently large q, the next question is whether the IAM model is still valid, i.e., can IAM describes the DCS for collisions at about 100 eV and over, at angles larger than 40° or 50°? One needs experimental data to check. But there is still another problem. For LIED, the returning electrons scatter with a molecular ion. The DCS data for electron collisions with molecular ions are rarely available in the literature for the obvious reason that target density for ions is much too small for differential measurements. Here large-angle scatterings come to help again. At the energies and large scattering angles that are of interest for LIED, the DCS is not sensitive to whether the outermost electron is removed or not, since such scattering is dominated by the force near the atomic center. The validity of this statement has been confirmed theoretically for atomic targets, and also in experiments on atomic targets with mid-infrared lasers where electron–atom collision DCS has been proved to be identical to the DCS extracted from the high-energy electron spectra generated by mid-infrared lasers, see Xu et al.69 Thus, to test the IAM model, we compare the calculations with electron–molecule collisions at large angles near and above about 100 eV. Such experimental DCS data are available from the earlier studies.70,71
In Fig. 4 the experimental DCS72,73 of N2 and O2 for scattering angles from 40° to 180° at collision energy of 100 eV are compared to the prediction of the IAM. The experimental data are normalized to the theory for optimal overlap. The known internuclear separation R for each molecule, 1.10 Å for N2 and 1.21 Å for O2, were used in the IAM calculation. The scattering amplitude for each atom is calculated with a model potential that fits the binding energy of the negative ion. We can see surprisingly good agreement between the IAM results and experimental data. How much does the remaining discrepancy affect the bond length retrieval in this example? We assume that the scattering amplitude for each atom is known, but we do not know the interatomic distance and the normalization factor in the experimental data. Using GA we find the interatomic distance R that best fits the measured DCS. The best retrieved R is 1.15 Å for N2 and 1.22 Å for O2. We have also used collision data at 150 eV and 200 eV, and concluded that the bond length extracted is always within better than 0.05 Å of the known values for these two molecules.
 | ||
| Fig. 4 Comparing the experimental DCS (red filled squares) with the IAM prediction (the blue lines), for 100 eV electrons colliding with N2 and O2, respectively. Experimental data from ref. 72 and 73. | ||
In short, we have confirmed that IAM can be applied to describe DCS for electron–molecular ion collisions from about 100 eV and up, for scattering angles larger than about 30° or 40°. Furthermore, the atomic scattering amplitude is the same for the neutral atom and the atomic cation. With these, the ingredients for using LIED for imaging are all set.
3.3 The first LIED experiment that revealed sub-angstrom spatial resolution
The first experiment that used mid-infrared lasers to generate high-energy photoelectron momentum spectra was reported by Blaga et al.16 recently. An optical parametric amplifier pumped by a Ti–sapphire front-end system (0.8 μm, 4.4 mJ, 50 fs and 1 kHz) generates continuously tunable mid-infrared laser pulses from 1.7 to 2.3 μm. The pulse length is 50 fs and pulse energies can be focused to about 250 TW cm−2. For this initial study, nitrogen and oxygen molecules are used. Photoelectrons are collected using field-free time-of-flight electron spectrometer, with angular resolution of 1.6°. The spectra were collected by rotating the laser polarization axis with respect to the spectrometer axis in steps of 2°. Fig. 5a shows a typical experimental photoelectron momentum spectrum from N2. The data are then analyzed using the procedure outlined above. | ||
| Fig. 5 Results from the first LIED experiment. (a) The photoelectron momentum spectra of N2 taken with a 2 μm, 50 fs laser pulse with intensity of 260 TW cm−2. The DCS extracted from the outer circle with radius |pr| = 2.71 a.u. is shown in (c). The photoelectron energy distribution is shown in (b). The DCS was extracted from photoelectron energies around 500 eV. The interatomic distance is fitted from the DCS data in (c) directly. To illustrate the sensitivity of the method, the molecular contrast factor vs. the interatomic separation is shown in (d) for N2, assuming a 10% increase or decrease from the known value of 1.10 Å. This sensitivity illustrated that sub-angstrom spatial resolution is obtained by large momentum transfer collisions which can be accomplished by lower collision energies at large scattering angles. (e) Comparing the molecular contrast factor from the experimental data with the one obtained from the IAM model, using R from the equilibrium N–N distance of 1.10 Å (dotted lines), with respect to the 1.14 Å obtained from the best fit to the data (solid lines). (f) The same as (e) but for O2. Note that the large discrepancy between the experimental data with the result from the IAM calculated with the neutral O–O distance (1.21 Å). The best fit to the data gives the O–O distance to be 1.10 Å. The 0.1 Å difference is the amount the bond length shrinks between the time the electron was born and the time rescattering took place, which is about 5 fs. Some figures were adopted from ref. 16. | ||
In Fig. 5a, 2D electron momentum spectra along the axis of laser polarization and perpendicular to it are shown for a broad range of electron momenta. Since the molecules are not aligned, the spectra have cylindrical symmetry with respect to the polarization axis of the laser. The inner circle marks electrons that have energies below 2Up, which has the most electron counts. The outer circle marks those electrons that return with momentum pr that have been elastically scattered. For LIED, we consider “pure” rescattered electrons only, i.e., only those electrons outside the small circles – they are not contaminated by the low-energy unscattered direct electrons.
With the experimental 2D electron momentum spectra available, the DCS for a given momentum pr is obtained from Fig. 5a by reading off the relative yields along the circumference of the outer circle. The displacement of this circle from the origin of the momentum plot gives the value of |−Ar|. For a given pr, |−Ar| can be calculated from a simple classical theory since the return time is related to the electron momentum at the time of collision. The DCS thus extracted are shown in Fig. 5c. Note that only the relative yields are needed in the extracted DCS. The shaded area in Fig. 5b shows the energy region of the photoelectrons where the DCS data were taken for the LIED analysis.
In Fig. 5c, the red curve shows the DCS calculated using the IAM for the given pr = 2.71, using the known bond length 1.10 Å of N2. Although the theory curve (after normalization at one point) goes through the extracted DCS, the data have large error bars due to the weak electron signals. Fig. 5d demonstrates the sensitivity of the method. It displays how the fringe of the molecular contrast factor changes as R is increased or decreased by 10%, or by about 0.1 Å from the equilibrium distance. By fitting the overall shape of the DCS to the IAM model with R and normalization factor as unknowns, the fluctuations of individual experimental points become less crucial.
For N2, using the electron spectra reported by Blaga et al., the N–N length retrieved using the LIED procedure is 1.14 Å. Compared to the known equilibrium N–N distance of 1.10 Å in N2 and 1.12 Å in N2+, this value is within the expected error of 0.05 Å estimated from the e−–N2 collision data. Fig. 5e shows the direct comparison of the molecular contrast factor extracted from the experimental data, compared to the one calculated using the value of best-fitted R and of the equilibrium R. Similar results have been extracted from DCS at other energies and lasers of different intensities. From the electron spectra of N2, we conclude that LIED does give a spatial resolution within about 0.05 Å.
In Blaga et al., high-energy electron spectra from oxygen molecules were also investigated. The same analysis shows (Fig. 5f) that the bond length retrieved from LIED is 1.10 Å using a 2 μm laser. This is to be compared to 1.21 Å known for the neutral O2. Such a large difference was not expected if the O–O distance remains constant during the time O2 was exposed to the laser since the error of the method was estimated to be less than 0.05 Å. Additional experiments at 1.7 μm and 2.3 μm were performed. The retrieved bond length was 1.11 and 1.02 Å, respectively. For comparison, the equilibrium bond length of O2+ is 1.12 Å.
The large deviation of the retrieved O–O bond length was interpreted as due to bond rearrangement of the two oxygen atoms after tunnel ionization. Since the valence orbital of O2 is an anti-bonding πg orbital, the removal of an electron is expected to make the O–O length shrinks toward new equilibrium length of 1.12 Å of O2+, but only after the vibrational energy on the new potential curve of O2+ is dissipated. Before this new equilibrium is reached, in a classical model the two oxygen atoms execute a harmonic oscillation, i.e., their distance changes with time, after the electron is removed. When the freed electron comes back to recollide with the O2+, it takes the image of the O–O distance at that instant. Using a simple classical model for the motion of a free electron in the laser field (see Fig. 2a), the electron returns to recollide with the ion within one optical cycle. Thus when the image was being taken it reflects the O–O distance at about one optical cycle after the electron is removed by tunnel ionization. For 2 μm laser, this is about 5 fs. Thus in Blaga et al. for the first time the movement of atoms by 0.1 Å in about five femtoseconds was observed – an unprecedented spatial and temporal resolution demonstrated by the LIED method. We comment that the vibrational period of O2+ is 17 fs. In a classical model, the amplitude of the vibration is about 0.1 Å, taken to be the difference between the equilibrium distances of O2 and O2+. In 5 fs, i.e., in about a quarter period, the O–O distance becomes close to 1.12 Å, which is consistent with the retrieved data. More detailed discussions on this result are given in Blaga et al.
We comment that only one laser was used in Blaga et al. The pump–probe “delay” time of five femtoseconds, where the pump is ionization, and the probe is the re-collision, is based on a classical model of the electron motion in the laser field. The main result of the experiment is the demonstration of 0.1 Å in spatial resolution in LIED. In future pump–probe experiments, the time delay is determined by the two pulses which is controlled by the experimentalists. For large molecules, sub-ten femtosecond temporal resolution is likely not needed except for processes occurring near conical intersections.
4 Summary and outlook
4.1 Comparison of present tools for probing dynamic systems
X-ray and electron diffraction have been used to measure the equilibrium structure of a large number of molecules. Currently, the prevailing method for studying time-evolving structural change of molecules is to extend these X-rays and electron beams to shorter durations, to hundreds or tens of femtoseconds. Both efforts require substantial new technologies. In the case of X-ray free-electron lasers, they are costly large facilities, while for an ultrafast or femtosecond electron diffraction method the duration is still limited to about 100 fs. These two methods, while are very powerful tools for many other applications, they still have not been employed to study dynamics of molecules at sub-angstrom spatial resolution and tens to a few-femtosecond temporal resolution.For more than two decades, optical pump–probe experiments have been routinely carried out at temporal resolution of tens of femtoseconds, but these measurements cannot be “inverted” to reveal atomic positions in a molecule directly. In recent years, with the emergence of a few-femtoseconds intense IR lasers and attosecond XUV pulses, together with free-electron lasers in the XUV region, many pump–probe experiments have been carried out.74–79 These new experiments mostly also face the same limitations as in optical pump–probe experiments in that the results yield little information about the time evolution of the change of the positions of atoms in the molecule, i.e., the images of the sticks and balls that make a “molecular movie”.
4.2 Works ahead for LIED
In this article, we described LIED, an “implicit” electron diffraction method using intense femtosecond mid-infrared lasers, as a potentially powerful new platform for imaging ultrafast dynamics of molecules. In this method, the emission, acceleration and guidance of electrons to form diffraction images are all carried out directly by the laser pulse alone. The first experiment using LIED has been carried out, demonstrating sub-angstrom spatial and a few-femtosecond temporal resolution. Since the basic theory for LIED is new, and the theory is not as “obvious” as the conventional electron or X-ray diffraction methods, there are still very few LIED measurements. Further development of LIED toward a useful tool for dynamic imaging would require more experimental groups to devote their efforts to perfect experimental techniques. Below we address some essential experiments that are needed for furthering the progress of LIED, and our view of its future as a tool for imaging ultrafast dynamics of molecules.(i) In LIED, the diffraction image is extracted from the angular distributions of high-energy photoelectrons. Since the yield for high-energy photoelectrons is low, the counts available for the extraction of DCS are few, thus affecting the statistics. Thus the first task is to increase the statistics of high-energy electrons. This probably can be done by applying a weak field to deflect the abundant low-energy electrons away from the detector. Since high-energy electrons have energies of several hundreds of electron volts they are not likely affected by the weak fields, see Fig. 5b. It is to be noted that any diffraction experiments, be X-ray or electron diffraction, the scattering cross section from each molecule is always small since all diffraction experiments depend on close-collision events. Many techniques have been developed for the manipulation of weak signals from X-ray and electron diffraction experiments. These techniques probably can be adopted in LIED as well.
(ii) It is desirable to perfect LIED experiments beyond the proof-of-principle stage. More experiments should be carried out to demonstrate its capability for spatial resolution, and for larger molecules. Thus high-energy electron spectra by mid-infrared lasers for three- or four-atom molecules are desirable immediately, first with randomly distributed molecules. These data can be compared directly with those obtained from the gas-phase electron diffraction method. Next, the same molecules can be aligned or oriented by infrared lasers. Using LIED, from such molecules both the bond lengths and bond angles can be extracted. In fact, gas-phase electron diffraction from impulsively aligned molecules has been reported by the group of Martin Centurion80 recently. Even if the molecules are only oriented or aligned in 1D, it would still be instructive to use LIED to extract the equilibrium structure parameters, with lasers linearly polarized along different directions with respect to the orientation or alignment axis. A large set of data can be collected and analyzed, and the resulting structure parameters can be compared to check their consistency.
(iii) In Blaga et al.,16 genetic algorithm was used for the inversion of the DCS data to obtain the bond length. For larger molecules, the retrieval of the increasing number of structure parameters from the DCS will become more challenging. According to eqn (6), the DCS retrieved from the electron spectra differ from gas-phase diffraction experiments only by the additional angle-dependent tunneling ionization factors, N(ΩL). These factors can be calculated using molecular tunnel ionization theory or the strong field ionization approximation, but it is better that they are obtained from experiments for more complex molecules. For complex molecules, it is also known that tunneling ionization may occur from several inner orbitals, besides from the highest occupied molecular orbital, as demonstrated in the HHG spectra.81–83 In the case of LIED, this effect would imply that eqn (6) should be replaced by a sum over the contributions from all of these orbitals. Since the DCS within the IAM model is independent of the outershell structure, the effect of summation is to replace N(ΩL) in eqn (6) as the total tunneling ionization rates, which can be measured experimentally. In the future, advanced data retrieval tools developed by the X-ray diffraction and electron diffraction communities should also be looked into, to check if they can be applied to the analysis of LIED data.
4.3 Perspectives of LIED vs. time-resolved X-ray and electron diffraction for molecules
After LIED has demonstrated its prowess, it would be desirable to use LIED as the probe pulse in a typical pump–probe experiment. In such experiments, an optical pump laser initiates a dynamic system. The dynamic system could be probed with a femtosecond X-ray method, by electron diffraction, or by LIED with intense mid-infrared lasers. All of them are aiming at probing the atomic positions of a molecule that change with time on femtosecond timescales.To determine the atomic positions in a molecule requires that the impinging particles or photons be scattered off very close to the nucleus of each atom, thus all three methods have to deal with small scattering DCS. Since the cross section for photon interaction with molecules is five to six orders of magnitude smaller than for electron interaction, the pulse energy needed for using XFEL for imaging is higher. In fact, facilities like LCLS generate so many photons that diffraction images are to be taken before the molecule is destroyed.7 In the time-resolved electron diffraction method, the challenge is not too many electrons, but rather that there are too few. At present there are technical difficulties in pushing durations of electron pulses below 100 fs. One proposed method to reduce it further is to use relativistic electron beams, increasing it from the current 30 keV to above 3 MeV. This will require a larger facility, and the diffraction images will have to be taken at much smaller scattering angles. The rapid development in technology undoubtedly will improve both X-ray and electron beams to shorter pulses and higher pulse energies, to make them more available in the years to come. On the other hand, are there alternatives?
Since LIED has not been widely examined in the laboratories yet, its full potential or limitation is difficult to assess. Until now, the small number of high-energy electrons is limiting the statistics, but their number is small only when compared to the copious low-energy electrons. A typical spectrum in Blaga et al. was taken within a few hours.
Looking into the future, there are several emerging laser technologies that may significantly increase the returning electron flux for the LIED experiments. Recall that LIED and HHG are both based on the same elementary rescattering processes, thus any advances in generating more intense HHG at higher photon energies will also directly benefit LIED. Since HHG is an important tool for the generation of table-top XUV to soft X-ray light pulses, continuing research effort in this area is expected. In all LIED and in most HHG experiments so far, a single-color infrared or mid-infrared laser is used. To take advantage of the λ2 dependence of the energies of the returning electrons, long-wavelength lasers can be used. This has the unfortunate disadvantage that the returning electron flux is also significantly reduced as stated earlier. However, simulations84,85 have shown that because of wave synthesizing – by combining Ti–Sapphire 800 nm laser pulses with mid-infrared laser pulses with some favorable phases and amplitudes – an increase of two orders of magnitude in the returning electron flux is possible (as compared to the mid-infrared alone), while at the same time, the returning electron energy may reach the 100–200 eV region. Wave synthesizing is a flourishing research area86–89 and much progress has been made. Thus there is hope for substantial increase of the returning electron flux for LIED measurement without much increase in the input laser power. Another way to increase high-energy electrons is to increase the repetition rate of the IR and mid-IR lasers. Most of the mid-IR lasers used so far operate at one kHz, but 100 kHz or MHz lasers are in the horizon.90–93 Historically, laser technology always advances at a much faster pace than other technologies, thus it is likely that present limits imposed by existing lasers may be removed in the next few years.
4.4 Route to uncovering femtosecond molecular dynamics
It is important to emphasize that each LIED (or X-ray and electron diffraction) measurement can only offer the distributions of atomic positions of a molecule in a dynamic system at a given time interval. Stitching these distributions together forms a “molecular movie” where the breaking or rearrangement of bonds (the sticks) between pairs of atoms is played out. However, such a simple picture is limited to simple systems where the pump pulse excites a single electronic potential surface only. In molecular physics, a pump pulse creates a time-dependent many-particle wave packet. This wave packet is expanded in general in terms of linear combination of products of electronic wavefunction and rovibrational wavefunction. For femtosecond probe pulses, the rotational motion can be considered frozen. Thus a diffraction measurement is used to extract the vibrational wave packet only. If two or more electronic potential surfaces are populated in the pump step, then the DCS may include the interference of scattering amplitudes from the two surfaces. Such situations have been analyzed theoretically by Wilson and co-workers94 using X-ray and electron diffraction as the probe pulse in the late 1990s. Due to the lack of experiments, their formulation has not been tested so far.History has shown that it takes many tools to study the properties of an isolated molecule at equilibrium. It will take even more measurements to probe a dynamic system which is represented by a time-dependent many-body wave packet. As stated earlier, this wave packet is expanded in terms of approximate eigenstates of a molecule at fixed atomic positions. In quantum mechanics, each measurement is a projection operation, thus only partial information of the system is obtained. It is therefore nearly impossible to “reconstruct” the whole wave packet based on a few measurements. To “paint” a picture of how a dynamic system evolves would require many measurements for each wave packet. The measurements may include fragmentation of molecules or photoelectron angular distributions, by exposing the dynamic system to an UV or XUV light pulse. They may include measuring the HHG spectra, or the low-energy electron spectra, by exposing the dynamic system to a strong field. Since a master laser can be split into many arms, one arm can be used as a pump pulse, and the other(s) used as probe pulse(s), many such measurements can be performed on a single wave packet. In this way, the advantage of using LIED to map out the atomic positions is clear since it would use the same all-optical setup. With a slew of arsenal to interrogate a wave packet that was generated under the same conditions, a more complete picture of the dynamic system may emerge. We stress that data from LIED alone would not provide the essential understanding needed for a chemical reaction or a biological function. For this purpose, other tools that probe outer-shell phenomena of the molecule are needed. On the other hand, to understand these outer-shell processes, information about the positions of individual atoms in a molecule is needed. This is the role that can be provided by LIED.
Last but not the least, it goes without saying that theory also will have to play an essential role in order to understand a dynamic system. Experiments involving outer-shell electrons of a molecule cannot be understood without theoretical simulations.95,96 Thanks to theoretical tools developed over the past half a century in quantum chemistry, some of these tools can be used also for dynamic systems. The role of theory perhaps is best illustrated in Fig. 6. In this close-loop cartoon we show how quantum chemistry can help bridging the gap between two different measurements. Here a molecule (or a wave packet initiated by a pump pulse) is exposed to an intense mid-infrared laser pulse. Experimentally, the high-energy electron momentum spectra and HHG spectra are measured. Based on the QRS theory, the DCS is extracted from the electron spectra. Using GA or other retrieval software, the atomic positions can be extracted. Once these positions are known, using quantum chemistry codes, photo-recombination cross sections and the phases of the transition dipoles can be calculated. With these results, together with the QRS theory, theoretical HHG spectra can be calculated which are then compared to the measured HHG spectra. Similar calculations can be performed for measurements carried out by other tools if the atomic positions are given. With an iterative procedure, the consistency of the model for the dynamical system can be evaluated.
 | ||
| Fig. 6 LIED is a method of imaging the atomic positions of a molecule. LIED, as well as electron or X-ray diffraction methods, does not probe the main features in a chemical reaction or a biological function. The latter are outer-shell phenomena, involving the breaking and rearrangement of chemical bonds, as well as distributions of electronic charges. However, without the knowledge of the positions of atoms in a molecule, no chemistry can be studied. Since femtosecond chemistry is often carried out with pump–probe technique, this cartoon illustrates how LIED can be combined with another probe, HHG measurement in this example, in a similar setup. The pump beam initiates an isomerization process in acetylene. A probe pulse at a given delay time is used to generate photoelectron spectra. Using the QRS theory the DCS can be extracted and GA is used to retrieve the positions of atoms in the molecule at the given time delay. In the meanwhile, HHG spectra are measured from a probe pulse at the same time delay. From the retrieved atomic positions in the molecule, using quantum chemistry code to obtain photo-recombination cross section, together with the QRS, the theoretical HHG spectra can be calculated and compared to the measured HHG spectra. Good agreement with the HHG experimental data would imply that the theory describes the outer-shell “structure” correctly. Other method of probing outer-shell phenomena can also be combined with LIED, for example, by measuring photoelectron angular distributions, by the momentum distributions and charge states distributions of the fragments. We comment that quantitative interpretation of any outer shell phenomena is not possible without elaborate theoretical calculations. The route to dynamic imaging of molecules is tedious. It will take many different measurements and much more theoretical efforts than molecules at equilibrium. Figures reprinted with permission from ref. 32. Copyright(2010) Institute of Physics. | ||
In summary, the route to full understanding of a time-evolving molecular system is long and tedious. It will take many different experiments to gain a good glimpse of a real chemical event. While the ball-and-stick model does not tell us much about the chemistry of a molecule, chemistry cannot be studied without knowing the nature of the balls and the sticks. LIED, like X-ray and electron diffraction, is such a tool. Further development in the next few years will tell whether LIED will emerge as a piece of useful table-top tool in chemical laboratories.
Acknowledgements
We thank our colleagues who have involved in different stages of the development of the quantitative rescattering theory, including Anh-Thu Le, Zhangjin Chen, Toru Morishita, Robert Lucchese and Cheng Jin. We also thank Cosmin Blaga and other members of the group of Lou DiMauro and Pierre Agostini at Ohio State University for performing the first measurement to demonstrate sub-angstrom spatial resolution predicted in LIED. This work was partially supported by Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy.References
- A. H. Zewail and J. M. Thomas, 4D Electron Microscopy: Imaging in Space and Time, Imperial College Press, London, 2010 Search PubMed.
- M. Fushitani, Annu. Rep. Prog. Chem., Sect. C, 2008, 104, 272–297 RSC.
- D. Strasser, F. Goulay and S. R. Leone, J. Chem. Phys., 2007, 127, 184305 CrossRef.
- C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Geβner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464–1468 CrossRef CAS.
- H. Xu, T. Okino and K. Yamanouchi, J. Chem. Phys., 2009, 131, 151102 CrossRef.
- A. Hishikawa, A. Matsuda, M. Fushitani and E. J. Takahashi, Phys. Rev. Lett., 2007, 99, 258302 CrossRef.
- R. Neutze, R. Wouts, D. van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757 CrossRef CAS.
- H. Ihee, V. A. Lobastov, U. M. Gomez, B. M. Goodson, R. Srinivasan, C.-Y. Ruan and A. H. Zewail, Science, 2001, 291, 458–462 CrossRef CAS.
- P. Reckenthaeler, M. Centurion, W. Fuβ, S. A. Trushin, F. Krausz and E. E. Fill, Phys. Rev. Lett., 2009, 102, 213001 CrossRef.
- B. J. Siwick, J. R. Dwyer, R. E. Jordan and R. J. D. Miller, Science, 2003, 302, 1382–1385 CrossRef CAS.
- H. N. Chapman, P. Fromme, A. Barty, T. A. White, R. A. Kirian and A. Aquila, et al. , Nature, 2011, 470, 73–77 CrossRef CAS.
- M. Eichberger, H. Schäfer, M. Krumova, M. Beyer, J. Demsar, H. Berger and G. Moriena, et al. , Nature, 2010, 468, 799–802 CrossRef CAS.
- G. Sciaini and R. J. D. Miller, Rep. Prog. Phys., 2011, 74, 096101 Search PubMed.
- T. Elsaesser and M. Woerner, Acta Crysallogr., Sec. A: Found. Crystallogr., 2010, 66, 168–178 Search PubMed.
- J. Xu, Z. Chen, A.-T. Le and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 023814 Search PubMed.
- C. I. Blaga, J. Xu, A. D. DiChiara, E. Sistrunk, K. Zhang, Z. Chen and A.-T. Le, et al. , Nature, 2012, 483, 194–197 Search PubMed.
- M. M. Seibert, T. Ekeberg, F. R. N. C. Maia, M. Svenda, J. Andreasson, O. Jönsson and D. Odić, et al. , Nature, 2011, 470, 78–81 CrossRef CAS.
- J. M. Glownia, J. Cryan, J. Andreasson, A. Belkacem, N. Berrah, C. I. Blaga and C. Bostedt, et al. , Opt. Express, 2010, 18, 017620 Search PubMed.
- M. Krikunova, T. Maltezopoulos, A. Azima, M. Schlie, U. Frühling, H. Redlin and R. Kalms, et al. , New J. Phys., 2009, 11, 123019 Search PubMed.
- A. Azima, S. Düsterer, R. Radcliffe, H. Redlin, N. Stojanovic, W. Li and H. Schlarb, et al. , Appl. Phys. Lett., 2009, 94, 144102 Search PubMed.
- C. H. Yoon, P. Schwander, C. Abergel, I. Andersson, J. Andreasson, A. Aquila and S. Bajt, et al. , Opt. Express, 2011, 19, 16542–16549 Search PubMed.
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek and A. Brachmann, et al. , Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- F. Filsinger, G. Meijer, H. Stapefeldt, H. N. Chapman and J. Küpper, Phys. Chem. Chem. Phys., 2011, 13, 2076–2087 RSC.
- J. Kim, K. H. Kim, J. H. Lee and H. Ihee, Acta Crysallogr., Sec. A: Found. Crystallogr., 2010, 66, 270–280 Search PubMed.
- S. Pabst, P. J. Ho and R. Santra, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 043425 CrossRef.
- Stereochemical Applications of Gas-Phase Electron Diffraction, ed. I. Hargittai and M. Hargittai, VCH, New York, 1988, vol. I and II Search PubMed.
- M. Aidelsburger, F. O. Kirchner, F. Krausz and P. Baum, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19714–19719 Search PubMed.
- P. Musumeci, J. T. Moody, C. M. Scoby, M. S. Gutierrez, M. Westfall and R. K. Li, J. Appl. Phys., 2010, 108, 114513 Search PubMed.
- F. Carbone, P. Musumeci, O. J. Luiten and C. Hebert, Chem. Phys., 2012, 392, 1–9 Search PubMed.
- A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS.
- A. L. Cavalieri, N. Müller, T. Uphues, V. S. Yakovlev, A. Baltuška, B. Horvath and B. Schmidt, et al. , Nature, 2007, 449, 1029–1032 CrossRef CAS.
- C. D. Lin, A. T. Le, Z. Chen, T. Morishita and R. Lucchese, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 122001 Search PubMed.
- T. Morishita, A. T. Le, Z. Chen and C. D. Lin, New J. Phys., 2008, 10, 025011 Search PubMed.
- Z. Chen, A. T. Le, T. Morishta and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 033409 Search PubMed.
- M. V. Frolov, N. L. Manakov and A. F. Starace, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 033406 Search PubMed.
- A. Čerkić, E. Hasović, D. B. Milošević and W. Becker, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 033413 Search PubMed.
- O. I. Tolstikhin, T. Morishita and S. Watanabe, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 033415 Search PubMed.
- J. Xu, H.-L. Zhou, Z. Chen and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 052508 Search PubMed.
- T. Morishita, T. Umegaki, S. Watanabe and C. D. Lin, J. Phys.: Conf. Ser., 2009, 194, 012011 Search PubMed.
- D. Ray, B. Ulrich, I. Bocharova, C. Maharjan, P. Ranitovic, B. Gramkow and M. Magrakvelidze, et al. , Phys. Rev. Lett., 2008, 100, 143002 Search PubMed.
- M. Okunishi, T. Morishita, G. Prümper, K. Shimada, C. D. Lin, S. Watanabe and K. Ueda, Phys. Rev. Lett., 2008, 100, 143001 Search PubMed.
- M. Okunishi, H. Niikura, R. R. Lucchese, T. Morishita and K. Ueda, Phys. Rev. Lett., 2011, 106, 063001 Search PubMed.
- S. Micheau, Z. Chen, A. T. Le, J. Rauschenberger, M. F. Kling and C. D. Lin, Phys. Rev. Lett., 2009, 102, 073001 CrossRef CAS.
- C. Cornaggia, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 161002 Search PubMed.
- J. Tate, T. Auguste, H. G. Muller, P. Salières, P. Agostini and L. F. DiMauro, Phys. Rev. Lett., 2007, 98, 013901 Search PubMed.
- P. Colosimo, G. Doumy, C. I. Blaga, J. Wheeler, C. Hauri, F. Catoire and J. Tate, et al. , Nat. Phys., 2008, 4, 386–389 Search PubMed.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994–1997 CrossRef CAS.
- K. J. Schafer, B. Yang, L. F. DiMauro and K. C. Kulander, Phys. Rev. Lett., 1993, 70, 1599–1602 CrossRef CAS.
- M. Lewenstein, P. Balcou, M. Y. Ivanov, A. L'Huillier and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 2117–2132 CrossRef.
- Z. Chen, T. Morishita, A.-T. Le and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 043402 Search PubMed.
- M. Lein, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, R135–R173 CrossRef CAS.
- S. Haessler, J. Caillat and P. Salières, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 203001 Search PubMed.
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867–871 CrossRef CAS.
- C. Vozzi, M. Negro, F. Calegari, G. Sansone, M. Nisoli, S. D. Silvestri and S. Stagira, Nat. Phys., 2011, 7, 822–826 Search PubMed.
- V. H. Le, A. T. Le, R. H. Xie and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 013414 Search PubMed.
- T. Morishita, A. T. Le, Z. Chen and C. D. Lin, Phys. Rev. Lett., 2008, 100, 013903 Search PubMed.
- Z. Chen, A. T. Le, T. Morishita and C. D. Lin, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 061001 Search PubMed.
- M. Okunishi, R. Itaya, K. Shimada, G. Prümper, K. Ueda, M. Busuladžić and A. Gazibegović-Busuladžić, et al. , J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 201004 Search PubMed.
- S. J. Brotton, P. McKenna, G. Gribakin and I. D. Williams, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 062706 Search PubMed.
- X. M. Tong and C. D. Lin, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 2593 Search PubMed.
- K. A. Berrington, W. B. Eissner and P. H. Norrington, Comput. Phys. Commun., 1995, 92, 290 Search PubMed.
- M. Meckel, D. Comtois, D. Zeidler, A. Staudte, D. Pavičić, H. C. Bandulet and H. Pépin, et al. , Science, 2008, 320, 1478–1482 CrossRef CAS.
- S. K. Lee, Y. F. Lin, L. Yan and W. Li, J. Phys. Chem. A, 2012, 116, 1950–1955 Search PubMed.
- X. M. Tong, Z. X. Zhao and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 033402 CrossRef.
- S.-F. Zhao, C. Jin, A.-T. Le, T. F. Jiang and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 051402(R) Search PubMed.
- J. Muth-Böhm, A. Becker and F. H. M. Faisal, Phys. Rev. Lett., 2000, 85, 2280–2283 CrossRef CAS.
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543–557 CrossRef CAS.
- H. Miyagi, T. Morishita and S. Watanabe, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 022708 Search PubMed.
- J. Xu, C. I. Blaga, A. D. DiChiara, E. Sistrunk, K. Zhang, Z. Chen and A.-T. Le, et al. , Phys. Rev. Lett., 2012 Search PubMed (submitted).
- M. J. Brunger and S. J. Buckman, Phys. Rep., 2002, 357, 215–458 Search PubMed.
- S. Trajmar, D. Register and A. Chutjian, Phys. Rep., 1983, 97, 219–356 Search PubMed.
- D. Herrmann, K. Jost, J. Kessler and M. Fink, J. Chem. Phys., 1976, 64, 1–5 Search PubMed.
- T. W. Shyn and W. E. Sharp, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 1369–1372 Search PubMed.
- H. J. Wörner, J. B. Bertrand, D. V. Kartashov, P. B. Corkum and D. M. Villeneuve, Nature, 2010, 466, 604–607 CrossRef CAS.
- H. J. Wörner, J. B. Bertrand, B. Fabre, J. Higuet, H. Ruf, A. Dubrouil and S. Patchkovskii, et al. , Science, 2011, 334, 208–212 Search PubMed.
- W. Li, X. Zhou, R. Lock, S. Patchkovskii, A. Stolow, H. C. Kapteyn and M. M. Murnane, Science, 2008, 322, 1207–1211 Search PubMed.
- W. Li, A. A. Jaroń-Becker, C. W. Hogle, V. Sharma, X. Zhou, A. Becker and H. C. Kapteyn, et al. , Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20219–20222 CrossRef CAS.
- Y. H. Jiang, A. Rudenko, O. Herrwerth, L. Foucar, M. Kurka, K. U. Kühnel and M. Lezius, et al. , Phys. Rev. Lett., 2010, 105, 263002 CrossRef CAS.
- T. K. Allison, H. Tao, W. J. Glover, T. W. Wright, A. M. Stooke, C. Khurmi and J. van Tilborg, et al. , J. Chem. Phys., 2012, 136, 124317 Search PubMed.
- C. J. Hensley, J. Yang and M. Centurion, Phys. Rev. Lett., 2012 Search PubMed (submitted).
- C. Jin, J. B. Bertrand, R. R. Lucchese, H. J. Wörner, P. B. Corkum, D. M. Villeneuve, A. T. Le and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 013405 Search PubMed.
- C. Jin, H. J. Wörner, V. Tosa, A. T. Le, J. B. Bertrand, R. R. Lucchese, P. B. Corkum, D. M. Villeneuve and C. D. Lin, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 095601 Search PubMed.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972–977 CrossRef CAS.
- L. E. Chipperfield, J. S. Robinson, J. W. G. Tisch and J. P. Marangos, Phys. Rev. Lett., 2009, 102, 063003 Search PubMed.
- S.-W. Huang, G. Cirmi, J. Moses, K.-H. Hong, S. Bhardwaj, J. R. Birge and L.-J. Chen, et al. , J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 074009 Search PubMed.
- H.-S. Chan, Z.-M. Hsieh, W.-H. Liang, A. H. Kung, C.-K. Lee, C.-J. Lai and R.-P. Pan, et al. , Science, 2011, 331, 1165–1168 Search PubMed.
- T. Siegel, R. Torres, D. J. Hoffmann, L. Brugnera, I. Procino, A. Zar and J. G. Underwood, et al. , Opt. Express, 2010, 18, 6853–6862 Search PubMed.
- H. C. Bandulet, D. Comtois, E. Bisson, A. Fleischer, H. Pépin, J. C. Kieffer and P. B. Corkum, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 013803 Search PubMed.
- S.-W. Huang, G. Cirmi, J. Moses, K.-H. Hong, S. Bhardwaj, J. R. Birge and L.-J. Chen, et al. , Nat. Photonics, 2010, 81, 013803 Search PubMed.
- M. C. Chen, M. R. Gerrity, S. Backus, T. Popmintchev, X. Zhou, P. Arpin and X. Zhang, et al. , Opt. Express, 2009, 17, 17376–17383 Search PubMed.
- A. Vernaleken, J. Weitenberg, T. Sartorius, P. Russbueldt, W. Schneider, S. L. Stebbings and M. F. Kling, et al. , Opt. Lett., 2011, 36, 3428–3430 Search PubMed.
- C. M. Heyl, J. Güdde, A. L'Huillier and U. Höfer, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 074020 Search PubMed.
- J. Boullet, Y. Zaouter, J. Limpert, S. Petit, Y. Mairesse, B. Fabre and J. Higuet, et al. , Opt. Lett., 2009, 34, 1489–1491 Search PubMed.
- M. Ben-Nun, J. Cao and K. R. Wilson, J. Phys. Chem., 1997, 101, 8743–8761 Search PubMed.
- Y. Arasaki, K. Takatsuka, K. Wang and V. McKoy, J. Chem. Phys., 2010, 132, 124307 CrossRef.
- A.-T. Le, T. Morishita, R. R. Lucchese and C. D. Lin, Phys. Rev. Lett., 2012 Search PubMed (submitted).
| This journal is © the Owner Societies 2012 |
