Dissociation dynamics of fluorinated ethene cations: from time bombs on a molecular level to double-regime dissociators

Abstract

The dissociative photoionization mechanism of internal energy selected C₂H₃F⁺, 1,1-C₂H₂F₂⁺, C₂HF₃⁺ and C₂F₄⁺ cations has been studied in the 13–20 eV photon energy range using imaging photoelectron photoion coincidence spectroscopy. Five predominant channels have been found; HF loss, statistical and non-statistical F loss, cleavage of the C–C bond post H or F-atom migration, and cleavage of the C=C bond. By modelling the breakdown diagrams and ion time-of-flight distributions using statistical theory, experimental 0 K appearance energies, E₀, of the daughter ions have been determined. Both C₂H₃F⁺ and 1,1-C₂H₂F₂⁺ are veritable time bombs with respect to dissociation viaHF loss, where slow dissociation over a reverse barrier is followed by an explosion with large kinetic energy release. The first dissociative ionization pathway for C₂HF₃ and C₂F₄ involves an atom migration across the C=C bond, giving CF–CHF₂⁺ and CF–CF₃⁺, respectively, which then dissociate to form CHF₂⁺, CF⁺ and CF₃⁺. The nature of the F-loss pathway has been found to be bimodal for C₂H₃F and 1,1-C₂H₂F₂, switching from statistical to non-statistical behaviour as the photon energy increases. The dissociative ionization of C₂F₄ is found to be comprised of two regimes. At low internal energies, CF⁺, CF₃⁺ and CF₂⁺ are formed in statistical processes. At high internal energies, a long-lived excited electronic state is formed, which loses an F atom in a non-statistical process and undergoes statistical redistribution of energy among the nuclear degrees of freedom. This is followed by a subsequent dissociation. In other words only the ground electronic state phase space stays inaccessible. The accurate E₀ of CF₃⁺ and CF⁺ formation from C₂F₄ together with the now well established Δ_fH^o of C₂F₄ yield self-consistent enthalpies of formation for the CF₃, CF, CF₃⁺ and CF⁺ species.

---

1. Introduction

The C–F bond is one of the strongest in organic molecules. Exceptions include the C–H bond in acetylene, the C=C double and C≡C triple bonds.¹ This makes fluorinated alkanes and alkenes particularly appealing subjects in studies of their bonding, electronic spectroscopy and dissociation properties, because the strong bonding also results in sparsely spaced electronic levels. In addition, the small size of the fluorine atom makes these organic compounds amenable to computational chemistry studies, in which thermochemical properties such as enthalpies of formation can be determined.² In contrast to saturated perfluorocarbons,³ which photoionize dissociatively even at their ionization energy, the unsaturated fluorinated ethenes form stable molecular ions.⁴ Partly because of this great stability, early studies of fluorinated ethene cations have shown that they are metastable with respect to dissociation at low internal energies⁵ and can exhibit isolated state behaviour.^6,7

The dissociative photoionization of mono- and 1,1-difluoroethene was first investigated using threshold coincidence techniques by Güthe et al.,⁸ who reported complete kinetic energy release distributions (KERD) for the HF and F loss reaction channels based on the time-of-flight (TOF) spectra of the daughter ions. However, the insufficient mass resolution in the experiment did not allow for the determination of the appearance energy of the F-loss product, C₂H₂F⁺, from 1,1-C₂H₂F₂⁺. In a second paper, Güthe et al.⁹ further explored the metastable nature of the parent ion in the lowest energy dissociation channel, i.e.HF elimination from both C₂H₃F⁺ and 1,1-C₂H₂F₂⁺. Lifetimes on the order of several μs were found using both linear and reflectron time-of-flight mass spectrometers. They reported dissociation rate constants for both ions over a range from threshold to 400 meV above threshold, the smallest of which, 8 × 10⁴ s⁻¹, was observed with the linear TOF. A tight 4-membered ring transition state with a calculated reverse barrier of 163 kJ mol⁻¹ had been suggested for HF loss from 1,1-C₂H₂F₂⁺,¹⁰ in contrast with the smaller measured reverse barrier of only 95 kJ mol⁻¹. Analogously to HCl loss from C₂H₅Cl¹¹ or H₂ loss from C₂H₄,¹² Güthe et al. proposed H atom tunnelling to explain this discrepancy. The bimodal, statistical as well as non-statistical behaviour of F-loss from 1,1-C₂H₂F₂⁺ was investigated by examination of the KERDs using the maximum entropy method.¹³ Only the lower energy dissociative photoionization modus was found to be a statistical adiabatic reaction from the ionic ground state of the parent molecule, which formed a narrow KERD component.

The dissociative photoionization dynamics of trifluoroethene have not previously been studied. Tetrafluoroethene was the subject of a threshold coincidence study by Jarvis et al.⁴ They reported that F loss from C₂F₄⁺ is accompanied by high kinetic energy (KE) release, too large to be justified by a purely impulsive model, and they suggested two explanations. First, that the used heat of formation for C₂F₃⁺ was too high, and dissociation occurs below 15.85 eV. Second, that C₂F₄⁺ may decay via a ‘modified impulsive’ mechanism, where energy is deposited exclusively into the rotational and translational modes.

In this work, the imaging photoion photoelectron coincidence (iPEPICO) experiment¹⁴ at the VUV beamline¹⁵ of the Swiss Light Source (SLS) is used to prepare and study the dissociation dynamics of internal energy selected ions of monofluoroethene, 1,1-difluoroethene, trifluoroethene and tetrafluoroethene in the 13–20 eV photon energy range with a resolution much higher than in previous studies, i.e. only a few meV. The residence time of photoions in the acceleration region of the TOF mass spectrometer is several μs. If, while the ion resides in the acceleration region, there is significant dissociation then the fragment ion peak shapes are asymmetric and their analysis can yield dissociation rate constants,¹⁶ which are measured in the 10³ s⁻¹ < k < 10⁷ s⁻¹ range. This effect is distinct and different from a symmetrical TOF peak broadening due to kinetic energy release. The iPEPICO experiment yields both the threshold photoelectron spectrum (TPES) as well as parent and daughter ion fractional abundances as a function of the photon energy, which translates into an ion internal energy scan when the ion signal is evaluated in coincidence with threshold electrons. Metastable and parallel fragmentations can be modelled in the framework of the statistical theory of unimolecular reactions: the asymmetric TOF distributions yield the rate curve, k(E), as a function of internal energy which can be extrapolated to the 0 K appearance energy, E₀, below which k(E) vanishes. Accurate appearance energies of the daughter ions at 0 K can thus be established even when the low reaction rates result in incomplete dissociation of the parent ions at threshold, an effect often referred to as the kinetic shift.¹⁷ For fast dissociations in small molecules, the disappearance energy of the energy-selected parent ion signal yields the 0 K appearance energy, i.e. the energy at which all photoions, including those formed from neutrals with zero internal energy, are above the threshold.¹⁸

What does this appearance energy mean? Most ionic dissociations consist of simple bond breaking, which takes place along purely attractive potential energy curves. In such instances, the 0 K appearance energy equals the dissociative photoionization energy, E_dp. This E_dp value can be used in thermochemical cycles to determine 0 K enthalpies of formation for daughter ions, when the precursor parent enthalpy of formation is known, or vice versa (see Fig. 1a).¹⁹ In reactions that involve rearrangements, such as HF-loss, we also have to consider the barrier in the backward direction. Neglecting tunnelling, the appearance energy and the dissociative photoionization energy together can yield the value of this backward or reverse barrier (E_rb in Fig. 1b).

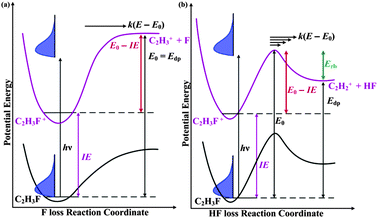Fig. 1 Energy diagram for the dissociations of (a) C₂H₃F⁺ into C₂H₃⁺ +F without and (b) C₂H₃F⁺ into C₂H₂⁺ + HFwith a reverse barrier. IE is the ionization energy, E_dp is the dissociative photoionization energy, E_rb is the height of the reverse barrier, E₀ is the 0 K appearance energy at which the products are first energetically accessible in the absence of tunnelling, and E₀ − IE is the height of the forward barrier. When there is no reverse barrier present, E₀ = E_dp.

A process is considered statistical if the complete phase space is accessible to the system. The ion density of states is dominated by the ground electronic state of the parent cation, which implies that the dissociation takes place from this ground electronic state. The adiabatic ionization energies of monofluoroethene, 1,1-difluoroethene, trifluoroethene and tetrafluoroethene are 10.37, 10.30, 10.14²⁰ and 10.11 eV,²¹ respectively. The dissociative photoionization channels all take place above 13 eV at energies corresponding to excited valence states of the four parent cations or in Franck–Condon gaps. If decay processes from these excited states to the ground state are slower than other processes, such as fluorescence or even dissociation, some excited states may have an isolated character and follow a non-statistical path. This has been suggested for several halogen containing ions, such as C₂F₄,⁴CF₃I,²²SiCl₄,²³ as well as Sn(CH₃)₃Cl, Sn(CH₃)₃Br²⁴ and even CH₃OH.^25,26 There are features uncharacteristic of statistical processes present in the breakdown diagrams of all four fluorinated ethene ions studied in this paper. Most notably, the fractional abundance of the daughter ions arising from F loss often follows the band intensities of the TPE spectrum of the molecule.

Two intriguing aspects of the dissociative photoionization of fluorinated ethenes are of particular interest to this work. First, we elaborate on the previously observed metastability of the parent ion when HF is lost. The slow dissociation rates correspond to parent ion lifetimes in the μs range, and the large reverse barriers to HF formation lead to impulsive dissociations with more than 1 eV kinetic energy being released. Since the leaving neutral and the fragment ion have comparable masses, a significant portion of this kinetic energy is deposited in the ion and leads to TOF peak broadening. Thus, these metastable parent ions are veritable time bombs with long delays in decay, but with eventual explosive fragmentation. Second, non-statistical dissociations are often associated with impulsive processes occurring on ion surfaces with a strongly repulsive character, as in ground electronic states of CF₄⁺ or CCl₄⁺,^23,27 or with fluorescence, i.e. an alternative relaxation pathway, as in N₂O⁺.^28,29 However, we will show that this is not always the case; long lived excited electronic states can in fact dissociate statistically when only the ground electronic state phase space is inaccessible to the system, and the long lifetimes allow for the statistical redistribution of the internal energy among the nuclear degrees of freedom.

2. Experimental approach

The imaging photoelectron photoion coincidence (iPEPICO) spectrometer¹⁴ has been described in detail elsewhere, and only a brief overview is given here. The pure sample is introduced into the chamber through an effusive source at room temperature, with typical pressures in the experimental chamber being 2–4 × 10⁻⁶ mbar during measurement. The background pressure is in the order of 10⁻⁷ mbar. The sample is ionized by the incident monochromatic vacuum ultra violet (VUV) synchrotron radiation dispersed by a grazing incidence monochromator. The photon energy resolution is 3 meV at 10 eV and the photon energy is calibrated in the first and second order against argon and neon autoionization states. Higher orders of radiation are effectively removed using a compact gas filter.¹⁵

Following photoionization, the photoelectrons and photoions are accelerated in opposite directions by a constant extraction field of 120 V cm⁻¹. The photoelectrons are velocity map imaged onto a DLD40 Roentdek position sensitive delay-line detector with a kinetic energy resolution of 1 meV at threshold. After acceleration in the 5 cm long 120 V cm⁻¹ first acceleration region, the ions undergo a further acceleration to −1800 V, which provides the necessary space focusing conditions. Ions then enter the 55 cm field free drift region and are finally detected by a Jordan TOF C-726 microchannel plate assembly.

Threshold electrons are velocity map imaged onto the centre of the position sensitive detector. Some of the kinetic energy (also referred to as hot) electrons have a velocity vector that is oriented along the flight tube axis and also arrive at the centre of the detector. The hot electron contamination of the threshold signal is accounted for by a simple subtraction process, as introduced by Sztáray and Baer.³⁰ The signal from a small ring around the central spot, as captured by the delay-line detector, is subtracted from the central threshold signal. This method enables the use of high extraction fields without sacrificing the quality of the true threshold signal. Electron hit positions and times, together with the ion hits, are recorded in a triggerless mode of a HPTDC time-to-digital converter card. Electrons and ions are correlated ‘on the fly’, obtaining time-of-flight distributions without deadtime. This multistart–multistop mode of data acquisition,³¹ which is particularly suited to high intensity synchrotron work, enables data acquisition with high ionization rates. The primary experimental data are the threshold ion TOF distributions as a function of photon energy, containing both the fractional ion abundances as well as the rate information in the form of asymmetric daughter ion peak shapes. The former can be concisely plotted in the breakdown diagram, i.e. the fractional ion abundances as a function of the photon energy, which includes most experimental information for fast dissociations.

3. Computational methods

3.1 Statistical modelling of unimolecular dissociations

The framework used to analyse the experimental data has been described in detail elsewhere, and only the most relevant aspects are mentioned here.¹⁶ The initial thermal energy distribution of the parent neutral molecule is assumed to be transposed onto the ion manifold without significant distortion in threshold ionization. This assumption is valid when the depth of the potential energy well is larger than the width of the thermal energy distribution^32,33 (see Fig. 1). Exceptions to this rule seem to be restricted to smaller molecules, such as CH₃I and CFBr₃.^34,35 If the first dissociation step is fast, every ion above the dissociative photoionization energy will dissociate and form a fragment ion and its 0 K appearance energy will be found where the parent ion signal vanishes. In order to model such processes, only the thermal energy distribution of the neutral molecule is needed, which can be calculated based on ab initio harmonic frequencies and rotational constants. By contrast, the dissociation rates do play a role in slow reactions, in which not all ions with sufficient energy dissociate, as well as in parallel processes, in which the ratio of the rates determines the branching ratio and hence the ion fractional abundances in the breakdown diagram. For slow dissociation reactions, the TOF distributions provide direct rate information, and are modelled along with the breakdown diagram. The absolute rate curves are fitted to reproduce the experimental rates in the observed energy range, and are extrapolated to obtain 0 K appearance energies. The relative rate information is used in a similar fashion for modelling the breakdown diagram of parallel, competing dissociations. In such cases, the higher-energy parallel dissociation channel may be relatively fast at threshold, but still slower than the faster lower-energy channel. Modelling the resulting competitive shift, i.e. the fact that the second daughter ion only appears at higher energies than its thermochemical threshold, is crucial to determine an accurate 0 K appearance energy for the higher-energy channel, as will be shown for C₂F₄ in Section 4.4.

Statistical rates as a function of internal energy are calculated using the transition state theory expression,

k(E) = σN^‡(E − E₀)/hρ(E) (1)

where σ is the symmetry number, h is Planck's constant, N^‡(E − E₀) is the number of states of the transition state and ρ(E) is the density of states of the fragmenting ion.³⁶ The slow dissociations reported here take place along a potential energy curve with a well-defined energy maximum (i.e. a saddle point on the potential energy surface), meaning that there is an unambiguous transition state structure. This calls for the application of rigid activated complex Rice–Ramsperger–Kassel–Marcus (RAC-RRKM) theory.³⁷ The ion and transition state harmonic frequencies are then used to calculate the density and number of states, respectively, and the transitional mode frequencies are scaled by a factor to reproduce the experimentally observed rate curve. In such cases, this scaling factor and the 0 K appearance energy are the only two fitting parameters in the data analysis. When two fast parallel channels are open, the slope of the breakdown curve for the second daughter ion is determined mostly by the relative activation entropies of the two channels (ΔΔS^‡), as has been found for the trihalides of methane.³⁸ Thus, in a similar approach, a rate curve is first obtained for the first dissociation, and ΔΔS^‡ fitted with help of the transitional modes to reproduce the slope of the breakdown curve of the second daughter as well as the second onset, E₀′.

This approach is used to determine accurate 0 K appearance energies (E₀) for the two or three lowest energy dissociative ionization channels. These energies can then be used in thermochemical derivations or in understanding the potential energy surfaces and the dissociation mechanism. For higher energy parallel channels, such modelling of the experimental data is of limited use, since these dissociations are apparent either at much higher energies above threshold due to inefficient competition with the lower energy ones, or because they compete non-statistically with them. For such reactions, only the phenomenological appearance energy (AE) is reported, which is an upper limit to the 0 K appearance energy of the daughter ion, allowing for energetics considerations to unveil the reaction mechanism.

3.2 Ab initio calculations

Density functional theory (DFT) calculations with the B3LYP functional and the 6-311++G(d,p) basis set were used to obtain vibrational frequencies and rotational constants needed in the modelling. The Gaussian 03 and 09 computational chemistry suites³⁹ were also employed in calculating reaction paths and transition states by constrained optimizations, in which a bond angle (e.g. a C–C–H angle for hydrogen atom transfer in the parent ion) or a bond length (e.g. a C–F distance for fluorine atom loss) were scanned. Having obtained suitable reaction paths, geometry optimizations as well as Synchronous Transit-Guided Quasi-Newton (STQN)⁴⁰ calculations were performed to locate transition state structures. G3B3⁴¹ calculations were also carried out at the minima and the saddle points in order to determine more accurate ab initio energetics for the different dissociative photoionization channels. A summary of the most relevant pathways is found in Fig. 2. When experimental and G3B3 calculated onset energies are compared, they typically agree to within 10 meV. Slightly worse accuracy is expected for saddle point energies, as well.

Fig. 2 Schematic of the main photoionization dissociation pathways in (a) monofluorethene, (b) 1,1-difluoroethene, (c) trifluoroethene and (d) tetrafluoroethene. Calculated G3B3 values, in eV, are shown for minima and saddle points on the ground electronic state potential energy surfaces. For C₂F₄, the blue plot shows TD-DFT values for the 1st electronic excited state. Continuous lines show observed reactions, dashed lines indicate reactions absent from the dissociative photoionization mechanism. IE denotes the experimental adiabatic ionization energy of the parent molecule, also in eV.

4. Results and discussion

4.1 Monofluoroethene

The breakdown diagram for C₂H₃F in the 13–21 eV photon energy range and the modelled breakdown curves of the first two daughter ions together with the experimental points in the photon energy range of 13.2–14.0 eV are shown in Fig. 3. The TOF signal for the first daughter ion, C₂H₂⁺, the product of HF loss, has an asymmetric peak shape complete with a long pseudo-exponential tail toward higher times-of-flight, indicating HF loss to be a metastable process (Fig. 4). However, even at zero parent fractional abundances, i.e. at energies for which k(E) > 10⁷ s⁻¹, the C₂H₂⁺ peak is still broad, but symmetric. This is a consequence of the impulsive nature of HF loss, and the resulting TOF difference between forward and backward scattered ions.

The G3B3 calculated reaction energy at 0 K for CHF=CH₂ → HC≡CH⁺ + HF is 12.32 eV (cf. 12.31 eV, based on the heats of formation for C₂H₃F⁺, −132.2 kJ mol⁻¹,⁴²C₂H₂⁺, 1329 kJ mol⁻¹,^42,43 and HF, −273.3 kJ mol⁻¹),⁴⁴ whereas for the formation of H₂C=C⁺ + HF it is 14.12 eV. Therefore the acetylene ion is formed, as reported in an earlier PEPICO study of Dannacher et al.⁷ Our ab initio results also show that the energetically more favourable 1,2-HF elimination proceeds via a tight 4-membered ring transition state involving a H migration across the C=C bond, with a large reverse barrier in the exit channel (see [1] → [7]^‡ → [8] in Fig. 2a). By simultaneous fitting of the breakdown diagram and the daughter TOF peaks to obtain the rate curve (Fig. 5a), the experimental 0 K appearance energy for HF loss has been determined to be 13.45 eV. The slow rates seen in Fig. 5 are a consequence of the large density of states of the dissociating ion resulting from the large barrier, as well as the small number of states of the tight transition state. Once the system has surmounted this barrier, there is significant excess energy in the reaction coordinate. This energy is not redistributed among the rovibrational modes, causing the fragments C₂H₂⁺ and HF to fly apart with considerable translational kinetic energy. The experimental 0 K appearance energy and the calculated endothermicity of the dissociative photoionization yield a reverse barrier to HF loss of 1.14 eV. This can be compared with a purely ab initio derived barrier of 1.34 eV (Fig. 2a).

Fig. 3 (a) Breakdown diagram and TPES of C₂H₃F over the range 13.2 to 21.0 eV. G3B3 calculated onsets at 0 K for selected fragment ions are also included. (b) Modelled breakdown curve (solid lines) with experimental points (open shapes) for the parent ion C₂H₃F⁺, and the onsets for only the first two daughter ions, C₂H₂⁺ and C₂H₂F⁺, in the energy range 13.2–14.0 eV.

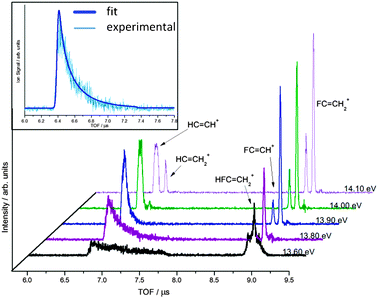Fig. 4 Selected time-of-flight distributions for C₂H₃F in the 13.6–14.1 eV photon energy range. The parent ion is observed at 8.8 μs and the first HF-loss daughter fragment HC=CH⁺ at 6.6 μs. The asymmetric peak shape is a consequence of slow dissociation in the acceleration region. The C₂H₂F⁺ ion due to metastable H loss is also seen in the 8.7–8.8 μs range as a shoulder to the parent peak. At higher energies the formation of C₂HF⁺ and C₂H₃⁺, due to H₂ and F loss, is clearly seen in the 8.6–8.7 and 6.7–6.8 μs TOF ranges, respectively. Above 14 eV, the kinetic energy release in the HC=CH⁺ ion is evident in a broadened peak. Inset is the modelled TOF fit (thicker line) for the metastable peak of HC=CH⁺, associated with HF loss at 13.70 eV.

Fig. 5 Plot of log₁₀k(E)vs. hν for (a) HF loss and H loss from C₂H₃F⁺, (b) HF loss and F loss from 1,1-C₂H₂F₂⁺. The experimental rates, observed in the 10³ s⁻¹ < k < 10⁷ s⁻¹ range, are extrapolated to obtain the E₀.

The G3B3 calculated onset for H-atom loss, CHF=CH₂ → C₂H₂F⁺ + H + e⁻, is 13.67 eV when the hydrogen atom is lost from the fluorinated carbon [1] → [5], and 14.71 eV when it is lost from the CH₂ group. The 0 K appearance energy of this daughter ion (m/z 45) is experimentally determined to be 13.60 eV, suggesting that the former hydrogen atom loss process giving rise to C₂H₂F⁺ is not kinetically hindered. Indeed, no reverse barrier to hydrogen atom loss could be found in our calculations, thus the metastable decay close to threshold (see rate data in Fig. 5a) is mostly due to the large barrier and the correspondingly large density of states in the parent ion. The observation of this metastability supports results reported by Güthe et al.⁸ Since the H-loss transition state is looser than the HF-loss one, the competition between the first two channels favours the former, with the C₂H₂F⁺ fractional abundance some 20% higher than that C₂H₂⁺ between 14–18 eV. Above 18.4 eV the loss of 20 amu becomes the dominant channel. This is identified as the formation of HC=CH⁺ + H + F + e⁻, for which the G3B3 calculated onset is 18.19 eV. The reaction endothermicity of CHF=CH₂ → H₂C=C⁺ + H + F + e⁻ is calculated to be 19.99 eV, and is subsequently discounted as the origin of the signal below 20 eV. Consequently the m/z 26 daughter ion C₂H₂⁺ is derived from the sequential dissociation of C₂H₃⁺ by H loss as well as from C₂H₂F⁺ by F loss in this energy range.

From their threshold to about 0.5 eV above, the fractional ion abundances of C₂HF⁺ and C₂H₃⁺ rise less steeply than those of the first two daughter ions, C₂H₂⁺ and C₂H₂F⁺. The appearance energy, AE, of C₂HF⁺ and C₂H₃⁺ is measured to be 13.7 and 13.9 eV, respectively. The thermochemical onset for 2,2-H₂ elimination yielding FHC=C⁺ is calculated to be 15.62 eV and cannot take place in this energy range. Therefore the structure of C₂HF⁺ must be CF=CH⁺, which is confirmed by the calculated 1,2-H₂ elimination threshold of 13.68 eV. Contrary to 1,1-difluoroethene, in which only 2,2-H₂ elimination is structurally possible, H₂ loss can compete effectively with the other dissociation channels in monofluoroethene. The agreement between the calculated and the experimental onsets also suggest that H₂ loss is not slow at threshold, quite unlike HF loss. This is only possible if H₂ loss has no reverse barrier along the reaction coordinate, or if it is very narrow and there is fast tunnelling through it.

The mechanism of F loss yielding C₂H₃⁺ has been discussed extensively in the literature.^7,8,45,46 This process is observed at its thermochemical threshold, and its rise is consistent with a statistical competitive fast reaction with a loose transition state. As can be seen in the TOF distributions (Fig. 4), the parent ion ceases to be metastable in this energy range and the F-loss signal is readily identified in our experiment, in contrast to a previous report.⁸ However, at 15.5 eV, there is a sudden increase in the C₂H₃⁺ abundance which fits poorly into the statistical picture. Previously, it was proposed that isolated C̃ state behaviour (i.e. the dissociation dynamics are dominated by those of the electronic C̃ state of the parent ion) contributes to this signal.^7,45,46 However, the C̃ peak in the TPES is observed at an onset of 16.18 eV, whereas this sudden rise occurs some 0.7 eV lower, still in the energy range of the B̃ peak. Furthermore, the C₂H₃⁺ ion abundance follows the C̃ peak only very approximately. Consequently, we confirm the double nature of the F-loss process, but also suggest that the C̃ state is not playing a simple and direct role in the non-statistical range. Instead of C̃ state participation, it is more likely that Rydberg series converging to the C̃ state have different autoionization pathways leading to the C₂H₃⁺ product. Based on the KER analysis of the C₂H₃⁺ ion yield at 16.85 eV, Momigny and Locht⁴⁶ conclude that approximately two thirds of the ion flux dissociates on the C̃ state producing the electronically excited ã³A state of C₂H₃⁺, which can then internally convert to its ground state, thereby keeping most of the excess energy. However one-third of the ion flux arrives at the ground state of C₂H₃F⁺, which correlates with the ground X̃¹A state of C₂H₃⁺, allowing for a larger kinetic energy release. Such a bimodal behaviour has also been proposed by Gridelet et al. for the F-loss pathway from 1,1-C₂H₂F₂⁺.¹³ Indeed, there is a very swift decrease in half the C₂H₃⁺ signal together with a jump in the C₂H₂⁺ fractional abundance at around hν = 18.5 eV. Taking into account the 0 K heats of formation of C₂H₃⁺,⁴⁷C₂H₂⁺,^42,43 and H,⁴⁸ (1120, 1329 and 216 kJ mol⁻¹, respectively), C₂H₃⁺ is expected to lose a further H atom at an internal energy of 4.4 eV, i.e. at a photon energy of 18.4 eV, whilst the G3B3 value for the dissociative photoionization C₂H₃F → HC=CH⁺ + F + H + e⁻ is 18.19 eV. As will be shown later for C₂F₄, the breakdown diagram of a sequential dissociation corresponds to the internal energy distribution in the first dissociation step, and can be used to study the excess energy redistribution. Thus, we attempted to analyse the C₂H₃⁺vs.C₂H₂⁺ breakdown curves in the 18–19 eV range to determine the C₂H₃⁺ internal energy distribution. There is a difference of about 1 eV in the excess energy available for kinetic energy release depending on whether the excited or ground state C₂H₃⁺ intermediate is formed. Both pathways yielded an acceptable fit to the C₂H₂⁺ breakdown curve within the signal-to-noise ratio of the experimental data. Ergo, the comparatively noisy high-energy breakdown curves of the three different open channels (H + F loss, F + H loss with an X̃¹A or ã³A C₂H₃⁺ intermediate) and the small differences in their energies (1.3 and 1 eV more excess energy available for KER in the first two) do not allow for a sufficiently detailed description of the reaction mechanism yielding C₂H₂⁺.

CF⁺ (m/z 31) appears around a photon energy of 14.87 eV, which is 0.3 eV higher than the G3B3 calculated endothermicity for CHF=CH₂ → CF⁺ + CH₃ + e⁻, 14.56 eV. It is 0.17 eV higher than the previously reported thermochemical value of 14.704 eV⁸ and lies between previous appearance energies of 14.5 eV⁷ and 14.90 eV.⁸Methyl radical loss is preceded by H atom migration, and ab initio calculations were used to obtain a plausible pathway to CF⁺ production. The transition state to CF–CH₃⁺ was calculated to lie at 12.07 eV, well below the overall barrier to CF⁺ formation. The highest energy major channel observed in this work is C=C bond cleavage to form CHF⁺ + CH₂. It has a calculated onset energy of 17.38 eV and is seen experimentally at 18.4 eV. This value is ca. 2 eV lower than the appearance energy of 20.02 eV reported by Güthe et al.⁸ The thermochemical threshold to CHF⁺ + CH₂, 17.099 eV,⁴⁹ is in reasonable agreement with our calculated G3B3 value, confirming the competitive shift in the CHF⁺ signal. At such high internal energies numerous processes can take place at rates comparable to intramolecular vibrational relaxation. Therefore, the fact that we observe a further parallel channel opening up at all is remarkable.

4.2 1,1-Difluoroethene

The breakdown diagram of 1,1-C₂H₂F₂⁺ in the 13.9–21.0 eV energy range with ab initio dissociative photoionization energies for selected channels, as well as the experimental and modelled breakdown curves for the HF and F loss reactions in the 13.9–14.7 eV energy range, are shown in Fig. 6. Similarly to monofluoroethene, HF loss is the lowest energy channel and the G3B3 calculated endothermicity lies 1.4 eV lower than that for F-atom loss. The calculated reaction energy for F₂C=CH₂ → FC=CH⁺ + HF + e⁻ at 0 K is 13.04 eV and the experimental 0 K onset energy, obtained by simultaneous modelling of the breakdown diagram and the daughter ion TOF spectra, is 14.05 eV. This agrees with the value of 14.1 eV reported by Güthe et al.,⁸ and indicates a reverse barrier of 1.01 eV in [2] → [14]^‡ → [15]. The daughter ion TOF peak shapes indicate metastable behaviour, and our calculations predict a tight transition state. The purely calculated E_rb of 1.19 eV is, as for C₂H₃F⁺, somewhat higher than the value based on the experimental E₀. This small discrepancy of 0.18 eV could be explained by tunnelling through the reverse barrier, which effectively lowers the observed E₀. Our values agree with the previously measured E_rb of 0.98 eV but not with the reported ab initio value of 1.69 eV.^9,10 This indicates that most of the reported 0.71 eV difference was primarily due to the inadequate description of the potential energy surface at the UHF/6-31G(d)//UHF/STO-3G level of theory.

Fig. 6 (a) Breakdown diagram and TPES of 1,1-C₂H₂F₂ over the range 13.9 to 21.0 eV. The G3B3 calculated onsets at 0 K for selected fragment ions are also included. (b) Modelled fit (solid line) with experimental points (open shapes) for the parent ion, 1,1-C₂H₂F₂⁺, and the onsets for the first two daughter ions, FC=CH⁺ and C₂H₂F⁺ in the 13.9–14.7 eV energy range.

The calculated onset energy for the formation of C₂H₂F⁺ (m/z 45) by F loss is 14.40 eV. The corresponding breakdown curve, however, is noisy due to the background subtraction required because the large asymmetric TOF signal of FC=CH⁺ overlaps with the FC=CH₂⁺ signal from F-loss (Fig. 7). We performed a potential energy scan along the C–F bond stretch coordinate to obtain the potential energy curve for F-atom loss. Fig. 2(b) shows that a transition state at a C–F bond length of 1.8 Å is predicted [11]^‡, in which the leaving fluorine atom straddles the C=C bond. This transition state may lead either to F-loss (in which there is no overall reverse barrier) or to the CH₂F–CF⁺ isomer ion [9]. F-loss may proceed without encountering this transition state, and this path is selected for the modelling of the dissociation rates. Fig. 6(b) shows the breakdown curve modelling, which led to the F-loss 0 K appearance energy of 14.47 ± 0.1 eV. As previously observed by Güthe et al.,⁸C₂H₂F⁺ [12] is the most abundant daughter ion between 16–17 eV as a result of a non-statistical process. As with C₂H₃F, there appears to be two pathways at play. At lower energies, F loss is a statistical process on the ionic ground state potential energy surface, but quickly loses out to reactions involving CF and CH₂F loss above 14.7 eV. The diminishing C₂H₂F⁺ fractional abundance starts rising again around 15.3 eV, in coincidence with the onset of the B̃ state in the TPES. This apparent similarity is indicative of isolated-state, non-statistical decay from this state of C₂H₂F₂⁺. However, as is the case for monofluorethene, the breakdown curves only approximately follow the TPES, indicating a complex mechanism.

Fig. 7 Time-of-flight distributions for 1,1-C₂H₂F₂ from the parent ion, at 10.4 μs to the fragment, FC=CH⁺, at 8.8 μs. The asymmetric peak shape of the daughter ion is a consequence of slow dissociation in the acceleration region. The fast F-loss daughter peak, C₂H₂F⁺, is seen emerging from the metastable FC=CH⁺ peak as the energy increases and is found at 8.7 μs. Inset shows the TOF fit for the metastable FC=CH⁺ peak at 14.49 eV.

The G3B3 onset energies for CH₂F⁺ and CF⁺ are close to one another at 14.82 eV and 14.92 eV, and their experimental onsets are 14.70 and 14.86 eV, respectively. These daughter ions are the products of the same process with the charge localised on one or the other fragment. The CF⁺ and CH₂F⁺ fragments are formed in competition with fast F and HF loss, suggesting a loose transition state and no overall reverse barrier to dissociation. As already mentioned, in the transition state structure the F atom can move over and attach to the CH₂ group in [11]^‡, [2] → [11]^‡ → [9] → [10]. C–C bond rupture in [11]^‡ can also lead to CF⁺. The ionization energy (IE) of CF has been determined by Dyke et al. to be 9.11 ± 0.01 eV,⁵⁰ whereas that of CH₂F is reported to be 9.04 ± 0.01 eV by Andrews et al.⁵¹ In the absence of a competitive shift, the offset in onset values would correspond to the ionization energy difference. If there is a competitive shift, i.e. the CF⁺ signal is delayed and rises only at higher energies because it is outcompeted by the other parallel channels, this offset can only be considered as an upper limit to the ionization energy difference. Both quantities appear to be well established; hence in lieu of a detailed kinetic model, only a lower limit to the IE of CH₂F is given as 8.95 eV. At energies above 15.3 eV, the signal for these two ions decreases because the non-statistical F-loss channel is preferred.

The calculated onsets of the H-loss products (m/z 63), HFC=CF⁺ and F₂C=CH⁺, are 15.24 eV and 15.52 eV, respectively. Experimentally, the H-loss product appears only at a higher photon energy of ca.15.9 eV, primarily because it is outcompeted by the other fast processes at lower energies. This also leads to its slow rise with increasing hν. At an energy ∼1 eV lower than in monofluoroethene, cleavage of the C=C bond occurs. The calculated onset for production of CH₂⁺ + CF₂ is 15.96 eV, and its experimental appearance energy is 16.9 eV. By contrast, the CH₂ loss is calculated at 17.42 eV but is not seen experimentally until 18.9 eV. The faster rise of CH₂⁺ than that of C₂HF₂⁺ from H loss suggests a looser transition state for the C=C bond rupture. Unlike monofluoroethene, however, the positively charged fragment first seen resulting from C=C cleavage is not the fluorine-containing moiety, but CH₂⁺. This observation is explained by the 1.3 eV difference between the IE of these fragments (CH₂⁵² 10.39 ± 0.01 eV, CHF⁵³ 10.06 ± 0.05 eV, and CF₂⁵⁴ 11.36 ± 0.005 eV).

Based on energetics considerations, the second rise in the CF⁺ signal at 19 eV is suggested to stem mostly from the C–C bond cleavage in the H-loss fragment ion, HFC=CF⁺ (calculated onset is 18.96 eV). This is supported by a decrease in the C₂HF₂⁺ abundance in this energy range, i.e. a decrease in the H-loss signal. Finally, the decrease in the F-loss signal C₂H₂F⁺ between 19 and 20 eV is due to two possible consecutive reactions from C₂H₂F⁺: a further H-loss to FC=CH⁺ (18.91 eV), or, after a rearrangement to HFC=CH⁺, a loss of F to HC=CH⁺ (18.92 eV) in agreement with the mechanism suggested by Güthe et al.⁸

4.3 Trifluoroethene

To the best of our knowledge, this is the first report of the fragmentation pathways of ionized trifluoroethene by coincidence techniques. The breakdown diagram and the threshold photoelectron spectrum in the 13.5–21.5 eV photon energy range are shown in Fig. 8(a). The adiabatic ionization energy of the neutral molecule has been determined to be 10.14 eV.²⁰ The lowest-energy G3B3 calculated 0 K dissociative photoionization energy of 13.47 eV corresponds to the 1,2-HF elimination. In contrast to monofluoroethene and 1,1-difluoroethene, this reaction is not observed and C₂F₂⁺ is virtually absent in the breakdown diagram.

Fig. 8 (a) Breakdown diagram and TPES of C₂HF₃ over the range 13.45 to 21.5 eV. The G3B3 calculated onsets at 0 K for selected fragment ions are also included. The calculated onset for the 1,2-HF abstraction at 13.47 eV denoted by the black dashed line is included for reference, though the product ion is not seen experimentally. (b) Experimental points (open shapes) with modelled breakdown curve (solid line) for C₂HF₃⁺, and the onsets for the first three daughter ions, CHF₂⁺, CF⁺ and CHF⁺ in the energy range 13.50–15.25 eV.

The first observed daughter ion, CHF₂⁺, corresponds to the loss of the CF fragment which requires an initial F-atom migration [3] → [16]^‡ → [18]. The G3B3 calculated onset energy is 13.86 eV and the experimental 0 K appearance energy is measured to be 13.856 ± 0.007 eV, so there appears to be no reverse barrier in the exit channel. Fig. 8(b) shows the experimental data, the modelled breakdown diagram, and the obtained 0 K appearance energies determined for the first three dissociation channels. The TOF peaks corresponding to CHF₂⁺ are almost symmetric, so we conclude that the parent ion is barely metastable along this reaction coordinate and dissociation is therefore fast. When a rearrangement precedes the loss of HF in ionized mono- and 1,1-difluoroethene, these reactions have slow rate constants. Therefore it might seem counterintuitive that the rates for CF loss from ionized trifluoroethene are not slow. To shed light on this issue, we obtained ab initio potential energy curves leading to these fragments (Fig. 2c). The F-transfer transition state in this series has a 3-membered ring structure [11]^‡, [16]^‡ and [24]^‡ whereas HF-loss proceeds via a 4-membered ring transition state structure [7]^‡ and [14]^‡. The figure also shows that the reaction coordinate changes character as the reaction proceeds. Initially, it starts as a F-atom migration across the C=C bond leading to a HF₂C–CF⁺ minimum, but this is followed by a C–C bond cleavage to form CHF₂⁺ + CF, [3] → [16]^‡ → [17] → [18]. The F-transfer transition state [16]^‡ lies at 12.74 eV and the H-transfer transition state has been found to lie at 12.93 eV, so both pathways are possible, though the lower energy F-transfer is more favourable. The reverse barrier associated with the F-migration is much smaller than the dissociation endothermicity, so there is no overall reverse barrier to production of CHF₂⁺ + CF or CF⁺ + CHF₂. Thus, the 0 K appearance energy of CHF₂⁺, 13.856 ± 0.007 eV, corresponds to the dissociative photoionization energy.

The second daughter ion observed is CF⁺, corresponding to the loss of the CHF₂ fragment, [3] → [16]^‡ → [17] → [19]. The experimentally determined 0 K appearance energy for this ion is 14.16 ± 0.02 eV, with the G3B3 onset energy calculated to be 14.33 eV. As these first two dissociative photoionization reactions differ only in which moiety the positive charge is localized on, the difference in the E₀ values, 0.30 ± 0.02 eV, yields the difference in the ionization energies of the CF and CHF₂ radicals. The ionization energy of CF is well established, 9.11 eV ± 0.01,⁵⁰ whilst values for CHF₂ span a large range of experimental values, 8.78,⁴⁹ 8.74,⁵⁵ and 10.5 eV,⁵⁶ and a calculated value of 8.4 eV.⁵⁷ By anchoring to the CF value, we determine the IE of the CHF₂ radical to be 8.81 ± 0.02 eV. The abundance of CF⁺ has two maxima, the first at ca. 15.3 eV (fractional abundance of 25%) and a much larger one at ca. 20.5 eV (80%). The shape of its breakdown curve can help understand its production mechanism. At low energies, CF⁺ is produced by the HFC=CF₂ + hν → CF⁺ + CHF₂ +e⁻ reaction. At 17 eV, a new channel opens up in which the third daughter ion, CHF⁺, which is produced initially by C=C bond cleavage to form CHF⁺ + CF₂, loses an H atom in a sequential process to produce CF⁺. At 19.1 eV, the steepness of the CF⁺ yield further increases as C=C bond rupture becomes possible from the F-loss daughter ion CHF=CF⁺.

The 0 K appearance energy of the third daughter ion CHF⁺ is 14.54 ± 0.02 eV. G3B3 calculations give 14.94 eV, corresponding to cleavage of the C=C bond of the parent ion, with CF₂ as the neutral fragment, [3] → [21]. This process occurs at relatively low photon energies for trifluoroethene and is an example of the perfluoro-effect,⁵⁸i.e. a decrease in the C=C bond strength as the number of F substituents increases. The onset for CH₂⁺ production from 1,1-difluoroethene is at ca. 17 eV, the onset of CHF⁺ from monofluoroethene does not occur until 18 eV. For all three molecules, however, this never becomes a dominant channel, with the maximum fractional abundance (CH₂⁺ from 1,1-difluoroethene) never exceeding 35%.

The final major fragment ion formed from trifluoroethene is F-loss to HFC=CF⁺, [3] → [20]. Its appearance energy is 15.36 eV and it turns on at its calculated thermochemical threshold. This reaction channel is associated with non-statistical F-loss, because the F-loss curve increases too sharply over a narrow energy range to be statistical. This channel is the most abundant yield between 15.6 and 19.0 eV, and the signal emulates closely that of the TPES. This range of energies coincides with the Ẽ/F̃/G̃ excited states of the ion where ionization occurs from C–F orbitals.²⁰ Unlike the F-loss channel observed from C₂H₃F⁺ and 1,1-C₂H₂F₂⁺, the contribution of the statistical F loss is not seen and is suggested to be minor at all energies. Higher-energy channels with abundances less than 25% occur after these four major channels: these are the production of CF₂⁺ + CHF at 17.2 eV and C₂HF⁺ + 2 F at 18.9 eV. G3B3 dissociative photoionization energies for these channels have been calculated to be 16.09 and 19.00 eV, respectively.

4.4 Tetrafluoroethene

The first three dissociative photoionization channels of C₂F₄ open in a Franck–Condon gap, as shown in the breakdown diagram and threshold photoelectron spectrum (Fig. 9a). This observation is in agreement with the findings of an earlier TPEPICO study by Jarvis et al.⁴ The first channel, formation of CF₃⁺ with CF as the accompanying neutral, has a calculated onset energy of 13.75 eV. Surprisingly, although analogously to the C₂HF₃ system, the CF₃⁺ TOF peak is symmetric and narrow, therefore the fluorine migration and subsequent C–C bond cleavage is a fast process without a large reverse barrier. At somewhat higher energies, CF⁺ is the second daughter ion, again mirroring the second dissociative photoionization channel in trifluoroethene. The adiabatic ionization energy of C₂F₄ is 10.11 ± 0.01 eV,²¹ meaning that the total depth of the potential energy well to CF₃⁺ + CF is about 3.64 eV, leading to a high density of states in the dissociating ion. In contrast with trifluoroethene, no reasonably chosen transition state is loose enough to lead to rates larger than 10⁷ s⁻¹ at such high internal energies. This indicates that the F-transfer mechanism plays a crucial role in ensuring that there is no kinetic shift. Rearrangement to a CF₃CF⁺ intermediate, [4] → [24]^‡ → [23], can take place at a much lower energy than the E₀ of CF₃⁺. Even though the transition state for this process is relatively tight, the rates are fast at an excess energy of 1–2 eV, i.e. at the dissociative photoionization onset: ab initioRRKM rates, based on the G3B3 calculated transition state, are in excess of 10⁹ s⁻¹ at threshold. C–C bond rupture can then proceed through a loose transition state with a lower density of states in the dissociating intermediate, giving rise to fast rates and no kinetic shift for [4] → [24]^‡ → [23] → [22] or [25]. In the absence of this CF₃CF⁺ intermediate [23], the dissociation would be slow and a kinetic shift apparent in the spectrum. Fig. 9(b) shows the modelled breakdown curves, and the E₀ for CF₃⁺ production has been determined to be 13.717 ± 0.007 eV.

Fig. 9 (a) Breakdown diagram and TPES of C₂F₄ taken over the range 13.5 to 18.0 eV. The G3B3 calculated onsets at 0 K for selected fragment ions are also included. (b) Experimental points (open shapes) with modelled breakdown curve (sold line) for the parent ion, C₂F₄⁺, and the onsets for the first three daughter ions, CF₃⁺, CF⁺ and CF₂⁺ in the energy range 13.4 to 15.2 eV.

The appearance energy of CF₃⁺ and that of the second daughter, CF⁺, are very close, as the ionization energy of CF₃, somewhat controversially reported as 8.61 eV,⁵⁹ 8.6–8.7 eV,⁶⁰ 9.04 eV,⁶¹ 9.05 ± 0.004 eV,⁶² 9.02 ± 0.03 eV and 9.08 ± 0.03 eV,³⁵ is only slightly lower than that of CF, 9.11 ± 0.01 eV.⁵⁰ The E₀ to CF⁺ + CF₃ formation is determined to be 13.740 ± 0.010 eV based on the statistical modelling. The difference between the barriers to these two daughter ions is 0.023 eV, and, together with the IE of CF, the IE of CF₃ is determined to be 9.090 ± 0.015 eV. This lies towards the higher end of previous reported onset values. While our CF₃⁺E₀ agrees well with the result from the photoionization efficiency (PIE) curve of C₂F₄ of 13.721 ± 0.005 eV,⁶² our CF⁺ onset differs considerably from the value of 13.777 ± 0.005 eV reported by Asher and Ruscic.⁶² Presumably, the reason is that the competitive shift in the CF⁺ channel was not considered in the PIE work, leading to a higher reported value. As a consequence, an onset energy difference (0.055 ± 0.003 eV) was reported, which corresponds well to the offset in breakdown curves we observe, but not to the E₀ difference. Thus, we feel that the C₂F₄ photoionization experiment warrants a revision of the IE of CF₃ to 9.090 ± 0.015 eV.

The third channel is formation of CF₂⁺ + CF₂, with a calculated appearance energy of 14.41 eV. This reaction arises from cleavage of the C=C bond, [4] → [27], and occurs at a lower photon energy than the same process in trifluoroethene, due to the perfluoro effect.⁵⁸ This parallel channel is in competition with the first two channels. The rate curves were obtained for CF₃⁺ and CF⁺ formation based on the density of states of intermediate [23], which were then used in conjunction with a rate equation based on the parent ion [4] density of states to describe C=C bond breaking. This approach yields a 0 K appearance energy of CF₂⁺ of 14.16 ± 0.04 eV.

There is a sharp increase in the abundance of the fourth channel, F atom loss and production of C₂F₃⁺, at 15.56 eV, at the end of a substantial Franck–Condon gap. Unlike the first three channels, a straightforward statistical treatment is not appropriate for this non-statistical process, because, similarly to F loss from C₂HF₃⁺, the breakdown curve rises too steeply to be statistical.⁶³ Two pieces of evidence stand out. First, there is an excellent correlation between the peaks in the TPES and the breakdown curve here. Second, the steepness of the crossover region is not only inconsistent with a parallel competing channel, but, as will be shown later, also corresponds to the room temperature internal energy distribution of C₂F₄⁺; significantly unlike a crossover due to a slowly changing rate constant ratio of competing statistical processes. The overall breakdown diagram appears to be comprised of two separate outcomes or regimes. The first one consists of the CF₃⁺ + CF, CF⁺ + CF₃ and CF₂⁺ + CF₂ channels discussed so far, which arise from dissociations on the ground state surface of the parent ion, C₂F₄⁺, partly through the intermediate structure CF₃CF⁺. Below a photon energy of 15.5 eV, only reactions belonging to this first regime are observed. Above this energy, a regime change occurs, and the two of the observed reactions belong to the excited, isolated-state second regime: loss of a fluorine atom yielding CFCF₂⁺ + F, which is followed by the sequential formation of CF⁺ + CF₂ + F above 17.2 eV.

As seen in the breakdown diagram in the range 15.9–18.0 eV, regime-two reactions dominate the regime-one reactions by a constant factor of roughly 2 ∶ 1. The threshold photoionization mechanism is suggested to play a vital role and can be discussed in the framework proposed for iodomethane previously.³⁴ Following photoabsorption, the neutral C₂F₄ molecule is excited to a Rydberg state with favourable Franck–Condon factors. Three non-radiative decay pathways are possible: (1) crossing to a repulsive neutral curve leading to neutral fragments, which are not detected in our experiment, (2) whilst on this repulsive surface, the system can return to the ground state Rydberg manifold eventually leading to the ground state parent ion which dissociates via regime one, and (3) direct autoionization to an excited electronic state, in this case the à state of C₂F₄⁺, which dissociates according to regime two by F loss and then by consecutive CF₂ loss.

Here we discuss three aspects of the double-regime dissociation mechanism of C₂F₄⁺. First, in Fig. 2(d), TD-DFT potential energy levels are shown for production of CF₃⁺ + CF, the simple C=C bond breaking and the F-loss channels. Excited state potential energy curves were obtained along the minimum energy path for the ground electronic state, and the TD-DFT minima and maxima are reported here. These points are therefore not necessarily stationary points on the excited state surface, but we believe they are reasonably good representations of them. Some EOM-UCCSD/aug-cc-pVTZ calculations along these curves showed the same general characteristics with only small differences in excitation energy. Since the C–F bond is very strong, F loss cannot compete effectively on the ground electronic surface; the dynamics are dominated by the CF₃⁺ + CF, CF⁺ + CF₃ and CF₂⁺ + CF₂ exit channels. However, if the first excited state is only weakly coupled to the ground state, which is hardly surprising given the 4–6 eV gap between the two states, F loss, [26]* → [28], becomes possible. This is not because the à state converges to energetically disallowed excited state products, as was invoked in the non-statistical model for Sn(CH₃)₃X²⁴ and methanol,²⁶ but because of large reverse barriers for the other competing processes on the excited state surface. Thus, the three regime-one exit channels, [26]^* ↛ [31]^‡ → [22], [26]^* ↛ [31]^‡ → [25] and [26]^* ↛ [29]^‡ → [27], are kinetically ‘blocked’ on the à state surface.

Second, the narrow width of the regime crossover at 15.9 eV corresponds to the width of the thermal energy distribution of C₂F₄⁺. This observation prompted us to consider the regime-two processes independently of the preceding channels, and plot a ‘regime-two breakdown diagram’ as shown in Fig. 10. This was achieved by disregarding regime-one product ions at hν > 16 eV, then re-normalizing the signal so that the F-loss daughter ion, C₂F₃⁺, converges to 100% closely above 16 eV. This is done to obtain a regime-two ‘pseudo parent ion’ signal. The temperature of the internal energy distribution in the ‘pseudo parent’ that gives the best fit is 340 K, somewhat higher than room temperature. Consequently, in contrast with CH₃I where autoionization to the electronically excited state was found to be enhanced at low internal energies,³⁴ here we find that the direct autoionization process (3) appears slightly enhanced at high internal energies and the thermal energy distribution is somewhat widened. Note that regime-two ions are only distinct from regime-one ions above the F-loss threshold of 15.5 eV. Below this energy, the long-lived electronically excited parent ions will eventually undergo internal conversion to the ground ion state and dissociate to fragment ions via regime one.

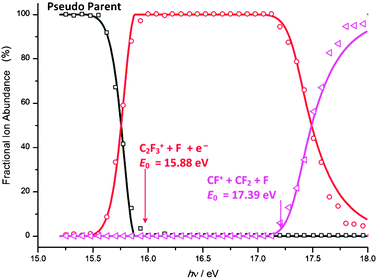Fig. 10 Experimental points (open shapes) with modelled breakdown curve (solid line) for the regime 2 of the breakdown diagram of C₂F₄⁺. As ions formed through regime 2 (C₂F₃⁺ and CF⁺) are decoupled from those of regime 1, all previous ion abundances are grouped together to form the pseudo-parent-ion abundance.

Third, in a particularly serendipitous turn, C₂F₃⁺, produced by non-statistical F-loss, undergoes a further sequential dissociation above 17 eV to form CF⁺, [26]^* → [28] → [30]. However, sequential F-loss from the regime-one CF₂⁺ could interfere with the regime-two CF⁺ signal, as evidenced by the small rise in the CF⁺ abundance close to 18 eV. Due to the larger kinetic energy release and the different product energy partitioning meaning that more than half of the excess energy is lost in the first C=C bond rupture step, this regime-one process will be very slow to rise with increasing photon energy, confirmed by the almost constant CF₂⁺ abundance above 17.5 eV. Therefore, regime-two processes are virtually distinct from regime-one processes.

Repulsive surfaces and impulsive mechanisms are often invoked to explain effective competition between non-statistical and statistical channels.⁶⁴ It was only recently that some evidence has been published highlighting the statistical redistribution of internal energy which is possible in isolated-state processes.²⁶ The breakdown curve of a sequential dissociation yields the product energy distribution of the dissociating ion.^16,24 By modelling the second step in the regime-two breakdown diagram in Fig. 10, it becomes evident that it is only the electronic ground state phase space which is inaccessible to our system, and statistical redistribution of the excess energy among the nuclear degrees of freedom can indeed occur. The derived E₀ values of 15.88 ± 0.03 eV and 17.39 ± 0.06 eV for C₂F₃⁺ + F and CF⁺ + CF₂ + F, respectively, can be compared with the G3B3 calculated dissociative photoionization energies of 15.61 and 17.41 eV. The enthalpies of formation for C₂F₄, CF⁺, CF₂ and F as listed in Table 1 yield an onset for C₂F₄ → CF⁺ + CF₂ + F of 17.32 ± 0.06 eV supporting the E₀ derived in this work. This agreement is excellent, confirming the validity of the ‘pseudo-parent assumption’ and the applicability of the statistical approach to regime two. To summarize, the internal energy distribution of the F-loss daughter ion, C₂F₃⁺, determines its breakdown curve in the sequential CF₂-loss process. The latter is described well assuming a statistical redistribution of the excess energy in the F-loss step. Therefore the F-loss is found to be non-statistical only in the sense that the ground electronic state is inaccessible. The statistical approximation is valid for the nuclear degrees of freedom, and F loss is not an impulsive process as was previously proposed.⁴

Table 1 Thermochemical values in kJ mol⁻¹

	ΔfH^o0 K	ΔfH^o298 K^h	H ^o298 K − H^o0 K (G3B3)^a	E 0/eV^a	Corresponding process
a This work. b Feller et al.^65,66 c Chase, JANAF tables.^67 d Ruscic et al.^68 e Bodi et al.^35 f Dixon and Feller.^69 g Unpublished work on CH2F2, the E0 of the reaction CH2F2 → CHF2^+ + H + e^− was found to be 13.070 ± 0.002 eV.^70 h (H^o298 K − H^o0 K) values for C, H2 and F2 are 1.05, 8.47 and 8.82 kJ mol^−1, respectively.^67 i Value determined using ΔfH^o0 K (CF2) = −195.0 kJ mol^−1.^69
1,1-C2H2F2	−343.1 ± 2.5^b	−350.2 ± 2.5^b	12.27
F	77.3 ± 0.3^c	79.4 ± 0.3^c	6.52^c
CH2=CF^+	976 ± 9^a	973 ± 9^a	12.25	14.47 ± 0.1	C2H2F2 → CH2=CF^+ + F + e^−
C2F4	−669.4 ± 3.3^b	−672.8 ± 3.3^b	16.43
CF3	−462.8 ± 2.1^d	−465.7 ± 2.1^d	11.55
CF3^+	413.4 ± 2.0^e	410.2 ± 2.0^e	11.14
CF	240.7 ± 3.9^a	243.9 ± 3.9^a	8.70	13.717 ± 0.007	C2F4 → CF3^++CF+e^−
CF^+	1119.1 ± 4.0^a	1122.3 ± 4.0^a	8.68	13.740 ± 0.010	C2F4 → CF^+ + CF3 + e^−
CF2	−199.7 ± 5.6^a	–199.2 ± 5.6^a	10.35	14.16 ± 0.04	C2F4 → CF2^+ + CF2 + e^−
CF2	−195.0 ± 2.9^f	−194.5 ± 2.9^f	10.35
CHF2^+	602.4 ± 2.0^g	598.7 ± 2.0^g	10.39	13.856 ± 0.007	C2HF3 → CHF2^+ + CF + e^−
C2HF3	−493.8 ± 4.4^a	–499.1 ± 4.4^a	14.31
CHF2	−246.7 ± 6.6^a	−249.8 ± 6.6^a	10.97	14.16 ± 0.03	C2HF3 → CF^+ + CHF2 + e^−
CHF^+	1104.1 ± 5.6^a^,^i	1104.2 ± 5.6^a^,^i	9.80	14.54 ± 0.02	C2HF3 → CHF^+ + CF2 + e^−

---

4.5 Trends and insights into bonding

We consider five statistical dissociation channels on the ground electronic state and non-statistical F-loss from excited electronic states in C₂H_4–nF_n⁺. The former channels comprise: (1) C–H bond cleavage, (2) statistical C–F bond cleavage, (3) HF loss by way of a four-membered ring transition state, (4) C–C bond cleavage by way of a three-membered ring transition state, and (5) C=C bond cleavage.

The C–H bond becomes progressively stronger with increasing n. In trifluoroethene, with a G3B3 calculated H-loss onset of 15.48 eV, the C–H bond is already too strong to compete successfully with the other dissociation channels. The F-loss potential energy well also deepens in the group with increasing n. In mono- and difluoroethene, statistical F-loss competes effectively, whereas statistical F-loss is at most a minor channel in trifluoroethene, and absent in C₂F₄⁺. In fact, non-statistical F-loss establishes a second dissociation regime in C₂F₄⁺, in which only the ground electronic state is inaccessible to the reactive flux.

Four-membered ring CHFC transition states may lead to HF loss in n = 1–3, which is the least endothermic channel, albeit with a decreasing margin as n increases, and is absent in the trifluoroethene breakdown diagram because of the large barrier to forming the transition structure. In short, the four-membered ring transition structure is destabilised as n increases. Three-membered ring transition states lead to F/H-migration and subsequent C–C bond breaking. The F-transfer transition state in trifluoroethene is calculated to be 0.19 eV lower in energy than H-transfer, but H-transfer may still compete if the tunnelling through the barrier is sufficiently fast. With increasing F-substitution, the three-membered ring transition states are found to be stabilised, and the resulting fragments dominate the low-energy breakdown diagram in n = 3 and 4. In contrast with the four-membered ring HF-loss transition state, F-migration takes place at internal energies below the C–C bond energy. This means that the corresponding dissociative photoionization processes are fast, and their endothermicities can be determined based on the breakdown diagram.

Finally, the C=C bond energy decreases from n = 3 to n = 4 as predicted by the perfluoro effect.⁵⁸ C=C bond rupture is a minor channel in monofluoroethene, a significant one in n = 2 and 3, and becomes one of the major regime-one channels in tetrafluoroethene.

4.6 Thermochemistry

For the dissociative photoionization reaction AB + hν → A⁺ + B + e⁻, the enthalpy of the unimolecular reaction, Δ_rH^o, and the appearance energy of the daughter ion A⁺, E₀, are equivalent only at 0 K and in the absence of a reverse barrier (Fig. 1a);

E₀ = Δ_rH^o_0 K = ∑(Δ_fH^o_0 K)_products − ∑(Δ_fH^o_0 K)_reactants (2)

Therefore, using 0 K appearance energies with established enthalpies of formation for neutral parent molecules, neutral fragments and daughter ions, the 0 K enthalpy of formation of the least well-determined species can be obtained.

To convert the enthalpy of formation of a molecular species or ion [AB] between 0 K and 298 K we use

(Δ_fH^o_298 K − Δ_fH^o_0 K)_[AB] = (H^o_298 K − H^o_0 K)_[AB] − ∑(H^o_298 K − H^o_0 K)_{constituent elements} (3)

where the thermal correction for a non-linear molecule is defined asThe electron value of (H_{298 K} − H_{0 K}) is neglected in eqn (3), i.e. we use the stationary electron (or ion) convention for ions at T > 0 K.⁴⁹

We cannot deduce any thermochemical values from C₂H₃F⁺ because of the slow HF loss and insufficient resolution of the H-loss signal due to the broadened parent TOF signal. Values derived from the other three molecules can be found in Table 1. In 1,1-difluoroethene, the E₀ value for F loss, 14.47 ± 0.1 eV, and Δ_fH^o_0 K (1,1-C₂H₂F₂) = −343.1 ± 2.5 kJ mol⁻¹⁶⁶ yield Δ_fH^o_0 K (CH₂=CF⁺) = 976 ± 9 kJ mol⁻¹, converted to 973 ± 9 kJ mol⁻¹ at 298 K. This last value can be compared with the previous room temperature value of 951 kJ mol⁻¹.⁴⁹

For tetrafluoroethene, Δ_fH^o_0 K (C₂F₄) = −669.4 ± 3.3 kJ mol⁻¹,⁶⁶ the C₂F₄ → CF₃⁺ + CF + e⁻E₀ value of 13.717 ± 0.007 eV, and Δ_fH^o_0 K (CF₃⁺) = 413.4 ± 2.0 kJ mol⁻¹,³⁵ yield Δ_fH^o_0 K (CF) = 240.7 ± 3.9 kJ mol⁻¹. This is an improved value upon that of Asher and Ruscic,⁶² of 251.0 ± 4.6 kJ mol⁻¹, partly because they used a now outdated JANAF value which was 14 kJ mol⁻¹ too high and partly because they overestimated the CF⁺/CF₃⁺ onset energy difference; thus they underestimated the CF₃ ionization energy by 0.04 eV. From the C₂F₄ → CF⁺ + CF₃ + e⁻E₀ value of 13.740 ± 0.010 eV, using Δ_fH^o_0 K (CF₃) = −462.8 ± 2.1 kJ mol⁻¹,⁶⁸ we present an improved value of Δ_fH^o_0 K (CF⁺) = 1119.1 ± 4.0 kJ mol⁻¹. This is in close agreement to the Burcat value of 1121.9 ± 0.9 kJ mol⁻¹ at 0 K,⁴² though some distance from the Lias and JANAF values of 1131.0 and 1140.0 ± 0.5 kJ mol⁻¹ respectively.^49,67 Using the C₂F₄ → CF₂⁺ + CF₂ + e⁻E₀ value of 14.16 ± 0.04 eV, the IE of CF₂ of 11.362 ± 0.03 eV⁵⁴ and Δ_fH^o_0 K (C₂F₄) of −669.4 ± 3.3 kJ mol⁻¹,⁶⁶ we obtain Δ_fH^o_0 K (CF₂) = −199.7 ± 5.6 kJ mol⁻¹. This value may be compared with previous values: −182.5 ± 6.3 kJ mol⁻¹ (JANAF),⁶⁷ −185.3 ± 4.2 kJ mol⁻¹ (Berman),⁷¹ −191.7 ± 1.3 kJ mol⁻¹ (Burcat),⁴² −195.0 ± 2.9 kJ mol⁻¹ (Dixon and Feller)⁶⁹ and −205.0 kJ mol⁻¹ (Lias).⁷²

In data yet to be published, the E₀ value of the reaction CH₂F₂ → CHF₂⁺ + H + e⁻ was found to be 13.070 ± 0.002 eV.⁷⁰ Thus, using Δ_fH^o_0 K (H) = 216.0 kJ mol^−1 67 and Δ_fH^o_0 K (CH₂F₂) = −442.6 ± 2.0 kJ mol⁻¹,⁷³Δ_fH^o_0 K (CHF₂⁺) = 602.4 ± 2.0 kJ mol⁻¹ can be derived. This value was then used, together with the now obtained Δ_fH^o_0 K (CF) = 240.7 ± 3.9 kJ mol⁻¹ and the E₀ value for C₂HF₃ → CHF₂⁺ + CF + e⁻ of 13.856 ± 0.007 eV in trifluoroethene, to derive Δ_fH^o_0 K (C₂HF₃) = −493.8 ± 4.4 kJ mol⁻¹. Burcat and Ruscic⁴² and Lias et al.⁴⁹ report −485.5 and −485.7 kJ mol⁻¹, respectively, for this quantity. From the Δ_fH^o_0 K (C₂HF₃) and Δ_fH^o_0 K (CF⁺) derived herein, and the C₂HF₃ → CF⁺ + CHF₂ + e⁻ 0 K appearance energy of 14.16 ± 0.02 eV, we obtain Δ_fH^o_0 K (CHF₂) = −246.7 ± 6.6 kJ mol⁻¹. This value can be compared with that of Lias et al. −233.8 ± 5 kJ mol⁻¹,⁴⁹ Burcat and Ruscic −235.7 kJ mol⁻¹,⁴² and a more recent ab initio study of −239.4 ± 2.6 kJ mol⁻¹.⁷³ From the C₂HF₃ → CHF⁺ + CF₂ + e⁻ threshold of 14.54 ± 0.02 eV, and Δ_fH^o_0 K (C₂HF₃) derived in this work, the Δ_fH^o_0 K (CHF⁺) was found to be 1104.1 ± 5.6 kJ mol⁻¹.

5. Conclusions

The unimolecular dissociation of energy-selected fluorinated ethene cations have been investigated in the 13–25 eV energy range. Four statistical channels, namely HF loss, F loss, direct cleavage of the C=C double bond as well as cleavage of the C–C bond post F or H migration have been discussed in detail, in addition to the non-statistical F-loss channel.

The studied fluorinated ethenes may be divided into two groups, the ‘time bombs’ (monofluoroethene and 1,1-difluoroethene) and the ‘fast dissociators’ (trifluoroethene and tetrafluoroethene). In the time bombs, the least endothermic HF loss channel is blocked by a tight 4-membered ring transition state structure. As a result, the parent ions have long lifetimes in the μs timescale at the onset of dissociative photoionization, succeeded by impulsive loss of HF with about 1 eV kinetic energy release. The latter is due to the large reverse barrier, reproduced well by the RAC-RRKM modelled appearance energies. In tri- and tetrafluoroethene, the two main channels at low energies are the post F/H-transfer C–C bond cleavages, in which the charge stays on either fragment. These processes are found to take place without an overall reverse barrier, and by taking into account the competitive shifts in the breakdown curves and deriving accurate 0 K appearance energies, we obtain the ionization energy differences for these fragments directly. This is particularly useful in C₂F₄, where it leads to a new, self-consistent set of thermochemical values for the CF/CF₃/CF⁺/CF₃⁺ system (Δ_fH^o_0 K = 240.7 ± 3.9, −462.8 ± 2.1, 1119.1 ± 4.0 and 413.4 ± 2.0 kJ mol⁻¹, respectively). The ionization energy of CHF₂ has been re-determined to be 8.81 ± 0.02 eV. The ionization energy of CF₃ has also been determined, and at 9.090 ± 0.015 eV is slightly higher than previous values.

As the C–F bond gets progressively stronger with increasing fluorine substitution, while the F/H-atom migration transition state becomes stabilized, statistical F loss becomes less competitive. There is evidence of a higher energy, non-statistical F-loss channel in all four molecules studied, but it is a dominant and exclusive F-loss channel in C₂F₄⁺. Thanks to a fortunate partitioning of the dissociative photoionization products, we could construct and model a second, regime-two breakdown diagram, in which a sequential CF₂ loss is also included from the F-loss fragment ion, C₂F₃⁺. By measuring the product energy distribution of the F-loss daughter, we could establish that only the ground electronic state of C₂F₄⁺ is inaccessible in the non-statistical F loss channel. Therefore, the dissociating excited state C₂F₄^*+ ion is long-lived, and that the excess energy is statistically redistributed among the nuclear degrees of freedom.

Acknowledgements

We thank Drs Melanie Johnson and Thomas Gerber for assistance and useful discussions. J. H. thanks the University of Birmingham for a research studentship. The research leading to these results has received funding from the European Community's Seventh Framework Programme (FP7/2007–2013) under grant agreement no. 226716. The experimental work was carried out at the VUV beamline of the Swiss Light Source of the Paul Scherrer Institut.

Notes and references

1. S. J. Blanksby and G. B. Ellison, Acc. Chem. Res, 2003, 36, 255.
2. K. Takeshita, Theor. Chem. Acc., 1999, 101, 343.
3. G. K. Jarvis, K. J. Boyle, C. A. Mayhew and R. P. Tuckett, J. Phys. Chem. A, 1998, 102, 3219.
4. G. K. Jarvis, K. J. Boyle, C. A. Mayhew and R. P. Tuckett, J. Phys. Chem. A, 1998, 102, 3230.
5. K. R. Jennings, Org. Mass Spectrom., 1970, 3, 85.
6. J.-P. Stadelmann and J. Vogt, Int. J. Mass Spectrom. Ion Phys., 1980, 35, 83.
7. J. Dannacher, A. Schmelzer, J.-P. Stadelmann and J. Vogt, Int. J. Mass Spectrom. Ion Phys., 1979, 31, 175.
8. F. Güthe, R. Locht, B. Leyh, H. Baumgärtel and K.-M. Weitzel, J. Phys. Chem. A, 1999, 103, 8404.
9. F. Güthe, H. Baumgärtel and K.-M. Weitzel, J. Phys. Chem. A, 2001, 105, 7508.
10. G. Frenking, W. Koch, M. Schaale and H. Baumgärtel, Int. J. Mass Spectrom. Ion Processes, 1984, 61, 305.
11. J. Booze, K.-M. Weitzel and T. Baer, J. Chem. Phys., 1991, 94.
12. M. Malow, F. Güthe and K.-M. Weitzel, Phys. Chem. Chem. Phys., 1999, 1, 1425.
13. E. Gridelet, D. Dehareng, R. Locht, A. J. Lorquet, J. C. Lorquet and B. Leyh, J. Phys. Chem. A, 2005, 109, 8225.
14. A. Bodi, M. Johnson, T. Gerber, Z. Gengeliczki, B. Sztáray and T. Baer, Rev. Sci. Instrum., 2009, 80, 034101.
15. M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610, 597.
16. B. Sztáray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233.
17. C. Lifshitz, Mass Spectrom. Rev., 1982, 1, 309.
18. K.-M. Weitzel, M. Malow, G. K. Jarvis, T. Baer, Y. Song and C. Y. Ng, J. Chem. Phys., 1999, 111, 8267.
19. T. Baer, B. Sztáray, J. P. Kercher, A. F. Lago, A. Bodi, C. Skull and D. Palathinkal, Phys. Chem. Chem. Phys., 2005, 7, 1507.
20. G. Bieri, W. V. Niessen, L. Åsbrink and A. Svensson, Chem. Phys., 1981, 60, 61.
21. T. J. Buckley, R. D. Johnson, R. E. Huie, Z. Zhang, S. C. Kuo and R. B. Klemm, J. Phys. Chem., 1995, 99, 4879.
22. I. Powis, O. Dutuit, M. Richard-Viard and P. M. Guyon, J. Chem. Phys., 1990, 92, 1643.
23. D. M. Smith, R. P. Tuckett, K. R. Yoxall, K. Codling, P. A. Hatherly, J. F. M. Aarts and M. Stankiewicz, J. Chem. Phys., 1994, 101, 10559.
24. T. Baer, A. Guerrero, J. Z. Davalos and A. Bodi, Phys. Chem. Chem. Phys., 2011, 13, 17791.
25. J. Berkowitz, J. Chem. Phys., 1978, 69, 3044.
26. S. Borkar, B. Sztáray and A. Bodi, Phys. Chem. Chem. Phys., 2011, 13, 13009.
27. D. M. Smith, R. P. Tuckett, K. R. Yoxall, K. Codling and P. A. Hatherly, Chem. Phys. Lett., 1993, 216, 493.
28. D. A. Shaw and D. M. P. Holland, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 145103.
29. I. Nenner, P. M. Guyon, T. Baer and T. R. Govers, J. Chem. Phys., 1980, 72, 439115.
30. B. Sztáray and T. Baer, Rev. Sci. Instrum., 2003, 74, 3763.
31. A. Bodi, B. Sztáray, T. Baer, T. Gerber and M. Johnson, Rev. Sci. Instrum., 2007, 78, 084102.
32. J. P. Kercher, W. R. Stevens, Z. Gengeliczki and T. Baer, Int. J. Mass Spectrom., 2007, 267, 159.
33. S. Borkar and B. Sztáray, J. Phys. Chem. A, 2010, 114, 6117.
34. A. Bodi, N. S. Shuman and T. Baer, Phys. Chem. Chem. Phys., 2009, 11, 11013.
35. A. Bodi, Á. Kvaran and B. Sztáray, J. Phys. Chem. A, 2011, 115, 13443.
36. T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press Inc., New York, 1996.
37. W. R. Stevens, B. Sztáray, N. S. Shuman, T. Baer and J. Troe, J. Phys. Chem. A, 2009, 113, 573.
38. N. S. Shuman, L. Y. Zhao, M. Boles, T. Baer and B. Sztáray, J. Phys. Chem. A, 2008, 112, 10533.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Rob, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. J. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian03, Gaussian, Inc, Wallingford, CT, 2003.
40. C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, J. Comput. Chem., 1996, 17, 49.
41. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. J. Raghavachari, J. Chem. Phys., 1999, 110, 7650.
42. A. Burcat and B. Ruscic, Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables, ANL-05/20 and TAE 960, Technion-IIT; Aerospace Engineering, and Argonne National Laboratory, Chemistry Division, ftp://ftp.technion.ac.il/pub/supported/aetdd/thermodynamics mirrored at http://garfield.chem.elte.hu/Burcat/burcat.html, Accessed September, 2011.
43. S. G. Lias, Ionization Energy Evaluation, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, http://webbook.nist.gov, Accessed 24 November, 2011.
44. J. D. Cox, D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corp, New York, 1984.
45. M. Roorda, A. J. Lorquet and J. C. Lorquet, J. Phys. Chem., 1991, 95, 9118.
46. J. Momigny and R. Locht, Chem. Phys. Lett., 1993, 211, 161.
47. A. Bodi, W. R. Stevens and T. Baer, J. Phys. Chem. A, 2011, 115, 726.
48. B. Ruscic, R. E. Pinzon, M. L. Morton, G. v. Laszewski, S. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 9979.
49. S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, J. Phys. Chem. Ref. Data, 1988, 17.
50. J. M. Dyke, A. E. Lewis and A. Morris, J. Chem. Phys., 1984, 80, 1382.
51. L. Andrews, J. M. Dyke, N. Jonathan, N. Keddar, A. Morris and A. Ridha, J. Phys. Chem., 1984, 88, 2364.
52. M. Litorja and B. Ruscic, J. Chem. Phys., 1998, 108, 6748.
53. K. K. Irikura, J. W. Hudgens and R. D. Johnson III, J. Chem. Phys., 1995, 103, 1303.
54. F. Innocenti, M. Eypper, E. P. F. Lee, S. Stranges, D. K. W. Mok, F. Chau, G. C. King and J. M. Dyke, Chem.–Eur. J., 2008, 14, 11452.
55. D. H. Aue and M. T. Bowers, in Gas Phase Ion Chemistry, ed. M. T. Bowers, Academic Press, New York, 1979, vol. 2, p. 1.
56. M. Goto, K. Nakamura, H. Toyoda and H. Sugai, Jpn. J. Appl. Phys., Part 1, 1994, 33, 3602.
57. D. V. Dearden, J. W. Hudgens, R. D. Johnson, B. P. Tsai and S. A. Kafafi, J. Phys. Chem., 1992, 96, 585.
58. C. R. Brundle, M. B. Robin, N. A. Kuebler and B. Harold, J. Am. Chem. Soc., 1972, 94, 1451.
59. E. A. Walters, J. T. Clay and J. R. Grover, J. Phys. Chem. A, 2005, 109, 1541.
60. G. K. Jarvis and R. P. Tuckett, Chem. Phys. Lett., 1998, 295, 145.
61. G. A. Garcia, P. M. Guyon and I. Powis, J. Phys. Chem. A, 2001, 105, 8296.
62. R. L. Asher and B. Ruscic, J. Chem. Phys., 1996, 106, 210.
63. C. Lifshitz and F. A. Long, J. Phys. Chem., 1963, 67, 2463.
64. C. Galloy, C. Lecomte and J. C. Lorquet, J. Chem. Phys., 1982, 77, 4522.
65. D. Feller, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2011, 115, 1440.
66. D. Feller, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2011, 115, 3182.
67. M. W. Chase, J. Phys. Chem. Ref. Data, Monogr., 1998, 9.
68. B. Ruscic, J. V. Michael, P. C. Redfern, L. A. Curtiss and K. Raghavachari, J. Phys. Chem. A, 1998, 102, 10889.
69. D. A. Dixon and D. Feller, J. Phys. Chem. A, 1998, 102, 8209.
70. J. Harvey, A. Bodi and R. P. Tuckett, to be published.
71. D. W. Berman, D. W. Bomse and J. L. Beauchamp, Int. J. Mass Spectrom. Ion Phys., 1981, 39, 263.
72. S. G. Lias, Z. Karpas and J. F. Liebman, J. Am. Chem. Soc., 1985, 107, 6080.
73. J. Csontos, Z. Rolik, S. Das and M. Kállay, J. Phys. Chem. A, 2010, 114, 13093.

---