Combining atomic force-fluorescence microscopy with a stretching device for analyzing mechanotransduction processes in living cells

Abstract

Mechanical forces affect biological systems in their natural environment in a widespread manner. Mechanical stress may either stimulate cells or even induce pathological processes. Cells sensing mechanical stress usually respond to such stressors with proliferation or differentiation. Hence, for in vitro studies, the ability to impose a controlled mechanical stress on cells combined with appropriate analytical tools providing an immediate answer is essential to understand such fundamental processes. Here, we present a novel uniaxial motorized cell stretching device that has been integrated into a combined fluorescence microscope (FM)-atomic force microscope (AFM) system, thereby enabling high-resolution topographic and fluorescent live cell imaging. This unique tool allows the investigation of mechanotransduction processes, as the cells may be exposed to deliberately controlled mechanical stress while simultaneously facilitating fluorescence imaging and AFM studies. The developed stretching device allows applying reproducible uniaxial strain from physiologically relevant to hyperphysiological levels to cultured cells grown on elastic polydimethylsiloxane (PDMS) membranes. Exemplarily, stretching experiments are shown for transfected squamous cell carcinoma cells (SCC-25) expressing fluorescent labeled cytokeratin, whereby fluorescence imaging and simultaneously performed AFM measurements reveal the cytokeratin (CSK) network. Topographical changes and mechanical characteristics such as elasticity changes were determined via AFM while the cells were exposed to mechanical stress. By applying a cell deformation of approx. 20%, changes in the Young's modulus of the cytoskeletal network due to stretching of the cells were observed. Consequently, integrating a stretching device into the combined atomic force-fluorescence microscope provides a unique tool for dynamically analyzing structural remodeling and mechanical properties in mechanically stressed cells.

---

1. Introduction

Mechanical forces such as strain, tension, compression, and shear stress play a crucial role in a variety of mammalian cells. Mechanotransduction – the conversion of mechanical forces to a specific cell response – is critical in healthy cells as well as in many diseases. Processes such as cell proliferation, secretion of signaling molecules, differentiation, growth, movement, and gene expression may be induced in living cells by applying mechanical stress. Exemplarily, mechanical stress is a pivotal parameter in pulmonary physiology. The alveolar epithelium is continuously exposed to mechanical stress during breathing. Breathing stretches the lung cyclically, while a single breath is sufficient for surfactant secretion, preventing the alveolar space from collapsing.¹ Similarly, bone tissue senses mechanical forces while walking and exercising. Furthermore, it has been shown that fracture healing is tightly correlated with mechanical strain.² Additionally, cardiac myocytes produce muscle mass due to stretching,³ and in the bladder stretching stimulates urinary afferent nerves.⁴ Mechanical stress is usually detected and transmitted by the cytoskeleton (CSK),⁵ a three dimensional intracellular network consisting mainly of F-actin, microtubules, and intermediate filaments (IFs). The CSK may thus be considered as a ‘linker architecture’, which translates mechanical forces into changes in local mechanical properties and cellular behavior.⁶ The involvement of the cytoskeletal network in signal transduction arising from external forces has already been a subject of several studies.^7–9 Evidently, understanding mechanotransduction and the involved molecular mechanism requires applying controlled forces in combination with analytical tools such as fluorescence imaging and atomic force microscopy (AFM). Several custom-built^10–12 and commercially available cell stretching devices have been reported.^13,14 In most cases, optical microscopy was used to image changes in the cell shape due to stretching. Yet, to date only little information is available on how cells perceive mechanical strain and how they respond to different stretching modes and amplitudes. Additionally, the activation of intracellular signaling cascades due to the impact of mechanical strain is not fully elucidated.¹⁵

Changes in surface and elastic properties caused by the external loadings may readily be investigated by AFM. AFM has the inherent advantage that mechanobiological and topographical studies on living cells may be obtained in buffered solution, i.e., at physiological conditions. Besides, AFM studies of biological processes such as endo- and exocytosis of cells,^16–18 elastic properties such as the stiffness¹⁹ and/or the Young's modulus may be accessed.^20,21 Additionally, by staining the constituents and/or cellular components of interest with fluorescent dyes, information on structural and molecular changes that are related to mechanical stimulation may be obtained via fluorescence microscopy (FM). For instance, fluorescent proteins may be used during live cell imaging in mechanobiology.²²

Consequently, the combination of FM and AFM with a suitably miniaturized stretching device has the unique advantage that the cells may reproducibly be stretched, while high-resolution imaging via complementary analytical imaging modalities is performed. An AFM-compatible cell stretching device termed ‘microcrack’ has been reported by De Jong et al.,²³ however, it cannot be applied in combination with optical microscopy. The commercially available NanoRack Sample Stretching stage (Asylum Research, Santa Barbara, CA, USA) allows AFM studies with mechanical stress control, however, studies with living cells cannot be performed with this device. To date, to the best of our knowledge, no cell stretching system is available, which readily facilitates the combination of AFM with simultaneous FM live cell imaging via an inverted fluorescence microscope.

The following requirements have to be fulfilled for combined AFM-FM imaging while performing stretching experiments: (i) the stretching device has to be small and lightweight for facilitating its integration into the AFM sample plate holder within the combined AFM/inverted microscope system. (ii) For AFM imaging, the soft silicone membrane with cells adherent to the membrane surface has to be supported by a solid substrate such as glass. (iii) The stretching device should be motorized in order to ensure reproducible stretch amplitudes applied to the silicone membrane, and therefore, to the attached cells. (iv) The stretching device should be modular, which allows exchanging the clamped PDMS sheet, sterilizing, cell seeding, and incubation.

With respect to these requirements, a device has been developed enabling controlled membrane stretching via a stepper motor with a minimal step size of 3.75°, which translates into a 0.07% stretch of the PDMS sheet, yet accommodating the AFM/FM setup for in vitro cell studies. With the uniaxial cell stretcher developed for combined AFM/FM measurements, changes in cell shape and elastic properties can be determined at controlled mechanical loadings of living cells, while bright field (BF) and fluorescence images may simultaneously be recorded.

2. Experimental

2.1 Cell culture and preparation

Cells are seeded onto PDMS membranes, which were previously coated with fibronectin overnight. Prior to seeding, the PDMS membrane and the cell stretch device were sterilized in 70% isopropyl alcohol for 30 min. Then, the membrane was reversibly clamped into the stretching device (Fig. 1(e)). The squamous cell carcinoma cell line SCC-25 was used as a model.²⁴ These cells were stable when transfected with cytokeratin 18 linked to a yellow fluorescence protein. Cytokeratin 18, is an intermediate filament protein, and hence, useful as a biomarker. Cells were cultured in Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% fetal bovine serum (FBS). Cells were used after 2–3 days in culture (37 °C, 5% CO₂), which corresponds to approximately 70% of confluence.

Fig. 1 (A) Image of the cell stretching device. (a) Teflon membrane chamber with the observation window in the middle; (b) two sliding brackets (marked with crosses) for clamping the PDMS sheet. (c) Spiral coil where the brackets are attached. (d) Stepper motor attached to a flexible axle (e). (f) Connector of the stretching device to the flexible axle. (g) Removed brackets screwed onto an assembly tool that allows clamping the PDMS membrane. (B) Schematic of the entire assembly including the stretching device, the top-down AFM head, and the objective of the inverted microscope.

2.2 Motorized stretch device

The mechanical force for stretching the PDMS membrane was provided by a 3.75° stepper motor (42SH-32KCA, ELV Electronic, GER). A programmable microcontroller (PIC16F887, Mikrochip Techn. Inc., Chandler, AZ, USA) triggers the motor; the software, which controls, for example, the pausing time during stretching, step width, and stretch velocity was compiled with mikroC for PIC (version 3.0, MikroElektronika). Besides the time between the steps, which may be individually adapted (during the measurements presented herein approx. 150–250 ms), the number of steps and the velocity of the motor may be regulated. Furthermore, any stretch or relaxation movement may be paused at any time and continued again.

2.3 Fluorescence microscopy

For combined AFM/FM measurements, the AFM was mounted on top of an inverted optical microscope (IX81, Olympus America Inc., Melville, NY, USA). A mercury lamp (model U-LH100HG, 19 V, 100 W) was used as light source for fluorescence excitation. Bright field (BF) and fluorescence images were recorded with an LCPlanFI-Olympus 40×/0.6 objective and an EZ CCD-camera (Photometrics, Tucson, AZ, USA). Data acquisition is obtained by the Metamorph software version 7.5.5.0 (Visitron systems GmbH, Puchheim, Germany). FM images were analyzed using ImageJ software (version 1.440, National Institute of Health, USA, http://rsb.info.nih.gov/ij).

2.4 Atomic force microscopy

AFM studies were performed with a model 5500 system from Agilent Technologies (Chandler, AZ, USA). For all measurements, V-shaped silicon nitride cantilevers with a nominal spring constant of 0.06 N m⁻¹ (Bruker, Camarillo, CA, USA) were used. The tips had a pyramidal shape with a half opening angle of 35°. Prior to cell measurements, the spring constants of the cantilevers were determined using the thermal noise method.²⁵ AFM images were recorded in low force contact mode at a scan rate of 0.2–0.5 Hz, while exerted forces were in the order of 5 nN. All experiments were performed in bath solution (BS in mM: 140 NaCl, 5 KCl, 1 MgCl₂, 2 CaCl₂, 5 glucose, 10 HEPES; pH 7.4) at room temperature.

For elasticity measurements, a 30 × 30 μm² area was imaged via a 32 × 32 force-mode operation (1024 indentations) at 0.5 Hz. The spacing between each force curve is approximately 1 μm. Indentations were performed with a load rate of 5 μm s⁻¹. For all elasticity studies, an area between neighboring cells was selected, where the CSK network was clearly evident in the FM images. After uniaxial stretching, the same area was imaged by the force–volume assay (one cell area per dish was measured).

To determine the Young's modulus from the force displacement curves, the deflection–displacement curve is converted into a force–distance curve. The sample distance may be calculated from the piezo displacement subtracting the deflection of the cantilever. The determination of the contact point between the AFM tip and a soft sample is challenging, and several methods have been described in the literature.^26,27 In the presented study, the contact point was determined using regression lines.²⁸ It is assumed that the cantilever does not encounter any repulsive forces until contact with the sample surface occurs. Hence, in the presented study, the contact point is placed in the region where the cantilever starts to deflect.²⁸ To calculate the Young's modulus from the force curves, a modified Hertz model is used.²⁹ The Hertz–Sneddon model describes the elastic deformation of a soft sample by a stiff cone as follows,

where F is the loading force, α the half-opening angle of the pyramidal tip (for Si_xN_y tips 35°), E the Young's modulus, δ the indentation into the sample (corresponding to the absolute value of the tip–sample distance after contacting the sample), and ν the Poisson ratio of the surface (0.5 for soft biological materials).

The Young's modulus E is directly proportional to the force F and inversely proportional to the second power of the indentation. Plotting F vs. δ² and applying a linear fitting algorithm, the Young's modulus is obtained from the calculated slope. It has to be noted that linear fitting is only applied to the data reflecting the part where the cantilever indents into the sample. This is critical to determine the elastic modulus of the sample rather than an underlying layer. Here, this is especially important for obtaining the Young's modulus of the cytoskeletal network and not from the underlying PDMS sheet. By using the described model for analyzing each force–distance curve of the force–volume assay, a corresponding elasticity image is obtained.

3. Results and discussion

3.1 Design of the uniaxial cell stretching device

Fig. 1(A) shows an image of the cell stretcher assembly. The basis of the stretch device is a high quality stainless steel plate that readily integrates into the magnetic sample holder of the AFM. The entire stretching device measures 1.4 cm in height, and has a diameter of 8.8 cm. It is comprised of two main components, the adapted cell stretcher (including the membrane chamber with observation window Fig. 1(a), brackets Fig. 1(b) and spiral coil Fig. 1(c)) and the stepper motor Fig. 1(d) attached to a flexible axle Fig. 1(e). The flexible axle is connected to the cell stretcher connector Fig. 1(f). The membrane is reversibly clamped between two sliding brackets (marked with crosses), which may be separately removed from the stretching device by a locking screw (marked with an arrow). The brackets, which are connected to a spiral coil Fig. 1(c), can be moved in opposite directions leading to a change in the membrane length, and hence, to a mechanical strain at the adherent cells. The lateral displacement during stretching (in particular, when cells are not exactly in the center part of the membrane) can be shifted back to the center by moving the AFM sample plate. The size of the window Fig. 1(b) integrated in the stretching device is 10 × 10 mm fitting in size of a 40× microscope objective from the bottom for locating and imaging cells. A small glass slide covers the window Fig. 1(b) and supports the PDMS membrane, which is needed for AFM imaging. The axle flexibility allows the sample plate to be moved in the z-direction, which is essential for approaching the sample towards the AFM cantilever, as well as movement in the x and y directions to move the sample relative to the objective of the microscope.

The modular design of the stretching device provides the distinct advantage that the sample plate with the device for mounting the PDMS membrane may be sterilized, and cells may be seeded and cultured at the required physiological conditions in a cell culture incubator without the motorized component. After cell cultivation, the device is combined with the stepper motor and mounted on the AFM scan head, which is attached to the inverted microscope. A scheme of the assembly with the AFM on top, the cell stretching device, and the inverted microscope is shown in Fig. 1(B).

3.2 Calibration of membrane deformation

Living cells are capable of adapting to mechanical stimulation, which is imposed upon the cells via stretching the PDMS membrane.^30,31 Strain analysis was performed by coating the PDMS sheet with tetraspeck fluorescent microspheres (1 μm in diameter, Invitrogen Corporation, Carlsbad, CA, USA) to calibrate the stretching level. The displacement of the adherent beads at the surface of the flexible membrane is optically determined by FM. Images were acquired at a magnification of 40× after moving the motor each time by 50 steps. After every 50 motor steps, the selected area of interest was centered prior to recording fluorescence images. The distance between two microbeads of the non-stretched and stretched PDMS membrane was measured and evaluated using ImageJ software after each stretching (i.e., after moving the motor by 50 steps), and plotted as normalized values (Fig. 2(A)). For evaluation, 7 stretching steps between two microbeads were analyzed (Fig. 2(B)). While stretching, the fluorescent spots followed paths oriented parallel to the strain axis. A highly reproducible linear relationship between motor steps and the stretch level of the membrane was determined to be 7% for 100 steps each. The mean slopes of independent calibration curves did not significantly vary (range: 0.05–0.08 per single step). Hence, it was safely assumed that the strain is almost uniform at locations across the viewable area of the observation window.

Fig. 2 Calibration of membrane deformation using fluorescent microspheres as markers. (A) Representative calibration function for a uniaxial stretch. The pixel change of 7 fluorescent spot-pairs was analyzed and plotted as a normalized function of motor steps. 100 motor steps lead to a membrane stretch of approx. 7%; (B) exemplary fluorescence images of a non-stretched and stretched (after 300 steps) membrane with microspheres observed with a 40× objective. Data are represented as mean ± SD. Scale bar corresponds to 10 μm.

3.3 Stretching of living cells

Stretching living cells while simultaneously monitoring the stretching process of a single cell with FM is challenging. Here, fluorescence images at defined intervals of uniaxial stretching are shown. As a model for demonstrating stretching experiments on live cells, cells of a squamous cell carcinoma (SCC-25 cells) were used. Fig. 3 shows a series of fluorescence images of labeled SCC-25 cells before and after stretch amplitudes of 12% and 25%. AFM topography images are shown in the ESI (Fig. S1†). Cell strain more than 60% is feasible with the present device, which is a much higher stretch level than needed for most studies of cellular response to mechanical stretching. For instance, 6–18% stretch affects bone remodeling,³² while cell deformation of 8–46% leads to increased lamellar body fusion in alveolar type II cells.³³ Muscles undergo deformations of >50% during contraction and expansion.³⁴ Hence, the presented stretch device may be used for various stress–response studies using a variety of different cell types cultured on fibronectin-coated PDMS membranes.

Fig. 3 Fluorescence images of living SCC-25 cells subjected to stretching. FM images were acquired before and after stretching (CSK staining via cytokeratin 18 linked to a yellow fluorescence protein). Cell deformation was analyzed via ImageJ software. Scale bar corresponds to 20 μm.

3.4 AFM/FM imaging of SCC-25 cells

Low force contact mode AFM imaging was used to assess the topography of non-stretched and stretched SCC-25 cells. Fig. 4 shows the BF/fluorescence image and the corresponding AFM deflection images of non-stretched and stretched SCC-25 cells. After AFM imaging of the non-stretched area (white rectangle shown in the BF and fluorescence images in Fig. 4(A), the AFM tip was withdrawn (20 μm) and the PDMS sheet was stretched via the stepper motor (here, 250, 430, and 700 steps; time between steps: 200 ms). Fig. 4(B–D) show the corresponding FM/AFM images after horizontally stretching the PDMS sheet along the x-direction (bold arrow). After re-centering the area of interest, the AFM tip is approached again and AFM images were recorded for each stretching step. As the calibrated relationship between motor steps and membrane deformation cannot be directly translated into single cell deformation,³⁵ the distance between discernible cellular features in the area where the AFM images were recorded (black line in the BF images) were measured. The deformation of the cell measured parallel to the stretch axis ranged from approx. 16% (250 motor steps, Fig. 4(B)) to 30% (430 motor steps, Fig. 4(C)), and finally to 50% (700 motor steps, Fig. 4(D)). Cytoskeletal elements are clearly evident in the AFM images, in particular for non-stretched cells, and correlate well with the FM images (white arrows in Fig. 5(A) and (B)). It appears that stretching the cells results in a less detailed structure, which maybe related to a disruption of connective elements or a rearrangement of cytoskeletal components. The loss of CSK elements detectable in the AFM images is already discernable at stretch values of 30%, and is clearly evident at a stretch level of 50% (Fig. 4(D) and 5(C)).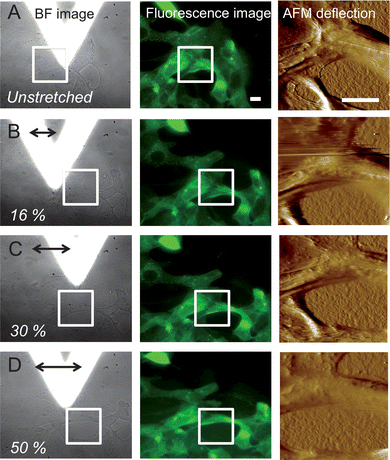

Fig. 4 Bright field/fluorescence images and corresponding AFM deflection images of SCC-25 cells before (A) and after defined stretching levels (B, C, and D). White rectangles show the area where low force contact mode AFM imaging was performed. Cell deformation was measured using ImageJ software. Z-range of the deflection image: 0–1 V; scale bar: 20 μm. CSK staining via cytokeratin 18 linked to a yellow fluorescence protein.

Fig. 5 (A) Fluorescence image and the corresponding AFM deflection image (B) of non-stretched SCC-25 cells, where cytoskeletal elements are evident (white arrows). After 50% cell deformation, the AFM deflection image (C) lacks information regarding specific CSK elements, indicating that they are disrupted due to stretching. Z-range of the deflection image: 0–1 V; scale bar: 10 μm.

3.5 Elasticity changes of the CSK network

To examine elasticity changes of the CSK part of SCC-25 cells in response to substrate strain, AFM force–volume assays were performed before and after defined stretching levels. Fig. 6(A) shows the AFM topography image (entire scan area) and the corresponding 32 × 32 force volume map Fig. 6(B) of a non-stretched area, where the CSK network is clearly visible. As described in the literature, the elastic modulus of living cells determined by AFM is in the range of 100 Pa to 100 kPa³⁶ depending on the investigated cell area and cell type. For example, stiffness measurements of glial cells of nerve tissues revealed a significant difference in stiffness between the cell membrane above the nucleus and areas reflecting F-actin, which appears much stiffer.³⁷ The obtained elastic values of the investigated SCC-25 cell–cell cytoskeletal filaments resulted in values in the same range. After deformation by approx. 20%, the same area was investigated via the force volume assay (Fig. 6(C) and (D)). As indicated by the blue rectangle, a small shift is apparent. The white arrows indicate the CSK network. After uniaxial cell stretching by 20%, a decrease in the elastic modulus of the CSK network is observed. Two exemplary force distance curves (Fig. 6(E) and (F) and their respective points are marked with crosses inside the circle in Fig. 6(B) and (D)) are extracted from the force maps. Each force distance curve was fitted following the Sneddon model. Fitting the force distance curves (black) to the Sneddon model (red) leads to a higher elastic modulus before stretching compared to the values after stretching (for calculation of the force a deflection sensitivity of 92 nm V⁻¹ and a spring constant of 0.06 N m⁻¹ was used). An elastic modulus of 45 kPa of non-stretched filaments (Fig. 6(E)) and 21 kPa after 20% strain (Fig. 6(F)) was obtained (note: these values are just an example from one single force curve and do not refer to the whole map). This decrease in the elastic modulus suggests that thin connective filaments are disrupted³⁸ and/or rearranged as previously reported in the literature.^38,39 Similar data confirmed that deformations up to 20% lead to stress-induced fiber reassembly and disassembly.^40,41 However, the cause for the reduced elastic modulus after cell stretch is not yet verified. Either the integrity of the CSK was lost or the stretch-induced CSK fiber remodeling resulted in a fiber arrangement with a reduced Young's modulus. In addition, the magnitude of the elastic modulus is also affected by the AFM tip geometry^42,43 and by the indentation depth,¹⁹ which may contribute to the observed effects. Future research will focus on quantification and statistical evaluation of elasticity changes, which is beyond of the scope of this study, as the objective herein is to demonstrate the fundamental versatility of the developed cell stretching device for elasticity studies at living cells.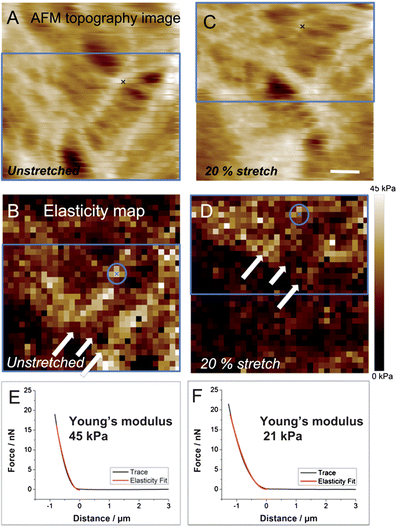

Fig. 6 AFM topography image and corresponding elasticity map of non-stretched (A and B) and 20% stretched (C and D) SCC-25 cells. Blue rectangles indicate the same area of (A) and (C) (B and D, respectively). White arrows point toward keratin, which show higher elasticity values before cell deformation. (E) and (F) show extracted force distance curves from the AFM map before (E) and after (F) 20% cell stretching (marked with crosses). Scale bar: 5 μm.

4. Conclusions and outlook

A miniaturized cell stretching device was developed for mechanically stimulating living cells at physiologically relevant levels applicable to a wide variety of adherent cell types. The unique advantage of the presented cell stretcher is its integration into a combined AFM/FM system, thereby enabling stretching experiments along with simultaneous real-time fluorescence and AFM studies. The stretching device is integrated into the sample stage of a top–down AFM, which is combined with an inverted microscope. This combination of optical microscopy, atomic force microscopy, and a cell stretching device providing controlled strain levels offers the opportunity to correlate simultaneously several crucial parameters, i.e., structural and molecular changes may be observed via high-resolution FM while mechanical changes are investigated immediately after stretching by AFM. Transfected squamous cell carcinoma cells (SCC-25 cells) were used as model samples for investigating the changes in elastic modulus due to mechanical stress. Uniaxial stretching from small strain values (i.e., 1%) to substantial deformations (i.e., up to 40%) of living cells provides detailed insights into the biological response of cells after mechanical stimulation. Based on such studies, it is anticipated that enhanced knowledge of the cellular response to mechanical stress will advance the fundamental understanding of the involved molecular and structural processes. It is anticipated that this will facilitate the prevention of and therapy for mechanically induced lung and/or cardiovascular diseases and injuries in the future.

Acknowledgements

The authors thank M. Elsner and E. Schoch for their contributions to the continuous development of the miniaturized cell stretching device. The machine shop at the University of Ulm is thanked for fabricating the mechanical components of the stretching device. T. Felder is acknowledged for the cell cultivation. The Boehringer Ingelheim – University Ulm Biocenter (BIU) is acknowledged for financial support.

Notes and references

1. P. Dietl, M. Frick, N. Mair, C. Bertocchi and T. Haller, Biol. Neonate, 2004, 85, 299–304.
2. M. van Griensven, S. Diederichs, S. Roeker, S. Boehm, A. Peterbauer, S. Wolbank, D. Riechers, F. Stahl and C. Kasper, Adv. Biochem. Eng./Biotechnol., 2009, 112, 95–123.
3. J. Sadoshima and S. Izumo, Annu. Rev. Physiol., 1997, 59, 551–571.
4. M. Takeda, T. Mochizuki, M. Yoshiyama, H. Nakagomi, H. Kobayashi, N. Sawada, H. Zakohji, S. Du and I. Araki, LUTS: Lower Urinary Tract Symptoms, 2010, 2, 51–60.
5. P. A. Janmey, Physiol. Rev., 1998, 78, 763–781.
6. D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485–492.
7. M. Tamada, M. P. Sheetz and Y. Sawada, Dev. Cell, 2004, 7, 709–718.
8. B. C. Di Paolo, G. Lenormand, J. J. Fredberg and S. S. Margulies, Am. J. Physiol., 2010, 299, C345–C353.
9. B. Geiger, J. P. Spatz and A. D. Bershadsky, Nat. Rev. Mol. Cell Biol., 2009, 10, 21–33.
10. S. P. Arold, J. Y. Wong and B. Suki, Ann. Biomed. Eng., 2007, 35, 1156–1164.
11. A. A. Lee, T. Delhaas, L. K. Waldman, D. A. McKenna, F. J. Villarreal and A. D. McCulloch, Am. J. Physiol., 1996, 271, C1400–C1408.
12. O. R. Rana, C. Zobel, E. Saygili, K. Brixius, F. Gramley, T. Schimpf, K. Mischke, D. Frechen, C. Knackstedt, R. H. G. Schwinger, P. Schauerte and E. Saygili, Am. J. Physiol., 2008, 294, H532–H540.
13. A. J. Banes, J. Gilbert, D. Taylor and O. Monbureau, J. Cell Sci., 1985, 75, 35–42.
14. A. Gerstmair, G. Fois, S. Innerbichler, P. Dietl and E. Felder, J. Appl. Physiol., 2009, 107, 613–620.
15. Y. S. Edwards, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 2001, 129, 245–260.
16. Y.-L. Pan, J.-Y. Cai, L. Qin and H. Wang, Acta Biochim. Biophys. Sin., 2006, 38, 646–652.
17. E. Hecht, S. M. Usmani, S. Albrecht, O. H. Wittekindt, P. Dietl, B. Mizaikoff and C. Kranz, Anal. Bioanal. Chem., 2011, 399, 2369–2378.
18. C.-C. Tsai, C.-C. Yang, P.-Y. Shih, C.-S. Wu, C.-D. Chen, C.-Y. Pan and Y.-T. Chen, J. Phys. Chem. B, 2008, 112, 9165–9173.
19. E. U. Azeloglu, J. Bhattacharya and K. D. Costa, J. Appl. Physiol., 2008, 105, 652–661.
20. M. Radmacher, IEEE Eng. Med. Biol., 1997, 16, 47–57.
21. C. Rotsch and M. Radmacher, Biophys. J., 2000, 78, 520–535.
22. Y. Wang, J. Y.-J. Shyy and S. Chien, Annu. Rev. Biomed. Eng., 2008, 10, 1–38.
23. K. L. De Jong, H. C. MacLeod, P. R. Norton, N. O. Petersen and M. F. Jasnin, Rev. Sci. Instrum., 2006, 77, 023701.
24. J. G. Rheinwald and M. A. Beckett, Cancer Res., 1981, 41, 1657–1663.
25. J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873.
26. K. A. Melzak, S. Moreno-Flores, K. Yu, J. Kizhakkedathu and J. L. Toca-Herrera, Microsc. Res. Tech., 2010, 73, 959–964.
27. D. C. Lin, E. K. Dimitriadis and F. Horkay, J. Biomech. Eng., 2007, 129, 904–912.
28. F. Gaboriaud, S. Bailet, E. Dague and F. Jorand, J. Bacteriol., 2005, 187, 3864–3868.
29. I. N. Sneddon, Int. J. Eng. Sci., 1965, 3, 47–57.
30. C. Rotsch, K. Jacobson and M. Radmacher, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 921–926.
31. S. J. Tumminia, K. P. Mitton, J. Arora, P. Zelenka, D. L. Epstein and P. Russell, Invest. Ophthalmol. Visual Sci., 1998, 39, 1361–1371.
32. L. Tang, Z. Lin and Y.-M. Li, Biochem. Biophys. Res. Commun., 2006, 344, 122–128.
33. M. Frick, C. Bertocchi, P. Jennings, T. Haller, N. Mair, W. Singer, W. Pfaller, M. Ritsch-Marte and P. Dietl, Am. J. Physiol., 2004, 286, L210–L220.
34. D.-H. Kim, P. K. Wong, J. Park, A. Levchenko and Y. Sun, Annu. Rev. Biomed. Eng., 2009, 11, 203–233.
35. X. Trepat, M. Grabulosa, F. Puig, G. N. Maksym, D. Navajas and R. Farre, Am. J. Physiol., 2004, 287, L1025–L1034.
36. A. R. Harris and G. T. Charras, Nanotechnology, 2011, 22, 345102.
37. T. G. Kuznetsova, M. N. Starodubtseva, N. I. Yegorenkov, S. A. Chizhik and R. I. Zhdanov, Micron, 2007, 38, 824–833.
38. N. Wang and D. Stamenovic, Am. J. Physiol., 2000, 279, C188–C194.
39. N. Gavara, P. Roca-Cusachs, R. Sunyer, R. Rarre and D. Navajas, Biophys. J., 2008, 95, 464–471.
40. L. Lu, Y. Feng, W. J. Hucker, S. J. Oswald, G. D. Longmore and F. C.-P. Yin, Cell Motil. Cytoskeleton, 2008, 65, 281–294.
41. A. Nekouzadeh, K. M. Pryse, E. L. Elson and G. M. Genin, J. Biomech., 2008, 41, 2964–2971.
42. K. D. Costa and F. C. Yin, J. Biomech. Eng., 1999, 121, 462–471.
43. F. Rico, P. Roca-Cusachs, N. Gavara, R. Farre, M. Rotger and D. Navajas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 21914.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2an36001b

---