Total internal reflection Raman spectroscopy
David A.
Woods
and
Colin D.
Bain
*
University of Durham, Department of Chemistry, University Science Laboratories, South Road, Durham, UK DH1 3LE. E-mail: c.d.bain@durham.ac.uk
First published on 14th October 2011
Abstract
Total internal reflection (TIR) Raman spectroscopy is an experimentally straightforward, surface-sensitive technique for obtaining chemically specific spectroscopic information from a region within approximately 100–200 nm of a surface. While TIR Raman spectroscopy has long been overshadowed by surface-enhanced Raman scattering, with modern instrumentation TIR Raman spectra can be acquired from sub-nm thick films in only a few seconds. In this review, we describe the physical basis of TIR Raman spectroscopy and illustrate the performance of the technique in the diverse fields of surfactant adsorption, liquid crystals, lubrication, polymer films and biological interfaces, including both macroscopic structures such as the surfaces of leaves, and microscopic structures such as lipid bilayers. Progress, and challenges, in using TIR Raman to obtain depth profiles with sub-diffraction resolution are described.
 David A. Woods | David Woods is currently finishing a PhD in physical chemistry at University of Durham U.K., using total internal reflection Raman spectroscopy to look at surfactant adsorption at the solid–liquid interface. Prior to his PhD he obtained an M.Chem. degree from University of Durham (2007). |
 Colin D. Bain | Colin Bain is Professor of Chemistry and Director (Science) of the Institute of Advanced Study at Durham University, U.K. His general research area is the structure and properties of thin organic films at wet interfaces, including the development of new experimental platforms and analytical techniques for characterising interfaces on short time scales. Recent awards for his research include the Tilden Prize (2008), Craig Lectureship (2008) and Thomas Graham Lectureship (2011). |
1 Introduction
The behaviour of surfaces controls a wide range of physical and chemical processes, including detergency, wetting, stability of emulsions, reactions at electrodes, lubrication, non-stick and anti-fouling coatings, heterogeneous catalysis, and membrane processes in living organisms. A wide range of analytical techniques have been developed to probe surfaces. Many of the most common techniques, including tensiometry, ellipsometry, quartz crystal microbalance and atomic force microscopy, are not intrinsically chemically specific meaning that the different molecular species cannot easily be distinguished. For this reason, the use of complementary spectroscopic techniques is desirable. Spectroscopic techniques that are based on second-order nonlinear optical effects, such as sum-frequency spectroscopy and second harmonic generation, are innately surface selective. Others can be made surface sensitive by careful control of the region probed. One way of achieving this control is confocal microscopy, which restricts the collection of emitted light to certain regions of the sample. Another way, which is particularly useful for the study of surfaces, is to restrict the excitation light to the region of interest, for example by use of the evanescent wave from totally internally reflected (TIR) light. ATR-IR (attenuated total reflection infrared spectroscopy)1–3 and TIRF (total internal reflection fluorescence)4 are sufficiently well-established to have entered the lexicon of the surface chemist. By contrast, the subject of this review, TIR Raman spectroscopy, has been used much less extensively despite numerous benefits compared to other forms of surface vibrational spectroscopy. One reason for the neglect of TIR Raman is the dominance of surface enhanced Raman spectroscopy (SERS) where the excitation of plasmons in metallic substrates of an appropriate morphology leads to large enhancements of Raman signals from molecules adsorbed on the metal surfaces.5,6SERS has been very well reviewed elsewhere and we do not discuss it further here. Rather this review will focus on Raman scattering from flat surfaces, where the only enhancement in the signal comes from the linear optics of an evanescent wave.7 With modern technology, TIR Raman spectra can be acquired from sub-monolayers of organic molecules in seconds, making TIR Raman spectroscopy a practical, useful and versatile alternative in applications where SERS is impractical or undesirable.TIR Raman spectroscopy was first demonstrated by Ikeshoji and coworkers in 1973,8 from carbon disulphide beneath a glass substrate (spectra are shown in Fig. 1). Subsequent early work looked at dyes adsorbed to a transparent electrode, showing a shift in Raman spectrum with potential;9dyes at the quartz–water interface;10dyes at the air–water interface;11 and dyes at the CCl4–water interface (including the determination of orientation from multiple polarisations).12,13 However, the signal was still weak—even with resonance enhancement from the dye— and obscured by large amounts of Raman scattering from the substrate. The development of SERS meant that very little work was done subsequently using TIR Raman at electrode interfaces and attention switched to dielectric materials. Iwamoto et al. demonstrated the surface sensitivity of non-resonant TIR Raman by recording spectra from a 1.1 μm thick polystyrene film without seeing peaks from the polyethylene film upon which it was mounted.14,15 They also provided the first demonstration of TIR Raman spectroscopy from biological samples.16 Their key improvement was the careful choice of a substrate that did not fluoresce and so reduced the background signal to manageable levels. Around the same time Hölzer and co-workers17 published a series of papers using TIR Raman spectroscopy to study polymers attached to surfaces, including polyethylene (to determine the degree of crystallinity) and partially polymerised styrene/polystyrene mixtures18,19 (to determine the degree of polymerisation). Pagannone and Suëtaka both studied the angular dependence of the Raman scattered radiation.20,21 The angular distribution of scattered light is a function of the polarisation of the emitted light,22 the polarisation of incident radiation and the orientation of molecules in the probed layer, but the greatest signal is always measured at the critical angle (see Fig. 2 for an example).
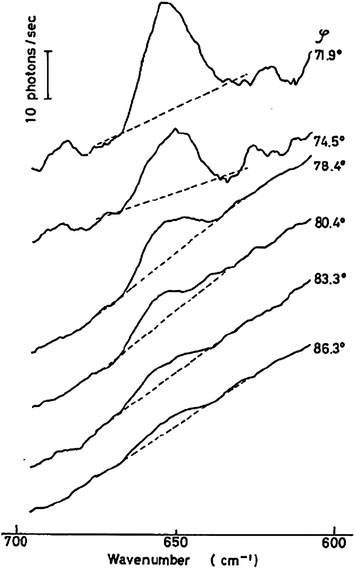 | ||
| Fig. 1 The first reported TIR Raman spectra, of CS2 at the glass–liquid interface for a variety of angles of incidence. Reproduced from ref. 8 with permission. | ||
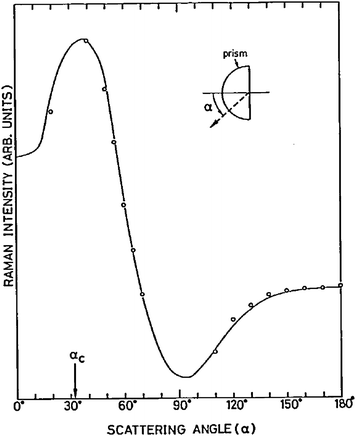 | ||
| Fig. 2 Angular dependence of scattered Raman radiation from the 1530 cm−1 band of a 5-nm thick copper phthalocyanine film on glass. The solid line is a calculated dependence. The critical angle is labelled as αc. Reprinted from ref. 21, Copyright (1984), with permission from Elsevier. | ||
Waveguides are a well-established technology that is readily adaptable for Raman scattering. In a conventional waveguide, a high-index core carries an optical wave in a well-defined transverse mode with a low-index cladding in which the wave is evanescent. If this cladding is sufficiently thin, the evanescent field penetrates into the surrounding medium and can be used to excite Raman scattering which then couples back into the waveguide. In waveguides, the maximum in the electric field occurs within the core of the waveguide and the field in the surrounding medium is much weaker (especially in low order modes). The enhancement in sensitivity in waveguide Raman comes principally from the large interaction area at the surface of the waveguide.23 Increased sensitivity to thin films can be achieved if the cladding is omitted and the guiding layer is placed directly in contact with the sample, provided the sample has a low-enough index for the field to be evanescent.24,25 Early work on waveguide Raman has been reviewed in ref. 2 and 26. There has been little recent work on waveguide Raman, though it has the potential to be integrated profitably with other surface analytical techniques that exploit waveguides, such dual phase interferometry.
This review focuses on more recent studies of TIR Raman scattering that use prisms or high numerical aperture (NA) objectives to deliver the laser beam to a buried interface. First, we briefly set out the theory of Raman scattering and total internal reflection. Second, we describe a typical experimental arrangement using a hemispherical prism to deliver the pump light, based on the TIR Raman apparatus in Durham, UK, as well as alternative experimental arrangements. Third we compare the advantages and disadvantages of TIR Raman to competing forms of vibrational surface spectroscopy: ATR-IR and sum-frequency generation. Fourth, we survey the literature on the use of TIR Raman at a variety of buried interfaces: the solid–liquid interface, including surfactant adsorption, lipid bilayers, liquid crystals and adsorption onto particles; the liquid–liquid interface, covering adsorption of fluorescent dyes; and the solid–solid interface, including tribological contacts, strained silicon surfaces and polymer thin-films and biological surfaces. Finally we discuss the potential of TIR Raman for depth profiling, and compare it with confocal Raman spectroscopy.
2 Theory
Raman spectroscopy is the term applied to linear (single photon) inelastic scattering associated with transitions between rotational or vibrational energy levels. Evanescent wave Raman scattering is exclusively used to study vibrational structure in condensed phases, where rotational structure is not resolved. An incident photon interacts with a molecule, exciting it to a short-lived virtual state. The molecule then relaxes to a different vibrational quantum level (v), releasing a photon at a slightly lower energy (Stokes scattering, Δv = +1) or higher energy (anti-Stokes scattering, Δv = −1). Stokes scattering is more intense than anti-Stokes scattering since there is a greater thermal population of molecules in the ground vibrational state. Where the virtual state corresponds to an electronic state of the molecule, the probability of inelastic scattering is enhanced (resonance Raman). Classically, Raman scattering arises from radiation from the electric dipole induced in a molecule (or material) by an incident electric field, E. In the linear regime, the induced dipole, p, is given by| p = α·E, | (1) |
An oscillating electric dipole (p, with amplitude p0) in a vacuum emits light with a time averaged power per solid angle, I, of27
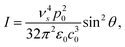 | (2) |
In linear Raman scattering (eqn (1) and 2), the scattered intensity depends quadratically on the electric field of the incident field (the pump laser) and on the fourth power of the frequency of the scattered light ν4s. Raman spectrometers detect the number of photons rather than the intensity of light, so the Raman signal scales proportionally to ν3s. Nevertheless, the sensitivity of the technique improves rapidly with shorter wavelength excitation.
Total internal reflection Raman spectroscopy is a variant of Raman spectroscopy where the incident excitation is an evanescent electric field at an interface. The following paragraphs describe the conditions of total internal reflection leading to the evanescent field.
When light strikes an interface it is split into a reflected and a transmitted wave. At the interface the components of the electric and magnetic fields tangential to the interface must be continuous. These boundary conditions allow the calculation of transmission and reflection coefficients t and r, representing the ratio of the electric field of the transmitted and reflected light to the incident electric field. For incident light with an electric field polarised perpendicular to the plane of incidence (i.e. the xz-plane containing the incident and reflected beams), referred to as S polarised,
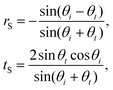 | (3) |
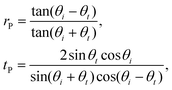 | (4) |
| nt sin θt = ni sin θi, | (5) |
| θc = arcsin nt/ni. | (6) |
Above the critical angle there is no net transmission of energy across the interface, however the boundary conditions still require there to be an electric field beyond the interface. This electric field is termed an evanescent wave, and decays exponentially with increased distance, z, from the interface.
| Et(z) = E0te−ktβz, | (7) |
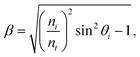 | (8) |
The electric field decays with a characteristic length of (ktβ)−1. Since Raman scattering is proportional to the square of the electric field, TIR Raman scattering probes a region adjacent to the interface with a characteristic thickness of (ktβ)−1/2.
Above the critical angle the transmission coefficients are complex quantities given explicitly by,
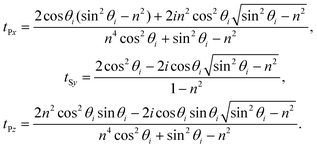 | (9) |
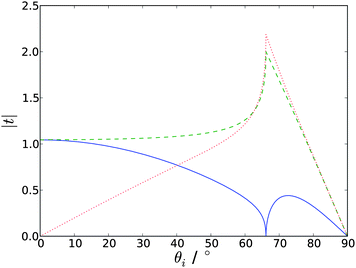 | ||
| Fig. 3 Absolute values of the Fresnel factors as a function of incident angle, at the silica-water interface (ni = 1.461, nt = 1.336). tpx is the solid blue line, tsy the dashed green line and tpz the dotted red line. | ||
3 Experiment
The TIR Raman spectrometer at Durham University,29,30 is illustrative of a design in which the beam is delivered externally to the collection optics in order to have a well-defined angle of incidence. The pump laser is a continuous-wave, frequency-doubled solid-state laser with a wavelength of 532 nm yielding between 0.1 and 1 W at the sample, depending on the application (and, in particular, on the damage threshold of the sample). A half-wave plate selects the incident polarisation to be S or P. The beam is gently focussed by a gradient index lens into a hemispherical prism to a diameter of ∼10 μm at the interface between the prism and the sample. The Raman scattered light is collected through the incident medium with a high NA ultra-long working distance objective attached to a commercial Raman spectrometer. The spectrometer allows the polarisation of the scattered light to be selected in either the x or y-directions. Fig. 4 illustrates the geometry of the incident light and the collection optics.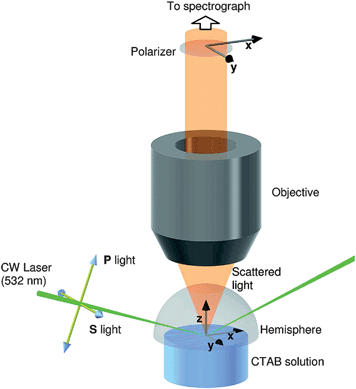 | ||
| Fig. 4 Schematic of the sample, incident light and collection optics in the TIR Raman spectrometer at Durham University. The directions of the electric field vectors for the available polarisations of incident and collected light are also shown. Reprinted with permission from ref. 29. Copyright 2008 American Chemical Society. | ||
The selection of a hemispherical prism for the total internal reflection element minimises optical aberrations in the incident beam and maintains the numerical aperture of the collection objective. Fused silica is a good choice of prism material when the sample is aqueous; typical parameters are an angle of incidence of 73° giving an illuminated region of 30 × 10 μm, a decay length for the electric field dp = 200 nm and a sampling depth for Raman scattering of dp/2 = 100 nm.
Other substrates used successfully in TIR Raman include CaF2, SrTiO3, sapphire and a variety of high index glasses. Ideally, the substrate should not have a strong Raman spectrum in the region of interest, since it will tend to dominate the recorded spectra (the evanescent wave only confers surface selectivity in the sample, not in the incident prism). For example, glasses are good substrates when studying molecules with large Stokes shifts but show a variety of broad strong bands at wavelengths below 1600 cm−1, while sapphire is clear of interfering bands above 800 cm−1.15 Where there is spectral overlap, crystalline compounds (such as sapphire or CaF2) are preferred, since they have sharper peaks than amorphous substrates. A major concern with TIR Raman spectroscopy is fluorescence from the substrate, which can often dominate the Raman scattering. Many optical glasses (but not fused silica) are prone to fluorescence due to impurities in the glass, as is sapphire. Excitation in the red or near-IR reduces fluorescence, at the cost of reduced Raman signal (due to the ν3 dependence of Raman scattering) and, for near-IR lasers, reduced detector efficiency. Pulsed lasers and time-gated excitation can discriminate Raman scattering from fluorescence,31 but this approach has not yet been applied to TIR Raman. Some substrates, such as sapphire and MgF2, are birefringent which complicates the optics and gives two different critical angles for different polarisations. Not all substrate materials can be fashioned into a transparent, optical element with a flat surface suitable for TIR Raman. In these cases an alternative option is to coat a suitable optical element with a thin film of the material on interest; this approach is discussed further in section 5.
An alternative approach to TIR Raman is to use annular illumination,32,33 typically through a hemispherical lens (often termed a solid immersion lens or SIL). The beam passes along the standard beam path of the Raman microscope, and is delivered to the sample through the same objective lens as that used to collect Raman scattered light. If the numerical aperture of the objective lens is high enough then some of the beam will be incident above the critical angle. Placing a circular block in the beam path gives annular illumination, removing light that would reach the sample at less than the critical angle. The advantage of this technique is that the insertion of the circular mask into the sample is straightforward and needs few changes to the default beam path. The main disadvantages are that the polarisation of the incident beam is scrambled and that the angle of incidence is less well-defined than for a custom beam path. Loss of much of the incident laser power at the mask is a further disadvantage, although the laser is often attenuated anyway to reduce damage to the sample. The irradiated area is much smaller than with the external beam path described above, leading to a reduction in sensitivity. A simpler variant of this approach is to use a full angular range of illumination and collect the Raman spectrum arising from both the evanescent wave and the transmitted light,34 providing the enhancement of the signal from the surface but no surface selectivity.
4 Comparison with other vibrational spectroscopies
The technique most similar to TIR Raman spectroscopy is ATR-IR spectroscopy, which measures the adsorption of infrared radiation within an evanescent wave. TIR Raman has better surface selectivity, since the penetration depth is proportional to the wavelength of light in the prism, which is in the visible or near-IR for Raman scattering and in the mid-IR for ATR-IR. TIR Raman spectra are also simpler to interpret for two reasons: first, in ATR-IR the penetration depth varies with wavelength, and second, strong bands in ATR-IR are distorted by the rapid variations in the refractive index of the sample. Both TIR Raman and ATR-IR have sufficient sensitivity to detect monolayers of organic molecules in a single spot, though ATR-IR frequently uses a multiple bounce internal reflection element (IRE) to enhance sensitivity (analogous to waveguide Raman discussed above).ATR-IR requires a substrate material that is transparent at the wavelengths of interest in the infrared, which is usually more limiting than the requirement of Raman that the material is transparent close to the wavelength of the excitation light (which can be selected by the researcher). As mentioned earlier, the choice of substrate material in Raman spectroscopy is limited by fluorescence, an issue that does not arise in ATR-IR. While the average fluorescent background can be subtracted from Raman spectra, the noise in the background cannot; it is this noise that degrades the quality of the Raman spectrum. The problem of fluorescence applies to the sample as well as the substrate: Beattie et al. found the surfactant 2-mercaptobenzothiazole fluoresced strongly when adsorbed as a dimer,35 whereas such problems were not observed in ATR-IR.36
For applications at the solid–water interface, one of the most important considerations is the intensity of the water background, and this is one of the areas where Raman and IR differ most strongly. Table 1 compares Raman and IR cross-sections of the O–H stretching modes in water and C–H stretching modes in hydrocarbons. For IR, C–H bands have a 3 × lower cross-section than the O–H band, whereas for Raman the cross-section is around 10 × greater (with excitation in the visible). Therefore, although Raman scattering is a comparatively weak effect compared to infrared absorption, it has much better sensitivity for hydrocarbons relative to water, making it preferable when studying aqueous solutions. The O–H bend around 1600 cm−1 also interferes with sample peaks and here the relative performance of Raman and ATR-IR depends on the specific vibrational mode under study (for example, carbonyl stretches are relatively more intense in IR than Raman). Using a deuterated solvent or sample may also be an option to reduce overlap with solvent peaks in both Raman and ATR-IR, although it does add to the cost of the experiment.37,38 A further issue is the small signal from a single bounce of the infrared beam; when studying rapidly changing processes multiple bounces are usually necessary to obtain sufficient signal.37,39
| Raman cross-section/cm−2 molecule−1 sr−1 | IR cross-section/cm−2 molecule−1 | |
|---|---|---|
| water | 4 × 10−30 (550 nm excitation) | 1 × 10−18 |
| 4 × 10−28 (250 nm excitation) | ||
| C–H | 6 × 10−29 (532 nm excitation) | 3 × 10−19 |
| 3 × 10−24 (239 nm excitation) |
Two other aspects in which TIR Raman has some advantages over ATR-IR are in microscopy, due to the ease of focussing coherent visible lasers over incoherent IR sources, and in kinetic measurements where it is more difficult to maintain a constant and controllable change over the large surface area of a typical IRE used in an ATR-IR experiment.37,39
Infrared-visible sum-frequency generation (SFG) is another form of surface vibrational spectroscopy that has gained widespread use despite the greater cost and complexity of the instrumentation compared to ATR-IR.44–49 In SFG, a pulsed infrared laser is overlapped at the sample with a pulsed laser in the visible or near-IR and light emitted at the sum of the two pump frequencies is detected. Wavelength scanning systems based on picosecond lasers are available commercially and broad-band femtosecond systems are increasingly popular. SFG is a second-order nonlinear technique and gives no signal from centrosymmetric and isotropic media. It is intrinsically surface sensitive (since most bulk materials are SF-inactive) and consequently is especially powerful when used to study how interfaces affect the orientation of the molecules comprising the bulk medium. The symmetry rules of SFG make it sensitive to interface structure but poor at quantifying composition. It is therefore complementary to ATR-IR and TIR Raman and particularly strong when used in combination with one of these techniques.29
SFG is also the preferred tool for probing structure at the air–water interface:47 the relative intensity of the peaks from ‘ice-like’ and ‘water-like’ O–H stretches provides local structural information and non-hydrogen bonded O–H bonds at the surface give a characteristic sharp peak at high wavenumbers; the tilt of O–H oscillators to the surface can be inferred from the polarisation-dependence of the SF signal; surface charge can be inferred from the phase of the water signal in the electrical double layers; there is no competing signal from bulk water. While Nickolov et al. used TIR Raman to compare water structure at hydrophilic (sapphire) and hydrophobic (an ω-tricosenoic acid monolayer) interfaces,50,51 based on the intensity and position of the ice-like and water-like peaks around 3200 cm−1 and 3420 cm−1, the information from SFG is both more detailed and more surface sensitive.
Third-order nonlinear effects, such as coherent anti-Stokes Raman scattering (CARS) and stimulated Raman scattering (SRS), have been developed into chemically sensitive microscopies with sub-micron spatial resolution and with enhanced sensitivity compared to linear Raman scattering. Unlike SFG, CARS and SRS have no intrinsic surface sensitivity and any advantages as surface spectroscopies over TIR Raman would arise from improved signal levels or better spatial resolution (arising from the nonlinear mixing processes involved in the signal generation). SRS also been combined with TIR illumination to look at the water structure at the air–water interface.52 The enhancement occurs transiently before the formation of a plasma from the liquid induced by the excitation laser; these unusual experimental conditions may not represent the properties of room temperature water. Both SRS53 and CARS54,55 have been combined with waveguide excitation to achieve surface sensitivity. At time of writing of this review, the advantages of third-order Raman techniques over linear TIR Raman for surface analysis have not been demonstrated experimentally.
5 Solid–liquid and solid–air interfaces
A recent study that provides a good illustration of the features of TIR Raman is the adsorption of a cationic surfactant, CTAB, from aqueous solutions onto silica.29 The surfactant is present in solution and in an adsorbed film <3 nm thick. The limited penetration depth of the evanescent wave discriminates the adsorbed surfactant from that in the bulk, while the Raman signal from bulk surfactant in the evanescent wave at high surfactant concentrations provides a means of calibrating the adsorbed amount. The strongest Raman signal from CTAB arises from the C–H stretches, which overlap the tail of the O–H stretch of water; the relatively weak Raman cross-section of water nevertheless permitted the adsorbed amount to be determined with a precision of 0.01 mg m−2 (∼1% of the saturated layer). The polarised spectra were largely insensitive to surface concentration and the relative intensities of peaks in different polarisations did not vary with concentration, showing that the orientation and local structure of the molecules in the adsorbed layer were independent of surface coverage. Sum-frequency spectroscopy provided complementary information about the conformation of CTAB at the silica interface, with a lack of C–H signal indicating that the adsorbed molecules were in a centrosymmetric environment. The combination of TIR Raman and sum-frequency generation was particularly powerful, since SFG alone provides no information about the amount of surfactant adsorbed, while TIR Raman cannot distinguish between adsorption in monolayers or centrosymmetric aggregates (such as admicelles or bilayers). In general, SFG is more sensitive to conformation than Raman or IR absorption spectroscopy.We have extended TIR Raman to look at adsorption and desorption kinetics of surfactants at solid-liquid interfaces,30,56 with a sampling frequency of 0.5 Hz—sufficient to follow the kinetics in real time—with a standard deviation from point to point of 1–5% of a saturated layer. For measuring the adsorption kinetics of single-component systems, techniques such as ellipsometry, optical reflectometry and QCM offer higher sampling rates (up to 1 kHz) with little increase in noise, but for multi-component systems TIR Raman is one of the most useful techniques available. The ability of TIR Raman to distinguish different chemical components even with highly overlapping spectra was illustrated for the competitive adsorption of the surfactants CTAB and Triton X-100 on silica.56 A wall-jet cell was employed to provide controlled hydrodynamics. The mass transport equations are one-dimensional on the axis of the wall-jet, so the small sampling area of TIR Raman compared to ATR-IR makes quantitative analysis of kinetic data much simpler. Fig. 5(a) shows a series of spectra acquired at 2-s intervals during the displacement of CTAB by Triton X-100. The set of kinetic spectra were processed by a chemometric technique known as target factor analysis57 to obtain the adsorbed amounts of CTAB and Triton X-100 as a function of time (Fig. 5(b)). The long tail in the adsorption kinetics arises from a synergistic interaction between CTAB and TX-100 on the silica surface. Fig. 5(c) illustrates the desorption of a mixed layer of CTAB and TX-100 from the surface and shows a transient spike in the adsorbed amount, attributed to differences in the rate of transport away from the surface for the two surfactants. Similar spikes have been reported by ellipsometry,58 but it is only with TIR Raman that the composition of the adsorbed layer can be followed in time.
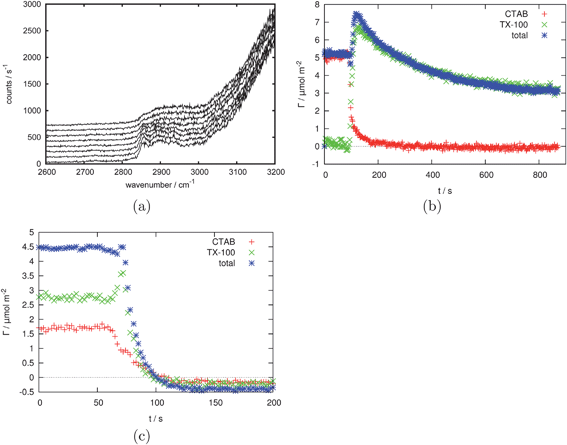 | ||
Fig. 5 (a) 10 consecutive example spectra (1 s acquisition time, 1500 mW laser power (∼1000 mW at sample, S polarised) taken every 2 s during the replacement of an adsorbed layer of CTAB by an adsorbed layer of Triton X-100. (b) CTAB and Triton X-100 surface excess based on the data shown in part (a) showing the replacement of 2 mM CTAB by 2 mM Triton X-100. (c) The desorption of a 2 mM total concentration 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of CTAB and Triton X-100. Reprinted with permission from ref. 56. Copyright 2011 American Chemical Society. 1 mixture of CTAB and Triton X-100. Reprinted with permission from ref. 56. Copyright 2011 American Chemical Society. | ||
Phospholipid bilayers deposited on planar substrates are a popular model system for the study of cellular membranes. Okamura et al. used TIR Raman to study a Langmuir–Blodgett film of 9 monolayers of the saturated lipid DPPC at the quartz–air interface.59 The ratio of intensities of three bands—the methylene symmetric stretch (d+), antisymmetric stretch (d−) and the Fermi resonance of the antisymmetric stretch and the methylene scissoring mode—allowed the study of conformational order (the ratio of gauche and trans conformers) with respect to the surface pressure at which the lipid was deposited onto the substrate. Single phospholipid bilayers in contact with an aqueous buffer are of greater biological relevance than multilayers in air. Lee et al. extended the TIR Raman technique to lipid bilayers formed in situ by fusion of lipid vesicles to a silica substrate. They studied phase transitions of lipids with temperature60 as well as the formation of lipid bilayers from mixed lipid surfactant systems.61 In the latter case, deuteration of the lipid was used to distinguish the two components. Lipids are structurally similar to organic surfactants, but form thicker films at the solid–water interface so the experimental sensitivity is somewhat better than that shown in Fig. 5. Lipid bilayers are more ordered than the adsorbed films of simple detergents and TIR Raman spectroscopy provides conformational markers with which to probe this order. The ratio of intensities of the d− and d+ modes of the CH2 groups is a measure of hydrocarbon chain packing while the ratio of the intensities of the S- and P-polarised spectra for both the CH2 stretching (2800–3000 cm−1) and scissoring (1450 cm−1) modes provides an indication of chain tilt, with a greater intensity in the S- polarised spectra indicating that the chains are orientated closer to the surface normal. The C–H twisting mode at 1300 cm−1 shows the opposite dependence.60 Shifts in vibrational frequency can also provide information about chain order. Such spectral markers are not unique to TIR Raman and are also used in other vibrational spectroscopic techniques such ATR-IR62 and sum-frequency spectroscopy28 (the markers in SFG are different, but convey similar information). The use of S- and P-polarisations is a unique feature of TIR/ATR-based techniques since the surface provides a reference plane for the orientation of molecules; the tilt of molecules cannot be obtained from polarised spectra of lipid vesicles in the bulk.
Morikawa and coworkers used TIR Raman to study the behaviour of a nematic liquid crystal at a solid surface, including the time dependence of the structure following a change in an electric field.63 The spectra were taken through a glass substrate coated with a transparent 50-nm indium tin oxide electrode and covered with a 60-nm silicon oxide layer. They determined the angle of the director in the liquid crystal molecule from the intensities of different Raman polarisations (see Fig. 6). The kinetics of reorientation following a brief application of an electric field could be could be measured on a 1 ms timescale: the electric field was pulsed periodically and Raman scattering was excited by a 15 ns laser pulse with a variable delay. Comparison with transmission IR spectroscopy showed a difference between the behaviour of the surface layer (probed with TIR Raman) and the bulk (probed with transmission IR). TIR Raman worked well for this application because the depth of penetration of the evanescent wave (∼50 nm) was comparable to the thickness of the liquid crystal perturbed by the interface. The authors noted that they were still seeing averaged behaviour within the evanescent wave, and suggested that more detail might be resolved by varying the angle of incidence (see section 8).
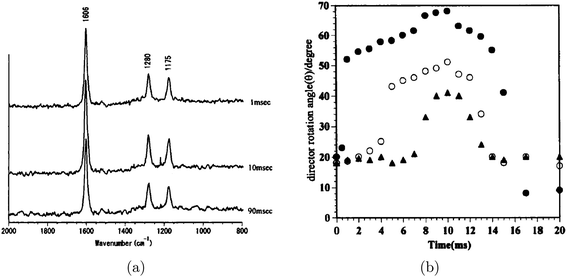 | ||
| Fig. 6 (a) Time resolved TIR Raman spectra of the liquid crystal 4-n-hexyl-4′-cyanobiphenyl measured using Px polarisation at a variety of time delays (shown on the graph) after application of an electric field. Spectra were accumulated over many pulses (up to 15 mins at 5 or 10 Hz) with the same time delay after the application of the electric field. (b) Director rotation angles for the same liquid crystal derived from the intensity ratios of different Raman polarisations. The three different symbols represent different amplitudes of the applied electric field. Reprinted from “Time-resolved Total Internal Reflection Raman Scattering Study on Electric-Field-Induced Reorientation Dynamics of Nematic Liquid Crystal of 4-Hexyl-4′-Cyanobiphenyl”, ref. 63, with permission from Taylor and Francis, Ltd. | ||
Willets and co-workers looked at individual multi-walled carbon nanotubes held perpendicular to the surface within the evanescent field by affixing them to an AFM tip.64 By varying the angle to incidence they were able to vary the depth sensitivity of the Raman scattering from the nanotube. The spectra showed two bands: a G band intrinsic to multi-walled nanotubes, and a D band associated with defects in the structure. The intensity of the D band increased at shorter penetration depths showing that there were more defects closer to the end of the nanotube. The spectra were also strongly sensitive to the orientation of the nanotube to the surface, with no signal usually seen for S polarised incident light and a nanotube perpendicular to the surface. The combination of AFM and TIR Raman provides a novel means of probing a single microscopic object on length scales below the diffraction limit.
When looking at the solid–liquid interface (or the solid–solid interface) only a limited range of substrates can be used; the constraints are discussed in the experimental section. The use of thin layers of non-transparent particles can relax these constraint (contact with the aqueous sample solution limits the laser-induced heating that takes place). Beattie and co-workers investigated the adsorption of a variety of surfactants onto sphalerite,35 a form of ZnS with Fe impurities. Fig. 7 shows the adsorption of a mixture of 2-mercaptobenzothiazole and dibutyl dithiophosphate; the rate of adsorption was relatively slow, which is often the case for adsorption onto particulate surfaces. This method of studying adsorption onto non-transparent particles has been used extensively with ATR-IR,65 but only rarely with TIR Raman. In comparison with TIR Raman on planar substrates, the penetration depth of the evanescent wave is less well-defined, due to interaction of the electric field with the particulate film; and no orientational information can be obtained, since the adsorbed layer is adsorbed on all sides of the particles, which were randomly oriented relative to the excitation light. Very recently, we have used TIR Raman spectroscopy to study surfactant adsorption onto a model cellulose surface, deposited on a silica substrate by Langmuir–Blodgett deposition.66 By slowly varying the concentration of surfactant over the period of ∼1 h we were able to record detailed adsorption isotherms over an almost continuous range of concentrations.
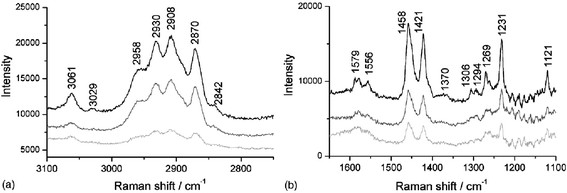 | ||
Fig. 7
TIR
Raman spectra of a 5 mM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 2-mercaptobenzothiazole and dibutyl dithiophosphate adsorbing onto sphalerite. Spectra are shown at 5 min (light grey line), 15 min (dark grey line) and 25 min (black line). (a) the CH stretching region and (b) the fingerprint region. Reprinted from ref. 35, Copyright (2006), with permission from Elsevier. 1 mixture of 2-mercaptobenzothiazole and dibutyl dithiophosphate adsorbing onto sphalerite. Spectra are shown at 5 min (light grey line), 15 min (dark grey line) and 25 min (black line). (a) the CH stretching region and (b) the fingerprint region. Reprinted from ref. 35, Copyright (2006), with permission from Elsevier. | ||
The solid-air interface is not one that at first sight would obviously benefit from use of evanescent wave techniques: after all, there is no need for an evanescent wave to obtain surface selectivity. Nevertheless, even for solid-air interfaces TIR Raman has several advantages over confocal Raman spectroscopy. First, the pump laser does not pass through the collection optics, which reduces the background scattering. Second, the pump energies are higher in TIR Raman but the power density at the sample is lower, reducing sample damage. Third, the polarisation of the electric field can be controlled either parallel or perpendicular to the surface. Fourth, the Fresnel coefficients lead to higher interfacial electric fields (and hence higher signal levels) for the same laser power. In a comparison of confocal and TIR Raman scattering from a Langmuir–Blodgett monolayer of a fatty acid on silica, Beattie et al. found that the signal to background was two orders of magnitude better with evanescent wave excitation.28
6 Liquid–liquid and liquid–air interfaces
The study of surface-active agents at a liquid–liquid interface is extremely challenging by TIR Raman spectroscopy. While it is usually possible to select solid substrates with non-overlapping spectra, most organic solvents have strong spectra that swamp those of organic surfactants. All studies of the liquid–liquid interface to date have used resonance Raman, to enhance selectively the signal from the adsorbed surfactant, which often requires the use of aromatic organic dyes. Fujiwara and Watarai looked at the adsorption of the dye meso-tetrakis(N-methylpyridyl)porphyrinatomanganese(III) adsorbing to the toluene–aqueous interface in the presence of an anionic surfactant.67Fig. 8 shows the design of the optical cell used at the liquid–liquid interface. Only the resonantly enhanced manganese complex and not the surfactant was seen in the Raman spectra. They measured relative adsorbed amounts, but not an exact surface excess, and also calculated mean tilt angles for the adsorbed dye molecules. Yamamoto and Watarai then went on to study tetraphenylprophyrin at the dodecane–water interface using a variety of evanescent wave scattering techniques including TIR Raman,68 observing peak shifts depending on the counterions present. However the study was mainly concerned with domain formation in the adsorbed layer which was imaged using TIR Rayleigh scattering. One nonpolar organic liquid that is relatively free of interfering Raman bands is CCl4, though it is toxic and a rather poor proxy for hydrocarbon oils. Takenaka and Nakanaga recorded the adsorption of a mixture of an number of dyes at the CCl4–aqueous interface.12,13,69 For the dye methyl orange co-adsorbing with CTAB,12 the tilt of the dye molecules in the monolayer was estimated at 50–60° based on the relative intensities of polarised spectra. The absolute adsorbed amount was obtained from surface tension measurements and not from the Raman intensity. Again, it was only possible to study the resonantly enhanced dye, and not the CTAB. An interesting experimental enhancement used in these papers was an extra mirror to increase the laser power by directing the totally reflected light back at the sample, and another extra mirror to capture Raman scattering emitted away from the objective.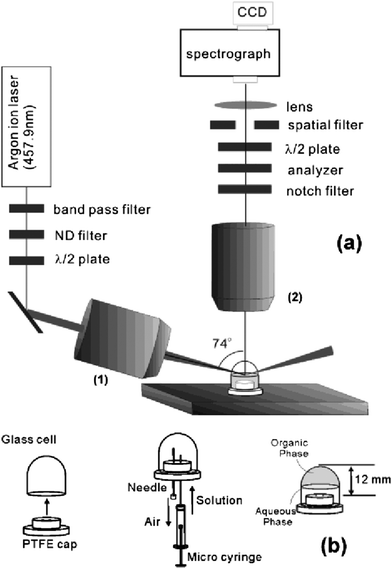 | ||
| Fig. 8 (a) Optics configuration and (b) optical cell design for resonant enhanced TIR Raman spectroscopy at the liquid–liquid interface. Reprinted with permission from ref. 67. Copyright 2003 American Chemical Society. | ||
TIR Raman spectroscopy is not currently the preferred spectroscopic technique for studying the liquid–liquid interface. Instead, genuinely surface selective techniques such as second harmonic generation or sum-frequency spectroscopy allow the interface to be probed without any contribution from the incident medium. Alternatively total internal reflection fluorescence spectroscopy can be used where the surfactant contains a fluorophore, since most pure solvents do not fluoresce. Perera and Stevens recently reviewed spectroscopic techniques for studying the liquid–liquid interface,70 and a wide range of references can be found there. Finally, non-spectroscopic techniques such as ellipsometry are viable for probing the liquid–liquid interface.71
The liquid–air interface has barely been studied using TIR Raman spectroscopy since the surface selectivity of the evanescent wave is working in the wrong direction: the liquid contributes strongly to the Raman signal while the evanescent wave decays into air. External reflection infrared spectroscopy72,73 and SFG74,46 are more suitable techniques, as both show surface selectivity. In the case of SFG, the surface selectivity arises from the preferential orientation of molecules at the liquid-air interface while in reflection IR spectroscopy, the line-shapes of molecules at the surface and in the bulk are different and can be separated by chemometric methods (the former depends on the imaginary part of the refractive index and the latter on the real part).75 Takenaka and coworkers used TIR Raman to look at monolayers on water of deuterated stearic acid and deuterated cadmium stearate under various amounts of compression.76 Acquisition times were between 1 and 2 h and it was necessary to use deuterated layers to avoid spectral overlap between the O–H and C–H stretching bands. Greene conducted a preliminary study of the adsorption of CTAB at the air–water interface, and found the C–H peaks of CTAB barely visible above the background from water.77
7 Solid–solid interface
The solid-solid interface is difficult to study by conventional techniques. One important practical problem is boundary lubrication, where a monolayer film is confined in a small contact (no more than a few hundred μm in diameter) between two hard solids. Reflection IR has been used to measure hydrodynamic lubrication with a minimum thickness of around 20 nm,78 but it is not yet possible to study monolayer films. Laser based spectroscopies have advantages when studying small areas and both SFG79,80 and Raman scattering28,81 have been used to in TIR mode to study lubricated contacts under pressure and shear. An important limitation with all spectroscopic techniques is the need to have transparent substrates (either in the IR or visible region), whereas metal substrates are most relevant to real applications. A typical experiment at a solid–solid contact uses a high refractive index solid (for example sapphire or SF10 glass) in contact with a curved surface of a lower refractive index solid (e.g.MgF2 or silica). Either or both of the two solids can be coated with a thin film, for example by Langmuir–Blodgett deposition. The Raman spectrum can be collected through either of the solids. Information about the ordering can be acquired based on the ratio of the symmetric and antisymmetric methylene stretch,28 as with the lipid systems discussed earlier. In addition to Langmuir–Blodgett deposited films, Beattie et al. looked at hydrocarbon layers as they were squeezed out from between two solid surfaces.81 They were able to detect small pockets of hydrocarbon remaining in gaps in the rough surface at a quantity well below a monolayer.A number of groups have looked at a strained silicon thin film under partial TIR conditions using illumination through a high numerical aperture objective.34,82 Lermen and co-workers reported that for their optical alignment, approximately half the Raman signal came from the evanescent wave and half from transmitted light.34 The shift in the characteristic silicon peak at 520 cm−1 allowed the identification of stressed and unstressed silicon. Samples include the area around a scratch in a silicon wafer,82 and a thin film of strained silicon separated from the bulk silicon substrate by a 150 nm SiO2 layer.34 In the latter case the peak from the bulk silicon was not completely eliminated, but was less prominent than when illuminated without any total internal reflection.
Grausem et al. used light collected from a small optical fibre probe brought into an evanescent wave to perform high resolution Raman imaging of a patterned sample.83 In the region around the collection probe there is a frustrated evanescent wave (energy is transmitted into the tip). This experiment is primarily taking advantage of the superior lateral resolution available using near-field illumination, rather than the surface sensitivity arising from total internal reflection. Damage to the sample probe caused by the excitation laser is a problem in such measurements.
The final use of TIR Raman spectroscopy at the solid–solid interface is to look at thin films of one substance on top of a second thicker layer; the optical element is in contact with the thin film. Such experiments can be seen as a precursor to the depth profiling experiments described in the next section, however most of these experiments were conducted simply to demonstrate the efficacy of TIR Raman in detecting only the thin layer. Iwamoto and coworkers were the first to demonstrate such selectivity using a thin film of polystyrene on a polyethylene base.14,15 Ishizaki and Kim looked at two different polymer systems: a thin films of polystyrene on poly(vinyl methyl ether) and a fluorinated polyimide.84 In the latter case near infrared excitation light was need to avoid fluorescence from the sample. Greene looked at polyethylene naphthalate on polyethylene terephthalate (PET)7 and Michaels looked at a thin poly(3,4-ethylenedioxythiophene)/poly(styrenesulfonate) (PEDOT:PSS) film on PET.33 Michaels acquired Raman images (Fig. 9) by scanning the hemispherical lens and taking spectra at each point, revealing a partially covered surface. The choice of samples is not limited to synthetic polymers: Greene and Bain looked at epicuticular leaf waxes in vivo.85 They used the ratio of the symmetric and antisymmetric methylene stretches to distinguish crystalline waxes in the top layer from amorphous waxes when the top layer had been removed with a cellulose acetate (Fig. 10). The limited penetration depth (40 nm) achieved with a cubic zirconia reflection element avoided fluorescence from the underlying pigments, which is often a problem in Raman spectroscopy of plant material.
 | ||
| Fig. 9 TIR Raman image of a micropatterned PEDOT:PSS film on PET, generated from the peak areas of (a) the PEDOT:PSS marker band at 440 cm−1 and (b) the PET marker band at 1726 cm−1. The scale bar is 1 μm. The image was acquired by scanning the position of the excitation/collection optics across the sample. Reproduced with permission from ref. 33. | ||
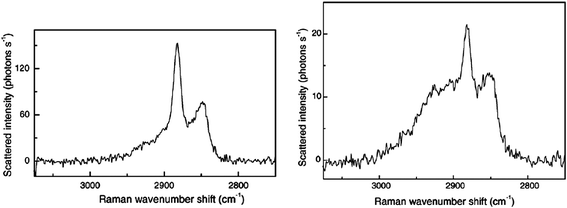 | ||
| Fig. 10 TIR Raman spectra from the epicuticular wax layer of a leaf. (a) Crystalline wax of the top layer and (b) amorphous wax below the crystalline wax. Reprinted from ref. 85, Copyright (2005), with permission from Elsevier. | ||
8 Depth profiling
The variation in the penetration depth with angle of incidence raises the prospect of using TIR Raman spectroscopy for depth profiling thin film on the 100-nm level. The Raman signal, I, from a specific angle of incidence, θi, and Stokes shift,![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , is given by86
, is given by86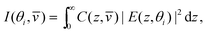 | (10) |
A limiting case that simplifies the analysis greatly is when the refractive index is constant in the low-index medium. This case is realistic for many situations: for example, many polymers have refractive indices around 1.5. In this case the intensity of Raman scattering is
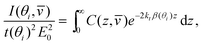 | (11) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ). One way of solving problems such as eqn (11) is to divide the sample into a series of layers, j, of equal thickness, Δz. Then
). One way of solving problems such as eqn (11) is to divide the sample into a series of layers, j, of equal thickness, Δz. Then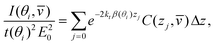 | (12) |
| a = Gc, | (13) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) )/(θi|2kE20)), c is a column vector representing the Raman cross-section at different values of z and G is a matrix with each row corresponding to a different incident angle, and each column corresponding to a different value of z (elements are calculated as e−2ktβzj). Eqn (13) applies for a specific wavelength of scattered light; however for simplicity the dependence of
)/(θi|2kE20)), c is a column vector representing the Raman cross-section at different values of z and G is a matrix with each row corresponding to a different incident angle, and each column corresponding to a different value of z (elements are calculated as e−2ktβzj). Eqn (13) applies for a specific wavelength of scattered light; however for simplicity the dependence of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is no longer written. Superficially, the problem of calculating the material dependence with z requires a straightforward matrix inversion:
is no longer written. Superficially, the problem of calculating the material dependence with z requires a straightforward matrix inversion:| c = G−1a, | (14) |
The solution is to regularise G (Tikhonov regularisation is commonly used and illustrated here, but other approaches exist): a pseudoinverse for G is created using87
| G+ = (GTG + L2I)−1GT, | (15) |
| c+ = G+a, | (16) |
Modelling the experimental response to varying depth profiles illustrates the limitations of TIR Raman for depth profiling. Fig. 11 shows the intensity dependence with respect to angle of incidence for a variety of film thicknesses (assuming a sharp step in the concentration profile). The dependence is strong enough that it should be possible to fit a characteristic thickness to a layer, especially if the signal from an infinitely thick layer is known and can be used as a reference. The dependence with respect to the functional form of the concentration profile is much weaker; Fig. 12 shows that there is almost no sensitivity to a blurring of the interface (modelled using 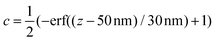 ), and only a slight difference compared to an exponential concentration profile.
), and only a slight difference compared to an exponential concentration profile.
 | ||
| Fig. 11 Modelled intensity dependence with respect to angle of incidence for a range of different film thicknesses. (a) Uniform films adjacent to the surface with a thickness, t; (b) Uniform films stretching from tstart to z = ∞. ni = 1.72 (SF10 glass), nr = 1.5 (a typical polymer). The dashed vertical line shows the critical angle. | ||
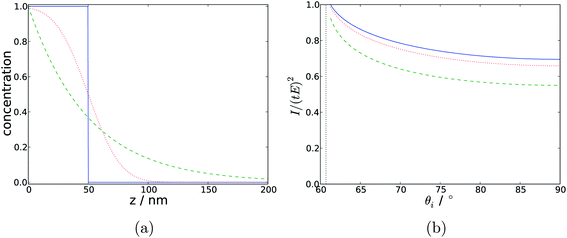 | ||
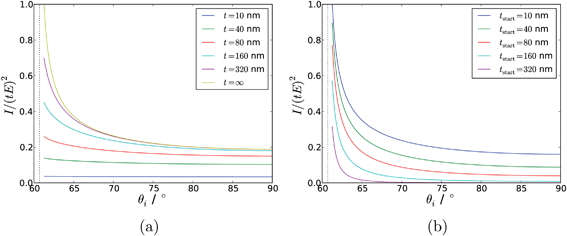
| Fig. 12 (a) Concentration profiles with respect to depth, for a step function (solid blue), an exponential decay (dashed green) and a profile derived from the error function (dotted red). (b) Modelled Raman intensity with respect to angle of incidence arising from those concentration profiles. In all cases the characteristic thickness is 50 nm. | ||
Due to the difficulty in deriving unique depth profiles from TIR Raman, very little work has been published on the subject. Initial work using variable angles looked at homogeneous samples,15,86 and aimed to recover the correct dependence on Raman signal with respect to angle of incidence. However, Fontaine and Furtak found that even in this simplest case there was a wide range of experimental difficulties that affect the measurement.86 For example, back reflections from the exit side of a symmetric optical element can strongly affect the intensity of the electric field in the sample. Additionally, when very close to the critical angle the small spread of angles in the incident beam can lead to some light being transmitted, which has a large impact on the spectrum since it samples to an infinite depth (as shown in Fig. 13); strategies to mitigate this effect are discussed in ref. 86.
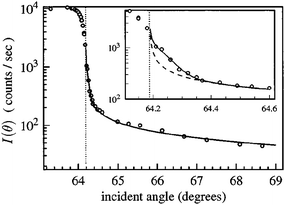 | ||
| Fig. 13 The angle dependence of the Raman intensity from two thick polymer layers around the critical angle (marked as a vertical dotted line). The inset focusses on small variations from the critical angle. The dashed line shows the expected signal from a single angle of incidence while the solid line shows the expected signal calculated using a spread of incident angle which cause non-evanescent fields in the sample. Reproduced from ref. 86 with permission. | ||
Rather than attempting the matrix inversion as required by eqn (16), the more common approach is to model the sample as a small number of well-defined layers, changing the layer thicknesses to fit the data. Iwamoto deliberately picked two-layer samples with identical refractive indices, and obtained reasonable estimates of the thickness of the first layer.15 However, there was a considerable difference between the predicted and measured values for the angle dependence of the spectra, attributed to the spread of angles.
Fontaine and Furtak subsequently looked at two-layer polymer films and were able to identify the position of the break between the layers with a precision of ±2 nm.90 It should be noted that this latter study mostly exploited the position of waveguide modes below the critical angle, rather than the changing penetration depth above the critical angle. A recent development is the production of a scanning angle Raman spectrometer,91 allowing greater automation of the measurement of Raman spectra at a range of angles. For a homogeneous benzonitrile sample the measured Raman signal agreed well with the expected angular variation of signal, providing the angular spread of the converging incident light was accounted for.
Other total internal reflection techniques could also be used for depth profiling. The use of ATR-IR is slightly more mature than for TIR Raman, however the majority of work within the last decade has looked only at qualitative changes in spectra with angle of incidence and has not attempted a full depth profile.92,93 Analysis is more complicated than for TIR Raman since the refractive index (and hence the penetration depth) varies across the spectral range, whereas for Raman there is only one incident wavelength. Additionally when absorption of incident light by the sample is appreciable the Laplace transform (eqn (11)) no longer applies. A range of attempts have been made to extract quantitative depth profiles from ATR-IR,94 often by assuming set functional forms for the concentration profiles with respect to depth, for example exponential95 and step-function forms96,97 (the step function has an analytical solution for the Laplace transform).
For depth profiling, the most important alternative to TIR Raman spectroscopy is confocal Raman microscopy. A recent review by Everall discussed the limitations of confocal Raman microscopy in some detail:98,99 the depth resolution is approximately 1–2 μm. Much better depth resolution (see Fig. 11) can potentially be achieved with TIR Raman; however a quantitative analysis is only feasible for simple cases where the functional form of the concentration profile is well-known. At one level, TIR Raman and confocal Raman are complementary: TIR Raman can only probe structure near a planar interface (z ≤ λ), but with a surface sensitivity of 100 nm or less; confocal microscopy has poorer depth resolution but can study much thicker samples, limited only by the working distance of the objective.
References
- S. G. Kazarian and K. L. A. Chan, Appl. Spectrosc., 2010, 64, 135A–151A CAS.
- R. A. Dluhy, S. M. Stephens, S. Widayati and A. D. Williams, Spectrochim. Acta, Part A, 1995, 51, 1413–1447 CrossRef.
- B. L. Mojet, S. D. Ebbesen and L. Lefferts, Chem. Soc. Rev., 2010, 39, 4643–4655 RSC.
- D. Axelrod, Fluorescence Microscopy of Living Cells in Culture Part B. Quantitative Fluorescence Microscopy–Imaging and Spectroscopy, Academic Press, 1989, vol. 30, pp. 245–270 Search PubMed.
- P. L. Stiles, J. A. Dieringer, N. C. Shah and R. P. Van Duyne, Annu. Rev. Anal. Chem., 2008, 1, 601–626 Search PubMed.
- A. Kudelski, Surf. Sci., 2009, 603, 1328–1334 CrossRef CAS.
- P. R. Greene and C. D. Bain, Spectroscopy Europe, 2004, Aug/Sep, 8–15 Search PubMed.
- T. Ikeshoji, Y. Ono and T. Mizuno, Appl. Opt., 1973, 12, 2236–2237 Search PubMed.
- M. Fujihira and T. Osa, J. Am. Chem. Soc., 1976, 98, 7850–7851 Search PubMed.
- T. Takenaka and K. Yamasaki, J. Colloid Interface Sci., 1980, 78, 37–43 Search PubMed.
- T. Takenaka and H. Fukuzaki, J. Raman Spectrosc., 1979, 8, 151–154 CAS.
- T. Takenaka and T. Nakanaga, J. Phys. Chem., 1976, 80, 475–480 CrossRef CAS.
- T. Nakanaga and T. Takenaka, J. Phys. Chem., 1977, 81, 645–649 CrossRef CAS.
- R. Iwamoto, M. Miya, K. Ohta and S. Mima, J. Am. Chem. Soc., 1980, 102, 1212–1213 CrossRef CAS.
- R. Iwamoto, M. Miya, K. Ohta and S. Mima, J. Chem. Phys., 1981, 74, 4780–4790 CrossRef CAS.
- R. Iwamoto, K. Ohta, M. Miya and S. Mima, Appl. Spectrosc., 1981, 35, 584–587 Search PubMed.
- W. Hölzer, O. Schröter and A. Richter, J. Mol. Struct., 1990, 217, 253–264 Search PubMed.
- W. Carius and O. Schröter, Phys. Status Solidi A, 1980, 59, K115–K118 Search PubMed.
- W. Carius, W. Hölzer and O. Schröter, Makromol. Chem. Rapid Commun., 1983, 4, 469–470 Search PubMed.
- G. Mattei, B. Fornari and M. Pagannone, Solid State Commun., 1980, 36, 309–312 Search PubMed.
- M. Ohsawa, K. Hashima and W. Suëtaka, Appl. Surf. Sci., 1984, 20, 109–120 Search PubMed.
- L. D'Hooge and J. Vigoureux, Chem. Phys. Lett., 1979, 65, 500–506 Search PubMed.
- Y. Levy, C. Imbert, J. Cipriani, S. Racine and R. Dupeyrat, Opt. Commun., 1974, 11, 66–69 Search PubMed.
- J. F. Rabolt, N. E. Schlotter and J. D. Swalen, J. Phys. Chem., 1981, 85, 4141–4144 Search PubMed.
- J. S. Kanger, C. Otto, M. Slotboom and J. Greve, J. Phys. Chem., 1996, 100, 3288–3292 Search PubMed.
- T. Plowman, S. Saavedra and W. Reichert, Biomaterials, 1998, 19, 341–355 CrossRef CAS.
- D. A. Long, The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules, John Wiley & Sons, Ltd., 2002 Search PubMed.
- D. A. Beattie, S. Haydock and C. D. Bain, Vib. Spectrosc., 2000, 24, 109–123 Search PubMed.
- E. Tyrode, M. W. Rutland and C. D. Bain, J. Am. Chem. Soc., 2008, 130, 17434–17445 CrossRef CAS.
- D. A. Woods, J. Petkov and C. D. Bain, J. Phys. Chem. B, 2011, 115, 7353–7363 Search PubMed.
- E. V. Efremov, J. B. Buijs, C. Gooijer and F. Ariese, Appl. Spectrosc., 2007, 61, 571–578 CrossRef CAS.
- L. G. Tisinger and A. J. Sommer, Microsc. Microanal., 2004, 10, 1318–1319.
- C. A. Michaels, J. Raman Spectrosc., 2010, 41, 1670–1677 Search PubMed.
- G. M. Lerman, A. Israel and A. Lewis, Appl. Phys. Lett., 2006, 89, 223122 Search PubMed.
- D. Beattie, M. Lidström Larsson and A. R. Holmgren, Vib. Spectrosc., 2006, 41, 198–204 Search PubMed.
- M. L. Larsson, A. Holmgren and W. Forsling, J. Colloid Interface Sci., 2001, 242, 25–30 Search PubMed.
- S. C. Clark and W. A. Ducker, J. Phys. Chem. B, 2003, 107, 9011–9021 Search PubMed.
- A. Khan, W. A. Ducker and M. Mao, J. Phys. Chem. B, 2006, 110, 23365–23372 Search PubMed.
- R. F. Tabor, J. Eastoe and P. Dowding, Langmuir, 2009, 25, 9785–9791 Search PubMed.
- G. W. Faris and R. A. Copeland, Appl. Opt., 1997, 36, 2686–2688 Search PubMed.
- M. O. Trulson and R. A. Mathies, J. Chem. Phys., 1986, 84, 2068–2074 CrossRef CAS.
- W. K. Thompson, Trans. Faraday Soc., 1965, 61, 2635–2640 RSC.
- A. E. Klingbeil, J. B. Jeffries and R. K. Hanson, J. Quant. Spectrosc. Radiat. Transfer, 2007, 107, 407–420 Search PubMed.
- Y. R. Shen, Nature, 1989, 337, 519–525 CrossRef CAS.
- C. D. Bain, J. Chem. Soc., Faraday Trans., 1995, 91, 1281–1296 RSC.
- G. L. Richmond, Chem. Rev., 2002, 102, 2693–2724 CrossRef CAS.
- Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154 CrossRef CAS.
- H. C. Allen, N. N. Casillas-Ituarte, M. R. Sierra-Hernandez, X. Chen and C. Y. Tang, Phys. Chem. Chem. Phys., 2009, 11, 5538–5549 RSC.
- F. M. Geiger, Annu. Rev. Phys. Chem., 2009, 60, 61–83 CrossRef CAS.
- Z. S. Nickolov, J. C. Earnshaw and J. J. McGarvey, Colloids Surf., A, 1993, 76, 41–49 Search PubMed.
- Z. S. Nickolov, J. C. Earnshaw and J. J. McGarvey, J. Raman Spectrosc., 1993, 24, 411–416 Search PubMed.
- H. Yui, H. Fujiwara and T. Sawada, Chem. Phys. Lett., 2002, 360, 53–58 Search PubMed.
- J. S. Kanger, C. Otto and J. Greve, J. Phys. Chem., 1996, 100, 16293–16297 Search PubMed.
- G. I. Stegeman, R. Fortenberry, C. Karaguleff, R. Moshrefzadeh, W. M. Hetherington, III, N. E. Van Wyck and J. E. Sipe, Opt. Lett., 1983, 8, 295–297 CAS.
- W. M. K. P. Wijekoon, Z. Z. Ho and W. M. Hetherington, J. Chem. Soc., Faraday Trans., 1993, 89, 1067–1069 RSC.
- D. A. Woods, J. Petkov and C. D. Bain, J. Phys. Chem. B, 2011, 115, 7341–7352 Search PubMed.
- E. R. Malinowski, Factor Analysis in Chemistry, John Wiley & Sons, 2nd edn, 1991 Search PubMed.
- J. Brinck, B. Jönsson and F. Tiberg, Langmuir, 1998, 14, 5863–5876 CrossRef CAS.
- E. Okamura, J. Umemura and T. Takenaka, J. Raman Spectrosc., 1991, 22, 759–762 Search PubMed.
- C. Lee and C. D. Bain, Biochim. Biophys. Acta, Biomembr., 2005, 1711, 59–71 CrossRef CAS.
- C. Lee, H. Wacklin and C. D. Bain, Soft Matter, 2009, 5, 568–575 RSC.
- D. J. Neivandt, M. L. Gee, M. L. Hair and C. P. Tripp, J. Phys. Chem. B, 1998, 102, 5107–5114 Search PubMed.
- T. Morikawa, E. Shirai, J. Tanno, H. Takanashi, A. Yasuda and K. Itoh, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1998, 312, 69–94 Search PubMed.
- I. Kaplan-Ashiri, E. J. Titus and K. A. Willets, ACS Nano, 2011, 5, 1033–1041 Search PubMed.
- A. J. McQuillan, Adv. Mater., 2001, 13, 1034–1038 CrossRef.
- D. A. Woods, J. Petkov and C. D. Bain, Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2011 DOI:10.1016/j.colsurfa.2011.07.027/.
- K. Fujiwara and H. Watarai, Langmuir, 2003, 19, 2658–2664 Search PubMed.
- S. Yamamoto and H. Watarai, J. Phys. Chem. C, 2008, 112, 12417–12424 Search PubMed.
- T. Takenaka, Chem. Phys. Lett., 1978, 55, 515–518 Search PubMed.
- J. Perera and G. Stevens, Anal. Bioanal. Chem., 2009, 395, 1019–1032 CrossRef CAS.
- J. P. R. Day and C. D. Bain, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041601 Search PubMed.
- R. A. Dluhy, N. A. Wright and P. R. Griffiths, Appl. Spectrosc., 1988, 42, 138–141 CAS.
- R. A. Campbell, S. R. W. Parker, J. P. R. Day and C. D. Bain, Langmuir, 2004, 20, 8740–8753 Search PubMed.
- G. R. Bell, C. D. Bain and R. N. Ward, J. Chem. Soc., Faraday Trans., 1996, 92, 515–523 RSC.
- R. A. Campbell, J. P. Day and C. D. Bain, Appl. Spectrosc., 2005, 59, 993–1001 Search PubMed.
- T. Kawai, J. Umemura and T. Takenaka, Chem. Phys. Lett., 1989, 162, 243–247 CrossRef CAS.
- P. R. Greene, Ph.D. thesis, University of Oxford, 2003.
- P. Cann and H. Spikes, Tribol. Lett., 2005, 19, 289–297 Search PubMed.
- R. Fraenkel, G. E. Butterworth and C. D. Bain, J. Am. Chem. Soc., 1998, 120, 203–204 Search PubMed.
- D. A. Beattie, R. Fraenkel, S. A. Winget, A. Petersen and C. D. Bain, J. Phys. Chem. B, 2006, 110, 2278–2292 Search PubMed.
- D. A. Beattie, S. Winget and C. D. Bain, Tribol. Lett., 2007, 27, 159–167 Search PubMed.
- S. Webster, D. N. Batchelder and D. A. Smith, Appl. Phys. Lett., 1998, 72, 1478–1480 CrossRef CAS.
- J. Grausem, B. Humbert, M. Spajer, D. Courjon, A. Burneau and J. Oswalt, J. Raman Spectrosc., 1999, 30, 833–840 Search PubMed.
- F. Ishizaki and M. Kim, Jpn. J. Appl. Phys., 2008, 47, 1621–1627 Search PubMed.
- P. R. Greene and C. D. Bain, Colloids Surf., B, 2005, 45, 174–180 Search PubMed.
- N. H. Fontaine and T. E. Furtak, J. Opt. Soc. Am. B, 1997, 14, 3342–3348 Search PubMed.
- J. F. Power, Rev. Sci. Instrum., 2002, 73, 4057–4141 Search PubMed.
- P. C. Hansen, Inverse Probl., 1992, 8, 849 CrossRef.
- P. C. Hansen, SIAM Rev., 1992, 34, 561–580 Search PubMed.
- N. H. Fontaine and T. E. Furtak, Phys. Rev. B: Condens. Matter, 1998, 57, 3807–3810 Search PubMed.
- K. J. McKee and E. A. Smith, Rev. Sci. Instrum., 2010, 81, 043106 Search PubMed.
- K. L. A. Chan and S. G. Kazarian, Appl. Spectrosc., January 2007, 61, 48–54 Search PubMed.
- T. Frosch, K. L. A. Chan, H. C. Wong, J. T. Cabral and S. G. Kazarian, Langmuir, 2010, 26, 19027–19032 Search PubMed.
- L. J. Fina, Appl. Spectrosc. Rev., 1994, 29, 309–365 CAS.
- L. J. Fina and G. Chen, Vib. Spectrosc., 1991, 1, 353–361 Search PubMed.
- R. A. Shick, J. L. Koenig and H. Ishida, Appl. Spectrosc., 1 August 1993, 47, 1237–1244 Search PubMed.
- R. A. Shick, J. L. Koenig and H. Ishida, Appl. Spectrosc., 1 August 1996, 50, 1082–1088 Search PubMed.
- N. J. Everall, Appl. Spectrosc., 2009, 63, 245A–262A CAS.
- N. J. Everall, Analyst, 2010, 135, 2512–2522 RSC.
| This journal is © The Royal Society of Chemistry 2012 |
