Modelling of magnetodipolar striction in soft magnetic elastomers
Oleg V.
Stolbov
*a,
Yuriy L.
Raikher
a and
Maria
Balasoiu
bc
aInstitute of Continuous Media Mechanics, Ural Division of RAS, 1 Korolyov street, Perm, 614013, Russia. E-mail: sov@icmm.ru; Fax: +7 342 237 84 81; Tel: +7 342 237 83 23
bLaboratory of Neutron Physics, Joint Institute of Nuclear Research, Dubna, Moscow region 141980, Russia
cHoria Hulubei National Institute of Physics and Nuclear Engineering, P.O. Box MG-6, Bucharest-Magurele, Romania
First published on 27th July 2011
Abstract
The origin of the so called magnetostriction effect, i.e., the deformation of a soft magnetic elastomer (SME) in response to a uniform magnetic field is discussed. We note that up to now there exists a number of cases, where the theory is unable to explain the facts well established for real SMEs. In our view, the essential issue, formerly not adequately accounted for, is the type of structural short-range order in the magnetic microparticle assembly. Two-dimensional model problems are formulated and solved, which demonstrate the validity of the hypothesis.
1. Introduction
Deformational properties of magnetorheological elastomers and, especially, of the subfamily of these smart materials which is termed ferrogels,1,2 magnetoelastics,3,4 elastomer-ferromagnetic composites,5 soft magnetic elastomers (SMEs),6,7etc.—is the key issue ensuring their applications. Among various field and traction conditions, which can be arranged in magnetomechanical tests, the deformation in response to a uniform magnetic field seems to be the most interesting and as well most contradictive with respect to the experiment vs. theory comparison. Indeed, the density of the body force arising in a SME under a non-uniform field and the deformation that it induces, do not cause ambiguities, except maybe for the assumptions under which the internal magnetic field is evaluated. On the contrary, in verification of the magnetodeformational effect under a uniform field, the experiment vs. theory mismatches are widespread. One finds a typical example of that in a classical work on SMEs,8 where, experimentally, the sample elongates in the direction of the field (Fig. 4 of ref. 8), while the theory predicts compression.In fact, even the very name of the effect needs to be refined. In the same paper,8 the deformation of a SME under a uniform field was referred to as magnetostriction (MS), and since then the term had got into wide circulation in the literature on the subject. However, since long ago this word has been used in solid state physics to designate the magnetization-strain coupling caused by the quantum spin–orbit interaction in crystalline ferromagnets, see ref. 9, for example. Given that the latter mechanism is inherently present in the ferromagnet grains, which make the solid phase of SMEs, one sees that the notion of magnetostriction with respect to these materials is indeed ambiguous. With allowance for the fact that in SMEs the major role is played by the mesoscopic inter-grain magnetodipolar and not by the microscopic intra-grain spin–orbit interaction, we surmise that the term magnetodipolar striction (MDS) can help to distinguish the meso-MS from its microscopic (solid-state) analog. As the magnitude of the latter in SMEs is several orders lower than the MDS effect in what follows we neglect micro-MS entirely.
Adoption of MDS as a more accurate term is a step in the right direction, but further refinement is yet necessary. Qualitatively, with respect to the macroscopic (continuum) description, the long-range interparticle magnetodipolar interaction causes two types of contributions to the free energy of a SME. The first one, we name it externalMDS, is determined by the overall geometry and net magnetization of the sample. In fact, it is the well-known demagnetizing field that creates the surface magnetic pressure jump in ellipsoidal bodies and some internal forces in non-ellipsoidal ones. The contribution of the second type, i.e., the internalMDS, is specific to SMEs and is determined by the local positions of the particles relative to one another; it does not produce any surface energy terms. Therefore, the effect of internal MDS reflects the inner structure of the material, and should be accounted for in the equation of state of a SME. In the free energy density, the internal MDS causes the “cross” terms, i.e., the products of magnetization times strain, while the contributions due to the external MDS never have such a form.
Notably, some magnetomechanical problems in SMEs can be solved successfully assuming that the role of internal MDS is negligible, and taking into account only the external MDS. This is done in the framework of a relatively simple macroscopic theory, where SME is considered as a magnetizable elastic continuum, whose equations of magnetic and elastic state are uncoupled. Implicitly, this means that the local spatial distribution of the particles is “frozen”, i.e., always the same as in the initial state. The achieved agreement with experiment is fairly good, see references 6, 10 and 11, for example. We remark also the work,12 where the model, although having been first stated in discrete terms, before application to experiment is in fact reduced to a continuum one.
Striking contradictions emerge, however, as soon as one tries to go beyond phenomenology and to investigate the problem at the structural level. Evidently, this approach should render the deformational response of the sample, correctly accounting for both external and internal MDS. By now, several interesting theoretical works on the structural magnetomechanics of SMEs have been published.12–14 Surprisingly, even the qualitative theoretical predictions of this kind agree with experiments quite poorly. We note, for example, the measurements reported in a quite thorough work.15 There a series of prolate SME cylinders of identical shape (aspect ratio ∼2.5) always responded to the axially applied field by elongation, whatever was the internal texture of the material: random, longitudinal or transverse. Meanwhile, the structure theories13,14 predict invariably negative internal MDS for the material itself and negative net MDS for the aspect ratio of a SME sample greater than 1.5 and lower than 0.3, see ref. 16. Moreover, the evidence of ref. 15 contradicts not only formal theories but a qualitative analysis as well. Indeed, consider a pre-textured SME (subjected to a strong field while curing) as a set of parallel particle chains separated by an elastomer and tightly coupled to it. Having been magnetized along their direction, the chains would repel each other making the sample to shrink along the field and to expand transversely.
A non-contradictive explanation of the facts has been outlined in ref. 15, 17. The main point is that in real SMEs the particles are not completely separated even if, upon curing the matrix, a magnetic field was not imposed. In other words, none of the procedures employed (stirring, sonication, etc.) are able to perfectly disperse the ferromagnetic microparticles, e.g. 2–5 μm iron carbonyl grains, which are the fillers in common SMEs. This means that some particle aggregates (clusters) are always present in the material, and their number but augments when an external field is applied. On the other hand, no field, whatever strong, imposed while the curing process is able to organize the particles inside a polymer in well separated, perfectly linear filaments. In result, structurally, any SME is a mixture of isolated particles with a variety of clusters including sufficiently anisometric ones.
The dominating mechanism of intrinsic MDS becomes clear from quite a simple schematization.15,17 Let, for a time being, the isolated particles be insignificant and let the existing clusters be replaced by prolate magnetizable particles distributed at arbitrary angles with respect to the sample axis. When a uniform axial field is applied, the model particles, due to their anisotropic magnetic susceptibility, strive to orient themselves parallel to the field thus stretching the sample in the field direction. This means positive internal and net MDS, the particular magnitudes of which depend on the details of the particle spatial and angular distributions.
2. 2D simulation: simple limiting cases
In order to distinguish between the contributions of the isolated particles—as shown in ref. 13 and 14 they induce negative internal MDS—and the clusters, a numerical modelling is performed. The test is carried out on a rectangular elastic monolayer filled with about 70 identical magnetically soft particles. From the magnetic viewpoint the particles are considered as spherical, in the mechanical aspect they are treated as disks. Each particle abuts on its polymer environment gaplessly and does not slip, i.e., is “glued” to the matrix. The shear elastic moduli of both the particles (Gp) and the matrix (G) are taken to be finite, and the SME is considered as an incompressible medium with piece-wise elastic properties. On the other hand, the particles are assumed to be much more rigid than the matrix (Gp ∼ 104G) that makes them virtually solid, thus making the dependence of the results on Gp negligible. The calculation is performed with the aid of finite-element method, where the mesh is made sufficiently dense, so that each particle contains 8–15 nodes inside.The boundary conditions for the SME sample in Fig. 1 are chosen in such a way that its two adjacent sides are always straight (cannot deform along their respective normals) but can freely change their length (slide tangentially); the two other sides are assumed to be free. Given that, each of the plots shown in Fig. 1 presents a quarter of a full model sample, whose particle spatial distribution is symmetrical with respect to the horizontal and vertical inner axes.
 | ||
| Fig. 1 Panels (a) and (c): samples at H0 = 0; panels (b) and (d): samples magnetized by the field H0 ∼ (G/μ0)1/2; the number of particles is N = 70, their surface density is 9%; the field is directed upward in the plane of the layer, contour squares mark the initial shape of the layer. | ||
A constant magnetic field H0 is imposed along Oy side of the sample. The particles (e.g.iron carbonyl) are assumed to have very high internal magnetic susceptibility, so that their external one, χ, is isotropic and entirely determined by the particle shape. The field strength H0 is far from the ferromagnet saturation, so that the linear magnetization relation μ = χVH holds, where H is the local field, and μ the magnetic moment of the particle of volume V.
The applied uniform field is augmented up to a certain value H0 by small increments, and at each such stage the configuration of the system that corresponds to the equilibrium between the magnetic and elastic stress distributions (both of them change) is determined. The illustration is given in Fig. 1 that shows the results for two conceivable limiting situations. Two square samples with the same filling fraction are shown in the left and right columns, respectively. The left-hand sample is deliberately configured in such a way that the particles, otherwise positioned at random, are isolated from one another as much as possible. In the right-hand sample the particles are united in close “dumbbells”, whose centers of mass are distributed according to the same isolation principle, while the “dumbbell” directions are distributed uniformly inside the angle interval [π/4, 3π/4] with respect to the field direction. To see the effect of the magnetizing field, the panels of Fig. 1 should be considered in pairs: (a) → (b) and (c) → (d). As the images show, the samples, being identical, except for the presence of the particle spatial correlations, respond to the field in opposite ways. Quite expectedly, the gas-like structure causes negative MDS (shrinking along the field), while the response of the structure with intentionally created short-range correlations is positive.
3. 2D random ensemble
To get closer to real SMEs, we consider a system with less artificial structure. Namely, a square elastomer layer is filled at random with a given number (166) of magnetically soft particles. Here no restrictions are imposed on the interparticle distances, except for forbidding the geometric overlap. Under these conditions, each statistical realization is an ensemble, where some particles are well isolated (“gas” component), while the others are grouped (“cluster” component). The latter includes all kinds of clusters, among which some are definitely anisometric and some are not.For this system the finite-element calculation is performed in the small-strain limit. Namely, first, the magnetostatic equations are solved at the initial mesh delivering the values of H at the site of each particle and the magnetic moment μ = χVH of the latter. From the values and directions of the induced magnetic moments, the interparticle dipolar forces are evaluated, and the force exerted on a particle is smeared over the space occupied by it, i.e., over its inner and boundary mesh nodes. Then the elastic equilibrium problem is solved for a medium with piece-wise constant modulus under the given distribution of the volume forces. In result, the spatial distributions of the displacement vector u and pressure p are found. The strain is characterized by the average displacement of the free side of the sample oriented perpendicularly to the field:
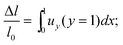 | (1) |
 | (2) |
The values of ε obtained in 30 realizations of the spatial pattern with the fixed number of particles are presented as a histogram in Fig. 2a. Although the spread of the data is substantial, the results evidence a small positive MDS on the average.
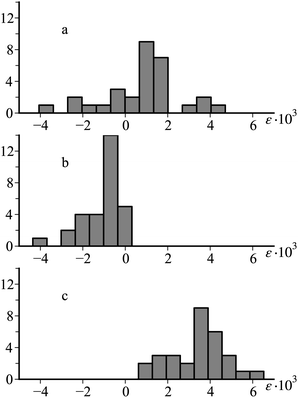 | ||
| Fig. 2 Deformation histograms of the model sample, vertical axis is scaled in the number of realizations; a – all the particles possess the same magnetic susceptibility, b – only the “gas” component is magnetic, c – only the “cluster” component is magnetic. | ||
From the developed viewpoint, the histogram in Fig. 2a emerges as the joint response of the “gas” and “cluster” components of the particle ensemble. To elucidate the respective contributions, we modify the calculation. Each realization (the initial particle distribution) just after having been generated, is subjected to cluster analysis, which divides it in the “gas” and “cluster” components and saves these data. Fig. 3 shows an example of a random spatial structure after the cluster analysis.
Then the same magnetoelastic problem is solved anew. One time it is done assuming that all the particles in clusters are non-magnetic (χ = 0), by that the contribution from the “gas” component is revealed. The second run is the inversion of the first: the condition χ = 0 is imposed on the “gas” particles, letting only the clusters to work. The results for such splitting of the MDS effect are shown in Fig. 2b and c, respectively. As seen, those two statistical sets are unambiguously different: while the isolated particles induce shrinking (negative elongation) in the direction of the field, the MDS due to clusterized particles is positive.
In this connection a remark is worthwhile. Apparently, the “gas” pattern of Fig. 1b and the data of Fig. 2b refer to the situations, which are essentially the same. This is not the case, however, for Fig. 1d and the data of Fig. 2c. Indeed, Fig. 1d presents the strain in a system filled with nothing but clusters intentionally prepared to be rotated by the field. Meanwhile, the system described by Fig. 2c consists of the clusters, which emerged just due to a non-zero probability for a particle to be placed close to another one during the ensemble generation process. In other words, the ensemble shown in Fig. 1c,d is entirely artificial, while the positive MDS predicted by Fig. 2c turns out to be an inherent property of an assembly of clusters formed in result of random filling of the sample.
4. Conclusions
A magnetic field exerted on a soft magnetic elastomer (SME) “switches on” the interparticle dipolar forces, which, in turn, induce in the polymer matrix the counteraction elastic stresses. The equilibrium deformation (the magnetodipolar striction – MDS) is determined by the balance between the magnetostatic energy that strives to decrease by chaining particles along the field, and the elastic energy that resists enhancement by trying to preserve the initial shape of the sample. In this magnetoelastic problem, the magnetic part could be schematically split in two terms. One is non-local and as such is but weakly sensitive to spatial rearrangements of the particles on the mesoscopic scale. In the continuum approach, where SME is modelled by a homogeneous magnetizable elastic medium, this non-local term (demagnetizing field, external MDS) is the only cause of deformation.The structural viewpoint, which takes into account the fact that in a SME the filler particles possess certain spatial freedom and can regroup, reveals an additional striction mechanism that ensures “field-tuning” of the SME internal organization. This effect modifies the magnetic and elastic properties on the mesoscopic (local) scale leading to internal MDS. The latter is very sensitive to the short-range interparticle spatial order and can either support or counteract the ever present external MDS.
The fact that experimentally only positive MDS (elongation in the field direction) is observed on non-pretextured samples, we attribute to the ubiquitous presence of a substantial number of multi-particle clusters in real SMEs; the electron microscopy evidence of that is plenty in the literature.4,18,19 The rotation of the pre-existing clusters to the direction of the field is then the prevailing mesoscopic effect in MDS that adds to the macroscopic (external) one.
The above-given qualitative evidence is essential for development of a macroscopic description that is necessary for applications of SMEs, e.g. design of smart dampers and actuators. The above-described complexity of the magnetodeformational behaviour of SMEs means that the magnetostriction, susceptibility and alike material coefficients entering the sought for continuum models should be considered as the functions of the applied stress/strain and field. For differently structured SMEs, these parameters should be evaluated specifically. Apparently, even for a set of materials produced from the same elastomer and the same quantity of magnetic particles the envisaged variety of observed properties can be impressively wide.
Finally, advancing the presented concept, one comes to a conclusion that, as soon as structure engineering of SMEs, similar to that of metamaterials, would become possible, this would enable synthesis of SMEs, whose magnetodipolar striction is pre-planned both in sign and magnitude.
 | ||
| Fig. 3 The coordinate frame and an example of a generated random distribution of the 166 particles in a square monolayer; the diameter of a particle is 0.04; at the adjacent sides (x = 1 and y = 0) normal displacements are forbidden; “gas” component (empty circles), “cluster” component (dark circles). | ||
Acknowledgements
The work was done under auspices of projects 09-P-1-1010 from Russian Academy of Sciences, 02.740.11.0442, AATP 2.1.1/4463 from Russian Ministry of Education and Science, 11-02-96000 from Russian Foundation for Basic Research, and ST247 from ERA.net-RUS; M. B. acknowledges JINR-Romania project 58/2010/it.18, No.146/2011/its.23,24 and JINR theme 04.4.1069.2009/2011.References
- M. Zrínyi, L. Barsi and A. Büki, J. Chem. Phys., 1996, 104, 8750–8756 CrossRef.
- J. A. Galicia, F. Cousin, E. Dubois, O. Sandre, V. Cabuil and R. Perzynski, Soft Matter, 2009, 5, 2614–2624 CAS.
- L. V. Nikitin, L. S. Mironova, G. V. Stepanov and A. N. Samus, J. Polym. Sci. A, 2001, 43, 443–450 Search PubMed.
- G. V. Stepanov, S. S. Abramchuk, D. A. Grishin, L. V. Nikitin, E. Y. Kramarenko and A. R. Khokhlov, Polymer, 2007, 48, 488–495 CrossRef CAS.
- G. Y. Zhou and Z. Y. Jiang, Smart Mater. Struct., 2004, 13, 309–316 CrossRef.
- Y. L. Raikher and O. V. Stolbov, J. Appl. Mech. Tech. Phys., 2005, 46, 434–443 CrossRef CAS.
- Y. L. Raikher and O. V. Stolbov, J. Phys.: Condens. Matter, 2008, 20, 204126 CrossRef.
- J. M. Ginder, S. M. Clark, W. F. Schlotter and M. E. Nichols, Int. J. Mod. Phys. B, 2002, 16, 2412–2418 CrossRef CAS.
- S. Chikazumi, Physics of Magnetism, Wiley, 1964 Search PubMed.
- Y. L. Raikher and O. V. Stolbov, J. Magn. Magn. Mater., 2005, 289, 62–65 CrossRef CAS.
- Y. L. Raikher and O. V. Stolbov, J. Phys. D: Appl. Phys., 2008, 41, 152002 CrossRef.
- G. Diguet, E. Beaugnon and J. Y. Cavaillé, J. Magn. Magn. Mater., 2009, 321, 396–401 CrossRef CAS.
- L. Borcea and O. Bruno, J. Mech. Phys. Solids, 2001, 49, 2877–2919 CrossRef.
- D. S. Wood and P. J. Camp, Phys. Rev. E, 2011, 83, 011402 CrossRef.
- X. Guan, X. Dong and J. Ou, J. Magn. Magn. Mater., 2008, 320, 158–163 CrossRef CAS.
- K. Morozov, M. Shliomis and H. Yamaguchi, Phys. Rev. E, 2009, 79, 040801(R) Search PubMed.
- Y. L. Raikher and O. V. Stolbov, Computational Continuum Mechanics [in Russian], 2009, 2, 85–95 Search PubMed.
- K. Shimada, S. Shuchi and H. Kanno, J. Intell. Mater. Syst. Struct., 2005, 16, 15–20 CrossRef CAS.
- W. Jiang, J. Yao, X. Gong and L. Chen, Chin. J. Chem. Phys., 2008, 21, 87–92 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2011 |
