Templated self-assembly of patchy particles

Abstract

We explore the use of templated self-assembly to facilitate the formation of complex target structures made from patchy particles. First, we consider the templating of high-symmetry shell structures around a spherical core particle. We find that nucleation around the core particle can inhibit aggregate formation, a process which often hinders self-assembly. In particular, this new assembly pathway allows dodecahedral shells to form readily, whereas these structures never form in the absence of the template. Secondly, we consider the self-assembly of multi-shell structures, where the central icosahedral core is known to form readily on its own, and which could then template the growth of further layers. We are able to find conditions under which two- and three-shell structures successfully assemble, illustrating the power of the templating approach.

---

1 Introduction

It has been a long-held goal to use self-assembly to create complex, ordered structures on the micro- and nanoscale.¹ Biological systems with their dazzling array of ordered and precise self-assembled structures² show what can be possible given sufficient control of the design and the interactions between the building blocks. Thus, with the goal of taking the first steps to achieving similar control in synthetic systems, researchers working on nanoparticles and colloids are making great efforts to synthesize “patchy” particles that have interactions only in specific directions.^3–10

The formation of icosahedral virus capsids, proteinaceous shells with specific size and structure that are designed to encapsulate the viral genome, provides one of the archetypal examples of biological self-assembly, and also one of the most studied.¹¹ If similar structures are to be achieved in synthetic systems, it will be important to understand the basic physical principles of such self-assembly and the design rules for the interactions between the constituent particles. So far, theory^12–15 and simulations^16–29 have been most concerned with understanding the assembly of smaller (T = 1, 3 or 4) empty capsids. However, functional viruses are not empty, but contain the genomic material. For icosahedral RNA viruses, the capsid proteins and the RNA typically co-assemble, and experiments have indicated that the kinetics of such assembly can be different from that of empty capsids.³⁰ Indeed, this ability of capsid proteins to encapsulate is not limited to the viral genome, but has been exploited to achieve capsid assembly around nanoparticles,^31–33 nanoemulsion droplets³⁴ and anionic polymers.³⁵ Furthermore, for larger and more complex capsids, assembly can be dependent on the presence of “scaffolding” proteins, which are thought to template the correct assembly of the capsid.^36,37

Although less studied, simulations^38–41 and theory^42–44 have begun to address the assembly of filled capsids. Particularly relevant to the present study are the simulations of Hagan and coworkers, who have shown that the change in assembly mechanism from homogeneous nucleation of the capsid proteins in the empty capsid case to heterogeneous nucleation around a core enhances the ability of the capsids to assemble.³⁸

When considering the design of synthetic systems of patchy particles which assemble into capsid-like structures, one has to consider the potential differences in the interactions between the biological and synthetic cases. For capsids, the interfaces responsible for the protein-protein interactions not only have to be in contact, but have to have the correct relative orientation. However, first-generation patchy colloids and nanoparticles are unlikely to have this “torsional” component in the potential. Simulations have indicated that the one-component self-assembly of simple monodisperse targets is still feasible in the absence of torsional constraints;^45–47 however, there can be significant differences in the mechanisms of assembly and the nature of the kinetic traps compared to virus capsids. In particular, the lack of a torsional component in the interparticle potential to enforce convexity in the growing clusters leads to disordered aggregation competing with correct assembly.^46,47 Furthermore, as the size of the target structure increases, the difficulty of assembly increases much more rapidly when torsional constraints are not present. For example, the self-assembly of 20-particle dodecahedra occurs readily with a protein-like potential with torsional constraints,²⁴ but is seemingly impossible without.⁴⁷

Here, we will explore whether templated assembly might potentially provide a way to allow the formation of more complex targets using synthetic patchy particles. We will consider both assembly around a single central core particle (Section 3) and also the assembly of two- and three-shell structures (Section 4), where the central shell is known to readily assemble on its own.⁴⁶ If the materials for the different particles were chosen appropriately, the template could then be selectively removed by chemical⁴⁸ or thermal⁴⁹ treatment, if desired.

We should also note that templating has been a useful strategy in supramolecular chemistry,^50,51 and even for the macroscopic assembly of magnetic subunits into polyhedral shells.⁵²

2 Methods

2.1 Potential

To model the patchy particles, we use the potential that we have used in our previous work on self-assembly,^46,47 but with the additional feature that we consider multiple particle types. The model has also been used to study the crystallization of patchy colloids,^53–56 and, with an additional torsional component to the potential, the self-assembly of protein complexes.^24,57

In the model, the repulsion between particles i and j is based upon an isotropic Lennard-Jones potential

but where the attraction is modulated by an orientational term, V_ang. Thus, the complete potential iswhere Ω_i is the orientation of particle i, andwhere θ_αij is the angle between the normal to patch α on particle i and the interparticle vector r_ij, and the ‘max’ selects the pair of patches that have the strongest interaction for the current geometry. We assume that the particle sizes are additive, i.e. σ_ij = (σ_ii + σ_jj)/2. We also generally choose σ_pw, a measure of the width of a patch, to be the same for all patches, except in the case of the central particle in Section 3. By contrast, we allow the well-depth of the patch-patch interactions, ε_αβ to vary (ε_ref = max[ε_α,β]). In addition, for computational efficiency, we cut and shift the potential at 3.5σ_max (where σ_max is σ for the largest particle in the system), and also shift the crossover distance in eqn (2) so that it still occurs when the potential is zero.

We note that in this model, we have effectively coarse-grained out the solvent degrees of freedom, and so when we talk about a gas phase in our model, this would correspond to a dilute solution.

2.2 Simulations

We use the virtual move Monte Carlo algorithm of Whitelam and Geissler^58,59 to simulate the dynamics. We choose this algorithm for a number of reasons. Firstly, as with other Monte Carlo algorithms based on local moves, the algorithm gives diffusive dynamics, as is appropriate for a model of colloids and nanoparticles in solution. Secondly, it can generate collective motion of the particles. Thirdly, the algorithm is designed to generate the correct relative diffusion rates for clusters of different size. The latter two features represent potential advantages over the single-particle Monte Carlo we typically used in our previous studies.^24,46,47 However, as the main mode of cluster growth in those studies was by monomer addition, this was not a significant drawback. Here, however, we felt that it was important not to artificially disfavour growth by the addition of clusters, particularly in the case of the multi-shell-structures studied in Section 4. As the actual algorithm is quite involved, we do not give the details here, but refer the interested reader to the original papers.^58,59 We note that we use a maximum translational move size of 0.3σ_min (where σ_min is σ for the smallest particle in the system), as we have found this to give a good balance between moves that lead to internal rearrangements within clusters and moves that lead to diffusive behaviour of complete clusters.⁶⁰

3 Assembly around a core particle

In this section, we consider the growth of symmetric shell-like clusters around a spherical core particle A. The two cases that we consider are of an icosahedral and a dodecahedral outer shell, as depicted in Fig. 1. The B particles that make up the outer shell have m identical patches whose positions are such that they point directly at the neighbouring B particles in the target geometry. These patches only interact with the equivalent patches on other B particles and with an interaction strength ε_BB. The B particles also have a second type of patch which points directly towards the centre of the target clusters. These patches only interact with the A particles and have an interaction strength ε_AB. For this AB interaction, there is no dependence on the orientation of particle A – its contribution to the attraction is isotropic (or equivalently, 1/σ_pw,A = 0).

Fig. 1 Target geometries: (a) AB₁₂, a centred icosahedron and (b) AB₂₀, a centred dodecahedron.

Fig. 2 shows the results for the assembly of centred icosahedra as a function of patch width and temperature for two different values of ε_AB. For comparison, the yield of icosahedra in simulations with only B particles present is shown in Fig. 2(c). In this case, which we have considered in detail previously,⁴⁶ there are two basic mechanisms of assembly. Firstly, at temperatures close to the clustering temperature, T_c, at which icosahedral clusters become stable with respect to a gas of monomers, and at smaller σ_pw, assembly of the icosahedra proceeds by direct nucleation. By contrast, for wider patches and lower temperatures, large aggregates form first, but these can then undergo further internal rearrangements leading to the formation and budding off of complete icosahedra. However, at even lower temperatures, the time scale for the rearrangements of the aggregates becomes so long that no icosahedra are able to form, and at even wider patch widths liquid aggregates are thermodynamically stable with respect to icosahedra.

Fig. 2 (a) and (b) Yields (averaged over five repeats) of centred and uncentred icosahedra, and the number of particles in aggregates after 10⁶MC cycles as a function of patch width (measured in radians) and the temperature for a system of 120 B particles and 10 A particles at a density of B particles of 0.15 σ⁻³_BB, where σ_AA/σ_BB = 0.95 and (a) ε_AB/ε_BB = 0.5 and (b) ε_AB/ε_BB = 1.0. For comparison, in (c) we have plotted the yield of icosahedra and the number of particles in aggregates under identical conditions but where only B particles are present. Clusters are identified as centred and uncentred icosahedra if they have the correct number of particles and within two of the expected number of bonds, i.e. 28–30 and 40–42 bonds for uncentred and centred icosahedra, respectively, where an interaction is considered a bond if it is at least 40% of the well depth. Aggregates are defined as clusters containing at least 25 particles.

In our simulations with both A and B particles present, there is the potential for competition between the formation of centred and uncentred icosahedra. Interestingly, we find that for ε_AB/ε_AA = 0.5 (Fig. 2(a)), centred icosahedra are the dominant product in the region of parameter space that we previously identified as being dominated by direct nucleation for the pure B system, and that uncentred icosahedra preferentially form in the region dominated by the budding-off mechanism. A closer comparison shows that the centred icosahedra start to form at a somewhat higher temperature than for the pure B system, which is unsurprising due to the extra stabilization due to interactions with the central particle. In the region T_c(B₁₂) < T < T_c(AB₁₂), there is no competition between the two forms as the only cluster stable with respect to the monomeric gas is the centred icosahedron and so growth is expected to occur by templated assembly around the central particle.

As one moves below T_c(B₁₂), the uncentred icosahedra can also start to form, and in the region where aggregation is initially more rapid than cluster formation, the uncentred icosahedra preferentially form. This preference arises because the formation of liquid aggregates is driven by the BB interactions and the A particles are generally excluded from the interior of these aggregates. Again, at too low temperatures, the system gets trapped in aggregates, rather than forming clusters.

For ε_AB/ε_BB = 1, (Fig. 2(b)) the increased stabilization of the centred relative to the uncentred icosahedra is such that the centred icosahedra start to form at significantly higher temperatures than for the pure B system, and the uncentred icosahedra rarely form in any part of the parameter space.

The effect of ε_AB/ε_BB is explored further in Fig. 3, where we look at the dependence of the competition between centred and uncentred icosahedra on ε_AB/ε_BB at a value of the patch width for which the yield of centred icosahedra is high in Fig. 2(a, b). At ε_AB/ε_BB = 1, there is a wide range of temperature over which centred icosahedra successfully assemble, and the templated assembly of the icosahedron around A particles dominates over direct nucleation of B₁₂icosahedra. Below this temperature window, the system forms kinetic aggregates (at this patch width, the local structure of these aggregates is not that similar to the target, so little product results from rearrangement of these aggregates, unlike at larger patch widths).

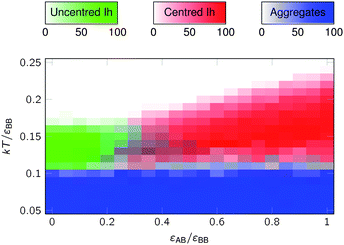Fig. 3 The yields of centred and uncentred icosahedra after 10⁶MC cycles as a function of ε_AB/ε_BB and temperature for a system of 120 B particles and 10 A particles at a density of B particles of 0.15 σ⁻³_BB, where σ_pw = 0.35 and σ_AA/σ_BB = 0.95. Definitions of icosahedra and aggregates are the same as in Fig. 2.

As ε_AB/ε_BB decreases, T_c(AB₁₂) decreases, but the temperature at which aggregation begins remains relatively unchanged, because this is mainly determined by ε_BB. Hence, the window over which successful AB₁₂ assembly occurs decreases. Furthermore, at sufficiently small ε_AB/ε_BB, T_c(AB₁₂) becomes lower than T_c(B₁₂) and at this point the energy gained from an A particle being inside the B₁₂ icosahedron does not offset the loss of entropy. A simple estimate of the value of ε_AB/ε_BB for this crossover can be found using the approximation that T_c ∝ E_gs/(n − 1) where E_gs is the ground state energy of the cluster and n is the number of particles in the cluster; this expression has been found to provide a surprisingly accurate description of the dependence of transition temperatures on relative patch strength.^24,57,61 Using E_gs(B₁₂) ≈ −30ε_BB and E_gs(AB₁₂) ≈ −30ε_BB − 12ε_AB gives a crossover value of ε_AB/ε_BB = 5/22 = 0.227.

However, even before this value of ε_AB/ε_BB is reached, the mechanism of assembly of AB₁₂ will have started to change. At ε_AB = ε_AA, E(AB_n−1) ≤ E(B_n) for any n and so it is favourable for the B particles to grow around the templating A particle. However, as ε_AB/ε_BB decreases, the value of n at which it becomes more energetically favourable to form AB_n–1 rather than B_n increases, and the role of A as a template diminishes. Consequently, at ε_AB/ε_BB = 0.227, the direct nucleation of uncentred icosahedra already dominates.

So far, we have considered cases where the A particle is the right size to fit inside an icosahedron. In Fig. 4, we consider the effect of the size of the A particle on the ease with which centred icosahedra form. It can be seen that there is a limited size range over which the centred icosahedra form. When σ_AA/σ_BB is too large, although templated growth of AB_n clusters will occur, the curvature of the central particle is too small to allow the particles to form icosahedra. When σ_AA/σ_BB is too small, although the initial nucleation of the icosahedra still occurs on the A particle, not all the particles in the growing icosahedra can maintain contact with the A particle. Thus although AB₁₂ clusters still result, the A particle is now in an off-centre position touching only a subset of the B particles. Fig. 4(a) and (b) differentiate between the yields of AB₁₂ clusters with the A particle centred or off-centred. It is noticeable that the off-centred clusters persist to lower σ_AA/σ_BB but that the temperature window over which they can form decreases with decreasing σ_AA/σ_BB, because the energetic stabilization of the cluster provided by the A particle decreases, as it can contact fewer and fewer of the B particles. Only at the smallest values of σ_AA/σ_BB do unfilled icosahedra begin to form.

Fig. 4 The percentage yields of (a) centred icosahedra and (b) 13-mers after 10⁶MC cycles as a function of σ_AA/σ_BB and temperature for a system of 120 B particles and 10 A particles at a density of B particles of 0.15 σ⁻³_BB, where σ_pw = 0.35 and ε_AB/ε_BB = 1. The definitions of icosahedra and aggregates are the same as in Fig. 2, and 13-mers are simply clusters with 13 particles.

Although icosahedral clusters can readily assemble in our simulations with or without a templating central particle, the same is not true for other target clusters. In particular, we previously found that it was impossible to get appropriately-designed patchy particles to form 20-particle dodecahedral shells.⁴⁷ The essential problem is that the system always prefers to form aggregates rather than clusters, because the aggregates are first to become thermodynamically stable as the temperature is decreased, i.e. T_aggreg > T_c(B₂₀), and so there is no temperature window for which the target clusters are the only species stable with respect to the gas. Furthermore, even when the dodecahedral clusters are more stable, i.e. for T < T_c the aggregates form more rapidly than dodecahedral clusters.

Here we investigate whether we can get dodecahedral clusters to form using templated self-assembly, the idea being that the addition of templating particles could stabilize the dodecahedra sufficiently such that T_c(AB₂₀) > T_aggreg, thus resolving the thermodynamic problem noted above. Moreover, templated growth around the central particles will help kinetically, by forcing the clusters to grow with the correct curvature.

It can be seen from Fig. 5(a) that there is now a clear region of parameter space where centred dodecahedra form. As expected, no uncentred dodecahedra form, and so the competition is simply between templated assembly and aggregation. The role of ε_AB in stabilizing the target structure and enabling assembly is clear from Fig. 5(b), which shows the yield of AB₂₀ dodecahedra as a function of ε_AB/ε_BB. In the temperature window T_aggreg < T < T_c(AB₂₀), dodecahedra now readily form, as the target clusters are the only species stable with respect to the gas. Below this window, aggregation dominates because it occurs more rapidly than cluster formation, and because the aggregates are so structurally different from the target that rearrangement of the aggregates to form the target will never occur.

Fig. 5 The yield of centred and uncentred dodecahedra and the number of particle in aggregates (a) as a function of patch width and temperature at ε_AB/ε_BB = 1.0 and (b) as a function of ε_AB/ε_BB and temperature at σ_pw = 0.35. The system consists of 10 A particles and 200 B particles at a density of B particles of 0.15 σ⁻³_BB, where σ_BB/σ_AA = 1.80. The simulations were of length 10⁶MC cycles. Clusters are identified as centred and uncentred dodecahedra if they have the correct number of particles and within two of the expected number of bonds, i.e. 28–30 and 48–50 bonds for uncentred and centred dodecahedra, respectively. Aggregates are defined as clusters containing at least 41 particles.

As ε_AB/ε_BB decreases, there is a corresponding decrease in T_c, and so the window of successful assembly first narrows and then disappears at ε_AB/ε_BB = 0.15, where T_c ≈ T_aggreg. Below this value, similar to the pure B system, dodecahedra are never found to assemble and aggregation always dominates.

4 Multi-shell assembly

The above results for the dodecahedra illustrate the potential role of templated self-assembly in enabling the assembly of more complex target structures in systems of patchy particles without torsionally-specific interactions. In this section we take this one step further to consider the self-assembly of multi-shell structures, where the outer shell(s) surround a polyhedral core that we already know to assemble readily.

Similar highly-symmetric multi-shell structures are seen in biology. For example, some icosahedral viruses have capsids with two or more proteinaceous shells, either in their native state⁶² or in malformed structures.^63,64 Furthermore, multi-enzyme complexes have been discovered that have an open multi-shell structure, e.g. in some species the pyruvate dehydrogenase complex has a dodecahedral inner core of 20 E1 trimers which can be surrounded by 60 E2 tetramers⁶⁵ or E3 dimers⁶⁶ to give a complex with overall icosahedral symmetry. However, the particles that we consider, unlike these proteins, do not have the advantage of torsionally-specific interactions.

The two example structures that we consider are illustrated in Fig. 6. At the centre of both is an icosahedron of 12 A particles. In the first example, this icosahedron is surrounded by a dodecahedron of 20 B particles. In the second example, in addition to the dodecahedral shell, there is a further outer shell of 30 C particles with the structure of an icosidodecahedron.

Fig. 6 Multi-shell target structures: (a) A₁₂B₂₀, a dodecahedron surrounding an icosahedron, and (b) A₁₂B₂₀C₃₀, an icosidodecahedron surrounding a dodecahedron which itself surrounds an icosahedron. There are two views of each structure, the ones on the right having the outer shell partially transparent to give a clearer view of the core. The clusters were produced by self-assembly at T = 0.14ε_AAk⁻¹, and so show some deviations from the ideal structure due to thermal vibrations. The relative particle sizes were chosen to allow the structures to form without any strain, i.e. σ_BB = 1.213σ_AA and σ_CC = 1.851σ_AA. The individual A, B and C particles are illustrated in (c).

The general principle for choosing the geometry of the patches for these particles is that in the ideal target cluster there will be patches pointing directly at the neighbours both in the current shell and in the adjacent shell(s). So, the A particles will have five patches that interact with strength ε_AA with the equivalent patches on other A particles and that are responsible for forming the icosahedron. Each A particle will also have a further 5 patches that point at the pentagon of B particles that surrounds each vertex of the icosahedron in the target structure. These latter patches interact with strength ε_AB with the three patches on the B particles that point to the three A particles of the triangular face of the icosahedron that each B particle sits above in the target cluster. Finally, the B particles also have a further three patches that interact with strength ε_BB with the equivalent patches on other B particles and that are responsible for forming the dodecahedron. Thus, the ground state energy of the A₁₂B₂₀ cluster is approximately −30ε_AA − 60ε_AB − 30ε_BB.

For the A₁₂B₂₀C₃₀ cluster, the B particles have an additional three patches that point at the triangle of C particles that surrounds each vertex of the dodecahedron in the target structure. These latter patches interact with strength ε_BC with the two patches on the C particles that point to the two B particles of the edge of the dodecahedron that each C particle sits above in the target cluster. The C particles also have a further four patches that interact with strength ε_CC with the equivalent patches on other C particles and that are responsible for forming the icosidodecahedron. Thus, the ground state energy of the A₁₂B₂₀C₃₀ cluster is approximately −30ε_AA − 60ε_AB − 30ε_BB − 60ε_BC − 60ε_CC.

The number of potential parameters when considering the assembly of these multi-shell clusters is considerably larger than for the structures in Section 3. Therefore, we always keep the size of the particles fixed at their ideal values (as given in Fig. 6), and for all patches σ_pw = 0.4. We always use a volume fraction of 0.0785, which is equivalent to a number density of 0.15 σ⁻³_AA in a one-component system of A particles. We then consider the effects of varying the interaction strengths of the patches on the self-assembly behaviour.

Results for the self-assembly of A₁₂B₂₀ are considered in Fig. 7 as a function of ε_AB and ε_BB for two temperatures. At the first temperature we consider, T = 0.14ε_AAk⁻¹ < T_c(A₁₂), i.e. icosahedral A₁₂ clusters are stable irrespective of the values of ε_AB and ε_BB. Thus, in the bottom left-hand corner of Fig. 7(a)–(c) corresponding to small ε_AB and ε_BB, the formation of isolated A₁₂ clusters is observed. As either ε_AB or ε_BB is increased, A₁₂B₂₀ clusters become stabilized and a region of parameter space is reached where it becomes favourable to form these clusters. Close to where they first become stable, A₁₂B₂₀ clusters readily form, with yields of 80% or more being common. In this region, the majority of A₁₂ clusters are part of complete A₁₂B₂₀ clusters and provide a stable intermediate for the templated growth of the target cluster. The mechanism of assembly is likely to be hierarchical with A₁₂ clusters forming first, followed by the growth of the second shell by the addition of B monomers.

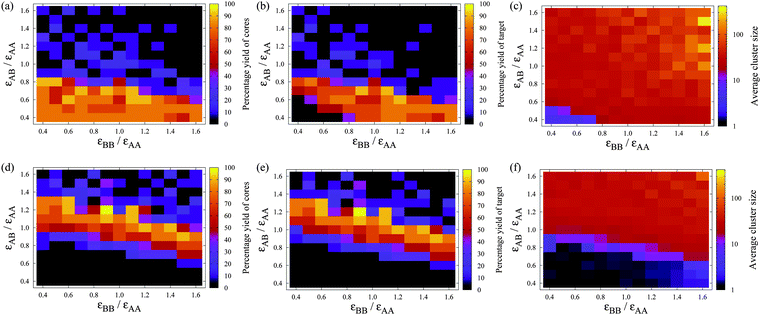Fig. 7 The dependence of the self-assembly of A₁₂B₂₀ on ε_AB and ε_BB at a given temperature: (a)–(c) T = 0.14ε_AAk⁻¹, and (d)–(f) T = 0.18ε_AAk⁻¹. (a) and (d) show the yield of A₁₂ icosahedra (irrespective of whether they are bonded to B atoms), (b) and (e) show the yield of A₁₂B₂₀, and (c) and (f) show the average cluster size, all after 625 000 MC cycles. Each simulation contains 120 A and 200 B particles, so that a maximum of ten target clusters could be formed. The volume fraction is 0.0785.

However, as ε_AB, and to a lesser extent ε_BB, is increased further, malformed structures also become stable with respect to the gas phase and the yield of both A₁₂ cores and A₁₂B₂₀ clusters falls off dramatically. It is noticeable that, unlike the one-component self-assembling systems^46,47 and even the systems considered in Sect. 3, this fall-off in the yield is not associated with the formation of system-spanning aggregates, but instead the average cluster size remains similar to that of the target cluster. Thus, there is a major difference in the configurations responsible for kinetic trapping and this is because the trapping is dominated by interactions between different particle types rather than interactions between like particles. For example, we can see from Fig. 5 that for aggregation between just B particles, kT/ε_BB must be below approximately 0.07, which at T = 0.14ε_AAk⁻¹ corresponds to ε_BB/ε_AA > 2. Kinetic trapping is instead caused by the rapid binding between the A and B particles, before the A particles have assembled into icosahedra, due to the strength of the AB interactions, which in turn interferes with assembly for a number of reasons. Firstly, there are kinetic effects. The B particles make it more difficult for the A particles to which they are bound to come together, both because they slow down the diffusion of the clusters and because the steric effect of the B particles means that it is less likely that a collision will lead to binding. Furthermore, in collisions between clusters, these clusters would also have to have ‘matching’ structures for them to be able to come together to generate a cluster that retains the correct structure (i.e. that is still a sub-cluster of the target structure). Secondly, there is the thermodynamic problem that, due to the stabilizing effects of the AB interactions, clusters with incorrectly formed structures for the A core are now stable with respect to the gas phase. Although the clusters formed have on average a similar size to the target clusters, the system is typically a mixture of larger clusters with of the order of 60 particles and smaller clusters with less than 10 particles.

At the second temperature that we consider, T = 0.18ε_AAk⁻¹, isolated A₁₂ icosahedra are unstable, and so can only form due to the stabilization provided by the second shell of B particles. Hence, in the bottom left-hand corner of Fig. 7(d)–(f) the system is now a mainly monomeric vapour. Similar to the results for the lower temperature, as ε_AB and ε_BB are increased, there is a band in Fig. 7(e) associated with reliable self-assembly of the A₁₂B₂₀ target, before the yield again falls off due to kinetic trapping. However, this band occurs at larger values of ε_AB and ε_BB as compared to Fig. 7(b) because stronger AB and BB interactions are required to compensate for the higher temperature. Furthermore, as A₁₂ clusters are no longer a stable intermediate, the mechanism of assembly must be more cooperative. Indeed, it is noticeable from a comparison of Fig. 7(d) and (e) that virtually all A₁₂ clusters that form do so as part of the target structure.

These results show that the templating strategy is again successful in leading to the formation of structures (dodecahedral shells) that are otherwise impossible to form. In the next example, A₁₂B₂₀C₃₀, we take this a stage further to show that templating can be used to create even more complex structures. Given the large number of parameters for this system, we choose ε_AB and ε_BB from within the region where A₁₂B₂₀ clusters were found to reliably form at the relevant temperature in the previous example. In Fig. 8 we then show the self-assembly behaviour as a function of ε_BC and ε_CC at two different temperatures.

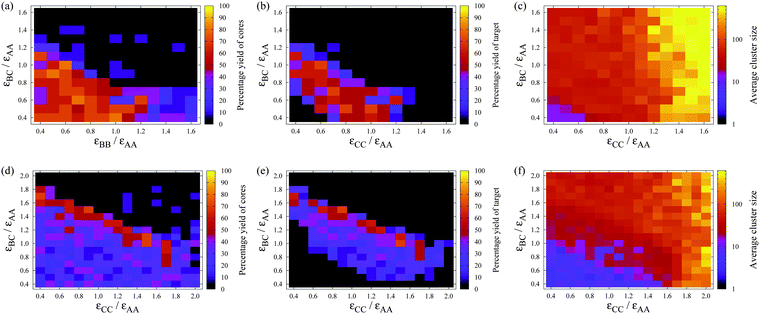Fig. 8 The dependence of the self-assembly of A₁₂B₂₀C₃₀ on ε_BC and ε_CC at (a)–(c) T = 0.12ε_AAk⁻¹, ε_AB/ε_AA = 0.5 and ε_BB/ε_AA = 0.7, and (d)–(f) T = 0.18ε_AAk⁻¹, ε_AB/ε_AA = 1.1 and ε_BB/ε_AA = 1.1. (a) and (d) show the yield of A₁₂B₂₀ (irrespective of whether they are bonded to C atoms), (b) and (e) show the yield of A₁₂B₂₀C₃₀ and (c) and (f) show the average cluster size, all after 625 000 MC cycles. Each simulation contains 120 A, 200 B and 300 C particles, so that a maximum of ten target clusters could be formed. The volume fraction is 0.0785.

The self-assembly behaviour of this system is broadly similar to that for the two-shell target. Again there is a diagonal band of successful assembly as a function of the two interaction strengths (Fig. 8(b) and (e)) with the interactions insufficient to stabilize the target at low ε_BC and ε_CC, but so strong that the system becomes kinetically trapped in incorrect configurations at high ε_BC and ε_CC.

However, there are also a number of differences between the two systems. Firstly, the maximum yields are somewhat lower (about 70%) but this is unsurprising given the greater complexity of the target. Perhaps more surprising is that it decreases by so little; this is testament to the robustness of the templated self-assembly approach. Secondly, there is a stronger dependence of the behaviour on ε_CC than there was on ε_BB in the previous example, but this is simply because there are four such patches on each C particle (rather than the three for B particles). Consequently, ε_CC plays a greater role in the stability of the target structure (but also malformed structures). Thirdly, at large ε_CC the formation of large aggregates is now found to occur. Because of their four self-interactions, C particles can start to aggregate at higher values of kT/ε_CC. An aggregate from this region is illustrated in Fig. 9. Binding of B particles to the aggregates of C particles prevents the formation of any A₁₂B₂₀ clusters, but A₁₂ icosahedra can still form because they have no interactions with the C particles.

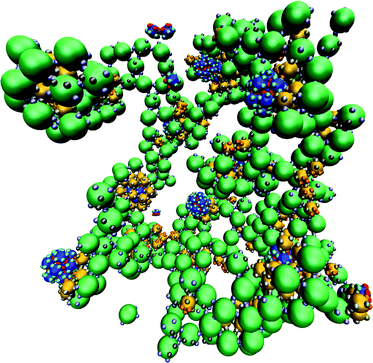Fig. 9 Kinetic aggregates formed for the A₁₂B₂₀C₃₀ target when T = 0.12ε_AAk⁻¹, ε_AB/ε_AA = 0.5, ε_BB/ε_AA = 0.7, ε_BC/ε_AA = 1.2, and ε_CC/ε_AA = 1.6.

There is also an interesting difference between the self-assembly behaviour of the systems at the two temperatures considered. Although for both temperatures ε_AB and ε_BB were chosen with the aim of making A₁₂B₂₀ clusters stable, this seems to have been only partially successful for the higher temperature with yields of only 30–40% in the bottom left of Fig. 8(d). Presumably, the lower yield is partly related to the fact that we have chosen to keep the overall volume fraction of particles the same in the two examples, meaning that there is a lower concentration of A and B particles compared to the two-shell case, and hence a lower driving force for A₁₂B₂₀ formation. Consequently, at T = 0.12ε_AAk⁻¹, the assembly mechanism can be hierarchical with A₁₂B₂₀ clusters a stable intermediate, leading to a relatively broad band of high yield for the target in Fig. 8(b). By contrast, at T = 0.18ε_AAk⁻¹ a more cooperative assembly mechanism is required to achieve high yields, because of the lower stability of A₁₂B₂₀ clusters. In this case, as the interaction strengths increase, there is initially a broad band of weak assembly of the target in Fig. 8(e) with only the 30–40% of particles that are able to form A₁₂B₂₀ clusters going on to form the target. Only at higher interaction strengths is there a narrow band of higher yield, presumably because the free energy barrier to direct nucleation of the A₁₂B₂₀C₃₀ target is now lower.

5 Conclusions

In this paper, we have used computer simulations to investigate the efficacy of a templating strategy to facilitate the self-assembly of high symmetry monodisperse shell structures from model patchy particles. Importantly, in contrast to the interactions between proteins, these particles lack a torsional component to the patch-patch interactions, thus providing a model for the synthetic patchy colloids and nanoparticles that many groups are seeking to develop, and allowing us to explore what structures it might be possible to assemble with such particles if the patch positions and the interaction strengths could be precisely controlled. Previous work has shown that although simple target structures, e.g. 12-particle icosahedra, can readily form, it is hard to form more complicated structures, because the lack of torsional specificity in the interactions means that the structure of the growing clusters is not tightly controlled. Consequently, there is typically a competition between correct assembly and the formation of disordered aggregates.

The potential advantage of using a templating strategy is that it opens up a new assembly mechanism, namely heterogeneous nucleation around the template rather than direct homogeneous nucleation. The simple icosahedral example allowed us to explore under what conditions the templating pathway can dominate. Templating is generally more successful under conditions away from where aggregation offers a competing pathway, e.g. higher temperatures and narrower patch widths. Furthermore, the region dominated by templated assembly can be enhanced by increasing the interaction strength between the template and the assembling particles, and thus opening up a larger temperature window over which the target structure is the only species stable with respect to the monomeric gas.

We have then demonstrated the potential for templating to aid the formation of more complex structures by assembling dodecahedral and multi-shell clusters. The dodecahedral example is particularly noteworthy, because without the template, dodecahedra are never able to form as aggregation always dominates over assembly.⁴⁷ However, the stabilization of the target structure by the template allows a temperature window to be opened up where the centred dodecahedra are the only species stable with respect to the monomeric gas, and in this region the dodecahedra can now assemble relatively easily. In addition to this thermodynamic effect, in removing aggregates as a competing state, templating also aids the dynamics of assembly by helping clusters to grow with the correct curvature and structure, even though their interactions are not torsionally specific. For example, although the angles between the patches allows dodecahedron-forming particles to form hexagonal as well as pentagonal rings, the former are likely to be disfavoured because they are less congruent with binding to the template. Similarly, if as a cluster grows around a template, it incorporates some kind of defect, the propagation of this defect during further growth of the cluster is likely to inhibit the binding to the template and hence reduce the stability of the growing cluster, making the annealing out of that defect more likely. Nevertheless, even given these advantages, it is impressive that templated assembly can allow us to form such complex structures as the three-shell A₁₂B₂₀C₃₀ cluster in relatively high yields.

In our simulations, we are straightforwardly able to increase the number of particle types and types of patches, and to introduce specificity into the patch-patch interactions. By contrast, even though the synthetic strategies for producing patchy particles are rapidly improving, some of the particles whose behaviour we have analysed here would be very challenging to synthesise, particularly in terms of the control of patch position and identity—DNA-mediated interactions provide a potential route to achieve the required specificity in the patch-patch interactions.⁶⁷ Nevertheless, our results also indicate that the use of templated self-assembly provides a means to greatly increase the repertoire of structures into which such particles could assemble.

6 Acknowledgements

The authors are grateful to the EPSRC and the Royal Society for financial support. We also thank Aleks Reinhardt for his expertise and support throughout this project.

References

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
2. D. S. Goodsell, Bionanotechnology, Wiley-Liss, Hoboken, 2004.
3. S. C. Glotzer and M. Solomon, Nat. Mater., 2007, 6, 557–562.
4. K.-H. Roh, D. C. Martin and J. Lahann, J. Am. Chem. Soc., 2006, 128, 6796–6797.
5. Y.-S. Cho, G.-R. Yi, S.-H. Kim, S.-J. Jeon, M. T. Elsesser, H. K. Yu, S.-M. Yang and D. J. Pine, Chem. Mater., 2007, 19, 3183–3193.
6. G. A. DeVries, M. Brunnbauer, Y. Hu, A. M. Jackson, B. Long, B. T. Neltner, O. Uzun, B. H. Wunsch and F. Stellacci, Science, 2007, 315, 358–361.
7. L. Wang, L. Xia, G. Li, S. Ravaine and X. S. Zhao, Angew. Chem., Int. Ed., 2008, 47, 4725–4728.
8. A. Perro, E. Duguet, O. Lambert, J.-C. Taveau, E. Bourgeat-Lami and S. Ravaine, Angew. Chem., 2009, 121, 367–371.
9. D. J. Kraft, W. S. Vlug, C. M. van Kats, A. van Blaaderen, A. Imhof and W. K. Kegel, J. Am. Chem. Soc., 2009, 131, 1182–1186.
10. A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168.
11. A. Zlotnick and S. J. Stray, Trends Biotechnol., 2003, 21, 536–542.
12. D. Endres and A. Zlotnick, Biophys. J., 2002, 83, 1217–1230.
13. D. Endres, M. Miyahara, P. Moisant and A. Zlotnick, Protein Sci., 2005, 14, 1518–1525.
14. A. Zlotnick, J. Mol. Recognit., 2005, 18, 479–490.
15. R. Zandi, P. van der Schoot, D. Reguera, W. Kegel and H. Reiss, Biophys. J., 2006, 90, 1939–948.
16. M. F. Hagan and D. Chandler, Biophys. J., 2006, 91, 42–54.
17. H. D. Nguyen, V. S. Reddy and C. L. Brooks III, Nano Lett., 2007, 7, 338–344.
18. H. D. Nguyen and C. L. Brooks III, Nano Lett., 2008, 8, 4574–4581.
19. H. D. Nguyen, V. S. Reddy and C. L. Brooks III, J. Am. Chem. Soc., 2009, 131, 2606–2614.
20. T. Zhang and R. Schwartz, Biophys. J., 2006, 90, 57–64.
21. B. Sweeney, T. Zhang and R. Schwartz, Biophys. J., 2008, 94, 772–783.
22. D. C. Rapaport, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051905.
23. D. C. Rapaport, Phys. Rev. Lett., 2008, 101, 186101.
24. A. W. Wilber, J. P. K. Doye, A. A. Louis and A. C. F. Lewis, J. Chem. Phys., 2009, 131, 175102.
25. I. G. Johnston, A. A. Louis and J. P. K. Doye, J. Phys.: Condens. Matter, 2010, 22, 104101.
26. D. J. Wales, Philos. Trans. R. Soc. London, Ser. A, 2005, 363, 357–377.
27. S. N. Fejer, T. R. James, J. Hernandez-Rojas and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 2098–2104.
28. S. N. Fejer, D. Chakrabarti and D. J. Wales, ACS Nano, 2010, 4, 219–228.
29. K. Van Workum and J. F. Douglas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031502.
30. J. M. Johnson, D. A. Willits, M. J. Young and A. Zlotnick, J. Mol. Biol., 2004, 335, 455–464.
31. B. Dragnea, C. Chen, E.-S. Kwak, B. Stein and C. C. Kao, J. Am. Chem. Soc., 2003, 125, 6374–6375.
32. C. Chen, M.-C. Daniel, Z. T. Quinkert, M. De, B. Stein, V. D. Bowman, P. R. Chipman, V. M. Rotello, C. C. Kao and B. Dragnea, Nano Lett., 2006, 6, 611–615.
33. J. Sun, C. DuFort, M.-C. Daniel, A. Murali, C.i. Chen, K. Gopinath, B. Stein, M. De, V. M. Rotello, A. Holzenburg, C. C. Kao and B. Dragnea, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1354–1359.
34. C. B. Chang, C. M. Knobler, W. M. Gelbart and T. G. Mason, ACS Nano, 2008, 109, 281–286.
35. Y. Hu, R. Zandi, A. Anavitarte, C. M. Knobler and W. M. Gelbart, Biophys. J., 2008, 94, 1428–1436.
36. A. Maraver, A. Oña, F. Abaitua, D. Gonález, R. Clemente, A. Ruiz-Diaz, J. R. Castón, F. Pazos and J. F. Rodriguez, J. Virol., 2003, 77, 6438–6449.
37. B. Deng, C. M. O'Connor, D. H. Kedes and Z. H. Zhou, J. Struct. Biol., 2008, 161, 419–427.
38. M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051904.
39. O. M. Elrad and M. F. Hagan, Nano Lett., 2008, 8, 3850–3857.
40. A. Kivenson and M. F. Hagan, Biophys. J., 2010, 99, 619.
41. O. M. Elrad and M. F. Hagan, Phys. Biol., 2010, 7, 045003.
42. P. van der Schoot and R. Bruinsma, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061928.
43. T. Hu and B. I. Shklovskii, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051901.
44. M. F. Hagan, J. Chem. Phys., 2009, 130, 114902.
45. Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413.
46. A. W. Wilber, J. P. K. Doye, A. A. Louis, E. G. Noya, M. A. Miller and P. Wong, J. Chem. Phys., 2007, 127, 085106.
47. A. W. Wilber, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2009, 131, 175101.
48. Y. A. Vlasov, X.-Z. Bo, J. C. Sturm and D. J. Norris, Nature, 2001, 414, 289–293.
49. K. P. Velikov, C. G. Christova, R. P. A. Dullens and A. van Blaaderen, Science, 2002, 296, 106–109.
50. H. N. Miras, G. J. T. Cooper, D.-L. Long, H. Bögge, A. Müller, C. Streb and L. Cronin, Science, 2010, 327, 72–74.
51. M. C. O'Sullivan, J. K. Sprafke, D. V. Kondratuk, C. Rinfray, T. D. W. Claridge, A. Saywell, M. O. Blunt, J. N. O'Shea, P. H. Beton, M. Malfois and H. L. Anderson, Nature, 2011, 469, 72–75.
52. B. T. Burnley and J. P. L. Cox, Mater. Sci. Eng., C, 2005, 25, 529–540.
53. J. P. K. Doye, A. A. Louis, I.-C. Lin, L. R. Allen, E. G. Noya, A. W. Wilber, H. C. Kok and R. Lyus, Phys. Chem. Chem. Phys., 2007, 9, 2197–2205.
54. E. G. Noya, C. Vega, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2007, 127, 054501.
55. E. G. Noya, C. Vega, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2010, 132, 234511.
56. G. Doppelbauer, E. Bianchi and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 104105.
57. G. Villar, A. W. Wilber, A. J. Williamson, P. Thiara, J. P. K. Doye, A. A. Louis, M. N. Jochum, A. C. F. Lewis and E. D. Levy, Phys. Rev. Lett., 2009, 102, 118106.
58. S. Whitelam and P. Geissler, J. Chem. Phys., 2007, 127, 154101.
59. S. Whitelam, E. H. Feng, M. F. Hagan and P. Geissler, Soft Matter, 2009, 5, 1251–1262.
60. A. W. Wilber, PhD thesis, University of Oxford, UK, 2009.
61. G. Villar, A. W. Wilber, A. J. Williamson, J. Andreani, J. P. K. Doye and A. A. Louis, to be submitted.
62. J. Z. Chen, E. C. Settembre, S. T. Aoki, X. Zhang, A. R. Bellamy, P. R. Dormitzer, S. C. Harrison and N. Grigorieff, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10644–10648.
63. G. Cardone, J. G. Purdy, N. Cheng, R. C. Craven and A. C. Steven, Nature, 2009, 457, 694–698.
64. L. Lavelle, M. Gingery, M. Phillips, W. M. Gelbart and C. M. Knobler, J. Phys. Chem. B, 2009, 113, 3813–3819.
65. J. L. S. Milne, D. Shi, P. B. Rosenthal, J. S. Sunshine, G. J. Domingo, X. Wu, B. R. Brooks, R. N. Perham, R. Henderson and S. Subramaniam, EMBO J., 2002, 21, 5587–5598.
66. J. L. S. Milne, X. Wu, M. J. Borgnia, J. S. Lengyel, B. R. Brooks, D. Shi, R. N. Perham and S. Subramaniam, J. Biol. Chem., 2006, 281, 4364–4370.
67. M. M. Maye, D. Nykypanchuk, M. Cuisinier, D. van der Lelie and O. Gang, Nat. Mater., 2009, 8, 388–391.

---