 Open Access Article
Open Access ArticleMinimum-energy vesicle and cell shapes calculated using spherical harmonics parameterization†
Khaled
Khairy
*a and
Jonathon
Howard
*b
aJanelia Farm Research Campus, 19700 Helix Drive, Ashburn, VA, USA. E-mail: khairyk@janelia.hhmi.org; Tel: +1 571 209 4217
bMax-Planck Institute of Molecular Cell Biology and Genetics, Pfotenhauerstrasse 108, Dresden, Germany. E-mail: howard@mpi-cbg.de; Fax: +49 351 210 2020; Tel: +49 351 210 2500
First published on 21st January 2011
Abstract
An important open question in biophysics is to understand how mechanical forces shape membrane-bounded cells and their organelles. A general solution to this problem is to calculate the bending energy of an arbitrarily shaped membrane surface, which can include both lipids and cytoskeletal proteins, and minimize the energy subject to all mechanical constraints. However, the calculations are difficult to perform, especially for shapes that do not possess axial symmetry. We show that the spherical harmonics parameterization (SHP) provides an analytic description of shape that can be used to quickly and reliably calculate minimum energy shapes of both symmetric and asymmetric surfaces. Using this method, we probe the entire set of shapes predicted by the bilayer couple model, unifying work based on different computational approaches, and providing additional details of the transitions between different shape classes. In addition, we present new minimum-energy morphologies based on non-linear models of membrane skeletal elasticity that closely mimic extreme shapes of red blood cells. The SHP thus provides a versatile shape description that can be used to investigate forces that shape cells.
1 Introduction
Amphiphilic molecules such as lipids spontaneously aggregate in aqueous solution. One stable aggregate is the membrane bilayer composed of two monomolecular leaflets, with the lipid molecules oriented such that their hydrophobic sides face each other and their hydrophilic sides face the aqueous solution. Membrane bilayers form the boundaries of vesicles and, despite their simple structure, can adopt a large variety of shapes. Such bilayer vesicles are considered the prototype for the boundaries of organelles and cells, and have consequently been the focus of many studies.1,2 To explain vesicle shapes, theoretical studies first stressed the effect of the bending stiffness of the membrane.3–5 Later, the coupling between the two membrane leaflets was included.6,7 In the case of red blood cells, which have an underlying cytoskeleton that reinforces the bilayer, shear and stretch elasticities of the membrane were added as well.8–12 In all variants, the energy function, once constructed, is minimized under constraints such as area and volume, yielding theoretically predicted shapes.4,9,13–16 Such minimum-energy surfaces have successfully accounted for many of the shapes adopted by membrane vesicles, and by red blood cells under various buffer conditions9,11 and pathologies.17There are three general categories of methods for calculating minimum-energy membrane conformations.18 The first is solving the Euler–Lagrange equations constructed from the integrals of the energy and constraint expressions.2,19 This method has so far been restricted to shapes that are axially symmetric.13,14 The second is a brute force technique in which the surface is represented as a simply connected triangular mesh.9,20–22 It permits general (nonaxisymmetric) shapes, but limits the accuracy of geometric property calculations and renders energy minimization CPU-intensive. This approach may become more attractive with future developments of faster computer clusters and clouds. The third approach is to use an appropriate set of basis functions.17,18,23 The parameter set is small and can be varied within a numerical optimization strategy to minimize the energy expression directly. An especially intuitive basis is provided by the spherical harmonics basis functions.24 This basis was used for vesicle mechanics studies in the pioneering work of Heinrich et al.25 The spherical harmonics are the three dimensional equivalent of the one dimensional Fourier series, they form an orthonormal basis and their characteristics are well studied. However, they can only represent stellar objects, i.e. objects that have a point inside that can see all points on the surface without crossing the surface (Fig. 1a, left). This poses a serious limitation to modeling cells and vesicles because only nearly spherical shapes can be represented.
 | ||
| Fig. 1 The spherical harmonics parameterization (SHP). (a) Spherical harmonics functions are single-valued; their direct combinations can only represent stellar surfaces, i.e., surfaces that contain a point inside that can “see” every point on the surface. SHP, however, can represent both stellar and non-stellar objects. Left: stellar object, right: non-stellar object. (b) Surface reconstruction of a human red blood cell discocyte segmented from 3D confocal microscopy images.30 The top row and lower left shapes represent direct spherical harmonic expansions (eqn (1)) with approximations of increasing Lmax values; number of coefficients = (Lmax + 1)2. Even at the high order of Lmax = 22 (lower left), the centre of the discocyte suffers from artefacts (ringing). Colour: local curvature. Lower right: SHP of the cell at Lmax = 10. 30 non-zero coefficients capture the essential features of the cell with no apparent artefacts. | ||
To circumvent the above problems, we implemented the spherical harmonics method in parametric form (spherical harmonics parameterization SHP).26,27 SHP represents both stellar and non-stellar closed surfaces (Fig. 1a, right), and requires far fewer parameters than the direct spherical harmonics representation even for stellar objects (Fig. 1b). SHP has been used successfully in computer vision for performing quantitative shape analysis.28,29
In this work, we use SHP to map out shape space defined by the bilayer couple model. In this model, the bending energy is minimized for fixed values of the reduced volume (the volume normalized by that of a sphere of equal surface area) and the relative area difference between the bilayers. Due to the computational advantages of SHP, we explore transitions from one class of shapes to another, finding that the transitions are smooth. We also use SHP to calculate minimum-energy surfaces produced by a lipid–cytoskeletal composite membrane with highly non-linear elastic properties, such as that of the human red blood cell. Recently, RBC shapes were obtained for particular resting shapes of the membrane associated cytoskeleton.9,17 However, the influence of the resting shape on the final morphology has not been fully investigated. We have used the SHP method to show that a prolate resting shape for the membrane-associated cytoskeleton is able to predict observed detailed morphological features that do not appear for oblate or biconcave resting shapes.
2 Methods
2.1 Shape description: spherical harmonics parameterization
A function r of the spherical coordinates (θ,ϕ) may be represented as a series expansion,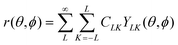 | (1) |
| yLK(θ,ϕ) = NLKPL,K(cos θ)cos (Kϕ), when K ≥ 0 |
| yLK(θ,ϕ) = NLKPL,K(cos θ)sin (|K|ϕ), when K < 0 | (2) |
As stated above, this representation is limited to stellar surfaces. We represent a general surface ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) that is topologically equivalent to the sphere, parametrically26 by expanding, in spherical harmonics basis functions, its individual Cartesian coordinates,
that is topologically equivalent to the sphere, parametrically26 by expanding, in spherical harmonics basis functions, its individual Cartesian coordinates,
 | (3) |
2.2 Bilayer couple energy of vesicles
A continuum formulation for vesicle shape energy is provided by the strict bilayer couple model.7,32 It predicts shapes by minimization of the bending energy, given by | (4) |
 , and reduced area difference Δa = M/4πRo3, with
, and reduced area difference Δa = M/4πRo3, with  . For a sphere v = Δa = 1. We implemented the above simplified model to demonstrate the numerical power of SHP and for comparison with established work. However, the accurate modeling of a bilayer vesicle requires the “generalized bilayer couple model” in which the hard constraint of area difference is relaxed by replacing it with an explicit area-difference-elasticity term.2,25,33
. For a sphere v = Δa = 1. We implemented the above simplified model to demonstrate the numerical power of SHP and for comparison with established work. However, the accurate modeling of a bilayer vesicle requires the “generalized bilayer couple model” in which the hard constraint of area difference is relaxed by replacing it with an explicit area-difference-elasticity term.2,25,33
2.3 Human red blood cell membrane energy
In the case of human red blood cells, it is assumed—similar to the generalized bilayer couple model above—that the cell membrane energy contains the bending energy (of eqn (4)), and a resistance of the membrane to adopting a shape whose difference in area between the outer and inner leaflets (ΔA) deviates from the unstressed area difference (ΔA0). In addition, the membrane skeletal network, which is largely composed of the protein spectrin, is associated with the bilayer from the cytoplasmic side, and provides it with stretch and shear resistance (energy EMS).8–12 The energy function that is to be minimized is given by,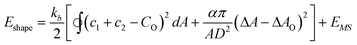 | (5) |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) /kb, where
/kb, where ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is the modulus corresponding to the stretching of the membrane leaflets due to the deviation from the preferred area difference. Co, ΔA and ΔAo are the spontaneous curvature, the difference in area between the outer and inner leaflets and the preferred difference respectively. Integration of the first term of eqn (5) is performed over the whole shape. EMS is the energy associated with the stretch and shear of the membrane skeleton. Here we closely follow the expression given in ref. 9 and 34,
is the modulus corresponding to the stretching of the membrane leaflets due to the deviation from the preferred area difference. Co, ΔA and ΔAo are the spontaneous curvature, the difference in area between the outer and inner leaflets and the preferred difference respectively. Integration of the first term of eqn (5) is performed over the whole shape. EMS is the energy associated with the stretch and shear of the membrane skeleton. Here we closely follow the expression given in ref. 9 and 34, | (6) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) . Δa0 is a measure of the tendency of the membrane to bend in or outwards and combines local and non-local effects (ESI, S6†).
. Δa0 is a measure of the tendency of the membrane to bend in or outwards and combines local and non-local effects (ESI, S6†).
2.4 Computing
We implemented the discrete versions of eqn (4)–(6) (ESI, S7†) in Matlab using SHP. For the numerical integration we used Gaussian quadrature36 with 3600 base points (ESI, S3†). We performed direct numerical constrained minimization using sequential quadratic programming37,38 (ESI, S8†) on a single 1.6 GHz Intel CPU under Windows XP 64Bit.3 Results and discussion
3.1 Bilayer couple minimum energy shapes
We calculated minimum-energy shapes of vesicles according to eqn (4) subject to fixed volume, surface area and difference in area between the inner and outer leaflets. To explore a broad range of both axisymmetric and nonaxisymmetric shapes, we varied the relative area difference from 0.6 to 1.3 in small intervals, 0.1%, at three different reduced volumes v = 0.8, 0.7 and 0.59. This maps out a large part of shape space corresponding to most of the observed shapes (Fig. 2a, lines I, II, and III respectively). The three lines are overlaid on a section of the phase diagram published in Fig. 3 of ref. 14. | ||
| Fig. 2 Phase diagram of the bilayer coupling model (adapted from the phase diagram of Fig. 3 in ref. 14), and simulated morphologies. (a) Part of the phase diagram adapted from Seifert et al. with the main morphological regions (phases) labeled. This part has been studied by Seifert et al. 1991 and Ziherl and Svetina 2005. Lines I, II and III show the fixed reduced volumes of 0.8, 0.7 and 0.59 along which we calculated minimum energy shapes using the bilayer coupling model and SHP shape representation. The three lines correspond to right, middle and left columns in (b) respectively. Dark circles indicate the locations at which shapes are shown in (b). (b) Right column: v = 0.8. Middle column: v = 0.7. Left column: v = 0.59. Numbers next to the shapes are Δa values. | ||
For the more spherical family of shapes corresponding to v = 0.8, we used Lmax = 3; this has 48 parameters. As the area difference was reduced from 1.3 to 0.6 in 0.1% steps, the minimum energy shape changed from bowling-pin morphology through dumbbell to ellipsoid, discocyte and stomatocyte (Fig. 2b, right column, corresponding top Fig. 2a, line I). The computational procedure was as follows. We started with a sphere and the first part of the optimization consisted of a series of steepest descent steps to satisfy the reduced volume and area difference constraints. This required 30 seconds. The second part consisted of bending energy minimizations satisfying those constraints at all times (ESI, S8†). A minimum energy shape resulting from one step was then used as starting shape for the next. The complete series was generated in 70 minutes. To test that a sufficiently broad range of shapes was explored for the minimization procedure, we raised Lmax to 5, with a total of 108 parameters. The same sequence was obtained with no significant decrease in the minimum bending energy, and no significant amplitudes in L orders above 3. The shape sequence in the right most column of Fig. 2b is in accord with the findings of Seifert et al. (1991) for the axisymmetric part, and with the findings of Ziherl and Svetina (2005)20 for the nonaxisymmetric part (fourth shape from the bottom).
Although axisymmetric shapes require only (Lmax + 1)2 + 2 parameters, starting with such a restricted set of parameters is only acceptable if the symmetry of the minimum energy shape is known beforehand. Usually, it is not. Therefore we kept our calculations general and made the full set available for optimization. Nevertheless, the number, order (L) and degree (K) of non-zero coefficients reflect symmetry, and result in a sparse representation for symmetric and smooth shapes. For example, the number of coefficients with amplitude >1% of the largest coefficient, for the top five shapes in the v = 0.8 sequence, was from top to bottom of Fig. 2b right: 13, 13, 11, 8 and 11. This clearly represents only a subset of the available 48. Truncating these coefficients from the series resulted in less than 0.01% increase in bending energy.
We then explored shapes with smaller reduced volume v = 0.7, in which the morphologies are more “deflated”. As the relative area difference was decreased from 1.25 to 0.6, the minimum energy shapes changed from dumbbell, biconcave discoid, discocyte to stomatocyte (Fig. 2a, line II, and Fig. 2b, middle column). This series is again in close agreement with the Seifert et al. phase diagram for the axisymmetric shapes. Non-axisymmetric morphologies for this constant reduced volume line are also in agreement with Heinrich et al. 199325 (Fig. 2b, middle column; second and third shapes from the top), as well as the values for the minimum bending energy Eb(S) (data not shown). The sequence 0.6 < Δa < 1.25 required 60 minutes, and was generated with Lmax = 3.
The third reduced volume that we explored was v = 0.59, corresponding to even more deflated morphologies (Fig. 2a, line III and Fig. 2b, column left). As the relative area difference was reduced from 1.4 to 0.6, the minimum-energy shapes ranged from dumbbell, through paddle-shape, plectrum, to discocyte and finally stomatocyte. The changing symmetry was handled naturally with SHP, and we found a smooth morphing of one shape into another. Our results agree with those of Seifert et al. (1991) for the axisymmetric shapes at Lmax = 3, including the dumbbell shape (Fig. 2b, left column: top shape). Our nonaxisymmetric sequence (Fig. 2b, left column: shapes 2–4 from the top), for which we used Lmax = 5, agreed with Fig. 1 of ref. 20.
3.2 Human red blood cell morphology
Modeling cell shape is more complex than modeling vesicles because the lipid bilayer surrounding cells also contains a thin membrane-associated network of cytoskeletal proteins that contribute shear stiffness (the fluid membrane cannot support shear) as well as additional bending stiffness. A paradigm system for such studies is the human red blood cell (RBC) whose shapes can be measured accurately by three-dimensional confocal microscopy. In addition to stomatocytes and discocytes (Fig. 3a, top two panels), RBCs can also form spiculated morphologies known as echinocytes, which come in several forms (Fig. 3a, lower three panels). Some features of echinocytes have been successfully modeled by incorporating models for the membrane skeleton.8,9,11 An important membrane skeleton parameter is its resting (relaxed) shape. By varying the morphology of the resting membrane skeleton from spherical to oblate and then discocytic, a large number of subclasses of echinocytic shapes has been modeled.34 With the computational advantages of SHP, which allows us to explore other resting shapes, we found that a prolate ellipsoid resting shape (v = 0.95) leads to the prediction of slightly out-of-plane spicules in the observed echinocyte I (arrow in Fig. 3a, middle panel and Fig. 3b, middle panel). To our knowledge this has not been observed computationally before.![Experimentally induced and theoretically predicted sequences of RBC morphology. (a) 3D confocal images of DiI-labeled RBCs in solutions of increasing concentrations of NaCl (concentrations in mM shown on the images). (b) Theoretically predicted shapes that minimize the shape energy of eqn (5) under constraints of total surface area 140 µm2, and volume 100 µm3. The sequence was obtained by changing the value of the effective reduced area difference Δa0; from top to bottom by [%]: 0.072, 0.143, 1.717, 1.788 and 2.003. Δa0 indicates the tendency of the membrane towards blebbing (small values) or budding (large values). All calculations assumed a prolate ellipsoidal relaxed membrane skeleton with a reduced volume of 0.95.](/image/article/2011/SM/c0sm01193b/c0sm01193b-f3.gif) | ||
| Fig. 3 Experimentally induced and theoretically predicted sequences of RBC morphology. (a) 3D confocal images of DiI-labeled RBCs in solutions of increasing concentrations of NaCl (concentrations in mM shown on the images). (b) Theoretically predicted shapes that minimize the shape energy of eqn (5) under constraints of total surface area 140 µm2, and volume 100 µm3. The sequence was obtained by changing the value of the effective reduced area difference Δa0; from top to bottom by [%]: 0.072, 0.143, 1.717, 1.788 and 2.003. Δa0 indicates the tendency of the membrane towards blebbing (small values) or budding (large values). All calculations assumed a prolate ellipsoidal relaxed membrane skeleton with a reduced volume of 0.95. | ||
For simulating RBC morphology, we calculated minimum energy shapes corresponding to eqn (5) for a range of Δa0values. When using a prolate ellipsoid, our results are in excellent qualitative agreement with the observed RBC morphologies (Fig. 3b). As in the case of the bilayer coupling, the number of parameters was small, so the calculations were fast (40–60 minutes). For example, a discocyte requires only 4 nonzero parameters and is readily calculated at Lmax = 3. A flat spiculated cell (echinocyte I) contains features available at Lmax = 10, yet only 6 nonzero coefficients essentially capture the morphology. For more complicated shapes (Fig. 3b, bottom 2), Lmax was set to 12, and the optimization was performed overnight (12 hours). However, only 13% of the coefficients are nonzero.
Importantly, our simulations reproduced the out-of-plane spicules of the echinocyte I (Fig. 3, middle panels) when we introduced the prolate ellipsoidal undeformed membrane skeleton geometry. We did not computationally observe such out-of-plane spicules when oblate or discocytic resting skeleton shapes were assumed. It should be noted that out-of-plane spicules can be clearly experimentally observed in about half the cells (ESI, S9†), and the features persist over the time span of an imaging experiment (0.5 to 1 hours).
Conclusions
To understand cell and organelle morphology, we need efficient and accurate morphological tools that facilitate the construction and testing of theoretical membrane mechanics models. In this work we have shown that SHP is a powerful way for representing vesicle and cell morphology, and enables traversing shape phase diagrams smoothly and at high resolution on a conventional PC workstation. The main morphologies that emerge from the bilayer coupling model were represented within a unifying framework without separate treatments for particular symmetries. Also the more involved problem of the human red blood cell was calculated efficiently. SHP enabled the calculation of RBC shapes for a model in which the undeformed membrane-associated cytoskeleton was prolate ellipsoidal, instead of discoid39 or oblate.9,17 We found that even the subtle out-of-plane spicules feature observed for echinocyte I was successfully reproduced using this model.SHP can describe arbitrary genus-zero morphologies. It is not restricted to symmetric shapes and has an advantage over methods that calculate shape properties from surface triangular meshes in terms of accuracy and efficiency. Its primary limitation is that it is an approximation up to some expansion order. This limitation, however, will become less of a problem as computational power increases.
Acknowledgements
We wish to thank JiJinn Foo for providing the RBC images, and also Frank Juelicher and Udo Seifert for helpful discussions. This work was funded by the Max-Planck Society.References
- R. Lipowsky, Nature, 1991, 349, 475–481 CrossRef CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CAS.
- P. B. Canham, J. Theor. Biol., 1970, 26, 61–81 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 Search PubMed.
- E. A. Evans, Biophys. J., 1974, 14, 923–931 CrossRef CAS.
- M. P. Sheetz and S. J. Singer, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 4457–4461 CrossRef CAS.
- S. Svetina and B. Zeks, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS.
- R. Mukhopadhyay, H. W. G. Lim and M. Wortis, Biophys. J., 2002, 82, 1756–1772 CrossRef CAS.
- H. W. G. Lim, M. Wortis and R. Mukhopadhyay, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16766–16769 CrossRef.
- M. Bobrowska-Hagerstrand, H. Hagerstrand and A. Iglic, Biochim. Biophys. Acta, Biomembr., 1998, 1371, 123–128 CrossRef CAS.
- A. Iglic, J. Biomech., 1997, 30, 35–40 CrossRef CAS.
- D. Kuzman, S. Svetina, R. E. Waugh and B. Zeks, Eur. Biophys. J., 2004, 33, 1–15 CrossRef CAS.
- H. J. Deuling and W. Helfrich, Biophys. J., 1976, 16, 861–868 CrossRef CAS.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS.
- P. Ziherl and S. Svetina, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 761–765 CrossRef CAS.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097 CrossRef CAS.
- K. Khairy, J. Foo and J. Howard, Cell. Mol. Bioeng., 2008, 1, 173–181 Search PubMed.
- M. Bloor and M. Wilson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4218–4229 CrossRef CAS.
- Z. Ou-Yang and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280–5288 CrossRef.
- P. Ziherl and S. Svetina, Europhys. Lett., 2005, 70, 690–696 CrossRef CAS.
- M. Jaric, U. Seifert, W. Wintz and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 6623–6634 CrossRef CAS.
- W. Wintz, H. Doebereiner and U. Seifert, Europhys. Lett., 1996, 33, 403–408 CrossRef CAS.
- V. Heinrich, M. Brumen, R. Heinrich and S. Svetina, J. Phys. II, 1992, 2, 1081–1108 CrossRef CAS.
- E. W. Hobson, The Theory of Spherical and Ellipsoidal Harmonics, Chelsea Pub. Co., New York, 1955 Search PubMed.
- V. Heinrich, S. Svetina and B. Zeks, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3112–3123 CrossRef CAS.
- B. S. Duncan and A. J. Olson, Biopolymers, 1993, 33, 219–229 CrossRef CAS.
- C. Brechbühler, G. Gerig and O. Kuebler, Comput. Vis. Image Understand., 1995, 61, 154–170 Search PubMed.
- M. Styner, J. A. Lieberman, R. K. McClure, D. R. Weinberger, D. W. Jones and G. Gerig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4872–4877 CrossRef CAS.
- L. Shen, H. Farid and M. A. McPeek, Evolution, 2009, 63, 1003–1016 CrossRef.
- K. Khairy and J. Howard, Med. Image Anal., 2008, 12, 217–227 CrossRef.
- W. Bosh, Phys. Chem. Earth, 2000, 25, 655–659 Search PubMed.
- S. Svetina and B. Zeks, Biomed. Biochim. Acta, 1983, 42, S86–S90 CAS.
- L. Miao, U. Seifert, M. Wortis and H. G. Doebereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389–5407 CrossRef CAS.
- G. H. W. Lim, PhD thesis, Simon Fraser University, 2003.
- E. A. Evans and R. Skalak, Mechanics and Thermodynamics of Biomembranes, CRC, Boca Raton, FL, 1980 Search PubMed.
- P. Davis and P. Rabinowitz, Methods of Numerical Integration, Academic Press, New York, 1975 Search PubMed.
- T. F. Coleman and Y. Li, SIAM J. Optim., 1996, 6, 418–445 CrossRef.
- R. A. Waltz, J. L. Morales, J. Nocedal and D. Orban, Math. Program., 2006, 107, 391–408 CrossRef.
- P. R. Zarda, S. Chien and R. Skalak, J. Biomech., 1977, 10, 211–221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1: the spherical harmonics series expansion; S2: calculation of associated Legendre functions and derivatives; S3: calculation of surface properties from SHP description; S4: testing convergence of SHP calculations with Gaussian quadrature; S5: testing accuracy of SHP with Gaussian quadrature against analytical methods; S6: a note on the preferred curvature and area difference; S7: numerical implementation of the membrane skeleton energy; S8: numerical optimization under constraints using sequential quadratic programming; S9: examples of echinocyte type I shapes. See DOI: 10.1039/c0sm01193b |
| This journal is © The Royal Society of Chemistry 2011 |
