Self-ordered arrays of linear defects and virtual singularities in thin smectic-A films

Abstract

Large-area ordered arrays can be created by the self-assembly of linear defects in thin smectic-A films deposited in air on crystalline substrates. Such structures could find applications in nanoparticle assembly and soft lithography. The smectic layers are bent in concentric cylinders under the effect of conflicting strong anchoring conditions at the substrate surface and free interface, and neighboring cylindrical domains are separated by curvature walls. We have studied the internal structure of such domains near the surface of muscovite mica using synchrotron X-ray diffraction. Our findings show that the domains are centered on virtual singularities, running below the substrate plane, and rest upon a surface region of submicrometric thickness where layers are flat and vertical, satisfying the planar anchoring condition imposed by the substrate.

---

Introduction

Creating large-scale ordered structures from the self-assembly of small building blocks such as copolymers¹ and liquid crystals² is an exciting possibility for material science and nanotechnology. The “bottom-up” organization of organic materials is faster, less expensive and can produce more complex geometries than traditional “top-down” microfabrication methods such as lithography. Liquid crystal structures offer the additional benefit of responsiveness to external stimuli such as electromagnetic, mechanical and thermal fields, which can produce structural changes at various length scales (phase transitions, orientational transitions, pattern growth).³ In the past few years, thermotropic smectic-A (SmA) liquid crystals have been used to create self-ordered templates for soft lithography⁴ or direct the dispersion and assembly of colloids⁵ and nanoparticles.⁶ Rod-like SmA molecules form layers of nanometric thickness comparable to the molecule length, and align parallel to each other along a preferential direction (“director”) normal to the layers, determined by the boundary conditions (“anchoring”).³

Under the effect of incompatible but equally strong anchoring conditions, the layered structure becomes distorted. Layers are easily bent in the bulk but compression and dilation—requiring a high energy per unit volume—are confined to singular lines and walls (“defects”) of nanometric extent.⁷ Colloids and nanoparticles interact with defects⁵ and may become trapped at the intersection of defects and boundaries.⁸ It is therefore crucial to understand defect–surface interaction, especially in SmA liquid crystals where interfaces are expected to deeply affect the defect structure.^8–10

In free SmA films subject to degenerate planar anchoring at one surface (with layers orthogonal to the surface) competing with a homeotropic anchoring at the SmA/air interface (with layers parallel to the interface), characteristic toroidal focal conic domains appear and self-assemble into 2D hexagonal lattices.¹¹ Such structures are now well documented^10,12,13 and constitute the basis for proposed applications.^4,5 More recently, regular arrays of parallel linear domains have been obtained on crystalline surfaces that induce unidirectional planar anchoring, such as molybdenite^9,14,15 and mica.¹⁶

In thin films and droplets of SmA deposited in air on mica linear arrays are perpendicular to the direction x of planar anchoring and can cover surface areas as large as several mm² (Fig. 1(a)). Such self-ordered structure may be used in the same type of applications as hexagonal lattices, expanding the variety of available geometries and length scales.

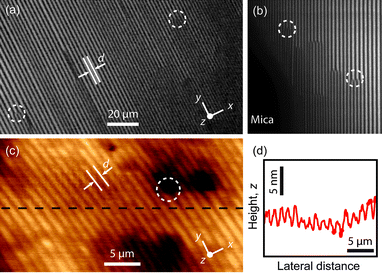Fig. 1 Arrays of parallel linear domains of SmA 8CB on mica. The domain axis, y, is perpendicular to the direction x of planar anchoring. d is the distance between neighboring disclinations. Circles mark regions where domains split or merge. (a) Optical micrograph of an array between crossed polarizers. (b) Detail of a drop edge. (c) AFM topographic image of the free interface. (d) Modulation of height z as a function of the distance along the dashed line of (c).

A possible structure of linear domains on crystalline mica, first proposed in ref. 14, is schematized in Fig. 2(a): SmA layers are wrapped in concentric cylinders around a singular line (center of curvature or “disclination”)³ tangent to the substrate and perpendicular to x. Both homeotropic anchoring at the free interface and planar anchoring along x at the mica substrate are satisfied. We call d the distance between neighbouring disclinations and h the thickness of a domain above the disclination, where molecules are normal to the substrate across the entire thickness. Since the surface tension of the free interface is high, γ ≈ 30 mJ m⁻²,¹⁷ disclinations are attracted to each other to reduce the interface area. As a result, curved layers are generally not hemi-cylinders, but truncated cylinders with h > d/2 (Fig. 2(a)). Curvature walls v are formed at the boundary between neighboring domains, where layers undergo rapid changes of thickness and orientation over a nanometric scale.⁷ Experimentally, d increases from 0.5 µm to 3.5 µm as h increases from ∼0.8 µm to ∼10 µm, whereas thicker films only show focal conic domains.¹⁶

Fig. 2 (a) Model array of cylindrical domains with disclination centres (blue dots) tangent to the substrate, separated by curvature walls v. SmA molecules (short green rods) are normal to the free interface and parallel to x on the substrate. h is the domain thickness and d the distance between neighboring disclinations. (b) Mirror symmetric domain of height h, size d and length l. The scattering vector q is perpendicular to the disclination, at an angle α from the substrate. q is normal to the free interface for ω < α < π − ω. The scattering intensity, I(α) ∝ f(α,ω)ld, is proportional to the distance f(α)d between the disclination and the domain boundaries. (c) Polar plot of the shape function f, with coordinates f_x = f·cos α and f_z = f·sin α. The plot describes vertical lines for α < ω and α > π − ω and an arc of circle for ω < α < π − ω.

In the present work, we have used synchrotron X-ray diffraction to investigate the internal structure of the linear domains.¹⁴ At the substrate interface, we show the existence of a region with thickness below optical resolution where layers deviate from the cylindrical shape and appear to be flat and vertical to the substrate. In this region, each curvature wall v splits up into couple of new curvature walls that separate the cylindrical layers from the vertical layers. Remarkably, this requires the cylinders to be bent around virtual singularities,¹⁸ located below the substrate.

Materials and methods

Linear arrays of SmA 8CB were created following the procedure described in detail in ref. 16. We deposited droplets of SmA 8CB of volume smaller than 0.1 µl on freshly cleaved surfaces of muscovite mica, which were clean and atomically smooth and exposed a single crystallographic plane over an area of several mm². The droplet wetted the substrate in the nematic phase, and was left spreading for more than 1 h. After cooling down to the SmA phase, the thickness of the droplet was smaller than 10 µm, as verified by the absence of focal conic domains.¹⁶ The actual thickness depended on the initial volume and the wetting time. In the following, we will denote as ‘thick’, ‘thin’ and ‘very thin’ films of thickness respectively above 5 µm, between 2 and 5 µm, and below 2 µm. The final shape of the droplet was generally non-circular with a maximum diameter varying from 2 to 5 mm depending on the initial volume and spreading time. We prepared two types of samples: single droplets and lines of 4–5 droplets of similar thickness deposited along the cylinder axis, y (Fig. 1 and 2). In the latter type of sample, droplets coalesced to form a strip along the y axis.

X-ray diffraction experiments were conducted on the D2AM beam line of the European Synchrotron Radiation Facility (ESRF, Grenoble, France), providing the high brilliance necessary to study droplets with small volume. The photon energy was set to 8 keV and the beam width to 0.2 mm. The scattering geometry, optimized to study linear arrays of 8CB, is described in detail in ref. 14. The scattering vector q was perpendicular to the y direction, at an angle α from the substrate (Fig. 2(b)). Its modulus q = (0.20 ± 0.05) Å⁻¹ satisfied the condition of Bragg reflection for 8CB with a layer thickness (period) of 3.1 nm. Due to the small value of q, the incident and scattered beams were almost grazing to the surface creating a footprint with dimensions ∼0.2 × 7 mm² elongated in the y direction, which was scanned on the sample along the x direction. The footprint length exceeded the diameter of a single droplet.

After corrections (background subtraction: geometrical corrections due to changing beam footprint and penetration depth leading to a step-like transmission factor),¹⁴ the Bragg intensity I was proportional to the number of layers perpendicular to q in the volume of the sample illuminated by the beam. The layer orientation was determined by continuously rotating q in the xz plane from parallel orientation (α = 0°, to probe layers vertical to the substrate) to normal orientation (α = 90°, horizontal layers). This was obtained by varying the angle of incidence with respect to the substrate from 0° to 1.4° and moving the detector, while keeping q constant. The scattered intensity was zero for α < 7° because the beam underwent internal reflection in the 8CB film and the beam penetration became negligible (the angle of incidence became lower than the critical angle of 0.17°). For angles α > 70°, the intensity I(α) rapidly increased due to the additional contribution of the Fresnel reflectivity of the substrate and flat horizontal SmA layers that appear over a time scale of a few hours in thin regions of the SmA film.¹⁹ In the following, we will only consider α ranging from 10° to 70°.

Topographic images of the free 8CB–air interface (Fig. 1(c) and (d)) were obtained with an Atomic Force Microscope (AFM, model Dimension from Veeco) operating in non-contact mode.^9,13,14 We used rectangular cantilevers (model Point Probe from Nanosensors) with a resonance frequency of about 300 kHz, laterally scanned over the surface at slow speed <30 µm s⁻¹ and vertically oscillated with an amplitude (few nm) close to the amplitude of free oscillation to avoid direct tip–sample contact.

Planar anchoring of 8CB on mica rapidly deteriorates towards homeotropic at high level of humidity.¹⁹ Therefore, spreading of the droplets, AFM and X-ray measurements were done in sealed enclosures containing silica gel or saturated with inert N₂ or He gas. All measurements were taken at room temperature in the SmA phase of 8CB.

Results

Polarized optical micrographs of linear arrays (Fig. 1(a) and (b)) showed parallel dark lines, where the director was normal to the surface across the entire film thickness, separated by bright regions where the director was tilted from the normal. According to the model presented in Fig. 2(a), dark lines correspond to regions above the disclinations and regions of maximum brightness to curvature walls. In topographic AFM images of the free interface (Fig. 1(c)), lines of maximum height z above the substrate are located above disclinations and lines of minima correspond to curvature walls v.

Both optical and AFM images showed that neighbouring disclinations did not change continuously their mutual distance d along the y direction, but they abruptly split or merged, forming respectively narrower or wider domains. d changed in small regions with dimensions ∼d, reminiscent of dislocations in a layered structure (circles in Fig. 1).³ Moreover, AFM images showed that the height h of the free interface above the disclinations did not change along y over distances much larger than d. Therefore, linear domains are invariant along y and relatively ‘rigid’: varying d and h along the y direction requires interrupting the domain, whereas variations along x can be obtained by assembling domains with different thicknesses (h and h′ in Fig. 2(a)). Variations of h along x produced the modulation of height Δz observed in AFM images, which was very shallow compared to the size d of the domains (Fig. 1(d)). The modulation is too small to be due to a convolution effect between the AFM tip and the interface,¹⁴ which implies that: (i) the modulation Δz of height for a single domain was Δz ≪ d, and (ii) the difference of thickness Δh between neighboring domains was Δh ≪ d. For simple geometrical reasons (see Fig. 2(a)) these conditions imply that domains have approximately the mirror symmetric shape described in Fig. 2(b): the thickness h is much larger than the distance d, in agreement with previous results,¹⁶ curvature walls v are almost vertical and located midway between disclinations, and most cylindrical layers end on the walls rather than on the substrate. The shape of such domain in an xz cross-section is uniquely determined by the aspect ratio h/d or, equivalently, by the angle ω defined in Fig. 2(b), such that q is normal to the free interface for ω < α < π − ω. Since h is larger than d, the angle ω = a cos(d/2h) is expected to be large, approaching π/2 in the limit of d/h → 0.

Calling l the domain length along the y direction, optical and AFM images showed that d decreased as the droplet thickness decreased going from the drop centre to the edge (Fig. 1(b)). The decrease along y was concentrated at the edges: the central part of the droplet contained domains with large l and d, sometimes extending almost from one edge of the droplet to the opposite, whereas both l and d rapidly decreased in a narrow peripheral region around the edge where rigid domains (with fixed d and h) frequently split into thinner and narrower domains. This shows that the droplet had a “pancake-like” thickness profile, i.e. constant over a large area surrounding the centre. Such profile is common for droplets of nematic liquid crystals that wet and spread on a solid surface under hybrid planar/homeotropic anchoring conditions.²⁰ In fact, optical micrographs of our droplets showed that the overall droplet shape did not change at the nematic–SmA transition.

Fig. 3(a) shows the scattering curves, I(α), obtained from for a single, approximately circular droplet with maximum diameter ∼5 mm at different locations x of the incident beam. Curves obtained in the range 0° < α < 90° were symmetric to those obtained for 90° < α < 180°, confirming that the domains had mirror symmetry around curvature walls v (Fig. 2(b)). We also measured the intensity I as a function of the angle ϕ between the diffraction plane and the domain axis, at several values of α and a fixed value of the magnitude q = 0.2 Å⁻¹.¹⁴ The I(ϕ) curves always showed a narrow peak centered at ϕ = 0, i.e., the intensity was maximum when the scattering vector q was perpendicular to the disclinations. This confirms that the normal of the curved SmA layers rotates in the xz plane orthogonal to the disclinations (Fig. 2(b)). In the following, measurements of I as a function of α were done at ϕ = 0.

Fig. 3 Intensity I diffracted by a single droplet as a function of the rotation angle α. Different symbols indicate different positions x of the beam on the sample (color symbols—droplet center x ≈ 0, white and black symbols—outer regions). Shaded areas with α < 10° correspond to total internal reflection of the beam in the droplet. (a) Scattering curves I(α). The inset shows the geometry of the droplet and footprint. (b) Normalized intensity S = I/I₀, with I₀ = ∫I(α)dα and α = 20–40°. Inset: I₀ as a function of x.

As the beam moved from the centre (defined as x ≈ 0) towards an edge of the droplet, I(α) varied because the scattering volume changed (Fig. 3(a), inset). However, all curves could be reduced to a single master curve S(α,x) = I(α,x)/I₀(x) in the interval α = 20–40°, when normalized by the integrated intensity I₀(x) = ∫I(α,x)dα in this interval (Fig. 3(b)). Such master curve can be understood using the model of Fig. 2. A linear domain with dimensions d and l and angle ω produces the scattered intensity I = klf(α,ω)d, where k is a constant and f(α,ω)d is the distance of the disclination from the domain boundaries (curvature walls and free interface) along the direction of the scattering vector q(α). The function f(α,ω) is a shape factor, identical for all domains with the same shape (i.e., same ω), and closely reproduces the shape of the domain boundaries when represented in polar coordinates f_x = f·cos α and f_z = f·cos α (Fig. 2(c)). The polar plot consists of an arc of circle for ω < α < π − ω, corresponding to the free interface, connected through inflection points to two vertical lines for α < ω and α > π − ω, corresponding to vertical curvature walls. In an assembly of domains, the total intensity I(α) ∝ ΣI_i = Σ_in_ia_if_i depends on the number n_i of domains with the same shape located in the footprint and on the area a_i = l_id_i of their bases on the substrate. When the angle α becomes smaller than the smallest ω_i of the array, f_i becomes independent from ω_i and I(α,x) ∝ A(x)f(α), where A(x) is the area of the droplet in the footprint. Since the integral I₀ of I calculated on any interval between α = 0 and α = min(ω_i) is also proportional to A(x), the normalized curve S = I/I₀ in this interval is independent from A(x) and x: S = f(α). Experimentally, the plot of I₀ as a function of x (Fig. 3(b), inset) shows a plateau near the droplet centre where the intersection of the beam footprint with the droplet (area A) is maximum.

The presence of a master curve for α < 40° confirms the isomorphism of the linear domains at small angles, but its shape shows that the model of Fig. 2 does not correctly predict the shape of the domain boundaries. At small angles, S(α) decreases more rapidly than expected as α decreases and experimental polar plots of S(α) are not vertical, but highly curved (Fig. 4). According to the model, the intensity at small angles is due to the end portions of cylinders, close to a vertical orientation, which end either on the mica surface or the vertical curvature wall v (Fig. 2(b)). Clearly, these portions of the cylinders are missing from the domain and a new domain structure must be considered near the substrate.

Fig. 4 Polar plots of the normalized intensity S(α) of Fig. 3, with coordinates S_x = S·cos α and S_z = S·sin α and the same meaning of the symbols. (a) Droplet centre (x ≈ 0). (b) Droplet edge. The solid line is an arc of circle.

On the other hand, the results obtained for large angles, 40° < α < 70°, can be explained without changing the domain structure near the free interface, by introducing a distribution of sizes d, h and l and angles ω for the domains falling in the footprint. The normalized intensity S(x,α) for large α depended on the position x of the beam. For a fixed α, S was almost constant with x near the droplet centre (−0.5 mm < x < 1 mm) (Fig. 4(a)), and decreased as the beam moved towards the edges (x < −0.5 and x > 1) (Fig. 4(b)) indicating that the main parameter influencing I(α) was the film thickness. As x moved towards the edge, S became increasingly similar to the arc of circle predicted for the range ω < α < π/2, with an inflection point near ω ≈ 50° (Fig. 4(b)). To explain this behaviour, one should consider that the thickness H(x) and diameter L(x) of the droplet in the footprint decreased as the beam moved towards the edges (Fig. 3(a), inset). For a given value of x, the thickness of the domains in the footprint was dispersed in the range h ∈ [0,H]. Since ωa priori depends on h,¹⁶ω was also more dispersed at the drop centre than at the edges. Therefore, the arc of circles observed near the edges was due to domains having ω ≈ 50° with little dispersion. Polar plots obtained at the centre were due to the combination of domains with a large dispersion of ω, so that the normalized intensity S was the combination of arcs of circle differing by radius and angles of aperture. At the drop centre, polar plots did not show any inflection point, which suggests that ω was dispersed in a wide range of interval extending up to 70°. S was almost independent from x at the centre of the droplet due to its pancake-like shape: here the maximum thickness H and thickness profile were almost uniform.

The influence of thin peripheral domains was reduced in experiments done on strips of droplets elongated along the y direction, which allowed the development of much longer flattened central domains with almost uniform value of h. For large α, polar plots of S resembled arcs of circle with a single value of ω (Fig. 5(a)). The value appeared to increase with h as predicted by earlier models:¹⁶ from ω ≈ 40° for thin regions to ω > 60° for thick regions. This increase of ω with h did not affect the polar plots of S at small α, which showed the same lack of intensity discussed above, due to missing portions of the cylindrical layers near the surface.

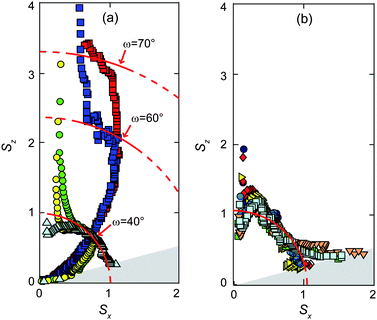Fig. 5 (a) Polar plot of the normalized intensity S obtained from strips of droplets aligned along y, at various positions x of the beam. Squares, circles and triangles denote respectively thick, thin and very thin strips. (b) Scattering from a single very thin droplet.

The behaviour at small α changed for very thin films of 8CB. In the curves obtained for very thin strips of droplets, the arc of circle appeared to continue into the region of internal reflection α < 10°, without any inflection point. We obtained the same results with a single droplet prepared on purpose to be very thin (small initial volume, long spreading time) (Fig. 5(b)). This indicates that ω decreased below 10° and the domain structure changed for very small thicknesses.

Discussion

The most interesting result in our measurements is that the scattered intensity I decreases more rapidly than expected when the angle α decreases. The deviation of I from the model curves (i.e., vertical lines in polar plots) is not limited to a particular range of angles, but continuously increases as α is decreased from the angle ω down to the minimum measurable value of α ≈ 10°. We first tried to explain the large deviation at small angles by replacing the end portions of the cylindrical layers, reaching the substrate with a vertical orientation and scattering at small angles, with a new sub-domain of ‘misaligned’ layers, located close to or intersecting the surface. We considered both curved (Fig. 6(a)) and flat (plane) layers (Fig. 6(b)) and we imposed the following conditions:

Fig. 6 Example of sub-domains containing (a) layers bent around a new disclination (central blue dot) and (b) flat horizontal layers. Domains of type (a) can be in contact with the substrate over an extended area if the disclination is tangent to the substrate. Domains of type (b) cannot touch the substrate without violating the planar anchoring condition. (c) Polar plot of the shape function f(α), normalized by the value f(0), for cases (a) (dotted line) and (b) (solid line). The angle ω has the same meaning as in Fig. 2(b).

(1) The domain shape and location comply with the overall mirror symmetry around vertical walls v observed in our experiments. This condition is satisfied for a symmetric domain ‘nested’ along v.

(2) Layers inside the domain have a uniform (undeformed) thickness, while layer dilation is confined in a new curvature wall w that constitutes the domain boundary (Fig. 6(a) and (b)).⁷

(3) There is an equal number of layers ending on w on both sides. This condition avoids dislocations and their high energy of deformation.

(4) Layers always end with a vertical orientation on the substrate to satisfy the planar anchoring condition.

(5) Flat layers are almost horizontal (Fig. 6(b)) or almost vertical (Fig. 7), and the angle between the layer normal and the substrate is respectively larger than 70° or smaller than 10°. Otherwise, flat layers would produce a strong peak of scattered intensity between 10° and 70°, which was never observed.

Fig. 7 Surface domains containing flat vertical layers, separated from the cylindrical layers by curvature walls w. The cylinders are bent around virtual disclinations (blue dots) located at a depth p below the surface. To avoid dislocations, the vertical layer at a lateral distance x from the disclination meets the cylindrical layer of radius R = p + x on w. Layers meet on curvature walls v and w with disorientation angles θ_v and θ_w, respectively.

In the presence of curved or flat horizontal layers, the calculated intensity was reduced in a limited interval of angles (Fig. 6(c)). The amplitude of the reduction and the interval of angles depended on the type, location and extension of subdomain considered, but the intensity remained unchanged in the limit of α → 0 (Fig. 6(c)). Since we could not reproduce the observed overall deviation, i.e. at all angles, of the scattered intensity from the model prediction, we considered a global modification of the array structure: we placed the center of curvature of the cylindrical layers on a virtual disclination, running at a depth p beneath the substrate and parallel to it (Fig. 7). A subdomain is now required at the substrate to prevent the cylindrical layers from reaching the substrate with a non-vertical orientation. Two hypotheses can be envisaged: either layers of the subdomain are flat and vertical (Fig. 7), or they are curved. In the latter case different region of a single layer may have different radii and centers of curvature, spanning a virtual focal surface.¹⁸ We have considered the first case, because it is much simpler to analyse and reproduces all the main features observed in the experimental scattering curves. We have also noticed that the inverse approach, i.e., starting from a subdomain of flat vertical layers at the surface while excluding dislocations (point (3) above) on the curvature wall w, necessarily leads to virtual disclinations or focal surfaces. To avoid dislocations, the shape of w must be such that the cylindrical layer with radius R = p + |x| centred on the virtual disclination must continue without interruption across w into the vertical layer that ends on the substrate at a lateral distance |x| from the disclination (Fig. 7). The number of layers on both sides of w is therefore |x|/a, where a is the thickness of a SmA layer. The height z of the w wall above the substrate is given by the intersection of the cylinder and vertical layer: z = (p² + 2p|x|)^½ − p with 0 < |x| < d/2. The maximum height is z* = z(p,d/2) ≤ d/2.

Fig. 8(a)–(d) shows the curvature walls w between the surface region with flat vertical layers and the cylindrical layers for different depths p of the disclination and thickness h of the linear domain. The overall shape of the linear domain is now specified by two aspect ratios, p/d and h/d. Domains with the same value of these parameters are isomorphic, and their scattering curves I(α) are proportional to the same shape function f(α, p/d, h/d) (Fig. 8(e)). In analogy with previous models, obtained for p = 0, the h/d ratio can be replaced by the angle ω such that the scattering vector q is normal to the free interface for ω < α < π − ω (Fig. 7). Notice that the polar plot of the shape function f(α,ω, p/d) is curved for all α and does not reproduce the vertical shape of the v wall for α < ω, whereas it still contains an arc of circle for ω < α < π − ω. Polar plots of I(α) derived from this model are in good agreement with the results obtained for thick and thin droplets and strips, with a constant value of p/d ≈ 0.02 and different values of h/d (Fig. 8(f)). The maximum height of the wall w above the substrate can thus be calculated: z*(p = 0.02d, x = d/2) ≈ 0.12d ≪ h. Since d ranges between 0.5 µm and 3.5 µm, the thickness of the surface region ranges between 60 nm and 400 nm which would hardly be revealed by polarizing or confocal optical microscopy. Nonetheless, the presence of such region has a profound effect on X-ray diffraction.

Fig. 8 (a)–(d) Shape of boundary wall w between flat vertical layers and the cylindrical layers for various depths p of the virtual disclination and thickness h of the domain. (e) Polar plots of the shape function f(α,ω, p/d) for the examples ((a)–(d)). (f) The normalized intensity S obtained for single droplets and strips agrees with model curves with fixed p/d = 0.02. Dotted, dashed and solid lines correspond respectively to h/d = 1.5, 2 and 10. For thick films, there is a dispersion of the h/d values (shaded area). A quarter of circle (dash-dotted line) is compared to the data obtained for very thin droplets and strips.

Experimentally, the shape function f(α, p/d,ω) at small angles α < 40° appears to be almost independent from the height h of the domains falling in the footprint, as demonstrated in Fig. 8(f). Therefore, linear domains with different h had the same value of the parameter p/d: their surface regions had the same shape. We call θ_v the angle of disorientation between cylindrical layers that meet on the curvature wall v (Fig. 7). This angle is small at the free interface (θ_v ≈ π − 2ω) and would reach a maximum value θ_v = π at the solid substrate if flat vertical layers were not present. Instead, θ_v reaches its maximum value at a height z* from the substrate, where the vertical wall v splits into the w wall. The independence from h of f(α, p/d, ω) at small angles (isomorphism of the surface region) indicates that the splitting occurs at a specific angle of disorientation θ_v = 2·atan(z*/d) ≈ 0.92π, rather than at a specific height z* (Fig. 7). It is well known²¹ that the energy per unit area of a curvature wall rapidly increases with θ_v. For this reason, curvature walls are unstable and are usually replaced by a set of focal conic domains. Such 2D curved textures appear to be incompatible with the strong unidirectional planar anchoring imposed by the crystalline substrate, and require a high energy to be nucleated in thin films.²² Instead, on mica the portion of the v wall with the highest energy (0.92 π < θ_v < π) is replaced by a couple of curvature walls w where cylindrical layers and flat vertical layers meet with smaller disorientation angles, θ_w < π/2 (Fig. 7). The energy per surface area on w is thereby greatly reduced. This should compensate the energy cost of replacing the small area lz* = 0.12 · ld of the removed portion of the v wall with the large area of the w walls, ∼l(z*² + d²)^½ ≈ ld. Moreover, replacing the disclination and the surrounding cylinders with flat layers removes both the core energy of the disclination and the surrounding region with the highest density of curvature energy (due to small cylinders).¹⁶

The presence of virtual disclinations in 8CB/mica samples is a manifestation of the complex interaction of SmA defects with solid substrates, still incompletely understood. On molybdenite, the interaction leads to formation of flattened hemi-cylinders and rotating grain boundaries, instead of virtual disclinations.^9,14 The difference with mica is likely due to differences in SmA/substrate interaction and nanoscale structure of the interface: 8CB molecules adsorbed on molybdenite are strongly anchored in a planar and highly ordered lattice,²³ whereas molecules adsorbed on mica show a distribution of orientations.¹⁹ The interaction between defects and substrate can take place through an evolution of the curvature elastic constant and compression modulus of the SmA close to the substrate, where the local order parameter may increase or decrease from the bulk value. On molybdenite, a thin nematic layer has been evidenced in 8CB close to a molybdenite substrate, which may modify the elastic constant K.¹⁵ In order to better understand the influence of anchoring strength, angular order and pretilt on the defect structure and interaction at the substrate, a study of non-crystalline, more disordered surfaces becomes particularly interesting. Preliminary optical observations show that linear arrays qualitatively similar to those obtained on mica and molybdenite can also be obtained on rubbed polymers. Therefore, the presence of a high degree of order at the substrate does not seem to be a necessary requirement for arrays to form.

Our results indicate that ω decreases as h decreases (Fig. 5), in agreement with previous calculations,¹⁶ while the S(α) curve at small angles remains the same (‘thick’ and ‘thin’ films in Fig. 8(f)) as expected for a fixed value of the parameter p/d (see curves ‘b’, ‘c’ and ‘h’ in Fig. 8(e)). However, as ω decreases, the maximum height (d/2)tan ω of the vertical wall v above the substrate also decreases, approaching the maximum height z* of the w wall. When ω = atan(2z*/d) ≈ 13.5°, the v wall disappears and the top portion of the w wall become exposed to air, violating the homeotropic anchoring (Fig. 8(c)). At this point, three scenarios are possible: (a) the ratio p/d (and therefore z*) decreases so that v does not disappear, (b) both w and v walls disappear (p/d = 0, ω = 0) leaving hemicylindrical domains centred on real disclinations, or (c) an anchoring transition occurs at the SmA/air or SmA/mica interface and the layers become flat and aligned along the direction of strongest anchoring.^9,16 Our measurements show that the S(α) curves dramatically change at small angles for very thin films (Fig. 8(f)), indicating that the ratio p/d changes and ω enters the region of internal reflection (α < 10°), possibly becoming zero. Although we were not able to distinguish between cases (a) and (b) due to the absence of data in this region, the curves show a distribution of layer orientation which allows us to exclude the case (c). Forthcoming scattering measurements in transmission at the ESRF, aimed at determining the intensity variations for α < 10°, should clarify this point.

Conclusions

Large-area ordered arrays of linear defects in SmA films deposited on crystalline surfaces are due to the combined effects of strong conflicting anchoring conditions and confinement to small film thicknesses. We anticipate this general result to be valid also for other types of substrates that induce a strong unidirectional planar anchoring, such as rubbed polymers on glass or silica coatings obtained by oblique evaporation, which may be used to create even larger and more periodic arrays suitable for applications in nanoparticle assembly and soft lithography. Linear domains on mica contain curvature walls and virtual singularities—seldom observed in thermotropic SmA liquid crystals—and depend on the specific interaction of the SmA with the substrate. This interaction can have subtle effects, as demonstrated by the different defect arrangement of 8CB near the substrate of mica and molybdenite, in a thin surface region which could hardly be revealed by optical means. Therefore, synchrotron X-ray diffraction is an important tool for the nanoscale study of defect–surface interaction.

References

1. R. A. Segalman, Science, 2008, 321, 919.
2. I. Musevic, M. Skarabot, U. Tkalec, M. Ravnik and S. Zumer, Science, 2006, 313, 954.
3. P. G. De Gennes and J. Prost, The Physics of Liquid Crystals, Oxford, 1974.
4. Y. H. Kim, D. K. Yoon, H. S. Jeong, J. H. Kim, E. K. Yoon and H. T. Jung, Adv. Funct. Mater., 2009, 19, 3008; Y. H. Kim, D. K. Yoon, H. S. Jeong and H. T. Jung, Soft Matter, 2010, 6, 1426.
5. D. K. Yoon, M. C. Choi, Y. H. Kim, M. W. Kim, O. D. Lavrentovich and H. T. Jung, Nat. Mater., 2007, 6, 866.
6. R. Pratibha, W. Park and I. I. Smalyukh, J. Appl. Phys., 2010, 107, 063511.
7. M. Kléman, Points, Lines and Walls in Liquid Crystals, Magnetic Systems and Various Ordered Systems, Wiley, New York, 1983.
8. M. Mitov, C. Portet, C. Bourgerette, E. Snoeck and M. Verelst, Nat. Mater., 2002, 1, 229.
9. J. P. Michel, E. Lacaze and M. Goldmann, Phys. Rev. Lett., 2006, 96, 027803.
10. W. Guo and C. Bahr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011707.
11. J. B. Fournier, I. Dozov and G. Durand, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2252; C. Blanc and M. Kleman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 6739; L. Z. Ruan, J. R. Sambles and I. W. Stewart, Phys. Rev. Lett., 2003, 91, 033901.
12. M. C. Choi, T. Pfohl, Z. Y. Wen, Y. L. Li, M. W. Kim, J. N. Israelachvili and C. R. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17340; W. Guo, S. Herminghaus and C. Bahr, Langmuir, 2008, 24, 8174; W. Guo and C. Bahr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 061701.
13. V. Designolle, S. Herminghaus, T. Pfohl and C. Bahr, Langmuir, 2006, 22, 363.
14. J.-P. Michel, E. Lacaze, M. Alba, M. de Boissieu, M. Gailhanou and M. Goldmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 011709.
15. E. Lacaze, J. P. Michel, M. Alba and M. Goldmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041702.
16. B. Zappone and E. Lacaze, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061704.
17. H. Schuring, C. Thieme and R. Stannarius, Liq. Cryst., 2001, 28, 241.
18. J. B. Fournier, Phys. Rev. Lett., 1993, 70, 1445.
19. B. Jerome and Y. R. Shen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 4556.
20. P. G. DeGennes, Rev. Mod. Phys., 1985, 57, 827.
21. C. E. Williams and M. Kléman, J. Phys. Colloq., 1975, 3, 315.
22. C. Blanc and M. Kleman, The European Physical Journal E, 2001, 4, 241.
23. E. Lacaze, M. Alba, M. Goldmann, J. P. Michel and F. Rieutord, Eur. Phys. J. B, 2004, 39, 261.

---