Interaction anisotropy and shear instability of aspirin polymorphs established by nanoindentation

Abstract

Nanoindentation is applied to the two polymorphs of aspirin to examine and differentiate their interaction anisotropy and shear instability. Aspirin provides an excellent test system for the technique because: (i) polymorphs I and II exhibit structural similarity in two dimensions, thereby facilitating clear examination of the differences in mechanical response in relation to well-defined differences between the two crystal structures; (ii) single crystals of the metastable polymorph II have only recently become accessible; (iii) shear instability has been proposed for II. Different elastic moduli and hardness values determined for the two polymorphs are correlated with their crystal structures, and the interpretation is supported by measured thermal expansion coefficients. The stress-induced transformation of the metastable polymorph II to the stable polymorph I can be brought about rapidly by mechanical milling, and proceeds via a slip mechanism. This work establishes that nanoindentation provides “signature” responses for the two aspirin polymorphs, despite their very similar crystal structures. It also demonstrates the value of the technique to quantify stability relationships and phase transformations in molecular crystals, enabling a deeper understanding of polymorphism in the context of crystal engineering.

---

Introduction

Polymorphism in molecular crystals is an intensively studied phenomenon.¹ Its practical importance arises from the fact that different crystal structures of the same compound can exhibit significantly different materials properties. This has particular implications, for example, in the pharmaceutical industry, where polymorphism must be rigorously monitored at all stages of the production process, because of chemical, regulatory and legal issues.^2,3 Current research in polymorphism spans a broad range of disciplines, including for example crystal structure analysis and prediction,⁴crystallisation monitoring and control,⁵ and structure-property correlation.⁶ Despite this extensive activity, however, quantitative understanding of the mechanical properties of polymorphic molecular crystals remains rare. This knowledge gap has an obvious impact in applications where polymorphs might be subjected to mechanical stress. For example, stress-induced phase transformations are highly undesirable for pharmaceutical ingredients during milling or tabletting.⁷ A quantitative description of mechanical properties also has relevance in computer modelling of molecular crystals, since tensorial properties such as elastic stiffness or thermal expansion provide a basis against which to evaluate and optimise atomistic models in terms of derivatives of calculated energy, rather than single-point calculations.

Nanoindentation is established as an effective method to assess the mechanical response of solids with high precision, and on extremely small volumes.⁸ A limited number of studies have been made on organic crystals,^9–18 including our own report on saccharin,¹⁹ and there have been other attempts to link measured values of elastic modulus and hardness to molecular and crystal structures.^20–23 However, very little has been done with polymorphs of molecular crystals—indeed, we are aware of only one other published report where nanoindentation has been explicitly applied to a polymorphic molecular system.²⁴ Thus, there exists a clear opportunity for advancement in this area, since polymorphic systems should provide an ideal basis to establish correlations between crystal structure and mechanical response. In this work, we apply nanoindentation to the two polymorphs of aspirin (acetylsalicylic acid). Aspirin provides an excellent test case for several reasons: (i) the two polymorphs (I and II) exhibit structural similarity in two dimensions, thereby facilitating clear examination of the differences in mechanical response in relation to well-defined differences between the two crystal structures; (ii) single crystals of aspirin form II have become accessible only recently; (iii) the mechanical properties of form II are thought to be implicated in its apparent metastability. In this paper, we use the comparative data established by nanoindentation to suggest a rational explanation for the observed phase stability and transformation between the two crystal forms. Our study establishes that nanoindentation can provide “signature” responses for the two aspirin polymorphs, despite their very similar crystal structures, and it demonstrates also the value of the technique for application to chemical problems associated with polymorphism in the context of crystal engineering.

Aspirin polymorphism

Aside from its obvious chemical and pharmaceutical importance,^25,26aspirin exhibits a fascinating and perplexing structural chemistry. The possible occurrence of aspirin polymorphs has been debated since the 1960s.²⁷ Recently, Ouvrard and Price²⁸ predicted a new crystal form, referred to as form II, with the long-known crystal form²⁹ labelled accordingly as form I. Independently, Munson and co-workers reported differences in solid-state NMR spectra measured for freeze-dried aspirin,³⁰ while Vishweshwar et al.³¹ reported single-crystal X-ray diffraction data that claimed³² to show the existence of form II. Some of us went on to show that aspirin crystals can exist as intergrowths containing domains of the two structure types,³³ and a detailed crystallographic investigation based on diffuse X-ray scattering has been made subsequently by Chan et al.³⁴

A brief summary of the structural situation is as follows: aspirin molecules are linked into centrosymmetric dimers by O–H⋯O hydrogen bonds between their carboxyl groups, and these dimers are arranged into 2-dimensional layers parallel to the (100) planes that are essentially identical in the two polymorphs. The distinction between forms I and II is the manner in which the layers are arranged relative to each other. The form I structure is related to that of form II by a relative shift of adjacent layers parallel to one of the crystallographic axes (specifically ½c in Fig. 1). Previous computational estimates of the lattice energies at various levels of theory have all concluded that the energetic difference between the two polymorphs is insignificantly small.^28,35,36

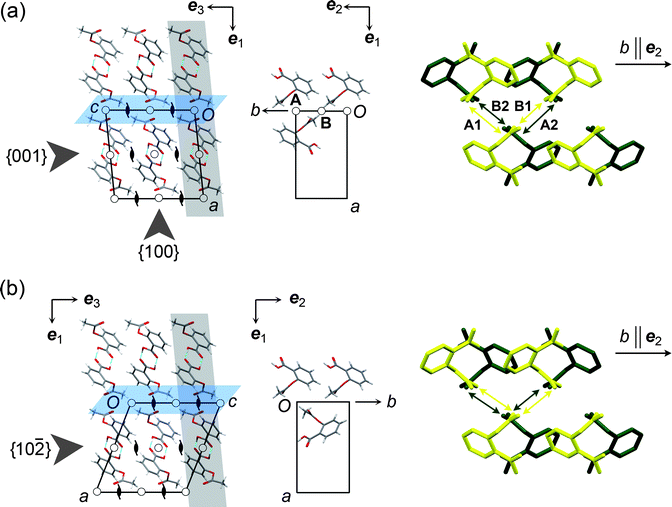Fig. 1 Crystal structures of the aspirin polymorphs: (a) form I, (b) form II. In the two figures, the grey slabs highlight planes parallel to {001} or {102̄}. The slip planes are coloured blue. The projection drawings in the centre show molecules within a single grey slab that are involved in significant stabilising interactions across the slip plane. In form I, these interactions (A and B) are across inversion centres. The figures to the right are projections down the c axis (ee₃3 in the Cartesian reference system), showing compression and elongation of the interactions during relative motion along b in the direction of the arrow. Yellow and green molecules lie in adjacent planes parallel to {001} or {102̄} (i.e. in adjacent grey slabs in the left-hand figure). H atoms are omitted. In I, movement of the upper molecules compresses interaction A1 and elongates interaction B1 in the front plane (yellow). For the rear plane (green), movement in the same direction elongates A2 and compresses B2. In form II, however, all interactions shown by the arrows are equivalent and 2₁-related, so movement in either direction along eee₂22 causes equivalent compression and elongation of interactions in the front and rear planes.

With regard to the crystallisation of aspirin, some of us have reported that form II domains can be systematically introduced into aspirin crystals by solution crystallization in the presence of aspirin anhydride.³⁷ By extension, single crystals were obtained that appear to be structurally pure aspirin form II—that is, without form I domains or any apparent disordered regions—within the detection limits of laboratory CCD X-ray instruments. The isolated single crystals were found to be stable under ambient conditions for months, as well as under the application of hydrostatic pressure up to 2.2 GPa.³⁷ Nonetheless, it is apparent that form II is metastable with respect to form I, since we have observed transformation of form II bulk powders under ambient conditions during our studies of the compound.‡ It has been suggested that instability of form II may arise because of a low shear modulus.²⁸ This has been questioned by Bauer et al. on the basis of experimentally measured elastic constants for form I and predicted constants for form II,³⁵ which showed no reason to suspect shear instability. Recourse to predictions for form II was a requirement in the absence of samples for experimental study, and the question regarding shear instability therefore remains open.

Results and discussion

Expectations from the crystal structures

Calculated attachment energies, E_att, (Table S2 in ESI†) confirm the expectation that the {100} planes, which are the most widely separated and have the lowest E_att, should be slip planes for both polymorphs. The potential slip systems are therefore either {100}<010> or {100}<001>, meaning slip parallel to the {100} plane along either the b or c crystallographic axes. The latter is clearly implicated in the transformation between the two forms. Our analysis of pairwise intermolecular interaction energies³⁸ (Tables S3–S9 in ESI†) shows two distinct significantly stabilizing interactions between molecules in neighbouring layers across {100} in form I, denoted A and B in Fig. 1a. Both interactions are formed around crystallographic inversion centres. Interaction A, calculated to be the more stabilising of the two, involves C–H⋯O contacts between the aromatic ring and the acetyl carbonyl group, while interaction B involves C–H⋯O contacts between the methyl group and another acetyl carbonyl. By contrast, the significant stabilizing interactions between layers across {100} in form II are all of the same type, involving C–H⋯O contacts between the acetyl substituents of molecules related by a crystallographic 2₁ screw axis (Fig. 1b). Thus, although the structures of the two polymorphs are closely related, a clear difference exists in the intermolecular interactions across the expected slip planes, specifically in the positions of the symmetry elements relative to molecules involved in significantly stabilising interactions.

Nanoindentation

Nanoindentation analyses were carried out on the structurally equivalent {001} face of I and {102̄} face of II. These faces correspond to indentation approximately parallel to the crystallographic direction of the interlayer shift relating forms I and II (<001>, Fig. 1). To provide an indication of the mechanical anisotropy for I, which could be compared to the values obtained from previous studies on form I single crystals,^39,40 indentation was also performed on the {100} face. Representative load, P, versus displacement, h, curves and the indent impressions on each crystal face are shown in Fig. 2 and 3. Full experimental details are provided in the ESI†. The maximum load applied in our experiments was 6 mN, with accompanying indentation depths of ∼1 μm. Indentation on {100} of II was complicated by the fact that the face exhibited only a very small size on the crystals that we could obtain, thereby making it difficult to hold rigidly while indenting. Indentation left only featureless dents (see ESI†), and we could not derive modulus or hardness values that we consider to be sufficiently reliable for discussion.

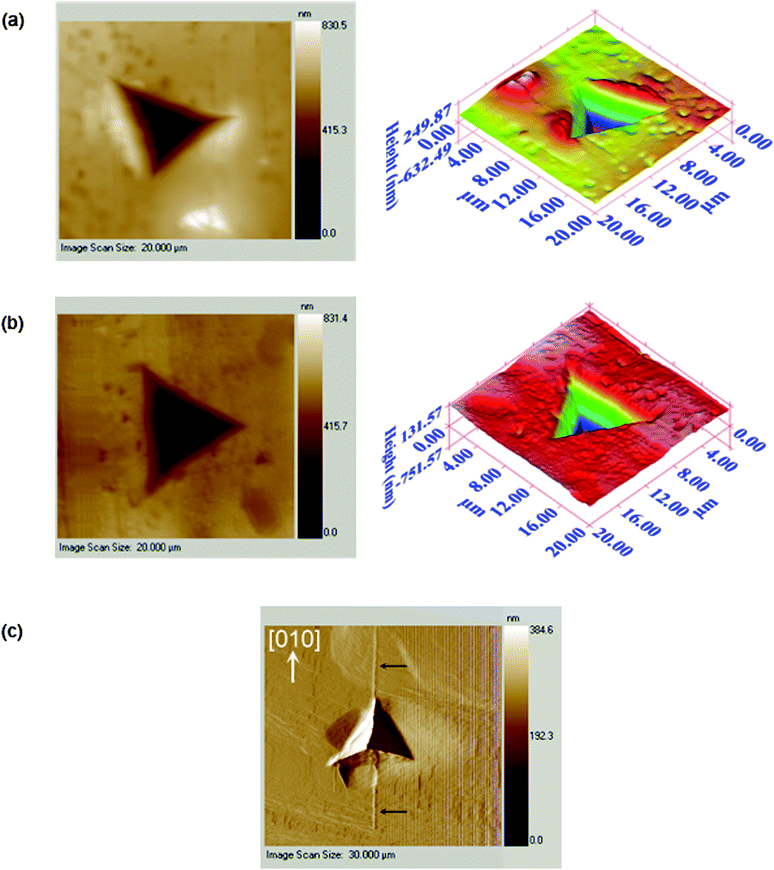Fig. 2 Images of the nanoindentation indents: (a) {001} of I; (b) {102̄} of II; (c) {100} of I showing cracking along <010> at higher loads.

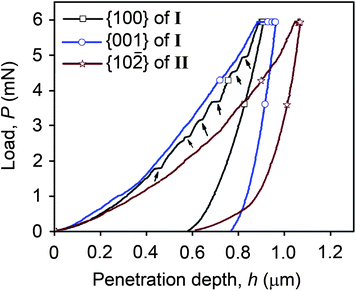Fig. 3 Representative P–h curves for all three faces examined, with pop-ins indicated by arrows for the loading curve of {100} of I.

All of the P–h curves (Fig. 3) show large residual depths upon unloading, which is a manifestation of significant plastic deformation undergone by the crystals during indentation. The loading parts of the P–h curves obtained for both {001} of I and {102̄} of II are smooth, while distinct displacement bursts are evident for {100} of I. These displacement bursts, which indicate heterogeneous deformation, occur consistently at penetration depths of 0.434, 0.564, 0.680 and 0.770 ± 0.02 μm, with the magnitude of the pop-in length being either 23 ± 4 nm at lower loads, or 35 ± 4 nm at higher loads. The latter implies that the pop-ins are related to the underlying crystal packing since they are integral multiples of d₁₀₀ (11.373 Å). Similar correlation of pop-in lengths with d_hkl was observed for saccharin.¹⁹ For I, the indent impression on {100} shows significant “pile-up”, which arises from incompressible plastic deformation of material from beneath the indenter to the top surface along the edges of the indenter. Cracking is also observed specifically along <010> at higher loads. Fracture or significant pile-up is not observed for either {001} of I or {102̄} of II. The maximum penetration depth, h_max, for {102̄} of II is higher than {001} of I, indicating a softer nature for form II compared to I. The average values of hardness (H) and elastic modulus (E) for the examined faces are shown in Table 1. Most notably, the mechanical properties of the two polymorphs are found to be significantly different for indentation along the potential shearing direction: {001} of I is stiffer and harder than {102̄} of II, with a difference of 48% for the elastic moduli and 37% for the hardness indices.

Table 1 Determined values of hardness (H) and elastic modulus (E) for the three crystal faces examined^a

	H (GPa)	E (GPa)
a See ESI† for details of the determination of these values.
{100} of I	0.257 ± 0.007	5.97 ± 0.291
{001} of I	0.240 ± 0.008	9.57 ± 0.201
{102̄} of II	0.152 ± 0.004	4.96 ± 0.226

---

Recently, Haware et al. have examined elastic properties of single crystals of aspirin form I in directions normal to the (100), (010) and (001) planes using powder X-ray diffraction and an in situ compression stage.³⁹ Measurement of changes in d-spacing gave values of 1.3(3), 1.6(6) and 4.6(8) GPa, respectively, for the elastic modulus along each direction. The trend in these values was in line with an accompanying computational estimation. Our observation for I that {001} has a greater modulus than {100} is consistent with these assessments. In another recent study, Olusanmi et al. have reported nanoindentation analyses on aspirin form I,⁴⁰ which gave average elastic modulus values of 5.02 ± 0.57 GPa and 2.95 ± 0.13 GPa for indentation on the {100} and {001} faces, respectively. These measurements refer to indentation depths of ∼6 μm at a maximum load of 100 mN. The trend in these values is neither consistent with the results of Haware et al. nor our results. This could be due to several factors, most notable being the following two: (i) Olusanmi et al. have used as-received particles whereas we have used carefully grown single crystals. Images given by them suggest that the particles they have used may have experienced considerable surface damage (Fig. 1b and 12 of their paper⁴⁰) and also that they may contain significant porosity (Figs. 11 and 13); (ii) the indentation loads applied by them are considerably higher that the loads that we have applied, which led to cracking along <010> during indentation on the {100} face. We have also observed cracking on {100} of I at higher loads (Fig. 2c), but not under the conditions from which our modulus values are derived. As is well known, cracking makes a material considerably compliant and hence tests for modulus measurements should be performed in a such a way that cracking does not occur during loading. Certainly, we note that the P–h curve reported by Olusanmi et al. for indentation on the {100} face of I (Fig. 9 in ref. 40) appears highly atypical compared to others reported in the literature.

Correlation of mechanical response with crystal structure

During indentation, molecules either stretch (elastic deformation) or slide relative to each other (plastic deformation). The difference in the measured elastic moduli for I and II demonstrates significant variation in the interaction characteristics under the indenter. We consider the expected relative motion of the molecules along different directions on the basis of the intermolecular interactions in order to suggest some structural basis for the deformation processes involved. For convenience, we refer to a Cartesian axis system, ee_iii, having eee₂22 parallel to the crystal b axis <010>, ee₃3 parallel to the crystal c axis <001> and ee₁1 perpendicular to both (Fig. 1). Axes eee₂22 and ee₃3 lie parallel to the planes of the hydrogen-bonded dimer layers, while ee₁1 is parallel to the layer stacking direction.

Since the hydrogen-bonded dimer layers within I and II are identical, the interactions between molecules within these layers should have closely comparable characteristics in the two forms. The differences described for the crystal structures exist in the regions between the layers, and mechanical differences should therefore be expected when molecules in neighbouring layers move relative to each other. Considering adjacent layers moving relative to each other along eee₂22: it is evident from Fig. 1a that one of the two distinct stabilising interlayer interactions (say A1) formed by a given molecule in I is compressed while the other (B1) is elongated. For molecules in the next plane parallel to {001}, the situation is reversed; motion in the same direction along eee₂22 serves to elongate interaction A2 and compress interaction B2. Since the interaction types (A and B) and associated potential energy profiles are different, a given molecule must favour one of the two possible circumstances, and there exists some hindrance in I for relative motion of adjacent hydrogen-bonded layers parallel to eee₂22. In a typical nanoindentation experiment, several thousands of such molecular layers are involved. Thus, even if the hindrance between a pair of adjacent layers is small, the cumulative effect has a significant influence on the elastic modulus. The same hindrance does not exist for II because the two significantly stabilising interlayer interactions made by a given molecule are symmetrically equivalent (Fig. 1b), and the same compression and elongation of the interlayer interactions is therefore experienced by all molecules for relative motion in either direction along eee₂22. For interlayer stretching parallel to ee₃3 there is also little distinction between the two structures so that no great difference should be expected for relative interlayer motion in this direction.

The expectation of hindrance to the relative molecular motion along eee₂22 in I is corroborated by measurements of the thermal expansion, derived from lattice constants of form I and II single crystals at temperatures in the range 100–298 K (Fig. 4 and Supplementary Tables S10–S13†). The anisotropy of the thermal expansion is much more pronounced for I than for II, and the thermal expansion parallel to eee₂22 for I is about half that of any other direction in the two polymorphs.

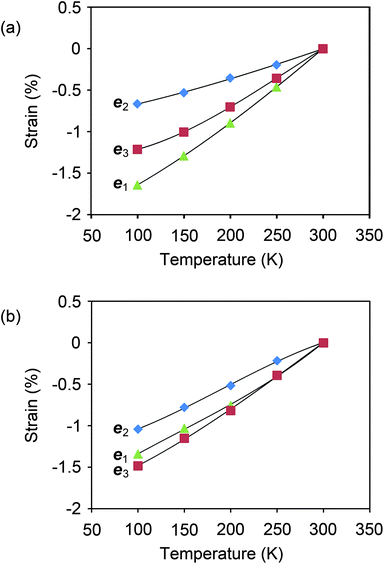Fig. 4 Thermal expansion measured for single crystals of aspirin I and II. The expansion is referred to the Cartesian reference system ee₃3 ‖ c, eee₂22 ‖ b, ee₁1 ‖ eee₂22 × ee₃3, and the lines drawn between data points provide a guide to the eye. (a) The expansion in I is highly anisotropic, with expansion along eee₂22 approximately half as large as any other direction in either polymorph. This result is in agreement with an assessment made previously by Bauer et al.³⁵ (b) The expansion in II is considerably less anisotropic.

For indentation on the {001} face of I or the {102̄} face of II, the established elastic moduli probe a combination of the elastic deformation characteristics along the principal indentation direction parallel to ee₃3 and inclined to it by virtue of the pyramidal indenter shape. The latter directions can be decomposed into a component along ee₃3 plus some component along ee₁1 and/or eee₂22. On the basis of the preceding analysis, the two polymorphs would be expected to show minimal difference for elastic deformation along ee₃3 and for any component along ee₁1, but any component of the elastic deformation along eee₂22 should be significantly more restricted for I. This is consistent with the measured elastic moduli for indentation on the {001}/{102̄} faces, since II is observed to have a smaller modulus than I. Thus, the elastic moduli and thermal expansion coefficients of the two polymorphs reflect inherent differences between the nature and symmetries of the intermolecular interactions in the two structures along the {100} planes; it is the component of the elastic deformation along eee₂22 that accounts principally for the significantly different values. Both the elastic modulus and the coefficient of thermal expansion are directly dependent on the intermolecular interactions and are inversely related to each other. Hence, the observation that thermal expansion parallel to eee₂22 for I is about 50% lower than that of any other direction is consistent with the elastic modulus of {001} of I being nearly twice that of either {102̄} of II or {100} of I.

Plastic deformation and polymorph transformation

The observed differences in hardness for the faces examined indicate an orientation and structure dependence for the micromechanisms of plasticity. In molecular crystals (as in inorganic crystals), plastic deformation occurs via slip, which is aided by movement of dislocations under the influence of applied stress.⁴¹ Generally, higher mobility of dislocations within the crystal leads to more facile plastic deformation. Typically, slip occurs on planes that are most widely spaced, with the smallest E_att (so that the frictional resistance for slip is the least) and in directions that are closest packed (so that the slip vector is the smallest). Roberts et al., on the basis of a simple model that relates hardness to cohesive energies of organic solids, have previously suggested {100}<001> as a probable slip system in aspirin form I.²² The smooth nature of the P–h curves obtained for nanoindentation on {001} of I and {102̄} of II are consistent with facile and smooth slip along the system {100}<001>, while the distinct pop-ins observed on {100} of I occur because the applied stress (compressive in nature) is normal to the slip planes. Consequently, the resolved shear stress on the slip planes is zero, necessitating alternative slip mechanisms. Upon the build up of sufficient stress, slip occurs intermittently in multiples of d₁₀₀.

Crucially, the larger magnitude of plastic deformation, and hence lower hardness, measured for {102̄} of II compared to {001} of I suggests that slip in II occurs more readily. The chemical implications are that the transformation from form II to form I takes place through slip along the system {100}<001>. We have observed that the transformation can occur under stress-free and ambient conditions, which implies that the activation energy barrier for the II → I transformation is small, although it proceeds over a relatively long time scale—commonly, we observe periods of several months for complete transformation to occur in crystalline powders.‡ Our nanoindentation results, however, imply that the transformation should be rapid when shear stress is applied. To verify this hypothesis, crystalline powders of form II were subjected to mechanical grinding. Powder X-ray diffraction (See Supplementary Fig. S2†) establishes that the diagnostic peaks (19.9 and 25.5° 2θ for Cu-Kα radiation) for form II are absent after grinding, thereby demonstrating that II → I transformation does indeed take place quickly under the influence of shear stress.

In their study of form I, Olusanmi et al. also propose {100} as the slip planes, but suggest that the likely direction of slip is along <010>, since this has the shortest lattice translation (b ≈ 6.5 Å).⁴⁰ However, it is crucial in the case of aspirin to realise that slip along <001> provides a shorter translation (½c ≈ 5.75 Å). Although this is not a lattice translation for form I, it is an energetically viable translation that transforms form I to form II. Thus, it is more reasonable that {100}<001> should be the most probable slip system.

Regarding the composition of aspirin crystals

The intergrown aspirin crystals that we described previously³³ could be viewed as snapshots along the pathway of the II → I transformation process. In this current study, we have observed single crystals of II that contain domains with a nanoindentation signature corresponding to I. This is despite the fact that single-crystal X-ray diffraction (using laboratory CCD instruments) suggests the crystals to be structurally pure form II. This provides a good illustration of the limits of diffraction methods for characterising smaller domains within crystals and illustrates a further valuable feature of nanoindentation as a local probe to test for crystal homogeneity. In the pharmaceutical industry, crystallographic techniques (both powder and single-crystal) are the tools usually used to establish phase purity and thereby claim intellectual property rights for new polymorphs. The presence of form I and II domains beyond the recognition of crystallographic tools, coupled with the view of a continuous slip-mediated pathway between forms I and II, revives the question of principle that we raised previously⁴² regarding the identity of the individual aspirin forms.

Conclusions

Nanoindentation provides valuable information on the mechanical properties of polymorphic molecular crystals, with implications for the understanding of stability relationships and phase transformations in the molecular solid state. The technique removes the principal practical barrier associated with conventional techniques for probing mechanical response, namely the requirement to grow exceptionally large single crystals. The polymorphs of aspirin have a close structural relationship, but nanoindentation establishes that the metastable form II of aspirin is considerably softer than the stable form I. Shear slip along {100}<001> provides a mechanistic rationale for the observed solid-state II → I transformation. This transformation takes place over months under ambient conditions but can be accelerated by mechanical grinding. In general terms, our work shows that nanoindentation has significant potential for the study and understanding of polymorphism in the context of crystal engineering.

Acknowledgements

S.V. thanks the Department of Science and Technology for a Young Scientist fellowship. M.S.R.N.K. thanks University Grants Commission for a D. S. Kothari postdoctoral research fellowship. K.A.S. and A.D.B. acknowledge funding from the Danish Council for Independent Research | Natural Sciences. G.R.D thanks the Department of Science and Technology for the award of a J. C. Bose fellowship.

Notes and references

1. J. Bernstein, Polymorphism in Molecular Crystals, 2002, Oxford University Press, New York.
2. H. G. Brittain, Polymorphism in Pharmaceutical Solids, 2009, Informa Healthcare, New York.
3. R. Hilfiker, Polymorphism in the Pharmaceutical Industry, 2006, Wiley, Weinheim.
4. K. Sanderson, Nature, 2007, 450, 771.
5. C. E. Hughes, S. Hamad, K. D. M. Harris, C. R. A. Catlow and P. C. Griffiths, Faraday Discuss., 2007, 136, 71.
6. C. Malla Reddy, K. A. Padmanabhan and G. R. Desiraju, Cryst. Growth Des., 2006, 6, 2720.
7. G. G. Z. Zhang, D. Law, A. A. Schmitt and Y. Qiu, Adv. Drug Delivery Rev., 2004, 56, 371.
8. A. Gouldstone, N. Chollacoop, M. Dao, J. Li, A. M. Mino and Y.-L. Shen, Acta Mater., 2007, 55, 4015.
9. P. J. Halfpenny, K. J. Roberts and J. N. Sherwood, J. Mater. Sci., 1984, 19, 1629.
10. D.-H. C. Wendy and G. C. Weatherly, J. Mater. Sci. Lett., 1989, 8, 1350.
11. W. C. Duncan-Hewitt, D. L. Mount and A. Yu, Pharm. Res., 1994, 11, 616.
12. S. Finnie, K. V. R. Prasad, D. B. Sheen and J. N. Sherwood, Pharm. Res., 2001, 18, 674–681.
13. X. Liao and T. S. Wiedmann, J. Pharm. Sci., 2005, 94, 79.
14. X. Liao and T. S. Wiedmann, J. Pharm. Sci., 2004, 93, 2250.
15. L. J. Taylor, D. G. Apadopoulos, P. J. Dunn, A. C. Bentham, J. C. Mitchell and M. J. Snowden, Powder Technol., 2004, 143, 179.
16. K. J. Ramos and D. F. Bahr, J. Mater. Res., 2007, 22, 2037.
17. K. J. Ramos, D. E. Hooks and D. F. Bahr, Philos. Mag., 2009, 89, 2381.
18. S. Chattoraj, L. Shi and C. C. Sun, CrystEngComm, 2010, 12, 2466.
19. M. S. R. N. Kiran, S. Varughese, C. Malla Reddy, U. Ramamurty and G. R. Desiraju, Cryst. Growth Des., 2010, 10, 4650.
20. R. J. Roberts and R. C. Rowe, Int. J. Pharm., 1989, 52, 213.
21. R. J. Roberts, R. C. Rowe and P. York, Powder Technol., 1991, 65, 139.
22. R. J. Roberts, R. C. Rowe and P. York, J. Mater. Sci., 1994, 29, 2289.
23. R. J. Roberts, R. C. Rowe and P. York, Int. J. Pharm., 1995, 125, 157.
24. K. M. Picker-Freyer, X. Liao, G. Zhang and T. S. Wiedmann, J. Pharm. Sci., 2007, 96, 2111.
25. K. C. Nicolaou, and T. Montagnon, Molecules That Changed The World, 2008, Wiley, Weinheim.
26. K. Schrör, Acetylsalicylic Acid, 2009, Wiley, Weinheim.
27. R. Tawashi, Science, 1968, 160, 76.
28. C. Ouvrard and S. L. Price, Cryst. Growth Des., 2004, 4, 1119.
29. P. J. Wheatley, J. Chem. Soc., 1964, 6036–6048.
30. D. Sperger, B. Chen, T. Offerdahl, S. Hong, L. Schieber, J. Lubach, D. Barich and E. Munson, AAPS Journal, 2005, 7(S2), 1991.
31. P. Vishweshwar, J. A. McMahon, M. Oliveira, M. L. Peterson and M. J. Zaworotko, J. Am. Chem. Soc., 2005, 127, 16802.
32. A. D. Bond, R. Boese and G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 615.
33. A. D. Bond, R. Boese and G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 618.
34. E. J. Chan, T. R. Welberry, A. P. Heerdegen and D. J. Goosens, Acta Crystallogr., Sect. B: Struct. Sci., 2010, B66, 696.
35. J. D. Bauer, E. Haussühl, B. Winkler and D. Arbeck, Cryst. Growth Des., 2010, 10, 3132.
36. T. Li, J. Pharm. Sci., 2007, 96, 755.
37. A. D. Bond, K. A. Solanko, S. Parsons, S. Redder and R. Boese, CrystEngComm, 2011, 13, 399.
38. A. Gavezzotti, J. Phys. Chem. B, 2002, 106, 4145; A. Gavezzotti, J. Phys. Chem. B, 2003, 107, 2344.
39. R. V. Haware, P. Kim, L. Ruffino, B. Nimi, C. Fadrowsky, M. Doyle, S. X. M. Boerrigter, A. Cuitino and K. Morris, Int. J. Pharm., 2011 DOI:10.1016/j.ijpharm.2011.06.021 , in press.
40. D. Olusanmi, K. J. Roberts, M. Ghadiri and Y. Ding, Int. J. Pharm., 2011, 411, 49.
41. J. N. Sherwood, The Plastically Crystalline State (Orientationally Disordered Crystals), 1979, Wiley, Chichester.
42. A. D. Bond, R. Boese and G. R. Desiraju, Am. Pharm. Rev., May/June 2007.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details, including crystallisation protocols and a full description of the nanoindentation studies; tables of calculated attachment energies and intermolecular interaction energies; residual indent impressions for {100} of II. Crystallographic data for form II at 123 and 298 K have been deposited with the Cambridge Crystallographic Data Centre. CCDC reference numbers 820697 and 820698. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1sc00430a

‡ We have observed this transformation using powder X-ray diffraction for numerous bulk samples stored under ambient conditions in our laboratories. The diagnostic peaks for form II diminish with time and are typically absent after a period of months.

---