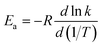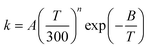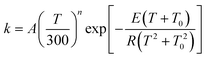DOI:
10.1039/C1SC00225B
(Edge Article)
Chem. Sci., 2011,
2, 2199-2213
Multi-structural variational transition state theory. Kinetics of the 1,4-hydrogen shift isomerization of the pentyl radical with torsional anharmonicity†
Received
7th April 2011
, Accepted 25th June 2011
First published on 10th August 2011
Abstract
We present a new formulation of variational transition state theory (VTST) called multi-structural VTST (MS-VTST) and the use of this to calculate the rate constant for the 1,4-hydrogen shift isomerization reaction of 1-pentyl radical and that for the reverse reaction. MS-VTST uses a multi-faceted dividing surface and provides a convenient way to include the contributions of many structures (typically conformers) of the reactant and the transition state in rate constant calculations. In this particular application, we also account for the torsional anharmonicity. We used the multi-configuration Shepard interpolation method to efficiently generate a semi-global portion of the potential energy surface from a small number of high-level electronic structure calculations using the M06 density functional in order to compute the energies and Hessians of Shepard points along a reaction path. The M06-2X density functional was used to calculate the multi-structural anharmonicity effect, including all of the structures of the reactant, product and transition state. To predict the thermal rate constant, VTST calculations were performed to obtain the canonical variational rate constant over the temperature range 200–2000 K. A transmission coefficient is calculated by the multidimensional small-curvature tunneling (SCT) approximation. The final MS-CVT/SCT thermal rate constant was determined by combining a reaction rate calculation in the single-structural harmonic oscillator approximation (including tunneling) with the multi-structural anharmonicity torsional factor. The calculated forward rate constant agrees very well with experimentally-based evaluations of the high-pressure limit for the temperature range 300–1300 K, although it is a factor of 2.5–3.0 lower than the single-structural harmonic oscillator approximation over this temperature range. We anticipate that MS-VTST will be generally useful for calculating the reaction rates of complex molecules with multiple torsions.
Introduction
Computational modeling methods for the kinetics of complex reactions by direct-dynamics algorithms that include tunneling can be expensive when applied with reliable electronic structure methods because of the need to obtain Hessian information, at least along a large portion of the minimum-energy reaction path (MEP). Furthermore, when kinetics modeling is based on the harmonic-oscillator approximation, errors can accumulate from the anharmonic internal rotational motions (i.e., torsions) in complex molecules, especially at high temperature. In the present article, we present and illustrate a new formulation of variational transition state theory (VTST) with multidimensional tunneling that is especially designed for treating complex molecules with many conformers generated by torsions, as is often needed for combustion modeling.
Combustion reactions of hydrocarbon fuels play a significant role as energy sources. However, the mechanisms of most combustion reactions have not been fully elucidated. This hampers the rational design of hydrocarbon fuels and pollution and energy efficiency issues are not optimally decided. The situation has now been complicated by the use of biofuel additives. Therefore, understanding the kinetics of hydrocarbon combustion reactions is becoming more and more important. At the same time, computational chemistry is advancing to the stage where it has quantitative predictive capability for the reaction rates of complex species. This predictive capability is also important for other research areas involving gas-phase reactions of complex organic molecules, e.g., atmospheric chemistry. The goal of the work reported here is to develop and apply a more accurate method of calculating the rates of such reactions, in particular, reactions with potential energy barriers and multiple conformations of reactants, transition states, or both.
The 1,4-hydrogen shift isomerization reaction of 1-pentyl radical is a prototype for an important class of reaction in the combustion of hydrocarbons. Alkyl isomerization reactions have been investigated both experimentally1–3 and computationally.4 The first direct measurement of the 1,4-hydrogen shift isomerization of 1-pentyl was reported in 2002 by Miyoshi et al.2 Hydrogen shift reactions are expected to be dominated by tunneling contributions at 500 K and below. The evaluation of such contributions requires more global information about the potential energy surface than is required to evaluate the over-barrier contributions. Torsions can lead to multiple structures for the transition state. In the case at hand, the reactant 1-pentyl, the product 2-pentyl and the saddle point all display multi-structural character due to internal rotation in the reactants and products and pseudorotation in the transition state. The harmonic oscillator approximation, using only one structure to represent the transition state or reactants, is inaccurate for rate-constant calculations. Therefore, a multi-structural approach is required.
In the present work, we propose an efficient method, based either on conventional transition state theory (TST)5 or—by using the reaction path and reaction-path potential6 on VTST,5,7 to compute the thermal rate constants of molecules with multi-structural anharmonicity and multidimensional tunneling and we apply it to the 1,4-hydrogen shift reaction of 1-pentyl radical. In order to include tunneling for this hydrogen shift reaction, instead of applying expensive straight direct dynamics calculations8,9 to obtain the reaction path and reaction-path potential, we used the multi-configuration Shepard interpolation (MCSI) method10,11 to efficiently generate the potential energy surface from a small number of high-level electronic structure calculations. The M06 density functional12 is used to optimize the geometry and compute the energies, gradients and Hessians of stationary Shepard points (reactant well, product well and saddle point), as well as non-stationary Shepard points along the reaction path. The Shepard-interpolated potential surface is used to compute the transmission coefficient by utilizing the multidimensional small-curvature tunneling (SCT) approximation.13,14
A key aspect of the present calculations is that we analyze all of the different conformers (hereafter called structures) of the critical configurations (1-pentyl, 2-pentyl and the saddle point) that are generated by internal rotation or pseudorotation. For this purpose, the M06-2X density functional12 was used to obtain all of the structures. Then, the conformational–vibrational–rotational partition function was calculated by the multi-structural all-structures15 (MS-AS) and multi-structural reference-structure15 (MS-RS) methods. The thermal rate constant over the temperature range 200–2000 K was evaluated by the POLYRATE program16 employing a new formulation of VTST, called multi-structural variational transition state theory.
We do not consider pressure effects18 in the present article; without considering pressure effects, transition state theory predicts the equilibrium limit of reaction rates, which is sometimes called the high-pressure limit for unimolecular reactions.
Theory
1. Rate constant
VTST has been widely applied to barrier reactions in the gas phase,7,17 barrierless reactions in the gas phase19–21 and reactions at gas-solid interfaces,22 in solids,23 in liquid solutions24,25 and in enzymes,26,27 and the most appropriate formalism is different for each case.28,29 In the present article, we recognize a distinction between two kinds of gas-phase barrier reactions, which we may loosely categorize as small-molecule reactions and complex-molecule reactions. In the small-molecule case, both the reactants and transition states have only one conformation or they have more than one conformer, but only one is low enough in energy to merit consideration or the others can be accounted for by a separable torsional anharmonicity approximation. An example with only one conformation for both the reactant and transition state would be Cl·+ CH4 → H· + CH3Cl. The previous formulation7,14,17,30–33 of VTST for gas-phase reactions with a barrier is applicable to this kind of case and we label this formulation of VTST as single-structural VTST. An example of a complex reaction would be the case considered in this paper, namely the isomerization of 1-pentyl radical to 2-pentyl radical. Here, the reactant has 15 distinguishable conformations and the transition state has four. We label these conformations as “structures” and, here, we propose a multi-structural formulation of VTST theory that includes them. Firstly, we need to review single-structural VTST.
1.1. Single-structural VTST.
In single-structural VTST, as is usually applied, the quasi-classical thermal rate constant of canonical variational theory (CVT: the formulation of VTST in which a best compromise transition state is found for each temperature) is7,14,17,30–33| | 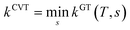 | (1) |
where s is the progress variable parameter for a sequence of trial transition states and kGT is the generalized transition state rate constant at temperature T for a transition state at s. In practice, we usually take s as the signed distance along the minimum energy path (MEP), which is the path6 of steepest descent in isoinertial coordinates from the saddle point down toward the reactants joined at s = 0 to the path of steepest descent down toward the products. By quasi-classical, we mean that the bound vibrations are quantized, but the motion along the reaction coordinate is classical. To include quantum effects on reaction coordinate motion (e.g., tunneling), we multiply by a transmission coefficient:where /T or /…T in a superscript denotes the inclusion of tunneling and κ is the transmission coefficient.
The transmission coefficient that we usually use is called a ground-state (G) transmission coefficient17,32 and it is taken as the ratio of the quantum mechanical thermally averaged flux through the ground-state level34,35 of the transition state dividing surface divided by the same quantity computed with the classical reaction coordinate motion. The quantity averaged in the divisor is equal to a Heaviside step function at the threshold energy implied by CVT. This threshold energy is the value of the vibrationally adiabatic ground-state potential energy curve6,32VGa at the temperature-dependent CVT transition state, where
where
VMEP denotes the minimum potential energy of the transition state dividing surface at
s relative to that of the reactants and
εG denotes the local zero-point vibrational energy of the modes transverse to the reaction coordinate at
s. Note that potential energy is also called the Born–Oppenheimer energy, classical energy and zero-point-exclusive energy.
The other factor, kCVT, in eqn (2) is computed from eqn (1), where the generalized transition state theory rate constant of eqn (1) may be written as
| | 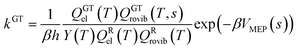 | (4) |
where
β is (
kBT)
−1,
kB is Boltzmann's constant,
h is Planck's constant,
Q is a partition function,
GT denotes a generalized transition state at location
s along the reaction coordinate, R denotes reactant, “el” denotes electronic, “rovib” denotes rotational-vibrational, and
| | 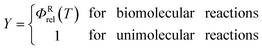 | (5) |
where
ΦRrel is the relative transitional partition function of two reactants (note that
ΦRrel may be written as
QRrel/
V, where
V is the volume). Note that
QGTrovib is missing a degree of freedom, in particular, the reaction coordinate, which is the degree of freedom normal to the transition state dividing surface. In
eqn (4), the zero of energy for the reactant partition functions is the minimum potential energy of reactants (which we set to equal to zero by convention), not the reactant zero-point level; and the zero of energy of
QGTel and
QGTrovib is at
VMEP, not at a zero-point level. All of the symmetry numbers for the overall rotation are included in the rotational partition functions.
36 The symmetry numbers for the internal rotation are included in
QRrovib. Full details of
eqns (1)–(5) are given elsewhere
14,32,33 and general background may be found in introductory treatments.
38
Note that, when using eqn (4), there are two approximations that can be employed to evaluate QGTrovib and QRrovib. If neither the generalized TS nor the reactant include any torsional motion, QGTrovib and QRrovib are taken as a product of a rotational partition function and a vibrational one that can be calculated using the harmonic approximation. This will be called the SS-HO approximation, where SS denotes single-structural. If the generalized TS or the reactant includes any torsional mode, the corresponding partition functions should be calculated by using the single-structural torsional method proposed previously37 or the one introduced below, called SS-T. The details of calculations using the SS-HO and SS-T approximations are presented below.
The theory reviewed above has usually just been labeled as VTST, although it will be labeled SS-VTST when we are specifically distinguishing it from the multi-structural generalization, which is presented next.
1.2. Multi-structural VTST.
Note that eqn (1) corresponds to minimizing the generalized free energy of activation.7 For a multi-structural case, we want a generalization where all quantities are computed along a single reaction path. However, in the limit of conventional transition state theory, we want the hypersurface (through which the transition state reactive flux is calculated) to pass through all of the conformations of the transition state, being normal to each of the imaginary normal modes at each of the saddle points. This requires a new formulation of generalized transition state theory that effectively has a multi-faceted dividing surface. We present a practical formulation of the new generalization here.
We label the distinguishable saddle point structures as c = 1, 2, …, C (where C is the number of saddle point structures). Similarly we label the distinguishable structures of the reactants and products by j = 1, 2, …, J (where J is the total number of reactant structures) and l = 1, 2, …, L (where L is the total number of product structures), respectively. Correspondingly, UjR and UlP denote the potential energies of structures j and l with respect to the lowest potential energy structure of the reactants, which is always numbered as j = 1; thus U1R is zero by definition. Also, we use the convention that the l = 1 structure is the lowest potential energy structure of the products.
We choose the reaction path to be the MEP through the saddle point with lowest value of VGa that connects the reactants to products and we label this structure with c = c*. For a unimolecular reaction with a simple barrier and a single product, this MEP terminates at a reactant structure for negative s and at a product structure for positive s; we label these structures with j = j* and l = l*. (For a bimolecular reaction, the MEP for negative s would terminate at a well in the entrance valley of the potential energy surface.) The potential energy relative to structure j = 1 as the reactant moves along the MEP that passes through structure c of the saddle point is called V. Then, we replace eqn (1) and 4 by
| | 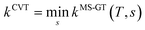 | (6) |
where
| | 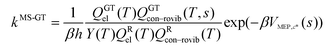 | (7) |
where
QXcon–rovib, with X =
GT or R, denotes a conformational–rotational–vibrational partition function (as in section 1.1, it is missing a degree of freedom when X =
GT);
QRel and
QRcon-rovib have their zero of energy at the lowest potential energy of the
j = 1 structure of the reactant and
QGTeland
QGTcon-rovib have their zero of energy at the
s-dependent
V. By writing
eqn (7), we assume that reaction barriers are much larger than the internal rotational barriers of the reactant, so that all the conformational structures of the reactant are in local equilibrium with each other during the reaction. If this is not true, one needs to use a multiwell
18 formalism.
For the reactants, we have
| | 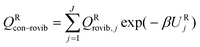 | (8) |
For the generalized transition state, we approximate QGTcon–rovib as the s-dependent rotational–vibrational partition function of the structure c = c* (computed just as QGTrovib for eqn (4)) times the ratio of the multi-structural result to the single-structural result at the saddle point, which is denoted ‡. This yields
| | | QGTcon–rovib = QGTrovib,c*(T,s)F‡MS(T) | (9) |
where
| | 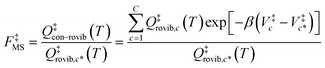 | (10) |
where
V‡c denotes the potential energy of saddle point structure
c with respect to the potential energy of the lowest energy structure,
j = 1, of the reactant and
Q‡rovib,c has its zero of energy at
V‡c. Note that
V‡c* is not necessarily the lowest energy saddle point energy.
For computational purposes, we rewrite the generalized transition state theory rate constant of eqn (6) as
| | | kMS-CVT = FMS(T)kSS-CVT1,c*(T) | (11) |
where
| | 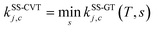 | (12) |
where
kSS-GTj,c and
kSS-CVTj,c are the single-structural generalized transition state rate constant and the single-structural
CVT rate constant, respectively, computed using the
MEP through structure
c of the saddle point and using structure
j for the reactants. Note that
eqn (11) corresponds to
j = 1 and
c =
c*. Comparing
eqn (11) and
(12) to
eqns (6)–(10) yields
| | 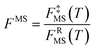 | (13) |
where
| | 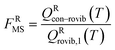 | (14) |
2. Transmission coefficient
Eqn (2) is used for the transmission coefficient for either the single-structural case of eqn (1) or the multi-structural case of eqn (6). In either case, one uses the MEP through the saddle point with the lowest VGa that connects the reactants to produces, and κCVT/T is the ratio of a thermally averaged approximate quantal transmission probability divided by a thermally averaged quasi-classical one.14,32,33 Although it is not done here, one could extend the theory to average variational effects and tunneling probabilities over more than one reaction path.
3. Vibrational anharmonicity
When using eqns (8), (9), (10), (13) and (14), QGTcon–rovib, Q‡con–rovib, and QRcon–rovib can be calculated by using the recently proposed internal-coordinate multi-structural approximation15 in either its full version, called the multi-structural-all-structures (MS-AS) approximation, or its more practical version, called the multi-structural reference-structure (MS-RS) approximation. When employing MS-AS calculations, we denote such partition functions as QMS-AS, Rcon–rovib and QMS-AS, ‡con–rovib. Similarly, we denote the reactant and transition state partition functions as QMS-RS, Rcon–rovib and QMS-RS, ‡con–rovib when using the MS-RS method. Then eqns (10), (11), (13) and (14) can be rewritten as| | 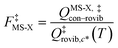 | (15) |
| | 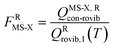 | (16) |
| | 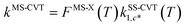 | (17) |
| | 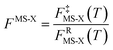 | (18) |
where X could be either AS or RS.
In addition, in the present article, we consider two versions each of the MS-AS and MS-RS approximations. The first versions are the MS-AS-HO and MS-RS-HO, which treat the included structures harmonically. This includes multi-structural anharmonicity (which is the difference between the MS-AS-HO or MS-RS-HO result and the single-structural HO result) but not the torsional, bend or stretch anharmonicity. The second versions are called MS-AS-T and MS-RS-T, where T denotes torsional anharmonicity, and these are reviewed below.
We note that the MS-AS-T and MS-RS-T methods explicitly only include the multi-structural and torsional anharmonicity. However, other forms of anharmonicity can be implicitly included by using scale factors for vibrational frequencies or, for example, using the Morse approximation for stretches31 and the quadratic-quartic38,39 approximation for bends. In the present article, we make the former choice, i. e., scaling.
Calculation methods
1. Electronic structure calculations
The M06-2X density functional with the 6-311+G(2df,2p) basis set40 was applied to optimize the geometry and obtain the frequency for all of the conformers of the reactant 1-pentyl radical, the product 2-pentyl radical and the transition state. These structures are generated by internal rotation around C–C bonds or by pseudorotation of the ring. The 6-311+G(2df,2p) basis set for H and C is also called MG3S and we will use this shortened name for brevity.
For the global minimum conformers of 1-pentyl, 2-pentyl and the transition state, the M06, M06-2X, and M08-SO41 density functionals were used to optimize the geometries of the reactants, products and transition states to obtain the reaction energies and barrier heights. In addition, two multi-level methods, BMC-CCSD42 and MCG3-TS,43 and the ab initio CCSD(T)-F12b44,45 method were used to calculate single-point energies at the M06-2X and M08-SO stationary points.
In addition to the already mentioned MG3S basis set, several other basis sets were also utilized for the electronic structure calculations, including 6-31+G(d,p),46 maug-cc-pVTZ,47 aug-cc-pVTZ,48 jul-cc-pVTZ,49 and def2-TZVP.50 The M06 and M06-2X density functional calculations were performed by using the Gaussian 09 program,51 and the M08-SO density functional calculations were carried out via Gaussian 03 locally modified by MN-GFM-4.1.52 CCSD(T)-F12a calculations were performed using Molpro53 and the BMC-CCSD and MCG3-TS calculations were carried out using MLGAUSS.54 The integration grid employed for the density functional calculations of frequencies had 99 radial shells and 974 angular points per shell. The frequencies used for the partition function and FMS-X calculations were obtained by using M06-2X/MG3S density functional calculations and multiplying the directly calculated values by an empirical frequency scaling factor55 of 0.970.
2. The conformational–vibrational–rotational partition function calculations
The most structurally complete conformational–vibrational–rotational partition functions were calculated by the MS-AS method15 mentioned above. In the MS-AS-HO and MS-AS-T versions of this method we have| | 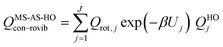 | (19) |
and| | 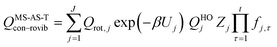 | (20) |
where Qrot,j is the classical rotational partition function of structure j, QHOj is the usual normal-mode harmonic oscillator vibrational partition function calculated at structure j, Zj is a factor designed to ensure that the partition function reaches the correct high-T limit (within the parameters of the model) and fj,τ is an internal coordinate torsional anharmonicity function that, in conjunction with Zj, adjusts the harmonic partition function of structure j for the presence of the torsional motion τ. As mentioned above, the frequencies used for QHOj, Zj, and fj,τ calculations were scaled by an empirical frequency scaling factor.55 We use the label MS-AS-HO to denote the partition function calculated without Zj and fj,τ, that is, with all Zj and all fj,τ equal to unity. When using either the MS-AS-HO or the MS-AS-T versions of the MS-AS method, it is not necessary to assign each torsional motion to a specific normal mode. The MS-AS-T approximation reduces to the MS-AS-HO approximation in the low-temperature limit and it approaches the free-rotor result for torsions in the high-temperature limit. The Zj and fj,τ factors are designed to interpolate the partition function (between these limits) in the intermediate temperature range. In principle, more accurate interpolations could be carried out15 if one calculated the barrier heights for torsional motions that interconvert the reactant structures with one another and the transition state structures with one another, but an advantage of the method employed here is that we forego this expensive step in the present application.
In the notation of ref. 15, when applying the MS-AS-T method, we assume that some of the torsions are strongly coupled, as specified further in the Results and Discussion section. We use eqns (19) and (20) to obtain the conformational–vibrational–rotational partition functions for the reactant, transition state and product, labeled as QMS-AS-X, Rcon–rovib, QMS-AS-X, ‡con–rovib, and QMS-AS-X, Pcon–rovib, respectively, where X is either HO or T.
Note that if one includes only a single conformer in eqns (19) and (20), that is, if J equals one, the corresponding equations reduce to
| | | QSS-HOrovib = Qrot,1QHOvib | (21) |
and
| | 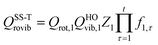 | (22) |
which can be used to calculate the SS-HO and SS-T partition functions for the SS-VTST calculations.
We also calculated the conformational–vibrational–rotational partition functions by the MS-RS-HO and MS-RS-T methods.15 These methods only include the structures that can be obtained by a one-at-a-time torsion from a reference structure. This restriction yields15
| | 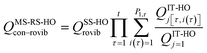 | (23) |
| | 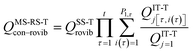 | (24) |
where
| | 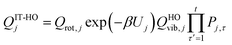 | (25) |
| | 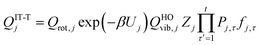 | (26) |
where we use
j = 1 as the reference structure. The
Pj,τ factor in
eqns (25) and
(26) denotes the number of distinguishable minima along torsion
τ in structure
j.
3. Transmission coefficient calculation using the MCSI algorithm
The transmission coefficient κ(T) that incorporates the tunneling for the hydrogen shift reaction was evaluated using the small-curvature tunneling approximation13 (SCT). The MEP and ground-state vibrationally adiabatic potential curve (VGa) were obtained by the MCSI method10,11,56–60 using the MCSI61 and MC-TINKERATE62 programs. Although the reactant, product and transition state all have a multi-structural character, we only need one structure of each to do MCSI calculations. We always use the transition state structure c* with the lowest VGa as the saddle point to determine the VMEP and VGa curves in the MCSI calculations. We choose the two structures, j* and l*, that are connected to the transition state c* as the reactant and product wells, respectively, in the MCSI interpolation of the potential energy surface and they were determined by following the paths of steepest descent.
To build the potential energy surface by the MCSI method, nine electronic structure Shepard points were used. All of the information about Shepard points, namely energies, gradients and Hessians, was obtained by M06/6-31+G(d,p) calculations. The first Shepard point was placed at saddle point c*, as optimized by M06/6-31+G(d,p). The six non-stationary Shepard points were placed close to the minimum energy reaction path (MEP) using a similar strategy to that in a previous paper47 and they were at the following locations: 6.91, 12.21, and 17.30 kcal mol−1 below the saddle point on the 1-pentyl radical side and 6.26, 14.03, 19.96 kcal mol−1 below the saddle point on the 2-pentyl radical side. The final two Shepard points are the reactant well and product well structures, j* and l*, mentioned at the end of the previous paragraph.
The MCSI method involves interpolating the off-diagonal element of a diabatic potential matrix,56,63 where the diagonal elements are given by molecular mechanics. We use the MM3 method64–66 for the molecular mechanics. It was found that using a Morse potential for the C–H bond in the MM3 force field for the Shepard interpolation provided smoother VGacurves than using quadratic stretch potentials and so we used Morse stretches in all of the MM3 calculations. The parameters are: bond energy: 98 kcal mol−1,67 bond length: 1.12 angstrom64–66 and force constant: 4.74 N cm−1.64–66
As discussed in the previous work,58,60 we used three different internal coordinate sets for the MCSI calculations: set q for molecular mechanics calculations, set r for Shepard interpolation and set s to calculate the Shepard weighting function. In the present work, the set q is the standard set of MM3 internal coordinates, the set r consists of 42 non-redundant internal coordinates (15 bond distances, 20 bond angles and 7 dihedral angles), and the set s consists of three intra-atomic distances shown in Fig. 1.
 |
| | Fig. 1 Three intra-atomic distances r1, r2 and r3 used to calculate the weight function (set s) for Shepard interpolation. | |
4. Thermal rate constant calculation
All of the rate constant calculations were carried out using the MC-TINKERATE62 and POLYRATE16,68 programs. All of the multi-structural anharmonicity calculations were carried out using the MSTor program.69
First, the single-structural CVT17 forward rate constant using harmonic approximation was calculated by eqn (12). Here, the transition state and reactant wells are c = c* and j = j* = 1, which are the same structures used in the MCSI calculations, since j* = 1 in the present work. We labeled the single-structural CVT forward rate constant as kSS-CVT.
In the next step, we calculated F‡MS-X and FRMS-X (X = AS-T or RS-T) using eqns (15) and (16). The final thermal rate constant was determined by eqn (27)
| | | kMS-CVT/SCT = κSCT(T)FMS-X(T)kSS-CVT(T) | (27) |
where the transmission coefficient
κSCT was calculated as discussed above and
FMS-X is defined in
eqn (18).
Because we used the SCT approximation13,14,68 for the ground-state transmission coefficient, the MS-CVT/T rate constant may be labeled kMS-CVT/SCT.
The thermal reverse rate constant was calculated by using the partition function of the product instead of that of the reactant. The ratio of the forward to reverse rate constant gives the equilibrium constant.
Results and discussion
1. Structures, energies and conformational–vibrational–rotational partition functions of the reactant, product and saddle point
Table 1 lists the zero-point-exclusive barrier heights and energies of reaction for the 1,4-hydrogen shift isomerization reaction of 1-pentyl radical, as calculated by various theoretical methods. The results obtained by the CCSD(T)-F12b/jul-cc-pVTZ//M06-2X/MG3S (our best estimate), BMC-CCSD//M06-2X/MG3S and MCG3-TS//M06-2X/MG3S methods agree very well with each other. However, the M06-2X and M08-SO density functionals, with the 6-31+G(d,p), MG3S, maug-cc-pVTZ, aug-cc-pVTZ and def2-TZVP basis sets, predict larger barrier heights. It was found that the M06 functional with the 6-31+G(d,p) basis gives results that are reasonably close to the CCSD(T)-F12b/jul-cc-pVTZ//M06-2X/MG3S calculation. Therefore, we chose M06/6-31+G(d,p) for the single-structural components of the kinetics calculation, that is, to calculate kSS-CVTand κSCT. However, we expect M06-2X/MG3S to be more accurate for conformational energy differences, so we calculated FMS-X based on M06-2X/MG3S results.
Table 1 Calculated forward and reverse zero-point-exclusive barrier heights and the energies of reaction for the 1,4-hydrogen shift isomerization of 1-pentyl radical as calculated by various methods (in kcal mol−1)
| Method |
V
f
‡
|
V
r
‡
|
ΔE |
| CCSD(T)-F12b/jul-cc-pVTZ//M06-2X/MG3S |
24.65 |
27.32 |
−2.67 |
| BMC-CCSD//M06-2X/MG3S |
24.60 |
27.11 |
−2.51 |
| MCG3-TS//M06-2X/MG3S |
24.12 |
26.91 |
−2.79 |
| M06-2X/6-31+G(d,p) |
25.27 |
28.27 |
−3.00 |
| M06-2X/MG3S |
25.83 |
28.97 |
−3.14 |
| M06-2X/aug-cc-pVTZ |
25.94 |
28.99 |
−3.05 |
| M06-2X/maug-cc-pVTZ |
25.93 |
28.98 |
−3.05 |
| M06-2X/def2-TZVP |
25.83 |
28.91 |
−3.08 |
| M08-SO/MG3S |
25.99 |
29.34 |
−3.35 |
| M08-SO/aug-cc-pVTZ |
25.87 |
29.42 |
−3.41 |
| M08-SO/maug-cc-pVTZ |
25.94 |
29.30 |
−3.36 |
| M08-SO/def2-TZVP |
26.04 |
29.45 |
−3.40 |
| M06/6-31+G(d,p) |
24.61 |
28.42 |
−3.81 |
| M06/MG3S |
25.18 |
28.73 |
−3.55 |
Based on M06-2X calculations, 1-pentyl radical, 2-pentyl radical and the transition state have fifteen, twelve and four distinguishable structures, respectively (Fig. 2). The five carbon atoms in the molecule (1-pentyl and 2-pentyl) are numbered as: H2C(1)–H2C(2)–H2C(3)–H2C(4)–H3C(5) and H3C(1)–H2C(2)–H2C(3)–HC(4)–H3C(5). In the 1-pentyl and 2-pentyl radicals, there exist four torsions, which are around the C(1)–C(2), C(2)–C(3), C(3)–C(4) and C(4)–C(5) bonds. Table 2 and Fig. 2 show the naming convention that is used for labeling of the structures. For instance, “1a+g−t” means the conformer of 1-pentyl radical with the first, second and third dihedral angles in the ranges of 140 to 163, −85 to −55 and −173 to 173 degrees, respectively, and “2g−a+” means the conformer of 2-pentyl radical with the first and second dihedral angles in the ranges of −85 to −55 and 140 to 172 degrees, respectively. The numbering of the structures is specified in Table 3.
|
The dihedral angles used for torsions are H–C(1)–C(2)–C(3), C(1)–C(2)–C(3)–C(4) and C(2)–C(3)–C(4)–C(5) for 1-pentyl and C(1)–C(2)–C(3)–C(4) and C(2)–C(3)–C(4)–C(5) for 2-pentyl, respectively.
|
|
1
|
1-pentyl radical |
|
|
2
|
2-pentyl radical |
|
|
TS
|
transition state |
|
| |
|
|
|
|
Abbreviation
|
Dihedral angle range (deg)
|
| Antiperiplanar |
a+
|
[140,172] |
|
a−
|
[−172, −140] |
| Gauche |
g+
|
[55, 85] |
|
g−
|
[−85, −55] |
| Syn |
s
|
[85, 112] or [−112, −85] |
| Synperiplanar |
p
|
[5, 30] or [−30, −5] |
| Trans |
t
|
[−173, −180] and [180, 173] |
Table 3 Sequence numbers and energiesa (kcal mol−1) of the structures of the reactant, product and transition state
| Structures |
Number |
Energy |
|
V
|
V + εG |
|
V is the M06-2X/MG3S zero-point-exclusive energy of the structures and V + εG is the zero-point-inclusive energy that is calculated by adding the zero-point energy, which is calculated using M06-2X frequencies multiplied by a scale factor from ref. 55.
|
| 1-pentyl radical |
|
1a−g+t, 1a+g−t |
j = 1, 2 |
0 |
89.01 |
|
1a−g+g+, 1a+g−g− |
j = 3, 4 |
0.08 |
89.55 |
|
1a−g+g−, 1a+g−g+ |
j = 5, 6 |
1.00 |
92.14 |
|
1a+tg+, 1a−tg− |
j = 7, 8 |
0.66 |
91.02 |
|
1a+tt, 1a−tt |
j = 9, 10 |
0.21 |
89.52 |
|
1a+tg−, 1a−tg+ |
j = 11, 12 |
0.74 |
91.20 |
|
1stg+, 1stg− |
j = 13, 14 |
0.84 |
91.64 |
|
1stt
|
j = 15 |
0.36 |
90.11 |
| 2-pentyl radical |
|
2g−a+, 2g+a− |
l = 1, 2 |
−3.14 |
85.96 |
|
2g−g−, 2g+g+ |
l = 3, 4 |
−3.12 |
86.04 |
|
2tg−, 2tg+ |
l = 5, 6 |
−2.85 |
86.85 |
|
2t+a−, 2t−a+ |
l = 7, 8 |
−2.98 |
86.25 |
|
2sg−, 2sg+ |
l = 9, 10 |
−2.77 |
86.99 |
|
2g+p, 2g−p |
l = 11, 12 |
−0.59 |
90.93 |
| Transition sate |
|
TS-1, TS-2 |
c = 1, 2 |
25.83 |
112.69 |
|
TS-3, TS-4 |
c = 3, 4 |
25.83 |
112.80 |
 |
| | Fig. 2 Fifteen structures of 1-pentyl radical (a); twelve structures of 2-pentyl radical (b); and four structures of the transition state (c). A vertical dashed line is used to separate the mirror image structures. | |
In 1-pentyl radical, the torsional motion around the C(1)–C(2), C(2)–C(3) and C(3)–C(4) bonds can contribute to generate distinguishable conformers and there are 15 structures. However, in the 2-pentyl radical, the C(1) and C(5) tails in the molecule are both methyl groups, the internal rotations of which do not generate distinct structures. Therefore, only the torsional motions around the C(2)–C(3) and C(3)–C(4) bonds produce distinguishable conformers and there are twelve structures. The transition state structures (Fig. 2(c)) contain a relatively rigid five-membered ring and a methyl tail group. The ring structure character reduces the number of conformers to four (two pairs of mirror images). Unlike the structures of 1-pentyl and 2-pentyl, these transition state structures are not connected to each other through torsion motions around C–C bonds; rather, they are connected by pseudorotation, as in cycloalkanes.
The multi-structural character of these critical configurations on the potential surface makes the kinetics of the reaction complicated. The new formulation of VTST presented in this article provides a practical way to compute the rate constants while calculating only a single reaction path based on that the saddle point with the lowest zero-point-inclusive energy. We found that this structure is the TS-1 structure, which is c* = 1 and the reactant and product wells connected with TS-1 are 1a+g−t (j* = 1) and 2g−a+ (l* = 1), respectively.
The next step is to calculate the partition functions of 1-pentyl, 2-pentyl and the transition state. The difficulty comes from treating the multi-structural character and torsional anharmonicity correctly. In the literature, the torsional anharmonicity has been treated by a variety of approximations based on hindered-rotor models (several references are cited in our previous papers15,37). Representative recent approximations include methods that assume a one-to-one correspondence between the torsions and normal modes70,71 or require multidimensional phase space integrals over high-dimensional potential energy surfaces.70 In the present work, the torsions between C(1)–C(2) and C(2)–C(3) in 1-pentyl are strongly coupled and assigning the torsions to specific normal modes is impossible; this kind of problem has been addressed previously by van Speybroeck and coworkers.72 Here, we treat this kind of situation with our recently presented15 MS-AS-T and MS-RS-T approximations that apply internal coordinate correction factors to multi-structural harmonic treatments to treat the non-separable torsions and the transition to the high-temperature limit of free internal rotation. A brief summary of these methods is given above in connection with eqns (19)–(26). A key feature of the new method is that it does not involve scans of the individual torsion angles, which would be inadequate for 1-pentyl radical because, for example, when one rotates the molecule around the CH2–C4H9 bond, the other torsions cannot be fixed. In general, scans of the individual torsions are inadequate to find all the structures.
We employed eqns (21) and (22) to calculate the partition functions of the structures TS-1, 1a+g−t, and 2g−a+ using the SS-HO and SS-T approximations, respectively. The conformational–rovibrational partition functions of 1-pentyl, 2-pentyl, and their transition state were evaluated by both the MS-AS-X and MS-RS-X (X = HO or T) methods15,69 using eqns (19)–(26). The MS-AS-T and MS-RS-T approximations provide more accurate partition functions than either the single-structural or MS-AS-HO and MS-RS-HO approximations. Tables 4–6 list information for each structure of the 1-pentyl radical, 2-pentyl radical and transition state that is used for the partition function calculations carried out by the MSTor program.69All of the calculated partition functions are given in Tables 7–9.
Table 4 Information used for the 1-pentyl radical partition function using the MS-AS-T methoda
| Torsion |
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
|
I
|
W
|
M
|
We used NS : SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method. 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
|
| Structures 1 and 2 (U = 0) |
| C(1)–C(2) |
133 |
1.71 |
281 |
2.53 |
| C(2)–C(3) |
142 |
10.91 |
2047 |
2.53 |
| C(3)–C(4) |
99 |
15.98 |
1040 |
3 |
| C(4)–C(5) |
228 |
2.92 |
998 |
3 |
| Structures 3 and 4 (U = 0.077 kcal mol−1) |
| C(1)–C(2) |
161 |
1.71 |
426 |
2.48 |
| C(2)–C(3) |
131 |
17.09 |
2819 |
2.48 |
| C(3)–C(4) |
108 |
18.38 |
1418 |
3 |
| C(4)–C(5) |
247 |
3.05 |
1228 |
3 |
| Structures 5 and 6 (U = 1.00 kcal mol−1) |
| C(1)–C(2) |
157 |
1.71 |
382 |
2.56 |
| C(2)–C(3) |
132 |
15.88 |
2521 |
2.56 |
| C(3)–C(4) |
110 |
14.79 |
1188 |
3 |
| C(4)–C(5) |
254 |
3.06 |
1297 |
3 |
| Structure 7 and 8 (U = 0.66 kcal mol−1) |
| C(1)–C(2) |
126 |
1.67 |
81 |
4.40 |
| C(2)–C(3) |
110 |
14.45 |
533 |
4.40 |
| C(3)–C(4) |
125 |
11.48 |
1177 |
3 |
| C(4)–C(5) |
229 |
3.04 |
1049 |
3 |
| Structures 9 and 10 (U = 0.21 kcal mol−1) |
| C(1)–C(2) |
118 |
1.66 |
76 |
4.28 |
| C(2)–C(3) |
119 |
11.40 |
523 |
4.28 |
| C(3)–C(4) |
117 |
11.91 |
1079 |
3 |
| C(4)–C(5) |
227 |
2.87 |
976 |
3 |
| Structure 11 and 12 (U = 0.74 kcal mol−1) |
| C(1)–C(2) |
109 |
1.67 |
64 |
4.30 |
| C(2)–C(3) |
107 |
14.52 |
536 |
4.30 |
| C(3)–C(4) |
123 |
11.34 |
1135 |
3 |
| C(4)–C(5) |
228 |
3.04 |
1041 |
3 |
| Structures 13 and 14 (U = 0.84 kcal mol−1) |
| C(1)–C(2) |
103 |
1.67 |
82 |
3.57 |
| C(2)–C(3) |
109 |
15.34 |
845 |
3.57 |
| C(3)–C(4) |
124 |
11.53 |
1161 |
3 |
| C(4)–C(5) |
229 |
3.04 |
1051 |
3 |
| Structures 15 (U = 0.36 kcal mol−1) |
| C(1)–C(2) |
108 |
1.65 |
90 |
3.56 |
| C(2)–C(3) |
121 |
11.88 |
816 |
3.56 |
| C(3)–C(4) |
116 |
11.96 |
1068 |
3 |
| C(4)–C(5) |
232 |
2.88 |
1024 |
3 |
Table 5 Information used for the 2-pentyl radical partition function using the MS-AS-T methoda
| Torsion |
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
|
I
|
W
|
M
|
We used NS : SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method. 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
|
| Structures 1 and 2 (U = 0) |
| C(1)–C(2) |
216 |
3.06 |
943 |
3 |
| C(2)–C(3) |
145 |
10.93 |
1160 |
3.44 |
| C(3)–C(4) |
63 |
13.66 |
275 |
3.44 |
| C(4)–C(5) |
121 |
2.94 |
285 |
3 |
| Structures 3 and 4 (U = 0.022 kacl/mol) |
| C(1)–C(2) |
223 |
3.06 |
1001 |
3 |
| C(2)–C(3) |
116 |
18.82 |
2157 |
2.92 |
| C(3)–C(4) |
77 |
15.68 |
795 |
2.92 |
| C(4)–C(5) |
136 |
3.04 |
371 |
3 |
| Structures 5 and 6 (U = 0.29 kcal mol−1) |
| C(1)–C(2) |
227 |
2.91 |
990 |
3 |
| C(2)–C(3) |
105 |
16.34 |
1240 |
2.94 |
| C(3)–C(4) |
72 |
10.27 |
362 |
2.94 |
| C(4)–C(5) |
114 |
3.02 |
260 |
3 |
| Structure 7 and 8 (U = 0.16 kcal mol−1) |
| C(1)–C(2) |
228 |
2.85 |
975 |
3 |
| C(2)–C(3) |
117 |
12.13 |
551 |
4.24 |
| C(3)–C(4) |
62 |
10.78 |
138 |
4.24 |
| C(4)–C(5) |
122 |
2.82 |
278 |
3 |
| Structures 9 and 10 (U = 0.37 kcal mol−1) |
| C(1)–C(2) |
238 |
3.07 |
1147 |
3 |
| C(2)–C(3) |
140 |
12.86 |
1484 |
3.56 |
| C(3)–C(4) |
61 |
15.24 |
336 |
3.56 |
| C(4)–C(5) |
98 |
3.03 |
190 |
3 |
| Structures 11 and 12 (U = 0.37 kcal mol−1) |
| C(1)–C(2) |
204 |
3.05 |
836 |
3 |
| C(2)–C(3) |
175 |
18.97 |
2660 |
3.59 |
| C(3)–C(4) |
135 |
10.42 |
879 |
3.59 |
| C(4)–C(5) |
223 |
3.05 |
1003 |
3 |
Table 6 Information used for the transition state partition function using the MS-AS-T methoda
| Torsion |
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
|
I
|
W
|
M
|
We used NS : SC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method. 0 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
|
| Structures 1 and 2 (U = 0) |
| C(4)–C(5) |
191 |
2.98 |
718 |
3 |
| Structures 3 and 4 (U = −0.0028 kcal mol−1) |
| C(4)–C(5) |
187 |
3.03 |
700 |
3 |
Table 7 Calculated conformational–vibrational–rotational partition function of 1-pentyl radical using single-structural and multi-structural methodsa
|
T/K |
SS-HOb |
SS-Tc |
MS-RS-HO |
MS-RS-T |
MS-AS-HO |
MS-AS-Td |
All of the partition functions in this table have their zero of energy at the bottom of the potential well for the j = 1 structure of 1-pentyl.
The partition function of the structure j = 1, 1a+g−t calculated using SS-HO approximation.
The partition function of the structure j = 1, 1a+g−t calculated using SS-T approximation.
MS-AS-T partition function is calculated using the MSTor program with NS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 2 SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. 2.
|
| 200 |
3.40E − 92 |
4.24E − 92 |
2.09E − 91 |
2.16E − 91 |
2.04E − 91 |
2.50E − 91 |
| 250 |
3.06E − 72 |
4.05E − 72 |
2.08E − 71 |
2.14E − 71 |
2.14E − 71 |
2.63E − 71 |
| 298.15 |
3.24E − 59 |
4.52E − 59 |
2.37E − 58 |
2.45E − 58 |
2.54E − 58 |
3.12E − 58 |
| 300 |
8.52E − 59 |
1.19E − 58 |
6.25E − 58 |
6.44E − 58 |
6.69E − 58 |
8.22E − 58 |
| 400 |
1.13E − 41 |
1.72E − 41 |
9.26E − 41 |
9.66E − 41 |
1.05E − 40 |
1.28E − 40 |
| 600 |
1.01E − 23 |
1.71E − 23 |
9.51E − 23 |
1.01E − 22 |
1.14E − 22 |
1.34E − 22 |
| 1000 |
1.65E − 07 |
2.78E − 07 |
1.76E − 06 |
1.78E − 06 |
2.20E − 06 |
2.21E − 06 |
| 1500 |
1.88E + 03 |
2.68E + 03 |
2.14E + 04 |
1.82E + 04 |
2.74E + 04 |
2.13E + 04 |
| 2000 |
4.05E + 09 |
4.63E + 09 |
4.79E + 10 |
3.29E + 10 |
6.18E + 10 |
3.71E + 10 |
| 2400 |
2.60E + 13 |
2.49E + 13 |
3.13E + 14 |
1.82E + 14 |
4.06E + 14 |
2.01E + 14 |
First, we discuss the MS-AS-T calculations for the 1-pentyl radical, 2-pentyl radical and the transition state. There are four torsions in 1-pentyl and 2-pentyl radicals. For 1-pentyl, two of the torsions around the C(1)–C(2) and C(2)–C(3) bonds are involved in a strongly coupled15 (SC) group. The other two torsions, around C(3)–C(4) and C(4)–C(5) bonds are considered to be nearly separable15 (NS). For 2-pentyl, the torsions around the C(2)–C(3) and C(3)–C(4) bonds are treated as a strongly coupled (SC) group. The other two torsions, around the C(1)–C(2) and C(4)–C(5) bonds, are considered to be nearly separable (NS). Tables 7 and 8 give the conformational–vibrational–rotational partition functions of the 1-pentyl and 2-pentyl radicals using NS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC =2
SC =2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. In the transition state, there is only one torsion around the bond between the methyl group and the five-membered ring. The conformational–vibrational–rotational partition functions are given in Table 9.
2. In the transition state, there is only one torsion around the bond between the methyl group and the five-membered ring. The conformational–vibrational–rotational partition functions are given in Table 9.
Table 8 Calculated conformational–vibrational–rotational partition functions of the 2-pentyl radical using single-structural and multi-structural methodsa
|
T/K |
SS-HOb |
SS-Tc |
MS-RS-HO |
MS-RS-T |
MS-AS-HO |
MS-AS-Td |
All of the partition functions in this table have their zero of energy at the bottom of the potential well for the l = 1 structure of 2-pentyl.
The partition function of the structure l = 1, 2g−a+ calculated using SS-HO approximation.
The partition function of the structure l = 1, 2g−a+ calculated using SS-T approximation.
MS-AS-T partition function is calculated using the MSTor program with NS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 2 SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. 2.
|
| 200 |
4.30E − 92 |
6.16E − 92 |
4.00E − 91 |
5.63E − 91 |
4.00E − 91 |
5.81E − 91 |
| 250 |
4.17E − 72 |
6.25E − 72 |
4.27E − 71 |
6.24E − 71 |
4.22E − 71 |
6.29E − 71 |
| 298.15 |
4.27E − 59 |
6.59E − 59 |
4.71E − 58 |
7.00E − 58 |
4.98E − 58 |
7.50E − 58 |
| 300 |
1.22E − 58 |
1.88E − 58 |
1.34E − 57 |
2.00E − 57 |
1.31E − 57 |
1.98E − 57 |
| 400 |
1.69E − 41 |
2.67E − 41 |
2.08E − 40 |
3.11E − 40 |
2.00E − 40 |
2.99E − 40 |
| 600 |
1.57E − 23 |
2.38E − 23 |
2.17E − 22 |
3.09E − 22 |
2.06E − 22 |
2.84E − 22 |
| 1000 |
2.56E − 07 |
3.18E − 07 |
3.94E − 06 |
4.53E − 06 |
3.70E − 06 |
4.01E − 06 |
| 1500 |
2.88E + 03 |
2.64E + 03 |
4.70E + 04 |
3.94E + 04 |
4.40E + 04 |
3.43E + 04 |
| 2000 |
6.18E + 09 |
4.19E + 09 |
1.04E + 11 |
6.39E + 10 |
9.68E + 10 |
5.57E + 10 |
| 2400 |
3.95E + 13 |
2.15E + 13 |
6.72E + 14 |
3.31E + 14 |
6.29E + 14 |
2.89E + 14 |
Table 9 Calculated conformational–vibrational–rotational partition function of the transition state using single-structural and multi-structural methodsa
|
T/K |
SS-HOb |
SS-Tc |
MS-RS-HO |
MS-RS-T |
MS-AS-HO |
MS-AS-Td |
All partition functions in this table have their zero of energy at the bottom of the potential well for the c = 1 structure of the transition state.
The partition function of the TS-1 calculated using SS-HO approximation.
The partition function of the TS-1 calculated using SS-T approximation.
MS-AS-T partition function is calculated using the MSTor program with NS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 1 SC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. 0.
|
| 200 |
2.39E − 90 |
2.55E-90 |
8.05E − 90 |
8.60E − 90 |
8.05E − 90 |
8.60E − 90 |
| 250 |
5.63E − 71 |
6.13E-71 |
1.93E − 70 |
2.11E − 70 |
1.93E − 70 |
2.11E − 70 |
| 298.15 |
2.40E − 58 |
2.66E-58 |
8.33E − 58 |
9.26E − 58 |
8.33E − 58 |
9.26E − 58 |
| 300 |
6.12E − 58 |
6.80E-58 |
2.13E − 57 |
2.37E − 57 |
2.13E − 57 |
2.37E − 57 |
| 400 |
2.32E − 41 |
2.65E − 41 |
8.17E − 41 |
9.37E − 41 |
8.17E − 41 |
9.37E − 41 |
| 600 |
5.37E − 24 |
6.29E − 24 |
1.92E − 23 |
2.25E − 23 |
1.92E − 23 |
2.25E − 23 |
| 1000 |
2.64E − 08 |
3.02E − 08 |
9.55E − 08 |
1.09E − 07 |
9.55E − 08 |
1.09E − 07 |
| 1500 |
1.53E + 02 |
1.63E + 02 |
5.54E + 02 |
5.89E + 02 |
5.54E + 02 |
5.89E + 02 |
| 2000 |
2.22E + 08 |
2.19E + 08 |
8.06E + 08 |
7.95E + 08 |
8.06E + 08 |
7.95E + 08 |
| 2400 |
1.14E + 12 |
1.06E + 12 |
4.13E + 12 |
3.85E + 12 |
4.13E + 12 |
3.85E + 12 |
Tables 7–9 show that at low temperature (200–250 K), the differences of the partition functions calculated by the multi-structural-all-structure harmonic oscillator method (MS-AS-HO) and MS-AS-T for 1-pentyl and the transition sate are within 6–19%. For 2-pentyl, the deviations are larger at 31–33%. As the temperature increases, the MS-HO approximation changes from being an underestimate to being an overestimate. By 2400 K, the MS-AS-HO results overestimate the MS-AS-T ones by 102% for 1-pentyl, 7% for the transition state and 118% for 2-pentyl. We will use the more accurate MS-AS-T method for the final kinetics calculations.
Next, we discuss the MS-RS-T calculations for the 1-pentyl and 2-pentyl radicals. (The transition state conformers are not generated by torsions, thus MS-RS is considered to be the same as MS-AS for the TS partition function calculations on the reaction considered in this paper, but these methods are not the same for the reactants or products.) When employing the MS-RS method, we need to identify all of the structures obtained by independent internal rotations from a reference structure. In this work, we use the global minimum structures 1a+g−t and 2g−a+ as the reference structures for 1-pentyl and 2-pentyl radicals, respectively. For 1-pentyl, the internal rotation around the C(1)–C(2) bond in the reference structure 1a+g−t does not generate any distinguishable structures, but the independent rotations around the C(2)–C(3) and the C(3)–C(4) bonds produce the other four structures used in the MS-RS calculations. They are 1a−g+g+, 1a−g+g−, 1a−tt and 1a−g+t. For 2-pentyl, independent rotations around the C(2)–C(3) and the C(3)–C(4) bonds in the reference structure 2g−a+ generate the other four structures: 2g+a−, 2ta+, 2g−g− and 2g−s. The detailed information about each structure of the 1-pentyl and 2-pentyl radicals used for the MS-RS calculation are listed in the electronic supplementary information†and the MS-RS-T partition functions are given in Tables 7 and 8. It is found that the deviations of the MS-RS-T partition functions for the 1-pentyl radical from the MS-AS-T ones are 6% at 200 K, increasing to 25% at 400–600 K, then decreasing to 9% at 2400 K. For the 2-pentyl radical, the deviations are smaller at 200–1000 K, but they increase to 15% by 2400 K. However, the MS-RS-T method needs much less structural information than the MS-AS-T method and it saves considerable time in the calculations.
2. Transmission coefficient
Fig. 3 displays the VMEP and VGa curves. Both the VMEP and VGa curves are well converged, with only six non-stationary Shepard points, which is consistent with earlier work.56 The transmission coefficient calculated using the SCT approximation is also well converged. Therefore, only nine high-level electronic structure theory Hessians along the reaction path were needed to interpolate the potential curves used for the following rate constant calculations.
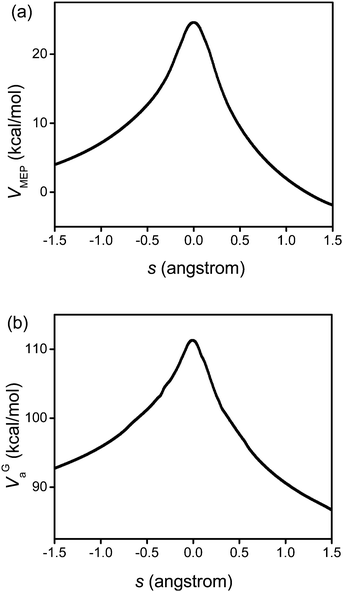 |
| | Fig. 3 Calculated VMEP and ground-state vibrationally adiabatic potential (VGa) vs. the reaction coordinate s (scaled to a reduced mass of one amu) for the 1,4-hydrogen shift isomerization reaction of 1-pentyl radical. This figure is based on M06/6-31+G(d,p). | |
Because the MCSI method uses just a few Hessian calculations, it saves considerable computation time relative to straight direct dynamics calculations. Also, compared to the IVTST-M algorithm,73 the MCSI method provides a more accurate interpolation of the VMEP and VGa curves; IVTST-M needs relatively large number of Hessians for a converged result and those Hessians are only located close to the saddle point, but the Hessians in the MCSI calculations are widely spaced along the reaction path. This makes the interpolation more reliable and robust.
Fig. 4 shows an Arrhenius plot of the SCT transmission coefficient. This shows that the reaction has a very large tunneling contribution at temperatures below 500 K. In particular, the quantum effects on the reaction coordinate motion increase the rate constant by factors of 7.6, 29, 821 and 2.6 × 104 at 500, 400, 300 and 250 K, respectively. However, above 1000 K, the quantum effects on the reaction coordinate motion increase the rate by less than 60%.
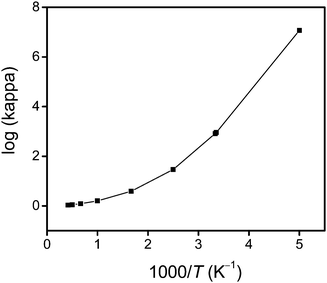 |
| | Fig. 4 The calculated common logarithm of the SCT transmission coefficient κ vs. reciprocal temperature (times a thousand). | |
3. SS-VTST rate constant calculations
The forward and reverse single-structural rate constants, kSS-CVT/SCT, were calculated using both the SS-HO and the SS-T approximations and they are labeled as kCVT/SCTSS-HO and kCVT/SCTSS-T, respectively. The results are given in the first and second rate constant columns of Tables 10 and 11. The SS results of Tables 10 and 11 replace the older single-structure results of ref. 4. The calculated rate constant in ref. 4 agreed well with experiments, but that resulted from a cancellation of three errors: (1) the reactant structure used was not the lowest-energy structure; (2) the VGa curve was poorly interpolated due to a poor choice of interpolation variable, causing the transmission coefficient to be underestimated; and (3) multi-structural and torsional anharmonicity were neglected.
Table 10 Forward SS-VTST and MS-VTST thermal rate constants (in s−1) for the 1,4-hydrogen shift isomerization reaction of 1-pentyl radical to produce 2-pentyl radical at various temperaturesa
|
T/K |
k
CVT/SCTSS-HO
|
k
CVT/SCTSS-T
|
k
CVT/SCTMS-RS-HO
|
k
CVT/SCTMS-RS-T
|
k
CVT/SCTMS-AS-HO
|
k
CVT/SCTMS-AS-T
|
|
Includes variational effects, torsional anharmonicity and tunneling.
|
| 200 |
5.27E − 06 |
4.51E − 06 |
2.89E − 06 |
2.98E − 06 |
2.96E − 06 |
2.58E − 06 |
| 250 |
9.19E − 04 |
7.56E − 04 |
4.63E − 04 |
4.92E − 04 |
4.50E − 04 |
4.01E − 04 |
| 298.15 |
4.80E − 02 |
3.81E − 02 |
2.28E − 02 |
2.45E − 02 |
2.13E − 02 |
1.92E − 02 |
| 300 |
5.12E − 02 |
4.07E − 02 |
2.43E − 02 |
2.62E − 02 |
2.27E − 02 |
2.06E − 02 |
| 400 |
2.11E + 01 |
1.58E + 01 |
9.07E + 00 |
9.97E + 00 |
8.00E + 00 |
7.52E + 00 |
| 600 |
3.27E + 04 |
2.26E + 04 |
1.24E + 04 |
1.37E + 04 |
1.04E + 04 |
1.03E + 04 |
| 1000 |
2.59E + 07 |
1.76E + 07 |
8.78E + 06 |
9.91E + 06 |
7.03E + 06 |
7.98E + 06 |
| 1500 |
9.34E + 08 |
6.98E + 08 |
2.96E + 08 |
3.71E + 08 |
2.32E + 08 |
3.17E + 08 |
| 2000 |
6.02E + 09 |
5.19E + 09 |
1.85E + 09 |
2.65E + 09 |
1.43E + 09 |
2.35E + 09 |
| 2400 |
1.56E + 10 |
1.51E + 10 |
4.71E + 09 |
7.53E + 09 |
3.62E + 09 |
6.81E + 09 |
Table 11 SS-VTST and MS-VTST thermal rate constants (in s−1) for the 1,4-hydrogen shift isomerization reaction of 2-pentyl radical to produce 1-pentyl radical at various temperaturesa
|
T/K |
k
CVT/SCTSS-HO
|
k
CVT/SCTSS-T
|
k
CVT/SCTMS-RS-HO
|
k
CVT/SCTMS-RS-T
|
k
CVT/SCTMS-AS-HO
|
k
CVT/SCTMS-AS-T
|
|
Includes variational effects, torsional anharmonicity and tunneling. Note that the reaction in this table is the reverse of that in Table 10.
|
| 200 |
1.94E − 10 |
1.44E − 10 |
7.02E − 11 |
5.33E − 11 |
7.03E − 11 |
5.18E − 11 |
| 250 |
2.14E − 07 |
1.56E − 07 |
7.17E − 08 |
5.37E − 08 |
7.26E − 08 |
5.32E − 08 |
| 298.15 |
3.45E − 05 |
2.47E − 05 |
1.08E − 05 |
8.11E − 06 |
1.11E − 05 |
8.20E − 06 |
| 300 |
4.09E − 05 |
2.95E − 05 |
1.29E − 05 |
9.67E − 06 |
1.32E − 05 |
9.73E − 06 |
| 400 |
7.93E − 02 |
5.73E − 02 |
2.27E − 02 |
1.74E − 02 |
2.36E − 02 |
1.81E − 02 |
| 600 |
5.87E + 02 |
4.54E + 02 |
1.52E + 02 |
1.25E + 02 |
1.60E + 02 |
1.36E + 02 |
| 1000 |
1.67E + 06 |
1.67E + 06 |
3.91E + 05 |
3.89E + 05 |
4.16E + 05 |
4.38E + 05 |
| 1500 |
1.15E + 08 |
1.34E + 08 |
2.54E + 07 |
3.23E + 07 |
2.74E + 07 |
3.73E + 07 |
| 2000 |
1.03E + 09 |
1.49E + 09 |
2.22E + 08 |
3.55E + 08 |
2.38E + 08 |
4.08E + 08 |
| 2400 |
3.12E + 09 |
5.33E + 09 |
6.66E + 08 |
1.26E + 09 |
7.15E + 08 |
1.45E + 09 |
4. Multi-structural anharmonicity torsional factors
As mentioned in section 1 of the Results and Discussion, for the transition state, MS-RS is the same as MS-AS in the present work. Thus, here we denote both F‡MS-X-T as F‡MS-AS-T. Table 12 gives the F‡MS-AS-T factors at various temperatures and it is found that the F‡MS-AS-T factors range 3.4–4.2. The magnitude can be qualitatively rationalized by the existence of four conformers for the transition state and the similar energies and frequencies of these conformers. FRMS-X-T and FPMS-X-T (X = RS or T) are also given in Table 12. The table shows that the deviations between FRMS-AS-T and FRMS-RS-T are larger than those between FPMS-AS-T and FPMS-RS-T. This observation is consistent with the deviations of the conformational–rotational–vibrational partition functions calculated using the two methods mentioned in section 1 of the Results and Discussion. In addition, it shows that the reactant and product wells have larger multi-structural anharmonicity factors than the transition state over the whole temperature range. This result is consistent with their larger number of conformers. However, there is no simple relationship between the multi-structural anharmonicity factor and the number of conformers. For instance, the 1-pentyl radical has 15 conformers, but its FRMS-AS-T and FRMS-RS-T factors are 7.4–9.6 and 6.4–7.6, instead of 15 at 200–300 K.
Table 12 Multi-structure torsional anharmonicity factors with respect to the structure TS-1 as the transition state, 1a+g−t as the reactant well and 2g−a+ as the product well
|
T/K |
F
‡MS-AS-X
|
F
RMS-RS-X
|
F
RMS-AS-X
|
F
PMS-RS-X
|
F
PMS-AS-X
|
| HO |
T |
HO |
T |
HO |
T |
HO |
T |
HO |
T |
| 200 |
3.37 |
3.60 |
6.15 |
6.36 |
6.00 |
7.36 |
9.30 |
13.26 |
9.31 |
13.50 |
| 250 |
3.43 |
3.75 |
6.80 |
6.98 |
6.99 |
8.58 |
10.25 |
15.00 |
10.13 |
15.10 |
| 298.15 |
3.47 |
3.86 |
7.31 |
7.54 |
7.84 |
9.62 |
11.02 |
16.27 |
10.78 |
16.23 |
| 300 |
3.48 |
3.87 |
7.34 |
7.57 |
7.85 |
9.65 |
11.02 |
16.32 |
10.74 |
16.27 |
| 400 |
3.52 |
4.04 |
8.19 |
8.56 |
9.29 |
11.34 |
12.29 |
17.93 |
11.82 |
17.65 |
| 600 |
3.58 |
4.19 |
9.42 |
9.98 |
11.29 |
13.20 |
13.83 |
18.69 |
13.13 |
18.14 |
| 1000 |
3.62 |
4.12 |
10.67 |
10.71 |
13.33 |
13.34 |
15.40 |
16.34 |
14.46 |
15.67 |
| 1500 |
3.62 |
3.86 |
11.38 |
9.64 |
14.57 |
11.29 |
16.33 |
12.41 |
15.25 |
11.90 |
| 2000 |
3.63 |
3.59 |
11.83 |
8.11 |
15.26 |
9.14 |
16.76 |
9.36 |
15.68 |
9.01 |
| 2400 |
3.62 |
3.39 |
12.04 |
6.97 |
15.62 |
7.71 |
17.01 |
7.56 |
15.90 |
7.31 |
In the kCVT/SCTMS-AS-T calculation, F‡MS-AS-T/FRMS-AS-T varies from 0.49 at 200 K to 0.31 at 1000 K, then back up to 0.44 at 2400 K. A corresponding analysis for the reverse reaction yields F‡MS-AS-T/FPMS-AS-T equal to 0.27, 0.26, and 0.46 at these three temperatures.
All of the multi-structural torsional anharmonicity factors F‡MS-AS-T, FRMS-AS-T and FPMS-AS-T depend on the frequencies used for partition function calculations by the MSTor program.69 As mentioned above, the frequencies used in the present work are the ones obtained from the M06-2X/MG3S density functional calculations multiplied by the scale factor of 0.970.46 This scale factor is designed to yield an accurate zero-point energy and, thus, applying it makes the VGa curve more reliable for the transmission coefficient calculations. However, when calculating the conformational–rotational–vibrational partition functions using the multi-structural methods, the contributions from the low-frequency modes dominate and the current scaling factor is not needed to improve the results for those low frequencies. Therefore, we tested the effect of calculating the multi-structural torsional anharmonicity factors without using the scale factor. The ratio of the multi-structural torsional anharmonicity factors calculated with the scaling factors over that without the scaling factors, that is (FXMS-AS-T)scale/(FXMS-AS-T)noscale (where X = ‡, R or P), are listed in the electronic supplementary information†. One finds that the effect is 6% or less for 1-pentyl, 2% or less for the transition state and 7% or less for 2-pentyl. Thus, neither the forward or reverse rate constants are sensitive to scaling the frequencies of the low frequency modes.
5. Final thermal rate constants
We employed the kCVT/SCTSS-HO and κSCT(T) results discussed in sections 2, 3 and 4 of the Results and Discussion to calculate the final thermal rate constant in the high-pressure limit using eqn (27). The results are given in the final four columns of Tables 10 and 11, and Fig. 5 shows how the final forward and reverse thermal rate constants vary with the temperature. Fig. 5a compares our final result to the experimentally-based recommendations of the high-pressure limit for the forward reaction from refs 1 and 2; the figure demonstrates that the calculated forward rate constants are in excellent agreement with the experimental results of Yamauchi and Miyoshi et al.1,2 over the whole temperature range of 300–1300 K for which they make an experimental recommendation. The experimental evaluations of the high-pressure limit are less certain above 800 K due to fall-off effects.2Fig. 5b shows the calculated results for the reverse reaction.
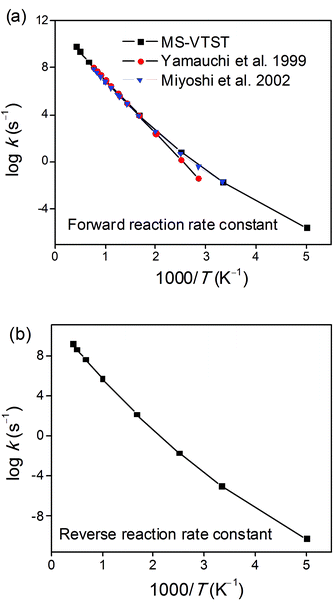 |
| | Fig. 5 Arrhenius plots of calculated (a) forward and (b) reverse rate constant kCVT/SCTMS-AS-T calculated by MS-VTST (black curve) and previous experimental data for the 1,4-hydrogen shift isomerization reaction of the 1-pentyl radical to produce the 2-pentyl radical. | |
The next issue to consider is a comparison of the MS-CVT/SCT rate constants calculated with the less expensive MS-RS-T approximation to those calculated with the full MS-AS-T approximation. Table 10 shows deviations of only 16% at 200 K, increasing to 33% at 400–600 K, then decreasing again to 11% at 2400 K. The performance is even better for the reverse reaction, where Table 11 shows errors of 8% or less at 200–600 K, increasing to 13% at 1500–2400 K. However, one's sense of encouragement in the accuracy of the less expensive reference structure method must be tempered by the realization that it results in part from a cancellation of errors. Further testing is warranted.
Based on the calculated thermal rate constant, we calculated the Arrhenius activation energies and fitted the rate constant to obtain a formula to predict the rate at any temperature in the high-pressure limit. The Arrhenius activation energy is calculated using| | 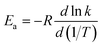 | (28) |
and the results are given in Table 13. Table 13 shows that the Ea increases with temperature, but much more slowly than a linear increase in T, whereas linear behavior is predicted by the very popular fitting expression| | 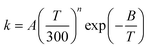 | (29) |
Table 13 Forward and reverse activation energies (in kcal mol−1) calculated by MS-VTST for the 1,4-hydrogen shift isomerization reaction of the 1-pentyl radical to produce the 2-pentyl radical at various temperatures
|
T/K |
300 |
400 |
600 |
1000 |
1500 |
2000 |
| Forward (MS-VTST) |
12.6 |
15.6 |
18.7 |
21.7 |
23.4 |
26.1 |
| Reverse (MS-VTST) |
16.4 |
19.0 |
22.9 |
25.4 |
27.9 |
29.5 |
Therefore, as recommended previously,74 we abandon this popular form and instead fit the calculated rate constants to the more physical functional form given by74
| | 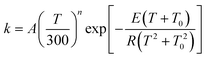 | (30) |
We obtain A = 1.06 × 108 s−1, n = 3.2897, E = 11.436 kcal mol−1 and T0 = 185.34 K for the forward reaction, and we obtain A = 8.81 × 106 s−1, n = 4.01577, E = 13.865 kcal mol−1 and T0 = 165.90 K for the reverse reaction. A plot is shown in the electronic supplementary information†.
Conclusions
We have addressed the challenge of developing an efficient and accurate way to predict the thermal rate constant of a reaction with multiple conformational states, and we illustrated the new method here by calculating the rate constant of the 1,4-hydrogen shift reaction of the 1-pentyl radical and the reverse reaction. The calculation involved several steps. First, we applied the multi-configuration Shepard interpolation (MCSI) method to obtain the potential energy surface of the reaction by using molecular mechanics to interpolate density functional calculations in the reaction valley that passes through the transition state with the lowest zero-point-inclusive energy. Then a single-structural variational transition state calculation was carried out and the multi-dimensional tunneling contribution was calculated by the SCT approximation. Finally, the multi-structural effect, including the torsional anharmonicity, was added based on the optimizations and frequency calculations for all of the structures of the reactants, products and transition state. These steps together constitute a new formulation of variational transition state theory labelled MS-VTST.
We found that multi-structural anharmonicity in the harmonic approximation lowers the forward-reaction rate by factors of 0.56, 0.32 and 0.23 at 200, 600 and 2400 K, respectively, and torsional anharmonicity lowers it (again with respect to the single-structural harmonic approximation) by factors of 0.49, 0.32 and 0.44 at these three temperatures. A large transmission coefficient is found for this reaction at lower temperatures, in particular, 1.2 × 107 and 3.90 at 200 and 600 K, respectively. The calculated final forward thermal rate constant agrees very well with experimentally-based data1,2 over the entire temperature range (300–1300 K). The MS-VTST method used here can be applied to calculate thermal rate constants for other complex unimolecular or bimolecular reactions involving molecules of even larger size.
Acknowledgements
The authors are grateful to Dr Osanna Tishchenko for help in using the MCSI method. Also, we appreciate helpful discussions with Dr John Alecu. This work was supported by the U. S. Department of Energy, Office of Basic Energy Sciences, under grant no. DE-FG02-86ER13579 and by the Combustion Energy Frontier Research Center under award no. DE-SC0001198.
Notes and references
- N. Yamauchi, A. Miyoshi, K. Kosaka, M. Koshi and H. Matsui, J. Phys. Chem. A, 1999, 103, 2723 CrossRef CAS.
- A. Miyoshi, J. Widjaja, N. Yamauchi, M. Koshi and H. Matsui, Proc. Combust. Inst., 2002, 29, 1285 CrossRef CAS.
- W. Tsang, J. A. Walker and J. A. Manion, Proc. Combust. Inst., 2007, 31, 141 CrossRef.
- J. Zheng and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 11919 CrossRef CAS.
-
(a) H. Eyring, Chem. Rev., 1935, 17, 65 CrossRef CAS;
(b) D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771 CrossRef CAS.
-
(a) R. A. Marcus, J. Chem. Phys., 1966, 45, 4493 CrossRef CAS;
(b) D. G. Truhlar and A. Kuppermann, J. Am. Chem. Soc., 1971, 93, 1840 CrossRef.
-
(a) B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593 CrossRef CAS;
(b) D. G. Truhlar and B. C. Garrett, Annu. Rev. Phys. Chem., 1984, 35, 159 CrossRef CAS.
- K. K. Baldridge, M. S. Gordon, R. Steckler and D. G. Truhlar, J. Phys. Chem., 1989, 93, 5107 CrossRef CAS.
-
D. G. Truhlar in The Reaction Path in Chemistry: Current Approaches and Perspectives, ed. D. Heidrich, Kluwer, Dordrecht, 1995, pp. 229–255 Search PubMed.
- Y. Kim, J. C. Corchado, J. Villa, J. Xing and D. G. Truhlar, J. Chem. Phys., 2000, 112, 2718 CrossRef CAS.
- O. Tishchenko and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 1454 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS ; erratum: 2008, 119, 525.
- Y.-P. Liu, G. C. Lynch, T. N. Truong, D.-H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408 CrossRef CAS.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Rev. Comput. Chem., 2007, 23, 125 CrossRef CAS.
- J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Phys. Chem. Chem. Phys., 2011, 13, 10885 RSC.
-
J. Zheng, S. Zhang, B. J. Lynch, J. C. Corchado, Y.-Y. Chuang, P. L. Fast, W.-P. Hu, Y.-P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. F. Ramos, B. A. Ellingson, V. S. Melissas, J. Villà, I. Rossi, E. L. Coitiño, J. Pu, T. V. Albu, D. G. Truhlar, POLYRATE-version 2010-A, University of Minnesota, Minneapolis, 2010 Search PubMed.
-
(a) D. G. Truhlar and B. C. Garrett, Acc. Chem. Res., 1980, 13, 440 CrossRef CAS;
(b) D. G. Truhlar, A. D. Isaacson, R. T. Skodje and B. C. Garrett, J. Phys. Chem., 1982, 86, 2252 CrossRef CAS.
- A. Fernández-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Truhlar, Chem. Rev., 2006, 106, 4518 CrossRef.
- S. N. Rai and D. G. Truhlar, J. Chem. Phys., 1983, 79, 6046 CrossRef CAS.
- Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 9776 CrossRef CAS.
- J. Zheng, S. Zhang and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 11509 CrossRef CAS.
- J. G. Lauderdale and D. G. Truhlar, Surf. Sci., 1985, 164, 558 CrossRef CAS.
- S. E. Wonchoba and D. G. Truhlar, Phys. Rev. B: Condens. Matter, 1996, 53, 11222 CrossRef CAS.
- Y.-Y. Chuang, C. J. Cramer and D. G. Truhlar, Int. J. Quantum Chem., 1998, 70, 887 CrossRef CAS.
- Y. Kim, J. R. Mohrig and D. G. Truhlar, J. Am. Chem. Soc., 2010, 132, 11071 CrossRef CAS.
- C. Alhambra, J. Corchado, M. L. Sánchez, M. Garcia-Viloca, J. Gao and D. G. Truhlar, J. Phys. Chem. B, 2001, 105, 11326 CrossRef CAS.
- D. G. Truhlar, J. Gao, M. Garcia-Viloca, C. Alhambra, J. M. Corchado, L. Sanchez and T. D. Poulsen, Int. J. Quantum Chem., 2004, 100, 1136 CrossRef CAS.
-
D. G. Truhlar in Isotope Effects in Chemistry and Biology, ed. A. Kohen and H. H. Limbach, Marcel Dekker Inc., New York, 2006, pp. 579–620 Search PubMed.
-
D. G. Truhlar, B. C. Garrett in Hydrogen Transfer Reactions, ed. J. T. Hynes, J. P. Klinman, H. H. Limbac and R. L. Schowen, Wiley-VCH, Weinheim, Germany, 2007, vol. 2, pp. 833–874 Search PubMed.
- B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 1079 CrossRef CAS ; errata: 1980, 84, 682; 1983, 87, 4553.
- A. D. Isaacson and D. G. Truhlar, J. Chem. Phys., 1982, 76, 1380 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730 CrossRef CAS ; erratum: 1983, 87, 4554.
-
D. G. Truhlar, A. D. Isaacson, B. C. Garrett in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, FL, 1985, vol. 4, pp. 65–137 Search PubMed.
- D. C. Chatfield, R. S. Friedman, D. G. Truhlar, B. C. Garrett and D. W. Schwenke, J. Am. Chem. Soc., 1991, 113, 486 CrossRef CAS.
- D. C. Chatfield, R. S. Friedman, D. G. Truhlar, B. C. Garrett and D. W. Schwenke, Faraday Discuss. Chem. Soc., 1991, 91, 289 RSC.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813 CrossRef.
-
(a) Y.-Y. Chuang and D. G. Truhlar, J. Chem. Phys., 2000, 112, 1221 CrossRef CAS ; errata: 2004, 121, 7036; 2006, 124, 179903/1-2;
(b) B. A. Ellingson, V. A. Lynch, S. L. Mielke and D. G. Truhlar, J. Chem. Phys., 2006, 125, 84305 CrossRef.
-
(a)
M. M. Kreevoy and D. G. Truhlar in Investigation of Rates and Mechanisms of Reactions, ed. C. F. Bernasconi, John Wiley and Sons, New York, 4th edn, 1986, Part 1, pp. 13–95 Search PubMed;
(b)
K. J. Laidler, Chemical Kinetics, Harper Collins Publishers, New Yorok, 3rd edn, 1987 Search PubMed.
-
(a) D. G. Truhlar, J. Mol. Spectrosc., 1971, 38, 415 CrossRef CAS;
(b) B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 1915 CrossRef CAS.
-
(a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS;
(b) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P.v. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS;
(c) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849 CrossRef CAS.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 1643 CrossRef CAS.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 43 RSC.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P.V. R. Schleyer, J. Comput. Chem., 1983, 4, 294 CrossRef CAS.
- E. Papajak, H. R. Leverentz, J. Zheng and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 1197 CrossRef CAS.
-
(a) T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS;
(b) R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
-
(a) E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 10 CrossRef CAS;
(b) E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 597 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
-
(a)
J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, CT, 2003 Search PubMed;
(b)
Y. Zhao and D. G. Truhlar, MN-GFM: Minnesota Gaussian Functional Module, version 4.1, University of Minnesota, Minneapolis, MN, 2008 Search PubMed.
-
H.-J. Werner, P. J. Knowles, F. R. Manby, M. Schütz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, Molpro, version 2010.1, University of Birmingham, Birmingham, 2010 Search PubMed.
-
Y. Zhao, D. G. Truhlar, MLGAUSS, version 2.0, University of Minnesota, Minneapolis, 2007 Search PubMed.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872 CrossRef CAS.
- T. V. Albu, J. C. Corchado and D. G. Truhlar, J. Phys. Chem. A, 2001, 105, 8465 CrossRef CAS.
- H. Lin, J. Z. Pu, T. V. Albu and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 4112 CrossRef CAS.
- K. H. Kim and Y. Kim, J. Chem. Phys., 2004, 120, 623 CrossRef CAS.
- H. Lin, Y. Zhao, O. Tishchenko and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 1237 CrossRef CAS.
- O. Tishchenko and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13530 CrossRef CAS.
-
O. Tishchenko, M. Higashi, T. V. Albu, J. C. Corchado, Y. Kim, J. Villà, J. Xing, H. Lin and D. G. Truhlar, MCSI, version 2010, University of Minnesota, Minneapolis, 2010 Search PubMed.
-
T. V. Albu, O. Tishchenko, J. C. Corchado, Y. Kim, J. Villà, J. Xing, H. Lin, M. Higashi and D. G. Truhlar, MC-TINKERATE, version 2010, University of Minnesota, Minneapolis, 2010 Search PubMed.
- R. Valero, L. Song, J. Gao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 1 CrossRef CAS.
- N. L. Allinger, Y. H. Yuh and J. H. Lii, J. Am. Chem. Soc., 1989, 111, 8551 CrossRef CAS.
- J. H. Lii and N. L. Allinger, J. Am. Chem. Soc., 1989, 111, 8566 CrossRef CAS.
- J. H. Lii and N. L. Allinger, J. Am. Chem. Soc., 1989, 111, 8576 CrossRef CAS.
-
J. M. Hornback, in Organic Chemistry, ed., Brooks/Cole, Pacific Grove, CA, 2nd edn, 2005, p. 91 Search PubMed.
- D.-h. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y.-P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1992, 71, 235 CrossRef CAS.
-
J. Zheng, S. L. Mielke, K. L. Clarkson and D. G. Truhlar, MSTor, version 2011, University of Minnesota, Minneapolis, 2011 Search PubMed.
- S. Sharma, S. Raman and W. H. Green, J. Phys. Chem. A, 2010, 114, 5689 CrossRef CAS.
- A. Ghysels, T. Verstraelen, K. Hemelsoet, M. Waroquier and V. Speybroeck, J. Chem. Inf. Model., 2010, 50, 1736 CrossRef CAS.
-
(a) K. Van Cauter, V. Van Speybroeck, P. Vansteenkiste, M.-F. Reyniers and M. Waroquier, ChemPhysChem, 2006, 7, 131 CrossRef CAS;
(b) P. Vansteenkiste, D. Van Neck, V. Van Speybroeck and M. Waroquier, J. Chem. Phys., 2006, 124, 044314 CrossRef CAS.
- J. C. Corchado, E. L. Coitino, Y. Y. Chuang, P. L. Fast and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 2424 CrossRef CAS.
- J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 7782 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Information used for calculating the conformational–rotational–vibrational partition functions of 1-pentyl, 2-pentyl and the transition state by MS-RS-HO and MS-RS-T methods, the transmission coefficient of the reaction using SCT approximation, the optimized geometries of the 1-pentyl radical, the 2-pentyl radical and the transition state structures, the effect of scaling factors on the multi-structural torsional anharmonicity factors and a plot of the calculated MS-VTST rate constants with the fitting curves. See DOI: 10.1039/c1sc00225b |
|
| This journal is © The Royal Society of Chemistry 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 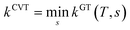
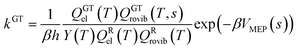
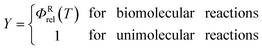
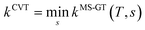
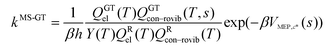
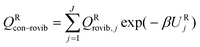
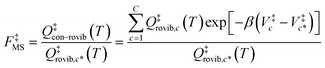
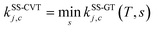
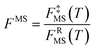
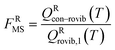
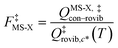
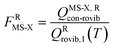
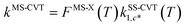
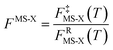
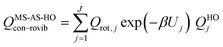
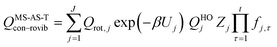
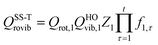
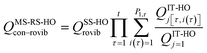
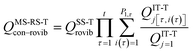
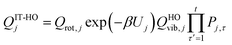
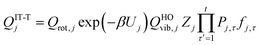


![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
2 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
0 and M06-2X/MG3S for this table. The units are cm−1 for torsional barrier heights W and frequencies. The unit is amu Å2 for internal moments of inertia, I, and the local periodicity M is unitless. See ref. 15 for details of the method.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 2
SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC =2
SC =2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. In the transition state, there is only one torsion around the bond between the methyl group and the five-membered ring. The conformational–vibrational–rotational partition functions are given in Table 9.
2. In the transition state, there is only one torsion around the bond between the methyl group and the five-membered ring. The conformational–vibrational–rotational partition functions are given in Table 9.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 2
SC = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SC = 1
SC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.
0.