Energy transfer at metal surfaces: the need to go beyond the electronic friction picture
Christof
Bartels
*ab,
Russell
Cooper
ac,
Daniel J.
Auerbach
c and
Alec M.
Wodtke
abc
aGeorg-August-Universität, Institut für Physikalische Chemie, Göttingen, Germany. E-mail: cbartel@gwdg.de; Fax: +49 551 39-20073; Tel: +49 551 39-12605
bMax-Planck-Institut für biophysikalische Chemie, Göttingen, Germany
cDepartment of Chemistry and Biochemistry, University of California Santa Barbara, Santa Barbara, CA 93106-9510, USA
First published on 31st May 2011
Abstract
Interactions of molecules at metal surfaces can result in energy exchange with the electrons of the metal. This complicates theoretical strategies designed to simulate surface reactivity, most of which today are based on the Born–Oppenheimer approximation. One widely applied electronically nonadiabatic theory designed to make the leap beyond the Born–Oppenheimer approximation is “molecular dynamics with electronic friction”, where weak coupling of adsorbate motion to metal electrons is treated as a frictional force field modifying the molecular dynamics in a systematic and simple way. This minireview describes recent experiments on energy transfer between small molecules and simple, well-ordered surfaces, which suggest that at least for certain systems, energy can be selectively transferred between a molecule and a single electron of the solid, a process that might better be described as an electron transfer reaction than as friction. These results point out that theoretical approaches that go beyond electron weak coupling and electronic friction will be needed to properly treat electronically nonadiabatic effects in surface chemistry.
Introduction
The Born–Oppenheimer approximation1 (BOA) forms the foundation for the majority of all approaches to theoretical chemistry. For many gas-phase reactions, especially at low total energies, there is excellent agreement between experimental and theoretical results, confirming the validity of the BOA for these systems.2–4 The situation is different for certain reactions at metal surfaces, where nonadiabatic coupling plays a crucial role in the energy transfer between the adsorbate and the substrate, and the BOA breaks down.5,6 Several theoretical approaches were developed to account for such effects, most of which are based on an electronic friction approach or which otherwise employ a weak coupling approximation.7–10 These models were successful in explaining many experimental results.11–16 In cases where friction theories are valid, their use is highly advantageous since friction theories represent a simple modification of the dynamics on an electronically adiabatic potential energy surface.Recent experiments give evidence that there also exists a “more severe” kind of Born–Oppenheimer breakdown,17–24 where friction theories—or theories that otherwise rely on a weak coupling approximation—are insufficient. This represents a particularly interesting class of molecule–surface interaction as it implies the need to develop novel approaches to dynamics that go beyond the BOA.
In this paper, we first present experiments showing the breakdown of the BOA for molecule–surface interactions. We point out why friction-based theoretical approaches are not sufficient to describe several key observations. We review modern theoretical models that go beyond the friction picture. Finally we speculate about possible future experiments that might help shed light on our understanding of nonadiabatic energy transfer at surfaces.
As this short introduction makes clear, this minireview is highly focused. We refer the reader to a number of more general reviews for a broader introduction to this field.6,25–32
Adsorbate vibrational relaxation lifetimes
Violation of the BOA in adsorbate interactions at metal surfaces has been inferred from the analysis of infrared lineshapes. For the C–O stretch vibration of carbon monoxide adsorbed on a single-crystal NaCl(100) surface, the linewidth can be as small as 0.09 cm−1, perhaps the narrowest linewidth ever measured for a molecule on a surface.33–37 This value sets a lower limit—limited by inhomogeneous broadening—of 50 ps to the vibrational lifetime.37 The true lifetime is, in fact, many orders of magnitude longer: a value of 43 ms was measured with time-resolved infrared fluorescence.38In stark contrast, linewidths of CO adsorbed on metal surfaces appear much broader. Many substrates including Ni, Ru, Pt and Cu have been investigated, and linewidths of a few cm−1 are consistently reported.6 The exclusion of other broadening mechanisms led to the conclusion that these lines are lifetime-broadened, with corresponding lifetimes of ∼1 ps. In other work on the M–H wagging mode of hydrogen atoms adsorbed on W(100) and Mo(100) surfaces, characteristically asymmetric Fano lineshapes were observed and explained as originating from coupling to electron-hole pair (EHP) excitation.39–41
When direct time resolved methods became available after the development of short pulse picosecond lasers,42,43 a value of 2.0 ± 1.0 ps was obtained for the lifetime of the C–O stretch vibration of CO in the c(2 × 2) overlayer on Cu(100);44 see Fig. 1. Lifetimes in the range of a few picoseconds were also observed for CO on other metal substrates.45–49 The obvious conclusion from comparing these results is that there are damping mechanisms for CO on metals that are not available for CO on NaCl.
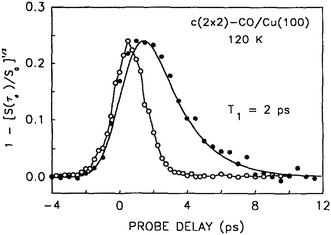 | ||
| Fig. 1 This shows the 2 ps decay of the CO/Cu stretch vibration, measured directly using picosecond pump–probe sum frequency generation spectroscopy. The laser pulse autocorrelation is shown as open circles. Reprinted with permission from ref. 44. Copyright 1992, American Institute of Physics. | ||
The basic theoretical picture that has been developed to explain vibrational lifetimes involves coupling from vibration to electron-hole pairs (V-EHP).11,12,50 Specifically, as a CO molecule approaches a metal surface, its 2π* affinity level (lowest unoccupied molecular orbital—LUMO) drops in energy due to an image-charge induced Coulomb interaction. Simultaneously, the level broadens into a resonance because the tunneling of electrons between the metal and the affinity level gives it a finite lifetime. The resulting state in the chemisorbed CO molecule is located near the Fermi energy, and the chemisorption bond is formed by partial charge transfer from the metal onto the molecule via the 2π* orbital. Since the 2π* orbital is anti-bonding in nature, as the molecule vibrates, the resonance state moves up and down in energy, causing charge to flow on and off the molecule. Using an Anderson-Newns Hamiltonian51,52 and time-dependent perturbation theory (Fermi's golden rule), it can be shown that the electron-vibration coupling through the 2π* orbital leads to damping of the vibrational motion, with the damping rate given by 1/τ = 2πΩ(δn)2, where Ω is the vibrational frequency, and δn is the fluctuation of the number of electrons in the affinity level during one vibrational period.12 From the experimentally determined dynamic dipole moments of chemisorbed and free CO molecules, the authors estimated that δn = 0.03, from which a lifetime of τ = 1.8 ps is obtained for CO on Cu(100), in perfect agreement with the experiment. More sophisticated cluster-based models were developed, incorporating ab initio discrete variational SCF53,54 and ab initio Hartree–Fock calculations.14,15 Both models support the general picture introduced above, and both yield similar results for the vibrational lifetime of CO on Cu(100), 1.3 ps and 1.7 ps, respectively.
Electronic friction models, which incorporate the dissipation of vibrational energy to EHP excitations in an average way by a friction coefficient, had long been used to describe the interaction between adsorbates and metal surfaces.7–10 Such models were successfully applied to calculate the vibrational lifetimes of adsorbed molecules,55 diffusion,56,57 sticking probabilities,58 and chemi-currents.59 The most popular version of electronic friction theory now employed—molecular dynamics with electronic friction60—was also shown to give good agreement with experimental lifetimes, to be conceptually equivalent with a Fermi golden rule approach and perhaps most importantly, to allow the calculation of friction coefficients from ab initio electronic structure theory.60,61
Molecular-beam surface scattering experiments
The use of molecular beams provides an appealing approach to the study of energy transfer between molecules and surfaces. A molecular beam is generated by expanding a gas at high stagnation pressure through a small nozzle into a vacuum chamber. The supersonic expansion leads to redistribution of the thermal energy such that the resulting beam is translationally and rotationally cooled.62 For a beam formed in a nozzle at ∼300 K, essentially all molecules are in their electronic and vibrational ground states, the spread of molecular velocities is small (Δv/v ∼ 5–10%), and rotational temperatures of less than 20 K can be obtained.62,63 The mean velocity of the molecules can be adjusted over a fairly wide range using seed gases with higher or lower molecular weight and varying the nozzle temperature. Laser-based excitation and detection schemes may be used to prepare molecules in specific quantum states and to measure the quantum state distribution of the molecules after scattering from the surface.Molecular beam experiments provided the first direct observation of vibrational excitation in molecule–surface collisions.5NO molecules in their vibrational ground state were scattered from a Ag(111) surface, and their vibrational distribution was analyzed after the collision for various surface temperatures, TS, and translational incidence energies, EI. Arrhenius-like TS dependence and strong threshold-less EI dependence of the vibrational excitation probability, P, are hallmarks of this experiment; see Fig. 2 for an example of threshold-less incidence energy dependence. The Arrhenius temperature dependence, P = A exp(−ΔEvib/kTS), results from the thermal availability of EHPs that have enough energy to promote NO from v = 0 to v = 1. The absence of a threshold in the incidence energy dependence shows that kinetic energy is not converted to vibration, but rather that vibration is excited by energy transfer from the surface. Similar observations have been made for NO scattering from Cu(110),64 Au(111),22 and HCl scattering from Au(111).65
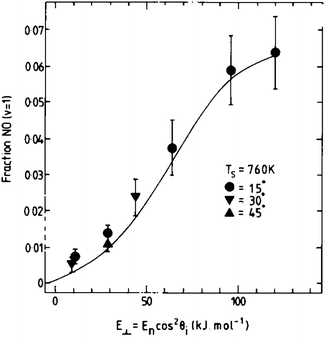 | ||
| Fig. 2 The probability of vibrational excitation in NO/Ag(111) collisions exhibits a characteristic threshold-less incidence energy dependence. Reproduced from ref. 13. | ||
These data contrast experimental observations on excitation of the NH3 “umbrella inversion” vibrational mode after scattering from a Au(111) surface.66 Here, the excitation probabilities are high, even for multiquantum excitation, and even at moderate incidence energies; the excitation probabilities are practically independent of surface temperature; and the excitation probabilities exhibit clear thresholds at incidence energies that match the vibrational excitation energies. The NH3/Au system is an example of a mechanically inelastic collision, which can be perfectly understood in an electronically adiabatic picture.67 The scattering and dissociative adsorption of H2/D2 from a Cu(111) surface is another example of an adiabatic mechanism.68,69
The incidence energy dependence for NO/Ag(111) was successfully reproduced using a one-dimensional analytical model,13 as shown by the solid line in Fig. 2. The model is based on a modified Anderson-Newns Hamiltonian,51,52 where the molecular vibrational excitation is due to de-excitation of an EHP in the metal, mediated by temporary formation of a negative ion. The strength of the nonadiabatic coupling between the molecular vibration and the charge state of the molecule is derived from a displaced harmonic oscillator approach. The probability for vibrational excitation is obtained by integrating over a classical trajectory. Despite its differences with electronic friction methods—for example there is no weak coupling approximation in this model—we point out that this approach is still restricted to single quantum transitions.
It is obvious that electronic friction models will fail to describe experiments in which the nonadiabatic coupling is not weak and/or the interaction time is not short. The restriction to single quantum transitions is also potentially problematic, since one can imagine many vibrational quanta of energy coupling to a single EHP. Experimental evidence for strong nonadiabatic coupling and for multiquantum transitions has indeed been observed over the last decade, as we will show in the next section.
Recent experiments suggesting the existence of a strong coupling regime
We now describe three related but different experiments that suggest a need for a new kind of theory of electronically nonadiabatic interactions, one that correctly describes strong interaction incompatible with the electronic friction model and other related models that rely on a weak coupling approximation.Vibrationally promoted electron transfer
The first of these three experiments probes the relaxation of highly vibrationally excited NO molecules upon scattering from metallic Au(111) and insulating LiF surfaces.18 The molecular beam conditions were chosen such that the kinetic energy was only 5 kJ mol−1 for scattering from Au but 38 kJ mol−1 for scattering from LiF. Stimulated emission pumping (SEP)70,71 was used to prepare NO in highly excited vibrational states, e.g. v = 12, 15. The scattered molecules were state-selectively detected using resonance-enhanced multiphoton ionization (REMPI).For molecules scattered from the gold surface, only a few percent emerge in their initial vibrational state. Relaxation from v = 15 to every state from v = 14 to v = 5 is observed, with the most probable transitions being to v = 7,8. This corresponds to a loss of seven to eight vibrational quanta, or more than 1.8 eV of vibrational energy. In a similar experiment, efficient multiquantum relaxation was also observed for NO scattering from Cu(111) and O/Cu(111).72,73 In contrast, for scattering of NO (v = 12) from LiF, there is little vibrational relaxation at any incidence energy studied, even at kinetic energies more than seven times as high as in the Au experiments. Small probabilities are found for relaxation to v = 11, 10, 9 (approximately 0.1, 0.05, 0.02 of the v = 12 signal) but the survival probability of the initial vibrational state is still as high as ∼90%; see Fig. 3.
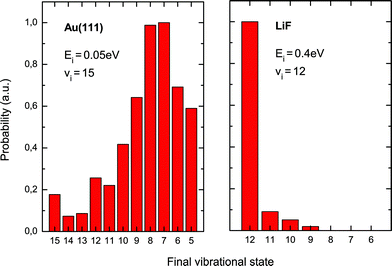 | ||
| Fig. 3 Efficiency of vibrational energy transfer is very different on Au and LiF. These data show scattering of high-vNO molecules from Au and from LiF. While NO (v = 15) loses several quanta of vibrational energy on Au, the incident state (v = 12) has a high survival probability on LiF. Adapted from ref. 18. | ||
The multiquantum vibrational relaxation seen in this work was explained by a vibrational autodetachment mechanism.19,21 Using known potential curves for gas-phase NO and NO− and correcting these gas-phase energy curves by the work function of Au, one may show that for NO at its equilibrium internuclear distance of 1.15 Å, there exists a 1.1 eV barrier for approach by the neutral to the anion curve crossing. That is, there is a substantial barrier to electron transfer. However at the outer turning point of a v = 15 classical vibration, the barrier disappears. This is due to the fact that the electron binding energy to NO depends strongly on internuclear separation: stretched NO bonds bind electrons more strongly. Thus, when NO approaches the surface in a high vibrational state, an electron can be transferred from the Fermi level of the substrate to the LUMO of the molecule to form NO− near the outer turning point of the vibration. As the bond subsequently compresses, the potential energy of the LUMO goes up dramatically (2–4 eV). Ejection of the electron from the LUMO to the unoccupied orbitals of the metal's conduction band high above the Fermi level is now possible. Owing to the large difference in equilibrium internuclear separation, the vibrational wave function will be projected to very different v states in the anion. When the electron jumps back to the surface, the vibrational wavefunctions will be at a different phase, and several vibrational states will be populated for the final neutral NO.74–76 Note that the electron cannot escape the surface, as the vibrational energy of the molecule does not exceed the surface work function.
A more sophisticated numerical implementation of this simple electron transfer mechanisms was later suggested.77–79 The model builds on a quantum-mechanical description of vibrational motion on the NO and NO− diabats, and it includes the coupling between them as a perturbation, which leads to electron hopping between the metal and the molecule. The metallic continuum is approximated by a number of discrete levels. The coupled electron-nuclear dynamics are calculated using independent electron surface hopping (IESH),80 with more than 1011 adiabatic states being taken into account. The authors find that vibrational relaxation is essentially absent in scattering from a surface without nonadiabatic coupling, and that when the nonadiabatic coupling is turned on, most of the vibrational energy is transferred in multiquantum transitions. The predicted vibrational state distributions are in approximate agreement with experiment.
It was argued that electronic friction theories cannot account for the widely accepted charge transfer mechanism, whereas the IESH approach intrinsically incorporates charge transfer. Moreover, electronic friction does not yield a broad vibrational distribution but only an average value for the loss of vibrational energy. In general, it cannot describe multiquantum relaxation, where several quanta of vibrational energy are transferred to a single electron.79
Recently, a perturbative approach with some features of electronic friction was used in an attempt to describe multiquantum vibrational relaxation of NO(v ≫ 0) on Au(111).16 This model accounts for quantized vibrations, wave packet interference and other quantum effects. In particular, it exhibits a selection rule, Δv = ±1, characteristic of friction-like methods. It was shown that a sequential single quantum relaxation appears similar to experimental observations like those shown in Fig. 3. The implication of this work is that the observed multiquantum vibrational relaxation is the consequence of many sequential single quantum transitions. We find this agreement interesting. Further insight could be gained by seeing if other experimentally observed aspects of NO/Au scattering can be captured by this approach, for example the vibrational insensitivity to trapping,81 as has been accomplished already with the IESH method,78 or the vibrational overtone excitation.22
We now present other related experiments that shed additional light on the nature of vibrationally promoted electron transfer, showing clearly that for multiquantum energy transfer, sequential single-quantum energy transfer is unimportant compared to direct multiquantum transitions.
Vibrationally promoted electron emission
When Cs covers Au(111) at sub-monolayer levels one obtains a low work function surface (Φ = 1.61 ± 0.08 eV).82 Scattering highly vibrationally excited NO from such a surface results in vibrationally promoted electron emission.19–21 In this experiment, a pulsed molecular beam of NO molecules at a kinetic energy of 29 meV is crossed with two laser beams for the preparation of vibrational states in the range v = 0–18 by SEP and Franck–Condon pumping. Note that molecules in the highest vibrational state (v = 18) carry more than 3.7 eV vibrational energy.20 If a large fraction of the molecule's vibrational energy can be transferred to a single electron, it can overcome the work function, escape the crystal and be detected. If, however, the vibrational energy were to be dissipated in sequential single quantum transitions, the excitation of a single electron above the work function would not occur.Fig. 4 shows the spectroscopic assignment of the observed electron emission signal. SEP uses one laser for excitation to an excited electronic state and a second laser for de-excitation to a highly vibrationally excited state of the ground electronic state. Electron emission (up-going signal) is detected as a function of the de-excitation laser's wavelength for two excitation transitions [Q21(0.5) and Q11(0.5)]. These spectra are compared to fluorescence depletion spectra (down-going signal) observed under identical conditions. The observed spectral resonances agree with known transitions of the A2Σ+(v = 3) to X2Π(v = 18) system of NO to better than the linewidth of the laser.19
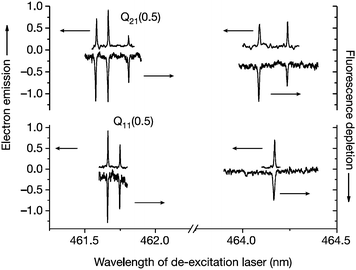 | ||
| Fig. 4 Exoelectrons are observed whenever NO vibration is excited. The up-going signal corresponds to electron emission; the down-going signal to the fluorescence depletion that indicates vibrational excitation in the electronic ground state. Reproduced from ref. 19. | ||
The electron emission signal as a function of the initial vibrational state is shown in Fig. 5. A threshold at v = 8 is observed. The energy of v = 8 is close to the substrate work function—gray bar in Fig. 5. Here one clearly sees that only when the vibrational energy exceeds the work function can exoelectrons be seen. This is a clear indicator that the vibrational energy of the molecule is directly converted to electron kinetic energy.
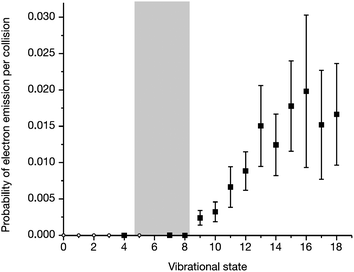 | ||
| Fig. 5 The threshold for electron emission approximately matches the surface work function, indicated by the gray bar. Reproduced from ref. 19. | ||
In a subsequent experiment, the dependence of the exoelectron quantum yield on the velocity of the incident molecules was observed by seeding the molecular beam in a variety of carrier gases.83 Over the range of 425 to 2500 m s−1, the electron yield varies inversely with velocity. This result was interpreted as indicating that (1) the nonadiabatic interactions take place in a defined region above the surface in which the molecule moves with constant velocity, and (2) that the nonadiabaticity is independent of velocity. The electron yield is then predicted to be proportional to the time the molecule spends in the “active” region. This picture is consistent with the vibrational autodetachment mechanism proposed earlier.21
Recently, electron energy distributions have been obtained which provide even stronger evidence for this interpretation. Here, a retarding-field hemispherical electron energy analyzer was employed, enabling the measurement of exoelectron kinetic energies.23 A molecular beam of NO molecules at a velocity of 430 m s−1 was prepared in v = 16 using SEP and scattered from a Cs-covered gold surface. The molecular vibrational energy of 3.3 eV exceeds the surface work function by 1.7 ± 0.1 eV. The measured exoelectron kinetic energy distribution is shown in Fig. 6. The most probable kinetic energy is seen at 0.5 eV, which corresponds to an excitation energy of 2.1 eV, assuming that the electron originates from the Fermi level. This value represents 64% of the available vibrational energy. In other words, about 11 quanta of vibrational energy are transferred to the kinetic energy of a single electron. The highest kinetic energies observed, Ekin ≈ 1.5 eV, correspond to excitation energies of 3.1 eV, or 95% of the initial vibrational energy, corresponding to conversion of the energy of 15 of the 16 vibrational quanta to electron kinetic energy.
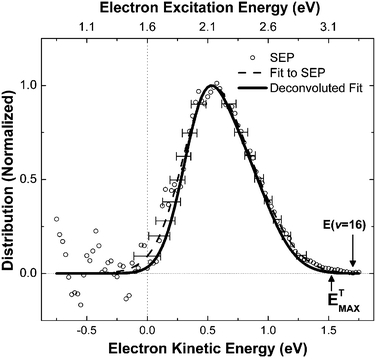 | ||
| Fig. 6 This shows the kinetic energy of the exoelectrons. Assuming excitation from the Fermi level, about 64% (Ekin = 0.5 eV) of vibrational energy is transferred to a single electron, and fractions of up to 95% (Ekin = 1.5 eV) are also observed. Reproduced from ref. 23 with permission of the PCCP Owner Societies. | ||
Thus far, only very limited attempts have been made to theoretically characterize the electron energy distribution observed in these experiments. Indeed, so far one can only make educated guesses based on comparison to IESH calculations done for the NO/Au(111) system.78,79 While IESH predicts a substantial probability that conduction electrons can be excited to ∼1.5 eV—that is, to an energy comparable to the Cs/Au work function—this effect appears to be still significantly smaller than is seen in experiments on Cs/Au. It is worth noting that friction theory predicts a much smaller excitation probability.78 IESH also predicts that the mean vibrational energy deposited into electronic excitation decreases with increasing incidence velocity,78 a result that is qualitatively similar to experimental observations for Cs/Au.
The presence of a cesium overlayer of course changes the chemical properties of the surface dramatically, and one might claim that the coupling of multiple vibrational quanta to a single electron is only possible on this peculiar surface. However very similar coupling is observed for vibrational excitation on a pure Au(111) surface, as will be shown in the following.
Vibrational overtone excitation
An important aspect of the experiments described above is the transfer of multiple quanta of vibration to a single electron. This process can hardly be described by the weak coupling models, as all of these approaches lead to a Δv = ±1 propensity. While multiquantum vibrational energy transfer to a single electron appears clearly for vibrational relaxation of highly vibrationally excited NO, it is not as obvious that the vibrational excitation of NO in collisions with metal surfaces follows a similar dynamic. This issue has recently been addressed experimentally.The experiments were performed on a scattering apparatus with a specially designed sample holder, which allows the sample to be heated over a wide range;63 see Fig. 7. The accessibility of high surface temperatures permits experiments that probe vibrational excitation of NO (v = 0) into both v = 1 and 2 during collisions with a hot Au(111) single crystal surface. Moreover, absolute excitation probabilities can be measured, which provide useful information about the absolute magnitude of nonadiabatic coupling.22
 | ||
| Fig. 7 This sample holder allows the sample to be heated to high temperatures. Heating is essential for the observation of overtone excitation in molecule–surface collisions due to the very low availability of EHPs at room temperature. Reprinted with permission from ref. 63. Copyright 2007, American Institute of Physics. | ||
Narrow angular distributions of the scattered molecules at all temperatures and for both v = 1 and v = 2 indicate that the collisions happen in a direct, “single bounce” mechanism for which short collision times are assumed. A trapping-desorption mechanism, which would yield a broad angular distribution, can be excluded.
The absolute probabilities measured for v = 1 and v = 2 excitation are shown in Fig. 8. The TS dependence follows an Arrhenius form with a slope equal to the vibrational energy gap of the channel in question. Application of a state-to-state kinetic model showed that sequential single quantum excitation was of minor relative importance in comparison to direct overtone excitation.22 Analysis of the Arrhenius TS dependence leads to a similar conclusion. We note that the pre-exponential factors, A0–v, always lie between 0 and 1 and that in a sequential single quantum mechanism, the overall prefactor is the product of two prefactors, one for each single quantum step.24 Thus, it is unlikely that A0–2 > A0–1 (as is observed in the experiment: A0–1 = 0.38 and A0–2 = 0.46) if sequential single quantum excitation were dominant. The experiments, rather, strongly suggest that direct overtone excitation, where a single EHP excites two quanta of vibration, is the dominant nonadiabatic excitation mechanism.
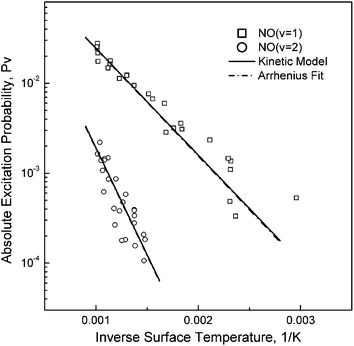 | ||
| Fig. 8 The surface temperature dependence of vibrational excitation shows Arrhenius behavior. Note that the prefactors are very similar for the two curves, indicating that the difference in excitation probability is largely due to thermal effects. Reproduced from ref. 24 with permission of the PCCP Owner Societies. | ||
This state-to-state rate model has been extended to analyze the TS dependence more thoroughly.24 In the framework of this model, the observed Arrhenius behavior for the excitation probabilities emerges as the low-temperature limit of a more general solution that approaches thermal equilibrium in the strong coupling limit. The model only fits the experimental data when the rate for direct overtone excitation is assumed to be much larger than that for multiple sequential single quantum excitations. Furthermore, the coupling strength for direct overtone excitation appears to be nearly as large (68%) as the coupling strength for single quantum excitation.
We emphasize that the finding that the vibrational excitation probabilities are higher for v = 1 than for v = 2 for all temperatures investigated is due to a thermal effect. The difference originates from the different number of EHPs with energies of one and two vibrational quanta, respectively. After accounting for this thermal factor, the results clearly show that the v = 2 excitation probability is remarkably high, providing strong evidence against a Δv = ±1 propensity rule. This experiment thus provides another clear example where multiple vibrational quanta are coupled to a single EHP; in this case the decay of a single thermally excited EHP is coupled to multiple quanta of vibrational excitation.
Prospects for future work
The possibility of measuring absolute probabilities for vibrational excitation and relaxation in molecular collisions with surfaces under highly defined conditions, and with potential variation of surface temperature, incidence angles and energies etc. provides an opportunity to provide key benchmark data important to the development of the next generation of nonadiabatic theories that are applicable in the strong coupling limit. In the final section of this paper we describe a number of promising experiments that relate to this need.The Newns model predicts a dependence of the vibrational excitation probabilities on the metal's work function and on the density of states near the Fermi energy. A systematic comparison of a series of metals with different densities of states at the Fermi level and different work functions is expected to provide us with important experimental data needed to test these ideas. Now that absolute excitation probabilities are available for NO scattering from Au, it is a simple matter to quantitatively obtain relative excitation probabilities on other surfaces, using a specially designed sample holder for multiple samples. In this way, the laboratory signals for new metals can be immediately compared to the NO/Au scattering system.
Similar experiments on refractory metals over a much wider range of TSprobe nonadiabatic interactions over the entire band of the metal. For example, using refractory metals, overtone excitation experiments like those presented here could be extended above TS = 2000 K. Based on our knowledge of detection sensitivities for vibrationally excited NO, we can expect to observe vibrational overtone excitation up to v = 5 or higher, if the coupling strengths are similar to what has been seen for NO (v = 0,1,2) on Au. By probing V-EHP coupling over such a wide energy range differential coupling over the band structure of the metal might be observable.
It is also possible to systematically modify surface electronic structure and study how this influences the molecular coupling to the solid. For example, one may imagine growing thin metallic layers by molecular beam epitaxy (MBE). Thin films with atomically uniform thickness have been grown over macroscopic areas.84 Such thin layers constitute one-dimensional potential wells for the conduction electrons, leading to quantization of their perpendicular momentum. The resulting quantum well states (QWS) have been experimentally verified using angle-resolved photoemission spectroscopy,85–87 and it is known that they can cause modulation of chemical reactivity88 or superconductivity84 as a function of layer thickness.
State-to-state molecular beam scattering experiments from such thin layers might lead to a deeper understanding of how the molecular energy exchange with solids can be tailored and controlled. By varying the metallic film thickness, one can control the energies of the QWSs, which might be expected to have a strong influence on the vibrational relaxation and excitation probabilities. For example, the spacing of the two lowest vibrational levels is 0.36 eV for HCl, which we estimate to be comparable to the energies needed for EHP formation in Pb films with about 30–40 atomic layers.88 Similar ideas might be developed using samples of quantum well states in GaN/AlGaN/GaN structures, buried a small number of nm below the surfaces, where the excited electronic states can still communicate with an adsorbate.
Another approach to modifying the surface electronic structure is to deposit nanoparticles of controlled composition and size onto an inert surface. Many nanoparticles exhibit a discrete electronic energy spectrum, and the electronic structure can be controlled by the particle size.89–91 Using a magnetron sputter source92 and a homebuilt mass filter,93 it should be possible to produce electronically quantized materials on surfaces that can be used in state-to-state scattering experiments. The possible enhancement or depression of vibrational relaxation or excitation at specific layer thicknesses or nanoparticle sizes is expected to provide additional insight into the mechanisms of nonadiabatic energy transfer.
One of the most heavily studied systems in surface dynamics is the H2/Cu dissociative adsorption; see for example ref. 94–97. The history of this system shows how extremely detailed our understanding of surface dynamics can be developed within an electronically adiabatic theoretical approach. It was argued that electronic adiabaticity is a general characteristic of H2/metal systems because their potential energy surfaces do not exhibit deep chemisorption wells, and the H2 molecule has negative electron affinity, such that electron transfer that could drive EHP excitation does not occur.98 Although chemical accuracy (1 kcal mol−1) was achieved in simulations of hydrogen dissociation on Cu(111),97 the limitations of the Born–Oppenheimer Static Surface (BOSS) model became apparent in simulations of vibrational excitation of H2 on Cu(111).99
Recent calculations show that the dissociative adsorption of HCl on Au(111) may occur at modest energies.100 In the meantime, there is extensive data showing that HCl on Au is subject to electronically nonadiabatic influences. Studying HCl dissociation on Au may be an excellent opportunity to examine the role of nonadiabatic interactions on reaction probabilities.
Translational inelasticity is at the heart of trapping, the initiating step of nearly all surface chemistry; yet the role of electronically nonadiabatic effects in translational inelasticity is another area where few experiments have been carried out. Using nearly mono-energetic H-atom beams produced from HI photolysis and Rydberg atom tagging to make high resolution measurements of scattering translational energy distributions, one may obtain high quality benchmark data on scattering systems that are accessible to first principles theoretical analysis.
Finally, we would like to point out that up to now ultrashort pulses of atoms and molecules are essentially unknown. We speculate that the development of a source of picosecond pulses of atoms or molecules would usher in a new era of pump–probe experiments, combining lasers with such sources. This would among other things allow the first scattering experiments to be carried out using laser-excited surfaces, a subject that would significantly enrich the study of electronically nonadiabatic interactions in surface dynamics.
From the experimenters' point of view, the following ideas for future theoretical development seem worthwhile to pursue: As at least one friction-like model16 was successful in calculating the vibrational relaxation probabilities for NO/Au(111) correctly, it would be interesting to see whether a similar model can also reproduce the vibrational overtone excitation observed for NO/Au(111). Another idea would be to take the incident molecule's spin into account. For example, it is known that the NO anion has singlet and triplet states, but even IESH, which semiquantitatively explains more than any competing approach, only considers one electronic state and neglects spin. Finally, it would be valuable to incorporate vacuum electronic states into the IESH model, in order to include the possibility of exoelectron excitation into the simulations. This would allow for a comparison with experiments on vibrationally promoted electron emission, which provide the most direct experimental evidence for the transfer of multiple quanta of vibrational energy to a single electron.
Conclusions
We have shown three experiments that suggest that in certain molecule–surface systems, energy is transferred between multiple quanta of molecular vibration and a single electron. This process cannot be understood in terms of a harmonic electronic friction theory nor in terms of related theories employing a weak coupling approximation. Indeed, the implications of the experiments are that the energy transfer process might be better described as an electron transfer reaction. In addition, we have suggested several experiments that we hope will contribute benchmark data to the development of new theories on nonadiabatic energy transfer beyond the electronic friction picture.Notes and references
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 84, 457–484 CAS.
- S. D. Chao, S. A. Harich, D. X. Dai, C. C. Wang, X. M. Yang and R. T. Skodje, J. Chem. Phys., 2002, 117, 8341–8361 CrossRef CAS.
- S. A. Harich, D. Dai, X. M. Yang, S. D. Chao and R. T. Skodje, J. Chem. Phys., 2002, 116, 4769–4772 CrossRef CAS.
- M. H. Qiu, Z. F. Ren, L. Che, D. X. Dai, S. A. Harich, X. Y. Wang, X. M. Yang, C. X. Xu, D. Q. Xie, M. Gustafsson, R. T. Skodje, Z. G. Sun and D. H. Zhang, Science, 2006, 311, 1440–1443 CrossRef.
- C. T. Rettner, F. Fabre, J. Kimman and D. J. Auerbach, Phys. Rev. Lett., 1985, 55, 1904–1907 CrossRef CAS.
- R. Ryberg, Adv. Chem. Phys., 1989, 76, 1–44 Search PubMed.
- W. L. Schaich, J. Chem. Phys., 1974, 60, 1087–1093 Search PubMed.
- W. L. Schaich, Surf. Sci., 1975, 49, 221–235 Search PubMed.
- E. G. d'Agliano, P. Kumar, W. Schaich and H. Suhl, Phys. Rev. B: Solid State, 1975, 11, 2122–2143 CrossRef.
- A. Nourtier, J Phys-Paris, 1977, 38, 479–502 Search PubMed.
- B. N. J. Persson and M. Persson, Surf. Sci., 1980, 97, 609–624 Search PubMed.
- B. N. J. Persson and M. Persson, Solid State Commun., 1980, 36, 175–179 CrossRef CAS.
- D. M. Newns, Surf. Sci., 1986, 171, 600–614 CrossRef CAS.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1992, 96, 3939–3949 CrossRef CAS.
- M. Head-Gordon and J. C. Tully, Phys. Rev. B: Condens. Matter, 1992, 46, 1853–1856 CrossRef CAS.
- S. Monturet and P. Saalfrank, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075404 CrossRef.
- H. Hou, Y. Huang, S. J. Gulding, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 1999, 284, 1647–1650 CrossRef CAS.
- Y. H. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114 CrossRef CAS.
- J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Nature, 2005, 433, 503–505 CrossRef CAS.
- J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, J. Vac. Sci. Technol., A, 2005, 23, 1085–1089 Search PubMed.
- J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2006, 124, 064702 CrossRef.
- R. Cooper, I. Rahinov, Z. S. Li, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Chem. Sci., 2010, 1, 55–61 RSC.
- J. LaRue, T. Schäfer, D. Matsiev, L. Velarde, N. H. Nahler, D. J. Auerbach and A. M. Wodtke, Phys. Chem. Chem. Phys., 2011, 13, 97–99 RSC.
- D. Matsiev, Z. S. Li, R. Cooper, I. Rahinov, C. Bartels, D. J. Auerbach and A. M. Wodtke, Phys. Chem. Chem. Phys., 2011, 13, 8153–8162 RSC.
- J. A. Barker and D. J. Auerbach, Surf. Sci. Rep., 1985, 4, 1–99 CrossRef.
- Y. J. Chabal, Surf. Sci. Rep., 1988, 8, 211–357 CrossRef CAS.
- G. E. Ewing, Int. Rev. Phys. Chem., 1991, 10, 391–425 Search PubMed.
- R. G. Tobin, Surf. Sci., 1987, 183, 226–250 CAS.
- J. C. Tully, Annu. Rev. Phys. Chem., 2000, 51, 153–178 CrossRef CAS.
- A. M. Wodtke, J. C. Tully and D. J. Auerbach, Int. Rev. Phys. Chem., 2004, 23, 513–539 CrossRef CAS.
- A. M. Wodtke, D. Matsiev and D. J. Auerbach, Prog. Surf. Sci., 2008, 83, 167–214 CrossRef CAS.
- M. S. Mizielinski and D. M. Bird, J. Chem. Phys., 2010, 132, 184704 CrossRef.
- H. H. Richardson and G. E. Ewing, J. Phys. Chem., 1987, 91, 5833–5835 CrossRef CAS.
- H. H. Richardson, H. C. Chang, C. Noda and G. E. Ewing, Surf. Sci., 1989, 216, 93–104 Search PubMed.
- C. Noda, H. H. Richardson and G. E. Ewing, J. Chem. Phys., 1990, 92, 2099–2105 CrossRef CAS.
- C. Noda and G. E. Ewing, Surf. Sci., 1990, 240, 181–192 CrossRef CAS.
- R. Disselkamp, H. C. Chang and G. E. Ewing, Surf. Sci., 1990, 240, 193–210 CrossRef CAS.
- H. C. Chang and G. E. Ewing, Phys. Rev. Lett., 1990, 65, 2125–2128 CrossRef CAS.
- Y. J. Chabal, Phys. Rev. Lett., 1985, 55, 845–848 Search PubMed.
- J. E. Reutt, Y. J. Chabal and S. B. Christman, Phys. Rev. B, 1988, 38, 3112–3132 Search PubMed.
- D. C. Langreth, Phys. Rev. Lett., 1985, 54, 126–129 Search PubMed.
- E. J. Heilweil, M. P. Casassa, R. R. Cavanagh and J. C. Stephenson, Annu. Rev. Phys. Chem., 1989, 40, 143–171 CrossRef CAS.
- H. Ueba, Prog. Surf. Sci., 1997, 55, 115–179 CrossRef CAS.
- M. Morin, N. J. Levinos and A. L. Harris, J. Chem. Phys., 1992, 96, 3950–3956 CrossRef CAS.
- J. D. Beckerle, M. P. Casassa, R. R. Cavanagh, E. J. Heilweil and J. C. Stephenson, Phys. Rev. Lett., 1990, 64, 2090–2093 CrossRef CAS.
- J. D. Beckerle, R. R. Cavanagh, M. P. Casassa, E. J. Heilweil and J. C. Stephenson, J. Chem. Phys., 1991, 95, 5403–5418 CrossRef CAS.
- M. Bonn, C. Hess, S. Funk, J. H. Miners, B. N. J. Persson, M. Wolf and G. Ertl, Phys. Rev. Lett., 2000, 84, 4653–4656 CrossRef CAS.
- M. Bonn, C. Hess and M. Wolf, J. Chem. Phys., 2001, 115, 7725–7735 CrossRef CAS.
- F. Fournier, W. Q. Zheng, S. Carrez, H. Dubost and B. Bourguignon, J. Chem. Phys., 2004, 121, 4839–4847 CrossRef CAS.
- P. Avouris and B. N. J. Persson, J. Phys. Chem., 1984, 88, 837–848 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1961, 1, 41–53 Search PubMed.
- D. M. Newns, Phys. Rev., 1969, 178, 1123–1135 CrossRef CAS.
- T. T. Rantala, A. Rosén and B. Hellsing, J. Electron Spectrosc. Relat. Phenom., 1986, 39, 173–181 Search PubMed.
- T. T. Rantala and A. Rosén, Phys. Rev. B, 1986, 34, 837–842 Search PubMed.
- B. Hellsing, M. Persson and B. I. Lundqvist, Surf. Sci., 1983, 126, 147–153 Search PubMed.
- B. N. J. Persson and A. I. Volokitin, J. Chem. Phys., 1995, 103, 8679–8683 Search PubMed.
- J. T. Kindt, J. C. Tully, M. Head-Gordon and M. A. Gomez, J. Chem. Phys., 1998, 109, 3629–3636 CrossRef CAS.
- K. Schönhammer and O. Gunnarsson, Phys. Rev. B, 1980, 22, 1629–1637 CrossRef.
- J. R. Trail, M. C. Graham, D. M. Bird, M. Persson and S. Holloway, Phys. Rev. Lett., 2002, 88, 166802 CrossRef CAS.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS.
- J. C. Tully, M. Gomez and M. Head-Gordon, J. Vac. Sci. Technol., A, 1993, 11, 1914–1920 CrossRef CAS.
- G. Scoles, ed., Atomic and Molecular Beam Methods - Volume I, Oxford University Press, 1988 Search PubMed.
- Q. Ran, D. Matsiev, A. M. Wodtke and D. J. Auerbach, Rev. Sci. Instrum., 2007, 78, 104104 CrossRef.
- E. K. Watts, J. L. W. Siders and G. O. Sitz, Surf. Sci., 1997, 374, 191–196 CrossRef CAS.
- Q. Ran, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Phys Rev Lett, 2007, 98 Search PubMed.
- B. D. Kay, T. D. Raymond and M. E. Coltrin, Phys. Rev. Lett., 1987, 59, 2792–2794 CrossRef CAS.
- L. Liu and H. Guo, Chem. Phys., 1996, 205, 179–190 Search PubMed.
- C. T. Rettner, D. J. Auerbach and H. A. Michelsen, Phys. Rev. Lett., 1992, 68, 2547–2550 CrossRef CAS.
- A. Hodgson, J. Moryl, P. Traversaro and H. Zhao, Nature, 1992, 356, 501–504 CrossRef CAS.
- C. E. Hamilton, J. L. Kinsey and R. W. Field, Annu. Rev. Phys. Chem., 1986, 37, 493–524 CrossRef CAS.
- M. Silva, R. Jongma, R. W. Field and A. M. Wodtke, Annu. Rev. Phys. Chem., 2001, 52, 811–852 CrossRef CAS.
- H. Hou, C. T. Rettner, D. J. Auerbach, Y. Huang, S. J. Gulding and A. M. Wodtke, Faraday Discuss., 1999, 181–200 Search PubMed.
- H. Hou, Y. Huang, S. J. Gulding, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 1999, 110, 10660–10663 CrossRef CAS.
- J. W. Gadzuk, J. Chem. Phys., 1983, 79, 6341–6348 CrossRef CAS.
- S. Holloway and J. W. Gadzuk, Surf. Sci., 1985, 152, 838–850 Search PubMed.
- S. Holloway and J. W. Gadzuk, J. Chem. Phys., 1985, 82, 5203–5215 CrossRef CAS.
- N. Shenvi, S. Roy, P. Parandekar and J. Tully, J. Chem. Phys., 2006, 125, 154703 CrossRef.
- N. Shenvi, S. Roy and J. C. Tully, Science, 2009, 326, 829–832 CrossRef CAS.
- N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107 CrossRef.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- A. M. Wodtke, H. Yuhui and D. J. Auerbach, Chem. Phys. Lett., 2005, 413, 326–330 CrossRef CAS.
- J. L. LaRue, J. D. White, N. H. Nahler, Z. Liu, Y. Sun, P. A. Pianetta, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2008, 129, 024709 CrossRef CAS.
- N. H. Nahler, J. D. White, J. LaRue, D. J. Auerbach and A. M. Wodtke, Science, 2008, 321, 1191–1194 CrossRef CAS.
- Y. Guo, Y. F. Zhang, X. Y. Bao, T. Z. Han, Z. Tang, L. X. Zhang, W. G. Zhu, E. G. Wang, Q. Niu, Z. Q. Qiu, J. F. Jia, Z. X. Zhao and Q. K. Xue, Science, 2004, 306, 1915–1917 Search PubMed.
- T. Miller, A. Samsavar, G. E. Franklin and T. C. Chiang, Phys. Rev. Lett., 1988, 61, 1404–1407 Search PubMed.
- J. J. Paggel, T. Miller and T. C. Chiang, Science, 1999, 283, 1709–1711 Search PubMed.
- L. Aballe, C. Rogero, P. Kratzer, S. Gokhale and K. Horn, Phys. Rev. Lett., 2001, 8715, 156801 Search PubMed.
- X. C. Ma, P. Jiang, Y. Qi, J. F. Jia, Y. Yang, W. H. Duan, W. X. Li, X. Bao, S. B. Zhang and Q. K. Xue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9204–9208 Search PubMed.
- C. Y. Cha, G. Ganteför and W. Eberhardt, J. Chem. Phys., 1993, 99, 6308–6312 Search PubMed.
- G. Wrigge, M. A. Hoffmann and B. von Issendorff, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 063201 Search PubMed.
- J. Zheng, C. W. Zhang and R. M. Dickson, Phys. Rev. Lett., 2004, 93, 077402 CrossRef.
- H. Haberland, M. Karrais and M. Mall, Z. Phys. D: At., Mol. Clusters, 1991, 20, 413–415 CrossRef CAS.
- B. von Issendorff and R. E. Palmer, Rev. Sci. Instrum., 1999, 70, 4497–4501 Search PubMed.
- H. A. Michelsen, C. T. Rettner and D. J. Auerbach, in Springer Series in Surface Science, Vol. 34: Surface Reactions, ed. R. J. Madix, Springer-VerlagBerlin Heidelberg, 1994 Search PubMed.
- A. Groß, Surf. Sci. Rep., 1998, 32, 291–340 CrossRef.
- G. J. Kroes, Science, 2008, 321, 794–797 CrossRef CAS.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G. J. Kroes, Science, 2009, 326, 832–834 CrossRef CAS.
- P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E. J. Baerends, G. J. Kroes and D. Farias, Science, 2006, 312, 86–89 CrossRef CAS.
- G. J. Kroes, C. Diaz, E. Pijper, R. A. Olsen and D. J. Auerbach, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20881–20886 Search PubMed.
- D. H. Zhang, personal communication.
| This journal is © The Royal Society of Chemistry 2011 |
