Adsorptions of hydrogen on graphene and other forms of carbon structures: First principle calculations

Abstract

Carbon can exist in various structural forms (graphite, graphene, graphene-nanoribbon and flake) and these are technologically very important materials. On the other hand, hydrogen incorporation in these materials can significantly affect their structural and electronic properties. As it is difficult to observe hydrogenation processes directly in experiment and to measure the electronic states at atomic scale, first-principle calculations are widely used to investigate the interaction between hydrogen and various carbon-based structures in past years. In this article, we briefly review work done in recent years, theoretical understanding on the interaction between hydrogen and different forms of carbon materials and present a number of strategies to modify the properties of carbon-based systems.

---

Yunhao Lu

Y H Lu received his Bachelor of Science degree and PhD from Zhejiang University, China, in 2003 and 2008, respectively. Subsequently, he worked as a research fellow in the Computational Physics Group of National University of Singapore, where he focused on computational materials science. He joined Zhejiang University, China, in 2010 and has been a faculty member since. His current research interests include new materials based on carbon, surfaces and interfaces of oxides and optical properties of semiconductors.

Yuan Ping Feng

Y P Feng received his Bachelor of Science degree from Lanzhou University, China, in 1982 and PhD from Illinois Institute of Technology in 1987. After a 3-year postdoc stint at Purdue University, he joined the National University of Singapore in 1990 and has been a faculty member since. His research interest is in computational condensed matter & materials physics, focusing mainly on the understanding of fundamental properties of materials for advanced technologies, and prediction of new materials based on ab initio electronic structure calculations.

---

1. Introduction

Carbon is a key element of life and is the basis of all organic chemistry. Its bonding is so flexible that there exists an unlimited number of carbon-based structures with diverse physical properties. These physical properties are related to the dimensionality of these structures. Graphite, a three dimensional (3D) allotrope of carbon, has been well studied for a long time. For certain applications, fewer and fewer layers of graphite are required and their properties have been studied. An explosion of interest was ignited by the discovery of graphene,¹ a single layer of graphite. Graphene is a single sheet of carbon arranged in a honeycomb structure. This is an exact two dimensional (2D) system as thin as one atomic layer, which no one actually expected to exist in the free state before. The most interesting property of graphene is its electronic structure.² Its low-energy excitations are massless chiral Dirac fermions. In neutral graphene, the chemical potential crosses exactly the Dirac point. This peculiar dispersion ensures high carrier mobility in graphene which can reach as high as 1/300 of the speed of light based on theoretical prediction. Moreover, the planar structure of graphene is comparable to the current industrial top-down technologies. It is promising to fabricate high-performance electronic devices based on graphene with shorter channel lengths and higher speeds without encountering the adverse short channel effects that restrict the performance of silicon based devices.³

On the other hand, hydrogen is the lightest element in the cosmos and the energy source of nuclear fusion that keeps our universe alive. The combination of hydrogen and carbon brings us many essential products in our life, from plastic bags to keyboards, or from tyres to aircraft. Many of the theoretically interesting and practically useful properties of carbon-based systems are results of interactions between hydrogen and carbon which have been extensively investigated in recent years. First-principles calculations have played a crucial role in providing theoretical understanding on the unique properties of these systems and in predicting new carbon-based materials. Here, we review results of recent first-principles studies on interactions between hydrogen and different forms of carbon materials, i.e., graphite (3D), graphene (2D), graphene-nanoribbon (1D) and graphene-nanoflake (0D).

2. Graphite

The reaction between hydrogen and graphite has been experimentally investigated for about half of a century. Breisach et al.⁴ first analyzed the products of graphite thermally reacted with hydrogen at different temperatures by gas-chromatography in 1963 and found a minimum reaction temperature of above 600 K. Recently, carbon-based nanomaterials have been investigated as promising materials for hydrogen strorage.⁵ The interaction between hydrogen and graphite thus has attracted much attention and a lot of efforts were made to understand adsorption sites and the energy of hydrogen in graphite layers. Fukunaga et al.⁶ performed neutron diffraction experiments to locate the D atoms in the deuterated nanographite produced by mechanical alloying. Their results show two types of deuterium positions in the nanographite. Thermal desorption mass spectroscopy⁷ and electron energy-loss spectroscopy⁸ of the deuterated nanographite also confirmed these results. It was suggested that 80% of the total amount of hydrogen is located in the graphite layers and the remaining 20% at the edges of graphite. First-principles calculations indicated that it is more favorable for hydrogen to exist as atomic hydrogen rather than as molecular hydrogen between the graphite layers and the relaxation of the carbon atoms allows the hydrogen atom to find effective reaction pathways and stable adsorption sites in the graphite layers.⁹ The relaxation of the constituent carbon atoms is crucial in determining the final configuration of the hydrogen atom and surprisingly, the most stable position of hydrogen atom is between two carbon atoms directly above and below it, respectively. However, the hydrogen atom is closer to one of them, rather than exactly in the middle of them. As shown in Fig. 1, the C atom that is nearer to the H atom relaxes 0.26–0.33 Å towards the hydrogen atom, while the other C atom, which is located much farther away in the other layer hardly moves. The H atom finally takes a position 1.11–1.15 Å from one of the C atoms and 1.87–1.98 Å from the other. Due to the large relaxation of the nearest C atom, the migration of atomic hydrogen in graphite requires coordinated motion of the lattice distortion. A hydrogen jump has to be viewed as a cooperative process involving a coupled motion of the H atom and the relaxation of the associated C atom, which helps appreciably to enhance the atom diffusion. An activation energy of about 0.4 eV was found for a H atom to diffuse from one C atom to a neighbouring one.^10,11 In the case of carbon vacancy assisted diffusion of H atoms in bulk graphite, the H atom has a strong tendency to move toward the vacancy, rather than away from it. The energy barrier for diffusion of one H atom between two adjacent carbon atoms near the vacancy is twice of the energy needed for an atomic H to diffuse in defect-free graphite while the barrier energy for H diffusing into the vacancy is only 0.5 eV, similar to that of an atomic H diffusing in defect-free graphite.¹¹

Fig. 1 The geometry of the H atom in the graphite layers.⁹

Ferromagnetism was also observed in proton irradiated graphite examples^12–14 and first-principle calculations confirmed that the macroscopic magnetic signal is due to vacancy-hydrogen complexes.^11,15,16

The interaction between hydrogen atom and the (101̄0) graphite edge is much stronger than that between interstitial hydrogen and graphite. This process is also exothermic and has relatively small barriers.¹⁷ On armchair edges, when H₂ is oriented parallel to and immediately above one of the graphite sheets, the barrier hindering dissociation is 1.7 eV. However, when the H–H bond is perpendicular to the graphene sheets, the barrier drops down to 0.5 eV.¹⁸ On zigzag edges, on the contrary, the dissociation is barrierless when H₂ is constrained to dissociate over the site formed by two parallel graphene planes.¹⁹ These results indicate different scattering and adsorption behaviors of H₂ on the armchair edge and on the zigzag edge.²⁰ One H atom can be chemisorbed directly on an edge carbon, with a binding energy of roughly 5 eV and two hydrogen atoms can be co-chemisorbed on the same edge carbon atom, with a binding energy of roughly 3.9 eV per C–H bond at a 50% coverage.¹⁷ As it requires much energy to insert a gas-phase H₂ between the layers of graphite, it is possible that H₂ dissociatively adsorbs at the edge sites and then H atoms could migrate along or between the sheets, into the interstitial region.

As the van der Waals (vdW) interaction between layers of graphite is very weak and has little effect on the graphite (0001) surface, the interaction of hydrogen molecule or atom with graphite (0001) surface is very similar to that between layers of graphite or graphene, which is discussed in next section.

3. Graphene

The discovery of graphene, the first truly two-dimensional crystal, and its exotic electronic properties²¹ initiated an explosion of interest in carbon materials. However, the interaction between hydrogen molecule/atom and graphene was investigated much earlier, motivated by systematic studies of other carbon nanostructures, e.g.carbon nanotubes.^22–26

3.1 H₂ molecule

The interaction between H₂ and graphene is similar to that between H₂ and the graphite (0001) surface as the hydrogen molecule is physically adsorbed on graphene through vdW interactions. Although it is well-known that DFT functionals cannot accurately describe all the characteristics of molecular interactions,²⁷ especially vdW interactions,^28–30 in some cases, the LDA does yield good agreement with experimental results through fortuitous error cancellations between exchange and correlation energy approximations.^28,30,31 A vdW corrected DFT functional gave a binding energy of 60 meV for a hydrogen molecule adsorbed on a graphene layer, which falls between the values by uncorrected LDA (86–92 meV) and GGA (4 meV) functionals,³⁰ and is very close to the experimental value (40 meV).³² This interaction is weakened at elevated temperature.^33,34 The axis of the hydrogen molecule was found parallel to the graphene plane. Fig. 2(a) shows the potential energy as a function of the graphene-hydrogen separation with the three mostly commonly used functionals.³⁵ The interaction is attractive in certain regions but becomes repulsive at short separation. The interaction between H₂ and the graphene layer is mainly the London dispersion and can be somewhat understood by the overlapping between the σ orbital of H₂ and π states of graphene, and formation of bonding and antibonding states. As the hydrogen approaches the graphene surface, this interaction is initially attractive as a weak dipole is induced on the hydrogen molecule at large separation as shown in Fig. 2(b). However, at small separation, the electron density becomes highly distorted (Fig. 2(c)) and the repulsive force due to the filled antibonding states creates an energy barrier for adsorption of molecular hydrogen. If the energy barrier is overcome, the hydrogen molecule dissociates and becomes chemisorbed on the graphene. For physisorption of a hydrogen molecule on a planar graphene, the adsorption energy does not depend much on adsorption sites. Furthermore, the potential energy curve of a H₂–H₂ interaction is almost repulsive.²⁴ These results suggest that the close-packed trigonal lattice is more favorable than the square lattice as a physisorption structure of molecular hydrogen on a planar graphene sheet. It was also found that the curvature is important for the interaction between molecular hydrogen and graphene and the physisorption energy of H₂ on curved graphene can be enhanced up to about three times of that on planar graphene.²⁴

Fig. 2 (a) Variation of potential energy with the separation between the graphene sheet and the center of mass of the hydrogen molecule obtained using the LDA VWN functional (empty square), the GGA PW91 functional (filled circle) and the GGA PBE functional (empty triangle). Inset: close up of the potential-energy minima. (b) & (c) Contour maps of the change in electron density for a hydrogen molecule placed 7 Å and 2 Å, respectively, from the graphene sheet. The H–H bond of H₂ is parallel to the graphene plane and crosses the center of hexagonal carbon ring perpendicularly to the C–C bond. Four carbon atoms in the graphene matrix are labeled by black points at the bottom of the figure. Scale bar is in units of e Å⁻³.³⁵

Until now, direct dissociation of a hydrogen molecule on a graphene or graphite (0001) surface without catalysts has not been reported, due to the high activation barrier. First-principles calculation predicted an activation barrier of 4.3 eV for H₂ dissociation on an unrelaxed graphene.²⁶ If the carbon atoms are allowed to relax, the activation barrier estimated by GGA decreases to 3.3 eV, while the minimum barrier energy determined by LDA is lower (2.38 eV).¹¹ The relaxation of carbon atoms results in an effective reaction pathway for dissociation of H₂ on graphene. If there exist carbon vacancies in the graphene sheet, the dissociation barrier of hydrogen molecule can be as low as 0.63 eV. This is because chemisorption of atomic hydrogen on carbon atoms around a carbon vacancy is much more energetically favored.¹¹ Adsorption of hydrogen also enhances the magnetic properties of graphene due to carbon vacancies because saturation of a dangling bond around a carbon vacancy doubles the magnetic moment of the naked vacancy.¹⁵ It was also proposed that a moderate stress³⁶ or electric field³⁷ applied to the graphene plane can lower the reaction barrier of H₂ dissociation by a factor of 6 and change the process from endothermic to exothermic.

3.2 H atom

3.2.1 Single H atom. It is interesting that a single H atom can also be physically adsorbed on graphene, in a broad region around 4 Å above the plane which does not depend on the adsorption site,^38,39 even though the physisorption energy is somewhat underestimated compared to the experimental results. A physisorbed H atom can diffuse on the graphene with essentially no energy barrier. It can recombine with another H atom and desorb at a relatively low temperature.³⁹ The physisorption region and chemisorption region of the H atom on graphene are separated by an energy barrier at about 1.5 Å above a carbon atom.^38,39At larger separation, the interaction between atomic H and graphene is purely repulsive because there is no unpaired electron available on (singlet) graphene to bind with the (doublet) hydrogen. At a small separation, however, the unpaired electron induced by the buckling of carbon atoms gives rise to an attractive, barrierless interaction with the H 1s lone electron.⁴⁰

When a single H atom approaches the graphene plane, it interacts with a π electron of graphene, triggering orbital rehybridization of a C atom from a planar sp² to a partially tetrahedral sp³ configuration. This pulls the rehybridized C atom out of the layer plane^38,39 and induces apparent distortions of the second and third neighbors of the hydrogen-bonded carbon atom.^40,41 Since only about 0.2 eV of energy are required for this electronic and nuclear rearrangement, sticking of a hydrogen atom turns out to be a thermally activated process though it hardly occurs at and below room temperature.⁴² The lowest energy diffusion pathway for a single hydrogen atom is from one carbon atom to the neighboring one along the bond between them, with an energy barrier of 1.19 eV. In comparison, the energy barrier for the path across the center of the hexagonal carbon ring is 1.84 eV.¹¹ This implies that H atom prefers to move along the C–C bonds, rather than traverse above the hexagonal carbon rings.

Adsorption of single atomic hydrogen on graphene opens a substantial gap between the occupied and unoccupied graphene bands and is accompanied by a spin-polarized gap state,⁴³ as shown in Fig. 3. An H atom binds covalently to an sp³carbon puckered out from the sheet, leaving an electron localized on the lattice, resulting in a magnetic moment of 1 μ_B. On the other hand, if the graphene plane is constrained to be flat and sp²-sp³ rehybridization is forbidden, the self-interaction error should be considered to get the correct magnetic properties due to fractional electron occupations in the two bands closest to the Fermi energy.⁴⁴ The magnetism of a single H atom adsorbed graphene sheet can be explained by a tight-binding model for bipartite lattices⁴⁵ and apparently only single-atom defects unequally distributed over the two sublattices may result in a net magnetic moment in graphene-based materials.¹⁶

Fig. 3 (a) Top view, (b) side view, and (c) band structure of H (light sphere) adsorbed on a graphene sheet. The system is modeled using a supercell consisting of 32 carbon atoms. Spin-up and spin-down channels are represented by dark (blue) and light (red) lines, respectively.⁴³

Although the geometries of hydrogen atoms on graphene have been identified experimentally,^46,47 direct observation of local magnetism of this system is difficult, possibly due to accumulation of extra charge around chemisorbed H, which tends to quench the magnetism and recover the Dirac point.⁴⁸ This magnetic property is also not stable against certain defects, such as the Stone-Wales defect, anywhere in the graphene sheet, which quench the spin-polarized state through rotation of the C–C bonds even at low concentration.⁴³

3.2.2 H dimer. If one more H atom is introduced so that two H atoms are adsorbed on graphene simultaneously, it was found that the secondary H atom prefers to be adsorbed on the different sublattice from the first one,^40,49,50 without any sticking barrier.^51,52 Its binding energy is much larger than that of a single H atom. The two most stable adsorption structures are ortho and para configurations,^49,50 which are in agreement with the hydrogen dimers identified experimentally.^47,52–55 However, only one of them can recombine directly for desorption.⁵⁴ Adsorption of two H atoms on two different sublattices gives rise to a nonmagnetic state.⁵⁰ In contrast, when two H atoms are adsorbed on the same sublattice, the ground state of the H–H pair is a triplet with a magnetic moment of 2μ_B. These findings agree with Lieb's theorem⁵⁶ for the repulsive Hubbard model of a bipartite lattice and a half-filled band.

3.2.3 H clusters and graphane. Further adsorption of chemisorbed H atoms leads to a collective stabilization mediated by cooperative alternate puckering in the underlying carbon sheet. After chemisorptions of several H atoms, the further H adsorption becomes more and more favorable.^40,41,57 Eventually, hydrogen adsorbate clusters form on graphene⁵⁵ through a unique formation mechanism which is different from diffusing mechanism.⁵² Once hydrogen atoms are adsorbed on the surface, the adsorption barriers for hydrogen in the vicinity of the already adsorbed H atoms on the graphene are much reduced or even vanishing. Additional hydrogen atoms thus prefer to stick to the carbon atoms close to the already adsorbed H atoms and lead to growth of the clusters. It is expected that the global ground state of the partially hydrogenated graphene displays macroscopic phase separation between graphene and graphane regions.^55,58

If the hydrogen adsorbate clusters on graphene become large enough or all carbon atoms of graphene are bonded with hydrogen, graphane can be obtained, which was first proposed by first-principle calculation⁵⁹ and confirmed experimentally later.⁶⁰ The most stable configuration of graphane is a hexagonal network and the hydrogen atoms are bonded to carbon on both sides of the plane in an alternating manner, as shown in left panel of Fig. 4. As all carbon atoms are in sp³ hybridization, graphane becomes a good insulator^59,61 with a direct gap at Γ (Fig. 4, right panel), which can be modified by applying a strain in the elastic range.⁶² The gap size can be reduced by adjacent vacancy-defects without mid-gap states.⁶³ Due to the sp²-sp³ transformation, the spin–orbit couplings (SOC) induced band splittings near its valence band maximum may be increased by 4 orders of magnitude.⁶⁴ Moreover, it was predicted that an excitonic Bose-Einstein condensate may be observed experimentally in graphane due to strong electron-hole interaction.⁶⁵ However, metastable configurations may exist in real samples⁶⁶ and H frustrated domains with extensive corrugations may form in the early stages of the hydrogenation process.⁶⁷ These frustrations prevent the formation of large domains of perfect graphane-like structures. As a result, a partial H adsorbed graphene with random distribution patterns is generated. The random distribution patterns induce a random symmetry-breaking potential and allow the system to remain conductive at nonzero temperature via variable-range hopping.⁶⁸ On the other hand, this partial hydrogenation can change the mechanical properties of graphene drastically even at low coverage.⁶⁹Hydrogenation of bilayer graphane was also investigated using first-principles calculations and similar properties were predicted.^70,71

Fig. 4 Left panel: Structure of graphane in the chair conformation.⁵⁹ The carbon atoms are shown in gray and the hydrogen atoms in white. The figure shows the hexagonal network with carbon in the sp³ hybridization. Right panel: The GGA band structure (full lines) and the GW band structure (red dots) of graphane in the chair conformation.⁶¹ The top of the valence bands is chosen as the zero energy.

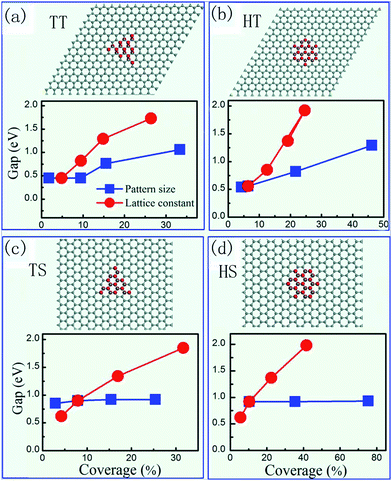
Although random partial hydrogenation cannot transform graphene to a semiconductor, it was predicted that a uniform bandgap can be opened by periodic modulations of the graphene lattice,⁷² and hydrogenation provides an effective way of achieving this.^73–76 Yang et al.⁷⁵ found that the geometry of edges of 2D H clusters on graphene is essential for the opening of an energy gap and the gap size is sensitively dependent on the shape, size and periodicity of the 2D patterns, as shown in Fig. 5. The periodic hydrogen structures have been successfully fabricated in experiment, confirming the band gap opening.^77,78Graphene quantum dots with interesting magnetic properties can also be obtained with hydrogen vacancy domains of different sizes and shapes.^79–81 Zhou et al.⁸² even proposed an extreme case 2D hydrogen pattern, named as graphone, where half of the carbon atoms within the same sublattice are hydrogenated. The localized and unpaired electrons in the unhydrogenated carbon atoms make graphone a high Curie temperature ferromagnetic semiconductor with a small indirect gap.⁸² The stability of interfaces between graphene and hydrogenated graphene (graphane) has been studied.^83,84 It was found that an atomically sharp graphene/graphane interface can be spontaneously generated against thermal disordering at a sufficiently high temperature.⁸³ The interface is stable even when the width of graphene is down to the limit of a single carbon chain.⁸⁴ Therefore, it is possible to make perfect graphene nanoribbons using the electrically insulating matrix of fully hydrogenated graphene (graphane) without cutting graphene.⁸⁵ In addition, the SOC is strongly amplified at the graphene/graphane interface, which may find applications in devices which are capable of converting spin polarizations to valley polarizations and vice versa.⁸⁶

Fig. 5 Energy gap vs. H coverage of graphene superlattice with armchair edges.⁷⁵ (a) Triangular pattern in triangular lattice (TT), (b) hexagonal pattern in triangular pattern lattice (HT), (c) triangular pattern in square lattice (TS), and (d) hexagonal pattern in square lattice (HS).

4. Carbon nanotube and graphene nanoribbon

4.1 Carbon nanotube

Carbon nanotube (CNT) is a well-known 1D carbon allotrope, which was first identified 20 years ago.⁸⁷ The interaction between hydrogen and CNT has been intensively investigated in the past as CNT was once viewed as the most promising medium for hydrogen storage.^88,89 However, undecorated CNTs do not meet the DOE target for hydrogen storage at ambient conditions. Some modifications in the structures or conditions are therefore necessary to make them ideal for storage requirements. More details can be found in a recent review paper written by Banerjee et al.⁹⁰ and references included. Here, we only give a brief introduction to the interaction between hydrogen and CNT, focusing mainly on results of first-principle calculations.

4.1.1 H₂ molecule. Single wall CNTs (SWCNTs) can be viewed as rolled-up cylinders of graphene and a H₂ molecule can be physically adsorbed on both inside and outside walls of the nanotube,^23,35 similar to adsorption on graphene. The interaction between H₂ and SWCNTs is site-independent but the most stable orientation of the H–H bond seems density-functional dependent.^35,91 However, the curvature of nanotube plays an important role in the hydrogen and CNT interaction. The curvature of the nanotube induces some degree of sp³ rehybridization that is absent in graphene. The sp³ rehybridization results in charge redistribution, and a small charge transfer between H₂ and SWCNTs.³⁵ Studies on molecular hydrogen on curved graphene revealed that the physisorption energy can be significantly increased over that on a planar graphene.²⁴Hydrogen molecule placed inside the nanotube has a larger binding energy than that on graphene or outer wall of the CNT, as the curvature of the nanotube makes more carbon atoms interact with the hydrogen molecule when it is adsorbed on the inner wall of the CNT.³⁵ Defects also affect adsorption of H₂ on SWCNTs, and the adsorption energy can be increased by 50% in the presence of structural defects in SWCNTs.⁹²

4.1.2 H atom. H atoms can be chemically adsorbed on SWCNTs if the hydrogen molecule has sufficient kinetic energy to overcome a substantial activation barrier and dissociates on the nanotube wall. The associated binding energy and electronic structure is dependent on the radius,⁹³ chirality,⁹⁴ coverage^57,95,96 and deformation^97,98 of the nanotube. H atoms were found to adsorb on SWCNTs in a row-by-row manner and the adsorbed H atoms form a belt around the axis of the tube.⁵⁷ For both zigzag and armchair nanotubes, hydrogenation of carbon atoms takes place alternatively on the inner and outer walls. The stable structure has a very weak curvature dependence and a large band gap.⁹⁹ Full hydrogen coverage is possible only for nanotubes of small sizes.⁹³ The distribution of hydrogen atoms on the CNT surfaces has a significant effect on the magnetic order of the hydrogenated SWCNTs.^98,100 Similar to graphene, H adsorption on both sublattices is more stable than on only one sublattice and flat bands appear at the Fermi energy in the latter structure, resulting in spontaneous magnetism.¹⁰⁰ Although most hydrogenated SWCNTs are insulating, zigzag nanotubes which are hydrogenated uniformly at half coverage are metallic with very high density of states at the Fermi level.⁹⁹ For double wall CNTs, the electronic properties of the inner tube remain unchanged when the outer tube is heavily hydrogenated. However, at low hydrogen coverage, adsorption of hydrogen on the outer tube affects the electronic structure of the inner tube.⁹⁵ Chemisorption of hydrogen weakens the C–C bonds of CNTs, which may lead to breaking of C–C bonds and disintegration of the tube wall in some cases.^101,102

4.2 Graphene nanoribbon

For graphene-based devices such as tunneling field-effect transistors, a band gap is required which can be created by the lateral confinement of charge carriers in graphene nanoribbons (GNRs),^103–105 Edge passivation of GNRs is crucial for thermodynamic stability of GNRs.¹⁰⁶ It is known that the formation energy of GNRs with hydrogen-terminated edges is much lower than that of GNRs with bare-edges.¹⁰⁷Hydrogen adsorption is energetically favored for all edge orientations even though the adsorption energy is larger on unreconstructed zigzag edges than on the armchair edge, and hydrogenation may lift reconstruction at the zigzag edge.¹⁰⁸ The edge structure and stability of hydrogen-terminated GNRs were found to be dependent on the hydrogen concentration in the environment.^109,110 At moderate hydrogen concentration, the most stable structures are the mono- and di-hydrogenated armchair edges as well as the zigzag edge with one di- and two mono-hydrogenated sites.¹¹¹ Fully mono-hydrogenated zigzag ribbons are stable only at extremely low ultravacuum pressures.¹¹¹ At high hydrogen concentration, graphene may spontaneously break into nanoribbons with di-hydrogenated armchair edges,¹¹¹ which has been observed experimentally.^112,113 Xiang et al.⁵⁸ suggested that H atoms first adsorb on the outermost bare carbon chain of one edge, and then on the outermost bare carbon chain of the other edge. This process of alternating hydrogenation could continue until all carbon atoms are hydrogenated. This mechanism may be useful for narrowing GNRs to a desired width.¹¹⁴

The electronic structures of GNRs are very sensitive to their edge terminations.¹¹⁵ It was shown that all armchair GNRs (AGNRs) with homogeneous mono-hydrogenated edges have finite band gaps which oscillate with the width, while zigzag GNRs (ZGNRs) with homogeneous mono-hydrogenated edges also have finite band gaps if antiferromagnetic ordering on both edges exists.^116,117 A hydrogen vacancy at the edge of ZGNRs introduces defect levels far away from the Fermi level and therefore does not affect the electronic and transport properties of ZGNRs near the Fermi level.¹¹⁸ The edge carbon atoms can be terminated by one or two hydrogen atoms, forming sp² and sp³-like bonds, respectively, at the edges as shown in left panel of Fig. 6. The band gaps of AGNRs vary continually over a wide range as a function of the percentage of sp³-like bonds at the edges (Fig. 6, right panel).¹¹⁹ For ZGNRs, the homogeneous sp³-like bonds at the edges open up a gap and destroy the magnetic ordering for narrow nanoribbon, whereas they become a metallic magnet with sufficiently large widths if antiferromagnetism across the ZGNR can be ordered ferromagnetically by an applied magnetic field.¹²⁰ Moreover, an intrinsic ferromagnetic order can be established in ZNGRs easily through saturation of carbon atoms on one edge by two hydrogen atoms and those on the other edge by one hydrogen atom.^121,122Hydrogen adsorption at the central part of GNRs has a great influence on the electronic and transport properties of the GNRs. Cantele et al.¹²³ reported that although the edge metallic states may be preserved for ZGNRs, bulk conducting channels can be easily destroyed by hydrogenation, resulting in devices with close to unity spin-polarized conductance. López-Bezanillaet al.¹²⁴ predicted that the sp³ nature of bonding of hydrogen on AGNRs gives rise to strong energy-dependent backscattering and its conduction decays rapidly with increasing density of these defects. Related to Lieb's theorem⁵⁶ discussed earlier, the hydrogen adsorption induced magnetic moments interact ferromagnetically or antiferromagnetically depending on whether hydrogens are adsorbed on one or both graphene sublattices. In addition, it was found that the magnitude of these interactions in GNRs is strongly dependent on the positions of the H atoms relative to the edges.¹²⁵ If all carbon atoms are hydrogenated, the GNRs become graphane nanoribbons with a direct wide-band-gap independent of the chirality.¹²⁶ If the hydrogen atoms on the edges are removed, adjacent dangling bonds of bare zigzag nanoribbons have antiferromagnetic ordering at the same edge while bare armchair nanoribbons remain nonmagnetic.¹²⁷ We also investigated hybrid graphane-graphene nanoribbons (partially hydrogenated GNRs) and found that the band structures of armchair hybrid nanoribbons are dominated by the graphene part and do not show spin-polarization.¹²⁸ On the other hand, the band gap and the spin-split defect level of zigzag hybrid nanoribbons can be controlled by the width of graphane or graphene section.¹²⁸ Apart from these, hydrogen terminations can significantly affect optical excitations¹⁰⁶ and thermal conductivity^129,130 of GNRs.

Fig. 6 Left panel: Perspective view of 9-AGNR showing edge atoms passivated by one or two hydrogen atoms and resulting sp² and sp³-like edge bonds. Right panel: Variation of band gaps of N-AGNR (N = 8,9,10) with percentage of sp³-like bonds.¹¹⁹

5. Graphene nanoflake and fullerene

5.1 Graphene nanoflake

Gan et al.¹⁰⁸ investigated the shape of 0D hydrogenated graphene nanoflakes systematically and found that the shape of unreconstructed graphene nanoflakes is determined by the hydrogen chemical potential. The equilibrium shapes of graphene nanoflakes are hexagonal with straight armchair edges at very low or very high hydrogen chemical potentials, as shown in Fig. 7(a) and (i), respectively. For intermediate values of the hydrogen chemical potential, the equilibrium shape of graphene nanoflake can be nearly hexagonal with zigzag facets and rounded edges, or up to twelve facets, as shown in Fig. 7(b)–(h). If the zigzag edges reconstruct, the thermodynamically favored shape of graphene nanoflakes still exhibits six fold symmetry, but with rounded rather than faceted edges. Graphene nanoflakes may be useful for spintronics as a spin-polarized current can be produced by pure hydrogenated graphene nanoflakes.^131,132

Fig. 7 Equilibrium shape of a graphene flake as a function of H₂ chemical potential. The values of H₂ chemical potential are as indicated. The red (blue) lines correspond to parts with (without) hydrogen termination.¹⁰⁸

5.2 Fullerene

Graphene flakes of certain shapes can be wrapped up into buckyballs, forming 0D fullerene, which was actually the first synthetic carbon allotrope.¹³³ Although the interaction between H₂ and neutral fullerene is weak, the binding strength of molecular hydrogen on either positively or negatively charged fullerenes can be dramatically enhanced due to the polarization of the hydrogen molecules by the high electric field near the surface of the charged fullerene.¹³⁴

6. Summary and outlook

In this article, we present a brief review on work related to the interactions between hydrogen and different forms of carbon materials, with a focus on results of first-principle calculations. Although the interaction between H₂ and various carbon structures is weak, the effect of H₂ on these systems cannot be ignored. The amount and patterns of hydrogens determine the electronic properties of the carbon systems. Hydrogenation can transform graphene-like systems from metallic to semiconducting or from nonmagnetic to magnetic. Both edge structures and electronic properties of nanoribbons and nanoflakes can be controlled by hydrogen adsorption. The process of hydrogenation are also discussed.

Further exploration in this area is probably to find an effective way to precisely control the hydrogenation processes for tuning electronic structures of graphene-like systems and understand its mechanism. For example, it was reported that the hydrogenation rate of graphene structure is layer-dependent,^135,136 which may be used to control the hydrogenation process. However, the relationship between hydrogenation process and number of layers has not been well established. On the other hand, the stacking order of graphene layers is shown to be important for magnetic property of multilayer graphene including defects.¹⁶ The mechanisms behind these phenomena are still unclear and further investigations are required. First-principle calculations enable us to understand the formation processes and the origins of unique electronic structures. They will provide proper explanation at the atomic scale, as these dynamic processes are often not directly observable in experiments and the localized electronic states are not easy to be measured. Given the more accurate functional (e.g. hybrid functional) accounting for weak interactions, the interactions between graphene-like structures and hydrogen can be fully understood and precise control of the hydrogenation processes can be realized based on quantitative knowledge obtained from first principle calculations.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
3. F. Schwierz, Nat. Nanotechnol., 2010, 5, 487.
4. P. Breisach and P. C. Marx, J. Am. Chem. Soc., 1963, 85, 3518.
5. T. A. Roman, W. A. Dino, H. Nakanishi, H. Kasai, T. Sugimoto and K. Tange, in Condensed Matter Theories, Vol 21, ed. H. Akai, A. Hosaka, H. Toki and F. B. Malik, Nova Science Publishers, Inc, Hauppauge, Editon edn, 2007, vol. 21, p. 275.
6. T. Fukunaga, K. Itoh, S. Orimo, M. Aoki and H. Fujii, J. Alloys Compd., 2001, 327, 224.
7. S. Orimo, T. Matsushima, H. Fujii, T. Fukunaga and G. Majer, J. Appl. Phys., 2001, 90, 1545.
8. T. Kimura, S. Muto, K. Tatsumi, T. Tanabe and T. Kiyobayashi, J. Alloys Compd., 2006, 413, 150.
9. W. A. Dino, Y. Miura, H. Nakanishi, H. Kasai and T. Sugimoto, J. Phys. Soc. Jpn., 2003, 72, 1867.
10. C. P. Herrero and R. Ramirez, J. Phys. D: Appl. Phys., 2010, 43, 255402.
11. Y. Lei, S. A. Shevlin, W. Zhu and Z. X. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 134114.
12. P. Esquinazi, A. Setzer, R. Höhne, C. Semmelhack, Y. Kopelevich, D. Spemann, T. Butz, B. Kohlstrunk and M. Lösche, Phys. Rev. B: Condens. Matter, 2002, 66, 024429.
13. P. Esquinazi, D. Spemann, R. Höhne, A. Setzer, K. H. Han and T. Butz, Phys. Rev. Lett., 2003, 91, 227201.
14. J. Barzola-Quiquia, P. Esquinazi, M. Rothermel, D. Spemann, T. Butz and N. García, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 161403.
15. P. O. Lehtinen, A. S. Foster, Y. Ma, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2004, 93, 187202.
16. O. V. Yazyev, Phys. Rev. Lett., 2008, 101, 037203.
17. X. W. Sha and B. Jackson, J. Am. Chem. Soc., 2004, 126, 13095.
18. W. A. Dino, Y. Miura, H. Nakanishi, H. Kasai, T. Sugimoto and T. Kondo, Solid State Commun., 2004, 132, 713.
19. W. A. Dino, H. Nakanishi, H. Kasai, T. Sugimoto and T. Kondo, eJ Surf Sci Nanotechnology, 2004, 2, 4.
20. N. B. Arboleda, H. Kasai, H. Nakanishi, W. A. Dino and T. Sugimoto, J. Appl. Phys., 2004, 96, 6331.
21. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
22. S. Hynek, W. Fuller and J. Bentley, Int. J. Hydrogen Energy, 1997, 22, 601.
23. J. S. Arellano, L. M. Molina, A. Rubio and J. A. Alonso, J. Chem. Phys., 2000, 112, 8114.
24. Y. Okamoto and Y. Miyamoto, J. Phys. Chem. B, 2001, 105, 3470.
25. M. K. Kostov, H. Cheng, A. C. Cooper and G. P. Pez, Phys. Rev. Lett., 2002, 89.
26. Y. Miura, H. Kasai, W. Dino, H. Nakanishi and T. Sugimoto, J. Appl. Phys., 2003, 93, 3395.
27. A. W. C. van den Berg, S. T. Bromley, J. C. Wojdel and J. C. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155428.
28. P. Lazić, Ž. Crljen, R. Brako and B. Gumhalter, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 245407.
29. M. Khantha, N. A. Cordero, L. M. Molina, J. A. Alonso and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125422.
30. A. J. Du and S. C. Smith, Nanotechnology, 2005, 16, 2118.
31. S. Rigamonti and C. R. Proetto, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235319.
32. G. Vidali, G. Ihm, H. Y. Kim and M. W. Cole, Surf. Sci. Rep., 1991, 12, 133.
33. S. Patchkovskii, J. S. Tse, S. N. Yurchenko, L. Zhechkov, T. Heine and G. Seifert, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10439.
34. T. Heine, L. Zhechkov and G. Seifert, Phys. Chem. Chem. Phys., 2004, 6, 980.
35. D. Henwood and J. D. Carey, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245413.
36. H. McKay, D. J. Wales, S. J. Jenkins, J. A. Verges and P. L. de Andres, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075425.
37. Z. M. Ao and F. M. Peeters, Appl. Phys. Lett., 2010, 96, 253106.
38. L. Jeloaica and V. Sidis, Chem. Phys. Lett., 1999, 300, 157.
39. X. W. Sha and B. Jackson, Surf. Sci., 2002, 496, 318.
40. S. Casolo, O. M. Lovvik, R. Martinazzo and G. F. Tantardini, J. Chem. Phys., 2009, 130, 054704.
41. D. W. Boukhvalov, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 035427.
42. Y. Ferro, F. Marinelli and A. Allouche, Chem. Phys. Lett., 2003, 368, 609.
43. E. J. Duplock, M. Scheffler and P. J. D. Lindan, Phys. Rev. Lett., 2004, 92, 225502.
44. S. Casolo, E. Flage-Larsen, O. M. Løvvik, G. R. Darling and G. F. Tantardini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205412.
45. M. Inui, S. A. Trugman and E. Abrahams, Phys. Rev. B: Condens. Matter, 1994, 49, 3190.
46. N. P. Guisinger, G. M. Rutter, J. N. Crain, P. N. First and J. A. Stroscio, Nano Lett., 2009, 9, 1462.
47. L. Hornekaer, W. Xu, R. Otero, E. Laegsgaard and F. Besenbacher, Chem. Phys. Lett., 2007, 446, 237.
48. J. A. Vergés and P. L. de Andres, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075423.
49. T. Roman, W. A. Dino, H. Nakanishi, H. Kasai, T. Sugimoto and K. Tange, Carbon, 2007, 45, 218.
50. Y. Ferro, D. Teillet-Billy, N. Rougeau, V. Sidis, S. Morisset and A. Allouche, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085417.
51. N. Rougeau, D. Teillet-Billy and V. Sidis, Chem. Phys. Lett., 2006, 431, 135.
52. L. Hornekær, E. Rauls, W. Xu, Ž. Šljivančanin, R. Otero, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 97, 186102.
53. A. Andree, M. Le Lay, T. Zecho and J. Kupper, Chem. Phys. Lett., 2006, 425, 99.
54. L. Hornekær, Ž. Šljivančanin, W. Xu, R. Otero, E. Rauls, I. Stensgaard, E. Lægsgaard, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2006, 96, 156104.
55. R. Balog, B. Jorgensen, J. Wells, E. Laegsgaard, P. Hofmann, F. Besenbacher and L. Hornekaer, J. Am. Chem. Soc., 2009, 131, 8744.
56. E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201.
57. D. Stojkovic, P. Zhang, P. E. Lammert and V. H. Crespi, Phys. Rev. B: Condens. Matter, 2003, 68, 195406.
58. H. J. Xiang, E. J. Kan, S. H. Wei, M. H. Whangbo and J. L. Yang, Nano Lett., 2009, 9, 4025.
59. J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401.
60. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610.
61. S. Lebègue, M. Klintenberg, O. Eriksson and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245117.
62. M. Topsakal, S. Cahangirov and S. Ciraci, Appl. Phys. Lett., 2010, 96, 091912.
63. B. S. Pujari and D. G. Kanhere, J. Phys. Chem. C, 2009, 113, 21063.
64. J. Zhou, Q. F. Liang and J. M. Dong, Carbon, 2010, 48, 1405.
65. P. Cudazzo, C. Attaccalite, I. V. Tokatly and A. Rubio, Phys. Rev. Lett., 2010, 104, 226804.
66. D. K. Samarakoon and X. Q. Wang, ACS Nano, 2009, 3, 4017.
67. M. Z. S. Flores, P. A. S. Autreto, S. B. Legoas and D. S. Galvao, Nanotechnology, 2009, 20, 465704.
68. B. Dora and K. Ziegler, New J. Phys., 2009, 11, 095006.
69. Q. X. Pei, Y. W. Zhang and V. B. Shenoy, Carbon, 2010, 48, 898.
70. O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245422.
71. L. A. Chernozatonskii, P. B. Sorokin, A. G. Kvashnin and D. G. Kvashnin, JETP Lett., 2009, 90, 134.
72. T. G. Pedersen, C. Flindt, J. Pedersen, N. A. Mortensen, A.-P. Jauho and K. Pedersen, Phys. Rev. Lett., 2008, 100, 136804.
73. L. A. Chernozatonskii, P. B. Sorokin and J. W. Bruning, Appl. Phys. Lett., 2007, 91, 183103.
74. L. A. Chernozatonskii, P. B. Sorokin, E. E. Belova, J. Bruning and A. S. Fedorov, JETP Lett., 2007, 85, 77.
75. M. Yang, A. Nurbawono, C. Zhang, Y. P. Feng and Ariando, Appl. Phys. Lett., 2010, 96, 193115.
76. L. A. Chernozatonskii and P. B. Sorokin, J. Phys. Chem. C, 2010, 114, 3225–3229.
77. R. Balog, B. Jorgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Laegsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekaer, Nat. Mater., 2010, 9, 315.
78. P. Sessi, J. R. Guest, M. Bode and N. P. Guisinger, Nano Lett., 2009, 9, 4343.
79. H. Sahin, C. Ataca and S. Ciraci, Appl. Phys. Lett., 2009, 95, 222510.
80. A. K. Singh, E. S. Penev and B. I. Yakobson, ACS Nano, 2010, 4, 3510.
81. M. H. Wu, X. J. Wu, Y. Gao and X. C. Zeng, J. Phys. Chem. C, 2010, 114, 139.
82. J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867.
83. L. A. Openov and A. I. Podlivaev, JETP Lett., 2009, 90, 459.
84. V. Tozzini and V. Pellegrini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 113404.
85. A. K. Singh and B. I. Yakobson, Nano Lett., 2009, 9, 1540.
86. M. J. Schmidt and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165439.
87. S. Iijima, Nature, 1991, 354, 56.
88. A. C. Dillon and M. J. Heben, Appl. Phys. A: Mater. Sci. Process., 2001, 72, 133–142.
89. A. C. Dillon, K. M. Jones, T. A. Bekkedahl, C. H. Kiang, D. S. Bethune and M. J. Heben, Nature, 1997, 386, 377–379.
90. S. Banerjee, S. Murad and I. K. Puri, Proc. IEEE, 2006, 94, 1806–1814.
91. S. S. Han and H. M. Lee, Carbon, 2004, 42, 2169–2177.
92. V. Gayathri and R. Geetha, Adsorption-Journal of the International Adsorption Society, 2007, 13, 53–59.
93. X. B. Yang and J. Ni, Physical Review B, 2006, 74.
94. V. Barone, J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 120, 7169–7173.
95. P. A. Denis, F. Iribarne and R. Faccio, J. Chem. Phys., 2009, 130.
96. F. H. Yang, A. J. Lachawiec and R. T. Yang, J. Phys. Chem. B, 2006, 110, 6236–6244.
97. O. Gulseren, T. Yildirim and S. Ciraci, Phys. Rev. Lett., 2001, 87, 116802.
98. D. Stojkovic, P. E. Lammert and V. H. Crespi, Phys. Rev. Lett., 2007, 99.
99. O. Gulseren, T. Yildirim and S. Ciraci, Phys. Rev. B: Condens. Matter, 2002, 66, 121401.
100. X. Y. Pei, X. P. Yang and J. M. Dong, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73.
101. J. S. Arellano, L. M. Molina, A. Rubio, M. J. Lopez and J. A. Alonso, J. Chem. Phys., 2002, 117, 2281–2288.
102. S. Berber and D. Tomanek, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80.
103. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
104. C. Stampfer, J. Güttinger, S. Hellmüller, F. Molitor, K. Ensslin and T. Ihn, Phys. Rev. Lett., 2009, 102, 056403.
105. P. Zhao, J. Chauhan and J. Guo, Nano Lett., 2009, 9, 684.
106. V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748.
107. S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041408.
108. C. K. Gan and D. J. Srolovitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125445.
109. Y. Kobayashi, K.-i. Fukui, T. Enoki, K. Kusakabe and Y. Kaburagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 193406.
110. P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. Lett., 2008, 101, 115502.
111. T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2008, 101, 096402.
112. X. Wang, Y. Ouyang, X. Li, H. Wang, J. Guo and H. Dai, Phys. Rev. Lett., 2008, 100, 206803.
113. X. L. Li, X. R. Wang, L. Zhang, S. W. Lee and H. J. Dai, Science, 2008, 319, 1229.
114. X. R. Wang and H. J. Dai, Nat. Chem., 2010, 2, 661–665.
115. F. Cervantes-Sodi, G. Csányi, S. Piscanec and A. C. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165427.
116. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97.
117. L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2007, 99.
118. T. B. Martins, A. J. R. da Silva, R. H. Miwa and A. Fazzio, Nano Lett., 2008, 8, 2293.
119. Y. H. Lu, R. Q. Wu, L. Shen, M. Yang, Z. D. Sha, Y. Q. Cai, P. M. He and Y. P. Feng, Appl. Phys. Lett., 2009, 94, 122111.
120. S. Bhandary, O. Eriksson, B. Sanyal and M. I. Katsnelson, arXiv:1005.5714v1, 2010.
121. B. Xu, J. Yin, Y. D. Xia, X. G. Wan, K. Jiang and Z. G. Liu, Appl. Phys. Lett., 2010, 96.
122. K. Kusakabe and M. Maruyama, Phys. Rev. B: Condens. Matter, 2003, 67, 092406.
123. G. Cantele, Y. S. Lee, D. Ninno and N. Marzari, Nano Lett., 2009, 9, 3425.
124. A. Lopez-Bezanilla, F. Triozon and S. Roche, Nano Lett., 2009, 9, 2537.
125. D. Soriano, F. Munoz-Rojas, J. Fernandez-Rossier and J. J. Palacios, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165409.
126. Y. F. Li, Z. Zhou, P. W. Shen and Z. F. Chen, J. Phys. Chem. C, 2009, 113, 15043.
127. H. Şahin, C. Ataca and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205417.
128. Y. H. Lu and Y. P. Feng, J. Phys. Chem. C, 2009, 113, 20841.
129. W. J. Evans, L. Hu and P. Keblinski, Appl. Phys. Lett., 2010, 96, 203112.
130. X. X. Ni, G. C. Liang, J. S. Wang and B. W. Li, Appl. Phys. Lett., 2009, 95, 192114.
131. H. Şahin and R. T. Senger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205423.
132. O. Hod, J. E. Peralta and G. E. Scuseria, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 233401.
133. H. W. Kroto, J. R. Heath, S. C. Obrien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162.
134. M. Yoon, S. Y. Yang, E. Wang and Z. Y. Zhang, Nano Lett., 2007, 7, 2578–2583.
135. Z. Q. Luo, T. Yu, K. J. Kim, Z. H. Ni, Y. M. You, S. Lim, Z. X. Shen, S. Z. Wang and J. Y. Lin, ACS Nano, 2009, 3, 1781.
136. S. Ryu, M. Y. Han, J. Maultzsch, T. F. Heinz, P. Kim, M. L. Steigerwald and L. E. Brus, Nano Lett., 2008, 8, 4597.

---