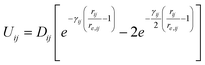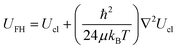Multi-scale theoretical investigation of hydrogen storage in covalent organic frameworks

Abstract

The quest for efficient hydrogen storage materials has been the limiting step towards the commercialization of hydrogen as an energy carrier and has attracted a lot of attention from the scientific community. Sophisticated multi-scale theoretical techniques have been considered as a valuable tool for the prediction of materials storage properties. Such techniques have also been used for the investigation of hydrogen storage in a novel category of porous materials known as Covalent Organic Frameworks (COFs). These framework materials are consisted of light elements and are characterized by exceptional physicochemical properties such as large surface areas and pore volumes. Combinations of ab initio, Molecular Dynamics (MD) and Grand Canonical Monte-Carlo (GCMC) calculations have been performed to investigate the hydrogen adsorption in these ultra-light materials. The purpose of the present review is to summarize the theoretical hydrogen storage studies that have been published after the discovery of COFs. Experimental and theoretical studies have proven that COFs have comparable or better hydrogen storage abilities than other competitive materials such as MOF. The key factors that can lead to the improvement of the hydrogen storage properties of COFs are highlighted, accompanied with some recently presented theoretical multi-scale studies concerning these factors.

---

E. Tylianakis

E. Tylianakis was born in 1970. He received his BSc from Physics Department of University of Crete and his PhD in 1997, from Department of Chemistry of the same University working on polymer dynamics by the aid of NMR relaxation techniques. He entered the Materials Science & Technology Department in 2001. His research focuses on theoretical studies of gas adsorption and separation by using classical simulations.

Emmanouel Klontzas

Emmanouel Klontzas was born in Agios Nikolaos Crete Hellas. He obtained his BA from Materials Science and Engineering, University of Ioannina in 2004. He received his PhD in 2009 from the Department of Chemistry, University of Crete. During his PhD he worked on computational modeling of hydrogen storage in Metal Organic Frameworks (MOFs) and Covalent Organic Frameworks (COFs). Currently he is a visiting professor in the Department of Chemistry, University of Crete and his research is focusing on the design and modeling of nanoporous materials for gas storage and separation.

George E. Froudakis

George E. Froudakis was born in Iraklion of Crete, Greece (1968) and began his studies in Physics at the University of Crete where he graduates his BSc (1990). During his PhD (1995) he studied the structure and stability of low symmetry semiconductor clusters. He joined the Chemistry Department of Crete University in 2001 where he teaches Computational and Quantum Chemistry. His research concerns ab initio and multi-scale theoretical calculations in nanomaterials. The last few years his main interest is in designing novel nano-materials suitable for hydrogen storage.

---

Introduction

Hydrogen storage

It is well known that our planet is running out of petroleum resources and a new energy carrier has to be found. In addition the new energy carrier has to be clean and environmentally friendly to prevent pollution. Hydrogen is believed to be an excellent candidate since it is regarded as an ideal energy carrier due to its advantages in comparison with other possible fuels. In particular, it is easy to produce and has high energy content per mass, higher than any other fuel. In addition it is environmentally friendly since the by-product that is produced from its “burning” procedure is mainly water. Nevertheless, one of the main issues that have not allowed commercial use yet has been the difficulty of storage. The US Department of Energy (DOE) has set some targets for hydrogen storage tanks in order to be commercialised for automobile applications. These targets for 2015 require that the gravimetric density at the system level should be 5.5 wt% and the volumetric capacity should be 40 g of H₂ L⁻¹.¹ Towards this direction, appropriate materials for hosting hydrogen need to be developed. We must mention that the above targets correspond to system level capacities and appropriate materials must have higher storage capacities in order to achieve system level targets.

Hydrogen can be stored in solid materials by chemisorption or by physisorption. In the first case molecular hydrogen dissociates and is stored in atomic form, whereas in the second case hydrogen is stored in the molecular form. Metal hydrides (e.g., LaNi₅H₆, Mg₂NiH₄) and complex hydrides (e.g., alanates, borohydrides, amides) are well known systems for reversible hydrogen storage by chemisorption. The hydrogen can be released by dehydrogenation of the hydride. Conventional metal hydrides provide high reversibility and volumetric capacity but very low gravimetric capacity (<2 wt% for La-based or Ti-based alloys).^2,3 Light complex hydrides have got higher gravimetric capacities but suffer from low reversibility due to poor hydrogenation–dehydrogenation kinetics and thermodynamics^4,5e.g. in the case of Mg-based alloys. Chemical hydrates, such as NaAlH₄, LiBH₄, and LiAlH₄, belong to the category of chemisorption materials. These materials preserve potentially good gravimetric and volumetric capacities, but these capacities are limited by the ideal hydrolysis that is required in order to have 100% conversion to hydrogen.

Besides chemisorption, the other possible storage mechanism is physisorption. The hydrogen molecule interacts weakly with the surface atoms of the storage material. The interaction energies lay in the order of few kcal mol⁻¹, which is at least an order of magnitude less than in the chemisorption case. The interactions can be attributed to dispersive and weak electrostatic forces.

In the recent past, considerable interest was focused on carbon-based materials^6–9 like fullerenes, nanofibres, and nanotubes¹⁰ for hydrogen storage. The large surface area and pore volume of these materials together with their advanced structural stability made them good adsorbent candidates. For conventional porous carbon, the hydrogen uptake is proportional to its surface area and pore volume. In addition, single-walled carbon nanotubes (SWNTs), which have diameters of typically a few nanometres, were suggested as suitable materials for gas storage.^11–13 Despite the fact that a lot of scientific effort was dedicated to these directions, the results both in experimental and in theoretical terms did not confirm the original enthusiasm.

From the very beginning it was expected that large surface area will promote storage by physisorption. Following this trivial idea, most of the research was focused on the porous materials that possess large surface area by design. Due to their superior structural formation, Metal Organic Frameworks (MOFs) have been considered as hydrogen storage materials upon their discovery. They are synthesized from metal or metal oxide vertexes interconnected by organic linkers. These materials were initially discovered by Yaghi and co-workers^14,15 and form 3-dimensional networks of very high porosity. A variety of linker molecules can be used to create an entire family of materials having different pore sizes and containing different chemical functionalities within the linkers but all with the same basic framework topology. In addition, different metal corners and different organic linkers can yield a wide variety of other framework topologies.^16–20 In many cases these materials fulfilled the expectations. Various experimental and theoretical studies^21–25 have shown impressive storage capacity of several MOFs at low temperature and high pressure. However, the storage capacity obtained at ambient temperature and pressure is still far from the DOE targets.

2D and 3D COFs

Theoretical and experimental studies on gas adsorption in MOF materials, which combine large surface area, aromaticity and metal sites, has led to some useful conclusions that will help the quest of the ideal storage material. The existence of metal atoms should be accompanied with exposed metal sites. Otherwise, they add weight in the structure without increasing the storage capacity, which is the case in most of MOFs. Studies have shown that the metal clusters, despite what it was believed in the beginning, had similar hydrogen binding strength with the organic linkers while the latter are much lighter.^26,27 An obvious improvement in the gravimetric capacity of these nanoporous materials (MOFs) would possibly come from substituting the metal cluster with another lighter building block or by discovering a novel family of materials that will exhibit the large surface area and the aromaticity of the organic linkers that MOFs have, but without the drawback of the presence of heavy unexposed metals. That new family of materials which fulfils some of the previous demands was synthesized, again, by Yaghi and co-workers,²⁸ namely, three-dimensional Covalent Organic Frameworks (3D-COFs).

The 3D-COFs were synthesized by targeting two nets based on triangular and tetrahedral nodes: ctn and bor. These materials are entirely constructed from strong covalent bonds (C–C, C–O, C–B, and B–O) and have high surface areas (4210 m² g⁻¹ for COF-103) and extremely low densities (0.17 g cm⁻³ for COF-108). From the first look, COFs present all the advantages of MOFs considering hydrogen storage (surface area, pore volume, rigidity of the structure) while the light elements that construct their molecular framework lower the relative weight of the structure, compared with that of the MOFs. For these reasons, COF materials have recently attracted attention as hydrogen storage materials.

The reticular structure of COFs can also be tailored in a wide variety of shapes, and materials composed of layers with hexagonal symmetry have recently been obtained.²⁹ The microscopic structure of these 2D-COFs presents one-dimensional pores whose size can be varied in a wide range. Diameters between 8 and 32 Å, i.e. comparable with those of medium sized carbon nanotubes, have been reported.

Multi-scale methodology

Nowadays theoretical studies have been proven to be equally useful to experimental techniques for material science. They can be very helpful by explaining what is happening in the experiments but also they can guide expensive, difficult and time consuming experimental studies. Improved and technically accurate multiscale computational techniques can perform experiments in silico with outstanding accuracy.^30,31

The application of such methods for the investigation of the hydrogen storage properties of nano-materials has been identified as crucial to the direction of finding an efficient solution to the hydrogen storage problem.^32–35 The basic categories of computational methods that can be used in the study of molecular systems are quantum mechanic calculations and simulations based on classical physics. Quantum chemistry (QM) methods, called ab initio, do not enforce any parameters to the system but solve the Schrödinger equation by first principles. The great advantage of the ab initio methods is that they can provide structural, electronic, and dynamic properties of the system with high accuracy. On the other hand, their computational cost increases dramatically with the number of the electrons of the system. Ab initio methods are used mainly to investigate the energetics of the interaction that can exist between hydrogen and the adsorbent. Such calculations result in the knowledge of the interaction strength, the nature of the interactions of hydrogen with the pore walls and provide the available binding sites in the material.

Classical simulations offer the possibility to measure the hydrogen adsorption capacity of nano-structures under different thermodynamic conditions. In this way we can predict absorption isotherms and compare directly with the experiment.^30,31 These simulations include several types of calculations like Monte Carlo (MC), Molecular Dynamics (MD) and Molecular Mechanics (MM). The great advantage of these methods is their ability to treat larger systems since they are computationally inexpensive compared with the ab initio methods. Furthermore, they can take into consideration the pressure and temperature dependence of the simulations. The major disadvantage of the classical simulations is that their results and their accuracy depend on parameters.

It is clear from the previous analysis of quantum and classical approaches that both have strong advantages together with critical disadvantages. Over the last few years, a new methodology is developed trying to combine the large size of the systems with the desired accuracy without ending up in prohibitively large calculations. It is based on a multi-scale methodology and it is schematically presented in Fig. 1.

Fig. 1 Multi-scale methodology scheme, showing the different levels of theory and the corresponding size of systems under study.

The 1^st scale consists of the minimum parts of the COF skeleton, the building units. There we can apply very accurate ab initio methods like Density Functional Theory (DFT), Möller–Plesset (MP) and Couple Cluster (CC) for calculating the binding of the hydrogen molecules. The 2^nd scale contains larger molecular models (more than 50 atoms) or a unit cell of the periodic structure where Density Functional Theory (DFT) or mixed methods involving QM and MM (QM/MM) can be applied. From these 2 scales we can predict all the necessary information for fitting an ab initio based interatomic potential describing the interaction between the hydrogen molecule and the COF pore. Then we can perform classical Molecular Dynamics (MD) or Monte Carlo (MC) simulations at the 3^rd scale, taking into account thousands of atoms. In our case, Grand Canonical Monte Carlo (GCMC) simulations can reproduce isotherms for hydrogen adsorption under different thermodynamic conditions that can be compared directly to the experiment.

Ab initio

The quantum mechanical methods used for calculating the binding energy of H₂ to the framework are generally based on Density Functional Theory or Möller–Plesset perturbation theory. DFT has the advantage of low computational cost together with the disadvantage of questionable accuracy when treating weak interactions. “Classical” functionals like PBE and PW91 claim to treat the weak interactions fairly.^36,37 In any case, direct comparison with at least MP2 is performed in most of the studies for evaluating the accuracy of binding energies of DFT in each particular system. Nevertheless in many cases DFT methods describe well the trends in binding energies in such systems. New approaches in DFT that include nonempirical³⁸ or empirical³⁹ corrections for the dispersion interactions in existing functionals seem very promising in predicting more accurately the energetics in hydrogen interaction with the host material.

To calculate the interaction potential of the hydrogen molecule with framework materials accurate ab initio methods like MP2 or even CC are used. This part of the multi-scale treatment is the most critical since all the classical calculations that will follow are very sensitive to the interatomic potentials. For this study we need to separate each part of the framework from its environment and treat it as individual cluster. In this way very accurate ab initio methods can be applied and the Potential Energy Surface (PES) of the interaction with hydrogen can be scanned. The tricky part is the termination of the remaining cluster that has to be done in a way that will represent sufficiently the missing environment.

Grand canonical Monte Carlo method

In material science, classical Monte Carlo simulations have been found to be a very important and widely used tool^40,41 taking into account thousands of atoms and producing results that can be directly compared with the experiment. Among the various ensembles that MC simulations^42,43 adopt for the description of the system under study, the grand canonical ensemble (GCMC) is the one most widely used for adsorption studies since it is the only one that allows the total number of particles, N, to vary. According to this ensemble, the chemical potential, µ, the volume, V, and the temperature, T, are kept constant ((µ,V,T) ensemble), while the number of the molecules, N, is allowed to fluctuate. The fluctuation of the total number of particles makes this method a unique tool for the adsorption study of a given sorbate within a given system. The chemical potential used corresponds to a specific condition of pressure and temperature and can be determined either from the use of the appropriate equation of state⁴⁴ or from Widom⁴⁵ test particle method. According to the latter method, NVT ensemble Monte Carlo study for bulk hydrogen is used. At frequent time intervals and after equilibrium is reached, a ghost atom is randomly inserted into the system and the energy change due to the insertion is used for the calculation of the chemical potential for the thermodynamic state under examination.

During the GCMC simulations, three types of trial moves are attempted i.e., particle creation at a randomly chosen position, randomly chosen particle destruction and randomly chosen particle displacement and/or rotation. Due to particle creation and destruction, the number of particles, N, within the pore fluctuates. For each trial, if the final configuration of the system is of lower energy than the previous, the move is accepted. In the opposite case, the energy difference of the configurations before and after the trial move is used for the calculation of the possibility of accepting the trial move.

The correct form of the function that describes the interactions between the particles of our system is a key point of this method. The common practice in that kind of simulations is to take into consideration the interactions of the atoms between the sorbate molecules and between the sorbate and solid atoms. The interactions between the atoms of the solid itself are not taken into consideration since they are assumed to be frozen.

A variety of potential functions are well known^46–50 for describing the Van der Waals interactions. Among these potential functions the Lennard–Jones (L–J) potential model⁴⁶ is the one most widely used. According to this potential the interaction energy between two non-bonded atoms i and j can expressed be as follows:

where ε_ij is the potential well depth and σ_ij the interatomic distance at which a zero potential energy occurs. The whole set of these parameters used for these studies can be either taken from literature^51–55 or calculated specifically for each case. Once the potential parameters, σ and ε, for a given atom type have been calculated, mixing rules can be applied for the calculations of these parameters for a pair of heteroatoms.

Another function that describes the potential between sorbate and framework atoms that has extensively been used is the Morse potential:

where D_ij is the well depth, γ_ij is the stiffness parameter that defines the well shape and r_e,ij is the equilibrium distance.

Besides the interatomic potential that will be used another point of debate is the necessity or not of using quantum corrections to the simulation. The quantum correction enlarges the effective diameter of a molecule in comparison to its classical counterpart and therefore reduces the adsorption ability of nanopores. The approach often used to describe the quantum effects during Monte Carlo simulations is based on the Feynman–Hibbs effective potential.⁵⁶ According to this approach, the effective potential is described by

where µ is the reduced mass of the pair of interacting species and U_cl is the classical potential used for the description of the interactions between the pair of species.

In addition to the Van der Waals forces, electrostatic interactions have been proven to play significant role in the interaction energy of the system. This is due to the fact that adsorbates may either have permanent dipole moment due to partial charges on their atoms or be easily polarized molecules. In both cases the electrostatic terms of the potential cannot be regarded as negligible. The electrostatic interactions are usually described by ordinary Coulomb potential.

Hydrogen storage in COF

Interaction sites vs. energy

The 1^st part of a multi-scale treatment of hydrogen storage in COFs is to find the interaction sites of the framework and calculate the relative binding energies. Due to the large size of COF cells, the model system must be reduced in size in order to perform accurate ab initio calculations. One way to achieve the reduction of the size is by using the supramolecular approach which was used by Klontzas et al.³⁰ They studied B₃O₃, C₂O₂B and phenyl rings that can be found in the structure of the four different 3D COFs (102, 103, 105, and 108) by selecting a unique molecular model for the representation of the phenyl ring (model A, Fig. 2) and two different models for the representation of the B₃O₃ ring (model B and model C, Fig. 2 respectively). The number of the molecular models that were adopted depended also on the computational method (model B for DFT and model C for MP2 respectively). The smaller model was chosen for the MP2 calculations due to the higher computational cost of the perturbation theory. For C₂O₂B rings, the model D shown in Fig. 2 was selected. Both the perpendicular and parallel approaching orientations of the H₂ molecule (with respect to the ring plane) for each binding site were examined. In the case of model A, they chose to examine only the model similar to the tetrahedral tetra(4-dihydroxyborylphenyl)methane (TBPM) building block (with the tetrahedral carbon atom) instead of the silane analogue because the selection of the tetrahedral atom would have minor effect on the calculated binding energies. All unsaturated bonds were terminated with hydrogen atoms.

Fig. 2 Molecular clusters that have been used for the quantum mechanics calculations and represent the different fragments of COF skeleton. Carbon, oxygen, boron and hydrogen atoms are shown as grey, red, pink and white colors respectively.

The Resolution of Identities (RI) approximation⁵⁷ was applied in all calculations. The Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional^36,37 along with the polarized triple-ζ valence basis set def2-TZVPP⁵⁸ was used in the calculations. For checking the validity of the DFT methodology, high accuracy RI-MP2 calculations along with the def2-TZVPP basis set were also performed.

All calculations (DFT and MP2) were performed with the TURBOMOLE⁵⁹ program package. Binding energies are corrected for the Basis Set Superposition Error (BSSE)⁶⁰ with the counterpoise method. These corrections are essential since the BSSE may become critical for non-bonding interactions as it was shown in earlier investigations of hydrogen storage in MOFs.²⁶

Table 1 shows that the H₂ binding energies in the different sites did not exceed 1 kcal·mol⁻¹ in the case of MP2 level. The energetically most favourable sites were located over the center of the phenyl rings when hydrogen approaches with a perpendicular orientation. Binding over B₃O₃ ring was favourable over the center of the ring and over B atom with similar binding energies and with the parallel approaching orientation for H₂. In the case of C₂O₂B rings binding energies were comparable to those on the center of the phenyl ring, with the parallel approaching orientation of H₂ over the center of ring to be favoured. A comparison of these binding energies with those calculated in previous studies for IRMOFs^26,27 showed that no major discrepancies existed. So the authors concluded that the binding energies were not the major reason for an increased hydrogen adsorption in 3D COFs.

Table 1 BSSE corrected Interaction Energies (IE) and optimal distances (dist.) for H₂ over possible binding sites obtained from the PES scans

Methods	RI-PBE/def2-TZVPP				RI-MP2/def2-TZVPP
Approach	Vertical		Parallel		Vertical		Parallel
Binding sites	IE/kcal·mol^−1	Dist./Å	IE/kcal·mol^−1	Dist./Å	IE/kcal·mol^−1	Dist./Å	IE/kcal·mol^−1	Dist./Å
S1	−0.4	3.1	−0.2	3.5	−1.1	2.7	−0.7	3.1
S2	−0.3	3.2	−0.2	3.7	−0.7	2.9	−0.4	3.4
S3	−0.3	3.2	−0.2	3.8	−0.7	3.0	−0.4	3.4
S4	−0.1	3.3	−0.3	3.3	−0.3	3.0	−0.5	3.2
S5(O)	−0.2	3.2	−0.2	3.6	−0.4	3.0	−0.3	3.4
S6(B)	−0.1	3.3	−0.2	3.5	−0.2	3.2	−0.5	3.2
S7(B)	−0.1	3.4	−0.2	3.4	−0.5	3.0	−0.7	3.1
S8(O)	−0.2	3.1	−0.2	3.5	−0.9	2.7	−0.6	3.2
S9	−0.1	3.3	−0.3	3.3	−0.6	2.8	−1.0	2.9

---

The analysis of the hydrogen binding sites presented in the previous paragraph showed that COFs did not offer considerably stronger binding in comparison with reported values in IRMOFs. That was the reason for which they expected that COFs and MOFs with comparable surface areas would accommodate similar amounts of hydrogen, resulting in analogous volumetric uptake. Since COFs consisted of lighter atoms they are expected to present significantly enhanced gravimetric capacity in comparison to MOFs (same amount of H₂ in reduced weight).

Srepusharawoot et al.⁶¹ studied hydrogen adsorption in COF-1 by performing ab initio calculations. They performed total energy calculations in the periodic system of COF-1 by using Density Functional Theory with the Local Density Approximation (LDA)⁶² and they carried out MP2 calculations in a molecular fragment of COF-1 to validate the obtained binding energies from DFT calculations. They found out that LDA predicted the trend of the calculated binding energies but overestimated the corresponding values when compared with MP2 binding energies. According to MP2 binding energies, the highest binding energies of H₂ were found over the center of the C₆H₄ ring and over the oxygen atom of the B₃O₃ ring. In both cases H₂ approached the binding sites with the head-on configuration. They found also a disagreement between the trend of the binding energies predicted from DFT and MP2 for the binding sites over C₆H₄ ring and they proposed that this disagreement was due to the close proximity of the adjacent layers of the two dimensional structure of COF-1.

Assfour and Seifert⁶³ carried out computer simulations (MD and MP2) on both 2D and 3D COF to study hydrogen adsorption. In order to locate the binding sites on the periodic 2D and 3D COF structures, they performed molecular dynamics simulations by the dispersion corrected density functional based tight binding theory method^64,65 by adding randomly up to 30 hydrogen molecules in the structure and performed simulated annealing down to 5 K. They located seven different adsorption sites with the largest binding energies in which they performed MP2 calculations. In order to perform these calculations, they selected smaller molecular fragments which were optimized with DFT method and then total energy MP2 calculations were carried out to find the corresponding counterpoise corrected binding energies and the interaction geometry between hydrogen and the selected molecular fragment. It was found that binding energies for the adsorption of H₂ on C₆H₄ ring of COF-102 and COF-103 were −3.12 kJ mol⁻¹ and −2.84 kJ mol⁻¹ respectively, where the binding energy over the B₃O₃ ring was −0.94 kJ mol⁻¹. It was also mentioned that the interaction orientation of hydrogen was vertical and parallel for C₆H₄ ring and B₃O₃ ring respectively. They also calculated H₂ binding energies on the building blocks of COF-105 and COF-108 which were found to be in the range of binding energies for COF-102 and COF-103. Finally they proposed that the small differences in the binding energies could be attributed to the selection of the size of the molecular cluster and the basis set.

From the above mentioned studies we can conclude that the binding energies in the pristine COF structures are similar to those that have been found in MOF and they have not major contribution to the high hydrogen loadings that have been predicted from GCMC calculations. The interactions of hydrogen with the building moieties of COF are dominated by weak van Waals and dispersion interactions and by weak electrostatic interactions between the permanent quadrupole moments of hydrogen with the framework.

Grand canonical Monte Carlo simulation

A series of studies have been performed by many research groups in an effort to quantify the performance of COFs in adsorbing hydrogen. All the results from that kind of studies indicate that these materials are very promising candidates for hydrogen storage. In fact, the so far reported gravimetric uptake of hydrogen from COFs exceeds the level of exotic 20 wt% in some cases, rendering them among the best performing materials studied for hydrogen storage applications. This uptake is almost 4 times larger than the 2015 DOE system target for automotive applications. From the volumetric point of view almost all 3D-COF materials perform well, reaching a maximum 45 g l⁻¹ in the case of COF-102.

Following a multi-scale theoretical approach Klontzas et al.³⁰ studied hydrogen adsorption from a series of 3D-COFs, i.e. COF-102, 103, 105, 108 and found extraordinary gravimetric uptakes for these materials. This multi-scale methodology offers the advantage of fixing the potential parameters to describe better the system under examination. This is achieved when the classical potential is able to calculate correctly the energetics of our systems, as have already determined from first principles calculations. Potential parameters are determined by scanning the hydrogen binding energy at different distances from the framework. This energy is calculated at the MP2 level of theory and afterwards the parameters of the potential are chosen in such way to be able to reproduce the energy taken from ab initio calculations. Following this approach, the classical potential is sensitive to the particularities of the system under examination and it is avoided the use of identical set of potential parameters for all the different studies.

Especially for COF-108, as it can be seen in Fig. 3, Monte Carlo simulations at cryogenic temperature showed that this material exhibits almost 21 wt%, whereas at ambient temperature the very promising value of 4.5 wt% was reached. In terms of volumetric uptake, the results were not that fascinating. At 77 K the materials barely fulfilled the DOE target reaching at most the value 45 g l⁻¹ in the case of COF-102, whereas at room temperature the performance was far below the target and the value is only 8 g l⁻¹.

Fig. 3 Gravimetric and volumetric isotherms of hydrogen adsorption at 77 and 300 K for COF-102, COF-103, COF-105, COF-108.

An entirely different performance was observed for these systems in terms of volumetric vs. gravimetric uptake. This performance was attributed to the topological characteristics of these materials since they possess large pore volume and this becomes a disadvantage when we consider the volumetric uptake leading to poor performance. The chemical reason for this observation is the fact that for materials of large free volume, the solid–fluid potential energy gain is not enough to result in a sizable excess adsorption. This disadvantage has also been noticed in the case of hydrogen adsorption on other large-pore COFs and MOFs.^66–68

The above observations can also justify the different behavior between COF-102, COF-103 vs. COF-105, COF-108. These two groups of materials have different topological characteristics. Indeed, the latter two compounds have larger pore volume (90% and 91%, respectively) than the first two (76% and 78%, respectively). Therefore, COF-105 and COF-108 reach much higher gravimetric uptake whereas COF-102 and COF-103 show larger volumetric capacity. This difference in the amount of pore volumes is also reflected on their densities, where we can observe a large deviation (0.41, 0.38, 0.18, and 0.17 g cm⁻³ for COF-102, COF-103, COF-105, and COF-108, respectively²⁸).

Garberoglio⁶⁹ performed GCMC simulations for a series of light gases including hydrogen for the same COFs as Klontzas et al..³⁰ The results of this study were expressed in terms of excess adsorption and were quite similar with the ones of ref. 30.

Similar simulations have been performed for 2D-COFs. Garberoglio and Vallauri⁷⁰ reported computer simulation results for adsorption and diffusion of hydrogen and methane in such systems i.e. COF-6, COF-8 and COF-10. They followed the same theoretical methodology as in their previous study for 3D-COFs.⁶⁹ The results show that the calculated adsorption isotherms of H₂ at T = 77 K and T = 298 K were generally half than those of MOFs or 3D-COFs under the same conditions both on a gravimetric and a volumetric basis. In particular the isotherms for these materials showed a maximum in the excess adsorption occurring around 25 bar for COF-6 and 45 bar for COF-8 and COF-10. COF-10 yields the larger excess gravimetric uptake, reaching 4.2 wt%, followed by COF-8 and COF-6. That amount of hydrogen adsorbed upon saturation is lower compared with 3D-COFs,³⁰ and MOFs, as observed in computer simulations.^71,72

The reason for the discrepancy of gravimetric uptake between the families of 2-D and 3-D COFs was attributed to the different framework densities and surface areas. The densities of the 2D-COF materials are on average larger than the densities of other organic frameworks leading to lower gravimetric uptake. In addition, in the structure of 2D-COFs the adsorption can occur only along the surface of the one-dimensional pores, resulting in a smaller surface area with respect to 3D organic frameworks. In fact the experimental surface areas for 2D-COFs studied in this article²⁹ ranges from 965 to 1050 m² cm⁻³, significantly smaller than the corresponding values of 3-D COFs²⁸ or other MOFs.^73,74 This results in lower hydrogen uptake on both gravimetric and volumetric basis.

The same behavior is observed when the adsorption of hydrogen at T = 298 K is analyzed. The amount of hydrogen adsorbed on a gravimetric basis at the pressure of P = 100 bar is half of that adsorbed in 3D-COFs and it is by far less than the DOE target.

Garberoglio and Vallauri⁷⁰ have also investigated the mechanism of diffusion in order to assess similarities and/or differences with the behavior observed in carbon nanotubes that have a similar pore structure and where transport is known to occur very rapidly.^75,76 Their results point out that gas diffusion in 2D COFs is one order of magnitude more rapid than in metal–organic frameworks or zeolites, but still not as fast as in carbon nanotubes. The adsorption and diffusion characteristics of these materials are related to the peculiar structure of the solid–fluid potential energy surface. In particular, the presence of very small potential barriers for the motion along the tube axis has been indicated as the principal reason for the rapid transport of hydrogen.^75,76 In the case of hydrogen interacting with a (10,10) carbon nanotube, the motion along the tube axis does not meet potential barriers higher than 10–20 K, which are easily crossed at room temperature. This is not the case for the diffusion along the pores in 2D-COFs. The existence of large potential barriers highly hinders the motion along the pores. As consequence diffusion in this direction takes place by jumps separated by quite long residence times, making the procedure slower.

The reduced ability of 2D-COF to adsorb hydrogen in comparison to the corresponding 3D-COF was also verified by Yang and Zhong⁷⁷ who performed GCMC simulations in order to investigate the adsorption behavior of CO₂, CH₄ and H₂ in two 2D-COFs with different pore size, namely COF-8 and COF-10.

Comparison with experimental results and MOFs

Garberoglio⁶⁹ compared the adsorption performance of MOFs and COFs. As mentioned earlier in this text, the excess amount of hydrogen adsorbed gravimetrically by COF-105 and COF-108 is slightly larger than 10% at P = 100 bar and 77 K. This is significantly larger than the gravimetric capacity of the highly adsorbing MOFs (like IRMOF-14) at the same conditions⁷¹ where the excess amount does not exceed 7.5 wt%. Garberoglio also noted that isotherms of COFs at 298 K display a structure qualitatively similar to the corresponding isotherms of adsorption in MOFs. At that temperature the excess adsorption does not exceed 0.8% in weight at a pressure of 100 bar. Despite the fact that this value is quite far from the DOE target, it is nonetheless a considerable improvement with respect to the value observed in MOFs. A high hydrogen sorbent MOF (IRMOF-14) does not adsorb more than 0.6% in weight of hydrogen at the same thermodynamic conditions.

In the case of 2D-COFs the performance is not that good since as it has already been mentioned the calculated adsorption isotherms of H₂ at T = 77 K and T = 298 K show that the uptake is generally half than the one in MOF or 3D covalent organic frameworks both on a gravimetric and a volumetric basis.

Despite the large amount of theoretical studies concerning hydrogen adsorption in COF, only a few experimental articles have been found in literature. One of them published by Furukawa and Yaghi³¹ presents a systematic study for a number of COFs. Measurements were performed at 1–85 bar and 77–298 K for seven porous COFs. The authors classified the systems into three groups based on their structural dimensions and corresponding pore sizes. Among the COFs of this study, data for COF-102 and COF-103 were presented as well. These materials had already been studied theoretically by Klontzas et al.³⁰ Results from these works are presented in Fig. 4. A comparison between experimental and calculated isotherms reveals the exceptional agreement between theory and experiment. This is even more fascinating if one keeps in mind that the theoretical results were presented first, several months before the publication of the corresponding experimental results.

Fig. 4 Calculated (taken from ref. 30) and experimental (taken from ref. 31) isotherms at 77 K for hydrogen adsorption in COF-102.

Improving storage strategies

Increasing the interaction strength

Doping with metals. As it has been clearly noted in this text 3D-COFs have been proved to be very good candidates for hydrogen storage. The major reason for their high hydrogen uptake is the special characteristics of the materials such as low density, high surface area, pore size, and framework topology rather than the existence of enhanced interaction sites in the pore surface. A further step to achieve improved storage capacity in these materials is the introduction of charged species on the pore surface. This strategy has been also used successfully in the past, both in carbon-based materials and MOFs to improve their storage capabilities.^{32–34,78–80} This improvement was achieved through the introduction of lithium ions in the material. Hydrogen interacts with the lithium ion through charge induced dipole with quadruple moment contributions. On top of this, a lithium cation can interact simultaneously with multiple hydrogen molecules with interaction energies⁸¹ up to 6 kcal mol⁻¹.

As in the case of MOFs, lithium intercalation has been achieved either by interaction of the Li with the p system of the organic linkers or by forming ionic bonds between lithium and functional groups of the organic linker. Cao et al.⁸² followed the first strategy for Li incorporation and studied the effects by performing GCMC simulations for a series of undoped and doped 3D-COF structures i.e. COF-102, 103, 105 and 108. The Li doped optimized geometries for the different building units of 3D-COFs can be seen in Fig. 5. They used Morse potential, the shape of which was fitted to first-principle calculations, performed at the second-order Möller–Plesset (MP2) level of theory using the cc-PVTZ basis set. In this way the potential parameters between H₂ and COFs were determined specifically for these systems. In the case of the undoped structures the theoretical isotherms were in good agreement with the corresponding theoretical results already reported in this text.²⁸

Fig. 5 Optimized geometries for Li-doped building blocks of 3D covalent organic frameworks. Li violet, H white, B pink, C green, O red, and Si yellow (taken from ref. 82).

From the simulated isotherms that are presented in Fig. 6 for the Li decorated structures it can be observed that there was a significant improvement of the amount of the adsorbed H₂. Among the four frameworks, COF-105 and COF-108 show more than double increase and reached 6.84 and 6.73 wt%, respectively, at T = 298 K and p = 100 bar. Moreover, it was confirmed that these two doped materials adsorb in terms of gravimetric uptake significantly higher amount than all the Li-doped MOFs reported in literature. Fig. 6 presents also H₂ isotherms for MOF-C6 and MOF-C30 for the shake of comparison.³⁴ Similar conclusions were drawn for the volumetric adsorption since all four Li-doped COFs achieve an enhancement of approximately a factor of two in volumetric adsorption capacity at T = 298 K and p = 100 bar (25.98, 25.00, 13.75, and 13.57 g l⁻¹ for Li-doped COFs 102, 103, 105, and 108, respectively) compared to the corresponding undoped material. This enhancement of storage capacity was also reflected to the storage in terms of excess values, which were also significantly improved, and reached, 4.25 wt% and 21.11 g l⁻¹ for Li doped COF-102 at ambient temperature.

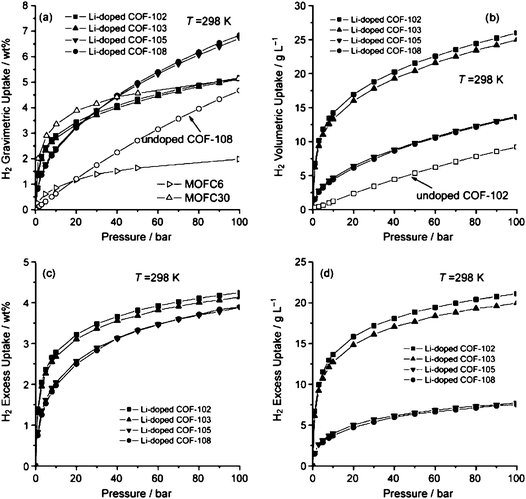Fig. 6 H₂ adsorption isotherms for Li-doped COFs at T = 298 K. (a) Total gravimetric isotherms. The H₂ isotherms for MOF-C6 and MOF-C30 are also presented for comparison.³⁴ (b) Total volumetric isotherms. (c) Excess gravimetric isotherms. (d) Excess volumetric isotherms (taken from ref. 82).

A study for Li doped and undoped COF-202 was performed by Lan et al.⁸³ They used the same multi-scale theoretical methodology as Cao et al. have used in the previous mentioned study. From the GCMC simulations it was shown that undoped COF-202 reached the gravimetric and volumetric capacity of 7.83 wt% and 44.37 g l⁻¹ at 77 K and 100 bar respectively. At 298 K and 100 bar, the gravimetric and volumetric capacity reached 1.52 wt% and 8.08 g l⁻¹ respectively. As the authors mentioned, the capacities at 77 K were comparable to the best performed MOF and 3D COF and reach the DOE targets, where the performance at room temperature was away from the corresponding DOE targets. Afterwards they studied the possible Li loading of COF-202 by performing DFT calculations and they decided to perform GCMC simulations in doped COF-202 structures with one and two Li atoms per phenyl ring. The results obtained from these simulations showed that the gravimetric capacity at room temperature and 100 bar reached 3.32 wt% and 4.39 wt% for single and double Li doping respectively. Similar enhancement was observed also for volumetric capacity. Nevertheless, the capacities were found to be lower than the corresponding Li doped 3D COF in the study of Cao et al., where the authors attributed this difference mainly to the different physicochemical characteristics (e.g., free volume, framework density) of these materials.

Choi et al.⁸⁴ explored hydrogen storage mechanisms on pure and Li⁺- and Mg²⁺-decorated COFs via first principles calculations. It was found that Li⁺-decorated material could adsorb up to 3 dihydrogen molecules while the average interaction energy per adsorbed molecule was found to be 6.45 kcal mol⁻¹. The Mg²⁺-doped material adsorbed up to 6 molecules (twice the number determined in the case of Li⁺), with average interaction energy of 6.91 kcal mol⁻¹ per adsorbed molecule. The authors also estimated the saturation values of gravimetric hydrogen storage capacities at room temperature and reasonable pressures using a method proposed by Sagara et al.,⁸⁵i.e. by counting the number of hydrogen molecules effectively adsorbed on each metal ion in the unit cell of COF-108. In this way the calculated maximum saturation values of hydrogen sorption capacity were 6.5 and 6.8 wt%, for Li⁺- and Mg²⁺- decorated COF-108s, respectively.

Functionalization. Li doping proved to be an effective way for the improvement of hydrogen uptake of framework structures but this strategy presents severe experimental difficulties when applied in MOFs. An experimentally feasible way of incorporating Li is by forming ionic bonds between lithium and functional groups of the organic linker. In this case, lithium can interact with multiple hydrogen molecules as in the doped case but with somewhat decreased interaction energies. This methodology has been initially applied theoretically in MOFs³³ and there was experimental evidence for the formation of lithium alkoxide groups in MOF^86–88 and MIL (Materiaux Institut Lavoisier)⁸⁹ confirming the validity of the strategy.

Klontzas et al.⁹⁰ applied this strategy to improve the storage capacity by introducing into the 3D-COF structures lithium alkoxide groups. Three lithium alkoxide groups were added in every HHTP building unit and the functionalized building block is presented in Fig. 7. Then a multiscale theoretical study was performed to evaluate the hydrogen storage capacity of the modified COF-105. Initially, DFT calculations showed that up to five H₂ can interact directly with the lithium alkoxide group. The first H₂ interact with Li, and the interaction energy was calculated to be 2.95 kcal mol⁻¹, a value that is almost three times larger than the interaction of H₂ with the unmodified material.

Fig. 7 Optimized molecular model of the lithium alkoxide modified HHTP building unit; carbon, silicon, oxygen, boron, hydrogen, and lithium atoms are shown as gray, yellow, red, pink, white, and purple colors, respectively.

Then the H₂ storage capacity of the modified COF-105 was studied by performing GCMC simulations at 77 and 300 K for pressures up to 100 bars. As it can be clearly seen from Fig. 8 it was found that the proposed structure functionalization led to significant improvement of hydrogen uptake in both gravimetric and volumetric terms. The effect of the functionalization was more pronounced for the volumetric uptake than the gravimetric. The reason for this is that the proposed modification with the –OLi group increased the weight of the material, since a single hydrogen molecule of the framework is substituted by a group of significantly larger weight. This was not the case for the volumetric uptake since the system volume does not change upon the structural modification. In addition the improvement of the uptake was more important for the low loading range, where the modified COF-105 reaches the DOE target for gravimetric uptake even at room temperature.

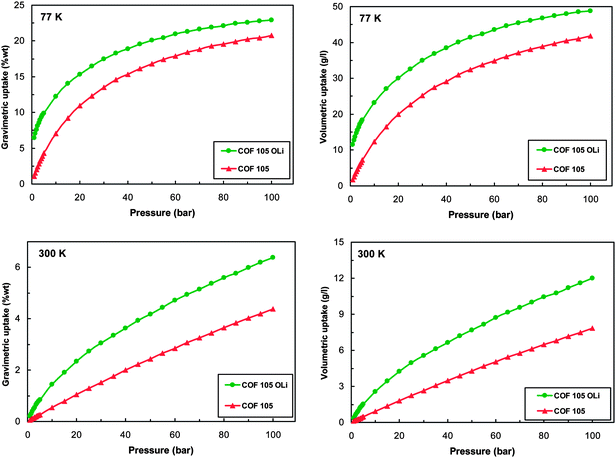Fig. 8 Gravimetric and volumetric isotherms of hydrogen adsorption at 77 and 300 K for original and OLi group modified COF-105.

Li et al.⁹¹ proposed a new way for improving hydrogen storage in COFs by substitutional doping of the bridge C₂O₂B rings with different metal-participated rings. In this way, they aimed at avoiding the clustering of metal atoms. First-principles calculations on both crystalline phase and molecular fragments showed that the H₂ binding energy can be significantly enhanced. In particular for the N₂Al and Mg₂N doped COF-108 crystals the binding energies approached 2.39 kcal mol⁻¹ (almost three times more than in the pure crystal), which would be beneficial for efficient hydrogen storage at ambient temperatures. The isotherms obtained from GCMC simulations further confirmed that such substitutional doping would improve the room temperature hydrogen storage performance by a factor of two to three since it enabled reaching values up to 2.73 wt% in the Mg₂N doped crystal.

Increasing pore volume and surface area

New COFs. In a recent study, Klontzas et al.⁶⁶ proposed four novel 3D-COF structures with enhanced storage performance. They all come from COF-102 by carrying out the appropriate structural changes in such a way that their storage properties would be superior to the parent framework. Particularly, they substituted the phenylene moieties of COF-102 with the more extended diphenyl, triphenyl, napthalene, and pyrene aromatic moieties, without changing the net topology creating in this way the so-called COF-102-2, COF-102-3, COF-102-4, and COF-102-5 (Fig. 9). The construction of the initial crystal structures was followed by an optimization procedure, using molecular mechanics methods. The resulting building units and COF structures are presented in Fig. 9. After the optimization of these new structures, GCMC simulations were used to obtain the total gravimetric and volumetric hydrogen uptake at 77 K and room temperature for pressures up to 100 bar. The results of these simulations can be seen in Fig. 10.

Fig. 9 The different organic moieties that have been used for the construction of the COF materials. By using the same topology as COF-102 and the same connectivity and alternating the organic moieties there have been constructed a series of periodic COF cells ranging from COF-102 to COF-102-5. Carbon, oxygen, boron, and hydrogen atoms are shown as gray, red, pink, and white colors, respectively.

Fig. 10 Gravimetric and volumetric isotherms of hydrogen adsorption at 77 and 300 K for COF-102, COF-102-2, COF-102-3, COF- 102-4, and COF-102-5.

All the proposed structures showed enhanced gravimetric capacity with respect to the corresponding gravimetric uptake of the parent COF-102 structure, both at cryogenic and room temperature. COF-102-3 showed the best performance and reached 26.7 and 6.5 wt% at 77 and 300 K, respectively at 100 bar, values that exceed the DOE target of 5.5 wt% even at room temperature. On the other hand, the proposed materials showed lower volumetric performance than COF-102. This was attributed to the larger pore volume that they possess, i.e. 94%, 89%, 87%, 83% and 76% for COF-102-3, COF-102-2, COF-102-5, COF-102-4 and COF-102, respectively. As it can be seen, the order of the materials in terms of free volume is the same as in terms of maximum gravimetric uptake. On the contrary, in terms of volumetric uptake that order is reversed. Indeed, from the volumetric point of view, very large pores result in empty space inside the material, which is dominated by weak fluid–fluid interactions.

Hydrogen storage in COF by spillover

Another approach that has attracted a lot of attention has been the hydrogen storage by spillover. The spillover effect on hydrogen is currently under investigation in order to discover the underlying mechanism, which involves the dissociation over the supported metal catalyst and the diffusion of spilt-over hydrogen through the porous media. Experimental data have shown that spillover can enhance hydrogen storage in bridged porous carbon, MOF and COF materials by 2–3 times compared with the pristine materials.^92,93 It has been proposed that hydrogen dissociate over metal catalyst and then can be diffused from the supporting substrate to the adsorptive material through oxygen-rich bridging materials (this material acts as “glue”). Suri et al.⁹⁴ performed an ab initio study to find the hydrogen capacity of COF-1. They concluded that 1H atom per carbon atom of the benzene molecule could be bound with an average binding energy of 2.41 eV. No hydrogen was bound on B₃O₃ rings. In this way they predicted a saturation storage density of 4.5 wt% for COF-1.

Conclusions

COF materials have been considered as candidate materials for hydrogen storage. Especially 3D-COFs due to their unique characteristics exhibit excellent performance especially at 77 K, where COF-108 exceeded 20 wt% storage capacity at 100 bar. On the other hand, COF performance at ambient pressure and temperature is quite low and similar to other MOFs. In order to enhance their storage capabilities, strategies such as doping with alkali atoms or functionalization of the organic moieties have been applied. These strategies led to a clear enhancement of the amount of hydrogen that can be stored in the modified 3D-COF, exceeding in some cases the established target of 6 wt% at ambient temperature. Further work shall be focused on the introduction of stronger interaction sites in COF materials, since their physicochemical characteristics such as surface area and free volume are already among the highest.

In parallel the validity of multiscale theoretical approaches for predicting the adsorption characteristics of COF materials has been well established based on the observed agreement with the experimental data. Such approaches can contribute toward the targeted synthesis of new COF materials which have been predicted to give even higher performances in terms of hydrogen storage capability.

References

1. Hydrogen, Fuel Cells & Infrastructure Technologies Program: Multiyear Research, Development and Demonstration Plan: Planned program activities for 2003–2010, United States Department of Energy, 2005, ch. 3.3, Revision 1, http://www1.eere.energy.gov/hydrogenandfuelcells/mypp/pdfs/storage.pdf.
2. L. Zhou, Progress and problems in hydrogen storage methods, Renewable Sustainable Energy Rev., 2005, 9, 395–408.
3. A. Züttel, Hydrogen storage methods, Naturwissenschaften, 2004, 91, 157–172.
4. M. Fichtner, Nanotechnological aspects in materials for hydrogen storage, Adv. Eng. Mater., 2005, 7, 443–455.
5. W. Grochala and P. P. Edwards, Thermal decomposition of the non-interstitial hydrides for the storage and production of hydrogen, Chem. Rev., 2004, 104, 1283–1316.
6. S. Patchkovskii, J. S. Tse, S. N. Yurchenko, L. Zhechkov, T. Heine and G. Seifert, Graphene nanostructures as tunable storage media for molecular hydrogen, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10439–10444.
7. R. Ströbel, J. Garche, P. T. Moseley, L. Jörissen and G. Wolf, Hydrogn storage by carbon materials, J. Power Sources, 2006, 159, 781–801.
8. A. V. Eletskii, Sorption properties of carbon nanostructures, Phys.-Usp., 2004, 47, 1119–1154.
9. Z. Yang, Y. Xia and R. Mokaya, Enhanced hydrogen storage capacity of high surface area zeolite-like carbon materials, J. Am. Chem. Soc., 2007, 129, 1673–1679.
10. S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354, 56–58.
11. A. C. Dillon, K. M. Jones, T. A. Bekkedahl, C. H. Kiang, D. S. Bethune and M. J. Heben, Storage of hydrogen in single-walled carbon nanotubes, Nature, 1997, 386, 377–379.
12. C. Liu, Y. Y. Fan, M. Liu, H. T. Cong, H. M. Cheng and M. S. Dresselhaus, Hydrogen storage in single-walled carbon nanotubes at room temperature, Science, 1999, 286, 1127–1129.
13. Y. Ye, C. C. Ahn, C. Witham, B. Fultz, J. Liu, A. G. Rinzler, D. Colbert, K. A. Smith and R. E. Smalley, Hydrogen adsorption and cohesive energy of single-walled carbon nanotubes, Appl. Phys. Lett., 1999, 74, 2307–2309.
14. N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keefee and O. M. Yaghi, Hydrogen storage in microporous metal–organic frameworks, Science, 2003, 300, 1127–1129.
15. J. L. C. Rowsell and O. M. Yaghi, Strategies for hydrogen storage in metal–organic frameworks, Angew. Chem., Int. Ed., 2005, 44, 4670–4679.
16. C. Janiak, Engineering coordination polymers towards applications, Dalton Trans., 2003, 2781–2804.
17. B. Kesanli, Y. Cui, M. R. Smith, E. W. Bittner, B. C. Bockrath and W. Lin, Highly interpenetrated metal–organic frameworks for hydrogen storage, Angew. Chem., Int. Ed., 2005, 44, 72–75.
18. B. Q. Ma, K. L. Mulfort and J. T. Hupp, Microporous pillared paddle-wheel frameworks based on mixed-ligand coordination of zinc ions, Inorg. Chem., 2005, 44, 4912–4914.
19. A. Erxleben, Structures and properties of Zn(II) coordination polymers, Coord. Chem. Rev., 2003, 246, 203–228.
20. M. J. Rosseinsky, Recent developments in metal–organic framework chemistry: design, discovery, permanent porosity and flexibility, Microporous Mesoporous Mater., 2004, 73, 15–30.
21. A. R. Millward and O. M. Yaghi, Metal organic frameworks with exceptionally high capacity for storage of carbon dioxide at room temperature, J. Am. Chem. Soc., 2007, 127, 17998–17999.
22. A. G. Wong-Foy, A. J. Matzger and O. M. Yaghi, Exceptional H₂ saturation uptake in microporous metal–organic frameworks, J. Am. Chem. Soc., 2006, 128, 3494–3494.
23. S. S. Kaye, A. Dailly, O. M. Yaghi and J. R. Long, Impact of preparation and handling on the hydrogen storage properties of Zn₄O(1,4-benzenedicarboxylate)₃ (MOF-5), J. Am. Chem. Soc., 2007, 129, 14176–14177.
24. S. S. Han, W.-Q. Deng and W. A. Goddard, Improved designs of metal organic frameworks for hydrogen storage, Angew. Chem., Int. Ed., 2007, 46, 6289–6292.
25. H. Frost, T. Düren and R. Q. Snurr, Effects of surface area, free volume, and heat of adsorption on hydrogen uptake in metal–organic frameworks, J. Phys. Chem. B, 2006, 110, 9565–9570.
26. E. Klontzas, A. Mavrandonakis, G. E. Froudakis, Y. Carissan and W. Klopper, Molecular hydrogen interaction with IRMOF-1: a multiscale theoretical study, J. Phys. Chem. C, 2007, 111, 13635–13640.
27. O. Hubner, A. Gloss, M. Fichtner and W. Klopper, On the interaction of dihydrogen with aromatic systems, J. Phys. Chem. A, 2004, 108, 3019–3023.
28. H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortes, A. P. Cote, R. E. Taylor, M. O'Keeffe and O. M. Yaghi, Designed synthesis of 3D covalent organic frameworks, Science, 2007, 316, 268–272.
29. A. P. Côté, H. M. El-Kaderi, H. Furukawa, J. R. Hunt and O. M. Yaghi, Reticular synthesis of microporous and mesoporous 2D covalent organic frameworks, J. Am. Chem. Soc., 2007, 128, 12914–12915.
30. E. Klontzas, E. Tylianakis and G. E. Froudakis, Hydrogen storage in 3D covalent organic frameworks. A multiscale theoretical investigation, J. Phys. Chem. C, 2008, 112, 9095–9098.
31. H. Furukawa and O. M. Yaghi, Storage of hydrogen, methane, and carbon dioxide in highly porous covalent organic frameworks for clean energy applications, J. Am. Chem. Soc., 2009, 131, 8875–8883.
32. G. K. Dimitrakakis, E. Tylianakis and G. E. Froudakis, Pillared graphene: a new 3-D network nanostructure for enhanced hydrogen storage, Nano Lett., 2008, 8, 3166–3170.
33. E. Klontzas, A. Mavrandonakis, E. Tylianakis and G. E. Froudakis, Improving hydrogen storage capacity of MOF by functionalization of the organic linker with lithium atoms, Nano Lett., 2008, 8, 1572–1576.
34. S. S. Han and W. A. Goddard, Lithium-doped metal–organic frameworks for reversible H₂ storage at ambient temperature, J. Am. Chem. Soc., 2007, 129, 8422–8423.
35. S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard, Covalent organic frameworks as exceptional hydrogen storage materials, J. Am. Chem. Soc., 2008, 130, 11580–11581.
36. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter, 1992, 45, 13244–13249.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Kack, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schroder and T. Thonhauser, A density functional for sparse matter, J. Phys.: Condens. Matter, 2009, 21, 084203.
39. K. Sillar, A. Hofmann and J. Sauer, Ab initio study of hydrogen adsorption in MOF-5, J. Am. Chem. Soc., 2009, 131, 4143–4150.
40. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, Orlando, FL, 2001.
41. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, New York, NY, 1988.
42. W. W. Wood, Early History of Computer Simulation in Statistical Mechanics, Molecular Dynamics Simulations of Statistical Mechanics Systems, Proceedings of the 97th International “Enrico Fermi” School of Physics, ed. G. Ciccotti and W. G. Hoover, North-Holland, Amsterdam, 1986.
43. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. N. Teller and E. Teller, Equations of state calculations by fast computing machines, J. Chem. Phys., 1953, 21, 1087–1092.
44. D. Y. Peng and D. B. Robinson, A new two-constant equation of state, Ind. Eng. Chem. Fundam., 1976, 5, 59–64.
45. B. Widom, Some topics in the theory of fluids, J. Chem. Phys., 1963, 39, 2802–2812.
46. J. E. Lennard-Jones, Proceedings of the Physical Society, Cohesion, 1931, vol. 43, pp. 461–482.
47. I. F. Silvera and V. V. Goldman, The isotropic intermolecular potential for H₂ and D₂ in the solid and gas phases, J. Chem. Phys., 1978, 69, 4209–4213.
48. W. A. Steele, The physical interaction of gases with crystalline solids: I. Gas solid energies and properties of isolated adsorbed atoms, Surf. Sci., 1973, 36, 317–352.
49. L. Mattera, C. S. Rosatelli, F. Tommasini, U. Valbusa and G. Vidali, Selective adsorption of ¹H₂ and ²H₂ on the (0001) graphite surface, Surf. Sci., 1980, 93, 515–525.
50. A. D. Crowell and J. S. Brown, Laterally averaged interaction potentials for ¹H₂ and ²H₂ on the (0001) graphite surface, Surf. Sci., 1982, 123, 296–304.
51. J. J. Potoff and J. I. Siepmann, Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide and nitrogen, AIChE J., 2001, 47, 1676–1682.
52. W. L. Jorgensen, J. D. Madura and C. J. Swenson, Optimized intermolecular potential functions for liquid hydrocarbons, J. Am. Chem. Soc., 1984, 106, 6638–6646.
53. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035.
54. S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING a generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909.
55. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rivers, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236.
56. R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965.
57. F. Weigend, M. Haser, H. Patzelt and R. Ahlrichs, RI-MP2: optimized auxiliary basis sets and demonstration of efficiency, Chem. Phys. Lett., 1998, 294, 143–152.
58. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
59. TURBOMOLE version 5.8, http://www.turbomole.com/.
60. S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553.
61. P. Srepusharawoot, R. H. Scheicher, C. M. Araujo, A. Blomqvist, U. Pinsook and R. Ahuja, Ab initio study of molecular hydrogen adsorption in covalent organic framework-1, J. Phys. Chem. C, 2009, 113, 8498–8504.
62. D. M. Ceperley and B. Alder, Ground state of the electron gas by a stochastic method, Phys. Rev. Lett., 1980, 45, 566–569.
63. B. Assfour and G. Seifert, Hydrogen adsorption sites and energies in 2D and 3D covalent organic frameworks, Chem. Phys. Lett., 2010, 489, 86–91.
64. T. Frauenheim, G. Seifert, M. Elstner, Z. Hajnal, G. Jungnickel, D. Porezag, S. Suhai and R. Scholz, A self-consistent charge density-functional based tight-binding method for predictive materials simulations in physics, chemistry and biology, Phys. Status Solidi B, 2000, 217, 41–62.
65. L. Zhechkov, T. Heine, S. Patchkovskii, G. Seifert and H. A. Duarte, An efficient a posteriori treatment for dispersion interaction in density functional-based tight binding, J. Chem. Theory Comput., 2005, 1, 841–847.
66. E. Klontzas, E. Tylianakis and G. E. Froudakis, Designing 3D COFs with enhanced hydrogen storage capacity, Nano Lett., 2010, 10, 452–454.
67. H. Frost and R. Q. Snurr, Design requirements for metal–organic frameworks as hydrogen storage materials, J. Phys. Chem. C, 2007, 111, 18794–18803.
68. A. Mavrandonakis, E. Tylianakis, A. K. Stubos and G. E. Froudakis, Why Li doping in MOFs enhances H₂ storage capacity? a multi-scale theoretical study, J. Phys. Chem. C, 2008, 112, 7290–7294.
69. G. Garberoglio, Computer simulation of the adsorption of light gases in covalent organic frameworks, Langmuir, 2007, 23, 12154–12158.
70. G. Garberoglio and R. Vallauri, Adsorption and diffusion of hydrogen and methane in 2D covalent organic frameworks, Microporous Mesoporous Mater., 2008, 116, 540–547.
71. G. Garberoglio, A. I. Skoulidas and J. K. Johnson, Adsorption of gases in metal organic materials: comparison of simulations and experiments, J. Phys. Chem. B, 2005, 109, 13094–13103.
72. T. Sagara, J. Klassen and E. Ganz, Computational study of hydrogen binding by metal–organic framework-5, J. Chem. Phys., 2004, 121, 12543–12547.
73. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage, Science, 2002, 295, 469–472.
74. J. L. Rowsell, A. R. Millward, K. S. Park and O. M. Yaghi, Hydrogen sorption in functionalized metal–organic frameworks, J. Am. Chem. Soc., 2004, 126, 5666–5667.
75. A. I. Skoulidas, D. M. Ackerman, J. K. Johnson and D. S. Sholl, Rapid transport of gases in carbon nanotubes, Phys. Rev. Lett., 2002, 89, 185901.
76. H. Chen, J. K. Johnson and D. S. Sholl, Transport diffusion of gases is rapid in flexible carbon nanotubes, J. Phys. Chem. B, 2006, 110, 1971–1975.
77. Q. Yang and C. Zhong, Molecular simulation study of the stepped behaviors of gas adsorption in two-dimensional covalent organic frameworks, Langmuir, 2009, 25, 2302–2308.
78. G. E. Froudakis, Why alkali-metal-doped carbon nanotubes possess high hydrogen uptake, Nano Lett., 2001, 1, 531–533.
79. G. Mpourmpakis, E. Tylianakis, D. Papanikolaou and G. E. Froudakis, Theoretical study of alkaline metal cations in carbon nanotubes, Rev. Adv. Mater. Sci., 2006, 11, 92–97.
80. G. Mpourmpakis, E. Tylianakis, D. Papanikolaou and G. E. Froudakis, A multi scale theoretical study of Li⁺ interaction with carbon nanotubes, J. Nanosci. Nanotechnol., 2006, 6, 3731–3735.
81. R. C. Lochan and M. Head-Gordon, Computational studies of molecular hydrogen binding affinities: the role of dispersion forces, electrostatics, and orbital interactions, Phys. Chem. Chem. Phys., 2006, 8, 1357–1370.
82. J. Lan, D. Cao, W. Wang and B. Smit, Lithium-doped 3D covalent organic frameworks: High-capacity hydrogen storage materials, Angew. Chem., Int. Ed., 2009, 48, 4730–4733.
83. J. Lan, D. Cao and W. Wang, Li-Doped and Nondoped Covalent Organic borosilicate framework for hydrogen storage, J. Phys. Chem. C, 2010, 114, 3108–3114.
84. Y. J. Choi, J. W. Lee, J. H. Choi and J. K. Kang, Ideal metal-decorated three dimensional covalent organic frameworks for reversible hydrogen storage, Appl. Phys. Lett., 2008, 92, 173102.
85. T. Sagara, J. Ortony and E. Ganz, New isoreticular metal–organic framework materials for high hydrogen storage capacity, J. Chem. Phys., 2005, 123, 214707.
86. K. L. Mulfort and J. T. Hupp, Alkali metal cation effects on hydrogen uptake and binding in metal–organic frameworks, Inorg. Chem., 2008, 47, 7936–7938.
87. K. L. Mulfort, O. K. Farha, S. L. Stern, A. A. Sarjeant and J. T. Hupp, Post-synthesis alkoxide formation within metal–organic framework materials: a strategy for incorporating highly coordinatively unsaturated metal ions, J. Am. Chem. Soc., 2009, 131, 3866–3868.
88. K. L. Mulfort and J. T. Hupp, Chemical reduction of metal–organic framework materials as a method to enhance gas uptake and binding, J. Am. Chem. Soc., 2007, 129, 9604–9605.
89. D. Himsl, D. Wallacher and M. Hartmann, Improving the hydrogen-adsorption properties of a hydroxy Modified MIL-53(A1) structural analogue by lithium doping, Angew. Chem., Int. Ed., 2009, 48, 4639–4642.
90. E. Klontzas, E. Tylianakis and G. E. Froudakis, Hydrogen storage in lithium-functionalized 3-D covalent-organic framework materials, J. Phys. Chem. C, 2009, 113, 21253–21257.
91. F. Li, J. Zhao, B. Johansson and L. Sun, Improving hydrogen storage properties of covalent organic frameworks by substitutional doping, Int. J. Hydrogen Energy, 2010, 35, 266–271.
92. Y. Li and R. T. Yang, Hydrogen storage in metal–organic and covalent-organic frameworks by spillover, AIChE J., 2008, 54, 269–279.
93. L. Wang and R. Yang, New sorbents for hydrogen storage by hydrogen spillover—a review, Energy Environ. Sci., 2008, 1, 268–278.
94. M. Suri, M. Dornfeld and E. Ganz, Calculation of hydrogen storage capacity of metal–organic and covalent-organic frameworks by spillover, J. Chem. Phys., 2009, 131, 174703.

---