Structure–reactivity relationships and substituent effect additivity in the aqueous oxidation of chlorophenols by cerium(IV)

Abstract

The oxidation of all 19 chlorophenols and unsubstituted phenol by cerium(IV) was studied in an acidic aqueous solution in order to carry out a systematic test of chlorine substituent effects on the reactivity. All reactions were found to show 2 ∶ 1 cerium(IV)  ∶ phenol stoichiometry and a simple second-order rate equation. Rate constants did not correlate well with characteristic parameters such as pK values, carbon-13 NMR chemical shifts or Hammett substituent constants. Nevertheless, a strict additivity of chlorine substituent effects was found in both characteristic and reactivity parameters. The data suggest that a proton-coupled electron transfer mechanism could be operative. 2,4,6-Trichlorophenol was found to show exceptionally high reactivity towards cerium(IV).

---

Introduction

Chlorophenols constitute a group of widely used compounds that are currently listed as priority pollutants by European and American environmental protection agencies.^1,2 Their removal from industrial wastewater usually requires special techniques as they are resistant to chemical oxidation or microbial degradation.^3–16 From an environmental point of view, the stoichiometric oxidant in a chemical treatment method should be an abundant and cost-effective reagent, the by-product of which does not cause major environmental concerns. Hydrogen peroxide and peroxomonosulfate ion (oxone) seem ideal oxidants for this purpose and a number of catalytic systems have been reported using these compounds. The best results were obtained with iron complexes as catalysts.^{3,6–8,10–12} Mechanistic details of such catalyzed processes are not easy to explore. A useful but not very often used tool in those kinetic studies is a systematic change of the number of chlorine substituents on the oxidizable substrates.

In one of our earlier studies, an interesting structure–reactivity relationship was revealed in the Fe^IIITPPS-catalyzed (Fe^IIITPPS: iron(III) meso-tetra(4-sulfonatophenyl)porphine) oxidation of chlorophenols by hydrogen peroxide.¹⁰ Using various substituted chlorophenols, the logarithm of the rate constant of the reaction between the active form of the catalyst and the chlorophenols was shown to correlate with the ¹³C NMR chemical shift of the carbon atom that is directly connected to the oxygen in the chlorophenol.¹⁰ No similar relationship with the pK values of various phenols was found in the same work.¹⁰ The correlation must have far-reaching mechanistic implications, but the lack of similar examples from the earlier literature was a serious obstacle to making a convincing point about the consequences. Based on some independent information on the homolytic bond dissociation energies of chlorophenols,¹⁷ it was suggested that the observed trend might be indicative of hydrogen atom transfer in the rate determining step.¹⁰ The interpretation of these results would be much easier in comparison with similar substituent effect studies in stoichiometric redox reactions of chlorophenols in non-catalytic systems.

The three major one-electron oxidation pathways of phenols are hydrogen atom transfer (HAT), proton-coupled electron transfer (PCET), and sequential proton-loss electron transfer (SPLET). In water, SPLET is equivalent to the acid dissociation of the phenol followed by electron transfer from the phenolate anion. This is easily identified by the pH dependence as this sort of mechanism should show inverse first-order dependence on the concentration of hydrogen ion in the acidic region. No such distinction is easily made between HAT and PCET and recent research has focused a lot of attention on this question.^18–28

The aim of the present work was a thorough study of the effect of chlorine substituents on the one-electron oxidation of phenols using all possible chlorinated phenols. Cerium(IV) was found to be an ideal oxidant for this purpose as it is a strong one-electron oxidant which can only be used in highly acidic medium, ensuring that any rate contributions from pathways involving the phenolate ion (SPLET) could only be minor. This paper reports our detailed stoichiometric and kinetic results and correlation analysis between rate constants and selected characteristic parameters.

Experimental section

Materials

Chlorinated phenols were purchased from Aldrich, Lancaster Synthesis and Supelco. When necessary (i.e. when the purchased material was not completely white), they were purified by vacuum sublimation before use. The purity of all compounds has been tested in ¹H and ¹³C NMR measurements. Throughout this paper, different chlorophenols will be abbreviated by giving only the positions of the chlorine substituents on the phenol (e.g. 236 means 2,3,6-trichlorophenol). Solutions of Ce(IV) were prepared by dissolving Ce(SO₄)₂ in sulfuric acid. The Ce(IV) concentrations of these solutions were standardized by iodometry. All other chemicals used in this study were of analytical reagent grade and purchased from commercial sources. Doubly deionized and ultrafiltered water from a Millipore Q system was used to prepare the stock solutions and samples.

Instruments and softwares

Shimadzu UV-2501PC (scanning), Shimadzu UV-3101PC (scanning), Shimadzu MultiSpec-1500 (diode-array), Perkin Elmer Lambda 25 (scanning), Perkin Elmer Lambda 2S (scanning), and HP-8543 (diode-array) spectrophotometers were used in this study using standard quartz cells with 1.000 cm optical path length. All kinetic measurements were performed with an Applied Photophysics DX-17 MV sequential stopped-flow apparatus in the absorbance mode using 1.00 cm optical path length. The dead time of the instrument was measured to be 1.09 ± 0.02 ms by published methods.^29,30 pH was measured by standard combination glass electrodes (Hanna Instruments or Metrohm) connected to either a precision Hanna Instruments pH-meter or a computer-controlled Metrohm Titrino system. The calibration of the electrodes was based on relevant IUPAC recommendations.³¹¹H and ¹³C NMR spectra were recorded on Varian VRX-300, Varian VRX-400, Bruker DRX-360 and Bruker DRX-400 instruments and were calibrated using the residual signal of the solvent CDCl₃. In addition to the operating softwares of individual instruments, Scientist³² and Matlab³³ were used in the fitting procedures.

Results

Acid dissociation constants and chemical shifts

The acid dissociation constants of all studied chlorophenols were determined in this study in order to use strictly identical conditions and measuring methods. A combined pH-potentiometric and spectrophotometric method was used, whereby the UV-vis spectra of chlorophenols were recorded as a function of measured pH. Fig. S1 in the ESI† gives a series of spectra for 2356 as an example. The data were evaluated based on the following equation with the use of linear algebraic transformations detailed in the ESI†:In this equation, A_λ,pH is the absorbance measured at wavelength λ and pH, c_tot is the analytical concentration of the phenol, [small script l] is the path length, ε_λ,HA and ε_λ,A are the molar absorption coefficients for the protonated and deprotonated forms of the phenol at wavelength λ. All determined pK values are shown in Table 1 along with some relevant literature data for comparison.^34–36 The standard error for the determined parameter pK was smaller than 0.01 when calculated by the usual statistical analysis. This is viewed as unreasonably small as the actual accuracy of the pH measurements was 0.01 in all cases. Therefore, the conservative estimate of 0.02 will be used for the standard errors for all pK values determined in this work. ¹H NMR and ¹³C chemical shifts were determined for all chlorophenols in CDCl₃ by routine measurements. The results are listed in Table 1 and Table S1 in the ESI.†

Table 1 pK values, ¹³C NMR chemical shifts and rate constants in the oxidation by cerium(IV) determined for different chlorophenols used in this study

	pK^a	Literature pK^b		δC1^c/ppm	k/M^−1s^−1
		Ref: d,e	Ref: f
a Measured in this work, standard error: ±0.02 (see text for detailed explanation). b Literature data typically measured at varying ionic strength and medium, sometimes with the addition of non-aqueous solvents up to 50%. c Precision: ±0.1 ppm, solvent: CDCl3. d NIST Database (ref. 34). e SC Database (ref. 35). f Ref. 36.
Phenol	9.86	9.79^d	10.02	155.3	(3.72 ± 0.03) × 10^4
2-Chlorophenol	8.33	8.53^d	8.48	151.5	(9.07 ± 0.05) × 10^3
3-Chlorophenol	8.85	8.78^d	9.02	155.9	(3.48 ± 0.01) × 10^4
4-Chlorophenol	9.34	9.20^d	9.38	153.8	(4.43 ± 0.02) × 10^4
2,3-Dichlorophenol	7.64	7.70^d	7.45	152.8	(9.08 ± 0.11) × 10^3
2,4-Dichlorophenol	7.83	7.89^d	7.75	150.3	(5.72 ± 0.05) × 10^3
2,5-Dichlorophenol	7.40	7.51^d	7.35	152.0	(9.79 ± 0.03) × 10^3
2,6-Dichlorophenol	6.77	6.79^d	6.79	148.1	(1.58 ± 0.01) × 10^3
3,4-Dichlorophenol	8.56	8.59^d	8.39	154.6	(4.54 ± 0.05) × 10^4
3,5-Dichlorophenol	7.99	8.18^d	7.93	156.5	(3.48 ± 0.04) × 10^4
2,3,4-Trichlorophenol	7.00	—	7.59	151.4	(1.00 ± 0.05) × 10^4
2,3,5-Trichlorophenol	6.68	—	7.23	153.0	(1.06 ± 0.06) × 10^4
2,3,6-Trichlorophenol	5.75	—	6.12	149.2	(1.84 ± 0.01) × 10^3
2,4,5-Trichlorophenol	6.97	6.71^e	7.33	150.8	(1.63 ± 0.03) × 10^4
2,4,6-Trichlorophenol	6.15	6.42^e	6.42	147.1	(2.27 ± 0.08) × 10^4
3,4,5-Trichlorophenol	7.82	—	7.74	154.2	(5.6 ± 0.3) × 10^4
2,3,4,5-Tetrachlorophenol	6.31	—	6.96	151.0	(2.3 ± 0.2) × 10^4
2,3,4,6-Tetrachlorophenol	5.32	—	—	147.9	(2.21 ± 0.08) × 10^3
2,3,5,6-Tetrachlorophenol	5.31	—	5.44	150.1	(2.7 ± 0.1) × 10^3
Pentachlorophenol	4.66	5.25^e	5.26	148.3	(6.0 ± 0.9) × 10^3

---

Reaction stoichiometry

The stoichiometry of the reaction between cerium(IV) and each chlorophenol was studied by spectrophotometric titration in 0.10 M H₂SO₄. A solution of the studied phenol was titrated in a cell and the spectra were recorded after the addition of each increment. As an example, the titration of 246 is shown in Fig. 1, which also displays the UV-vis spectra of Ce(IV) and Ce(III). In all cases, the reaction was shown to feature Ce(IV)  ∶ phenol stoichiometry of 2 ∶ 1 corresponding to an overall two-electron oxidation of the phenols. This is valid for conditions under which the phenol is in excess and the product of this initial reaction was shown to be oxidized further by Ce(IV) on a time scale longer (from several minutes to hours) than that of the direct reaction between the original reagents. This clearly demonstrated the need for titrating a phenol solution with small increments of Ce(IV) solution in the spectrophotometric titrations, results from a reverse titration would have been difficult to interpret. The kinetics of the process was always studied at phenol excess, where the 2 ∶ 1 stoichiometry clearly prevails.

Fig. 1 Spectrophotometric titration of an aqueous solution of 2,4,6-trichlorophenol with cerium(IV) sulfate. Initial solution: V = 2.00 cm³, [246] = 0.690 mM. Titrant: [Ce(IV)] = 4.75 mM. Increments: 0.100 cm³. Optical path length: 1.000 cm, T = 25.0 °C. Inset: molar absorbance values of Ce(IV) and Ce(III).

No efforts were made to positively identify the two-electron oxidation products formed from the phenols beyond some observations in the reactions of 246 and 26. In the case of 246, the confirmed 2 ∶ 1 stoichiometry corresponds to a two-electron oxidation of the organic molecule, which usually leads to 2,6-dichloro-1,4-benzoquione according to well established literature information.^{8,10,12,37–40} Further experimental confirmation of this product was made possible by the fact that neither 246 nor the product Ce(III) has significant absorption above 320 nm. The UV-vis spectrum of the product of the reaction between 246 and Ce(IV) was indistinguishable from the independently known spectrum of an authentic sample of 2,6-dichloro-1,4-benzoquione.³⁷ Furthermore, two characteristic reactions (a photoreaction³⁷ and oxidation by H₂O₂ solution¹⁰) of this quinone were also confirmed to occur in test experiments after masking cerium(III) with EDTA (Fig. S3 in the ESI†). In the case of 26 (Fig. S4 in the ESI†), a similar analysis showed that the product was different from 2,6-dichloro-1,4-benzoquinone, which was formed in the FeTPPS-catalyzed oxidation of 26.¹⁰ The confirmed stoichiometry also rules out the formation of 2,6-dichloro-1,4-benzoquinone as it would require a four-electron oxidation of 26. The most logical two-electron oxidation product of 26 would be 3-chloro-1,2-benzoquinone. This is in agreement with the intense peak observed at 434 nm in the product spectrum, which is usually characteristic of ortho-quinones, and is also in agreement with the literature information.^41–44 However, these observations by no means imply a positive product identification similar to the case of 246.

Reaction kinetics

The kinetics of the reactions was studied at chlorophenol excess by the stopped-flow method. In all cases, the following simple second-order rate equation was found to be valid:In most cases, the chlorophenol could be used in large excess over Ce(IV). The absorption of the limiting reagent Ce(IV) was followed at 320 nm, where only Ce(IV) absorbs. An exponential decay was observed in these cases, which proved that the reaction was first-order with respect to Ce(IV). The concentrations of chlorophenols were varied by about an order of magnitude in different experiments, and the direct proportionality of the observed rate constants with the concentration of the excess reagent (Fig. 2) proved the first-order nature of the process with respect to the chlorophenol. It should be kept in mind that the slopes of these straight lines give an estimate of 2k because of the stoichiometry.⁴⁵

Fig. 2 Pseudo first-order rate constants as a function of chlorophenol concentration in the oxidation of various chlorophenols by cerium(IV) ion. Medium: 0.10 M H₂SO₄. T = 25.0 °C.

245, 345, 2345, 2346, 2356 and 23456 were not soluble enough in water to cover a sufficiently large concentration range in kinetic experiments while still using a large excess of the chlorophenol over Ce(IV). In these cases, most measurements were carried out under second-order conditions. The absorbance-time traces were fitted to the following equation:⁴⁵

where

Δ = [Cl–Ph]₀ − 0.5[Ce(IV)]₀, γ = [Ce(IV)]₀/[Cl–Ph]₀, k_app = kΔ (4)

In eqn (3), ε represents the molar absorption coefficient of Ce(IV) in 0.10 M H₂SO₄. The successful fit to this equation alone proves adherence to eqn (2). Nevertheless, kinetic curves measured at 4–6 different initial concentrations of the chlorophenols were used in each case to estimate the rate constant.

All the determined rate constants are listed in Table 1. The values refer to measurements done in 0.10 M H₂SO₄ without any additional salts. Some detailed kinetic information for chlorophenols not covered in Fig. 2 are shown in Fig. S5–S8 in the ESI.† The rate did not depend on the acidity in the H₂SO₄ concentration range between 0.10 M (pH = 0.86) and 0.50 M (pH = 0.25).

Structure–reactivity correlations

Correlations were sought between two characteristic parameters, pK and the ¹³C NMR chemical shift of the carbon atom connected directly to the oxygen in each chlorinated phenol (δ¹³C₁) and the logarithm of the second-order rate constant of the oxidation of the phenol by Ce(IV). Fig. 3 shows that the two characteristic parameters are significantly different as they do not correlate with each other. On closer inspection, the graph reveals that the chlorophenols can be divided into three groups depending on the number of chlorine substituents in the meta position. There is strong correlation between the two characteristic parameters within each group.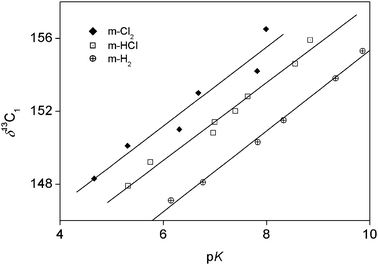

Fig. 3 ¹³C chemical shifts of the phenolic carbon as a function of the pK values for the studied chlorophenols.

Fig. 4 shows that the correlation between the logarithm of the rate constants and δ¹³C₁ is weak. The figure also displays similar data from an earlier work obtained in the Fe^IIITPPS-catalyzed oxidation of chlorophenols where a strong correlation was observed for comparison.¹⁰ There is no spectacular correlation between pK values and rate constants, either (Fig. S9 in the ESI†). Average chemical shifts of aromatic carbon atoms were also used as site-independent molecular descriptors, but failed to give any reasonable correlation with the rate constants (Fig. S10 in the ESI†).

Fig. 4 Rate constants of the oxidation chlorophenols by cerium(IV) as a function of the ¹³C chemical shift of the phenolic carbon. Grey triangles: similar plot obtained in the reaction of chlorophenols with hydrogen peroxide catalyzed by Fe^III(TPPS).¹⁰

Additivity of substituent effects

The additivity of substituent effects was tested for both characteristic parameters and for the kinetic data as well by seeking substituent constants that best adhere to Hammett-type relationships.⁴⁶ The first equation (3σ equation) assumed total additivity of substituent effects:

Y = Y₀ + n_oσ_o + n_mσ_m + n_pσ_p (5)

where σ_o, σ_m and σ_p are characteristic of the effect of ortho, meta and para substituents, and Y₀ is the reference value of the property characteristic for unsubstituted phenol. It must be noted that Y₀ was also optimized to give the best fit for all points rather than simply assigned the value of unsubstituted phenol. This was necessary in order to avoid assigning a special role to any particular compound in the fitting procedure.

An approach containing more parameters has also been tried. In this approach, it was not assumed that two ortho substituents, for example, have the same effect on the property together as two independent ortho substituents would have. The corresponding equation (5σ equation) is given as:

The additivity tests were done based on the 20-element data set by seeking the best-fitting σ values with linear least-squares fitting for each of the three properties pK, δ¹³C₁, and log k. The best fitting σ_o, σ_m and σ_p values for eqn (5), together with the correlation coefficients, are displayed in Table 2. The goodness of the fits are illustrated in Fig. 5–7, where the analyzed property is displayed as a function of the appropriate sum of substituent constants Σ and Σ′. The definitions of these quantities follow from eqn (5) and (6):

Σ = n_oσ_o + n_mσ_m + n_pσ_p (7)

As the values of σ_o, σ_m and σ_p have been determined to give the best fit, points in this representation should be scattered around a straight line that has a slope of unity. Deviations from these straight lines represent the deviations from additivity. The correlation coefficients given in Table 2 give a numerical idea about the goodness of fit.

Fig. 5 pK values for the studied chlorophenols as a function of the sum of substituent constants. 3σ: with the use of eqn (5). 5σ: with the use of eqn (6).

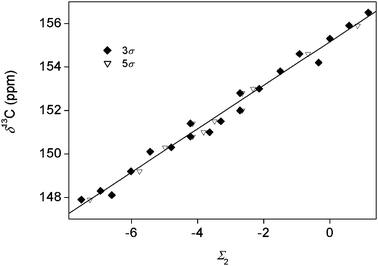Fig. 6 ¹³C NMR chemical shifts for the studied chlorophenols as a function of the sum of substituent constants. 3σ: with the use of eqn (5). 5σ: with the use of eqn (6).

Fig. 7 Rate constant measured in the oxidation of the studied chlorophenols by cerium(IV) as a function of the sum of substituent constants excluding 2,4,6-trichlorophenol. 3σ: with the use of eqn (5). 5σ: with the use of eqn (6).

Table 2 Substituent constant values and correlation coefficients from the additivity studies of pK, chemical shift and rate constant values

	σ o	σ m	σ p	r 3σ ^2	r 5σ ^2
pK	−1.54 ± 0.03	−0.79 ± 0.03	−0.45 ± 0.06	0.9938	0.9949
δ ^13C	−3.3 ± 0.1	0.58 ± 0.10	−1.50 ± 0.16	0.9865	0.9893
log k	−0.53 ± 0.07	0.03 ± 0.07	0.24 ± 0.11	0.9519	0.9543

---

Discussion

The rate equation of the oxidation of chlorophenols by cerium(IV) shows that the phenolate anion cannot be a reactive species in these processes. Very clearly, inverse first-order acidity-dependence would be expected in this case under the highly acidic conditions used here. In addition, the true second order rate constant of the process would be higher than the diffusion controlled limit of 10¹⁰ M⁻¹ s⁻¹ for some of the studied compounds (phenol, 2, 3, 4, 23, 24, 25, 34, 35, 234, 245, 345) if electron transfer was initiated form the phenolate ion. This observation rules out the SPLET mechanism of one-electron transfer. It is also notable that none of the kinetic studies showed saturation of rate with increasing concentration of chlorophenol, which indicates that there is no substantial association (complex formation) between the reactants. The most notable deviation from the expected straight lines in the pseudo first-order rate constant-chlorophenol concentration plots occurs for 246 (shown in Fig. 2), where a careful look at the plot might hint of some curvature. However, this is statistically insignificant. Actually, it would have been very useful to do experiments at higher concentrations of 246 because any saturation character would have been more pronounced in that region. Unfortunately, this was not possible because the experiments already approached the solubility limit of 246. Therefore, there is no experimental reason to believe that there is a significant saturation character for this plot.

Fig. 3 shows that the two characteristic parameters (pK and δ¹³C₁) analyzed here are under different influences. A closer look at this figure reveals that the points actually give linear correlation in three distinct series depending on the number of metachloro substituents. The fact that the correlation is quite good within each of the three series (m-H₂, m-HCl, and m-Cl₂) indicates that the para and the ortho substituents have very similar effects on the pK and on δ¹³C₁. This will be analyzed further at the discussion of the additivity tests.

Fig. 4 shows very poor correlation between the logarithm of rate constants and the δ¹³C₁ values. An even worse correlation is found between log k and pK values (Fig. S9 in the ESI†). The points in Fig. 4 can be broken down to three clusters depending on the number of orthochloro substituents. Basically, o-Cl₂ phenols (except 246) are oxidized relatively slowly and o-H₂ phenols relatively fast, with o-HCl phenols occupying a middle position in this respect. This is quite different from the earlier case when we studied the Fe^IIITPPS/H₂O₂ system as shown by the grey points in Fig. 4.¹⁰ Even if one assumes a weak correlation for the rate constants of the cerium(IV) oxidation, this correlation is in the opposite direction (log k is smaller with larger δ¹³C₁) than in the case of Fe^IIITPPS/H₂O₂ system.¹⁰ In addition, the product in one of the reactions was proved to be quite different: 26 is oxidized to 2,6-dichloro-1,4-benzoquinone in the case of Fe^IIITPPS/H₂O₂,¹⁰ whereas this is clearly not the case in the present study of cerium(IV) oxidation. On these grounds, it is very safe to conclude that these two reactions have quite different mechanisms. Since there is some reason to argue that the Fe^IIITPPS/H₂O₂ system oxidizes phenols by HAT,¹⁰ the cerium(IV) oxidation could follow the PCET pathway.

Fig. 5–7 show that the additivity of substituent effects is excellent for pK values, but the δ¹³C₁ and log k data (excluding 246 in this last case) also show fits that are better than in most published examples of substituent effect relationships. It should be noted that the correlation coefficients only show a very modest improvement when eqn (6) is used. This, again, proves that the additivity of substituent effects is quite good for each of the studied properties and the fit cannot be improved by including further parameters.

The determined σ values summarized in Table 2 deserve more attention. The σ values obtained from different properties are not directly comparable as the absolute changes in pK, δ¹³C₁ and log k are different. From the σ values obtained based on pK values, it is clear that distance is the primary factor in determining the acidity of the phenolic OH groups. All three σ constants are negative (any substitution with chlorine decreases the pK), which is probably due to the electron withdrawing effect of a chlorine substituent. The σ values decrease in the σ_o > σ_m > σ_p order. The two other properties show different behavior. The δ¹³C₁ values reflect a behavior similar to the textbook direction rules in aromatic electrophilic substitution, which is based on a balance between electron withdrawing and inductive effects. Ortho and (to a smaller degree) para substituents decrease the chemical shift, which means that they increase the electron density on the phenolic carbon. The σ_o/σ_p ratio is 2.2 for δ¹³C₁, which is not very far away from the similar ratio calculated based on pK values (3.4). This is the primary origin of the good correlation between pK and δ¹³C₁ within each of the three series shown in Fig. 3. The σ_m value obtained from δ¹³C₁ is positive, which means that meta substitution removes some electron density from the phenolic carbon. The magnitude of the effect, however, is much smaller than para or ortho effects. This is, again, in excellent agreement with the classic interpretation of the inductive effect.

Sigma values obtained from rate constants show a third trend. First of all, the rate constant of 246 did not follow the pattern set by the remaining 19 compounds. Therefore, the statistical analysis was done and Fig. 6 is shown based on 19 points. A version of this graph with all 20 points is shown as Fig. S11 in the ESI†, and illustrates that the effect of even a single point can hide an otherwise significant correlation in the statistical analysis. The largest substituent effect, similarly to the previous two cases, is exerted by the orthogroup, and the negative value of σ_o indicates that ortho substitution decreases the reactivity in the cerium(IV) oxidation. Earlier, there have been numerous attempts to characterize ortho substituents with Hammett constants.^47–52 These efforts did not yield widely accepted σ_o values, which is classically interpreted as a consequence of steric effects. However, this interpretation would not be without contradictions in our special case. First of all, chlorine is a single atom, which is much closer in steric bulk to a hydrogen atom than any other chemical groups with several connected atoms. In addition, the effect compared to the effect of the para substituents is actually weaker than similar ratios for characteristic parameters (pK and δ¹³C₁). Therefore, there is not much experimental ground for implying steric effects in this process.

Meta substitution has no significant effect on the reactivity as shown by the σ_m value, which is not significantly different from 0. Para substitution, on the other hand, clearly increases the reactivity: σ_p is positive and its value is about a half of −σ_o. Based on these observations, 4, 34 and 345 are expected to have the largest rate constants, which is in full agreement with the data shown in Table 1. It is also observed that the effects are strongly position-dependent: there is a 50-fold difference in rate constants and a pK change of more than 2.0 determined just within the series of six trichlorophenols. The chlorine substituents are not directly involved either in acid dissociation or in the rate determining step of the cerium(IV) reaction. Therefore, their effect must be exerted solely by modifying the electronic structure of the aromatic system. As pointed out previously, this can be often understood in terms of electron withdrawing and inductive effects.

As mentioned above, 246 did not fit the trend of rate constants defined by the rest of the chlorophenols. This is a quite unexpected finding and a warning for the future design of experiments because 246 has been used as a typical chlorophenol in many earlier studies.^3,7,11 246 is not exceptional in its characteristic parameters, but the fact that it is the chlorophenol with the lowest δ¹³C₁ should not go unnoticed. Therefore, it is the chlorophenol with the most electron rich phenolic carbon atom and it is not unfeasible that the oxidation mechanism for 246 is different from the remaining group of 19 compounds. It is also to be recalled that 246 is the case when some hints of rate saturation are seen in the rate equation which might be attributable to the complexation of reactants. No similar phenomena were observed experimentally for any of the 19 other compounds.

The generally accepted Hammett substituent constants^45,46,48,52 for chlorine are σ_p = 0.23 and σ_m = 0.37. This fits the values obtained from the pK data in this work (σ_p/σ_m = 1.61 from the accepted values and 1.75 from the pK data of Table 2), which is perhaps not surprising as the Hammett substituent constants were originally defined based on the pK values of substituted benzoic acids.⁴⁶ The Hammett constants are primarily used to interpret kinetic data. In the series of reactions studied in this work, they are unsuitable for this purpose, which is illustrated by a Hammett plot for the six chlorophenols not containing any ortho substituents (Fig. S12, ESI†). This plot does not show any correlation.

Conclusion

In this work, we have shown that the oxidation of chlorophenols by cerium(IV) follows 1 ∶ 2 stoichiometry and a simple second-order rate equation in the acidic region. pK values and ¹³C NMR chemical shifts have been determined as characteristic parameters. The rate constants do not correlate well with these characteristic parameters or with the conventional Hammett substituent constants. However, all three sets of parameters follow well defined additivity rules. 2,4,6-Trichlorophenol shows a substantially different behavior than other chlorophenols do, which should be taken into account when selecting typical chlorophenols as model compounds in future studies.

Acknowledgements

The authors thank the Tempus Foundation and Hungarian Science Foundation (OTKA) for financial support under grant No. K68668. The research was supported by the EU and co-financed by the European Social Fund through the Social Renewal Operational Programme under the project CHEMIKUT (TÁMOP-4.2.2-08/1-2008-0012). The financial support of TEVA Hungary Ltd. is also highly appreciated. Some experiments were carried out using the facilities of Iowa Sate University and Ames Laboratory in Ames, Iowa, US.

References

1. L. H. Keith and W. A. Telliard, Environ. Sci. Technol., 1979, 13, 416.
2. Decision No 2455/2001/EC of the European Parliament and of the Council of 20 November 2001 establishing the list of priority substances in the field of water policy and amending Directive 2000/60/EC.
3. A. Sorokin, J. L. Séris and B. Meunier, Science, 1995, 268, 1163.
4. F. J. Benitez, J. Beltran-Hereida, J. L. Acero and F. J. Rubio, Ind. Eng. Chem. Res., 1999, 38, 1341.
5. L. Padilla, V. Matus, P. Zenteno and B. Gonzalez, J. Basic Microbiol., 2000, 40, 243.
6. B. Meunier, Science, 2002, 296, 270.
7. S. Sen Gupta, M. Stadler, C. A. Noser, A. Ghosh, B. Steinhoff, D. Lenoir, C. P. Horwitz, K. W. Schramm and T. J. Collins, Science, 2002, 296, 326.
8. G. Lente and J. H. Espenson, Chem. Commun., 2003, 1162.
9. M. Fukushima, A. Sawada, M. Kawasaki, H. Ichikawa, K. Morimoto and K. Tatsumi, Environ. Sci. Technol., 2003, 37, 1031.
10. G. Lente and J. H. Espenson, New J. Chem., 2004, 28, 847.
11. G. Lente and J. H. Espenson, Int. J. Chem. Kinet., 2004, 36, 449.
12. G. Lente and J. H. Espenson, Green Chem., 2005, 7, 28.
13. G. Díaz-Díaz, M. Celis-García, M. C. Blanco-López, M. J. Lobo-Castanon, A. J. Miranda-Ordieres and P. Tunón-Blanco, Appl. Catal., B, 2010, 96, 51.
14. K. C. Christoforidis, M. Louloudi, E. R. Milaeva and Y. Deligiannakis, J. Catal., 2010, 270, 153.
15. K. C. Christoforidis, M. Louloudi and Y. Deligiannakis, Appl. Catal., B, 2010, 95, 297.
16. Q. Raffy, R. Ricoux, E. Sansiaume, S. Pethe and J. P. Mahy, J. Mol. Catal. A: Chem., 2010, 317, 19.
17. S. I. Ahonkhai, I. Wiater and R. Louw, Organohalogen Compd., 2000, 46, 74.
18. J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142.
19. I. J. Rhile and J. M. Mayer, J. Am. Chem. Soc., 2004, 126, 12718.
20. C. Isborn, D. A. Hrovat, W. S. Borden, J. M. Mayer and B. K. Carpenter, J. Am. Chem. Soc., 2005, 127, 5794.
21. J. P. Aguer, G. Mailhot and M. Bolte, New J. Chem., 2006, 30, 191.
22. F. d'Acunzo, C. Galli, P. Gentili and F. Sergi, New J. Chem., 2006, 30, 583.
23. C. Costentin, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 2006, 128, 4552.
24. O. V. Zalomaeva and A. B. Sorokin, New J. Chem., 2006, 30, 1768.
25. G. Litwinienko and K. U. Ingold, Acc. Chem. Res., 2007, 40, 222.
26. C. Galli, P. Gentili, A. S. Nunes Pontes, J. A. F. Gamelas and D. V. Evtuguin, New J. Chem., 2007, 31, 1461.
27. N. Song and D. M. Stanbury, Inorg. Chem., 2008, 47, 11458.
28. O. V. Zalomaeva, I. D. Ivanchikova, O. A. Kholdeeva and A. B. Sorokin, New J. Chem., 2009, 33, 1031.
29. B. Tonomura, H. Nakatani, M. Ohnishi, J. Yamaguchi-Ito and K. Hiromi, Anal. Biochem., 1978, 84, 370.
30. G. Peintler, A. Nagy, A. K. Horváth, T. Körtvélyesi and I. Nagypál, Phys. Chem. Chem. Phys., 2000, 2, 2575.
31. A. K. Covington, R. G. Bates and R. A. Durst, Pure Appl. Chem., 1985, 57, 531.
32. SCIENTIST, Version 2.0, Micromath Software, Salt Lake City, UT, USA, 1995.
33. MatLab for Windows, Version 4.2c1, The Mathworks, Inc., Natick, MA, USA, 1994.
34. NIST Standard Reference Database 46 Version 8: Critically Selected Stability Constants of Metal Complexes (http://www.nist.gov/ts/msd/srd/nist46.cfm).
35. The IUPAC Stability Constants Database, SC-Database (http://www.acadsoft.co.uk/).
36. L. Lepri, P. G. Desideri and D. Heimler, J. Chromatogr., 1980, 195, 339.
37. G. Lente and J. H. Espenson, J. Photochem. Photobiol., A, 2004, 163, 249.
38. W. H. Hunter and M. Morse, J. Am. Chem. Soc., 1926, 48, 1615.
39. H. Lübbecke and P. Boldt, Angew. Chem., Int. Ed. Engl., 1976, 15, 608.
40. R. S. Shukla, A. Robert and B. Meunier, J. Mol. Catal. A: Chem., 1996, 113, 45.
41. R. Willstätter and H. E. Muller, Ber. Dtsch. Chem. Ges., 1911, 44, 2182.
42. R. D. Kaushik, R. P. Singh and V. Shashi, Asian J. Chem., 2003, 15, 1485.
43. M. P. Shurygina, Y. A. Kurskii, N. O. Druzhkov, S. A. Chesnokov, L. G. Abakumova, G. K. Fukin and G. A. Abakumov, Tetrahedron, 2008, 64, 9784.
44. G. Albarran, W. Boggess, V. Rassolov and R. H. Schuler, J. Phys. Chem. A, 2010, 114, 7470.
45. J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, 2nd edn, McGraw-Hill, New York, 1995, p. 25 and p. 226.
46. L. P. Hammett, Chem. Rev., 1935, 17, 125.
47. M. Charton, J. Am. Chem. Soc., 1969, 91, 6649.
48. C. H. Yoder, R. H. Tuck and R. E. Hess, J. Am. Chem. Soc., 1969, 91, 539.
49. M. Charton, Prog. Phys. Org. Chem., 1971, 8, 235.
50. C. D. Schaeffer, Jr. and C. H. Yoder, J. Org. Chem., 1971, 36, 2201.
51. T. Fujita and T. Nishioka, Prog. Phys. Org. Chem., 1976, 12, 49.
52. C. Hansch and A. Leo, Substituent Constants for Correlation Analysis in Chemistry and Biology, Wiley, New York, 1979.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures, tables and mathematical derivations referred to in the text of the article. See DOI: 10.1039/c0nj00529k

---