Prediction of solid oxide fuel cell cathode activity with first-principles descriptors

Abstract

In this work we demonstrate that the experimentally measured area specific resistance and oxygen surface exchange of solid oxide fuel cell cathode perovskites are strongly correlated with the first-principles calculated oxygenp-band center and vacancy formation energy. These quantities are therefore descriptors of catalytic activity that can be used in the first-principles design of new SOFC cathodes.

---

Broader context

Achieving adequate oxygen reduction reaction (ORR) rates at reduced temperatures is a critical challenge for the next generation Solid Oxide Fuel Cells (SOFCs). SOFC cathode catalysts are typically perovskites, where the ORR takes place by coupling to the material surface and bulk properties in a poorly understood manner. Here we show this complex catalytic reaction is in fact governed by a single bulk phase descriptor, the bulk oxygenp-band center or bulk vacancy formation energy. We demonstrate that the experimentally measured area specific resistance and oxygen surface exchange of SOFC perovskites are both strongly correlated with our first-principles-based descriptors, although not with the commonly used metal d-band center. We explain the success of our descriptor in terms of a rigid band model and oxygen redox chemistry. These descriptors allow the catalytic activity of perovskite SOFC cathodes to be predicted directly by first-principles, enabling first-principles design of new SOFC cathodes.

SOFCs are a promising technology for efficient energy generation from a wide-range of hydrocarbon fuels, but applications of SOFCs are severely limited by their high operating temperature (typically 800∼1000 °C).^1–5 Lowering the SOFC operating temperatures to 600∼800 °C, or even lower, would dramatically reduce materials costs, degradation rates, start-up times, and packaging requirements. Lower SOFC operating temperatures would thereby enable new applications and more rapid commercialization in present areas of opportunity (e.g., distributed power generation, auxiliary truck power, or combined SOFC/gas turbines). The present high operating temperature of SOFCs is in part required by the need to efficiently catalyze the oxygen reduction reaction (ORR),^4–6 O₂ (gas) + 4e⁻ → 2O²⁻ (solid phase), which occurs at the SOFC cathode during operation. Developing lower-temperature SOFC's therefore requires the identification of new catalyst material with dramatically improved ORR capabilities.³ Here we show this complex catalytic reaction is in fact governed by a single bulk phase descriptor, the bulk oxygenp-band center or bulk vacancy formation energy. We demonstrate that the experimentally measured area specific resistance and oxygen surface exchange of SOFC perovskites are both strongly correlated with our first-principles-based descriptors, although not with the commonly used metal d-band center.^7–9 We explain the success of our descriptor in terms of a rigid band model¹⁰ and oxygen redox chemistry. These descriptors allow the catalytic activity of perovskite SOFC cathodes to be predicted directly by first-principles, enabling first-principles design of new SOFC cathodes.

Limited understanding of the ORR on the multicomponent perovskites used in SOFCs has been a fundamental impediment to detailed molecular modeling.¹¹ Attempts to understanding the rate limiting ORR steps on perovskite surfaces^5,12–14 have faced major challenges due to the complexity of the materials and difficulties in performing in situ characterization of well-controlled samples. Therefore, the rate limiting steps and structure-property relationships underlying the ORR on perovskites are still not well understood (although rate limiting steps have been recently identified for a few systems by non-linear impedance spectroscopy^15,16). Because of this limited understanding a complete molecular level model of the ORR in SOFCs has not yet been developed for even a single system, and the goal of first-principles design of new SOFC catalysts has appeared to be unobtainable for the present.

To overcome the challenges associated with full molecular models of the ORR we here propose a first-principles based descriptor approach for SOFC catalyst design. The descriptor approach searches for a functional relationship between a simple calculated property (the descriptor) and catalytic activity. This approach has been successfully applied to predict ORR on metal elemental and alloy surfaces,^17,18 where the d-band center or oxygen surface binding energy has been shown to correlate with catalytic activity. Improved metal ORR catalysts can now be designed by searching for descriptors that correlate with optimal performance.^17–20 For binary transition metal oxides (MO_x), early experimental works have shown oxygen surface bond strength is correlated with activities of hydrogen oxidation, CO oxidation, and oxygen surface exchange.²¹ Very recently, Suntivich et al.²² observed that the ORR activity of perovskites operated in a low-temperature aqueous environment is correlated with the σ*-orbital (e_g) occupation and the extent of B-site transition-metal-oxygen covalency. However, we find that a quite different descriptor is effective for high-temperature ORR catalysis on perovskites, perhaps due to the critical role for vacancies in the high-temperature process.

In this work we identify an electronic structure descriptor for the ORR activity of electron rich perovskites for application in SOFC cathodes. The descriptor is specific to the active oxygen sublattice and consists of the oxygen (O) p-band center measured relative to the Fermi energy. We demonstrate that this theoretical descriptor correlates with, and can therefore be used to predict, the overall ORR activity. We stress that the O p-band is a bulk property, making it possible to predict ORR activity without detailed knowledge of the perovskite surfaces that is presently very challenging to obtain. In perovskites with disordered cation and/or anion vacancy distributions (e.g., (Ba,Sr)(Co,Fe)O_3-δ) even the bulk can be challenging to model. However, these disordered systems can be studied using special quasirandom structures (SQS)²³ and are still computationally manageable. To further support the correlation, we also show that the descriptor correlates strongly with oxygen surface exchange rates (which represent a key step in the ORR) and a number of energies essential to the ORR (e.g., vacancy formation energies). These results together demonstrate that the descriptor controls the key energetics underlying the ORR, thereby explaining why the descriptor is so effective.

To demonstrate the effectiveness of the bulk O p-band descriptor we show in Fig. 1 the area specific resistance (ASR) of a series of SOFC perovskite-type cathode materials reported in the literature plotted against their first-principles calculated bulk O p-band center (measured relative to the Fermi energy). The ASR is a characteristic resistance describing the contribution to the cell impedance from the cathode ORR and it is therefore a measure of the catalyst's overall ORR activity, including both surface and bulk kinetic processes. The ASR is an imperfect measure of the intrinsic catalytic activity of the bulk and surface material as it can be affected by many extrinsic factors relating to microstructure and environment. Unfortunately, no more direct intrinsic measure of SOFC catalyst ORR capabilities is well established for a significant range of materials. To counteract the extrinsic effects on ASR an effort was made to collect ASR data from cathodes tested under similar conditions^3,24–42 (PO₂ = 0.2∼1.0 bar, temperature = 959∼1073 K, under open circuit voltage). In addition, at least two values were used for each data point (except for the undoped LaCoO₃ and LaMnO₃ systems, where we there was only one experimental value available). We therefore believe that the ASR values presented here at least qualitatively represent and intrinsic ORR capability of the materials discussed. As shown in Fig. 1, the log of the ASRs of perovskite SOFC cathodes are almost all linearly correlated with the calculated bulk O p-band centers of stoichiometric perovskites, demonstrating that the bulk O p-band center is a descriptor for the ORR activity in these materials. Note that the calculated O p-band centers of the sampled SQS²³ span an effective range of ∼0.3 eV, which is represented by horizontal bars in Fig. 1 and Fig. 2. The one exception to the linear trend is the (La,Sr)MnO₃ (LSM) family marked with circles (LSM and LMO). That these do not follow the same trend as the other materials is to be expected as they are known to work by a surface oxygen transport mechanism,^11,43 as opposed to the bulk oxygen transport mechanisms which are believed to dominate the other materials in Fig. 1 (due to their greater concentration of oxygen vacancies). Changes of behaviour with oxygen transport mechanism suggests that one might see different trends than observed in this study for the hyperstoichiometric Ruddlesden-Popper phases (e.g., Re₂NiO4),^5,44,45 which transport oxygen through an interstitial mechanism under many conditions. Compounds with interstitial oxygen transport have not been considered in this work (bulk oxygen motion in all compounds studied here is mediated by vacancy transport) and their correlation with the p-band center remains to be studied.

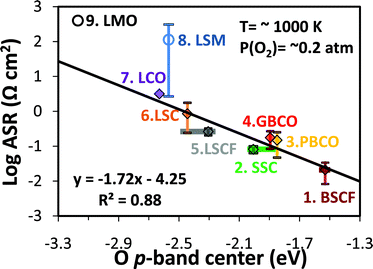Fig. 1 Experimental area specific resistances at ∼1000 K^3,24–42vs. the calculated bulk O p-band center of perovskites with simulated composition: 1.Ba_0.5Sr_0.5Co_0.75Fe_0.25O₃ (BSCF), 2.Sm_0.5Sr_0.5CoO₃ (SSC), 3.PrBaCo₂O₆ (PBCO), 4.GdBaCo₂O₆ (GBCO), 5.La_0.625Sr_0.375Co_0.25 Fe_0.75O₃ (LSCF), 6.La_0.75Sr_0.25CoO₃ (LSC), 7.LaCoO₃ (LCO), 8.La_0.75Sr_0.25MnO₃ (LSM), and 9.LaMnO₃ (LMO). Values with vertical errors bars are the average of multiple data values with an error bar equal to the standard deviation in the mean of the ASR. Experimental ASR data references and experimental compositions are listed in Table S1 of the Supporting Online Material.† The range of the calculated O p-band centers for different special quasirandom structures (SQS, see SI Section S2†) for the disordered BSCF, SSC, and LSCF structures are represented with horizontal bars, and the data points are calculated using Boltzmann factor weighted averages at 1000 K of the SQS energies.

Fig. 2 Experimental surface exchange coefficients (k*s) measured under P(O₂) = 0.2∼1.0 bar at T ∼ 1000 K^{29,33,46–53}vs. the calculated bulk O p-band center of perovskites (simulated composition are the same as those in Fig. 1): 1.BSCF, 2.SSC, 3.PBCO, 4.GBCO, 5.LSCF, 6.LSC, 7.LCO, 8.LSM, and 9.LMO. Values with vertical errors bars are the average of multiple data values with an error bar equal to the standard deviation in the mean. Experimental k* data references and experimental compositions are listed in Table S1 of the Supporting Online Material.† The range of the calculated O p-band centers for different SQS (see SI Section S2†) for the disordered BSCF, SSC, and LSCF structures are represented with horizontal bars, and the data points are calculated using Boltzmann factor weighted averages at 1000 K of the SQS energies.

The equivalent of Fig. 1 but for materials adjusted to include the experimental oxygen nonstoichiometry, is shown in Figure S3 in the Supplementary Information (SI).† Figure S3 shows even stronger correlations than Fig. 1. The increased fidelity of the descriptor for more realistic stoichiometries both supports that the descriptor is sensitive to the key ORR related properties of the materials and suggests how limited experimental data on stoichiometry could be incorporated to provide more accurate descriptor based prediction.

To further support the relevance of the bulk O p-band descriptor for ORR we have correlated the descriptor with a property closely related to the ORR, the oxygen surface exchange coefficient (k*). Incorporation of oxygen in the cathode surface is considered to play a fundamental role in the SOFC ORR and k* values have been shown to correlate with ORR activity.^21,51,55,56Fig. 2 shows the log of experimental k*s^{29,33,46–53} for SOFC cathode perovskites plotted against the calculated bulk O p-band centers. The linear correlation demonstrates that the O p-band center is an excellent descriptor for k* and that the O p-band center controls the chemical processes underlying oxygen surface exchange. The deviation of the LSM and LMO seen in the ASR data (Fig. 1) does not occur here. This result is consistent with our explanation that the deviation in ASR is due to a change in ORR mechanism to involve surface transport, which does not play a role in k*s.

For an electronic structure descriptor like the O p-band center to describe catalytic behavior the descriptor must correlate with reaction energies and barriers of relevant surface reactions. To assure that such correlations exist for the bulk O p-band and SOFC ORR catalysts, we have explored the correlation of a number of ORR relevant reaction energies with the bulk O p-band. For example, Fig. 3 demonstrates that the LaBO₃ (B = Mn, Co, and Ni) bulk oxygen vacancy (E_{bulk_vac}, Fig. 3a), (001) BO₂ surface oxygen vacancy (E_{surf_vac}, Fig. 3b) and (001) BO₂ O-above-B-site adsorption energies (E_O-B, Fig. 3b) are all linearly correlated with the bulk O p-band center. Here LaFeO₃ is not included due to its insulating nature, which leads to deviation from the linear correlations, as shown in SI Figure S1.† The data in Fig. 3 includes values for a range of U_eff (0–9 eV) and B cations, and the enlarged data points represent the calculated reaction energies at the optimal U_eff from ref. 57 and 54. Trends with changing U_eff or with the B ion at the optimal U_eff all follow the same linear relationships. In addition, the calculated activation barriers of oxygen/vacancy hopping, and O₂ dissociation with and without oxygen vacancies on BO₂ surfaces, are also linearly correlated with the bulk O p-band center (see SI Table S2†). In Section 4 of the SI, we show the surface O p-band center of the stoichiometric top two surface layers is also correlated with the calculated ORR relevant energies, but we found almost no further improvement on the correlations by using the surface O p-band center as compared to the bulk O p-band center. All these results indicate the bulk O p-band center is capable of describing reaction energies and activation barriers for electron rich perovskite systems, consistent with the effectiveness of the bulk O p-band center as a descriptor for SOFC cathode catalysts. These results also demonstrate that a number of energetic parameters could serve as descriptors in place of the bulk O p-band center, including the (001) surface O binding energy to the B-cation and the bulk oxygen vacancy formation energy (the correlation of k* and ASR with the latter is shown explicitly in SI Figure S5 and S6†).

Fig. 3 (a) The LaBO₃ bulk oxygen vacancy (empty symbols) and (b) (001) BO₂ surface oxygen vacancy (solid symbols) and O above B site adsorption energies (empty symbols) as a function of the bulk O p-band center, where B = Mn(ferromagnetic (FM)): blue squares, Mn(A-type ferromagnetic (AAFM)): light blue squares, Co(FM): pink diamonds, and Ni(FM): green circles. The bulk O p-band center is calculated from the projected density of states (DOS) of all the oxygen in the undefected bulk. Each point corresponds to different B metal cations at different U_eff values (see SI Figure S1† for the corresponding U_eff value), and the enlarged points represent the results at the optimal U_eff from ref. 54.

The effectiveness of the O p-band descriptor can be qualitatively understood in terms of a simple rigid band model (schematically illustrated in Fig. 4), which has been successfully used to describe at least some electron rich perovskites.¹⁰ In this model, processes involving O addition to the system correspond to moving electrons from the Fermi level to the O p-band (and oxygen removal corresponds to moving electrons in the opposite direction). Since O addition and removal govern many key aspects of ORR in SOFCs, the O p-band provides an effective descriptor of ORR and related processes. This model is supported by the observation that the slopes of the reaction energy vs. O p-band are close to the expected number of electrons transferred to/from the O p-band in each reaction process (see SI Table S2†). Because bonding does not occur in the same manner as on transition metal catalyst surfaces (d-band hybridization with adsorbate s/p orbitals), there is no a priori reason to expect that the Hammer-Nørskov d-band model for metal catalysts will work particularly well for these systems. To assess the effectiveness of the d-band center as a descriptor in these materials, we show in Fig. 5 the log of the experimental k*vs. the d-band centers of the SOFC cathode perovskites. A much poorer linear correlation is observed (R² = 0.06), in contrast to the highly correlated results (R² = 0.87) shown in Fig. 2 for k*vs. the O p-band centers. Comparisons of calculated reaction energy/activation barrier correlations vs. the O p-band and the d-band center demonstrate that the O-p band center also exhibit significantly better correlations than the d-band center (see SI Table S2†).

Fig. 4 Schematic electronic structure plots to illustrate the correlation of the ORR energetics vs. the O p-band center based on the rigid band model.¹⁰ The shaded areas (red and blue in color) represent the occupied transition metal 3d and oxygen 2p states, and the empty areas represent the unoccupied states. The bold and dotted lines are the Fermi energy level before removing O²⁻ and before adding O²⁻, respectively. When oxygen is removed (added) in bulk or on the surfaces, the oxygen2p states are decreased (increased) with respect to the transition metal cation states along with an upshift (downshift) of E_fermi. Therefore, reaction energies correlate with the number of interchanged electrons between the Fermi energy level and O p band.

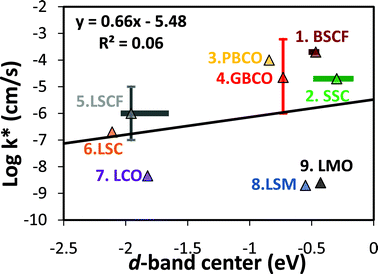Fig. 5 Experimental surface exchange coefficients (k*s) measured under P(O₂) = 0.2∼1.0 bar at T ∼ 1000 K^{29,33,46–53}vs. the calculated bulk d-band center of perovskites (simulated composition are the same as those in Fig. 1): 1.BSCF, 2.SSC, 3.PBCO, 4.GBCO, 5.LSCF, 6.LSC, 7.LCO, 8.LSM, and 9.LMO. Values with vertical errors bars are the average of multiple data values with an error bar equal to the standard deviation in the mean. Experimental k* data are the same as Fig. 2. The range of the calculated d-band centers for different SQS for the disordered BSCF, SSC, and LSCF structures are represented with horizontal bars, and the data points are calculated using Boltzmann factor weighted averages at 1000 K of the SQS energies. The R² value of the k*vs. the calculated d-band centers for the SOFC cathode perovskites is 0.06.

Conclusions

In summary, we have shown that key properties of the SOFC cathode oxygen reduction reaction on perovskite cathodes can be described by a single descriptor, either the bulk O p-band or the bulk oxygen vacancy formation energy. These descriptors can predict both area specific resistance (which represents ORR activity), oxygen exchange rates, and they correlate well with a range of energies relevant for the oxygen reduction reaction. The effectiveness of these descriptors can be explained in terms of the movement of electrons to and from oxygen interacting with the perovskite. The descriptors are relatively straightforward to calculate with first-principles methods and, because they are a bulk property, do not require knowing surface structure and chemistry. Because of the complexity of the perovskite magnetic, electronic, and defect structures, some care must be taken in determining the descriptors, and improved electronic structure methods are still needed to establish them more reliably, However, these descriptors can be calculated accurately and quickly enough to be a practical tool for first-principles based design of optimal catalysts for SOFC cathodes.

Calculation methods

Calculations were preformed with the Vienna Ab initio Simulation Package^58,59 using Density Functional Theory (DFT) and the Projector-Augmented plane-Wave method.⁶⁰ Exchange–correlation was treated in the Perdew-Wang-91⁶¹ Generalized Gradient Approximation (GGA) using the soft O_s oxygen pseudopotential. Energy convergence was within 3 meV per perovskite formula unit using a Monkhorst–Pack 4 × 4 × 4 k-point mesh. The GGA + U calculations⁶² are performed with the simplified spherically averaged approach,⁶³ where the U_eff (U_eff = Coulomb U - exchange J) is applied to d electrons. Bulk calculations are simulated with 2 × 2 × 2 cubic supercells where ions are relaxed internally to include BO₆ octahedron distortion. The cells are chosen to be cubic to mimic the average cubic symmetry that exists at SOFC operating temperatures. All calculations of O p-band centers in Fig. 1 and 2 are performed in the ferromagnetic state in order to use a consistent and tractable set of magnetic structures and to simulate the conductive nature of electron-rich perovskites at SOFC temperatures. The high-concentrations of disordered mixtures of multiple cations on one or more sublattices (specifically, Ba_0.5Sr_0.5Co_0.75Fe_0.25O₃, Sm_0.5Sr_0.5CoO₃, and La_0.625Sr_0.375Co_0.25Fe_0.75O₃) are modeled with the Special Quasi-random Structures (SQS) approach,²³ where the cations are arranged within a 2 × 2 × 2 perovskite supercell to be as random as possible in terms of local correlations. An effective O p-band center is determined by the weighted average of the SQS O p-band centers by the Boltzmann factor for the energy of the SQS evaluated at 1000 K. More detailed discussions on the simulation approach for surfaces and the disordered bulk phases, and the effect of U_eff and magnetic ordering on reaction energetics, are described in SI Section 2 and 3.†

Acknowledgements

Work at the University of Wisconsin gratefully acknowledges financial support from the U.S. National Science Foundation MRSEC program under award number 0079983, the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under award number DE-SC0001284, and computing support from NSF National Center for Supercomputing Applications (NCSA - DMR060007). The work at MIT was supported by DOE SISGR DE-SC0002633.

References

1. B. C. H. Steele, Nature, 1999, 400, 619–621.
2. N. P. Brandon, S. Skinner and B. C. H. Steele, Annu. Rev. Mater. Res., 2003, 33, 183–213.
3. Z. P. Shao and S. M. Haile, Nature, 2004, 431, 170–173.
4. A. J. Jacobson, Chem. Mater., 2010, 22, 660–674.
5. A. Chroneos, B. Yildiz, A. Tarancon, D. Parfitt and J. A. Kilner, Energy Environ. Sci., 2011, 4, 2774–2789.
6. S. C. Singhal and K. Kendall, High-temperature Solid Oxide Fuel Cells: Fundamentals, Design and Applications, Elsevier Science, 2004.
7. B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240.
8. J. Greeley and M. Mavrikakis, Nat. Mater., 2004, 3, 810–815.
9. J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
10. M. H. R. Lankhorst, H. J. M. Bouwmeester and H. Verweij, Phys. Rev. Lett., 1996, 77, 2989–2992.
11. S. B. Adler, Chem. Rev., 2004, 104, 4791–4843.
12. Y. M. Choi, D. S. Mebane, M. C. Lin and M. L. Liu, Chem. Mater., 2007, 19, 1690–1699.
13. Y. Choi, M. C. Lin and M. L. Liu, Angew. Chem., Int. Ed., 2007, 46, 7214–7219.
14. L. Wang, R. Merkle and J. Maier, J. Electrochem. Soc., 2010, 157, B1802–B1808.
15. J. R. Wilson, D. T. Schwartz and S. B. Adler, Electrochim. Acta, 2006, 51, 1389–1402.
16. S. B. Adler, X. Y. Chen and J. R. Wilson, J. Catal., 2007, 245, 91–109.
17. J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
18. V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. F. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247.
19. J. L. Zhang, M. B. Vukmirovic, Y. Xu, M. Mavrikakis and R. R. Adzic, Angew. Chem., Int. Ed., 2005, 44, 2132–2135.
20. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Norskov, Nat. Chem., 2009, 1, 552–556.
21. A. Bielański and J. Haber, Oxygen in catalysis, Marcel Dekker, Inc., New York, 1991.
22. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550.
23. S. H. Wei, L. G. Ferreira, J. E. Bernard and A. Zunger, Phys. Rev. B: Condens. Matter, 1990, 42, 9622.
24. S. Lee, Y. Lim, E. A. Lee, H. J. Hwang and J.-W. Moon, J. Power Sources, 2006, 157, 848–854.
25. C.-H. Chen, C.-L. Chang and B.-H. Hwang, Mater. Chem. Phys., 2009, 115, 478–482.
26. C. Xia, W. Rauch, F. Chen and M. Liu, Solid State Ionics, 2002, 149, 11–19.
27. H. Lv, Y. J. Wu, B. Huang, B. Y. Zhao and K. A. Hu, Solid State Ionics, 2006, 177, 901–906.
28. S. W. Baek, J. H. Kim and J. Bae, Solid State Ionics, 2008, 179, 1570–1574.
29. G. Kim, S. Wang, A. J. Jacobson, L. Reimus, P. Brodersen and C. A. Mims, J. Mater. Chem., 2007, 17, 2500–2505.
30. C. Zhu, X. Liu, C. Yi, D. Yan and W. Su, J. Power Sources, 2008, 185, 193–196.
31. D. Chen, R. Ran, K. Zhang, J. Wang and Z. Shao, J. Power Sources, 2009, 188, 96–105.
32. A. Chang, S. J. Skinner and J. A. Kilner, Solid State Ionics, 2006, 177, 2009–2011.
33. A. Tarancon, S. J. Skinner, R. J. Chater, F. Hernandez-Ramirez and J. A. Kilner, J. Mater. Chem., 2007, 17, 3175–3181.
34. N. Li, Z. Lü, B. Wei, X. Huang, K. Chen, Y. Zhang and W. Su, J. Alloys Compd., 2008, 454, 274–279.
35. S. P. Jiang, Solid State Ionics, 2002, 146, 1–22.
36. J. M. Ralph, C. Rossignol and R. Kumar, J. Electrochem. Soc., 2003, 150, A1518–A1522.
37. A. Esquirol, N. P. Brandon, J. A. Kilner and M. Mogensen, J. Electrochem. Soc., 2004, 151, A1847–A1855.
38. T. Horita, K. Yamaji, N. Sakai, H. Yokokawa, A. Weber and E. Ivers-Tiffee, J. Electrochem. Soc., 2001, 148, A456–A462.
39. M. Shiono, K. Kobayashi, T. Lan Nguyen, K. Hosoda, T. Kato, K. Ota and M. Dokiya, Solid State Ionics, 2004, 170, 1–7.
40. Y. Takeda, R. Kanno, M. Noda, Y. Tomida and O. Yamamoto, J. Electrochem. Soc., 1987, 134, 2656–2661.
41. E. Perry Murray and S. A. Barnett, Solid State Ionics, 2001, 143, 265–273.
42. T. Ioroi, T. Hara, Y. Uchimoto, Z. Ogumi and Z. Takehara, J. Electrochem. Soc., 1998, 145, 1999–2004.
43. J. Fleig, Annu. Rev. Mater. Res., 2003, 33, 361–382.
44. D. Parfitt, A. Chroneos, J. A. Kilner and R. W. Grimes, Phys. Chem. Chem. Phys., 2010, 12, 6834–6836.
45. A. Kushima, D. Parfitt, A. Chroneos, B. Yildiz, J. A. Kilner and R. W. Grimes, Phys. Chem. Chem. Phys., 2011, 13, 2242–2249.
46. L. Wang, R. Merkle, J. Maier, T. Acarturk and U. Starke, Appl. Phys. Lett., 2009, 94, 071908.
47. I. C. Fullarton, J. P. Jacobs, H. E. van Benthem, J. A. Kilner, H. H. Brongersma, P. J. Scanlon and B. C. H. Steele, Ionics, 1995, 1, 51.
48. A. A. Taskin, A. N. Lavrov and Y. Ando, Appl. Phys. Lett., 2005, 86, 091910.
49. J. E. tenElshof, M. H. R. Lankhorst and H. J. M. Bouwmeester, Solid State Ionics, 1997, 99, 15–22.
50. J. A. Lane, S. J. Benson, D. Waller and J. A. Kilner, Solid State Ionics, 1999, 121, 201–208.
51. R. A. De Souza and J. A. Kilner, Solid State Ionics, 1999, 126, 153–161.
52. T. Ishigaki, S. Yamauchi, J. Mizusaki, K. Fueki and H. Tamura, J. Solid State Chem., 1984, 54, 100–107.
53. A. V. Berenov, J. L. MacManus-Driscoll and J. A. Kilner, Solid State Ionics, 1999, 122, 41–49.
54. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
55. S. B. Adler, J. A. Lane and B. C. H. Steele, J. Electrochem. Soc., 1996, 143, 3554–3564.
56. J. Maier, Physical Chemistry of Ionic Materials: Ions and Electrons in Solids, John Wiley & Sons, Ltd, New York, 2004.
57. Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101.
58. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558.
59. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
60. P. E. Blochl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
61. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244.
62. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
63. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1ee02032c

---