 Open Access Article
Open Access ArticleA prototype cell for extracting energy from a water salinity difference by means of double layer expansion in nanoporous carbon electrodes
D.
Brogioli
*a,
R.
Zhao
bc and
P. M.
Biesheuvel
bc
aDipartimento di Medicina Sperimentale, Università degli Studi di Milano-Bicocca, Via Cadore, 48, 20052, Monza, Italy. E-mail: dbrogioli@gmail.com
bDepartment of Environmental Technology, Wageningen University, Bomenweg 2, 6703 HD, Wageningen, The Netherlands
cWetsus, centre of excellence for sustainable water technology, Agora 1, 8900 CC, Leeuwarden, The Netherlands
First published on 24th January 2011
Abstract
Electrical energy can be obtained from the controlled mixing of fresh (river) and saline (sea) water. Existing technologies such as pressure retarded osmosis and reverse electrodialysis make use of ion-exchange membranes which must be crossed by either the water or the ions. Recently a new physical principle has been experimentally demonstrated, which allows extraction of electrical energy without making use of membranes, based on the temporary storage of ions inside two porous electrodes kept at different electrical potentials, and the repeatable expansion/contraction of the electrostatic double layers formed inside the electrodes upon changing the salt concentration [D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501]. To make further investigations and to improve the energy recovery, we developed a simple prototype cell of much larger dimensions. Because of the larger dimensions (thus higher currents), testing is more facile, while this design can be the basis for further scaling-up of this technology. In order to reduce the internal resistance of the cell, the electrodes are no longer placed side-by-side, but parallel to one another, separated only by a 250 μm-thick open spacer channel to form a “sandwich”-like flow cell. In a lab-scale experimental stack consisting of 8 such cells (with outer dimensions 6 × 6 × 1 cm3) we extract about 2 J per charging/discharging cycle in 500 mM/1 mM NaCl salt solution, an amount which is 20 times higher per cycle per unit electrode mass than previously obtained. The extracted energy increases with the operating voltage, in line with predictions of the Gouy-Chapman-Stern model for double layer formation.
Broader contextSalinity differences between river water and sea water can be used to generate electrical energy. The free energy content of a liter of water that is dissipated when it flows into the sea is about 2 kJ, an astonishing amount corresponding to the energy released by the same amount of water falling down a height of 200 m. To harvest this source of sustainable energy, we present results using supercapacitor technology which does not require membranes. Two electrodes are dipped into the sea water and are charged, then the solution is changed to fresh water. This leads to the increase of the electrical energy stored in the capacitor. We show that the surplus energy can be extracted in a cyclic operation mode in which fresh and sea water sequentially flow through the capacitor cell. |
When salt water and fresh water are mixed, the entropy of the system increases. This entropy change can be intercepted and used to convert part of the thermal energy of the fluids into electrical energy. In particular, this idea can be used to extract energy from the controlled mixing of river and sea water. The thermodynamic limit of this energy extraction is determined by the free energy change upon mixing, which is around 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kJ when one liter of fresh water is mixed with an equal amount of sea water.1 Worldwide, the potential for energy extraction from this resource (for all river effluents combined) amounts to around 2 TW, close to present-day global electricality use.2,3 Several technologies were suggested for harvesting this source of renewable energy.4,5 In pressure-retarded osmosis (PRO)6,7 the water moves through a semi-permeable membrane under the influence of the osmotic pressure difference, leading to the development of a hydrostatic head which can subsequently be converted into electricality by using a turbine. Alternatively, it is not the water which is transported through the membrane but the ions, which is the approach used in reverse electrodialysis (RED)2,8 and in a recent capacitive technology using ion-exchange membranes.3 In RED, compartments fed alternately by fresh or salt water are separated by a sequence of positively and negatively charged ion-exchange membranes. The potential which develops across each membrane sums up to a large overall potential which, together with a redox solution being cycled along the electrodes, results in a continuous current and thus electrical power. Both PRO and RED require membranes, which are prone to the usual problems of fouling, while permeabilities and selectivities still need to be improved before successful applications.2,8 An alternative method, based on the vapor pressure difference between fresh and saline water, has also been proposed.9 Up to now, no industrial scale plant has been built, but salinity difference power has received renewed interest, and research and development is ongoing both for PRO10 and RED.2,8
kJ when one liter of fresh water is mixed with an equal amount of sea water.1 Worldwide, the potential for energy extraction from this resource (for all river effluents combined) amounts to around 2 TW, close to present-day global electricality use.2,3 Several technologies were suggested for harvesting this source of renewable energy.4,5 In pressure-retarded osmosis (PRO)6,7 the water moves through a semi-permeable membrane under the influence of the osmotic pressure difference, leading to the development of a hydrostatic head which can subsequently be converted into electricality by using a turbine. Alternatively, it is not the water which is transported through the membrane but the ions, which is the approach used in reverse electrodialysis (RED)2,8 and in a recent capacitive technology using ion-exchange membranes.3 In RED, compartments fed alternately by fresh or salt water are separated by a sequence of positively and negatively charged ion-exchange membranes. The potential which develops across each membrane sums up to a large overall potential which, together with a redox solution being cycled along the electrodes, results in a continuous current and thus electrical power. Both PRO and RED require membranes, which are prone to the usual problems of fouling, while permeabilities and selectivities still need to be improved before successful applications.2,8 An alternative method, based on the vapor pressure difference between fresh and saline water, has also been proposed.9 Up to now, no industrial scale plant has been built, but salinity difference power has received renewed interest, and research and development is ongoing both for PRO10 and RED.2,8
In this letter we present laboratory-scale results of a new technology that does not need membranes, which we call “capacitive energy extraction based on double-layer expansion” (CDLE) and which was first proposed by Brogioli11 and experimentally tested in a microfluidic flow cell in which micro-joule power was generated. In this technology, two porous “supercapacitor” electrodes12–14 are first contacted with salt water and are charged by connecting each electrode to one pole of an external capacitor (EC) operating at a voltage difference V0. The EC is an essential element of the technology and must operate at a low overvoltage which can be achieved when the EC-capacity is much larger than the capacity of the flow cell. It must be stressed that the EC is not a source of energy and slowly discharging. Instead, it operates as an ideally reversible storage device for electronic charge, at a certain voltage. While the EC charges the flow cell during flow of saline water, the EC is re-charged again when fresh water flows through the cell and the current direction is reversed. Thus, the EC can be seen as equivalent to the fly-wheel for internal combustion engines.
In the flow cell, brought in contact with saline water, and with an EC-voltage V0 applied, the following events take place in the electrodes. First of all, electrons start to flow through the external circuit, making one electrode positive and the other negative. Subsequently, at the interfaces within the porous electrode where the electron-conducting matrix is in contact with the aqueous solution filling the pores, electrostatic double layers (EDL) develop where the electronic charge is compensated by an ion charge excess in the diffuse layer of the EDL, with an EDL containing positive ion countercharge in the cathode, and vice versa in the anode. Formation of the EDL continues until Vcell (initially smaller than V0) becomes equal to V0. Subsequently the electrodes are brought into contact with fresh water which modifies the structure of the EDL (i.e. the diffuse layer will expand) which leads to an increase in the cell potential, Vcell, to values beyond V0 resulting in a flow of electrons in the reverse direction, re-charging the EC.
An analogy can help to describe the physical principle of CDLE. Consider an electrostatic capacitor, made of two conductive plates with a dielectrical medium in between. When the plates constituting the capacitor are charged, one relative to the other, the electrostatic force is attractive. We can perform mechanical work and bring the plates further apart. This work is converted into electrostatic energy, appearing as an increase of voltage between the plates, while the accumulated charge remains constant. This kind of device is thus able to transform mechanical work into electrostatic energy.
In the EDL capacitor described in this paper, one charged plate of the above example is substituted by the ion countercharge (diffuse layer of ions, or “ion cloud”). When this capacitor is brought into contact with fresh water, the salt ions diffuse away from the electrode surface. This ion outward displacement, performed by diffusion, increases the average distance between the electrode surface and the ion cloud forming the second charged plate. In analogy with the previous case, the voltage across the capacitor increases.
In order to use the electrical energy extracted from this system, consisting of the flow cell and the EC, a device must be placed in the external circuit to harvest the energy, either by making direct use of it (e.g., to drive an electricalal device) or by storing it, as in a battery or redox flow cell. In electricalal terms, this device is called a “load.” In our experiments the load is simply a passive resistance, denoted by R in Fig. 1, producing heat upon current flow in either direction. It is important to realize that in both steps of the cycle (both during charging in saline water, and during discharging in fresh water) electrical energy can be harvested because in both steps the electrons flow spontaneously through the resistance, with only the current direction reversed. The total electrical energy which is dissipated in the load R equals the area enclosed by each charge-voltage cycle shown in Fig. 4.
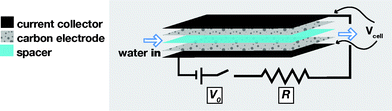 | ||
| Fig. 1 Schematic view of the flow cell for capacitive energy extraction from the sequential flow of saline and fresh water, and of the required electrical circuit. The external capacitor provides a constant voltage of V0 while the load R represents the device for energy-harvesting. | ||
Up to now, only a proof of principle has been given of CDLE,11 in a microfluidic flow cell with small porous electrodes made of 0.4 mg activated carbon, placed one behind the other. In this system it was possible to recover 5 μJ in one charging/discharging cycle. Brogioli11 analyzed the upscaling potential of the principle of CDLE suggesting that it may be feasible to harvest energy in an economically attractive manner. One of the key parameters in this evaluation is the energy that can be extracted per cycle per gram of electrode material. In the present work we transfer the CDLE principle from the scale of a microfluidic device to the scale of a much larger “prototype” cell, constructed from commonly available and inexpensive materials, and constructed in such a way that further technological improvement and scaling-up is possible. Because of the larger cell dimensions and amount of electrode material (about 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times more), much more current can be generated and the results of the experiments are much more reliable, without relying on μA noisy measurements. As we will show, the prototype cell is not only larger, but also more efficient with the per-cycle per-gram energy recovery increased by a factor of 20 as compared to that reported by Brogioli.11
000 times more), much more current can be generated and the results of the experiments are much more reliable, without relying on μA noisy measurements. As we will show, the prototype cell is not only larger, but also more efficient with the per-cycle per-gram energy recovery increased by a factor of 20 as compared to that reported by Brogioli.11
In the protype cell, besides increasing system dimensions, one of the main modifications is to reduce the internal resistance of the flow cell by placing the electrodes parallel to one another, separated only by a thin spacer layer of less than half a mm thickness, permeable by ions and water, but electricalally insulating for electrons. We use electrode materials used in state-of-the-art supercapacitors, with a high specific surface area for EDL formation. The flow cell has been designed such that the liquid can easily contact the electrodes, simultaneously with robust current transfer from one electrode to the other via current collectors and the external circuit, see Fig. 1.
Our laboratory-scale setup consists of eight parallel flow cells15 (see Fig. 1) consisting each of dense graphite current collectors (thickness δ = 250 μm), porous carbon electrodes (δ = 270 μm, 8.5 g in total in the stack, mass density 0.58 g ml−1, porosity 65%, BET-area 1330 m2 g−1), and an open-meshed polymer spacer (δ = 250 μm, porosity > 80%). Each graphite current collector is used for two adjacent cells and is alternatingly connected to the positive or negative pole of the external circuit. All materials are cut in pieces of dimensions 6 × 6 cm2 and assembled, after which the entire stack of all layers is firmly compressed and placed in a Teflon housing. An aqueous NaCl solution is pumped into a small hole (1.5 × 1.5 cm2) located in the exact middle of the stack, and flows radially outward through the spacer channels, leaving the cell on all four sides. The total flow rate, which is 1 ml s−1, is constant during all experiments. The electrical circuit includes a potentiostat, that simulates the EC, operating at a voltage V0, and a resistance R = 11 Ω, constituting the load, in series with the flow cell. The current I is measured by the potentiostat, and the voltage across the cell, Vcell, is calculated from Vcell = V0 − R·I.
To describe the experimental data we will use the classical Gouy-Chapman-Stern (GCS) theory, in which the EDL is decomposed into an inner (Stern) layer, and a diffuse (Gouy-Chapman) layer. For a given surface charge density σ, defined as charge per internal electrode surface area, σ = Q/am, the potential VSt over the Stern layer is
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monovalent salt solution, the potential Vd over the diffuse layer is14,16,17
1 monovalent salt solution, the potential Vd over the diffuse layer is14,16,17| Vd = 2VTasinh(ασλD), | (2) |
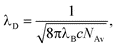 | (3) |
In a first set of experiments, the equilibrium electrode charge was measured versus the cell potential for different values of the ionic strength of the solution flowing through our prototype cell. Fig. 2 reports the resulting equilibrium cell potential Vcellversus the charge per gram of electrode material Q. Data at 1 mM and 500 mM were obtained in the following way. The potentiostat is directly connected to the cell, and operated in chrono-amperometric mode (integrating current with time) first stepping up in voltage (steps of 0.2 V) up to 1 V and then down again, each time with a resting period of 30 min. To compare, we also show data from Zhao et al.15 for the same electrode material and for intermediate values of the salt concentrations, namely at 5 and 20 mM, which were also obtained in amperometric mode but in this case for each data point the potential is increased from 0 V directly up to Vcell, so that each experimental data point represents an independent measurement. It can be clearly observed from the four data sets that the charge increases with cell voltage as well as with salt concentration, while both dependencies are well described by the GCS-theory. Fig. 2 shows that, for a given charge, lowering the ionic strength leads to a higher cell potential, due to an expansion of the EDL, see eqns (2) and (3), which is the principle at the basis of energy extraction using CDLE.
 | ||
| Fig. 2 Equilibrium values for electrode charge versuscell potential for different values of the ionic strength (NaCl solutions). Lines according to the Gouy-Chapman-Stern theory (parameter settings in the text). | ||
In the previous experiment, for a given ionic strength the cell voltage was varied and the equilibrium charge determined. In the next experiment we simulate more closely the CDLE process. Namely, we start with flowing saline water into the cell and apply a certain EC-voltage, V0. It is important to note that in our experiment, the EC is simulated by a power supply operating at a constant voltage, V0. After some time we disconnect (i.e. “open”) the external circuit to fix (i.e. “trap”) the stored charge and repeatedly switch the inflowing solution from saline water (500 mM) to fresh water (1 mM) and back. Ideally, this should lead to a repeatable increase in voltage when going to fresh water, and a decrease upon contacting with saline water, in line with the data of Fig. 2. This experiment is then a more conclusive evidence that indeed it is possible to modulate the cell voltage by repeatedly switching from saline to fresh water. The results presented in Fig. 3 show that indeed this scenario holds true, but with certain differences compared to Fig. 2 and compared to similar experiments reported by Brogioli.11Fig. 3 presents results for three values of the EC-voltage (0.3, 0.5 and 0.7 V) and shows that indeed after disconnecting the electrical circuit and switching to fresh water (downward arrows) the cell voltage increases and decreases again after starting a flow of saline water (upward arrows). It must be noted that in this experiment a gradual loss of cell potential was observed, which we ascribe to a small leakage current, and thus to a gradual loss of stored charge. The leakage current was estimated at 0.3, 0.7 and 2.1 mA, respectively, for EC-voltages V0 of 0.3, 0.5 and 0.7 V. This leakage current is recalculated to a cell potential decline and used to correct the raw data.
 | ||
| Fig. 3 Variation of cell potential upon salinity switching in a cell with fixed charge. Three experiments are reported, at different EC-voltages V0. Horizontal lines shows the EC-voltage, V0, and the cell potential predicted by GCS theory, for concentration 1 mM and η = 0.99. The arrows represent the time at which salinity switching takes place (up: to 500 mM; down: to 1 mM solution). | ||
Fig. 3 shows that when the concentration is reduced to 1 mM, the cell potential increase, Δϕ*, is 0.1–0.16 V. Interestingly, this range of values is much higher than the 33 mV-increase for Δϕ* previously reported.11 But still Δϕ* is less than predicted by GCS theory, which based on the equilibrium data in Fig. 2 suggests that Δϕ* must be about 0.2 V. This can be derived from Fig. 2 by observing that for a cell voltage of 0.5 V, the equilibrium charge is about 20 C g−1 at 500 mM. For this charge, the cell voltage at 1 mM is about 0.7 V, which would imply that Δϕ* is about 0.2 V. What is the cause of this difference? We have assumed the reason is that upon switching to fresh water not all ions absorbed within the pores of the electrode during the previous step are washed out completely again; instead, we assume that a small fraction 1 − η of the ions initially present is not removed upon switching to fresh water, so that the effective concentration is not 1 mM (for fresh water) but 1 mM + (1 − η)·500 mM. To describe the data in Fig. 3 we take a value of η = 0.99, thus the effective concentration of the fresh water is not 1 mM but 6 mM. Other possible explanations for this difference are the contribution of protons and hydroxyl ions in surface charge compensation,18 or chemical charge regulation of the carbon surface groups.
Though Δϕ* is much higher than in the work of Brogioli,11 unfortunately the approach to equilibrium is also much slower. This can be quantified by the characteristic time, τ*, which takes for the cell potential to change to half the value of Δϕ*, which for the data obtained with the prototype cell is 800 s at 1 mM and 80 s at 500 mM. Both these times are much longer than that reported by Brogioli,11 where τ* was of the order of several seconds. This is due to the fact that in our experiments the charge and discharge times RC are longer: the capacitance is much bigger, and is not compensated by a proportionally lower internal resistance. Actually, the resistance in the experiments performed by Brogioli11 may have been lower than in the prototype cell, because the electrodes were thinner and contained more macropores, thereby reducing mass transfer limitations within the electrode. Reducing the resistance of the prototype cell demands further study because optimizing the dynamics of the process is very important to make the technology commercially relevant.
To finally fully test the principle of CDLE, similar to the experiments reported by Brogioli,11 we used the electrical circuit shown in Fig. 1, with the potentiostat (operating in chrono-amperometric mode) simulating an ideally rechargeable EC operating at a constant voltage V0 and without any appreciable overpotential. One difference with the previous experiment is that the charge is no longer fixed and the voltage change is measured upon salinity switching, but instead in two steps of the cycle, charge is allowed to flow and the voltage across the load R is calculated from the current. In the two switching steps (from fresh to salt water, and back), the charge is fixed using an open electrical circuit. In this way the voltage across the resistance, Vcell–V0, is maximized, and thus the power production.
Each experiment consists of the following four steps:
1. Charging: We start the flow of saline water through the cell and charge the electrodes for 3 h.
2. Switching step I: We open the circuit and let the fresh water flow for 30 min.
3. Discharging: We close the circuit and monitor the current for up to 15 h.
4. Switching step II: We open the circuit and start the flow of saline water for 15 min.
In these CDLE experiments, full cycles were repeatedly made at EC-voltages from V0 = 0.3 V to V0 = 0.7 V. The evolution of the cell voltage versus time is similar to that shown in Fig. 3 and is not repeated here, but see Fig. 6 to be discussed later for the power production as function of time. Instead, to evaluate the electrical energy that is harvested, it is more informative to directly plot the cell potential, Vcell, versus the stored charge, as shown in Fig. 4, reporting results for different EC-voltages V0. In this representation, the cycles show a close analogy with classical thermodynamic cycles for pressure versus volume of thermomechanical systems.19,20 In particular, the area enclosed by the cycle represents the extracted energy. As explained, the process is run counterclockwise with the vertical edges representing the two switching steps; the right one representing switching to a low salinity feed solution, and the left one switching back to high salinity water. The upper line represents the cell potential decay towards V0 when flushing with fresh water, with current running in one direction, and the lower line represents the cell potential increase towards V0 in saline water with current now running in the other direction. The difference between the cell voltage and the EC-voltage (horizontal dashed line) equals the voltage across the resistance which is of different sign during charging in saline water and during discharging in fresh water, but note that energy is extracted both during charging and during discharging because the current direction is also reversed. Fig. 4 shows how the enclosed area (harvested energy) increases with increasing EC-voltage, as plotted in more detail in Fig. 5.
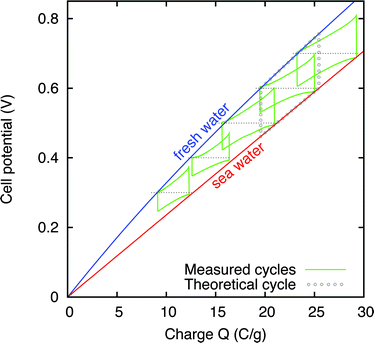 | ||
| Fig. 4 Charge-voltage cycle at different EC-voltages V0, represented by dotted lines. The area enclosed by each cycle represents the extracted electrical energy from switching between 1 mM and 500 mM salt solutions. The lines labelled with “sea water” and “fresh water” represent the charge-voltage relations obtained from GCS theory, respectively, for 500 mM and 1 mM with η = 0.99. | ||
 | ||
| Fig. 5 Extracted electrical energy per cycle based on the CDLE-principle, as a function of the EC-voltage, V0. Solid line is based on GCS theory. | ||
In our experiment with the prototype cell, the extracted energy is of the order of 2 J for EC-voltages of V0 > 0.5 V, which is of the order of 106 times the amount extracted in the micro-scale setup, as previously reported.11 The energy per cycle per gram of electrode (where mass is defined as that of all electrodes of one charge sign, i.e., either of the cathode or of the anode) can be calculated as about 0.47 J per gram of electrode: compared to the first reported experiments this is an improvement by a factor of 20.
It is relevant to note that in the experiment there is some leakage current so that when each cycle is run through several times (starting initially at Vcell = 0 V) we have lost knowledge of the exact charge stored, i.e., how far to the left or right each cycle must be plotted in Fig. 4. This is to some extent not essential because the energy that can be harvested (the enclosed area) does not depend on the total charge stored, but only on the change in charge between start and end of the (dis-)charging steps. Therefore we have taken the liberty to shift each cycle left–right to fit within the two theoretical curves based on GCS-theory which envelope our set of charge-voltage cycles.
The area delimited by dots in Fig. 4 represents one theoretical cycle for an EC-voltage of V0 = 0.6 V. As can be noticed, the enclosed area of each of the experimental cycles is smaller than that of the corresponding theoretical cycle. This may be due to several effects, including a voltage drop across the internal cell resistance, incomplete charging, and leakage current. However, the origin of the mismatch of the experimental cycles is not very well understood, because the external resistance of 11 Ω is two orders of magnitude larger than the internal resistance of the flow cell, and thus the current should be low enough to generate low internal voltage drops, and thus the energy dissipation in the cell should be small.
What is in general the effect of the chosen load on the power production? In this work, since the main goal is to quantify the maximum energy that can be extracted from a single cycle, we selected a load with a resistance much higher than the internal resistance of the cell. However, the duration of each cycle is then also very long. A higher power production per unit time can be obtained with a lower resistance of the load R. For steady-state operation and when the internal cell resistance is constant, it can be derived that power production is maximized when the internal cell resistance is equal to the resistance of the load.
Fig. 5 shows in detail the values of the extracted energy as a function of EC-voltage V0. It also shows the calculation of the energy that can be extracted in a cycle, based on the GCS theory, for concentrations 500 mM and 1 mM, with efficiency η = 0.99. As the comparison shows, in reality we extract about half the energy content theoretically available in a cycle.
Finally we present in Fig. 6 curves for the produced power per unit projected electrode area (of all electrodes of one charge sign) for the charging and for the discharging step, for one of the cycles of Fig. 4. The power is calculated by multiplying at each moment the current with the voltage drop across the external resistance, R, where the voltage drop equals current times resistance, and finally divided by the area. We observe that the maximum power is produced at the start of each step. This is different from the power curves as given by Sales et al.3 where the maxima occur slightly later. This difference is due to the fact that in Sales et al.3 switching steps were not included. The maximum power produced in the present work is lower than in Sales et al.3 which is related to the higher external resistance which we use (11 Ω vs. 1 Ω); however the extracted energy per cycle is higher.
 | ||
| Fig. 6 Power production as a function of time during charging and discharging (EC-voltage V0 = 0.3 V). | ||
It is important to note that our results must be considered with some care, since our experiments suffered from leakage currents which though small were important because of the long times involved. Note also that several of the cycles presented in Fig. 4 were replicated a few times and only the best result is presented. So our data must not be considered as definitive, but they still show enough indications that with our prototype setup it is possible to reach an energy recovery of the order of several Joules. Compared to a previous work using the CDLE-principle, this then implies an increase in per-cycle per-gram energy recovery by a factor of about 20.
Acknowledgements
The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 256868. Part of this research was performed in the TTIW-cooperation framework of Wetsus, Centre of Excellence for Sustainable Water Technology. Wetsus is funded by the Dutch Ministry of Economic Affairs, the European Union Regional Development Fund, the Province of Friesland, the City of Leeuwarden, and the EZ/Kompas program of the “Samenwerkingsverband Noord-Nederland”. We thank the members of the “Blue Energy” Program in Wetsus for their participation in this research.References
- R. Semiat, Environ. Sci. Technol., 2008, 42, 8193 CrossRef CAS.
- J. W. Post, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2008, 42, 5785 CrossRef CAS.
- B. B. Sales, M. Saakes, J. Post, C. J. N. Buisman, P. M. Biesheuvel and H. V. M. Hamelers, Environ. Sci. Technol., 2010, 44, 5661 CrossRef CAS.
- R. E. Pattle, Nature, 1954, 174, 660 CrossRef CAS.
- R. W. Norman, Science, 1974, 186, 350 CrossRef CAS.
- O. Levenspiel and N. de Vevers, Science, 1974, 183, 157 CrossRef CAS.
- S. Loeb, Science, 1975, 189, 654 CrossRef CAS.
- J. N. Weinstein and F. B. Leitz, Science, 1976, 191, 557 CrossRef CAS.
- M. Olsson, G. L. Wick and J. D. Isaacs, Science, 1979, 206, 452 CrossRef CAS.
- K. Gerstandt, K. V. Peinemann, S. E. Skilhagen, T. Thorsen and T. Holt, Desalination, 2008, 224, 64 CrossRef CAS.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845 CrossRef CAS.
- M. Levi, G. Salitra, N. Levy, D. Aurbach and J. Maier, Nat. Mater., 2009, 8, 872 CrossRef CAS.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef CAS.
- R. Zhao, P. M. Biesheuvel, H. Miedema, H. Bruning and A. van der Wal, J. Phys. Chem. Lett., 2010, 1, 205 Search PubMed.
- Z. Jiang and D. Stein, Langmuir, 2010, 26, 8161 CrossRef CAS.
- R. J. Hunter, Foundations of colloid science, Clarendon press, Oxford, 1993, pp. 316 Search PubMed.
- K. M. Joshi and R. Parsons, Electrochim. Acta, 1961, 4, 129 CrossRef CAS.
- P. M. Biesheuvel, J. Colloid Interface Sci., 2009, 332, 258 CrossRef CAS.
- N. Boon and R. van Roij, Mol. Phys., accepted.
| This journal is © The Royal Society of Chemistry 2011 |
