Definitive solid-state ^185/187Re NMR spectral evidence for and analysis of the origin of high-order quadrupole-induced effects for I = 5/2

Abstract

Rhenium-185/187 solid-state nuclear magnetic resonance (SSNMR) experiments using NaReO₄ and NH₄ReO₄ powders provide unambiguous evidence for the existence of high-order quadrupole-induced effects (HOQIE) in SSNMR spectra. Fine structure, not predicted by second-order perturbation theory, has been observed in the ^185/187Re SSNMR spectrum of NaReO₄ at 11.75 T, where the ratio of the Larmor frequency (ν₀) to the quadrupole frequency (ν_Q) is ∼2.6. This is the first experimental observation that under static conditions, HOQIE can directly manifest in SSNMR powder patterns as additional fine structure. Using NMR simulation software which includes the quadrupole interaction (QI) exactly, extremely large ^185/187Re nuclear quadrupole coupling constants (C_Q) are accurately determined. QI parameters are confirmed independently using solid-state ^185/187Re nuclear quadrupole resonance (NQR). We explain the spectral origin of the HOQIE and provide general guidelines that may be used to assess when HOQIE may impact the interpretation of the SSNMR powder pattern of any spin-5/2 nucleus in a large, axially symmetric electric field gradient (EFG). We also quantify the errors incurred when modeling SSNMR spectra for any spin-5/2 nucleus within an axial EFG using second-order perturbation theory. Lastly, we measure rhenium chemical shifts in the solid state for the first time.

---

Introduction

All quadrupolar nuclei (i.e., I > 1/2) possess a nuclear electric quadrupole moment (Q), which will couple with the electric field gradient (EFG) at the nucleus.¹ The coupling between Q and the EFG, known as the quadrupole interaction (QI), provides information that can be used to complement other solid-state nuclear magnetic resonance (SSNMR) observables, such as the isotropic chemical shift (CS). Unfortunately, the QI may also drastically broaden the SSNMR signal in powdered samples, sometimes to the extent that the experiment becomes impractical. Despite this potential drawback, SSNMR experiments using quadrupolar nuclei are valuable, as these nuclei can be found in many important areas of chemical research, including biochemistry (e.g., ¹⁴N, ¹⁷O, ²³Na, ²⁵Mg, ⁴³Ca, ⁶⁷Zn), and materials science (e.g., ^6/7Li, ¹¹B, ¹⁷O, ²⁷Al).² The precise determination of the QI is therefore of critical importance to correctly characterize a wide variety of systems using SSNMR spectroscopy. Until now, it was most common to use second-order perturbation theory to model SSNMR line shapes (to see how first- and second-order perturbation theory modifies the Zeeman eigenstates, see the ESI, Fig. S1a†); however, as the sensitivity of SSNMR experiments continues to increase, experiments using previously “inaccessible” nuclei are becoming more common and additional care needs to be taken when analyzing the SSNMR spectra of quadrupolar nuclei that experience a very large QI.

Rhenium, a group 7 transition metal, was first detected in 1925, occurs naturally within molybdenum sulfide ores in the earth's crust (∼10⁻⁷% abundance), and may exist in at least nine oxidation states (ranging from −1 to +7).^3,4 Compounds containing rhenium in a relatively reduced oxidation state, such as Re(III), exhibit metal–metal bonding interactions: for example, K₂Re₂Cl₈ is recognized as containing the first example of a metal–metal quadruple bond.⁵Rhenium metal possesses very high thermal stability, and is present within the high-temperature alloys used to make jet engine parts.⁴ In addition, rhenium-containing compounds have been used as catalysts in many types of organic reactions.^6–8 The nuclei of the two stable isotopes of rhenium (¹⁸⁵Re/¹⁸⁷Re) are NMR-active, are present in high natural abundance (37.398(16)% and 62.602(16)% for ¹⁸⁵Re and ¹⁸⁷Re, respectively),⁹ and are quadrupolar (I(^185/187Re) = 5/2). In addition, they possess relatively high magnetogyric ratios (γ(¹⁸⁵Re) = 6.1057 × 10⁷ rad s⁻¹ T⁻¹; γ(¹⁸⁷Re) = 6.1682 × 10⁷ rad s⁻¹ T⁻¹).¹⁰ Despite the potential wealth of diagnostic information that could be extracted using ^185/187Re SSNMR experiments, very few literature reports exist, and they are nearly exclusively restricted to compounds that exhibit very high symmetry,^11–13 or are from experiments carried out at liquid helium temperatures.^14–16 The paucity of ^185/187Re SSNMR studies may be attributed to the very large Q for both NMR-active nuclides (Q(¹⁸⁵Re) = 2180(20) mb; Q(¹⁸⁷Re) = 2070(20) mb).¹⁷ In fact, the line-width factor for ¹⁸⁵Re is the highest of the stable elements (1.5 × 10⁴ relative to ¹H).¹⁰ As such, a very small EFG can result in a rhenium QI that broadens the SSNMR powder pattern to the point that it is undetectable. A partial remedy to this problem is to perform the SSNMR experiments within as high an applied magnetic field (B₀) as possible.

As very high magnetic fields (i.e., B₀ > 18.8 T) are becoming increasingly available, SSNMR experiments on previously inaccessible nuclei are now potentially feasible, but remain technically challenging as they often require sensitivity-enhancing pulse sequences^18,19 and/or variable offset cumulative spectrum (VOCS) data acquisition.^20–22 Recently, we have shown that subtle “high-order” (i.e., greater than second-order) quadrupole-induced effects (HOQIE) are present in the SSNMR spectra for ¹²⁷I (I = 5/2) at B₀ = 11.75 T and 21.1 T for some alkaline earth iodides.²³ In those cases, the observed HOQIE manifested as a non-uniform frequency-dependent shift of the ¹²⁷I SSNMR spectrum. While high-order perturbation theory may have been useful for modeling these ¹²⁷I SSNMR line shapes, we used a simulation code that included Zeeman and QI effects exactly,^24,25 as well as ¹²⁷I NQR experiments, to precisely measure the EFG tensor magnitude, as well as the isotropic iodine chemical shift.

As part of an effort to more generally and completely understand the origin and ramifications of HOQIE on SSNMR spectra for I = 5/2 nuclides, we report here ^185/187Re SSNMR spectra for NH₄ReO₄ and NaReO₄ in standard and ultrahigh B₀. Prior ^185/187Re SSNMR measurements on these two compounds highlighted some of the largest QIs ever measured using NMR, although quantitative EFG tensor information could not be extracted for NaReO₄.²² While repeating the prior ^185/187Re SSNMR measurements on NaReO₄ at 11.75 T, we observed previously undetected fine structure. Using both second-order perturbation theory and exact QI simulations, we comment upon the origin of the fine structure and also outline some guidelines that are generally applicable when modeling the SSNMR spectra for any I = 5/2 nucleus which experiences a large, axially symmetric QI.

Experimental

1 Sample preparation

Both NaReO₄ (99.99%) and NH₄ReO₄ (99.999%) were purchased from Sigma-Aldrich and were received as powders. Sample purity was confirmed by the manufacturer (ESI, Additional Experimental†). Both compounds are stable under normal conditions. All samples were tightly packed into 4 mm o.d. Bruker magic angle spinning (MAS) ZrO₂ rotors.

2 Solid-state ^185/187Re NMR

Experimental data were acquired at the National Ultrahigh-field NMR Facility for Solids in Ottawa and at the University of Ottawa. The Ultrahigh-field Facility experiments used a standard bore Bruker AVANCE II spectrometer, which operates at B₀ = 21.1 T (ν₀(¹H) ≈ 900.08 MHz, ν₀(¹⁸⁵Re) = 202.738 MHz, and ν₀(¹⁸⁷Re) = 204.781 MHz), and a 4 mm Bruker HX MAS probe. The experiments performed at the University of Ottawa used a wide bore Bruker AVANCE spectrometer, which operates at B₀ = 11.75 T (ν₀(¹H) ≈ 500.13 MHz, ν₀(¹⁸⁵Re) = 112.652 MHz, and ν₀(¹⁸⁷Re) = 113.787 MHz), and a 4 mm Bruker HXY MAS probe. The ^185/187Re SSNMR signals were referenced to a 0.1 mol dm⁻³ solution of NaReO₄ in D₂O at 0.0 ppm. The ^185/187Re pulse lengths used for experiments on NH₄ReO₄ were established using the solution reference, and include a scaling of the optimized solution pulse by 1/[I + 1/2] = 1/3 to selectively excite the central transition (m_I = 1/2 ↔ −1/2; CT) of the solid. Due to the excessive width of the ^185/187Re SSNMR signals of NaReO₄ (vide infra), the high- and low-frequency pulse lengths were calibrated using the high- and low-frequency CT and satellite transition (ST) discontinuities of the actual powder sample. For further details on the frequency-dependence of the pulse lengths used to acquire the ^185/187Re SSNMR signals of NaReO₄, see the ESI, Table S1.†

The ^185/187Re SSNMR signals were acquired using either Solomon (i.e., “solid”) echo (i.e., π/2–τ₁–π/2–τ₂–acq)^26–28 or Hahn echo (i.e., π/2–τ₁–π–τ₂–acq)²⁹pulse sequences (see also the ESI†). Typical parameters were as follows: π/2 = 1.1 to 1.7 μs; spectral window = 2 MHz; τ₁ = 12.75 to 13.8 μs; recycle delay ≈ 100 ms, and between 512 and 1024 complex time-domain data points were collected per scan. All final SSNMR spectra were prepared using VOCS data acquisition methods.^20–22 This involves stepping the radiofrequency transmitter at uniform offset values, with the acquisition of a ‘sub-spectrum’ at each step. The offsets used here were 200 and 300 kHz for Hahn and Solomon echo experiments, respectively. For each transmitter setting, between 8192 and 17 500 transients were collected. Each processed sub-spectrum was combined in the frequency domain via co-addition to produce the final spectrum. Due to the temperature dependence of the ^185/187Re QI for these compounds, all experiments were performed at T = 291.8(0.2) K, as monitored via a Bruker ‘type-T’ thermocouple and regulated using a standard Bruker variable temperature unit. For full experimental details, see the ESI, Table S1.†

3 Solid-State ^185/187Re NQR

All experiments were carried out at the University of Ottawa using the AVANCE spectrometer outlined above. In addition, NQR experiments used a 4 mm Bruker HX MAS probe, and all spectra were acquired using the Hahn echo pulse sequence at T = 291.8(0.2) K. Non-optimized, short (≤ 1.6 μs), high-powered pulses were used as the radiofrequency was varied until a particular resonance was detected. The offset used while searching for ^185/187Re NQR signals was 200 kHz. For further details, see the ESI, Table S1.†

Results and discussion

1 Rhenium-185/187 solid-state NMR

i Sodium perrhenate, NaReO₄. Under ambient conditions, this material crystallizes in the scheelite-type tetragonal structure (space group, I4₁/a).³⁰ The oxygen atoms in the [ReO₄⁻] cluster arrange themselves in a distorted tetrahedral fashion about the central Re: there are four equivalent Re–O bond distances (r_ReO = 1.728 Å); however, the O–Re–O bond angles range from 108.5° to 111.4°.³¹ As the structure is not perfectly tetrahedral, the expected EFG at the Re nucleus is nonzero. Indeed, prior ^185/187Re NQR measurements on this system highlight a substantial, axially symmetric (i.e., the asymmetry parameter, η_Q=0) and temperature-dependent rhenium QI.^32,33 Previous ^185/187Re NMR measurements are consistent with a large rhenium QI (C_Q(¹⁸⁵Re) ∼278 MHz and C_Q(¹⁸⁷Re) ∼268 MHz, where C_Q is the nuclear quadrupole coupling constant), but were not used to precisely determine the rhenium EFG/CS tensor magnitudes.²² Prior rhenium NQR data collected at T = 296 K found that ν_Q(¹⁸⁵Re) = 44.997(0.005) (C_Q(¹⁸⁵Re) = 299.98(0.04) MHz) and ν_Q(¹⁸⁷Re) = 42.606(0.005) MHz (C_Q(¹⁸⁷Re) = 284.04(0.04) MHz) for NaReO₄, where ν_Q is the quadrupole frequency (see the footnotes to Table 1 for the definition of ν_Q used here, as well as the ESI, Fig. S1b,† for an energy level diagram for I = 5/2 under NQR conditions).³⁴ It is clear that there is a large discrepancy between the previously reported NQR and SSNMR results for the rhenium QI of NaReO₄. This compound was chosen for study in order to investigate the possible impact of HOQIE in the ^185/187Re SSNMR spectra and to potentially observe rhenium CS effects.

Table 1 Experimental ^185/187Re EFG tensor parameters and isotropic chemical shifts obtained via exact modeling of the quadrupole interaction^a

Compound	ν 1(^185Re)/MHz	ν 2(^185Re)/MHz	ν 1(^187Re)/MHz	ν 2(^187Re)/MHz	|CQ(^185Re)| ^b/MHz	|CQ(^187Re)|/MHz	η Q	δ iso ^c/ppm
a Measurement errors are within parentheses and parameter definitions are as follows: CQ = eQV33/h; ηQ = (V11–V22)/V33, where |V11| ≤ |V22| ≤|V33|; δiso = (δ11 + δ22 + δ33)/3, where δ33 ≤ δ22 ≤ δ11. The frequencies ν1 and ν2 correspond to the doubly-degenerate single quantum NQR resonance frequencies, which for I = 5/2 and ηQ = 0 can be defined as: ν1 = νQ = 3CQ/20 and ν2 = 2νQ = 3CQ/10. All measurements were carried out at T = 291.8(0.2) K. SSNMR line shape simulations were performed using exact theory.^24 EFG tensor parameters using NQR data were determined using the procedure outlined by Semin.^54 b While CQ may take any real value, |CQ| is measured experimentally using NQR/SSNMR. On the basis of our data, we find that the maximum possible value for the ^185Re nuclear electric hexadecapole interaction in NaReO4 is ca. 750 Hz.^35 c Rhenium chemical shifts are relative to 0.1 mol dm^−3NaReO4 in D2O (δiso(^185/^187Re) = 0 ppm).
NaReO4	45.102(0.006)	90.204(0.009)	42.681(0.005)	85.362(0.008)	300.68(0.02)	284.54(0.02)	<0.003	70(40)
NH4ReO4	—	35.068(0.010)	—	33.186(0.008)	116.90(0.04)	110.62(0.03)	<0.003	0(40)

---

Rhenium-185/187 NQR experiments were performed (ESI, Fig. S2†) and the resulting transition frequencies (Table 1) allow us to confirm that η_Q(^185/187Re) = 0. As the ratio between the m_I = ±3/2 ↔ ±5/2 and m_I = ±1/2 ↔ ±3/2 transition frequencies (|Δm_I| = 1) is exactly 2 within experimental error, we may conclude that there is no evidence of a nuclear electric hexadecapole interaction.³⁵ Using our new NQR data, we establish that C_Q(¹⁸⁵Re)=300.68(0.02) MHz and C_Q(¹⁸⁷Re) = 284.54(0.02) MHz at 291.8 K. The slight discrepancy between our C_Q(^185/187Re) values and those measured earlier by NQR can be fully attributed to the difference in the respective measurement temperatures.³⁶

To measure the rhenium EFG and CS tensors for this sample using SSNMR, we carried out ^185/187Re SSNMR experiments on powdered NaReO₄ at B₀ = 11.75 and 21.1 T (Fig. 1 and 2). In the present study, the ^185/187Re SSNMR signals typically overlap one another due to their similar Larmor frequencies. After careful line shape analysis using exact QI simulation software²⁴ (it is noted here that other exact QI models exist),^37–40 quantitative agreement between the rhenium EFG tensor parameters determined using our ^185/187Re NQR and NMR measurements was established. In addition, we were able to measure for the first time an isotropic rhenium CS in a solid sample (δ_iso = 70(40) ppm relative to 0.1 mol dm⁻³NaReO₄ in D₂O). This opens up the possibility that ^185/187Re SSNMR experiments could be used to report on the local rhenium bonding environment or the oxidation state (under favorable conditions) in solid samples. Indeed, the sparse solution ^185/187Re NMR literature data highlight a chemical shift range of ∼6800 ppm.^41,42 We were not able to measure rhenium chemical shift anisotropy (CSA) for this sample.

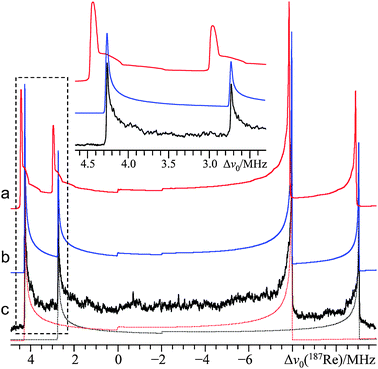
Fig. 1 Second-order perturbation theory simulation (a, d), exact simulation (b, e), and experimental static VOCS Hahn echo (c, f) ^185/187Re SSNMR spectrum of powdered NaReO₄, acquired at B₀ = 11.75 T (ν₀(¹⁸⁷Re) = 113.787 MHz; ν₀(¹⁸⁵Re) = 112.652 MHz) and T = 291.8 K. The second-order perturbation theory spectrum includes only the ¹⁸⁷Re signal, to enhance clarity. The high frequency region is depicted in (a, b, c) and the low frequency region is in (d, e, f). Please note that the horizontal scaling is not equivalent between (a, b, c) and (d, e, f): in the inset, the experimental spectrum is displayed using equivalent horizontal scaling for both regions. Below (c and f), the exact simulation line shapes associated with each of ¹⁸⁵Re and ¹⁸⁷Re are deconvoluted: the long dashed red trace is ¹⁸⁷Re, while the short dashed black trace is ¹⁸⁵Re. Low-frequency splittings (denoted by double-headed arrows and guide lines) are not predicted by second-order perturbation theory. The discontinuities due to the m_I = 1/2 ↔ 3/2 STs are marked by “*”, while the remainder of the discontinuities are due to the m_I = 1/2 ↔ −1/2 transition. All simulations use identical EFG tensor parameters, which were also measured independently using ^185/187Re NQR experiments. Minor discontinuities in the slope of trace (a) are due to the POWDER algorithm⁵⁵ used for powder averaging.

Fig. 2 Second-order perturbation theory simulation (a), exact simulation (b), and experimental static VOCS Solomon echo (c) ^185/187Re SSNMR spectra of powdered NaReO₄, acquired at B₀ = 21.1 T (ν₀(¹⁸⁷Re) = 204.781 MHz; ν₀(¹⁸⁵Re) = 202.738 MHz) and T = 291.8 K. Below c, the exact simulation signals associated with each of ¹⁸⁵Re and ¹⁸⁷Re are deconvoluted: the dotted red trace is ¹⁸⁷Re, while the dotted black trace is ¹⁸⁵Re. Low-frequency splittings are not observed; however, the expected positions of the discontinuities in the analytical simulation are subject to a non-uniform, frequency-dependent shift, which is evidence of HOQIE. All simulations used identical EFG tensor parameters, which were also measured independently using ^185/187Re NQR experiments. The inset (top, middle) corresponds to the region within the dashed line box, and is meant to highlight the significant difference between the exact and second-order perturbation theory models. For the inset, the deconvolution traces have been omitted to enhance clarity.

Upon inspection of Fig. 1 and 2, it is immediately clear that the predominantly CT line shapes at both applied fields are very broad (∼16 and 26 MHz for the spectra acquired at B₀ = 21.1 and 11.75 T, respectively), but the most striking aspect of the spectrum at 11.75 T is the presence of unexpected high-intensity discontinuities (i.e., not predicted using second-order perturbation theory; Fig. 1f). It is intriguing that the extra discontinuities do not appear in the ^185/187Re SSNMR spectrum acquired at 21.1 T. This B₀-dependent system response is consistent with the expected behavior of a second-order (or greater) quadrupole-induced effect and can be fully attributed to HOQIE (vide infra). While it is perhaps clear that up to two additional low-frequency discontinuities could be due to the inner (m_I = 1/2 ↔ 3/2) ST (one from each of ¹⁸⁵Re and ¹⁸⁷Re), second-order perturbation theory still fails rather spectacularly when one applies the correct ¹⁸⁷Re EFG tensor parameters (from NQR and exact line shape simulations) and includes the STs within the model (Fig. 1a and d). The high-frequency ¹⁸⁷Re CT discontinuity position is overestimated by ∼1 MHz, as are both the position of the corresponding low-frequency CT discontinuity and that of the m_I = 1/2 ↔ 3/2 ST. Line shape modeling using exact QI software leads to both the correct number and frequency positions for all eight observed discontinuities for NaReO₄ using the parameters in Table 1. Most importantly, the exact QI model predicts the experimentally observed fine structure in the low-frequency spectral region for both ¹⁸⁵Re and ¹⁸⁷Re (Fig. 1f). These additional features are field-dependent, are attributed to the m_I = 1/2 ↔ 3/2 ST transition (vide infra), and do not interfere with the CT ^185/187Re SSNMR spectra at 21.1 T (Fig. 2).

Although second-order perturbation theory does not predict the correct placement of the CT discontinuities for NaReO₄, even at 21.1 T (Fig. 2a), it does predict the correct number of discontinuities at the higher applied field. At 21.1 T, the additional fine structure observed at 11.75 T is not present and it appears that HOQIE manifest as a non-uniform frequency-dependent shift in the positions of the discontinuities (with a notable bias towards a positive-frequency shift; the effective parameters determined using second-order perturbation theory are summarized in the ESI, Table S2†). It is therefore clear that the unusual B₀-dependent behavior is due to HOQIE, and that the fine structure observed at 11.75 T must be due to a 3rd-order QI effect on the ST and/or a 4th-order QI effect on the CT and/or ST (as 3rd-order effects on the CT are known to be zero).⁴³ Beyond 4th-order effects are also potentially significant, but are expected to be much smaller than the leading-order contributions. It is possible that fourth-order perturbation theory may be able to produce accurate line shape models in the regime where the value of ν_Q becomes somewhat comparable to the Larmor frequency (ν₀). Overall, it is seen that second-order perturbation theory cannot lead to the correct values for either δ_iso or C_Q(^185/187Re) under these conditions and in fact both quantities will be underestimated relative to their true values (vide infra).

ii Ammonium perrhenate, NH₄ReO₄. As with NaReO₄, NH₄ReO₄ has the tetragonal scheelite-type structure (space group, I4₁/a).⁴⁴ Due to the anomalous dependence of its ^185/187Re NQR transition frequencies with respect to temperature and pressure, NH₄ReO₄ has been featured in numerous rhenium NQR studies^32,45–50 and one rhenium SSNMR²² account. All prior reports suggest a large and axially symmetric rhenium QI. Relative to NaReO₄, the [ReO₄]⁻cluster in NH₄ReO₄ is significantly less distorted from tetrahedral: there are four equivalent Re–O bond distances (r_ReO = 1.734 Å) and the unique O–Re–O bond angles are 108.8 and 110.8°. Based upon this information, one would expect the rhenium QI in NH₄ReO₄ to be reduced relative to that of NaReO₄ and indeed this is the case. We have chosen this material for study to establish potential HOQIE in the SSNMR spectra for the case of a more modest rhenium QI and to observe chemical shift effects.

To provide a second independent measure of the ^185/187Re EFG tensor parameters in NH₄ReO₄, rhenium NQR experiments were performed (see ESI, Fig. S3†) and the measured NQR transition frequencies are summarized in Table 1. Using the rhenium NQR data in tandem with the multiple field ^185/187Re SSNMR data (Fig. 3) (SSNMR data analyzed using exact QI line shape modeling), it is observed that C_Q(¹⁸⁵Re) = 116.90(0.04) MHz, C_Q(¹⁸⁷Re) = 110.62(0.03) MHz, and η_Q(^185/187Re) = 0 at T = 291.8 K for this sample. After adjusting for the well-known temperature dependence of the rhenium QI in NH₄ReO₄, these measurements are fully consistent with prior NQR findings. Unlike the ^185/187Re SSNMR spectra of NaReO₄ recorded at 11.75 T, there is no evidence of unexpected additional fine structure in the ^185/187Re CT SSNMR spectrum of NH₄ReO₄. Using exact QI simulation software, we were able to measure the isotropic rhenium chemical shift for this sample as 0(40) ppm. At the lower applied field, the extracted isotropic chemical shifts using second-order perturbation theory and exact theory do not agree with one another. As was the case in our prior study using ¹²⁷I SSNMR data,²³ and with the ^185/187Re SSNMR spectral simulations for NaReO₄ at 21.1 T, the second-order simulation produces a chemical shift that is smaller than the true value (for the values extracted using second-order perturbation theory, see the ESI, Table S2†). Unlike the rhenium SSNMR line shape simulations for NaReO₄, however, the rhenium EFG tensor parameters extracted for NH₄ReO₄ using both second-order perturbation theory and exact theory match, within experimental error, when modeling the spectrum acquired at 11.75 T. At 21.1 T, quantitative agreement is found between second-order and exact theory for all the reported parameters in Table 1. Hence, there is no evidence of HOQIE in the spectra for NH₄ReO₄ at 21.1 T and second-order perturbation theory would be sufficient to model this SSNMR line shape. The quantitative agreement for this final case is sensible, as at 21.1 T, the ratio between ν₀ and ν_Q for NH₄ReO₄ exceeds 10 to 1, which is a regime where HOQIE are not expected to be significant (i.e., the high-field approximation is valid).

Fig. 3 Exact simulation (a, c), experimental static VOCS Hahn echo (b), and static VOCS Solomon echo (d) ^185/187Re SSNMR spectra of powdered NH₄ReO₄, acquired at (b) B₀ = 11.75 T and (d) B₀ = 21.1 T. Below b and d, the exact simulation signals associated with each of ¹⁸⁷Re (dotted red trace) and ¹⁸⁵Re (dashed black trace) are deconvoluted. All experiments were performed at T = 291.8 K.

As the two CT ^185/187Re signals for NH₄ReO₄ are separated at 21.1 T (Fig. 3d), and as the central “step” discontinuity is clearly defined for both isotopes, we attempted to include rhenium CSA in the line shape models for this sample. Unfortunately, the rhenium CS tensor span was too small to be measured and it is noted that the span must be less than ca. 80 ppm. A small tensor span is consistent with the nearly tetrahedral local symmetry about the rhenium atoms.

iii Origin of the fine structure present in the ^185/187Re SSNMR spectrum of NaReO₄ at 11.75 T. While HOQIE have been observed for several different ν₀/ν_Q ratios in the current study, and while it appears as though the onset of these effects leads to a non-uniform frequency-dependent shift in the resulting SSNMR powder pattern, the ^185/187Re SSNMR spectrum of NaReO₄ acquired at 11.75 T presents previously unobserved fine structure. This fine structure was attributed to HOQIE and we now briefly outline its origin and the ν₀/ν_Q regime where it may manifest in an SSNMR spectrum where I = 5/2 and η_Q = 0.

In Fig. 4, line shape simulations are presented which were generated using the exact simulation software. We examined the regime where the ν₀/ν_Q ratio value ranges from 4.0 to 2.0 in steps of −0.2. As we wish to comment upon the origin of the fine structure for this particular case, we have set ν₀ to 113.787 MHz (the value of the NMR resonance condition for the ¹⁸⁷Re solution standard at 11.75 T). At ν₀/ν_Q = 4, it is noted that the inner ST discontinuity (i.e., m_I = 1/2 ↔ 3/2) is expected to have a relatively high intensity, and there is no additional fine structure. However, as the ν₀/ν_Q value is further decreased, the inner low-frequency ST splits into two discontinuities. Eventually, the discontinuities shift to such an extent that they will both occur within the spectral region which is normally (using second-order perturbation theory) attributed to the CT. For the experimental case of ^185/187Re SSNMR of NaReO₄ at 11.75 T, the ν₀/ν_Q value is roughly 2.6 : 1, which closely resembles the ratio used to generate the trace indicated using a dagger in Fig. 4. Hence, we may conclude that the experimentally observed fine structure is due to a high-order splitting in the m_I =1/2 ↔ 3/2 ST for each of the ¹⁸⁵Re and ¹⁸⁷Re nuclides. One can expect this type of fine structure to exist (although it will not likely interfere with the CT signal until ν₀/ν_Q < 3) once ν₀/ν_Q becomes less than 4. This effect on the ST appears to be similar in nature to the splittings observed in certain STMAS experiments, which were attributed to a third-order quadrupole-induced effect.⁵¹ Fine structure due to third-order effects is also predicted to arise in ¹⁴N (I = 1) MAS NMR spectra when the value of C_Q becomes large, although it appears that this has not been experimentally validated.⁵²

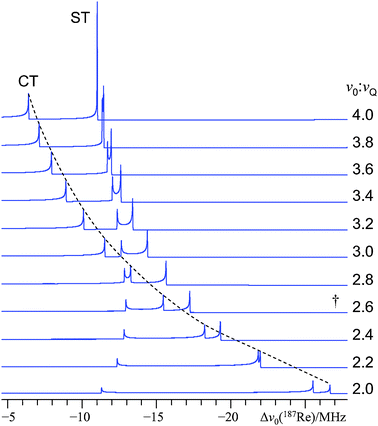Fig. 4 Exact simulations of the low-frequency spectral region (part of the CT and m_I = 1/2 ↔ 3/2 ST discontinuities only), which highlight the onset and origin of the HOQIE fine structure for NaReO₄. For this particular simulation, the ¹⁸⁷Re nucleus at 11.75 T has been assumed; hence, ν₀ = 113.787 MHz. By adjusting ν_Q, the ν₀/ν_Q ratio is varied from 4.0 (top trace) to 2.0 (bottom trace) in steps of −0.2. The dashed line trace clarifies the evolution of the low-frequency CT discontinuity as a function of ν₀/ν_Q. The spectrum corresponding closely to the best-fit spectrum in Fig. 1 is demarked with a dagger above it.

2 General guidelines for NMR spectral analysis when any I = 5/2 nucleus experiences a very large, axial QI

It is well known that second-order perturbation theory is a valid method to model many SSNMR line shapes associated with half-integer quadrupolar nuclei; however, care must be taken to ensure that the high-field condition is satisfied (often taken as ν₀ > 10ν_Q). For a large enough QI (i.e., ν₀ < 4ν_Q), it was established above, using experiment and theory, that additional fine structure is present in the SSNMR spectrum. Under these conditions, second-order perturbation theory does not even predict the correct number of discontinuities, and it is not meaningful to quantify the differences in the extracted NMR parameters between perturbation theory and exact theory. Between these two cases, therefore, there exists a region where the high field approximation is not clearly valid, but the additional fine structure is not observable. We comment here upon the errors in the SSNMR parameters extracted (namely C_Q and δ_iso) in this intermediate regime when using second-order perturbation theory as compared to exact theory. Methodology details for this section can be found in the ESI, Additional Experimental.†

We consider here the case where a nuclear spin having I = 5/2 is subjected to an axial EFG and B₀. The inclusion of additional effects, such as η_Q ≠ 0, CSA, dipole–dipole, etc., is beyond the scope of the current study. For cases where the high-field approximation is traditionally viewed as being valid (ν₀ > 10ν_Q), it is found that the error in the extracted C_Q value is at most ca. 0.1% (Fig. 5a). However, the error in the isotropic chemical shift, even within the high-field condition, can be as large as 40 ppm (Fig. 5b). For a fictitious example where ν₀ = 100 MHz and ν_Q = 10.0 MHz (i.e., C_Q = 66.7 MHz), this would mean an error in the C_Q value of ∼67 kHz, while the error in the shift would be 4.0 kHz. As the value of the ratio between ν₀ and ν_Q is decreased (i.e., increasing C_Q or decreasing ν₀), a point is reached where the extracted C_Q and δ_iso values exceed typical experimental measurement errors. The point at which this would occur is of course highly dependent upon the measurement conditions and the sample. As an additional example, for the case where ν₀ = 4ν_Q, the error in the chemical shift extracted using second-order perturbation theory exceeds 1500 ppm (Fig. 5b). At the onset of the additional fine structure (ν₀ ≈ 4ν_Q), the error in the C_Q value determined using second-order perturbation theory will be slightly in excess of 0.6% (Fig. 5a). These findings echo the observations noted previously for spin-5/2 nuclei (although not restricted to η_Q = 0): when using second-order perturbation theory to model the SSNMR line shapes, the error in the chemical shift becomes detectable at a relatively greater ν₀/ν_Q value than the error in C_Q.^23,53 Importantly, it is observed and calculated that the errors in both parameters will always be such that second-order perturbation theory underestimates the true value of the parameter.

Fig. 5 Illustrations of the errors associated with using second-order perturbation theory to model SSNMR line shapes for the case where I = 5/2 and η_Q = 0, relative to an exact simulation. (a) Error in the C_Q value as a function of the ν₀/ν_Q ratio, and (b) error in the isotropic chemical shift value as a function of the ν₀/ν_Q ratio. High field conditions are traditionally assumed to be satisfied if ν₀/ν_Q > 10. The lines connecting the data points are guides for the eyes only.

Conclusions

We have presented unambiguous evidence of HOQIE in SSNMR spectra and show that they can manifest in unexpected ways (i.e., not always as simple shifts in the frequencies of the spectral discontinuities). The ^185/187Re NMR spectrum of NaReO₄ at B₀ = 11.75 T displays additional fine structure in the low-frequency region, which is not predicted by second-order perturbation theory, but which is predicted using an exact QI model. The fine structure is not observed experimentally at 21.1 T, and is not predicted to be present at this field using exact QI line shape simulations, which is in accord with the expected behavior of a quadrupole-induced effect on a SSNMR line shape (i.e., higher B₀ leads to smaller QI spectral effects). We confirm our NMR QI parameters, and rule out (within experimental error) hexadecapole interaction effects by performing ^185/187Re NQR experiments for both samples. We use exact QI simulations to establish that the fine structure will potentially become observable when the ν₀/ν_Q value drops below 4, and that the fine structure originates from the m_I = 1/2 ↔ 3/2 ST, which also happens to overlap with the CT. For ν₀/ν_Q values greater than 4, we find that the true values of δ_iso and C_Q will be underestimated when the spectra are modeled using second-order perturbation theory. Knowledge of HOQIE may be of critical importance for the accurate line shape analysis of SSNMR spectra of many quadrupolar nuclei that may experience large QIs, including ^63/65Cu, ⁶⁷Zn, ⁷⁵As, ^79/81Br, ⁹¹Zr, ¹⁰⁵Pd, ¹¹⁵In, ¹²⁷I, ²⁰⁹Bi, and others.

Acknowledgements

D.L.B. thanks the Natural Sciences and Engineering Research Council (NSERC) of Canada for funding. C.M.W. thanks NSERC for an Alexander Graham Bell CGS D2 scholarship. We are grateful to Dr Victor Terskikh and Dr Eric Ye for technical support. Access to the 900 MHz NMR spectrometer was provided by the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a national research facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Québec, the National Research Council Canada, and Bruker Biospin and managed by the University of Ottawa (www.nmr900.ca). NSERC is acknowledged for a Major Resources Support grant.

References

1. C. P. Slichter, Principles of Magnetic Resonance, ed. M. Cardona, P. Fulde, K. von Klitzing, H. J. Queisser and H. K. V. Lotsch, Springer-Verlag, New York, 3rd edn, 1990, pp. 485–502.
2. S. E. Ashbrook, Phys. Chem. Chem. Phys., 2009, 11, 6892.
3. F. A. Cotton and G. Wilkinson, in Advanced Inorganic Chemistry: A Comprehensive Text, Wiley, Toronto, 4th edn, 1980, p. 883.
4. A. V. Naumov, Russ. J. Non-Ferrous Metals, 2007, 48, 418.
5. F. A. Cotton, Acc. Chem. Res., 1969, 2, 240.
6. Y. Kuninobu and K. Takai, Chem. Rev., 2011, 111, 1938.
7. R. Hua and J.-L. Jiang, Curr. Org. Synth., 2007, 4, 151.
8. A. T. Herrmann, T. Saito, C. E. Stivala, J. Tom and A. Zakarian, J. Am. Chem. Soc., 2010, 132, 5962.
9. I. L. Barnes, T. L. Chang, P. De Bièvre, J. W. Gramlich, R. J. C. Hageman, N. E. Holden, T. J. Murphy, K. J. R. Rosman and M. Shima, Pure Appl. Chem., 1991, 63, 991.
10. R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795.
11. M. Bernasson, P. Descouts and G. A. Styles, Helv. Phys. Acta, 1970, 43, 393.
12. J. E. Schirber, L. J. Azevedo and A. Narath, Phys. Rev. B, 1979, 20, 4746.
13. D. G. Klobasa and P. K. Burkert, Magn. Reson. Chem., 1987, 25, 154.
14. A. Narath and D. C. Barham, Phys. Rev., 1968, 176, 479.
15. S. Wada and K. Asayama, J. Phys. Soc. Jpn., 1973, 34, 1163.
16. Y. Nishihara, Y. Yamaguchi, S. Waki and T. Kohara, J. Phys. Soc. Jpn., 1983, 52, 2301.
17. P. Pyykkö, Mol. Phys., 2008, 106, 1965.
18. R. Siegel, T. T. Nakashima and R. E. Wasylishen, Concepts Magn. Reson. A, 2005, 26A, 62.
19. R. Siegel, T. T. Nakashima and R. E. Wasylishen, Concepts Magn. Reson. A, 2005, 26A, 47.
20. D. Massiot, I. Farnan, N. Gautier, D. Trumeau, A. Trokiner and J. P. Coutures, Solid State Nucl. Magn. Reson., 1995, 4, 241.
21. A. Medek, V. Frydman and L. Frydman, J. Phys. Chem. A, 1999, 103, 4830.
22. R. W. Schurko, S. Wi and L. Frydman, J. Phys. Chem. A, 2002, 106, 51.
23. C. M. Widdifield and D. L. Bryce, J. Phys. Chem. A, 2010, 114, 10810.
24. A. D. Bain, Mol. Phys., 2003, 101, 3163.
25. A. D. Bain and B. Berno, Prog. Nucl. Magn. Reson. Spectrosc., 2011 DOI:10.1016/j.pnmrs.2010.12.002.
26. I. Solomon, Phys. Rev., 1958, 110, 61.
27. I. D. Weisman and L. H. Bennett, Phys. Rev., 1969, 181, 1341.
28. A. C. Kunwar, G. L. Turner and E. Oldfield, J. Magn. Reson., 1986, 69, 124.
29. E. L. Hahn, Phys. Rev., 1950, 80, 580.
30. A. Atzesdorfer and K.-J. Range, Z. Naturforsch. B: Chem. Sci., 1995, 50, 1417.
31. J. Spitaler, C. Ambrosch-Draxl, E. Nachbaur, F. Belaj, H. Gomm and F. Netzer, Phys. Rev. B: Condens. Matter, 2003, 67, 115127.
32. A. A. Boguslavskii, R. S. Lotfullin, R. V. Magera and V. V. Pechenov, Fiz. Tverd. Tela, 1974, 16, 2453.
33. R. A. Johnson and M. T. Rogers, in Advances in Nuclear Quadrupole Resonance: Papers Presented at the International Symposium on Nuclear Quadrupole Resonance, Sept. 28-–29, 1972, Queen Elizabeth College, University of London, England, ed. J. A. S. Smith, 1974, 297.
34. M. T. Rogers and K. V. S. R. Rao, J. Chem. Phys., 1973, 58, 3233.
35. S. L. Segel, J. Chem. Phys., 1978, 69, 2434.
36. S. Günther, O. Lutz, A. Nolle and P. G. Schrade, Z. Naturforsch., 1978, 33a, 1018.
37. G. M. Muha, J. Magn. Reson., 1983, 53, 85.
38. R. B. Creel and D. A. Drabold, J. Mol. Struct., 1983, 111, 85.
39. R. B. Creel, J. Magn. Reson., 1983, 52, 515.
40. B. C. Sanctuary, T. K. Halstead and P. A. Osment, Mol. Phys., 1983, 49, 753.
41. A. Müller, E. Krickemeyer, H. Bögge, M. Penk and D. Rehder, Chimia, 1986, 40, 50.
42. Y. Do, E. D. Simhon and R. H. Holm, Inorg. Chem., 1985, 24, 4635.
43. A. D. Bain, J. Magn. Reson., 2006, 179, 308.
44. I. P. Swainson and R. J. C. Brown, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 76.
45. K. V. S. R. Rao and M. T. Rogers, J. Magn. Reson., 1972, 8, 392.
46. P. K. Burkert and M. F. Eckel, Z. Naturforsch., 1973, 28b, 379.
47. R. A. Johnson and M. T. Rogers, J. Magn. Reson., 1974, 15, 584.
48. R. J. C. Brown, J. Magn. Reson., 1975, 18, 558.
49. R. J. C. Brown, J. G. Smeltzer and R. D. Heyding, J. Magn. Reson., 1976, 24, 269.
50. R. J. C. Brown and S. L. Segel, J. Chem. Phys., 1977, 67, 3163.
51. S. E. Ashbrook and S. Wimperis, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 53.
52. S. Cavadini, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 56, 46.
53. C. M. Widdifield, R. P. Chapman and D. L. Bryce, in Annu. Rep. Nucl. Magn. Reson. Spectrosc, ed. G. A. Webb, 2009, vol. 66, 195–326.
54. G. K. Semin, Russ. J. Phys. Chem. A, 2007, 81, 38.
55. D. W. Alderman, M. S. Solum and D. M. Grant, J. Chem. Phys., 1986, 84, 3717.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental; detailed ^185/187Re NQR/SSNMR experimental acquisition parameters; energy level diagrams for I = 5/2 under various relative Zeeman/QI strengths; experimental ^185/187Re NQR spectra of NaReO₄ and NH₄ReO₄; experimental ^185/187Re EFG/CS parameters obtained via second-order perturbation theory; V₃₃/B₀ angle corresponding to the low-frequency CT discontinuity using exact QI theory; table of values used to constructFig. 5. See DOI: 10.1039/c1cp20572b

---