The role of molecular modeling in confined systems: impact and prospects
Received
11th August 2010
, Accepted 20th October 2010
First published on 29th November 2010
Abstract
Molecular modeling at the electronic and atomistic levels plays an important and complementary role to experimental studies of confinement effects. Theory and atomistic simulation can provide fundamental understanding, determine the limits of well known macroscopic laws such as Kelvin's equation, provide predictions for systems that are difficult to study via experiment (e.g. adsorption of highly toxic gases), and can be used to gain detailed molecular level information that may not be accessible in the laboratory (e.g. the local structure and composition of confined phases). We describe the most important and useful methods that are based firmly on quantum mechanics and statistical mechanics, including ab intio and classical density functional theories, and Monte Carlo and molecular dynamics simulation. We discuss their strengths and limitations. We then describe examples of applications of these methods to adsorption and equilibrium properties, including testing the Kelvin equation, determination of pore size distributions and capillary phenomena. Applications to self and transport diffusion, including single-file and anomalous diffusion, and viscous flow in nanoporous materials are described. The use of these methods to understand confinement effects on chemical reactions in heterogeneous media is treated, including effects on reaction equilibria, rates and mechanism. Finally we discuss the current status of molecular modeling in this area, and the outlook and future research needs for the next few years. The treatment is suitable for the general technical reader.
1. Introduction
Our ability to model physical and chemical processes at the atomic and sub-atomic levels has progressed rapidly over the last three decades, due to development of theoretical methods based on statistical mechanics and quantum mechanics, rapid increases in computer speed and memory, more efficient algorithms and a steady improvement in force field development. Among the most useful theoretical methods for surface science are ab initio and classical density functional theories and molecular simulation methods, that is the numerical solution of the equations of statistical mechanics using Monte Carlo or molecular dynamics techniques. Theory and simulation can provide fundamental understanding of observed phenomena, and can be used to make predictions for systems that are difficult or impossible to study experimentally, for example adsorption of toxic or biological agents, or behavior at very high temperature or pressure. In addition, theory and simulation can give detailed molecular level information that is difficult or impossible to determine from laboratory experiments. Examples are the molecular structure of adsorbed phases, detailed mapping of diffusion of guest molecules in highly disordered microporous materials, the pressure tensor in a pore and the wave function of the electrons. These methods also find important applications in determining the limits of well known macroscopic laws, which may break down for nano-scale systems. Examples are the concept of surface tension1 and Gibbs' surface thermodynamics in general, related equations such as those of Kelvin,2 Young and Laplace,1 Fick's Law of diffusion3–6 and the Second Law of Thermodynamics.‡,§7–13
Theory and experiment each have different strengths and limitations, but these are complementary to a large extent and there is much to be gained by constructing research programs that combine the two. Significant difficulties in experimental studies of adsorption and confinement effects include identifying the nature and composition of the host adsorbate phase, long-lived metastable states, and preferential adsorption of trace impurities on the pore walls, while in theoretical and simulation studies the main difficulties are uncertainties about the pore morphology and topology of the real materials (in the case of non-crystalline materials), and about the force fields involved. A further limitation for simulation at present is that current computers are not yet powerful enough to carry out molecular dynamics simulations for longer than about a microsecond of real time. While this is sufficient for studies of relatively small adsorbate molecules, the self-assembly of larger surfactant or protein molecules on solid surfaces and in pores requires longer times. Such studies are likely to become possible in the next decade, when more powerful machines are available. While metastability also occurs in theoretical calculations, free energy calculations enable this to be detected and the true equilibrium state determined; moreover, the nature and composition of the host phase is readily determined.
This paper is an introduction and overview of the most useful theoretical and molecular simulation methods for studying confinement effects, and is intended for the general technical reader rather than specialists. We restrict ourselves to methods that are firmly based on statistical mechanics or quantum mechanics. In Section 2 we briefly describe the methods, pointing out their limitations as well as strengths. In the following sections we discuss some applications of these methods to study adsorption and phase transitions (Section 3.1), diffusion and transport (Section 3.2), and confinement effects on chemical reactions (Section 3.3). Finally, in Section 4 we discuss the current state of molecular modeling for confined systems, and future prospects.
2. Overview of methods
Theory and modeling methods can be conveniently classified into four groups, depending on the level of detail of their description of matter: (a) electronic level methods, in which matter is regarded as made up of fundamental particles (electrons, protons, etc.) and obeys the laws of quantum mechanics; (b) atomistic level methods, with matter made up of atoms that obey the laws of statistical mechanics; (c) meso-scale methods, where matter is regarded as made up of ‘blobs’ of matter with each blob containing a few or many atoms; and (d) the continuum scale, with matter treated as a continuum that can be sub-divided without limit, and obeying well established macroscopic laws (conservation of matter, energy and momentum, Fick's Law of diffusion, and so on). Clearly the level of description becomes less detailed as we progress from electronic level methods to the continuum ones. At the atomistic level all detail of the electronic structure is lost, while at the meso- and continuum scales atomic detail is lost. However, the length and time scales that can be accessed with these methods increase as we go from the electronic to the continuum levels of description. With currently available supercomputers, electronic scale methods such as density functional theory can comfortably describe system sizes up to about 100 atoms or more and a few tens of picoseconds, while atomistic simulation methods (Monte Carlo and molecular dynamics) can model system sizes up to tens of billions of atoms, box lengths of a few microns or more, and up to a few microseconds of real time, these scales being dependent on the number and complexity of the molecules involved. Meso-scale methods, such as Brownian and dissipative particle dynamics, can describe systems that are larger and for longer times by several orders of magnitude, but at the cost of loss of atomic detail and reduced rigor.
In this paper we focus on those methods from the first two categories, the electronic and atomistic levels of description, which we believe are most useful in modeling of confined systems.
2.1 Electronic level methods
The ab initio (“from the beginning”) methods,14,15 as their name implies, require no experimental input other than a knowledge of the atomic species involved. These methods are needed when there is a significant movement or rearrangement of the electrons, as in chemical reactions in porous materials, in photonic or electronic devices, and in electrical conduction in electrodes, supercapacitors, etc.16 These methods are the most rigorous in principle, but computationally the most demanding, so that their application is still limited to rather small systems and short times. There is a considerable range to the computational burden, depending on the level of rigor of the treatment. In the case of guest phases within porous materials one needs a system size of at least several dozen atoms in order to capture the phenomena of interest in a realistic way, and at present this makes it difficult to use the most rigorous methods.
For many applications to confined systems, ab initio density functional theory17,18 (DFT) provides the best compromise between rigor and computational burden at present. The accuracy obtained with DFT varies with the application, but is often in the range 0.1 to 1 kcal mol−1 in energy.18 The basic concept of DFT is to describe the system via the density of electrons, ρe, as a function of position r in the system, rather than by the more traditional Ne-body wave function, Φ. This has two advantages. First, the electron density depends only on 3 variables (x,y,z), as opposed to the 3Ne variables that the wave function depends on. Second, the electron density is a physical observable, accessible in experiments such as electron paramagnetic resonance.19
DFT is based on two theorems, proposed and formally proved in 1964 by Hohenberg and Kohn.20 The first theorem states that the ground state energy of the system, E, is a functional of the electron density, E[ρe], so that E depends on the electron density at all r, and is uniquely determined for a given electron density profile function. The energy E can be written as
| | | E[ρe] = T[ρe] + U[ρe] + Exc[ρe] | (1) |
where
T[
ρe] is the kinetic energy of a system on non-interacting particles of density
ρe,
U[
ρe] is the classical electrostatic energy due to coulombic interactions, and
Exc[
ρe] includes all many-body contributions to the total energy, in particular the exchange and correlation energies. Knowledge of the electron density is sufficient to calculate all of the ground state properties of the system.
The second theorem of Hohenberg and Kohn20 states that the true electron density profile for the ground state is the one that minimizes the energy. This provides a variational principle that permits calculation of ρe(r), provided that we have some knowledge of the form of the functional dependence of the energy on the electron density. The latter problem was resolved in a paper by Kohn and Sham,21 who proposed that the electron density could be expressed in terms of a sum over one electron orbitals, ψi(r),
| | 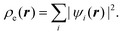 | (2) |
These Kohn–Sham orbitals are determined
via a minimization of the ground state energy
E, with the electron density given by
eqn (2). The exchange–correlation energy,
Exc[
ρe], requires some approximation for this method to be computationally tractable. A simple and surprisingly good approximation is the local density approximation, which is based on the known exchange–correlation energy of the uniform electron gas at the local density at point
r.
22,23 With the electron density known, the energy components in
eqn (1) can be calculated.
Density functional theory has some limitations, including reduced accuracy in calculating excited electronic states and band gaps in semi-conductors and insulators.16,18 Another limitation is a relatively poor description of the effects of dispersion forces between molecules. However, there have been recent advances in this latter area.24–26
DFT can be combined with atomistic classical molecular dynamics simulation (see next section), with DFT being used to compute the intermolecular forces acting on the atomic nuclei from electronic structure calculations after each time step. The best known of these ab initio molecular dynamics methods is that due to Car and Parrinello.27 These methods have been applied widely to studies of chemical reactions,28 material properties,16,18 and other areas of biochemistry and physics,29 and have the advantage over DFT alone of giving the dynamics of the system, for example the rate of chemical reactions, in addition to the mechanism. Because of the computational burden of the DFT calculations, these methods are restricted to quite short times at present.
A variety of higher level ab initio methods are available,14,15,28 and provide higher accuracy than DFT, but at the expense of increased computational intensity, and as a consequence they are limited to smaller system sizes. Most of these methods use the Hartree–Fock (HF) model (self-consistent mean field theory) as a starting point. In HF theory the electron–electron interaction is replaced by the interaction of the electron with a mean field interaction due to the other electrons.29 The neglect of detailed electron–electron correlations leads to errors that are too serious for most chemical calculations. The higher level methods are based on an expansion about the HF result, and include cluster expansions (coupled cluster theory), expansions in the difference in the potential energies between the exact and HF electron energies (Møller–Plesset30 and related perturbation theories),28 and determinantal expansions (configuration interaction theory). While these methods generally achieve higher accuracy than DFT, the computational effort rises rapidly with the number of electrons involved, so that they are limited to small systems, often too small to be useful in studies of confined systems. One important use of these higher level methods is in the calculation of inter- and intra-molecular force fields, an area where DFT is of limited accuracy.
Another approach which offers high accuracy is Quantum Monte Carlo (QMC),31–34 which avoids some of the limitations of the expansion approaches. In QMC, as in classical MC, stochastic sampling is used to solve the path integrals of quantum mechanics. QMC is capable, in principle, of solving the Schrödinger equation exactly, with only statistical errors. This method is also computationally demanding, and is at present limited to systems of about 30–40 atoms, but this situation will improve with advances in computational architecture, and QMC is likely to prove useful for studies of confined systems in the near to mid term.
In addition to these higher level methods, more approximate approaches, usually called semi-empirical methods,14,15 exist, and are often useful in describing systems requiring larger length and time scales. These methods rely on a simplification of the many electron problem, e.g. by introducing some experimental information or by only considering the valence electrons explicitly, with the core electrons treated by reducing the nuclear charge or by modeling the combined repulsion due to the core electrons and nuclei. A minimum basis set is usually used for the valence electrons. Such calculations run much faster than full ab initio ones, and make it possible to study much larger systems consisting of large segments of pores with adsorbed phases,35 and large molecules such as polymers and biological molecules. Examples of such semi-empirical methods include tight-binding,36 which relies on the use of the superposition of wave functions for isolated atoms on each atomic site, MNDO (Modified Neglect of Differential Overlap)37 and INDO/S (Intermediate Neglect of Differential Overlap/Screened approximation).38 These latter two methods restrict the treatment to the valence electrons. Which of these methods is most appropriate depends on the application and the level of accuracy desired.
2.2 Atomistic theories: classical density functional theory
Classical density functional theory (C-DFT) was first introduced by Ebner et al. in 1976¶,39–41 a little more than a decade after the formulation of the Kohn–Sham21 quantum mechanical density functional theory. Whereas the latter is used to determine the ground state properties of electronic systems, C-DFT provides a route to determine the equilibrium properties of inhomogeneous fluids, including free energies, density profiles and phase diagrams of confined systems. Here we introduce the C-DFT formalism and discuss recent advances in the methodology that have increased its applicability to studying fluid behavior in highly complex, confined systems.
Confined phases are often best treated as open systems, free to exchange molecules and energy with a bulk phase. The grand canonical ensemble, with chemical potential, μ, volume, V and temperature, T as the independent variables, is then the appropriate one, and these variables define the thermodynamic state of the system. At equilibrium the chemical potential and temperature are uniform throughout both the bulk and confined phases. The thermodynamic potential, or free energy, for these variables is the grand potential, Ω = A − G, where A and G are the Helmholtz and Gibbs free energies, respectively; it is this function that must be a minimum for the equilibrium state for the given values of μ, V and T. For a uniform, bulk fluid Ω = −PV, where P is the pressure.
We assume a system of spherical molecules, for simplicity of notation||.42–45 In C-DFT a grand potential functional, Ω[ρ′(rN)], and a Helmholtz energy functional, A[ρ′(rN)], are introduced that are functionals of the N-body probability density distribution function ρ′(rN), where rN ≡ r1,r2,r3,…rN are the positions of the N molecules, and are given by:
| | Ω[ρ′(rN)] = ∫drNρ′(rN)[![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) + Vext(rN) − μN + kBT lnρ′(rN)] + Vext(rN) − μN + kBT lnρ′(rN)] | (3) |
and
| | A[ρ′(rN)] = ∫drNρ′(rN)[![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) + kBT lnρ′(rN)] + kBT lnρ′(rN)] | (4) |
where
kB is Boltzmann's constant,
N is the average number of molecules,
Vext(
rN) is an external potential field that arises from the confining geometry and
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
is the intermolecular potential energy of interaction of the molecules, both of which depend on the positions of all the molecules. The
N-body external potential
Vext is just a sum of one body external potentials,
vext(
ri), acting on molecules 1,2,…
i,…. In
eqn (3) and (4)ρ′(
rN) is, in general, not the equilibrium probability density, but a probability density that obeys the same normalization condition as the equilibrium one. It is now possible to prove two theorems
41 that parallel those of
ab initio DFT: (1) at thermodynamic equilibrium, when the probability density becomes
ρ′(
rN) =
ρ(
rN),
Ω[
ρ′(
rN)] =
Ω[
ρ(
rN)] =
Ω, the thermodynamic grand potential, and
A[
ρ′(
rN)] =
A[
ρ(
rN)] =
Ai ≡
A − ∫d
rf(
r)
vext(
r), where
f(
r) is the one body distribution function.
Ai is the
intrinsic Helmholtz energy,
i.e. the Helmholtz energy minus the
explicit external potential term given by the integral; and (2)
Ω[
ρ(
rN)] =
Ω is the minimum of
Ω[
ρ′(
rN)] while
A[
ρ(
rN)] =
Ai is the minimum of
A[
ρ′(
rN)]. The second theorem follows from the Gibbs inequality.
In the above Ω and A are functionals of the full N-body probability density, ρ′(rN). It is possible to prove41 that a given one-body external potential, vext(ri), gives rise to a unique one-body density profile, ρ(r), and to a corresponding unique N-body probability density, ρ(rN); the proof follows from the uniqueness theorem of statistical mechanics.46,47 It follows that Ω[ρ′] and A[ρ′] can be taken as functionals of the one body density profile, ρ′(r), in what follows.
From eqn (3) and (4) and the above discussion we can write Ω[ρ′] as
| | | Ω[ρ′] = A[ρ′] + ∫drρ′(r)[vext(r) − μ] | (5) |
Since
Ω[
ρ′] must be a minimum at equilibrium we can determine the equilibrium density profile,
ρ(
r), using the variational principle,
| | 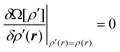 | (6) |
with the differentiation carried out at constant (
μ,V,T) and fixed
vext(
r).
The above equations provide a formal starting point for a density functional theory. We now consider a fluid system with attractive forces, with the intrinsic Helmholtz energy functional approximation as a perturbation about a hard sphere reference system,
| | | A[ρ(r)] = Aidhs[ρ(r)] + Aexhs[ρ(r)] + Aatt[ρ(r)] | (7) |
where
Aidhs[
ρ(
r)] and
Aexhs[
ρ(
r)] are the ideal and excess functionals for the hard sphere system, respectively, and
Aatt[
ρ(
r)] is the Helmholtz energy functional for the attractive portion of the potential. If it is assumed that the attractive portion of the potential can be written as a sum of effective pair-wise potentials,
ϕatt(|
r −
r′|), then
| | | Aatt[ρ(r)] = ½∫∫drdr′ρ(2)(r, r′)ϕatt(|r − r′|), | (8) |
where
ρ(2)(
r,
r′) is the pair distribution function.
Eqn (8) can be simplified in the
mean-field approximation (
i.e.,
ρ(2)(
r,
r′) ≈
ρ(
r)
ρ(
r′)), if correlations can be neglected in the calculation of
Aatt. In many implementations, the attractive potential is evaluated using the Weeks–Chandler–Andersen form of the Lennard-Jones potential.
48
The ideal part of the hard sphere reference system is known exactly and is only a functional of the local density (the density at r),
| | | Aidhs[ρ(r)] = kBT∫drρ(r)[ln(Λ3ρ(r)) − 1] | (9) |
where Λ is the de Broglie wavelength. The excess part is written for a uniform hard sphere fluid:
| | Aexhs[ρ(r)] = kBT∫drρ(r)fexhs[![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r)], (r)], | (10) |
where
fexhs is the excess Helmholtz free energy per molecule, which is determined using a suitable equation of state for hard-spheres, and
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif)
(
r) is a smoothed or weighted average of the density,
| | ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r) = ∫dr′ρ(r′)w[|r − r′|], (r) = ∫dr′ρ(r′)w[|r − r′|], | (11) |
with weighting function,
w. The density profile can then be determined from
eqn (6).
The choice of the weighting function has serious implications in the accuracy of the C-DFT. In the earliest implementations of C-DFT, a local density approximation (i.e. ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r) ≈ ρ(r), the local fluid density at point r) was used. The local version of C-DFT is useful for studies of fluid–fluid interfaces, including liquid crystal phases and surfactant solutions, although it predicts fluid densities that are, in general, too low. More seriously, the local theory fails for highly inhomogeneous fluids and solids, particularly crystals and fluids near solid surfaces, where very large density variations occur over atomic scale distances.
(r) ≈ ρ(r), the local fluid density at point r) was used. The local version of C-DFT is useful for studies of fluid–fluid interfaces, including liquid crystal phases and surfactant solutions, although it predicts fluid densities that are, in general, too low. More seriously, the local theory fails for highly inhomogeneous fluids and solids, particularly crystals and fluids near solid surfaces, where very large density variations occur over atomic scale distances.
Tarazona49 introduced a non-local version of the fluid density functional theory, in which weighting functions were developed that were implicit functions of the weighted density. Since then, several other methods have been proposed for the determination of the smoothed density, and these, together with applications of C-DFT, have been the subjects of reviews**.50,51 The most powerful of these theories is that due to Rosenfeld,52,53 which provides a more accurate description than Tarazona's version in highly confined systems and is readily extended to mixtures.
The non-local version of the C-DFT gives a complete thermodynamic description of both bulk and confined fluids. Due to its high degree of accuracy, ease of implementation and computational efficiency, it has been used extensively to study adsorption phenomena of porous systems with simple geometries such as atomically-smooth slit, cylindrical and spherically shaped pores, which have two-dimensional symmetry, reducing the necessary integration to only one-dimension. For many real porous systems, including nearly all microporous systems, the molecular roughness of the pore walls has significant effects on the behavior of confined fluids.54,55 The reduced symmetry of these systems often makes the integration of the C-DFT equations computationally intractable.
To include the effects of surface roughness, Ravikovitch and Neimark56 have recently proposed a modified version of C-DFT using Rosenfeld's weighting functionals for mixtures, known as quenched solid non-local density functional theory (QS-NLDFT). Instead of treating the fluid–solid interactions through an external potential, the confining solid is modeled as a second component that is quenched (i.e., its density profile is held constant). Thus, the external potential component in eqn (5) is removed, and the grand potential and intrinsic Helmholtz potential become functionals of both the fluid and solid densities, ρf(r) and ρs(r), respectively:
| | | Ω[ρf(r);ρs(r)] = A[ρf(r);ρs(r)] − μf∫drρf(r) − μs∫drρs(r). | (12) |
Since the solid density profile is constant, minimization of the grand potential is only carried out with respect to the fluid density and the normal methods for obtaining the fluid density remain applicable. The QS-NLDFT formalism allows for an arbitrary one-dimensional, piece-wise continuous solid density profile to be assumed for the pore wall. Atomically smooth pore walls can be simply modeled with a uniform solid density profile outside the regions of the pore, while effective wall roughness is introduced by choosing a non-uniform profile.
A second major development towards a more flexible density functional theory was prompted by the recent observation that the thermodynamics of continuum fluids can be quantitatively captured by molecules restricted to lattice sites if the ratio of the adsorbate molecule's diameter to lattice spacing is sufficiently large, while realizing significant computational savings.57 Lattice versions of C-DFT-like theories had been previously developed and applied to confined systems.58,59 However, they required that the lattice spacing be at least as large as the diameter of the confined fluid molecule, coarse-graining the system and imposing a translational order that is not well suited to describe fluid-like phases. As a result, these approaches are useful for studying only qualitative behavior. Siderius and Gelb60 developed a lattice version of C-DFT, in which the lattice spacing can be arbitrarily discretized with respect to the characteristic molecular dimensions. In the spirit of the original continuum C-DFT, they derived an expression for the grand potential of a lattice system with N molecules on M sites,
| | 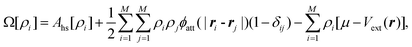 | (13) |
constrained such that
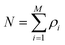
, replacing the integration in
eqn (5) with the sum over the lattice sites. Following Tarazona's approach, they also developed non-local weighting and free energy functionals for the reference hard sphere fluid, which were parameterized with the use of lattice Monte Carlo simulations. Full details of their method may be found in the supporting information of
ref. 60. The computational savings due to the discretization enables the lattice C-DFT to be used in systems with low dimensional symmetry and can be applied to study fluid behavior in three-dimensional porous structures.
2.3 Atomistic simulation methods: Monte Carlo and molecular dynamics
In atomistic simulations the equations of statistical mechanics are solved numerically for the model system of interest. Provided that a large enough sample of the system is used, and the simulation run is long enough, this should result in an essentially exact solution for the model system with only statistical errors. Here the ‘model’ would usually include the equations used for the intermolecular forces and any simplification in representing the pore walls (e.g. atomically detailed walls, but with atoms fixed in space, or smooth, structureless walls, etc.). A straightforward approach to solving the equations of statistical mechanics would be to evaluate the N-body integrals that appear in the classical partition function; these depend on all of the configurational degrees of freedom of the particles in the system (i.e., center of mass positions, orientations, and internal bond angles, etc.). In principle, these integrals may be evaluated exactly by enumerating every possible configuration of the system, calculating the ensemble weights of the configurations from the configurational energies, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) , and then computing the desired thermodynamic properties by taking ensemble-weighted averages. For systems with realistic complexity, the number of unique configurations is nearly innumerable and this direct approach is well beyond computational capabilities of even the fastest massively parallel supercomputers for the foreseeable future.
, and then computing the desired thermodynamic properties by taking ensemble-weighted averages. For systems with realistic complexity, the number of unique configurations is nearly innumerable and this direct approach is well beyond computational capabilities of even the fastest massively parallel supercomputers for the foreseeable future.
However, two approaches exist that provide highly accurate estimates (often with uncertainties comparable to experiment) of the thermodynamic and transport properties for complex systems within a matter of hours or days on modern computers. These are the Monte Carlo (MC) and the molecular dynamics (MD) methods. The MC method is a stochastic simulation technique that uses importance sampling to explore configurational phase space, in which particle configurations are generated with a probability proportional to their weight in the desired statistical ensemble. Thus, states with higher ensemble weights (lower configurational energies) that contribute significantly to the average thermodynamic quantities are sampled most frequently. The MD method is a deterministic technique that integrates Newton's equations of motion for the system of particles, allowing the system to explore a natural dynamic trajectory. The thermodynamic properties calculated from MC and MD methods should be equivalent provided that large enough samples of the system and long enough simulation times are used. In MD the fraction of time spent for sampling states with a given configurational energy is proportional to its weight in the ensemble, and thus the MD method reproduces the same ensemble averages as the MC method. In practice, the MC method is often more computationally efficient for sampling thermodynamic properties, since the motions of the particles are not restricted by physical timescales. However, if both thermodynamic and dynamic properties are of interest, then MD is the method of choice. In the following sections, we describe the foundations of these methods, limiting our discussion to basic overviews of the methods and advances that have made them particularly well suited for studying confined systems. For a more comprehensive discussion on MC and MD as well as details of their implementation, we refer readers to ref. 61 and 62.
2.3.1 Monte Carlo methods.
The idea of numerically estimating sums or integrals by sampling the integrand has a long history in mathematics and science,63 and these methods were earlier known as statistical sampling methods. Such methods were used by Lord Kelvin in 190164 to verify the equipartition of energy, using as human calculator his long suffering assistant, William Anderson, who carried out 5000 trajectory calculations by hand.64 Statistical sampling was also used in the 1930s in Rome by Enrico Fermi to calculate the properties of the newly discovered neutron, using a mechanical calculating device.65 The name Monte Carlo was coined by Nicholas Metropolis in the mid-1940s. In statistical mechanics Monte Carlo is generally used now to refer to the importance sampling method developed and published in 1953 by Nicholas Metropolis and co-workers working at the Los Alamos National Laboratory, who provided a clear account of the method in their seminal paper.66 Since then, the MC method has gained widespread use, largely due to its ease of implementation and ability to be easily generalized to different ensembles without approximation. However, the method is most naturally defined in the canonical or NVT ensemble, where the number of particles, N, the volume of the system, V, and the temperature, T, are held constant.
In the Metropolis–Hastings version of the algorithm, the configurational phase space described by the coordinates of the N particle system is sampled by randomly selecting particles and attempting to change one of their coordinates by a random amount. Consider the system of interest with some initial molecular configuration m, with particles (atoms or molecules) having coordinates (x1,x2,x3,…xN)m ≡ (xN)m for short, with potential energy of interaction ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)m. Here xi represents the set of coordinates needed to specify the position, orientation and conformation of molecule i; for a spherical molecule, such as argon, these would just be the 3 Cartesian coordinates for the center of mass, but for a larger molecule such as n-hexane there would be additional coordinates needed to define the orientation of the equilibrium conformer relative to space-fixed axes and additional coordinates to define the intramolecular structure of the molecule. We now choose a molecule at random and move or rotate it a random amount to produce a new configuration, n, with coordinates (x1,x2,x3,…xN)n ≡ (xN)n with potential energy
(xN)m. Here xi represents the set of coordinates needed to specify the position, orientation and conformation of molecule i; for a spherical molecule, such as argon, these would just be the 3 Cartesian coordinates for the center of mass, but for a larger molecule such as n-hexane there would be additional coordinates needed to define the orientation of the equilibrium conformer relative to space-fixed axes and additional coordinates to define the intramolecular structure of the molecule. We now choose a molecule at random and move or rotate it a random amount to produce a new configuration, n, with coordinates (x1,x2,x3,…xN)n ≡ (xN)n with potential energy ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)n. The change in potential energy of interaction due to the move is Δ
(xN)n. The change in potential energy of interaction due to the move is Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) =
= ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)n −
(xN)n − ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)m. The condition of detailed balance states that at equilibrium the rate of change from configuration m to n must equal the rate for the reverse change, from configuration n to m. This condition is necessary for thermodynamic equilibrium to be maintained once it is reached. The rate of change from m to n is proportional to the probability that the system is initially in state m, ρm, multiplied by the probability of acceptance of the change, pmn(m → n); similarly, the rate of the reverse change from n to m is proportional to ρn, the probability of observing the system in state n multiplied by the probability of acceptance of the change, pnm(n → m), i.e. ρmpmn(m → n) = ρnpnm(n → m) or
(xN)m. The condition of detailed balance states that at equilibrium the rate of change from configuration m to n must equal the rate for the reverse change, from configuration n to m. This condition is necessary for thermodynamic equilibrium to be maintained once it is reached. The rate of change from m to n is proportional to the probability that the system is initially in state m, ρm, multiplied by the probability of acceptance of the change, pmn(m → n); similarly, the rate of the reverse change from n to m is proportional to ρn, the probability of observing the system in state n multiplied by the probability of acceptance of the change, pnm(n → m), i.e. ρmpmn(m → n) = ρnpnm(n → m) or
| | 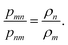 | (14) |
Eqn (14) is the
detailed balance condition. It is the essential equation on which the Monte Carlo method rests. In MC, the algorithm must be designed to obey detailed balance. We note that
eqn (14) holds for any set of independent variables,
i.e. any permitted move in any ensemble. For example it holds for particle insertion attempts using the grand canonical variables (
μ,
V,
T), or for volume change moves with the isobaric–isothermal (
N,
P,
T) variables. In these cases it is only necessary to use the appropriate expression for the probability distribution
ρi on the right side of
eqn (14). The derivation of detailed balance given above is heuristic in nature. Nevertheless, the result is intuitively reasonable; we expect the probability of a change from configuration
m to configuration
n to directly depend on the probability of state
n. More rigorous derivations based on the theory of stochastic processes are given in the standard texts.
61,62
If the canonical variables (N,V,T) are used the probability density is the familiar Boltzmann distribution law,
| | 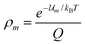 | (15) |
where
Q = ∑
ie−![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) i/kBT
i/kBT is the canonical partition function. Thus if we choose the canonical set of independent variables
eqn (14) gives
| | 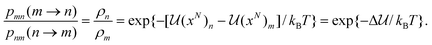 | (16) |
The algorithm proposed by Metropolis
et al.66 is designed to satisfy detailed balance, as given by
eqn (16) and consists of the following steps. Each time a particle move is attempted, the change in configurational interaction energy in going from configuration
m to
n, Δ
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
, is calculated. If the energy change is negative,
i.e. the energy is more attractive as a result of the move, the attempted move is accepted, while if it is positive,
i.e. less attractive, the move is accepted with a probability
Pacc= e−Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) /kBT
/kBT. These two cases can be summarized by the acceptance probability:
| | Pacc = min(1,e−Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) /kBT) /kBT) | (17) |
It is readily verified, by substitution in
eqn (16) for these two cases, that this algorithm obeys detailed balance. This procedure is repeated millions of times to generate an adequate sampling of configurational phase space. If performed correctly, the canonical or Boltzmann distribution is sampled and equilibrium properties of the system can be calculated by simply averaging over the configurations, without the need for re-weighting as would be necessary if the configurations were sampled uniformly.
While the various ensembles in statistical mechanics yield equivalent thermodynamic properties, judicious choice of the ensemble can often make the problem at hand much easier and faster to solve and can provide a more direct route for comparison with experiment. For example, in grand canonical ensemble Monte Carlo67,68 (GCEMC), the independent variables are (μ,V,T), and phase space is sampled by fixing the chemical potential, μ, as well as temperature and volume, allowing the number of particles to fluctuate. This has the physical interpretation of simulating the equilibrium reached between a fictitious reservoir containing a bulk phase and the simulated system, and it is a particularly useful ensemble for studying adsorption phenomena in model materials, and interfacial properties in general. As for the canonical ensemble discussed above, particle moves are made to equilibrate the system, but in addition, particle insertion and deletion attempts must be made to bring the system to chemical equilibrium with the reservoir. The acceptance criterion for accepting or rejecting these insertion attempts is obtained by substituting the grand canonical probability distribution for ρn and ρm in eqn (14). This gives
| | 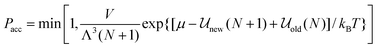 | (18) |
where Λ is the de Broglie wavelength,
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) new
new is the configurational energy of interaction after the insertion, so that the system now contains N + 1 molecules, and
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) old
old is the energy of the original
N particle system. Similarly the criterion for particle deletion is:
| | 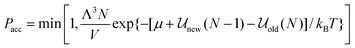 | (19) |
Simulation in the isothermal–isobaric (N,P,T) ensemble69,70 is often useful for determining an appropriate equation of state for pure component or fluid mixtures, where the pressure is fixed instead of the volume by performing changes in the volume of the simulation cell. Again, the acceptance criterion for the volume change trials is obtained from eqn (14) using the probability distribution expression for the (N,P,T) ensemble. The chemical potential can be readily calculated in this ensemble for fluid phases,71 providing a direct relationship between the pressure and chemical potential. For complex phase equilibria problems, it is often advantageous to simulate all of the different phases explicitly. In Gibbs ensemble Monte Carlo72 (GEMC), each phase is simulated in a different simulation cell at the same temperature. Chemical equilibrium is maintained by exchanging particles between cells, while the volumes of the individual simulation cells are allowed to fluctuate, such that either the total volume of all the simulation cells or the pressure may be held constant. By simulating all of the phases explicitly, the number of calculations necessary to obtain equilibrium properties, such as adsorption isotherms, may be greatly reduced.
In addition to the most commonly used ensembles described above, specialized ensembles and Monte Carlo techniques have been developed to study specific phenomena, such as mixtures with large size differences between solvent and solute73 (e.g. colloidal particles, protein molecules, or micelles in aqueous solution) or calculations of free energies and phase coexistence. Reaction ensemble Monte Carlo (RxMC)74,75 can be used to study simultaneous phase and reaction equilibria by adding reactive MC moves into the aforementioned ensembles. In these moves reactant molecules are removed from the simulation cell while the product molecules are simultaneously inserted such that the stoichiometry of the reaction is preserved. Product molecules are usually inserted in vacancies formed by removal of reactant molecules, where possible. The Metropolis acceptance criteria for such a reaction move are:
| | 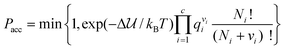 | (20) |
where Δ
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
is the change in the intermolecular potential energy due to the reaction move,
c is the total number of species in the reaction,
qi is the molecular (ideal gas reference state) partition function for species
i, and
Ni and
νi are the number of molecules and the stoichiometric coefficient of species
i. These reaction ensemble methods determine the composition at chemical equilibrium and they have been widely used to study the effects of confinement in pores on reaction equilibria, and can be used to study effects of other reaction environments, such as reactions in liquid or supercritical
solvents, in reverse micelles, in nanocomposites,
etc. For a recent review of the method and its applications see
ref. 76.
Advantages of MC over MD are that it is straightforward to carry out calculations using different sets of independent variables—(N,V,T), (N,P,T), (μ,V,T), etc.—since the probability densities are well known for each of these ensembles, and we only need to substitute for these in the detailed balance equation (eqn (14)). Since the particle and other moves are artificial rather than natural, it is possible to apply various special techniques to speed up equilibration, making it possible to study phenomena that take too long to observe in MD at present. Disadvantages of MC relative to MD are that only equilibrium properties, not dynamic properties, can be obtained in MC, and MC codes are more difficult to efficiently parallelize than MD.
2.3.2 Molecular dynamics methods.
Unlike the MC method, in which the movement of the particles is stochastic, particles in MD follow well-defined dynamic trajectories according to Newton's Second Law, F = ma. The MD method was developed in the 1950s by Berni Alder and Tom Wainwright at the Lawrence Radiation Laboratory at Livermore (now Lawrence Livermore National Laboratory). In its initial 1957 implementation,77 the method was used to examine the phase behavior of hard sphere systems. Several years later, Aneesur Rahman at Argonne National Laboratory, extended the method to realistic fluids with continuous intermolecular potentials.78 The equations of motion for the N particle system are solved using finite difference methods79 by calculating the total force acting on each particle,| | 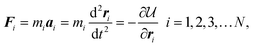 | (21) |
where mi, ai, and ri are the mass, acceleration and position vector of the ith particle, respectively. The basic MD method conserves the total energy of the system, E, and is therefore naturally performed in the microcanonical (N,V,E) ensemble.
The Verlet algorithm79 for solving eqn (21) is still widely used, and we outline this method here. Initial positions and configurations are assigned to each molecule, and initial velocities are assigned according to a Maxwell–Boltzmann distribution. For small molecules the simulation is usually started with the molecules on lattice sites, to avoid molecular overlap and initial configurations of very high energy. For larger molecules an energy minimization routine is usually applied to determine suitable initial conformations. Knowing the position of the molecule or atom i at time t, the position at some later time t + δt is estimated from a Taylor series expansion about the initial position:
| | 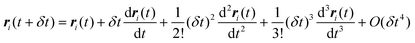 | (22) |
Similarly, the position of molecule
i at some earlier time
t −
δt is given by
| | 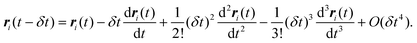 | (23) |
Adding
eqn (22) and (23) gives:
| | 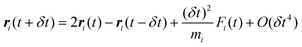 | (24) |
where
eqn (21) has been used to simplify the second order term.
Eqn (24) provides a means to calculate the position at time
t +
δt knowing only the position at
t and
t −
δt, together with the total force, which can be determined from a given force field. The velocity of molecule
i can be determined by subtracting
eqn (23) from
(22):
| | 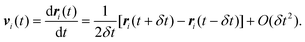 | (25) |
Various modifications of the above algorithm have been proposed.
61,62 The best choice usually depends on the energy conservation needed, computational cost and the time step. The time step
δt must be small enough to obtain rapid convergence in the above series, so that energy is conserved during the run. A rule of thumb is that the energy should remain constant within 0.01% over the course of the run. For flexible molecules, where the vibrations are rapid, this typically requires a time step of about 1 femtosecond (10
−15 s). Thus to observe one microsecond (10
−6 s) of real time, 10
9 time steps are needed. This is feasible on current supercomputers.
Although MD simulations may be performed in other ensembles, extreme care must be taken in implementing these methods to ensure that the correct dynamics are preserved. For example, to perform simulations in the canonical ensemble, the temperature must be held constant instead of the total energy. The Andersen thermostat80 has been widely used to control the temperature in MD. It maintains the temperature by mimicking the effect of a heat bath surrounding the simulation cell, in which energy is exchanged between the cell and heat bath through intermolecular collisions. In the Andersen thermostat, the collisions with particles from the heat bath are modeled as random stochastic forces acting on the simulated particles. Although this method maintains the correct equilibrium distribution, and hence gives the equilibrium properties correctly, the introduction of stochastic forces violates Newton's Third Law and thus the total momentum of the simulated system is not conserved and the method does not produce the correct dynamical trajectories and dynamical properties. The Nosé–Hoover thermostat81,82 controls the temperature using modified equations of motion to introduce a feedback force which adjusts the kinetic energy of the system to achieve the desired temperature. Although there is some additional computational overhead in comparison with the Andersen thermostat, the perturbations to the system are continuous and result in deterministic trajectories which lead to the correct canonical distribution at equilibrium. It is also possible to run MD simulations at constant pressure by coupling the system to a barostat, or at fixed chemical potential by coupling the system to a particle bath (chemostat), but these methods suffer from similar problems to those of thermostats. The difficulty in implementing MD in different ensembles is a limitation of the method, although in principle it can be overcome by simulating very large systems, taking advantage of parallel computational architectures and the equivalence of the statistical ensembles in the thermodynamic limit. If dynamical properties are of primary interest it is often best to equilibrate the system with a thermostat, barostat or chemostat, and then follow this by a microcanonical simulation to calculate the properties.
The most common boundary conditions in MC and MD are periodic and are used to simulate systems with three full dimensions of translational symmetry and reduce spurious boundary effects. In non-equilibrium molecular dynamics (NEMD), the boundary conditions may be carefully chosen to study steady-state and transient phenomena. For the study of steady-state diffusion in confined systems, dual control-volume grand canonical molecular dynamics83 (DCV-GCEMD) may be used to impose chemical potential gradients across a MD simulation cell by conducting GCEMC simulations in reservoir cells attached to opposing ends of the main MD simulation cell. The dual control volume method has also been extended to include RxMC moves in the reservoirs to study simultaneous adsorption, diffusion, and reaction.84 Rheological properties of fluids, such as viscosity, may be examined by using moving hard-wall boundary conditions to impose different strain rates on confined fluids.85
3. Applications
Atomistic theories and simulation methods have been used extensively to study confinement effects on a wide variety of equilibrium and transient phenomena. Thermodynamic properties such as freezing behavior, adsorption, differential enthalpies of adsorption, free energies, chemical reaction equilibria and other types of phase equilibria can be obtained from atomistic level methods, such as Monte Carlo simulations and classical density functional theory. Molecular dynamics methods have been used to study diffusive behavior in porous materials under both equilibrium and non-equilibrium conditions, simultaneous diffusion and reaction, and the dynamics of capillary condensation and nucleation phenomena. The electronic scale methods are well suited for studying the effect of confinement on reaction pathways and rates, and electrical and electronic properties; they have also been used to study properties such as adsorption in porous materials in circumstances where appropriate classical intermolecular potentials may be unavailable. Indeed, the applications of these methods are widespread and cover a vast array of topics—many more than we shall attempt to cover here. In the following sections we provide representative examples of these methods in action applied to studying confined systems. We first examine adsorption and phase equilibrium properties, for which the primary tools are the MC and C-DFT methods. Next, we discuss the application of molecular dynamics simulation to study diffusion, transport, and rheological properties of confined fluids. Finally, we describe applications of the methods to examine confinement effects on chemical reaction equilibrium and dynamics, with focus on the electronic level methods (ab initio DFT). Our examples are undoubtedly biased (and limited) by our expertise and knowledge. As such, we have made our best efforts to provide only a few examples of research in these areas that are of historical importance and representative of the ability of the methods or recent advances that are paving the way for improved understanding.
3.1 Adsorption and equilibrium properties
3.1.1 Test of the Kelvin equation.
Although atomistic simulation methods are becoming more and more accessible to novice users though a multitude of user-friendly simulation software packages, their implementation is still somewhat time-consuming, and there remains a need for simple and accurate theories that can be more readily applied. Providing these tools unavoidably requires making various levels of approximations to keep the theories simple and tractable. Since molecular simulation provides essentially exact solutions to the proposed models, it plays a central role in testing the scope of applicability of more approximate methods. Such tests avoid the ambiguity associated with direct comparisons with experiment, where the intermolecular force field and other aspects of the model (e.g. assumptions about the nature of the pore walls) are being tested in addition to approximations in the theory itself.
A notable example is the well-documented limitations of the Kelvin equation and its modified forms in systems with small mesopores and micropores. The Kelvin equation, named after its originator Lord Kelvin2 (William Thomson), relates the capillary condensation pressure, Pc, to the saturation pressure of the bulk fluid, P0, and the pore width, H,
| | 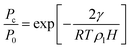 | (26) |
where
γ is the gas–liquid surface tension,
R is the gas constant and
ρl is the liquid density.
Eqn (26) is the Kelvin equation for a slit shaped pore and is strictly valid in the thermodynamic limit (
N,
V → ∞,
N/
V = constant). However, for gas–liquid interfaces that are highly curved, as in narrow pores, the equation must break down because (a) the surface tension and liquid density will deviate from their bulk values due to surface curvature, and (b) the concept of an interface breaks down, so that surface tension no longer has meaning.
45,86 Although the breakdown of the Kelvin equation for small mesopores can be observed in experiments,
87,88 the curvature at which these effects become significant is difficult to determine experimentally due to the difficulty of measuring surface tension and liquid density in pores. Molecular simulation is more suited to such tests.
Surface tension arises because molecules in the surface layer experience stronger attractive forces on the liquid as opposed to the gas side of the interface. For a convex liquid interface, as in a droplet or in a non-wetting pore, we expect the surface tension to be lower than for the planar interface, γ∞, because there are fewer liquid phase molecules to interact with. By contrast, for a concave liquid surface (e.g. a liquid–gas interface in a pore where the liquid wets the walls) we expect the surface tension to be higher than γ∞. This is borne out by the results of molecular simulations. An example is shown in Fig. 1 for the case of liquid drops, and suggests that deviations will become important for a radius of curvature below 8σ, where σ is the diameter of the fluid molecule. For nitrogen or argon as adsorbates this would correspond to a pore diameter of about 55–60 Å. Fig. 1 also shows that for even smaller radii the concept of an interface, and of surface tension, breaks down, so that for drops below about 2.5–3.0σ in radius the calculated surface tension becomes negative, an unphysical result. That surface tension becomes undefined for very small drops is clear from its statistical mechanical definition, γ = (∂A/∂S)T,N,V, where A = −kBTln Q is the Helmholtz energy, Q is the canonical partition function, Q = ∑ie−Ei/kBT, and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is the surface area. While Q, and hence A, are always well defined however small the system, surface tension is not, since it requires the presence of a well defined interface.
is the surface area. While Q, and hence A, are always well defined however small the system, surface tension is not, since it requires the presence of a well defined interface.
![The variation of reduced surface tension, , with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f1.gif) |
| | Fig. 1 The variation of reduced surface tension, 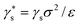 , with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.] , with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.] | |
Other simulation and C-DFT studies have confirmed the failure of eqn (26), and empirical corrections to it, for capillary condensation in pores.89–91Fig. 2 shows the limitation of the Kelvin equation in predicting the pore filling pressure for small carbonaceous pores. The results from these studies suggest that the Kelvin equation breaks down for pores below approximately 8 nm in width, depending on the state conditions and the specific nature of the interactions between adsorbed phases and host material, and that the Kelvin and modified Kelvin equations predict pore sizes that are too small. For a more complete discussion on the accuracy of the Kelvin equation and its modified forms, we refer readers to ref. 92.
![Filling pressures predicted by the Kelvin equation (dotted line), local C-DFT (dashed line) and non-local C-DFT (solid line) at various pore widths for N2 in carbon slit pores. [Adapted from ref. 90.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f2.gif) |
| | Fig. 2 Filling pressures predicted by the Kelvin equation (dotted line), local C-DFT (dashed line) and non-local C-DFT (solid line) at various pore widths for N2 in carbon slit pores. [Adapted from ref. 90.] | |
3.1.2 Determining the pore size distributions of heterogeneous materials.
Historically one of the most widespread uses of the Kelvin equation has been the estimation of the pore size distribution (PSD) of porous materials from adsorption isotherms.92 Due to the limitations of the Kelvin equation in predicting the condensation pressure in small pores, more general methods have been sought over the past several decades. In 1989 Seaton et al.93 proposed the use of a local version of C-DFT to calculate the PSD. In their method, the amount adsorbed, Γ, may be related to the PSD, f(H), of the adsorbent material,| | 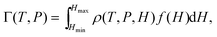 | (27) |
where ρ(T,P,H) is the average density of the adsorbed phase in a pore of width H. To determine the PSD, eqn (27) may be inverted using nonlinear least squares regression methods, specifying the amount adsorbed in the material using the experimentally determined isotherm. The mean density is calculated prior to the inversion using a regularly shaped pore model, such as infinitely long slit or cylindrically shaped pores. A kernel of ρ(T,P,H) values is generated by calculating individual pore isotherms in model pores of different widths, varying between Hmin and Hmax. In principle, any theory may be used to do this as long as it is accurate in describing individual pore isotherms in the desired range of pore widths. In the initial implementation of the method, Seaton et al. used a local version of C-DFT to generate the kernel. Later a more accurate non-local version of C-DFT was implemented independently by Lastoskie et al.90 and Olivier et al.,94 which lead to significantly improved predictions of the local isotherms in small micropores.
While the use of C-DFT with eqn (27) greatly improved estimates of the pore size distribution, especially for microporous materials, there are several limitations of the method that arise from the models used to construct the ρ(T,P,H) distribution and the assumptions made in the formulation of eqn (27). Real porous materials contain pores that have finite lengths and wall thicknesses, and they may also contain interconnected pores with a variety of irregular and regular shapes. These attributes were unaccounted for with the use of the original independent slit pore models and they may have a substantial impact on the quality of the PSDs determined using these methods.
Yin et al.95 demonstrated that changing the density of the pore walls from that of crystalline graphite (i.e., 2.23 g cm−3) had a significant effect on isotherms calculated using GCEMC simulations. It had previously been shown experimentally from X-ray diffraction measurements and transmission electron microscopy imaging that microporous carbons contain highly defective pore walls that are only a few atomic layers thick.96 To take this into account, a C-DFT model of slit-shaped pores with finite wall thickness was first proposed by Ravikovitch et al.97 and later extended by Bhatia98 to include a distribution of wall thicknesses. However, this only led to minor improvements in the estimation of the PSD. In 2006, Ravikovitch and Neimark56 introduced quenched solid non-local density functional theory described in Section 2.2, which allowed for a non-uniform density profile to be used for the solid pore walls, incorporating an effective surface roughness into the slit pore model. This resulted in significant improvements in the PSD estimates for highly heterogeneous materials such as amorphous silica materials56 and microporous carbons,99 reducing artifacts in the PSDs that were seen in previous non-local C-DFT versions, such as false gaps in the pore size distribution that were caused by layering transitions in the local isotherms of the slit pores, as illustrated in Fig. 3. In the real materials, these layering transitions are often suppressed by the highly heterogeneous nature of the pore surface, while they can occur in the simple slit pore models due the presence of smooth walls.
![(a) Comparison of the experimental isotherms (circles) and the fits obtained using non-local C-DFT (solid line) and QS-NLDFT (dashed line) for argon at 87.3 K on CM-E2 microporous carbon synthesized from coconut shell. Both the non-local C-DFT and QS-NLDFT are based on Rosenfeld's52,53 fundamental measure theory. (b) The estimates of the PSD for CM-E2 obtained using non-local C-DFT (circles) and QS-NLDFT (squares). The effect of spurious layering transitions is seen in the non-local C-DFT fit to the experimental isotherm at P/Po ≈ 10−3 (a). The final result is an artificial gap in the PSD at H ≈ 10 Å (b). The QS-NLDFT model corrects this behavior by adding effective surface roughness to the slit pore model. [Adapted from ref. 99.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f3.gif) |
| | Fig. 3 (a) Comparison of the experimental isotherms (circles) and the fits obtained using non-local C-DFT (solid line) and QS-NLDFT (dashed line) for argon at 87.3 K on CM-E2 microporous carbon synthesized from coconut shell. Both the non-local C-DFT and QS-NLDFT are based on Rosenfeld's52,53 fundamental measure theory. (b) The estimates of the PSD for CM-E2 obtained using non-local C-DFT (circles) and QS-NLDFT (squares). The effect of spurious layering transitions is seen in the non-local C-DFT fit to the experimental isotherm at P/Po ≈ 10−3 (a). The final result is an artificial gap in the PSD at H ≈ 10 Å (b). The QS-NLDFT model corrects this behavior by adding effective surface roughness to the slit pore model. [Adapted from ref. 99.] | |
Recently there have also been independent efforts by Jagiello and Olivier100 and Siderius and Gelb60 to develop C-DFT models using pores of finite length. While the finite length slit pores introduce significant edge effects into the density profiles of adsorbed fluids and change the adsorption characteristics of the pore, it is unclear whether such models can be effectively incorporated into methods to determine the PSD due to the variable pore lengths that real materials have. Moreover, it remains to be seen if incorporating such effects will lead to improved estimates of PSDs.
3.1.3 Adsorption and capillary phenomena.
The study of adsorption phenomena in porous materials is one of many common applications of atomistic methods in examining confined systems. If accurate intermolecular potentials are used to describe the adsorbate–adsorbate and adsorbate–solid matrix interactions, GCEMC or GEMC simulations may be used to study adsorption of complex molecules in highly heterogeneous materials. Classical DFT methods, on the other hand, have historically been used to study adsorption of simple molecules (e.g., argon, nitrogen, methane and hydrogen) in slit or cylindrical pore geometries due to the computational limitations in calculating the necessary integrals in three-dimensional systems. While C-DFT and DFT-like theories can be extended to study more complex adsorbates, such as polymeric101,102 and ionic103,104 systems, serious limitations on the adsorbent matrix geometry are imposed by the computational constraints. The lattice C-DFT developed by Siderius and Gelb60 (described in Section 2.2), provides a computationally tractable method for calculating adsorption isotherms in complex materials using C-DFT. In the first application of the lattice C-DFT, they showed that this method produces results comparable in accuracy to GCEMC simulations for hydrogen adsorption on the isoreticular metal–organic framework (MOF) 1, as shown in Fig. 4. The benefit of using the C-DFT to calculate the isotherms is that the full set of thermodynamic properties may be readily obtained and metastable states may be examined. If simulation methods were used to calculate such properties, many additional simulations may be required.
![Theoretical predictions of H2 adsorption on isoreticular MOF-1 at 298 K, using the lattice C-DFT of Siderius and Gelb (solid-line), lattice grand canonical Monte Carlo simulations (diamonds) and off-lattice grand canonical simulations taken from the literature (circles). [Adapted from ref. 60.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f4.gif) |
| | Fig. 4 Theoretical predictions of H2 adsorption on isoreticular MOF-1 at 298 K, using the lattice C-DFT of Siderius and Gelb (solid-line), lattice grand canonical Monte Carlo simulations (diamonds) and off-lattice grand canonical simulations taken from the literature (circles). [Adapted from ref. 60.] | |
Capillary condensation phenomena, such as sorption hysteresis, where experimentally observed adsorption and desorption isotherms do not collapse onto a single equilibrium isotherm, have also been studied extensively using C-DFT and simulation methods.92 The canonical view of sorption hysteresis is that borne out of a discontinuous, first-order, gas–liquid phase transition occurring in porous media. Along the adsorption branch, the adsorbed phase remains metastable in a gas-like phase past the equilibrium pressure Peq (or chemical potential, μeq), because of a barrier in the grand free energy between the metastable and equilibrium states. A similar picture is thought to describe the hysteresis along the desorption branch. Monson and co-workers105–107 showed that this classical view may not be entirely accurate for systems with a realistic degree of morphological disorder in the pore structure. Using a classical, coarse-grained, lattice density functional theory and lattice Monte Carlo simulations, in which fluid and solid atoms each occupy a single lattice site, they showed that in systems with disordered solid matrices, there are multiple paths connecting the adsorption and desorption branches through metastable states. These paths, called scanning curves, are seen upon reversal of the direction of the adsorption or desorption branches in the region of hysteresis as illustrated in Fig. 5, and have been observed experimentally in Vycor glasses.108 For disordered systems of macroscopic size, they hypothesized that the number of such local metastable states may become nearly infinite and that the system may never reach the true equilibrium state. Furthermore, they demonstrated that for their model, thermodynamic consistency is not strictly maintained along the sorption isotherms in the hysteresis region. Thus, in their view, in a real system the classical van der Waals view of metastability may not be valid and hysteresis may signify an out of equilibrium transition whose specific nature is highly system dependent.
![(left) Adsorption and desorption isotherms given as dimensionless fluid density (ρf = number of molecules/number of lattice sites) versus the reduced chemical potential, μ/wff, for wmf/wff = 1.5 and T* = 0.8, where wmf and wff are the matrix–fluid and fluid–fluid lattice interaction parameters, respectively. The adsorption branches of the isotherms are shown (filled circles), along with two scanning curves starting from the adsorption branch (open circles). (right) Location of local minima in the grand potential (crosses) and the equilibrium isotherm (solid line) formed connecting the states of lowest grand potential. The density of the solid matrix was set to 0.25 for the calculations. [Reprinted with permission from ref. 105, Copyright 2001, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f5.gif) |
| | Fig. 5 (left) Adsorption and desorption isotherms given as dimensionless fluid density (ρf = number of molecules/number of lattice sites) versus the reduced chemical potential, μ/wff, for wmf/wff = 1.5 and T* = 0.8, where wmf and wff are the matrix–fluid and fluid–fluid lattice interaction parameters, respectively. The adsorption branches of the isotherms are shown (filled circles), along with two scanning curves starting from the adsorption branch (open circles). (right) Location of local minima in the grand potential (crosses) and the equilibrium isotherm (solid line) formed connecting the states of lowest grand potential. The density of the solid matrix was set to 0.25 for the calculations. [Reprinted with permission from ref. 105, Copyright 2001, American Physical Society.] | |
The impact of adsorbent flexibility on capillary phenomena has also been of recent interest. It is often assumed in both experimental and theoretical investigations that the adsorbent is rigid and does not deform upon sorption of the adsorbate phase. However, a number of simulation and experimental studies have shown that pore width in carbonaceous adsorbents can change on uptake of an adsorbent.109,110 More flexible adsorbents, such as metal–organic framework MIL-53, undergo reversible conformational changes upon adsorption and desorption, resulting in large changes of the pore dimensions.111,112
Günther et al.113 examined the impact of small pore deformations induced during sorption using MC simulations in the semi-grand canonical ensemble,114 where the number of molecules of the flexible solid matrix was held constant, while the number of adsorbate molecules was allowed to fluctuate as in GCEMC simulations. Using an atomically detailed slit-shaped pore, they modeled pore wall flexibility by tethering the atoms on the pore wall surface to fcc lattice sites using a harmonic constraint, with a spring constant, κ. The spring constant was used to control the effective stiffness of the pore wall, with a completely rigid wall in the limit that κ → ∞ and a fluid wall as κ → 0. Fluid–fluid and fluid–wall interactions were modeled using the Lennard-Jones potential, with the same parameters for both the wall and fluid atoms. Using this simple model, they demonstrated that the bulk pressure at which capillary condensation occurs in the pore, P0+, using their nomenclature, may change by several percent depending on the rigidity of the pore wall. Furthermore, they showed that the induced model strain, ξ = H(P)/H(0) − 1, of the pore walls during the sorption process was in semi-quantitative agreement with the experimentally determined lattice strain, ε, measured using in situ X-ray diffraction for C5H12 sorption on mesoporous silica MCM-41, as shown in Fig. 6.
![Sorption strain for cyclopentane, C5H12, as a function of the reduced pressure, where P0+ is the bulk pressure at which condensation occurs. The filled circles are experimental results from in situ X-ray diffraction experiments, while open circles are results of the model with κ = 30ε/σ2 and the solid line is a visual guide. [Reprinted with permission from ref. 113. Copyright 2008, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f6.gif) |
| | Fig. 6 Sorption strain for cyclopentane, C5H12, as a function of the reduced pressure, where P0+ is the bulk pressure at which condensation occurs. The filled circles are experimental results from in situ X-ray diffraction experiments, while open circles are results of the model with κ = 30ε/σ2 and the solid line is a visual guide. [Reprinted with permission from ref. 113. Copyright 2008, American Physical Society.] | |
In both the model and experimental systems, the strain increased with pressure inside the pore filling region, as the fluid molecules collided with the walls, causing swelling of the pore to occur. However, at the condensation pressure, the strain sharply decreased as the pore contracted due to attractive interactions between the fluid and wall molecules, and then it resumed its increasing trend as the pressure continued to increase. Subsequently, Günther et al.115 also examined the behavior of the sorption strain at different thermodynamic states. While the apparent discontinuity in the sorption strain was not observed at temperatures above the pore critical temperature, the general trend illustrated in Fig. 6 appeared to be universal throughout the range of thermodynamic conditions examined. By analyzing the density profiles of the adsorbate molecules confined within the pore, they further argued that the behavior of the strain was highly correlated with the packing of the adsorbate molecules in the porous structure, as opposed to being strictly a state-dependent phenomenon.
3.2 Diffusion and dynamic properties
3.2.1 Self, collective, and transport diffusivities for pure components.
In both experiment and simulation, three diffusivities are of general interest. These are the self-diffusivity (also known as the tracer diffusivity), the collective diffusivity (also known as the corrected or Maxwell–Stefan diffusivity), and the transport diffusivity that appears in Fick's first law. Self-diffusion refers to the diffusion of a single, tagged molecule through a fluid that is in equilibrium. In molecular dynamics, the self-diffusion coefficient, DS, can be obtained from the time integral of the velocity autocorrelation function (VACF),| | 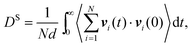 | (28) |
where vi(t) is the center of mass velocity vector of molecule i at time t, N is the number of molecules, and d is the dimensionality of the system under consideration. For the particular case of the self-diffusion coefficient, the familiar Einstein relationship is commonly used,| | 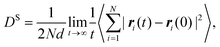 | (29) |
where ri(t) is the center of mass position vector of molecule i and the bracketed term is known as the mean-squared displacement (MSD). Eqn (28) and (29) are equivalent expressions, and either can be used to evaluate the self-diffusivity. Experimentally, the self-diffusivity can be measured by pulsed-field gradient nuclear magnetic resonance (PFG-NMR)5 and quasi-elastic neutron scattering (QENS).116,117
The collective and transport diffusivities refer to the flux of molecules due to concentration gradients in the fluid. For pure components, the flux (J) is related to the transport diffusivity (DT) as:
In
eqn (30),
c is the concentration (molecules per m
3) and
J and
DT have units of molecules m
−2 s
−1 and m
2 s
−1, respectively.
Eqn (30) is Fick's first law of diffusion, first derived by Adolf Fick in 1855
3 and is the commonly used diffusion coefficient in continuum scale modeling.
Collective and transport diffusivities can be measured experimentally through QENS117 or other macroscopic techniques,118 where the concentration gradient (∇c) in eqn (30) is easily imposed. However, in thermodynamics and molecular dynamics simulation the driving force for transport diffusion is more easily interpreted as a chemical potential gradient (∇μ), and eqn (30) can be rewritten as:
| | 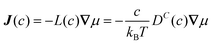 | (31) |
In
eqn (31),
L is referred to as the Onsager transport coefficient and
kBTL/c has the same unit as a diffusion coefficient (m
2 s
−1),
kB is the Boltzmann constant,
T is the temperature, and
DC is the
collective diffusion coefficient.
To link together the transport and collective diffusion coefficients in eqn (30) and (31), a thermodynamic correction factor (Γ) is commonly defined as:
| | 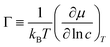 | (32) |
Using
eqn (32), we can now relate the chemical potential gradient to the concentration gradient:
| | 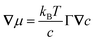 | (33) |
By substituting
eqn (33) into
eqn (31) and equating the right hand side of
eqn (31) with
eqn (30), a relationship between transport and collective diffusion coefficients is obtained:
| | 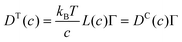 | (34) |
where
Γ is the thermodynamic factor from
eqn (32).
In simulation, collective or transport diffusion coefficients can be measured with either equilibrium molecular dynamics (EMD) or non-equilibrium molecular dynamics (NEMD). In the NEMD approach, the dual control volume grand canonical MD (DCV-GCEMD) method is used to impose a chemical potential gradient across the MD simulation cell.83,119,120 The EMD method is more straight-forward and easier to implement than the NEMD DCV-GCEMD method and relies on techniques previously discussed. In the EMD method, proposed by Maginn et al.,121eqn (32) is rewritten using the definition of fugacity (μ − μo ≡ kBTln(f/fo)):
| | 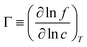 | (35) |
In
eqn (35)f is the fugacity of the bulk fluid in equilibrium with the adsorbed phase and
c is the concentration of the adsorbed phase. The thermodynamic factor in
eqn (35) can be calculated from measurement of the equilibrium adsorption isotherm, generally determined using GCEMC.
Experimentally, eqn (35) is also used to determine the transport diffusivity from the collective diffusivity, although pressure may be substituted for fugacity in the thermodynamic factor, if the bulk phase can be described as an ideal gas. From EMD simulation trajectories, the collective diffusion coefficient in eqn (34) can be measured using:
| | 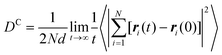 | (36) |
or equivalently in terms of the velocities:
| | 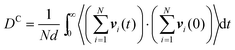 | (37) |
For the calculation of the mean-squared displacement in
eqn (29), the square of the displacement is averaged over all
i molecules, while in
eqn (36) the square is taken of the sum of all of the displacements over all molecules. Thus the collective diffusion coefficient can be thought of as related to the diffusive motion of the center of mass of the particles moving through a material.
122 While statistically accurate measurements of the self-diffusion coefficient can often be obtained from a single simulation, the measurement of the collective diffusivity is more difficult. Usually measurements must be obtained over multiple (often 20 or more) independent MD simulations.
122
Comparing diffusion coefficients between simulation and experiment can often be difficult, and quantitative comparison is even more difficult to obtain. However, several researchers123–125 have shown that in many cases for zeolites the comparisons can be drastically improved by removing the often used Darken assumption126 from the experimental data. The Darken assumption states that the collective diffusivity is independent of concentration. However, it has been pointed out124,127 that Darken actually explicitly stated that the collective diffusion coefficient was not independent of concentration.126 Beerdsen and Smit124 and Chong et al.125 have shown that if careful consideration of the loading dependence of the experimentally determined diffusivities is made, good agreement between simulation and experiment can be obtained for the self-, collective- and transport diffusivities, as shown in Fig. 7. Fig. 7(a) shows the self-diffusivity of methane in MFI-type silicate compared between several simulation studies and several experimental studies which used different methods (QENS, PFG-NMR, membrane permeation). Fig. 7(b) shows good agreement between simulation and QENS experiments for the collective and transport diffusion of ethane in silicate. As shown in Fig. 7(b) in the limit of zero loading, the self-, corrected-, and transport-diffusion coefficients become equivalent,127 but quite pronounced differences exist at higher loading. Thus, the self-, collective-, and transport diffusivities are not generally independent of concentration. The transport and collective diffusivities are almost always greater than the self-diffusivities due to the collective diffusivities having interparticle correlations which have a positive contribution.127 However, Kärger and co-workers128 have recently reported experimentally that methanol and ethanol in MOF ZIF-8 exhibit the opposite effect with their self-diffusivities greater than the collective and transport diffusivities due to strong fluid–solid electrostatic effects.
![The three different types of diffusivities compared between simulation and experiment. In (a) the self-diffusivity of methane in MFI-type silicate as a function of adsorbate loading is shown. Simulation results (closed symbols) are compared from various researchers: Beerdsen and Smit124 (circles), Goodbody et al.129 (squares), Nicholas et al.130 (triangles), June et al.131 (downward triangles). Experimental results (open symbols) using various techniques are also shown: Caro et al.132 using PFG-NMR (circles), Jobic et al. using PFG-NMR (squares) and QENS (triangles)133 and Kapteijn et al.118 using membrane permeation experiments (downward triangles). [Adapted from ref. 124.] All data are at 300 K except for the experimental results of Jobic et al.133 (PFG-NMR and QENS) which are at 250 K. In (b) the self-,collective-, and transport-diffusivities of ethane in silicate are shown at room temperature. Simulation data (closed symbols) are shown for all three, but experimental (open symbols) (QENS) comparison is also shown for the collective and transport diffusivities. The authors did not report experimental data for the self-diffusivity. [Adapted from ref. 125.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f7.gif) |
| | Fig. 7 The three different types of diffusivities compared between simulation and experiment. In (a) the self-diffusivity of methane in MFI-type silicate as a function of adsorbate loading is shown. Simulation results (closed symbols) are compared from various researchers: Beerdsen and Smit124 (circles), Goodbody et al.129 (squares), Nicholas et al.130 (triangles), June et al.131 (downward triangles). Experimental results (open symbols) using various techniques are also shown: Caro et al.132 using PFG-NMR (circles), Jobic et al. using PFG-NMR (squares) and QENS (triangles)133 and Kapteijn et al.118 using membrane permeation experiments (downward triangles). [Adapted from ref. 124.] All data are at 300 K except for the experimental results of Jobic et al.133 (PFG-NMR and QENS) which are at 250 K. In (b) the self-,collective-, and transport-diffusivities of ethane in silicate are shown at room temperature. Simulation data (closed symbols) are shown for all three, but experimental (open symbols) (QENS) comparison is also shown for the collective and transport diffusivities. The authors did not report experimental data for the self-diffusivity. [Adapted from ref. 125.] | |
3.2.2
Transport diffusivity in mixtures.
Diffusion can be formulated in several ways, including descriptions known as the Onsager,134,135 Maxwell–Stefan136–138 and Fick3 formulations. Each of these descriptions allows one to write down the flux of molecules in terms of either the chemical potential or concentration gradients. Combining any two of these descriptions allows one to define and calculate transport diffusion coefficients, which can be measured through simulation or experiment. Our description of pure components in Section 3.2.1 is formulated in terms of the Fick and Onsager descriptions. For mixtures, the Fick description combined with the Onsager description leads to what is called the mutual139,140 diffusion coefficient, which has been used to describe bulk liquid mixtures139–142 and has been applied to describe the diffusion of fluids in zeolites,143–146graphite slit pores,147 and other model nanopores.148 Here we give a brief description of the Maxwell–Stefan and Onsager formulations, which have been used by Krishna and coworkers149–152 to study the diffusion of multicomponent mixtures in confinement. For other formulations, we refer readers to several excellent reviews127,138,153,154 and other literature155–157 which give more detailed descriptions.
In the Onsager formulation, the flux of component i, Ji, is written in terms of the chemical potential gradient of component i, ∇μi, as:
| | 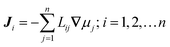 | (38) |
In
eqn (38),
Lij are known as the Onsager transport coefficients, and
n is the number of components in the mixture. Onsager
134,135 showed that
Lij have a reciprocal relationship,
Lij = Lji. The Onsager transport coefficients can be calculated using linear response theory,
155 as applied to transport processes by Mori:
158| | 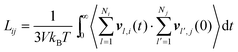 | (39) |
Eqn (39) can be rewritten in the Einstein form in terms of the position vectors:
| | 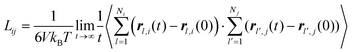 | (40) |
In the Maxwell–Stefan formulation, the relationship between the chemical potential and flux can be written as:
| | 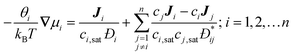 | (41) |
In
eqn (41),
ci is the concentration of component
i in the mixture (number of molecules per unit of accessible volume of adsorbent),
ci,sat is the concentration of component
i at saturation (
i.e., the amount adsorbed per unit of accessible volume of adsorbent at
T and
Po(
T), which can be obtained from the equilibrium adsorption isotherm using GCEMC),
θi = ci/
ci,sat is the fractional occupancy of species
i, defined in relation to its saturation concentration,
Đi, is the Maxwell–Stefan diffusivity of component
i (which includes the effects of interactions between component
i and the adsorbent), and
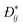
are known as the Maxwell–Stefan exchange coefficients (which include the effects of interactions between species
j on the motion of species
i).
Note that for a pure component, eqn (41) gives:
| | 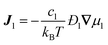 | (42) |
which is equivalent to
eqn (31). Thus the Maxwell–Stefan diffusivity,
Đ1 is equivalent to the collective diffusivity,
DC, for a pure component.
It can be shown150 that the Onsager reciprocal relations require that:
| | 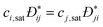 | (43) |
For a binary mixture,
eqn (38) and (41) lead to:
| | | J2 = −(L21∇μ1 + L22∇μ2) | (44) |
and
| | 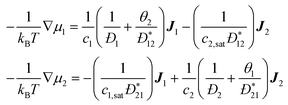 | (45) |
Enforcing consistency between
eqn (44) and (45) leads to the four Maxwell–Stefan coefficients which describe a binary mixture:
159| | 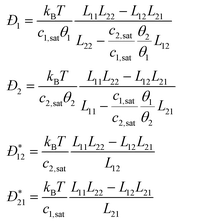 | (46) |
Krishna and van Baten
150 have shown that the benefit of using this formulation over the others described at the beginning of this section is that it is highly predictive. This is shown in
Fig. 8 for equimolar methane/argon mixtures diffusing in cylindrical
silica pores. For pores 2 nm and larger (
Fig. 8(a)), bulk liquid mixture simulations gave binary Maxwell–Stefan exchange coefficients equivalent to those in the silica pores. However, for pores 1 nm and smaller (
Fig. 8(b)), the binary Maxwell–Stefan exchange coefficients were related to the liquid mixture value by a scaling factor,
F, defined as:
| | 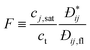 | (47) |
where
ct is the total adsorbed amount per unit of accessible volume of the pore and
Đij,fl is the binary Maxwell–Stefan exchange coefficient obtained from molecular dynamics simulations of the binary liquid mixture. In
Fig. 8,
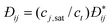
is plotted against the total concentration for the adsorbed phases. Krishna and van Baten
150 have shown that the predictability of this model extends to other types of
zeolites, metal–organic frameworks (MOF), and covalent organic frameworks (COF) as well as to the Maxwell–Stefan diffusivities
Đi.
![Maxwell–Stefan binary exchange coefficients, , for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as . Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f8.gif) |
| | Fig. 8 Maxwell–Stefan binary exchange coefficients, 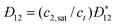 , for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as , for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as 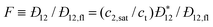 . Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.] . Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.] | |
3.2.3 Diffusion in confinement: single-file and anomalous diffusion.
The diffusion discussed so far, while in confinement, refers to diffusion in three dimensions; thus, all molecules are able to pass each other, and fluid–fluid and fluid–wall collisions lead to a random walk in three dimensions, and thus the diffusion mechanisms behave according to Fick's law. When the degree of confinement is enhanced such that the diffusion in three dimensions is restricted, slower modes of diffusion emerge. We refer to these slower modes as anomalous, because they do not strictly follow the same behavior as is predicted for diffusion in three dimensions. One way to characterize these slower modes of diffusion is to analyze the time dependence of the mean-squared displacement. For bulk fluids or fluids which are in pores large enough such that the molecules can pass each other easily in three dimensions (see the examples given in Section 3.2.1), the MSD increases linearly with time. For diffusion in one direction, z, e.g. along the axis of a carbon nanotube, the MSD can be expressed in terms of the self-diffusion coefficient as:| | 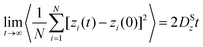 | (48) |
In eqn (48)zi is the position of molecule i at time t and DSz is the self-diffusion coefficient of the molecules in the z direction, N is the total number of fluid molecules and the term on the left hand side of eqn (48) is the MSD. When the pore diameter is small enough that the motion of the fluid is constrained to a single-dimension and the particles cannot pass each other, a one-dimensional random walk gives rise to a MSD which is predicted161–167 to be proportional to the square root of time (an early review of single-file diffusion can be found in ref. 168).| | 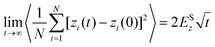 | (49) |
In eqn (49), ESz is referred to as the single-file mobility. Experimentally, single-file diffusion has been observed for small molecules in zeolites,5,169,170 for colloidal particles in confined channels171–173and recently for water in single-walled carbon nanotubes.174
Theoretically, several groups have been active in the investigation of single-file diffusion. Sholl and Fichthorn175 have investigated diffusion mechanisms of various fluids in zeolites and found evidence not only of single-file diffusion but also of bi-modal diffusion, where one component diffused in single-file and the other by a normal Fickian mechanism. Bi-modal diffusion has also been investigated by Percus and coworkers176 for hard disks confined within hard walls and Chen et al.177 for Lennard-Jones mixtures in atomically detailed carbon nanotubes. Percus and coworkers have also extensively investigated single-file diffusion of pure component fluids with hard potentials (hard spheres and hard disks) confined within hard walls.4,178–186
Hahn and Kärger investigated single-file diffusion of fluids with continuous potentials in cylindrical pores.187,188 They found that there was a significant size correlation effect that occurs for particles diffusing in cylindrical pores. This size effect is shown in Fig. 9a. For systems with short pores and small numbers of diffusing particles, a finite limiting value of the mean-squared displacement was observed. As the number of diffusing particles was increased with increased length of the pore, this value was moved to longer times. Thus, if one is to study single-file diffusion, a large enough system size is needed such that the time at which the limiting value of the mean-squared displacement occurs is at a time which is much greater than the needed observation time. From Fig. 9a, it is apparent that the number of diffusing particles needed is approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 or greater, although the needed system size depends on density.189
000 or greater, although the needed system size depends on density.189
![(a) Mean-squared displacements for single-file LJ fluids (σff = 0.383 nm, ε/k = 164 K, approximately that of CF4) in perfect cylindrical pores of effective diameter 0.623 nm at different system sizes (number of adsorbate molecules) at 20% relative occupancy and 300 K. For small numbers of molecules, a finite limiting value of the mean-squared displacement is observed as a result of strong correlation effects. For larger system sizes, the correlation effect appears at longer times. These results were from microcanonical MD simulations. The slope of the MSD for the largest system size at long times is 1, which is not the expected result for a single-file fluid (see text). [Adapted from ref. 187.] (b) Time dependence of the mean-squared displacement for single-file LJ fluids (σ = 0.383 nm, ε/k = 164 K, approximately that of CF4) in a perfect cylinder of effective diameter 0.623 nm at 20 % relative occupancy and 300 K from a microcanonical (N,V,E) MD simulation (line) using 10 000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f9.gif) |
| | Fig. 9 (a) Mean-squared displacements for single-file LJ fluids (σff = 0.383 nm, ε/k = 164 K, approximately that of CF4) in perfect cylindrical pores of effective diameter 0.623 nm at different system sizes (number of adsorbate molecules) at 20% relative occupancy and 300 K. For small numbers of molecules, a finite limiting value of the mean-squared displacement is observed as a result of strong correlation effects. For larger system sizes, the correlation effect appears at longer times. These results were from microcanonical MD simulations. The slope of the MSD for the largest system size at long times is 1, which is not the expected result for a single-file fluid (see text). [Adapted from ref. 187.] (b) Time dependence of the mean-squared displacement for single-file LJ fluids (σ = 0.383 nm, ε/k = 164 K, approximately that of CF4) in a perfect cylinder of effective diameter 0.623 nm at 20 % relative occupancy and 300 K from a microcanonical (N,V,E) MD simulation (line) using 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.] 000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.] | |
Another important observation from Fig. 9a is that the time dependence of the mean-squared displacement is linear for the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particle system, even though the particles were in single-file confinement. This is due to a violation of a random walk. This is further illustrated in Fig. 9b. In Fig. 9b, the MSDs for a single-file fluid using a MD simulation in the microcanonical (N,V,E) ensemble with and without random forces added to the adsorbate velocities are shown. The MSD for the microcanonical simulation without random forces exhibits a slope on a log–log scale equal to 1, which would normally be indicative of Fickian diffusion (see eqn (48)). However, the fluid is in single-file confinement, and the particles do not pass each other. When a random walk is imposed upon the system by adding random forces to the particles during the MD simulation, the slope of the MSD on the log–log scale becomes 1/2, indicative of single-file diffusion (see eqn (49)). It can be shown theoretically that the square root of time dependence of the mean-squared displacement results from a random walk.162 Perfectly cylindrical pores, as used in the work of Hahn and Kärger,187 are completely smooth. Thus, the standard microcanonical simulations without random forces exhibit purely specular reflection of the particles colliding with the wall, and any diffusive reflection of particles is absent. Because the fluid is constrained in a single dimension, fluid–fluid collisions do not create a random walk. Thus, the absence of a random walk from collisions for fluid–fluid and fluid–wall interactions results in the absence of the square root of time dependence of the MSD. Adding random forces to the particle velocities mimicks diffusive collisions with the walls, but it is not a real effect for perfectly cylindrical pores.
000 particle system, even though the particles were in single-file confinement. This is due to a violation of a random walk. This is further illustrated in Fig. 9b. In Fig. 9b, the MSDs for a single-file fluid using a MD simulation in the microcanonical (N,V,E) ensemble with and without random forces added to the adsorbate velocities are shown. The MSD for the microcanonical simulation without random forces exhibits a slope on a log–log scale equal to 1, which would normally be indicative of Fickian diffusion (see eqn (48)). However, the fluid is in single-file confinement, and the particles do not pass each other. When a random walk is imposed upon the system by adding random forces to the particles during the MD simulation, the slope of the MSD on the log–log scale becomes 1/2, indicative of single-file diffusion (see eqn (49)). It can be shown theoretically that the square root of time dependence of the mean-squared displacement results from a random walk.162 Perfectly cylindrical pores, as used in the work of Hahn and Kärger,187 are completely smooth. Thus, the standard microcanonical simulations without random forces exhibit purely specular reflection of the particles colliding with the wall, and any diffusive reflection of particles is absent. Because the fluid is constrained in a single dimension, fluid–fluid collisions do not create a random walk. Thus, the absence of a random walk from collisions for fluid–fluid and fluid–wall interactions results in the absence of the square root of time dependence of the MSD. Adding random forces to the particle velocities mimicks diffusive collisions with the walls, but it is not a real effect for perfectly cylindrical pores.
Another type of system which has been of interest for single-file diffusion are carbon nanotubes.6,189–192 Liu et al.6 and Mao and Sinnott191 found square-root of time dependence of the MSD for fluids diffusing in narrow single-walled carbon nanotubes but used stochastic Langevin thermostats. This thermostat adds random forces to the particles' velocities similarly to the work of Hahn and Kärger,187 and thus a corrugated pore with diffuse reflections of the particles off the nanotube wall was mimicked. Other researchers who used deterministic thermostats190,192 were not able to observe a square-root of time dependence of the mean-squared displacement for single-file fluids diffusing in carbon nanotubes. These observations may be related to the fact that carbon nanotubes, similarly to the perfect cylinders previously described, do not result in particles having large amounts of diffusive collisions with the wall. While, carbon nanotubes have small amounts of corrugation due to the atomic detail of the wall, this corrugation is not enough to produce diffusive collisions with the walls. Bhatia et al.193 have quantified the diffusive reflection of methane and hydrogen diffusing in atomically detailed carbon nanotubes using a Maxwell coefficient194 which relates specular and diffusive reflections. They found that the fluid–wall collisions were nearly completely specular. The smallest molecule studied, hydrogen, resulted in the greatest amount of diffusive collisions, but these contributed less than 1% of the total collisions, even at the largest densities studied. Thus, the diffusion of fluids in carbon nanotubes is predicted to be dominated by specular collisions of atoms with the carbon nanotube wall.
Liu et al.189 have demonstrated single-file diffusion in carbon nanotube bundles, without the aid of a stochastic thermostat. Using microcanonical simulations, they were able to observe single-file diffusion of argon in the interstices of carbon nanotube bundles, while the three dimensional self-diffusion of argon dominated inside the (25,0) carbon nanotubes. Some of their results are shown in Fig. 10. Their systems sizes were such that approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 argon atoms were in the interstitial channels of the bundle; thus the size correlation effects shown by Hahn and Kärger187 were alleviated. These interstitial channels were corrugated, as they were composed of the outside of three adjacent carbon nanotubes. This resulted in the MSD of the diffusing interstitial argon atoms having a square-root of time dependence (eqn 49), shown in Fig. 10b. The MSDs of the argon atoms diffusing in the carbon nanotubes had a linear time dependence, indicative of Fickian diffusion (eqn 48). The MSD of the entire system also had a linear time dependence at all but the lowest pressures, as it was dominated by the much faster diffusion inside the carbon nanotubes. Furthermore, the authors observed that when large system sizes were used, the flexibility of the CNTs had negligible influence on the diffusion of argon.
000 argon atoms were in the interstitial channels of the bundle; thus the size correlation effects shown by Hahn and Kärger187 were alleviated. These interstitial channels were corrugated, as they were composed of the outside of three adjacent carbon nanotubes. This resulted in the MSD of the diffusing interstitial argon atoms having a square-root of time dependence (eqn 49), shown in Fig. 10b. The MSDs of the argon atoms diffusing in the carbon nanotubes had a linear time dependence, indicative of Fickian diffusion (eqn 48). The MSD of the entire system also had a linear time dependence at all but the lowest pressures, as it was dominated by the much faster diffusion inside the carbon nanotubes. Furthermore, the authors observed that when large system sizes were used, the flexibility of the CNTs had negligible influence on the diffusion of argon.
![(a) Argon adsorbed in a (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. (b) The mean-squared displacements of argon in the (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. The slope of the mean-squared displacements for the atoms in the interstitial sites is ½ on the log–log scale, indicative of single-file diffusion while that for the atoms diffusing in the nanotubes as well as for the total bundle is 1, indicative of Fickian diffusion. Simulations using a rigid carbon nanotube bundle are indicated by the solid line, while simulations using a flexible nanotube bundle are indicated with open symbols. The MSDs for the rigid and flexible bundles are nearly identical, indicating that influence of the carbon nanotube flexibility on diffusion is negligible. [Adapted from ref. 189.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f10.gif) |
| | Fig. 10 (a) Argon adsorbed in a (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. (b) The mean-squared displacements of argon in the (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. The slope of the mean-squared displacements for the atoms in the interstitial sites is ½ on the log–log scale, indicative of single-file diffusion while that for the atoms diffusing in the nanotubes as well as for the total bundle is 1, indicative of Fickian diffusion. Simulations using a rigid carbon nanotube bundle are indicated by the solid line, while simulations using a flexible nanotube bundle are indicated with open symbols. The MSDs for the rigid and flexible bundles are nearly identical, indicating that influence of the carbon nanotube flexibility on diffusion is negligible. [Adapted from ref. 189.] | |
Eqn (49) represents the limiting case of anomalous diffusion which is single-file diffusion. Mao and Sinnott191 have reported dependencies of the mean-squared displacement which are intermediate between the single-file (square root) and Fickian (linear) modes for ethane and ethylene in carbon nanotubes. They found that the smaller, more spherical methane molecule exhibited a completely normal Fickian mode of diffusion, but ethane and ethylene seemed to exhibit a behavior intermediate between single-file and Fickian diffusion. Thus, ethane and ethylene, in some diameters of CNTs, exhibited time dependences of the mean-squared displacement which were between 1/2 and 1.
Experimentally, such a transition has not been observed. However, using both MD simulation and transition state theory, Hahn and Kärger188 presented results that suggested that all diffusion will eventually tend toward the Fickian limit if given enough time. For realistic continuous potentials, the single-file particles will eventually exhibit hopping, as particles begin to hop over their neighbors. The degree of hopping as well as the time scale this occurs on depends entirely on the degree of confinement. Long time (100 ns) MSDs shown in their work are illustrated in Fig. 11. Particles in the smallest diameter pores (0.70 and 0.74 nm) exhibited square root of time dependence of their MSDs, indicating single-file diffusion. However, as the pore diameter was increased slightly to 0.78 nm, a transition similar to that described by Mao and Sinnott191 was observed, where the time dependence of the MSD was between 1/2 and 1. Larger diameter pores exhibited a linear time dependence. Using transition state theory, they estimated particle hopping times in all of the pores. Those in the smallest pores exhibiting single-file diffusion presented hopping on microsecond time scales (beyond the time scale shown in Fig. 11 and beyond the current limit of atomistic MD simulations). The particles diffusing in the largest diameter pores exhibited hopping on picosecond time scales which resulted in MSDs with a linear time dependence and Fickian diffusion. From transition state theory and hopping times, Hahn and Kärger188 were able to calculate crossover times (the time at which single-file diffusion was predicted to crossover into Fickian diffusion) as well as the predicted diffusion coefficients that would result after this crossover time. These results are shown in Table 1. Comparisons are shown between the calculated values of the diffusion coefficients from the MSDs for the largest pores and the calculated values from transition state theory. Excellent agreement was obtained.
![Mean-squared displacements of LJ particles (σ = 0.383 nm, ε/kB = 164 K, approximately that of CF4) in different diameters, d, of perfect cylinders. [Adapted from ref. 188.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f11.gif) |
| | Fig. 11 Mean-squared displacements of LJ particles (σ = 0.383 nm, ε/kB = 164 K, approximately that of CF4) in different diameters, d, of perfect cylinders. [Adapted from ref. 188.] | |
Table 1 Hopping times between particle passes (τ), diffusivities obtained from transition state theory (Dtst) and from MD simulation (Dsim) and crossover times predicted from transition state theory (tc) for the systems shown in Fig. 11. From ref. 188
|
d
T/nm |
τ/s |
D
tst/m2 s−1 |
D
sim/m2 s−1 |
t
c/s |
| 0.70 |
7.0 × 10−6 |
2.6 × 10−13 |
— |
3.0 |
| 0.74 |
9.8 × 10−8 |
1.9 × 10−11 |
— |
5.6 × 10−4 |
| 0.78 |
5.8 × 10−9 |
3.2 × 10−10 |
— |
1.6 × 10−6 |
| 0.82 |
1.5 × 10−10 |
1.2 × 10−8 |
1.2 × 10−8 |
1.3 × 10−9 |
| 0.86 |
7.1 × 10−11 |
2.6 × 10−8 |
2.5 × 10−8 |
3.0 × 10−10 |
| 0.90 |
4.5 × 10−11 |
4.1 × 10−8 |
4.0 × 10−8 |
1.2 × 10−10 |
Regardless of whether or not initial single-file and other anomalous diffusion eventually always result in hopping and Fickian diffusion, the initial slow movement of particles diffusing in pores can influence the overall diffusion coefficients. Anomalous regions in the MSD can result in a maximum in the self-diffusion coefficients for fluids in porous materials, such as activated carbon.195 An example is shown in Fig. 12 for argon diffusing in a model of a saccharose-derived activated carbon.196 In materials with regularly shaped pores, such as carbon nanotubes, the self-diffusion coefficient is expected to decrease with increasing density as an increased density of fluid generally slows diffusion. In disordered porous materials, such as activated carbon, the diffusion of the fluid can be slowed at low densities due to the fluid being adsorbed in strongly attractive pores. As the smallest pores become full at intermediate densities, the larger pores begin to fill and the diffusion rate increases. At higher densities, as the larger pores become filled due to the increased density of the fluid in the pores, the diffusion rate is slowed. This results in a maximum in the self-diffusion coefficient and has been observed in several simulation studies195–198 as well as in experiment.199
![Self-diffusivity as a function of relative pressure for argon confined at 77 K in CS1000A (model of a saccharose-based porous carbon) from MD simulation. A maximum in the self-diffusion coefficient exists in the region roughly corresponding to the pore filling region of the isotherm. [Reprinted with permission from ref. 196. Copyright 2006, Taylor & Francis, Ltd.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f12.gif) |
| | Fig. 12 Self-diffusivity as a function of relative pressure for argon confined at 77 K in CS1000A (model of a saccharose-based porous carbon) from MD simulation. A maximum in the self-diffusion coefficient exists in the region roughly corresponding to the pore filling region of the isotherm. [Reprinted with permission from ref. 196. Copyright 2006, Taylor & Francis, Ltd.] | |
3.2.4 Other transport properties.
Dynamic properties such as the self-diffusion coefficient (see Section 3.2.1), viscosity,200,201 and thermal and electrical conductivities,62 which appear in many phenomenological macroscopic laws, can be calculated from time–correlation functions using Green–Kubo relationships. Here, we will only give a brief discussion of the viscosity in confinement and refer readers to other sources for a discussion of other properties.61,62,202,203
The shear viscosity, η, is defined as the ratio of the shear stress σxy = −Pxy, where P is the pressure tensor, to the shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂ux/∂y, where ux is the streaming velocity in the x direction of flow and y is the direction of the flow gradient.
≡ ∂ux/∂y, where ux is the streaming velocity in the x direction of flow and y is the direction of the flow gradient.
| | 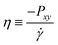 | (50) |
In
eqn (50),
Pxy is the
xy component of the pressure tensor.
In equilibrium MD simulations, the Green–Kubo relationship predicts that for a limiting, small shear rate, the shear viscosity is given by:202
| | 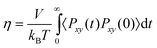 | (51) |
To calculate the shear viscosity as a function of the shear rate, non-equilibrium MD simulations can be used.
200,201,204 The shear-rate dependent viscosity can be determined from
| | 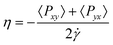 | (52) |
In
eqn (52), 〈
Pxy〉 and 〈
Pyx〉 are the averages of the
xy and
yx components of the pressure tensor and
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif)
is the shear rate.
In Fig. 13 we show an example from Cummings and co-workers200 for the calculation of the shear viscosity as a function of the shear rate for n-dodecane confined between mica surfaces. Non-equilibrium MD (NEMD) simulations have been compared with the surface force apparatus experiments of Granick and coworkers.205,206 Because of the timescale limitations of molecular dynamics simulations as well as thermal noise, the simulation results are limited to shear rates greater than 107 s−1. Experiments are limited by the stability of the mica surfaces and can only reach shear rates less than 105 s−1. Nevertheless, the experimental and simulation results seem to be consistent.
![Comparison of the shear viscosity (η) as a function of shear rate () from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f13.gif) |
| | Fig. 13 Comparison of the shear viscosity (η) as a function of shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ) from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.] ) from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.] | |
3.3 Confinement effect on chemical reactions
Confinement and surface interactions can have a profound effect on the equilibrium composition, reaction rate and even the reaction mechanism for reactive systems. Among the factors that may be important in determining such effects are strong interactions of the various molecular species with the pore walls, selective adsorption of certain reactants or products, geometrical constraints due to the pore size and shape, surface curvature and surface defects, and increased density and pressure in the confined phase.207 As a result of these many effects, it is difficult to achieve fundamental understanding from experiment alone, and molecular modeling can play an important role in complementing experimental studies.
Several new complications are involved in molecular modeling of confined reactive systems that do not arise in studies of non-reactive phases. First and foremost, chemical reactions usually involve breaking and forming chemical bonds, and thus a major rearrangement of the electrons. Any description of such processes requires quantum mechanics. One approach is to use a suitable ab initio computational method to estimate the potential energy surface (the potential energy map for the reactive mixture as a function of all possible bond lengths and angles), and then use optimization methods to determine the optimum reaction path or paths through this energy map. For reactions in nanopores, density functional theory (Section 2.1) is often the method of choice, since it provides a convenient compromise between accuracy and computational expense. Computational expense increases rapidly for the higher level (and more accurate) ab initio methods, and this may preclude studying systems of sufficient size to properly model confinement effects. A second complication is that reaction events are rare events; the reactant molecules must come together in a suitable orientation and with sufficient energy to overcome the transition state barrier. Thus, conventional MD cannot be used to determine reaction rates. Specialized rare event methods, such as Blue Moon MD,208,209 have been developed that bias the simulation so that it focuses on regions of phase space near the top of the transition barrier where reaction is likely; the bias is removed at the end of the simulation. A third complication for some reactions, particularly ones involving large molecules, such as polymers and proteins, is that there may be many possible reaction paths. In such cases, it is necessary to take an ensemble average over these possible paths in order to calculate the rate of reaction. Specialized methods, such as transition path sampling,210,211 have been developed for such cases, but are computationally demanding. For a more comprehensive discussion on the methods for modeling reactive systems we refer readers to recent reviews.28,212
In the remainder of this section we give several examples of modeling studies of confined chemical reactions.
3.3.1 Classical approaches to confined chemical reactions.
Although the investigation of specific chemical reaction pathways requires an explicit consideration of the electronic degrees of freedom using ab initio or semi-empirical methods, changes in the equilibrium product yields can be obtained from classical simulation methods, such as reaction ensemble Monte Carlo74,75 (RxMC) (Section 2.3.1), which incorporate reactive MC moves that insert and remove reactant and product molecules according to the stoichiometry of a specified reaction and the free energy difference between the products and reactants. The free energy is broken up into an ideal contribution, involving only the chemical nature of the isolated reactant and product species, and a configurational contribution resulting from the species interaction with the local environment. The first of these contributions can readily be obtained either from standard thermodynamic tables or from ab initio calculations,213 while the latter is obtained during the RxMC simulations using appropriate force fields to describe the intermolecular interactions.
Prompted by the experimental study of Kaneko et al.214 that showed enhancement of the nitric oxide dimerization reaction (2NO ↔ (NO)2) in activated carbon fibers, Turner et al.215 used RxMC moves in conjunction with Gibbs ensemble MC to study this reaction in carbon slit pores. At lower temperatures they found a nearly 40-fold enhancement in the fraction of dimers over the bulk phase for pore widths of ∼1 nm. They attributed this enhancement to the increased density in the confined environment, which according to Le Châtelier's principle, shifts the equilibrium to favor the products in the reaction due to the reduction in the total number of moles as the reaction proceeds forward. In addition, the dimer molecule preferentially adsorbed into the pores due to stronger interactions with the pore walls than the monomer species. These findings were in qualitative agreement with the findings of Kaneko et al.,214 although the experiment showed an even greater enhancement of the dimerization, with almost 100% dimers even at room temperature. A later experimental study of this reaction in carbon nanotubes, using FTIR spectroscopy, by Yates and coworkers216 also found 100% dimerization in the pores, thus confirming the prior experimental and simulation results. The cause of the under-prediction from the simulations was not entirely clear. It could result from uncertainties in the intermolecular potential models used, or from the effect of the wall interactions on the dimer bond energy.
Subsequently, the study of Turner et al. was extended by Lisal et al.213 to investigate the same reaction in slit pores for a wider range of temperatures and pressures; some of these results are shown in Fig. 14. In both studies, capillary condensation was observed to lead to a large increase in the concentration of dimers, again due to the sharp increase in density in the pores, as illustrated in Fig. 15. Thus, while a very small change in the pressure in the bulk phase has only a small effect on the reaction in the bulk phase, the enhancement of the forward reaction in the confined pore phase is amplified dramatically.
![Conversion of the NO dimerization reaction within slit-shaped carbon pores, ranging from 0.95–1.59 nm in width, predicted from RxMC simulation. The bulk phase pressure is 0.16 bar, and the corresponding conversion in the bulk phase is shown for comparison. [Adapted from ref. 215.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f14.gif) |
| | Fig. 14 Conversion of the NO dimerization reaction within slit-shaped carbon pores, ranging from 0.95–1.59 nm in width, predicted from RxMC simulation. The bulk phase pressure is 0.16 bar, and the corresponding conversion in the bulk phase is shown for comparison. [Adapted from ref. 215.] | |
![Effect of capillary condensation on the mole fraction of dimers and monomers as a function of bulk pressure for the NO dimerization reaction within a slit-shaped carbon pore of width H/σNO = 5.5, at 122.5 K. Open and closed circles correspond to monomers and dimers, respectively, and vertical jumps represent capillary condensation. [Adapted from ref. 215.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f15.gif) |
| | Fig. 15 Effect of capillary condensation on the mole fraction of dimers and monomers as a function of bulk pressure for the NO dimerization reaction within a slit-shaped carbon pore of width H/σNO = 5.5, at 122.5 K. Open and closed circles correspond to monomers and dimers, respectively, and vertical jumps represent capillary condensation. [Adapted from ref. 215.] | |
The RxMC method has been used to study the effects of confinement on other reactions,76 including ammonia synthesis215,217 (N2 + 3H2 ↔ 2NH3), the esterification reaction218 (CH3COOH + C2H5OH ↔ C2H5OOCCH3 + H2O), both in bare and functionalized carbon pores, and the propene metathesis reaction219,220 in zeolites. The ammonia synthesis reaction is favored by high pressure, and confinement leads to an enhanced yield of ammonia, through the same mechanism as for the nitric oxide dimer reaction.215,217 However, the effects are smaller due to the high temperature at which the reaction is carried out. RxMC simulation results for the esterification reaction in slit shaped carbon pores, both unadorned carbon walls and with walls decorated with –COOH groups, are shown in Fig. 16. The results show an enhancement in the yield of the ester from about 39 mol% in the bulk phase to 87–90% in the activated carbon pores. In this example the enhancement does not arise from increased density in the pores, but from selective adsorption of the ethyl acetate product on the pore walls. A number of experimental studies of this reaction in activated carbons have been reported,221,222 with results that are in generally good agreement with the simulations. Thus Chu et al.222 found a yield of 87.3% ester in activated carbon at 423 K, with the yield increasing with temperature.
![RxMC results for the esterification reaction at 523.15 K for the reaction carried out in the bulk phase, and in bare carbon slit pores, and carbon slit pores activated by decorating the carbon surfaces with –COOH groups (density 1.82 groups per nm2). The bulk phase pressure is 1.0 bar. [Adapted from ref. 218.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f16.gif) |
| | Fig. 16
RxMC results for the esterification reaction at 523.15 K for the reaction carried out in the bulk phase, and in bare carbon slit pores, and carbon slit pores activated by decorating the carbon surfaces with –COOH groups (density 1.82 groups per nm2). The bulk phase pressure is 1.0 bar. [Adapted from ref. 218.] | |
For reactions where the activation energy barrier, ΔE*, is high relative to the thermal energy kBT, and the system is coupled to the reaction coordinate sufficiently strongly so as to dissipate energy of the order kBT from the product in a time comparable to the velocity of the reaction coordinate, transition state theory (TST) together with the RxMC method can be used to make an estimate of the effect of confinement on reaction rate, using classical simulation methods.212 A useful rule of thumb is that transition state theory should be a good approximation if ΔE* ≥ 5kBT. The method requires knowledge of the transition state species, and a force field for it. RxMC simulation is then used to determine the equilibrium concentrations of the various species, including that of the transition state species, and the rate constant k is calculated from the TST expression:
| | 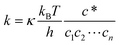 | (53) |
where
kB is Boltzmann's constant,
κ is the transmission coefficient which accounts for recrossing of the products through the activation barrier (
κ = 1 when no recrossing occurs),
h is Planck's constant,
c* is the concentration of the activated species, and
c1,
c2,… are the concentrations of the reactants. Turner
et al.212 applied this approach to determine the effect of confinement in slit-shaped carbon pores and in
carbon nanotube bundles on the reaction rate of the hydrogen iodide dissociation reaction, 2HI ↔ H
2 + I
2. The
activation barrier for this reaction is 42 kcal mol
−1, which well exceeds 5
kBT at moderate conditions, and
κ was assumed to be unity. The method gave good agreement with experimental results for the reaction rate for the bulk gas reaction for a temperature range of 583–595 K and pressures up to 300 bar. For the reaction in carbon nanopores a large increase in the reaction rate is observed, as shown in
Fig. 17 for
carbon nanotubes of two diameters. The results show an increase of a factor of 13 over the bulk phase reaction at 1 bar, rising to a factor of 47 at 200 bar in the case of the (8,8)
nanotube. The cause of this large increase is the strong dispersion force interaction between the transition state species and the carbon walls.
![TST-RxMC simulations of the hydrogen iodide decomposition rate at 573.15 K in the bulk phase (solid circles) and in carbon nanotubes of different diameters: (8,8) nanotube (open squares, internal diameter d = 1.09 nm) and (10,10) nanotube (open diamonds, d = 1.36 nm). Here k is the reaction rate constant at the pressure shown in the figure, k0 is the rate constant at the standard state condition of 1 bar. [Adapted from ref. 212.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f17.gif) |
| | Fig. 17
TST-RxMC simulations of the hydrogen iodide decomposition rate at 573.15 K in the bulk phase (solid circles) and in carbon nanotubes of different diameters: (8,8) nanotube (open squares, internal diameter d = 1.09 nm) and (10,10) nanotube (open diamonds, d = 1.36 nm). Here k is the reaction rate constant at the pressure shown in the figure, k0 is the rate constant at the standard state condition of 1 bar. [Adapted from ref. 212.] | |
3.3.2 Rotational isomerism of C4hydrocarbons: pore geometry constraints.
The constraint provided by the pore walls can restrict the possible intermediates and products of the reaction, thus changing both products and reaction mechanism. These are sometimes referred to as shape-catalytic effects, i.e. the effect of the shape and size of the pores on the reaction. An example of such a geometric constraint is provided by a study of rotational isomerism for C4hydrocarbons (n-butane, 1-butene and 1,3-butadiene) in slit-shaped graphitic carbon pores carried out by Santiso et al.223 In these reactions there are no bonds broken or formed, but rather different isomers occur through torsional rotation about the central C–C bond in the molecule. Santiso et al. used DFT with the Becke–Lee–Yang–Parr (BLYP) exchange correlation functional to determine the energy of a single C4 molecule as a function of the torsion angle, both in the ideal gas phase and confined in slit pores with pore widths ranging from 5.8 to 7.9 Å. Here we discuss only the results for n-butane. The energy for the isolated n-butane molecule is shown in Fig. 18. It is seen that the anti isomer is the most stable form, with the gauche isomer being metastable, while the eclipsed and syn isomers are unstable. The values found for the energy barriers for the eclipsed and syn isomers, and for the energy differences shown in Fig. 18, are in good agreement with experimental measurements and other theoretical calculations. Results for the energies as a function of torsion angle for the confined n-butane molecule are shown in Fig. 19. The effect of confinement for these pore widths is dramatic. While the anti isomer remains the most stable one, the syn isomer, which was the most unstable form for the isolated butane molecule, becomes metastable, and the gauche isomer, previously metastable, becomes increasingly unstable with decreasing pore width. The reason for these large changes in the energy map is readily understood from the molecular structure of the isomers. Confinement in a slit-shaped pore favors a product molecule that is planar or nearly so, i.e. the anti and syn forms. The eclipsed and gauche isomers are more non-planar and cannot fit easily into a narrow pore of this shape.
![Energy as a function of C–C torsion angle for an isolated n-butane molecule from DFT. Open triangles denote the 4 stationary points (the syn, gauche, eclipsed and anti isomers). [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f18.gif) |
| | Fig. 18 Energy as a function of C–C torsion angle for an isolated n-butane molecule from DFT. Open triangles denote the 4 stationary points (the syn, gauche, eclipsed and anti isomers). [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.] | |
![Energy as a function of C–C torsion angle for n-butane confined within slit carbon pores of various widths. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f19.gif) |
| | Fig. 19 Energy as a function of C–C torsion angle for n-butane confined within slit carbon pores of various widths. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.] | |
Santiso et al.223 also studied the effect of such confinement on the reaction rate constant k for the anti–gauche/anti–syn transition using transition state theory, and found a remarkably large effect of pore width on the rate, more than 40 orders of magnitude difference at low temperatures between the reaction rate in the gas phase and in the smallest pores. Some of these results are shown in Fig. 20. The rate constant is found to vary roughly with the exponential of the pore width. This remarkable effect of pore width is believed to arise from an enhancement of the activation energy due to interaction of the n-butane molecules with the pore walls, and a simple model of this behavior is proposed and tested. Similar confinement effects are found for 1-butene and 1,3-butadiene.
![Arrhenius plots of the rate constant for n-butane as calculated from transition state theory for the anti–gauche transition for the gas phase and larger pore widths, which becomes the anti–syn transition for smaller pores (see Fig. 19). Labels to the right are the pore width. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f20.gif) |
| | Fig. 20 Arrhenius plots of the rate constant for n-butane as calculated from transition state theory for the anti–gauche transition for the gas phase and larger pore widths, which becomes the anti–syn transition for smaller pores (see Fig. 19). Labels to the right are the pore width. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.] | |
3.3.3
Carbon dioxide-free methods for hydrogen production.
Many of the dominant methods for producing hydrogen on an industrial scale involve the creation of by-products, such as carbon dioxide, which are undesirable due to environmental considerations. One of the most appealing potential reactions for production of hydrogen is by direct thermal splitting of water (H2O → H2 + ½O2), due to the abundance of the reactants and the benign nature of the products. However, in addition to producing a relatively low yield of hydrogen (∼25%),224 this reaction in the bulk phase has a high activation barrier, and requires temperatures in excess of 2000 °C for the conversion to proceed on a practical timescale.225
Kostov et al.226 used DFT to investigate the feasibility of using vacancy defects in sp2-hybridized carbon materials as catalysts for the decomposition reaction. Using a defective graphene sheet and a defective (10,10) single-walled carbon nanotube (SWCNT), they used several complementary methods to identify stable intermediates (Laio–Parrinello metadynamics),227,228 reaction pathways and transition states (nudged elastic band method)229 on the potential energy surface obtained from DFT. These methods enabled several reaction mechanisms to be identified which improve the kinetics and yield of the dissociation reaction over those for the bulk phase reaction. Fig. 21 shows an example of intermediate configurations along a dissociation reaction pathway over a single vacancy in the (10,10) SWCNT. Starting from a physisorbed state (Fig. 21a), the oxygen forms a complex with a dangling bond in the vicinity of the vacancy (Fig. 21b and c), which eventually causes the water molecule to disassociate, producing diatomic hydrogen and filling the vacancy with the oxygen (Fig. 21d). Once the reactants and products had been identified, Kostov et al. used DFT to calculate the molecular partition functions in order to obtain ideal gas estimates of the Gibbs free energies for the reactions.230 As shown in Fig. 22, they used these data to predict the equilibrium conversion as a function of temperature in the ideal gas limit, for the bulk phase reaction, as well as for the reactions involving the vacancies in the graphene and nanotube. With addition of the vacancies, their results showed that hydrogen could be produced at temperatures far below the operational range of the bulk phase reaction. In addition, their calculations predicted a large effect of curvature of the graphene surface on the equilibrium yield, shifting the optimum temperature down by more than 1000 K, albeit at the cost of about 12% in the expected yield.
![Top and side views of (a) the initial state, (b) intermediate complex, (c) transition state, and (d) final conformation for a favorable dissociation pathway over a vacancy in a (10,10) nanotube. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f21.gif) |
| | Fig. 21 Top and side views of (a) the initial state, (b) intermediate complex, (c) transition state, and (d) final conformation for a favorable dissociation pathway over a vacancy in a (10,10) nanotube. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.] | |
![Ideal-gas equilibrium yields (fraction of water converted to hydrogen at equilibrium in % mole) for the dissociation of water in the bulk gas phase, over a single vacancy in graphene, and over a single vacancy in a (10,10) carbon nanotube. The values correspond to a pressure of 1 bar and an initial equimolar mixture of water and vacancies. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f22.gif) |
| | Fig. 22 Ideal-gas equilibrium yields (fraction of water converted to hydrogen at equilibrium in % mole) for the dissociation of water in the bulk gas phase, over a single vacancy in graphene, and over a single vacancy in a (10,10) carbon nanotube. The values correspond to a pressure of 1 bar and an initial equimolar mixture of water and vacancies. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.] | |
4. Outlook and conclusions
Major improvements in computer hardware and in modeling algorithms over the last few decades have made it possible to study increasingly complicated confinement effects, using larger and more representative systems and longer time scales. Since 1993 Prometeus GMBH has tested the performance of the world's top 500 general purpose supercomputers, and has published these data twice each year as TOP500††. The first such list (1993) ranked a Thinking Machine Corporation CM5 computer as the fastest, at 59.7 Gflops‡‡ (59.7 × 109 flops). In June 2010 the fastest machine was the Cray XT5 Jaguar, located at Oak Ridge National Laboratory, at 1.76 Pflops (1.76 × 1015 flops, a speedup of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fold over 16 years). The Office of Science at the U.S. Department of Energy plans to develop 250 Pflop machines by 2015, and an Exaflop (1018 flops) machine by 2018. Of equal importance to these improvements in computer hardware have been major advances in computational methods and algorithms. These have led to a further speedup of several orders of magnitude over the same time period. They have included the development of efficient parallelized quantum mechanics and molecular dynamics codes; examples of the former include CPMD (Car–Parinello Molecular Dynamics)§§ and Quantum ESPRESSO,231 and of the latter the NAMD (NAnoscale Molecular Dynamics)232 and LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)233 codes.
000 fold over 16 years). The Office of Science at the U.S. Department of Energy plans to develop 250 Pflop machines by 2015, and an Exaflop (1018 flops) machine by 2018. Of equal importance to these improvements in computer hardware have been major advances in computational methods and algorithms. These have led to a further speedup of several orders of magnitude over the same time period. They have included the development of efficient parallelized quantum mechanics and molecular dynamics codes; examples of the former include CPMD (Car–Parinello Molecular Dynamics)§§ and Quantum ESPRESSO,231 and of the latter the NAMD (NAnoscale Molecular Dynamics)232 and LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)233 codes.
These advances, amounting to roughly 12 orders of magnitude in the speed of execution over the last 30 years in the case of atomistic simulations, are leading to a shift away from the older and more approximate analytic theories towards direct molecular simulation, which bypass many of the approximations needed in analytic theories. Classical density functional theory remains valuable, however, because it is accurate and is less computationally expensive. The extension of C-DFT to three dimensions60 opens the way to describing more realistic pore structures and more complex molecules.
A number of difficulties remain in modeling confinement effects. In some areas, such as effects of confinement on the behavior of large, complex molecules (e.g.polymers, proteins, etc.) or on chemical reaction mechanisms and rates, computational intensity is still a problem. Improved multi-scale modeling methods are needed to investigate these areas in the near term. In the case of non-crystalline porous materials, lack of detailed knowledge of the atomic structure of the material introduces major uncertainties in the modeling.234,235 Depending on the system studied, the intermolecular force models may still be inadequate. Finally, improved algorithms are needed in order to take full advantage of the new supercomputers, which have hundreds of thousands of processors.
While there has been considerable progress in our understanding of equilibrium phenomena, such as adsorption, phase changes and reaction equilibrium in confined phases over the last three decades, much work is needed in understanding the mechanism and kinetics of non-equilibrium phenomena. Diffusion will occur by different mechanisms (e.g. Fickian, anomalous) in different regions for many materials, and ways to describe this quantitatively are needed. Confinement effects on heterogeneous reactions carried out in nanoporous catalyst materials are poorly understood at present, and it would be desirable to develop multi-scale (electronic–atomistic) methods that can capture these effects, including diffusion to and from reaction sites.
Acknowledgements
It is a pleasure to thank M. Schoen and D. Theodorou for helpful discussions and K. Phillips for critical reading of the manuscript. We are grateful to the U.S. National Science Foundation (grants CBET-0754979 and CBET-0932656), the Petroleum Research Fund of the American Chemical Society (grant 48623-AC6), the National Natural Science Foundation of China (grant 20876132) and Zhejiang Provincial National Science Foundation of China (grant Y408131) for support of our research. We wish to thank the National Science Foundation for supercomputer time through TeraGrid resources provided by the San Diego Supercomputing Center, National Center for Supercomputing Applications, and Indiana University under grant number TG-CHE080046N.
List of Acronyms
|
BLYP
| Becke–Lee–Yang–Parr exchange–correlation functional |
|
C-DFT
| Classical density functional theory |
| CNT |
Carbon nanotube
|
|
COF
| Covalent organic framework |
|
CPMD
| Car–Parinello molecular dynamics |
| DCV-GCEMD | Dual control-volume grand canonical ensemble molecular dynamics |
| DFT |
Ab initio density functional theory |
|
EMD
| Equilibrium molecular dynamics |
|
GCEMC
| Grand canonical ensemble Monte Carlo |
|
GEMC
| Gibbs ensemble Monte Carlo |
|
HF
| Hartree–Fock self-consistent mean field theory |
|
INDO/S | Intermediate neglect of differential overlap/screened approximation |
| LAMMPS | Large-scale Atomic/Molecular Massively Parallel Simulator |
|
MC
| Monte Carlo |
| MD | Molecular dynamics |
|
MNDO
| Modified neglect of differential overlap |
| MOF | Metal–organic framework |
|
MSD
| Mean-squared displacement |
|
NAMD
| Nanoscale molecular dynamics |
|
NEMD
| Non-equilibrium molecular dynamics |
|
PFG-NMR
|
Pulsed-field gradient nuclear magnetic resonance |
|
PSD
|
Pore size distribution |
|
QENS
|
Quasi-elastic neutron scattering
|
|
QMC
| Quantum Monte Carlo |
|
QS-NLDFT
| Quenched solid non-local (classical) density functional theory |
|
RxMC
| Reaction ensemble Monte Carlo |
| SWCNT |
Single-walled carbon nanotube
|
|
TST
| Transition state theory |
References
- S. M. Thompson, K. E. Gubbins, J. P. R. B. Walton, R. A. R. Chantry and J. S. Rowlinson, J. Chem. Phys., 1984, 81, 530–542 CrossRef CAS
 .
.
- W. Thomson, Philos. Mag., 1871, 42, 448–452
 .
.
- A. Fick, Philos. Mag., 1855, 10, 30–39
 .
.
- J. K. Percus, Phys. Rev. A: At., Mol., Opt. Phys., 1974, 9, 557–559 CrossRef CAS
 .
.
- K. Hahn, J. Kärger and V. Kukla, Phys. Rev. Lett., 1996, 76, 2762–2765 CrossRef CAS
 .
.
-
Y.-C. Liu, J. D. Moore, Q. Chen, T. Roussel, Q. Wang and K. E. Gubbins, in Diffusion Fundamentals III, ed. C. Chmelik, N. Kannelopoulos, J. Kärger and D. Theodorou, Leipziger Universitätsverlag, Athens, 2009, pp. 164–180 Search PubMed
 .
.
-
P. G. Tait, Sketch of Thermodynamics, David Douglas, Edinburgh, 2nd edn, 1877 Search PubMed
 .
.
- D. J. Evans and D. J. Searles, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 1645–1648 CrossRef
 .
.
- D. J. Evans and D. J. Searles, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 5839–5848 CrossRef CAS
 .
.
- D. J. Evans and D. J. Searles, Adv. Phys., 2002, 51, 1529–1585 CrossRef
 .
.
- D. J. Searles and D. J. Evans, J. Chem. Phys., 2000, 113, 3503–3509 CrossRef CAS
 .
.
- G. M. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Phys. Rev. Lett., 2002, 89, 050601 CrossRef CAS
 .
.
- E. M. Sevick, R. Prabhakar, S. R. Williams and D. J. Searles, Annu. Rev. Phys. Chem., 2008, 59, 603–633 CrossRef CAS
 .
.
-
C. J. Cramer, Essentials of Computational Chemsitry: Theories and Models, Wiley, Chichester, 2002 Search PubMed
 .
.
-
F. Jensen, Introduction to Computational Chemistry, Wiley, Chichester, 1999 Search PubMed
 .
.
-
R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, Cambridge, 2004 Search PubMed
 .
.
-
R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989 Search PubMed
 .
.
-
D. S. Sholl and J. Steckel, Density Functional Theory: A Practical Introduction, Wiley, Hoboken, 2009 Search PubMed
 .
.
-
J. A. Weil, J. R. Bolton and J. E. Wertz, Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, Wiley, New York, 1994 Search PubMed
 .
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
 .
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef
 .
.
- L. Hedin and B. I. Lundqvis, J. Phys. Chem., 1971, 4, 2064–2083
 .
.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS
 .
.
- R. W. Williams and D. Malhotra, Chem. Phys., 2006, 327, 54–62 CrossRef CAS
 .
.
- J. Grafenstein and D. Cremer, J. Chem. Phys., 2009, 130, 124105 CrossRef
 .
.
- A. Krishtal, K. Vanommeslaeghe, A. Olasz, T. Veszpremi, C. Van Alsenoy and P. Geerlings, J. Chem. Phys., 2009, 130, 033201
 .
.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1988, 60, 204–207 CrossRef CAS
 .
.
- E. E. Santiso and K. E. Gubbins, Mol. Simul., 2004, 30, 699–748 CrossRef CAS
 .
.
-
A. R. Leach, Molecular Modelling: Principles and Applications, Prentice Hall, Harlow, 2nd edn, 2001 Search PubMed
 .
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 0618–0622 CrossRef CAS
 .
.
- M. H. Kalos, Phys. Rev., 1962, 128, 1791–1795 CrossRef
 .
.
- M. H. Kalos, J. Comput. Phys., 1966, 1, 257–276 CrossRef
 .
.
- D. M. Ceperley, Rev. Mod. Phys., 1995, 67, 279–355 CrossRef CAS
 .
.
- D. M. Ceperley, Rev. Mod. Phys., 1999, 71, S438–S443 CrossRef
 .
.
- S. K. Jain, J. Fuhr, R. J. M. Pellenq, C. Bichara and K. E. Gubbins, Stud. Surf. Sci. Catal., 2007, 160, 169–176 CAS
 .
.
-
W. A. Harrison, Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond, Freeman, San Francisco, 1980 Search PubMed
 .
.
- M. J. S. Dewar and W. Thiel, J. Am. Chem. Soc., 1977, 99, 4899–4907 CrossRef CAS
 .
.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef CAS
 .
.
-
J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon Press, Oxford, 1982 Search PubMed
 .
.
- C. Ebner, W. F. Saam and D. Stroud, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 2264 CrossRef
 .
.
- R. Evans, Adv. Phys., 1979, 28, 143–200 CAS
 .
.
- E. Chacon, P. Tarazona and G. Navascues, J. Chem. Phys., 1983, 79, 4426–4430 CrossRef CAS
 .
.
- M. M. Telo da Gama, Mol. Phys., 1984, 52, 585–610 CrossRef CAS
 .
.
- M. M. Telo da Gama, Mol. Phys., 1984, 52, 611–630 CrossRef
 .
.
-
C. G. Gray, K. E. Gubbins and C. G. Joslin, Theory of Molecular Fluids 2. Applications, Secs. 8.2, 8.4, Clarendon Press, Oxford, 2010, in press Search PubMed
 .
.
-
C. G. Gray and K. E. Gubbins, Theory of Molecular Fluids, Clarendon Press, Oxford, 1984 Search PubMed
 .
.
- R. Henderson, Phys. Lett. A, 1974, 49, 197–198 CrossRef
 .
.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS
 .
.
- P. Tarazona, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 2672 CrossRef CAS
 .
.
- J. Wu, AIChE J., 2006, 52, 1169–1193 CrossRef CAS
 .
.
- J. Z. Wu and Z. D. Li, Annu. Rev. Phys. Chem., 2007, 58, 85–112 CrossRef CAS
 .
.
- Y. Rosenfeld, Phys. Rev. Lett., 1989, 63, 980–983 CrossRef CAS
 .
.
- Y. Rosenfeld, D. Levesque and J. J. Weis, J. Chem. Phys., 1990, 92, 6818–6832 CrossRef CAS
 .
.
- T. Vuong and P. A. Monson, Langmuir, 1998, 14, 4880–4886 CrossRef CAS
 .
.
- B. Coasne, F. R. Hung, R. J. M. Pellenq, F. R. Siperstein and K. E. Gubbins, Langmuir, 2005, 22, 194–202
 .
.
- P. I. Ravikovitch and A. V. Neimark, Langmuir, 2006, 22, 11171–11179 CrossRef CAS
 .
.
- A. Z. Panagiotopoulos, J. Chem. Phys., 2000, 112, 7132–7137 CrossRef CAS
 .
.
- E. Pitard, M. L. Rosinberg, G. Stell and G. Tarjus, Phys. Rev. Lett., 1995, 74, 4361–4364 CrossRef CAS
 .
.
- E. Kierlik, M. L. Rosinberg, G. Tarjus and E. Pitard, Mol. Phys., 1998, 95, 341–351 CrossRef CAS
 .
.
- D. W. Siderius and L. D. Gelb, Langmuir, 2009, 25, 1296–1299 CrossRef CAS
 .
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed
 .
.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2nd edn, 2002 Search PubMed
 .
.
-
J. M. Hammersley and D. C. Handscomb, Monte Carlo Methods, Methuen, London, 1964 Search PubMed
 .
.
- Lord Kelvin (W. Thomson), Philos. Mag., 1901, 2, 1–40
 .
.
-
E. Segrè, From X-Rays to Quarks, W. H. Freeman & Co, San Francisco, 1980 Search PubMed
 .
.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS
 .
.
- G. E. Norman and V. S. Filinov, High Temp., 1969, 7, 216–222
 .
.
- D. J. Adams, Mol. Phys., 1975, 29, 307–311 CAS
 .
.
- I. R. McDonald, Mol. Phys., 1972, 23, 41–58 CAS
 .
.
- W. W. Wood, J. Chem. Phys., 1968, 48, 415–434 CrossRef
 .
.
- K. S. Shing, Chem. Phys. Lett., 1985, 119, 149–151 CrossRef CAS
 .
.
- A. Z. Panagiotopoulos, Mol. Phys., 1987, 61, 813–826 CAS
 .
.
- A. Z. Panagiotopoulos, Int. J. Thermophys., 1989, 10, 447–457 CrossRef CAS
 .
.
- J. K. Johnson, A. Z. Panagiotopoulos and K. E. Gubbins, Mol. Phys., 1994, 81, 717–733 CrossRef CAS
 .
.
- W. R. Smith and B. Triska, J. Chem. Phys., 1994, 100, 3019–3027 CrossRef CAS
 .
.
- C. H. Turner, J. K. Brennan, M. Lisal, W. R. Smith, J. K. Johnson and K. E. Gubbins, Mol. Simul., 2008, 34, 119–146 CrossRef CAS
 .
.
- B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208–1209 CrossRef CAS
 .
.
- A. Rahman, Phys. Rev., 1964, 136, A405–A411 CrossRef
 .
.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS
 .
.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS
 .
.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CAS
 .
.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef
 .
.
- G. S. Heffelfinger and F. Van Swol, J. Chem. Phys., 1994, 100, 7548–7552 CrossRef CAS
 .
.
- M. Lisal, J. K. Brennan, W. R. Smith and F. R. Siperstein, J. Chem. Phys., 2004, 121, 4901–4912 CrossRef CAS
 .
.
- S. Bair, C. McCabe and P. T. Cummings, Phys. Rev. Lett., 2002, 88, 0583021
 .
.
-
S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area, and Porosity, Academic Press, London, New York, 2nd edn, 1982 Search PubMed
 .
.
- L. R. Fisher and J. N. Israelachvili, J. Colloid Interface Sci., 1981, 80, 528–541 CrossRef
 .
.
- H. K. Christenson, J. Fang and J. N. Israelachvili, Phys. Rev. B: Condens. Matter, 1989, 39, 11750–11754 CrossRef
 .
.
- J. P. R. B. Walton and N. Quirke, Mol. Simul., 1989, 2, 361–391
 .
.
- C. Lastoskie, K. E. Gubbins and N. Quirke, J. Phys. Chem., 1993, 97, 4786–4796 CrossRef CAS
 .
.
- L. D. Gelb and K. E. Gubbins, Langmuir, 1999, 15, 305–308 CrossRef CAS
 .
.
- L. D. Gelb, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573–1659 CrossRef CAS
 .
.
- N. A. Seaton, J. P. R. B. Walton and N. Quirke, Carbon, 1989, 27, 853–861 CrossRef CAS
 .
.
-
J. P. Olivier, W. B. Conklin and M. Vonszombathely, Characterization of Porous Solids III, 1994, 81–89, vol. 87 Search PubMed
 .
.
- Y. F. Yin, B. McEnaney and T. J. Mays, Carbon, 1998, 36, 1425–1432 CrossRef CAS
 .
.
- T. J. Bandosz, M. J. Biggs, K. E. Gubbins, Y. Hattori, T. Iiyama, K. Kaneko, J. Pikunic and K. T. Thomson, Chem. Phys. Carbon, 2003, 28, 41–228 Search PubMed
 .
.
-
P. I. Ravikovitch, J. Jagiello, D. Tolles and A. V. Neimark, Carbon 2001, Lexington, KY, 2001 Search PubMed
 .
.
- S. K. Bhatia, Langmuir, 2002, 18, 6845–6856 CrossRef CAS
 .
.
- A. V. Neimark, Y. Z. Lin, P. I. Ravikovitch and M. Thommes, Carbon, 2009, 47, 1617–1628 CrossRef CAS
 .
.
- J. Jagiello and J. P. Olivier, J. Phys. Chem. C, 2009, 113, 19382–19385 CrossRef CAS
 .
.
- P. Bryk, O. Pizio and S. Sokolowski, J. Chem. Phys., 2005, 122, 194904 CrossRef
 .
.
- S. Tripathi and W. G. Chapman, Phys. Rev. Lett., 2005, 94, 087801 CrossRef
 .
.
- D. Henderson, P. Bryk, S. Sokolowski and D. T. Wasan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 3896–3903 CrossRef CAS
 .
.
- D. Busath, D. Henderson and S. Sokolowski, J. Phys.: Condens. Matter, 2004, 16, S2193–S2201 CrossRef CAS
 .
.
- E. Kierlik, P. A. Monson, M. L. Rosinberg, L. Sarkisov and G. Tarjus, Phys. Rev. Lett., 2001, 87, 055701 CrossRef CAS
 .
.
- E. Kierlik, P. A. Monson, M. L. Rosinberg and G. Tarjus, J. Phys.: Condens. Matter, 2002, 14, 9295–9315 CrossRef CAS
 .
.
- L. Sarkisov and P. A. Monson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 011202 CAS
 .
.
- C. G. V. Burgess, D. H. Everett and S. Nuttall, Pure Appl. Chem., 1989, 61, 1845–1852 CAS
 .
.
- Y. Fujiwara, K. Nishikawa, T. Iijima and K. Kaneko, J. Chem. Soc., Faraday Trans., 1991, 87, 2763–2768 RSC
 .
.
-
K. Kaneko, Y. Suzuki, Y. Fujiwara and K. Nishikawa, in Characterization of Porous Solids II, ed. F. Rodriguez-Reinoso, J. Rouquerol, K. S. W. Sing and K. K. Unger, Elsevier Science Publishers B.V., Alicante, Spain, 1990, pp. 389–408 Search PubMed
 .
.
- P. L. Llewellyn, S. Bourrelly, C. Serre, Y. Filinchuk and G. Ferey, Angew. Chem., Int. Ed., 2006, 45, 7751–7754 CrossRef CAS
 .
.
- A. V. Neimark, F. X. Coudert, A. Boutin and A. H. Fuchs, J. Phys. Chem. Lett., 2010, 1, 445–449 Search PubMed
 .
.
- G. Günther, J. Prass, O. Paris and M. Schoen, Phys. Rev. Lett., 2008, 101, 086104 CrossRef
 .
.
- D. A. Kofke and E. D. Glandt, Mol. Phys., 1988, 64, 1105–1131 CAS
 .
.
- G. Günther and M. Schoen, Phys. Chem. Chem. Phys., 2009, 11, 9082–9092 RSC
 .
.
- H. Jobic, K. Hahn, J. Kärger, M. Bée, A. Tuel, M. Noack, I. Girnus and G. J. Kearley, J. Phys. Chem. B, 1997, 101, 5834–5841 CrossRef CAS
 .
.
- H. Jobic, J. Kärger and M. Bée, Phys. Rev. Lett., 1999, 82, 4260–4263 CrossRef CAS
 .
.
- F. Kapteijn, W. J. W. Bakker, G. H. Zheng, J. Poppe and J. A. Moulijn, Chem. Eng. J., 1995, 57, 145–153 CAS
 .
.
- M. G. Ahunbay, J. R. Elliott and O. Talu, J. Phys. Chem. B, 2002, 106, 5163–5168 CrossRef CAS
 .
.
- M. G. Martin, A. P. Thompson and T. M. Nenoff, J. Chem. Phys., 2001, 114, 7174–7181 CrossRef CAS
 .
.
- E. J. Maginn, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1993, 97, 4173–4181 CrossRef CAS
 .
.
- D. M. Ackerman, A. I. Skoulidas, D. S. Sholl and J. K. Johnson, Mol. Simul., 2003, 29, 677–684 CrossRef CAS
 .
.
- D. S. Sholl, Acc. Chem. Res., 2006, 39, 403–411 CrossRef
 .
.
- E. Beerdsen and B. Smit, J. Phys. Chem. B, 2006, 110, 14529–14530 CrossRef CAS
 .
.
- S. S. Chong, H. Jobic, M. Plazanet and D. S. Sholl, Chem. Phys. Lett., 2005, 408, 157–161 CrossRef CAS
 .
.
- L. S. Darken, Trans. Am. Inst. Min. Metall. Eng., 1948, 175, 184–201 Search PubMed
 .
.
- B. Smit and T. L. M. Maesen, Chem. Rev., 2008, 108, 4125–4184 CrossRef CAS
 .
.
- C. Chmelik, H. Bux, J. Caro, L. Heinke, F. Hibbe, T. Titze and J. Kärger, Phys. Rev. Lett., 2010, 104, 085902 CrossRef
 .
.
- S. J. Goodbody, K. Watanabe, D. Macgowan, J. P. R. B. Walton and N. Quirke, J. Chem. Soc., Faraday Trans., 1991, 87, 1951–1958 RSC
 .
.
- J. B. Nicholas, F. R. Trouw, J. E. Mertz, L. E. Iton and A. J. Hopfinger, J. Phys. Chem., 1993, 97, 4149–4163 CrossRef CAS
 .
.
- R. L. June, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1990, 94, 8232–8240 CrossRef CAS
 .
.
- J. Caro, M. Bulow, W. Schirmer, J. Kärger, W. Heink, H. Pfeifer and S. P. Zdanov, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 2541–2550 RSC
 .
.
- H. Jobic, M. Bée, J. Caro, M. Bulow and J. Kärger, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 4201–4209 RSC
 .
.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS
 .
.
- L. Onsager, Phys. Rev., 1931, 38, 2265–2279 CrossRef CAS
 .
.
- J. C. Maxwell, Philos. Mag., 1868, 35, 129–145
 .
.
- J. Stefan, Sitzungsber. Kais. Akad. Wiss. Wien, 2te Abt. A, 1871, 63, 63–124 Search PubMed
 .
.
- R. Krishna and J. A. Wesselingh, Chem. Eng. Sci., 1997, 52, 861–911 CrossRef CAS
 .
.
- M. Schoen and C. Hoheisel, Mol. Phys., 1984, 52, 33–56 CrossRef CAS
 .
.
- M. Schoen and C. Hoheisel, Mol. Phys., 1984, 52, 1029–1042 CrossRef CAS
 .
.
- D. L. Jolly and R. J. Bearman, Mol. Phys., 1980, 41, 137–147 CrossRef CAS
 .
.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, 2nd edn, Academic Press, London, 1986 Search PubMed
 .
.
- C. R. Kamala, K. G. Ayappa and S. Yashonath, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 061202 CrossRef CAS
 .
.
- C. R. Kamala, K. G. Ayappa and S. Yashonath, J. Phys. Chem. B, 2005, 109, 22092–22095 CrossRef CAS
 .
.
- M. J. Sanborn and R. Q. Snurr, Sep. Purif. Technol., 2000, 20, 1–13 CrossRef CAS
 .
.
- M. J. Sanborn and R. Q. Snurr, AIChE J., 2001, 47, 2032–2041 CrossRef CAS
 .
.
- C. R. Kamala, K. G. Ayappa and S. Yashonath, J. Phys. Chem. B, 2004, 108, 4411–4421 CrossRef CAS
 .
.
- L. Zhang, Y. C. Liu and Q. Wang, J. Chem. Phys., 2005, 123, 144701 CrossRef
 .
.
- A. I. Skoulidas, D. S. Sholl and R. Krishna, Langmuir, 2003, 19, 7977–7988 CrossRef CAS
 .
.
- R. Krishna and J. M. van Baten, Chem. Eng. Sci., 2009, 64, 3159–3178 CrossRef CAS
 .
.
- R. Krishna, Chem. Phys. Lett., 2000, 326, 477–484 CrossRef CAS
 .
.
- R. Krishna, Chem. Eng. Sci., 1990, 45, 1779–1791 CrossRef CAS
 .
.
- D. Dubbeldam and R. Q. Snurr, Mol. Simul., 2007, 33, 305–325 CrossRef CAS
 .
.
- F. J. Keil, R. Krishna and M. O. Coppens, Rev. Chem. Eng., 2000, 16, 71–197 Search PubMed
 .
.
-
D. N. Theodorou, R. Q. Snurr and A. T. Bell, in Comprehensive Supramolecular Chemistry, ed. G. Alberti and T. Bein, Pergamon, Oxford, 1996, vol. 7, pp. 507–548 Search PubMed
 .
.
-
J. Kärger and D. M. Ruthven, Diffusion in Zeolites and Other Microporous Solids, Wiley, New York, 1992 Search PubMed.
-
P. Heitjans and J. Kärger, Diffusion in Condensed Matter: Methods, Materials, Models, Springer, Berlin, New York, 2005 Search PubMed
 .
.
- H. Mori, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef
 .
.
-
D. N. Theodorou, personal communication
 .
.
- R. Krishna and J. M. van Baten, Chem. Eng. Sci., 2009, 64, 870–882 CrossRef CAS
 .
.
- D. G. Levitt, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8, 3050–3054 CrossRef
 .
.
- B. U. Felderhof, J. Chem. Phys., 2009, 131, 064504 CrossRef CAS
 .
.
- T. E. Harris, J. Appl. Probab., 1965, 2, 323–338 Search PubMed
 .
.
- F. Spitzer, Adv. Math., 1970, 5, 246–290 CrossRef
 .
.
- P. A. Fedders, Phys. Rev. B: Solid State, 1978, 17, 40–46 CrossRef
 .
.
- S. Alexander and P. Pincus, Phys. Rev. B: Condens. Matter, 1978, 18, 2011–2012 CrossRef
 .
.
- P. M. Richards, Phys. Rev. B: Solid State, 1977, 16, 1393–1409 CrossRef CAS
 .
.
- H. van Beijeren, K. W. Kehr and R. Kutner, Phys. Rev. B: Condens. Matter, 1983, 28, 5711–5723 CrossRef CAS
 .
.
- V. Gupta, S. S. Nivarthi, A. V. McCormick and H. T. Davis, Chem. Phys. Lett., 1995, 247, 596–600 CrossRef CAS
 .
.
- V. Kukla, J. Kornatowski, D. Demuth, I. Gimus, H. Pfeifer, L. V. C. Rees, S. Schunk, K. K. Unger and J. Kärger, Science, 1996, 272, 702–704 CAS
 .
.
- Q. H. Wei, C. Bechinger and P. Leiderer, Science, 2000, 287, 625–627 CrossRef CAS
 .
.
- C. Lutz, M. Kollmann and C. Bechinger, Phys. Rev. Lett., 2004, 93, 026001 CrossRef
 .
.
- B. H. Lin, M. Meron, B. X. Cui, S. A. Rice and H. Diamant, Phys. Rev. Lett., 2005, 94, 216001 CrossRef
 .
.
- A. Das, S. Jayanthi, H. S. M. V. Deepak, K. V. Ramanathan, A. Kumar, C. Dasgupta and A. K. Sood, ACS Nano, 2010, 4, 1687–1695 CrossRef CAS
 .
.
- D. S. Sholl and K. A. Fichthorn, J. Chem. Phys., 1997, 107, 4384–4389 CrossRef CAS
 .
.
- C. D. Ball, N. D. MacWilliam, J. K. Percus and R. K. Bowles, J. Chem. Phys., 2009, 130, 054504 CrossRef CAS
 .
.
- Q. Chen, J. D. Moore, Y. C. Liu, T. J. Roussel, Q. Wang, T. Wu and K. E. Gubbins, J. Chem. Phys., 2010, 133, 094501 CrossRef
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2000, 112, 3457–3458 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Phys. Chem. C, 2007, 111, 15995–15997 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2007, 127, 094702 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2006, 125, 244704 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2005, 122, 214503 CrossRef CAS
 .
.
- R. K. Bowles, K. K. Mon and J. K. Percus, J. Chem. Phys., 2004, 121, 10668–10673 CrossRef CAS
 .
.
- K. K. Mon, J. K. Percus and J. Yan, Mol. Simul., 2003, 29, 721–726 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2003, 119, 3343–3346 CrossRef CAS
 .
.
- K. K. Mon and J. K. Percus, J. Chem. Phys., 2002, 117, 2289–2292 CrossRef CAS
 .
.
- K. Hahn and J. Kärger, J. Phys. Chem., 1996, 100, 316–326 CrossRef CAS
 .
.
- K. Hahn and J. Kärger, J. Phys. Chem. B, 1998, 102, 5766–5771 CrossRef CAS
 .
.
- Y. C. Liu, J. D. Moore, T. J. Roussel and K. E. Gubbins, Phys. Chem. Chem. Phys., 2010, 12, 6632–6640 RSC
 .
.
- A. Striolo, Nano Lett., 2006, 6, 633–639 CrossRef CAS
 .
.
- Z. G. Mao and S. B. Sinnott, J. Phys. Chem. B, 2000, 104, 4618–4624 CrossRef
 .
.
- F. J. A. L. Cruz and E. A. Muller, Adsorption, 2009, 15, 13–22 CrossRef CAS
 .
.
- S. K. Bhatia, H. B. Chen and D. S. Sholl, Mol. Simul., 2005, 31, 643–649 CrossRef CAS
 .
.
-
M. Knudsen, The Kinetic Theory of Gases; Some Modern Aspects, Wiley, New York, 3rd edn, 1950 Search PubMed
 .
.
- J. D. Moore, J. C. Palmer, Y. C. Liu, T. J. Roussel, J. K. Brennan and K. E. Gubbins, Appl. Surf. Sci., 2010, 256, 5131–5136 CrossRef CAS
 .
.
- B. Coasne, S. K. Jain and K. E. Gubbins, Mol. Phys., 2006, 104, 3491–3499 CrossRef CAS
 .
.
- T. X. Nguyen, S. K. Bhatia, S. K. Jain and K. E. Gubbins, Mol. Simul., 2006, 32, 567–577 CrossRef CAS
 .
.
- J. Pikunic and K. E. Gubbins, Eur. Phys. J. E, 2003, 12, 35–40 CrossRef CAS
 .
.
- J. Kärger, H. Pfeifer, R. S. Vartapetian and A. M. Voloshchuk, Pure Appl. Chem., 1989, 61, 1875–1880 CrossRef
 .
.
- S. T. Cui, C. McCabe, P. T. Cummings and H. D. Cochran, J. Chem. Phys., 2003, 118, 8941–8944 CrossRef CAS
 .
.
- P. T. Cummings, H. Docherty, C. R. Iacovella and J. K. Singh, AIChE J., 2010, 56, 842–848 CAS
 .
.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586
 .
.
-
D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Cambridge University Press, Cambridge, 2nd edn, 2008 Search PubMed
 .
.
- S. T. Cui, S. A. Gupta, P. T. Cummings and H. D. Cochran, J. Chem. Phys., 1996, 105, 1214–1220 CrossRef CAS
 .
.
- S. Granick, Science, 1991, 253, 1374–1379 CrossRef CAS
 .
.
- H. W. Hu, G. A. Carson and S. Granick, Phys. Rev. Lett., 1991, 66, 2758–2761 CrossRef CAS
 .
.
- E. E. Santiso, M. K. Kostov, A. M. George, M. B. Nardelli and K. E. Gubbins, Appl. Surf. Sci., 2007, 253, 5570–5579 CrossRef CAS
 .
.
- E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477 CrossRef CAS
 .
.
- I. Coluzza, M. Sprik and G. Ciccotti, Mol. Phys., 2003, 101, 2885–2894 CrossRef CAS
 .
.
- C. Dellago, P. G. Bolhuis, F. S. Csajka and D. Chandler, J. Chem. Phys., 1998, 108, 1964–1977 CrossRef CAS
 .
.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS
 .
.
- C. H. Turner, J. K. Brennan, J. K. Johnson and K. E. Gubbins, J. Chem. Phys., 2002, 116, 2138–2148 CrossRef CAS
 .
.
- M. Lisal, J. K. Brennan and W. R. Smith, J. Chem. Phys., 2006, 124, 064712 CrossRef
 .
.
- K. Kaneko, N. Fukuzaki, K. Kakei, T. Suzuki and S. Ozeki, Langmuir, 1989, 5, 960–965 CrossRef CAS
 .
.
- C. H. Turner, J. K. Johnson and K. E. Gubbins, J. Chem. Phys., 2001, 114, 1851–1859 CrossRef CAS
 .
.
- O. Byl, P. Kondratyuk and J. T. Yates, J. Phys. Chem. B, 2003, 107, 4277–4279 CrossRef CAS
 .
.
- C. H. Turner, J. Pikunic and K. E. Gubbins, Mol. Phys., 2001, 99, 1991–2001 CrossRef CAS
 .
.
- C. H. Turner and K. E. Gubbins, J. Chem. Phys., 2003, 119, 6057–6067 CrossRef CAS
 .
.
- N. Hansen, S. Jakobtorweihen and F. J. Keil, J. Chem. Phys., 2005, 122, 164705 CrossRef
 .
.
- S. Jakobtorweihen, N. Hansen and F. J. Keil, J. Chem. Phys., 2006, 125, 224709 CrossRef CAS
 .
.
- Y. Izumi and K. Urabe, Chem. Lett., 1981, 663–666
 .
.
- W. L. Chu, X. G. Yang, X. K. Ye and Y. Wu, Appl. Catal., A, 1996, 145, 125–140 CrossRef CAS
 .
.
- E. E. Santiso, M. B. Nardelli and K. E. Gubbins, J. Chem. Phys., 2008, 128, 034704 CrossRef
 .
.
- A. Kogan, Int. J. Hydrogen Energy, 2000, 25, 1043–1050 CrossRef CAS
 .
.
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS
 .
.
- M. K. Kostov, E. E. Santiso, A. M. George, K. E. Gubbins and M. B. Nardelli, Phys. Rev. Lett., 2005, 95, 136105 CrossRef CAS
 .
.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS
 .
.
- M. Iannuzzi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 238302 CrossRef
 .
.
- G. Mills, H. Jonsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS
 .
.
-
T. L. Hill, Statistical Mechanics: Principles and Selected Applications, Dover Publications, New York, 1987 Search PubMed
 .
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef
 .
.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS
 .
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
 .
.
- J. C. Palmer, J. K. Brennan, M. M. Hurley, A. Balboa and K. E. Gubbins, Carbon, 2009, 47, 2904–2913 CAS
 .
.
- J. C. Palmer, A. Llobet, S. H. Yeon, J. E. Fischer, Y. Shi, Y. Gogotsi and K. E. Gubbins, Carbon, 2010, 48, 1116–1123 CrossRef CAS
 .
.
Footnotes |
| † Current Address: Weapons and Materials Research Directorate, United States Army Research Laboratory, Aberdeen Proving Ground, MD, USA 21005-5069. |
| ‡ Maxwell appears to be one of the first to note the breakdown of the Second Law. In his review of Tait's book (ref. 7) Maxwell writes: “Hence the Second Law of Thermodynamics is continually being violated and that to a considerable extent in any sufficiently small group of molecules belonging to any real body.” |
| § For nano-sized systems the Second Law of Thermodynamics is replaced by a fluctuation theorem that applies to small systems for short periods of time, as well as for macroscopic systems and longer times. The point is that fluctuations become increasingly important as the system is made smaller, leading to violation of the Second Law. The fluctuation theorem leads to the Second Law in the thermodynamic limit (N → ∞, ρ = N/V = constant). The predictions of this theorem have been confirmed by both molecular simulation and experiment: see ref. 12, G. M. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Phys. Rev. Lett., 2002, 89, 050601 and ref. 13, E. M. Sevick, R. Prabhakar, S. R. Williams and D. J. Searles, Annu. Rev. Phys. Chem., 2008, 59, 603–633. |
| ¶ The early history of the use of functionals and the density profile is described by Rowlinson and Widom, ref. 39. |
| || See references for the extension of C-DFT to non-spherical molecules. |
| ** A good overview of the development of density functional theory up to 2002 can be obtained from a Special Issue of J. Phys.: Condens. Matter, 2002, 14(46). |
| †† See http://www.top500.org (accessed July 25 2010). The list reports computer performance using a standardized LINPACK benchmark, to solve a set of n × n linear equations. Data for their list are mainly taken from the LINPACK Benchmark Report, J. Dongarra Performance of Various Computers Using Standard Linear Equations Software; Computer Science Technical Report Number CS–89–85; University of Tennessee, Knoxville TN; http://www.netlib.org/benchmark/performance.ps (accessed 25 July 2010). |
| ‡‡ A floating point operation (flop) is any mathematical operation (addition, subtraction, multiplication, division) done on a floating point number (a string of digits representing a real number, not a binary integer). |
| §§ See http://www.cpmd.org (accessed 25 July 2010). CPMD, Copyright IBM Corp., 1990–2010. Copyright MPI für Festkörperforschung Stuttgart 1997–2001. |
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 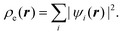
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) + Vext(rN) − μN + kBT lnρ′(rN)]
+ Vext(rN) − μN + kBT lnρ′(rN)]![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) + kBT lnρ′(rN)]
+ kBT lnρ′(rN)]![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) is the intermolecular potential energy of interaction of the molecules, both of which depend on the positions of all the molecules. The N-body external potential Vext is just a sum of one body external potentials, vext(ri), acting on molecules 1,2,…i,…. In eqn (3) and (4)ρ′(rN) is, in general, not the equilibrium probability density, but a probability density that obeys the same normalization condition as the equilibrium one. It is now possible to prove two theorems41 that parallel those of ab initio DFT: (1) at thermodynamic equilibrium, when the probability density becomes ρ′(rN) = ρ(rN), Ω[ρ′(rN)] = Ω[ρ(rN)] = Ω, the thermodynamic grand potential, and A[ρ′(rN)] = A[ρ(rN)] = Ai ≡ A − ∫drf(r)vext(r), where f(r) is the one body distribution function. Ai is the intrinsic Helmholtz energy, i.e. the Helmholtz energy minus the explicit external potential term given by the integral; and (2) Ω[ρ(rN)] = Ω is the minimum of Ω[ρ′(rN)] while A[ρ(rN)] = Ai is the minimum of A[ρ′(rN)]. The second theorem follows from the Gibbs inequality.
is the intermolecular potential energy of interaction of the molecules, both of which depend on the positions of all the molecules. The N-body external potential Vext is just a sum of one body external potentials, vext(ri), acting on molecules 1,2,…i,…. In eqn (3) and (4)ρ′(rN) is, in general, not the equilibrium probability density, but a probability density that obeys the same normalization condition as the equilibrium one. It is now possible to prove two theorems41 that parallel those of ab initio DFT: (1) at thermodynamic equilibrium, when the probability density becomes ρ′(rN) = ρ(rN), Ω[ρ′(rN)] = Ω[ρ(rN)] = Ω, the thermodynamic grand potential, and A[ρ′(rN)] = A[ρ(rN)] = Ai ≡ A − ∫drf(r)vext(r), where f(r) is the one body distribution function. Ai is the intrinsic Helmholtz energy, i.e. the Helmholtz energy minus the explicit external potential term given by the integral; and (2) Ω[ρ(rN)] = Ω is the minimum of Ω[ρ′(rN)] while A[ρ(rN)] = Ai is the minimum of A[ρ′(rN)]. The second theorem follows from the Gibbs inequality.
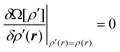
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r)],
(r)],![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r) is a smoothed or weighted average of the density,
(r) is a smoothed or weighted average of the density,![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r) = ∫dr′ρ(r′)w[|r − r′|],
(r) = ∫dr′ρ(r′)w[|r − r′|],![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (r) ≈ ρ(r), the local fluid density at point r) was used. The local version of C-DFT is useful for studies of fluid–fluid interfaces, including liquid crystal phases and surfactant solutions, although it predicts fluid densities that are, in general, too low. More seriously, the local theory fails for highly inhomogeneous fluids and solids, particularly crystals and fluids near solid surfaces, where very large density variations occur over atomic scale distances.
(r) ≈ ρ(r), the local fluid density at point r) was used. The local version of C-DFT is useful for studies of fluid–fluid interfaces, including liquid crystal phases and surfactant solutions, although it predicts fluid densities that are, in general, too low. More seriously, the local theory fails for highly inhomogeneous fluids and solids, particularly crystals and fluids near solid surfaces, where very large density variations occur over atomic scale distances.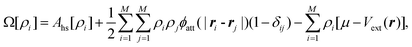
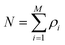 , replacing the integration in eqn (5) with the sum over the lattice sites. Following Tarazona's approach, they also developed non-local weighting and free energy functionals for the reference hard sphere fluid, which were parameterized with the use of lattice Monte Carlo simulations. Full details of their method may be found in the supporting information of ref. 60. The computational savings due to the discretization enables the lattice C-DFT to be used in systems with low dimensional symmetry and can be applied to study fluid behavior in three-dimensional porous structures.
, replacing the integration in eqn (5) with the sum over the lattice sites. Following Tarazona's approach, they also developed non-local weighting and free energy functionals for the reference hard sphere fluid, which were parameterized with the use of lattice Monte Carlo simulations. Full details of their method may be found in the supporting information of ref. 60. The computational savings due to the discretization enables the lattice C-DFT to be used in systems with low dimensional symmetry and can be applied to study fluid behavior in three-dimensional porous structures.
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) , and then computing the desired thermodynamic properties by taking ensemble-weighted averages. For systems with realistic complexity, the number of unique configurations is nearly innumerable and this direct approach is well beyond computational capabilities of even the fastest massively parallel supercomputers for the foreseeable future.
, and then computing the desired thermodynamic properties by taking ensemble-weighted averages. For systems with realistic complexity, the number of unique configurations is nearly innumerable and this direct approach is well beyond computational capabilities of even the fastest massively parallel supercomputers for the foreseeable future.
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)m. Here xi represents the set of coordinates needed to specify the position, orientation and conformation of molecule i; for a spherical molecule, such as argon, these would just be the 3 Cartesian coordinates for the center of mass, but for a larger molecule such as n-hexane there would be additional coordinates needed to define the orientation of the equilibrium conformer relative to space-fixed axes and additional coordinates to define the intramolecular structure of the molecule. We now choose a molecule at random and move or rotate it a random amount to produce a new configuration, n, with coordinates (x1,x2,x3,…xN)n ≡ (xN)n with potential energy
(xN)m. Here xi represents the set of coordinates needed to specify the position, orientation and conformation of molecule i; for a spherical molecule, such as argon, these would just be the 3 Cartesian coordinates for the center of mass, but for a larger molecule such as n-hexane there would be additional coordinates needed to define the orientation of the equilibrium conformer relative to space-fixed axes and additional coordinates to define the intramolecular structure of the molecule. We now choose a molecule at random and move or rotate it a random amount to produce a new configuration, n, with coordinates (x1,x2,x3,…xN)n ≡ (xN)n with potential energy ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)n. The change in potential energy of interaction due to the move is Δ
(xN)n. The change in potential energy of interaction due to the move is Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) =
= ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)n −
(xN)n − ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (xN)m. The condition of detailed balance states that at equilibrium the rate of change from configuration m to n must equal the rate for the reverse change, from configuration n to m. This condition is necessary for thermodynamic equilibrium to be maintained once it is reached. The rate of change from m to n is proportional to the probability that the system is initially in state m, ρm, multiplied by the probability of acceptance of the change, pmn(m → n); similarly, the rate of the reverse change from n to m is proportional to ρn, the probability of observing the system in state n multiplied by the probability of acceptance of the change, pnm(n → m), i.e. ρmpmn(m → n) = ρnpnm(n → m) or
(xN)m. The condition of detailed balance states that at equilibrium the rate of change from configuration m to n must equal the rate for the reverse change, from configuration n to m. This condition is necessary for thermodynamic equilibrium to be maintained once it is reached. The rate of change from m to n is proportional to the probability that the system is initially in state m, ρm, multiplied by the probability of acceptance of the change, pmn(m → n); similarly, the rate of the reverse change from n to m is proportional to ρn, the probability of observing the system in state n multiplied by the probability of acceptance of the change, pnm(n → m), i.e. ρmpmn(m → n) = ρnpnm(n → m) or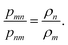
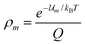
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) i/kBT is the canonical partition function. Thus if we choose the canonical set of independent variables eqn (14) gives
i/kBT is the canonical partition function. Thus if we choose the canonical set of independent variables eqn (14) gives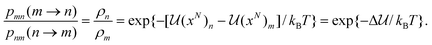
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) , is calculated. If the energy change is negative, i.e. the energy is more attractive as a result of the move, the attempted move is accepted, while if it is positive, i.e. less attractive, the move is accepted with a probability Pacc= e−Δ
, is calculated. If the energy change is negative, i.e. the energy is more attractive as a result of the move, the attempted move is accepted, while if it is positive, i.e. less attractive, the move is accepted with a probability Pacc= e−Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) /kBT. These two cases can be summarized by the acceptance probability:
/kBT. These two cases can be summarized by the acceptance probability:![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) /kBT)
/kBT)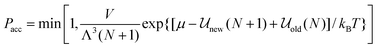
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) new is the configurational energy of interaction after the insertion, so that the system now contains N + 1 molecules, and
new is the configurational energy of interaction after the insertion, so that the system now contains N + 1 molecules, and ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) old is the energy of the original N particle system. Similarly the criterion for particle deletion is:
old is the energy of the original N particle system. Similarly the criterion for particle deletion is: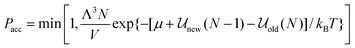
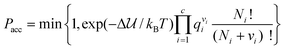
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) is the change in the intermolecular potential energy due to the reaction move, c is the total number of species in the reaction, qi is the molecular (ideal gas reference state) partition function for species i, and Ni and νi are the number of molecules and the stoichiometric coefficient of species i. These reaction ensemble methods determine the composition at chemical equilibrium and they have been widely used to study the effects of confinement in pores on reaction equilibria, and can be used to study effects of other reaction environments, such as reactions in liquid or supercritical solvents, in reverse micelles, in nanocomposites, etc. For a recent review of the method and its applications see ref. 76.
is the change in the intermolecular potential energy due to the reaction move, c is the total number of species in the reaction, qi is the molecular (ideal gas reference state) partition function for species i, and Ni and νi are the number of molecules and the stoichiometric coefficient of species i. These reaction ensemble methods determine the composition at chemical equilibrium and they have been widely used to study the effects of confinement in pores on reaction equilibria, and can be used to study effects of other reaction environments, such as reactions in liquid or supercritical solvents, in reverse micelles, in nanocomposites, etc. For a recent review of the method and its applications see ref. 76.
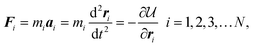
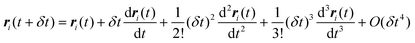
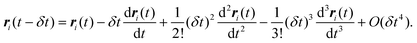
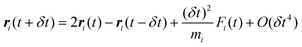
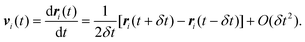
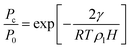
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is the surface area. While Q, and hence A, are always well defined however small the system, surface tension is not, since it requires the presence of a well defined interface.
is the surface area. While Q, and hence A, are always well defined however small the system, surface tension is not, since it requires the presence of a well defined interface.![The variation of reduced surface tension, , with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f1.gif)
 , with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.]
, with drop radius, Re, at two reduced temperatures, as determined by molecular dynamics simulation. Here γs is the surface tension, and σ and ε are the Lennard-Jones molecular size and energy well depth parameters, respectively. [Reprinted with permission from ref. 1. Copyright 1984, American Institute of Physics.]![Filling pressures predicted by the Kelvin equation (dotted line), local C-DFT (dashed line) and non-local C-DFT (solid line) at various pore widths for N2 in carbon slit pores. [Adapted from ref. 90.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f2.gif)
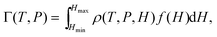
![(a) Comparison of the experimental isotherms (circles) and the fits obtained using non-local C-DFT (solid line) and QS-NLDFT (dashed line) for argon at 87.3 K on CM-E2 microporous carbon synthesized from coconut shell. Both the non-local C-DFT and QS-NLDFT are based on Rosenfeld's52,53 fundamental measure theory. (b) The estimates of the PSD for CM-E2 obtained using non-local C-DFT (circles) and QS-NLDFT (squares). The effect of spurious layering transitions is seen in the non-local C-DFT fit to the experimental isotherm at P/Po ≈ 10−3 (a). The final result is an artificial gap in the PSD at H ≈ 10 Å (b). The QS-NLDFT model corrects this behavior by adding effective surface roughness to the slit pore model. [Adapted from ref. 99.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f3.gif)
![Theoretical predictions of H2 adsorption on isoreticular MOF-1 at 298 K, using the lattice C-DFT of Siderius and Gelb (solid-line), lattice grand canonical Monte Carlo simulations (diamonds) and off-lattice grand canonical simulations taken from the literature (circles). [Adapted from ref. 60.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f4.gif)
![(left) Adsorption and desorption isotherms given as dimensionless fluid density (ρf = number of molecules/number of lattice sites) versus the reduced chemical potential, μ/wff, for wmf/wff = 1.5 and T* = 0.8, where wmf and wff are the matrix–fluid and fluid–fluid lattice interaction parameters, respectively. The adsorption branches of the isotherms are shown (filled circles), along with two scanning curves starting from the adsorption branch (open circles). (right) Location of local minima in the grand potential (crosses) and the equilibrium isotherm (solid line) formed connecting the states of lowest grand potential. The density of the solid matrix was set to 0.25 for the calculations. [Reprinted with permission from ref. 105, Copyright 2001, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f5.gif)
![Sorption strain for cyclopentane, C5H12, as a function of the reduced pressure, where P0+ is the bulk pressure at which condensation occurs. The filled circles are experimental results from in situ X-ray diffraction experiments, while open circles are results of the model with κ = 30ε/σ2 and the solid line is a visual guide. [Reprinted with permission from ref. 113. Copyright 2008, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f6.gif)
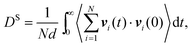
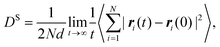
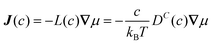
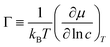
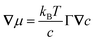
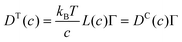
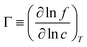
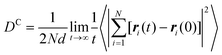
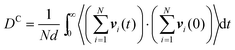
![The three different types of diffusivities compared between simulation and experiment. In (a) the self-diffusivity of methane in MFI-type silicate as a function of adsorbate loading is shown. Simulation results (closed symbols) are compared from various researchers: Beerdsen and Smit124 (circles), Goodbody et al.129 (squares), Nicholas et al.130 (triangles), June et al.131 (downward triangles). Experimental results (open symbols) using various techniques are also shown: Caro et al.132 using PFG-NMR (circles), Jobic et al. using PFG-NMR (squares) and QENS (triangles)133 and Kapteijn et al.118 using membrane permeation experiments (downward triangles). [Adapted from ref. 124.] All data are at 300 K except for the experimental results of Jobic et al.133 (PFG-NMR and QENS) which are at 250 K. In (b) the self-,collective-, and transport-diffusivities of ethane in silicate are shown at room temperature. Simulation data (closed symbols) are shown for all three, but experimental (open symbols) (QENS) comparison is also shown for the collective and transport diffusivities. The authors did not report experimental data for the self-diffusivity. [Adapted from ref. 125.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f7.gif)
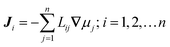
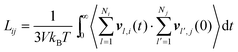
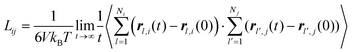
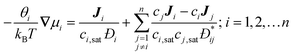
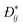 are known as the Maxwell–Stefan exchange coefficients (which include the effects of interactions between species j on the motion of species i).
are known as the Maxwell–Stefan exchange coefficients (which include the effects of interactions between species j on the motion of species i).
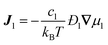
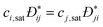
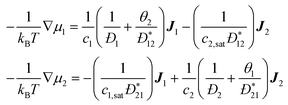
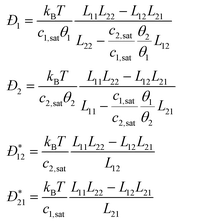
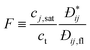
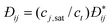 is plotted against the total concentration for the adsorbed phases. Krishna and van Baten150 have shown that the predictability of this model extends to other types of zeolites, metal–organic frameworks (MOF), and covalent organic frameworks (COF) as well as to the Maxwell–Stefan diffusivities Đi.
is plotted against the total concentration for the adsorbed phases. Krishna and van Baten150 have shown that the predictability of this model extends to other types of zeolites, metal–organic frameworks (MOF), and covalent organic frameworks (COF) as well as to the Maxwell–Stefan diffusivities Đi.
![Maxwell–Stefan binary exchange coefficients, , for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as . Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f8.gif)
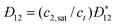 , for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as
, for the diffusion of an equimolar mixture of methane (C1, component 1) and argon (Ar, component 2) in cylindrical silica pores at 300 K. In (a) mesopore diameters of 2, 3 and 4 nm are shown and in (b) micropore diameters of 0.6, 0.75 and 1 nm are shown. The data are shown at 300 K as a function of the total fluid concentration, ct. A comparison is also shown for the value of Đ12 obtained for liquid mixtures of methane and argon (Đ12,fl). For mesopores, the binary exchange coefficients are approximately equivalent to the values calculated for liquid mixtures, while for micropores, a correction factor is needed to obtain agreement. The correction factor is defined as 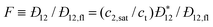 . Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.]
. Data for 1–4 nm pores are from ref. 160. Data for smaller pores are from ref. 150 but obtained using the same methods. The lines shown are fits to the liquid mixture data or those fits scaled by the correction factor F. [Reprinted with permission from ref. 150. Copyright 2009, Elsevier.]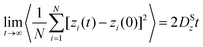
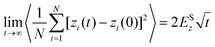
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 or greater, although the needed system size depends on density.189
000 or greater, although the needed system size depends on density.189![(a) Mean-squared displacements for single-file LJ fluids (σff = 0.383 nm, ε/k = 164 K, approximately that of CF4) in perfect cylindrical pores of effective diameter 0.623 nm at different system sizes (number of adsorbate molecules) at 20% relative occupancy and 300 K. For small numbers of molecules, a finite limiting value of the mean-squared displacement is observed as a result of strong correlation effects. For larger system sizes, the correlation effect appears at longer times. These results were from microcanonical MD simulations. The slope of the MSD for the largest system size at long times is 1, which is not the expected result for a single-file fluid (see text). [Adapted from ref. 187.] (b) Time dependence of the mean-squared displacement for single-file LJ fluids (σ = 0.383 nm, ε/k = 164 K, approximately that of CF4) in a perfect cylinder of effective diameter 0.623 nm at 20 % relative occupancy and 300 K from a microcanonical (N,V,E) MD simulation (line) using 10 000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f9.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.]
000 fluid atoms and a microcanonical MD simulation where random forces have been periodically added to alter the fluid velocities using 4000 fluid atoms (dashed). The slope of the MSD at the longest times is 1 without random forces but 1/2 when random forces are added. Reference lines (dotted) illustrating t1 and t1/2 dependence of the MSD are also shown. [Adapted from ref. 187.]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particle system, even though the particles were in single-file confinement. This is due to a violation of a random walk. This is further illustrated in Fig. 9b. In Fig. 9b, the MSDs for a single-file fluid using a MD simulation in the microcanonical (N,V,E) ensemble with and without random forces added to the adsorbate velocities are shown. The MSD for the microcanonical simulation without random forces exhibits a slope on a log–log scale equal to 1, which would normally be indicative of Fickian diffusion (see eqn (48)). However, the fluid is in single-file confinement, and the particles do not pass each other. When a random walk is imposed upon the system by adding random forces to the particles during the MD simulation, the slope of the MSD on the log–log scale becomes 1/2, indicative of single-file diffusion (see eqn (49)). It can be shown theoretically that the square root of time dependence of the mean-squared displacement results from a random walk.162 Perfectly cylindrical pores, as used in the work of Hahn and Kärger,187 are completely smooth. Thus, the standard microcanonical simulations without random forces exhibit purely specular reflection of the particles colliding with the wall, and any diffusive reflection of particles is absent. Because the fluid is constrained in a single dimension, fluid–fluid collisions do not create a random walk. Thus, the absence of a random walk from collisions for fluid–fluid and fluid–wall interactions results in the absence of the square root of time dependence of the MSD. Adding random forces to the particle velocities mimicks diffusive collisions with the walls, but it is not a real effect for perfectly cylindrical pores.
000 particle system, even though the particles were in single-file confinement. This is due to a violation of a random walk. This is further illustrated in Fig. 9b. In Fig. 9b, the MSDs for a single-file fluid using a MD simulation in the microcanonical (N,V,E) ensemble with and without random forces added to the adsorbate velocities are shown. The MSD for the microcanonical simulation without random forces exhibits a slope on a log–log scale equal to 1, which would normally be indicative of Fickian diffusion (see eqn (48)). However, the fluid is in single-file confinement, and the particles do not pass each other. When a random walk is imposed upon the system by adding random forces to the particles during the MD simulation, the slope of the MSD on the log–log scale becomes 1/2, indicative of single-file diffusion (see eqn (49)). It can be shown theoretically that the square root of time dependence of the mean-squared displacement results from a random walk.162 Perfectly cylindrical pores, as used in the work of Hahn and Kärger,187 are completely smooth. Thus, the standard microcanonical simulations without random forces exhibit purely specular reflection of the particles colliding with the wall, and any diffusive reflection of particles is absent. Because the fluid is constrained in a single dimension, fluid–fluid collisions do not create a random walk. Thus, the absence of a random walk from collisions for fluid–fluid and fluid–wall interactions results in the absence of the square root of time dependence of the MSD. Adding random forces to the particle velocities mimicks diffusive collisions with the walls, but it is not a real effect for perfectly cylindrical pores.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 argon atoms were in the interstitial channels of the bundle; thus the size correlation effects shown by Hahn and Kärger187 were alleviated. These interstitial channels were corrugated, as they were composed of the outside of three adjacent carbon nanotubes. This resulted in the MSD of the diffusing interstitial argon atoms having a square-root of time dependence (eqn 49), shown in Fig. 10b. The MSDs of the argon atoms diffusing in the carbon nanotubes had a linear time dependence, indicative of Fickian diffusion (eqn 48). The MSD of the entire system also had a linear time dependence at all but the lowest pressures, as it was dominated by the much faster diffusion inside the carbon nanotubes. Furthermore, the authors observed that when large system sizes were used, the flexibility of the CNTs had negligible influence on the diffusion of argon.
000 argon atoms were in the interstitial channels of the bundle; thus the size correlation effects shown by Hahn and Kärger187 were alleviated. These interstitial channels were corrugated, as they were composed of the outside of three adjacent carbon nanotubes. This resulted in the MSD of the diffusing interstitial argon atoms having a square-root of time dependence (eqn 49), shown in Fig. 10b. The MSDs of the argon atoms diffusing in the carbon nanotubes had a linear time dependence, indicative of Fickian diffusion (eqn 48). The MSD of the entire system also had a linear time dependence at all but the lowest pressures, as it was dominated by the much faster diffusion inside the carbon nanotubes. Furthermore, the authors observed that when large system sizes were used, the flexibility of the CNTs had negligible influence on the diffusion of argon.![(a) Argon adsorbed in a (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. (b) The mean-squared displacements of argon in the (25,0) single-walled carbon nanotube bundle at a relative pressure of P/Po = 1.2 × 10−4. The slope of the mean-squared displacements for the atoms in the interstitial sites is ½ on the log–log scale, indicative of single-file diffusion while that for the atoms diffusing in the nanotubes as well as for the total bundle is 1, indicative of Fickian diffusion. Simulations using a rigid carbon nanotube bundle are indicated by the solid line, while simulations using a flexible nanotube bundle are indicated with open symbols. The MSDs for the rigid and flexible bundles are nearly identical, indicating that influence of the carbon nanotube flexibility on diffusion is negligible. [Adapted from ref. 189.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f10.gif)
![Mean-squared displacements of LJ particles (σ = 0.383 nm, ε/kB = 164 K, approximately that of CF4) in different diameters, d, of perfect cylinders. [Adapted from ref. 188.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f11.gif)
![Self-diffusivity as a function of relative pressure for argon confined at 77 K in CS1000A (model of a saccharose-based porous carbon) from MD simulation. A maximum in the self-diffusion coefficient exists in the region roughly corresponding to the pore filling region of the isotherm. [Reprinted with permission from ref. 196. Copyright 2006, Taylor & Francis, Ltd.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f12.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≡ ∂ux/∂y, where ux is the streaming velocity in the x direction of flow and y is the direction of the flow gradient.
≡ ∂ux/∂y, where ux is the streaming velocity in the x direction of flow and y is the direction of the flow gradient.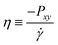
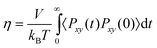
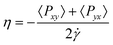
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) is the shear rate.
is the shear rate.
![Comparison of the shear viscosity (η) as a function of shear rate () from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f13.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ) from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.]
) from NEMD and experiment for a six-layer n-dodecane film confined between mica surfaces. Constant film thickness simulations200 have been performed at constant stress (open squares), constant streaming velocity (open circles), and constant streaming velocity at atmospheric pressure (open diamond). Surface force apparatus experiments206 are shown for results where amplitude was varied at constant frequency (closed squares) and frequency varied at constant amplitude (closed circles). The dashed line indicates the constant Newtonian viscosity plateau for bulk dodecane with calculated values of the bulk viscosity (open triangles). [Adapted from ref. 200.]![Conversion of the NO dimerization reaction within slit-shaped carbon pores, ranging from 0.95–1.59 nm in width, predicted from RxMC simulation. The bulk phase pressure is 0.16 bar, and the corresponding conversion in the bulk phase is shown for comparison. [Adapted from ref. 215.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f14.gif)
![Effect of capillary condensation on the mole fraction of dimers and monomers as a function of bulk pressure for the NO dimerization reaction within a slit-shaped carbon pore of width H/σNO = 5.5, at 122.5 K. Open and closed circles correspond to monomers and dimers, respectively, and vertical jumps represent capillary condensation. [Adapted from ref. 215.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f15.gif)
![RxMC results for the esterification reaction at 523.15 K for the reaction carried out in the bulk phase, and in bare carbon slit pores, and carbon slit pores activated by decorating the carbon surfaces with –COOH groups (density 1.82 groups per nm2). The bulk phase pressure is 1.0 bar. [Adapted from ref. 218.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f16.gif)
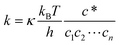
![TST-RxMC simulations of the hydrogen iodide decomposition rate at 573.15 K in the bulk phase (solid circles) and in carbon nanotubes of different diameters: (8,8) nanotube (open squares, internal diameter d = 1.09 nm) and (10,10) nanotube (open diamonds, d = 1.36 nm). Here k is the reaction rate constant at the pressure shown in the figure, k0 is the rate constant at the standard state condition of 1 bar. [Adapted from ref. 212.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f17.gif)
![Energy as a function of C–C torsion angle for an isolated n-butane molecule from DFT. Open triangles denote the 4 stationary points (the syn, gauche, eclipsed and anti isomers). [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f18.gif)
![Energy as a function of C–C torsion angle for n-butane confined within slit carbon pores of various widths. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f19.gif)
![Arrhenius plots of the rate constant for n-butane as calculated from transition state theory for the anti–gauche transition for the gas phase and larger pore widths, which becomes the anti–syn transition for smaller pores (see Fig. 19). Labels to the right are the pore width. [Reprinted with permission from ref. 223. Copyright 2008, American Institute of Physics.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f20.gif)
![Top and side views of (a) the initial state, (b) intermediate complex, (c) transition state, and (d) final conformation for a favorable dissociation pathway over a vacancy in a (10,10) nanotube. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f21.gif)
![Ideal-gas equilibrium yields (fraction of water converted to hydrogen at equilibrium in % mole) for the dissociation of water in the bulk gas phase, over a single vacancy in graphene, and over a single vacancy in a (10,10) carbon nanotube. The values correspond to a pressure of 1 bar and an initial equimolar mixture of water and vacancies. [Reprinted with permission from ref. 226. Copyright 2005, American Physical Society.]](/image/article/2011/CP/c0cp01475c/c0cp01475c-f22.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fold over 16 years). The Office of Science at the U.S. Department of Energy plans to develop 250 Pflop machines by 2015, and an Exaflop (1018 flops) machine by 2018. Of equal importance to these improvements in computer hardware have been major advances in computational methods and algorithms. These have led to a further speedup of several orders of magnitude over the same time period. They have included the development of efficient parallelized quantum mechanics and molecular dynamics codes; examples of the former include CPMD (Car–Parinello Molecular Dynamics)§§ and Quantum ESPRESSO,231 and of the latter the NAMD (NAnoscale Molecular Dynamics)232 and LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)233 codes.
000 fold over 16 years). The Office of Science at the U.S. Department of Energy plans to develop 250 Pflop machines by 2015, and an Exaflop (1018 flops) machine by 2018. Of equal importance to these improvements in computer hardware have been major advances in computational methods and algorithms. These have led to a further speedup of several orders of magnitude over the same time period. They have included the development of efficient parallelized quantum mechanics and molecular dynamics codes; examples of the former include CPMD (Car–Parinello Molecular Dynamics)§§ and Quantum ESPRESSO,231 and of the latter the NAMD (NAnoscale Molecular Dynamics)232 and LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator)233 codes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
