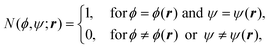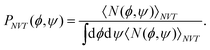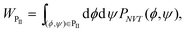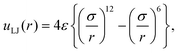Optimization of partial multicanonical molecular dynamics simulations applied to an alanine dipeptide in explicit water solvent†
Received
27th April 2010
, Accepted 28th July 2010
First published on 29th October 2010
Abstract
The partial multicanonical algorithm for molecular dynamics and Monte Carlo simulations samples a wide range of an important part of the potential energy. Although it is a strong technique for structure prediction of biomolecules, the choice of the partial potential energy has not been optimized. In order to find the best choice, partial multicanonical molecular dynamics simulations of an alanine dipeptide in explicit water solvent were performed with 15 trial choices for the partial potential energy. The best choice was found to be the sum of the electrostatic, Lennard-Jones, and torsion-angle potential energies between solute atoms. In this case, the partial multicanonical simulation sampled all of the local-minimum free-energy states of the PII, C5, αR, αP, αL, and Cax7 states and visited these states most frequently. Furthermore, backbone dihedral angles ϕ and ψ rotated very well. It is also found that the most important term among these three terms is the electrostatic potential energy and that the Lennard-Jones term also helps the simulation to overcome the steric restrictions. On the other hand, multicanonical simulation sampled all of the six states, but visited these states fewer times. Conventional canonical simulation sampled only four of the six states: The PII, C5, αR, and αP states.
I. Introduction
Biomolecules like proteins and peptides have complicated free-energy surfaces with many local minima. An important problem is to predict the structures of these biomolecules theoretically or computationally. Conventional molecular dynamics (MD) and Monte Carlo (MC) simulations in physical ensembles, such as the canonical ensemble,1–4 tend to get trapped in these local-minimum states and give inaccurate conformational results. Generalized-ensemble algorithms5–9 are powerful techniques to avoid this difficulty. One of the most well-known generalized-ensemble algorithms is the multicanonical ensemble algorithm.10–13 A non-Boltzmann weight factor is employed in this ensemble so that a free one-dimensional random walk can be realized in the potential-energy space. Thus, a simulation with this algorithm can escape from the free-energy-minimum states and sample a wide range of the conformational space. Because of this advantage, the multicanonical algorithm has frequently been applied to a biomolecule, which has a free-energy surface with many local minima. Modification of the multicanonical algorithm has also been proposed.14–33
The non-Boltzmann weight factor in the multicanonical algorithm is not a priori known and has to be determined by a preliminary simulation.34–36 As the system size increases, the distribution of the total potential energy P(E) gets narrower in proportion to 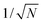 , where N is the number of atoms. Thus, the determination of the multicanonical weight factor to give a flat distribution becomes difficult in a large system. New techniques are desired to reduce the effort for the weight-factor determination with keeping the high sampling efficiency. The multicanonical algorithm covers a wide range of the total potential energy. The total potential energy of a biomolecular system includes bond-length, bond-angle, torsion-angle, improper torsion-angle, Lennard-Jones, and electrostatic energy terms for most of the force fields.37–41 However, it is redundant to sample a wide range of all these terms.
, where N is the number of atoms. Thus, the determination of the multicanonical weight factor to give a flat distribution becomes difficult in a large system. New techniques are desired to reduce the effort for the weight-factor determination with keeping the high sampling efficiency. The multicanonical algorithm covers a wide range of the total potential energy. The total potential energy of a biomolecular system includes bond-length, bond-angle, torsion-angle, improper torsion-angle, Lennard-Jones, and electrostatic energy terms for most of the force fields.37–41 However, it is redundant to sample a wide range of all these terms.
The author proposed recently the partial multicanonical ensemble algorithm for MD and MC simulations,25 in which only an important part of potential-energy terms, instead of the total potential energy, are sampled widely. The partial potential energy terms can, in principle, be chosen arbitrarily. The purpose of this article is to optimize the choice of the partial potential energy terms. For this purpose, the partial multicanonical MD simulations of an alanine dipeptide are performed in explicit water and many choices of the partial potential energy are tested. Conventional canonical and multicanonical MD simulations are performed, too. Their sampling efficiencies are compared with the partial multicanonical MD simulations. The author also discusses which potential energy term contributes most to sample many conformations. The alanine dipeptide has been studied theoretically extensively as a model biomolecule because of its simplicity (see, for example, ref. 23–25 and 42–49).
In section II the partial multicanonical algorithm is explained. The computational details of the alanine dipeptide simulations are described in section III. The results and discussion are presented in section IV. Section V is devoted to conclusions.
II. Methods
In the canonical ensemble, the distribution PNVT(E) of the total potential energy E is given bywhere n(E) is the density of states, β0 is the inverse of the product of the Boltzmann constant kB and the absolute temperature T0, at which simulations are performed. This ensemble has a bell-shaped distribution in the potential-energy space.
In the multicanonical ensemble,10–13 every state is sampled with a weight factor Wmuca(E) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp{−β0Emuca(E)} so that a uniform distribution of E may be obtained:
exp{−β0Emuca(E)} so that a uniform distribution of E may be obtained:
| | | Pmuca(E) = n(E) Wmuca(E) = n(E) exp{−β0Emuca(E)} = constant, | (2) |
where
Emuca(
E) and
Wmuca(
E) are referred to as the multicanonical energy and the multicanonical weight factor, respectively. The difference between
Emuca and
E is written as
δE(
E):
Emuca(
E)
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E
E +
δE(
E). The difference
δE(
E) is additional potential energy which is introduced to obtain a flat distribution of
E in
eqn (2). The case of
δE(
E) = 0 gives the regular canonical ensemble. The multicanonical simulation covers a wide range of
E and escapes from local-minimum free-energy states. The expectation value of a physical quantity
A at temperature
T is obtained by reweighting techniques
50 from
| | 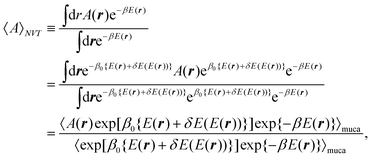 | (3) |
where 〈⋯〉
muca is the multicanonical ensemble average, which is defined as 〈⋯〉
muca ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
∫d
r⋯e
−β0{E(r)+δE(E(r))}/∫d
re
−β0{E(r)+δE(E(r))}. The vector
r is the set of coordinates
r ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
{
r1,…,
rN}. Because of the random walks in the potential-energy space, we can calculate physical quantities in a wide range of
T.
Although the multicanonical algorithm is a powerful technique, the multicanonical weight factor Wmuca(E) or the multicanonical energy Emuca(E) is not a priori known and has to be determined in advance of the simulation for data collection, for example, by the iterations of short simulations.34–36 The determination of the multicanonical weight factor is time consuming for a larger system. In order to alleviate the effort to determine the weight factor, the total potential energy is divided into two terms in the partial multicanonical algorithm:
where
E1 is the part of the total potential energy which needs to be sampled for a wide range of conformational space. The partial potential energy
E1 can be composed of any of the components of
E, in principle. The second term
E2 is the rest of the potential energy. The partial multicanonical algorithm ensures that the wide range of
E1 is efficiently sampled. The partial multicanonical simulation is performed with a weight factor
Wpmuca(
E1,
E2)
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
exp{−
β0Epmuca(
E1,
E2)} so that a uniform distribution of
E1 may be obtained:
| | 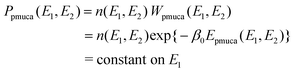 | (5) |
where
Epmuca(
E1,
E2) and
Wpmuca(
E1,
E2) are referred to as the partial multicanonical energy and the partial multicanonical weight factor, respectively. This equation means that
Ppmuca(
E1,
E2) depends on
E2 but is independent of
E1. The difference between
Epmuca and
E depends only on
E1 and is written as
δE1(
E1):
| | Epmuca(E1, E2) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E1 + E2 + δE1(E1) = E + δE1(E1). E1 + E2 + δE1(E1) = E + δE1(E1). | (6) |
The difference
δE1(
E1) is characteristic of the partial multicanonical simulation. If we define here a distribution
Ppmuca(
E1) of
E1 and the density of states
n(
E1) of
E1 as
| | Ppmuca(E1) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dE2Ppmuca(E1, E2), ∫dE2Ppmuca(E1, E2), | (7) |
| | n(E1) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dE2n(E1, E2)exp(−β0E2), ∫dE2n(E1, E2)exp(−β0E2), | (8) |
Eqn (5) is rewritten as
| | 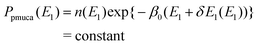 | (9) |
The expectation value of a physical quantity
A is obtained by the reweighting techniques
50 from
| | 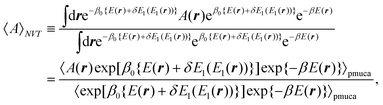 | (10) |
where 〈⋯〉
pmuca is the partial multicanonical ensemble average, which is defined as 〈⋯〉
pmuca ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
∫d
r⋯e
−β0{E(r)+δE1(E1(r))}/∫d
re
−β0{E(r)+δE1(E1(r))}. Note that 〈
A〉
NVT can be calculated correctly at a temperature
T only in the vicinity of
T0, although 〈
A〉
NVT can be calculated in a wide range of
T in the multicanonical algorithm. It is because a limited range of
E2 is sampled with the normal Boltzmann weight factor exp(−
β0E2) in the partial multicanonical algorithm.
The scheme of the partial multicanonical algorithm includes the canonical and the multicanonical algorithms. In the case of E1 = 0 and E2 = E, this algorithm becomes the regular canonical algorithm as a limiting case. This is because eqn (5) becomes the canonical distribution as Ppmuca(E) = n(E) exp(−β0E). In the case of E1 = E and E2 = 0, the multicanonical algorithm is obtained because eqn (5) becomes the multicanonical distribution as Ppmuca(E) = n(E) exp{−β0(E + δE)} = constant. Furthermore, if we take E1 as the sum of the potential energy between solute atoms Eslt–slt and that of the solute–solvent interaction Eslt–svn (i.e., E1 = Eslt–slt + Eslt–svn) and E2 as the potential energy between solvent atoms Esvn–svn (i.e., E2 = Esvn–svn), the partial multicanonical algorithm gives the selectively enhanced multicanonical algorithm.17 The partial multicanonical algorithm can be applied not only to an explicit solvent model but also to an implicit solvent model, in a similar way to the combination of the multicanonical algorithm and the RISM theory.51
A constant-temperature MD method is employed to perform a partial multicanonical MD simulation. One of the representative constant-temperature methods is the Nosé thermostat.1,2 The partial multicanonical Hamiltonian based on the Nosé thermostat is given by
| | 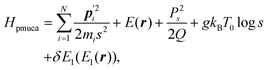 | (11) |
where
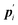
is the conjugate momentum for
ri. The real momentum
pi is related to the virtual momentum
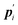
by
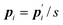
. The variable
s is the additional degree of freedom for the Nosé thermostat. The variable
Ps is the conjugate momentum for
s. The constant
mi is the mass of atom
i and
Q is the artificial “mass” related to
s. The real time interval Δ
t is related to the virtual time interval Δ
t′ by Δ
t = Δ
t′/
s. In the case of a system consisting of
N atoms,
g equals 3
N if the time development is performed in the real time
t, or
g equals 3
N + 1 if the time development is performed in virtual time
t′.
The equations of motion in the real time development are derived from the Hamiltonian in eqn (11). In the Nosé-Hoover formalism,1–3 a variable ζ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ṡ/s is introduced and the equations of motion are given by
ṡ/s is introduced and the equations of motion are given by
| | 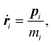 | (12) |
| | 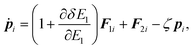 | (13) |
| | 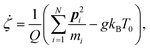 | (14) |
where the dot (˙) stands for the real time derivative d/d
t and forces are defined by
| | 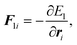 | (15) |
| | 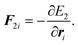 | (16) |
In the case of a rigid-body molecule system, the equations of motion in the partial multicanonical ensemble are given by
| | 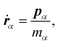 | (17) |
| | 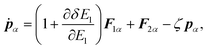 | (18) |
| | 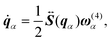 | (19) |
| | 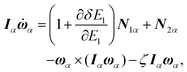 | (20) |
| | 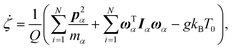 | (21) |
where subscript
α is an index of the rigid-body molecules,
rα is the coordinate of the center of mass of molecule
α,
pα is the momentum of molecule
α,
mα is the mass of molecule
α, and
qα is a quaternion of molecule
α, which indicates the orientation of the rigid-body molecule. Here, the quaternion
q = (
q0,
q1,
q2,
q3)
T is related to the Euler angle (
ϕ,
θ,
ψ) as follows:
| | 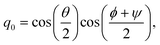 | (22) |
| | 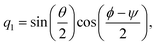 | (23) |
| | 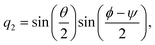 | (24) |
| | 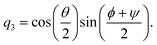 | (25) |
The elements of the matrix
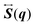
are given by
| | 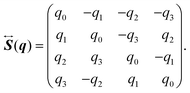 | (26) |
ω and
ω(4) are three-dimensional and four-dimensional angular velocity, respectively, which are given by
| | | ω(4) = (0, ω1, ω2, ω3)T, | (28) |
where
ω1,
ω2, and
ω3 are the angular velocities along each of the corresponding principal axes. The vector
Fα is the force acting on molecule
α, which is related to the force
Fi acting on atom
i in molecule
α by
| | 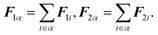 | (29) |
The torque
Nα is calculated by
| | 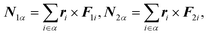 | (30) |
where
ri and
Fi are the coordinate and force of atom
i, respectively, in a rigid-body-fixed coordinate system for molecule
α. The
matrix Iα is a 3 × 3 diagonal
matrix consisting of the principle moments of inertia of molecule
α.
The equations of motion (13), (18), and (20) are obtained from the regular canonical-ensemble equations of motion by modifying the force from
to
| | 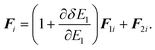 | (32) |
The partial multicanonical MD formalism has been described here based on the Nosé-Hoover thermostat. The partial multicanonical MD simulation can also be performed in a similar way based on the Gaussian thermostat by modifying the force from
eqn (31) to (32).
Instead of MD simulations, it is also possible to perform the partial multicanonical simulations using the MC method. In the partial multicanonical MC simulations, all atoms are updated from ri to 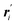 as trial moves by uniform random numbers. Let us suppose that the partial multicanonical energy is consequently changed from Epmuca(r) to
as trial moves by uniform random numbers. Let us suppose that the partial multicanonical energy is consequently changed from Epmuca(r) to 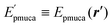 by these trial moves. The Metropolis criterion4 is employed here with the weight factor of exp(−β0Epmuca) instead of the Boltzmann weight factor exp(−β0E) in the canonical ensemble. These trial moves are accepted with the probability
by these trial moves. The Metropolis criterion4 is employed here with the weight factor of exp(−β0Epmuca) instead of the Boltzmann weight factor exp(−β0E) in the canonical ensemble. These trial moves are accepted with the probability
| | 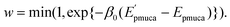 | (33) |
The partial multicanonical probability distribution
Ppmuca(
E1) can be obtained either by the MD simulation in
eqn (12)–(21) or by the MC simulation in
eqn (33).
III. Computational details
Molecular dynamics simulations were performed for a system consisting of one alanine dipeptide molecule ((S)-2-(acetylamino)-N-methylpropanamide) and 67 water molecules. The N-terminus and the C-terminus of the alanine residue were blocked by the acetyl group and the N-metyl group, respectively. Enough water molecules are used so that the alanine dipeptide molecule was always held perfectly within the simulation box. A cubic unit cell was employed with periodic boundary conditions. The side length was set to be 13.39 Å. Thus, the volume V of the unit cell was 2400 Å3. The initial condition of the backbone dihedral angles ϕ and ψ were ϕ = ψ = 180°, as shown in Fig. 1. The AMBER parm96 force field38 was used for the alanine dipeptide molecule and the TIP3P rigid-body model53 was employed for the water molecules. The electrostatic potential energy was calculated using the Ewald method. The Lennard-Jones interaction was calculated for all pairs of the atoms within the minimum image convention instead of introducing the spherical potential cutoff.
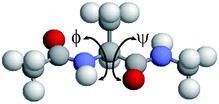 |
| | Fig. 1 Initial conformation of alanine dipeptide for the MD simulations. The dihedral angles are ϕ = ψ = 180°. The figure was created with RasMol.52 | |
The combination54 of the Nosé-Hoover thermostat1–3 and the symplectic quaternion scheme for the rigid-body water molecules55 was used. The time step was taken to be Δt = 0.5 fs. The temperature was set to T0 = 300 K.
The total potential energy is the sum of the potential energy between solute atoms Eslt–slt, that of the solute–solvent interaction Eslt–svn, and that between solvent atoms Esvn–svn as follows:
| | | E = Eslt–slt + Eslt–svn + Esvn–svn. | (34) |
Each term for the AMBER force field
37,38 is given by
| | 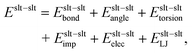 | (35) |
| | | Eslt–svn = Eslt–svnelec + Eslt–svnLJ, | (36) |
| | | Esvn–svn = Esvn–svnelec + Esvn–svnLJ, | (37) |
where the subscripts bond, angle, torsion, imp, elec, and LJ stand for the bond-length, bond-angle, torsion-angle, improper torsion-angle, electrostatic, and Lennard-Jones potential energy, respectively. Although these terms may vary for different force fields, the partial multicanonical algorithm can be applied in essentially the same way.
The purpose of this article is to find the best choice of the partial potential energy E1. For this purpose, the following 15 cases of the E1 choices were tested.
| | | case 2: E1 = Eslt–slt + Eslt–svn + Esvn–svn = E, | (39) |
| | | case 3: E1 = Eslt–slt + Eslt–svn, | (40) |
| | | case 4: E1 = Eslt–slt, | (41) |
| | | case 5: E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, | (42) |
| | | case 6: E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp, | (43) |
| | | case 7: E1 = Eslt–slttor + Eslt–sltelec, | (44) |
| | | case 8: E1 = Eslt–slttor + Eslt–sltLJ, | (45) |
| | | case 9: E1 = Eslt–sltelec + Eslt–sltLJ, | (46) |
| | | case 10: E1 = Eslt–slttor, | (47) |
| | | case 11: E1 = Eslt–sltelec, | (48) |
| | | case 12: E1 = Eslt–sltLJ, | (49) |
| | | case 13: E1 = Eslt–sltbond, | (50) |
| | | case 14: E1 = Eslt–sltangle, | (51) |
| | | case 15: E1 = Eslt–sltimp. | (52) |
Cases 1, 2, and 3 correspond to the conventional canonical MD simulation, the multicanonical MD simulation, and the selectively enhanced multicanonical MD simulation, respectively. In case 4,
E1 includes all of the solute–solute interactions. Case 5 is the same choice as in the preceding article (see
ref. 25). At that time the author expected this choice may work well because of the following reasons: even if we sample wide ranges of bond-length, bond-angle, and improper torsion-angle energy in
Eslt–slt , the conformation of the solute molecule is not expected to be changed very much. Sampling a wide range of
solvent energy
Esvn–svn would not change the solute structure very much, either. Sampling a wide range of the solute–
solvent potential energy
Eslt–svn may sample a wide range of the interface area between the solute molecule and
solvent molecules. The solute molecule of the
alanine dipeptide, however, is small and this effect may not necessarily have to be taken into account in this system. In case 6,
E1 includes the solute–solute energy terms which were not expected to be important in the preceding article.
25 Cases 7–9 include two of the three energy terms in case 5. Cases 10–15 include only one of the solute–solute energy terms.
To obtain an optimal partial multicanonical weight factor Wpmuca(E1, E2), both the iterative method34–36 and the Wang-Landau techniques56 were employed. This is because this combination is more efficient to determine Wpmuca(E1, E2) than employing only the iterative method. This technique updates Wpmuca(E1, E2) at every MD step n as Wpmuca(E1, E2, n) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp[−{E1 + E2 + δE1(E1, n)}/kBT0] to lower energy barriers. The difference δE1(E1, n) at time step n in the i-th iteration was updated using a histogram of E1 and is given by
exp[−{E1 + E2 + δE1(E1, n)}/kBT0] to lower energy barriers. The difference δE1(E1, n) at time step n in the i-th iteration was updated using a histogram of E1 and is given by
| | 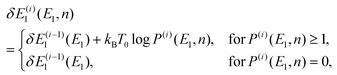 | (53) |
where
P(i)(
E1,
n) is the histogram of
E1 accumulated until one time step before
n, that is, until time step (
n − 1). Here, the time step in the
i-th iteration takes the values
n = 1,2,…,
N(i)t. For the first iteration (
i = 1), the partial multicanonical energy starts from the normal potential energy with
In the case of
i ≥ 2,
δE(i−1)1(
E1) was given by the histogram
P(i−1)(
E1) of the partial potential energy
E1 accumulated until the last time step in the (
i − 1)-th iteration as follows:
| | 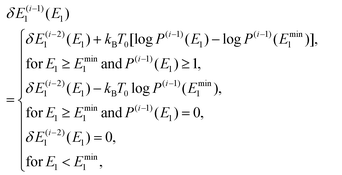 | (55) |
where log
P(i−1)(
E1) was shifted by log
P(i−1)(
Emin1) for the partial potential energy larger than a threshold
Emin1(
E1 ≥
Emin1) to make the potential-energy distribution wider towards the larger value of
E1 to overcome free-energy barriers. The threshold
Emin1 was determined as the minimum value of
E1 in the canonical MD simulation (MD simulation of the case 1). This procedure was iterated 5 times (
i = 1–5). In the first iteration the MD simulation was performed for 100 ps (
N(1)t = 200
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000). At later iterations, the MD simulations we carried out for longer times,
e.g., for 500 ps (
N(5)t = 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000) in the fifth iteration. An optimal weight factor,
Wpmuca(
E1,
E2), was obtained after these preliminary simulations for 1.5 ns in total.
A partial multicanonical MD simulation was performed for an equilibration process for 20 ps before sampling. A long partial multicanonical MD simulation was then performed for 10 ns for data collection. This simulation length is longer than the preceding partial multicanonical article,25 in which the data were collected for 6 ns.
For convenience, E1 was discretized into bins and histograms used to calculate δE1(E1). The bin size was set as ΔE1 = 5 kcal mol−1 for the multicanonical (case 2) and selectively enhanced multicanonical (case 3) simulation, ΔE1 = 2 kcal mol−1 for the cases 4, 6, and 13 simulation, and ΔE1 = 1 kcal mol−1 for the other partial multicanonical simulations. In order to calculate the derivative of δE1(E1), that is, ∂δE1(E1)/∂E1, it is necessary to interpolate the histogram. The histogram was interpolated by a third-order polynomial in E1 to make the derivative continuous at the boundaries between two adjacent bins (see ref. 22). Deviation of the value of the Hamiltonian from its initial value was suppressed by this polynomial.
IV. Results and discussion
The time series of the total potential energy E are shown in Fig. 2. Only four results are shown here for simplicity, which were obtained by the conventional canonical (E1 = 0), multicanonical (E1 = E), selectively enhanced multicanonical (E1 = Eslt–slt + Eslt–svn), and partial multicanonical (E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ) MD simulations. The potential energy E fluctuated in a narrow range in the canonical MD simulation, as shown in Fig. 2(a). The fluctuation ranges in the selectively enhanced multicanonical and partial multicanonical MD simulations were almost the same as that in the canonical simulation, as shown in Fig. 2(c) and (d). The energy fluctuation range of the selectively enhanced multicanonical and that of the partial multicanonical was 1.33 times wider and 1.10 times wider, respectively, than that of the canonical MD simulations. On the other hand, Fig. 2(b) shows that the multicanonical MD simulation covered a wide range of E. The energy range was 1.87 times wider than that of the canonical MD simulations.
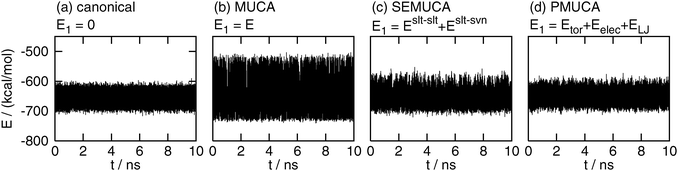 |
| | Fig. 2 The time series of total potential energy E obtained by (a) the canonical (E1 = 0), (b) the multicanonical (MUCA, E1 = E), (c) the selectively enhanced multicanonical (SEMUCA, E1 = Eslt–slt + Eslt–svn), and (d) the partial multicanonical (PMUCA, E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ) MD simulation. | |
Fig. 3 shows the time series of Eslt–slt + Eslt–svn. As expected, the selectively enhanced multicanonical MD simulation, of which E1 was set as E1 = Eslt–slt + Eslt–svn , performed a random walk in a wide range of Eslt–slt + Eslt–svn, as shown in Fig. 3(c). The fluctuation range was 2.06 times wider in the selectively enhanced multicanonical MD simulation than that in the canonical MD simulation. On the other hand, this energy fluctuated in a narrow range in the canonical, multicanonical, and partial multicanonical simulations. The energy ranges in the multicanonical and partial multicanonical simulations were only 1.25 times wider and 1.26 times wider, respectively, than that in the canonical MD simulation.
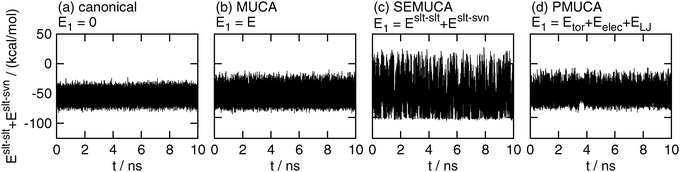 |
| | Fig. 3 The time series of partial potential energy Eslt–slt + Eslt–svn. See the caption of Fig. 2 for further details. | |
Fig. 4 shows the time series of Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. The partial multicanonical MD simulation in the case of E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ performed a random walk in a wide range of this energy, as shown in Fig. 4(d). This fluctuation range was 2.65 times wider than that in the canonical MD simulation. On the other hand, this energy fluctuated in a narrow range in the canonical, multicanonical, and selectively enhanced multicanonical simulations. The ranges in the multicanonical and selectively enhanced multicanonical simulations were only 1.19 times wider and 1.39 times wider, respectively, than the canonical MD simulation.
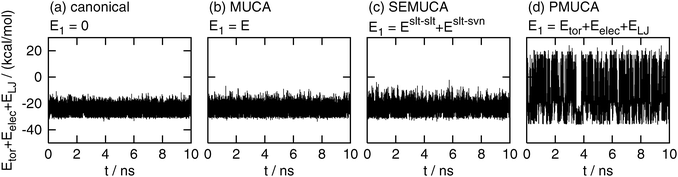 |
| | Fig. 4 Time series of the partial potential energy Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. See the caption of Fig. 2 for further details. | |
The probability distributions of the potential energy are shown in Fig. 5. The distribution of the total potential energy E in the selectively enhanced multicanonical and partial multicanonical simulation was slightly wider than that in the canonical simulation and shifted toward a higher value. The distribution of E in the multicanonical simulation was much wider than those in the other two simulations. Similar situations can be seen in Eslt–slt + Eslt–svn and Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. The selectively enhanced multicanonical algorithm sampled a wide range of Eslt–slt + Eslt–svn, whereas its distributions in the multicanonical and partial multicanonical simulations were almost the same as that in the canonical simulation. The partial multicanonical simulation covered a wider range of Eslt–slttor + Eslt–sltelec + Eslt–sltLJ than the canonical, multicanonical and selectively enhanced multicanonical simulations. Fig. 2–5 show that these generalized-ensemble MD simulations actually sampled a wide range of the potential energy which and only which are pre-designated to be sampled widely.
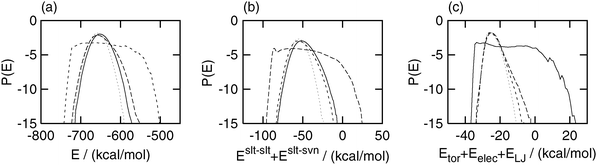 |
| | Fig. 5 Logarithms of the probability distributions of (a) total potential energy E, (b) partial potential energy Eslt–slt + Eslt–svn, and (c) partial potential energy Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. The dotted lines were obtained by the canonical (E1 = 0), the short-dashed lines were obtained by the multicanonical (E1 = E), the long-dashed lines were obtained by the selectively enhanced multicanonical (E1 = Eslt–slt + Eslt–svn), and the solid lines were obtained by the partial multicanonical (E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ) MD simulation. | |
The time series of the dihedral angle ϕ are shown in Fig. 6. The canonical MD simulation did not make a complete rotation, as shown in Fig. 6(a). It covered only 65% of the whole range of ϕ. There is potential energy barriers around ϕ = 0° and ϕ = 120° which cannot be overcome by the canonical simulation (these energy barriers correspond to the boundaries between the local-minimum free-energy states defined in Table 2 below). It means that the canonical MD simulation was trapped in the local-minimum free-energy states.
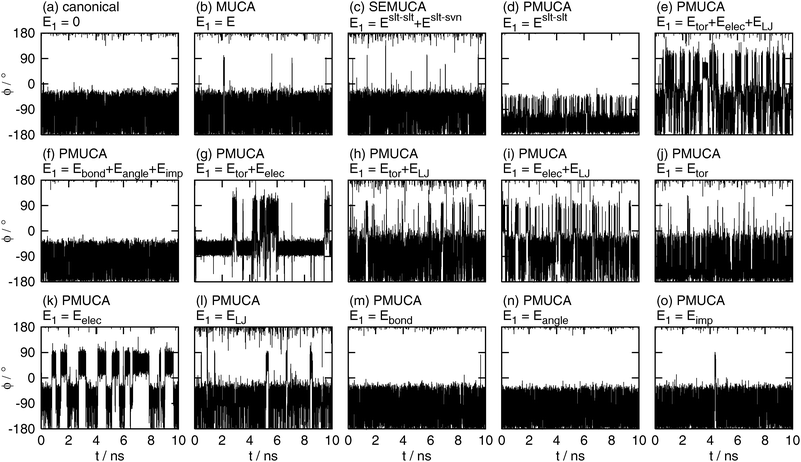 |
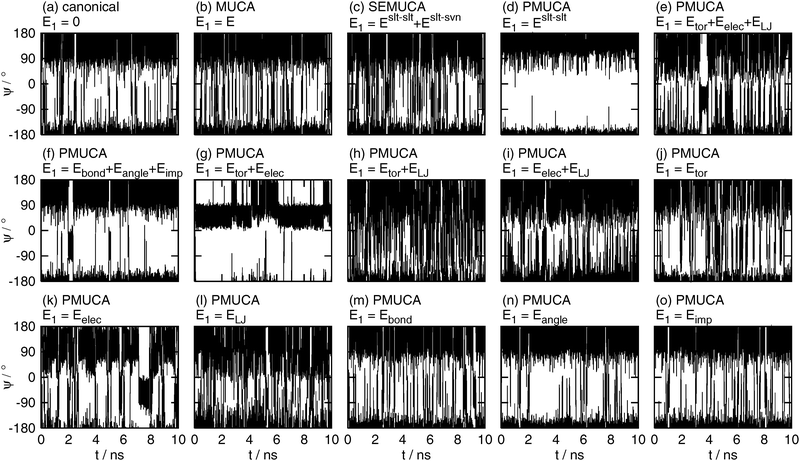
| | Fig. 6 The time series of the backbone dihedral angle ϕ obtained by (a) the canonical (E1 = 0), (b) the multicanonical (MUCA, E1 = E), (c) the selectively enhanced multicanonical (SEMUCA, E1 = Eslt–slt + Eslt–svn), the partial multicanonical (PMUCA) MD simulations in the cases of (d) E1 = Eslt–slt, (e) E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, (f) E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp, (g) E1 = Eslt–slttor + Eslt–sltelec, (h) E1 = Eslt–slttor + Eslt–sltLJ, (i) E1 = Eslt–sltelec + Eslt–sltLJ, (j) E1 = Eslt–slttor, (k) E1 = Eslt–sltelec, (l) E1 = Eslt–sltLJ, (m) E1 = Eslt–sltbond, (n) E1 = Eslt–sltangle, and (o) E1 = Eslt–sltimp. | |
As well as the canonical MD simulation, the MD simulations did not overcome these energy barriers at ϕ = 0° and ϕ = 120°, if E1 was selected as E1 = Eslt–slt (Fig. 6(d)), E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp (Fig. 6(f)), or E1 = Eslt–sltangle (Fig. 6(n)). It means that these choices of E1 do not contribute to enhance the sampling efficiency.
The multicanonical MD simulation did not make a complete rotation, either. It overcame the potential energy barrier around ϕ = 0°, but did not overcome that around ϕ = 120° and sampled 91% of the whole range of ϕ, as shown in Fig. 6(b). The multicanonical MD simulation surely have higher sampling efficiency than the canonical MD simulation. Note that these simulation results do not mean that the multicanonical algorithm cannot sample the whole range of ϕ. The results mean that longer preliminary simulations are required to determine a better multicanonical weight factor Wmuca(E). If a better weight factor Wmuca(E) were obtained with the longer preliminary simulations, the whole range of ϕ could be sampled. In this article, the multicanonical and the partial multicanonical algorithms are compared in the same condition of the effort to determine the weight factors for 1.5 ns.
The partial multicanonical MD simulations with E1 = Eslt–sltbond (Fig. 6(m)) and E1 = Eslt–sltimp (Fig. 6(o)) also sampled the range of 0° < ϕ < 120°, but only once. The sampling efficiency of these choices might be slightly better than the canonical MD simulation, but worse than the multicanonical MD simulation.
The whole range of ϕ was sampled in the cases of E1 = Eslt–slt + Eslt–svn (Fig. 6(c)), E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ (Fig. 6(e)), E1 = Eslt–slttor + Eslt–sltelec (Fig. 6(g)), E1 = Eslt–slttor + Eslt–sltLJ (Fig. 6(h)), E1 = Eslt–sltelec + Eslt–sltLJ (Fig. 6(i)), E1 = Eslt–slttor (Fig. 6(j)), E1 = Eslt–sltelec (Fig. 6(k)), and E1 = Eslt–sltLJ (Fig. 6(l)). These MD simulations overcame both energy barriers and covered the whole range of ϕ. These results mean that the partial multicanonical algorithm with appropriate choice of E1 shows higher sampling efficiency than the multicanonical algorithm. Table 1 shows how many times ϕ underwent a complete rotation (covering 360°) in these MD simulations for 10 ns. Here, one turn of rotation is defined when ϕ undergoes all values between −180 and 180° and count another turn when ϕ undergoes all values after that. The dihedral angle ϕ rotated particularly well if E1 was set as E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, E1 = Eslt–slttor + Eslt–sltLJ, E1 = Eslt–sltelec + Eslt–sltLJ, or E1 = Eslt–sltLJ. In these choices of E1, ϕ made seven turns or more. The Lennard-Jones potential energy is commonly included in these choices of E1. It indicates that sampling a higher value of the Lennard-Jones potential energy helps the MD simulation to overcome steric restrictions when the solute atoms collide with one another.
Table 1 Numbers of the complete rotations of the backbone dihedral angles ϕ and ψ during the 10 ns MD simulations. The numbers in parentheses are the ratio of the dihedral angle range sampled by the MD simulation to the whole range of the dihedral angle (360°) if the whole range was not sampled
| Choice of E1 |
ϕ
|
ψ
|
|
E
1 = 0 |
(0.65) |
27 |
|
E
1 = E |
(0.91) |
54 |
|
E
1 = Eslt–slt + Eslt–svn |
3 |
68 |
|
E
1 = Eslt–slt |
(0.49) |
(0.92) |
|
E
1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ |
8 |
46 |
|
E
1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp |
(0.56) |
9 |
|
E
1 = Eslt–slttor + Eslt–sltelec |
2 |
6 |
|
E
1 = Eslt–slttor + Eslt–sltLJ |
10 |
89 |
|
E
1 = Eslt–sltelec + Eslt–sltLJ |
7 |
53 |
|
E
1 = Eslt–slttor |
2 |
37 |
|
E
1 = Eslt–sltelec |
1 |
31 |
|
E
1 = Eslt–sltLJ |
9 |
57 |
|
E
1 = Eslt–sltbond |
(0.82) |
37 |
|
E
1 = Eslt–sltangle |
(0.56) |
18 |
|
E
1 = Eslt–sltimp |
(0.82) |
31 |
Fig. 7 shows the time series of the other backbone dihedral angle ψ. All MD simulations sampled the whole range of ψ except the case of E1 = Eslt–slt. The dihedral angle ψ rotated more easily than ϕ even in the canonical MD simulation. Table 1 also shows how many times ψ realized a complete rotation. The following choices of E1 made ψ rotate well (more than 40 turns): the multicanonical (E1 = E), selectively enhanced multicanonical (E1 = Eslt–slt + Eslt–svn), partial multicanonical with E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, E1 = Eslt–slttor + Eslt–sltLJ, E1 = Eslt–sltelec + Eslt–sltLJ, and E1 = Eslt–sltLJ. These choices of E1 also include the Lennard-Jones potential energy. This means again that sampling of a wide range of the Lennard-Jones energy helps the simulations to overcome the free-energy barriers.
 |
| | Fig. 7 Time series of the backbone dihedral angle ψ. See the caption of Fig. 6 for further details. | |
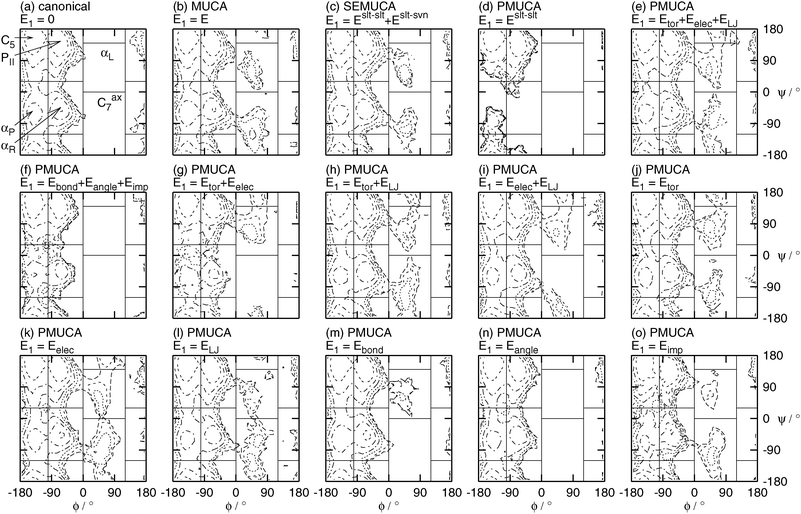
Fig. 8 shows the potential of the mean force or the free-energy surface A(ϕ,ψ) as a function of ϕ and ψ at T = 300 K. Fig. 8 also shows the borders between the adjacent states. These borders are listed in Table 2, too. The potential of mean force A(ϕ, ψ) was calculated from the probability distributions PNVT(ϕ, ψ) of ϕ and ψ in the canonical ensemble by
| | | A(ϕ, ψ) = −kBT log PNVT(ϕ, ψ). | (56) |
In the canonical MD simulation, the distribution
PNVT(
ϕ,
ψ) is easily calculated. On the other hand, to obtain the distribution
PNVT(
ϕ,
ψ) from the multicanonical simulation and that from the partial multicanonical simulation, the reweighting techniques in
eqn (3) and (10) were used, respectively. For example,
PNVT(
ϕ,
ψ) was calculated from the partial multicanonical MD simulation as follows: fist, an unnormalized histogram 〈
N(
ϕ,
ψ)〉
NVT of
ϕ and
ψ in the canonical ensemble was given by
| | | 〈N(ϕ,ψ)〉NVT = 〈N(ϕ,ψ; r)exp[β0{E(r) + δE1(E1(r))}]exp{−βE(r)}〉pmuca, | (57) |
where
ϕ and
ψ were discretized using the bin sizes of Δ
ϕ = Δ
ψ = 10° to calculate the histogram
N(
ϕ,
ψ;
r) and
| | 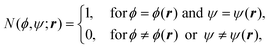 | (58) |
where
ϕ(
r) and
ψ(
r) stand for
ϕ and
ψ, respectively, for the coordinates
r.
Eqn (57) means that 〈
N(
ϕ,
ψ)〉
NVT is obtained by summing up the values of exp[
β0{
E(
r) +
δE1(
E1(
r))}]exp{−
βE(
r)} at (
ϕ(
r),
ψ(
r)). The probability distribution
PNVT(
ϕ,
ψ) was then obtained by normalizing 〈
N(
ϕ,
ψ)〉:
| | 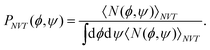 | (59) |
The peak position of
P(
ϕ,
ψ) of each state obtained by the partial multicanonical MD simulation with
E1 =
Eslt–slttor +
Eslt–sltelec +
Eslt–sltLJ is listed in
Table 3.
 |
| | Fig. 8 Contour maps of the potential of mean force A(ϕ, ψ) as a function of the backbone dihedral angles ϕ and ψ obtained by the reweighting techniques at T = 300 K. See the caption of Fig. 6 for further details. | |
Table 2 Dihedral angle ranges of (ϕ, ψ) for each state. The state labels are taken from ref. 46
| State |
ϕ
|
ψ
|
|
PII |
(−100°, 0°) |
(30°, −120°) |
| C5 |
(120°, −100°) |
(30°, −120°) |
|
α
R
|
(−100°, 0°) |
(−120°, 30°) |
|
α
P
|
(120°, −100°) |
(−120°, 30°) |
|
α
L
|
(0°, 120°) |
(0°, 140°) |
| Cax7 |
(0°, 120°) |
(140°, 0°) |
Table 3 Peak positions (ϕ, ψ) of the probability distribution PNVT(ϕ, ψ) for six states at T = 300 K. The results were obtained by the reweighting techniques from the partial multicanonical MD simulation in the case of E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp
| State |
(ϕ, ψ) |
|
PII |
(−65°, 145°) |
| C5 |
(−145°, 155°) |
|
α
R
|
(−65°, −45°) |
|
α
P
|
(−145°, −55°) |
|
α
L
|
(45°, 65°) |
| Cax7 |
(55°, −85°) |
The volume under the surface of P(ϕ, ψ) around each peak corresponds to the population W of each state. In order to calculate W, the whole (ϕ, ψ) plane was divided into six states as shown in Fig. 8 and Table 2. For example, the population WPII of the PII state is calculated by the integral of P(ϕ, ψ) in the area in which ϕ and ψ take the PII conformation:
| | 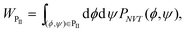 | (60) |
where the integration area of (
ϕ,
ψ) means the range for the corresponding state in
Table 2. The population of each state at
T = 300 K calculated by the reweighting techniques from the results of the partial multicanonical MD simulation is listed in
Table 4. The statistical uncertainties were estimated by the jackknife method
57 in which the production run was divided into ten segments. The populations of the P
II and C
5 states are higher than those of the
αR and
αP states. In the case of longer
peptides or
proteins, the
αR state corresponds to an
α-helix structure and the P
II and C
5 states correspond to a
β-strand structure. It is known that, in general, the AMBER parm96 force field tends to form a
β-strand structure.
58 The potential of mean force
A(
ϕ,
ψ) in
Fig. 8 and
Table 4 is consistent with this feature and
PNVT(
ϕ,
ψ) calculated by other methods such as the multibaric-multithermal MD algorithm.
24
Table 4 Population W of each state at T = 300 K obtained by the reweighting techniques from the results of the partial multicanonical MD simulation in the case of E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp
| State |
W
|
|
PII |
0.409(18) |
| C5 |
0.470(21) |
|
α
R
|
0.067(7) |
|
α
P
|
0.051(7) |
|
α
L
|
0.00062(12) |
| Cax7 |
0.0020(14) |
Fig. 8 shows that the PII, C5, αR, and αP states were sampled in the canonical MD simulation (Fig. 8(a)) and the partial multicanonical MD simulations in the cases of E1 = Eslt–slt (Fig. 8(d)), E1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp (Fig. 8(f)), and E1 = Eslt–sltangle (Fig. 8(n)). Neither the αL state nor the Cax7 state were sampled in these simulations because the range of ϕ between 0 and 120° was not sampled in Fig. 6. These choices of E1 are not appropriate to enhance the sampling efficiency.
All of the six states of the PII, C5, αR, αP, αL, and Cax7 states were sampled in the multicanonical (E1 = E, Fig. 8(b)), selectively enhanced multicanonical (E1 = Eslt–slt + Eslt–svn, Fig. 8(c)), and partial multicanonical MD simulations in the cases of E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ (Fig. 8(e)), E1 = Eslt–slttor + Eslt–sltelec (Fig. 8(g)), E1 = Eslt–slttor + Eslt–sltLJ (Fig. 8(h)), E1 = Eslt–sltelec + Eslt–sltLJ (Fig. 8(i)), E1 = Eslt–slttor (Fig. 8(j)), E1 = Eslt–sltelec (Fig. 8(k)), E1 = Eslt–sltLJ (Fig. 8(l)), E1 = Eslt–sltbond (Fig. 8(m)), and E1 = Eslt–sltimp (Fig. 8(o)).
Although these choices of E1 sampled all states, not all of these choices were good. In order to judge which choice of E1 works well, the author calculated how many times each simulation visits each state, as listed in Table 5. The number of visiting times is good information to find the best choice of E1 as well as the number of rotations of ϕ and ψ. The simulation, however, enters into the neighboring state's area moving by a few degrees of ϕ or ψ, but soon comes back to the original state's area. For example, a small part of the foot of the PII state peak extends over the area of the αL state in the canonical ensemble, as shown in Fig. 8(a), but this simulation essentially did not sample the αL state. To avoid counting such a situation as a visit, when the simulation comes into the area listed in Table 2 for more than 10 degrees, it counts for one visit. For example, when the simulation enters into the area of 10° < ϕ < 110° and 10° < ψ < 130°, it is regarded as one visit to the αL state, although the αL state area is originally 0° < ϕ < 120° and 0° < ψ < 140°. The numbers of visiting times are listed in Table 5. The PII, C5, αR, and αP states were already sampled well in the canonical MD simulation. Important states here are the αL and Cax7 states, because they were not sampled in the canonical MD simulation. These states were visited many times when E1 was chosen as E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, E1 = Eslt–slttor + Eslt–sltelec, E1 = Eslt–sltelec + Eslt–sltLJ, or E1 = Eslt–sltelec. In particular, when E1 was chosen as E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ, all of the PII, C5, αR, αP, αL and Cax7 states were visited more than 400 times. It means that the simulation did not get trapped in any local-minimum free-energy states and visited all states many times. The electrostatic potential energy between the solute atoms Eslt–sltelec was commonly chosen in these four choices of E1. We can see that covering higher energy values of Eslt–sltelec contributes the most to sampling so many states.
Table 5 The number of visiting times of each state
| Choice of E1 |
PII |
C5 |
α
R
|
α
P
|
α
L
|
Cax7 |
|
E
1 = 0 |
1318 |
1417 |
194 |
291 |
0 |
0 |
|
E
1 = E |
1305 |
1423 |
266 |
382 |
8 |
9 |
|
E
1 = Eslt–slt + Eslt–svn |
1421 |
1497 |
306 |
366 |
11 |
21 |
|
E
1 = Eslt–slt |
205 |
208 |
2 |
3 |
0 |
0 |
|
E
1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ |
1019 |
452 |
810 |
515 |
1141 |
862 |
|
E
1 = Eslt–sltbond + Eslt–sltangle + Eslt–sltimp |
1150 |
1170 |
112 |
131 |
0 |
0 |
|
E
1 = Eslt–slttor + Eslt–sltelec |
1017 |
115 |
834 |
53 |
541 |
402 |
|
E
1 = Eslt–slttor + Eslt–sltLJ |
1745 |
1390 |
1172 |
779 |
99 |
121 |
|
E
1 = Eslt–sltelec + Eslt–sltLJ |
1102 |
691 |
592 |
282 |
816 |
732 |
|
E
1 = Eslt–slttor |
1667 |
1661 |
740 |
759 |
46 |
24 |
|
E
1 = Eslt–sltelec |
495 |
249 |
459 |
240 |
995 |
970 |
|
E
1 = Eslt–sltLJ |
1509 |
1057 |
848 |
389 |
27 |
38 |
|
E
1 = Eslt–sltbond |
1208 |
1309 |
282 |
377 |
1 |
1 |
|
E
1 = Eslt–sltangle |
1246 |
1300 |
151 |
205 |
0 |
0 |
|
E
1 = Eslt–sltimp |
1040 |
1108 |
145 |
216 |
2 |
1 |
On the other hand, the Lennard-Jones potential energy between solute atoms Eslt–sltLJ, instead of Eslt–sltelec, was most important for the numbers of the complete rotations of ϕ and ψ, as listed in Table 1. It depends on whether the simulation can overcome the free energy barrier at ϕ = 120° or not. The backbone dihedral angle ϕ made nine turns of the rotation when E1 was chosen as E1 = Eslt–sltLJ, as shown in Fig. 6(l). It is more than one turn of the rotation in the case of E1 = Eslt–sltelec. However, the simulation visited the range of 0° < ϕ < 120° more frequently if E1 = Eslt–sltelec than E1 = Eslt–sltLJ. The reason why the number of rotation in the case of E1 = Eslt–sltelec is less than that in the case of Eslt–sltLJ is the simulation of E1 = Eslt–sltelec did not overcome the free energy barrier at ϕ = 120°.
In order to discuss the relation between the free energy barrier and the atomic conformation, the potential of the mean force and some typical atomic conformations, of which the dihedral angle ψ is larger than zero (ψ > 0°), are shown in Fig. 9. Both the potential of the mean force and the atomic conformations were obtained from the partial multicanonical MD simulation in the case of E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. The distance r between the O atom of the acetyl group and the O atom of the alanine at the PII state is r = 3.92 Å. Here, the Lennard-Jones pair potential energy uLJ is given by
| | 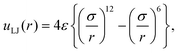 | (61) |
where
σ is the distance at which the interatomic potential is zero and
ε is the depth of the potential well. For these O atoms,
σ = 2.96 Å and the Lennard-Jones energy of this pair is
uLJ = −0.13 kcal mol
−1. The distance between the H atom which has a covalent bond with the N atom of the
alanine and the O atom of the
alanine is
r = 3.26 Å. The Lennard-Jones parameter of this pair is
σ = 2.01 Å and the Lennard-Jones energy is
uLJ = −0.012 kcal mol
−1. These facts mean that both pairs of the atoms at the P
II state do not collide with each other. The electrostatic potential
uelec between these pairs are
uelec = 27.3 kcal mol
−1 for the pair of the O atom of the
acetyl group and the O atom of the
alanine and
uelec = 15.7 kcal mol
−1 for the pair of the H atom and the O atom of the
alanine.
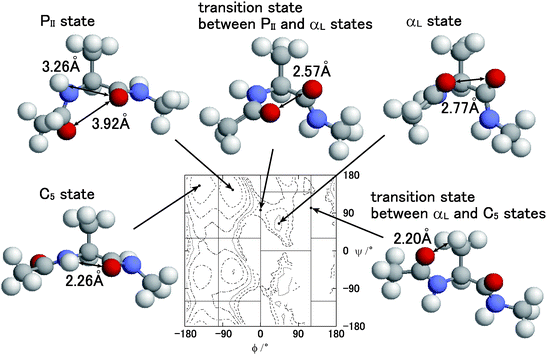 |
| | Fig. 9 Typical conformations of the alanine dipeptide and contour maps of the potential of mean force A(ϕ, ψ) at T = 300 K obtained by the partial multicanonical MD simulation in the case of E1 = Eslt–slttor + Eslt–sltelec + Eslt–sltLJ. | |
At the C5 state, the distance between the H atom and the O atom of the alanine is r = 2.26 Å. It is relatively close to that of the PII state, but they do not collide with each other yet, because σ = 2.01 Å and it is still shorter than r. Thus, the Lennard-Jones energy is low enough as uLJ = −0.057 kcal mol−1 and the electrostatic energy is uelec = −22.7 kcal mol−1. Because the distances of any pairs of atoms at the C5 states are not too close with each other, the C5 state is stable and its population is high as that of the PII state, as listed in Table 4.
The population of the αL state is much less than the PII and C5 states. The distance between the O atom of the acetyl group and the O atom of the alanine is 2.77 Å. This distance is shorter than the parameter σ = 2.96 Å of this pair. It means that these O atoms overlap slightly with each other, thus the Lennard-Jones energy of this pair is relatively high as uLJ = 0.61 kcal mol−1 and the electrostatic potential is uelec = 38.7 kcal mol−1. Both uLJ and uelec are higher than those of the PII and C5 states. This is the reason why the population of the αL state is less than the PII and C5 states.
The distance between the O atom of the acetyl group and the O atom of the alanine of the transition state at ϕ = 0° between the PII state and the αL state is 2.57 Å. They overlap each other more than those of the αL state. Thus, both Lennard-Jones energy and the electrostatic energy are higher than the αL state as uLJ = 2.62 kcal mol−1 and uelec = 41.7 kcal mol−1. The reason for the free energy barrier at ϕ = 0° is both the Lennard-Jones energy and the electrostatic energy.
The distance between the O atom of the acetyl group and the H atom of the alanine side chain of the transition state between the αL state and the C5 state at ϕ = 120° is 2.20 Å. These atoms overlap most among any non-bonding atom pairs shown in Fig. 9. The parameter σ of this pair is σ = 2.80 Å and the Lennard-Jones energy is highest as uLJ = 3.25 kcal mol−1. On the other hand, the electrostatic energy is as low as uelec = −5.2 kcal mol−1 because the charges of these atoms have opposite signs. The reason for the free energy barrier at ϕ = 120° is solely the Lennard-Jones energy, not the electrostatic energy. It means that the Lennard-Jones term Eslt–sltLJ should be included in E1 to overcome the free energy barrier at ϕ = 120°.
The free energy barrier at ϕ = 0° is also caused by the Lennard-Jones repulsive force but it is not as high as that at ϕ = 120°. The electrostatic interaction also causes the free energy barrier at ϕ = 0°. It is why the simulation in which E1 includes only the electrostatic interaction (E1 = Eslt–sltelec) can overcome the free energy barrier at ϕ = 0°. To overcome both free energy barriers at ϕ = 0° and ϕ = 120° efficiently, both Eslt–sltLJ and Eslt–sltelec should be included in E1. In fact, both simulations in the cases of E1 = Eslt–sltelec + Eslt–sltLJ + Eslt–slttor and E1 = Eslt–sltelec + Eslt–sltLJ visited all states many times. Strictly speaking, the simulation sampling the wide range of E1 = Eslt–sltelec + Eslt–sltLJ + Eslt–slttor visited all states slightly more than that of E1 = Eslt–sltelec + Eslt–sltLJ, as listed in Table 5. This fact indicates that sampling the wide range of the torsion angle potential energy Eslt–slttor also contributes somewhat to enhancing the sampling efficiency.
V. Conclusions
In the multicanonical ensemble, a free one-dimensional random walk is realized in the potential-energy space and a simulation does not get trapped in the local-minimum free-energy states in biomolecules. But still there is the problem of the multicanonical algorithm that the determination of the multicanonical weight factor becomes difficult for a large system. It is because the multicanonical simulation samples a wide range of total potential energy and thus a redundant effort is required to determine the weight factor. In order to alleviate this difficulty, the author recently proposed the partial multicanonical algorithm for MD and MC simulations.25 The partial multicanonical simulation samples a wide range of only a part of the potential energy terms which is necessary to sample the conformational space widely, so that one can save the effort to determine the weight factor. The partial multicanonical MD simulation can not only sample the local-minimum free-energy states but also overcome the free-energy barriers. Furthermore, its sampling efficiency is higher than the multicanonical algorithm by focusing to sample the wide range of the important energy terms.
To find the best choice of the partial potential energy E1 which should be sampled widely, 15 choices of E1 were tried in this article. The canonical, multicanonical, selectively enhanced multicanonical, and partial multicanonical MD simulations of an alanine dipeptide were performed in explicit water. The AMBER parm96 force field38 was used for the peptide molecule and the TIP3P rigid-body model53 was employed for the water molecules.
The canonical MD simulation sampled only four states of the PII, C5, αR, and αP states. The multicanonical and selectively enhanced multicanonical MD simulations also sampled the αL and Cax7 states. Although these simulations sampled all of the six states, the αL and Cax7 states were not visited frequently and their sampling was not enough.
The best choice of E1 in this system is the sum of the electrostatic, Lennard-Jones, and torsion-angle terms between the solute atoms. In this case, all states were sampled sufficiently many times. The most important term is the electrostatic potential energy, which makes the simulation visit all states many times. The Lennard-Jones potential is also important for overcoming the steric restriction. In the case of an alanine dipeptide, there are free energy barriers at ϕ = 0° and ϕ = 120° due to the steric restriction. Including the torsion-angle potential energy also contributes to enhancing the sampling efficiency.
The partial potential energy E1 in the multicanonical and selectively enhanced multicanonical algorithms also includes the electrostatic, Lennard-Jones, and torsion-angle terms. But these algorithms do not concentrate on widening the sampling energy ranges of these terms. Most of the effort to widen the sampling energy-ranges is spent on other unimportant energy terms. This is why the sampling efficiency of the multicanonical and selectively enhanced multicanonical algorithms is not as good as the partial multicanonical algorithm in the cases of E1 = Eslt–sltelec + Eslt–sltLJ + Eslt–slttor, E1 = Eslt–sltelec + Eslt–sltLJ, and E1 = Eslt–sltelec.
The best choice of E1 may depend on the system and force field. For example, in the case of aquaporin, a protein which includes water molecules, the solute–solvent interaction may be important and should be included in E1. However, the detailed discussion on the choice of E1 in this article will be useful for other systems. The partial multicanonical algorithm, of course, will be also useful for a MC simulation. This algorithm will be a great use for MD and MC simulations of a large system like a protein beyond the limit of the multicanonical algorithm. Furthermore the partial multicanonical algorithm can be employed for free-energy sampling problems59 in general such as supercooled liquids and glasses.
This idea, in which a simulation covers a wide range of only important potential energy terms, can be utilized not only for the multicanonical algorithm but also for multidimensional extensions14,15,18–24,30,31 of the multicanonical algorithm such as the multibaric–multithermal18–24 and multicanonical–multioverlap30 algorithms. Combining these algorithms, we can develop new stronger simulation techniques.
References
- S. Nosé, Mol. Phys., 1984, 52, 255 CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087 CrossRef CAS.
-
U. H. E. Hansmann and Y. Okamoto, in Ann. Rev. Comput. Phys. VI, ed. D. Stauffer, World Scientific, Singapore, 1999, p. 129 Search PubMed.
- A. Mitsutake, Y. Sugita and Y. Okamoto, Biopolymers, 2001, 60, 96 CrossRef CAS.
- B. A. Berg, Comput. Phys. Commun., 2002, 147, 52 CrossRef.
- Y. Okamoto, J. Mol. Graphics Modell., 2004, 22, 425 CrossRef CAS.
- S. G. Itoh, H. Okumura and Y. Okamoto, Mol. Simul., 2007, 33, 47 CrossRef CAS.
- B. A. Berg and T. Neuhaus, Phys. Lett. B, 1991, 267, 249 CrossRef.
- B. A. Berg and T. Neuhaus, Phys. Rev. Lett., 1992, 68, 9 CrossRef.
- U. H. E. Hansmann, Y. Okamoto and F. Eisenmenger, Chem. Phys. Lett., 1996, 259, 321 CrossRef CAS.
- N. Nakajima, H. Nakamura and A. Kidera, J. Phys. Chem. B, 1997, 101, 817 CrossRef CAS.
- C. Bartels and M. Karplus, J. Comput. Chem., 1997, 18, 1450 CrossRef CAS.
- J. Higo, N. Nakajima, H. Shirai, A. Kidera and H. Nakamura, J. Comput. Chem., 1997, 18, 2086 CrossRef CAS.
- Y. Iba, G. Chikenji and M. Kikuchi, J. Phys. Soc. Jpn., 1998, 67, 3327 CrossRef.
- N. Nakajima, Chem. Phys. Lett., 1998, 288, 319 CrossRef CAS.
- H. Okumura and Y. Okamoto, Chem. Phys. Lett., 2004, 383, 391 CrossRef CAS.
- H. Okumura and Y. Okamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 026702 CrossRef.
- H. Okumura and Y. Okamoto, J. Phys. Soc. Jpn., 2004, 73, 3304 CrossRef CAS.
- H. Okumura and Y. Okamoto, Chem. Phys. Lett., 2004, 391, 248 CrossRef CAS.
- H. Okumura and Y. Okamoto, J. Comput. Chem., 2006, 27, 379 CrossRef CAS.
- H. Okumura and Y. Okamoto, Bull. Chem. Soc. Jpn., 2007, 80, 1114 CrossRef CAS.
- H. Okumura and Y. Okamoto, J. Phys. Chem. B, 2008, 112, 12038 CrossRef CAS.
- H. Okumura, J. Chem. Phys., 2008, 129, 124116 CrossRef.
- B. A. Berg, H. Noguchi and Y. Okamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036126 CrossRef.
- S. G. Itoh and Y. Okamoto, Chem. Phys. Lett., 2004, 400, 308 CrossRef CAS.
- S. G. Itoh and Y. Okamoto, J. Chem. Phys., 2006, 124, 104103 CrossRef.
- S. G. Itoh and Y. Okamoto, Mol. Simul., 2007, 33, 83 CrossRef CAS.
- S. G. Itoh and Y. Okamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026705 CrossRef.
- Y. Yoshimoto, J. Chem. Phys., 2006, 125, 184103 CrossRef.
- T. Yamaguchi, T. Kiuchi, T. Matsuoka and S. Koda, Bull. Chem. Soc. Jpn., 2005, 78, 2098 CrossRef CAS.
- T. Morishita and M. Mikami, J. Chem. Phys., 2007, 127, 034104 CrossRef.
- B. A. Berg and T. Celik, Phys. Rev. Lett., 1992, 69, 2292 CrossRef.
- J. Lee, Phys. Rev. Lett., 1993, 71, 211 CrossRef CAS; J. Lee, Phys. Rev. Lett., 1993, 71, 2353 CrossRef CAS (E).
- Y. Okamoto and U. H. E. Hansmann, J. Phys. Chem., 1995, 99, 11276 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, Jr., D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179 CrossRef CAS.
-
P. A. Kollman, R. Dixon, W. Cornell, T. Fox, C. Chipot and A. Pohorille, in Computer Simulation of Biomolecular Systems 3, ed. A. Wilkinson, P. Weiner and W. F. van Gunsteren, Elsevier, Dordrecht, 1997, p. 83 Search PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474 CrossRef CAS.
- A. D. MacKerell, Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586 CrossRef CAS.
- I. R. Gould and P. A. Kollman, J. Phys. Chem., 1992, 96, 9255 CrossRef CAS.
- J. Apostolakis, P. Ferrara and A. Caflisch, J. Chem. Phys., 1999, 110, 2099 CrossRef CAS.
- P. E. Smith, J. Chem. Phys., 1999, 111, 5568 CrossRef CAS.
- A. D. MacKerell, Jr., M. Feig and C. L. Brooks III, J. Comput. Chem., 2004, 25, 1400 CrossRef CAS.
- J. D. Chodera, W. C. Swope, J. W. Pitera and K. A. Dill, Multiscale Model. Simul., 2006, 5, 1214 CrossRef.
- D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103 CrossRef.
- D. Branduardi, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef.
- M. Bonomi, A. Barducci and M. Parrinello, J. Comput. Chem., 2009, 30, 1615 CrossRef CAS.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1988, 61, 2635 CrossRef CAS; A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1989, 63, 1658 CrossRef CAS (E).
- A. Mitsutake, M. Kinoshita, Y. Okamoto and F. Hirata, Chem. Phys. Lett., 2000, 329, 295 CrossRef CAS.
- R. A. Sayle and E. J. Milner-White, Trends Biochem. Sci., 1995, 20, 374 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- H. Okumura, S. G. Itoh and Y. Okamoto, J. Chem. Phys., 2007, 126, 084103 CrossRef.
- T. F. Miller, M. Eleftheriou, P. Pattnaik, A. Ndirango, D. Newns and G. J. Martyna, J. Chem. Phys., 2002, 116, 8649 CrossRef.
- F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050 CrossRef CAS.
-
B. A. Berg, Introduction to Monte Carlo Simulations and Their Statistical Analysis, World Scientific, Singapore, 2004 Search PubMed.
- T. Yoda, Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 2004, 386, 460 CrossRef CAS.
- J. C. Schön, J. Chem. Phys., 1996, 105, 10072 CrossRef.
Footnote |
| † This article was submitted as part of a Themed Issue on solid state and cluster structure prediction. Other papers on this topic can be found in issue 30 of vol. 12 (2010). This issue can be found from the PCCP homepage [http://www.rsc.org/pccp] |
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 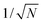 , where N is the number of atoms. Thus, the determination of the multicanonical weight factor to give a flat distribution becomes difficult in a large system. New techniques are desired to reduce the effort for the weight-factor determination with keeping the high sampling efficiency. The multicanonical algorithm covers a wide range of the total potential energy. The total potential energy of a biomolecular system includes bond-length, bond-angle, torsion-angle, improper torsion-angle, Lennard-Jones, and electrostatic energy terms for most of the force fields.37–41 However, it is redundant to sample a wide range of all these terms.
, where N is the number of atoms. Thus, the determination of the multicanonical weight factor to give a flat distribution becomes difficult in a large system. New techniques are desired to reduce the effort for the weight-factor determination with keeping the high sampling efficiency. The multicanonical algorithm covers a wide range of the total potential energy. The total potential energy of a biomolecular system includes bond-length, bond-angle, torsion-angle, improper torsion-angle, Lennard-Jones, and electrostatic energy terms for most of the force fields.37–41 However, it is redundant to sample a wide range of all these terms.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp{−β0Emuca(E)} so that a uniform distribution of E may be obtained:
exp{−β0Emuca(E)} so that a uniform distribution of E may be obtained:![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E + δE(E). The difference δE(E) is additional potential energy which is introduced to obtain a flat distribution of E in eqn (2). The case of δE(E) = 0 gives the regular canonical ensemble. The multicanonical simulation covers a wide range of E and escapes from local-minimum free-energy states. The expectation value of a physical quantity A at temperature T is obtained by reweighting techniques50 from
E + δE(E). The difference δE(E) is additional potential energy which is introduced to obtain a flat distribution of E in eqn (2). The case of δE(E) = 0 gives the regular canonical ensemble. The multicanonical simulation covers a wide range of E and escapes from local-minimum free-energy states. The expectation value of a physical quantity A at temperature T is obtained by reweighting techniques50 from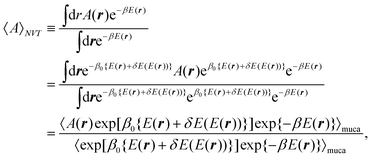
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dr⋯e−β0{E(r)+δE(E(r))}/∫dre−β0{E(r)+δE(E(r))}. The vector r is the set of coordinates r
∫dr⋯e−β0{E(r)+δE(E(r))}/∫dre−β0{E(r)+δE(E(r))}. The vector r is the set of coordinates r ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) {r1,…,rN}. Because of the random walks in the potential-energy space, we can calculate physical quantities in a wide range of T.
{r1,…,rN}. Because of the random walks in the potential-energy space, we can calculate physical quantities in a wide range of T.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp{−β0Epmuca(E1, E2)} so that a uniform distribution of E1 may be obtained:
exp{−β0Epmuca(E1, E2)} so that a uniform distribution of E1 may be obtained: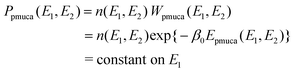
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) E1 + E2 + δE1(E1) = E + δE1(E1).
E1 + E2 + δE1(E1) = E + δE1(E1).![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dE2Ppmuca(E1, E2),
∫dE2Ppmuca(E1, E2),![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dE2n(E1, E2)exp(−β0E2),
∫dE2n(E1, E2)exp(−β0E2),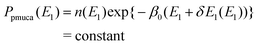
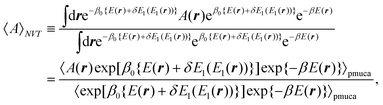
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ∫dr⋯e−β0{E(r)+δE1(E1(r))}/∫dre−β0{E(r)+δE1(E1(r))}. Note that 〈A〉NVT can be calculated correctly at a temperature T only in the vicinity of T0, although 〈A〉NVT can be calculated in a wide range of T in the multicanonical algorithm. It is because a limited range of E2 is sampled with the normal Boltzmann weight factor exp(−β0E2) in the partial multicanonical algorithm.
∫dr⋯e−β0{E(r)+δE1(E1(r))}/∫dre−β0{E(r)+δE1(E1(r))}. Note that 〈A〉NVT can be calculated correctly at a temperature T only in the vicinity of T0, although 〈A〉NVT can be calculated in a wide range of T in the multicanonical algorithm. It is because a limited range of E2 is sampled with the normal Boltzmann weight factor exp(−β0E2) in the partial multicanonical algorithm.
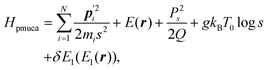
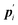 is the conjugate momentum for ri. The real momentum pi is related to the virtual momentum
is the conjugate momentum for ri. The real momentum pi is related to the virtual momentum 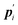 by
by 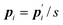 . The variable s is the additional degree of freedom for the Nosé thermostat. The variable Ps is the conjugate momentum for s. The constant mi is the mass of atom i and Q is the artificial “mass” related to s. The real time interval Δt is related to the virtual time interval Δt′ by Δt = Δt′/s. In the case of a system consisting of N atoms, g equals 3N if the time development is performed in the real time t, or g equals 3N + 1 if the time development is performed in virtual time t′.
. The variable s is the additional degree of freedom for the Nosé thermostat. The variable Ps is the conjugate momentum for s. The constant mi is the mass of atom i and Q is the artificial “mass” related to s. The real time interval Δt is related to the virtual time interval Δt′ by Δt = Δt′/s. In the case of a system consisting of N atoms, g equals 3N if the time development is performed in the real time t, or g equals 3N + 1 if the time development is performed in virtual time t′.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ṡ/s is introduced and the equations of motion are given by
ṡ/s is introduced and the equations of motion are given by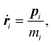
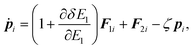
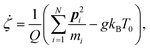
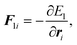
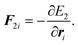
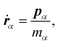
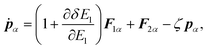
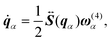
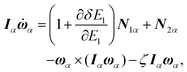
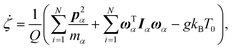
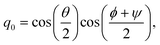
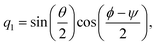
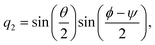
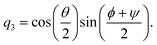
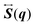 are given by
are given by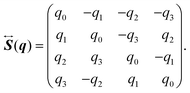
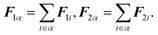
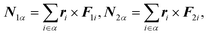
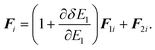
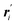 as trial moves by uniform random numbers. Let us suppose that the partial multicanonical energy is consequently changed from Epmuca(r) to
as trial moves by uniform random numbers. Let us suppose that the partial multicanonical energy is consequently changed from Epmuca(r) to 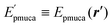 by these trial moves. The Metropolis criterion4 is employed here with the weight factor of exp(−β0Epmuca) instead of the Boltzmann weight factor exp(−β0E) in the canonical ensemble. These trial moves are accepted with the probability
by these trial moves. The Metropolis criterion4 is employed here with the weight factor of exp(−β0Epmuca) instead of the Boltzmann weight factor exp(−β0E) in the canonical ensemble. These trial moves are accepted with the probability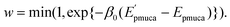

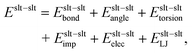
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) exp[−{E1 + E2 + δE1(E1, n)}/kBT0] to lower energy barriers. The difference δE1(E1, n) at time step n in the i-th iteration was updated using a histogram of E1 and is given by
exp[−{E1 + E2 + δE1(E1, n)}/kBT0] to lower energy barriers. The difference δE1(E1, n) at time step n in the i-th iteration was updated using a histogram of E1 and is given by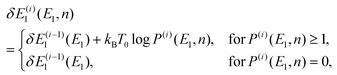
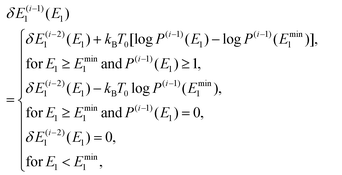
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). At later iterations, the MD simulations we carried out for longer times, e.g., for 500 ps (N(5)t = 1
000). At later iterations, the MD simulations we carried out for longer times, e.g., for 500 ps (N(5)t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) in the fifth iteration. An optimal weight factor, Wpmuca(E1, E2), was obtained after these preliminary simulations for 1.5 ns in total.
000) in the fifth iteration. An optimal weight factor, Wpmuca(E1, E2), was obtained after these preliminary simulations for 1.5 ns in total.