Size-selective molecular transport through silica colloidal nanopores†‡
Patricia Anne A.
Ignacio-de Leon
and
Ilya
Zharov
*
Department of Chemistry, University of Utah, 315 S. 1400 E. Salt Lake City, UT 84112-0850, USA. E-mail: i.zharov@utah.edu; Fax: 1-801-581-8433; Tel: 1-801-587-9335
First published on 24th November 2010
Abstract
Diffusion rate of dye-labelled PAMAM dendrimers through free-standing silica colloidal crystals was studied as a function of the dendrimer generation and nanopore size to determine the transport selectivity.
Research in the area of nanoporous materials ranges from fundamental studies of molecular transport through nanochannels1 to applications such as separations of biomacromolecules2 and drug molecules,3 controlled release4 and drug delivery,5 chemical sensing6 and biological nanoreactors.7 Many of these applications stem from the ability to control the molecular transport through the nanopores by modifying their surfaces with various moieties,8 as well as varying the nanopore size.9
The majority of the nanopores studied so far have cylindrical geometry resulting from the techniques used for their preparation, such as ion beam etching of silicon nitride,10 track-etching of polycarbonate,8 anodic oxidation of aluminium,11 soft lithographic techniques,12 and embedding carbon nanotubes.13Silica colloidal crystals constitute a unique nanoporous material formed viaself-assembly of silica nanospheres into a close-packed face-centered cubic (fcc) lattice.14 The tetrahedral and octahedral voids present in the close-packed system constitute ordered arrays of three-dimensional interconnected nanopores whose sizes can be controlled over a broad range in straightforward manner by varying the silica nanosphere diameter.15
Previously, we reported molecular transport through the colloidal nanopores controlled either by electrostatics16 or by molecular recognition.17 We demonstrated that the tortuous path molecules take to diffuse through the colloidal crystal significantly enhances the electrostatic transport selectivity.16a,b We also prepared polymer-modified colloidal films and membranes where molecular transport has been controlled by polymer conformation changing in response to temperature and pH.18
An important aspect of the molecular transport through silica colloidal crystals not studied so far is the size selectivity. To address this issue, we investigated the transport of macromolecules through the colloidal nanopores as a function of the nanopore and macromolecule size, in a way similar to recent studies of size selectivity for other mesoporous membranes.19 We used polyamidoamine (PAMAM) dendrimers as diffusion probes due to their high monodispersity, well-defined molecular architecture20 and size ranging from 2–20 nm. Full generation (G1, G2, etc.) PAMAM dendrimers are terminated with primary amines, which can be readily used in dye labeling.21 Thus, Rhodamine B isothiocyanate-labeled PAMAM dendrimers were prepared via the facile amide bond formation (Scheme 1). The extent of dye-labeling evaluated using UV absorbance (Table 1) was purposefully kept low to avoid altering the size of the diffusion probes.
 | ||
| Scheme 1 Preparation of dye-labeled dendrimers. | ||
| PAMAM | Diameter, nma | No. of –NH2 end groups per dendrimer | No. of dyes per dendrimer |
|---|---|---|---|
| a Rhodamine B diameter was reported21b to be of 1.6 nm, the diameters of the dendrimers are given as provided by the manufacturer (Dendritic Nanotechnologies, Inc.). | |||
| G1 | 1.9 | 8 | 2.87 |
| G2 | 2.6 | 16 | 2.79 |
| G3 | 3.6 | 32 | 2.72 |
| G4 | 4.4 | 64 | 3.00 |
| G5 | 5.7 | 128 | 5.72 |
Silica colloidal crystals were prepared by vertical deposition from colloidal solutions of preshrunk silica spheres (Table 2). Subsequent sintering afforded free-standing colloidal crystals (nano-frits).22Fig. 1a shows an SEM image of a colloidal crystal sintered at 1050 °C and demonstrates the absence of major defects, such as cracks, over a large area. Occasional point defects within the fcc lattice are present but do not persist beyond one or two layers of the spheres.
| [TEOS], M | [NH3], M | [H2O], M | Reaction temp. and time | Measured diameter, nm | ||
|---|---|---|---|---|---|---|
| As made | Preshrunk | Inside sintered membrane | ||||
| a Measured using Dynamic Light Scattering (DLS). | ||||||
| 0.2 | 0.4 | 16.0 | 25 °C (24 h) | 261 ± 20 | 235 ± 20 | 100 ± 6 |
| 0.2 | 1.1 | 17.0 | 25 °C (24 h) | 388 ± 30a | 345 ± 15 | 252 ± 10 |
| 0.2 | 4.0 | 5.0 | 10 °C (6 h) | 432 ± 27 | 427 ± 29 | 362 ± 27 |
 | ||
| Fig. 1 SEM image of a sintered membrane made from 235 nm (preshrunk diameter) silica spheres (size bar = 2.5 μm). | ||
The molecular transport in colloidal crystals prepared as described above occurs normal to the (111) plane of the fcc-packed structure. Thus, molecules enter the crystal through the concave triangular openings between the silica spheres. We define the ‘radius’ of these colloidal nanopores as the distance from the center of the opening to the nearest silica sphere surface, which is ca. 15% of the sphere radius.18b§ Thus, nano-frits composed of 100 and 362 nm spheres contain nanopores with 7.5 and 27.2 nm ‘radii’, respectively. Octahedral voids found in the (100) direction of the colloidal crystal are much larger, and thus the smaller ‘radii’ nanopores should determine the size selectivity of the system.
To determine whether size-selective molecular transport could be achieved in silica colloidal crystals and to investigate the effect of the nanopore size and surface charge, we studied the diffusion of the dendrimers of increasing generations and diameters (Table 1) through the nano-frits in a diffusion apparatus (Fig. 2S). Nano-frit membranes were prepared for diffusion experiments by sandwiching a nano-frit piece between two washers using an epoxy resin as adhesive (Fig. 1S). The membranes used in this work were sufficiently robust to last for several months.
We measured the diffusion rate RD (mol·sec−1) through a nano-frit of a known thickness L and area S (cm2) by recording the number of moles of a dendrimer that diffused through the nano-frit as a function of time. The molecular flux Jcolloid (mol·sec−1·cm−2) through the nano-frit was then calculated as Jcolloid = RD/S. A solution of Fick's law for diffusion, Deff = (Jcolloid × L)/(0.087 × ΔC), was then used to determine the effective diffusion coefficients Deff (cm2·sec−1) of the dendrimers.23
Fig. 2 shows the flux plots of various diffusing species through a nano-frit as a function of time. These plots are representative of the observed differences in the diffusion rates for the different dendrimer species employed through multiple nano-frits constructed and investigated. Tables 3 and 4 summarize the calculated Deff values for the dye-labeled PAMAM dendrimers used.
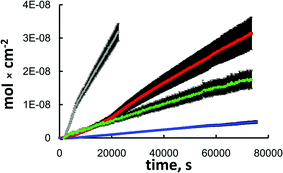 | ||
| Fig. 2 A representative flux plot for Rhodamine B (grey) and dye-labeled PAMAM G1 (red), G4 (green) and G5 (blue). Data shown are for a rehydroxylated nano-frit with 252 nm sphere size and 0.597 mm thickness. | ||
| Diffusing PAMAM species | As-sintered membrane | Rehydroxylated membrane | ||
|---|---|---|---|---|
| D eff (cm2/s) × 10−6 | %Deff ratio relative to G1 | D eff (cm2/s) × 10−6 | %Deff ratio relative to G1 | |
| G1 | 2.35 ± 0.42 | 100 | 1.92 ± 0.35 | 100 |
| G2 | 1.79 ± 0.31 | 76 ± 19 | 1.40 ± 0.25 | 73 ± 19 |
| G3 | 0.82 ± 0.15 | 35 ± 9 | 0.93 ± 0.18 | 48 ± 13 |
| G4 | 0.57 ± 0.10 | 24 ± 6 | 0.48 ± 0.10 | 25 ± 8 |
| G5 | 0.64 ± 0.17 | 27 ± 9 | 0.68 ± 0.14 | 35 ± 10 |
| Diffusing PAMAM species | As-sintered membrane | Rehydroxylated membrane | ||
|---|---|---|---|---|
| D eff (cm2/s) × 10−6 | %Deff ratio relative to G1 | D eff (cm2/s) × 10−6 | %Deff ratio relative to G1 | |
| G1 | 1.68 ± 0.27 | 100 | 2.20 ± 0.40 | 100 |
| G4 | 0.70 ± 0.13 | 42 ± 10 | 0.94 ± 0.19 | 43 ± 12 |
| G5 | 0.92 ± 0.19 | 55 ± 14 | 1.45 ± 0.22 | 66 ± 16 |
Comparison of the calculated Deff values for the same nano-frit showed that the diffusion rate decreased with increasing size of the diffusing species. This effect can be demonstrated quantitatively by calculating the ratio of diffusion coefficients for each of the higher generation dendrimers relative to G1. The results for the nano-frits sintered from 100 nm spheres (7.5 nm ‘radius’ nanopores) showed an abrupt change in diffusion rates from G2 to G3. While G2 dendrimer diffused about three-fourths as fast as G1, G3 has a diffusion rate ca. three times lower, and G4 and G5 have roughly the same diffusion rates, about four times slower than G1. This is noteworthy considering the fact that there is only about 3–4 nm difference between the diameters of G4 and G5 and of G1 dendrimers (Table 1). Moreover, the size of the colloidal nanopores is significantly larger than the dendrimer diameter, suggesting an additional effect of tortuosity on the size selectivity.
Examination of the nano-frits constructed from 362 nm silica spheres showed that the Deff is dependent on the nanopore size, with the smallest Deff values corresponding to diffusion through the 7.5 nm nanopores (Tables 3 and 4). The selectivities for G4 and G5 dendrimers are lower by a factor of ca. 2 for the nano-frits with the larger nanopores. Another set of nano-frits comprising 252 nm spheres (18.9 nm nanopore ‘radius’) was investigated and the results were intermediate between the two discussed above (see Fig. 2, data not tabulated).
Interestingly, for all nano-frits studied the Deff values of the G5 dendrimer are slightly higher than those for G4 dendrimer. As the size of the G5 dendrimer is larger, this increase in Deff may be the result of increased flexibility of the G5 dendrimer.
In order to confirm that the observed transport selectivities are due to the size discrimination and not electrostatic effects, the diffusion experiments were also performed using the rehydroxylated nano-frits. The difference between as-sintered and rehydroxylated nano-frits is that the former have a greater number of terminal siloxanes (Si–O–Si) on the surface.24 The rehydroxylation with ammonia converts the terminal siloxanes to the surface silanol (Si–OH) groups25 with pKa 6–8.26 Thus, in an aqueous medium, as-sintered nano-frits should possess a smaller negative surface charge compared to the rehydroxylated nano-frits. This is supported by zeta potential of −41.22 mV measured for silica nanoparticles produced by breaking down sintered nano-frits compared to −44.92 mV measured for silica nanoparticles produced by breaking down rehydroxylated nano-frits (zeta potential of −46.88 mV was measured for as-made silica spheres from the same batch).
If transport selectivity of the dendrimers through the nano-frits is affected by electrostatic effects, different diffusion rates through the rehydroxylated nano-frits would be expected due to the interactions between the negatively charged nanopore surface and the cationic dye-labeled dendrimers. However, a comparison of both calculated Deff and selectivity values (Tables 3 and 4) shows little difference in diffusion rates between the as-sintered and the rehydroxylated nano-frits. This confirms that the molecular transport selectivity exhibited by the nano-frits results exclusively from the size discrimination.
In conclusion, we demonstrated that molecular transport through silica colloidal crystals is size-selective and the selectivity is enhanced by the tortuous path diffusing molecules take through the colloidal crystal. Our results suggest that nano-frits have potential applications in size-selective separations. Work is currently being conducted to develop nano-frits with even smaller nanopore sizes to further enhance their size selectivity.
This work was supported by the NSF CAREER Award (CHE-0642615) to I. Z and by the NSF MWN grant (DMR-1008251), the latter is a part of our collaboration with Kazan Federal University, Russia (Prof. Ivan Stoikov), supported by RFBR (10-03-92661-NSF).
Notes and references
- (a) T. Ito, L. Sun and R. M. Crooks, Chem. Commun., 2003, 1482 RSC; (b) D. W. Deamer and D. Branton, Acc. Chem. Res., 2002, 35, 817 CrossRef CAS.
- S. Yu, S. B. Lee, M. Kang and C. R. Martin, Nano Lett., 2001, 1, 495 CrossRef CAS.
- J. B. Schlenoff and H. H. Ramaile, J. Am. Chem. Soc., 2003, 125, 6602 CrossRef.
- (a) F. Martina, R. Walczaka, A. Boiarskia, M. Cohena, T. Westa, C. Cosentinob and M. Ferrari, J. Controlled Release, 2005, 102, 123 CrossRef CAS; (b) J. T. Santini Jr., M. J. Cima and R. A. Langer, Nature, 1999, 397, 335 CrossRef CAS; (c) M. C. Berg, L. Zhai, R. E. Cohen and M. F. Rubner, Biomacromolecules, 2006, 7, 357 CrossRef CAS.
- (a) M. E. Davis, Nature, 2002, 417, 813 CrossRef CAS; (b) L. Sun and R. M. Crooks, J. Am. Chem. Soc., 2002, 122, 12340; (c) S. Yu, S. B. Lee, M. Kang and C. R. Martin, Nano Lett., 2001, 1, 495 CrossRef CAS.
- H. Bayley and C. R. Martin, Chem. Rev., 2000, 100, 2575 CrossRef CAS.
- (a) C. Lei, Y. Shin and E. J. Ackerman, J. Am. Chem. Soc., 2002, 124, 11242 CrossRef CAS; (b) C. Lei, Y. Shin, J. Liu and E. J. Ackerman, Nano Lett., 2007, 7, 1050 CrossRef CAS.
- (a) M. Nishizawa, V. P. Menon and C. R. Martin, Science, 1995, 268, 700 CrossRef CAS; (b) V. Smuleac, D. A. Butterfield and D. Bhattacharyya, Chem. Mater., 2004, 16, 2762 CrossRef CAS; (c) Y. Ito, Y. S. Park and Y. Imahishi, Langmuir, 2000, 16, 5376 CrossRef CAS; (d) T. Yamaguchi and T. Ito, J. Am. Chem. Soc., 2004, 126, 6202 CrossRef.
- (a) T. A. Desai, D. J. Hansford, L. Kulinsky, A. H. Nashat, G. Rasi, J. Tu, Y. Wang, M. Zhang and M. Ferrari, Biomed. Microdevices, 1999, 2, 11 CrossRef CAS; (b) S. Sershen and J. West, Adv. Drug Delivery Rev., 2002, 54, 1225 CrossRef CAS.
- J. Li, M. Gershow, D. Stein, E. Brandin and J. A. Golovchenko, Nat. Mater., 2003, 2, 611 CrossRef CAS.
- C.-S. Toh, B. M. Kayes, E. J. Nemanick and N. S. Lewis, Nano Lett., 2004, 4, 767 CrossRef CAS.
- O. A. Saleh and L. L. Sohn, Nano Lett., 2003, 3, 37 CrossRef CAS.
- L. Sun and R. M. Crooks, J. Am. Chem. Soc., 2000, 122, 12340 CrossRef CAS.
- S. Wong, V. Kitaev and G. A. Ozin, J. Am. Chem. Soc., 2003, 125, 15589 CrossRef CAS.
- P. Jiang, J. F. Bertone, K. S. Hwang and V. L. Colvin, Chem. Mater., 1999, 11, 2132 CrossRef CAS.
- (a) M. R. Newton, A. K. Bohaty, H. S. White and I. Zharov, J. Am. Chem. Soc., 2005, 127, 7268 CrossRef CAS; (b) M. R. Newton, A. K. Bohaty, Y. Zhang, H. S. White and I. Zharov, Langmuir, 2006, 22, 4429 CrossRef CAS; (c) J. J. Smith and I. Zharov, Langmuir, 2008, 24, 2650 CrossRef CAS; (d) A. Bohaty and I. Zharov, J. Porous Mater., 2010, 17, 465 CrossRef CAS.
- (a) J. Cichelli and I. Zharov, J. Am. Chem. Soc., 2006, 128, 8130 CrossRef CAS; (b) J. Cichelli and I. Zharov, J. Mater. Chem., 2007, 17, 1870 RSC; (c) A. Mollard, D. Ibragimova, I. S. Antipin, I. Stoikov and I. Zharov, Microporous Mesoporous Mater., 2010, 131, 378 CrossRef CAS.
- (a) O. Schepelina and I. Zharov, Langmuir, 2006, 22, 10523 CrossRef CAS; (b) O. Schepelina and I. Zharov, Langmuir, 2007, 23, 12704 CrossRef CAS; (c) A. E. Abelow and I. Zharov, Soft Matter, 2009, 5, 457 RSC; (d) O. Schepelina, N. Poth and I. Zharov, Adv. Funct. Mater., 2010, 20, 1962 CrossRef CAS.
- (a) C.-H. Hou, X. Wang, C. Liang, S. Yiacoumi, C. Tsouris and S. Dai, J. Phys. Chem. B, 2008, 112, 8563 CrossRef CAS; (b) X.-S. Peng, J. Jin and I. Ichinose, Adv. Funct. Mater., 2007, 17, 1849 CrossRef CAS.
- D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck and P. Smith, Macromolecules, 1986, 19, 2466 CrossRef.
- (a) G. T. Hermansen, Bioconjugate Techniques, Academic Press, San Fransisco, 1996 Search PubMed; (b) S. A. Klein, S. J. Wilk, T. J. Thornton and J. D. Posner, International Symposium on Advanced Nanodevices and Nanotechnology Journal of Physics: Conference Series, 2008, 109, 012022 Search PubMed.
- A. K. Bohaty, J. J. Smith and I. Zharov, Langmuir, 2009, 25, 3096 CrossRef CAS.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, New York, 2nd edn, 1997 Search PubMed.
- P. K. Jal, S. Patel and B. K. Mishra, Talanta, 2004, 62, 1005 CrossRef CAS.
- T. V. Le, E. E. Ross, T. R. C. Velarde, M. A. Legg and M. J. Wirth, Langmuir, 2007, 23, 8554 CrossRef CAS.
- J. M. Rosenholm, T. Czuryszkiewicz, F. Kleitz, J. B. Rosenholm and M. Linden, Langmuir, 2007, 23, 4315 CrossRef CAS.
Footnotes |
| † This article is part of the ‘Emerging Investigators’ themed issue for ChemComm. |
| ‡ Electronic supplementary information (ESI) available: Experimental details of materials preparation and diffusion experiments. See DOI: 10.1039/c0cc02101f |
| § This is different from the radius of tetrahedral and octahedral voids, 0.225 and 0.414 of the sphere radius, respectively, typically used to describe a close-packed face-centered cubic (fcc) lattice of hard spheres. |
| This journal is © The Royal Society of Chemistry 2011 |
