Dual-fluorophore ratiometric pH nanosensor with tuneable pK_a and extended dynamic range

Abstract

Ratiometric pH nanosensors with tuneable pK_a were prepared by entrapping combinations of two pH-sensitive fluorophores (fluorescein isothiocyanate dextran (FITC-D) and Oregon Green^®dextran (OG-D)) and a reference fluorophore (5-(and-6)-carboxytetramethylrhodamine dextran (TAMRA-D)), in a biocompatible polymer matrix. Dual-fluorophore pH nanosensors permit the measurement of an extended dynamic range, from pH 4.0 to 7.5.

---

Accurate determination of pH, and particularly its effects on submicron compartments of cells, is of great interest to the scientific community.^1–3 Advances in optical technology have driven the development of tools small enough to characterise diverse microenvironments.⁴ Initial efforts were directed towards reducing the dimensions of analyte sensitive optodes.⁵ However, it was soon established that the fluorophores at the tip of an optode are all that are required to make measurements.^6–8 Fluorescent pH polymeric nanosensors represent an advance that harnesses the benefits of both pulled optical fibres and free fluorophores, whilst overcoming some of their inherent weaknesses.^9–11

Fluorescent pH polymeric nanosensors are spherical probes, less than 1000 nm in diameter. They are composed of an inert matrix, such as polyacrylamide, which entraps, or is covalently bound to transducers in the form of fluorescent dyes.^6,12 The matrix shields the fluorophores from cellular interferents and protects cellular components from the dye. Free dyes have been found to interact with biological components, either triggering cellular toxicity, e.g. as a result of photoexcitation, and/or hindering sensing capabilities, due to protein binding.¹³

Polyacrylamide nanosensors typically consist of two fluorophores that emit at different wavelengths.¹¹ One fluorophore is an indicator which produces a signal proportional to the analyte concentration. In contrast, a second fluorophore provides a reference signal, insensitive to the analyte of interest. The combination of dyes permits accurate ratiometric measurements to be made.¹⁴ The fluorescence emission can be quantified with the use of analytical techniques such as fluorescence spectroscopy and widefield or confocal microscopy. Due to their small size, nanosensors can also provide high spatial resolution when compared to pulled optical fibres.¹⁵

pH-sensitive fluorescent nanosensors have previously been reported,^12,16–18 however, they are restricted when using commercially available fluorophores to a defined pK_a and a limited pH range of measurement.¹⁹ For pH-sensitive fluorophores the pK_a is generally the pH at which the fluorophore shows half its maximal response. More importantly, the pK_a is the pH at which the fluorophore exhibits its greatest sensitivity to changes in pH. Therefore, a nanosensor which contains a fluorophore that has a pK_a that can be tuned to a defined pH is highly desirable. For example, being able to derive maximal sensitivity from a sensor at selected pH would be of great value when monitoring cellular processes, such as apoptosis where small changes in pH are thought to be key.^20–22

Typically a pH-sensitive fluorophore responds in a sigmoidal manner to changes in pH, allowing the dynamic range and detection limit of the fluorophore to be determined. For a pH-sensitive fluorophore the dynamic range can be considered as the pH range between its minimal and maximal response. Whereas, the detection limit is the pH between the intersection of the lower and upper asymptote and the linear portion of the calibration curve.²³ The detection limit has predominantly been used to characterise the measurement range for ion-selective electrodes and in some cases optodes.^23,24

It has previously been reported that chemical sensors using a combination of absorbance based pH-sensitive dyes give optodes with an extended range of pH measurement^25–27 and indeed this is the principle behind Universal Indicator Solution.²⁸ Using an analogous approach we have applied this theory to fluorophore based pH measurements where we have immobilised two pH-sensitive fluorophores within a polyacrylamide nanoparticle to produce a pH-sensitive nanosensor with extended measurement range and tuneable pK_a.

Combinations of pH-sensitive fluorophores, fluorescein isothiocyanate dextran (FITC-D) and Oregon Green^®dextran (OG-D), and a reference fluorophore 5-(and-6)-carboxytetramethylrhodamine dextran (TAMRA-D) were immobilised in an acrylamide based nanosensor matrix. OG-D and TAMRA-D were synthesised through conjugation to amino dextran 10 000 M_w with succinimidyl ester forms of the fluorophores prior to entrapment.²⁹Dynamic light scattering of the nanoparticles showed a single distribution centred at a diameter of 40 nm, in agreement with previously published data (see the ESI† for experimental details).^8,15,30

The tuning of pK_a was demonstrated by varying the initial concentrations of FITC-D and OG-D during the preparation of nanosensors. Fig. 1 shows the change in pH calibration curves as the OG-D:FITC-D percentage is varied through successive increases in FITC-D concentration. This change is accompanied by an increase in the pK_a for the nanosensors, from 4.8 to 6.4, corresponding to a change from OG-D to FITC-D. These values are comparable to previously reported pK_a solution values for Oregon Green^® and fluorescein of 4.7 and 6.4, respectively.¹⁹

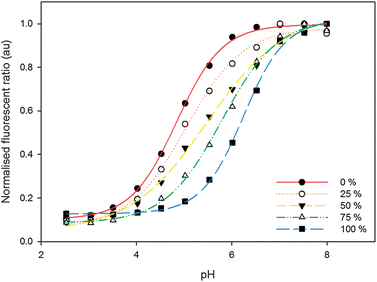Fig. 1 Normalised ratiometric calibration curves for nanosensors containing varying OG-D:FITC-D percentages and incorporating TAMRA-D as a reference. Percentage of FITC-D, with respect to OG-D, is increasing from the left. The calibration curves are fitted to a sigmoidal function each with R² values greater than 0.99 (see the ESI† for further details).

Taking the second derivative of the sigmoidal pH response curve allows improved visualisation of the dynamic range of pH measurement, Fig. 2a. The effective dynamic range, the region where the pH response is most sensitive to changes in pH, is the pH range between the maxima and minima points in the second derivative curve. Using this approach, nanosensors consisting of a single pH-sensitive fluorophore, only OG-D (0% FITC-D) or FITC-D (100% FITC-D), have an effective dynamic range of approximately 1.15 pH units, Fig. 2b. Whereas, for nanosensors containing both FITC-D and OG-D fluorophores combined in a 1 : 1 ratio the effective dynamic range is maximised, to 2.01 pH units. Therefore, through careful selection of the ratios of FITC-D to OG-D, the pK_a can be tuned to create a nanosensor with maximal sensitivity at a desired pH, Fig. 1, and an extended pH measurement range, Fig. 2a.

Fig. 2 (a) Normalised second derivatives of calibration curves for nanosensors containing varying OG-D:FITC-D and incorporating TAMRA-D as a reference. (b) Graph illustrating the change in pK_a and effective dynamic range with increasing proportions of FITC-D, with respect to OG-D. The effective dynamic range is fitted to a linear plot with a R² value of 0.98. Error bars represent standard error mean (n = 3).

Nanosensors containing both FITC-D and OG-D, in a 1 : 1 ratio, have overlapping emission curves, which peak at approximately 520 nm and increase in intensity when the pH is increased from 3.5 to 8.0, Fig. 3a. Using TAMRA-D as a reference dye, ratiometric measurements can be made over the range of pH 4.0 to 7.5, Fig. 3b.

Fig. 3 Emission (a) and calibration curves (b) for FITC-D, OG-D (1 : 1 ratio) and TAMRA-D nanosensors. Excitation/emission of FITC-D and OG-D at 488 nm/520 nm and TAMRA-D at 540 nm/577 nm. The calibration curve is fitted to a sigmoidal function with a R² value of 0.99 and pK_a of 5.5 (see the ESI† for further details). Error bars representative of the standard error mean fall within the data points. (c) Residual errors of sigmoidal fit.

In conclusion, fluorescent nanosensors with tuneable pK_a and size of approximately 40 nm have been demonstrated. When FITC-D and OG-D were combined in a 1 : 1 ratio and immobilised within the nanosensors the effective dynamic range was extended to 2.01 pH units as opposed to 1.15 pH units for sensors containing the individual fluorophores. We believe tuneable nanosensors will be of great value when applied to biological systems where nanosensors can be designed to have a specific pK_a, so that sensitivity in a narrow pH range can be maximised. Additionally, the development of sensors with an extended dynamic range will enable simultaneous measurement of both cytoplasmic and endosomal pH, potentially eliminating the need to perform multiple experiments with more than one type of nanosensor containing different pH-sensitive fluorophores.

The authors gratefully acknowledge Professor Phil Williams for helpful discussions. This research is supported by the Biotechnology and Biosciences Research Council (BBSRC) and an industrial CASE award from GlaxoSmithKline (GSK) Consumer Health (grant number BBG0176381).

Notes and references

1. A. Roos and W. F. Boron, Physiol. Rev., 1981, 61, 296–434.
2. J. Lin, TrAC, Trends Anal. Chem., 2000, 19, 541–552.
3. O. S. Wolfbeis, Anal. Chem., 2004, 76, 3269–3283.
4. C. McDonagh, C. S. Burke and B. D. MacCraith, Chem. Rev., 2008, 108, 400–422.
5. A. Song, S. Parus and R. Kopelman, Anal. Chem., 1997, 69, 863–867.
6. H. A. Clark, S. L. R. Barker, M. Brasuel, M. T. Miller, E. Monson, S. Parus, Z. Y. Shi, A. Song, B. Thorsrud, R. Kopelman, A. Ade, W. Meixner, B. Athey, M. Hoyer, D. Hill, R. Lightle and M. A. Philbert, Sens. Actuators, B, 1998, 51, 12–16.
7. H. A. Clark, M. Hoyer, S. Parus, M. A. Philbert and M. Kopelman, Mikrochim. Acta, 1999, 131, 121–128.
8. H. A. Clark, R. Kopelman, R. Tjalkens and M. A. Philbert, Anal. Chem., 1999, 71, 4837–4843.
9. J. W. Aylott, Analyst, 2003, 128, 309–312.
10. H. Ow, D. R. Larson, M. Srivastava, B. A. Baird, W. W. Webb and U. Wiesner, Nano Lett., 2005, 5, 113–117.
11. Y. E. K. Lee, R. Smith and R. Kopelman, Annu. Rev. Anal. Chem., 2009, 2, 57–76.
12. H. Sun, A. M. Scharff-Poulsen, H. Gu and K. Almdal, Chem. Mater., 2006, 18, 3381–3384.
13. M. L. Graber, D. C. Dilillo, B. L. Friedman and E. Pastorizamunoz, Anal. Biochem., 1986, 156, 202–212.
14. D. Sarkar, A. Mallick, B. Haldar and N. Chattopadhyay, Chem. Phys. Lett., 2010, 484, 168–172.
15. S. M. Buck, H. Xu, M. Brasuel, M. A. Philbert and R. Kopelman, Talanta, 2004, 63, 41–59.
16. H. A. Clark, M. Hoyer, M. A. Philbert and R. Kopelman, Anal. Chem., 1999, 71, 4831–4836.
17. H. H. Sun, T. L. Andresen, R. V. Benjaminsen and K. Almdal, J. Biomed. Nanotechnol., 2009, 5, 676–682.
18. A. Burns, P. Sengupta, T. Zedayko, B. Baird and U. Wiesner, Small, 2006, 2, 723–726.
19. R. Haugland, The Handbook: A Guide to Fluorescent Probes and Labeling Technologies, Invitrogen Corporation, 2005.
20. D. Lagadic-Gossmann, L. Huc and V. Lecureur, Cell Death Differ., 2004, 11, 953–961.
21. S. Matsuyama, J. Llopis, Q. L. Deveraux, R. Y. Tsien and J. C. Reed, Nat. Cell Biol., 2000, 2, 318–325.
22. J. Srivastava, D. L. Barber and M. P. Jacobson, Physiology, 2007, 22, 30–39.
23. R. P. Buck and E. Lindner, Pure Appl. Chem., 1994, 66, 2527–2536.
24. E. Bakker, M. Willer and E. Pretsch, Anal. Chim. Acta, 1993, 282, 265–271.
25. J. Lin and D. Liu, Anal. Chim. Acta, 2000, 408, 49–55.
26. P. Hashemi and R. A. Zarjani, Sens. Actuators, B, 2008, 135, 112–115.
27. B. D. Gupta and S. Sharma, Opt. Commun., 1998, 154, 282–284.
28. L. S. Foster and I. J. Gruntfest, J. Chem. Educ., 1937, 14, 274–276.
29. K. Zen, J. Biwersi, N. Periasamy and A. S. Verkman, J. Cell Biol., 1992, 119, 99–110.
30. P. G. Coupland, S. J. Briddon and J. W. Aylott, Integr. Biol., 2009, 1, 318–323.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c1an15042a

---