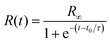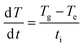Conductive shape memory nanocomposites for high speed electrical actuation

Abstract

A new shape memory nanocomposite that exhibits rapid electrical actuation capabilities is fabricated by incorporating continuous, non-woven carbon nanofibers (CNFs) into an epoxy based SMP matrix. The fiber morphology and nanometre size provide a percolating conductive network with a large interfacial area. This not only gives high electrical conductivity but also simultaneously enhances heat transfer and recovery stress.

---

Shape memory polymers (SMPs) are stimuli-responsive materials that have the ability to change between shapes on demand.^1–5 Although having a number of intrinsic advantages over shape memory alloys (SMAs) such as large deformation strain (actuation amplitude), low density and low manufacturing cost, some major limitations of SMPs still exist and impose great challenges to their broad utilization.^4,6 Some of the key limitations include: (1) small recovery stresses due to low rubbery moduli (0.1 to 10 MPa), (2) low recovery speed, primarily due to poor thermal conductivities, and (3) inertness to electromagnetic stimuli (in contrast with SMAs), due to the electrical insulation of most polymeric materials. Research efforts have begun to address these challenges. For example, with regard to challenge (3) listed above, electro-active materials systems have been developed⁷ by combining SMPs with conductive fillers including carbon black,^8–11 carbon nanotubes (CNTs),^12–14 short carbon fibers,^8,10,15 nickel,^9,16 and polypyrrole.^13,17 A brief summary of previously reported conductive SMP composites, their electrical properties and recovery performance is given in ESI†. Instead of using external heating, a DC voltage is applied to the material, which generates heat according to Joule's law and eventually triggers shape recovery. However, in all the examples reported to date the conductivity is still relatively low, due to the limited efficiency of discrete fillers to form percolating conductive networks. This results in a modest Joule heating effect and associated low recovery rate, rendering the materials insufficient for high-speed actuation applications. In addition, the conductive filler approach brings with it processing challenges, most importantly achievement of uniform distribution of fillers (prevent aggregation) and divergent viscosity at percolation. Here, we report the fabrication of a new shape memory nanocomposite that addresses each of these problems and exhibits surprisingly rapid electrical actuation capabilities. In contrast to previous conducting SMP systems in which discrete fillers were blended into a SMP matrix, we utilized continuous non-woven carbon nanofibers (CNFs) as a pre-defined network to impart electrical conductivity. The fiber morphology and nanometre size provide a percolating conductive network with a large degree of interconnectedness. This not only gives high electrical conductivity but also significantly enhances heat transfer, together resulting in high actuation speed.

The CNFs were prepared by a well-established method using poly(acrylonitrile) (PAN) as the precursor.^18,19 PAN was first electrospun into non-woven fibers with an average diameter of 511.3 ± 105.6 nm (Fig. 1A). The resulting PAN fiber mat was converted to CNFs via a two-step process. The first step, commonly known as the stabilization or pre-oxidization step, involved heating the PAN mat to an intermediate temperature of 280 °C in the presence of air. Although a fair amount of debate still exists,²⁰ it is generally accepted that PAN undergoes a cyclization reaction and forms a highly conjugated structure, this rendering the resulting material both insoluble and infusible. Macroscopically, the fiber mat changed its color from white to dark brown (Fig. 1A and B), and showed a dimensional shrinkage and a weight loss of 20% and 18%, respectively. In the second step, or the carbonization step, the stabilized PAN mat was heated to a high temperature of 1000 °C under a nitrogen environment. In this step, the stabilized PAN undergoes dehydrogenation and denitrogenation,²¹ and eventually becomes graphitic. The carbonized mat turned completely black (Fig. 1C), and showed a dimensional shrinkage and a weight loss (relative to the stabilized PAN mat) of 11% and 57%, respectively. By comparison with the same values for the first step, we postulated that this step proceeded primarily by fiber diameter reduction and no axial contraction normally associated with macroscopic dimensional change. This postulation was confirmed by microscopy, as we now reveal.

Fig. 1 Morphological studies of epoxy/CNF shape memory nanocomposites. (A)–(C) are scanning electron microscopy (SEM) images of (A) as-spun PAN, (B) stabilized PAN, and (C) carbonized PAN (CNF) fibers. The fiber diameters were measured by image analysis and the resulting histograms are plotted in (D). (E) SEM image of a fully cured epoxy/CNF nanocomposite.

The morphologies of PAN fibers at different states were characterized using scanning electron microscopy. As shown in Fig. 1A–C, the fiber structure was well preserved after each step. Fig. 1D shows the histograms of fiber diameters (obtained by image analysis) for the as-spun, stabilized, and carbonized PAN samples. It is noted that the average fiber diameter decreased slightly from 511.3 ± 105.6 nm to 411.4 ± 50.4 nm after stabilization, and further reduced to 135.4 ± 24.5 nm after carbonization. The polydispersity in fiber diameter showed a similar trend.

The CNF mat was then incorporated into a SMP matrix. For the latter, we have chosen an epoxy based SMP system previously reported by Xie and Rousseau.²² This system is chemically composed of diglycidyl ether of bisphenol-A (DGEBA), neopentyl glycol diglycidyl ether (NGDE), and poly(propylene glycol)bis(2-aminopropyl) ether (Jeffamine D230) of different compositions. This system features several advantages, including: (1) narrow glass transition easily tailored by copolymerizing DGEBA and NGDE at different ratios, (2) excellent cycle lifetime, and (3) good thermal and chemical stability. For the fabrication of shape memory nanocomposites, two epoxy formulations were used. The first formulation contains simply DGEBA and Jeffamine D230, and is referred to as D100. In the second formulation, half of the DGEBA was replaced by NGDE (therefore, the molar ratio of DGEBA/NGDE is 50/50), and is designated as D50N50. A stoichiometric amount of Jeffamine D230 was used in both cases, yielding molar equivalence between epoxide groups and both primary and secondary amine hydrogens.

The shape memory nanocomposites were fabricated using a relatively simple method. Similar processes have been reported by us as well as other researchers for shape memory elastomeric composites (SMECs),²³ nanofiber ion-exchange membranes²⁴ and transparent Nylon-4,6/epoxy composites.²⁵ In the current case, a piece of CNF mat was first kept immersed in the uncured resin mixture for 10 min. The liquid resin could easily wet the CNF mat due to its low starting viscosity and ostensibly favorable interfacial energetics. After removing the resin on the surfaces, the resin-impregnated CNF mat was cured at 100 °C for 1 h under a constant small compression and post-cured at 130 °C for 1.5 h (see ESI†). The SEM image of a fully cured epoxy/CNF nanocomposite (Fig. 1E) reveals an anticipated non-woven fiber/matrix morphology in which all the CNFs are evenly distributed in a void-free epoxy matrix. Unlike previously reported systems with nano-sized fillers, no procedures (strong shear, surface modification, or solvent processing) were needed to achieve uniform distribution and prevent filler aggregation, since the fiber morphology was pre-defined and not altered by the fabrication process. The average CNF weight fraction was measured gravimetrically to be 9.18% with a small standard deviation of 0.33%, indicating good reproducibility of our fabrication protocol. This translates to an average CNF volume fraction of ca. 4.72%, calculated using the densities of epoxy (1.06 g cm⁻³) and graphite (2.16 g cm⁻³).

The thermomechanical properties of the epoxy/CNF nanocomposites were characterized using dynamic mechanical analysis (DMA), with particular consideration of glass transition behavior and elastic moduli. Fig. 2 shows the storage modulus (E′) as a function of temperature for two nanocomposites (D100/CNF and D50N50/CNF) compared with neat epoxies of the same formulations (D100 and D50N50). For all the samples, a sharp transition in E′ corresponding to the glass transition of the epoxy was observed. The incorporation of CNFs showed little effect on the glass transition temperatures (T_g's), which was also shown by differential scanning calorimetry (DSC; Fig. S1 in ESI†). However, for both formulations, adding CNFs significantly raises the rubbery modulus (E′ plateau above T_g) from ca. 10 MPa to more than 200 MPa—a remarkable 20-fold increase that can potentially lead to much higher stresses in shape memory recovery. Indeed, the strengths of the nanocomposites were over 150% higher than those of the pure epoxy samples, although achieved with a compromise in ultimate strains (Fig. S2 in ESI†). This makes our epoxy/CNF nanocomposites suitable for applications where large recovery stresses are desired.

Fig. 2 Dynamic mechanical analysis (DMA) results of epoxy/CNF shape memory nanocomposites in comparison with pure epoxy samples of the same formulations.

Both the D100/CNF and D50N50/CNF nanocomposites prepared showed excellent thermally triggered shape memory properties with fast recovery kinetics. One experimental example is given in Fig. S3 (ESI†) for D50N50/CNF using isothermal water bath (60 °C) as the heating source. The fast recovery speed is attributed to (1) the narrow glass transition of epoxy and (2) increased thermal conductivity due to the incorporation of CNFs.²⁶ The latter can be seen from the fact that, for the same sample dimensions, D50N50/CNF nanocomposite recovered approximately 40% faster than D50N50 (Fig. S3†).

D50N50/CNF was further utilized to demonstrate the electrically triggered shape memory/actuation behavior. The electrical conductivity of D50N50/CNF was measured using a four-probe method to be 30.59 ± 0.81 S m⁻¹ (corresponding to a volumetric resistivity of 0.0327 ± 0.0008 Ω m). This is higher than most previously reported conductive SMPs with comparable filler contents (see Table S1 in ESI†). The structural origin of this high conductivity, as we proposed in the beginning, is the large degree of interconnectedness of the CNFs combined with negligible concentration of conductor termini (no free ends of CNFs were observed; Fig. 1C). This high electrical conductivity allows fast activation of shape recovery by applying a constant DC voltage. Experimentally, the recovery process was characterized using a modified bending test method, with the recovery ratio calculated based on the change of deformation angle as a function of time/temperature.^1,27–29 A “Π” shaped geometry, shown schematically in the inset of Fig. 3B was used to minimize the mechanical constraint imposed by the electrodes.⁹ In other words the shape recovery was carried out under a relatively unconstrained condition. Fig. 1A shows the recovery of D50N50/CNF from a fixed bent shape to its straight permanent shape under a constant DC voltage of 20 V (images taken at a frame rate of 30 Hz using a digital camera; a continuous movie is available in ESI†). Each image was then analyzed using ImageJ to obtain the deformation angle, θ(t) as shown in the first image (0 s) of Fig. 1A. The recovery ratio, R, is defined as:

Here θ_i, θ(t) and θ_e are the initial deformation angle of the fixed sample, the deformation angle at a given time t, and the deformation angle at the equilibrium/permanent state (in our case θ_e = 0), respectively. The recovery experiments were conducted under three different DC voltages (10, 15 and 20 V) and the resulting recovery profiles (Rvs. time plots) are shown in Fig. 3B. It can be observed that increasing the DC voltage leads to dramatically faster recovery. With a DC voltage of 20 V, the recovery accomplished in less than 2 s. To the authors' knowledge this is significantly faster than all previously reported conductive SMPs, which typically recover in 20 to 120 s with applied voltages ranging from 20 to 40 V (ESI†).‡

Fig. 3 Electrically activated shape recovery of epoxy/CNF nanocomposites. The sample used was D50N50/CNF with a “Π” shaped geometry, schematically shown as the inset in (B). (A) presents time-resolved photographs showing the fast recovery of a D50N50/CNF nanocomposite under a constant DC voltage of 20 V. (B) shows the recovery profiles (see main text for details on analysis) of D50N50/CNF under 3 different voltages of 20 V, 15 V and 10 V. The voltage was applied at time “0” for all the samples. The solid lines are fit curves using a three-parameter sigmoidal function. (C) plots the induction and recovery times (see main text for definition and analysis) for the three voltages studied.

The recovery data were further analyzed to reveal more detailed kinetics information. The datasets shown in Fig. 3B were fit using a standard sigmoidal function:

where R_∞, t₀ and τ are the three fitting parameters. The fit curves have R² values from 0.991 to 0.999 and are shown as the solid lines in Fig. 3B. The 2^nd derivatives of the fit curves were then calculated and plotted (Fig. S4 in ESI†). All the 2^nd derivative plots show a similar pattern consisting of two opposite peaks with the same height. Two characteristic times were defined using the 2^nd derivative plots. The induction time (time before rapid shape recovery takes place) is the time between “0” (when the voltage was applied) and the first (positive) peak on the 2^nd derivative plot. This corresponds to an induction period of the recovery profile (Fig. 3B), during which the sample was heated from environmental temperature to its T_g. The recovery time (time taken for the shape recovery) is defined as the time interval between the two peaks. This is the time period from the onset (when the material is heated just to its T_g) to the completion of the recovery, and corresponds to the section on the recovery profile where R rapidly increased with time (Fig. 3B).

The obtained induction and recovery times are plotted for the three DC voltages and shown in Fig. 3C. We observe that for a given DC voltage, the induction time is always longer than the recovery time therefore limits the overall recovery rate. Both the induction and recovery times decay exponentially with applied voltage. Furthermore, the induction times can be used to estimate the initial heating rate, with the assumptions that: (1) the resistivity has little temperature dependence and (2) shape recovery initiates precisely at the T_g, here defined as the onset temperature of E′ drop. The initial heating rate, dT/dt, can be calculated as:

where T_e and t_i are the environmental temperature (in this case room temperature) and induction time, respectively. With a T_g of 50.0 °C (determined from Fig. 2) and T_e of 22 °C, the initial heating rates were calculated to be 25.7, 11.09 and 4.73 °C s⁻¹ for 20, 15 and 10 V, respectively. As we can see these heating rates are quite high and cannot be easily achieved by external heating, even for SMPs with enhanced thermal conductivity.³⁰

Conclusions

To conclude, a unique shape memory nanocomposite with unprecedented high-speed electrical actuation capability has been developed by incorporating continuous, non-woven CNFs into an epoxy based SMP matrix. Besides the simple processing and excellent electrical conductivity, this non-woven CNF based filler system simultaneously enhances the recovery stress (by raising the rubbery modulus above T_g) and the thermal conductivity of the SMP. Smart devices utilizing this exciting material are currently being designed in our lab. We envision great potential of this material in applications encompassing actuators, sensors and deployable devices.

Acknowledgements

The authors acknowledge Nan Qin and Prof. Israel Cabasso (SUNY-ESF) for their help on using the tube furnace and Prof. Jeremy Gilbert (Syracuse University) for access to the SEM.

Notes and references

1. A. Lendlein and S. Kelch, Angew. Chem., Int. Ed., 2002, 41, 2034.
2. C. Liu, H. Qin and P. T. Mather, J. Mater. Chem., 2007, 17, 1543.
3. P. T. Mather, X. F. Luo and I. A. Rousseau, Annu. Rev. Mater. Res., 2009, 39, 445.
4. Q. H. Meng and J. L. Hu, Composites, Part A, 2009, 40, 1661.
5. D. Ratna and J. Karger-Kocsis, J. Mater. Sci., 2008, 43, 254.
6. I. A. Rousseau, Polym. Eng. Sci., 2008, 48, 2075.
7. Y. J. Liu, H. B. Lv, X. Lan, J. S. Leng and S. Y. Du, Compos. Sci. Technol., 2009, 69, 2064.
8. J. S. Leng, H. B. Lv, Y. J. Liu and S. Y. Du, Appl. Phys. Lett., 2007, 91, 144105.
9. J. S. Leng, W. M. Huang, X. Lan, Y. J. Liu and S. Y. Du, Appl. Phys. Lett., 2008, 92, 204101.
10. J. S. Leng, H. B. Lv, Y. J. Liu and S. Y. Du, J. Appl. Phys., 2008, 104, 104917.
11. F. K. Li, L. Y. Qi, J. P. Yang, M. Xu, X. L. Luo and D. Z. Ma, J. Appl. Polym. Sci., 2000, 75, 68.
12. J. W. Cho, J. W. Kim, Y. C. Jung and N. S. Goo, Macromol. Rapid Commun., 2005, 26, 412.
13. N. G. Sahoo, Y. C. Jung, H. J. Yoo and J. W. Cho, Compos. Sci. Technol., 2007, 67, 1920.
14. H. Koerner, G. Price, N. A. Pearce, M. Alexander and R. A. Vaia, Nat. Mater., 2004, 3, 115.
15. I. S. Gunes, G. A. Jimenez and S. C. Jana, Carbon, 2009, 47, 981.
16. J. S. Leng, X. Lan, Y. J. Liu, S. Y. Du, W. M. Huang, N. Liu, S. J. Phee and Q. Yuan, Appl. Phys. Lett., 2008, 92, 014104.
17. N. G. Sahoo, Y. C. Jung, N. S. Goo and J. W. Cho, Macromol. Mater. Eng., 2005, 290, 1049.
18. J. Sutasinpromprae, S. Jitjaicham, M. Nithitanakul, C. Meechaisue and P. Supaphol, Polym. Int., 2006, 55, 825.
19. Z. P. Zhou, C. L. Lai, L. F. Zhang, Y. Qian, H. Q. Hou, D. H. Reneker and H. Fong, Polymer, 2009, 50, 2999.
20. Z. Bashir, Carbon, 1991, 29, 1081.
21. W. X. Zhang, J. Liu and G. Wu, Carbon, 2003, 41, 2805.
22. T. Xie and I. A. Rousseau, Polymer, 2009, 50, 1852.
23. X. F. Luo and P. T. Mather, Macromolecules, 2009, 42, 7251.
24. J. Choi, K. M. Lee, R. Wycisk, P. N. Pintauro and P. T. Mather, Macromolecules, 2008, 41, 4569.
25. M. M. Bergshoef and G. J. Vancso, Adv. Mater., 1999, 11, 1362.
26. S. Ganguli, A. K. Roy and D. P. Anderson, Carbon, 2008, 46, 806.
27. J. R. Lin and L. W. Chen, J. Appl. Polym. Sci., 1998, 69, 1563.
28. J. R. Lin and L. W. Chen, J. Appl. Polym. Sci., 1998, 69, 1575.
29. C. Liu and P. T. Mather, J. Appl. Med. Polym., 2002, 6, 47.
30. C. Liu and P. T. Mather, Mater. Res. Soc. Symp. Proc., 2005, 855E, W4.7.1.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental methods, Table 1, Fig. S1–S4, dimensional dependence of recovery rate and recovery movie. See DOI: 10.1039/c001295e

‡ The recovery rate is dependent on specimen geometric dimensions. A brief analysis on dimensional dependence and comparison to literature is provided in ESI.

---